Comparison of Internal Clustering Validation Indices for Prototype-Based Clustering
Abstract
:1. Introduction
2. Methods
2.1. General Prototype-Based Clustering and Its Convergence
| Algorithm 1: Prototype-based partitional clustering algorithm. |
| Input: Dataset and the number of clusters K. Output: Partition of dataset into K disjoint groups. Select K points as the initial prototypes; repeat 1. Assign individual observation to the closest prototype; 2. Recompute the prototype with the assigned observations; until the partition does not change; |
| Algorithm 2: General K-means++-type initialization. |
| Input: Dataset and the number of clusters K. Output: Initial prototypes . 1. Select uniformly randomly, ; for , , do 2. Select with probability , ; end |
2.2. Cluster Validation Indices
2.3. On Computational Complexity
2.4. About Earlier Validation Index Comparisons
3. Experimental Setup
4. Results
4.1. CVIs for Synthetic Datasets
4.2. CVIs for Real Datasets
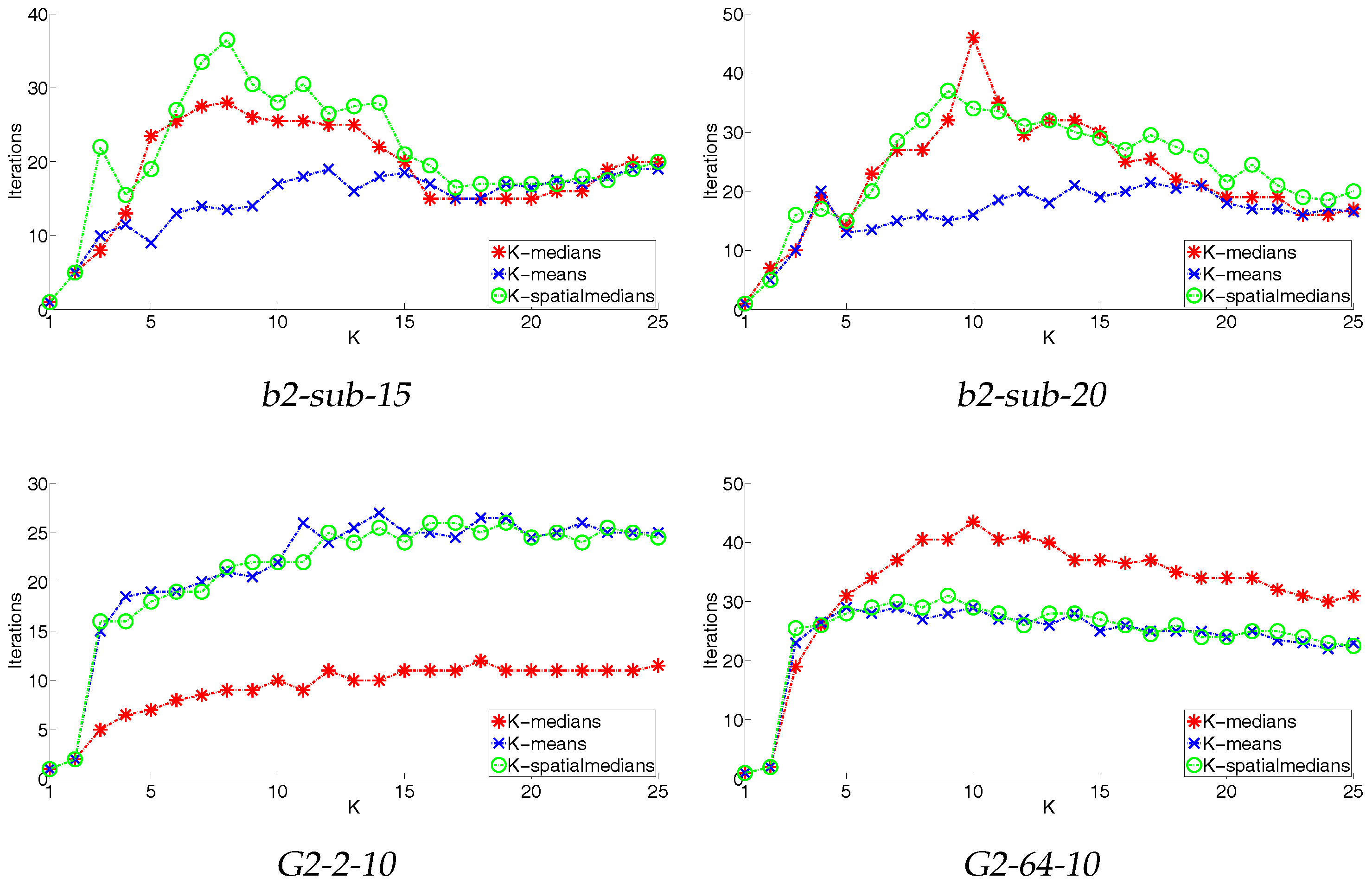
4.3. Convergence
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
| cb, se, ec | KCE | WB | CH | DB | PBM | RT | WG |
|---|---|---|---|---|---|---|---|
| Unbalance | 5, 20, 5 | 5, 20, 5 | 5, 20, 5 | 8, 8, 8 | 5, 25, 5 | 8, 2, 8 | 8, 8, 8 |
| a1 | 2, 20, 2 | 2, 20, 2 | 2, 20, 2 | 20, 19, 16 | 6, 24, 6 | 2, 18, 17 | 20, 20, 20 |
| Sim5D10 | 3, 5, 3 | 3, 5, 3 | 3, 3, 3 | 3, 3, 3 | 5, 10, 5 | 3, 3, 3 | 3, 3, 3 |
| Sim5D2 | 3, 5, 3 | 3, 5, 3 | 3, 3, 3 | 3, 3, 3 | 5, 16, 5 | 3, 3, 3 | 3, 3, 3 |
| S1 | 2, 15, 2 | 15, 15, 15 | 2, 15, 2 | 15, 15, 15 | 15, 15, 15 | 15, 15, 15 | 15, 15, 15 |
| S2 | 2, 15, 2 | 2, 15, 3 | 2, 15, 2 | 15, 15, 15 | 15, 15, 15 | 15, 15, 15 | 15, 15, 15 |
| S3 | 2,15, 2 | 2, 15, 2 | 2, 15, 2 | 7, 13, 15 | 4, 15, 4 | 4, 4, 15 | 15, 15, 15 |
| S4 | 2, 15, 2 | 2, 15, 3 | 2, 15, 2 | 17, 17, 15 | 5, 23, 5 | 17, 13, 15 | 16, 15, 16 |
| DIM032 | 16, 16, 16 | 16, 16, 16 | 16, 16, 16 | 16, 16, 16 | 16, 16, 16 | 16, 16, 16 | 16, 16, 16 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| DIM1024 | 16, 16, 16 | 16, 16, 16 | 16, 16, 16 | 16, 16, 16 | 16, 16, 16 | 16, 16, 16 | 16, 16, 16 |
| b2-sub-2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 20, 2 | 2, 2, 2 | 2, 2, 2 |
| b2-sub-3 | 3, 3, 3 | 3, 3, 3 | 3, 3, 3 | 3, 3, 3 | 3, 3, 3 | 3, 3, 3 | 3, 3, 3 |
| b2-sub-4 | 4, 4, 4 | 4, 4, 4 | 4, 4, 4 | 4, 4, 4 | 4, 4, 4 | 4, 4, 4 | 4, 4, 4 |
| b2-sub-5 | 5, 5, 5 | 5, 5, 5 | 5, 5, 2 | 5, 5, 5 | 5, 5, 5 | 5, 5, 5 | 5, 5, 5 |
| b2-sub-6 | 6, 6, 6 | 6, 6, 6 | 2, 6 ,2 | 5, 6, 5 | 6, 6, 6 | 5, 6, 6 | 6, 6, 6 |
| b2-sub-7 | 7, 7, 7 | 7, 7, 7 | 2, 7, 2 | 5, 6, 6 | 7, 14, 7 | 2, 2, 2 | 7, 7, 7 |
| b2-sub-8 | 8, 8, 8 | 8, 8, 8 | 2, 8, 2 | 6, 6, 7 | 8 ,17, 8 | 2, 2, 2 | 8, 8, 8 |
| b2-sub-9 | 9, 19, 9 | 9, 19, 9 | 2, 9, 2 | 6, 7, 8 | 9, 21, 9 | 2, 7, 7 | 9, 9, 9 |
| b2-sub-10 | 10, 21, 10 | 10, 21, 10 | 2, 21, 2 | 8, 8, 9 | 10, 25, 10 | 8, 8, 8 | 10, 10, 10 |
| b2-sub-11 | 11, 23, 11 | 11, 23, 11 | 2, 23, 3 | 9, 9, 10 | 11, 24, 11 | 9, 9, 8 | 11, 11, 11 |
| b2-sub-12 | 12, 25, 12 | 12, 25, 12 | 2, 25, 3 | 10, 10, 11 | 12, 25, 12 | 10, 10, 9 | 12, 12, 12 |
| b2-sub-13 | 13, 13, 13 | 13, 24, 13 | 2, 13, 2 | 11, 11, 12 | 13, 24, 13 | 11, 11, 11 | 13, 13, 13 |
| b2-sub-14 | 14, 14, 14 | 14, 14, 14 | 2, 14, 2 | 12, 12, 13 | 14, 14, 14 | 12, 12, 12 | 14, 14, 14 |
| b2-sub-15 | 15, 15, 15 | 15, 15, 15 | 2, 15, 2 | 13, 13, 14 | 15, 15, 15 | 13, 13, 13 | 15, 15, 15 |
| b2-sub-16 | 16, 16, 16 | 16, 16, 16 | 2, 16, 2 | 14, 14, 15 | 16, 16, 16 | 14, 14, 14 | 16, 16, 16 |
| b2-sub-17 | 17, 17, 17 | 17, 17, 17 | 2, 17, 2 | 15, 15, 16 | 17, 17, 17 | 15, 2, 2 | 17, 17, 17 |
| b2-sub-18 | 18, 18, 18 | 18, 18, 18 | 2, 18, 2 | 15, 15, 16 | 18, 18, 18 | 2, 2, 2 | 18, 18, 18 |
| b2-sub-19 | 19, 19, 19 | 19, 19, 19 | 2, 19, 2 | 16, 16, 17 | 19, 19, 19 | 2, 2, 2 | 19, 19, 19 |
| b2-sub-20 | 20, 20, 20 | 20, 20, 20 | 2, 20, 2 | 2, 2, 2 | 20, 21, 20 | 2, 2, 2 | 20, 20, 2 |
| G2-1-10 | 2, 25, 2 | 2, 25, 2 | 2, 25, 2 | 2, 2, 2 | 25, 25, 25 | 2, 2, 2 | 2, 2, 2 |
| G2-1-100 | 2, 25, 2 | 2, 25, 2 | 2, 25, 2 | 22, 25, 22 | 21, 25, 21 | 3, 3, 3 | 2, 2, 2 |
| G2-2-10 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 20, 2 | 2, 2, 2 | 2, 2, 2 |
| G2-2-100 | 2, 2, 2 | 2, 22, 2 | 2, 2, 2 | 21, 19, 25 | 8, 23, 2 | 10, 7, 7 | 2, 2, 2 |
| G2-4-10 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 |
| G2-4-100 | 2, 2, 2 | 2, 3, 2 | 2, 2, 2 | 2, 17, 23 | 2, 6, 2 | 2, 16, 16 | 2, 2, 2 |
| G2-8-10 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 |
| G2-8-100 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| G2-1024-10 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 |
| G2-1024-100 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 |

References
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Reddy, C.K. Data Clustering: Algorithms and Applications; CRC Press: New York, NY, USA, 2013. [Google Scholar]
- Xie, X.L.; Beni, G. A validity measure for fuzzy clustering. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 841–847. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Zaki, M.J.; Meira, W., Jr. Data Mining and Analysis: Fundamental Concepts and Algorithms; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Saarela, M.; Hämäläinen, J.; Kärkkäinen, T. Feature Ranking of Large, Robust, and Weighted Clustering Result. In Proceedings of the Pacific-Asia Conference on Knowledge Discovery and Data Mining, Jeju, Korea, 23–26 May 2017; pp. 96–109. [Google Scholar]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Khan, S.S.; Ahmad, A. Cluster center initialization algorithm for K-modes clustering. Expert Syst. Appl. 2013, 40, 7444–7456. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. K-means++: The advantages of careful seeding. In Proceedings of the 18th Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Xu, R.; Wunsch, D. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef] [PubMed]
- Hruschka, E.R.; Campello, R.J.; Freitas, A.A.; de Carvalho, A.C.P.L.F. A survey of evolutionary algorithms for clustering. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2009, 39, 133–155. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Tung, A. Spatial Clustering Methods in Data Mining: A Survey. In Geographic Data Mining and Knowledge Discovery; Miller, H., Han, J., Eds.; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Huber, P.J. Robust Statistics; John Wiley & Sons Inc.: New York, NY, USA, 1981. [Google Scholar]
- Rousseeuw, P.J.; Leroy, A.M. Robust Regression and Outlier Detection; John Wiley & Sons Inc.: New York, NY, USA, 1987; p. 329. [Google Scholar]
- Hettmansperger, T.P.; McKean, J.W. Robust Nonparametric Statistical Methods; Edward Arnold: London, UK, 1998; p. 467. [Google Scholar]
- Saarela, M.; Kärkkäinen, T. Analysing Student Performance using Sparse Data of Core Bachelor Courses. J. Educ. Data Min. 2015, 7, 3–32. [Google Scholar]
- Kärkkäinen, T.; Heikkola, E. Robust Formulations for Training Multilayer Perceptrons. Neural Comput. 2004, 16, 837–862. [Google Scholar] [CrossRef]
- Croux, C.; Dehon, C.; Yadine, A. The k-step spatial sign covariance matrix. Adv. Data Anal. Classif. 2010, 4, 137–150. [Google Scholar] [CrossRef]
- Äyrämö, S. Knowledge Mining Using Robust Clustering. Ph.D. Thesis, Jyväskylä Studies in Computing 63. University of Jyväskylä, Jyväskylä, Finland, 2006. [Google Scholar]
- Shannon, C.E. A mathematical theory of communication. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2001, 5, 3–55. [Google Scholar] [CrossRef]
- Strehl, A.; Ghosh, J. Cluster ensembles—A knowledge reuse framework for combining multiple partitions. J. Mach. Learn. Res. 2002, 3, 583–617. [Google Scholar]
- Zhao, Q.; Fränti, P. WB-index: A sum-of-squares based index for cluster validity. Data Knowl. Eng. 2014, 92, 77–89. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A cluster separation measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, PAMI-1, 224–227. [Google Scholar] [CrossRef]
- Caliński, T.; Harabasz, J. A dendrite method for cluster analysis. Commun. Stat. Theory Methods 1974, 3, 1–27. [Google Scholar] [CrossRef]
- Ray, S.; Turi, R.H. Determination of number of clusters in k-means clustering and application in colour image segmentation. In Proceedings of the 4th International Conference on Advances in Pattern Recognition and Digital Techniques, Calcutta, India, 27–29 December 1999; pp. 137–143. [Google Scholar]
- Rendón, E.; Abundez, I.; Arizmendi, A.; Quiroz, E.M. Internal versus external cluster validation indexes. Int. J. Comput. Commun. 2011, 5, 27–34. [Google Scholar]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. On clustering validation techniques. J. Intell. Inf. Syst. 2001, 17, 107–145. [Google Scholar] [CrossRef]
- Kuncheva, L.I.; Vetrov, D.P. Evaluation of stability of k-means cluster ensembles with respect to random initialization. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1798–1808. [Google Scholar] [CrossRef] [PubMed]
- Handl, J.; Knowles, J. An evolutionary approach to multiobjective clustering. IEEE Trans. Evolut. Comput. 2007, 11, 56–76. [Google Scholar] [CrossRef]
- Jauhiainen, S.; Kärkkäinen, T. A Simple Cluster Validation Index with Maximal Coverage. In Proceedings of the European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESAINN 2017), Bruges, Belgium, 26–28 April 2017; pp. 293–298. [Google Scholar]
- Kim, M.; Ramakrishna, R. New indices for cluster validity assessment. Pattern Recognit. Lett. 2005, 26, 2353–2363. [Google Scholar] [CrossRef]
- Maulik, U.; Bandyopadhyay, S. Performance evaluation of some clustering algorithms and validity indices. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1650–1654. [Google Scholar] [CrossRef]
- Arbelaitz, O.; Gurrutxaga, I.; Muguerza, J.; Pérez, J.M.; Perona, I. An extensive comparative study of cluster validity indices. Pattern Recognit. 2013, 46, 243–256. [Google Scholar] [CrossRef]
- Liu, Y.; Li, Z.; Xiong, H.; Gao, X.; Wu, J. Understanding of internal clustering validation measures. In Proceedings of the 2010 IEEE 10th International Conference on.Data Mining (ICDM), Sydney, Australia, 13–17 December 2010; pp. 911–916. [Google Scholar]
- Agrawal, K.; Garg, S.; Patel, P. Performance measures for densed and arbitrary shaped clusters. Int. J. Comput. Sci. Commun. 2015, 6, 338–350. [Google Scholar]
- Halkidi, M.; Vazirgiannis, M. Clustering validity assessment: Finding the optimal partitioning of a data set. In Proceedings of the IEEE International Conference on Data Mining (ICDM 2001), San Jose, CA, USA, 29 November–2 December 2001; pp. 187–194. [Google Scholar]
- Lughofer, E. A dynamic split-and-merge approach for evolving cluster models. Evol. Syst. 2012, 3, 135–151. [Google Scholar] [CrossRef]
- Lughofer, E.; Sayed-Mouchaweh, M. Autonomous data stream clustering implementing split-and-merge concepts—Towards a plug-and-play approach. Inf. Sci. 2015, 304, 54–79. [Google Scholar] [CrossRef]
- Ordonez, C. Clustering binary data streams with K-means. In Proceedings of the 8th ACM SIGMOD Workshop on Research Issues in Data Mining and Knowledge Discovery, San Diego, CA, USA, 13 June 2003; pp. 12–19. [Google Scholar]
- Bagirov, A.M.; Yearwood, J. A new nonsmooth optimization algorithm for minimum sum-of-squares clustering problems. Eur. J. Oper. Res. 2006, 170, 578–596. [Google Scholar] [CrossRef]
- Karmitsa, N.; Bagirov, A.; Taheri, S. MSSC Clustering of Large Data using the Limited Memory Bundle Method; Discussion Paper; University of Turku: Turku, Finland, 2016. [Google Scholar]
- Kärkkäinen, T.; Majava, K. Nonmonotone and monotone active-set methods for image restoration, Part 1: Convergence analysis. J. Optim. Theory Appl. 2000, 106, 61–80. [Google Scholar] [CrossRef]
- Kärkkäinen, T.; Kunisch, K.; Tarvainen, P. Augmented Lagrangian Active Set Methods for Obstacle Problems. J. Optim. Theory Appl. 2003, 119, 499–533. [Google Scholar] [CrossRef]
- Kärkkäinen, T.; Kunisch, K.; Majava, K. Denoising of smooth images using L1-fitting. Computing 2005, 74, 353–376. [Google Scholar] [CrossRef]
- Pakhira, M.K.; Bandyopadhyay, S.; Maulik, U. Validity index for crisp and fuzzy clusters. Pattern Recognit. 2004, 37, 487–501. [Google Scholar] [CrossRef]
- Desgraupes, B. “ClusterCrit: Clustering Indices”. R Package Version 1.2.3. 2013. Available online: https://cran.r-project.org/web/packages/clusterCrit/ (accessed on 6 September 2017).
- Milligan, G.W.; Cooper, M.C. An examination of procedures for determining the number of clusters in a data set. Psychometrika 1985, 50, 159–179. [Google Scholar] [CrossRef]
- Fränti, P.; Sieranoja, S. K-means properties on six clustering benchmark datasets. Algorithms 2017. submitted. [Google Scholar]
- Saarela, M.; Kärkkäinen, T. Do country stereotypes exist in educational data? A clustering approach for large, sparse, and weighted data. In Proceedings of the 8th International Conference on Educational Data Mining (EDM 2015), Madrid, Spain, 26–29 June 2015; pp. 156–163. [Google Scholar]
- Verleysen, M.; François, D. The Curse of Dimensionality in Data Mining and Time Series Prediction. In Proceedings of the International Work-Conference on Artificial Neural Networks (IWANN), Cadiz, Spain, 14–16 June 2005; Volume 5, pp. 758–770. [Google Scholar]
- Wartiainen, P.; Kärkkäinen, T. Hierarchical, prototype-based clustering of multiple time series with missing values. In Proceedings of the 23rd European Symposium on Artificial Neural Networks, Computational Intelligence and Machine Learning (ESANN 2015), Bruges, Belgium, 22–24 April 2015; pp. 95–100. [Google Scholar]
| Name | Notation | Intra | Inter | Formula |
|---|---|---|---|---|
| KCE [30] | KCE | |||
| WB-index [22] | WB | |||
| Calinski–Harabasz [24] | CH | |||
| Davies–Bouldin [23] | DB | |||
| Pakhira, Bandyopadhyay, and Maulik [45] | PBM | |||
| Ray–Turi [25] | RT | |||
| Wemmert– Gançarski ([46]) | WG |
| Data | Size | Dimensions | Clusters | Description |
| S | 5000 | 2 | 15 | Varying overlap |
| G2 | 2048 | 1–1024 | 2 | Varying overlap and dimensionality |
| DIM | 1024 | 32–1024 | 16 | Varying dimensionality |
| A | 3000–7500 | 2 | 20–50 | Varying number of clusters |
| Unbalance | 6500 | 2 | 8 | Both dense and sparse clusters |
| Birch | 100,000 | 2 | 1–100 | Varying structure |
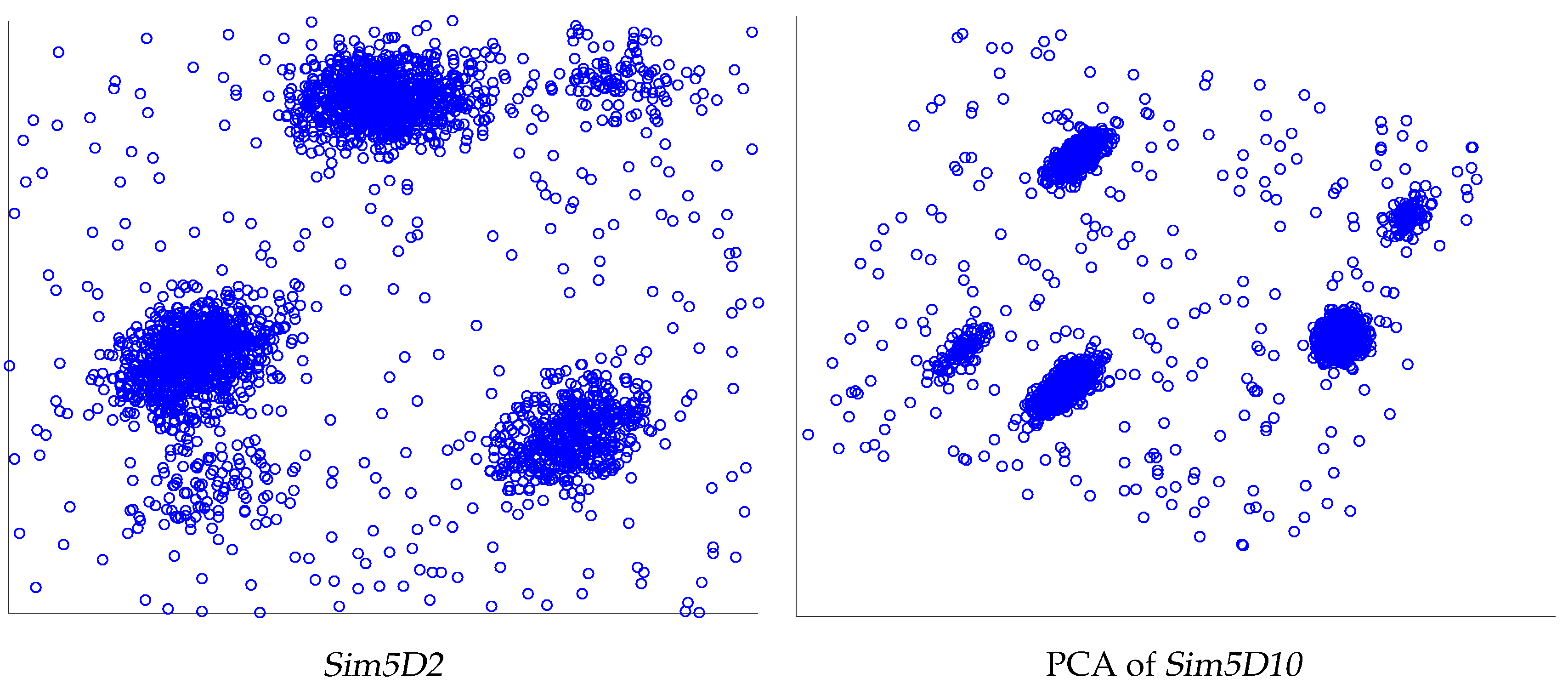
| Sim5 | 2970 | 2–10 | 5 | Small subclusters close to bigger ones |
| Data | Size | Dimensions | Classes | Description |
| Iris | 150 | 4 | 3 | Three species of iris |
| Arrhythmia | 452 | 279 | 13 | Different types of cardiac arrhythmia |
| Steel Plates | 1941 | 27 | 7 | Steel plates faults |
| Ionosphere | 351 | 34 | 2 | Radar returns from the ionosphere |
| USPS | 9298 | 256 | 10 | Numeric data from scanned handwritten digits |
| Satimage (Train) | 6435 | 36 | 6 | Satellite images |
| Index | City-Block | Squared Euclidean | Euclidean |
|---|---|---|---|
| KCE | 85.7% | 87.5% | 85.7% |
| WB | 87.5% | 80.4% | 87.5% |
| CH | 58.9% | 85.7% | 57.1% |
| DB | 60.7% | 60.7% | 62.5% |
| PBM | 87.5% | 64.3% | 89.3% |
| RT | 60.7% | 58.9% | 64.3% |
| WG | 94.6% | 96.4% | 92.9% |
| cb, se, ec | KCE | WB | CH | DB | PBM | RT | WG |
|---|---|---|---|---|---|---|---|
| Iris | 2, 3, 2 | 2, 3, 2 | 2, 3, 2 | 2, 2, 2 | 3, 22, 3 | 2, 2, 2 | 2, 2, 2 |
| Arrhythmia | 2, 2, 2 | 2, 5, 2 | 2, 2, 2 | 25, 24, 17 | 2, 14, 2 | 2, 25, 3 | 2, 25, 25 |
| Steel | 2, 2, 2 | 3, 5, 2 | 2, 2, 2 | 7, 3, 7 | 3, 7, 2 | 2, 2, 3 | 3, 2, 3 |
| Ionosphere | 2, 2, 2 | 2, 2, 2 | 2, 2, 2 | 11, 23, 2 | 3, 20, 3 | 4, 4, 4 | 4, 2, 2 |
| USPS | 2, 2, 2 | 2, 4, 2 | 2, 2, 2 | 2, 18, 11 | 2, 4, 4 | 2, 12, 7 | 2, 2, 7 |
| Satimage (Train) | 2, 3, 2 | 3, 6, 2 | 2, 3, 2 | 3, 3, 3 | 3, 6, 3 | 3, 3, 3 | 3, 3, 3 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hämäläinen, J.; Jauhiainen, S.; Kärkkäinen, T. Comparison of Internal Clustering Validation Indices for Prototype-Based Clustering. Algorithms 2017, 10, 105. https://doi.org/10.3390/a10030105
Hämäläinen J, Jauhiainen S, Kärkkäinen T. Comparison of Internal Clustering Validation Indices for Prototype-Based Clustering. Algorithms. 2017; 10(3):105. https://doi.org/10.3390/a10030105
Chicago/Turabian StyleHämäläinen, Joonas, Susanne Jauhiainen, and Tommi Kärkkäinen. 2017. "Comparison of Internal Clustering Validation Indices for Prototype-Based Clustering" Algorithms 10, no. 3: 105. https://doi.org/10.3390/a10030105
APA StyleHämäläinen, J., Jauhiainen, S., & Kärkkäinen, T. (2017). Comparison of Internal Clustering Validation Indices for Prototype-Based Clustering. Algorithms, 10(3), 105. https://doi.org/10.3390/a10030105





