Contract-Based Incentive Mechanism for Mobile Crowdsourcing Networks

Abstract

Mobile crowdsourcing networks (MCNs) are a promising method of data collecting and processing by leveraging the mobile devices’ sensing and computing capabilities. However, because of the selfish characteristics of the service provider (SP) and mobile users (MUs), crowdsourcing participants only aim to maximize their own benefits. This paper investigates the incentive mechanism between the above two parties to create mutual benefits. By modeling MCNs as a labor market, a contract-based crowdsourcing model with moral hazard is proposed under the asymmetric information scenario. In order to incentivize the potential MUs to participate in crowdsourcing tasks, the optimization problem is formulated to maximize the SP’s utility by jointly examining the crowdsourcing participants’ risk preferences. The impact of crowdsourcing participants’ attitudes of risks on the incentive mechanism has been studied analytically and experimentally. Numerical simulation results demonstrate the effectiveness of the proposed contract design scheme for the crowdsourcing incentive.

1. Introduction

According to the International Data Corporation, the worldwide smartphone market will reach 1.84 billion units in 2020. With the rapid development of IT technologies, mobile devices are always equipped with powerful processors, various sensors and large memories [1]. These devices can offer a novel paradigm to collect data about individuals, human society, and environments. Numerous mobile crowdsourcing applications have been created, such as OpenStreetMap [2] for constructing an openly licensed map of the world, CrowdDB [3] for querying and answering, Honeybee [4] for face detection, SignalGuru [5] for traffic signal detection, and Medusa [6] for environment sensing and data processing.

However, designing an efficient mobile crowdsourcing network (MCN) [7] is considerably challenging. First, while participating in tasks, mobile devices may consume their resources (i.e., battery, memory, and time) [1]. Mobile devices in MCNs are always controlled by rational users to maximize their own benefits. Moreover, the collected data usually contains location information with potential privacy and security threats. Mobile users (MUs) may not be willing to participate in crowdsourcing tasks without any extra incentives. Therefore, incentive mechanisms are necessary to achieve the win–win goal by considering the two parties’ requirements.

Recently, three primary incentive mechanisms have been suggested for MCNs, which are entertainment-based, service-based, and monetary-based mechanisms [8]. The entertainment-based incentive mechanism turns crowdsourcing tasks into playable games to attract crowdsourcing participants [9,10]. The service-based incentive mechanism attracts each crowdsourcing participant to make important contributions for crowdsourcing mutually [11,12,13]. The monetary-based incentive mechanism offers crowdsourcing participants rewards for their efforts [14,15,16]. Because the former two incentive mechanisms need to obtain the domain knowledge, the third incentive mechanism is more suitable for general crowdsourcing scenarios. Yang et al. [14] proposed two incentive mechanisms to attract MUs to participate in crowdsourcing tasks. Zhang et al. [15] designed three online incentive mechanisms for mobile crowdsourcing sensing. Zhao et al. [16] proposed the online incentive mechanism for crowdsourcing tasks with a budget constraint. However, most existing works have assumed that crowdsourcing participants will not deviate from the incentive mechanism.

Unfortunately, because of users’ mobility and mobile wireless environments’ dynamicity, certain crowdsourcing information (i.e., crowdsourcing efforts of MUs) may not be available to the service provider (SP), which causes network information asymmetry between the MUs and the SP. The SP may not monitor the MUs’ crowdsourcing action in real-time, and the MUs may deviate from the incentive mechanism. To tackle this problem, we propose a contract-based incentive mechanism. Contract theory [17] investigates how economic parties make decisions under uncertain conditions or make contracts with asymmetric information. Recently, it has been successfully applied to many practical problems, for example, cooperative spectrum trading [18], mobile crowdsourcing [19], and cooperative relay [20,21,22]. Duan and Lin et al. considered the cooperative incentive with resource-exchange spectrum trading [18]. Ho et al. investigated the adaptive contract design for crowdsourcing markets [19]. Zhang et al. proposed the incentive mechanism approach to solve the optimal compensation package with moral hazard [23]. Our prior works developed an efficient contract model for adverse selection in the presence of the wireless nodes’ hidden relay information [20] and moral hazard problems [21] caused by the wireless nodes’ hidden relay actions. However, none of these considered the risk attitudes of crowdsourcing participants (i.e., an SP, or mobile devices). Most existing works have assumed that the MUs are risk-neutral. Practically, some MUs may want to “gamble” too much by crowdsourcing sensing, and the crowdsourcing participants’ behavioral features will be influenced by their attitudes on risk.

Inspired by these existing works, this work investigates the crowdsourcing incentive mechanism in the presence of asymmetric information with risk attitudes. A contract-based incentive model is proposed to obtain the effort-incentive objective. The bonus ratio related to the MUs’ performance is introduced to motivate the MUs to work effectively. The optimal contract designs are investigated by jointly examining both the SP’s and MUs’ risk preferences. A moral hazard model is proposed to incentivize the MUs to participate in crowdsourcing tasks effectively with asymmetric information. The optimization incentive problem is formulated to maximize the SP’s expected utility subject to the feasible conditions of the MUs. The impact of the crowdsourcing participants’ risk preferences on the incentive mechanism has been studied analytically and experimentally. Simulations have demonstrated the proposed incentive mechanism’s performance.

The rest of the paper is organized as follows. Section 2 introduces the system model for the crowdsourcing incentive mechanism. The optimal contract design with risk attitudes is proposed and discussed in Section 3 and Section 4, respectively. Section 5 demonstrates the performance evaluation results, and Section 6 concludes this work.

2. System Model for Crowdsourcing Incentive Mechanism

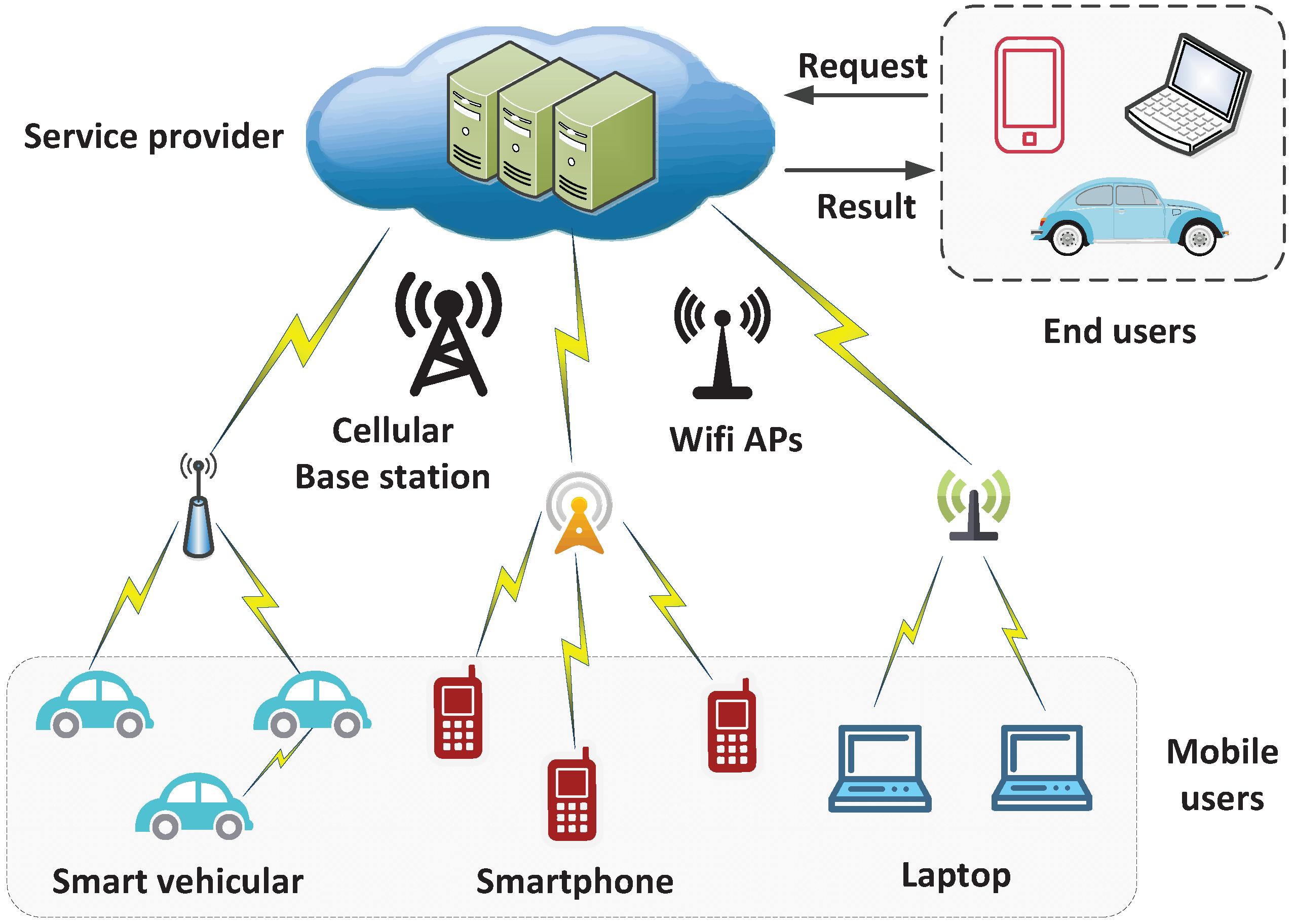
As shown in Figure 1, a MCN includes three basic entities: an SP, end users, and N MUs. End users first send their requests to the SP for help. Then, the SP divides the service requests into several small crowdsourcing tasks, which are published on the service platform. The MUs are recruited for crowdsourcing tasks by the SP. Once these crowdsourcing tasks are finished, the SP provides the end users with the final service.

However, because of the selfish characteristics of the SP and MUs, crowdsourcing participants only aim to maximize their own benefits. This paper investigates the incentive mechanism between the above two parties to create mutual benefits. Mobile crowdsourcing is modeled as a labor market. The SP, as the employer, offers the contract to recruit certain MUs for crowdsourcing. The contract is composed of a set of different items regarding the various combinations of the basic wage and performance bonus. Each MU, as an employee, chooses one item from the contract when participating in crowdsourcing tasks.

Moreover, in this context, to characterize the behaviour of crowdsourcing participants regarding their willingness to participate in crowdsourcing tasks, the participants’ behaviour can be categorized as risk-averse or risk-neutral [24]. A risk-averse MU does not want to obtain too great a profit by participating in crowdsourcing tasks. A risk-averse SP appreciates higher profit but demands a basic level of service, whereas a risk-neutral participant is an entity whose objective is only to maximize the SP’s profit.

2.1. Utility of Mobile Users

Suppose that the ith MU offers its crowdsourcing effort $e_i$ to obtain the reward from the SP. The SP can achieve profit ${\pi }_i$ with the help of the ith MU. As a result of some measurement errors, the SP’s achieved profit may be slightly different from the actual effort exerted by the MU. Therefore, we assume that the SP’s actual achieved profit ${\pi }_i$ is a noisy signal, which is given as

$${\pi }_i={\theta }_i{e}_i+\delta$$

(1)

where ${\theta }_i$ is the profit per unit crowdsourcing effort, and $\delta$ is a normally distributed random variable with $\delta \sim \mathcal{N}(0,{\sigma }^2)$.

The more the crowdsourcing resources the MUs consume, the greater the crowdsourcing cost the MUs pay. Moreover, we assume that $C_i\left(e_i\right)$ grows more rapidly in the large crowdsourcing effort than it does in the small crowdsourcing effort. Therefore, ${C_i}^{\prime }\left(e_i\right)>0$ and ${C_i}^{\prime \prime }\left(e_i\right)>0$. For simplicity, the crowdsourcing cost $C_i\left(e_i\right)$ of the ith MU is assumed to be quadratic:

$$C_i\left(e_i\right)=c_i{e}_i^2/2$$

(2)

where $c_i$ is the ith MU’s crowdsourcing cost coefficient, which can describe the ith MU’s crowdsourcing cost information (i.e., battery, memory, and computing power). We note that different crowdsourcing scenarios may have a different crowdsourcing cost.

We assume that the SP offers the payment $W_{M_i}$ to the ith MU in the linear form [25] defined as

$$W_{M_i}={\alpha }_i+{\beta }_i{\pi }_i-\frac{c_i}{2}{e}_i^2$$

(3)

where ${\alpha }_i$ is the ith MU’s basic wage, and ${\beta }_i\in [0,1]$ is the bonus coefficient related to the crowdsourcing performance. Considering the different crowdsourcing actions, MUs may obtain different bonuses.

The payment $W_{M_i}$ is approximately normally distributed with means

$$E\left[W_{M_i}\right]={\alpha }_i+{\beta }_i{\theta }_i{e}_i-\frac{c_i}{2}{e}_i^2$$

(4)

and variances

$$V_{ar}\left[W_{M_i}\right]={\beta }_i^2{\sigma }^2$$

(5)

In this section, we assume that each MU has a constant absolute risk-averse (CARA) preference; then, the ith MU’s negative exponential utility is defined as

$$u\left(W_{M_i}\right)=-e^{-{\eta }_M{W}_{M_i}}$$

(6)

where ${\eta }_M>0$ is the ith MU’s coefficient of absolute risk aversion (${\eta }_M=-u^{\prime \prime }\left(W_{M_i}\right)/u^{\prime }\left(W_{M_i}\right)$). A larger value of ${\eta }_M>0$ means that the MU has less incentive to participate in crowdsourcing tasks; ${\eta }_M=0$ means that the MU is risk-neutral. A risk-neutral MU’s decision is not affected by the degree of crowdsourcing uncertainty.

Then, the ith MU’s expected utility $u\left(W_{M_i}\right)$ can be written as

$$\begin{array}{cc}E\left[u\left(W_{M_i}\right)\right]\hfill & =E\left[-e^{-{\eta }_M{W}_{M_i}}\right]\hfill \\ \hfill & =\frac{-1}{\sqrt{2\pi V_{ar}\left[W_{M_i}\right]}}{\int }_{-\infty }^{\infty }{e}^{-\frac{W_{M_i}^2-2E\left[W_{M_i}\right]W_{M_i}+{\left(E\left[W_{M_i}\right]\right)}^2+2V_{ar}\left[W_{M_i}\right]{\eta }_M{W}_{M_i}}{2V_{ar}\left[W_{M_i}\right]}}d{W}_{M_i}\hfill \\ \hfill & =\frac{-1}{\sqrt{2\pi V_{ar}\left[W_{M_i}\right]}}·e^{\frac{1}{2}{V}_{ar}\left[W_{M_i}\right]{\eta }_M^2-E\left[W_{M_i}\right]{\eta }_M}·{\int }_{-\infty }^{\infty }{e}^{-\frac{{\left(W_{M_i}-E\left[W_{M_i}\right]+V_{ar}\left[W_{M_i}\right]{\eta }_M\right)}^2}{2V_{ar}\left[W_{M_i}\right]}}d{W}_{M_i}\hfill \\ \hfill & =-e^{-{\eta }_M\left[E\left[W_{M_i}\right]-\frac{1}{2}{V}_{ar}\left[W_{M_i}\right]{\eta }_M\right]},\hfill \\ \hfill & -e^{-{\eta }_M\left[{\alpha }_i+{\beta }_i{\theta }_i{e}_i-\frac{c_i}{2}{e}_i^2-\frac{{\eta }_M}{2}{\beta }_i^2{\sigma }^2\right]}\hfill \end{array}$$

(7)

2.2. Utility of Service Provider

Considering the MUs’ crowdsourcing effort $e_i$ and the SP’s reward allocation $W_{M_i}$, the SP’s total utility can be written as

$$W_S=\sum _{i=1}^N\left[\left(1-{\beta }_i\right){\pi }_i-{\alpha }_i\right]$$

(8)

with means

$$E\left[W_S\right]=\sum _{i=1}^N\left[\left(1-{\beta }_i\right){\theta }_i{e}_i-{\alpha }_i\right]$$

(9)

and variances

$$\begin{array}{cc}\hfill V_{ar}\left[W_S\right]& =\sum _{i=1}^N{\left(1-{\beta }_i\right)}^2{\sigma }^2\hfill \end{array}$$

(10)

Then, similarly to the MUs, the SP’s CARA risk preferences are also considered. Thus, the SP’s expected utility is represented as

$$E\left[u\left(W_S\right)\right]=E\left[-e^{-{\eta }_S{W}_S}\right]=-e^{-{\eta }_S\left[E\left[W_S\right]-\frac{1}{2}{V}_{ar}\left[W_S\right]{\eta }_S\right]}$$

(11)

where ${\eta }_S$ represents the SP’s absolute risk-averse degree. The larger ${\eta }_S$ is, the more the SP is afraid of risk. When ${\eta }_S=0$, the SP is risk-neutral.

2.3. Problem Formulation

Considering the MUs’ selfishness and the limited resources, the MUs may intend to shirk or act less carefully in crowdsourcing tasks. For example, because crowdsourcing tasks consume the MUs’ resources (i.e., battery, memory, and time), the MUs may like to obtain their benefits from the SP to maximize their own utilities with little crowdsourcing effort. Thus, the MUs may not take the full responsibilities for their tasks. Because of the asymmetry of network information, the MUs’ crowdsourcing actions are unobservable to the SP, which leads to the moral hazard problem. This moral hazard problem influences the crowdsourcing’s performance. Therefore, the SP needs to design a contract-based incentive mechanism to motivate the MUs to participate in crowdsourcing tasks efficiently and credibly.

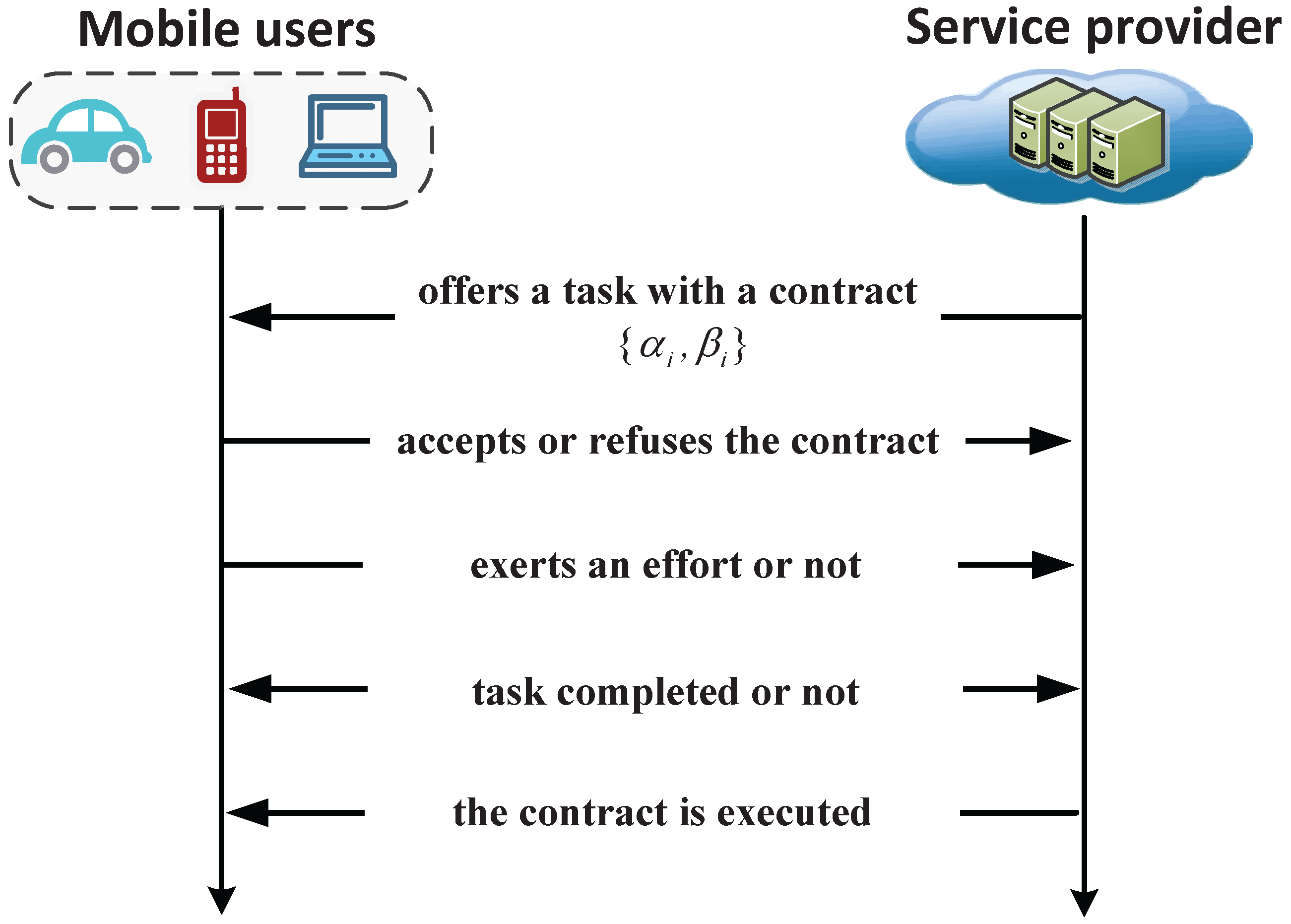
As shown in Figure 2, when the SP designs the optimal contract, the SP broadcasts a set of contract items to the potential MUs. Then, after receiving the contract, the MUs willing to accept certain contract items inform the SP of their choices. Next, after receiving the MUs’ confirmations, the SP informs the employed MUs’ crowdsourcing tasks, and the MUs help to participate in crowdsourcing sensing or computing. Finally, after receiving the data from the MUs, the SP checks for the required information. If the MUs succeed in the crowdsourcing tasks, the SP rewards the MUs according to their contracts. However, if the information fails to meet the requirement, the employed MUs obtain no reward. Because this requires limited interaction with potential MUs, this contract-based incentive mechanism is simple to implement, and can effectively reduce communication and computation overhead.

3. Contract-Based Crowdsourcing Incentive Mechanism

As a result of information asymmetry, the SP may not obtain the MUs’ exact crowdsourcing efforts after contracting between the SP and the MUs. Therefore, the designed contract should ensure that each MU selects the optimal effort $e_i^{*}$ to maximize its own utility. Then, the following incentive compatibility (IC) constraint should be satisfied:

$$\left(IC\right)\underset{e_i\ge 0}{max}E\left[u\left(W_{M_i}\right)\right]$$

(12)

We let $f_{M_i}={\alpha }_i+{\beta }_i{\theta }_i{e}_i-\frac{c_i}{2}{e}_i^2-\frac{{\eta }_M}{2}{\beta }_i^2{\sigma }^2$; then, the ith MU’s expected utility $u\left(W_{M_i}\right)$ in Equation (7) can be rewritten as

$$E\left[u\left(W_{M_i}\right)\right]=-e^{-{\eta }_M{f}_{M_i}}$$

(13)

Because $\frac{\partial E\left[u\left(W_{M_i}\right)\right]}{\partial f_{M_i}}={\eta }_M{e}^{-{\eta }_M{f}_{M_i}}>0$, the IC constraint in Equation (12) can be simplified as

$$\left(IC\right)\underset{e_i\ge 0}{max}{f}_{M_i}={\alpha }_i+{\beta }_i{\theta }_i{e}_i-\frac{c_i}{2}{e}_i^2-\frac{{\eta }_M}{2}{\beta }_i^2{\sigma }^2$$

(14)

Then, in order to ensure that the utility each MU has received is no lower than its retained utility $\overline{U}$, the following individually rational (IR) constraint should be satisfied:

$$\left(IR\right){\alpha }_i+{\beta }_i{\theta }_i{e}_i-\frac{c_i}{2}{e}_i^2-\frac{{\eta }_M}{2}{\beta }_i^2{\sigma }^2\ge \overline{U},1\le i\le N$$

(15)

Thus, on the basis of the above IC and IR constraints, the optimal contract is designed to achieve the maximum expected utility of the SP, which can be written as

$$\begin{array}{c}\underset{\{\{{\alpha }_i,{\beta }_i\}\ge 0\}}{max}E\left[u\left(W_S\right)\right],\hfill \\ s.t.\left(IC\right)\underset{e_i\ge 0}{max}{\alpha }_i+{\beta }_i{\theta }_i{e}_i-\frac{c_i}{2}{e}_i^2-\frac{{\eta }_M}{2}{\beta }_i^2{\sigma }^2,\hfill \\ \left(IR\right){\alpha }_i+{\beta }_i{\theta }_i{e}_i-\frac{c_i}{2}{e}_i^2-\frac{{\eta }_M}{2}{\beta }_i^2{\sigma }^2\ge \overline{U},1\le i\le N.\hfill \end{array}$$

(16)

Similarly to the case of MUs, we let

$$f_S=E\left[W_S\right]-\frac{V_{ar}\left[W_S\right]}{2}{\eta }_S=\sum _{i=1}^N\left[\left(1-{\beta }_i\right){\theta }_i{e}_i-{\alpha }_i-\frac{{\eta }_S}{2}{\sigma }^2{\left(1-{\beta }_i\right)}^2\right]$$

(17)

Then, we simplify the SP’s expected utility in Equation (11) to

$$E\left[u\left(W_S\right)\right]=-e^{-{\eta }_S{f}_S}$$

(18)

Because $\frac{\partial E\left[u\left(W_S\right)\right]}{\partial f_S}={\eta }_S{e}^{-{\eta }_S{f}_S}>0$, we simplify the SP’s optimization problem to

$$\begin{array}{c}\underset{\{\{{\alpha }_i,{\beta }_i\}\ge 0\}}{max}{f}_S={\displaystyle \sum _{i=1}^N}\left[\left(1-{\beta }_i\right){\theta }_i{e}_i-{\alpha }_i-\frac{{\eta }_S}{2}{\sigma }^2{\left(1-{\beta }_i\right)}^2\right],\hfill \\ s.t.\left(IC\right)\underset{e_i\ge 0}{max}{\alpha }_i+{\beta }_i{\theta }_i{e}_i-\frac{c_i}{2}{e}_i^2-\frac{{\eta }_M}{2}{\beta }_i^2{\sigma }^2,\hfill \\ \left(IR\right){\alpha }_i+{\beta }_i{\theta }_i{e}_i-\frac{c_i}{2}{e}_i^2-\frac{{\eta }_M}{2}{\beta }_i^2{\sigma }^2\ge \overline{U},1\le i\le N.\hfill \end{array}$$

(19)

From the first IC constraint, we have $e_i^{*}=\frac{{\beta }_i{\theta }_i}{c_i}$. Then, the optimal effort $e_i^{*}\left({\beta }_i\right)$ can be obtained from the above formula.

Because the SP’s expected utility in Equation (16) is decreasing in ${\alpha }_i$, the SP can obtain its maximum utility by decreasing ${\alpha }_i$ until ${\alpha }_i+{\beta }_i{\theta }_i{e}_i-\frac{c_i}{2}{e}_i^2-\frac{{\eta }_M}{2}{\beta }_i^2{\sigma }^2=\overline{U}$.

Accordingly, we can further simplify the SP’s utility maximization problem in Equation (19) to

$$\underset{\{\left\{{\beta }_i\right\}\ge 0\}}{max}\sum _{i=1}^N\left[\frac{{\theta }_i^2{\beta }_i}{c_i}-\overline{U}-\frac{{\beta }_i^2{\theta }_i^2}{2c_i}-\frac{{\eta }_M}{2}{\beta }_i^2{\sigma }^2-\frac{{\eta }_S}{2}{\sigma }^2{\left({\beta }_i-1\right)}^2\right]$$

(20)

We note that the SP’s optimization problem with $2N$ variables (${\alpha }_i,{\beta }_i$) in Equation (19) is simplified to the variables ${\beta }_i$ in Equation (20). Any local optimal solution (denoted as ${\widehat{\beta }}_i$) to the problem of Equation (19) satisfies

$${\left.\frac{d{f}_s}{d{\beta }_i}\right|}_{{\beta }_i={\widehat{\beta }}_i}=\frac{{\theta }_i^2}{c_i}-\frac{{\theta }_i^2}{c_i}{\widehat{\beta }}_i-{\eta }_M{\sigma }^2{\widehat{\beta }}_i-{\eta }_S{\sigma }^2\left({\widehat{\beta }}_i-1\right)=0$$

(21)

Then, the second-order derivative of the problem of Equation (19) is

$${\left.\frac{d^2{f}_s}{d{{\beta }_i}^2}\right|}_{{\beta }_i={\widehat{\beta }}_i}=-\frac{{\theta }_i^2}{c_i}-{\eta }_M{\sigma }^2-{\eta }_S{\sigma }^2<0$$

(22)

Thus, the optimal solution to Equation (19) is achieved as

$${\beta }_i^{*}=\frac{{\theta }_i^2+{\eta }_S{\sigma }^2{c}_i}{{\theta }_i^2+{\eta }_M{\sigma }^2{c}_i+{\eta }_S{\sigma }^2{c}_i}$$

(23)

Therefore,

Table 1. Optimal contract design parameters and settings.

Parameters	Settings
${\beta }_i^{*}$	$\frac{{\theta }_i^2+{\eta }_S{\sigma }^2{c}_i}{{\theta }_i^2+{\eta }_M{\sigma }^2{c}_i+{\eta }_S{\sigma }^2{c}_i}$
$e_i^{*}$	$\frac{{\beta }_i^{*}{\theta }_i}{c_i}$
${\alpha }_i^{*}$	$\overline{U}-{\beta }_i^{*}{\theta }_i{e}_i^{*}+\frac{c_i}{2}{\left(e_i^{*}\right)}^2+\frac{{\eta }_M}{2}{\left({\beta }_i^{*}\right)}^2{\sigma }^2$
${E\left[u\left(W_{M_i}\right)\right]}^{*}$	$-e^{-{\eta }_M\overline{U}}$
$f_S^{*}$	${\displaystyle \sum _{i=1}^N}\left[\left(1-{\beta }_i^{*}\right){\theta }_i{e}_i^{*}-{\alpha }_i^{*}-\frac{{\eta }_S}{2}{\sigma }^2{\left(1-{\beta }_i^{*}\right)}^2\right]$
${E\left[W_S\right]}^{*}$	$-e^{-{\eta }_S{f}_S^{*}}$

summarizes the optimal contract settings and the two parties’ optimal expected utilities.

4. Analysis and Discussion

In this section, the impact of the crowdsourcing participants’ risk preferences on the incentive mechanism is illustrated.

First, the optimal incentive mechanism of the risk-averse MUs is considered with ${\eta }_M\ne 0$. From Equation (23), we have

$$\frac{\partial {\beta }_i^{*}}{\partial {\eta }_M}=\frac{-{\sigma }^2{c}_i({\theta }_i^2+{\eta }_S{\sigma }^2{c}_i)}{{({\theta }_i^2+{\eta }_M{\sigma }^2{c}_i+{\eta }_S{\sigma }^2{c}_i)}^2}<0$$

(24)

$$\frac{\partial {\beta }_i^{*}}{\partial {\eta }_S}=\frac{{\eta }_M{\sigma }^4{c}_i^2}{{({\theta }_i^2+{\eta }_M{\sigma }^2{c}_i+{\eta }_S{\sigma }^2{c}_i)}^2}>0$$

(25)

and

$$\frac{\partial {\beta }_i^{*}}{\partial c_i}=\frac{-{\eta }_M{\sigma }^2{\theta }_i^2}{{({\theta }_i^2+{\eta }_M{\sigma }^2{c}_i+{\eta }_S{\sigma }^2{c}_i)}^2}<0$$

(26)

Thus, from the above formulas, we have that the ith MU’s optimal bonus coefficient ${\beta }_i^{*}$ is decreasing in its absolute risk-averse coefficient ${\eta }_M$ and in its crowdsourcing cost, andis increasing in the SP’s absolute risk-averse coefficient ${\eta }_S$. Given the SP’s absolute risk-averse coefficient ${\eta }_S$, an increasing ${\eta }_M$ can reduce the MU’s optimal bonus coefficient. The greater the SP’s absolute risk-averse coefficient ${\eta }_S$, the greater the risk transferred to the MUs, and the greater the MU’s optimal bonus coefficient ${\beta }_i^{*}$. Therefore, the MUs need to take a greater risk to obtain more utility.

Then, because $e_i^{*}=\frac{{\beta }_i^{*}{\theta }_i}{c_i}$, from the above illustrations, we can also have that the ith MU’s optimal effort $e_i^{*}$ is decreasing in its absolute risk-averse coefficient ${\eta }_M$ and increasing in the SP’s absolute risk-averse coefficient ${\eta }_S$. The greater the MU’s absolute risk-averse coefficient ${\eta }_M$, the lesser the value its crowdsourcing risk will take, and the lower the expected level of its effort.

In particular, the optimal incentive mechanism of the risk-neutral MUs is considered with ${\eta }_M=0$. From Equation (23), we have ${\beta }_i^{*}=1$, $e_i^{*}=\frac{{\theta }_i}{c_i}$ and $f_S^{*}={\displaystyle \sum _{i=1}^N}\left[\frac{{\theta }_i^2}{2c_i}-\overline{U}\right]$. We notice that the optimal expected utility of the SP has no relation to the MUs’ crowdsourcing effort. Furthermore, the greater the MU’s crowdsourcing cost, the lower the level of its effort.

5. Numerical Results

Numerical simulation results are presented to assess the proposed mechanism.

Figure 3 demonstrates the MUs’ optimal basic wage ${\alpha }_i^{*}$, bonus coefficient ${\beta }_i^{*}$ and crowdsourcing effort $e_i^{*}$ with the same crowdsourcing cost $c_i$. We notice that as ${\theta }_i$ becomes large, the ith MU’s profit per unit crowdsourcing effort increases; thus the optimal crowdsourcing effort $e_i^{*}$ increases and the SP may allocate a greater bonus ${\beta }_i^{*}$ to attract the MUs to offer enough crowdsourcing effort. Then, because ${\beta }_i^{*}$ increases, the SP only needs to offer a lesser basic wage ${\alpha }_i^{*}$ to the MUs for enough help.

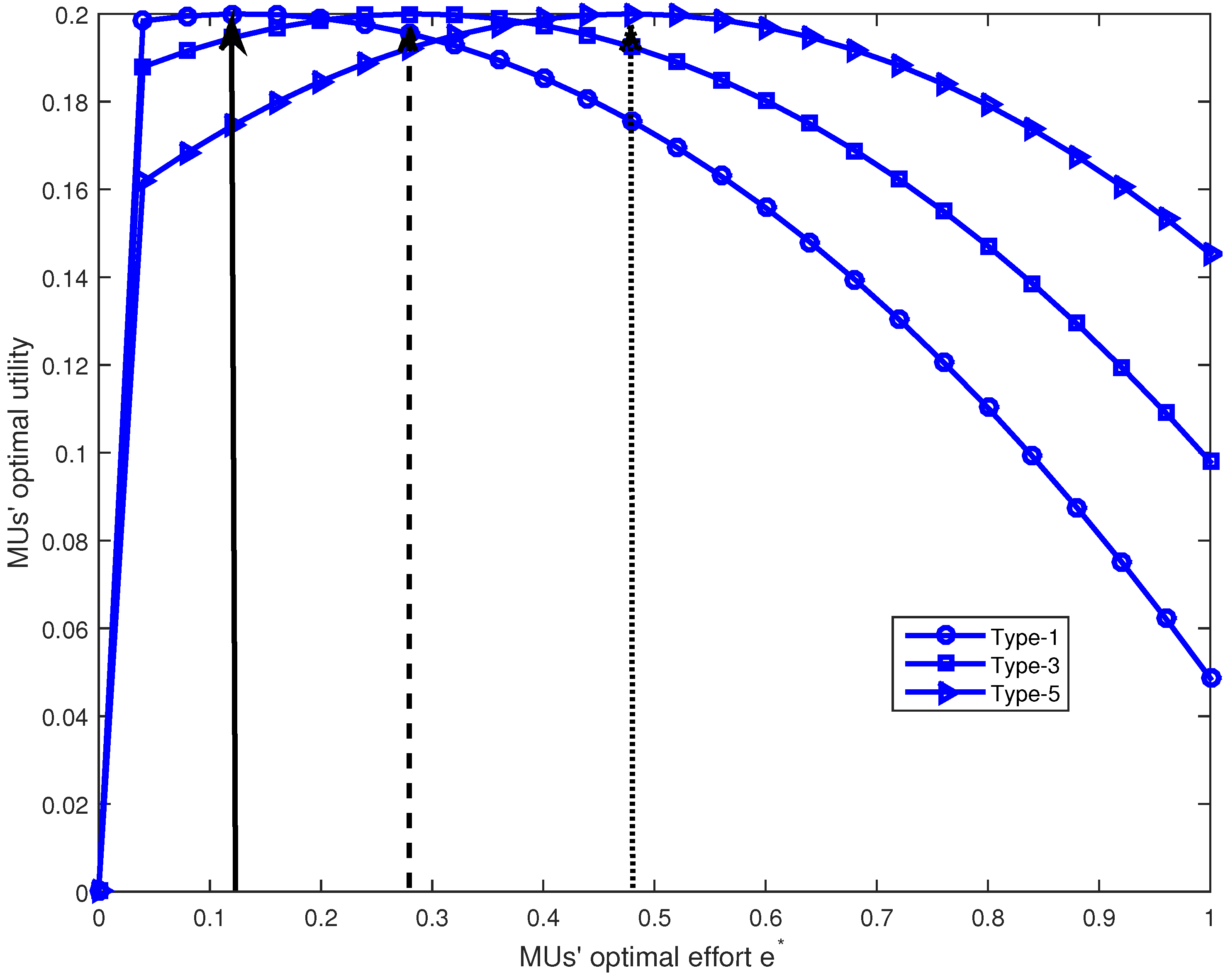
Figure 4 shows the performance of the crowdsourcing effort-incentive with three MUs. The simulation parameter setting is the same as for Figure 3. Each MU obtains its maximum utility by selecting the optimal crowdsourcing effort $e_i^{*}$. Thus, in the proposed optimal contract, the SP can attract the MUs to take full responsibility for their crowdsourcing tasks. The proposed contract-based incentive mechanism breaks information asymmetry and attracts the MUs to make maximum crowdsourcing efforts.

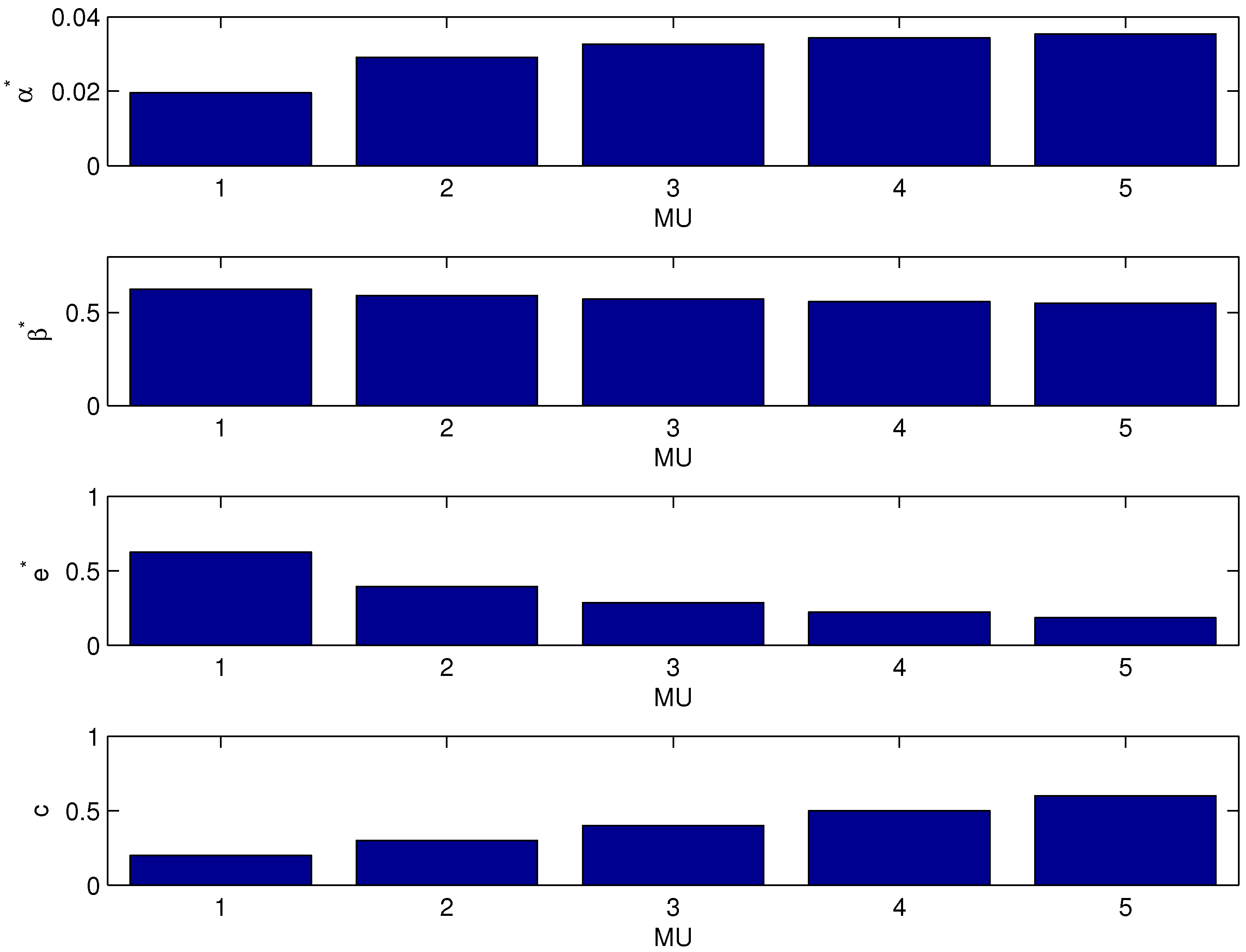
Figure 5 presents the MUs’ optimal basic wage ${\alpha }_i^{*}$, bonus coefficient ${\beta }_i^{*}$ and crowdsourcing effort $e_i^{*}$ with the same crowdsourcing profit ${\theta }_i$. As shown in Figure 4, the MUs’ optimal bonus coefficient ${\beta }_i^{*}$ and the crowdsourcing effort $e_i^{*}$ increase in the crowdsourcing cost coefficient $c_i$. The MUs’ optimal basic wage ${\alpha }_i^{*}$ increases in the crowdsourcing cost coefficient $c_i$. As $c_i$ becomes large, the $i^{th}$ MU’s crowdsourcing cost increases; thus the SP may offer a greater basic wage ${\alpha }_i^{*}$ to obtain enough crowdsourcing effort.

Figure 6 shows the MUs’ optimal bonus coefficient ${\beta }_i^{*}$ with the various SP’s risk-averse degree ${\eta }_S$ and MUs’ risk-averse degree ${\eta }_M$; ${\theta }_i$ is the same as that in Figure 3. We notice that the ith MU’s optimal bonus coefficient ${\beta }_i^{*}$ decreases in its absolute risk-averse coefficient ${\eta }_M$ and increases in the SP’s absolute risk-averse coefficient ${\eta }_S$. Similar results can be obtained for cases of the MUs’ optimal effort $e_i^{*}$, which verifies Equations (24) and (26). 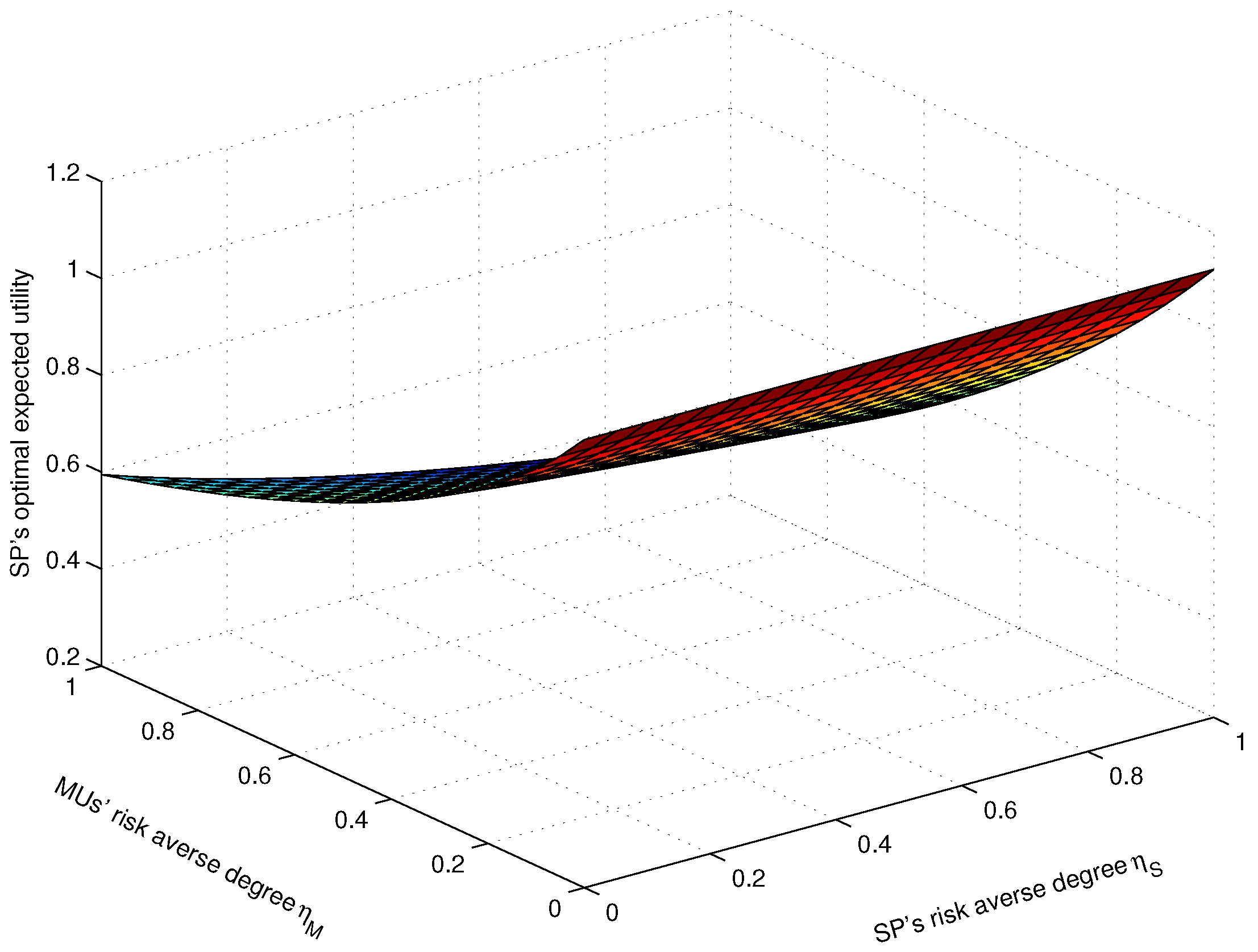Figure 7 illustrates the SP’s optimal expected utility with the SP’s variable risk-averse degree ${\eta }_S$ and MUs’ risk-averse degree ${\eta }_M$. As the SP’s variable risk averse degree ${\eta }_S$ and the MUs’ risk-averse degree ${\eta }_M$ become large, the SP’s optimal expected utility decreases. The greater the MUs’ risk-averse degree ${\eta }_M$, the lesser the SP’s optimal expected utility. Thus, in order to obtain more utilities, the SP needs to choose MUs with a lesser risk-averse degree.

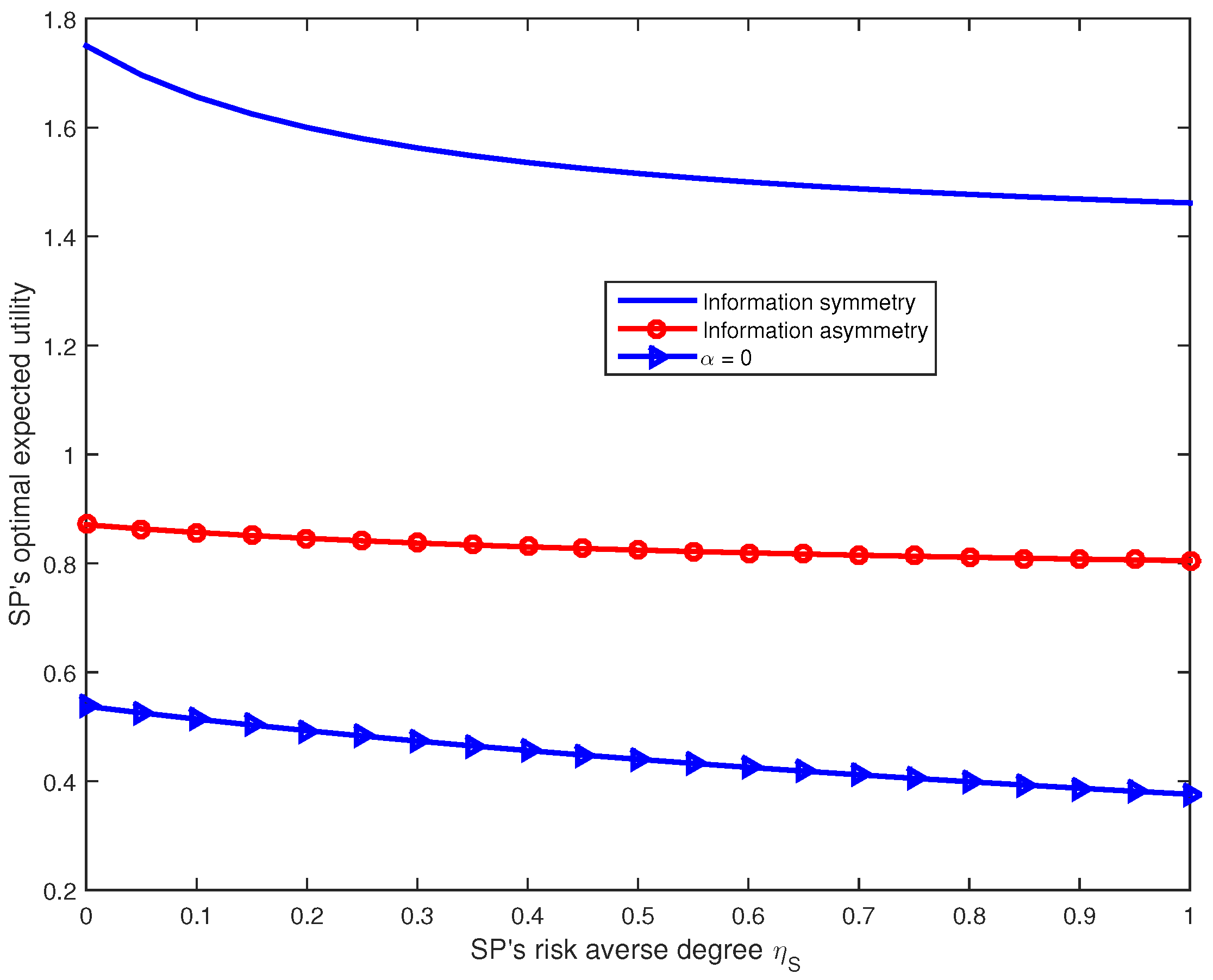
Finally, by introducing another two mechanisms, we evaluate the proposed incentive mechanism. The first incentive mechanism is the contract-based mechanism in the presence of symmetric information (i.e., the SP obtains information about the MUs’ crowdsourcing efforts). The second incentive mechanism is a linear pricing scheme with ${\alpha }_i=0$. In this linear pricing mechanism, the SP only specifies the performance-based bonus coefficient ${\beta }_i$, without the basic wage.

Figure 8 presents the SP’s optimal expected utility with the different incentive mechanisms. In these three incentive mechanisms, the contract-based mechanism under the symmetric information scenario obtains the maximum expected utility of the SP, which is considered to be the upper bound on the SP’s expected utility. Compared to the other two incentive mechanisms, the SP with the proposed contract scheme always achieves more utility than that with ${\alpha }_i=0$. Moreover, as ${\eta }_S$ increases, the SP becomes much more afraid of risk, and thus the SP obtains less utility.

6. Conclusions

In this paper, we investigate a novel contract-based crowdsourcing incentive mechanism between the SP and the MUs. Because of the selfish characteristics of the SP and the MUs, the incentive mechanism is proposed economically to achieve the win–win goal by considering the two parties’ requirements. Moreover, considering both the SP’s and MUs’ risk preferences, the optimal contract design is investigated under an asymmetric information scenario. A moral-hazard contract model is discussed to attract the MUs to take full responsibility for their tasks. The impact of the crowdsourcing participants’ risk preferences on the incentive mechanism has been studied analytically and experimentally. Simulation results show that the proposed contract-based incentive mechanism can effectively improve the performance of crowdsourcing.