Research on Misalignment Fault Isolation of Wind Turbines Based on the Mixed-Domain Features
Abstract
:1. Introduction
- The precise alignment in the wind turbine is very difficult;
- The wind speed fluctuation can cause the start-stop of wind turbine frequently, and, as time goes on, it will cause the shift of generator or the deformation of some parts, resulting in the misalignment of generator and gearbox.
- The time-domain analysis is one of the most simple and direct analysis methods, and it is effective in isolating the fault in a certain extent. Except for the poor anti-interference of serious faults, the numerical values in time-domain are close to that in normal state, so it is easy to make misjudgments only using time-domain analysis.
- The frequency-domain analysis of signal is the most commonly used method of mechanical equipment fault analysis. It can be used to get more intuitive fault information than by the time-domain analysis. However, the theoretical basis of frequency-domain analysis is the method of Fourier analysis, so it has sidedness, and cannot extract the features of vibration signal comprehensively.
- The vibration signal is expressed in the time-domain and frequency-domain at the same time for the time-frequency domain analysis, and it has very prominent advantages. The main methods of feature extraction based on time-frequency analysis are as follows: short time Fourier Transform, Wigner-Ville Distribution, Wavelet Transform, Blind Source Separation, Empirical Mode Decomposition (EMD) and so on.
2. Establishment of Mixed-Domain Feature Library
2.1. Feature Extraction of Vibration Signal in the Time-Domain
2.1.1. Dimensional Index
2.1.2. Dimensionless Index
2.2. Feature Extraction of Vibration Signal in the Frequency-Domain
2.3. Feature Extraction of Vibration Signal in the Time-Frequency Domain
3. Fault Isolation of Transmission System Based on PSO-SVM
3.1. The Principles of SVM
3.2. Particle Swarm Optimization
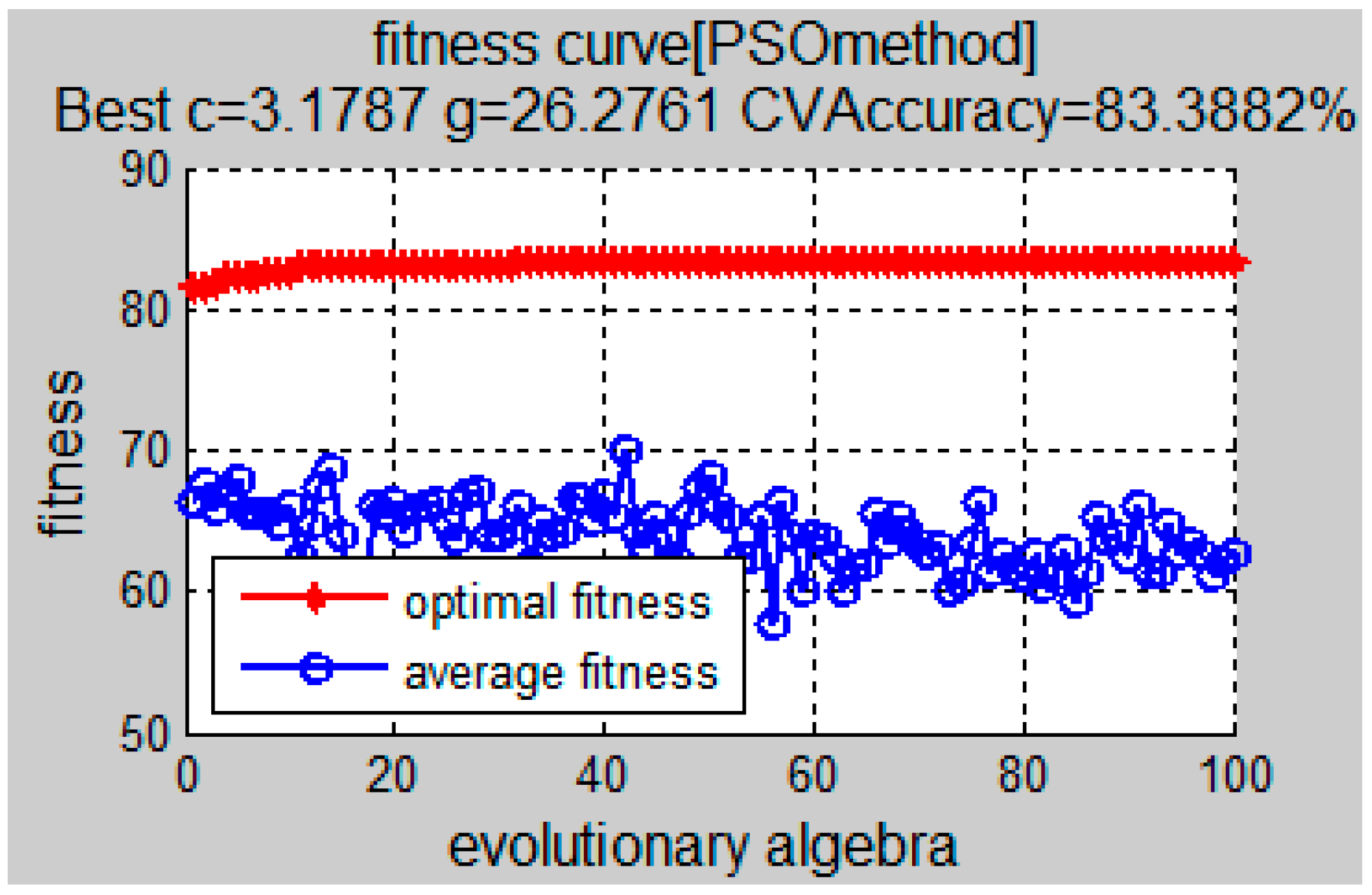
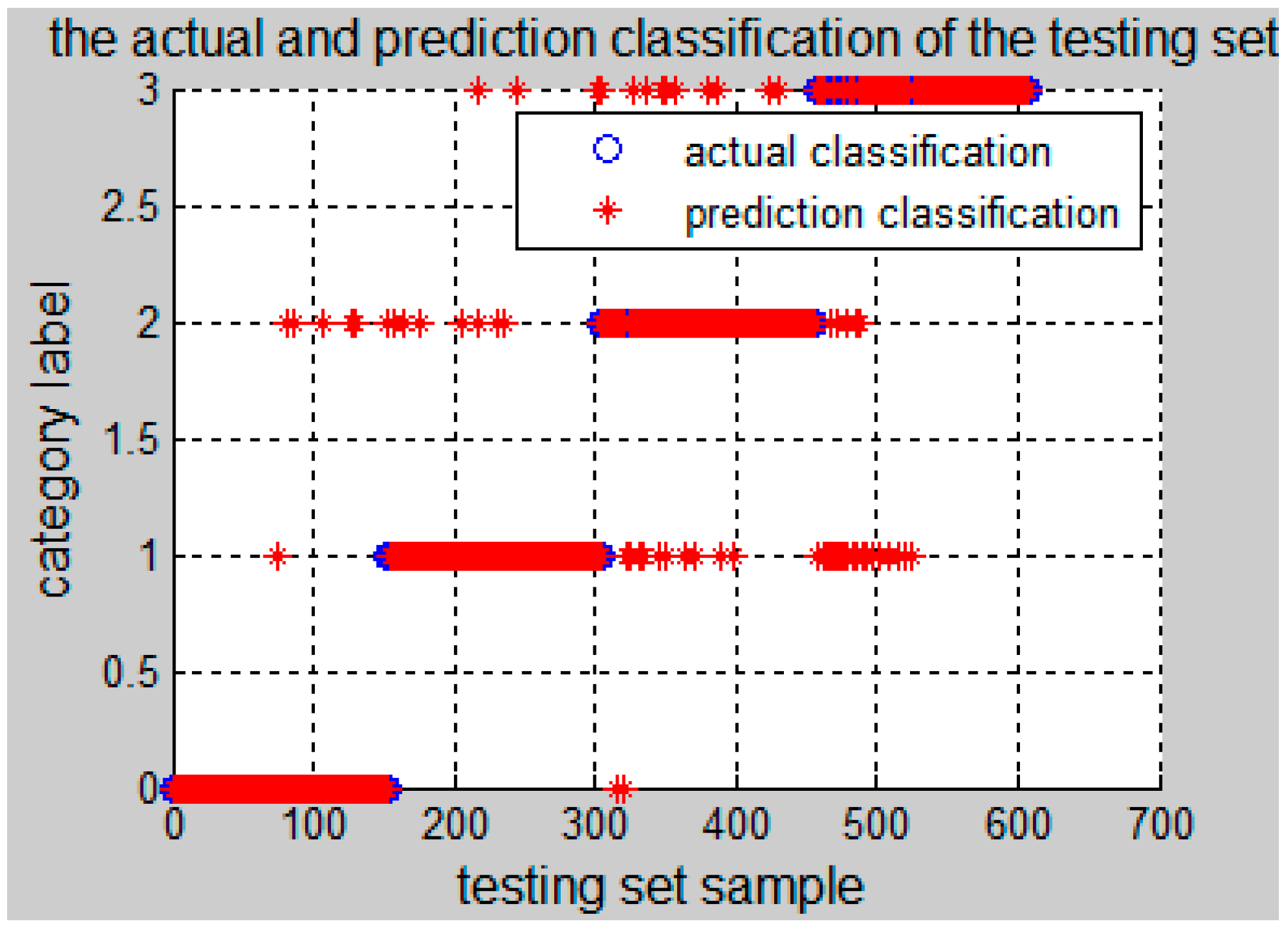
4. PSO-SVM Fault Isolation Results Based on Mixed-Domain Features
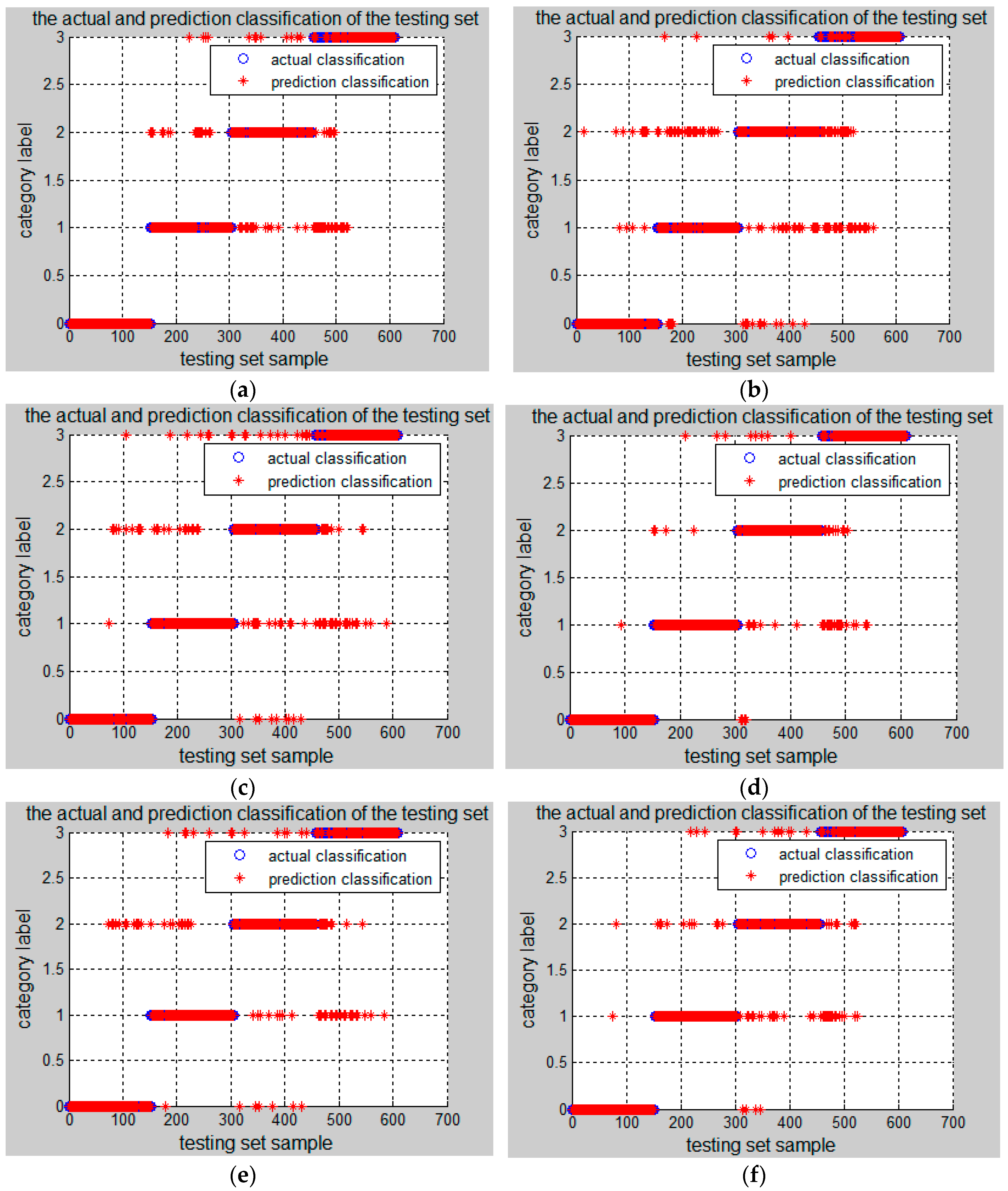
5. Comparison of Fault Isolation Results with Different Fault Features
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhang, T.; Dwight, R.; El-Akruti, K. Condition based maintenance and operation of wind turbines. In Proceedings of the 8th World Congress on Engineering Asset Management & 3rd International Conference on Utility Management & Safety, Hong Kong, China, 30 October–1 November 2013. [Google Scholar]
- Zappalá, D.; Tavner, P.J.; Crabtree, C.J.; Sheng, S. Side-band algorithm for automatic wind turbine gearbox fault detection and diagnosis. IET Renew. Power Gener. 2014, 8, 380–389. [Google Scholar] [CrossRef]
- Kusiak, A.; Li, W. The prediction and diagnosis of wind turbine faults. Renew. Energy 2011, 36, 16–23. [Google Scholar] [CrossRef]
- Bak-Jensen, B.; Kawady, T.A.; Abde1-Rahman, M.H. Coordination between fault-ride-through capability and over-current protection of DFIG generators for wind farms. J. Energy Power Eng. 2010, 4, 20–29. [Google Scholar]
- Amirat, Y.; Benbouzid, M.E.H.; Al-Ahmar, E.; Bensaker, B.; Turri, S. A brief status on condition monitoring and fault diagnosis in wind energy conversion systems. Renew. Sustain. Energy Rev. 2009, 13, 2629–2636. [Google Scholar] [CrossRef]
- Liao, M.; Liang, Y.; Wang, S.; Wang, Y. Misalignment in Drive Train of Wind Turbines. Mech. Sci. Technol. 2011, 30, 173–180. [Google Scholar]
- Xiao, Y.; Kang, N.; Hong, Y.; Zhang, G. Misalignment Fault Diagnosis of DFWT Based on IEMD Energy Entropy and PSO-SVM. Entropy 2017, 19, 6. [Google Scholar] [CrossRef]
- Chen, S. Application of Time Domain Analysis in Mechanical Equipment Fault Diagnosis. J. Mech. Transm. 2007, 31, 79–83. [Google Scholar]
- Zhen, L. Study on Fault Diagnosis Methods of Generator and Gearbox for Wind Turbines. Master’s Thesis, North China Electric Power University, Beijing, China, 2014. [Google Scholar]
- Zhang, C.; Chen, J.; Guo, X. A gear fault diagnosis method based on EMD energy entropy and SVM. J. Vib. Shock 2010, 29, 216–220. [Google Scholar]
- Long, J.; Wu, J. Fault Diagnosis of Rotor Misalignment for Windmill Generators. Noise Vib. Control 2013, 33, 222–225. [Google Scholar]
- Ding, S.; Chang, X.; Wu, Q.; Wei, H.; Yang, Y. Study on wind turbine gearbox fault diagnosis based on LVQ neural network. Mod. Electron. Tech. 2014, 37, 150–152. [Google Scholar]
- Ren, S. The Study of Fault Diagnosis Methods for Wind Turbine Gearbox Based on the Analysis Vibration Characteristics. Master’s Thesis, Hebei University of Technology, Tianjin, China, 2015. [Google Scholar]
- Wang, B. Research on Fault Diagnosis System for Gearbox of Wind Turbine. Master’s Thesis, North China Electric Power University, Beijing, China, 2012. [Google Scholar]
- Tang, B.; Song, T.; Li, F.; Deng, L. Fault diagnosis for a wind turbine transmission system based on manifold learning and Shannon wavelet support vector machine. Renew. Energy 2014, 62, 1–9. [Google Scholar] [CrossRef]
- Li, F.; Tang, B.; Yang, R. Rotating machine fault diagnosis using dimension reduction with linear local tangent space alignment. Measurement 2013, 46, 2525–2539. [Google Scholar] [CrossRef]
- Xu, Z. Research on Transmission Chain State Monitoring and Fault Diagnosis of Wind Turbine Based on Vibration Method. Master’s Thesis, Zhejiang University, Hangzhou, China, 2012. [Google Scholar]
- Ding, K.; Li, W. Practical Technology for Fault Diagnosis of Gear and Gearbox; China Machine Press: Beijing, China, 2006. [Google Scholar]
- Zhang, L.; Zhu, L.; Zhong, B. Study on the Features of Some Specific Parameters Utilized for Machine Condition Monitoring. J. Vib. Shock 2001, 20, 20–21. [Google Scholar]
- Yi, L. On-Site Practical Technology of Simple Vibration Diagnosis; China Machine Press: Beijing, China, 2003. [Google Scholar]
- Zhang, C.; Chen, J.; Guo, X. Gear fault diagnosis method based on EEMD energy entropy and support vector machine. J. Cent. South Univ. 2012, 3, 932–939. [Google Scholar]



| Feature Library | Feature | Index |
|---|---|---|
| Mixed-domain feature library | Time-domain | root mean square, square root amplitude, variance, standard deviation, kurtosis, waveform index, peak index, pulse index, margin index, kurtosis index |
| Frequency-domain | centroid frequency, mean square frequency, variance frequency | |
| Time-frequency domain | energy entropy of the first eight IMF components of IEMD decomposition |
| Type | RMS (×10) | Square Root Amplitude | Variance (×106) | SD (×10) | Kurtosis | Waveform Index | Peak Index | Pulse Index | Margin Index | Kurtosis Index |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 10,107 | 71,069 | 10,212 | 10,105 | 2.49 | 1.21 | 3.42 | 4.15 | 4.86 | 2.50 |
| 10,112 | 70,651 | 10,223 | 10,111 | 2.53 | 1.22 | 3.02 | 3.68 | 4.32 | 2.54 | |
| 10,117 | 69,920 | 10,229 | 10,114 | 2.55 | 1.22 | 3.28 | 4.01 | 4.74 | 2.56 | |
| 10,135 | 70,627 | 10,261 | 10,130 | 2.52 | 1.22 | 3.44 | 4.19 | 4.93 | 2.54 | |
| 10,136 | 69,844 | 10,267 | 10,132 | 2.59 | 1.23 | 3.03 | 3.72 | 4.40 | 2.60 | |
| 1 | 68,743 | 203,770 | 47,184 | 68,690 | 14.19 | 1.89 | 6.26 | 11.81 | 21.11 | 14.40 |
| 70,048 | 213,120 | 49,046 | 70,033 | 15.37 | 1.85 | 5.44 | 10.07 | 17.89 | 15.51 | |
| 70,194 | 208,350 | 49,209 | 70,149 | 14.69 | 1.90 | 5.21 | 9.90 | 17.57 | 14.94 | |
| 70,720 | 217,070 | 49,931 | 70,662 | 16.04 | 1.91 | 5.11 | 9.75 | 16.66 | 16.30 | |
| 71,651 | 227,770 | 51,201 | 71,555 | 12.08 | 1.84 | 5.57 | 10.24 | 17.53 | 12.23 | |
| 2 | 176,820 | 689,720 | 30,935 | 175,880 | 7.41 | 1.64 | 4.42 | 7.24 | 11.34 | 7.58 |
| 177,180 | 702,010 | 31,389 | 177,170 | 6.72 | 1.63 | 4.87 | 7.92 | 12.28 | 6.72 | |
| 177,930 | 680,850 | 31,660 | 177,930 | 7.52 | 1.67 | 4.78 | 8.00 | 12.50 | 7.52 | |
| 178,990 | 679,150 | 31,589 | 177,730 | 7.71 | 1.69 | 3.84 | 6.48 | 10.13 | 8.28 | |
| 179,010 | 706,130 | 32,048 | 179,020 | 6.77 | 1.64 | 5.04 | 8.26 | 12.77 | 6.77 | |
| 3 | 601,360 | 1,681,900 | 36,139 | 601,160 | 14.83 | 1.95 | 5.82 | 11.35 | 20.81 | 15.09 |
| 625,910 | 1,801,800 | 39,127 | 625,520 | 13.28 | 1.91 | 6.70 | 12.76 | 23.26 | 13.58 | |
| 656,970 | 2,154,200 | 43,123 | 656,680 | 11.11 | 1.79 | 7.30 | 13.09 | 22.27 | 11.22 | |
| 664,860 | 2,069,300 | 44,194 | 664,780 | 11.38 | 1.82 | 6.80 | 12.37 | 21.85 | 11.51 | |
| 671,750 | 2,101,200 | 45,063 | 671,290 | 12.30 | 1.83 | 6.82 | 12.50 | 21.81 | 12.50 |
| Type | FC | MSF | VF |
|---|---|---|---|
| 0 | −458 | 7,083,800 | 6,873,700 |
| −455 | 7,047,800 | 6,841,100 | |
| −457 | 7,077,400 | 6,868,500 | |
| −453 | 6,958,700 | 6,753,100 | |
| −448 | 6,988,700 | 6,787,900 | |
| 1 | −750 | 12,950,000 | 12,387,000 |
| −647 | 11,048,000 | 10,629,000 | |
| −697 | 12,436,000 | 11,950,000 | |
| −728 | 13,462,000 | 12,933,000 | |
| −715 | 12,794,000 | 12,283,000 | |
| 2 | −440 | 8,587,500 | 8,393,500 |
| −443 | 8,652,700 | 8,456,200 | |
| −475 | 9,280,300 | 9,053,800 | |
| −447 | 8,707,000 | 8,507,200 | |
| −451 | 8,785,300 | 8,581,700 | |
| 3 | −376 | 7,338,600 | 7,196,600 |
| −355 | 7,033,700 | 6,907,400 | |
| −388 | 8,190,100 | 8,039,200 | |
| −369 | 7,400,400 | 7,264,100 | |
| −346 | 6,958,600 | 6,838,700 |
| Type | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0 | 0.3109 | 0.3429 | 0.1709 | 0.0747 | 0.0476 | 0.072 | 0.097 | 0.0521 |
| 0.3166 | 0.352 | 0.1553 | 0.0784 | 0.0477 | 0.0688 | 0.0575 | 0.0176 | |
| 0.3186 | 0.3498 | 0.1657 | 0.0814 | 0.0478 | 0.0452 | 0.069 | 0.0172 | |
| 0.3256 | 0.341 | 0.2031 | 0.0895 | 0.0564 | 0.037 | 0.0933 | 0.0148 | |
| 0.3302 | 0.3386 | 0.1669 | 0.0748 | 0.0574 | 0.0522 | 0.0788 | 0.0129 | |
| 1 | 0.1484 | 0.3676 | 0.3623 | 0.193 | 0.1201 | 0.0863 | 0.0477 | 0.1012 |
| 0.1489 | 0.3669 | 0.3678 | 0.2267 | 0.0938 | 0.0481 | 0.028 | 0.1249 | |
| 0.1513 | 0.3678 | 0.3662 | 0.1839 | 0.1077 | 0.0665 | 0.0517 | 0.2216 | |
| 0.1558 | 0.3533 | 0.3675 | 0.2133 | 0.1479 | 0.0683 | 0.0637 | 0.1977 | |
| 0.1574 | 0.3601 | 0.3639 | 0.157 | 0.0807 | 0.062 | 0.2031 | 0.1429 | |
| 2 | 0.2335 | 0.3067 | 0.2325 | 0.1467 | 0.0843 | 0.0763 | 0.1386 | 0.3648 |
| 0.2361 | 0.3024 | 0.3679 | 0.289 | 0.1934 | 0.1157 | 0.1594 | 0.0478 | |
| 0.2423 | 0.3665 | 0.3417 | 0.2574 | 0.1862 | 0.0897 | 0.0395 | 0.0279 | |
| 0.2455 | 0.3476 | 0.3679 | 0.3096 | 0.1083 | 0.0873 | 0.0337 | 0.0536 | |
| 0.2487 | 0.3298 | 0.3134 | 0.2565 | 0.1254 | 0.0804 | 0.1309 | 0.3447 | |
| 3 | 0.1456 | 0.2285 | 0.2912 | 0.3322 | 0.2521 | 0.1672 | 0.2001 | 0.1162 |
| 0.1061 | 0.2784 | 0.3393 | 0.2876 | 0.2762 | 0.0813 | 0.2059 | 0.1677 | |
| 0.1074 | 0.2581 | 0.3357 | 0.3582 | 0.1606 | 0.1101 | 0.1396 | 0.1396 | |
| 0.1082 | 0.2853 | 0.3271 | 0.3022 | 0.1685 | 0.1765 | 0.0751 | 0.1556 | |
| 0.111 | 0.3268 | 0.3654 | 0.2737 | 0.2681 | 0.0886 | 0.0773 | 0.1014 |
| Item | Accuracy of Training Set | Accuracy of Testing Set | ||
|---|---|---|---|---|
| SVM | 1 | 0.01 | 63.2401% (769/1216) | 63.6513% (387/608) |
| GridSearch-SVM | 16 | 1.4142 | 93.4211% (1136/1216) | 90.9539% (553/608) |
| GA-SVM | 26.2168 | 6.7162 | 99.5066% (1210/1216) | 91.1184% (554/608) |
| PSO-SVM | 3.1787 | 26.2761 | 97.9441% (1191/1216) | 92.1053% (560/608) |
| Fault Features | Accuracy of Training Set | Accuracy of Testing Set | ||
|---|---|---|---|---|
| Time-domain | 22.5396 | 74.8823 | 88.0757% (1071/1216) | 84.2105% (512/608) |
| Frequency-domain | 7.71812 | 346.316 | 77.7138% (945/1216) | 74.5066% (453/608) |
| IEMD energy entropy | 7.88573 | 6.12414 | 87.4178% (1063/1216) | 82.4013% (501/608) |
| Time-domain + frequency-domain | 73.0786 | 20.0281 | 93.5033% (1137/1216) | 89.9671% (547/608) |
| Time-domain + IEMD energy entropy | 58.3106 | 1.42904 | 93.2566% (1134/1216) | 87.8289% (534/608) |
| Frequency-domain + IEMD energy entropy | 2.1093 | 10.0231 | 91.1184% (1108/1216) | 84.8684% (516/608) |
| Time-domain + frequency-domain + IEMD energy entropy | 3.1787 | 26.2761 | 97.9441% (1191/1216) | 92.1053% (560/608) |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Wang, Y.; Mu, H.; Kang, N. Research on Misalignment Fault Isolation of Wind Turbines Based on the Mixed-Domain Features. Algorithms 2017, 10, 67. https://doi.org/10.3390/a10020067
Xiao Y, Wang Y, Mu H, Kang N. Research on Misalignment Fault Isolation of Wind Turbines Based on the Mixed-Domain Features. Algorithms. 2017; 10(2):67. https://doi.org/10.3390/a10020067
Chicago/Turabian StyleXiao, Yancai, Yujia Wang, Huan Mu, and Na Kang. 2017. "Research on Misalignment Fault Isolation of Wind Turbines Based on the Mixed-Domain Features" Algorithms 10, no. 2: 67. https://doi.org/10.3390/a10020067
APA StyleXiao, Y., Wang, Y., Mu, H., & Kang, N. (2017). Research on Misalignment Fault Isolation of Wind Turbines Based on the Mixed-Domain Features. Algorithms, 10(2), 67. https://doi.org/10.3390/a10020067





