Stable Analysis of Compressive Principal Component Pursuit

Abstract

Compressive principal component pursuit (CPCP) recovers a target matrix that is a superposition of low-complexity structures from a small set of linear measurements. Pervious works mainly focus on the analysis of the existence and uniqueness. In this paper, we address its stability. We prove that the solution to the related convex programming of CPCP gives an estimate that is stable to small entry-wise noise. We also provide numerical simulation results to support our result. Numerical results show that the solution to the related convex program is stable to small entry-wise noise under board condition.

1. Introduction

Recently, there has been a rapidly increasing interest in recovering a target matrix that is a superposition of low-rank and sparse components from a small set of linear measurements. In many cases, this problem is shorted for matrix completion [1,2,3], which arises in a number of fields, such as medical imaging [4,5], seismology [6], and computer vision [7,8] and Kalman filter [9]. Mathematically, there exists a large-scale data matrix $M=L_0+S_0$, where $L_0$ is a low-rank matrix, and $S_0$ is a sparse matrix. One of the important problems here is how to extract the intrinsic low-dimensional structure from a small set of linear measurements. In a recent paper [10], E. J. Candès et al. proved that most low-rank matrices and the sparse components can be recovered, provided that the rank of the low-rank component is not too large, and that the sparse component is reasonably sparse. It is more important that they proved that these two components can be recovered by solving a simple convex optimization problem. In [11], John Wright et al. generalized this problem to decompose a matrix into multiple incoherent components:

$$\begin{array}{ccc}\mathrm{minimize}\hfill & & {\displaystyle \sum _i^{\tau }}{\lambda }_i{\parallel X_i\parallel }_{\left(i\right)}\hfill \\ \mathrm{subject}\mathrm{to}\hfill & & {\displaystyle \sum _i^{\tau }}{X}_i=M,\hfill \end{array}$$

(1)

where $\parallel X_i{\parallel }_{\left(i\right)}$ are norms that encourage various types of low-complexity structure. The authors also provide a sufficient condition that can promise the existence and uniqueness theorem of compressive principle component pursuit (CPCP). The result in [11] requires that the components are low-complexity structures.

However, in many applications, the observed measurements are always corrupted by different kinds of noise which may affect every entry of the data matrix. In order to further complete the theory developed in [11], it is necessary to research the stability of CPCP which can guarantee stable and accurate recovery in the presence of entry-wise noise. In this paper, we make a commendable attempt in this respect. We denote M as the observing matrix which can decompose into multiple incoherent components, and assume that

$$M={\displaystyle \sum _i^{\tau }}{X}_{i,0}+Z_0,$$

where $X_{i,0}$ are corresponding incoherent components and $Z_0$ is an independent and identically distributed (i.i.d.) noise. We assume that $Z_0$ is only limited by $\parallel Z_0{\parallel }_F\le \delta$ for some $\delta >0$. In order to recover the unknown low-complexity structures, we suggest solving the following relaxed optimization problem.

$$\begin{array}{ccc}\mathrm{minimize}\hfill & & {\displaystyle \sum _i^{\tau }}{\lambda }_i{\parallel X_i\parallel }_{\left(i\right)}\hfill \\ \mathrm{subject}\mathrm{to}\hfill & & \parallel {\displaystyle \sum _i^{\tau }}{X}_i{-M\parallel }_F\le \delta \hfill \end{array}$$

(2)

In this paper, we prove the solution of (2) is stable to small entry-wise noise. The rest of paper is organized as follows. In Section 2, we show some notations and the main result, which will be proven in Section 3 and Section 4. In Section 3, we give two important lemmas which are an important parts of our main result. In Section 4, The proof of Theorem 1 will be given. We further provide numerical results in Section 5 and conclude the paper in Section 6.

2. Notations and Main Results

In this section, we first give some important notions which will be used throughout this paper, and then provide the main result.

2.1. Notations

We denote the operator norm of matrix by $\parallel X\parallel$, the Frobenius norm by ${\parallel X\parallel }_F$, and the nuclear norm by ${\parallel X\parallel }_{*}$, and denote the dual norm of ${\parallel X\parallel }_{\left(i\right)}$ by ${\parallel X\parallel }_{\left(i\right)}^{*}$. The Euclidean inner product between two matrices is defined by the formula $⟨X,Y⟩=trace\left(X^{*}Y\right)$. Note that ${\parallel X\parallel }_F^2=⟨X,X⟩$. The Cauchy–Schwarz inequality gives $⟨X,Y⟩\le {\parallel X\parallel }_F{\parallel Y\parallel }_F$, and it is well known that we also have $⟨X,Y⟩\le {\parallel X\parallel }_{\left(i\right)}{\parallel Y\parallel }_{\left(i\right)}^{*}$ (e.g., [1,12]). ${\parallel X\parallel }_{\left(i\right)}$ majorized the Frobenius norm means ${\parallel X\parallel }_{\left(i\right)}\ge {\parallel X\parallel }_F$ for all X. Linear transformations which act on the space of matrices are denoted by ${\mathcal{P}}_{T}X$. It is easy to see that the operator of ${\mathcal{P}}_T$ is a high dimension matrix. The operator norm of the operator is denoted by $\parallel {\mathcal{P}}_T\parallel$. It should be noted that $\parallel {\mathcal{P}}_T\parallel ={\sup }_{\{\parallel X{\parallel }_F=1\}}{\parallel {\mathcal{P}}_{T}X\parallel }_F$.

For any matrix vector $x=\left[X_i\right],i=1,2,\cdots ,\tau$, where $X_i\in {\mathbb{R}}^{m\times n}$ is i-th matrix. We will consider two norms of this matrix pair, which can define as ${\parallel x\parallel }_{\diamond }:={\sum }_i^{\tau }{\lambda }_i{\parallel X_i\parallel }_{\left(i\right)}$ and ${\parallel x\parallel }_2:={\sum }_i^{\tau }{\parallel X_i\parallel }_F$. In order to simplify the stability analysis of CPCP, we also define the subspaces (the common component) $\gamma :=\left[{\mathrm{\Gamma }}_i\right],{\mathrm{\Gamma }}_i=\left({\sum }_l^{\tau }{X}_l\right)/\tau i=1,2,\cdots ,\tau$, and (the different component) ${\gamma }^{\perp }:=\left[{\mathrm{\Gamma }}_i^{\perp }\right],{\mathrm{\Gamma }}_i^{\perp }=X_i-{\mathrm{\Gamma }}_i$ $i=1,2,\cdots ,\tau$. In order to analyze the behavior of special projection operator, we define the projection operator ${\mathcal{P}}_{T_1}\times \cdots \times {\mathcal{P}}_{T_{\tau }}\left(x\right):=[{\mathcal{P}}_{T_1}\left(X_1\right),\cdots ,{\mathcal{P}}_{T_{\tau }}\left(X_{\tau }\right)]$.

we assume that $\parallel X_i{\parallel }_{\left(i\right)}i=1,2,\cdots ,\tau$ are decomposable norms. The definition of decomposable norms is below.

Definition 1 (Decomposable Norms).

if there exists a subspace T and a matrix Z satisfying

$$\begin{array}{c}\hfill \partial \parallel ·\parallel \left(X\right)=\left\{\mathrm{\Lambda }\right|{\mathcal{P}}_T\mathrm{\Lambda }=Z,\parallel {\mathcal{P}}_{T^{\perp }}\mathrm{\Lambda }{\parallel }^{*}\le 1\},\end{array}$$

(3)

where ${\parallel ·\parallel }^{*}$ denotes the dual norm of $\parallel ·\parallel$ and ${\mathcal{P}}_{T^{\perp }}$ is nonexpansive with respect to ${\parallel ·\parallel }^{*}$. Then, we say that the norm $\parallel ·\parallel$ is decomposable at X.

Definition 2 (Inexact Certificate).

We say Λ is an $(\alpha ,\beta )$-inexact certificate for a putative solution $(X_{1,\diamond },\cdots ,X_{\tau ,\diamond })$ to (1.1) with parameters $({\lambda }_1,\cdots ,{\lambda }_{\tau })$ if for each i, $\parallel {\mathcal{P}}_{T_i}\mathrm{\Lambda }-{\lambda }_i{Z}_i{\parallel }_F\le \alpha$, and $\parallel {\mathcal{P}}_{T_i^{\perp }}{\mathrm{\Lambda }\parallel }_{\left(i\right)}^{*}<{\lambda }_i\beta$.

2.2. Main Results

Pertaining to Problem (1), we have the result as follows.

Lemma 1

([11]). Assume there exists a feasible solution $x=(X_1,\cdots ,X_{\tau })$ to the optimization Problem (1). Suppose that each of the norms ${\parallel ·\parallel }_{\left(i\right)}$ is decomposable at $X_i$, and that each of the ${\parallel ·\parallel }_{\left(i\right)}$ majorizes the Frobenius norm. Then, x is the unique optimal solution if $T_1,\cdots ,T_{\tau }$ are independent subspaces with

$$\begin{array}{c}\hfill \parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel <\frac{1}{\tau -1}\forall i\ne j,\end{array}$$

and there exists an $(\alpha ,\beta )$-inexact certificate $\widehat{\mathrm{\Lambda }}$, with

$$\begin{array}{c}\hfill \beta +\frac{\alpha \sqrt{\tau }}{\sqrt{1-(\tau -1){max}_{ij}\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel }}\times \frac{1}{{min}_l{\lambda }_l}\le 1.\end{array}$$

The main contribution of this paper is the stability analysis of the solution of CPCP; the main Theorem of [13] can be regarded as a special case of our result (although the main idea of proof is similar to the paper [13], there are some important differences here). Next, we will provide the proposed related convex programming (2) is stable from small entry-wise noise under board condition. The main result of this paper is provided below.

Theorem 1.

Assume $x_{\diamond }=(X_{1,\diamond },\cdots ,X_{\tau ,\diamond })$, $\widehat{x}=(X_1,\cdots ,X_{\tau })$ are the solutions of the optimization Problems (1) and (2), respectively. Suppose that each of the norms ${\parallel ·\parallel }_{\left(i\right)}$ is decomposable at $X_{i,\diamond }$, and each of the ${\parallel ·\parallel }_{\left(i\right)}$ majorizes the Frobenius norm. Then, if $T_1,\cdots ,T_{\tau }$ are independent subspaces with

$$\begin{array}{c}\hfill \parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel <\frac{1}{\tau -1}\forall i\ne j\end{array}$$

and there exists an $(\alpha ,\beta )$-inexact certificate $\widehat{\mathrm{\Lambda }}$, with

$$\begin{array}{c}\hfill \beta +\frac{\alpha \sqrt{\tau }}{\sqrt{1-(\tau -1){max}_{ij}\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel }}\times \frac{1}{{min}_l{\lambda }_l}\le 1,\end{array}$$

(4)

then for any $Z_0$ which is limited by $\parallel Z_0{\parallel }_F\le \delta$, the solution $\widehat{x}$ to the convex programming (2) obeys

$$\begin{array}{c}\hfill \sum _i{\parallel {\widehat{x}}_i-x_{i,\diamond }\parallel }_2^2\le C(n,\tau ,\alpha ,\beta ){\delta }^2,\end{array}$$

(5)

where $C(n,\tau ,\alpha ,\beta )$ is a numerical constant only depending upon $n,\tau ,\alpha ,\beta$.

3. Main Lemmas

In this section, we present two main lemmas which are used to obtain Theorem 1. The paper [11] states that:

Lemma 2

([11]). Suppose $T_1,\cdots ,T_{\tau }$ are independent subspaces of ${\mathbb{R}}^{m\times n}$ and $Z_1\in T_1,\cdots ,Z_{\tau }\in T_{\tau }$, under the other conditions of Lemma 1. Then, the below equations

$$\begin{array}{c}\hfill {\mathcal{P}}_{T_i}\Delta ={\lambda }_i{Z}_i-{\mathcal{P}}_{T_i}\mathrm{\Lambda },i=1,\cdots ,\tau \end{array}$$

have a solution $\Delta \in T_1+\cdots +T_{\tau }$ obeying

$$\begin{array}{c}\hfill {\parallel \Delta \parallel }_F\le \sqrt{\frac{{\alpha }^2\tau }{1-(\tau -1){max}_{i\ne j}\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_i}\parallel }}.\end{array}$$

In order to bound the behavior of the norm of ${\parallel x\parallel }_{\diamond }$, we have the first main lemma that is used to obtain Theorem 1.

Lemma 3.

Assume $\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel <\frac{1}{\tau -1}\forall i\ne j$. Suppose there exists an $(\alpha ,\beta )$-inexact certificate $\widehat{\mathrm{\Lambda }}$ satisfying Lemma 1. Then, for any perturbation $h=\left[H_i\right]$ obeying ${\sum }_i{H}_i=0$

$$\begin{array}{c}\hfill \parallel x_0{+h\parallel }_{\diamond }\ge \parallel x_0{\parallel }_{\diamond }+{\displaystyle \sum _{i=1}^{\tau }}({\lambda }_i-C_{\alpha }-{\lambda }_i\beta ){\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i\parallel }_{\left(i\right)},\end{array}$$

wherein, let $C_{\alpha }=\sqrt{\frac{{\alpha }^2\tau }{1-(\tau -1){max}_{i\ne j}\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_i}\parallel }}$. It is easy to see that under the hypothesis of Lemma 1, the coefficients of $\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i{\parallel }_{\left(i\right)}$ satisfy ${\lambda }_i-C_{\alpha }-{\lambda }_i\beta >0$.

Proof. 

According to the property of convex function, for any subgradients $z=\left[Z_i\right]\in \partial {\parallel x_0\parallel }_{\diamond }$, we can obtain

$$\begin{array}{c}\hfill \parallel x_0{+h\parallel }_{\diamond }\ge {\parallel x\parallel }_{\diamond }+{\displaystyle \sum _{i=1}^{\tau }}{\lambda }_i<Z_i,H_i>.\end{array}$$

Now, because the norm of the subgradients is decomposable at $X_i$, there exists Λ, $Z_i$, α, and β obeying $\parallel {\mathcal{P}}_{T_i}\mathrm{\Lambda }-{\lambda }_i{Z}_i{\parallel }_F\le \alpha$, and $\parallel {\mathcal{P}}_{T_i^{\perp }}{\mathrm{\Lambda }\parallel }_{\left(i\right)}^{*}<{\lambda }_i\beta$. Let ${\Delta }_i:={\mathcal{P}}_{T_i}\Delta ={\lambda }_i{Z}_i-{\mathcal{P}}_{T_i}\mathrm{\Lambda }\in T_i$ (see Lemma 2). Note that

$$\begin{array}{ccc}\hfill \mathrm{\Lambda }+{\Delta }_i+{\mathcal{P}}_{T_i^{\perp }}({\lambda }_i{Z}_i-\mathrm{\Lambda })& =& \mathrm{\Lambda }+{\lambda }_i{Z}_i-{\mathcal{P}}_{T_i}\mathrm{\Lambda }+{\mathcal{P}}_{T_i^{\perp }}{\lambda }_i{Z}_i-{\mathcal{P}}_{T_i^{\perp }}\mathrm{\Lambda }\hfill \\ & =& {\lambda }_i{Z}_i+{\mathcal{P}}_{T_i^{\perp }}{\lambda }_i{Z}_i\hfill \\ & =& {\lambda }_i{Z}_i,\hfill \end{array}$$

where the second equation obeys $Z_i\in T_i$. According to the above equation, we will continue bounding ${\sum }_{i=1}^{\tau }{\lambda }_i<Z_i,H_i>$.

$$\begin{array}{ccc}{\displaystyle \sum _{i=1}^{\tau }}{\lambda }_i<Z_i,H_i>\hfill & =\hfill & {\displaystyle \sum _{i=1}^{\tau }}<\mathrm{\Lambda }+{\Delta }_i+{\mathcal{P}}_{T_i^{\perp }}({\lambda }_i{Z}_i-\mathrm{\Lambda }),H_i>\hfill \\ & =\hfill & {\displaystyle \sum _{i=1}^{\tau }}<\mathrm{\Lambda },H_i>+{\displaystyle \sum _{i=1}^{\tau }}<{\mathcal{P}}_{T_i}\Delta ,H_i>+{\displaystyle \sum _{i=1}^{\tau }}<{\mathcal{P}}_{T_i^{\perp }}({\lambda }_i{Z}_i-\mathrm{\Lambda }),H_i>\hfill \\ & =\hfill & <\mathrm{\Lambda },{i=1}^{\tau }{H}_i>+{\displaystyle \sum _{i=1}^{\tau }}<\Delta ,{\mathcal{P}}_{T_i}{H}_i>+{\displaystyle \sum _{i=1}^{\tau }}<{\lambda }_i{Z}_i-\mathrm{\Lambda },{\mathcal{P}}_{T_i^{\perp }}{H}_i>\hfill \\ & =\hfill & {\displaystyle \sum _{i=1}^{\tau }}<\Delta ,H_i>-{\displaystyle \sum _{i=1}^{\tau }}<\Delta ,{\mathcal{P}}_{T_i^{\perp }}{H}_i>+{\displaystyle \sum _{i=1}^{\tau }}<{\lambda }_i{Z}_i-\mathrm{\Lambda },{\mathcal{P}}_{T_i^{\perp }}{H}_i>\hfill \\ & \ge \hfill & {\displaystyle \sum _{i=1}^{\tau }}<{\lambda }_i{Z}_i-\mathrm{\Lambda },{\mathcal{P}}_{T_i^{\perp }}{H}_i>-{\displaystyle \sum _{i=1}^{\tau }}{\parallel \Delta \parallel }_F{\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i\parallel }_F\hfill \\ & \ge \hfill & {\displaystyle \sum _{i=1}^{\tau }}<{\lambda }_i{Z}_i-\mathrm{\Lambda },{\mathcal{P}}_{T_i^{\perp }}{H}_i>-{\displaystyle \sum _{i=1}^{\tau }}{\parallel \Delta \parallel }_F{\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i\parallel }_{\left(i\right)}\hfill \end{array}$$

With the definition of duality, there exists ${\widehat{Z}}_i\in \partial {\parallel X_{i,0}\parallel }_{\left(i\right)}$ with $\parallel {\widehat{Z}}_i{\parallel }_{\left(i\right)}^{*}\le 1$ such that $<Z_i^{*},{\mathcal{P}}_{T_i^{\perp }}{H}_i>={\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i\parallel }_{\left(i\right)}$. Moreover, with the Cauchy–Schwarz inequality, we have

$$\begin{array}{ccc}\hfill |<\mathrm{\Lambda },{\mathcal{P}}_{T_i^{\perp }}{H}_i>|& =& |<{\mathcal{P}}_{T_i^{\perp }}\mathrm{\Lambda },{\mathcal{P}}_{T_i^{\perp }}{H}_i>|\le \parallel {\mathcal{P}}_{T_i^{\perp }}{\mathrm{\Lambda }\parallel }_{\left(i\right)}^{*}{\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i\parallel }_{\left(i\right)}.\hfill \end{array}$$

Let $Z_i={\widehat{Z}}_i$. Then, we can obtain:

$$<{\lambda }_i{Z}_i-\mathrm{\Lambda },{\mathcal{P}}_{T_i^{\perp }}{H}_i>\ge ({\lambda }_i-\parallel {\mathcal{P}}_{T_i^{\perp }}{\mathrm{\Lambda }\parallel }_{\left(i\right)}^{*})\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i{\parallel }_{\left(i\right)}.$$

Combining with the inequalities above, we can obtain

$$\begin{array}{ccc}\hfill \parallel x_0{+h\parallel }_{\diamond }& \ge & \parallel x_0{\parallel }_{\diamond }+{\displaystyle \sum _{i=1}^{\tau }}({\lambda }_i-{\parallel \Delta \parallel }_F-\parallel {\mathcal{P}}_{T_i^{\perp }}{\mathrm{\Lambda }\parallel }_{\left(i\right)}^{*})\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i{\parallel }_{\left(i\right)}\hfill \\ & \ge & \parallel x_0{\parallel }_{\diamond }+{\displaystyle \sum _{i=1}^{\tau }}({\lambda }_i-C_{\alpha }-{\lambda }_i\beta ){\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i\parallel }_{\left(i\right)}.\hfill \end{array}$$

The Lemma 3 is established. ☐

For bounding the behavior of ${\sum }_i{\parallel {\widehat{x}}_i-x_{i,\diamond }\parallel }_F^2$, we have to bound the projection operator ${\mathcal{P}}_{T_1}\times \cdots \times {\mathcal{P}}_{T_{\tau }}\left(x\right)$. Therefore, we have the second main lemma that will be used to obtain Theorem 1.

Lemma 4.

Assume that $\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel <\frac{1}{\tau -1}\forall i\ne j$. For any matrix vector $x=\left[X_i\right]$, we have

$$\begin{array}{c}\hfill \parallel {\mathcal{P}}_{\gamma }({\mathcal{P}}_{T_1}\times \cdots \times {\mathcal{P}}_{T_{\tau }})\left(x\right){\parallel }_F^2\ge \frac{1-{max}_i\frac{1}{2}{\sum }_{j\ne i}(\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel +\parallel {\mathcal{P}}_{T_j}{\mathcal{P}}_{T_i}\parallel )}{\tau }{\parallel {\mathcal{P}}_{T_1}\times \cdots \times {\mathcal{P}}_{T_{\tau }}\left(x\right)\parallel }_F^2.\end{array}$$

It is easy to see that under the hypothesis of $\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel <\frac{1}{\tau -1}\forall i\ne j$, the constant $\frac{1-{max}_i\frac{1}{2}{\sum }_{j\ne i}(\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel +\parallel {\mathcal{P}}_{T_j}{\mathcal{P}}_{T_i}\parallel )}{{\tau }^2}$ is strictly greater than zero.

Proof. 

With respect to any matrix $x=\left[X_i\right]$, we have ${\mathcal{P}}_{\gamma }\left(x\right)=\left[{\mathrm{\Gamma }}_i\right]$, where ${\mathrm{\Gamma }}_i=\left({\sum }_{l=1}^{\tau }{X}_l\right)/\tau$. It is easy to see that $\parallel {\mathcal{P}}_{\gamma }{\left(x\right)\parallel }_F^2=\frac{1}{\tau }{\parallel {\sum }_{l=1}^{\tau }{X}_l\parallel }_F^2$. Then, we have

$$\begin{array}{ccc}\hfill \parallel {\mathcal{P}}_{\gamma }({\mathcal{P}}_{T_1}\times \cdots \times {\mathcal{P}}_{T_{\tau }})\left(x\right){\parallel }_F^2& =& \frac{1}{\tau }\parallel {\displaystyle \sum _{i=1}^{\tau }}{\mathcal{P}}_{T_i}{X}_i{\parallel }_F^2\hfill \\ & =& \frac{1}{\tau }({\displaystyle \sum _{i=1}^{\tau }}(\parallel {\mathcal{P}}_{T_i}{X}_i{\parallel }_F^2+\sum _{j\ne i}<{\mathcal{P}}_{T_i}{X}_i,{\mathcal{P}}_{T_j}{X}_j>\left)\right).\hfill \end{array}$$

Note that

$$\begin{array}{ccc}\hfill <{\mathcal{P}}_{T_i}{X}_i,{\mathcal{P}}_{T_j}{X}_j>& =& <{\mathcal{P}}_{T_i}{X}_i,{\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}{X}_j>\hfill \\ & \ge & -\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel \parallel {\mathcal{P}}_{T_i}{X}_i{\parallel }_F{\parallel {\mathcal{P}}_{T_j}{X}_j\parallel }_F.\hfill \end{array}$$

Together with $\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel <\frac{1}{\tau -1}\forall i\ne j$, we have

$$\begin{array}{ccc}\hfill \parallel {\mathcal{P}}_{\gamma }({\mathcal{P}}_{T_1}\times \cdots \times {\mathcal{P}}_{T_{\tau }})\left(x\right){\parallel }_F^2& \ge & \frac{1}{\tau }({\displaystyle \sum _{i=1}^{\tau }}\parallel {\mathcal{P}}_{T_i}{X}_i{\parallel }_F^2-\sum _{j\ne i}\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel \parallel {\mathcal{P}}_{T_i}{X}_i{\parallel }_F\parallel {\mathcal{P}}_{T_j}{X}_j{\parallel }_F\left)\right)\hfill \\ & \ge & \frac{1}{\tau }({\displaystyle \sum _{i=1}^{\tau }}(\parallel {\mathcal{P}}_{T_i}{X}_i{\parallel }_F^2-\sum _{j\ne i}\frac{\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel }{2}(\parallel {\mathcal{P}}_{T_i}{X}_i{\parallel }_F^2+\parallel {\mathcal{P}}_{T_j}{X}_j{\parallel }_F^2\left)\right)\hfill \\ & =& \frac{1}{\tau }{\displaystyle \sum _{i=1}^{\tau }}(1-\frac{1}{2}\sum _{j\ne i}(\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel +\parallel {\mathcal{P}}_{T_j}{\mathcal{P}}_{T_i}\parallel \left)\right)\parallel {\mathcal{P}}_{T_i}{X}_i{\parallel }_F^2\hfill \\ & \ge & \frac{1-{\max }_i\frac{1}{2}{\sum }_{j\ne i}(\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel +\parallel {\mathcal{P}}_{T_j}{\mathcal{P}}_{T_i}\parallel )}{\tau }(\sum _i\parallel {\mathcal{P}}_{T_i}{X}_i{\parallel }_F^2)\hfill \\ & \ge & \frac{1-{\max }_i\frac{1}{2}{\sum }_{j\ne i}(\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel +\parallel {\mathcal{P}}_{T_j}{\mathcal{P}}_{T_i}\parallel )}{\tau }{\parallel {\mathcal{P}}_{T_1}\times \cdots \times {\mathcal{P}}_{T_{\tau }}\left(x\right)\parallel }_F^2,\hfill \end{array}$$

where in the second inequality, we have used the inequity that for any $x,y$, $2xy\le (x^2+y^2)$. Therefore, Lemma 4 is established. ☐

4. Proof of Theorem 1

In this section, we will provide the proof of Theorem 1. Our main proof is based on two elementary and important properties of $\widehat{x}$, which is the solution of Problem (2). First, note that $x_0$ is also a feasible solution to Problem (2) and $\widehat{x}$ is the optimum solution; therefore, we can obtain $\parallel \widehat{x}{\parallel }_{\diamond }\le {\parallel x_0\parallel }_{\diamond }$. Second, according to triangle inequality, we can obtain

$$\begin{array}{ccc}\parallel \widehat{x}-x_0{\parallel }_2\hfill & =\hfill & \parallel \widehat{x}-M-(x_0-M){\parallel }_2\hfill \\ & \le \hfill & \parallel \widehat{x}{-M\parallel }_2+{\parallel x_0-M\parallel }_2\hfill \\ & \le \hfill & 2\delta .\hfill \end{array}$$

(6)

Let $\widehat{x}=x_0+h$, where $h=\left[H_i\right]$. According to the definition of subspace of γ, we denote $h^{\gamma }:={\mathcal{P}}_{\gamma }\left(h\right)$, $h^{{\gamma }^{\perp }}:={\mathcal{P}}_{{\gamma }^{\perp }}\left(h\right)$ for short. Our main aim is to bound ${\parallel h\parallel }_2={\parallel \widehat{x}-x_0\parallel }_2$, which can be rewritten as

$$\begin{array}{ccc}{\parallel h\parallel }_2^2\hfill & =\hfill & \parallel h^{\gamma }{\parallel }_2^2+{\parallel h^{{\gamma }^{\perp }}\parallel }_2^2\hfill \\ & =\hfill & \parallel h^{\gamma }{\parallel }_2^2+{\parallel {\mathcal{P}}_{T_1}\times \cdots \times {\mathcal{P}}_{T_{\tau }}{h}^{{\gamma }^{\perp }}\parallel }_2^2\hfill \\ & & +\parallel {\mathcal{P}}_{T_1^{\perp }}\times \cdots \times {\mathcal{P}}_{T_{\tau }^{\perp }}{h}^{{\gamma }^{\perp }}{\parallel }_2^2.\hfill \end{array}$$

(7)

Combining with (4), we have

$$\begin{array}{c}\hfill \parallel h^{\gamma }{\parallel }_2^2=\sum _i\parallel \frac{{\sum }_{j=1}^{\tau }{H}_j}{\tau }{\parallel }_2^2\le \frac{4{\delta }^2}{\tau }\end{array}$$

Therefore, it is necessary to bound the other two terms on the right-hand-side of (5). We will bound the second and third terms, respectively.

Norm equivalence theorem tells us that every two norms on a finite dimensional normed space are equivalent, which implies that there exists two constants $C(n,\tau )\ge c(n,\tau )>0$ satisfying

$$\begin{array}{c}\hfill {c(n,\tau )\parallel x\parallel }_2\le {\parallel x\parallel }_{\diamond }\le C(n,\tau ){\parallel x\parallel }_2.\end{array}$$

(8)

A. Estimate the third term of (5) Let Λ be a dual certificate obeying Lemma 1. Then, using triangle inequality, we have

$$\begin{array}{c}\hfill \parallel x_0{+h\parallel }_2\ge \parallel x_0+h^{{\gamma }^{\perp }}{\parallel }_2-{\parallel h^{\gamma }\parallel }_2.\end{array}$$

(9)

Combining with Lemma 3, we can obtain

$$\begin{array}{ccc}\hfill \parallel x_0+h^{{\gamma }^{\perp }}{\parallel }_2& \ge & \parallel x_0{\parallel }_d+{\displaystyle \sum _{i=1}^{\tau }}({\lambda }_i-C_{\alpha }-{\lambda }_i\beta ){\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i\parallel }_{\left(i\right)}\hfill \\ & \ge & \parallel x_0{\parallel }_d+(1-C_{\alpha }\frac{1}{{\min }_i{\lambda }_i}-\beta ){\displaystyle \sum _{i=1}^{\tau }}{\lambda }_i{\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i^{{\mathrm{\Gamma }}^{\perp }}\parallel }_{\left(i\right)}\hfill \\ & \ge & \parallel x_0{+h\parallel }_d+(1-C_{\alpha }\frac{1}{{\min }_i{\lambda }_i}-\beta ){\displaystyle \sum _{i=1}^{\tau }}{\lambda }_i{\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i^{{\mathrm{\Gamma }}^{\perp }}\parallel }_{\left(i\right)},\hfill \end{array}$$

wherein, to get the third inequality, we used the fact $\parallel \widehat{x}{\parallel }_d\le {\parallel x_0\parallel }_d$. For simplification, let

$$\begin{array}{c}\hfill C_1(\alpha ,\beta )\triangleq \left(1-C_{\alpha }\frac{1}{{\min }_i{\lambda }_i}-\beta \right)>0.\end{array}$$

Therefore, we have

$$\begin{array}{ccc}\hfill \parallel x_0+h^{{\gamma }^{\perp }}{\parallel }_2& \ge & \parallel x_0{+h\parallel }_d+C_1(\alpha ,\beta ){\displaystyle \sum _{i=1}^{\tau }}{\lambda }_i{\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i^{{\mathrm{\Gamma }}^{\perp }}\parallel }_{\left(i\right)}.\hfill \end{array}$$

Combining with (7), we can obtain

$$\begin{array}{c}\hfill C_1(\alpha ,\beta ){\displaystyle \sum _{i=1}^{\tau }}{\lambda }_i\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i^{{\mathrm{\Gamma }}^{\perp }}{\parallel }_{\left(i\right)}\le {\parallel h^{\gamma }\parallel }_2.\end{array}$$

Then

$$\begin{array}{c}\hfill {\displaystyle \sum _{i=1}^{\tau }}{\lambda }_i\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i^{{\mathrm{\Gamma }}^{\perp }}{\parallel }_{\left(i\right)}\le C_2(\alpha ,\beta ){\parallel h^{\gamma }\parallel }_2,\end{array}$$

(10)

where $C_2(\alpha ,\beta )=1/C_1(\alpha ,\beta )$. We will estimate the third term of (5). Using triangle inequality, we have

$$\begin{array}{ccc}\hfill \parallel {\mathcal{P}}_{T_1^{\perp }}\times \cdots \times {\mathcal{P}}_{T_{\tau }^{\perp }}{h}^{{\mathrm{\Gamma }}^{\perp }}{\parallel }_2& \le & \sum _i{\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i^{{\mathrm{\Gamma }}^{\perp }}\parallel }_F\hfill \\ & \le & \frac{1}{c(n,\tau )}{\displaystyle \sum _{i=1}^{\tau }}{\lambda }_i{\parallel {\mathcal{P}}_{T_i^{\perp }}{H}_i^{{\mathrm{\Gamma }}^{\perp }}\parallel }_{\left(i\right)}\hfill \\ & \le & \frac{C_2(\alpha ,\beta )}{c(n,\tau )}{\parallel h^{\gamma }\parallel }_2\hfill \\ & \le & C(n,\tau ,\alpha ,\beta )\delta ,\hfill \end{array}$$

where $C(n,\tau ,\alpha ,\beta ):=\frac{2C_2(\alpha ,\beta )}{c(n,\tau )\sqrt{\tau }}$. The second inequality is set up by (6); the fourth inequality is obtained by (8); the last one is obtained by the fact $\parallel h^{\gamma }{\parallel }_2\le \frac{2\delta }{\sqrt{\tau }}$. Therefore, we can obtain

$$\begin{array}{c}\hfill \parallel {\mathcal{P}}_{T_1^{\perp }}\times \cdots \times {\mathcal{P}}_{T_{\tau }^{\perp }}(h^{{\mathrm{\Gamma }}^{\perp }}){\parallel }_2^2\le C^2(n,\tau ,\alpha ,\beta ){\delta }^2,\end{array}$$

(11)

which implies that the third term of (5) can bound by $C\delta$.

B. Estimate the second term of (5) According to Lemma 4, we can obtain

$$\begin{array}{ccc}\hfill \parallel {\mathcal{P}}_{\gamma }({\mathcal{P}}_{T_1}\times \cdots \times {\mathcal{P}}_{T_{\tau }})(h^{{\gamma }^{\perp }}){\parallel }_2^2& \ge & \frac{1-{\max }_i\frac{1}{2}{\sum }_{j\ne i}(\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel +\parallel {\mathcal{P}}_{T_j}{\mathcal{P}}_{T_i}\parallel )}{\tau }\hfill \\ & & \parallel {\mathcal{P}}_{T_1}\times \cdots \times {\mathcal{P}}_{T_{\tau }}(h^{{\gamma }^{\perp }}){\parallel }_2^2\hfill \\ & =& \widehat{C}(\tau ,\alpha ,\beta )\parallel {\mathcal{P}}_{T_1}\times \cdots \times {\mathcal{P}}_{T_{\tau }}(h^{{\gamma }^{\perp }}){\parallel }_2^2,\hfill \end{array}$$

where $\widehat{C}(\tau ,\alpha ,\beta ):=\frac{1-{\max }_i\frac{1}{2}{\sum }_{j\ne i}(\parallel {\mathcal{P}}_{T_i}{\mathcal{P}}_{T_j}\parallel +\parallel {\mathcal{P}}_{T_j}{\mathcal{P}}_{T_i}\parallel )}{\tau }$. Note that

$$\begin{array}{ccc}\hfill 0& =& {\mathcal{P}}_{\gamma }(h^{{\gamma }^{\perp }})\hfill \\ & =& {\mathcal{P}}_{\gamma }{\mathcal{P}}_{T_1}\times \cdots \times {\mathcal{P}}_{T_{\tau }}{h}^{{\gamma }^{\perp }}+{\mathcal{P}}_{\gamma }{\mathcal{P}}_{T_1^{\perp }}\times \cdots \times {\mathcal{P}}_{T_{\tau }^{\perp }}{h}^{{\gamma }^{\perp }}.\hfill \end{array}$$

Therefore,

$$\begin{array}{ccc}\hfill \parallel {\mathcal{P}}_{\gamma }{\mathcal{P}}_{T_1}\times \cdots \times {\mathcal{P}}_{T_{\tau }}{h}^{{\gamma }^{\perp }}{\parallel }_2& =& \parallel {\mathcal{P}}_{\gamma }{\mathcal{P}}_{T_1^{\perp }}\times \cdots \times {\mathcal{P}}_{T_{\tau }^{\perp }}{h}^{{\gamma }^{\perp }}{\parallel }_2\hfill \\ & \le & \parallel {\mathcal{P}}_{T_1^{\perp }}\times \cdots \times {\mathcal{P}}_{T_{\tau }^{\perp }}{h}^{{\gamma }^{\perp }}{\parallel }_2.\hfill \end{array}$$

Taking the previous two inequalities, we have

$$\begin{array}{ccc}\parallel {\mathcal{P}}_{T_1}\times \cdots \times {\mathcal{P}}_{T_{\tau }}{h}^{{\gamma }^{\perp }}{\parallel }_2\hfill & \le \hfill & \frac{\parallel {\mathcal{P}}_{\gamma }{\mathcal{P}}_{T_1^{\perp }}\times \cdots \times {\mathcal{P}}_{T_{\tau }^{\perp }}{h}^{{\gamma }^{\perp }}{\parallel }_2}{\sqrt{\widehat{C}(\tau ,\alpha ,\beta )}}\hfill \\ & \le \hfill & \frac{\parallel {\mathcal{P}}_{T_1^{\perp }}\times \cdots \times {\mathcal{P}}_{T_{\tau }^{\perp }}{h}^{{\gamma }^{\perp }}{\parallel }_2}{\sqrt{\widehat{C}(\tau ,\alpha ,\beta )}}\hfill \\ & \le \hfill & C(n,\tau ,\alpha ,\beta )\delta ,\hfill \end{array}$$

(12)

where $C(n,\tau ,\alpha ,\beta )$ is an appropriate constant. Combining with (9), we can obtain

$$\begin{array}{ccc}\hfill {\parallel h\parallel }_2^2& =& \parallel h^{\mathrm{\Gamma }}{\parallel }_2^2+{\parallel {\mathcal{P}}_{T_1}\times \cdots \times {\mathcal{P}}_{T_{\tau }}{h}^{{\mathrm{\Gamma }}^{\perp }}\parallel }_2^2\hfill \\ & & +\parallel {\mathcal{P}}_{T_1^{\perp }}\times \cdots \times {\mathcal{P}}_{T_{\tau }^{\perp }}{h}^{{\mathrm{\Gamma }}^{\perp }}{\parallel }_2^2\hfill \\ & \le & \widehat{C}(n,\tau ,\alpha ,\beta ){\delta }^2.\hfill \end{array}$$

Therefore, Theorem 1 is established.

Remark 1.

if $\tau =2$, then Theorem 1 will degrade to the main result of [13].

5. Numerical Results

In this section, numerical experiments with varieties of the value of parameter σ, parameter ${\rho }_s$, and rank r are given. For each setting of parameters, we show the average errors over 10 trials. Our implementation was realized with MATLAB. All the computational results were obtained on a desktop computer with a 2.27-GHz CPU (Intel(R) Core(TM) i3) and 2 GB of memory. Without loss of generality, we assume that $\tau =2$. In [13], the authors certified this result with Accelerated Proximal Gradient (APG) by numerical experiments. In our numerical experiments, we will provide that this result is also proper with Principal Component Pursuit by Alternating Direction Method (PCP-ADM). In our simulations, our matrix is generated by the formulation as: $M=L_0+S_0+N_0$, and a rank-r matrix $L_0$ is a product $L_0=X{Y}^T$, where X and Y are $m\times r$ and $n\times r$ matrices in which entries are independently sampled from a $\mathcal{N}(0;1)$ distribution. According to PCP-ADM, we can generate $S_0$ by choosing a support set of size $k_s={\rho }_{s}mn$ uniformly at random, and set $S_0={\mathcal{P}}_{\mathrm{\Omega }}E$. Noise component $N_0$ is generated with entries independently sampled from a $\mathcal{N}(0;\sigma )$ distribution. Without loss of generality, we set $m=n=200$ and ${\rho }_s=0.01$, and other parameters which PCP-ADM requires are the same as parameters of PCP-ADM [10]. Here we briefly interpret PCP-ADM. In [10], in order to stably recover $\widehat{X}=(\widehat{L};\widehat{S})$, the ADM method operates on the augmented Lagrangian

$$\begin{array}{ccc}\hfill l(L,S,Y)& =& {\parallel L\parallel }_{*}+{\lambda \parallel S\parallel }_1+<Y,M-L-S>+\frac{\mu }{2}{\parallel M-L-S\parallel }_F^2.\hfill \end{array}$$

The details of the PCP-ADM can be found in [14,15].

In our simulations, the stopping criterion of the PCP-ADM algorithm can be

$$\begin{array}{c}\hfill \frac{{\parallel L+S-M\parallel }_F}{{\parallel M\parallel }_F}\le \mathrm{tolerance}\end{array}$$

or the maximum iteration number ($k_{max}=500$). In order to estimate the errors, we use the root-mean-squared (RMS) error as $\parallel \widehat{L}-L_0{\parallel }_F/n$, $\parallel \widehat{S}-S_0{\parallel }_F/n$ for the low-rank component and the sparse component, respectively. Figure 1 shows the RMS errors’ variation with different values of ${\sigma }^2$. It is noted that the RMS error grows approximately linearly with the noise level in Figure 1. This phenomenon verifies Theorem 1 by numerical experiments with PCP-ADM (this phenomenon also exists in [13] with APG, which is very different from PCP-ADM in principle).

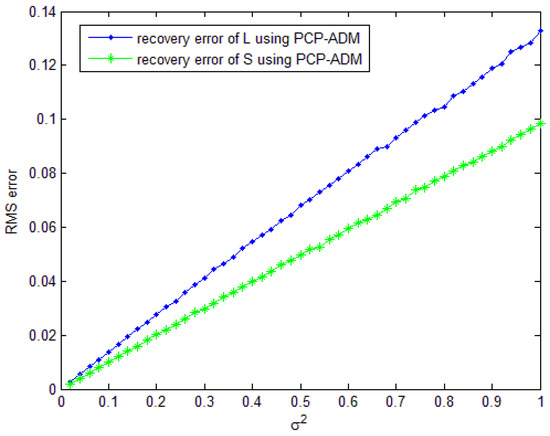
Figure 1. Root-mean-squared (RMS) errors as a function of ${\sigma }^2$ with $r=10;{\rho }_s=0.01;n=200$. PCP-ADM: Principal Component Pursuit by Alternating Direction Method.

6. Conclusions

In this paper, we have investigated the the stability of CPCP. Our main contribution is the proof of Theorem 1, which implies the solution to the related convex programming (1.2) is stable to small entrywise noise under board condition. It is an extension of the result in [13], which only allows $\tau =2$. Moreover, in the numerical experiments, we have investigated the performance of the PCP-ADM algorithm. Numerical results showed that it is stable to small entrywise noise.