Problems on Finite Automata and the Exponential Time Hypothesis

Abstract

We study several classical decision problems on finite automata under the (Strong) Exponential Time Hypothesis. We focus on three types of problems: universality, equivalence, and emptiness of intersection. All these problems are known to be CoNP-hard for nondeterministic finite automata, even when restricted to unary input alphabets. A different type of problems on finite automata relates to aperiodicity and to synchronizing words. We also consider finite automata that work on commutative alphabets and those working on two-dimensional words.

1. Introduction

Many computer science students will get the impression, at least when taught the basics on the Chomsky hierarchy in their course on Formal Languages, that finite automata are fairly simple devices, and hence it is expected that typical decidability questions on finite automata are easy ones. In fact, for instance, the non-emptiness problem for finite automata is solvable in polynomial time, as well as the uniform word problem. (Even tighter descriptions of the complexities can be given within classical complexity theory, but this is not so important for our presentation here, as we mostly focus on polynomial versus exponential time.) This contrasts to the respective statements for higher levels of the Chomsky hierarchy.

However, this impression is somewhat misled. Finite automata can be also viewed as edge-labeled directed graphs, and as many combinatorial problems are harder on directed graphs compared to undirected ones, it should not come as such a surprise that many interesting questions are actually NP-hard for finite automata.

We will study hard problems for finite automata under the perspective of the Exponential Time Hypothesis (ETH) and variants thereof, as surveyed in [1]. In particular, using the famous sparsification lemma [2], ETH implies that there is no $O(2^{o(n+m)})$ algorithm for Satisfiability (SAT) of m-clause 3CNF formulae with n variables, or 3SAT for short. Notice that for these reductions to work, we have to start out with 3SAT (i.e., with Boolean formulae in conjunctive normal form where each clause contains (at most) three literals), as it seems unlikely that sparsification also works for general formulae in conjunctive normal form; see [3]. Occasionally, we will also use SETH (Strong ETH); this hypothesis implies that there is no $O({(2-\epsilon )}^n)$ algorithm for solving the satisfiability problem (CNF-)SAT for general Boolean formulae in conjunctive normal form with n variables for any $\epsilon >0$.

Recall that the $O^{*}$ notation suppresses polynomial factors, measured in the overall input length. This notation is common in exact exponential-time algorithms, as well as in parameterized algorithms, as it allows to focus on the decisive exponential part of the running time. We refer the reader to textbooks like [4,5,6].

Let us now briefly yet more thoroughly discuss the objects and questions that we are going to study in the following. Mostly, we consider finite-state automata that read input words over the input alphabet Σ one-way, from left to right, and they accept when entering a final state upon reading the last letter of the word. We only consider deterministic finite automata (DFAs) and nondeterministic finite automata (NFAs). The language (set of words) accepted by a given automaton A is denoted by $L(A)$. For these classical devices, both variants of the membership problem are solvable in polynomial time and they are therefore irrelevant to the complexity studies we are going to undertake.

Rather, we are going to study the following three problems. In each case, we clarify the natural parameters that come with the input, as we will show algorithms whose running times depend on these parameters, and, more importantly, we will prove lower bounds for such algorithms based on (S)ETH.

Problem 1 (Universality).

Given an automaton A with input alphabet Σ, is $L(A)={\mathrm{\Sigma }}^{*}$? Parameters are the number q of states of A and the size of Σ.

Problem 2 (Equivalence).

Given two automata $A_1,A_2$ with input alphabet Σ, is $L(A_1)=L(A_2)$? Parameters are an upper bound q on the number of states of $A_1,A_2$ and the size of Σ.

Clearly, Universality reduces to Equivalence by choosing the automaton $A_2$ such that $L(A_2)={\mathrm{\Sigma }}^{*}$. Also, all these problems can be solved by computing the equivalent (minimal) deterministic automata, which requires time $O^{*}(2^q)$. In particular, notice that minimizing a DFA with s states takes time $O(s\log s)$ with Hopcroft’s algorithm, so that the running time of first converting a q-state NFA into an equivalent DFA ($O^{*}(2^q)$) and then minimizing a $2^q$-state DFA (in time $O(2^q{2}^{\log q})=O^{*}(2^q)$). Our results on these problems for NFAs are summarized in

Table 1. Universality/Equivalence; functions refer to exponents of bounding functions.

Σ	Universality/Equivalence
	Lower Bound	Upper Bound
unary	$o(\sqrt[3]{q})$	$O(\sqrt{q\log q})$	Theorem 2
binary	$o(q)$	q	Theorem 4
unbounded	$o(q)$	q	Theorem 4

. The functions refer to the exponents, so, e.g., according to the first row, we will show in this paper that there is no $2^{o(\sqrt[3]{q})}$ algorithm for Universality for q-state NFAs with unary input alphabets.

Problem 3 (Intersection).

Given k automata $A_1,\dots ,A_k$, each with input alphabet Σ, is ${\bigcap }_{i=1}^{k}L(A_i)=\varnothing$? Parameters are the number of automata k, an upper bound q on the number of states of the automata $A_i$, and the size of Σ.

For (Emptiness of) Intersection, our results are summarized in

Table 2. Intersection; functions refer to exponents of bounding functions.

# of States	Σ	Intersection
		Lower Bound	Upper Bound
2			O(1), i.e., in P
3	unary		O(1), i.e., in P
3	binary		O(1), i.e., in P
3	unbounded	$o(k)$	k	Proposition 2
q	unary	$o(\min (k\sqrt{\log q},\sqrt{q}))$	$\min (k\log q,1.5·q)$	Theorem 3 & Proposition 1
q	binary	$o(\min (k,2^q))$	$\min (k\log q,2^{2q}\log q)$	Proposition 3 & Proposition 4
q	unbounded	$o(k\log q)$	$k\log q$	Proposition 2

, whose entries are to be read similar to those of Table 1.

All these problems are already computationally hard for tally NFAs, i.e., NFAs on unary inputs. Hence, we will study these first, before turning towards larger input alphabets. The classical complexity status of these and many more related problems is nicely surveyed in [7]. The classical complexity status of the mentioned problems is summarized in

Table 3. The classical complexity status of three types of problems on nondeterministic finite automata.

NFA	Unary Inputs	Binary Inputs
Non-Universality	NP-complete	PSPACE-complete
Inequivalence	NP-complete	PSPACE-complete
Intersection Non-emptiness	NP-complete	PSPACE-complete

. Notice that (only) the last problem is also hard on deterministic finite automata.

In the second part of the paper, we are extending our research in two directions: we consider further hard problems on finite automata, more specifically, the question of whether a given DFA accepts an aperiodic language, and questions related to synchronizing words, and we also look at finite automata that work on objects different from strings.

In all the problems we study, we sometimes manage to show that the known or newly presented algorithms are in some sense tight, assuming (S)ETH, while there are also always cases where we can observe some gaps between lower and upper bounds. Without making this explicit in each case, such situations obviously pose interesting question for future research. Also, the mentioned second part of the paper can only be seen as a teaser to look more carefully into computationally hard complexity questions related to automata, expressions, grammars etc. Most of the results have been presented in a preliminary form at the conference CIAA in Seoul, 2016; see [8].

2. Universality, Equivalence, Intersection: Unary Inputs

The simplest interesting question on tally finite automata is the following one. Given an NFA A with input alphabet $\{a\}$, is $L(A)={\{a\}}^{*}$? In [9], the corresponding problem for regular expressions was examined and shown to be CoNP-complete. This problem is also known as NEC (Non-empty Complement). As the reduction given in [9] starts off from 3SAT, we can easily analyze the proof to obtain the following result. In fact, it is often a good strategy to first start off with known NP-hardness results to see how these can be interpreted in terms of ETH-based lower bounds. However, as we can also see with this example, this recipe does not always yield results that match known upper bounds. However, the analysis often points to weak spots of the hardness construction, and the natural idea is to attack these weak spots afterwards. This is exactly the strategy that we will follow in this first problem that we consider in this paper.

We are sketching the construction for NP-hardness (as a reduction from 3SAT as in the paper of Stockmeyer and Meyer) in the following for tally NFAs.

Let F be a given CNF formula with variables $x_1,\dots ,x_n$. F consists of the clauses $c_1,\dots ,c_m$. After a little bit of cleanup, we can assume that each variable occurs at most once in each clause. Let $p_1,\dots ,p_n$ be the first n prime numbers. It is known that $p_n\le (n\ln (n\ln n)))$. To simplify the following argument, we will only use that $p_n\sim n\ln n$, as shown in ([10], Satz, p. 214). If a natural number z satisfies

$$\forall i:1\le i\le n\Rightarrow \left(z\equiv 0\mathrm{mod}{p}_i\vee z\equiv 1\mathrm{mod}{p}_i\right),$$

then z represents an assignment α to $x_1,\dots ,x_n$ with $\alpha (x_i)=z\mathrm{mod}{p}_i$. Then, we say that z satisfies F if this assignment satisfies F. Clearly, if $z\in \{a^j\}{\{a^{p_k}\}}^{*}$ for some $2\le j<p_k$, then z cannot represent any assignment, as $z\mathrm{mod}{p}_k$ is neither 0 nor 1. (This case does not occur for $p_1=2$.) There is a DFA for $\{a^j\}{\{a^{p_k}\}}^{*}$ with $p_k+1\le p_n$ states. Moreover, there is even an NFA $A_0$ for

$$L_0:=\bigcup _{k=2}^n\bigcup _{j=2}^{p_k-1}\{a^j\}{\{a^{p_k}\}}^{*}$$

with at most $n{p}_n\sim n^2\ln n$ many states.

To each clause $c_j$ with variables $x_{i_j(1)},\dots ,x_{i_j(|c_j|)}$ occurring in $c_j$, for a suitable injective index function $i_j:\{1,\dots ,|c_j|\}\to \{1,\dots ,n\}$, there is a unique assignment $\alpha \in {\{0,1\}}^{|c_j|}$ to these variables that falsifies $c_j$. This assignment can be represented by the language

$$L_j:=\{a^{z_{k_j}}\}·{\{a^{p_{i_j(1)}\cdots p_{i_j(|c_j|)}}\}}^{*}$$

with $0\le z_{k_j}<p_{i_j(1)}\cdots p_{i_j(|c_j|)}$ being uniquely determined by $z_{k_j}\equiv \alpha (r)\mathrm{mod}{p}_{i_j(r)}$ for $r=1,\dots ,|c(j)|$. As $p_{i_j(1)}\cdots p_{i_j(|c_j|)}\le p_n^3$ (3SAT), $L_j$ can be accepted by a DFA with at most $p_n^3$ states. Hence, ${\bigcup }_{j=1}^m{L}_j$ can be accepted by an NFA with at most $m{p}_n^3\sim m{n}^3{(\ln n)}^3$ many states. In conclusion, there is an NFA A for ${\bigcup }_{j=0}^m{L}_j$ with at most $m{p}_n^3\sim m{n}^3{(\ln n)}^3$ many states with $L(A)\ne {\{a\}}^{*}$ iff F is satisfiable. For the correctness, it is crucial to observe that if $a^{\ell }\notin L(A)$ for some $\ell \ge p_1\cdots p_n$, then also $a^{\ell \mathrm{mod}(p_1\cdots p_n)}\notin L(A)$. Hence, if $L(A)\ne {\{a\}}^{*}$, then $a^{\ell }\notin L(A)$ for some $\ell <p_1\cdots p_n$. As $L_0\subset L(A)$, ℓ represents an assignment α that does not falsify each clause (by construction of the sets $L_j$), so that α satisfies the given formula. Conversely, if α satisfies F, then α can be represented by an integer z, $0\le z<p_1\cdots p_n$. Now, $a^z\notin L_0$ as it represents an assignment, but neither $a^z\in L_j$ for any $j>0$, as $\alpha (c_j)=1$. Observe that in the more classical setting, this proves that Non-Universality is NP-hard.

We like to emphasize a possible method to ETH-based results, namely, analyzing known NP-hardness reductions first and then refining them to get improved ETH-based results.

Unless ETH fails, for any $ϵ\in \left(0,\frac{1}{4}\right)$, there is no $O^{*}\left(2^{o(q^{1/4-ϵ})}\right)$-time algorithm for deciding, given a tally NFA A on q states, whether $L(A)={\{a\}}^{*}$.

Assume that, for any $ϵ>0$, there was an $O^{*}\left(2^{o(q^{1/4-ϵ})}\right)$-time algorithm ${\mathcal{A}}_{ϵ}$ for deciding, given a tally NFA A on q states, whether $L(A)={\{a\}}^{*}$. Consider some 3SAT formula with n variables and m clauses. We can assume (by the Sparsification Lemma) that this 3SAT instance is sparse. We already described the construction of [9] above. So, we can obtain in polynomial time an NFA with $q\approx m{n}^3{(\ln n)}^3$ many states as an instance of Universality. This instance can be solved in time $O^{*}(2^{o(q^{1/4-ϵ})})$ by ${\mathcal{A}}_{ϵ}$. Hence, ${\mathcal{A}}_{ϵ}$ can be used to solve the given 3SAT instance in time

$$O^{*}\left(2^{o(q^{1/4-ϵ})}\right)=O^{*}\left(2^{o({(m{(n·\ln n)}^3)}^{1/4-ϵ})}\right)\subseteq O^{*}\left(2^{o({((m+n)·\ln {(m+n)}^4)}^{1/4-ϵ})}\right)\subseteq O^{*}\left(2^{o(n+m)}\right),$$

in the interesting range of $ϵ\in \left(0,\frac{1}{4}\right)$, which contradicts ETH. To formally do the necessary computations in the previous theorem (and similar results below), dealing with logarithmic terms in the exponent, we need to understand the correctness of some computations in the $o(·)$ notation. We exemplify such a computation in the following.

Lemma 1.

$\forall ϵ\in (0,1)$: $o({(n\log n)}^{ϵ})\subseteq o(n)$.

Proof. 

This statement can be seen by the following line, using the rule of l’Hospital.

$$\underset{n\to \infty }{\lim }\frac{{(n\ln n)}^{ϵ}}{n}=\underset{n\to \infty }{\lim }\frac{ϵ{(1+\ln n)}^{ϵ-1}}{1}=\underset{n\to \infty }{\lim }\frac{ϵ}{{(1+\ln n)}^{1-ϵ}}=0$$

Notice that $1-ϵ\in (0,1)$ by our assumption. ☐

We are now trying to strengthen the assertion of the previous theorem. There are actually two weak spots in the mentioned reduction: (a) The ϵ-term in the statement of the theorem is due to logarithmic factors introduced by encodings with prime numbers; however, the encodings suggested in [9] leave rather big gaps of numbers that are not coding any useful information. (b) The $\sqrt[4]{·}$-term is due to writing down all possible reasons for not satisfying any clause, which needs about $\tilde{O}(m{n}^3)$ many states (ignoring logarithmic terms) on its own; so, we are looking for a problem that allows for cheaper encodings of conflicts. To achieve our goals, we need the following theorem, see [5], Theorem 14.6.

Theorem 1.

Unless ETH fails, there is no $O^{*}\left(2^{o(m+n)}\right)$-time algorithm for deciding if a given m-edge n-vertex graph has a (proper) 3-coloring.

As it seems to be hard to find proof details anywhere in the literature, we provide them in the following.

Proof. 

Namely, in some standard NP-hardness reduction (from 3SAT via 3-Not-All-Equal-SAT), we could first sparsify the given 3SAT instance, obtaining an instance with N variables and M clauses. Also, we can assume that $N\in O(M)$. The 3-NAE-SAT instance would replace each clause $c={\ell }_1\vee {\ell }_2\vee {\ell }_3$ of the 3SAT instance by $c^{\prime }={\ell }_1\vee {\ell }_2\vee x_c$ and $c^{\prime }={\ell }_3\vee \neg x_c$, where $x_c$ is a special new variable. Hence, this instance has $N^{\prime }=N+M$ variables and $M^{\prime }=2M$ clauses. The 3-coloring instance $G=(V,E)$ that we then obtain has $2N^{\prime }+3$ vertices and $3N^{\prime }+3$ edges in the variable gadgets, as well as $6M^{\prime }$ vertices and $9M^{\prime }$ edges in the clause gadgets, plus $3M^{\prime }$ edges to connect the clause with the variable gadgets. Hence, in particular $\left|E\right|\in O(M)$. This rules out $O^{*}\left(2^{o(m)}\right)$-time algorithms for solving 3-Coloring on m-edge graphs. ☐

The previous result can be used, together with the sketched ideas, to prove the following theorem.

Theorem 2.

Unless ETH fails, there is no $O^{*}\left(2^{o(q^{1/3})}\right)$-time algorithm for deciding, given a tally NFA A on q states, whether $L(A)={\{a\}}^{*}$.

Proof. 

We are now explaining a reduction from 3-Coloring to tally NFA Universality. Let $G=(V,E)$ be a given graph with vertices $v_1,\dots ,v_n$. E consists of the edges $e_1,\dots ,e_m$. Let $P=\{p\mid p$ is a prime and $2n\le p<4n\}$. To simplify the following argument, we will only use that the expected number of primes below n is at least $n/\ln n$, as shown in [10], Satz, p. 214. Hence we can assume P contains at least $n/\log n$ primes $p_1,\dots ,p_l$ for $l=\lceil n/\log n\rceil$. (For the sake of clarity of presentation, we ignore some small multiplicative constants here and in the following.)

We group the vertices of V into blocks of size $\log n$. A coloring within such a block can be encoded by a number between 0 and $3^{\log n}\le 2n$. Hence, a coloring is described by an l-tuple $z_1,\dots ,z_l$ of numbers.

If a natural number z satisfies

$$\forall i:1\le i\le n/\log n\Rightarrow z\equiv z_i\mathrm{mod}{p}_i,$$

where $z_i$ is representing the encoding of a block, then z is an encoding of a coloring of some vertex from V.

There is a DFA for $\{a^j\}{\{a^{p_k}\}}^{*}$ with at most $4n$ states, where j is number that does not represent a valid coloring of the k-th block. Similarly, there is also a DFA for ${\bigcup }_{j\mathrm{is}\mathrm{not}\mathrm{valid}}\{a^j\}{\{a^{p_k}\}}^{*}$ with this number of states (only the set of final states changes). Moreover, there is even an NFA $A_0$ for

$$L_0:=\bigcup _{k=1}^l\bigcup _{j\mathrm{is}\mathrm{not}\mathrm{valid}}\{a^j\}{\{a^{p_k}\}}^{*}$$

with at most $l{p}_{n+1}\sim n^2$ states.

To formally describe invalid colorings, we also need a function $\mathbf{blk}$ that associates the block number to a given vertex index (where the coloring information can be found), and partial functions ${\mathbf{col}}_j:\{0,\dots ,p_{\mathbf{blk}(j)}-1\}\to \{0,1,2\}$ for each vertex index j, yielding the coloring of vertex $v_j$. We can cyclically extend ${\mathbf{col}}_j$ by setting ${\mathbf{col}}_j(n):={\mathbf{col}}_j(n\mathrm{mod}{p}_{\mathbf{blk}(j)})$ whenever ${\mathbf{col}}_j$ is defined.

For each edge $e_j$ with end vertices $v_{\alpha (j)},v_{\omega (j)}$ with $1\le \alpha (j)<\omega (j)\le n$ there are three colorings of $\{v_{\alpha (j)},v_{\omega (j)}\}$ that violate the properness condition. We can capture such a violation in the language $L_j:=\{a^z:{\mathbf{col}}_{\alpha (j)}(z)={\mathbf{col}}_{\omega (j)}(z)\}$. $L_j$ is regular, as

$$L_j=M_j·{\{a^{p_{\mathbf{blk}(\alpha (j))}·p_{\mathbf{blk}(\omega (j))}}\}}^{*},$$

with

$$M_j:=\{a^z:0\le z<p_{\mathbf{blk}(\alpha (j))}·p_{\mathbf{blk}(\omega (j))}\wedge {\mathbf{col}}_{\alpha (j)}(z)={\mathbf{col}}_{\omega (j)}(z)\}$$

being finite, as $p_{\mathbf{blk}(\alpha (j))}{p}_{\mathbf{blk}(\omega (j))}\le 16n^2$. So, $L_j$ can be accepted by a DFA with at most $n^2$ states, ignoring constant factors. Hence, ${\bigcup }_{j=1}^m{L}_j$ can be accepted by an NFA with at most $m{n}^2$ many states. In conclusion, there is an NFA A for ${\bigcup }_{j=0}^m{L}_j$ with at most $m{n}^2$ many states with $L(A)\ne {\{a\}}^{*}$ iff G is 3-colorable.

For the correctness, it is crucial to observe that if $a^r\notin L(A)$ for some $r\ge p_1\cdots p_l$, then also $a^{r\mathrm{mod}(p_1\cdots p_l)}\notin L(A)$. Hence, if $L(A)\ne {\{a\}}^{*}$, then $a^r\notin L(A)$ for some $r<p_1\cdots p_l$. As $L_0\subset L(A)$, r represents a coloring c that does not color any edge improperly (by construction of the sets $L_j$). Conversely, if c properly colors G, then c can be represented by an integer z, $0\le z<p_1\cdots p_l$. Now, $a^z\notin L_0$ as it represents a coloring, but neither $a^z\in L_j$ for any $j>0$, as $c(v_{\alpha (j)})\ne c(v_{\omega (j)})$.

Observe that in the more classical setting, this proves that Universality is CoNP-hard.

As ETH rules out $O^{*}\left(2^{o(n+m)}\right)$-algorithms for solving 3-Coloring on m-edge graphs with n vertices, we can assume that we have ${(m+n)}^3$ as an upper bound on the number q of states of the NFA instance constructed as described above. If there would be an $O^{*}\left(2^{o(q^{1/3})}\right)$-time algorithm for Universality of q-state tally NFAs, then we would find an algorithm for solving 3-Coloring that runs in time $O^{*}\left(2^{o({({(n+m)}^3)}^{1/3})}\right).$ This would contradict ETH. ☐

How good is this improved bound? There is a pretty easy algorithm to solve the universality problem. First, transform the given tally NFA into an equivalent tally DFA, then turn it into a DFA accepting the complement and check if this is empty. The last two steps are clearly doable in linear time, measured in the size of the DFA obtained in the first step. For the conversion of a q-state tally NFA into an equivalent $q^{\prime }$-state DFA, it is known that $q^{\prime }=2^{\mathrm{\Theta }(\sqrt{q\log q})}$ is possible but also necessary [11]. The precise estimate on $q^{\prime }$ is

$$F(q)=\max \{lcm(x_1,\dots ,x_r)\mid x_1,\dots ,x_r\ge 1\wedge x_1+\cdots +x_r=q\},$$

also known as Landau’s function. It is tightly related to the prime number estimate for $p_n$ we have already seen. So, in a sense, the ETH bound poses the question if there are other algorithms to decide universality for tally NFAs, radically different from the proposed one, not using DFA conversion first. Let us mention that there have been indeed proposal for different algorithms to test universality for NFAs; we only refer to [12], but we are not aware of any accompanying complexity analysis that shows the superiority of that approach over the classical one. Conversely, it might be possible to tighten the upper bound.

Notice that this problem is trivial for tally DFAs by state complementation and hence reduction to the polynomial-time solvable emptiness problem.

We now turn to the equivalence problem for tally NFAs. As an easy corollary from Theorem 2, we obtain the next result.

Corollary 1.

Unless ETH fails, there is no $O^{*}\left(2^{o(q^{1/3})}\right)$-time algorithm for deciding equivalence of two NFAs $A_1$ and $A_2$ on at most q states and input alphabet $\{a\}$.

We are finally turning towards Tally-DFA-Intersection and also towards Tally-NFA-Intersection. CoNP-completeness of this problem, both for DFAs and for NFAs, was indicated in [13], referring to [9,14]. We make this more explicit in the following, in order to also obtain some ETH-based results.

Theorem 3.

Let k tally DFAs $A_1,\dots ,A_k$ with input alphabet $\{a\}$ be given, each with at most q states. If ETH holds, then there is no algorithm with that decides if ${\bigcap }_{i=1}^{k}L(A_i)=\varnothing$ in time $O^{*}\left(2^{o(\min (k\sqrt{\log q},\sqrt{q}))}\right)$.

Proof. 

We revisit our previous reduction (from an instance $G=(V,E)$ of 3-Coloring with $\left|V\right|=n$ and $\left|E\right|=m$ to some NFA instance for Universality), which delivered the union of many simple sets $L_i$, each of which can be accepted by a DFA $A_i$ whose automaton graph is a simple cycle. These DFAs $A_i$ have $O(n^2)$ states each. The complements $\overline{L_i}$ of these languages can be also accepted by DFAs $\overline{A_i}$ of the same size. Ignoring constants, originally the union of $O(n+m)$ many such sets was formed. Considering now the intersection of the complements of the mentioned simple sets, we obtain a lower bound if $k\ge n+m$ and $q\ge n^2$ or, a bit weaker, if $q\ge {(n+m)}^2$.

Finally, we can always merge two automata into one using the product construction. This allows us to halve the number of automata while squaring the size of the automata. This trade-off allows to optimize the values for k and q.

Assume we have an algorithm with running time $2^{o(k\sqrt{\log q})}$, then we get can reduce 3-Coloring with m edges to intersection of $(n+m)/\log (n+m)$ automata each of size bounded by ${({(n+m)}^2)}^{\log (n+m)}=2^{2{\log }^2(n+m)}$, and hence solving it in time $2^{o((n+m)/\log (n+m)·\sqrt{2{\log }^2(n+m)})}=2^{o(n+m)}$, a contradiction. Similarly, there can be no algorithm with running time $2^{o(\sqrt{q})}$. ☐

Proposition 1.

Let k tally DFAs $A_1,\dots ,A_k$ with input alphabet $\{a\}$ be given, each with at most q states. There is an algorithm that decides if ${\bigcap }_{i=1}^{k}L(A_i)=\varnothing$ in time $O^{*}\left(2^{\min (k\log q,1.5·q)}\right)$.

Proof. 

For the upper bound there are basically two algorithms; the natural approach to solve this intersection problem would be to first build the product automaton, which is of size $q^k$, and then solve the emptiness problem in linear time on this device. This gives an overall running time of $O^{*}\left(q^k\right)=O^{*}\left(2^{k\log q}\right)$; also see Theorem 8.3 in [15]. On the other hand, we can test all words up to length $q+2^{1.5q}$. As each DFA has at most q states in each DFA, processing a word enters a cycle in at most q steps. Also the size of the cycle in each DFA is bounded by q. The least common multiple of all integers bounded by q, i.e., $e^{\psi (q)}$, where ψ is the second Chebyshev function, is bounded by $2^{1.5q}$; see Propositions 3.2 and 5.1. in [16]. This yields an upper bound $O^{*}\left(2^{1.5q}\right)$ of the running time. ☐

Hence in the case where the exponent is dominated by k, the upper and lower bound differ by a factor of $\sqrt{\log q}$, and in the other case by a factor of $\sqrt{q}$.

Remark 1.

From the perspective of parameterized complexity, we could also (alternatively) only look at the parameter q, as in the case of DFAs $k\le q{(2q)}^q$ (after some cleaning; as there are no more than $q^q$ many functions $Q\to Q$ available as state transition functions, multiplied by $2^q$ choices of final state sets, as well as by the q choices of initial states); the corresponding bound for NFAs is worse. However, the corresponding $O^{*}\left(q^{q{(2q)}^q}\right)$ algorithm for solving Tally-DFA-Intersection for q-state DFAs is far from practical for any $q>2$. We can slightly improve our bound on k by observing that from the $2^q$ potential choices of final state sets for each of the $q^{q+1}$ choices of transition functions and initial states, at most one is relevant for the question at hand, as the intersection of languages accepted by DFAs with identical transition functions and initial states is accepted by one DFA with the same transition function and initial state whose set of final states is just the intersection of the sets of final states of the previously mentioned DFAs; if this intersection turns out to be empty, then also the intersection of the languages in question is empty. Hence, we can assume that $k\le q^{q+1}$. A further improvement is due to the following modified algorithm: First, we construct DFAs ${\overline{A}}_1,\dots ,{\overline{A}}_k$ that accept the complements of the languages accepted by $A_1,\dots ,A_k$. Then, we build an NFA $\overline{A}$ that accepts ${\bigcup }_{i=1}^{k}L({\overline{A}}_i)$. Notice that $\overline{A}$ has about at most $qk+1\le q^{q+2}$ states by using some standard construction. If we check the corresponding DFA for Universality, this would take, altogether, time $O^{*}\left(2^{\sqrt{q^{q+2}(q+2)\log q}}\right)$ for unary input alphabets.

3. The Non-Tally Case

In the classical setting, the automata problems that we study are harder for binary (and larger) input alphabet sizes (PSPACE-complete; for instance, see [17]). Also, notice that the best-known algorithms are also slower in this case. This should be reflected in the lower bounds that we can obtain for them (under ETH), too.

Let us describe a modification (and in a sense a simplification) of our reduction from 3-Coloring. Let $G=(V,E)$ be an undirected graph. We construct an NFA A (on a ternary alphabet $\mathrm{\Sigma }=\{a,b,c\}$ for simplicity) as follows. Σ corresponds to the set of colors with which we like to label the vertices of the graph. The state set is $\{s\}\cup (E\times V\times \mathrm{\Sigma })$. W.l.o.g., $V=\{v_1,\dots ,v_n\}$. For $e=uv$ and $x,y\in \mathrm{\Sigma }$, we add the following transitions.

• $s\stackrel{x}{⟶}(e,v_1,y)$ if $v_1\notin \{u,v\}$ or if $(u=v_1\vee v=v_1)\wedge y=x$;
• $(e,v_i,y)\stackrel{x}{⟶}(e,v_{i+1},y)$ (for $i=1,\dots ,n-1$) if $v_{i+1}\notin \{u,v\}$ or if $(u=v_{i+1}\vee v=v_{i+1})\wedge y=x$;
• $(e,v_n,y)\stackrel{x}{⟶}s$.

Moreover, s is the only initial and all states are final states. If $z=z_1{z}_2\cdots z_{n+1}\in L(A)$, then this corresponds to a coloring $c:V\to \mathrm{\Sigma }$ via $c(v_k)=z_k$, $k=1,\dots ,n$, that is not proper. Namely, z drives the A through the states s, $(e,v_1,y)$, $(e,v_2,y)$, …, $(e,v_n,y)$, s for some $e=v_i{v}_j\in E$ and some $y\in \mathrm{\Sigma }$. By construction, this is only possible if $c(v_i)=c(v_j)=z_i=z_j=y$, establishing the claim. Conversely, if $c:V\to \mathrm{\Sigma }$ is a coloring that is improper, then there is an edge, say, $e=v_i{v}_j$, such that $c(v_i)=c(v_j)=y$ for some $y\in \mathrm{\Sigma }$. Then, $z:=z_1{z}_2\cdots z_{n}a\in L(A)$, where $z_k=c(v_k)$, $k=1,\dots ,n$. Namely, this z will drive A through the states s, $(e,v_1,y)$, $(e,v_2,y)$, …, $(e,v_n,y)$, s.

Hence, for the constructed automaton A, $L(A)\ne {\mathrm{\Sigma }}^{*}$ if and only if there is some proper coloring $c:V\to \mathrm{\Sigma }$ of G. For such a proper coloring c, $z:=z_1{z}_2\dots z_{n}a\notin L(A)$, where $z_k=c(v_k)$, $k=1,\dots ,n$.

As $m\ge n$, the number of states of A is $O(m^2)$. So, we can conclude a lower bound of the form $O^{*}\left(2^{o(\sqrt{q})}\right)$. We are now further modifying this construction idea to obtain the following tight bound.

Theorem 4.

Assuming ETH, there is no algorithm for solving Universality for q-state NFAs with binary input alphabets that runs in time $O^{*}\left(2^{o(q)}\right)$.

Proof. 

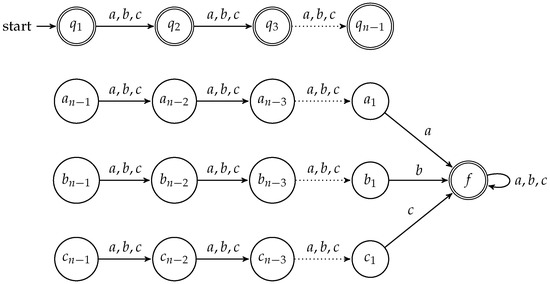
As we can encode the union of all the NFAs above more succinct we get a better bound. Let $G=(V,E)$ be an undirected graph, and $V=\{v_1,\dots ,v_n\}$ as above. Let $\mathrm{\Sigma }=\{a,b,c\}$ represent three colors. Then there is a natural correspondence of a word in ${\mathrm{\Sigma }}^n$ to a coloring of the graph, where the i-th letter in the words corresponds to the color of $v_i$. We construct an automaton with $3(n-1)+1$ states, as sketched in Figure 1. Notice that this figure only shows the backbone of the construction. Additionally, for each edge $(v_i,v_j)$ with $i<j$ in the graph, we add three types of transitions to the automaton: $q_i\stackrel{a}{⟶}{a}_{j-i}$, $q_i\stackrel{b}{⟶}{b}_{j-i}$, $q_i\stackrel{c}{⟶}{c}_{j-i}$. These three transitions are meant to reflect the three possibilities to improperly color the given graph due to assigning $v_i$ and $v_j$ the same color. Inputs of length n encode a coloring of the vertices. First notice that the automaton will accept every word of length not equal to n. Namely, words shorter than n can drive the automaton into one of the states $q_1$ through $q_{n-1}$. Also, as argued below, the automaton can accept all words longer than n, starting with an improper coloring coding of the word, as this can drive the automaton into state f. Further, our construction enables the check of an improper coloring. A coloring is improper if to vertices that are connected have the same color, so we should accept a word $w=w_1\dots w_n$ iff $i<j$ and $(i,j)\in E$ and $w_i=w_j$. Pick such a word and assume, without a loss of generality, that $w_i=a$. Then the automaton will accept w, since the additional edge $q_i\stackrel{a}{⟶}{a}_{j-i}$ allows for an accepting run terminating in the state f. Note that the automaton accepts all words of length at most $n-1$. Also, it accepts a word of length at least n iff the prefix of length n corresponds to a bad coloring. Hence the automaton accepts all words iff all colorings are bad.

The converse direction is also easily seen. Assume there is a valid coloring represented by a word $w_1\dots w_n$. Assume by contradiction that this word is accepted by the automaton. As the word has length n an accepting run has to terminate in f, and so one of the edges added to the automaton backbone as shown in Figure 1 has to be part of this run. Assume, without a loss of generality, that this is the edge $q_i\stackrel{a}{⟶}{a}_{j-i}$. Then $w_i=a$, as the edge was chosen and since this run leads to f, also the letter at position $i+(j-i)$ has to equal a. However, as $(i,j)\in E$ this is not valid coloring, hence the assumption that the word is accepted by the automaton was false. Hence, if there is a valid coloring the automaton does not accept all words.

It is simple to change the construction given above to get away with binary input alphabets (instead of ternary ones), for instance, by encoding a as 00, b as 01 and c as 10. ☐

We are now turning towards DFA-Intersection and also to NFA-Intersection. In the classical perspective, both are PSPACE-complete problems. An adaptation of our preceding reduction from 3-Coloring, considering $\left|E\right|$ DFAs each with $3\left|V\right|+1$ states obtained from a graph instance $(V,E)$, yields the next result, where upper and lower bounds perfectly match.

In the following proposition we have parameters k the number of automata, q the maximum size of these automata, and n the input length. The parameters $k,q$ are both upper bounded by n. Recall that the notation $O^{*}(2^{f(k,q)})$ drops polynomial factors in n even though n is not explicitly mentioned in the expression.

Proposition 2.

There is no algorithm that, given k DFAs (or NFAs) $A_1,\dots ,A_k$ with arbitrary input alphabet, each with at most q states, decides if ${\bigcap }_{i=1}^{k}L(A_i)=\varnothing$ in time $O^{*}\left(2^{\log (q)·o(k)}\right)$ unless ETH fails. Conversely, there is an algorithm that, given k DFAs (or NFAs) $A_1,\dots ,A_k$ with arbitrary input alphabet, each with at most q states, decides if ${\bigcap }_{i=1}^{k}L(A_i)\ne \varnothing$ in time $O^{*}\left(2^{\log (q)·k}\right)$.

Proof. 

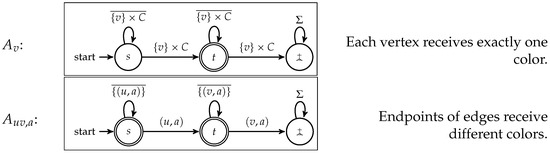
The hardness is by adaptation of the the 3-Coloring reduction we gave for Universality. For parameters k and q, we take a graph with $\left|V\right|+\left|E\right|=k{\log }_{3}q=\mathrm{\Theta }(k\log q)$. In this proof, we neglect the use of some ceiling functions for the sake of readability. For the DFAs, choose the alphabet $\mathrm{\Sigma }=V\times C$, $C=\{1,2,3\}$. The states are s, t, . For each vertex v, we define the DFA $A_v$, and for each edge $uv$ and each color a, we define the DFA $A_{uv,a}$, as described in Figure 2. Clearly, we have $\left|V\right|+\left|E\right|$ many of these DFAs $A_i$.

We can compute the intersection for each block of ${\log }_{3}q$ automata into a single DFA in polynomial time (with respect to q). This can be most easily seen by performing a multi-product construction. Hence, given a block of ${\log }_{3}q$ automata $A_i$ with transition function ${\delta }_i$, we output the new block automaton $A_B$ whose set of states $Q_B$ corresponds to all (q many) ternary numbers, interpreted as $({\log }_{3}q)$-tuples in {s, t, }${}^{{\log }_{3}q}$. We output a transition in the table of ${\delta }_B$ in the following situation:

$${\delta }_B((p_1,\dots ,p_{{\log }_{3}q}),(v,a))=({\delta }_1(p_1,(v,a)),\dots ,{\delta }_{{\log }_{3}q}(p_{{\log }_{3}q},(v,a))).$$

So, we have to look up $3q\left|\mathrm{\Sigma }\right|$ times the tables of the $A_i$’s, where each of the ${\log }_{3}q$ look-ups takes roughly $3\left|\mathrm{\Sigma }\right|$ time.

This way, we obtain an automaton with q states and we reduce the number of DFAs to $k=(|V|+\left|E\right|)/{\log }_{3}q$. Hence, we got k DFAs each with q states. If there was an algorithm solving DFA-Intersection in time $O^{*}\left(2^{\log (q)o(k)}\right)$, then this would result in an algorithm solving 3-Coloring in time $O^{*}\left(2^{o(|V|+|E|)}\right)$, contradicting ETH.

Conversely, given k DFAs $A_1,\dots ,A_k$ with arbitrary input alphabet, each with at most q states (q is fixed), we can turn these into one DFA with $O^{*}(q^k)$ states by the well-known product construction, which allows us to solve the DFA-Intersection question in time $O^{*}(2^{O(k\log q)})$. ☐

Remark 2.

The proof of the previous theorem also implies that no such algorithm even if restricted to any infinite subset of tuples $(q,k)\subseteq \{3,4,\dots \}\times \{1,2,3,\dots \}$ in time $O^{*}(2^{\log (q)o(k)})$ can exist, unless ETH fails. Especially, if q is fixed to a constant greater than 2, no algorithm in time $O^{*}\left(2^{o(k)}\right)$ can exist, unless ETH fails.

We can encode the large alphabet of the previous construction into the binary one, but we get a weaker result. In particular, the DFAs $A_v$ and $A_{uv,a}$ in this revised construction have $O(\log n)$ states, and not constantly many as before. This means that we have to spell out the paths between the states s and t, but this is not necessary with the trash state .

Proposition 3.

There is no algorithm that, given k DFAs $A_1,\dots ,A_k$ with binary input alphabet, each with at most q states, decides if ${\bigcap }_{i=1}^{k}L(A_i)=\varnothing$ in time $O^{*}\left(2^{o(k)}\right)$ or $O^{*}\left(2^{o(2^q)}\right)$, unless ETH fails.

Proof. 

We reduce this case to the case of unbounded alphabet size. Assume we are given k DFAs $A_1,\dots ,A_k$ over the alphabet Σ, where $\left|\mathrm{\Sigma }\right|=l$. We encode each letter of Σ by a word of length $\lceil \log l\rceil$ (block code) over the alphabet $\{0,1\}$.

In general, when converting an automaton from an alphabet Σ to an alphabet $\{0,1\}$, the size of the automaton might increase by a factor of $\left|\mathrm{\Sigma }\right|$, as one might need to build a tree distinguishing all words of length $\log l$.

But we already know that, for the unbounded alphabet size, the lower bound is achieved by using only the automata from that proof (see Figure 2). These automata are special, as there are at most $\left|C\right|=3$ many edges leaving each state, while all other edges loop.

Hence, we only increase the number of states (and also edges) by a factor or $4\log l$. ☐

The following proposition gives a matching upper bound:

Proposition 4.

There is an algorithm that, given k DFAs $A_1,\dots ,A_k$ with binary input alphabet, each with at most q states, decides if ${\bigcap }_{i=1}^{k}L(A_i)=\varnothing$ in time $O^{*}\left(2^{\log (q)·\min (k,2^{2q})}\right)$.

Proof. 

We will actually give two algorithms that solve this problem. One has a running time of $O^{*}\left(2^{k\log q}\right)$ and one a running time of $O^{*}\left(2^{2^q·\log q}\right)$. The result then follows.

(a) We can first construct the product automaton of the DFAs $A_1,\dots ,A_k$, which is a DFA with at most $q^k=2^{k\log q}$ many states. In this automaton, one can test emptiness in time linear in the number of states.

(b) For the other algorithm, notice that for a fixed number q, a large number k of automata seems not to increase the complexity of the intersection problem, as there are only finitely many different DFAs with at most q many states. Intersection is easy to compute for DFAs with the same underlying labeled graph. On binary alphabets, each state has exactly two outgoing edges. Thus, there are $q^2$ possible choices for the outgoing edges of each state. Hence in total there are ${(q^2)}^q=q^{2q}$ different such DFAs. By merging first all DFAs with the same graph structure we can assume that $k\le q^{2q}$. We can now proceed as in (a). ☐

Let us conclude this section with a kind of historical remark, linking three papers from the literature that can also be used as a starting point for ETH-based results on DFA-Intersection. Wareham presented several reductions when discussing parameterized complexity issues for DFA-Intersection in [15]. In particular, Lemma 6 describes a reduction from Dominating Set that produces from a given n-vertex graph (and parameter $\ell \ge n$) a set of $n+1$ DFAs, each of at most $\ell +1$ states and with an n-letter input alphabet, so that we can rule out $O^{*}(2^{o(\min (q,k))})$ algorithms for DFA-Intersection in this way. In the long version of [18], it is shown that SUBSET SUM, parameterized by the number n of numbers, does not allow for an algorithm running in time $O^{*}\left(2^{o(n)}\right)$, unless ETH fails. Looking at the proof, it becomes clear that (under ETH) there is also no algorithm $O^{*}\left(2^{o(N)}\right)$-algorithm for Subset Sum, parameterized by the maximum number N of bits per number. Karakostas, Lipton and Viglas, apparently unaware of the ETH framework at that time, showed in [19] that an $O^{*}\left(q^{o(k)}\right)$-algorithm for DFA-Intersection would entail a $O^{*}\left(2^{ϵ·N}\right)$-algorithms for Subset Sum, for any $ϵ>0$. Although the latter condition looks rather like SETH, it is at least an indication that we could also make use of other reductions in the literature to obtain the kinds of bounds we are looking for. Also, Wehar showed in [20] that there is no $O^{*}\left(q^{o(k)}\right)$-algorithm for DFA-Intersection, unless NL equals P. This indicates another way of showing lower bounds, connecting to questions of classical Complexity Theory rather than using (S)ETH.

4. Related Problems

Our studies so far only touched the tip of the iceberg. Let us mention and briefly discuss at least some related problems for finite automata in this section.

4.1. The Aperiodicity Problem

Recall that a regular language is called star-free (or aperiodic) if it can be expressed, starting from finite sets, with the Boolean operations and with concatenation. (So, Kleene star is disallowed in the set constructions, in contrast to the ‘usual’ form of regular expressions.) We denote the subclass of the regular languages consisting of the star-free languages by $\mathsf{SF}$.

It is known that a language is star-free if and only it its syntactic monoid is aperiodic [21], that is, it does not contain any nontrivial group. Here we will use a purely automata-theoric characterization: A language accepted by some minimum-state DFA A is star-free iff for every input word w, for every integer $r\ge 1$ and for every state q, ${\delta }^{*}(q,w^r)=q$ implies ${\delta }^{*}(q,w)=q$.

This allows a minimal automaton of a star-free language to contain a cycle, but if the non-empty word w along a cycle starting at q is a power of another non-empty word u, i.e., $w=u^r$ for some $r\ge 2$, then u also forms a cycle starting at q. For example, the language ${\{aaa\}}^{*}$ is not aperiodic as $a^3$ forms a cycle starting at any state of the minimal automaton, but a does not. However, ${\{abc\}}^{*}$ is aperiodic, as $abc,bca,cab$ are the only cycles in the minimal automaton (except for cycles starting at the sink state).

For this class $\mathsf{SF}$ (and in fact for any other subregular language class), one can ask the following decision problem. Given a DFA A, is $L(A)\in \mathsf{SF}$? This problem (called Aperiodicity in the following) was shown to be PSPACE-complete by Cho and Huynh in [22]. It relies on the following characterization of aperiodicity: Cho and Huynh present a reduction that first (again) proves that the DFA-Intersection-Nonemptiness is PSPACE-complete (by giving a direct simulation of the computations of a polynomial-space bounded TM) and then show how to alter this reduction in order to obtain the desired result. Unfortunately, this type of reductions is not very useful for ETH-based lower-bound proofs. However, in an earlier paper, Stern [23] proved that Aperiodicity is CoNP-hard. His reduction is from 3SAT (on n variables and m clauses), and it produces a minimum-state DFA with $O(nm)$ many states. Hence, we can immediately conclude a lower bound of $O\left(2^{o(\sqrt{q})}\right)$ for Aperiodicity on q-state DFAs. This can be improved as follows.

The basic idea of the proof of the next proposition is to reduce the intersection problem (in a restricted version) to aperiodicity. Given language $L_1,L_2,\dots ,L_k$, consider the language $L={(L_1\$L_2\$\dots \$L_k\$)}^{*}$, and let A be its minimal automaton. One direction is easy: if the intersection of the languages $L_1,\dots ,L_k$ contains a word u, then ${(u\$)}^k$ forms a cycle in A starting at the initial state, but $u\$$ does not. This gives the idea to show that if there is a word w in the intersection, then the language L is not aperiodic. The other direction is more involved and requires that the languages $L_1,\dots ,L_k$ are themselves aperiodic, and that k is a prime.

Theorem 5.

Assuming ETH, there is no algorithm for solving Aperiodicity for q-state DFAs on arbitrary input alphabets that runs in time $O\left(2^{o(q)}\right)$.

Proof. 

We will show this by reducing a restricted version of the intersection problem to Aperiodicity. Proposition 2 is stated only for general automata, but as the hardness part of the proof only uses automata which are aperiodic, the following claim holds:

Claim 1.

Let $q\ge 3$ be fixed. Let $L_1,\dots ,L_k$ be star-free languages given by their minimal automata $A_1,\dots ,A_k$ over some alphabet Σ, where the number of states of each $A_i$ is bounded by q. Then there is no algorithm deciding if ${\bigcap }_{i=1}^k{L}_i=\varnothing$ in time $O\left(2^{\log (q)·o(k)}\right)$ unless ETH fails.

We will use the claim only for $q=3$.

Let $L_1,\dots ,L_k$ be star-free languages given by their minimal automata $A_1,\dots ,A_k$, where $A_1=(\mathrm{\Sigma },Q_1,q_1^{\prime },F_1,{\delta }_1)$ and for $i\in \{2,\dots ,k\}$ we let $A_i=(\mathrm{\Sigma },Q_i,q_i,F_i,{\delta }_i)$. (For technical reasons explained later, the initial state of $A_1$ is $q_1^{\prime }$ whereas the initial states of the other $A_i$ are called $q_i$.) Without a loss of generality, we can assume that k is a prime. If not, one can simply add $L_k$ multiple times to the list of automata, until the length of the list is a prime. Moreover, we can assume that the state alphabets satisfy, for all $1\le i,j\le k$, $Q_i\cap Q_j\ne \varnothing \Rightarrow i=j$, i.e., the state alphabets are pairwise disjoint.

We let

$$L={(L_1\$L_2\$\dots \$L_k\$)}^{*}$$

and our main goal will be to show that L is star-free if and only if ${\bigcap }_{i=1}^k{L}_i=\varnothing$. This will complete the proof, as the number of states for an automata recognizing A can be bounded by $k{\max }_i\left|Q_i\right|+2=O(k)$ by the construction given below, and as by the reduction no algorithm deciding Aperiodicity in time $O\left(2^{o(k)}\right)$ can exist unless ETH fails.

If one of the $L_i$ is empty, a property that can be tested in linear time, then the intersection is empty and $L={\varnothing }^{*}$ hence is also star-free. So from now on, we assume that for all $i\in \{1,\dots ,k\}$, we have $L_i\ne \varnothing$.

In the following, we will first give an explicit construction of the minimal automaton A of L. We use the characterization from above that A is star-free iff for every input w and every integer $r\ge 1$ and every state q, ${\delta }^{*}(q,w^r)=q$ implies ${\delta }^{*}(q,w)=q$.

First we show the “easy direction”: given a word $\tilde{w}$ in the intersection, $w=\tilde{w}\$$, q being the initial state of A, and $r=k$, the condition for being aperiodic fails. Then we proceed with the “hard direction” given a word w and an integer $r\ge 1$ and a state q of A such that ${\delta }^{*}(q,w^r)=q$ and ${\delta }^{*}(q,w)\ne q$ implies that the maximal prefix of w in ${\mathrm{\Sigma }}^{*}$ is in the intersection ${\bigcap }_{i=1}^k{L}_i$, and hence the intersection is non-empty.

Step 1: Construction of the minimal automaton of L

The idea is to construct an automaton over the alphabet $\mathrm{\Sigma }\cup \{\$\}$, $\$\notin \mathrm{\Sigma }$, which is basically a large cycle consisting of the automata $A_i$. For $i\in \{1,\dots ,k-1\}$, we connect the accepting state(s) of $A_i$ to the initial state $q_{i+1}$ of $A_{i+1}$ via an edge labeled $, and finally we connect the accepting state(s) of $A_k$ to the initial state $q_1^{\prime }$ of $A_1$ via an edge labeled $.

The details of this construction are a bit more involved. By minimality, each of the $Q_i$ might contain at most one sink state, i.e., a state that has no path leading to an accepting state. Let $Q_i^{\prime }$ be the set of states of $A_i$ that contain a path to a state from $F_i$. As all languages $L(A_i)$ are non-empty, the initial state of $A_i$ is in $Q_i^{\prime }$. In particular, each $Q_i^{\prime }$ is non-empty. Let $A=(\mathrm{\Sigma }\cup \{\$\},Q,q_1,\{q_1\},\delta )$, where $Q={\bigcup }_{i=1}^k{Q}_i^{\prime }\cup$ {q₁, }, and $\delta \subseteq Q\times (\mathrm{\Sigma }\cup \{\$\})\times Q$ consists of the following sets:

• ${\delta }_i$ for $i\in \{1,\dots ,k\}$ (recall that the state sets are pairwise disjoint),
• $\{(q,\$,q_{i+1})\mid i\in \{1,\dots ,k-1\},q\in F_i\}$,
• $\{(q,\$,q_1)\mid q\in F_k\}$,
• $\{(q_1,\sigma ,q)\mid (q_1^{\prime },\sigma ,q)\in {\delta }_1\}$,
• $\{(q_1,\$,q_2)\}$ if $q_1^{\prime }\in F_1$,
• {( , σ, ) ∣ σ ∈ Σ},
• {(q, σ, ) ∣ for all $q,\sigma$ where there is no $q^{\prime }$ such that $(q,\sigma ,q^{\prime })$ is in one of the sets above}.

Since the initial state of $A_1$ was called $q_1^{\prime }$, we could add a new state $q_1$ and make sure there are no edges from $Q_1$ connecting to $q_1$. This is needed as otherwise we might recognize additional words looping within $Q_1$ from $q_1$ to $q_1$. Also we merge all sink states of the $A_i$ into a single sink state .

We need to show that the automaton is minimal. For this we need to show that no pair of states can be merged, i.e., there exists a word that leads to the final state for exactly one of them. First note that no word leads from to the final state $q_1$, and there is a path from every other state. Hence cannot be merged with any other state. Also note that $q_1$ cannot be merged with any other state as it is the only final state.

Hence we need to show that $q^{\prime },q^{″}\in {\bigcup }_{i=1}^k{Q}_i^{\prime }$, $q^{\prime }\ne q^{″}$, cannot be merged. If $q^{\prime }$ and $q^{″}$ are both in some $Q_i^{\prime }$, then these state corresponds to states in $A_i$ and by minimality of $A_i$ they cannot be merged. Assume that $q^{\prime }\in Q_i$ and $q^{″}\in Q_j$ for $i<j$, then there is a path from $q^{″}$ to the final state $q_1$ using exactly $k-i+1$ many $-transitions, and such a path cannot exist for $q^{\prime }$.

So A is the minimal automaton for L.

Step 2: “Easy direction”

Assume the intersection of the $A_i$ is nonempty and w is a word in the intersection. Then ${\delta }^{*}(q_1,{(w\$)}^k)=q_1$ and ${\delta }^{*}(q_1,(w\$))=q_2$ and since A is the minimal automaton for L, this implies that L is not star-free.

Step 3: “Hard direction”

Assume there is a common word w that forms a nontrivial cycle $w^r$ in A for $r>1$, i.e., there exists a state q such that ${\delta }^{*}(q,w^r)=q$ and ${\delta }^{*}(q,w)\ne q$. First we can rule out that q = , as all cycles through are trivial.

Assume that $w\in {\mathrm{\Sigma }}^{*}$, i.e., w does not contain a $ symbol. Then the cycle is contained completely within one of the $Q_i^{\prime }$ and hence there is a corresponding cycle in $A_i$ which cannot be nontrivial as the $A_i$ are aperiodic.

Recall that the states corresponding to the initial states of $A_1,\dots ,A_k$ are called $q_1,\dots ,q_k$ in A (strictly speaking for $q_1$ this is not correct, but $q_1$ behaves similar enough in the following). First note that if $w=uv$ forms a cycle starting at the state q, then $vu$ forms a cycle starting at the state ${\delta }^{*}(q,u)$. We will use this idea to find a cycle starting at one of the states $q_i$ for $i\in \{1,\dots ,k\}$ corresponding to an initial state of $A_i$. So w is of the form $w=u_1\$v\$u_2$, where $u_1,u_2\in {\mathrm{\Sigma }}^{*}$ and $v\in {(\mathrm{\Sigma }\cup \{\$\})}^{*}$. Since $u_1\$v\$$ is a word ending with a $ symbol, we have that ${\delta }^{*}(q,u_1\$v\$)=q_i$ is one of the states corresponding to an initial states of an $A_i$. By rotating $w^r$ one easily sees that ${\delta }^{*}(q_i,{(u_2{u}_1\$v\$)}^r)=q_i$. Also assume by contradiction that ${\delta }^{*}(q_i,u_2{u}_1\$v\$)=q_i$. We get ${\delta }^{*}(q,{(u_1\$v\$u_2)}^c)={\delta }^{*}(q,{(u_1\$v\$u_2)}^{c-1})$ by removing one loop through $q_i$. However, this implies by induction on c that ${\delta }^{*}(q,(u_1\$v\$u_2))=q$, contradicting the assumption that w forms a nontrivial cycle. Hence $u_2{u}_1\$v\$$ also forms a nontrivial cycle starting at $q_i$. We let $u=u_2{u}_1$.

Also since $u\$v\$$ ends with a $ symbol we have ${\delta }^{*}(q_i,u\$v\$)=q_{i^{\prime }}$ where $i^{\prime }=i+c(\mathrm{mod}k)$ (for $c\ne 0$ as $q_{i^{\prime }}\ne q_i$), and since the number of $ in ${(u\$v\$)}^t$ is proportional to t, we get ${\delta }^{*}(q_i,{(u\$v\$)}^t)=q_j$, where $j=i+c·t(\mathrm{mod}k)$ (this also uses the fact that ${\delta }^{*}(q_i,{(u\$v\$)}^r)=q_i$, hence no prefix can lead to the state ). Also since k is a prime, for each j, there exists a t such that ${\delta }^{*}(q_i,{(u\$v\$)}^t)=q_j$. However, then this implies that ${\delta }^{*}(q_j,u\$)=q_{j^{\prime }}$ where $j^{\prime }=j+1(\mathrm{mod}k)$ for all $j\in \{1,\dots ,k\}$. Hence $u\in L_j$ for all $j\in \{1,\dots ,k\}$ (note this is also true for $j=1$ as the out-going transitions from $q_1$ are the same as the ones from $q_1^{\prime }$), and so the intersection is not empty. ☐

If we use the automaton over the binary alphabet from Proposition 3 in the proof of the previous theorem, we require automata of logarithmic size instead of constant size for the hardness of the intersection problem. Hence, the number of states decreases by a factor of $\log q$. This will give us the following result.

Corollary 2.

Assuming ETH, there is no algorithm for solving Aperiodicity for q-state DFAs on binary input alphabets running in time $O(2^{o(q/\log q)})$.

We are not aware of any published exponential-time algorithm for solving Aperiodicity. However, as some NP-hard problems involving cycles in directed graphs admit subexponential-time algorithms, see [24,25], our lower bound could be even matched. Nonetheless, this stays an open question.

Proposition 5.

There is an algorithm for solving Aperiodicity that runs in time $O^{*}\left(q^q\right)=O^{*}\left(2^{q\log q}\right)$ on a given q-state DFA with arbitrary input alphabet.

Proof. 

Namely, first (as a preparatory step) create a table of size $q^q$, classifying those mappings $f:Q\to Q$ as good that have the property that for some state p of the given DFA A, $f(p)\ne p$ but $f^i(p)=p$ for some $i=2,\dots ,q$. The table creation needs time $O^{*}\left(q^q\right)$.

In a second column of our table, write down if a certain mapping f is realizable, i.e., does there exist a word $w\in {\mathrm{\Sigma }}^{*}$ such that ${\mu }_w=f$? In order to be able to reconstruct the word realizing f, either notify that f is the identity (and hence f is realized as ${\mu }_{\epsilon }$), or write down a realizable map g, i.e., $g={\mu }_u$ for some $u\in {\mathrm{\Sigma }}^{*}$, and a letter $a\in \mathrm{\Sigma }$, such that $f={\mu }_{ua}$. We build this second column by dynamic programming, starting with only one realizable entry, the identity, and then we keep looping through the whole alphabet (for all $a\in \mathrm{\Sigma }$) and all realizable mappings $g={\mu }_u$ and mark $f={\mu }_{ua}$ as realizable until no further changes happen to the table. Hence, this part of the algorithm will perform at most $q^q$ loops. Finally, we have to check in our table if there are any mappings that are both realizable and good. If so, we can construct a star witness, proving that $L(A)$ is not aperiodic. If not, we know that the language $L(A)$ is aperiodic. The overall running time of the algorithm is $O^{*}\left(q^q\right)=O^{*}\left(2^{q\log q}\right)$. ☐

Another related problem asks whether, given a DFA A, the language $L(A)$ belongs to $A{C}^0$, which means testing if $L(A)$ is quasi-aperiodic.Let us make this more precise. Let $L\subseteq {\mathrm{\Sigma }}^{*}$ be a language, M be its syntactic monoid. and $\eta :{\mathrm{\Sigma }}^{*}\to L$ its syntactic morphism. A regular language is in AC${}^0$ iff the syntactic morphism is quasi-aperiodic, i.e., for all $n\in \mathbb{N}$ the subset $\eta ({\mathrm{\Sigma }}^n)$ of M does not contain a non-trivial subgroup of M. Analyzing the PSPACE-hardness proof of Beaudry, McKenzie and Thérien given in [26], we see that the same lower bound result as stated for Aperiodicity holds for this question, as well. We can reduce testing if the syntactic monoid of a language is aperiodic to the question whether the syntactic morphism is quasi-aperiodic by adding a neutral letter. This will give us the same lower bound as deciding aperiodicity. For the upper bound, note that we only need to test if $\eta ({\mathrm{\Sigma }}^n)$ contains a group up to $n\le 2^{\left|M\right|}$.

Corollary 3.

Assuming ETH, there is no algorithm that runs in time $O\left(2^{o(q)}\right)$ and decides, given a q-state DFA A on arbitrary input alphabets, whether or not the syntactic morphism of $L(A)$ is quasi-aperiodic. Conversely, we can decide if a q-state automaton recognizes a language with a quasi-aperiodic syntactic morphism in time $O^{*}(2^{q\log q})$.

It would be also interesting to study other “hard subfamily problems” for regular languages, as exemplified with [27], within the ETH framework. In addition, it would be also interesting to systematically study the complexity of the problems under scrutiny in the previous section, restricted to subclasses of regular languages, as we did in Claim 1 of the proof of Theorem 5.

4.2. Synchronizing Words

A deterministic finite semi-automaton (DFSA) A can be specified as $A=(Q,\mathrm{\Sigma },\{{\mu }_a\mid a\in \mathrm{\Sigma }\})$, where, for each $a\in \mathrm{\Sigma }$, there is a mappting ${\mu }_a:Q\to Q$. Given some DFSA A, a synchronizing word $w\in {\mathrm{\Sigma }}^{*}$ enjoys

$$\forall p,p^{\prime }\in Q:{\mu }_w(p)={\mu }_w(p^{\prime }).$$

The Synchronizing Word (SW) problem is the question, given a DFSA A and an integer ℓ, whether there exists a synchronizing word w of length at most ℓ for A. This decision problem is related to the arguably most famous combinatorial conjecture in Formal Languages, which is Černý’s conjecture [28], stating (in a relaxed form) that there is always a synchronizing word of size at most $O(|Q{|}^2)$ for any DFSA, should there be a synchronizing word at all.

We have undertaken a multi-parameter analysis of this problem in [29]. The most straightforward parameters are $\left|\mathrm{\Sigma }\right|$, $q=\left|Q\right|$, and an upper bound ℓ on the length of the synchronizing word we are looking for. In [29], algorithms with running times of $O^{*}(2^q)$ and of $O^{*}({\left|\mathrm{\Sigma }\right|}^{\ell })$ were given, complemented by proofs that show that there is neither an $O^{*}(2^{o(q)})$-time (with unbounded input alphabet size) nor an $O^{*}({(|\mathrm{\Sigma }|-ϵ)}^{\ell })$-time algorithm (for any $ϵ>0$) under ETH or SETH, respectively.

From the reduction presented in ([29] Theorem 12), we cannot get any lower bounds for bounded input alphabets; the dependency on Σ for the mentioned $O^{*}(2^q)$-time algorithm is only linear.

We were not able to answer this question completely for SW, but (only) for a more general version of this problem. Given a DFSA $A=(Q,\mathrm{\Sigma },\{{\mu }_a\mid a\in \mathrm{\Sigma }\})$ and a state set $Q_{sync}$, a $Q_{sync}$-synchronizing word $w\in {\mathrm{\Sigma }}^{*}$ satisfies

$$\forall p,p^{\prime }\in Q_{sync}:{\mu }_w(p)={\mu }_w(p^{\prime }).$$

The $Q_{sync}$-Synchronizing Word ($Q_{SYNC}$-SW) problem is the question, given a DFSA A, a set of states $Q_{sync}$ and an integer ℓ, whether there exists a $Q_{sync}$-synchronizing word w of length at most ℓ for A. Correspondingly, the $Q_{sync}$-Synchronizing Word problem can be stated. Notice that while SW is NP-complete, $Q_{sync}$-SW is even PSPACE-complete; see [30].

Theorem 6.

There is an algorithm for solving $Q_{sync}$-SW on bounded input alphabets that runs in time $O^{*}\left(2^q\right)$ for q-state deterministic finite semi-automata. Conversely, assuming ETH, there is no $O^{*}\left(2^{o(q)}\right)$-time algorithm for this task.

Proof. 

It was already observed in [29] that the algorithm given there for SW transfers to $Q_{sync}$-SW, as this is only a breadth-first search algorithm on an auxiliary graph (of exponential size, with vertex set $2^Q$). The PSPACE-hardness proof contained in ([30] Theorem 1.22), based on [31], reduces from DFA-Intersection. Given k automata each with at most s states, with input alphabet Σ, one deterministic finite semi-automaton $A=(Q,\{{\mu }_a\mid a\in \mathrm{\Sigma }\})$ is constructed such that $\left|Q\right|\le sk+2$. Hence, an $O^{*}\left(2^{o(|Q|)}\right)$-time algorithm for $Q_{sync}$-SW would result in an $O^{*}\left(2^{o(sk)}\right)$-time algorithm for DFA-Intersection, contradicting Proposition 3. ☐

5. SETH-Based Bounds: Length-Bounded Problem Variants

Cho and Huynh studied in [32] the complexity of a so-called bounded version of Universality, where in addition to the automaton A with input alphabet Σ, a number k (encoded in unary) is input, and the question is if ${\mathrm{\Sigma }}^{\le k}\subseteq L(A)$. This problem is again CoNP-complete for general alphabets. The proof given in [32] is by reduction from the n-Step Halting Problem for NTMS, somehow modifying earlier constructions of [33]. Our reduction from 3-Coloring given above also shows the mentioned CoNP-completeness result in a more standard way. Our ETH-based result also transfers into this setting; possibly, there are now better algorithms for solving Bounded Universality, as this problem might be a bit easier compared to Universality. We will discuss this a bit further below.

Notice that in [29], another SETH-based result relating to synchronizing words was derived. Namely, it was shown that (under SETH) there is no algorithm that determines, given a deterministic finite semi-automaton $A=(Q,\mathrm{\Sigma },\{{\mu }_a\mid a\in \mathrm{\Sigma }\})$ and an integer ℓ, whether or not there is a synchronizing word for A, and that runs in time $O^{*}\left({(|\mathrm{\Sigma }|-\epsilon )}^{\ell }\right)$ for any $\epsilon >0$. Here, Σ is part of the input; the statement is also true for fixed binary input alphabets. We will use this result now to show some lower bounds for the bounded versions of more classical problems we considered above.

Theorem 7.

There is an algorithm with running time $O^{*}\left({\left|\mathrm{\Sigma }\right|}^{\ell }\right)$ that, given k DFAs over the input alphabet Σ and an integer ℓ, decides whether or not there is a word $w\in {\mathrm{\Sigma }}^{\le \ell }$ accepted by all these DFAs. Conversely, there is no algorithm that solves this problem in time $O^{*}\left({(|\mathrm{\Sigma }|-\epsilon )}^{\ell }\right)$ for any $\epsilon >0$, unless SETH fails.

Proof. 

The mentioned algorithm simply tests all words of length up to ℓ. We show how to find a synchronizing word of length at most ℓ for a given DFSA $A=(Q,\mathrm{\Sigma },\{{\mu }_a\mid a\in \mathrm{\Sigma }\})$ and an integer ℓ that runs in time ${O((\left|\mathrm{\Sigma }\right|-\epsilon )}^{\ell })$, assuming for the sake of contradiction that there is an algorithm with such a running time for Bounded DFA-Intersection. From A, we build ${\left|Q\right|}^2$ many DFAs $A_{s,f}$ (namely, with start state s and with unique final state f, while the transition function of all $A_{s,f}$ is identical, corresponding to $\{{\mu }_a\mid a\in \mathrm{\Sigma }\}$). Furthermore, let $A^{\ell }$ be the automaton that accepts any word of length at most ℓ. Now, we create $\left|Q\right|$ many instances of $I_f$ of Bounded DFA-Intersection. Namely, $I_f$ is given by $\{A_{s,f}\mid s\in Q\}\cup \{A^{\ell }\}$. Now, A has a synchronizing word of length at most ℓ if and only if for some $f\in Q$, $I_f$ is a YES-instance.

Clearly, the above reasoning implies that there is no $O^{*}\left({(|\mathrm{\Sigma }|-\epsilon )}^{\ell }\right)$-time algorithm for Bounded NFA-Intersection, unless SETH fails. More interestingly, we can use state complementation and a variant of the NFA union construction to show the following result.

Corollary 4.

There is an algorithm with running time $O^{*}\left({\left|\mathrm{\Sigma }\right|}^{\ell }\right)$ that, given some NFA over the input alphabet Σ and an integer ℓ, decides whether or not there is a word $w\in {\mathrm{\Sigma }}^{\le \ell }$ not accepted by this NFA. Conversely, there is no algorithm that solves this problem in time $O^{*}\left({(|\mathrm{\Sigma }|-\epsilon )}^{\ell }\right)$ for any $\epsilon >0$, unless SETH fails.

Clearly, this implies a similar result for Bounded NFA-Equivalence.

Corollary 5.

There is an algorithm with running time $O^{*}\left({\left|\mathrm{\Sigma }\right|}^{\ell }\right)$ that, given two NFAs $A_1,A_2$ over the input alphabet Σ and an integer ℓ, decides whether or not there is a word $w\in {\mathrm{\Sigma }}^{\le \ell }$ not accepted by exactly one NFA. Conversely, there is no algorithm that solves this problem in time $O^{*}\left({(|\mathrm{\Sigma }|-\epsilon )}^{\ell }\right)$ for any $\epsilon >0$, unless SETH fails.

From these reductions, we can borrow quite a lot of other results from [29], dealing with inapproximability and parameterized intractability.

• [29], Theorem 3, yields: Bounded NFA Universality is hard for W[2], when parameterized by ℓ. Similar results hold also for the intersection and equivalence problems that we usually consider.
• Using (in addition) recent results due to Dinur and Steurer [34], we can conclude that there is no polynomial-time algorithm that computes an approximate synchronizing word of length at most a factor of $(1-\epsilon )\ln (|\mathrm{\Sigma }|)$ off from the optimum, unless P equals NP. (This sharpens [29], Corollary 4. Neither is it possible to approximate the shortest word accepted by some NFA up to a factor of $(1-\epsilon )\ln (|\mathrm{\Sigma }|)$.

It would be interesting to obtain more inapproximability results in this way.

6. Two Further Ways to Interpret Finite Automata

Finite automata cannot be only used to process (contiguous) strings, but they might also jump from one position of the input to another position, or they can process two-dimensional words. We picked these two processing modes for the subsequent analysis, as they were introduced quite recently [35,36].

6.1. Jumping Finite Automata

A jumping finite automaton (JFA) formally looks like a usual string-processing NFA. However, the application of a rule to a word is different: If $p\stackrel{a}{⟶}{p}^{\prime }$ is a transition rule, then it can transform the input string u into $u^{\prime }$ provided that $u,u^{\prime }$ decompose as $u=u_{1}a{u}_2$ and $u^{\prime }=u_1{u}_2$. In other words, a JFA may first jump to an arbitrary position of the input and then apply the rule there. This model was introduced in [36] and further studied in [37]. It is relatively easy to see that the languages accepted by JFAs are just the inverses of the Parikh images of the regular languages, or, in other words, the commutative (or permutation) closure of the regular languages, or, yet in different terminology, the inverses of the Parikh images of semilinear sets. In particular, the emptiness problem for JFAs is as simple as for NFAs. Also, for the case of unary input alphabets, JFAs and NFAs just work the same. Hence, Universality is hard for JFAs, as well. Classical complexity considerations on these formalisms are contained in [37,38,39,40,41]; observe that mostly the input is given in the form of Parikh vectors of numbers encoded in binary, while we will consider the input given in unary-encoded Parikh vectors below (namely, as words, i.e., as elements of the free monoid), since JFAs were introduced this way in [36]. Yet another way to formally look at how JFAs operate incorporates the use of the shuffle operation. Recall that $w_1⧢w_2$ denotes the shuffle of $w_1$ and $w_2$, which can be seen as observing a concurrent left-to-right read of $w_1$ and $w_2$, listing all possible concurrent reads. For instance, $ab⧢ba=\{abba,abab,baba,baab\}$.

Notice however that even if a JFA might formally look like a DFA, there is a certain nondeterminism inherent to this mechanism, which is the position at which the next symbol is read (in the case of non-unary input alphabets). It can be therefore shown that the uniform word problem for JFAs is NP-hard. Analyzing the proof given in [37], Theorem 54, we can conclude:

Theorem 8.

Under ETH, there is no algorithm that, given a JFA A on q states and a word $w\in {\mathrm{\Sigma }}^{*}$, decides if $w\in L(A)$ in time $O^{*}\left(2^{o(q)}\right)$, $O^{*}\left(2^{o\left(\frac{\left|w\right|}{\log (|w|)}\right)}\right)$ nor $O^{*}\left(2^{o(|\mathrm{\Sigma }|)}\right)$.

Notice that this problem can be solved in time $O^{*}(n!)$ on arbitrary input alphabets, feeding all permutations of an input word of length n into the given automaton, interpreted as an NFA. There is also a dynamic programming algorithm solving Universal Membership for q-state JFAs (that is not improvable by Theorem 8, assuming ETH). This algorithm is based on the following idea. A word w allows the transition from state p to state $p^{\prime }$ iff for some decomposition $w\in w_1⧢w_2$, p can transfer to $\widehat{p}$ by reading $w_1$ and from $\widehat{p}$ one can go into $p^{\prime }$ when reading $w_2$. For the correct implementation of the shuffle possibilities, we need to store possible translations for all subsets of indices within the input word, yielding a table (and time) complexity of $O^{*}(2^{\left|w\right|})$. We have no other upper bound.

This also means (assuming P is not equal to NP) that there is no polynomial-time algorithm that computes, given a JFA A, another JFA $A^{\prime }$ that describes the Parikh mapping inverses of the complement of the Parikh images that A describes (otherwise, we would have a polynomial-time algorithm to solve Universality), nor is there a polynomial-time algorithm that computes, given two JFAs $A_1$ and $A_2$, a third JFA $A_3$ such that the intersection of the (commutative / JFA) languages associated to $A_1$ and $A_2$ is just the language accepted by the JFA $A_3$ (namely, otherwise we could solve the Universal Membership Problem in polynomial time; given a JFA A and a word w, first construct a JFA $A_w$ that accepts the permutation closure of $\{w\}$ and then check if the intersection of the JFA languages of A and of $A_w$ is empty). Recall that, by way of contrast, intersection is an easy operation even on NFAs. (This also indicates that the simple constructions for the corresponding closure properties of JFA languages as given in [36] are flawed.) However, the closure properties themselves hold true, as this was already known for the Parikh images of regular sets, also known as semi-linear sets, also see [42] and the references quoted therein.

What about the three decidability questions that are central to this paper for these devices? As the behavior of JFA is the same as that of NFA on unary alphabets, we can borrow all results from Section 2.

Theorem 9.

Let $k=\left|\mathrm{\Sigma }\right|$ be fixed. Unless ETH fails, there is no algorithm that solves Universality for q-state JFAs in time $O^{*}\left(2^{o\left(q^{\frac{k}{k+2}}\right)}\right)$.

Proof. 

We only sketch the idea in the case of binary alphabets, i.e., when $k=2$. We revisit our reduction from 3-Coloring for the case $k=1$ detailed above. The main bottleneck was the coding of badly colored edges. This is taken care of in the following way. We encode the vertices $v_1,\dots ,v_n$ no longer by n prime numbers, but by pairs of $\lceil \sqrt{n}\rceil$ many prime numbers, which are then expressed as powers of the input letters a and b, resp. Hence, to describe the $3m$ bad colorings of the m edges, we need no longer $O(m{n}^2)$ many states, but only $O(mn)$ many. We can extend this method such that, for arbitrary k, we would need $O(m{n}^{\frac{k}{2}})$ many states for all bad edge colorings. ☐

Notice that the expression that we claim somehow interpolates between the third root of q (in the exponent of 2), namely, when $k=1$, and then it also coincides with our earlier findings, and q itself (if k tends to infinity). We could make the construction for arbitrary alphabets more explicit by re-interpreting the proof of Proposition 2 as one dealing with Universality for JFAs.

Proposition 6.

Unless ETH fails, there is no algorithm that solves Universality for q-state JFAs in time $O^{*}\left(2^{o(\sqrt{q})}\right)$.

Proof. 

First observe that the DFAs $A_v$ and $A_{uv,a}$ that we constructed in the proof of Proposition 2 can be as well interpreted as JFAs, and also the automata $\overline{A_v}$ and $\overline{A_{uv,a}}$ that can be constructed by complementing the sets of final states can read the input in arbitrary sequence. It is easy to construct a JFA that accepts the union of all languages accepted by any JFA $\overline{A_v}$ or $\overline{A_{uv,a}}$. This union equals ${\mathrm{\Sigma }}^{*}$ (with Σ as in the referred proof) if and only if the given graph was not 3-colorable. ☐

We can obtain very similar results for Equivalence for JFAs.

Let us now briefly discuss Intersection. Interestingly enough, also the problem of detecting emptiness of the intersection of only two JFA languages is NP-hard. This and a related study on ETH-based complexity can be found in [37]. For the intersection of k JFAs, the proof of Proposition 2 actually shows the analogous result also in that case. For bounded alphabets, we can re-analyze the proof of Theorem 9 to obtain:

Corollary 6.

Let Σ be fixed. Unless ETH fails, there is no algorithm for solving JFA intersection in time $O^{*}\left(2^{o(k)+o\left(q^{\left|\mathrm{\Sigma }\right|/2}\right)}\right)$ for k JFAs with at most q states.

Namely, we can construct to a given 3-Coloring instance with n vertices and m edges a collection of $k=3m+1$ many JFAs, each with $n^{\left|\mathrm{\Sigma }\right|/2}$ many states.

6.2. Boustrophedon Finite Automata

In the last four decades, several attempts have been made to transfer automata theory into the area of image processing. Unfortunately, most (natural) attempts failed insofar, as even the most simple algorithmic questions (like the emptiness problem for the corresponding devices) turn out to be undecidable; see [43,44]. In order to avoid these negative results, simpler devices have been discussed in the literature; see [45] or [35] for more recent works.

Boustrophedon finite automata (BFAs) have been introduced to describe a simple processing of rectangular-shaped pictures with finite automata that scan these pictures as depicted in Figure 3.

Without going into formal details, let us mention that it has been shown in [35] that the non-emptiness problem for this type of finite automata is NP-complete. This might read like a very negative result, but as mentioned above, for picture-processing automata, mostly undecidability results can be expected for the non-emptiness problem; see [46] for 4-way DFAs. Even for the class of 3-way automata obviously related to BFAs, the known decidability result for non-emptiness does not give an NP algorithm; see [47]. This NP-hardness reduction is from Tally-DFA-Intersection. From this (direct) construction, we can immediately deduce:

Proposition 7.

There is no algorithm that, given some BFA A with at most q states, decides if $L(A)=\varnothing$ in time $O^{*}\left(2^{o(q^{1/3})}\right)$, unless ETH fails.

How good is this bound?

To give a more formal treatment, we need some more definitions. A two-dimensional word (also called a picture, a matrix or an array in the literature) over Σ is a tuple

$$W:=((a_{1,1},a_{1,2},\dots ,a_{1,n}),(a_{2,1},a_{2,2},\dots ,a_{2,n}),\dots ,(a_{m,1},a_{m,2},\dots ,a_{m,n})),$$

where $m,n\in \mathbb{N}$ and, for every i, $1\le i\le m$, and j, $1\le j\le n$, $a_{i,j}\in \mathrm{\Sigma }$. We define the number of columns (or width) and number of rows (or height) of W by ${\left|W\right|}_c:=n$ and ${\left|W\right|}_r:=m$, respectively. For the sake of convenience, we also denote W by ${\left[a_{i,j}\right]}_{m,n}$ or by a matrix in a more pictorial form. If we want to refer to the $j^{\mathrm{th}}$ symbol in row i of the picture W, then we use $W[i,j]=a_{i,j}$. By ${\mathrm{\Sigma }}^{++}$, we denote the set of all (non-empty) pictures over Σ. Every subset $L\subseteq {\mathrm{\Sigma }}^{++}$ is a picture language.

Let $W:={\left[a_{i,j}\right]}_{m,n}$ and $W^{\prime }:={\left[b_{i,j}\right]}_{m^{\prime },n^{\prime }}$ be two non-empty pictures over Σ. The column concatenation of W and $W^{\prime }$, denoted by $W⦶W^{\prime }$, is undefined if $m\ne m^{\prime }$ and is the picture

$$\begin{array}{cccccccc}{a}_{1,1}& a_{1,2}& \dots & a_{1,n}& b_{1,1}& b_{1,2}& \dots & b_{1,n^{\prime }}\\ a_{2,1}& a_{2,2}& \dots & a_{2,n}& b_{2,1}& b_{2,2}& \dots & b_{2,n^{\prime }}\\ ⋮& ⋮& \ddots & ⋮& ⋮& ⋮& \ddots & ⋮\\ a_{m,1}& a_{m,2}& \dots & a_{m,n}& b_{m^{\prime },1}& b_{m^{\prime },2}& \dots & b_{m^{\prime },n^{\prime }}\end{array}$$

otherwise. The row concatenation of W and $W^{\prime }$, denoted by $W\ominus W^{\prime }$, is undefined if $n\ne n^{\prime }$ and is the picture

$$\begin{array}{cccc}{a}_{1,1}& a_{1,2}& \dots & a_{1,n}\\ a_{2,1}& a_{2,2}& \dots & a_{2,n}\\ ⋮& ⋮& \ddots & ⋮\\ a_{m,1}& a_{m,2}& \dots & a_{m,n}\\ b_{1,1}& b_{1,2}& \dots & b_{1,n^{\prime }}\\ b_{2,1}& b_{2,2}& \dots & b_{2,n^{\prime }}\\ ⋮& ⋮& \ddots & ⋮\\ b_{m^{\prime },1}& b_{m^{\prime },2}& \dots & b_{m^{\prime },n^{\prime }}\end{array}$$

otherwise. Column and row catenation naturally extend to picture languages. Accordingly, we can define powers of languages, as well as a closure operation. $L^1=L$, $L^{i+1}=L^i⦶L$ for $i\ge 1$; then $L^{+}={\displaystyle \bigcup _{i=1}^{\infty }}{L}^i$.

$$L_1=L,L_{i+1}=L_i\ominus L\mathrm{for}i\ge 1;\mathrm{then}{L}_{+}=\bigcup _{i=1}^{\infty }{L}_i.\mathrm{Hence},{({\mathrm{\Sigma }}_{+})}^{+}={({\mathrm{\Sigma }}^{+})}_{+}={\mathrm{\Sigma }}^{++}.$$

Definition 1.

A boustrophedon finite automaton, or BFA for short, can be specified as a 7-tuple $M=(Q,\mathrm{\Sigma },R,s,F,\#,\square )$, where Q is a finite set of states, Σ is an input alphabet, $R\subseteq Q\times (\mathrm{\Sigma }\cup \{\#\})\times Q$ is a finite set of rules. A rule $(q,a,p)\in R$ is usually written as $qa\to p$. The special symbol $\#\notin \mathrm{\Sigma }$ indicates the border of the rectangular picture that is processed, $s\in Q$ is the initial state, F is the set of final states. Let $\square$ be a new symbol indicating an erased position and let ${\mathrm{\Sigma }}_{+}:=\mathrm{\Sigma }\cup \{\#,\square \}$. Then $C_M:=Q\times {\mathrm{\Sigma }}_{+}^{++}\times \mathbb{N}$ is the set of configurations of M.

A configuration $(p,A,\mu )\in C_M$ is valid if $1\le \mu \le {\left|A\right|}_r$ and, for every i, $1\le i\le \mu -1$, the $i^{th}$ row equals $\#{\square }^{{\left|A\right|}_c-2}\#$, for every j, $\mu +1\le j\le {\left|A\right|}_r$, the $j^{th}$ row equals $\#w\#$, $w\in {\mathrm{\Sigma }}^{{\left|A\right|}_c-2}$, and, for some ν, $0\le \nu \le {\left|A\right|}_c-2$, $w\in {\mathrm{\Sigma }}^{{\left|A\right|}_c-\nu -2}$, the ${\mu }^{th}$ row equals $\#{\square }^{\nu }w\#$, if μ is odd and $\#w{\square }^{\nu }\#$, if μ is even. Notice that valid configurations model the idea of observable snapshots of the work of the BFA.

• If $(p,A,\mu )$ and $(q,A^{\prime },\mu )$ are two valid configurations such that A and $A^{\prime }$ are identical but for one position $(i,j)$, where $A^{\prime }[i,j]=\square$ while $A[i,j]\in \mathrm{\Sigma }$, then $(p,A,\mu ){⊢}_M(q,A^{\prime },\mu )$ if $pA[i,j]\to q\in R$.
• If $(p,A,\mu )$ and $(q,A,\mu +1)$ are two valid configurations, then $(p,A,\mu ){⊢}_M(q,A,\mu +1)$ if the ${\mu }^{\mathrm{th}}$ row contains only # and $\square$ symbols, and if $p\#\to q\in R$.

The reflexive transitive closure of the relation ${⊢}_M$ is denoted by ${⊢}_M^{*}$.

The language $L(M)$ accepted by M is then the set of all $m\times n$ pictures A over Σ such that

$$(s,{\#}_m⦶A⦶{\#}_m,1){⊢}_M^{*}(f,{\#}_m⦶{\square }_m^n⦶{\#}_m,m)$$

for some $f\in F$.

First observe that although the emptiness problem is similar to the intersection problem, the only “communication” between the rows is via the state that is communicated and via the length information that is implicitly checked. In particular, we can first convert a given BFA into one, say, A, that only deals with one input letter, by replacing any input letter in any transition by, say, $\mathtt{a}$. Let A have state set Q, with $\left|Q\right|=q$ and let $s_0$ be the initial state of A.

Now, $L(A)\ne \varnothing$ if and only if there is some array in $L(A)$ that can be linearized as ${\mathtt{a}}^r\#{\mathtt{a}}^r\#\dots {\mathtt{a}}^r$. Here, from the start state $s_0$, first ${\mathtt{a}}^r\#$ would lead into $s_1$, then ${\mathtt{a}}^r\#$ would lead into $s_2$ etc., until ${\mathtt{a}}^r$ would lead into $s_n$ and then ${\mathtt{a}}^r$ leads into some final state f. By a simple pumping argument, we can assume that $n\le q$. So, we could try all permutations of at most q different states $s_1,\dots ,s_n$, and then construct the product automaton $A_{\times }$ from $A_0,\dots ,A_{n+1}$, where $A_0$ is as A, but starts with $s_0$ and has $s_1$ as its only accepting state, $A_1$ is like A, but starts with $s_1$ and has $s_2$ as its only accepting state, …, $A_{n-1}$ is like A, but starts with $s_{n-1}$ and has $s_2$ as its only accepting state, $A_n$ is like A, but starts with $s_n$ and from f there is another arc labeled # that leads into the only final state $f^{\prime }$, and finally $A_{n+1}$ is the 2-state NFA accepting ${\{a\}}^{*}\{\#\}$. Now, the string-processing NFA $A_{\times }$ does not accept the empty language if and only if there is some r such that ${\mathtt{a}}^r\#$ is accepted by each of the constructed automata $L(A_i)$, if and only if ${\mathtt{a}}^r\#{\mathtt{a}}^r\#\dots {\mathtt{a}}^r$ (with n rows) is accepted by A. The whole procedure can be carried out in time $O^{*}(q!q^q))=O^{*}(q^{2q})$, which is obviously far off from our lower bound.

A slightly better bound can be obtained by a graph-algorithm based procedure that results in the following statement.

Proposition 8.

Emptiness for q-state BFAs can be decided in time $O^{*}(q^q)$ (and polynomial space).

Proof. 

Namely, consider the following algorithm. For each $r=1,\dots ,q^q$, we successively build a directed graph $G^r$ with vertices $(p,i)$, $1\le p,i\le q$ and $s,f$. Construct an arc $(s,(p,1))$ if A on input ${\mathtt{a}}^r\#$ could enter state p. More generally, we have an arc $((p^{\prime },i),(p,i+1))$ for $i=1,\dots ,q-1$ if A, when started in state $p^{\prime }$, would be driven in state p by the input ${\mathtt{a}}^r\#$. Finally, for each $i=1,\dots ,q$, we have an arc $((p,i),f)$ if A, starting in p, would enter a final state upon reading ${\mathtt{a}}^r$. Now, A accepts ${\mathtt{a}}^r\#{\mathtt{a}}^r\#\dots {\mathtt{a}}^r$ (with at most q rows) if and only if the constructed graph $G^r$ has a path from s to f. Notice that with a little bit of bookkeeping, $G^r$ can be computed from $G^{r-1}$ in polynomial time. Also, observe that we can stop the loop after at most $q^q$ iterations, as we can view (in the case of deterministic BFAs) each word ${\mathtt{a}}^r$ as defining a mapping ${\mu }_{{\mathtt{a}}^r}:Q\to Q$ (from the state that we started out to some well-defined state we ended in), and there are no more than $|Q^Q|=q^q$ many such mappings. From this perspective, our algorithm can be viewed as looking for some r such that ${\mu }_{{\mathtt{a}}^r}({\mu }_{{\mathtt{a}}^r\#}^i(s_0))$ is a final state of A, for some $i=0,\dots ,q-1$. Now, nondeterministic BFAs can be viewed as providing some additional shortcuts in the transition graph, i.e., again at most $q^q$ iterations suffice. (In [35], a “column pumping lemma” was suggested that also shows that $q^q$ iterations suffice.) So, our algorithm performs $O^{*}(q^q)$ steps. Also, it only uses polynomial space, while the previous algorithm used space $O^{*}(q^q)$ already for the product automaton construction. ☐

7. Conclusions

So far, there has been no systematic study of hard problems for finite automata under ETH. Frankly speaking, we are only aware of the papers [29,37] on these topics. Returning to the survey of Holzer and Kutrib [7], it becomes clear that there are quite a many hard problems related to finite automata and regular expressions that have not yet been examined with respect to exact algorithms and ETH. This hence gives ample room for future research. Also, there are quite a many modifications of finite automata with hard decision problems. One (relatively recent) such example are finite-memory automata [48,49].

It might be also interesting to study these problems under different yet related hypotheses, Pătraşcu and Williams list some of such hypotheses in [50]. Notice that even the Strong ETH was barely used in this paper.

It should be also interesting to rule out certain types of XP algorithms for parameterized automata problems, as this was started out in [51] (relating to assumptions from Parameterized Complexity) and also mentioned in [1,5] (with assumptions like (S)ETH). In this connection, we would also like to point to the fact that if the two basic Parameterized Complexity classes FPT and W[1] coincide, then ETH would fail, which provides another link to the considerations of this paper.

More generally speaking, we believe that it is now high time to interconnect the classical Formal Language area with the modern areas of Parameterized Complexity and Exact Exponential-Time Algorithms, including several lower bound techniques. Both communities can profit from such an interconnection. For the Parameterized Complexity community, it might be interesting to learn about results as in [52], where the authors show that Intersection Emptiness for k tree automata can be solved in time $O(n^{c_{1}k})$, but not (and this is an unconditional not, independent of the belief in some complexity assumptions) in time $O(n^{c_{2}k})$, for some suitable constants $c_1>c_2$. Maybe, we can obtain similar results also in other areas of combinatorics. It should be noted that Intersection Emptiness is EXPTIME-complete even for deterministic top-down tree automata.

In relation to the idea of approximating automata, Holzer and Jacobi [53] recently introduced and discussed the following problem(s). Given an NFA A, decide if one of the six variants of an a-boundary of $L(A)$ is finite. By reduction from DFA-Intersection, they proved all variants to be PSPACE-hard. Membership of the problems can be easily seen by reducing the problems to a reachability problem of some DFA closely related to the NFA A. Although the hardness reductions in Lemma 15 slightly differ in each case i, all in all the number of states of the resulting NFA $A_i$ is just the total number of states of all DFAs used as input in the reduction, plus a constant. In particular, if the number of states per input DFA is bounded, say, by 3, and if we use unbounded input alphabets, then our previous results immediately entail that, unless ETH fails, none of the six variants of the a-boundary problems admit an algorithm with running time $O^{*}(2^{o(q)})$, where q is now the number of states of the given NFA A. This bound is matched by the sketched reduction to prove PSPACE-membership, as the subset construction to obtain the desired equivalent DFA gives a single-exponential blow-up.

In short, this area offers quite a rich ground for further studies.