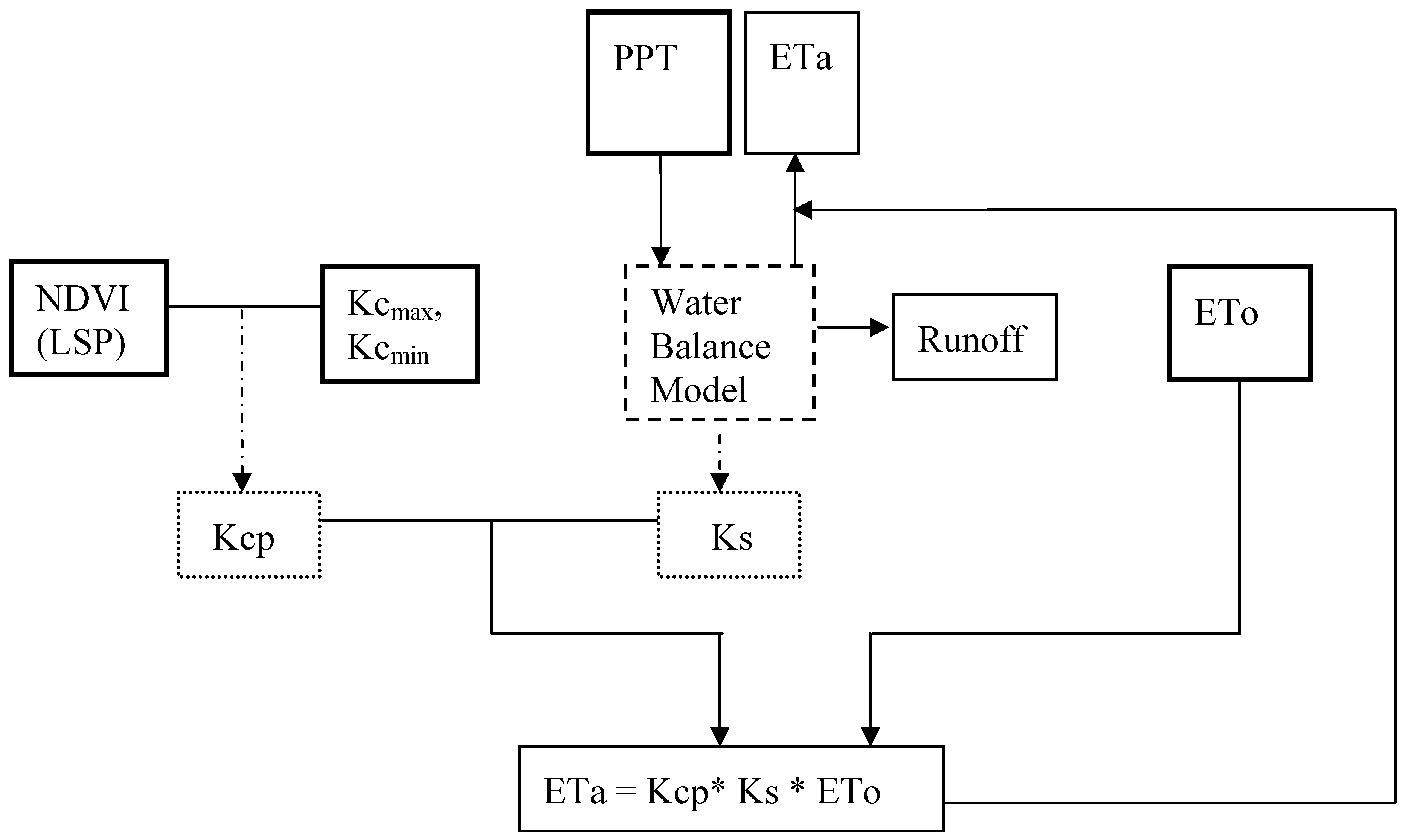
1. Introduction
Evapotranspiration (ET) is an important component of the hydrologic budget because it expresses the exchange of mass and energy between the soil-water-vegetation system and the atmosphere. The prevailing weather conditions influence the potential, or reference, ET through variables such as radiation, temperature, wind, and relativity humidity. In addition to these weather variables, actual ET (ETa) is also affected by land cover type, land cover condition, and soil moisture. ETa’s dependence on land cover and soil moisture, along with its direct relationship with carbon dioxide assimilation in plants, makes it an important variable to monitor and estimate crop yield and biomass for decision makers interested in food security, grain markets, water allocation, and carbon sequestration.
Although the estimation of ETa is the ultimate goal of many researchers for hydrological and agronomical applications, it is often difficult to quantify and requires expensive instrumentation. However, different hydrological modeling techniques are used to estimate ETa. The two broad modeling techniques can be grouped as either based on surface energy balance (e.g., [
1]; [
2]; [
3]; [
4]; [
5]) or water balance principles (e.g., [
6]; [
7]; [
8]). More recently, Wang et al. [
9] developed a regression equation to estimate ETa from a combination of net radiation, vegetation index, and temperature.
The choice of the model type depends on the availability of data and on the objective of the project. For example, the presence of cloud cover adversely impacts the surface energy balance models, but it does not impact the water balance model, which explicitly takes cloud information into consideration in the satellite-based rainfall estimation process. This feature guarantees a reliable daily ETa estimation in much of the rainfed vegetation systems regardless of cloud cover. This can be a significant advantage during the growing season in many parts of the world. On the other hand, the surface energy balance model has the advantage of estimating “total” ET irrespective of the water source, whereas the water balance model only estimates “rainfed” ET. This difference creates the opportunity to identify landscapes that meet their ET from external (e.g., stream diversion) or groundwater sources. In this study, a landscape is defined as the modeling spatial unit as determined by the resolution of the Land Surface Phenology (LSP).
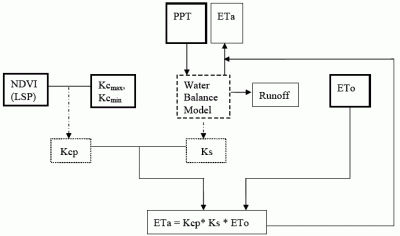
The main objective of this study is to present an improved modeling technique called
Vegetation
ET (VegET) that integrates commonly used water balance algorithms with remotely-sensed LSP-parameter (
Figure 1) to conduct operational vegetation water balance modeling at the spatial resolution of the LSP data set using readily available global data sets.
Background
The most widely used crop water balance technique for operational monitoring is the Food and Agriculture Organization (FAO) water balance algorithm by Doorenbos and Kassam [
10] that produces the crop water requirement satisfaction index (WRSI). The WRSI shows the relative relationship (ratio/percent) between the supply (from rainfall and existing soil moisture) and demand (crop demand to meet its physiological needs) using observed data from the beginning of the crop season (planting) until a specified date throughout the growing season.
The Famine Early Warning System Network (FEWS NET) demonstrated a regional implementation of the FAO WRSI in a grid-cell modeling environment [
7]. Furthermore, Senay and Verdin [
8] enhanced the geospatial model by introducing the concept of maximum allowable depletion (MAD) and soil water stress factor, commonly used in irrigation engineering, for better estimation of ETa as a function of soil water content in an operational setup (
http://earlywarning.usgs.gov/adds/). The WRSI crop water balance index has been demonstrated to be a reliable tool for crop performance monitoring of large areas in an operational manner.
However, the use of crop coefficients (Kc) in the model has certain limitations: 1) Kc factors are crop specific and require a prior knowledge of the crop planted in the area, 2) Kc factors are spatially specific since they are influenced by local climate, soils, and other geophysical conditions, and 3) the use of the Kc model requires knowledge (or assumption) of the crop calendar such as the start of season (SOS) and length of growing period (EOS) in each of the four crop developmental stages (initial, vegetative, mature, and senescence).
The VegET modeling approach presented in this paper removes the above constraints by the inclusion of the LSP parameter, which describes the seasonal progression of vegetation growth and development. LSP can be observed by spaceborne sensors and is a key biogeophysical parameter that links the water and carbon cycles with anthropogenic activities, providing an important approach to change detection in terrestrial ecosystems (e.g., [
11]; [
12]; [
13]; [
14]).
This paper will discuss the formulation of the LSP-based Kc parameter function in the VegET model and demonstrate its application using two years of daily meteorological data in the conterminous United States. To differentiate the LSP-based Kc from the commonly used “crop coefficient,” the designation Kcp (the “p” denoting the phenology-based coefficient) is used in this study.
3. Results and Discussion
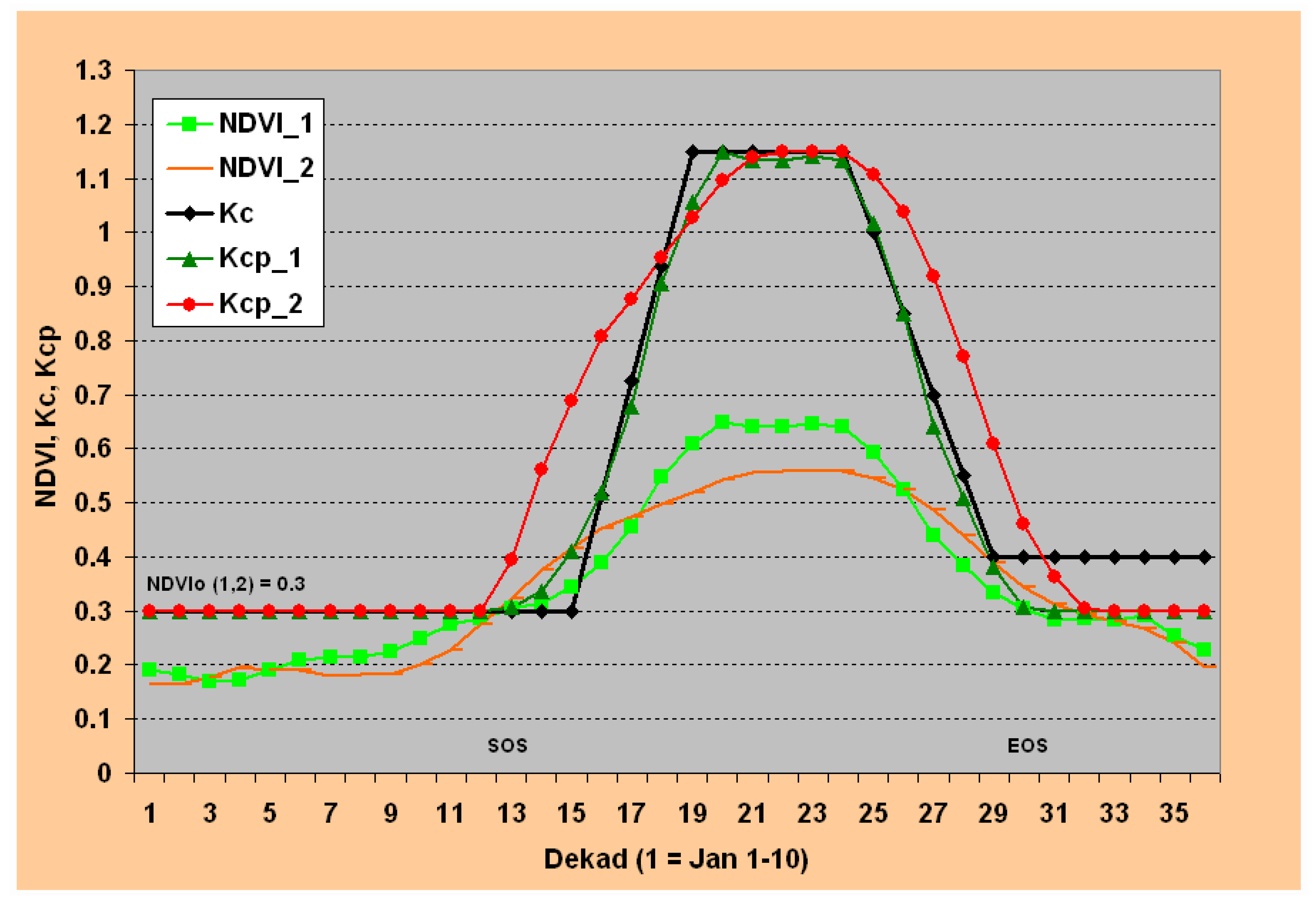
Figure 2 shows the temporal plots of dekadal NDVI climatology and the corresponding Kcp and Kc for two locations with a high proportion of herbaceous cover (potential crop pixels). The major difference between NDVI_1 and NDVI_2 profiles is that NDVI_1 contains a higher proportion of tree (T) cover (27%) and lower bare (B) cover (1%), while NDVI_2 contains a higher proportion of bare (21%) and lower tree (2%) covers. The herbaceous (H) component is comparable on both: 72% and 77% for NDVI_1 and NDVI_2, respectively. Also, NDVI_1 is located in northern Illinois with a “B1” marker, while NDVI_2 is located in northwestern North Dakota (“B21”) (
Figure 4). The numbers in the location marker such as “B1” and “B21” refer to the bare cover percentages. Both locations showed a comparable start of season by crossing the 0.3 NDVI threshold around dekad 12 (20–30 April). The overall seasonal pattern is comparable in that both experience their peak NDVI in the time period between dekad 19 and dekad 23. However, NDVI_1 shows a higher magnitude during the peak season while NDVI_2 shows a higher magnitude during the early and late season. Also, NDVI_1 crosses back the 0.3 NDVI threshold about 2 dekads earlier than NDVI_2 toward the end of season.
The corresponding Kcp patterns for NDVI_1 and NDVI_2 are shown as Kcp_1 and Kcp_2. The transformation of NDVI into Kcp patterns involves changes both in magnitude and temporal patterns. For example, in terms of peak magnitude, NDVI_1 is higher than NDVI_2. But the peak magnitude is about the same for Kcp_1 and Kcp_2 mostly because the assumption of cereal crops being grown on both locations with comparable ground cover will result in a comparable peak water-use coefficient under unlimited soil water condition. Temporally, the differences between NDVI and Kcp patterns are more pronounced during early and late seasons. On the other hand, during the dormant stages of the crops (before start of season and after end of season), the Kcp values are held constant to a minimum threshold value of 0.3. The NDVI patterns of the two locations are also close to each other during this period, unlike the peak season. From
Figure 2 it can be shown that NDVI_1 will be transformed into a crop water-use pattern (Kcp_1) characterized by a steep increase and decrease in water-use before and after the peak-season, respectively. On the other hand, NDVI_2 will be transformed into a water-use pattern (Kcp_2) characterized by a longer season with a gradual increase and decrease in water use before and after the peak growing season. The actual water use in each case will depend on the atmospheric demand (reference ET) and availability of soil moisture in the area, as shown in Equation 1.
A plot of a typical Kc profile for a cereal crop with a 170-day growing season shows that Kcp_1 closely matches with the Kc curve, indicating that the use of published Kc values will work well for this location. However, the use of a published Kc profile will not represent well the Kcp_2, which will potentially underestimate the overall vegetation water use in this example.
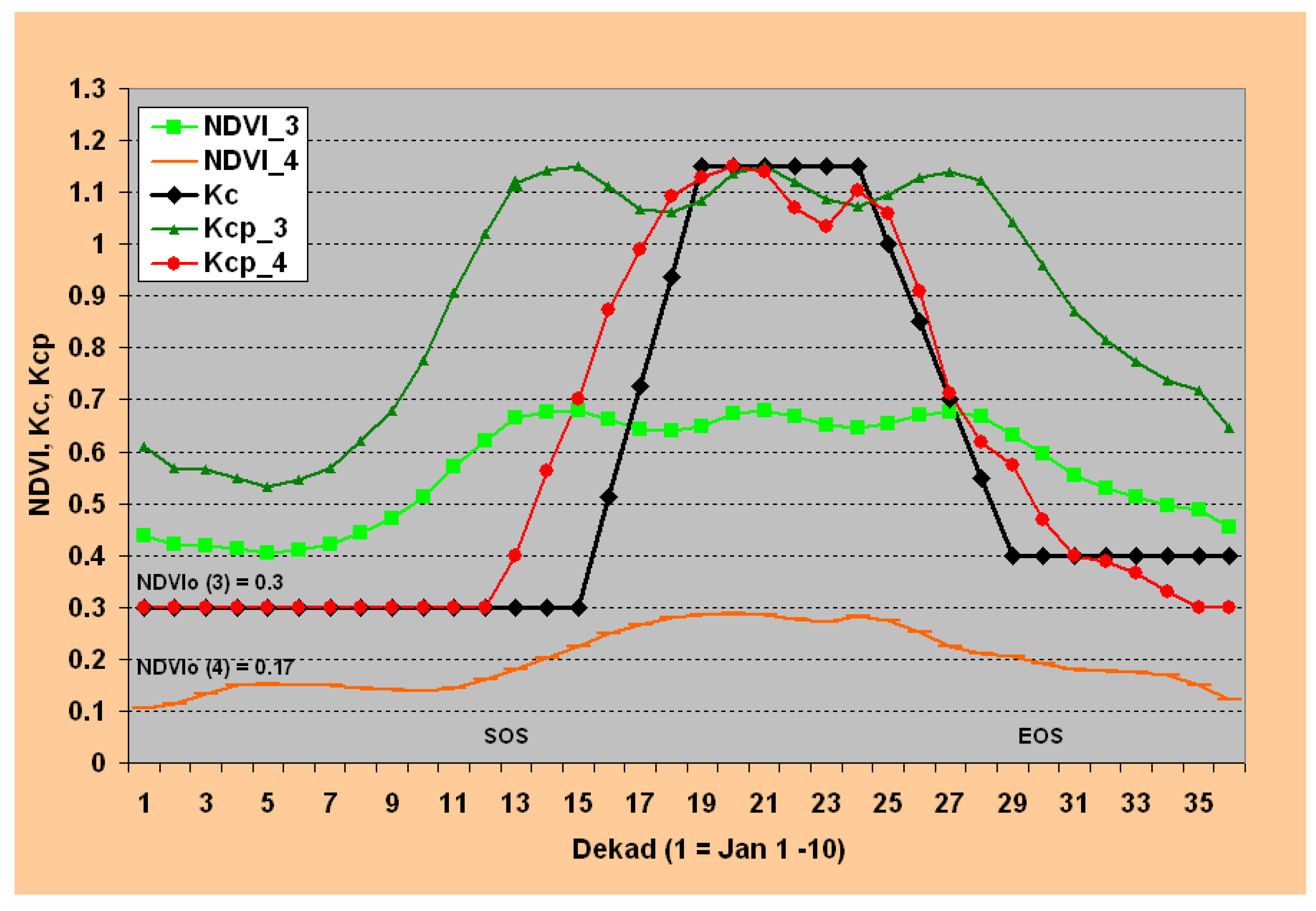
Figure 3 shows the temporal plots of dekadal NDVI climatology and the corresponding Kcp for two other locations with a relatively high proportion of tree cover (0%, 62%, 38% for bare (B), herbaceous (H), and tree (T), respectively) for NDVI_3 and a high proportion of bare areas (42%, 58%, 0% for B, H, T covers, respectively) for NDVI_4. The conversion from NDVI LSP to Kcp has a different effect on the two cover types, especially when compared to the traditional Kc-based water-use pattern. While the temporal pattern of the Kcp_4 (high bare cover) area closely follows the Kc pattern, the Kcp_4 (high tree cover) resembles that of the corresponding NDVI, except for the magnitude. Note that Kcp_4 is generated using Equation 7 to calculate the threshold NDVIo of 0.17, while Kcp_3 used the same NDVIo of 0.3 as in the case of Kcp_1 and Kcp_2 in
Figure 2. The main reason for this difference is that the maximum NDVI for NDVI_4 is less than 0.4, triggering the use of Equation 7 to estimate NDVIo. The cutoff value of 0.4 is established arbitrarily from visual inspection of several plots to handle sparsely vegetated areas. The peak NDVI is used as a measure of vegetation density. In this study, the peak NDVI magnitude was strongly correlated (r > 0.89) with the bare area percentage. From the examples of
Figure 2 and
Figure 3, NDVI_4 has the lowest peak NDVI (< 0.3) with the highest bare percentage (42%), while NDVI_3 has the highest peak NDVI (> 0.65) with a bare percentage of 0.0%.
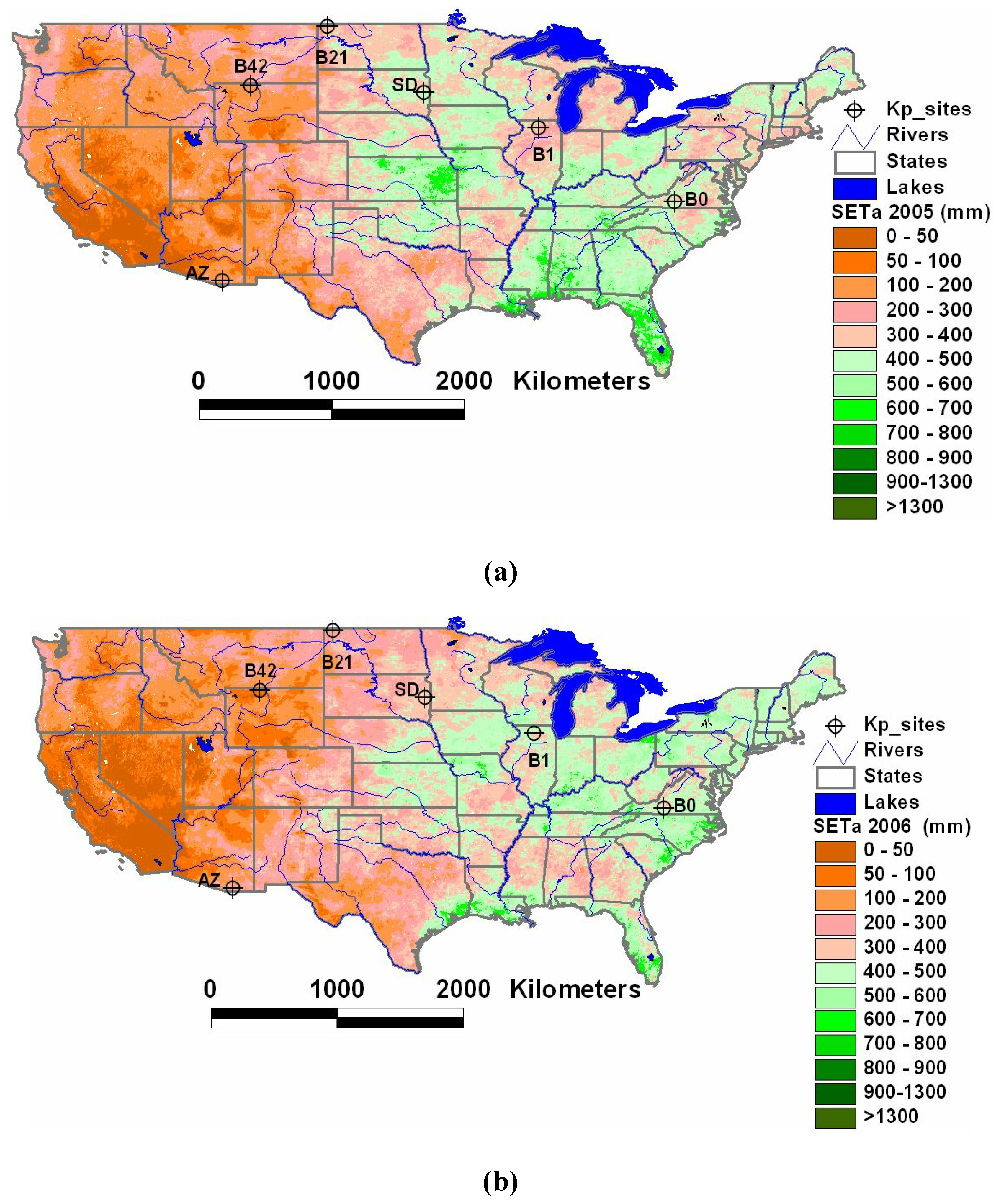
Figure 4 show the spatial distribution of seasonal (1 May through 30 September) ETa for the generic cereal crops generated using the VegET model for 2005 and 2006, respectively, at 5-km resolution. Generally, it can be observed that the eastern United States has a higher ETa than the western United States in both years, which can be attributed to higher rainfall and vegetation cover. More important for decision makers is that the VegET output shows a gradual subcounty spatial variability and a dramatic year-to-year variability in some places. For example, the 2005 ETa (
Figure 4) shows lower ETa (drought) in Illinois, Pennsylvania, and North Carolina with seasonal ETa values as low as 300 mm. By contrast, in 2006, the drought was located in the Dakotas, Oklahoma/Kansas, and Alabama/Georgia. These drought incidences have been reported by various organizations.
Figure 4.
Seasonal VegETa ETa (May–September) maps for 2005 (a) and 2006 (b). Kp_sites refer to locations where the Kcp (B1 – B42) and AmerixFlux (SD, AZ) latent flux data were extracted.
Figure 4.
Seasonal VegETa ETa (May–September) maps for 2005 (a) and 2006 (b). Kp_sites refer to locations where the Kcp (B1 – B42) and AmerixFlux (SD, AZ) latent flux data were extracted.
Furthermore, preliminary analysis with crop yield data has shown a strong correlation between seasonal ETa and wheat yield in South Dakota, where ETa has explained 60% of the spatial yield variation in 2005 and 2006. The yield decrease from 2005 to 2006 was correctly identified in most counties in South Dakota [
23].
It should be pointed out that the relatively low ET in the wet part of the northwest of the US can be explained by two important reasons: 1) the accumulation period for the ET map is between May and September, a generally dry time for the region and 2) the VegET model only monitors rainfed systems and does not take into account snowmelt sources that supply moisture to the natural vegetation and irrigation systems during the dry period. Although the VegET model was run assuming a generic cereal crop over the landscape, the relative ETa spatial distribution will also apply to other natural vegetation types that obtain their water from rainfall since the maximum crop coefficient value for cereal crop and natural vegetation such as grassland is comparable for similar ground cover fraction.
The low ETa for the western part of the United States is mainly a result of the shortage of precipitation and thus the lack of adequate soil water, which affects the Ks factor in Equation 2. From the cereal crop assumption covering the whole modeling unit, these seasonal ETa estimates, despite their low value in the arid and semiarid west, are probably exaggerated on the high side because of the assumption of Kc
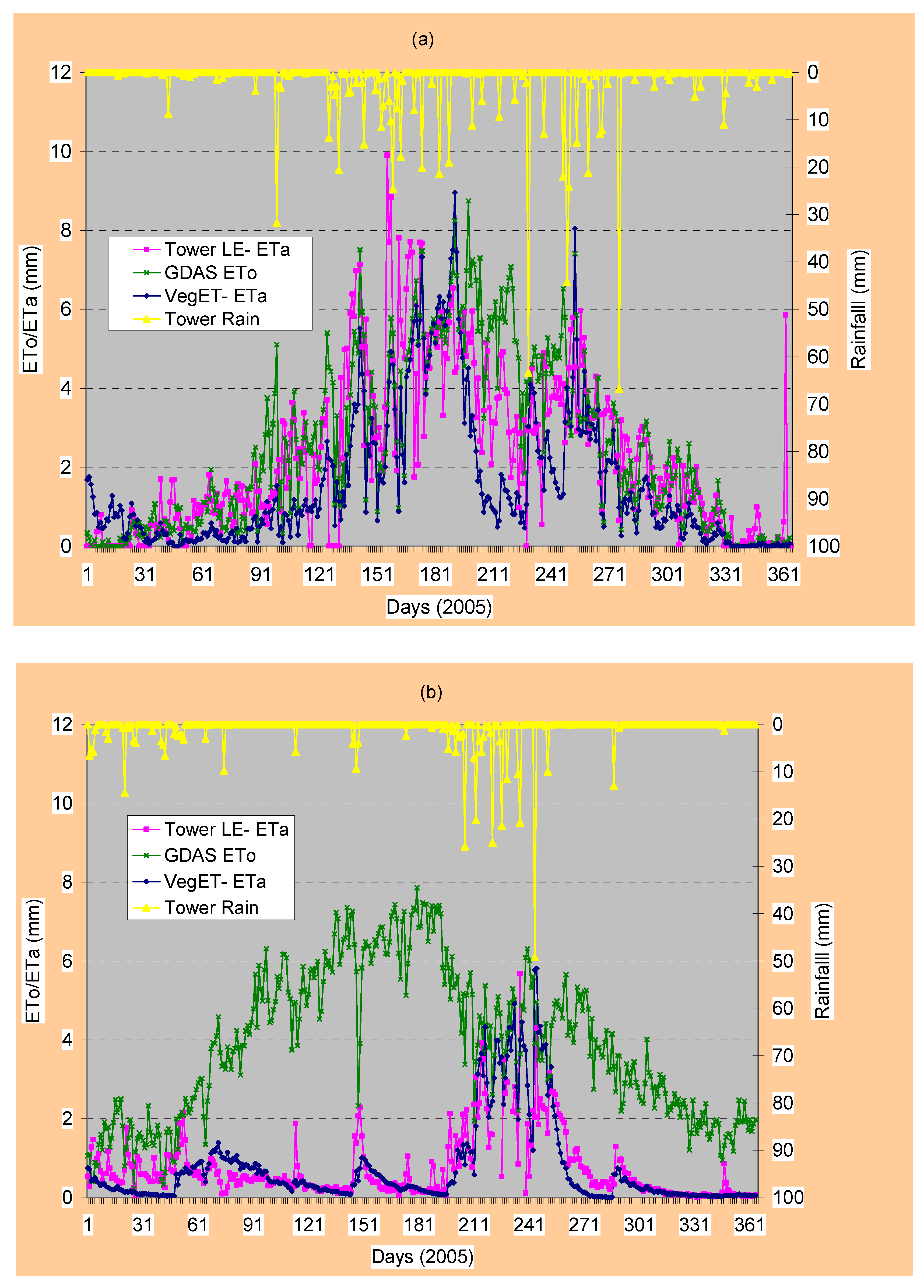
max for the entire modeling cell. However, the relative spatial distribution in water use (ETa) is expected to represent the situation in the field as it is demonstrated by flux tower data on two locations with different climate (
Figure 5a and
Figure 5b).
Figure 5a and
Figure 5b show a validation of the VegET ETa results using AmeriFlux tower eddy covariance latent heat flux measurements.
Figure 5a shows these relationships using flux tower data from Brookings, South Dakota, in a crop/grassland environment, while
Figure 5b shows the same relationship in the semiarid grassland of Audubon, Arizona. On both sites, the flux tower latent heat flux ETa and VegET ETa tracked well, capturing the seasonality of ETa with comparable magnitudes. The major difference between the two sites is that the ETa was much lower than the ETo during the dormant vegetation growing season in the Arizona site. This difference indicates the importance of rainfall/soil moisture or supplemental irrigation for achieving higher magnitudes of ETa in such environments. On the other hand, the relationship in Brookings, South Dakota, shows that, although both the VegET and flux tower latent heat ET track well, their magnitude is very close to ETo in much of the season. This indicates the limiting factor to increasing vegetation water use for more biomass production is the available energy in the form of net radiation.
The overall performance of the VegET when compared to the latent heat flux data points is encouraging in the two different environments. The day-to-day correlation coefficient between VegET ETa and flux tower latent heat flux (LE) is 0.72 and 0.74 for South Dakota and Arizona. The respective correlation coefficients improved to 0.87 and 0.88 when the data were aggregated on 10-day time periods. These results are particularly encouraging considering the flux tower latent heat ETa data contain some suspiciously high magnitudes and extreme fluctuations from day to day in some cases. For example, in South Dakota, flux tower LE ETa was higher than ETo in 188 days out of 365. The ETo is expected to provide the upper boundary of ETa under unlimited moisture conditions. This is an indication that the flux tower LE is probably overestimating at the South Dakota site. Another example that shows the extreme fluctuation is the unseasonably high flux tower LE ETa estimate of 5.8 mm on 31 December 2005 (day number 365,
Figure 5a). The problem with the Arizona flux tower data was that it was missing 11 days during the critical growing season (high ETa periods) and suspected too low values in the days next to the missing days. Overall, VegET ETa and flux tower latent heat flux data tracked very well even during the winter months at the Arizona site.
Figure 5.
Validation of VegET ETa using AmeriFlux data in a grass/cropland region of Brookings, South Dakota (a), and a semiarid grassland region of Audubon, Arizona (b), using daily data from 2005.
Figure 5.
Validation of VegET ETa using AmeriFlux data in a grass/cropland region of Brookings, South Dakota (a), and a semiarid grassland region of Audubon, Arizona (b), using daily data from 2005.
4. Conclusions
The main objective of the study was to present a simplified modeling technique called VegET that blends a commonly used vegetation water balance algorithm with LSP derived from remotely sensed data for estimating landscape ETa anywhere in the world.
A set of simplified linear equations are presented to convert NDVI-based LSPs into Kcp, which is comparable in purpose with that of the Kc described in [
6]. These equations contain some threshold parameters that the user can adjust depending on the source of the LSP.
The VegET model was run using daily weather data for two years for the conterminous United States using NDVI climatology derived from the AVHRR data set. The daily model runs were aggregated to produce two seasonal maps that reflected the general crop performance and drought incidences in 2005 and 2006. In addition, daily ETa estimates for AmeriFlux tower sites in Brookings, South Dakota, and Audubon, Arizona, tracked well the ETa estimates from flux tower measurements using the eddy covariance method. Despite concerns in the quality of the flux tower data, the day-to-day correlation coefficient between VegET ETa and raw tower latent heat flux data was greater than 0.71 on both flux tower sites. The correlation coefficient improved to greater than 0.87 using 10-day moving average data sets. Further research is required to evaluate the performance of the approach and the sensitivity of the few model parameters using more diverse data in different hydroclimatic regions of the world.
Particularly, the VegET model brings several advantages for operational monitoring of soil water changes and ET for drought monitoring and large area water balance modeling. The blending of a hydrological model and vegetation index will allow the possibility of quantifying ET at a higher spatial scale, even when the rainfall is at a coarser spatial scale. This is possible because ET is affected by land cover while rainfall is generally a function of location, especially at longer time steps (days and season). Since global data sets tend to be coarse for rainfall and ETo while NDVI is available at higher resolutions (less than 1 km), the approach will allow the use of global data sets for localized monitoring and decision making.
The other advantages of using the LSP in VegET is the potential for predicting ETa patterns with changing land use and land cover types. The exercise will simply involve the replacing of modeling units using predicted LSP from land use and land cover change models. For example, if a land cover is expected to convert from grassland to cropland, the VegET model will run using LSPs derived from cropland in the same region. Thus, the VegET model can be used for testing scenarios of climate change under different climate (rainfall and ETo) and land cover changes.
Because the VegET model runs on daily or longer time steps with little effort for model setup and operation, the VegET modeling approach was demonstrated to have a promising application for drought monitoring and early warning applications at various spatial and time scales for rainfed sytems. The model can be made operational easily for any location where there is spatially explicit data on NDVI climatology, rainfall, reference ET, and soils with little or no requirement to recalibrate or develop site-specific regression equations. All required data sets are now available for different parts of the world at different resolutions.