A Review of Virtual Sensing Algorithms for Active Noise Control
Abstract
:1. Introduction
2. Spatially Fixed Virtual Sensing Algorithms
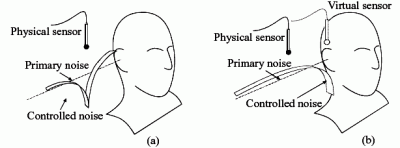
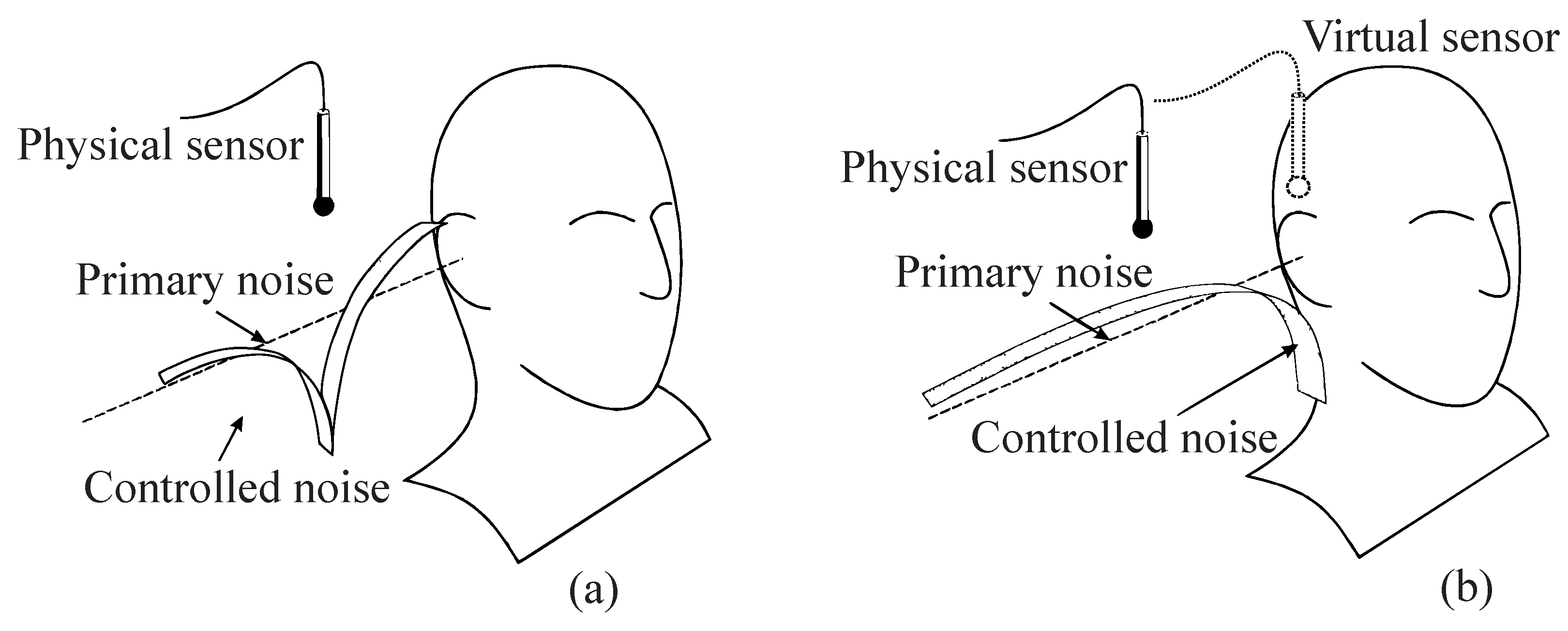
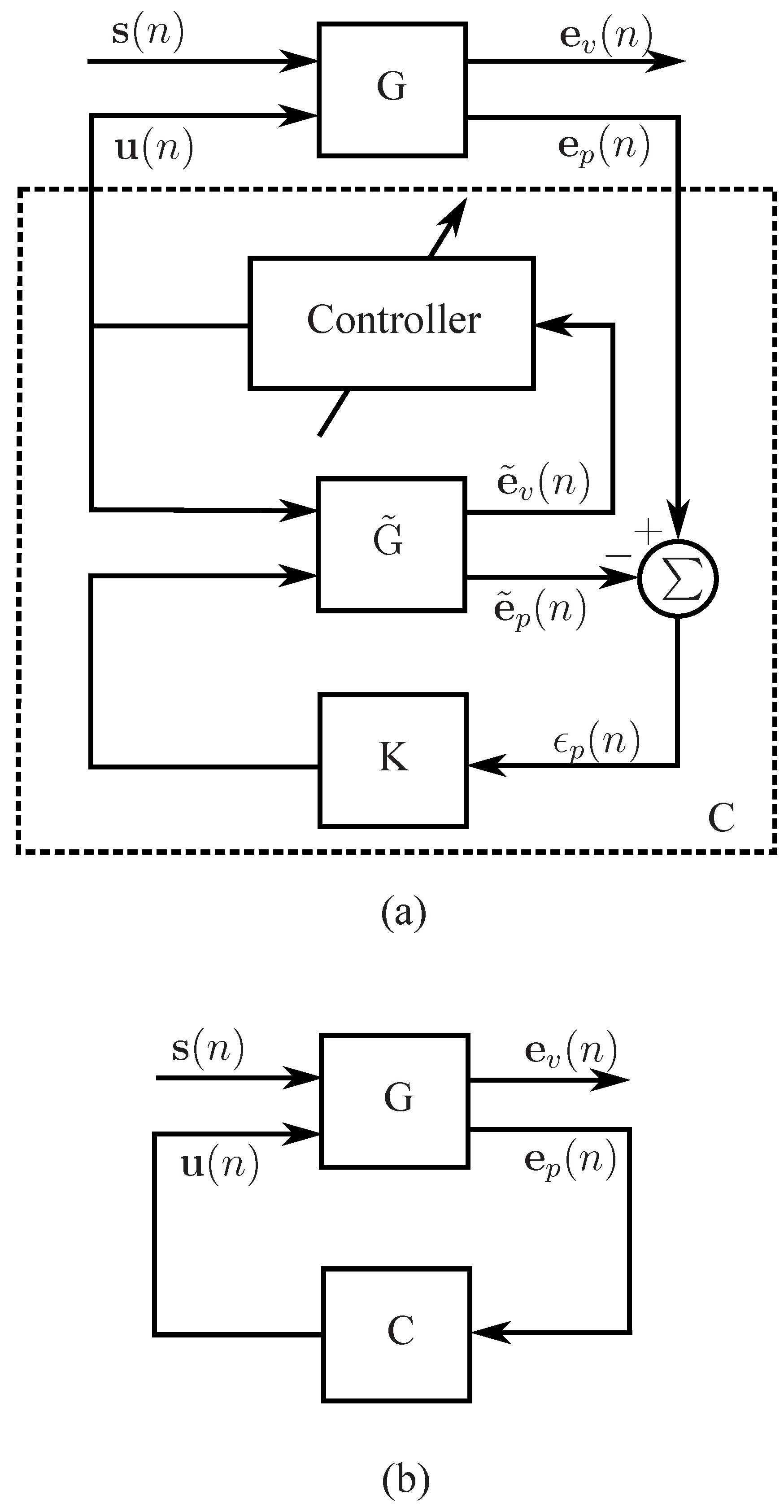
2.1. The virtual sensing problem
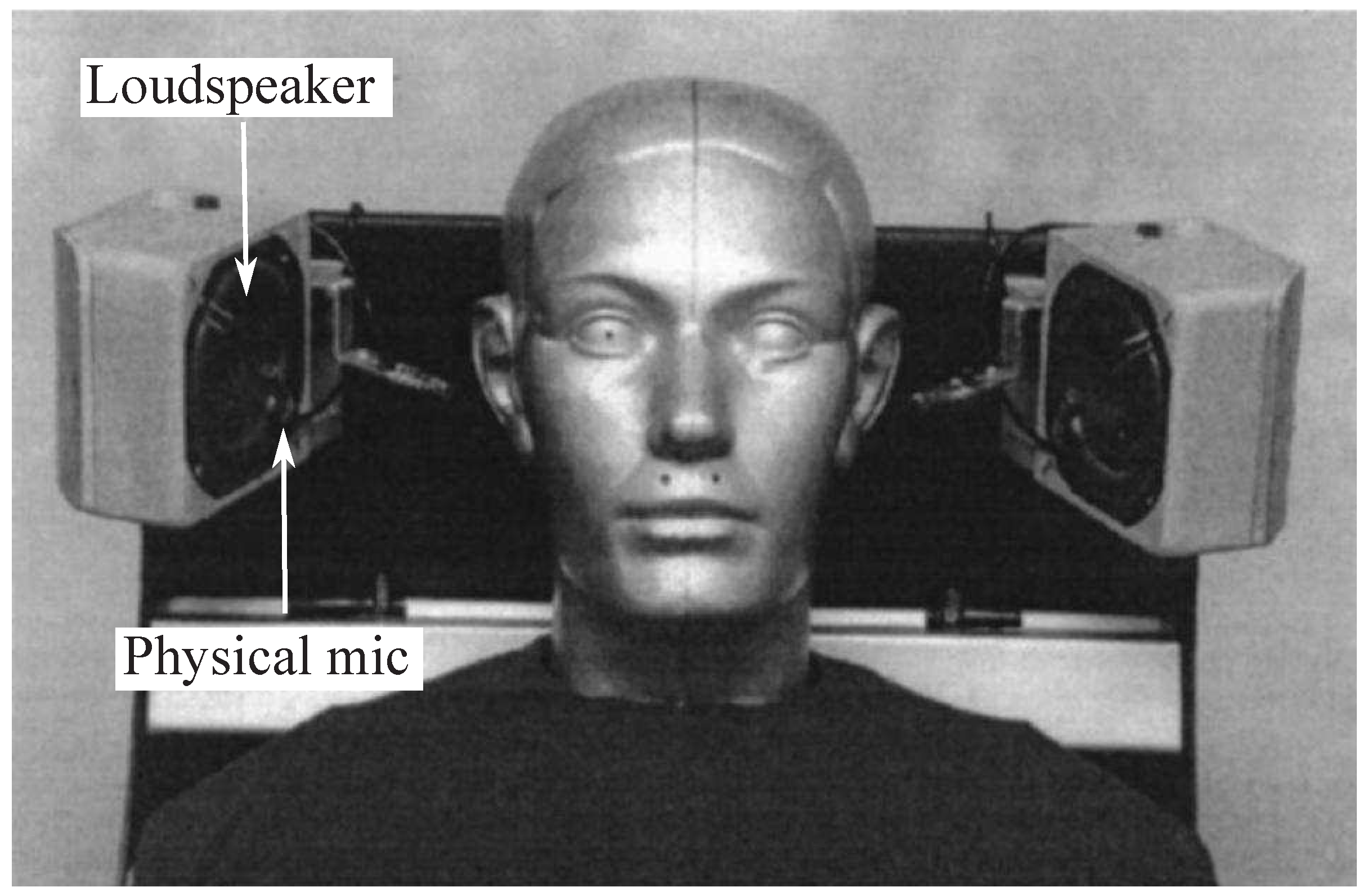
2.2. The virtual microphone arrangement
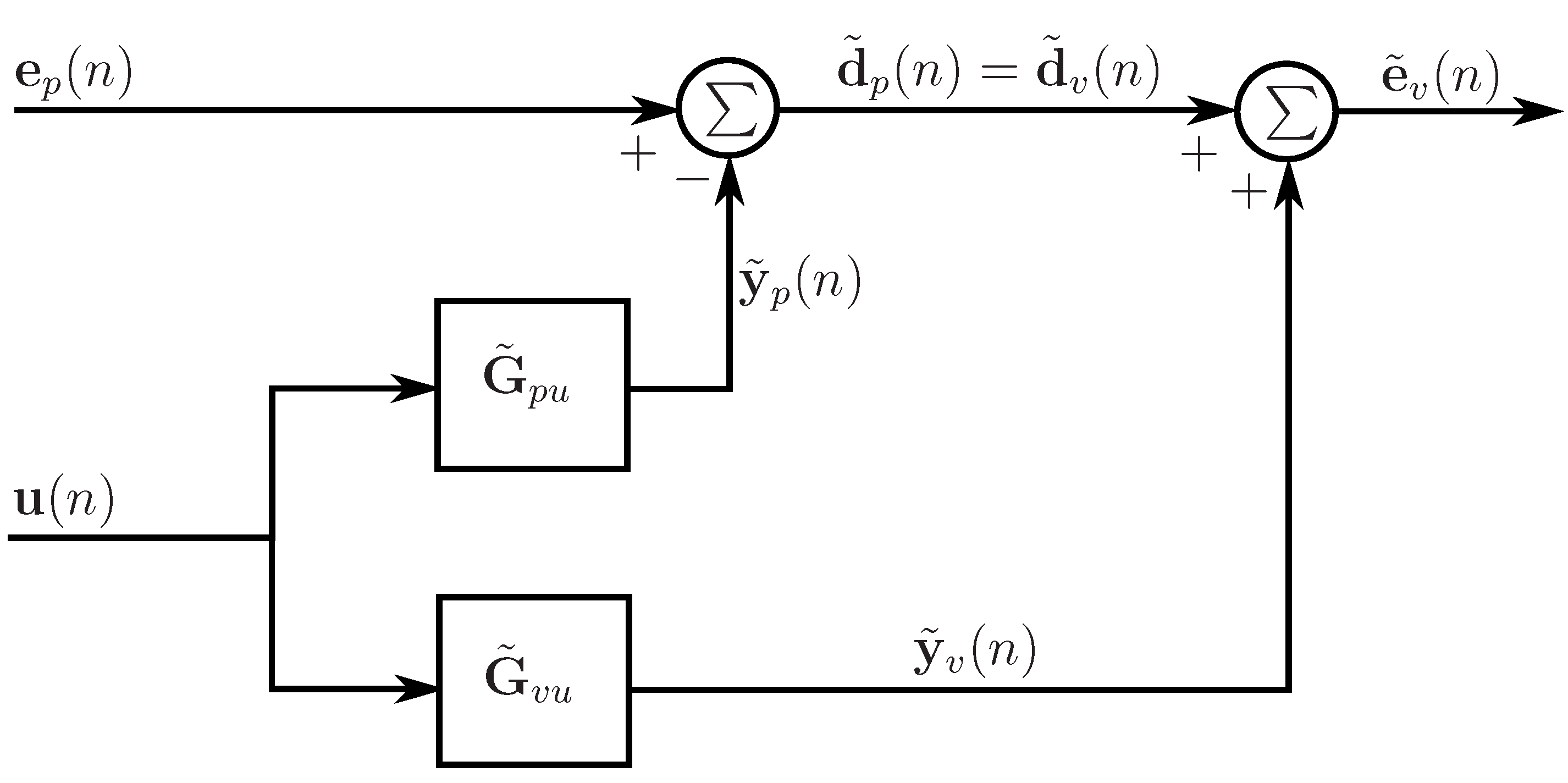
2.3. The remote microphone technique
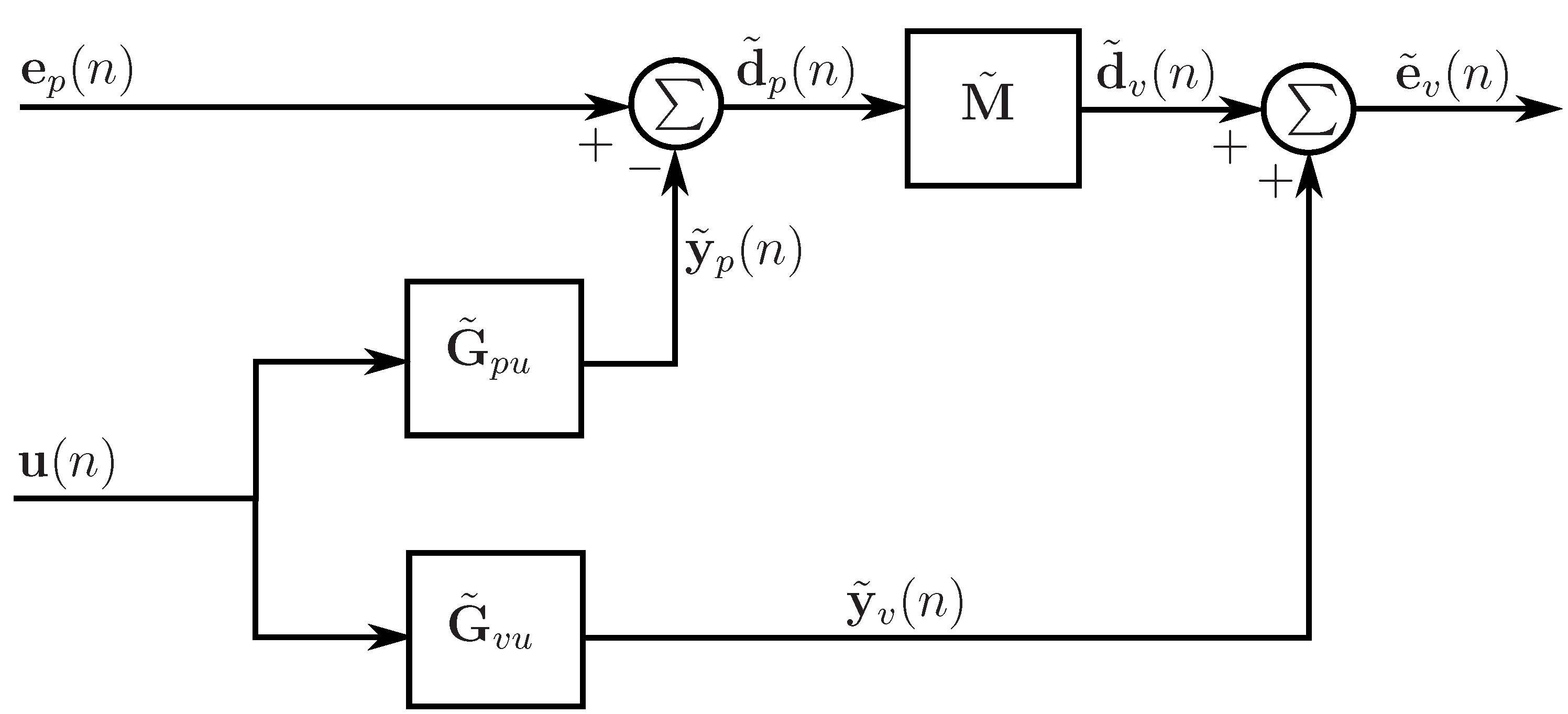
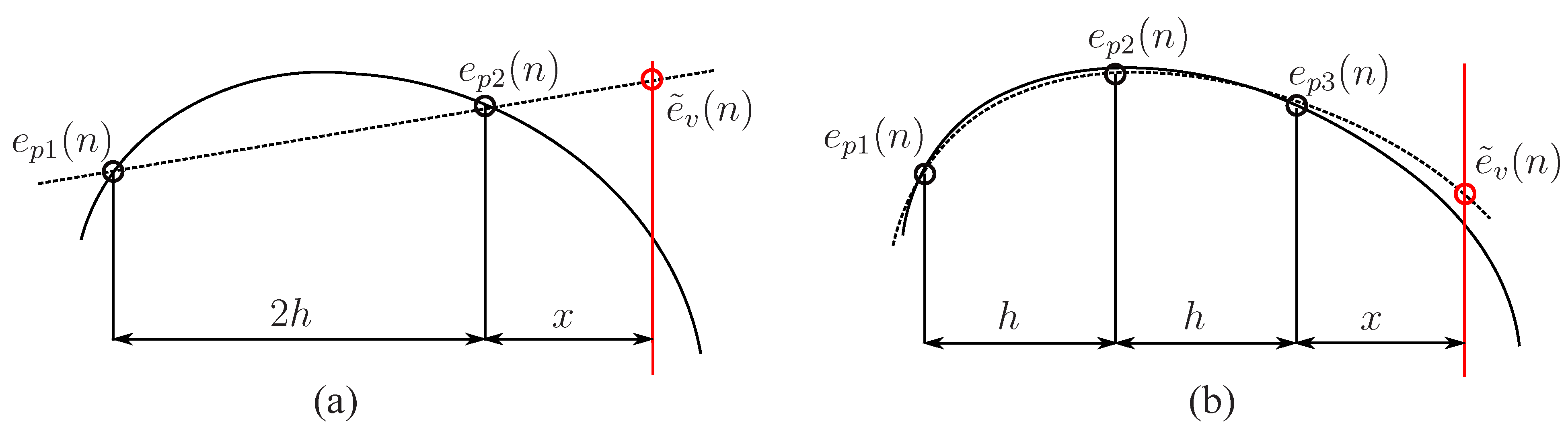
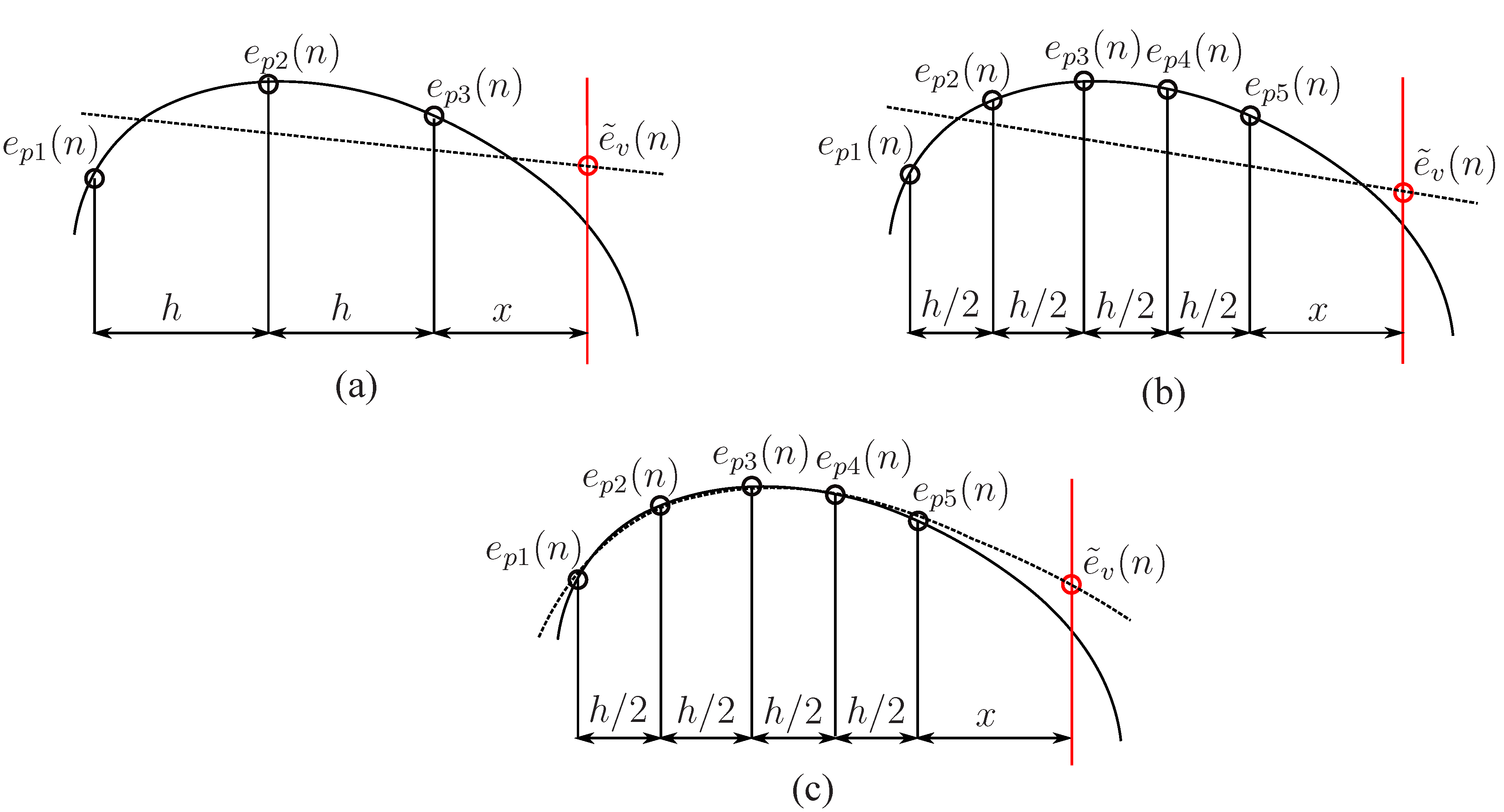
2.4. The forward difference prediction technique
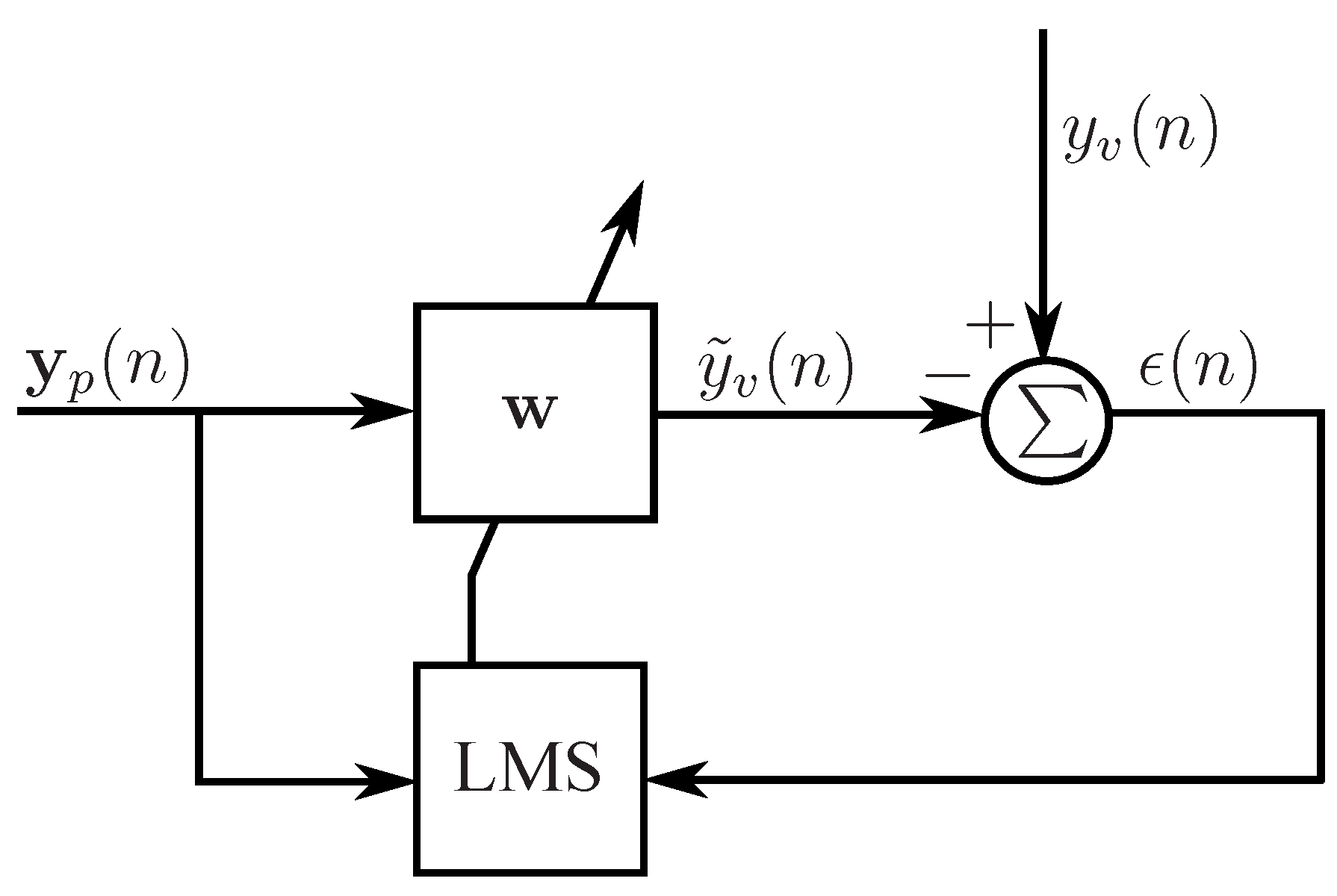
2.5. The adaptive LMS virtual microphone technique
2.6. The Kalman filtering virtual sensing method
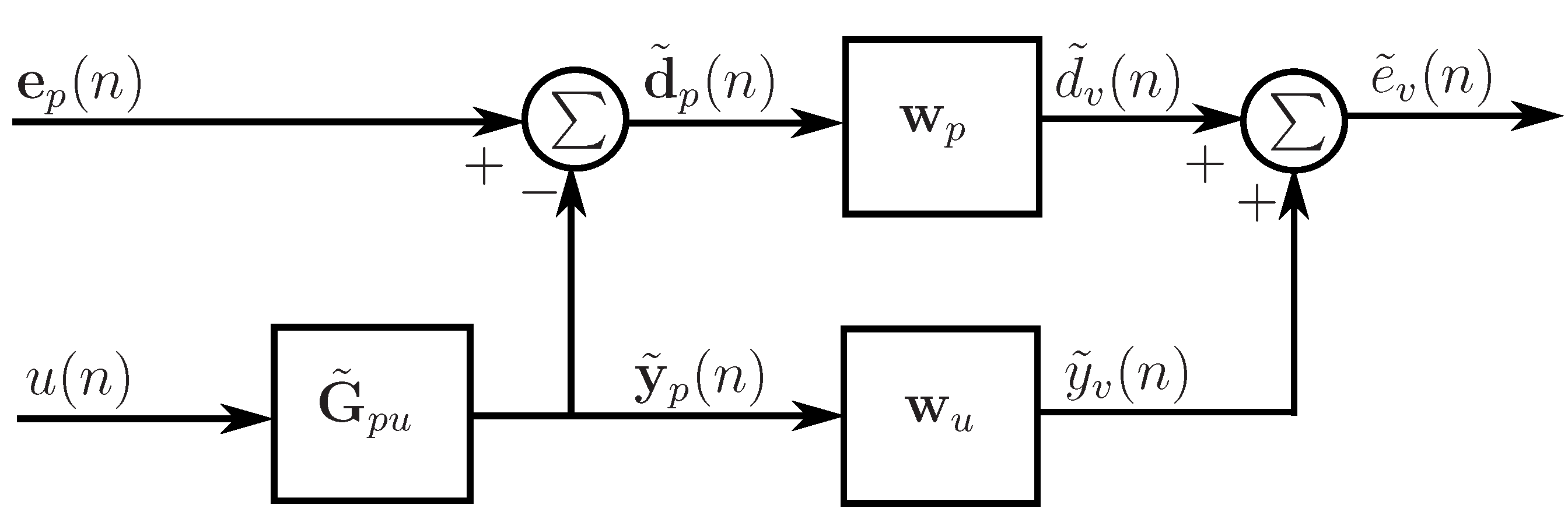
- Temporarily locate physical sensors at the spatially fixed virtual locations and measure an input-output data-set
- Use subspace identification techniques [54] to estimate an innovations model of the physical and virtual error signalsand estimate the covariance matrix of the white innovation signals
- Implement the Kalman filtering virtual sensing method aswhere the Kalman gain matrix and the virtual innovation gain matrix are calculated as followswith , the unique solution to the discrete algebraic Riccati equation given by
2.7. The stochastically optimal tonal diffuse field virtual sensing method
3. Moving Virtual Sensing Algorithms
3.1. The remote moving microphone technique
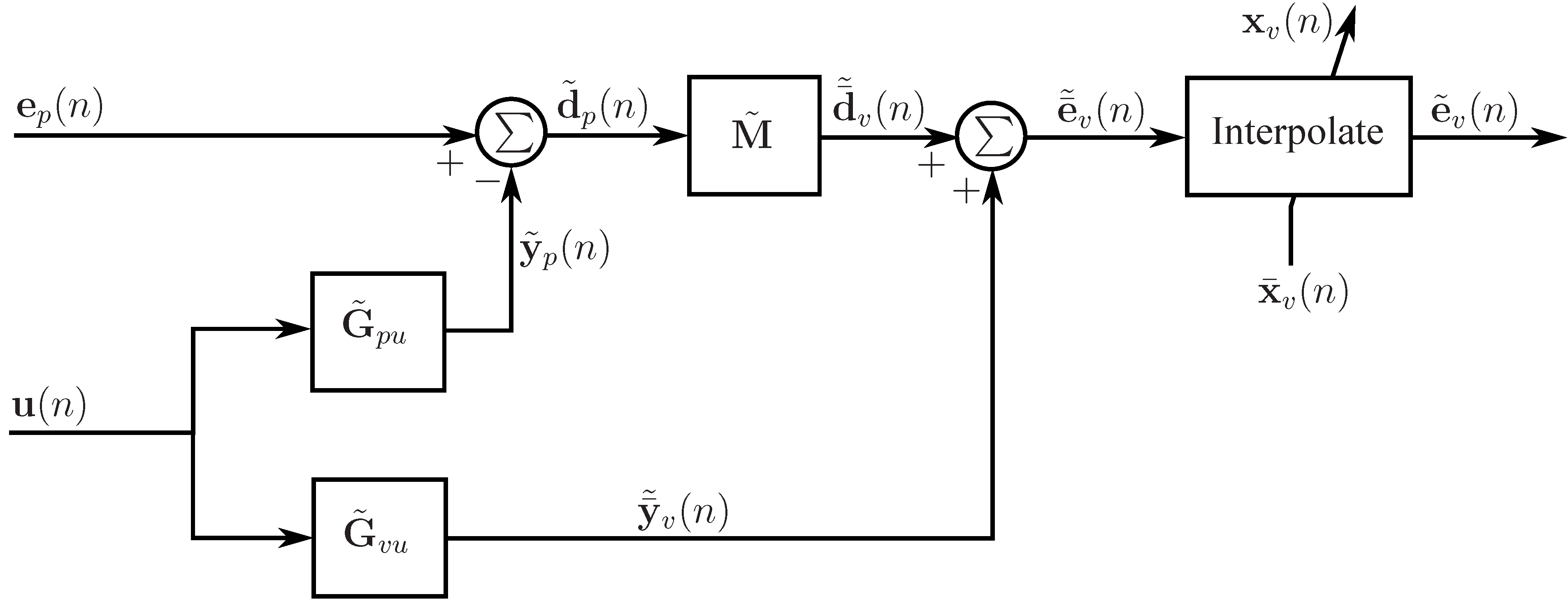
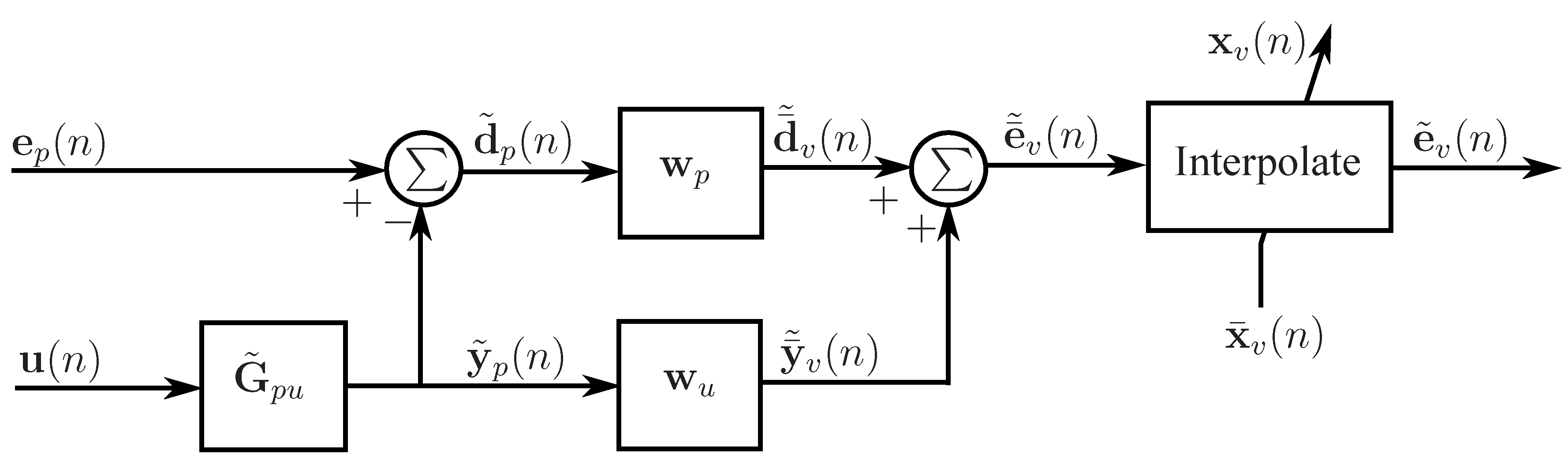
3.2. The adaptive LMS moving virtual microphone technique
3.3. The Kalman filtering moving virtual sensing method
4. Conclusion
| Algorithm | Characteristics | Advantages | Disadvantages |
|---|---|---|---|
| The virtual microphone arrangement [4] | Generates a spatially fixed virtual microphone using models of the secondary transfer functions at the physical and virtual locations and the assumption that the primary disturbance at the physical location is equal to the primary disturbance at the virtual location. | • Requires a preliminary identification stage. • Uses the assumption of equal primary sound pressure at the physical and virtual locations. • Is not robust to changes in the sound field that alter the transfer functions between the sensors and the sources. | |
| The remote microphone technique [5] | Generates a spatially fixed virtual microphone in an extension to the virtual microphone arrangement [4] using an additional filter to compute an estimate of the primary disturbance at the virtual microphone from the primary disturbance at the physical microphone. | • Theoretically obtains a perfect estimate of the tonal disturbance provided accurate models of the tonal transfer functions are obtained. • Does not use the assumption of equal primary sound pressure at the physical and virtual locations. | • Requires a preliminary identification stage. • Is not robust to changes in the sound field that alter the transfer functions between the sensors and the sources. |
| The forward difference prediction technique [6] | Generates spatially fixed virtual microphones and energy density sensors by fitting a polynomial to the signals from a number of physical microphones in an array. This polynomial is then extrapolated to the virtual location. | • Is a fixed gain technique. • Is robust to changes in the sound field that may alter the transfer functions between the sensors and the sources. • Does not require a preliminary identification stage or FIR filters or similar to model the complex transfer functions. | • Is only suitable for use in low frequency sound fields and for small virtual distances. • Is sensitive to phase and sensitivity mismatches and relative position errors between the physical microphones. • Second order estimate is ill-conditioned and is adversely affected by short wavelength extraneous noise. |
| The adaptive LMS virtual microphone technique [7] | Generates a spatially fixed virtual microphone by employing the LMS algorithm to adapt the weights of physical microphones in an array so that the weighted sum of these signals minimises the mean square difference between the predicted pressure and that measured at the virtual location. | • Can compensate for relative position errors and sensitivity mismatches adversely affecting the forward difference prediction technique | • Requires a preliminary identification stage. • Is not robust to changes in the sound field that alter the transfer functions between the sensors and the sources. |
| The Kalman filtering virtual sensing method [8] | Generates a spatially fixed virtual microphone using Kalman filtering theory. | • Uses a compact state space model instead of FIR or IIR filter matrices. •Is derived including measurement noise on the sensors. •Estimation is optimal given a known or measured noise covariance. | • Requires a preliminary identification stage. •Is limited to use in systems of relatively low order. |
| The stochastically optimal tonal diffuse field virtual sensing method [9] | Generates stochastically optimal spatially fixed virtual microphones and energy density sensors using the correlation functions between the physical and virtual quantities in a pure tone diffuse sound field. | • Is a fixed gain technique. •Can compensate for changes in the sound field that alter the transfer functions between the sensors and the sources. •Does not require a preliminary identification stage or FIR filters or similar to model the complex transfer functions. | • Estimation performance decreases with increasing virtual distance. •Only suitable for use in pure tone diffuse sound fields. |
| The remote moving microphone technique [10] | Generates a moving virtual microphone by interpolating the virtual error signals at a number of spatially fixed virtual locations estimated using the remote microphone technique [5]. | • Virtual microphone can track the desired location of attenuation as it moves through the sound field. | •Requires a preliminary identification stage. •Is not robust to changes in the sound field that alter the transfer functions between the sensors and the sources. |
| The adaptive LMS moving virtual microphone technique [11] | Generates a moving virtual microphone by interpolating the virtual error signals at a number of spatially fixed virtual locations estimated using the adaptive LMS virtual microphone technique [7]. | • Virtual microphone can track the desired location of attenuation as it moves through the sound field. | • Requires a preliminary identification stage. •Is not robust to changes in the sound field that alter the transfer functions between the sensors and the sources. |
| The Kalman filtering moving virtual sensing method [12] | Generates a moving virtual microphone by interpolating the virtual error signals at a number of spatially fixed virtual locations estimated using the Kalman filtering virtual sensing method [8]. | • Virtual microphone can track the desired location of attenuation as it moves through the sound field. •Implemented using a compact state space model instead of FIR or IIR filter matrices. •Is derived including measurement noise on the sensors. | • Requires a preliminary identification stage. •Is limited to use in systems of relatively low order. |
References and Notes
- Elliott, S.; Joseph, P.; Bullmore, A.; Nelson, P. Active cancellation at a point in a pure tone diffuse sound field. Journal of Sound and Vibration 1988, 120(1), 183–189. [Google Scholar] [CrossRef]
- Nelson, P.; Elliott, S. Active Control of Sound, 1st edition; Academic Press: London, 1992. [Google Scholar]
- Elliott, S.; Garcia-Bonito, J. Active cancellation of pressure and pressure gradient in a diffuse sound field. Journal of Sound and Vibration 1995, 186(4), 696–704. [Google Scholar] [CrossRef]
- Elliott, S.; David, A. A virtual microphone arrangement for local active sound control. In Proceedings of the 1st International Conference on Motion and Vibration Control, Yokohama, 1992; pp. 1027–1031.
- Roure, A.; Albarrazin, A. The remote microphone technique for active noise control. Proceedings of Active 99 1999, 1233–1244. [Google Scholar]
- Cazzolato, B. Sensing systems for active control of sound transmission into cavities. PhD thesis, School of Mechanical Engineering, The University of Adelaide, SA, 5005, 1999. [Google Scholar]
- Cazzolato, B. An adaptive LMS virtual microphone. In Proceedings of Active 02, Southampton, UK, 2002; pp. 105–116.
- Petersen, C.; Fraanje, R.; Cazzolato, B.; Zander, A.; Hansen, C. A Kalman filter approach to virtual sensing for active noise control. Mechanical Systems and Signal Processing 2008, 22(2), 490–508. [Google Scholar] [CrossRef]
- Moreau, D.; Ghan, J.; Cazzolato, B.; Zander, A. Active noise control with a virtual acoustic sensor in a pure-tone diffuse sound field. In Proceedings of the 14th International Congress on Sound and Vibration, Cairns, Australia, 2007.
- Petersen, C.; Cazzolato, B.; Zander, A.; Hansen, C. Active noise control at a moving location using virtual sensing. In Proceedings of the 13th International Congress on Sound and Vibration, Vienna, 2006.
- Petersen, C.; Zander, A.; Cazzolato, B.; Hansen, C. A moving zone of quiet for narrowband noise in a one-dimensional duct using virtual sensing. Journal of the Acoustical Society of America 2007, 121(3), 1459–1470. [Google Scholar] [CrossRef] [PubMed]
- Petersen, C. Optimal spatially fixed and moving virtual sensing algorithms for local active noise control. PhD thesis, School of Mechanical Engineering, The University of Adelaide, SA, 5005, 2007. [Google Scholar]
- Kuo, S.; Morgan, D. Active Noise Control Systems, Algorithms and DSP Implementation; John Wiley and Sons Inc: New York, 1996. [Google Scholar]
- Elliott, S. Signal Processing for Active Control; Academic Press: London, 2001. [Google Scholar]
- Kuo, S.; Gan, W.; Kalluri, S. Virtual sensor algorithms for active noise control systems. In Proceedings of the 2003 International Symposium on Intelligent Signal Processing and Communication Systems (ISPACS 2003), Awaji Island, Japan, 2003; pp. 714–719.
- Pawelczyk, M. Adaptive noise control algorithms for active headrest system. Control Engineering Practice 2004, 12(9), 1101–1112. [Google Scholar] [CrossRef]
- Pawelczyk, M. Design and analysis of a virtual-microphone active noise control system. In Proceedings of the 12th International Congress on Sound and Vibration, Lisbon, Portugal, 2005; pp. 1–8.
- Garcia-Bonito, J.; Elliott, S.; Boucher, C. A virtual microphone arrangement in a practical active headrest. Proceedings of Inter-noise 96 1996, 1115–1120. [Google Scholar]
- Garcia-Bonito, J.; Elliott, S.; Boucher, C. Generation of zones of quiet using a virtual microphone arrangement. Journal of the Acoustical Society of America 1997, 101(6), 3498–3516. [Google Scholar] [CrossRef]
- Garcia-Bonito, J.; Elliott, S. Strategies for local active control in diffuse sound fields. In Proceedings of Active 95, Newport Beach, CA, USA, 1995; pp. 561–572.
- Garcia-Bonito, J.; Elliott, S.; Boucher, C. A novel secondary source for a local active noise control system. In Proceedings of Active 97, Budapest, Hungary, 1997; pp. 405–418.
- Rafaely, B.; Garcia-Bonito, J.; Elliott, S. Feedback control of sound in headrest. In Proceedings of Active 97, Budapest, 1997; pp. 445–456.
- Rafaely, B.; Elliott, S.; Garcia-Bonito, J. Broadband performance of an active headrest. Journal of the Acoustical Society of America 1999, 106(2), 787–793. [Google Scholar] [CrossRef] [PubMed]
- Horihata, S.; Matsuoka, S.; Kitagawa, H.; Ishimitsu, S. Active noise control by means of virtual error microphone system. In Proceedings of Inter-Noise 97, Budapest, 1997; pp. 529–532.
- Pawelczyk, M. Noise control in the active headrest based on estimated residual signals at virtual microphones. In Proceedings of the 10th International Congress on Sound and Vibration, Stockholm, Sweeden, 2003; pp. 251–258.
- Pawelczyk, M. A double input-quadruple output adaptive controller for the active headrest system. In Proceedings of the Active Noise and Vibration Control Methods Conference, Cracow, Poland, 2003.
- Pawelczyk, M. Multiple input-multiple output adaptive feedback control strategies for the active headrest system: design and real-time implementation. International Journal of Adaptive Control and Signal Processing 2003, 17(10), 785–800. [Google Scholar] [CrossRef]
- Pawelczyk, M. Active noise control in a phone. In Proceedings of the 11th International Congress on Sound and Vibration, St Petersburg, Russia, 2004; pp. 523–530.
- Pawelczyk, M. Polynomial approach to design of feedback virtual-microphone active noise control system. In Proceedings of the 13th International Congress on Sound and Vibration, Vienna, Austria, 2006.
- Diaz, J.; Egana, J.; Vinolas, J. A local active noise control system based on a virtual-microphone technique for railway sleeping vehicle applications. Mechanical Systems and Signal Processing 2006, 20, 2259–2276. [Google Scholar] [CrossRef]
- Matuoka, S.; Kitagawa, H.; Horihata, S.; Ishimitu, S.; Tamura, F. Active noise control using a virtual error microphone system. Transactions of the Japan Society of Mechanical Engineers 1996, 62(601), 3459–3464. [Google Scholar] [CrossRef]
- Holmberg, U.; Ramner, N.; Slovak, R. Low complexity robust control of a headrest system based on virtual microphones and the internal model principle. In Proceedings of Active 02, ISVR, Southampton, UK, 2002; pp. 1243–1250.
- Popovich, S. Active acoustic control in remote regions. US Patent No 5,701,350, 1997. [Google Scholar]
- Hashimoto, H.; Terai, K.; Kiba, M.; Nakama, Y. Active noise control for seat audio system. In Proceedings of Active 95, Newport Beach, CA, USA, 1995; pp. 1279–1290.
- Friot, E.; Roure, A.; Winninger, M. A simplified remote microphone technique for active noise control at virtual error sensors. In Proceedings of Inter-Noise 01, The Hague, The Netherlands, 2001.
- Yuan, J. Virtual sensing for broadband noise control in a lightly damped enclosure. Journal of the Acoustical Society of America 2004, 116(2), 934–941. [Google Scholar] [CrossRef] [PubMed]
- Radcliffe, C.; Gogate, S. A model based feedforward noise control algorithm for vehicle interiors. Advanced Automotive Technologies ASME 52(DSC) 1993, 299–304. [Google Scholar]
- Berkhoff, A. Control strategies for active noise barriers using near-field error sensing. Journal of the Acoustical Society of America 2005, 118(3), 1469–1479. [Google Scholar] [CrossRef]
- Renault, S.; Rymeyko, F.; Berry, A. Active noise control in enclosure with virtual microphone. Canadian Acoustics 2000, 28(3), 72–73. [Google Scholar]
- Kestell, C. Active control of sound in a small single engine aircraft cabin with virtual error sensors. PhD thesis, School of Mechanical Engineering, The University of Adelaide, SA, 5005, 2000. [Google Scholar]
- Kestell, C.; Hansen, C.; Cazzolato, B. Virtual sensors in active noise control. Acoustics Australia 2001, 29(2), 57–61. [Google Scholar]
- Kestell, C.; Hansen, C.; Cazzolato, B. Active noise control in a free field with virtual error sensors. Journal of the Acoustical Society of America 2001, 109(1), 232–243. [Google Scholar] [CrossRef] [PubMed]
- Kestell, C.; Hansen, C.; Cazzolato, B. Active noise control with virtual sensors in a long narrow duct. International Journal of Acoustics and Vibration 2000, 5(2), 1–14. [Google Scholar]
- Munn, J.; Cazzolato, B.; Kestell, C.; Hansen, C. Virtual error sensing for active noise control in a one-dimensional waveguide: Performance prediction versus measurement (l). Journal of the Acoustical Society of America 2003, 113(1), 35–38. [Google Scholar] [CrossRef] [PubMed]
- Munn, J. Virtual sensors for active noise control. PhD thesis, Department of Mechanical Engineering, The University of Adelaide, SA, 5005, 2004. [Google Scholar]
- Munn, J.; Kestell, C.; Cazzolato, B.; Hansen, C. Real-time feedforward active control using virtual sensors in a long narrow duct. In Proceedings of Acoustics 2001: Noise and Vibration Policy the Way Forward, Canberra, Australia, 2001.
- Munn, J.; Kestell, C.; Cazzolato, B.; Hansen, C. Real-time feedforward active noise control using virtual error sensors. In Proceedings of the 2001 International Congress and Exhibition on Noise Control Engineering, The Hague, The Netherlands, 2001.
- Munn, J.; Cazzolato, B.; Hansen, C.; Kestell, C. Higher order virtual sensing for remote active noise control. In Proceedings of Active 02, Southampton, UK, 2002.
- Cazzolato, B.; Petersen, C.; Howard, C.; Zander, A. Active control of energy density in a 1D waveguide: A cautionary note. Journal of the Acoustical Society of America 2005, 117(6), 3377–3380. [Google Scholar] [CrossRef] [PubMed]
- Gawron, H.; Schaaf, K. Interior car noise: Active cancellation of harmonics using virtual microphones. In Proceedings of the 2nd International Conference on Vehicle Comfort: Ergonomic, Vibrational and Thermal Aspects, Bologna, Italy, 1992; pp. 739–748.
- Munn, J.; Cazzolato, B.; Hansen, C. Virtual sensing: Open loop vs adaptive LMS. Proceedings of the Annual Australian Acoustical Society Conference (2002) 2002, 24–33. [Google Scholar]
- Munn, J.; Cazzolato, B.; Hansen, C. Virtual sensing using an adaptive LMS algorithm. In Proceedings of Wespac VIII, Melbourne, Australia, 2003.
- Skogestad, S.; Postlethwaite, I. Multivariable feedback control: analysis and design; John Wiley: Hoboken, NJ, 2005. [Google Scholar]
- Haverkamp, L. State Space Identification: Theory and Practice. PhD thesis, System and Control Engineering Group, Delft University of Technology, 2001. [Google Scholar]
- Moreau, D. An analytical, numerical and experimental investigation of active noise control strategies in a pure tone diffuse sound field. In Technical report; School of Mechanical Engineering, The University of Adelaide, 2008. [Google Scholar]
- Moreau, D.; Cazzolato, B.; Zander, A. Active noise control at a moving location in a modally dense three-dimensional sound field using virtual sensing. In Proceedings of Acoustics 08, Paris, 2008.
© 2008 by the authors licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Moreau, D.; Cazzolato, B.; Zander, A.; Petersen, C. A Review of Virtual Sensing Algorithms for Active Noise Control. Algorithms 2008, 1, 69-99. https://doi.org/10.3390/a1020069
Moreau D, Cazzolato B, Zander A, Petersen C. A Review of Virtual Sensing Algorithms for Active Noise Control. Algorithms. 2008; 1(2):69-99. https://doi.org/10.3390/a1020069
Chicago/Turabian StyleMoreau, Danielle, Ben Cazzolato, Anthony Zander, and Cornelis Petersen. 2008. "A Review of Virtual Sensing Algorithms for Active Noise Control" Algorithms 1, no. 2: 69-99. https://doi.org/10.3390/a1020069
APA StyleMoreau, D., Cazzolato, B., Zander, A., & Petersen, C. (2008). A Review of Virtual Sensing Algorithms for Active Noise Control. Algorithms, 1(2), 69-99. https://doi.org/10.3390/a1020069