Numerical Approach to Modeling and Characterization of Refractive Index Changes for a Long-Period Fiber Grating Fabricated by Femtosecond Laser
Abstract
:1. Introduction
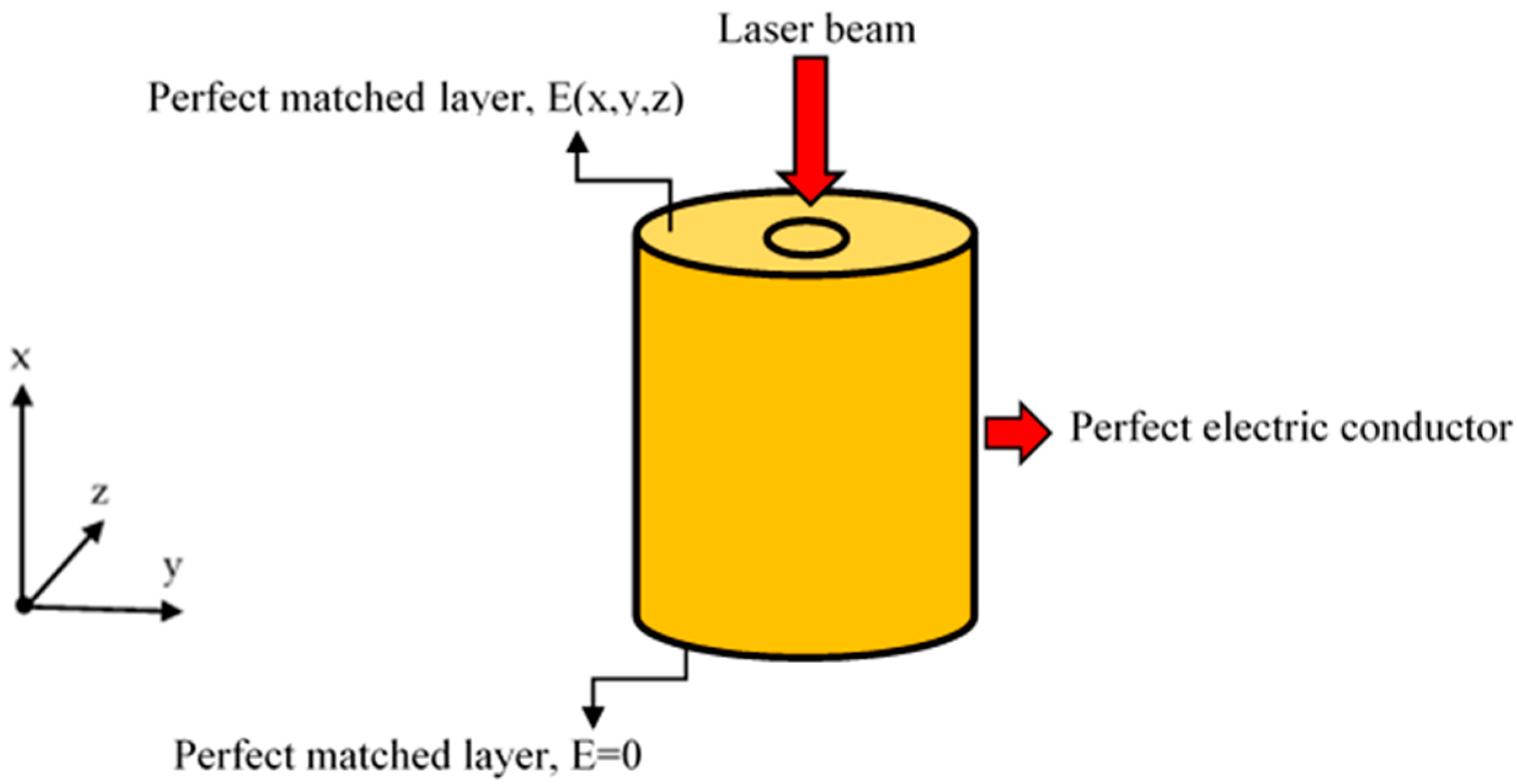
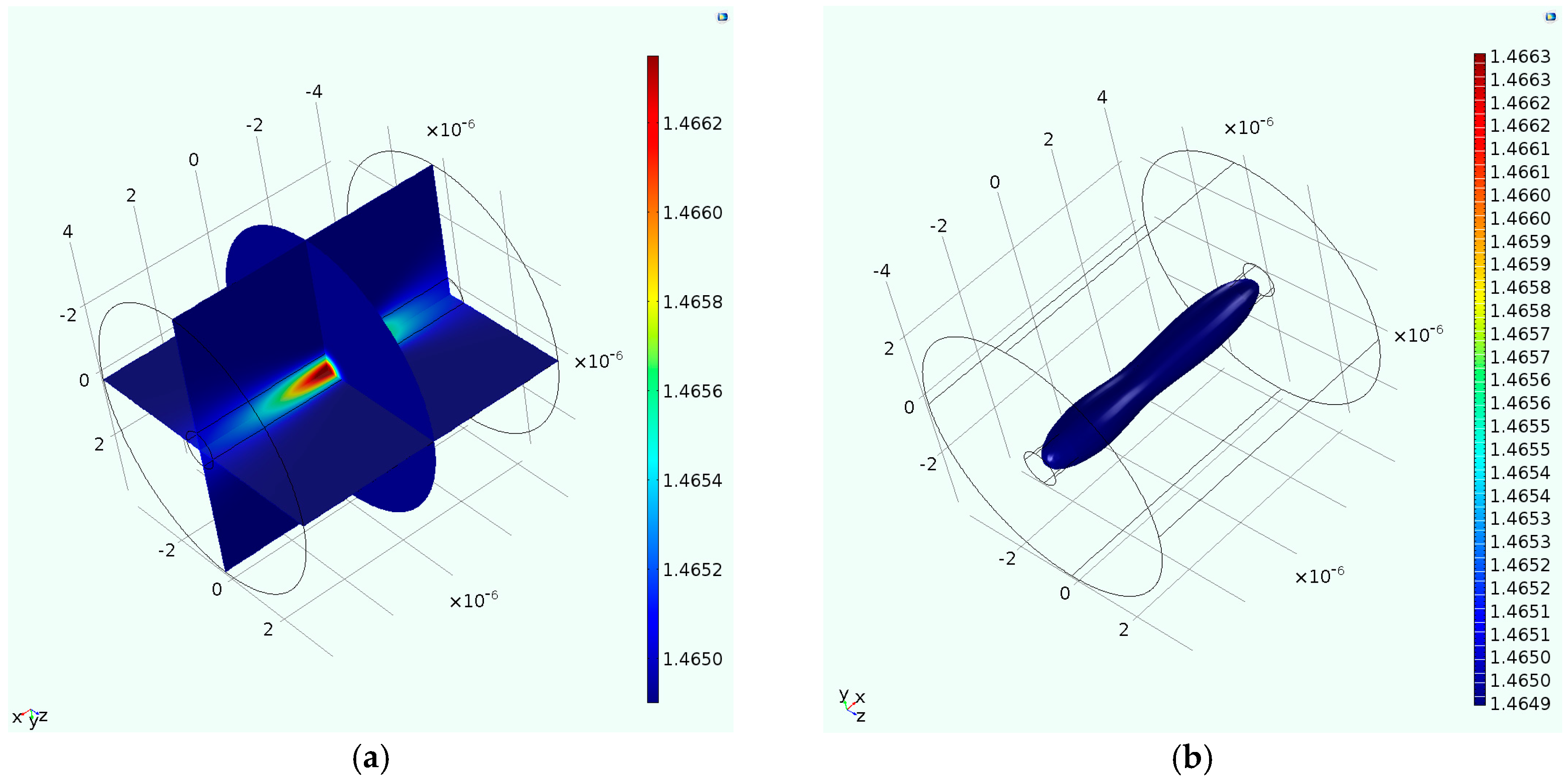
2. Intensity-Dependent Refractive Index Model
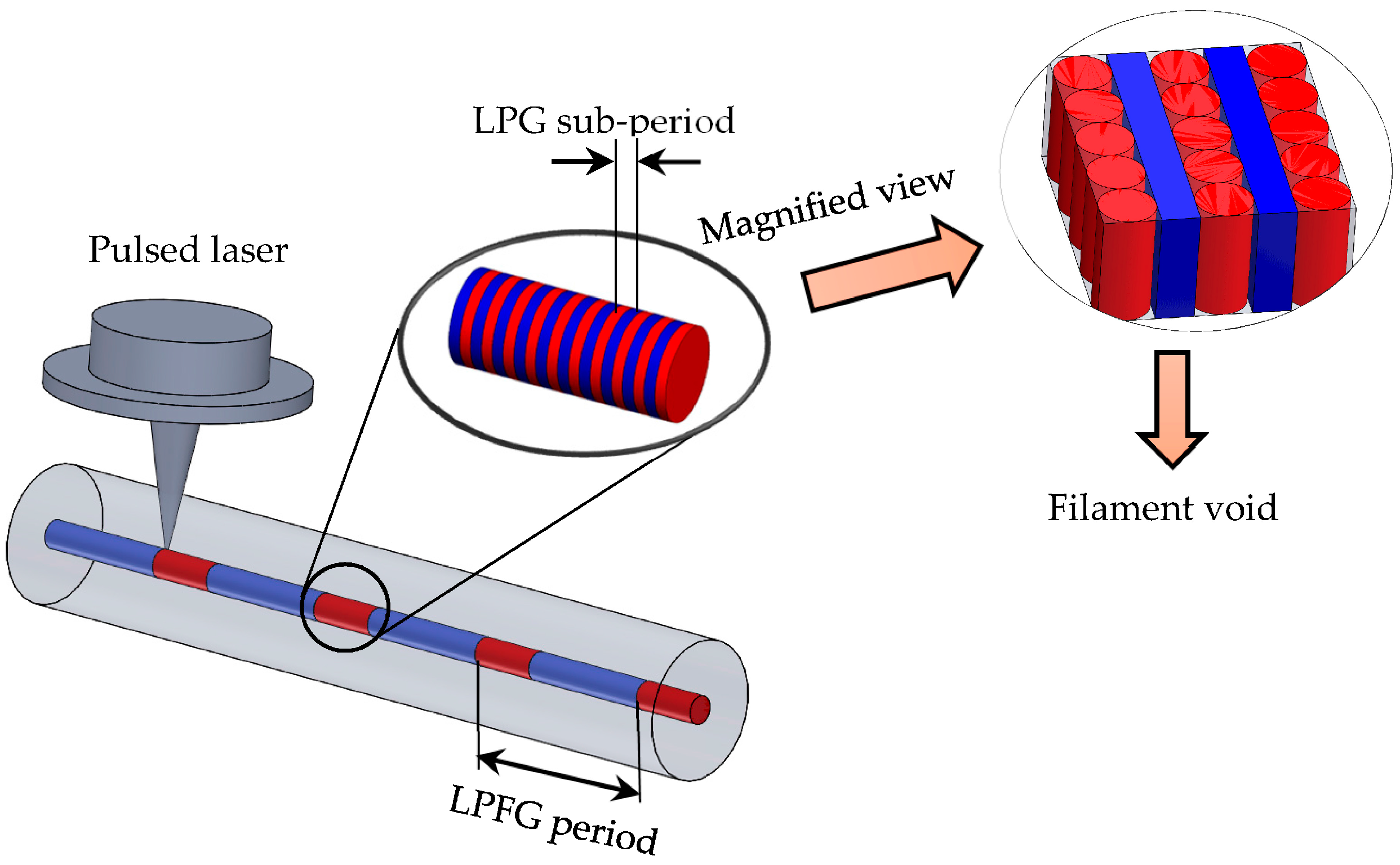
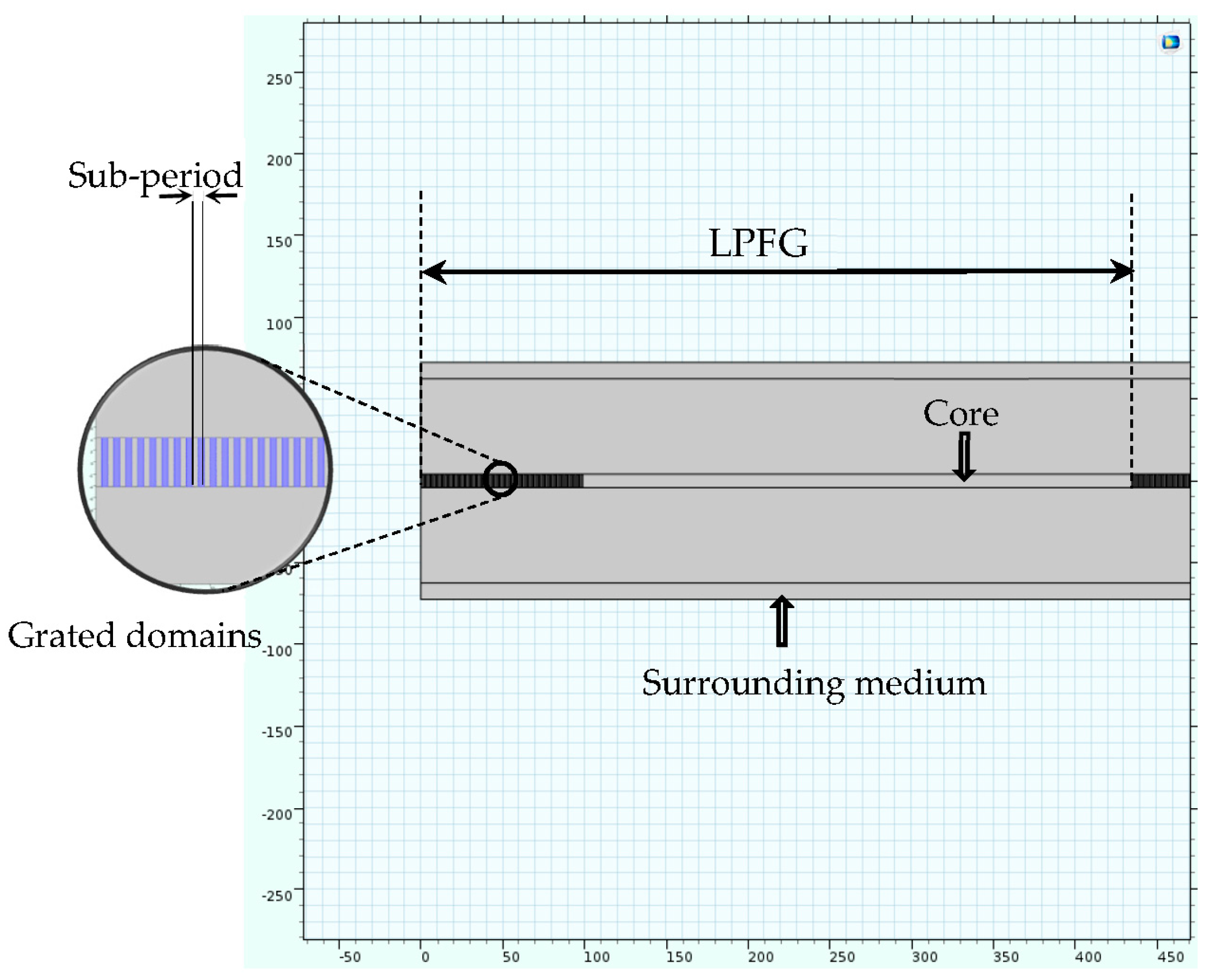
3. Long-Period Grating Model
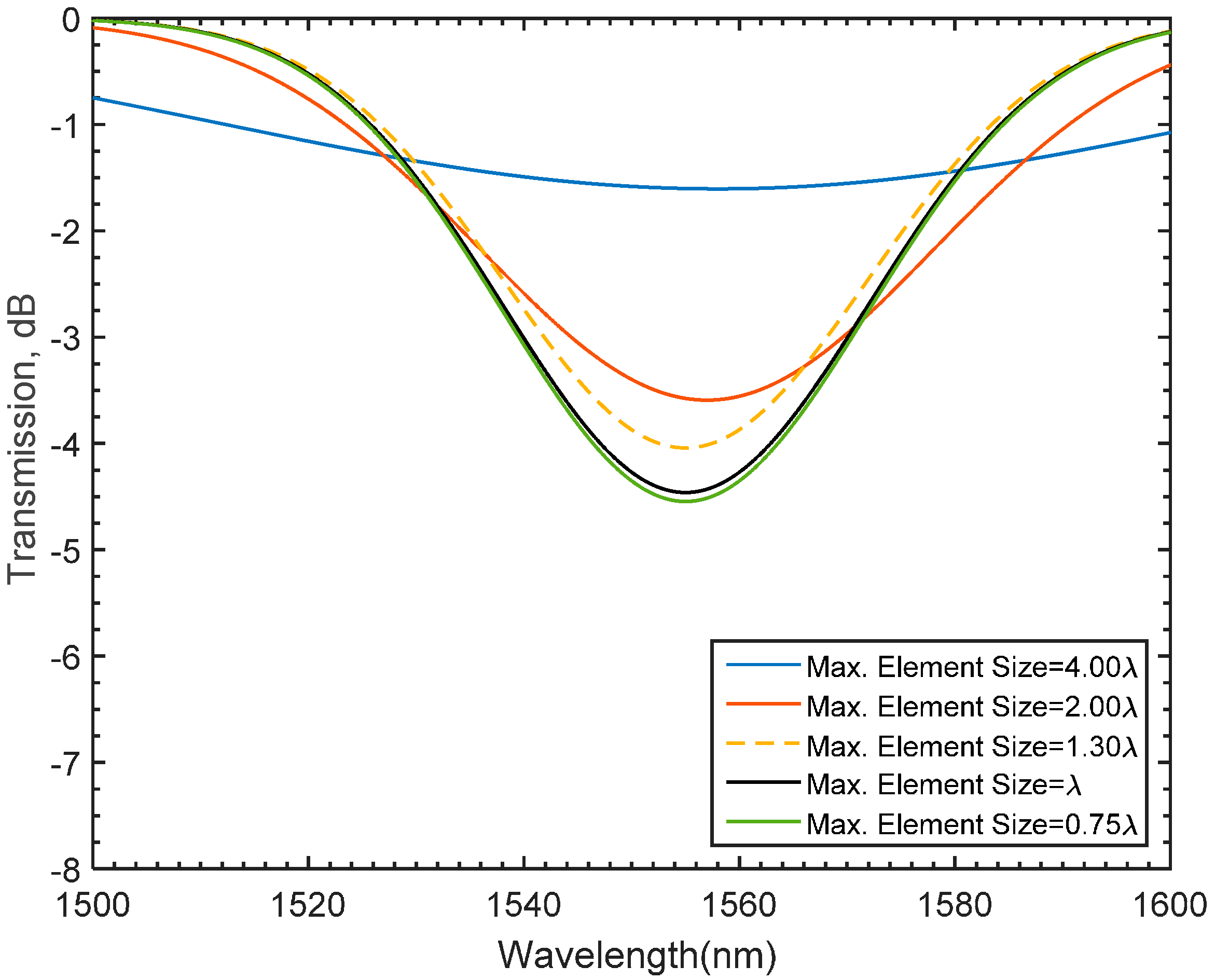
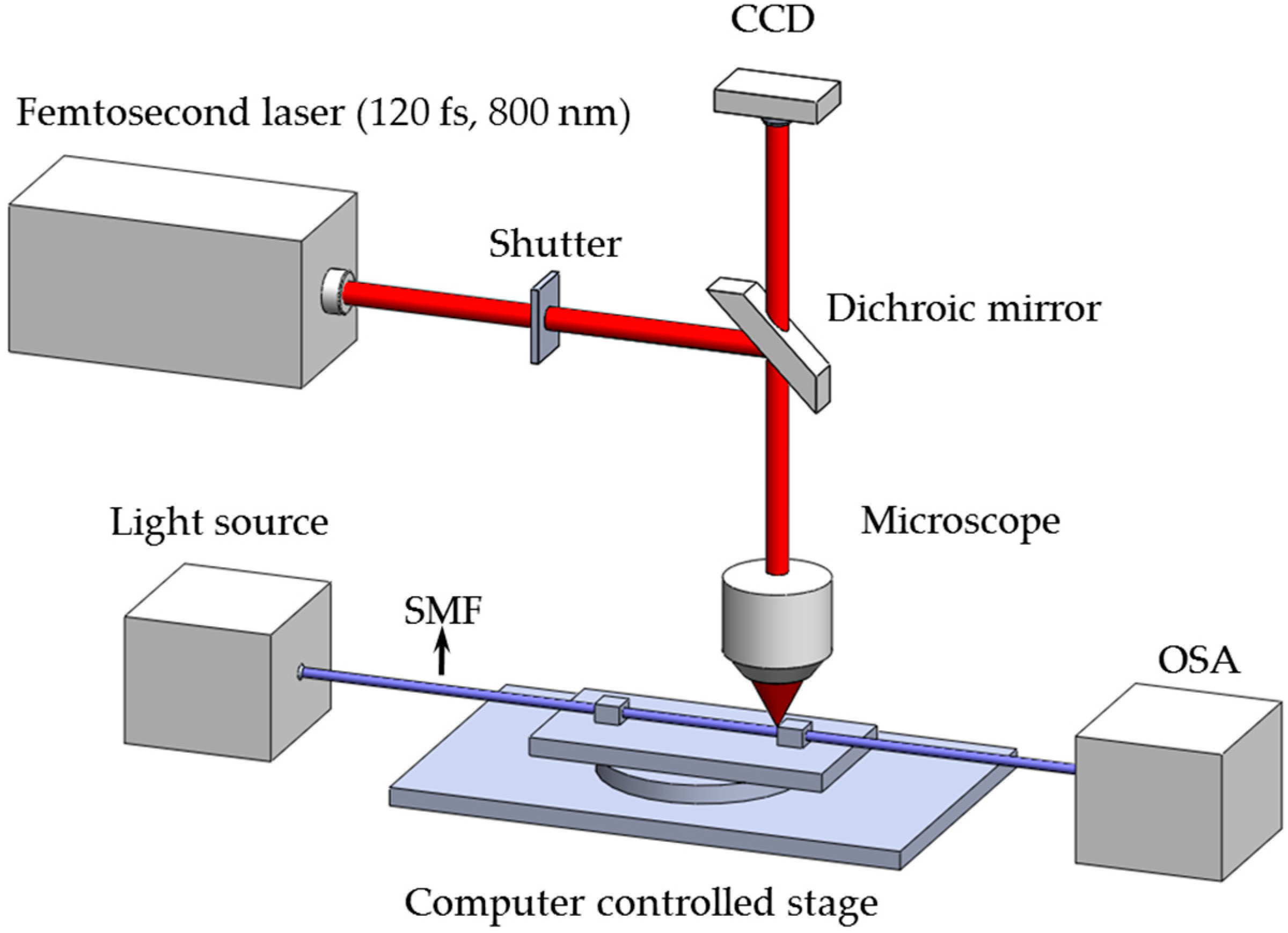
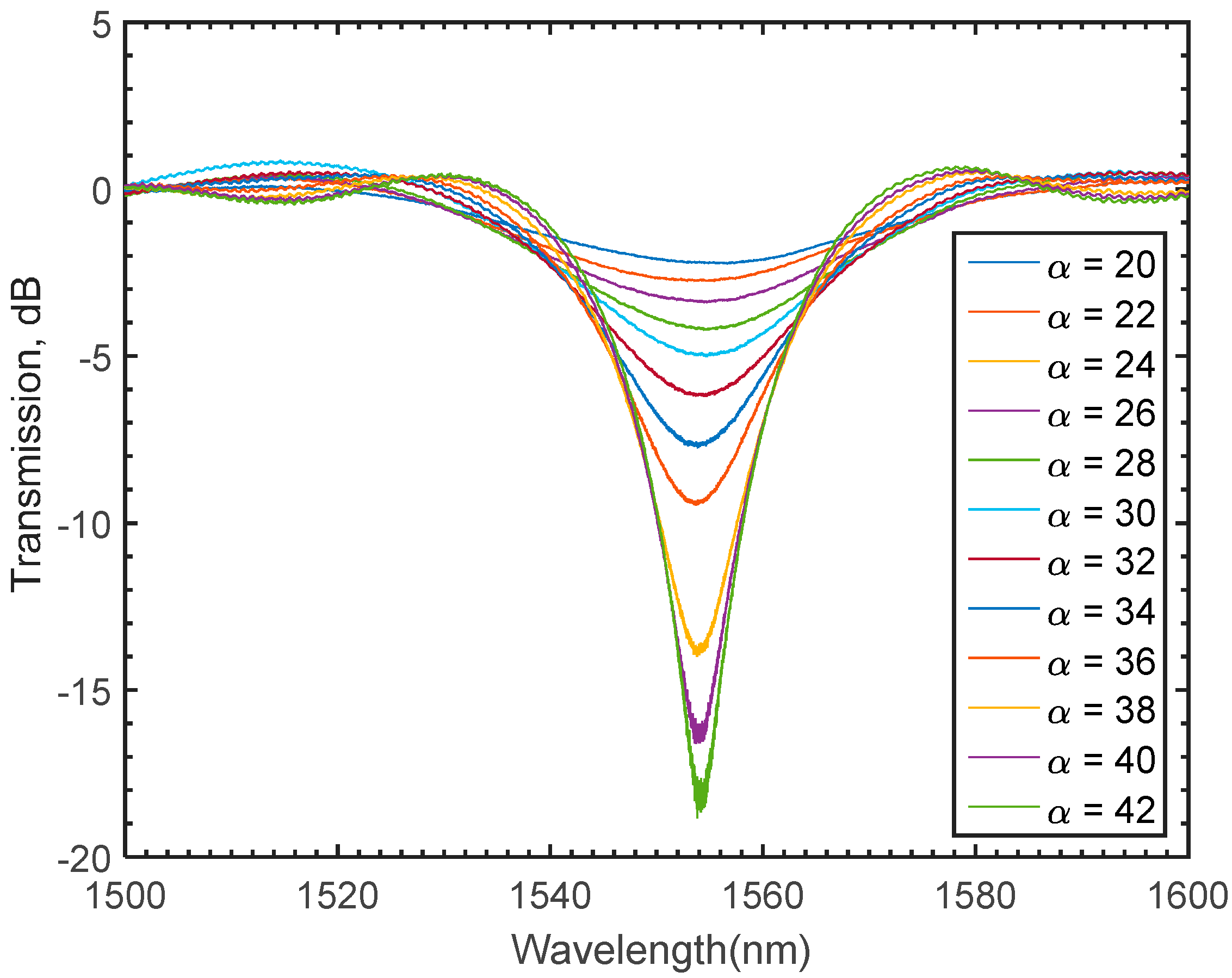
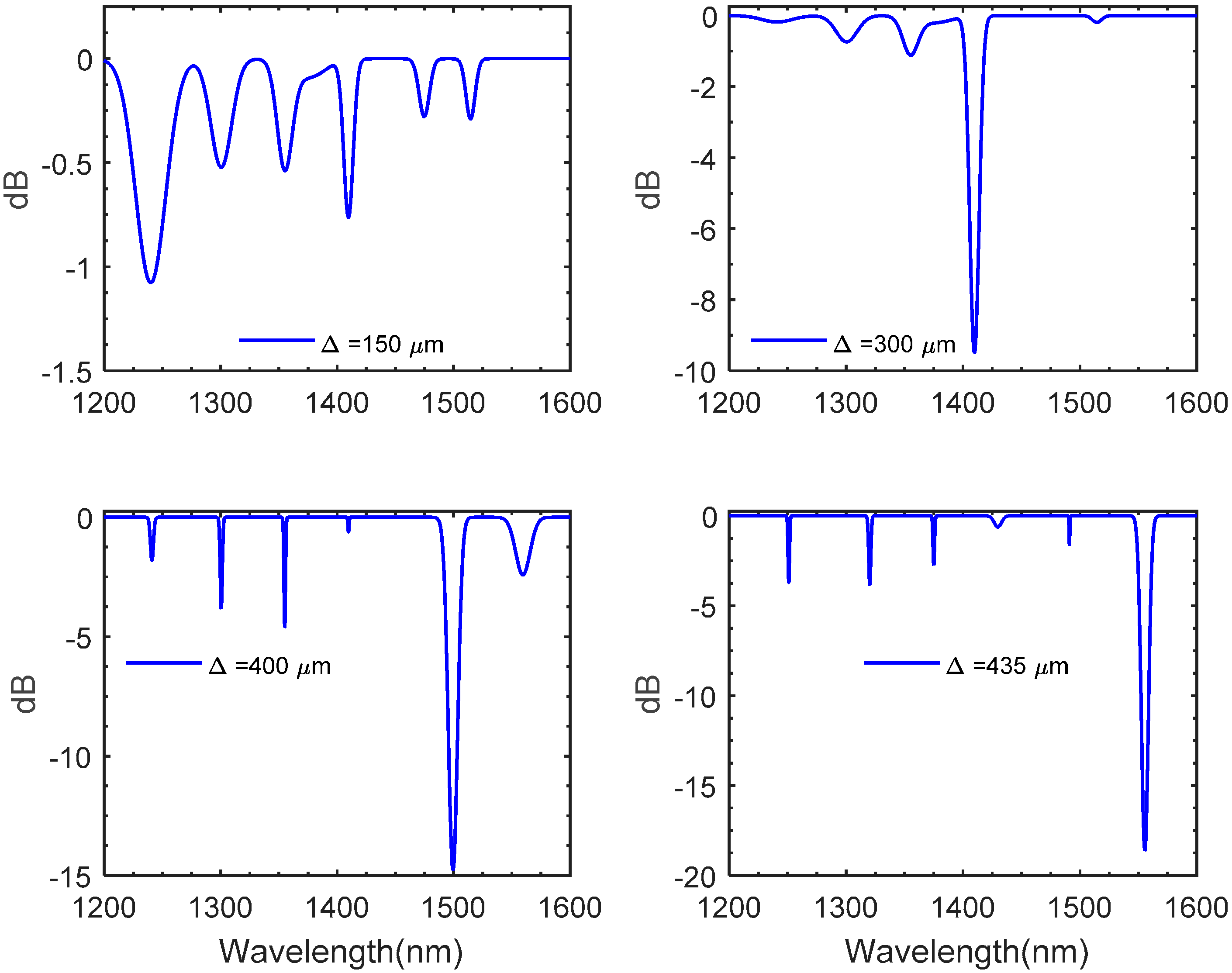
4. Spectral Growth Experimental Validation
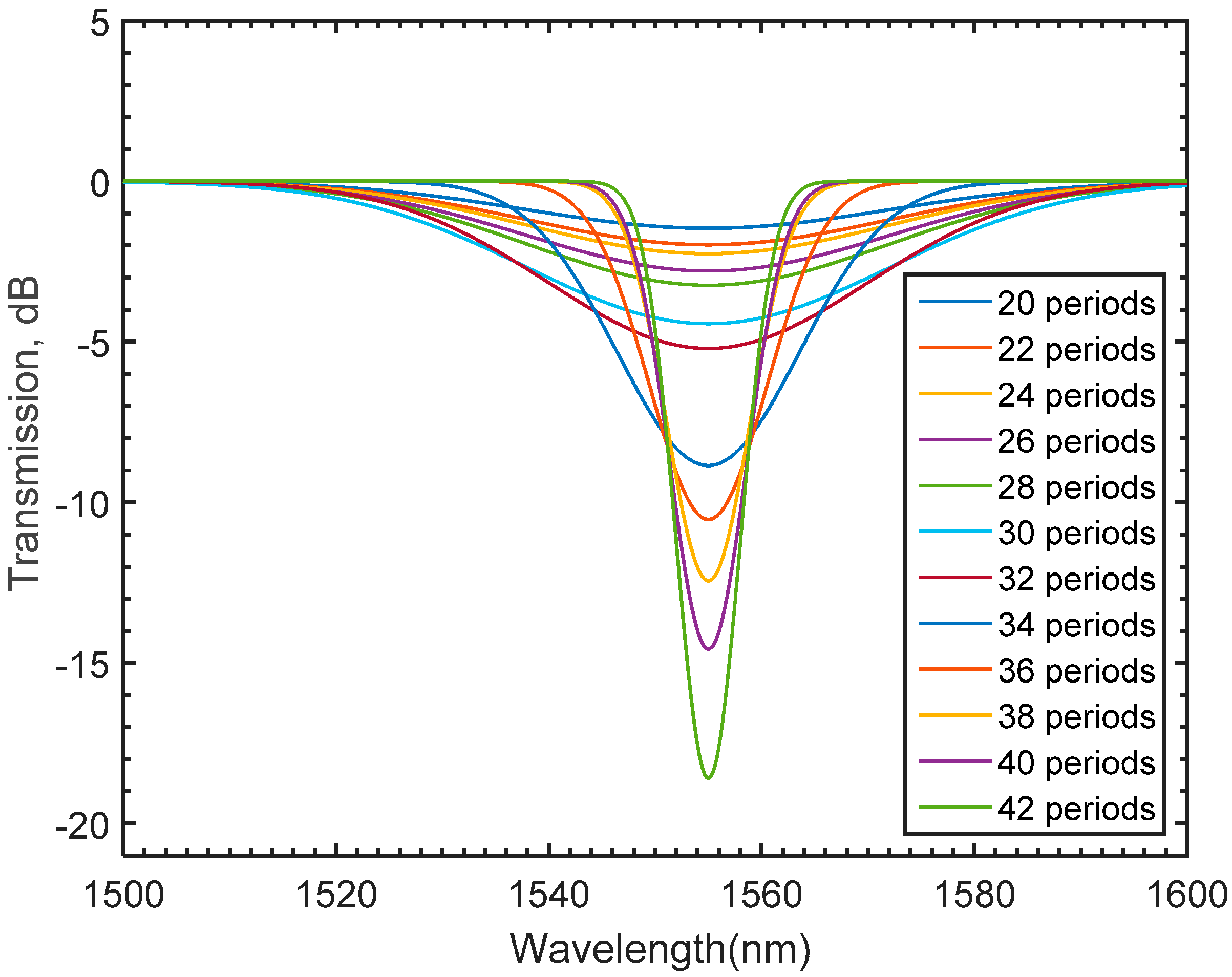
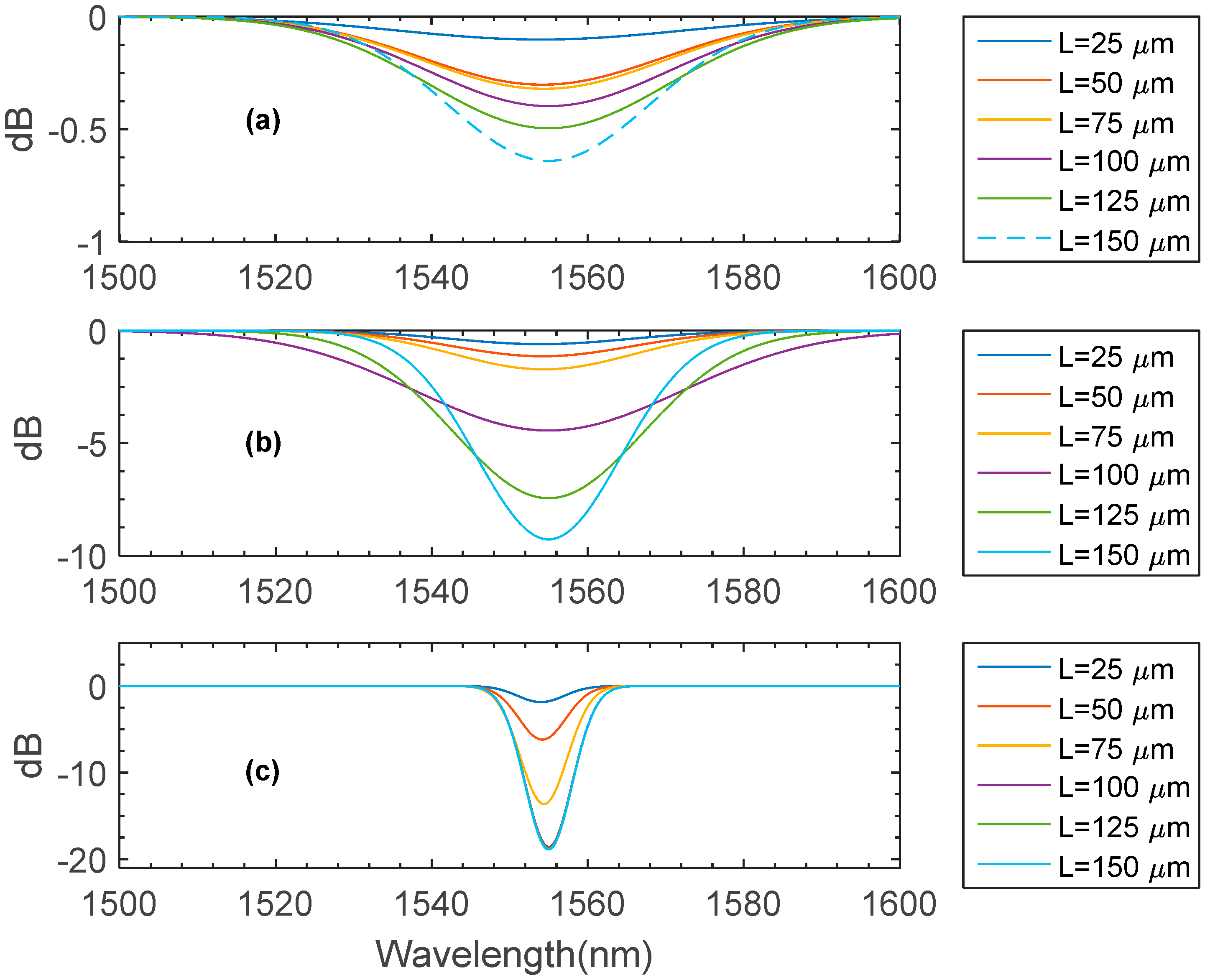
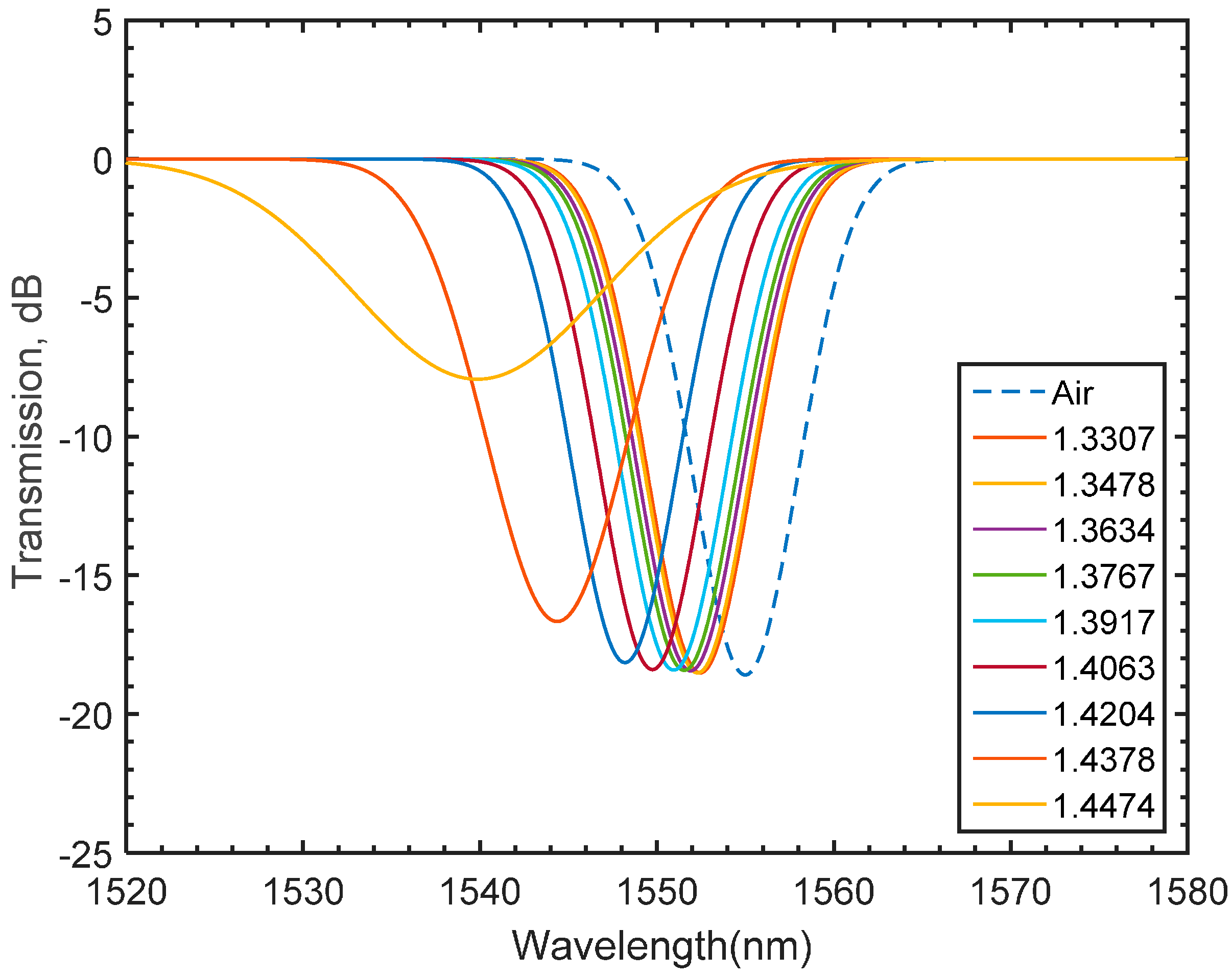
5. Varying the Grating Length and Grating Period
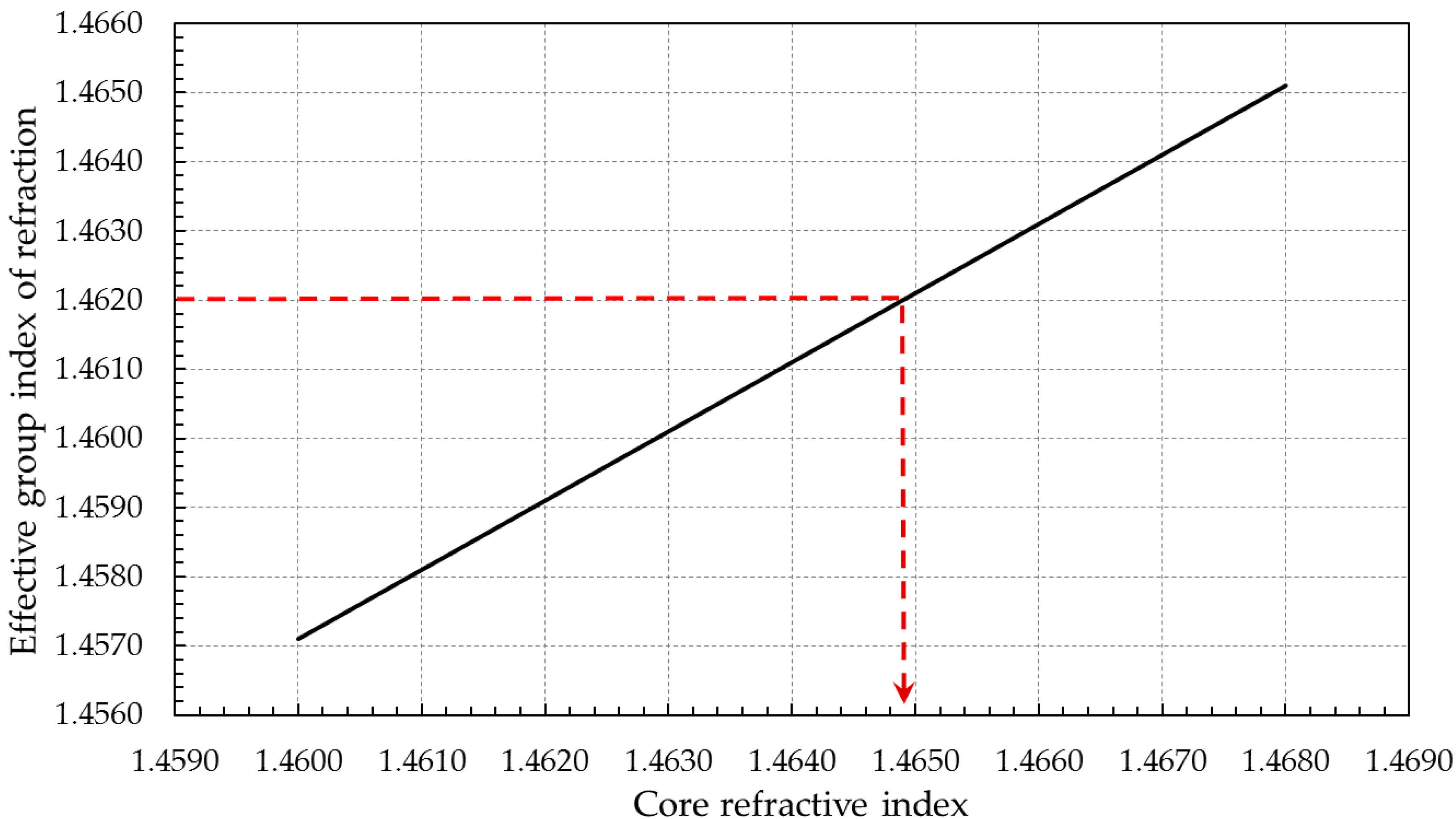
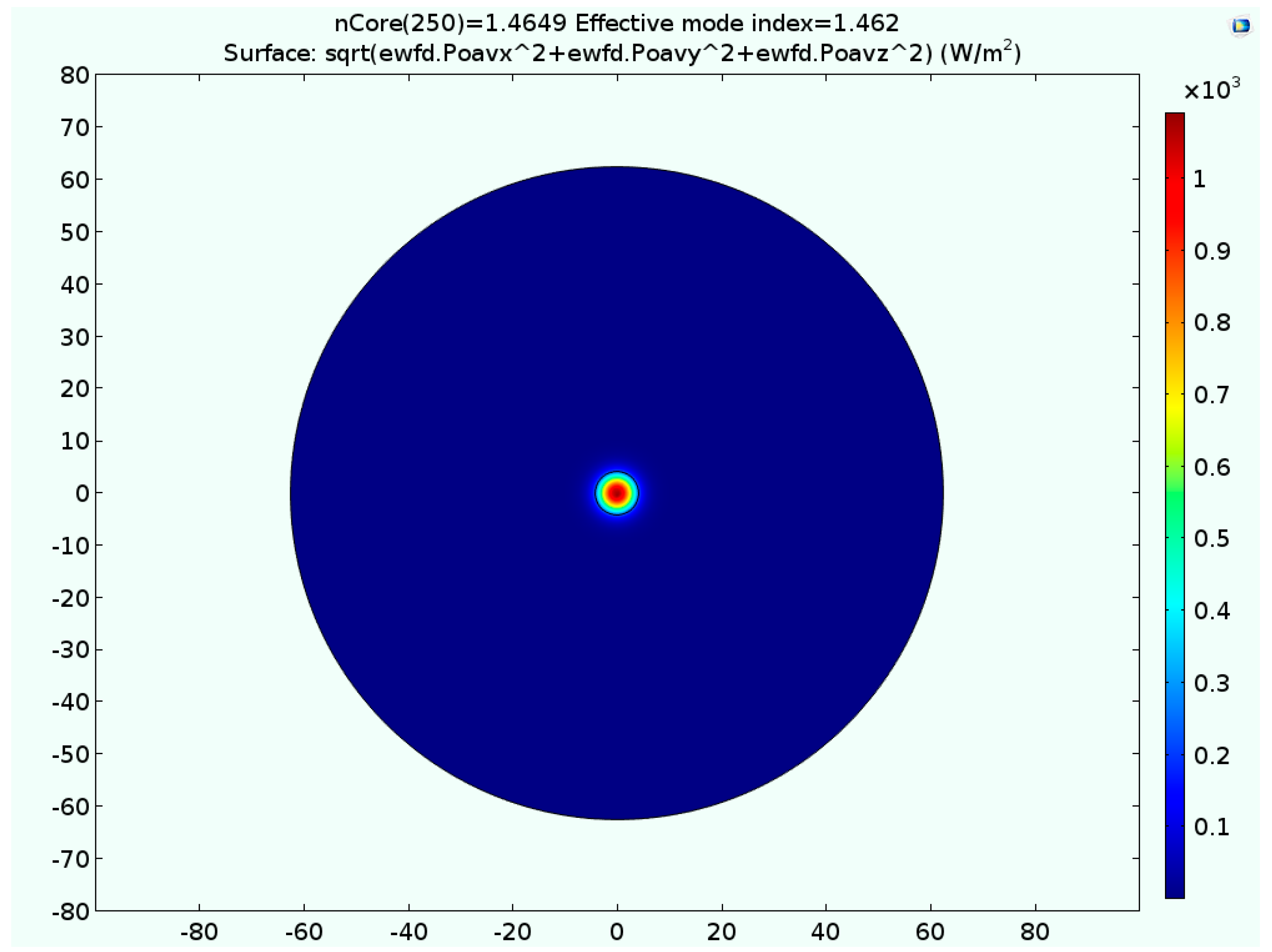
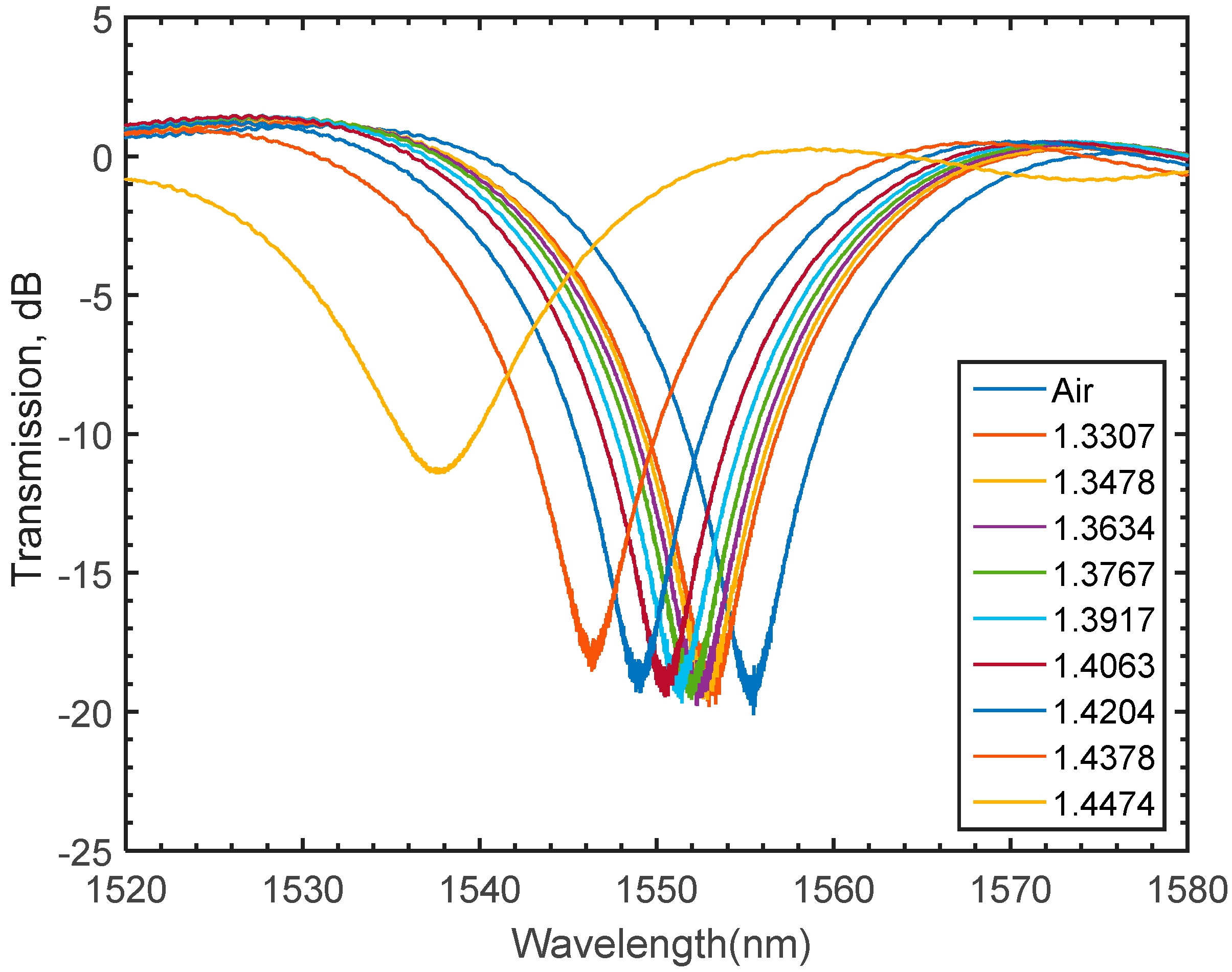
6. Experimental Validation of the Modeled Refractive Index LPFG Sensor
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Rao, Y.J.; Zhu, T.; Ran, Z.L.; Wang, Y.P.; Jiang, J.; Hu, A.Z. Novel long-period fiber gratings written by high frequency CO2 laser pulses and applications in optical fiber communication. J. Lightwave Technol. 2003, 229, 209–221. [Google Scholar] [CrossRef]
- James, S.W.; Tatam, R.P. Optical fiber long period grating sensors: Characteristics and applications. Meas. Sci. Technol. 2003, 14, 49–61. [Google Scholar] [CrossRef]
- Allsop, T.; Kalli, K.; Zhou, K.; Smith, G.N.; Komodromos, M.; Petrovic, J.; Webb, D.J.; Bennion, I. Spectral characteristics and thermal evolution of long-period gratings in photonic crystal fibers fabricated with a near-IR radiation femtosecond laser using point-by-point inscription. J. Opt. Soc. Am. B 2011, 28, 2105–2114. [Google Scholar] [CrossRef]
- Mihailov, S.J. Fiber Bragg grating sensors for harsh environments. Sensors 2012, 12, 1898–1918. [Google Scholar] [CrossRef] [PubMed]
- Davis, D.D.; Gaylord, T.K.; Glytsis, E.N.; Mettler, S.C.; Vengsarkar, A.M. Long-period fiber grating fabrication with focused CO2 laser pulses. Electron. Lett. 1998, 34, 302–303. [Google Scholar] [CrossRef]
- Vengsarkar, A.M.; Lemaire, P.J.; Judkins, J.B.; Bhatia, V.; Erdogan, T.; Sipe, J.E. Long-period fiber gratings as band-rejection filters. IEEE J. Lightwave Technol. 1996, 14, 58–65. [Google Scholar] [CrossRef]
- Kim, H.J.; Kown, O.J.; Lee, S.B.; Han, Y.G. Measurement of temperature and refractive index based on surface long-period gratings deposited onto a D-shaped photonic crystal fiber. Appl. Phys. B 2011, 102, 81–85. [Google Scholar] [CrossRef]
- Kondo, Y.; Nouchi, K.; Mitsuyu, T.; Watanabe, M.; Kazansky, P.G.; Hirao, K. Fabrication of long-period fiber gratings by focused irradiation of infrared femtosecond laser pulses. Opt. Lett. 1999, 4, 646–648. [Google Scholar] [CrossRef]
- Davis, K.; Miura, K.; Sugimoto, N.; Hirao, K. Writing waveguides in glass with a femtosecond laser. Opt. Lett. 1996, 21, 1729–1731. [Google Scholar] [CrossRef] [PubMed]
- Hindle, F.; Fertein, E.; Przygodzki, C.; Dürr, F.; Paccou, L.; Bocquet, R.; Niay, P.; Limberger, H.G.; Douay, M. Inscription of long-period gratings in pure silica and Germano-silicate fiber cores by femtosecond laser irradiation. IEEE Photon. Technol. Lett. 2004, 16, 1861–1863. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, L.; Wang, S.M.; Tsai, H.L.; Xiao, H. Femtosecond laser fabrication of long period fiber gratings and applications in refractive index sensing. Opt. Laser Technol. 2011, 43, 1420–1423. [Google Scholar] [CrossRef]
- Oberson, P.; Gisin, B.; Huttner, B.; Gisin, N. Refracted near-field measurements of refractive index and geometry of silica-on-silicon integrated optical wave guides. Appl. Opt. 1998, 37, 7268–7272. [Google Scholar] [CrossRef] [PubMed]
- Yablon, A.D. Multi-wavelength optical fiber refractive index profiling by spatially resolved Fourier transform spectroscopy. J. Lightwave Technol. 2010, 28, 360–364. [Google Scholar] [CrossRef]
- Liu, Z.; Dong, X.; Chen, Q.; Yin, C.; Xu, Y.; Zheng, Y. Non-destructive measurement of an optical fiber refractive-index profile by a transmitted-light differential interference contact microscope. Appl. Opt. 2004, 43, 1485–1492. [Google Scholar] [CrossRef] [PubMed]
- Bachim, B.; Gaylord, T.K. Microinterferometric optical phase tomography for measuring small, asymmetric refractive-index differences in the profiles of optical fibers and fiber devices. Appl. Opt. 2005, 44, 316–327. [Google Scholar] [CrossRef] [PubMed]
- Jholen, D.; Renner, H.; Ewald, A.; Brinjmeyer, E. Fiber Bragg grating Fabry–Perot interferometer for a precise measurement of the UV-induced index change. In Proceedings of the European Conference on Optical Communications, (ECOC’98), Madrid, Spain, 20–24 September 1998; pp. 393–394.
- Fertein, E.; Przygodzki, C.; Delbarre, H.; Hidayat, A.; Douay, M.; Niay, P. Refractive index changes of standard telecommunication fiber through exposure to femtosecond laser pulses at 810 cm. Appl. Opt. 2001, 40, 3506–3508. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, F.; Joe, H.-E.; Min, B.-K.; Jun, M.B.G. Characterization of refractive index change and fabrication of long period gratings in pure silica fiber by femtosecond laser radiation. Opt. Laser Technol. 2015, 74, 119–124. [Google Scholar] [CrossRef]
- Koshiba, M.; Saitoh, K. Finite-element analysis of birefringence and dispersion properties in actual and idealized holey-fiber structures. Appl. Opt. 2003, 42, 6267–6275. [Google Scholar] [CrossRef] [PubMed]
- Erdogan, T. Cladding-mode resonances in short- and long- period fiber gratings. J. Opt. Soc. Am. A 1997, 14, 1760–1773. [Google Scholar] [CrossRef]
- He, Y.J.; Hung, W.C.; Lai, Z.P. Using Finite Element and Eigenmode Expansion Methods to Investigate the Periodic and Spectral Characteristic of Superstructure Fiber Bragg Gratings. Sensors 2016, 16, 192. [Google Scholar] [CrossRef] [PubMed]
- Talanov, V.I. Self-focusing of waves in nonlinear media. JETP Lett. 1965, 2, 138. [Google Scholar]
- Fleck, J.A., Jr.; Kelley, P.L. Temporal aspect of the self-focusing of optical beams. Appl. Phys. Lett. 1969, 15, 313–315. [Google Scholar] [CrossRef]
- Feit, M.D.; Fleck, J.A., Jr. Beam nonparaxiality, filament formation, and beam breakup in the selffocusing of optical beams. J. Opt. Soc. Am. B 1988, 5, 633–640. [Google Scholar] [CrossRef]
- Moll, K.D.; Gaeta, A.L.; Fibich, G. Self-similar optical wave collapse: Observation of the townes profile. Phys. Rev. Lett. 2003, 90, 203902. [Google Scholar] [CrossRef] [PubMed]
- Fibich, G.; Ilan, B. Multiple filamentation of circularly polarized beams. Phys. Rev. Lett. 2002, 89, 013901. [Google Scholar] [CrossRef] [PubMed]
- Fibich, G.; Ren, W.; Wang, X.P. Numerical simulations of self-focusing of ultrafast laser pulses. Phys. Rev. E 2003, 67, 056603. [Google Scholar] [CrossRef] [PubMed]
- Joseph, R.M.; Taflove, A. Spatial soliton deflection mechanism indicated by FDTD Maxwell’s equations modeling. IEEE Photon. Technol. Lett. 1994, 6, 1251–1254. [Google Scholar] [CrossRef]
- Ziolkowski, R.W.; Judkins, J.B. Full-wave vector Maxwell equation modeling of the self-focusing of ultrashort optical pulses in a nonlinear Kerr medium exhibiting a finite response time. J. Opt. Soc. Am. B 1993, 10, 186–198. [Google Scholar] [CrossRef]
- Dutt, A.; Varshney, S.K.; Mahapatra, S. Design of tunable couplers using magnetic fluid filled three-core optical fibers. IEEE Photon. Technol. Lett. 2012, 24, 164–166. [Google Scholar] [CrossRef]
- Khurram, N.; Nguyen, L.V.; Alameh, K.; Chung, Y. Cladding modes analysis of photonics crystal fiber for refractive index sensors using Finite Element method. In Proceedings of the Lasers and Electro-Optics (CLEO) and Quantum Electronics and Laser Science Conference (QELS), San Jose, CA, USA, 16–21 May 2010; pp. 1–2.
- Coelho, J.M.P.; Nespereira, M.; Abreu, M.; Rebordao, J. 3D finite element model for writing long-period fiber gratings by CO2 laser radiation. Sensors 2013, 13, 10333–10347. [Google Scholar] [CrossRef] [PubMed]
- Jingsong, W.; Hui, Y. Laser beam induced nanoscale spot through nonlinear “thick” samples: A multi-layer thin lens self-focusing model. J. Appl. Phys. 2014, 116, 063107. [Google Scholar] [CrossRef]
- Anemogiannis, E.; Glytsis, E.N.; Gaylord, T.K. Transmission characteristics of long-period fiber gratings having arbitrary azimuthal/radial refractive index variations. J. Lightwave Technol. 2003, 21, 218–227. [Google Scholar] [CrossRef]
- Rahman, B.M.A.; Davies, J.B. Penalty function improvement of waveguide solution by finite elements. IEEE Trans. Microwave Theory Tech. 1984, 32, 922–928. [Google Scholar] [CrossRef]
- Tsuji, Y.; Koshiba, M. Guided-mode and leaky-mode analysis by imaginary distance beam propagation method based on finite element scheme. IEEE J. Lightwave Technol. 2000, 18, 618–623. [Google Scholar] [CrossRef]
- Rahman, B.M.A.; Agrawal, A. Finite Element Modeling Methods for Photonics, 1st ed.; Aretch House: Boston, MA, USA, 2013; pp. 5–15. [Google Scholar]
- Yablon, A.D.; Yan, M.F.; Wisk, P.; DiMarcello, F.V.; Fleming, J.W.; Reed, W.A.; Monberg, E.M.; DiGiovanni, D.J. Refractive index perturbations in optical fibers resulting from frozen-in viscoelasticity. Appl. Phys. Lett. 2004, 84, 19–21. [Google Scholar] [CrossRef]
- Hoo, Y.L.; Jin, W.; Xiao, L.; Ju, J.; Ho, H.L. Numerical study of refractive index sensing based on the anti-guide property of a depressed-index core photonic crystal fiber. Sens. Actuators B Chem. 2009, 136, 26–31. [Google Scholar]
- Tao, C.; Wei, H.; Zhu, Y.; Krishnaswamy, S. Grapefruit photonic crystal fiber sensor for gas sensing application. Opt. Eng. 2016. [Google Scholar] [CrossRef]
- Baghdasaryan, T.; Geernaert, T.; Thienpont, H.; Berghmans, F. Numerical modeling of femtosecond laser inscribed IR gratings in photonic crystal fibers. Opt. Express 2015, 23, 709–723. [Google Scholar] [PubMed]
- Jovanovic, N.; Thomas, J.; Williams, R.; Steel, M.; Marshall, G.; Fuerbach, A.; Nolte, S.; Tünnermann, A.; Withford, M. Polarization-dependent effects in point-by-point fiber Bragg gratings enable simple, linearly polarized fiber lasers. Opt. Express 2009, 17, 6082–6095. [Google Scholar] [CrossRef] [PubMed]
- FKatsriku, A.; Rahman, B.M.A.; Grattan, K.T.V. Numerical modeling of second harmonic generation in optical waveguides using the finite element method. IEEE J. Quantum Electron. 1997, 33, 1727–1733. [Google Scholar] [CrossRef]
- Hartl, I.; Li, X.; Chudoba, C.; Ghanta, R.; Ko, T.; Fujimoto, J.; Ranka, J.; Windeler, R. Ultrahigh-resolution optical coherence tomography using continuum generation in an air-silica microstructure optical fiber. Opt. Lett. 2011, 26, 608–610. [Google Scholar] [CrossRef]
- Agrawal, G. Nonlinear Fiber Optics, 5th ed.; Academic Press: New York, NY, USA, 2013. [Google Scholar]
- Lai, C.-H.; Chang, H.-C. Effect of perfectly matched layer reflection coefficient on modal analysis of leaky waveguide modes. Opt. Express 2011, 19, 562–569. [Google Scholar] [CrossRef] [PubMed]
- Koechner, W. Solid-State Laser Engineering, 6th ed.; Springer: New York, NY, USA, 2006; pp. 200–209. [Google Scholar]
- Marburger, J.H. Self-focusing theory. Prog. Quantum Electron. 1975, 4, 35–110. [Google Scholar] [CrossRef]
- Chiao, R.Y.; Garmire, E.; Townes, C.H. Self-trapping of optical beams. Phys. Rev. Lett. 1964, 13, 479. [Google Scholar] [CrossRef]
- Self-Focusing. Available online: https://www.comsol.com/model/self-focusing-14639 (accessed on 1 June 2016).
- Jin, J. The Finite Element Method in Electromagnetics, 3rd ed.; Wiley-IEEE Press: New York, NY, USA, 2014. [Google Scholar]
- Tzortzakis, S.; Sudrie, L.; Franco, M.; Prade, B.; Mysyrowicz, A.; Couairon, A.; Bergé, L. Self-Guided Propagation of Ultrashort IR Laser Pulses in Fused Silica. Phys. Rev. Lett. 2001, 87, 213902. [Google Scholar] [CrossRef] [PubMed]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saad, A.; Cho, Y.; Ahmed, F.; Jun, M.B.-G. Numerical Approach to Modeling and Characterization of Refractive Index Changes for a Long-Period Fiber Grating Fabricated by Femtosecond Laser. Materials 2016, 9, 941. https://doi.org/10.3390/ma9110941
Saad A, Cho Y, Ahmed F, Jun MB-G. Numerical Approach to Modeling and Characterization of Refractive Index Changes for a Long-Period Fiber Grating Fabricated by Femtosecond Laser. Materials. 2016; 9(11):941. https://doi.org/10.3390/ma9110941
Chicago/Turabian StyleSaad, Akram, Yonghyun Cho, Farid Ahmed, and Martin Byung-Guk Jun. 2016. "Numerical Approach to Modeling and Characterization of Refractive Index Changes for a Long-Period Fiber Grating Fabricated by Femtosecond Laser" Materials 9, no. 11: 941. https://doi.org/10.3390/ma9110941
APA StyleSaad, A., Cho, Y., Ahmed, F., & Jun, M. B.-G. (2016). Numerical Approach to Modeling and Characterization of Refractive Index Changes for a Long-Period Fiber Grating Fabricated by Femtosecond Laser. Materials, 9(11), 941. https://doi.org/10.3390/ma9110941





