A Review on Development and Applications of Bio-Inspired Superhydrophobic Textiles
Abstract
:1. Introduction
1.1. Wetting Process
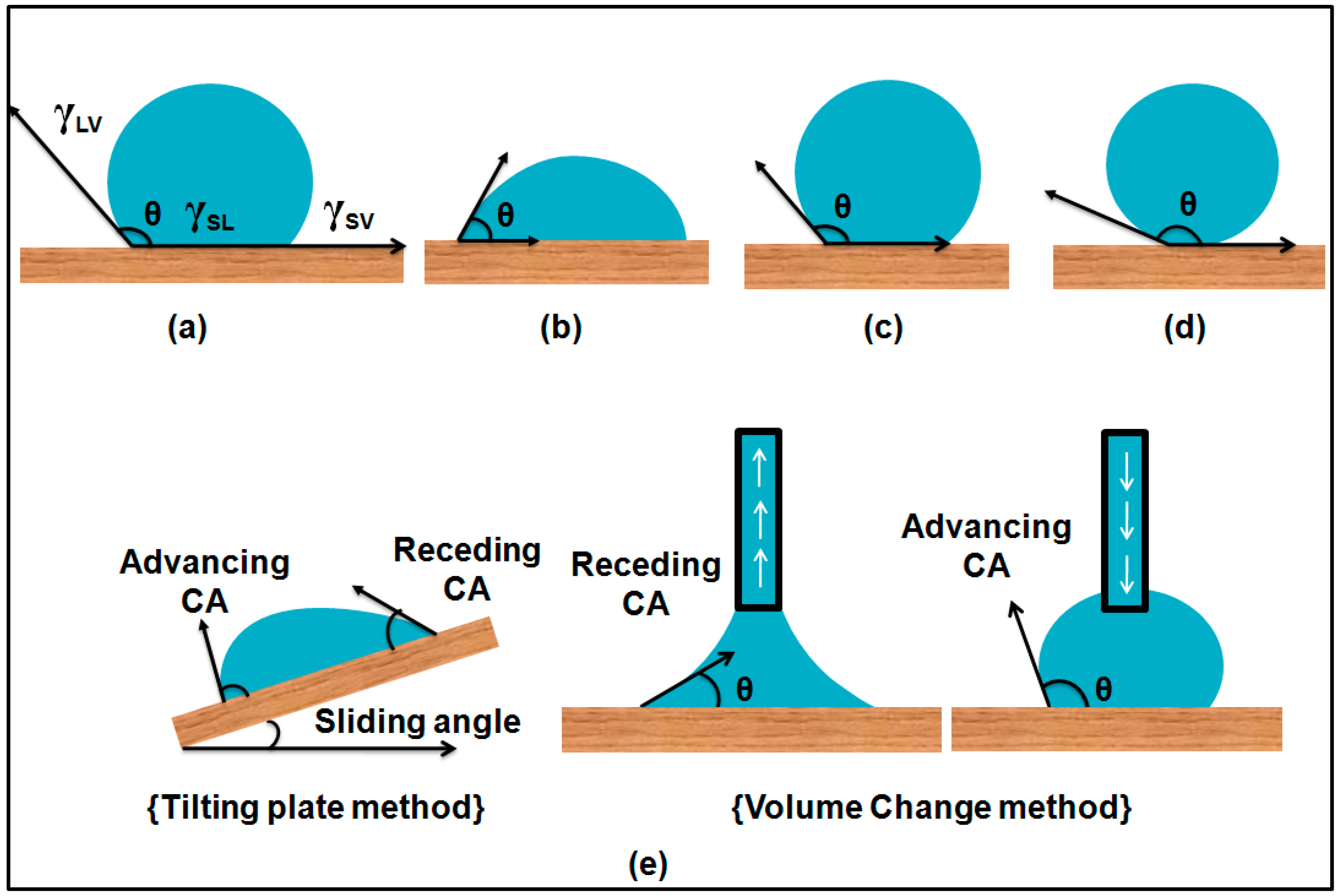
1.2. Young’s Equation and Contact Angles
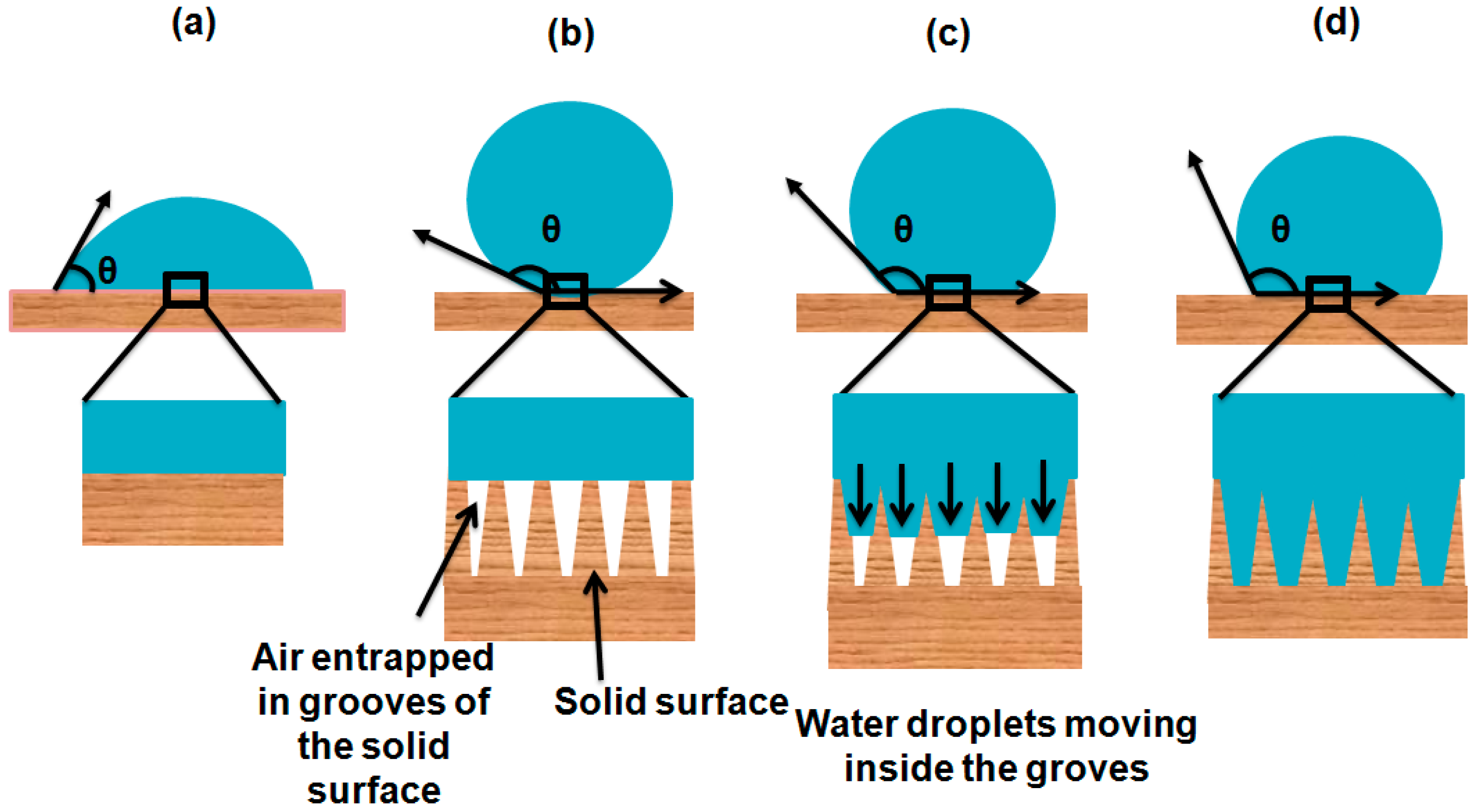
1.3. Wenzel Model
1.4. Cassie–Baxter Model
1.5. Dynamic Contact Angles and Contact Angle Hysteresis
1.6. Importance of Contact Angle Hysteresis
1.7. Stability of Cassie–Baxter State
1.8. Re-Entrant Topographies
2. Measurement of Contact Angle
2.1. Methods Used for Sessile Drops on Solid Surfaces
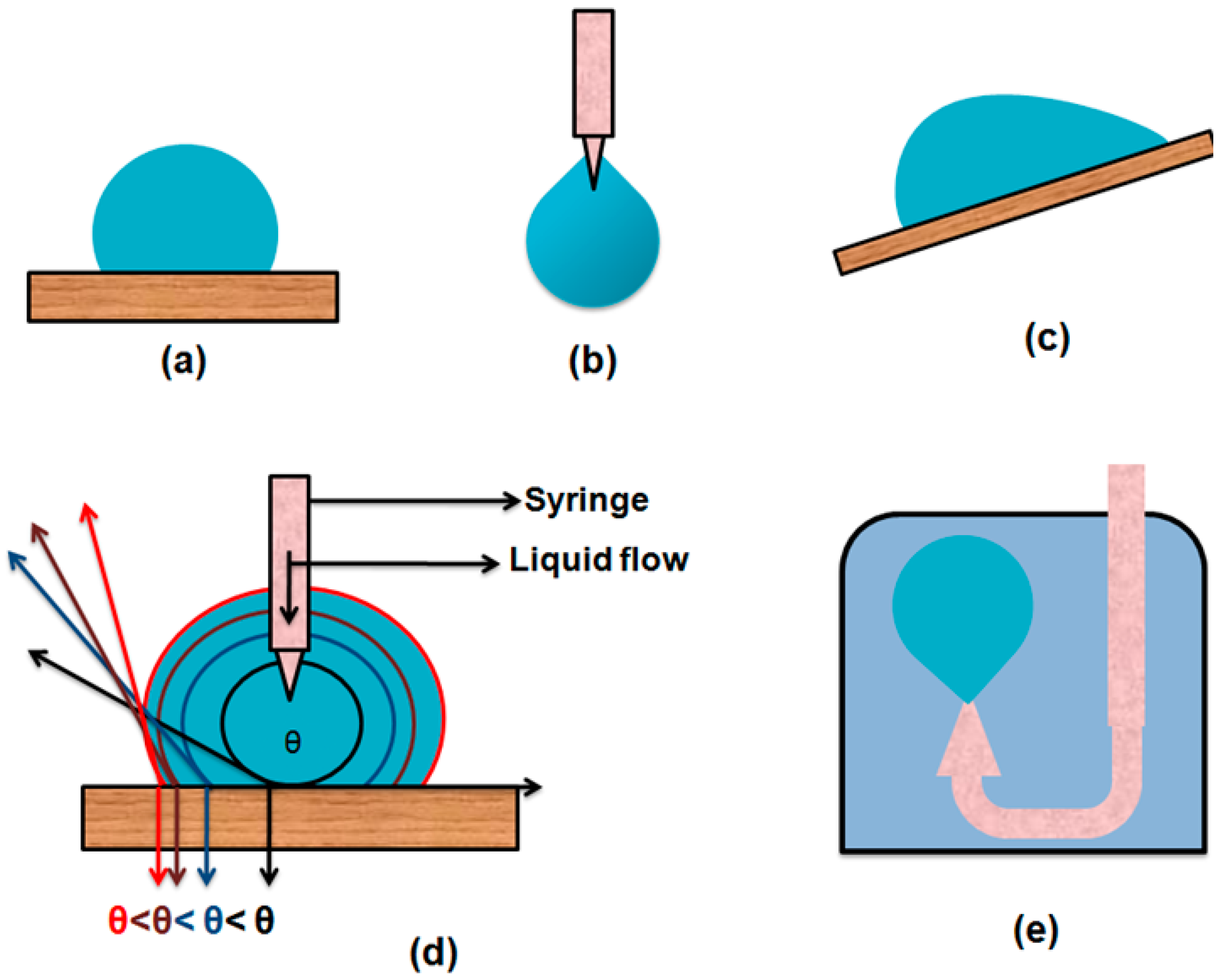
2.1.1. Direct Goniometer Method
- Only a few microliters of the liquid sample are required.
- Surface contact angle of very small substrate surface i.e., only few square millimeters can be measured.
- With the passage of time, modifications have been made in the method to get better accuracy and precision i.e., (1) integration of a camera to take images for future analysis and presentation; (2) use of high magnification lenses to get an in detail examination of the intersection profiles of contact lines of all the phases in contact; and (3) assembly of a motor driven micro syringe to control the volume of the liquid droplet [23,51,52].
- Zisman and his co-workers used a very simple method for the measurement of contact angle of sessile drops on solid surfaces by using a platinum wire. In this method an 8 cm long platinum wire of about 0.05–0.1 mm diameter is cleaned by heating with a Bunsen burner. This cleaned wire tip is dipped into the liquid and gently removed from the liquid to get a suspended drop on the tip of the platinum wire. This pendent drop is smoothly brought into contact with the solid surface, forming a sessile drop on the surface and the wire is gently removed from the drop. Furthermore, the contact angle was noted with the help of telescope-goniometer. Reproducibility for this method is claimed to be of ±2°.
- To avoid inconsistency and uncertainty in measuring the contact angle, it is suggested to establish general guidelines for the users.
- A background light as an illumination source is used, but it is necessary to use a light source of specific intensity to avoid the undesired heating and evaporation of the droplet.
- To measure the dynamic contact angle, a micro syringe with a stainless steel needle is used to increase or decrease the volume of the liquid droplet. During this process, the needle must remain in the droplet to avoid unnecessary vibrations.
- If the substrate is of a large area, it is important to measure the contact angles at different points to get an average value representing the whole surface of the substrate.
- An enclosed chamber should be used for all the measurements to prohibit airborne contamination and vapor pressure equilibrium of the liquid under study must be obtained for volatile liquids.
- The droplet may have unsymmetrical attachment with the surface; it is appropriate to measure the contact angles on both sides of the liquid droplet to get more accuracy.
- The accuracy and reproducibility of the contact angle measurements rely on the consistency of the user in assigning the tangent line. When measurements are taken by multiple users, a significant error and inconsistency might occur.
- The direct telescope-goniometric method has another serious limitation. On superhydrophilic surfaces, water droplets are almost flat and it is very difficult to assign a tangent line, thus accurate contact angles below 20° cannot be measured by this method.
2.1.2. Conventional Tilting Plate Method
2.1.3. Tangentometric Technique
2.2. Methods Used for the Measurement of Contact Angles on Solid Surfaces with Different Geometries
2.2.1. Captive Bubble Method
- This method ensures that the solid surface is immersed in the saturated environment.
- Minimum air born contamination on the solid–air interface.
- Easy to control the temperature of the system under study which makes it easier to study the effect of temperature on contact angles.
- For clean polymeric surfaces, the contact angle measurements are in good agreement with that of the sessile drop methods [61].
- It requires large amount of liquid as compared to the sessile drop methods.
- It is not easy to measure the contact angle of solid surfaces that swell when coming into contact with the liquid or substrates with soluble thin films present.
2.2.2. Tilting Plate Method
- When the solid plate is immersed in the test liquid, a disturbance in the liquid appears that may affect the exact measurement of the contact angle.
- Observation of the moving solid plate in the test liquid when the meniscus on one side becomes parralal to the plate requires highly skilled persons for accurate measurement of the contact angles [23].
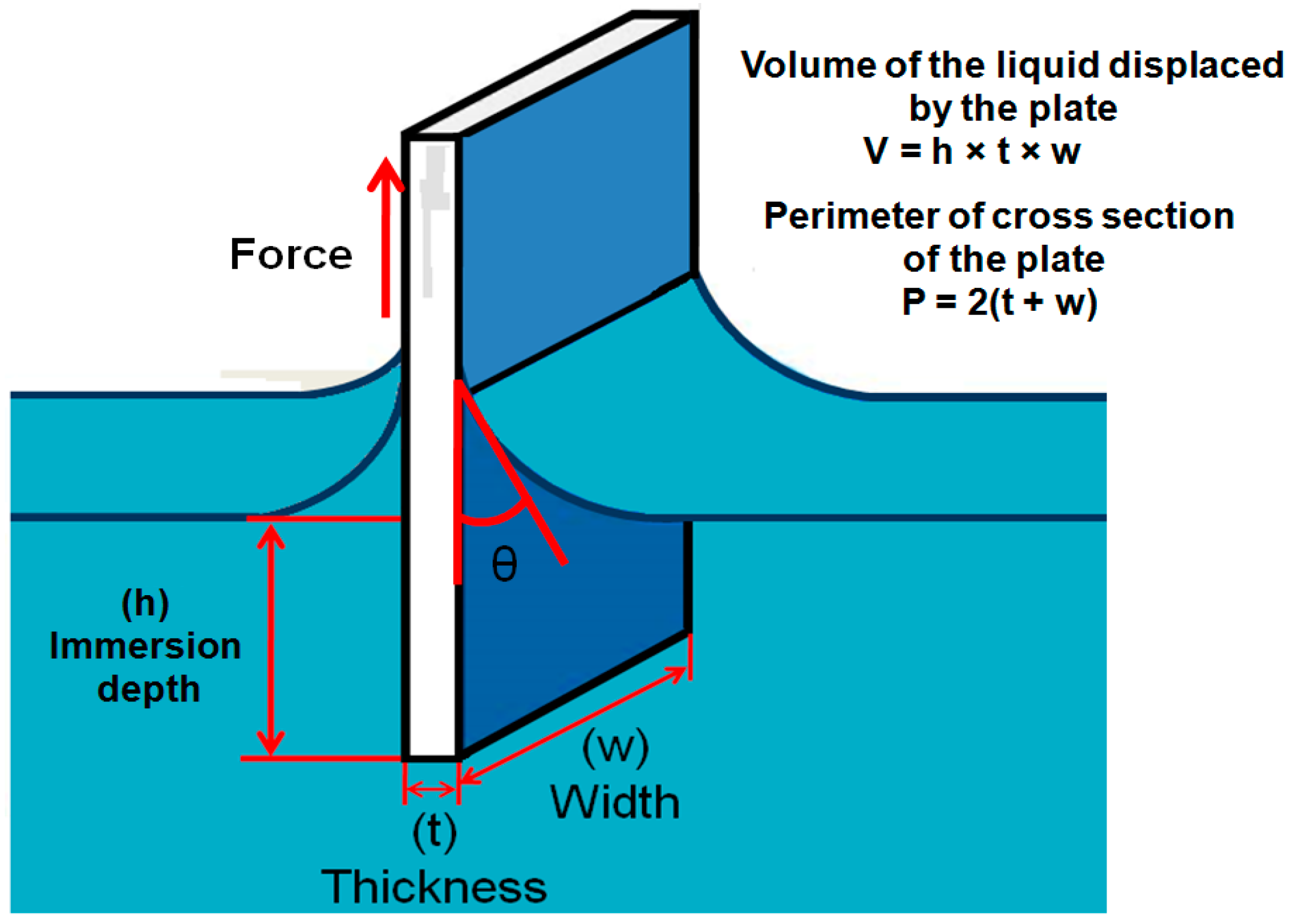
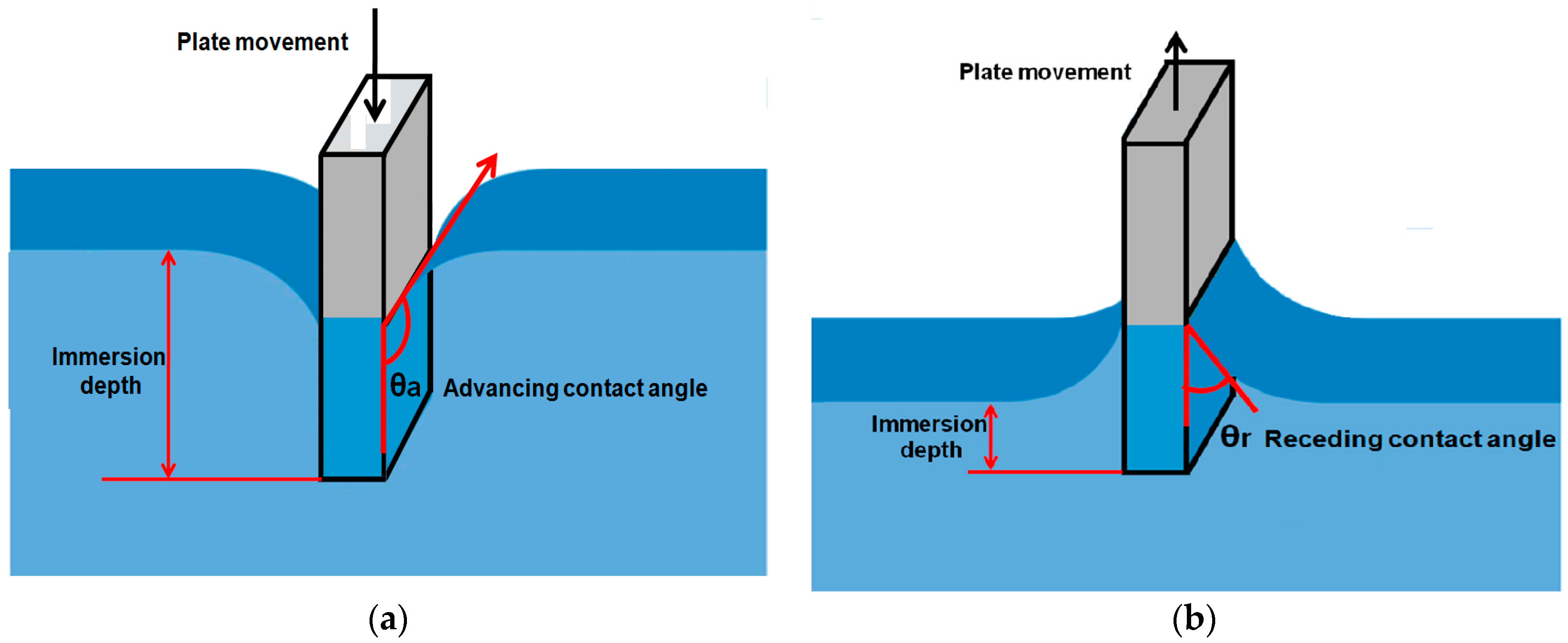
2.2.3. Wilhelmy Balance Method
- The contact angle is indirectly calculated from the measurement of weight force and length which can be measured with more accuracy that direct observation of the contact angle.
- The force can be measured from any depth in the liquid which is always an average value.
- Measurement of the contact angle by this method is more accurate and the advancing and receding angles can be measured by this approach as shown in the Figure 5.
- From this method, surface properties of the solid-like homogeneity and heterogeneity cannot be predicted.
- In this method, the solid sample must be of a known cross sectional area, making it limited for only rods, plates and fibers.
- It can be difficult to measure the precise perimeter of the wetted area of the solid sample.
- Along with the geometry, the solid sample must be the same in composition and topography in all sides which is difficult to obtain if one wants to study the films of anisotropic systems.
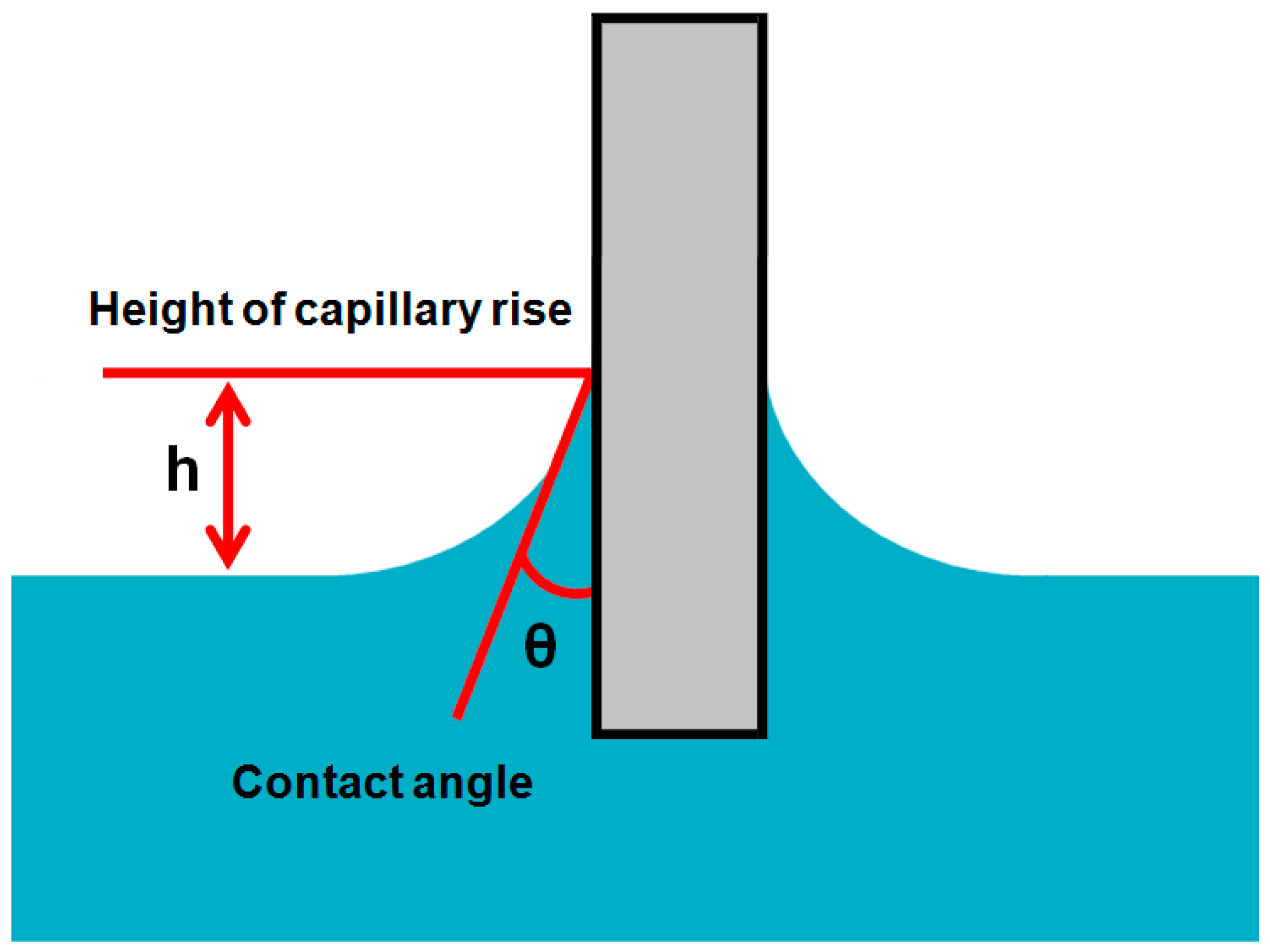
2.2.4. Capilary Rise on a Vertical Plate
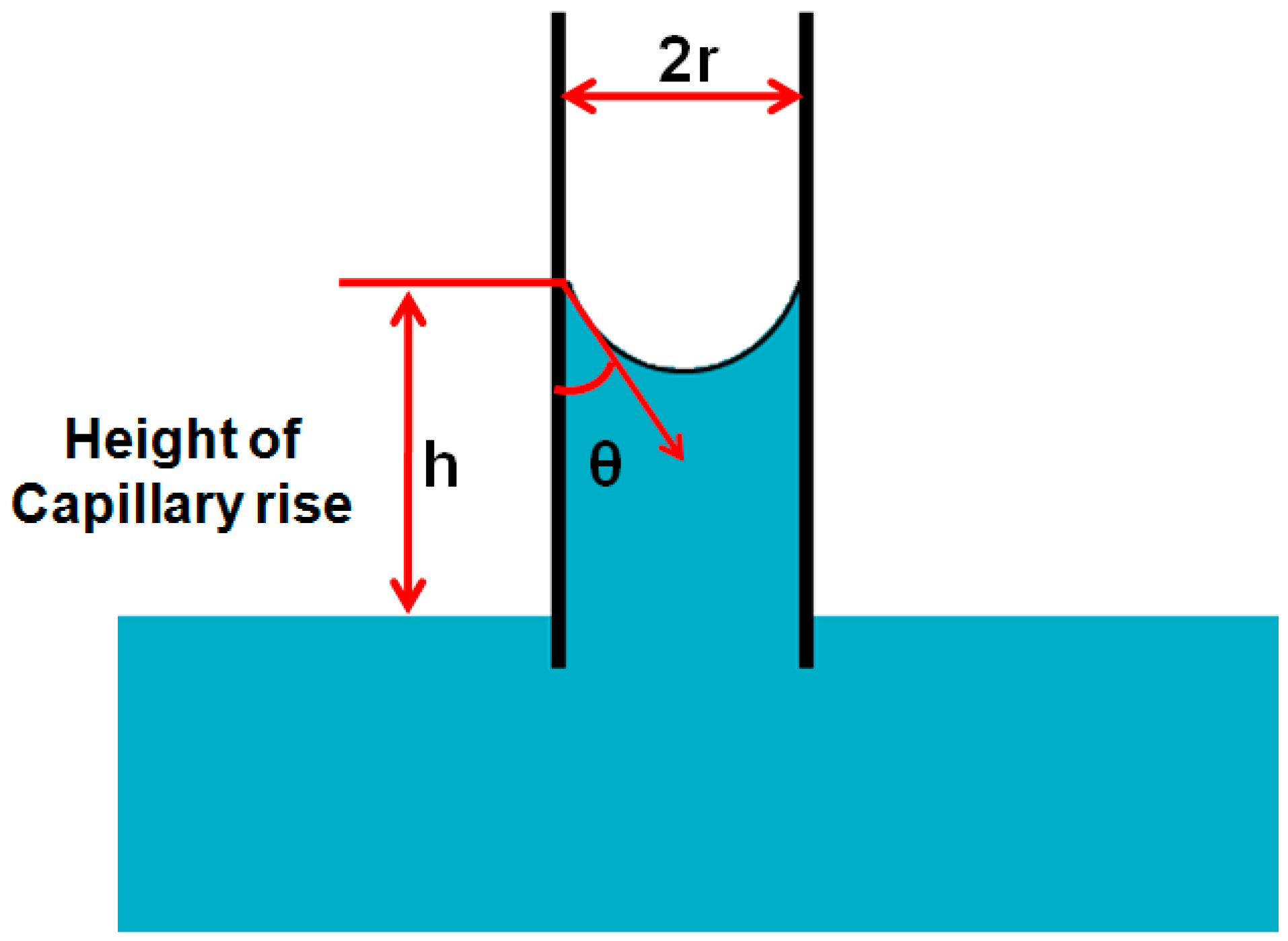
2.2.5. Capillary Rise in a Vertical Tube
2.2.6. Measurement of Contact Angle on Fibers
3. Theories for Analysis of Drop Profile
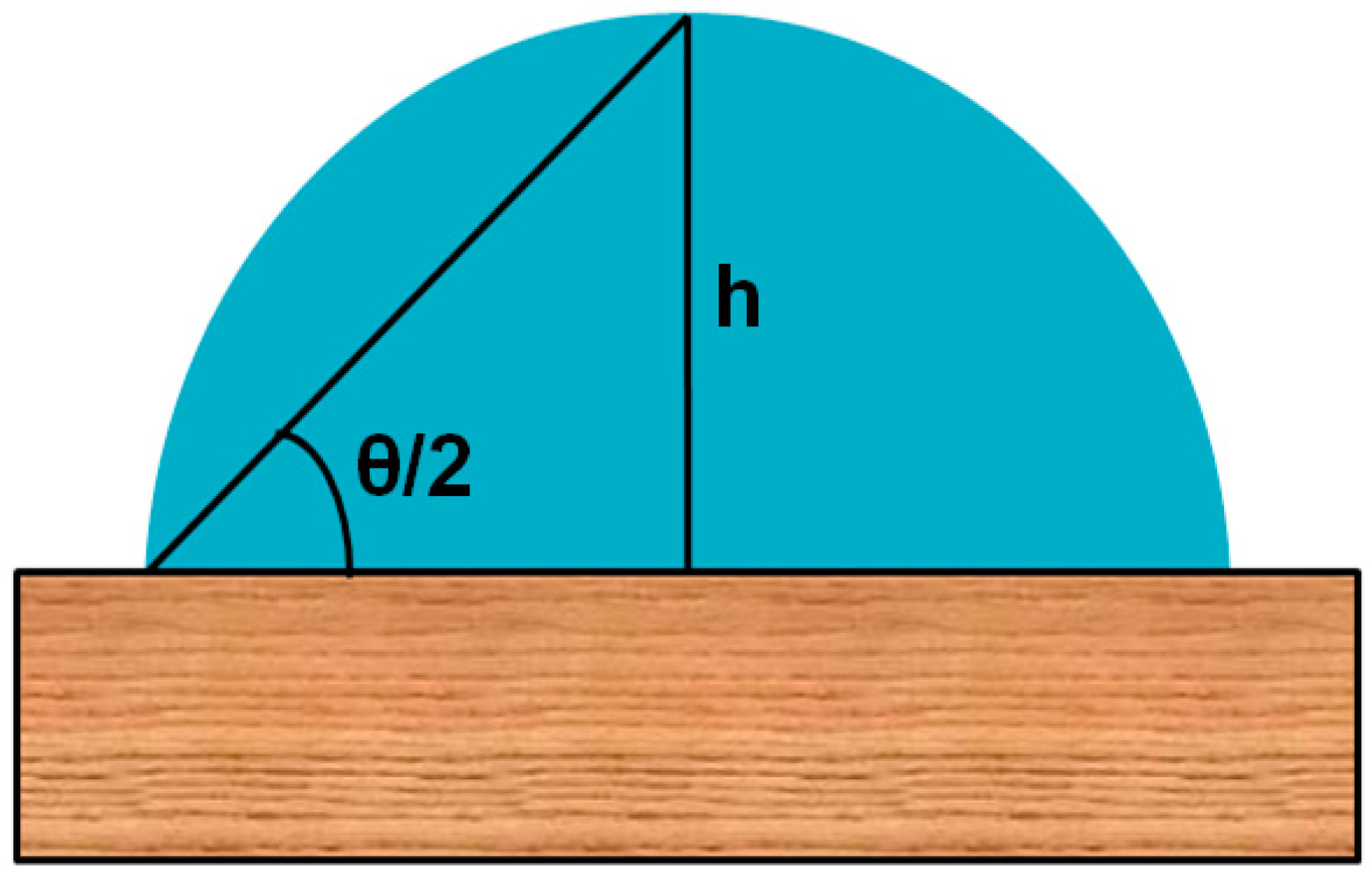
3.1. Drop Shape Analysis by θ/2 Method
3.2. Axisymmetric Drop Shape Analysis (ADSA)
4. Superhydrophobic Surfaces in Plants
5. Superhydrophobic Surfaces in Animals and Insects
6. Superhydrophobic Textiles
6.1. Robust Superhydrophobic Textiles
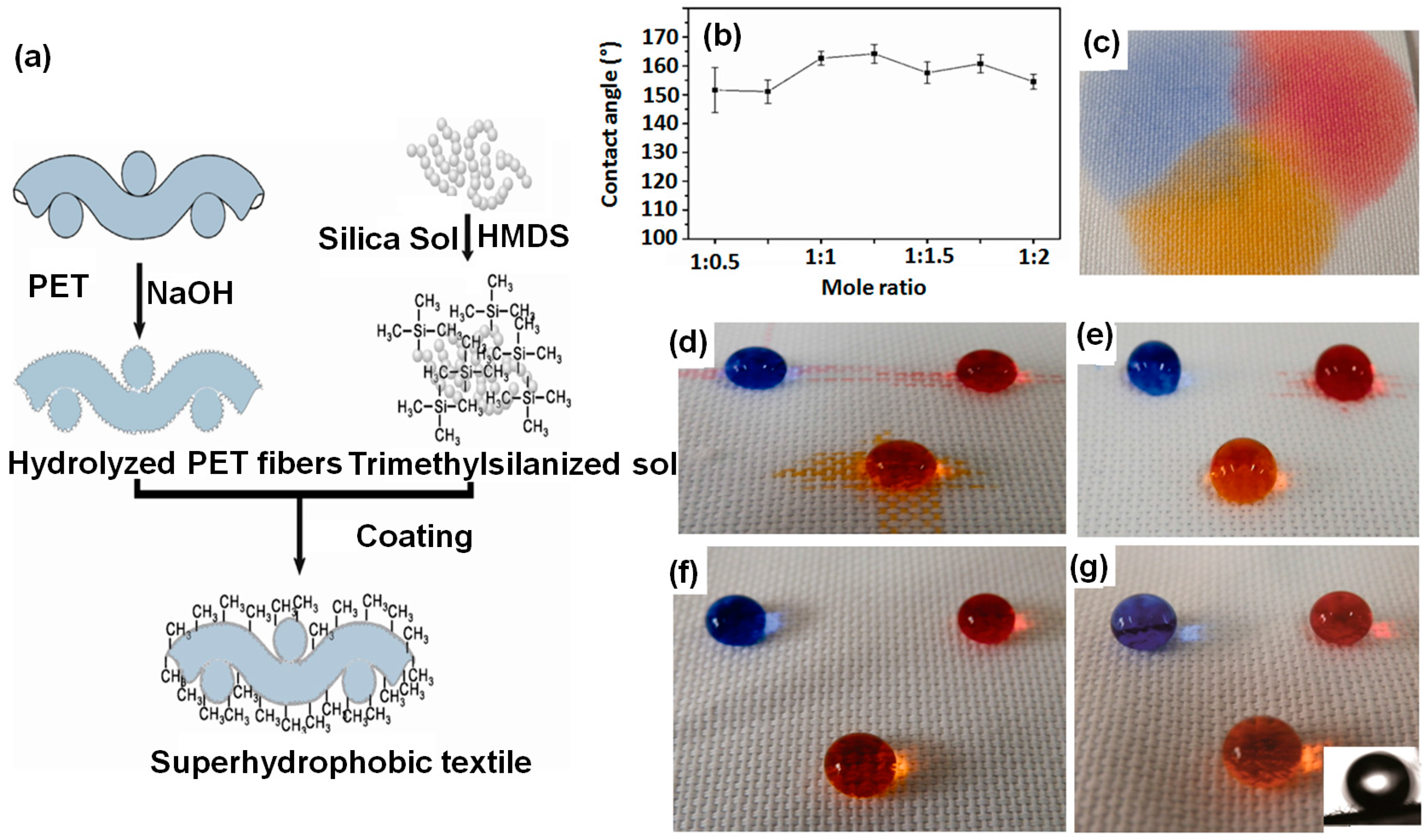
6.1.1. Sol–Gel Method
- Silica, modified silica and other metal oxide nano-sols with particle diameters ranging from 1 to 100 nm can make transparent and well adhered oxide layers on textiles.
- The oxide layers formed impart and enhance mechanical properties to the fabrics, e.g., wear and abrasion resistance.
- The metal oxide layers formed offer further possible ways to modify and enhance the surface functionality of the fabrics.
- The oxide layers formed by this method are stable against heat, light, microbial and chemical attacks.
- The oxide layers formed can carry other functional additives such as inorganic particles and polymers. It is easy to control the pore size, porosity level and immobilization of imbedded compounds.
- This process can be performed in conventional coating systems such as pad-dry-cure and simple dip-coating methods under normal temperature and pressure conditions.
6.1.2. Admicellar Polymerization Technique
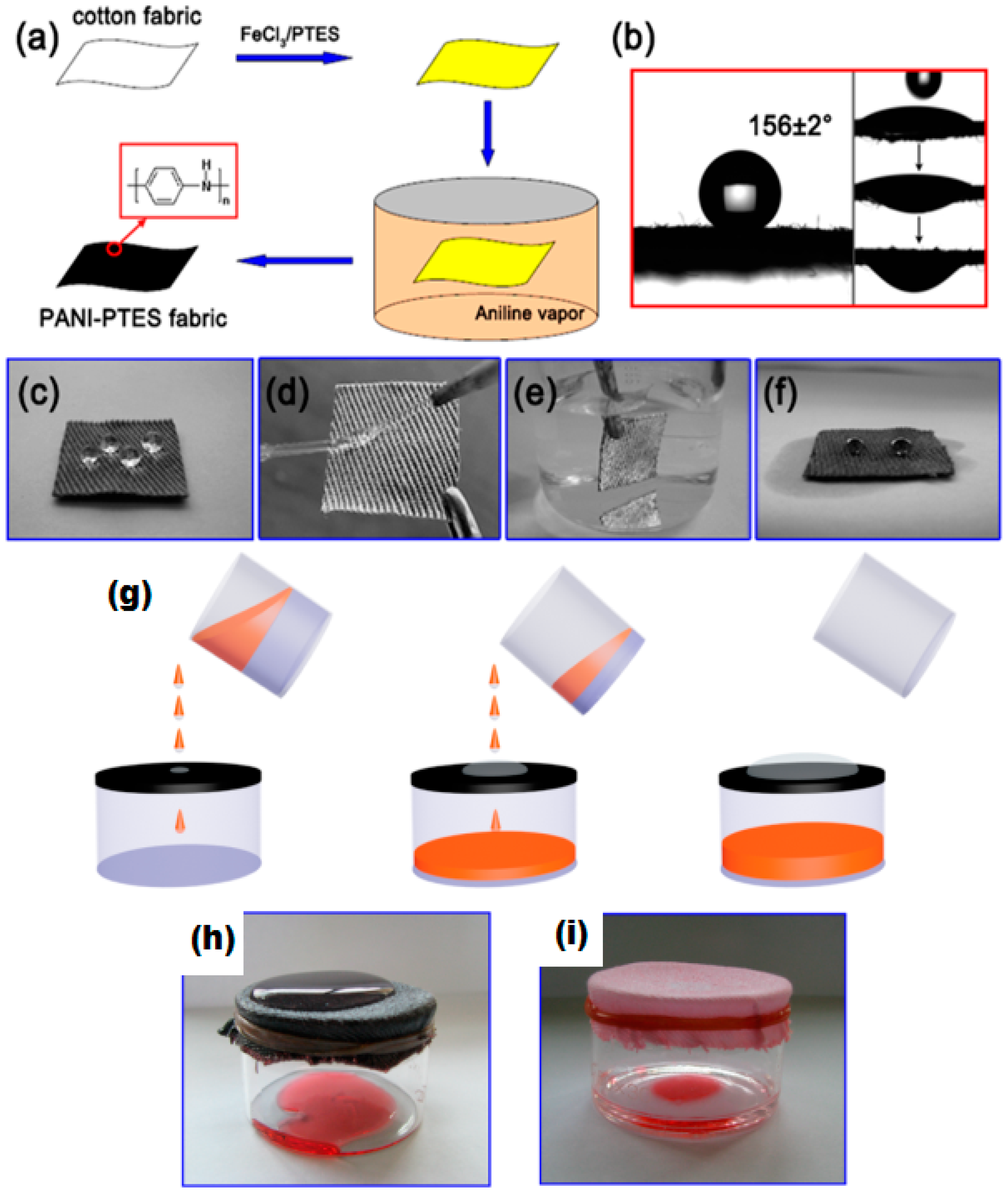
6.1.3. Direct Fluorination Modification
6.1.4. Electrospinning
6.1.5. Polymerization
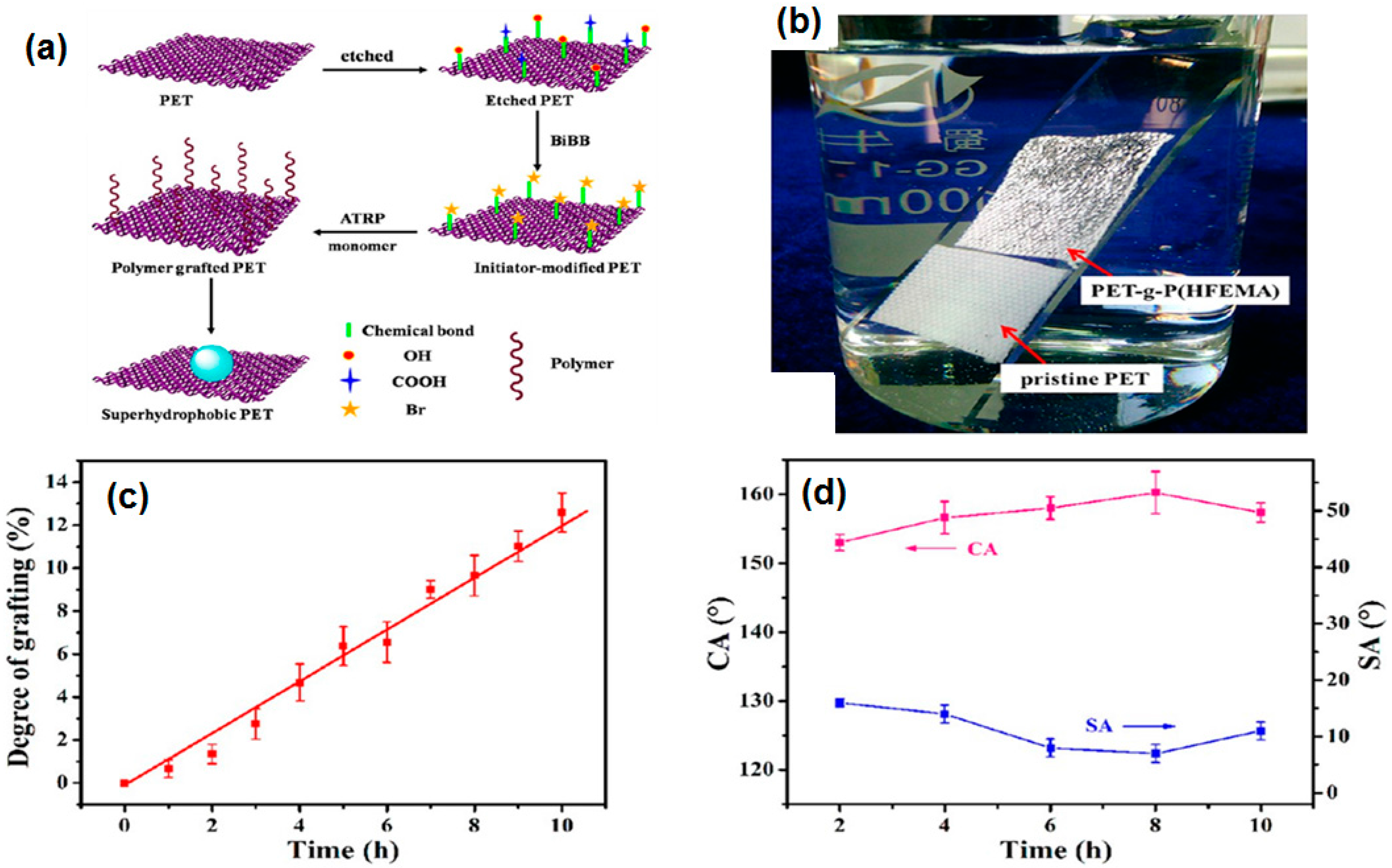
6.1.6. Initiated Chemical Vapor Deposition (iCVD) and Atom Transfer Radical Polymerization (ATRP)
6.2. Superhydrophobic Textiles for Oil–Water Separations
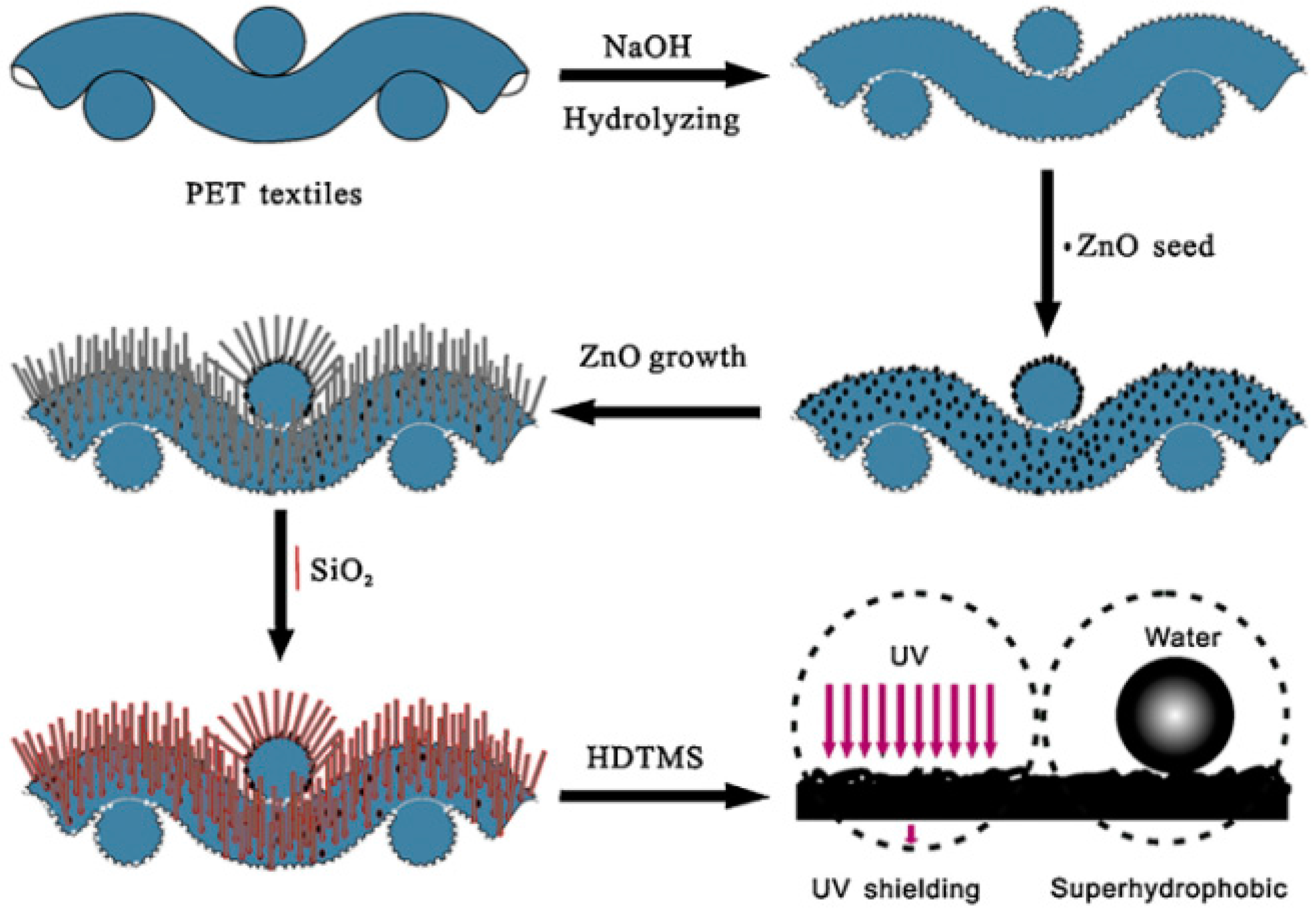
6.3. Superhydrophobic Textiles for Ultraviolet Radiation Shielding
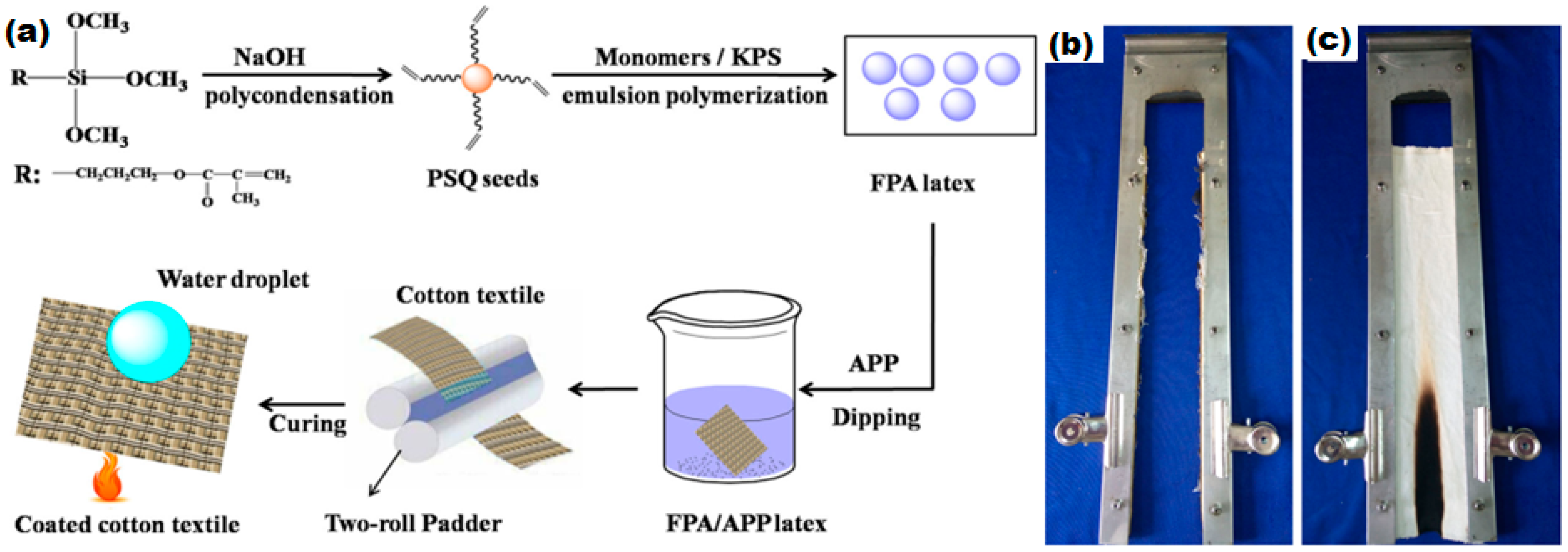
6.4. Flame Retardant Superhydrophobic Textiles
7. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Barthlott, W.; Neinhuis, C. Purity of the sacred lotus, or escape from contamination in biological surfaces. Planta 1997, 202, 1–8. [Google Scholar] [CrossRef]
- Neinhuis, C.; Barthlott, W. Characterization and distribution of water-repellent, self-cleaning plant surfaces. Ann. Bot. 1997, 79, 667–677. [Google Scholar] [CrossRef]
- Blossey, R. Self-cleaning surfaces—Virtual realities. Nat. Mater. 2003, 2, 301–306. [Google Scholar] [CrossRef] [PubMed]
- Xue, C.-H.; Jia, S.-T.; Zhang, J.; Tian, L.-Q.; Chen, H.-Z.; Wang, M. Preparation of superhydrophobic surfaces on cotton textiles. Sci. Technol. Adv. Mater. 2016, 9. [Google Scholar] [CrossRef]
- Barthlott, W.; Schimmel, T.; Wiersch, S.; Koch, K.; Brede, M.; Barczewski, M.; Walheim, S.; Weis, A.; Kaltenmaier, A.; Leder, A. The Salvinia paradox: Superhydrophobic surfaces with hydrophilic pins for air retention under water. Adv. Mater. 2010, 22, 2325–2328. [Google Scholar] [CrossRef] [PubMed]
- Bixler, G.D.; Bhushan, B. Bioinspired rice leaf and butterfly wing surface structures combining shark skin and lotus effects. Soft Matter 2012, 8, 11271–11284. [Google Scholar] [CrossRef]
- Gao, X.; Yan, X.; Yao, X.; Xu, L.; Zhang, K.; Zhang, J.; Yang, B.; Jiang, L. The Dry-Style Antifogging Properties of Mosquito Compound Eyes and Artificial Analogues Prepared by Soft Lithography. Adv. Mater. 2007, 19, 2213–2217. [Google Scholar] [CrossRef]
- Kwon, D.H.; Huh, H.K.; Lee, S.J. Wettability and impact dynamics of water droplets on rice (Oryza sativa L.) leaves. Exp. Fluids 2014, 55, 1–9. [Google Scholar] [CrossRef]
- Mayser, M.J.; Bohn, H.F.; Reker, M.; Barthlott, W. Measuring air layer volumes retained by submerged floating-ferns Salvinia and biomimetic superhydrophobic surfaces. Beilstein J. Nanotechnol. 2014, 5, 812–821. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Gao, N.; Barthlott, W. Mimicking natural superhydrophobic surfaces and grasping the wetting process: A review on recent progress in preparing superhydrophobic surfaces. Adv. Colloid Interface Sci. 2011, 169, 80–105. [Google Scholar] [CrossRef] [PubMed]
- Wenzel, R.N. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Cassie, A.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546–551. [Google Scholar] [CrossRef]
- Koch, K.; Bhushan, B.; Barthlott, W. Diversity of structure, morphology and wetting of plant surfaces. Soft Matter 2008, 4, 1943–1963. [Google Scholar] [CrossRef]
- Li, X.-M.; Reinhoudt, D.; Crego-Calama, M. What do we need for a superhydrophobic surface? A review on the recent progress in the preparation of superhydrophobic surfaces. Chem. Soc. Rev. 2007, 36, 1350–1368. [Google Scholar] [CrossRef] [PubMed]
- Callies, M.; Quéré, D. On water repellency. Soft Matter 2005, 1, 55–61. [Google Scholar] [CrossRef]
- Wenzel, R.N. Surface Roughness and Contact Angle. J. Phys. Chem. 1949, 53, 1466–1467. [Google Scholar] [CrossRef]
- Herminghaus, S. Roughness-induced non-wetting. Europhys. Lett. 2000, 52, 165–170. [Google Scholar] [CrossRef]
- Herminghaus, S. Roughness-induced non-wetting. Europhys. Lett. 2007, 79. [Google Scholar] [CrossRef]
- Bico, J.; Marzolin, C.; Quéré, D. Pearl drops. Europhys. Lett. 1999, 47, 220–226. [Google Scholar] [CrossRef]
- Quéré, D. Non-sticking drops. Rep. Prog. Phys. 2005, 68, 2495–2532. [Google Scholar] [CrossRef]
- Marmur, A. Wetting on hydrophobic rough surfaces: To be heterogeneous or not to be? Langmuir 2003, 19, 8343–8348. [Google Scholar] [CrossRef]
- Cassie, A. Contact angles. Discuss. Faraday Soc. 1948, 3, 11–16. [Google Scholar] [CrossRef]
- Yuan, Y.; Lee, T.R. Contact angle and wetting properties. In Surface Science Techniques; Springer: New York, NY, USA, 2013; pp. 3–34. [Google Scholar]
- Kota, A.K.; Li, Y.; Mabry, J.M.; Tuteja, A. Hierarchically structured superoleophobic surfaces with ultralow contact angle hysteresis. Adv. Mater. 2012, 24, 5838–5843. [Google Scholar] [CrossRef] [PubMed]
- Onda, T.; Shibuichi, S.; Satoh, N.; Tsujii, K. Super-water-repellent fractal surfaces. Langmuir 1996, 12, 2125–2127. [Google Scholar] [CrossRef]
- Jung, Y.C.; Bhushan, B. Dynamic effects induced transition of droplets on biomimetic superhydrophobic surfaces. Langmuir 2009, 25, 9208–9218. [Google Scholar] [CrossRef] [PubMed]
- Roach, P.; Shirtcliffe, N.J.; Newton, M.I. Progess in superhydrophobic surface development. Soft Matter 2008, 4, 224–240. [Google Scholar] [CrossRef]
- Kwon, Y.; Patankar, N.; Choi, J.; Lee, J. Design of surface hierarchy for extreme hydrophobicity. Langmuir 2009, 25, 6129–6136. [Google Scholar] [CrossRef] [PubMed]
- Patankar, N.A. On the modeling of hydrophobic contact angles on rough surfaces. Langmuir 2003, 19, 1249–1253. [Google Scholar] [CrossRef]
- Quéré, D.; Lafuma, A.; Bico, J. Slippy and sticky microtextured solids. Nanotechnology 2003, 14, 1109–1112. [Google Scholar]
- Feng, L.; Song, Y.; Zhai, J.; Liu, B.; Xu, J.; Jiang, L.; Zhu, D. Creation of a superhydrophobic surface from an amphiphilic polymer. Angew. Chem. 2003, 115, 824–826. [Google Scholar] [CrossRef]
- Gao, L.; McCarthy, T.J. A perfectly hydrophobic surface (θA/θR = 180/180). J. Am. Chem. Soc. 2006, 128, 9052–9053. [Google Scholar] [CrossRef] [PubMed]
- Gao, L.; McCarthy, T.J. A commercially available perfectly hydrophobic material (θA/θR = 180/180). Langmuir 2007, 23, 9125–9127. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Yao, T.; Wu, J.; Ma, C.; Fan, Z.; Wang, Z.; Cheng, Y.; Lin, Q.; Yang, B. Facile approach in fabricating superhydrophobic and superoleophilic surface for water and oil mixture separation. ACS Appl. Mater. Interfaces 2009, 1, 2613–2617. [Google Scholar] [CrossRef] [PubMed]
- Lafuma, A.; Quéré, D. Superhydrophobic states. Nat. Mater. 2003, 2, 457–460. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Mammen, L.; Butt, H.-J.; Vollmer, D. Candle soot as a template for a transparent robust superamphiphobic coating. Science 2012, 335, 67–70. [Google Scholar] [CrossRef] [PubMed]
- Leng, B.; Shao, Z.; de With, G.; Ming, W. Superoleophobic cotton textiles. Langmuir 2009, 25, 2456–2460. [Google Scholar] [CrossRef] [PubMed]
- Steele, A.; Bayer, I.; Loth, E. Inherently superoleophobic nanocomposite coatings by spray atomization. Nano Lett. 2008, 9, 501–505. [Google Scholar] [CrossRef] [PubMed]
- Chen, A.-F.; Huang, H.-X. Rapid Fabrication of T-Shaped Micropillars on Polypropylene Surfaces with Robust Cassie–Baxter State for Quantitative Droplet Collection. J. Phys. Chem. C 2016, 120, 1556–1561. [Google Scholar] [CrossRef]
- Wang, J.; Liu, F.; Chen, H.; Chen, D. Superhydrophobic behavior achieved from hydrophilic surfaces. Appl. Phys. Lett. 2009, 95. [Google Scholar] [CrossRef]
- Liu, T.; Kim, C. Turning a surface superrepellent even to completely wetting liquids. Science 2014, 346, 1096–1100. [Google Scholar] [CrossRef] [PubMed]
- Ahuja, A.; Taylor, J.; Lifton, V.; Sidorenko, A.; Salamon, T.; Lobaton, E.; Kolodner, P.; Krupenkin, T. Nanonails: A simple geometrical approach to electrically tunable superlyophobic surfaces. Langmuir 2008, 24, 9–14. [Google Scholar] [CrossRef] [PubMed]
- Tuteja, A.; Choi, W.; Ma, M.; Mabry, J.M.; Mazzella, S.A.; Rutledge, G.C.; McKinley, G.H.; Cohen, R.E. Designing superoleophobic surfaces. Science 2007, 318, 1618–1622. [Google Scholar] [CrossRef] [PubMed]
- Pan, S.; Kota, A.K.; Mabry, J.M.; Tuteja, A. Superomniphobic surfaces for effective chemical shielding. J. Am. Chem. Soc. 2012, 135, 578–581. [Google Scholar] [CrossRef] [PubMed]
- Choi, W.; Tuteja, A.; Chhatre, S.; Mabry, J.M.; Cohen, R.E.; McKinley, G.H. Fabrics with tunable oleophobicity. Adv. Mater. 2009, 21, 2190–2195. [Google Scholar] [CrossRef]
- Im, M.; Im, H.; Lee, J.-H.; Yoon, J.-B.; Choi, Y.-K. A robust superhydrophobic and superoleophobic surface with inverse-trapezoidal microstructures on a large transparent flexible substrate. Soft Matter 2010, 6, 1401–1404. [Google Scholar] [CrossRef]
- Choi, H.-J.; Choo, S.; Shin, J.-H.; Kim, K.-I.; Lee, H. Fabrication of superhydrophobic and oleophobic surfaces with overhang structure by reverse nanoimprint lithography. J. Phys. Chem. C 2013, 117, 24354–24359. [Google Scholar] [CrossRef]
- Bigelow, W.; Pickett, D.; Zisman, W. Oleophobic monolayers: I. Films adsorbed from solution in non-polar liquids. J. Colloid Sci. 1946, 1, 513–538. [Google Scholar] [CrossRef]
- Neumann, A.; Good, R.; Good, R.; Stromberg, R. Surface and Colloid Science. Plenum 1979, 11, 31–91. [Google Scholar]
- Hunter, R.J. Foundations of Colloid Science; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Smithwich, R.W. Contact-angle studies of microscopic mercury droplets on glass. J. Colloid Interface Sci. 1988, 123, 482–485. [Google Scholar] [CrossRef]
- Kwok, D.; Lin, R.; Mui, M.; Neumann, A. Low-rate dynamic and static contact angles and the determination of solid surface tensions. Colloids Surf. Physicochem. Eng. Asp. 1996, 116, 63–77. [Google Scholar] [CrossRef]
- Macdougall, G.; Ockrent, C. Surface energy relations in liquid/solid systems. I. The adhesion of liquids to solids and a new method of determining the surface tension of liquids. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1942, 180, 151–173. [Google Scholar] [CrossRef]
- Extrand, C.; Kumagai, Y. Contact angles and hysteresis on soft surfaces. J. Colloid Interface Sci. 1996, 184, 191–200. [Google Scholar] [CrossRef] [PubMed]
- Extrand, C.; Kumagai, Y. An experimental study of contact angle hysteresis. J. Colloid Interface Sci. 1997, 191, 378–383. [Google Scholar] [CrossRef] [PubMed]
- Pierce, E.; Carmona, F.; Amirfazli, A. Understanding of sliding and contact angle results in tilted plate experiments. Colloids Surf. Physicochem. Eng. Asp. 2008, 323, 73–82. [Google Scholar] [CrossRef]
- Krasovitski, B.; Marmur, A. Drops down the hill: Theoretical study of limiting contact angles and the hysteresis range on a tilted plate. Langmuir 2005, 21, 3881–3885. [Google Scholar] [CrossRef] [PubMed]
- Morra, M.; Occhiello, E.; Garbassi, F. Knowledge about polymer surfaces from contact angle measurements. Adv. Colloid Interface Sci. 1990, 32, 79–116. [Google Scholar] [CrossRef]
- Phillips, M.; Riddiford, A. Dynamic contact angles. II. Velocity and relaxation effects for various liquids. J. Colloid Interface Sci. 1972, 41, 77–85. [Google Scholar] [CrossRef]
- Taggart, A.F.; Taylor, T.C.; Ince, C.R. Experiments with Flotation Reagents; American Institute of Mining and Metallurgical Engineers, Incorporated: Englewood, CO, USA, 1929. [Google Scholar]
- Zhang, W.; Wahlgren, M.; Sivik, B. Membrane characterization by the contact angle technique: II. Characterization of UF-membranes and comparison between the captive bubble and sessile drop as methods to obtain water contact angles. Desalination 1989, 72, 263–273. [Google Scholar] [CrossRef]
- Smedley, G.T.; Coles, D.E. A refractive tilting-plate technique for measurement of dynamic contact angles. J. Colloid Interface Sci. 2005, 286, 310–318. [Google Scholar] [CrossRef] [PubMed]
- Bezuglyi, B.; Tarasov, O.; Fedorets, A. Modified tilting-plate method for measuring contact angles. Colloid J. 2001, 63, 668–674. [Google Scholar] [CrossRef]
- Moghaddam, M.S.; Claesson, P.M.; Wålinder, M.E.; Swerin, A. Wettability and liquid sorption of wood investigated by Wilhelmy plate method. Wood Sci. Technol. 2014, 48, 161–176. [Google Scholar] [CrossRef]
- Cain, J.; Francis, D.; Venter, R.; Neumann, A. Dynamic contact angles on smooth and rough surfaces. J. Colloid Interface Sci. 1983, 94, 123–130. [Google Scholar] [CrossRef]
- Shimokawa, M.; Takamura, T. Relation between interfacial tension and capillary liquid rise on polished metal electrodes. J. Electroanal. Chem. Interfacial Electrochem. 1973, 41, 359–366. [Google Scholar] [CrossRef]
- Budziak, C.; Vargha-Butler, E.; Neumann, A. Temperature dependence of contact angles on elastomers. J. Appl. Polym. Sci. 1991, 42, 1959–1964. [Google Scholar] [CrossRef]
- Budziak, C.; Neumann, A. Automation of the capillary rise technique for measuring contact angles. Colloids Surf. 1990, 43, 279–293. [Google Scholar] [CrossRef]
- Kwok, D.; Budziak, C.; Neumann, A. Measurements of static and low rate dynamic contact angles by means of an automated capillary rise technique. J. Colloid Interface Sci. 1995, 173, 143–150. [Google Scholar] [CrossRef]
- Jordan, D.; Lane, J. A thermodynamic discussion of the use of a vertical-plate balance for the measurement of surface tension. Aust. J. Chem. 1964, 17, 7–15. [Google Scholar] [CrossRef]
- Kloubek, J. Measurement of the dynamic surface tension by the maximum bubble pressure method. IV. Surface tension of aqueous solutions of sodium dodecyl sulfate. J. Colloid Interface Sci. 1972, 41, 17–22. [Google Scholar] [CrossRef]
- Schwartz, A.M.; Minor, F.W. A simplified thermodynamic approach to capillarity: I. Application to flow in capillary channels. J. Colloid Sci. 1959, 14, 572–583. [Google Scholar] [CrossRef]
- Bascom, W.; Romans, J. Microvoids in Glass-Resin Composites. Their Origin and Effect on Composite Strength. Ind. Eng. Chem. Prod. Res. Dev. 1968, 7, 172–178. [Google Scholar] [CrossRef]
- Roe, R.-J. Wetting of fine wires and fibers by a liquid film. J. Colloid Interface Sci. 1975, 50, 70–79. [Google Scholar] [CrossRef]
- Rapacchietta, A.; Neumann, A. Force and free-energy analyses of small particles at fluid interfaces: II. Spheres. J. Colloid Interface Sci. 1977, 59, 555–567. [Google Scholar] [CrossRef]
- Rapacchietta, A.; Neumann, A.; Omenyi, S. Force and free-energy analyses of small particles at fluid interfaces: I. Cylinders. J. Colloid Interface Sci. 1977, 59, 541–554. [Google Scholar] [CrossRef]
- Passerone, A.; Liggieri, L.; Rando, N.; Ravera, F.; Ricci, E. A new experimental method for the measurement of the interfacial tension between immiscible fluids at zero bond number. J. Colloid Interface Sci. 1991, 146, 152–162. [Google Scholar] [CrossRef]
- Fordham, S. On the calculation of surface tension from measurements of pendant drops. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1948, 194, 1–16. [Google Scholar] [CrossRef]
- Mills, O. Tables for use in the measurement of interfacial tensions between liquids with small density differences. Br. J. Appl. Phys. 1953, 4, 247–252. [Google Scholar] [CrossRef]
- Del Rio, O.; Neumann, A. Axisymmetric drop shape analysis: Computational methods for the measurement of interfacial properties from the shape and dimensions of pendant and sessile drops. J. Colloid Interface Sci. 1997, 196, 136–147. [Google Scholar]
- Malcolm, J.; Paynter, H. Simultaneous determination of contact angle and interfacial tension from sessile drop measurements. J. Colloid Interface Sci. 1981, 82, 269–275. [Google Scholar] [CrossRef]
- Maze, C.; Burnet, G. A non-linear regression method for calculating surface tension and contact angle from the shape of a sessile drop. Surf. Sci. 1969, 13, 451–470. [Google Scholar] [CrossRef]
- Fisher, L.R.; Israelachvili, J.N. Experimental studies on the applicability of the Kelvin equation to highly curved concave menisci. J. Colloid Interface Sci. 1981, 80, 528–541. [Google Scholar] [CrossRef]
- Rotenberg, Y.; Boruvka, L.; Neumann, A. Determination of surface tension and contact angle from the shapes of axisymmetric fluid interfaces. J. Colloid Interface Sci. 1983, 93, 169–183. [Google Scholar] [CrossRef]
- Kalantarian, A.; Saad, S.M.; Neumann, A.W. Accuracy of surface tension measurement from drop shapes: The role of image analysis. Adv. Colloid Interface Sci. 2013, 199, 15–22. [Google Scholar] [CrossRef] [PubMed]
- Cheng, P.; Li, D.; Boruvka, L.; Rotenberg, Y.; Neumann, A. Automation of axisymmetric drop shape analysis for measurements of interfacial tensions and contact angles. Colloids Surf. 1990, 43, 151–167. [Google Scholar] [CrossRef]
- Skinner, F.; Rotenberg, Y.; Neumann, A. Contact angle measurements from the contact diameter of sessile drops by means of a modified axisymmetric drop shape analysis. J. Colloid Interface Sci. 1989, 130, 25–34. [Google Scholar] [CrossRef]
- Moy, E.; Cheng, P.; Policova, Z.; Treppo, S.; Kwok, D.; Mack, D.; Sherman, P.; Neuman, A. Measurement of contact angles from the maximum diameter of non-wetting drops by means of a modified axisymmetric drop shape analysis. Colloids Surf. 1991, 58, 215–227. [Google Scholar] [CrossRef]
- Cabezas, M.; Bateni, A.; Montanero, J.; Neumann, A. A new drop-shape methodology for surface tension measurement. Appl. Surf. Sci. 2004, 238, 480–484. [Google Scholar] [CrossRef]
- Cabezas, M.; Bateni, A.; Montanero, J.; Neumann, A. A new method of image processing in the analysis of axisymmetric drop shapes. Colloids Surf. Physicochem. Eng. Asp. 2005, 255, 193–200. [Google Scholar] [CrossRef]
- Cabezas, M.G.; Bateni, A.; Montanero, J.M.; Neumann, A.W. Determination of surface tension and contact angle from the shapes of axisymmetric fluid interfaces without use of apex coordinates. Langmuir 2006, 22, 10053–10060. [Google Scholar] [CrossRef] [PubMed]
- Feng, L.; Li, S.; Li, Y.; Li, H.; Zhang, L.; Zhai, J.; Song, Y.; Liu, B.; Jiang, L.; Zhu, D. Super-hydrophobic surfaces: From natural to artificial. Adv. Mater. 2002, 14, 1857–1860. [Google Scholar] [CrossRef]
- Koch, K.; Bhushan, B.; Barthlott, W. Multifunctional surface structures of plants: An inspiration for biomimetics. Prog. Mater Sci. 2009, 54, 137–178. [Google Scholar] [CrossRef]
- Barthlott, W.; Neinhuis, C.; Cutler, D.; Ditsch, F.; Meusel, I.; Theisen, I.; Wilhelmi, H. Classification and terminology of plant epicuticular waxes. Bot. J. Linn. Soc. 1998, 126, 237–260. [Google Scholar] [CrossRef]
- Hüger, E.; Rothe, H.; Frant, M.; Grohmann, S.; Hildebrand, G.; Liefeith, K. Atomic force microscopy and thermodynamics on taro, a self-cleaning plant leaf. Appl. Phys. Lett. 2009, 95. [Google Scholar] [CrossRef]
- Byun, D.; Hong, J.; Ko, J.H.; Lee, Y.J.; Park, H.C.; Byun, B.-K.; Lukes, J.R. Wetting characteristics of insect wing surfaces. J. Bionic Eng. 2009, 6, 63–70. [Google Scholar] [CrossRef]
- Fang, Y.; Sun, G.; Cong, Q.; Chen, G.-H.; Ren, L.-Q. Effects of methanol on wettability of the non-smooth surface on butterfly wing. J. Bionic Eng. 2008, 5, 127–133. [Google Scholar] [CrossRef]
- Bixler, G.D.; Bhushan, B. Fluid drag reduction and efficient self-cleaning with rice leaf and butterfly wing bioinspired surfaces. Nanoscale 2013, 5, 7685–7710. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.; Jiang, L. Biophysics: Water-repellent legs of water striders. Nature 2004, 432, 36. [Google Scholar] [CrossRef] [PubMed]
- Jost, K.; Dion, G.; Gogotsi, Y. Textile energy storage in perspective. J. Mater. Chem. A 2014, 2, 10776–10787. [Google Scholar] [CrossRef]
- Avila, A.G.; Hinestroza, J.P. Smart textiles: Tough cotton. Nat. Nanotechnol. 2008, 3, 458–459. [Google Scholar] [CrossRef] [PubMed]
- Horrocks, A.R.; Anand, S.C. Handbook of Technical Textiles; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Mahltig, B.; Haufe, H.; Böttcher, H. Functionalisation of textiles by inorganic sol–gel coatings. J. Mater. Chem. 2005, 15, 4385–4398. [Google Scholar] [CrossRef]
- Hikita, M.; Tanaka, K.; Nakamura, T.; Kajiyama, T.; Takahara, A. Super-liquid-repellent surfaces prepared by colloidal silica nanoparticles covered with fluoroalkyl groups. Langmuir 2005, 21, 7299–7302. [Google Scholar] [CrossRef] [PubMed]
- Xue, C.-H.; Jia, S.-T.; Chen, H.-Z.; Wang, M. Superhydrophobic cotton fabrics prepared by sol–gel coating of TiO2 and surface hydrophobization. Sci. Technol. Adv. Mater. 2008, 9. [Google Scholar] [CrossRef]
- Zhu, Q.; Gao, Q.; Guo, Y.; Yang, C.Q.; Shen, L. Modified silica sol coatings for highly hydrophobic cotton and polyester fabrics using a one-step procedure. Ind. Eng. Chem. Res. 2011, 50, 5881–5888. [Google Scholar] [CrossRef]
- Harwell, J.H.; Hoskins, J.C.; Schechter, R.S.; Wade, W.H. Pseudophase separation model for surfactant adsorption: Isomerically pure surfactants. Langmuir 1985, 1, 251–262. [Google Scholar] [CrossRef]
- Ulman, K.N.; Shukla, S.R. Admicellar Polymerization and Its Application in Textiles. Adv. Polym. Technol. 2015. [Google Scholar] [CrossRef]
- Wang, S.; Russo, T.; Qiao, G.G.; Solomon, D.H.; Shanks, R.A. Admicellar polymerization of styrene with divinyl benzene on alumina particles: The synthesis of white reinforcing fillers. J. Mater. Sci. 2006, 41, 7474–7482. [Google Scholar] [CrossRef]
- Maity, J.; Kothary, P.; O’Rear, E.A.; Jacob, C. Preparation and comparison of hydrophobic cotton fabric obtained by direct fluorination and admicellar polymerization of fluoromonomers. Ind. Eng. Chem. Res. 2010, 49, 6075–6079. [Google Scholar] [CrossRef]
- Siriviriyanun, A.; O’Rear, E.A.; Yanumet, N. Improvement in the flame retardancy of cotton fabric by admicellar polymerization of 2-acryloyloxyethyl diethyl phosphate using an anionic surfactant. J. Appl. Polym. Sci. 2008, 109, 3859–3866. [Google Scholar] [CrossRef]
- Tragoonwichian, S.; O’Rear, E.A.; Yanumet, N. Broad ultraviolet protection by copolymerization of 2-[3-(2H-benzotriazol-2-yl)-4-hydroxyphenyl] ethyl methacrylate and 2-hydroxy-4-acryloyloxybenzophenone on cotton via admicellar polymerization. J. Appl. Polym. Sci. 2008, 108, 4004–4013. [Google Scholar] [CrossRef]
- Pongprayoon, T.; Yanumet, N.; Edgar, A. Admicellar polymerization of styrene on cotton. J. Colloid Interface Sci. 2002, 249, 227–234. [Google Scholar] [CrossRef] [PubMed]
- Hanumansetty, S.; Maity, J.; Foster, R.; O’Rear, E.A. Stain resistance of cotton fabrics before and after finishing with admicellar polymerization. Appl. Sci. 2012, 2, 192–205. [Google Scholar] [CrossRef]
- Hobbs, J.P.; Henderson, P.B.; Pascolini, M.R. Assisted permeation through surface fluorinated polymers. J. Fluor. Chem. 2000, 104, 87–95. [Google Scholar] [CrossRef]
- Ma, M.; Mao, Y.; Gupta, M.; Gleason, K.K.; Rutledge, G.C. Superhydrophobic fabrics produced by electrospinning and chemical vapor deposition. Macromolecules 2005, 38, 9742–9748. [Google Scholar] [CrossRef]
- Sas, I.; Gorga, R.E.; Joines, J.A.; Thoney, K.A. Literature review on superhydrophobic self-cleaning surfaces produced by electrospinning. J. Polym. Sci. B Polym. Phys. 2012, 50, 824–845. [Google Scholar] [CrossRef]
- Ma, M.; Hill, R.M.; Rutledge, G.C. A review of recent results on superhydrophobic materials based on micro-and nanofibers. J. Adhes. Sci. Technol. 2008, 22, 1799–1817. [Google Scholar] [CrossRef]
- Shirgholami, M.A.; Khalil-Abad, M.S.; Khajavi, R.; Yazdanshenas, M.E. Fabrication of superhydrophobic polymethylsilsesquioxane nanostructures on cotton textiles by a solution–immersion process. J. Colloid Interface Sci. 2011, 359, 530–535. [Google Scholar] [CrossRef] [PubMed]
- Xu, B.; Ding, Y.; Qu, S.; Cai, Z. Superamphiphobic cotton fabrics with enhanced stability. Appl. Surf. Sci. 2015, 356, 951–957. [Google Scholar] [CrossRef]
- Lovingood, D.D.; Salter, W.B.; Griffith, K.R.; Simpson, K.M.; Hearn, J.D.; Owens, J.R. Fabrication of Liquid and Vapor Protective Cotton Fabrics. Langmuir 2013, 29, 15043–15050. [Google Scholar] [CrossRef] [PubMed]
- Chen, F.; Liu, X.; Yang, H.; Dong, B.; Zhou, Y.; Chen, D.; Hu, H.; Xiao, X.; Fan, D.; Zhang, C. A simple one-step approach to fabrication of highly hydrophobic silk fabrics. Appl. Surf. Sci. 2016, 360, 207–212. [Google Scholar] [CrossRef]
- Sasaki, K.; Tenjimbayashi, M.; Manabe, K.; Shiratori, S. Asymmetric Superhydrophobic/Superhydrophilic Cotton Fabrics Designed by Spraying Polymer and Nanoparticles. ACS Appl. Mater. Interfaces 2015, 8, 651–659. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.-W.; Guo, C.; Yuan, Z.-H. The stability of superhydrophobic cotton fabrics prepared by sol-gel coating of SiO2 and TiO2. Surf. Rev. Lett. 2013, 20. [Google Scholar] [CrossRef]
- Mohamed, A.L.; El-Sheikh, M.A.; Waly, A.I. Enhancement of flame retardancy and water repellency properties of cotton fabrics using silanol based nano composites. Carbohydr. Polym. 2014, 102, 727–737. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Geng, T.; Guo, Y.; Zhang, Z.; Zhang, P. Facile fabrication of stable superhydrophobic SiO2/polystyrene coating and separation of liquids with different surface tension. Chem. Eng. J. 2013, 231, 414–419. [Google Scholar] [CrossRef]
- Xue, C.-H.; Ji, P.-T.; Zhang, P.; Li, Y.-R.; Jia, S.-T. Fabrication of superhydrophobic and superoleophilic textiles for oil–water separation. Appl. Surf. Sci. 2013, 284, 464–471. [Google Scholar] [CrossRef]
- Xue, C.-H.; Guo, X.-J.; Ma, J.-Z.; Jia, S.-T. Fabrication of robust and antifouling superhydrophobic surfaces via surface-initiated atom transfer radical polymerization. ACS Appl. Mater. Interfaces 2015, 7, 8251–8259. [Google Scholar] [CrossRef] [PubMed]
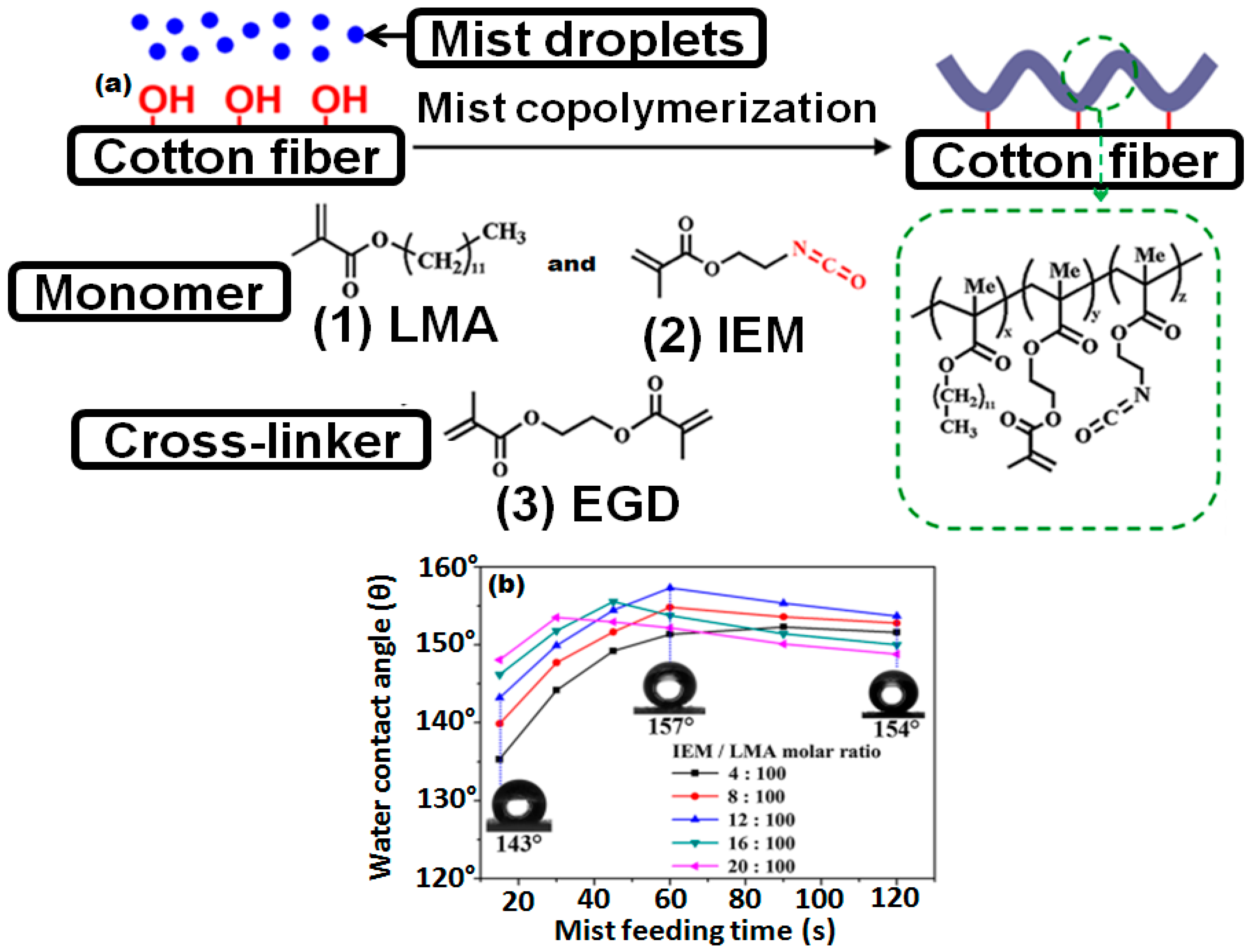
- Xi, G.; Wang, J.; Luo, G.; Zhu, Y.; Fan, W.; Huang, M.; Wang, H.; Liu, X. Healable superhydrophobicity of novel cotton fabrics modified via one-pot mist copolymerization. Cellulose 2016, 23, 915–927. [Google Scholar] [CrossRef]
- Wang, L.; Xi, G.; Wan, S.; Zhao, C.; Liu, X. Asymmetrically superhydrophobic cotton fabrics fabricated by mist polymerization of lauryl methacrylate. Cellulose 2014, 21, 2983–2994. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, H.; Gestos, A.; Fang, J.; Lin, T. Robust, superamphiphobic fabric with multiple self-healing ability against both physical and chemical damages. ACS Appl. Mater. Interfaces 2013, 5, 10221–10226. [Google Scholar] [CrossRef] [PubMed]
- Zimmermann, J.; Reifler, F.A.; Fortunato, G.; Gerhardt, L.C.; Seeger, S. A Simple, One-Step Approach to Durable and Robust Superhydrophobic Textiles. Adv. Funct. Mater. 2008, 18, 3662–3669. [Google Scholar] [CrossRef]
- Khalil-Abad, M.S.; Yazdanshenas, M.E. Superhydrophobic antibacterial cotton textiles. J. Colloid Interface Sci. 2010, 351, 293–298. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Zheng, H.; Wang, Y.; Wang, H.; Dong, Q.; Bai, R. A facile strategy for the fabrication of highly stable superhydrophobic cotton fabric using amphiphilic fluorinated triblock azide copolymers. Polymer 2010, 51, 1940–1946. [Google Scholar] [CrossRef]
- Artus, G.R.; Zimmermann, J.; Reifler, F.A.; Brewer, S.A.; Seeger, S. A superoleophobic textile repellent towards impacting drops of alkanes. Appl. Surf. Sci. 2012, 258, 3835–3840. [Google Scholar] [CrossRef]
- Li, Y.; Ge, B.; Men, X.; Zhang, Z.; Xue, Q. A facile and fast approach to mechanically stable and rapid self-healing waterproof fabrics. Compos. Sci. Technol. 2016, 125, 55–61. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, Z.; Xu, X.; Men, X.; Zhu, X. Fabrication of super-repellent cotton textiles with rapid reversible wettability switching of diverse liquids. Appl. Surf. Sci. 2013, 276, 571–577. [Google Scholar] [CrossRef]
- Yoo, Y.; You, J.B.; Choi, W.; Im, S.G. A stacked polymer film for robust superhydrophobic fabrics. Polym. Chem. 2013, 4, 1664–1671. [Google Scholar] [CrossRef]
- Liu, Y.; Chen, X.; Xin, J. Super-hydrophobic surfaces from a simple coating method: A bionic nanoengineering approach. Nanotechnology 2006, 17, 3259–3263. [Google Scholar] [CrossRef]
- Hansson, S.; Ostmark, E.; Carlmark, A.; Malmström, E. ARGET ATRP for versatile grafting of cellulose using various monomers. ACS Appl. Mater. Interfaces 2009, 1, 2651–2659. [Google Scholar] [CrossRef] [PubMed]
- Yuan, J.; Liu, X.; Akbulut, O.; Hu, J.; Suib, S.L.; Kong, J.; Stellacci, F. Superwetting nanowire membranes for selective absorption. Nat. Nanotechnol. 2008, 3, 332–336. [Google Scholar] [CrossRef] [PubMed]
- Adebajo, M.O.; Frost, R.L.; Kloprogge, J.T.; Carmody, O.; Kokot, S. Porous materials for oil spill cleanup: A review of synthesis and absorbing properties. J. Porous Mater. 2003, 10, 159–170. [Google Scholar] [CrossRef]
- Johnson, S.A.; Ollivier, P.J.; Mallouk, T.E. Ordered mesoporous polymers of tunable pore size from colloidal silica templates. Science 1999, 283, 963–965. [Google Scholar] [CrossRef] [PubMed]
- Tang, Z.; Kotov, N.A.; Magonov, S.; Ozturk, B. Nanostructured artificial nacre. Nat. Mater. 2003, 2, 413–418. [Google Scholar] [CrossRef] [PubMed]
- Park, S.H.; Xia, Y. Macroporous Membranes with Highly Ordered and Three-Dimensionally Interconnected Spherical Pores. Adv. Mater. 1998, 10, 1045–1048. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Z.; Wang, P. Smart surfaces with switchable superoleophilicity and superoleophobicity in aqueous media: Toward controllable oil/water separation. NPG Asia Mater. 2012, 4. [Google Scholar] [CrossRef]
- Feng, X.; Jiang, L. Design and creation of superwetting/antiwetting surfaces. Adv. Mater. 2006, 18, 3063–3078. [Google Scholar] [CrossRef]
- Chu, Z.; Feng, Y.; Seeger, S. Oil/water separation with selective superantiwetting/superwetting surface materials. Angew. Chem. Int. Ed. 2015, 54, 2328–2338. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Seeger, S. Polyester materials with superwetting silicone nanofilaments for oil/water separation and selective oil absorption. Adv. Funct. Mater. 2011, 21, 4699–4704. [Google Scholar] [CrossRef]
- Artus, G.R.; Jung, S.; Zimmermann, J.; Gautschi, H.P.; Marquardt, K.; Seeger, S. Silicone nanofilaments and their application as superhydrophobic coatings. Adv. Mater. 2006, 18, 2758–2762. [Google Scholar] [CrossRef]
- Zimmermann, J.; Artus, G.R.; Seeger, S. Long term studies on the chemical stability of a superhydrophobic silicone nanofilament coating. Appl. Surf. Sci. 2007, 253, 5972–5979. [Google Scholar] [CrossRef]
- Pan, Q.; Wang, M.; Wang, H. Separating small amount of water and hydrophobic solvents by novel superhydrophobic copper meshes. Appl. Surf. Sci. 2008, 254, 6002–6006. [Google Scholar] [CrossRef]
- Dunderdale, G.J.; England, M.W.; Sato, T.; Urata, C.; Hozumi, A. Programmable Oil/Water Separation Meshes: Water or Oil Selectivity Using Contact Angle Hysteresis. Macromol. Mater. Eng. 2016, 301, 1032–1036. [Google Scholar] [CrossRef]
- Song, W.; Xia, F.; Bai, Y.; Liu, F.; Sun, T.; Jiang, L. Controllable water permeation on a poly (N-isopropylacrylamide)-modified nanostructured copper mesh film. Langmuir 2007, 23, 327–331. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Huang, W.; Han, Y. A composite polymer film with both superhydrophobicity and superoleophilicity. Macromol. Rapid Commun. 2006, 27, 804–808. [Google Scholar] [CrossRef]
- Li, T.; Shen, J.; Zhang, Z.; Wang, S.; Wei, D. A poly (2-(dimethylamino) ethyl methacrylate-co-methacrylic acid) complex induced route to fabricate a super-hydrophilic hydrogel and its controllable oil/water separation. RSC Adv. 2016, 6, 40656–40663. [Google Scholar] [CrossRef]
- Li, J.; Yan, L.; Li, H.; Li, J.; Zha, F.; Lei, Z. A facile one-step spray-coating process for the fabrication of a superhydrophobic attapulgite coated mesh for use in oil/water separation. RSC Adv. 2015, 5, 53802–53808. [Google Scholar] [CrossRef]
- Wang, S.; Li, M.; Lu, Q. Filter paper with selective absorption and separation of liquids that differ in surface tension. ACS Appl. Mater. Interfaces 2010, 2, 677–683. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Wang, C.; Wang, S.; Li, J. Fabrication of superhydrophobic cotton textiles for water–oil separation based on drop-coating route. Carbohydr. Polym. 2013, 97, 59–64. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Ma, M.; Zang, D.; Gao, Z.; Wang, C. Fabrication of superhydrophobic/superoleophilic cotton for application in the field of water/oil separation. Carbohydr. Polym. 2014, 103, 480–487. [Google Scholar] [CrossRef] [PubMed]
- Zhou, X.; Zhang, Z.; Xu, X.; Guo, F.; Zhu, X.; Men, X.; Ge, B. Robust and durable superhydrophobic cotton fabrics for oil/water separation. ACS Appl. Mater. Interfaces 2013, 5, 7208–7214. [Google Scholar] [CrossRef] [PubMed]
- Bolaji, B.; Huan, Z. Ozone depletion and global warming: Case for the use of natural refrigerant—A review. Renew. Sustain. Energy Rev. 2013, 18, 49–54. [Google Scholar] [CrossRef]
- Hatch, K.L. American standards for UV-protective textiles. In Cancers of the Skin; Springer: New York, NY, USA, 2002; pp. 42–47. [Google Scholar]
- Reinert, G.; Fuso, F.; Hilfiker, R.; Schmidt, E. UV-protecting properties of textile fabrics and their improvement. Text. Chem. Color. 1997, 29, 36–43. [Google Scholar]
- Hoffmann, K.; Kaspar, K.; Gambichler, T.; Altmeyer, P. In vitro and in vivo determination of the UV protection factor for lightweight cotton and viscose summer fabrics: A preliminary study. J. Am. Acad. Dermatol. 2000, 43, 1009–1016. [Google Scholar] [CrossRef] [PubMed]
- Xin, J.; Daoud, W.; Kong, Y. A new approach to UV-blocking treatment for cotton fabrics. Text. Res. J. 2004, 74, 97–100. [Google Scholar] [CrossRef]
- Becheri, A.; Dürr, M.; Nostro, P.L.; Baglioni, P. Synthesis and characterization of zinc oxide nanoparticles: Application to textiles as UV-absorbers. J. Nanopart. Res. 2008, 10, 679–689. [Google Scholar] [CrossRef]
- Edwards, S.D.; Edwards, K.; Parker, T.L.; Evans, J.M. Ultraviolet Ray (UV) Blocking Textile Containing Particles. U.S. Patent 6037280A, 14 March 2000. [Google Scholar]
- Wang, R.; Xin, J.; Tao, X. UV-blocking property of dumbbell-shaped ZnO crystallites on cotton fabrics. Inorg. Chem. 2005, 44, 3926–3930. [Google Scholar] [CrossRef] [PubMed]
- Hoffmann, K.; Laperre, J.; Avermaete, A.; Altmeyer, P.; Gambichler, T. Defined UV protection by apparel textiles. Arch. Dermatol. 2001, 137, 1089–1094. [Google Scholar] [PubMed]
- Han, K.; Yu, M. Study of the preparation and properties of UV-blocking fabrics of a PET/TiO2 nanocomposite prepared by in situ polycondensation. J. Appl. Polym. Sci. 2006, 100, 1588–1593. [Google Scholar] [CrossRef]
- Aguilera, J.; Gálvez, M.V.; Sánchez-Roldán, C.; Herrera-Ceballos, E. New advances in protection against solar ultraviolet radiation in textiles for summer clothing. Photochem. Photobiol. 2014, 90, 1199–1206. [Google Scholar] [CrossRef] [PubMed]
- Xue, C.-H.; Yin, W.; Zhang, P.; Zhang, J.; Ji, P.-T.; Jia, S.-T. UV-durable superhydrophobic textiles with UV-shielding properties by introduction of ZnO/SiO2 core/shell nanorods on PET fibers and hydrophobization. Colloids Surf. Physicochem. Eng. Asp. 2013, 427, 7–12. [Google Scholar] [CrossRef]
- Duan, W.; Xie, A.; Shen, Y.; Wang, X.; Wang, F.; Zhang, Y.; Li, J. Fabrication of superhydrophobic cotton fabrics with UV protection based on CeO2 particles. Ind. Eng. Chem. Res. 2011, 50, 4441–4445. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, Z.; Wang, X.; Lin, T. Superhydrophobic and UV-blocking cotton fabrics prepared by layer-by-layer assembly of organic UV absorber intercalated layered double hydroxides. Appl. Surf. Sci. 2013, 286, 364–370. [Google Scholar] [CrossRef]
- Morgan, A.B.; Gilman, J.W. An overview of flame retardancy of polymeric materials: Application, technology, and future directions. Fire Mater. 2013, 37, 259–279. [Google Scholar] [CrossRef]
- Chen, S.; Li, X.; Li, Y.; Sun, J. Intumescent flame-retardant and self-healing superhydrophobic coatings on cotton fabric. ACS Nano 2015, 9, 4070–4076. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Zang, D.; Shi, J.; Gao, Z.; Wang, C.; Li, J. Superhydrophobic cotton textile with robust composite film and flame retardancy. RSC Adv. 2015, 5, 67780–67786. [Google Scholar] [CrossRef]
- Xue, C.-H.; Zhang, L.; Wei, P.; Jia, S.-T. Fabrication of superhydrophobic cotton textiles with flame retardancy. Cellulose 2016, 23, 1471–1480. [Google Scholar] [CrossRef]
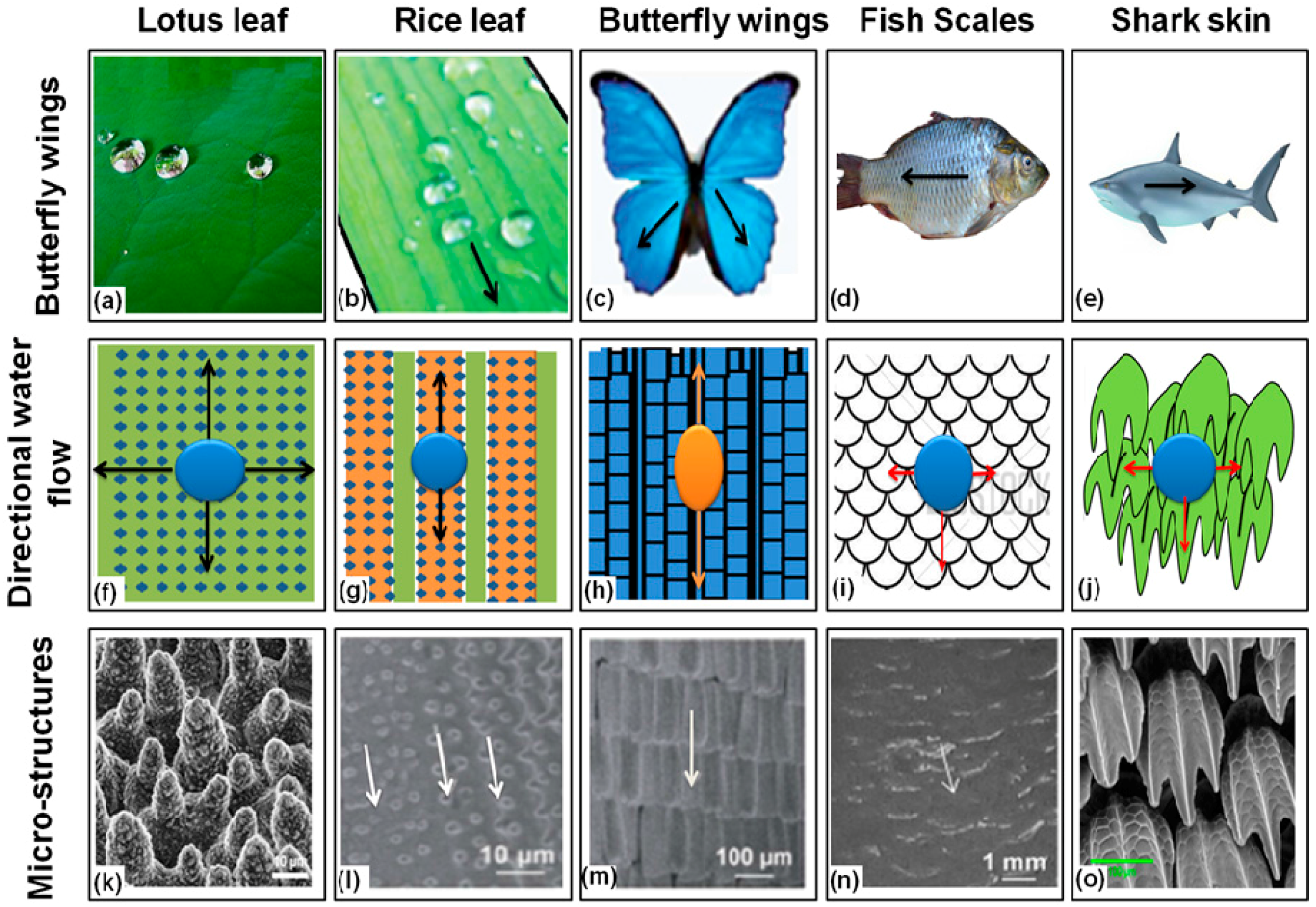


| Natural Surface | Surface Structure | Contact Angle (θ) | Properties |
|---|---|---|---|
| Lotus leaf | Hierarchical, wax tubules | 160° |
|
| Rice leaf | Sinusoidal grooves covered with micropapilla and nanobumps | 164° |
|
| Butterfly wing | Shingle-like scales with aligned microgrooves | 161° |
|
| Fish scale | Overlapping hinged scales | 58° |
|
| Shark skin | Overlapping dermal denticles with triangular riblets | n/a |
|
| Material Properties | Processing Conditions | System Design | Ambient Conditions |
|---|---|---|---|
| Surface tension | Electric field strength | Design of the needle | Temperature |
| Viscosity | Type of electrical signal | Geometry of the collector | Humidity |
| Conductivity | Solution charge polarity | Air velocity | |
| Polymer type | Tip to collector distance | Medium of the system | |
| Polymer MW | Flow rate |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, I.; Kan, C.-w. A Review on Development and Applications of Bio-Inspired Superhydrophobic Textiles. Materials 2016, 9, 892. https://doi.org/10.3390/ma9110892
Ahmad I, Kan C-w. A Review on Development and Applications of Bio-Inspired Superhydrophobic Textiles. Materials. 2016; 9(11):892. https://doi.org/10.3390/ma9110892
Chicago/Turabian StyleAhmad, Ishaq, and Chi-wai Kan. 2016. "A Review on Development and Applications of Bio-Inspired Superhydrophobic Textiles" Materials 9, no. 11: 892. https://doi.org/10.3390/ma9110892
APA StyleAhmad, I., & Kan, C.-w. (2016). A Review on Development and Applications of Bio-Inspired Superhydrophobic Textiles. Materials, 9(11), 892. https://doi.org/10.3390/ma9110892






