An 8-Channel Wavelength MMI Demultiplexer in Slot Waveguide Structures
Abstract
:1. Introduction
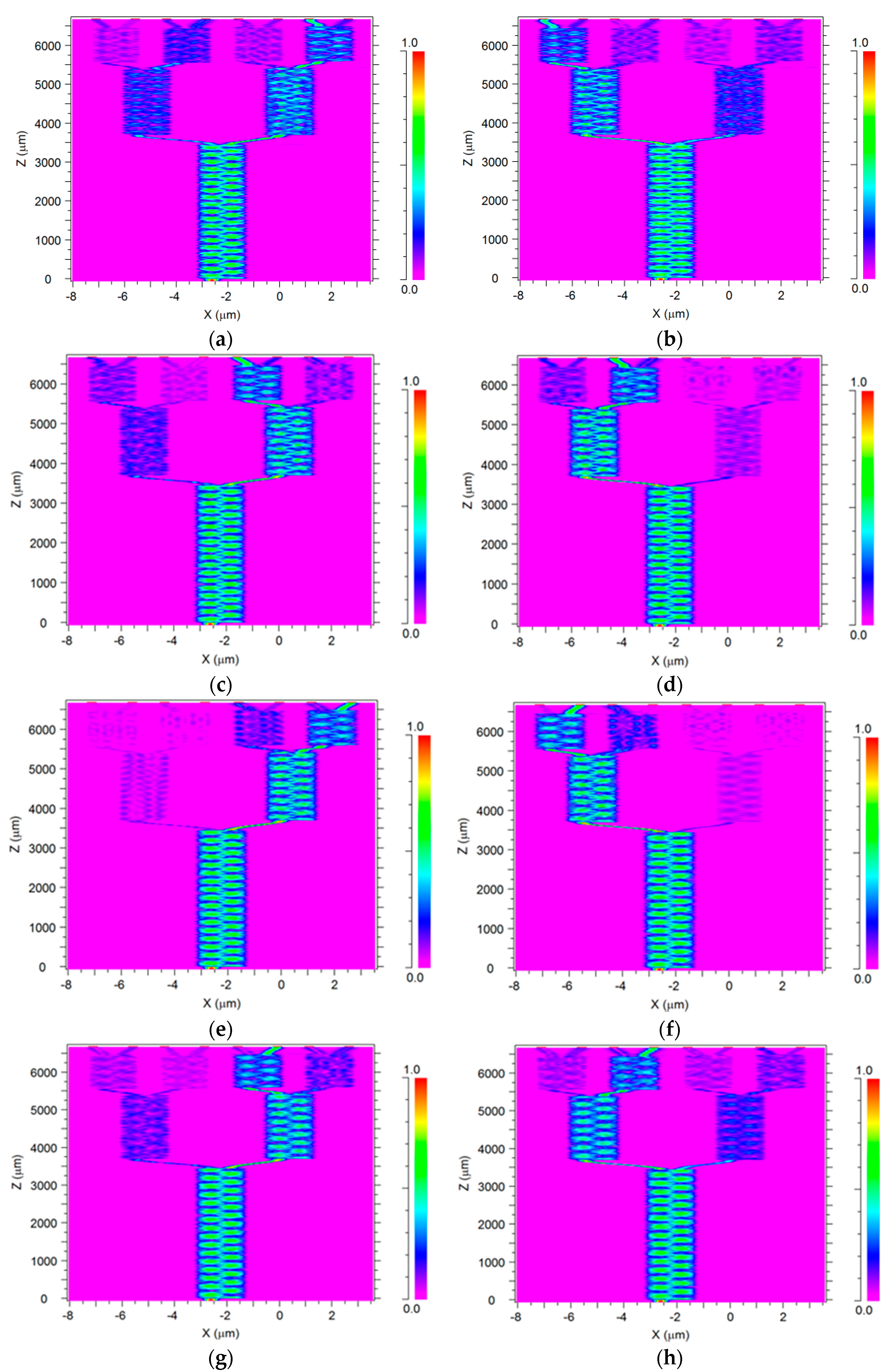
2. The 1 × 8 MMI Demultiplexer Structure and Theoretical Aspect
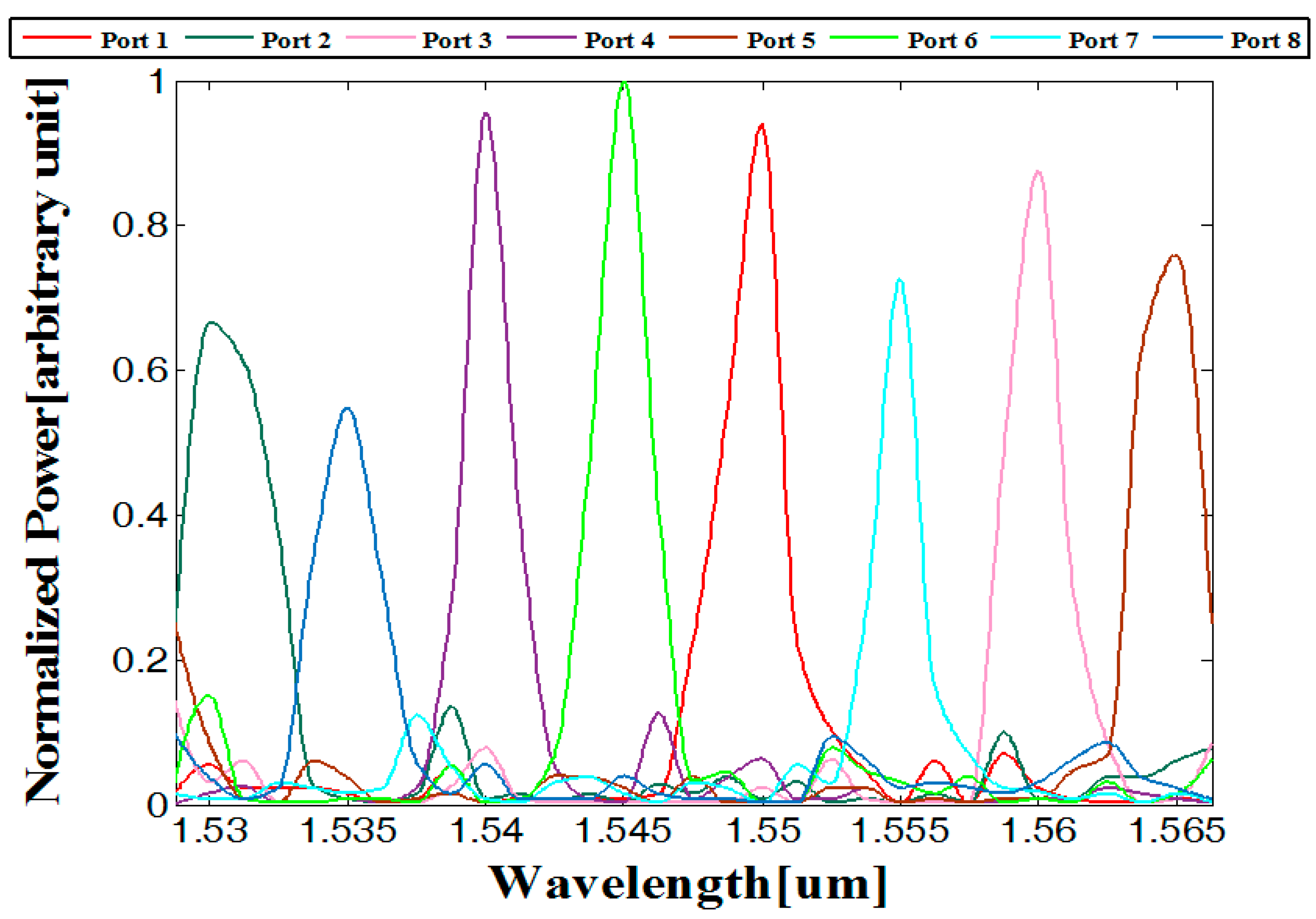
3. Results
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Bogdan, H. DWDM Fundamentals, Components, and Applications. J. Opt. Netw. 2002, 1, 184–185. [Google Scholar]
- Gong, J.M.; Zuo, X.; Zhao, Y. The steady SRS analysis theory of DWDM transmission system in single-mode silica fiber. Opt. Commun. 2015, 350, 257–262. [Google Scholar] [CrossRef]
- Ari, T.; Petteri, P.; Seppo, H.; Markku, T. A guided-wave Mach-Zehnder interferometer structure for wavelength multiplexing. IEEE Photon. Technol. Lett. 1991, 3, 516–518. [Google Scholar]
- Lin, K.C.; Lee, W.Y. Guided-wave 1.30/1.55 µm wavelength division multiplexer based on multimode interference. Electron. Lett. 1996, 32, 1259–1261. [Google Scholar] [CrossRef]
- Li, B.; Li, G.; Liu, E.; Jiang, Z.; Qin, J.; Wang, X. Low-loss 1 × 2 multimode interference wavelength demultiplexer in silicon-germanium alloy. IEEE Photon. Technol. Lett. 1999, 11, 575–577. [Google Scholar]
- Tsao, S.L.; Guon, H.C.; Tsai, C.W. A novel 1 × 2 single-mode 1300/1550 nm wavelength division multiplexer with output facet-tilted MMI waveguide. Opt. Commun. 2004, 232, 371–379. [Google Scholar] [CrossRef]
- Goto, N.; Yip, G.L. Y-branch wavelength multi-demultiplexer for λ = 1.30 µm and 1.55 µm. Electron. Lett. 2007, 26, 102–103. [Google Scholar] [CrossRef]
- Almeida, V.R.; Xu, Q.; Barrios, C.A.; Lipson, M. Guiding and confining light in void nanostructure. Opt. Lett. 2004, 29, 1209–1211. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Liow, T.Y.; Lo, G.Q.; Kwong, D.L. Silicon-based horizontal nanoplasmonic slot waveguide for on-chip integration. Opt. Express 2011, 19, 8888–8902. [Google Scholar] [CrossRef] [PubMed]
- Soref, R. The past, present, and future of silicon photonics. IEEE J. Sel. Top. Quantum Electron. 2006, 12, 1678–1687. [Google Scholar] [CrossRef]
- Jalai, B.; Fathpour, S. Silicon photonics. J. Lightwave Technol. 2006, 24, 4600–4615. [Google Scholar] [CrossRef]
- Olof, B. Image formation using self-imaging techniques. J. Opt. Soc. Am. 1973, 63, 416–418. [Google Scholar]
- Fujisawa, T.; Koshiba, M. Theoretical Investigion of ultrasmall polarization-insensitive multimode interference waveguide based on sandwiched structures. IEEE Photon. Technol. Lett. 2006, 18, 1246–1248. [Google Scholar] [CrossRef]
- Xiao, J.; Liu, X.; Sun, X. Design of an ultracompact MMI wavelength demultiplexer in slot waveguide structures. Opt. Express 2007, 15, 8300–8308. [Google Scholar] [CrossRef] [PubMed]
- Malka, D.; Sintov, Y.; Zalevsky, Z. Design of a 1 × 4 silicon-alumina wavelength demultiplexer based on multimode interference in slot waveguide structures. J. Opt. 2015, 17, 1–9. [Google Scholar] [CrossRef]
- Dike, J.N.; Ogbe, D.A. Optimizing the Efficiency of Fiber-Optics Technology in Telecommunications System. In Proceedings of the IEEE International Conference on Emerging & Sustainable Technologies for Power & ICT in Developing Society (NIGERCON), Owerri, Nigeria, 14–16 November 2013; pp. 135–142.
- Retno, W.P.; Irma, S.; Nji Raden, P.; Elhadj, D. Design of GaN-Based Low-Loss Y-Branch Power Splitter. Makara J. Technol. 2014, 18, 101–104. [Google Scholar]
- Komatsu, M.A.; Saitoh, K.; Koshiba, M. Design of highly-nonlinear horizontal slot waveguide with low and flat dispersion. Opt. Commun. J. Sci. Direct 2013, 298–299, 180–184. [Google Scholar] [CrossRef]
- Carnevale, S.D.; Kent, T.F.; Phillips, P.J.; Mills, M.J.; Rajan, S.; Myers, R.C. Polarization-induced pn diodes in wide-band-gap nanowires with ultraviolet electroluminescence. Nano Lett. 2012, 12, 915–920. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Li, X.; Fen, X.; Cui, K.; Liu, F.; Huang, Y. Designing gallium nitride slot waveguide operating within visible band. Opt. Quant Electron. 2015, 47, 3705–3713. [Google Scholar] [CrossRef]
- Malka, D.; Danan, Y.; Ramon, Y.; Zalevsky, Z. A Photonic 1 × 4 Power Splitter Based on Multimode Interference in Silicon-Gallium-Nitride Slot Waveguide Structures. Materials 2016, 9, 516. [Google Scholar] [CrossRef]
- Chu, R.; Cao, Y.; Chen, M.; Li, R.; Zehnder, D. An Experimental Demonstration of GaN CMOS Technology. IEEE Electron Device Lett. 2016, 37, 269–271. [Google Scholar] [CrossRef]
- Rostami, A.; Bahrami, A.; Nazari, F.; Alupour Banaei, H. Eight-channel wavelength division demultiplexer using multimode interference. In Proceedings of the Communications and Photonics Conference and Exhibition (ACP), Shanghai, China, 2–6 November 2009; p. 7630.
- Almedia, V.R.; Barrios, C.A.; Panepucci, R.R.; Lipson, M. All-optical control of light on a silicon chip. Nature 2004, 431, 1081–1084. [Google Scholar] [CrossRef] [PubMed]
- Soldano, L.B.; Pennings, E.C.M. Optical multimode interference devices based on self-imaging: Principles and applications. J. Lightwave Technol. 1995, 13, 615–627. [Google Scholar] [CrossRef]
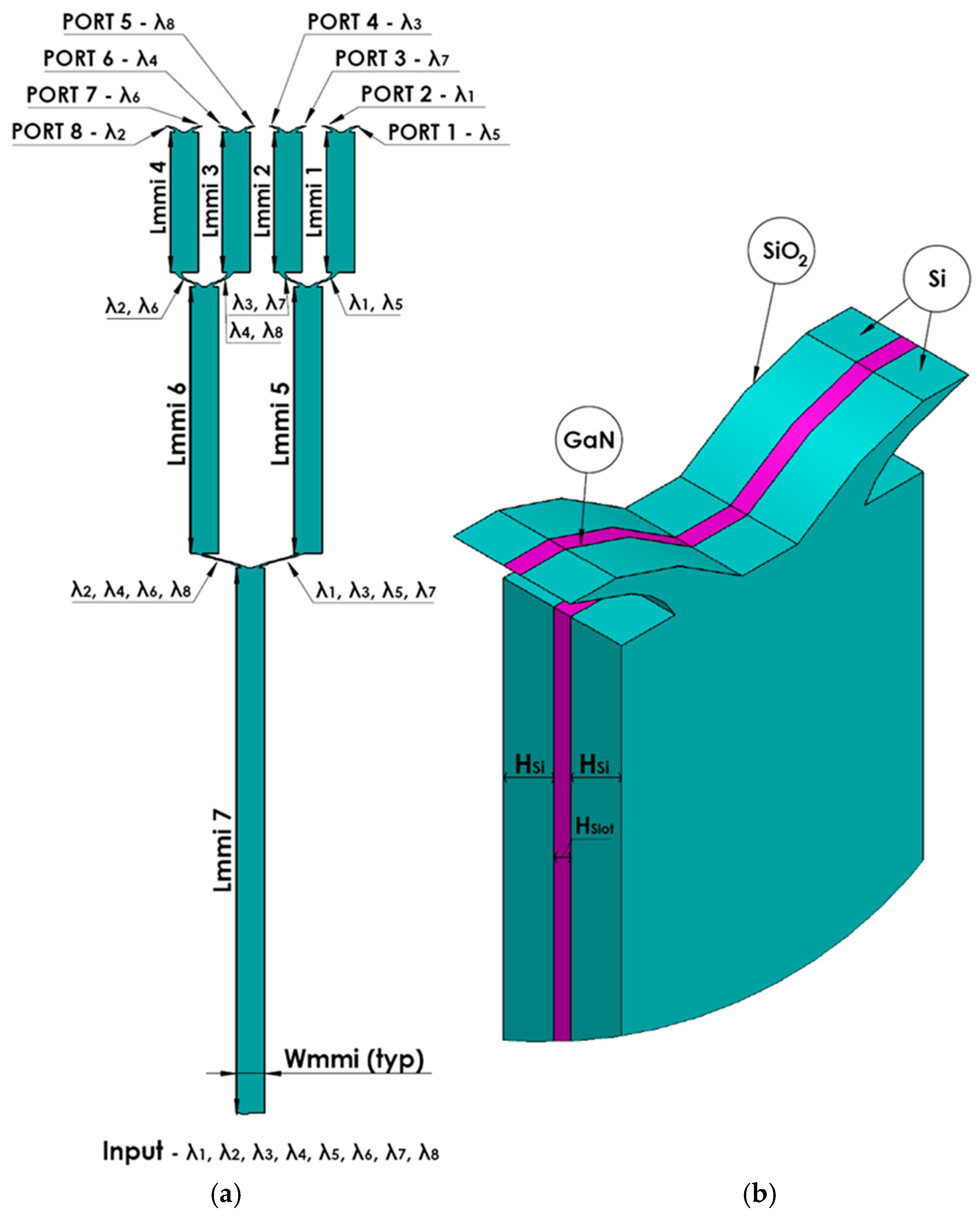
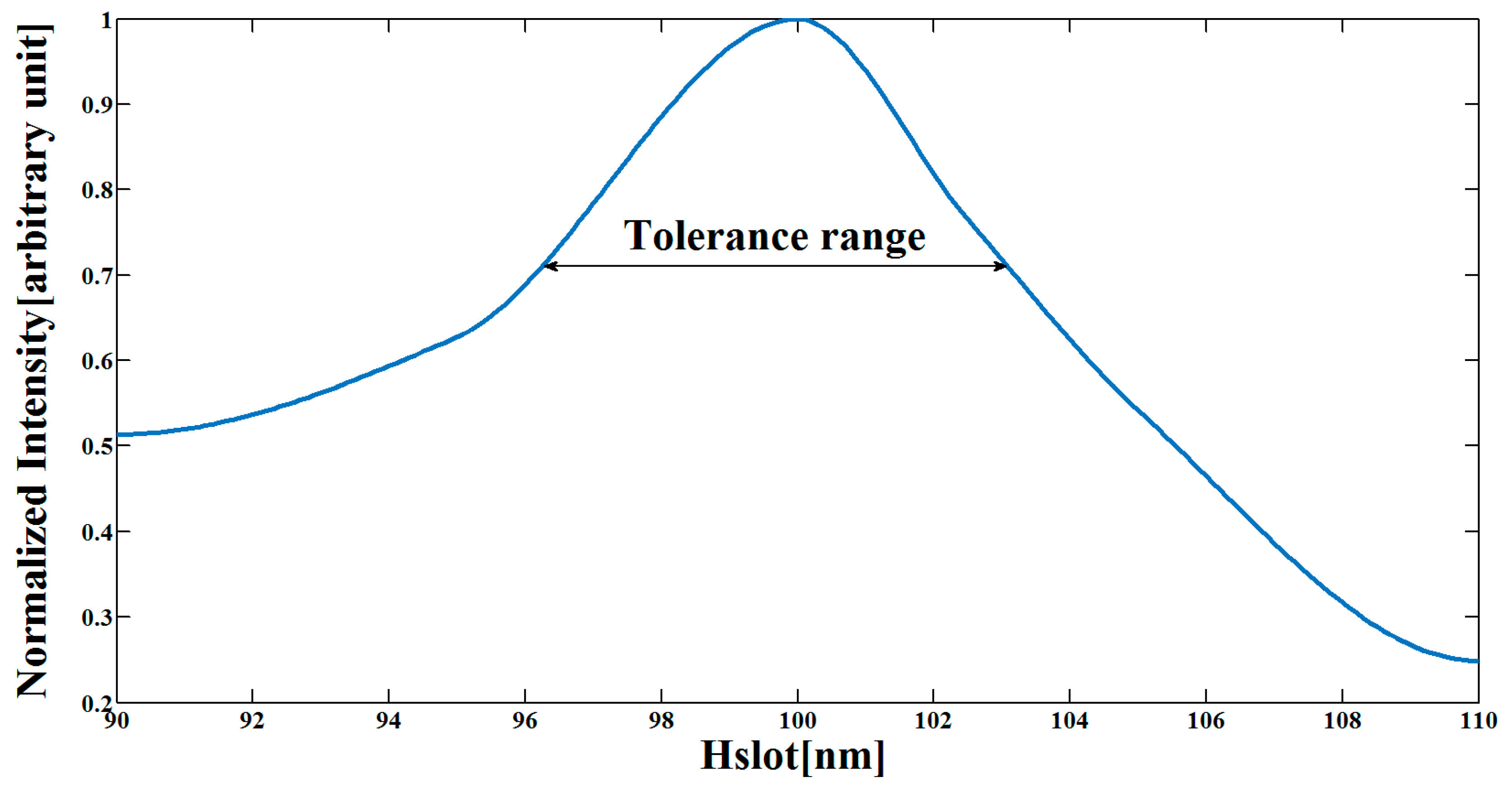
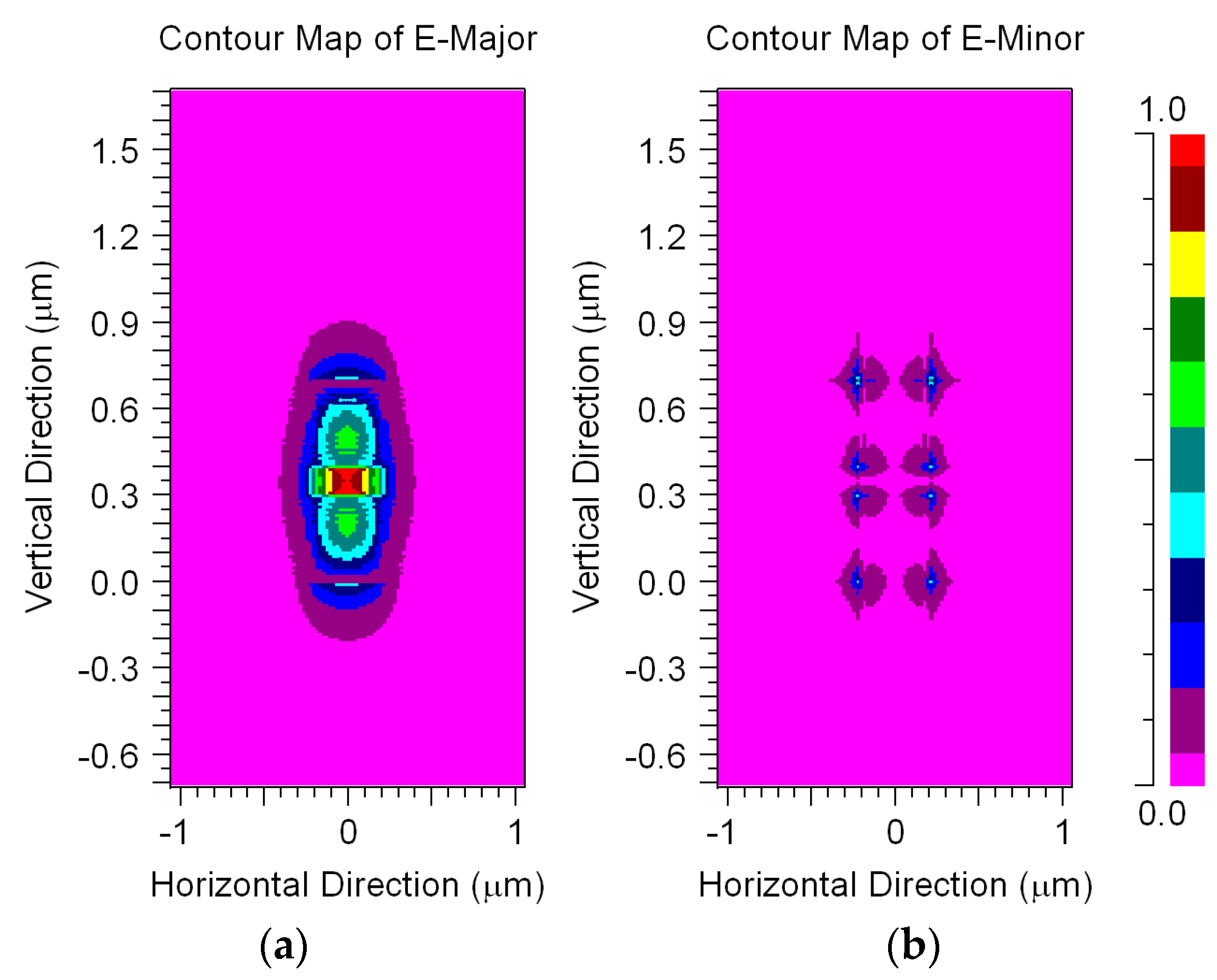
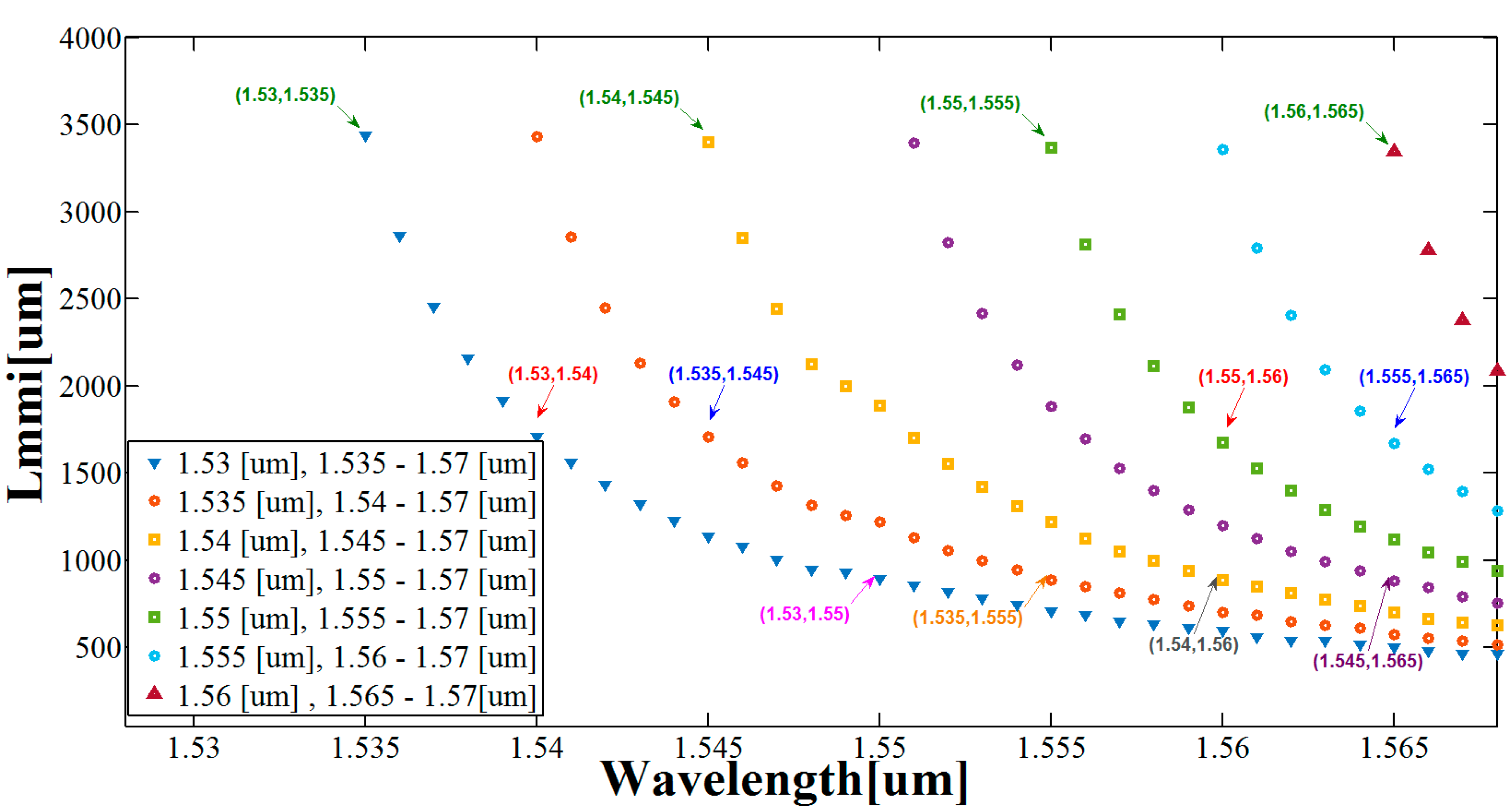
| λm (nm) | 1530 | 1535 | 1540 | 1545 | 1550 | 1555 | 1560 | 1565 |
|---|---|---|---|---|---|---|---|---|
| nSi | 3.4794 | 3.4790 | 3.4786 | 3.4781 | 3.4777 | 3.4773 | 3.4769 | 3.4765 |
| nSiO2 | 1.4443 | 1.4442 | 1.4441 | 1.4441 | 1.444 | 1.444 | 1.4439 | 1.4438 |
| nGaN | 2.3173 | 2.3172 | 2.3171 | 2.3170 | 2.3169 | 2.3168 | 2.3167 | 2.3165 |
| λm (nm) | 1530 | 1535 | 1540 | 1545 | 1550 | 1555 | 1560 | 1565 |
| Lπ (µm) | 9.295 | 9.27 | 9.245 | 9.22 | 9.2 | 9.175 | 9.15 | 9.125 |
| λm (nm) | 1530 | 1535 | 1540 | 1545 | 1550 | 1555 | 1560 | 1565 |
|---|---|---|---|---|---|---|---|---|
| Port number | 2 | 8 | 4 | 6 | 1 | 7 | 3 | 5 |
| Crosstalk (dB) | −19.97 | −19.53 | −18.89 | −18.04 | −18.86 | −19.41 | −18.7 | −13.77 |
| FWHM (nm) | 2.35 | 3.6 | 2.35 | 1.95 | 2.8 | 2.2 | 1.8 | 2.9 |
| Losses (dB) | 1.78 | 2.12 | 1.2 | 0.9 | 1.32 | 1.71 | 1.45 | 1.67 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ben Zaken, B.B.; Zanzury, T.; Malka, D. An 8-Channel Wavelength MMI Demultiplexer in Slot Waveguide Structures. Materials 2016, 9, 881. https://doi.org/10.3390/ma9110881
Ben Zaken BB, Zanzury T, Malka D. An 8-Channel Wavelength MMI Demultiplexer in Slot Waveguide Structures. Materials. 2016; 9(11):881. https://doi.org/10.3390/ma9110881
Chicago/Turabian StyleBen Zaken, Bar Baruch, Tal Zanzury, and Dror Malka. 2016. "An 8-Channel Wavelength MMI Demultiplexer in Slot Waveguide Structures" Materials 9, no. 11: 881. https://doi.org/10.3390/ma9110881
APA StyleBen Zaken, B. B., Zanzury, T., & Malka, D. (2016). An 8-Channel Wavelength MMI Demultiplexer in Slot Waveguide Structures. Materials, 9(11), 881. https://doi.org/10.3390/ma9110881





