A New Predictive Model of Centerline Segregation in Continuous Cast Steel Slabs by Using Multivariate Adaptive Regression Splines Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Dataset
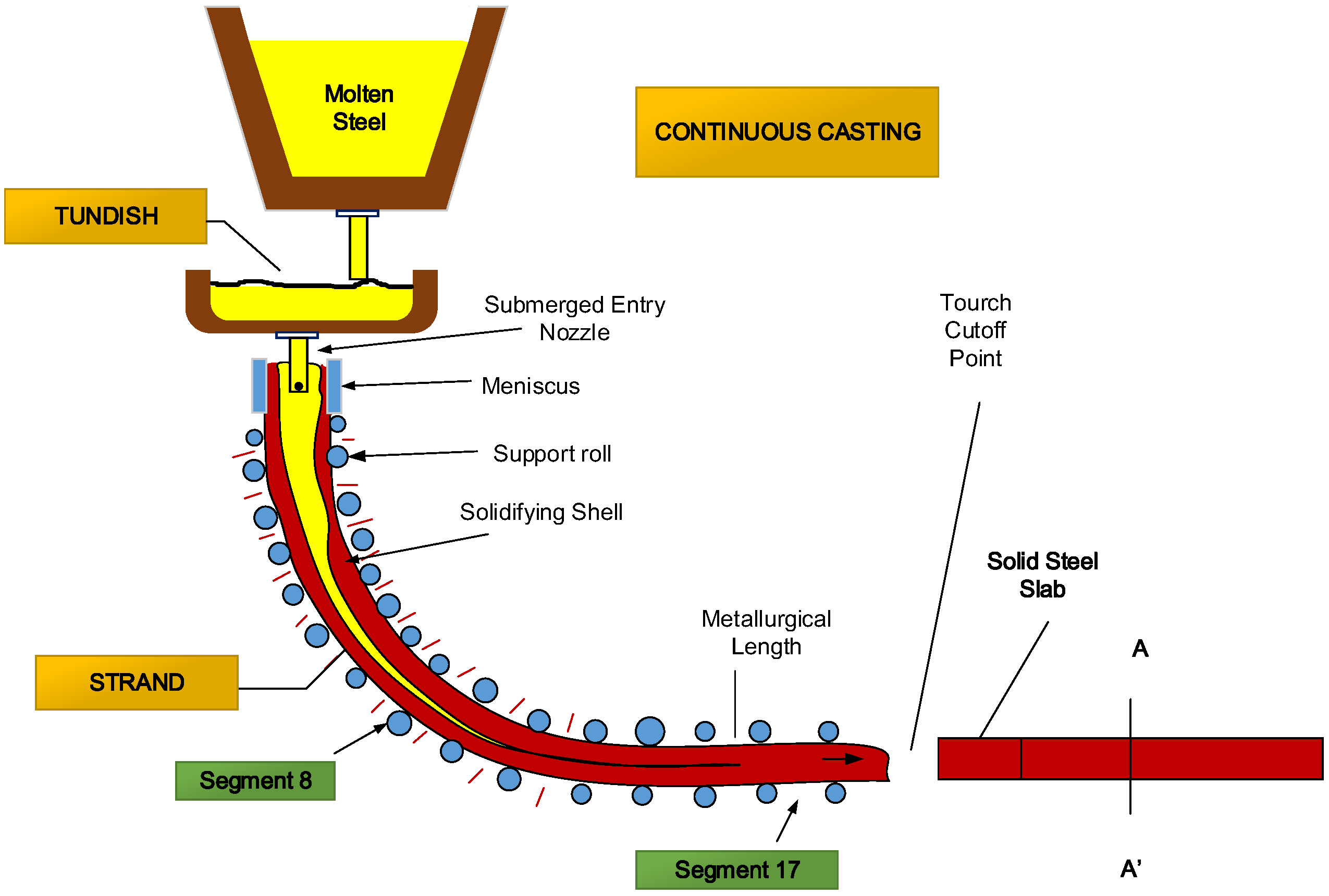
- (1)
- Variables related to the analysis of steel in the tundish, that is to say, the composition of the steel (solute). Three samples of the tundish per casting are sent to the laboratory for their analysis. Among these three samples, one of them is chosen as significant of the casting. The elements analyzed are:
- (a)
- Total manganese (Mn): The presence of sulfide is controlled by the addition of manganese. Manganese has a higher affinity for sulfur than iron so that instead of MnS, FeS is formed. FeS has a high melting point and good plastic properties. Manganese content should be about five times the sulfur concentration so that the reaction occurs. The end result, once removed causing gases, is a less porous casting, and therefore of higher quality.
- (b)
- Total sulfur (S): Its maximum limit is of about 0.04%. The sulfur along with iron gives place to iron sulfide, which with the austenite, results in a eutectic point with a low melting point and, therefore, it appears in the grain boundaries. When cast steel ingots are rolled in hot, this eutectic point is in liquid state, causing the shelling of the material. Although considered a detrimental element, their presence is positive for improved machinability in the machining processes. When the percentage of sulfur is high, it may cause pores in the welding process.
- (c)
- Total carbon (C): The term steel is commonly used to refer in metallurgical engineering to an iron alloy with a variable amount of carbon between 0.03% and 1.075% by weight of the alloy, depending on its applications and uses.
- (d)
- Total aluminum (Al): this alloying element is used in some high strength nitriding steels (with Cr-Al-Mo) at concentrations close to 1% and with percentages less than 0.008% as a deoxidizer in high alloy steels.
- (e)
- Total silicon (Si): this alloying element moderately increases the hardenability. Furthermore, it is used as a deoxidizing element. Additionally, it increases the resistance of low carbon steels.
- (f)
- Total phosphorus (P): this element is detrimental, either due to its dissolution in ferrite, which decreases the ductility, or due to formation of FeP. Its maximum limit is approximately 0.04%. Iron phosphide, along with the cementite and austenite, forms a ternary eutectic point called steadite, which is extremely fragile and has a relatively low melting point. Therefore, it appears in grain boundaries so that transmits brittleness to the material. Although it is considered a detrimental element in steels because it reduces their ductility and toughness, giving place to their brittle behavior, it is sometimes added to increase the tensile strength and improve machinability.
- (2)
- Variables related to the cooling conditions of the slab:
- (a)
- Specific flow (Specific_Flow (m3·s−1)): The continuous casting machine is cooled. On the one hand, there is a primary cooling at the mold by using a water jacket (water casing) bolted to the plates. On the other hand, there is a secondary cooling in the rollers area through water showers. The value of the water flow injected to the rollers depends on casting parameters: type of steel, casting speed, temperature, etc. The specific flow is an index that determines the secondary cooling as a function of these parameters.
- (b)
- Average casting speed (m·s−1) (Ave_Speed): This variable is the average output speed of the slab from the casting machine. It influences on the solidification and cooling that it is necessary to apply.
- (c)
- Superheating in the tundish (Overtemperature) (°C): Steel begins to solidify when the temperature reaches a value called liquidus temperature and is different depending on its composition. For each of the samples taken in the tundish, three samples per casting, their actual temperature is measured and the liquidus temperature associated with each sample is calculated. The difference between the actual temperature and the liquidus temperature is known as overtemperature. This parameter is an important variable in the casting of steel since it measures how hot the steel is, if it is possible to cast it, and how fast. Thus, the colder is the slab, the faster it is casted, but if the steel is very cold, it is impossible to proceed with the casting process. Therefore, this parameter is of fundamental importance on the solidification and consequently on segregation.
- (d)
- Temperatures in Segment 8 and Segment 17 (°C) (Temp_Seg8 and Temp_Seg17): The rollers path of the casting machine is divided into groups of rollers called segments, which are numbered starting at the mold exit. In Segment 8 and Segment 17, there are pyrometers that measure the surface temperature of the slab as it exits the machine. Segment 8 is located on the curved zone of the machine and Segment 17 once the slab has been straightened. Their measurements may be regarded as indirect indicators of how the cooling process is performed.
- (e)
- Mold oscillation frequency (Freq_Oscillation): The mold is part of the continuous casting machine to give shape to the slab and where solidification begins. The mold rests on two eccentrics that impart an oscillatory motion to prevent the skin of the slab formed in the walls of the mold remains stuck to them. The frequency of this oscillation motion is fixed depending on the kind of steel casted. Its value must move the mold with a speed greater than the exit speed of slab.
- (f)
- Percentage of negative strip (Ratio_Strip): During the oscillatory motion of the mold, there is a time that the mold is moved downward faster than the line speed, which leads to an entrance effect of the slab into the mold. This represents a positive effect, decreasing the likelihood of formation of transverse cracks on the slab surface. The overall time of this effect is called percentage of negative strip.
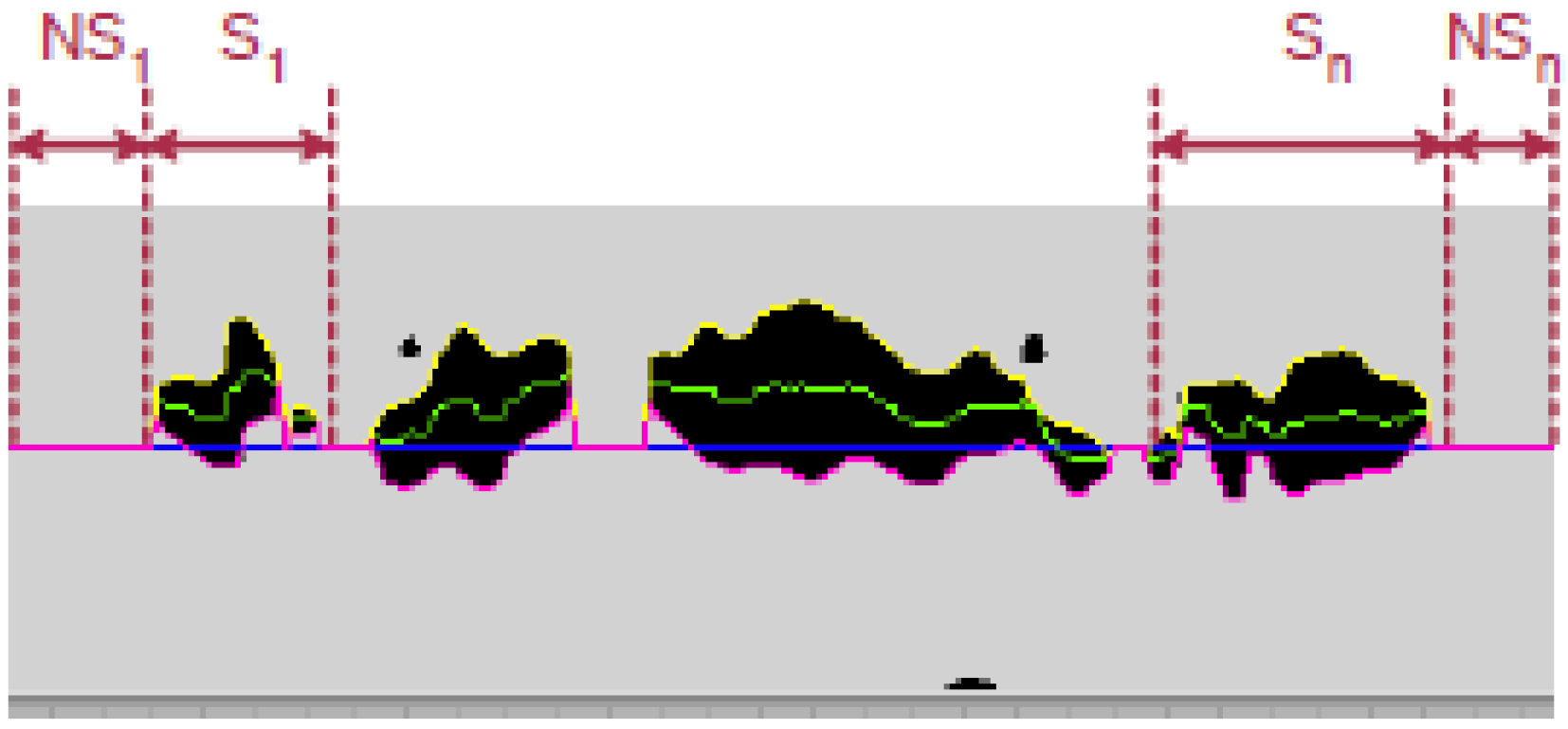
2.2. Segregation Evaluation

2.3. Segregation Models
2.4. Method Multivariate Adaptive Regression Splines (MARS) Approach
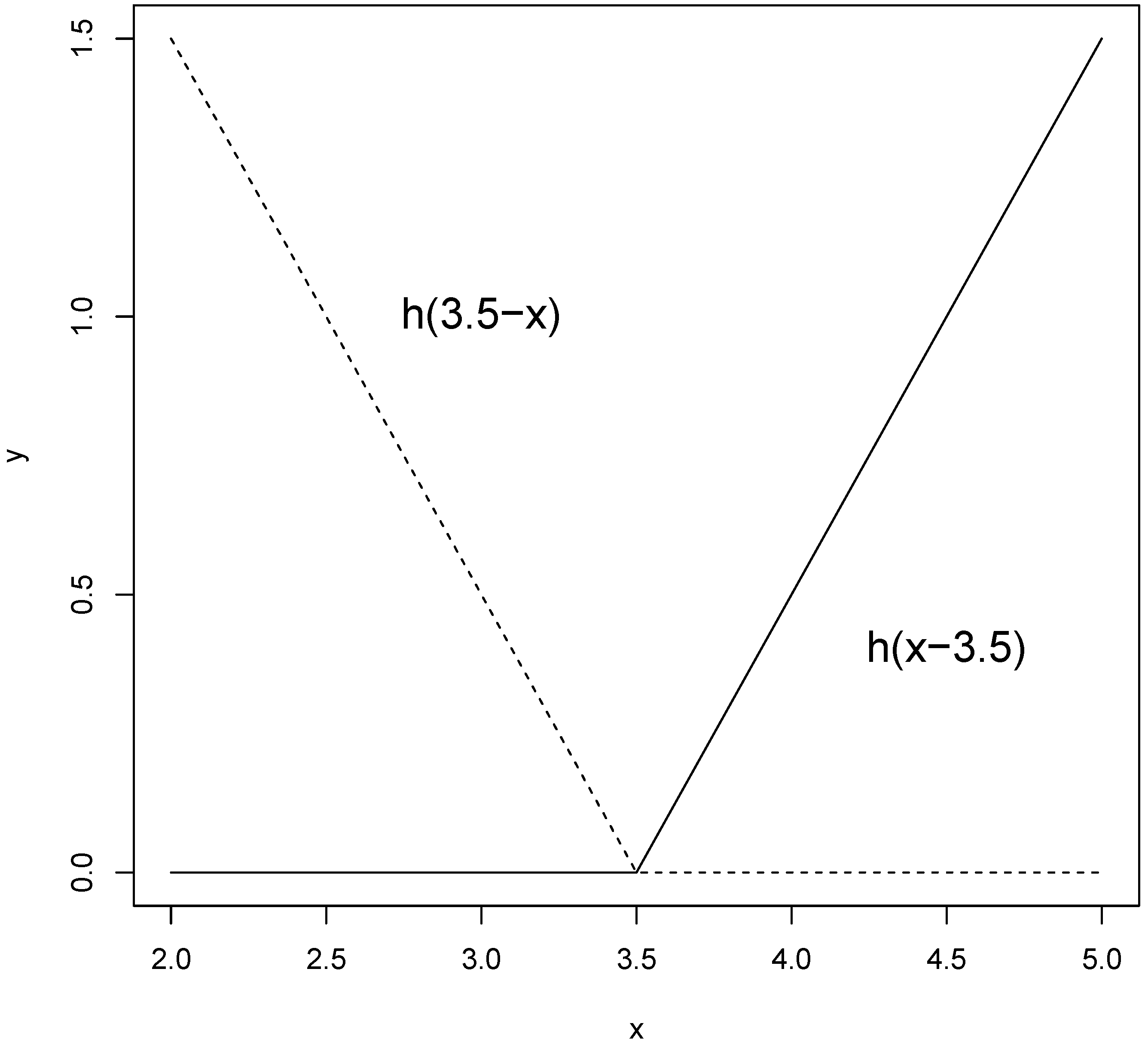
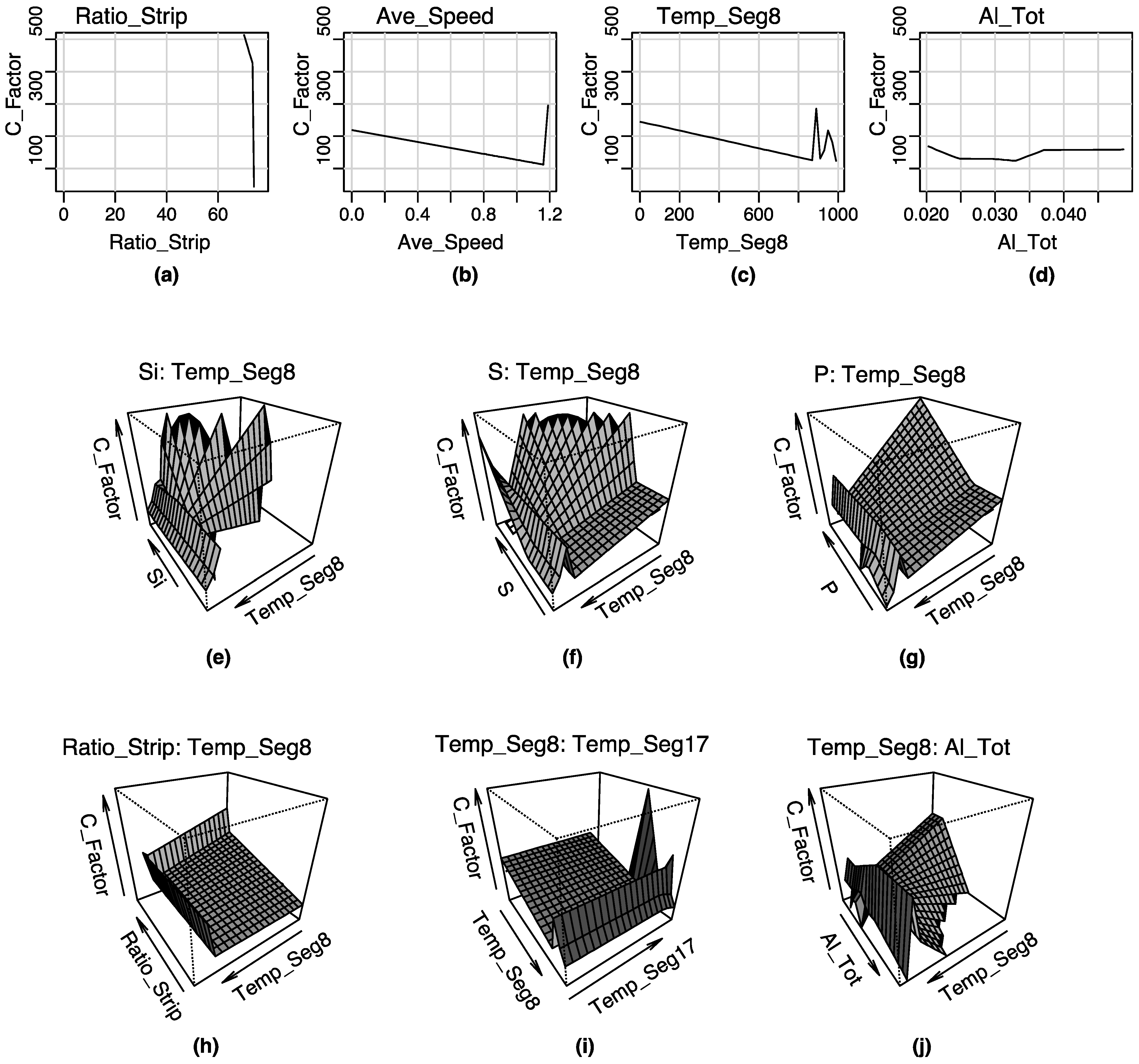
2.5. The Importance of Variables in the MARS Model
3. Analysis of Results and Discussion
3.1. Results of The Model
| Input variables | Name of the variable | Mean | Standard deviation |
|---|---|---|---|
| Total aluminum (measured as weight%) | Al | 0.030 | 0.006 |
| Total manganese (measured as weight%) | Mn | 1.357 | 0.050 |
| Total sulfur (measured as weight%) | S | 0.009 | 0.002 |
| Total carbon (measured as weight%) | C | 0.173 | 0.014 |
| Total phosphorus (measured as weight%) | P | 0.016 | 0.004 |
| Superheating (°C) | Overtemperature | 24.545 | 8.940 |
| Percentage of negative strip | Ratio_Strip | 68.517 | 21.519 |
| Specific flow (m3·s−1) | Specific_Flow | 0.633 | 0.074 |
| Average casting speed (m·s−1) | Ave_Speed | 0.957 | 0.143 |
| Mold oscillation frequency | Freq_Oscillation | 2.043 | 0.688 |
| Temperature in segment 8 (°C) | Temp_Seg8 | 816.472 | 265.506 |
| Temperature in segment 17 (°C) | Temp_Seg17 | 771.911 | 246.454 |
| Silicon (measured as weight%) | Si | 0.201 | 0.048 |
| Definition | ||
|---|---|---|
| 1 | 80.112 | |
| h (Ratio_Strip − 75.117) | −286.265 | |
| h (Ratio_Strip − 75.378) | 471.796 | |
| h (Ave_Speed – 1.16) | 6177.268 | |
| h (1.16 − Ave_Speed) | 91.964 | |
| h (Temp_Seg8 − 870) | 8.631 | |
| h (Temp_Seg8 − 889) | −20.522 | |
| h (889 – Temp_Seg8) | 0.563 | |
| h (Temp_Seg8 − 906) | 11.476 | |
| h (Al – 0.0247) | 8358.107 | |
| h (Al – 0.0371) | −7741.410 | |
| h (Si – 0.2276) × h (889 – Temp_Seg8) | 22.903 | |
| h (0.2276 – Si) × h (889 – Temp_Seg8) | −10.688 | |
| h (0.2483 − Si) × h (Temp_Seg8 − 870) | 6.243 | |
| h (S – 0.0091) × h (Temp_Seg8 − 889) | 433.489 | |
| h (0.0194 − P) × h (Temp_Seg8 – 906) | 240.291 | |
| h (Freq_Oscillation – 2.43) × h (Ratio_Strip – 75.378) | 697.928 | |
| h (75.378 – Ratio_Strip) × h (Temp_Seg8 − 953) | −30.322 | |
| h (75.378 – Ratio_Strip) × h (Temp_Seg8 – 938) | 12.800 | |
| h (889 – Temp_Seg8) × h (Temp_Seg17 – 883) | 0.433 | |
| h (881 – Temp_Seg8) × h (Al – 0.0247) | −35.436 | |
| h (Temp_Seg8 − 889) × h (0.0329 – Al) | 537.071 | |
| h (Temp_Seg8 − 906) × h (Al – 0.0304) | −219.353 | |
| h (Temp_Seg8 – 906) × h (0.0304 – Al) | −961.240 | |
| h (C − 0.1863) × h (0.0091 − S) × h (Temp_Seg8 – 889) | −97083.453 | |
| h (C – 0.19) × h (75.378 – Ratio_Strip) × h (Temp_Seg8 – 953) | −16338.606 | |
| h (C – 0.1739) × h (Temp_Seg8 – 889) × h(Al – 0.0329) | 114852.181 | |
| h (Mn – 1.3736) × h (0.0091 – S) × h (Temp_Seg8 – 889) | −16604.875 | |
| h (Mn – 1.3464) × h (889 – Temp_Seg8) × h (Temp_Seg17 – 883) | −11.470 | |
| h (1.3464 – Mn) × h (889 – Temp_Seg8) × h (Temp_Seg17 – 883) | 38.383 | |
| h (0.2276 – Si) × h (P – 0.0166) × h (889 – Temp_Seg8) | 503.269 | |
| h (Si – 0.2095) × h (75.378 – Ratio_Strip) × h (953 – Temp_Seg8) | −18.490 | |
| B33 | h (0.2095 − Si) ×h (75.378 – Ratio_Strip) × h (953 – Temp_Seg8) | 0.124 |
| h (0.2483 − Si) × h (Ratio_Strip – 75.977) × h (Temp_Seg8 – 870) | −4789.996 | |
| h (0.2483 − Si) × h (Temp_Seg8 – 870) × h (Temp_Seg17 – 815) | −0.133 | |
| h (S – 0.0089) × h (Freq_Oscillation – 2.16) × h (899 – Temp_Seg8) | 2206.549 | |
| h (S – 0.0089) × h (2.16 − Freq_Oscillation) × h (899 – Temp_Seg8) | 59.436 | |
| h (0.0091 − S) × h (75.115 – Ratio_Strip) × h (Temp_Seg8 − 889) | 20,180.563 | |
| h (S – 0.0091) × h (Overtemperature – 25) × h (Temp_Seg8 – 889) | −200.213 | |
| h (S – 0.0091) × h (25 − Overtemperature) × h (Temp_Seg8 – 889) | −36.885 | |
| h (0.015 – P) × h (75.378 – Ratio_Strip) × h (Temp_Seg8 – 870) | −1053.411 | |
| h (2.43 – Freq_Oscillation) × h (Ratio_Strip – 75.37) × h (Overtemperature – 29) | 613.802 | |
| h (75.378 – Ratio_Strip) × h (953 – Temp_Seg8) × h (Al – 0.0383) | 0.443 | |
| h (75.378 – Ratio_Strip) × h (953 – Temp_Seg8) × h (0.0383 – Al) | −0.306 | |
| h (Ratio_Strip – 75.378) × h (Temp_Seg8 − 870) × h (Al − 0.0314) | 2183.857 | |
| h (Temp_Seg8 – 906) × h (Temp_Seg17 − 815) × h (0.0304 – Al) | 3.265 |
| Variable | Nsubsets | GCV | RSS |
|---|---|---|---|
| Si | 45 | 100.0 | 100.0 |
| Temp_Seg8 | 45 | 100.0 | 100.0 |
| S | 44 | 91.8 | 92.1 |
| Ratio_Strip | 44 | 91.8 | 92.1 |
| Mn | 43 | 86.5 | 86.8 |
| Temp_Seg17 | 43 | 86.5 | 86.8 |
| Al | 42 | 81.0 | 81.4 |
| C | 33 | 58.5 | 57.3 |
| Overtemperature | 32 | 57.1 | 55.5 |
| P | 31 | 55.7 | 53.8 |
| Freq_Oscillation | 24 | 49.6 | 44.7 |
| Ave_Speed | 20 | 42.3 | 37.7 |
| Definition | ||
|---|---|---|
| 1 | 0.2156 | |
| h (C − 0.1873) | −177.2487 | |
| h (0.1873 − C) | −29.2927 | |
| h (Si – 0.2483) | −45.3392 | |
| h (P–0.0174) | 1102.0646 | |
| h (Ave_Speed – 1.16) | 245.0236 | |
| h (1.16 − Ave_Speed) | 8.2028 | |
| h (749 – Temp_Seg17) | −0.0064 | |
| h (Temp_Seg17 – 900) | −0.1186 | |
| h (Si – 0.02152) × h (Temp_Seg17 – 749) | 0.3908 | |
| h (0.2152−Si) × h (Temp_Seg17 − 749) | 1.0 | |
| h (S − 0.0074) × h (Temp_Seg17 − 749) | −4.3071 | |
| h (0.0146 − P) × h (Temp_Seg17 − 749) | −11.1187 | |
| h (P − 0.0166) × h (749 − Temp_Seg17) | 1.8191 | |
| h (0.0166 − P) × h (749 − Temp_Seg17) | 57.9514 | |
| h (Freq_Oscillation − 2.53) × h (Temp_Seg17 − 749) | 0.1544 | |
| h (Ratio_Strip − 75.572) × h (Temp_Seg17 − 749) | 0.0440 | |
| h (75.572 − Ratio_Strip) × h (Temp_Seg17 − 749) | 0.0222 | |
| h (Temp_Seg8 − 921) × h (Temp_Seg17 − 749) | 0.0015 | |
| h (921 − Temp_Seg8) × h (Temp_Seg17 − 749) | 0.0002 | |
| h (Temp_Seg8 − 943) × h (Temp_Seg17 − 749) | −0.0017 | |
| h (Temp_Seg17 − 749) × h (Al − 0.0325) | 3.2277 | |
| h (749 − Temp_Seg17) × h (0.0302 − Al) | 0.7147 | |
| h (C − 0.1863) × h (0.0146 − P) × h (Temp_Seg17 − 749) | 25,383.1351 | |
| h (0.1855 − C) × h (921 − Temp_Seg8) × h (Temp_Seg17 − 749) | −0.0074 | |
| h (1.4062 − Mn) × h (1.16 − Ave_Speed) × h (Temp_Seg17 − 749) | −0.7150 | |
| h (Mn − 1.3506) × h (921 − Temp_Seg8) × h (Temp_Seg17 − 749) | −0.0026 | |
| h (0.1979 − Si) × h (2.53 − Freq_Oscillation) × h (Temp_Seg17 − 749) | −3.1666 | |
| h (0.2152 − Si) × h (Freq_Oscillation − 2.45) × h (Temp_Seg17 − 749) | −6.1100 | |
| h (0.2152 − Si) × h (2.45 − Freq_Oscillation) × h (Temp_Seg17 − 749) | −2.4387 | |
| h (0.2152 − Si) × h (0.95 − Ave_Speed) × h (Temp_Seg17 − 749) | 7.9399 | |
| h (0.1981 − Si) × h (921 − Temp_Seg8) × h (Temp_Seg17 − 749) | 0.0111 | |
| h (0.1957 − Si) × h (Temp_Seg17 − 749) × h (Al − 0.0325) | 132.0068 | |
| h (0.0074 − S) × h (P − 0.0127) × h (Temp_Seg17 − 749) | 24,770.8361 | |
| h (S − 0.0074) × h (Ratio_Strip − 75.864) × h (Temp_Seg17 − 749) | 118.2158 | |
| h (S − 0.0074) × h (Ratio_Strip − 75.977) × h (Temp_Seg17 − 749) | −190.8619 | |
| h (S − 0.0116) × h (921 − Temp_Seg8) × h (Temp_Seg17 − 749) | 0.0704 | |
| h (P − 0.0156) × h (2.53 − Freq_Oscillation) × h (Temp_Seg17 − 749) | 5.5200 | |
| h (0.0166 − P) × h (Freq_Oscillation − 1.62) × h (749 − Temp_Seg17) | −71.7430 | |
| h (0.0166 − P) × h (1.62 − Freq_Oscillation) × h (749 − Temp_Seg17) | −30.9687 | |
| h (P − 0.0146) × h (Ratio_Strip − 75.667) × h (Temp_Seg17 − 749) | −20.3425 | |
| h (P − 0.0146) × h (75.667 − Ratio_Strip) × h (Temp_Seg17 − 749) | −4.8084 | |
| h (P − 0.0166) × h (Ave_Speed − 0.88) × h (749 − Temp_Seg17) | −78.9370 | |
| h (0.0166 − P) × h (Ave_Speed − 1) × h (749 − Temp_Seg17) | −41.3467 | |
| B45 | h (0.0166 − P) × h (1 − Ave_Speed) × h (749 − Temp_Seg17) | −280.7197 |
| h (P − 0.0166) × h (Overtemperature−9) × h (749 − Temp_Seg17) | −0.0209 | |
| B47 | h (P − 0.0146) × h (Temp_Seg8 − 879) × h (Temp_Seg17 − 749) | −0.1404 |
| B48 | h (P − 0.0146) × h (879 − Temp_Seg8) × h (Temp_Seg17 − 749) | −0.0658 |
| B49 | h (P − 0.0156) × h (Temp_Seg8 − 943) × h (Temp_Seg17 − 749) | 0.2179 |
| B50 | h (0.0156 − P) × h (Temp_Seg8 − 943) × h (Temp_Seg17 − 749) | 0.1261 |
| B51 | h (Freq_Oscillation − 2.04) × h (1.16 − Ave_Speed) × h (Temp_Seg17 − 749) | 0.1828 |
| B52 | h (2.53 − Freq_Oscillation) × h (Ave_Speed − 1.09) × h (Temp_Seg17 − 749) | −3.6134 |
| B53 | h (2.53 − Freq_Oscillation) × h (804 − Temp_Seg8) × h (Temp_Seg17 − 749) | 0.0013 |
| B54 | h (75.756 − Ratio_Strip) × h (921 − Temp_Seg8) × h (Temp_Seg17 − 749) | −0.0002 |
| B55 | h (Specific_Flow − 0.65) × h (Temp_Seg17 − 749) × h (0.0325 − Al) | −119.6246 |
| B56 | h (Overtemperature − 30) × h (Temp_Seg8 − 921) × h (Temp_Seg17 − 749) | −0.0005 |
| B57 | h (30 − Overtemperature) × h (Temp_Seg8 − 921) × h (Temp_Seg17 − 749) | −0.0001 |
| B58 | h (30 − Overtemperature) × h (Temp_Seg17 − 749) × h (0.0325 − Al) | 0.1517 |
| B59 | h (Temp_Seg8 − 910) × h (Temp_Seg17 − 749) × h (Al − 0.0325) | −0.1202 |
| B60 | h (910 − Temp_Seg8) × h (Temp_Seg17 − 749) × h (Al − 0.0325) | −0.0317 |
| Variable | Nsubsets | GCV | RSS |
|---|---|---|---|
| S | 30 | 100.0 | 100.0 |
| P | 29 | 55.3 | 56.0 |
| Temp_Seg17 | 28 | 47.6 | 48.2 |
| Ratio_Strip | 28 | 47.6 | 48.2 |
| Al | 27 | 45.6 | 45.8 |
| Temp_Seg8 | 21 | 29.6 | 29.1 |
| Ave_Speed | 20 | 26.6 | 26.2 |
| Si | 13 | 15.8 | 15.8 |
| Overtemperature | 10 | 12.7 | 12.7 |
| Freq_Oscillation | 44 | 78.3 | 70.5 |
| Mn | 43 | 77.3 | 69.0 |
| C | 39 | 73.0 | 62.9 |
| Specific_Flow | 8 | 31.6 | 24.6 |
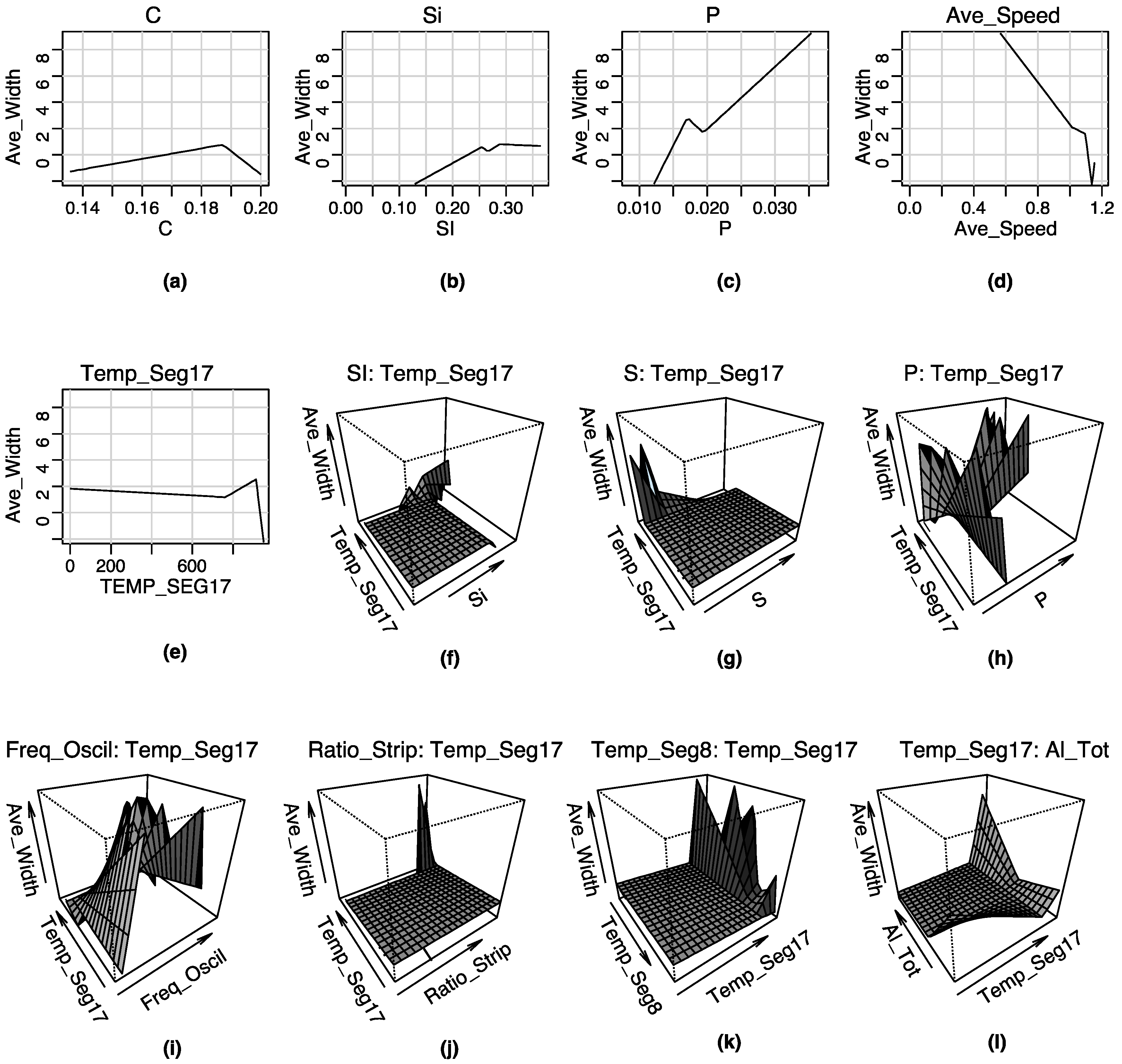
3.2. The Goodness-Of-Fit for This Approach
- (1)
- : the total sum of squares, proportional to the sample variance;
- (2)
- : the regression sum of squares, also called the explained sum of squares;
- (3)
- : the residual sum of squares.
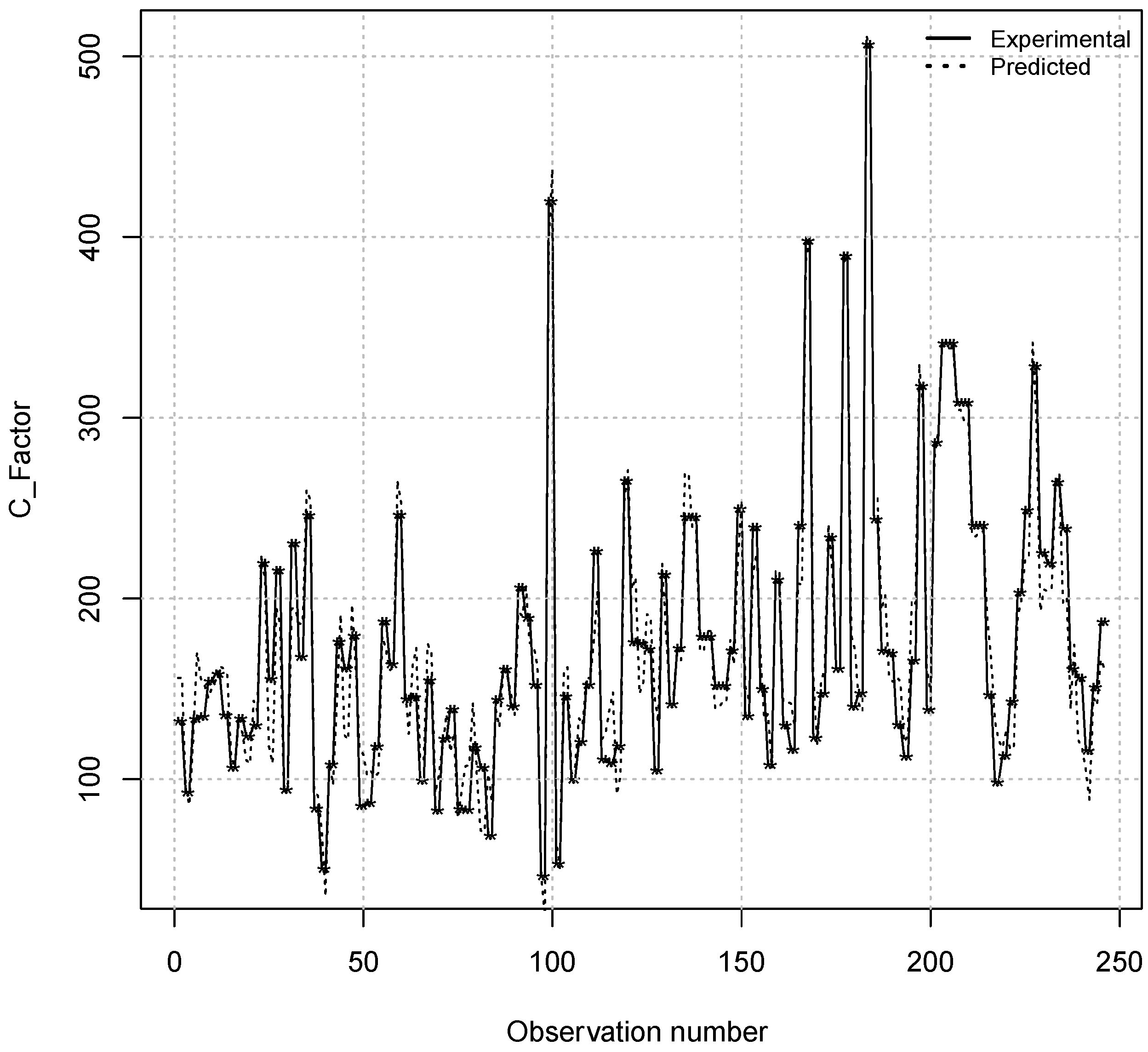
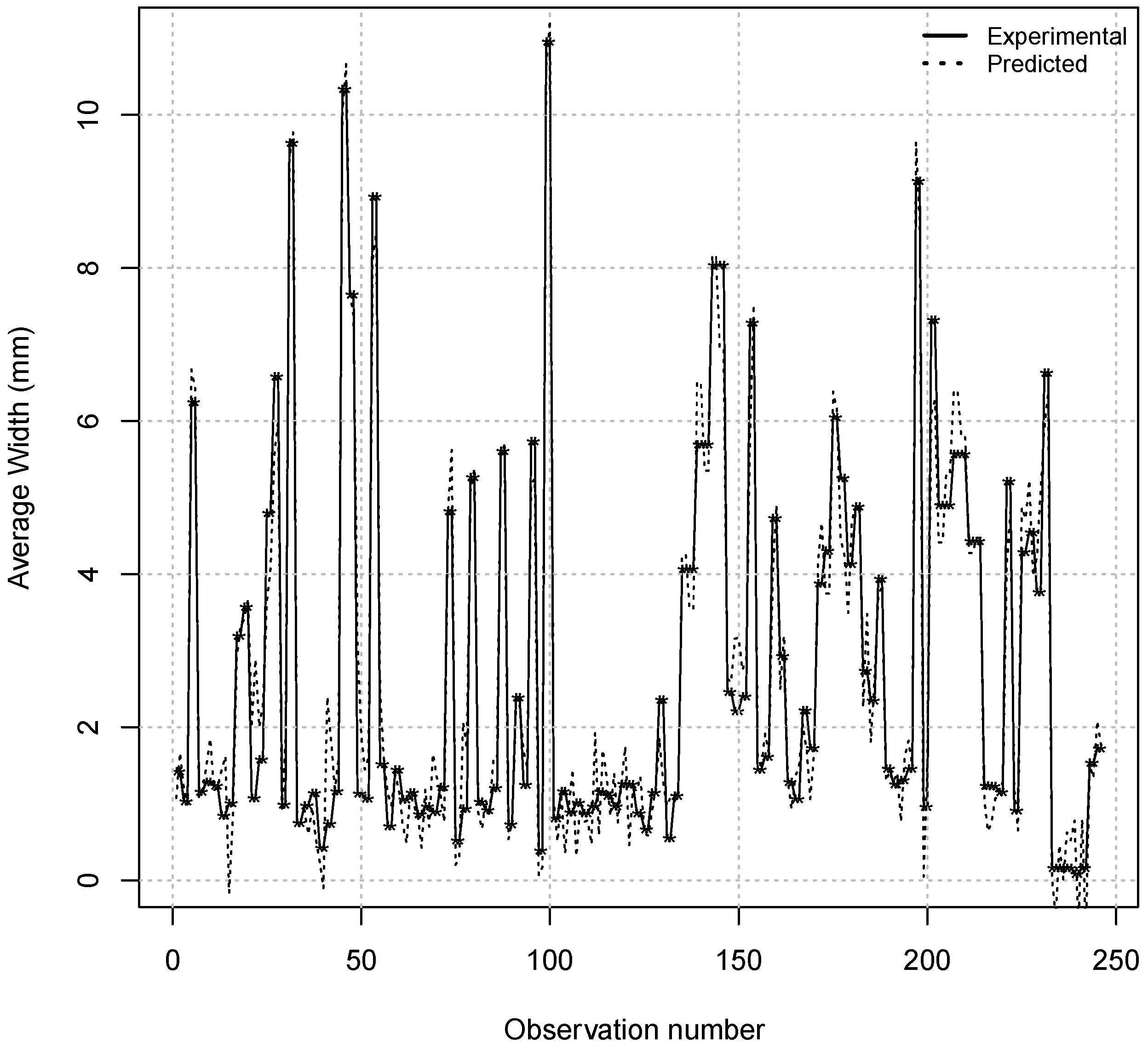
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ghosh, A. Principles of Secondary Processing and Casting of Liquid Steel; Oxford and IBH: New Delhi, India, 1990. [Google Scholar]
- Llewellyn, D.T. Steels: Metallurgy and Applications; Butterworth-Heinemann: Oxford, UK, 1992. [Google Scholar]
- Blair, M.; Stevens, T.L.; Linskey, B. Steel Castings Handbook; ASM International: New York, NY, USA, 1995. [Google Scholar]
- Díaz, A.M.; Sancho, L.F.; Sirgo, J.A.; López, A.M. Application of techniques of dimension reduction to predict the steel quality at the end of the secondary steelmaking. In Proceedings of 40th IEEE Industry Applications Conference, Annual General Meeting, Hong Kong, China, 2–6 October 2005; pp. 537–542.
- Krauss, G. Steels: Processing, Structure, and Performance; ASM International: New York, NY, USA, 2005. [Google Scholar]
- Sirgo, J.A.; Campo, R.; López, A.; Díaz, A.M.; Sancho, L.F. Measurement of centerline segregation in steel slabs. In Proceedings of 41st IEEE Industry Applications Conference, Tampa, FL, USA, 8–12 October 2006; pp. 516–520.
- Díaz, A.M.; Sancho, L.F.; Díaz, E.; López, A.M.; Sirgo, J.A. Application of self organizing maps to predict centerline segregation in steel slabs. In Proceedings of 41st IEEE Industry Applications Conference, Tampa, FL, USA, 8–12 October 2006; pp. 511–515.
- Verhoeven, J.D. Steel Metallurgy for the Non-Metallurgist; ASM International: New York, NY, USA, 2007. [Google Scholar]
- Brandt, D.A.; Warner, J.C. Metallurgy Fundamentals; Goodheart-Willcox: Chicago, IL, USA, 2009. [Google Scholar]
- Dantzig, J.A.; Rappaz, M. Solidification; CRC Press: New York, NY, USA, 2009. [Google Scholar]
- Mandal, S.K. Steel Metallurgy: Principles, Specifications and Applications; McGraw Hill Education: New Delhi, India, 2014. [Google Scholar]
- Réger, M.; Verő, B.; Józsa, R. Control of centerline segregation in slab casting. Acta Polytech. Hung. 2014, 11, 119–137. [Google Scholar]
- Gheorghies, C.; Crudu, I.; Teletin, C.; Spanu, C. Theoretical model of steel continuous casting technology. J. Iron Steel Res. Int. 2009, 16, 12–16. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines (with discussion). Ann. Statist. 1991, 19, 1–141. [Google Scholar] [CrossRef]
- Sekulic, S.S.; Kowalski, B.R. MARS: A Tutorial. J. Chemometr. 1992, 6, 199–216. [Google Scholar] [CrossRef]
- Friedman, J.H.; Roosen, C.B. An introduction to multivariate adaptive regression splines. Stat. Methods Med. Res. 1995, 4, 197–217. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer-Verlag: New York, NY, USA, 2003. [Google Scholar]
- Xu, Q.S.; Dazykowski, M.; Walczak, B.; Daeyaert, F.; de Jonge, M.R.; Heeres, J.; Koymans, L.M.H.; Lewi, P.J.; Vinkers, H.M.; Janssen, P.A.; et al. Multivariate adaptive regression splines–studies of HIV reverse transcriptase inhibitors. Chemometr. Intell. Lab. 2004, 72, 27–34. [Google Scholar]
- Vidoli, F. Evaluating the water sector in Italy through a two stage method using the conditional robust nonparametric frontier and multivariate adaptive regression splines. Eur. J. Oper. Res. 2011, 212, 583–595. [Google Scholar] [CrossRef]
- García Nieto, P.J.; Martínez Torres, J.; de Cos Juez, F.J.; Sánchez Lasheras, F. Using multivariate adaptive regression splines and multilayer perceptron networks to evaluate paper manufactured using Eucalyptus globulus. Appl. Math. Comput. 2012, 219, 755–763. [Google Scholar] [CrossRef]
- Álvarez Antón, J.C.; García Nieto, P.J.; de Cos Juez, F.J.; Sánchez Lasheras, F.; Blanco Viejo, C.; Roqueñí Gutiérrez, N. Battery state-of-charge estimator using the MARS technique. IEEE Trans. Power Electr. 2013, 28, 69–80. [Google Scholar] [CrossRef]
- Cheng, M.Y.; Cao, M.T. Accurately predicting building energy performance using evolutionary multivariate adaptive regression splines. Appl. Soft Comput. 2014, 22, 178–188. [Google Scholar] [CrossRef]
- Zhang, W.; Goh, A.T.C.; Zhang, Y.; Chen, Y.; Xiao, Y. Assessment of soil liquefaction based on capacity energy concept and multivariate adaptive regression splines. Eng. Geol. 2015, 188, 29–37. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H.; Honeycombe, R.W.K. Steels: Microstructure and Properties; Butterworth-Heinemann: Oxford, UK, 2011. [Google Scholar]
- Lejcek, P. Grain Boundary Segregation in Metals; Springer: Berlin, Germany, 2010. [Google Scholar]
- Komenda, J.; Runnsjö, G. Quantification of macrosegregation in continuously cast structures. Steel Research 1998, 69, 228–236. [Google Scholar]
- Jacobi, H.F. Investigation of centreline segregation and centreline porosity in CC-Slabs. Steel Res. 2003, 74, 667–678. [Google Scholar]
- Flemings, M.C.; Nerco, G.E. Macrosegregation: Part I. Trans. AIME 1967, 239, 1449–1461. [Google Scholar]
- Flemings, M.C.; Mehrabian, R.; Nerco, G.E. Macrosegregation: Part II. Trans. AIME 1968, 242, 41–49. [Google Scholar]
- Flemings, M.C. Solidification processing. Metall. Mater. Trans. 1974, 5, 2121–2134. [Google Scholar] [CrossRef]
- Schneider, M.C.; Beckermann, C. Simulation of micro-/microsegregation during solidification of a low-alloy steel. Iron Steel Inst. Jpn. Int. 1995, 35, 665–672. [Google Scholar] [CrossRef]
- Gu, J.P.; Beckermann, C. Simulation of convection and macrosegregation in a large steel ingot. Metall. Mater. Trans. 1999, A30, 1357–1367. [Google Scholar] [CrossRef]
- Ghosh, A. Segregation in cast products. Sadhana 2001, 26, 5–24. [Google Scholar] [CrossRef]
- Fujda, M. Centerline segregation of continuously cast slabs: Influence on microstructure and fracture morphology. J. Met. Mater. Min. 2005, 15, 45–51. [Google Scholar]
- Liu, J.; Baoa, Y.; Donga, X.; Lia, T.; Renb, Y.; Zhang, S. Distribution and segregation of dissolved elements in pipeline slab. J. Univ. Sci. Technol. B. Min. Metall. Mater. 2007, 14, 212–218. [Google Scholar] [CrossRef]
- Torgerson, W.S. Multidimensional Scaling: I, theory and method. Phychometrica 1952, 17, 401–419. [Google Scholar] [CrossRef]
- De Leeuw, J.; Heiser, W. Theory of multidimensional scaling. In Handbook of Statistics; Krishnaiah, P.R., Kanal, L.N., Eds.; North-Holland: Amsterdam, The Netherland, 1982; Volume 2, pp. 285–316. [Google Scholar]
- Sammon, J.W. A non linear mapping for data structure analysis. IEEE Trans. Comp. 1969, 18, 401–409. [Google Scholar] [CrossRef]
- Jolliffe, L.T. Principal Component Analysis; Springer-Verlag: New York, NY, USA, 1986. [Google Scholar]
- Fine, T.L. Feedforward Neural Networks Methodology; Springer-Verlag: New York, NY, USA, 1999. [Google Scholar]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer: New York, NY, USA, 1995. [Google Scholar]
- Vapnik, V. Statistical Learning Theory; Wiley-Interscience: New York, NY, USA, 1998. [Google Scholar]
- Freedman, D.; Pisani, R.; Purves, R. Statistics; W.W. Norton & Company: New York, NY, USA, 2007. [Google Scholar]
- Picard, R.; Cook, D. Cross-validation of regression models. J. Am. Stat. Assoc. 1984, 79, 575–583. [Google Scholar] [CrossRef]
- Efron, B.; Tibshirani, R. Improvements on cross-validation: the .632 + bootstrap method. J. Am. Stat. Assoc. 1997, 92, 548–560. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nieto, P.J.G.; Suárez, V.M.G.; Antón, J.C.Á.; Bayón, R.M.; Blanco, J.Á.S.; Fernández, A.M.D. A New Predictive Model of Centerline Segregation in Continuous Cast Steel Slabs by Using Multivariate Adaptive Regression Splines Approach. Materials 2015, 8, 3562-3583. https://doi.org/10.3390/ma8063562
Nieto PJG, Suárez VMG, Antón JCÁ, Bayón RM, Blanco JÁS, Fernández AMD. A New Predictive Model of Centerline Segregation in Continuous Cast Steel Slabs by Using Multivariate Adaptive Regression Splines Approach. Materials. 2015; 8(6):3562-3583. https://doi.org/10.3390/ma8063562
Chicago/Turabian StyleNieto, Paulino José García, Victor Manuel González Suárez, Juan Carlos Álvarez Antón, Ricardo Mayo Bayón, José Ángel Sirgo Blanco, and Ana María Díaz Fernández. 2015. "A New Predictive Model of Centerline Segregation in Continuous Cast Steel Slabs by Using Multivariate Adaptive Regression Splines Approach" Materials 8, no. 6: 3562-3583. https://doi.org/10.3390/ma8063562
APA StyleNieto, P. J. G., Suárez, V. M. G., Antón, J. C. Á., Bayón, R. M., Blanco, J. Á. S., & Fernández, A. M. D. (2015). A New Predictive Model of Centerline Segregation in Continuous Cast Steel Slabs by Using Multivariate Adaptive Regression Splines Approach. Materials, 8(6), 3562-3583. https://doi.org/10.3390/ma8063562







