Characterization of Fibrin and Collagen Gels for Engineering Wound Healing Models
Abstract
:1. Introduction
2. Experimental Section
2.1. Preparation of Fibrin and Collagen Gels
2.1.1. Fibrin Gels
2.1.2. Collagen Gels
2.2. Scanning Electron Microscopy
2.3. Confocal Reflection Imaging
2.4. Microstructural Analysis
2.5. Permeability Experiments
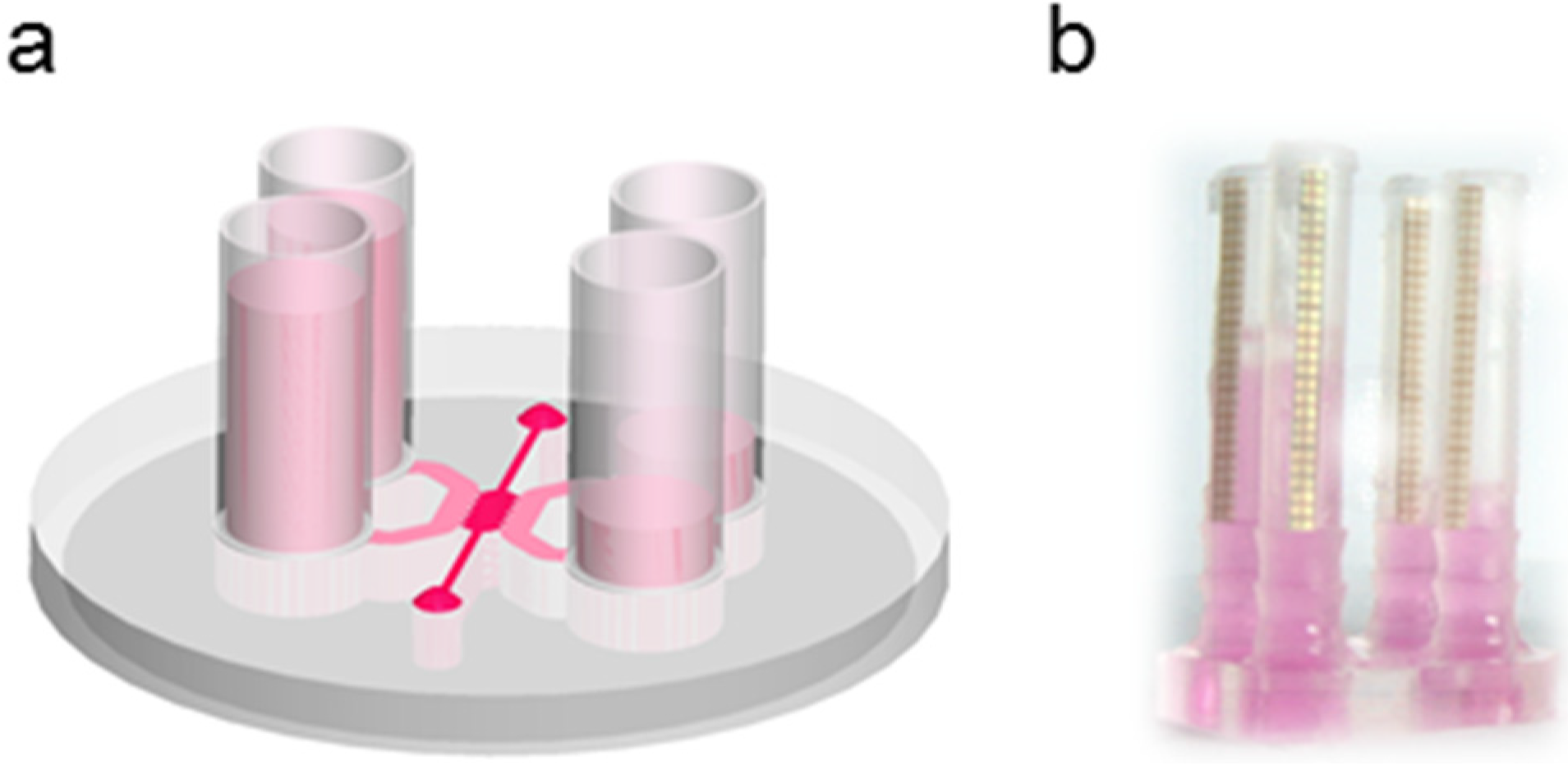
2.6. Rheology

3. Results and Discussion
3.1. Microstructural Study
| Collagen | Fibrin | |
|---|---|---|
| Void ratio (%) | 80.15 ± 1.82 | 71.46 ± 1.00 |
| Pore size (μm) | 2.84 ± 0.94 | 1.69 ± 0.33 |
| Fiber radius (nm) | 79.51 ± 33.16 | 66.53 ± 13.57 |


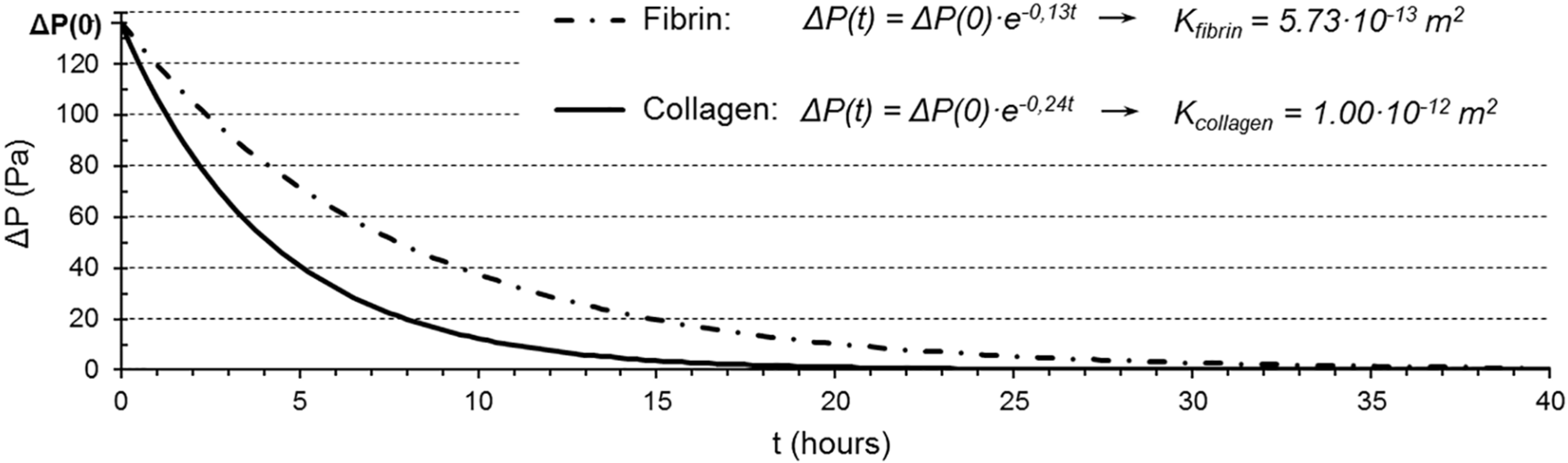
3.2. Permeability Quantification
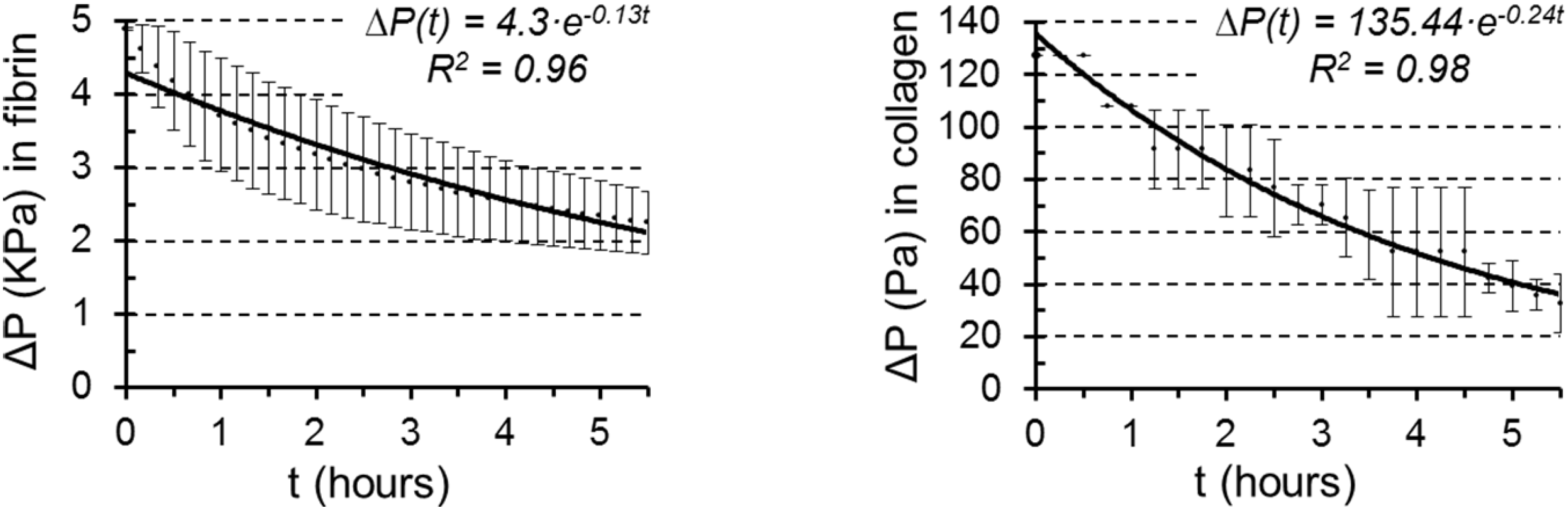
| Collagen | Fibrin | |
|---|---|---|
| Exponent coefficient, c (s−1) | 7.00·10−05 | 4.00·10−05 |
| Darcy’s permeability, K (m2) | 1.00·10−12 | 5.73·10−13 |
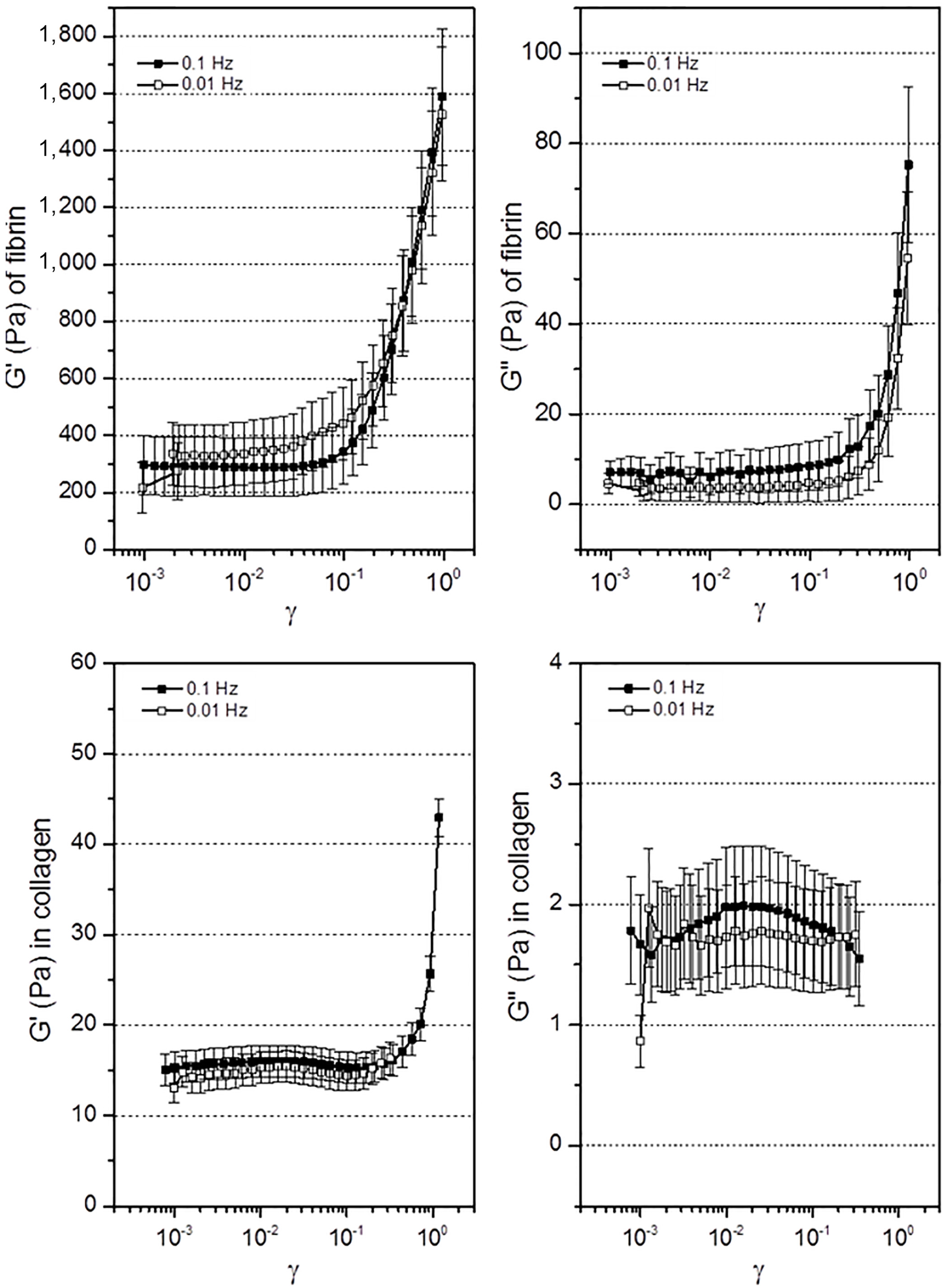
3.3. Mechanical Response
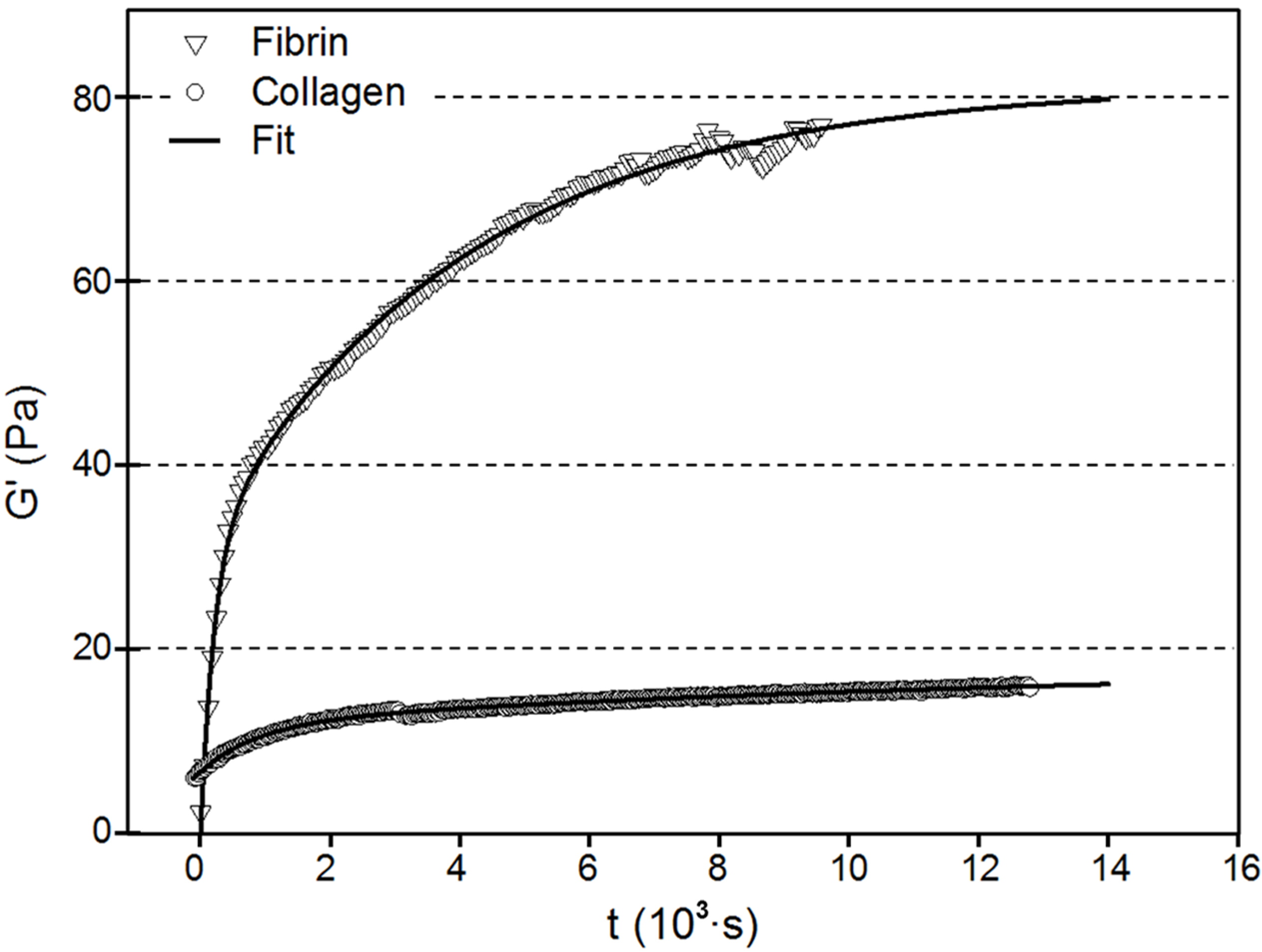
| Fibrin | Collagen | |||
|---|---|---|---|---|
| Value | Error | Value | Error | |
| G’1 | 31.12 | 0.48 | 11.70 | 0.10 |
| t1 | 211.87 | 11.09 | 896.75 | 22.16 |
| G’2 | 50.78 | 0.35 | 7.11 | 0.30 |
| t2 | 4,045.83 | 113.48 | 13,919.40 | 1,431.71 |
| xc | 117.52 | 4.63 | −591.82 | 15.62 |
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Diegelmann, R.F.; Evans, M.C. Wound Healing: An Overview of Acute, Fibrotic and Delayed Healing. Front. Biosci. 2004, 9, 283–289. [Google Scholar] [CrossRef] [PubMed]
- Guo, S.; Dipietro, L.A. Factors Affecting Wound Healing. J. Dent. Res. 2010, 89, 219–229. [Google Scholar] [CrossRef] [PubMed]
- Gahagnon, S.; Mofid, Y.; Josse, G.; Ossant, F. Skin Anisotropy in Vivo and Initial Natural Stress Effect: A Quantitative Study Using High-Frequency Static Elastography. J. Biomech. 2012, 45, 2860–2865. [Google Scholar] [CrossRef] [PubMed]
- Kamolz, L.-P.; Keck, M.; Kasper, C. Wharton’s Jelly Mesenchymal Stem Cells Promote Wound Healing and Tissue Regeneration. Stem Cell Res. Ther. 2014, 5, 62. [Google Scholar] [CrossRef] [PubMed]
- Moreno-Arotzena, O.; Mendoza, G.; Cóndor, M.; Rüberg, T.; García-Aznar, J.M. Inducing Chemotactic and Haptotactic Cues in Microfluidic Devices for Three-Dimensional in Vitro Assays. Biomicrofluidics 2014, 8, 064122. [Google Scholar] [CrossRef] [PubMed]
- Valero, C.; Javierre, E.; García-Aznar, J.M.; Gómez-Benito, M.J. A Cell-Regulatory Mechanism Involving Feedback between Contraction and Tissue Formation Guides Wound Healing Progression. PLoS One 2014, 9, e92774. [Google Scholar] [CrossRef] [PubMed]
- Anon, E.; Serra-Picamal, X.; Hersen, P.; Gauthier, N.C.; Sheetz, M.P.; Trepat, X.; Ladoux, B. Cell Crawling Mediates Collective Cell Migration to Close Undamaged Epithelial Gaps. Proc. Natl. Acad. Sci. USA 2012, 109, 10891–10896. [Google Scholar] [CrossRef] [PubMed]
- Murrell, M.; Kamm, R.; Matsudaira, P. Tension, Free Space, and Cell Damage in a Microfluidic Wound Healing Assay. PLoS One 2011, 6, e24283. [Google Scholar] [CrossRef] [PubMed]
- Singer, A.J.; Clark, R.A.F. Cutaneous Wound Healing. N. Engl. J. Med. 1999, 341, 738–746. [Google Scholar] [CrossRef] [PubMed]
- Polacheck, W.J.; Li, R.; Uzel, S.G.M.; Kamm, R.D. Microfluidic Platforms for Mechanobiology. Lab Chip 2013, 13, 2252–2267. [Google Scholar] [CrossRef] [PubMed]
- Griffith, L.G.; Swartz, M.A. Capturing Complex 3D Tissue Physiology in Vitro. Nat. Rev. Mol. Cell Biol. 2006, 7, 211–224. [Google Scholar] [CrossRef] [PubMed]
- Lambrechts, D.; Roeffaers, M.; Kerckhofs, G.; Hofkens, J.; van de Putte, T.; Schrooten, J.; van Oosterwyck, H. Reporter Cell Activity within Hydrogel Constructs Quantified from Oxygen-Independent Bioluminescence. Biomaterials 2014, 35, 8065–8077. [Google Scholar] [CrossRef] [PubMed]
- Grinnell, F. Fibroblast-Collagen-Matrix Contraction: Growth-Factor Signalling and Mechanical Loading. Trends Cell Biol. 2000, 10, 362–365. [Google Scholar] [CrossRef] [PubMed]
- Martino, M.M.; Briquez, P.S.; Ranga, A.; Lutolf, M.P.; Hubbell, J.A. Heparin-Binding Domain of Fibrin(ogen) Binds Growth Factors and Promotes Tissue Repair When Incorporated within a Synthetic Matrix. Proc. Natl. Acad. Sci. USA 2013, 110, 4563–4568. [Google Scholar] [CrossRef] [PubMed]
- Tomasek, J.J.; Gabbiani, G.; Hinz, B.; Chaponnier, C.; Brown, R.A. Myofibroblasts and Mechano-Regulation of Connective Tissue Remodelling. Nat. Rev. Mol. Cell Biol. 2002, 3, 349–363. [Google Scholar] [CrossRef] [PubMed]
- Ulrich, T.A.; de Juan Pardo, E.M.; Kumar, S. The Mechanical Rigidity of the Extracellular Matrix Regulates the Structure, Motility, and Proliferation of Glioma Cells. Cancer Res. 2009, 69, 4167–4174. [Google Scholar] [CrossRef] [PubMed]
- Miron-Mendoza, M.; Seemann, J.; Grinnell, F. The Differential Regulation of Cell Motile Activity through Matrix Stiffness and Porosity in Three Dimensional Collagen Matrices. Biomaterials 2010, 31, 6425–6435. [Google Scholar] [CrossRef] [PubMed]
- Swartz, M.A.; Fleury, M.E. Interstitial Flow and Its Effects in Soft Tissues. Annu. Rev. Biomed. Eng. 2007, 9, 229–256. [Google Scholar] [CrossRef] [PubMed]
- Ng, C.P.; Hinz, B.; Swartz, M.A. Interstitial Fluid Flow Induces Myofibroblast Differentiation and Collagen Alignment in Vitro. J. Cell Sci. 2005, 118, 4731–4739. [Google Scholar] [CrossRef] [PubMed]
- Polacheck, W.J.; German, A.E.; Mammoto, A.; Ingber, D.E.; Kamm, R.D. Mechanotransduction of Fluid Stresses Governs 3D Cell Migration. Proc. Natl. Acad. Sci. USA 2014, 111, 2447–2452. [Google Scholar] [CrossRef] [PubMed]
- Stroka, K.M.; Gu, Z.; Sun, S.X.; Konstantopoulos, K. Bioengineering Paradigms for Cell Migration in Confined Microenvironments. Curr. Opin. Cell Biol. 2014, 30C, 41–50. [Google Scholar] [CrossRef] [PubMed]
- Pathak, A.; Kumar, S. Independent Regulation of Tumor Cell Migration by Matrix Stiffness and Confinement. Proc. Natl. Acad. Sci. USA 2012, 109, 10334–10339. [Google Scholar] [CrossRef] [PubMed]
- Haeger, A.; Krause, M.; Wolf, K.; Friedl, P. Cell Jamming: Collective Invasion of Mesenchymal Tumor Cells Imposed by Tissue Confinement. Biochim. Biophys. Acta 2014, 1840, 2386–2395. [Google Scholar] [CrossRef] [PubMed]
- Rouillard, A.D.; Holmes, J.W. Mechanical Boundary Conditions Bias Fibroblast Invasion in a Collagen-Fibrin Wound Model. Biophys. J. 2014, 106, 932–943. [Google Scholar] [CrossRef] [PubMed]
- Miron-Mendoza, M.; Seemann, J.; Grinnell, F. Collagen Fibril Flow and Tissue Translocation Coupled to Fibroblast Migration in 3D Collagen Matrices. Mol. Biol. Cell 2008, 19, 2051–2058. [Google Scholar] [CrossRef] [PubMed]
- Buehler, M.J. Nature Designs Tough Collagen: Explaining the Nanostructure of Collagen Fibrils. Proc. Natl. Acad. Sci. USA 2006, 103, 12285–12290. [Google Scholar] [CrossRef] [PubMed]
- Rowe, S.L.; Stegemann, J.P. Interpenetrating Collagen-Fibrin Composite Matrices with Varying Protein Contents and Ratios. Biomacromolecules 2006, 7, 2942–2948. [Google Scholar] [CrossRef] [PubMed]
- Lai, V.K.; Frey, C.R.; Kerandi, A.M.; Lake, S.P.; Tranquillo, R.T.; Barocas, V.H. Microstructural and Mechanical Differences between Digested Collagen–fibrin Co-Gels and Pure Collagen and Fibrin Gels. Acta Biomater. 2012, 8, 4031–4042. [Google Scholar] [CrossRef] [PubMed]
- Münster, S.; Jawerth, L.M.; Leslie, B.A.; Weitz, J.I.; Fabry, B.; Weitz, D.A. Strain History Dependence of the Nonlinear Stress Response of Fibrin and Collagen Networks. Proc. Natl. Acad. Sci. USA 2013, 110, 12197–12202. [Google Scholar] [CrossRef] [PubMed]
- Storm, C.; Pastore, J.J.; MacKintosh, F.C.; Lubensky, T.C.; Janmey, P.A. Nonlinear Elasticity in Biological Gels. Lett. Nat. 2005, 435, 191–194. [Google Scholar] [CrossRef]
- Gersh, K.C.; Edmondson, K.E.; Weisel, J.W. Flow Rate and Fibrin Fiber Alignment. J. Thromb. Haemost. 2010, 8, 2826–2828. [Google Scholar] [CrossRef] [PubMed]
- Hartmann, A.; Boukamp, P.; Friedl, P. Confocal Reflection Imaging of 3D Fibrin Polymers. Blood Cells. Mol. Dis. 2006, 36, 191–193. [Google Scholar] [CrossRef] [PubMed]
- Ryan, E.A.; Mockros, L.F.; Weisel, J.W.; Lorand, L. Structural Origins of Fibrin Clot Rheology. Biophys. J. 1999, 77, 2813–2826. [Google Scholar] [CrossRef] [PubMed]
- Baniasadi, M.; Minary-Jolandan, M. Alginate-Collagen Fibril Composite Hydrogel. Materials (Basel). 2015, 8, 799–814. [Google Scholar] [CrossRef]
- Lai, V.K.; Lake, S.P.; Frey, C.R.; Tranquillo, R.T.; Barocas, V.H. Mechanical Behavior of Collagen-Fibrin Co-Gels Reflects Transition from Series to Parallel Interactions with Increasing Collagen Content. J. Biomech. Eng. 2012, 134, 011004. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.-L.; Leone, L.M.; Kaufman, L.J. Elastic Moduli of Collagen Gels Can Be Predicted from Two-Dimensional Confocal Microscopy. Biophys. J. 2009, 97, 2051–2060. [Google Scholar] [CrossRef] [PubMed]
- Lim, B.B.C.; Lee, E.H.; Sotomayor, M.; Schulten, K. Molecular Basis of Fibrin Clot Elasticity. Structure 2008, 16, 449–459. [Google Scholar] [CrossRef] [PubMed]
- Collet, J.-P.; Shuman, H.; Ledger, R.E.; Lee, S.; Weisel, J.W. The Elasticity of an Individual Fibrin Fiber in a Clot. Proc. Natl. Acad. Sci. USA 2005, 102, 9133–9137. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.L.; Dodge, M.R.; Kahn, H.; Ballarini, R.; Eppell, S.J. Stress-Strain Experiments on Individual Collagen Fibrils. Biophys. J. 2008, 95, 3956–3963. [Google Scholar] [CrossRef] [PubMed]
- Karande, T.S.; Ong, J.L.; Agrawal, C.M. Diffusion in Musculoskeletal Tissue Engineering Scaffolds: Design Issues Related to Porosity, Permeability, Architecture, and Nutrient Mixing. Ann. Biomed. Eng. 2004, 32, 1728–1743. [Google Scholar] [CrossRef] [PubMed]
- Wufsus, A.R.; Macera, N.E.; Neeves, K.B. The Hydraulic Permeability of Blood Clots as a Function of Fibrin and Platelet Density. Biophys. J. 2013, 104, 1812–1823. [Google Scholar] [CrossRef] [PubMed]
- Polacheck, W.J.; Charest, J.L.; Kamm, R.D. Interstitial Flow Influences Direction of Tumor Cell Migration through Competing Mechanisms. Proc. Natl. Acad. Sci. USA 2011, 108, 11115–11120. [Google Scholar] [CrossRef] [PubMed]
- Antoine, E.E.; Vlachos, P.P.; Rylander, M.N. Review of Collagen I Hydrogels for Bioengineered Tissue Microenvironments: Characterization of Mechanics, Structure, and Transport. Tissue Eng. Part B Rev. 2014, 20, 683–696. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Gu, L. Influence of Crosslink Density and Stiffness on Mechanical Properties of Type I Collagen Gel. Materials (Basel). 2015, 8, 551–560. [Google Scholar] [CrossRef]
- Stabenfeldt, S.E.; Gourley, M.; Krishnan, L.; Hoying, J.B.; Barker, T.H. Engineering Fibrin Polymers through Engagement of Alternative Polymerization Mechanisms. Biomaterials 2012, 33, 535–544. [Google Scholar] [CrossRef] [PubMed]
- Shin, Y.; Han, S.; Jeon, J.S.; Yamamoto, K.; Zervantonakis, I.K.; Sudo, R.; Kamm, R.D.; Chung, S. Microfluidic Assay for Simultaneous Culture of Multiple Cell Types on Surfaces or within Hydrogels. Nat. Protoc. 2012, 7, 1247–1259. [Google Scholar] [CrossRef] [PubMed]
- Rasband, W.S. ImageJ. U. S. National Institutes of Health: Bethesda, MD, USA, 1997. Available online: http://imagej.nih.gov/ij/ (accessed on 5 April 2015). [Google Scholar]
- Sudo, R.; Chung, S.; Zervantonakis, I.K.; Vickerman, V.; Toshimitsu, Y.; Griffith, L.G.; Kamm, R.D. Transport-Mediated Angiogenesis in 3D Epithelial Coculture. FASEB J. 2009, 23, 2155–2164. [Google Scholar] [CrossRef] [PubMed]
- Weisel, J.W. The Mechanical Properties of Fibrin for Basic Scientists and Clinicians. Biophys. Chem. 2004, 112, 267–276. [Google Scholar] [CrossRef] [PubMed]
- Engler, A.J.; Sen, S.; Sweeney, H.L.; Discher, D.E. Matrix Elasticity Directs Stem Cell Lineage Specification. Cell 2006, 126, 677–689. [Google Scholar] [CrossRef] [PubMed]
- Prentice-Mott, H.V.; Chang, C.-H.; Mahadevan, L.; Mitchison, T.J.; Irimia, D.; Shah, J.V. Biased Migration of Confined Neutrophil-like Cells in Asymmetric Hydraulic Environments. Proc. Natl. Acad. Sci. USA 2013, 110, 21006–21011. [Google Scholar] [CrossRef] [PubMed]
- Wolf, K.; Friedl, P. Extracellular Matrix Determinants of Proteolytic and Non-Proteolytic Cell Migration. Trends Cell Biol. 2011, 21, 736–744. [Google Scholar] [CrossRef] [PubMed]
- Shi, Z.-D.; Tarbell, J.M. Fluid Flow Mechanotransduction in Vascular Smooth Muscle Cells and Fibroblasts. Ann. Biomed. Eng. 2011, 39, 1608–1619. [Google Scholar] [CrossRef] [PubMed]
- Ulrich, T.A.; Jain, A.; Tanner, K.; MacKay, J.L.; Kumar, S. Probing Cellular Mechanobiology in Three-Dimensional Culture with Collagen-Agarose Matrices. Biomaterials 2010, 31, 1875–1884. [Google Scholar] [CrossRef] [PubMed]
- Pritchard, R.H.; Huang, Y.Y.S.; Terentjev, E.M. Mechanics of Biological Networks: From the Cell Cytoskeleton to Connective Tissue. Soft Matter 2014, 10, 1864–1884. [Google Scholar] [CrossRef] [PubMed]
- Shah, J.V.; Janmey, P.A. Strain Hardening of Fibrin Gels and Plasma Clots. Rheol. Acta 1997, 36, 262–268. [Google Scholar] [CrossRef]
- Mitsak, A.G.; Dunn, A.M.; Hollister, S.J. Mechanical Characterization and Non-Linear Elastic Modeling of Poly(glycerol Sebacate) for Soft Tissue Engineering. J. Mech. Behav. Biomed. Mater. 2012, 11, 3–15. [Google Scholar] [CrossRef] [PubMed]
- Legant, W.R.; Miller, J.S.; Blakely, B.L.; Cohen, D.M.; Genin, G.M.; Chen, C.S. Measurement of Mechanical Tractions Exerted by Cells in Three-Dimensional Matrices. Nat. Methods 2010, 7, 969–971. [Google Scholar] [CrossRef] [PubMed]
- Doyle, A.D.; Petrie, R.J.; Kutys, M.L.; Yamada, K.M. Dimensions in Cell Migration. Curr. Opin. Cell Biol. 2013, 25, 642–649. [Google Scholar] [CrossRef] [PubMed]
- Ehrbar, M.; Sala, A.; Lienemann, P.; Ranga, A.; Mosiewicz, K.; Bittermann, A.; Rizzi, S.C.; Weber, F.E.; Lutolf, M.P. Elucidating the Role of Matrix Stiffness in 3D Cell Migration and Remodeling. Biophys. J. 2011, 100, 284–293. [Google Scholar] [CrossRef] [PubMed]
- Kubow, K.E.; Conrad, S.K.; Horwitz, A.R. Matrix Microarchitecture and Myosin II Determine Adhesion in 3D Matrices. Curr. Biol. 2013, 23, 1607–1619. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno-Arotzena, O.; Meier, J.G.; Del Amo, C.; García-Aznar, J.M. Characterization of Fibrin and Collagen Gels for Engineering Wound Healing Models. Materials 2015, 8, 1636-1651. https://doi.org/10.3390/ma8041636
Moreno-Arotzena O, Meier JG, Del Amo C, García-Aznar JM. Characterization of Fibrin and Collagen Gels for Engineering Wound Healing Models. Materials. 2015; 8(4):1636-1651. https://doi.org/10.3390/ma8041636
Chicago/Turabian StyleMoreno-Arotzena, Oihana, Johann G. Meier, Cristina Del Amo, and José Manuel García-Aznar. 2015. "Characterization of Fibrin and Collagen Gels for Engineering Wound Healing Models" Materials 8, no. 4: 1636-1651. https://doi.org/10.3390/ma8041636
APA StyleMoreno-Arotzena, O., Meier, J. G., Del Amo, C., & García-Aznar, J. M. (2015). Characterization of Fibrin and Collagen Gels for Engineering Wound Healing Models. Materials, 8(4), 1636-1651. https://doi.org/10.3390/ma8041636






