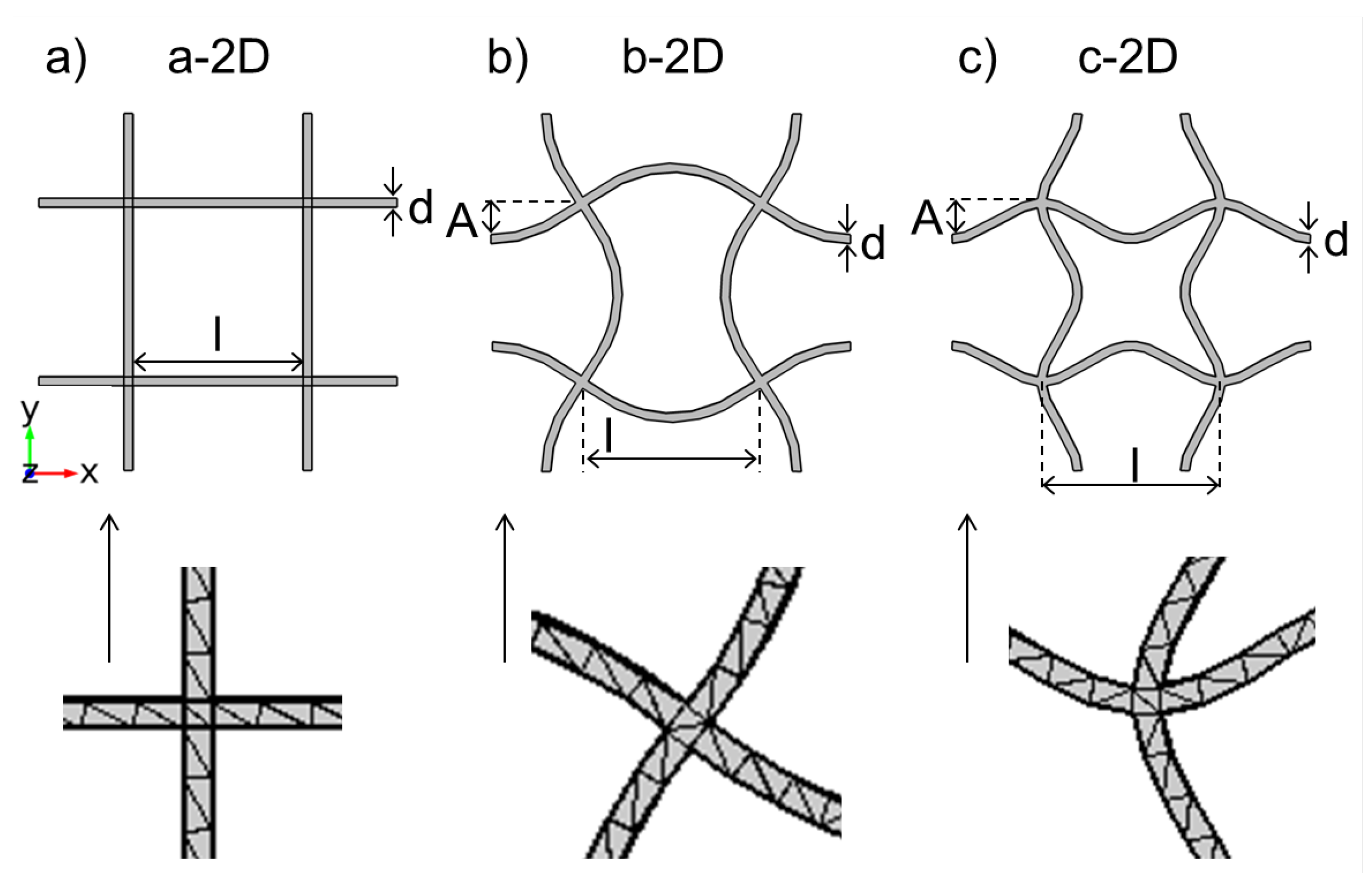
3.1. 2D Quadratic Unit Cells
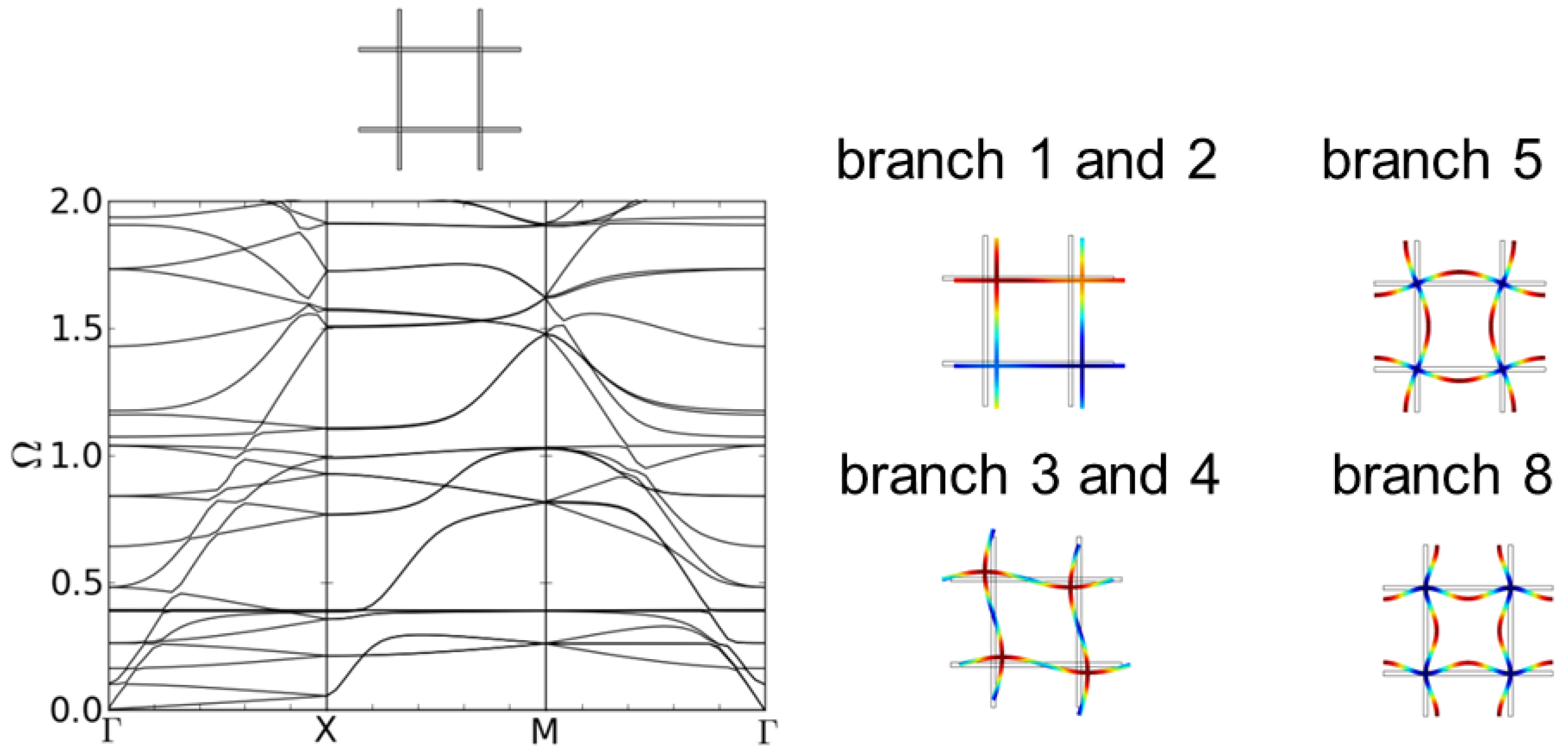
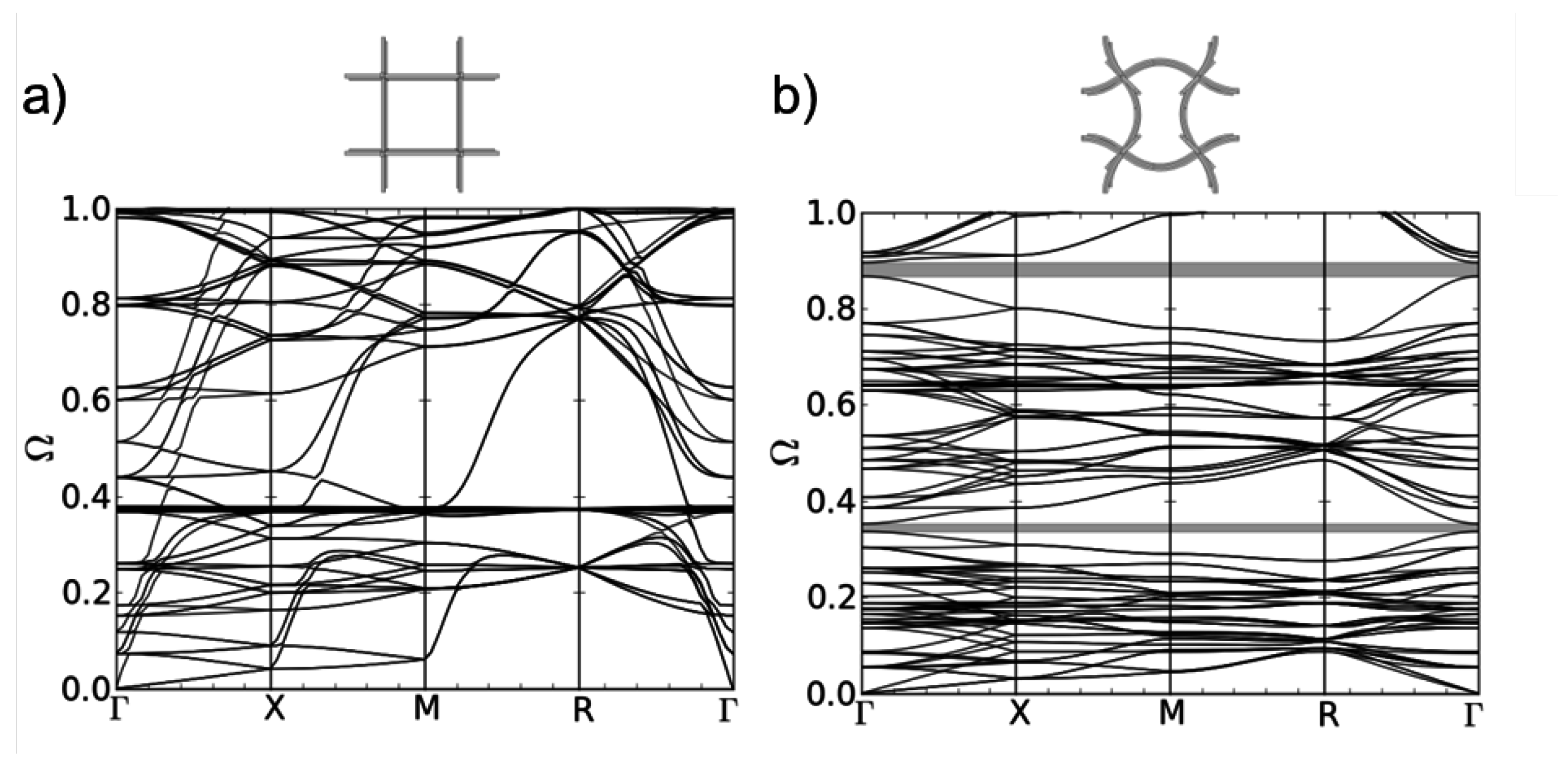
The dispersion results for the regular quadratic structure a-2D are shown in
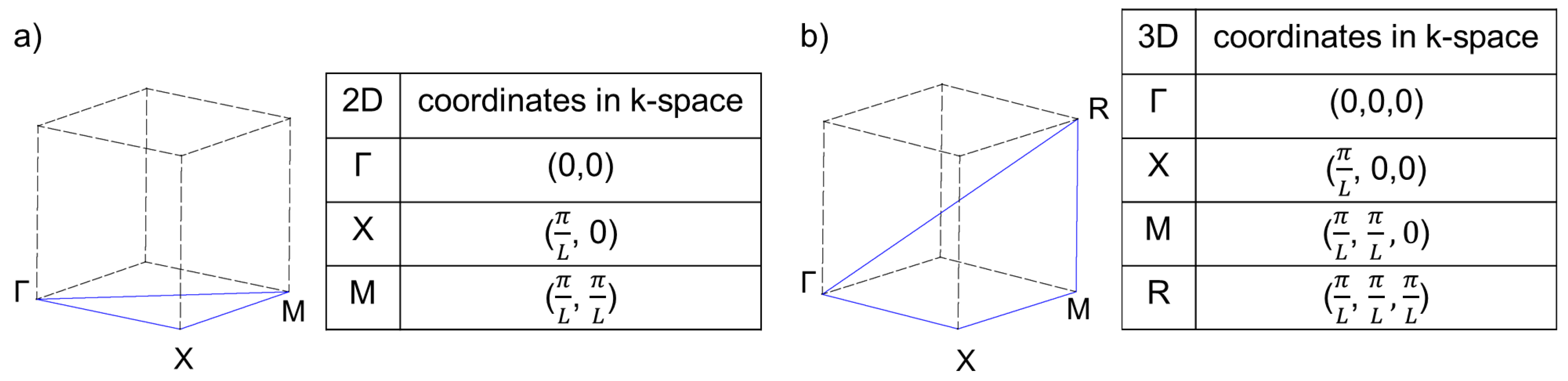
Figure 4. The normalized eigenfrequencies are plotted against the path Γ-X-M-Γ of the wave vector in
-space (see
Figure 1). No band gaps emerge. This is consistent with the results of Phani,
et al. [
9].
The corresponding eigenmode shapes for the first branches at point Γ in
-space can be seen in
Figure 4. While the first two eigenmodes correspond to a translation of the unit cell, for the third and fourth, the nodal points are moving and the struts begin to bend to follow the translation. The fifth eigenmode can be described as a bending of the struts due to a collective rotation of the nodal points that at the same time stay fixed at their initial position. The nodal points of the eighth eigenmode stay fixed at their initial position while the four struts between them bend alternatingly either all inwards or outwards.
Figure 4.
Dispersion relations of structure a-2D, a regular quadratic unit cell (l = 5.0 mm, d = 0.25 mm) and first eigenmodes at point Γ.
Figure 4.
Dispersion relations of structure a-2D, a regular quadratic unit cell (l = 5.0 mm, d = 0.25 mm) and first eigenmodes at point Γ.
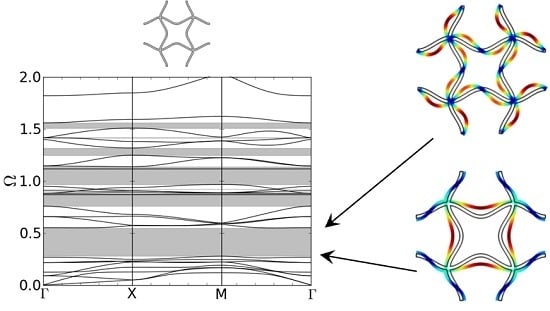
The dispersion curves for the quadratically based structure b-2D can be seen in
Figure 5a. In the considered frequency range, two band gaps develop. The first band gap emerges between the 8th and 9th dispersion branch. The corresponding eigenmodes are shown in
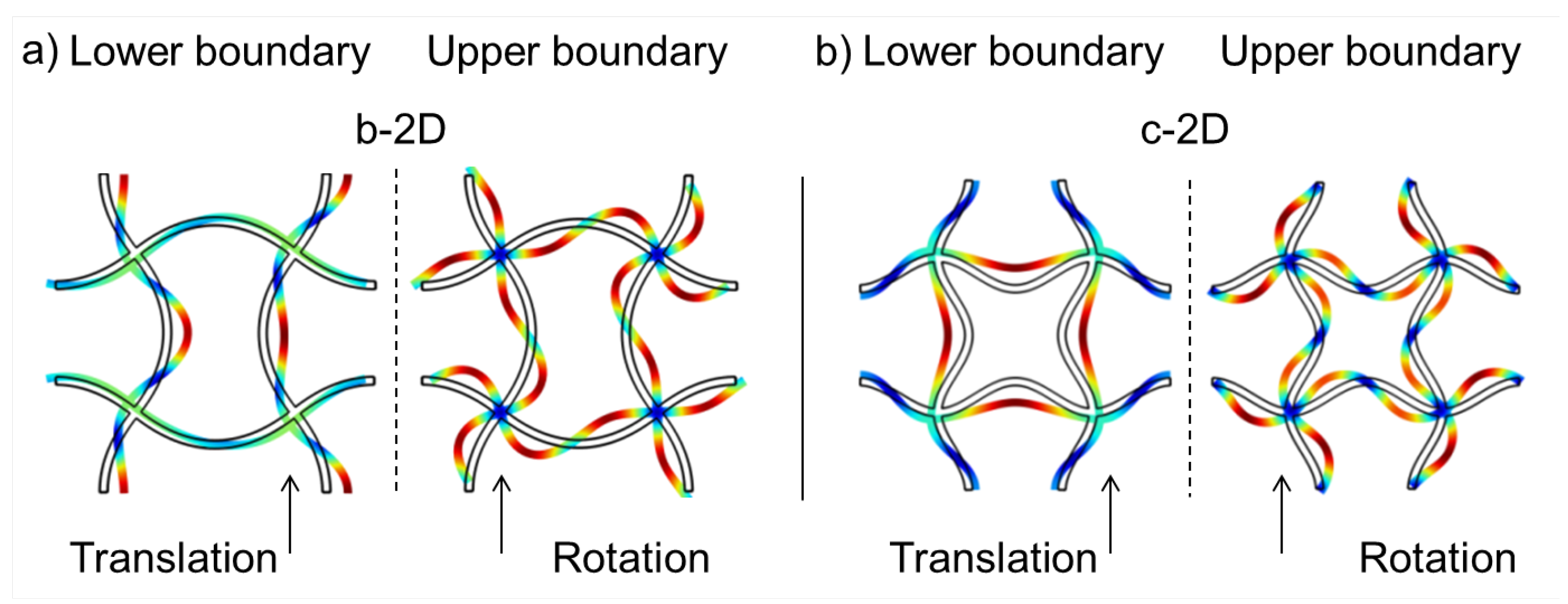
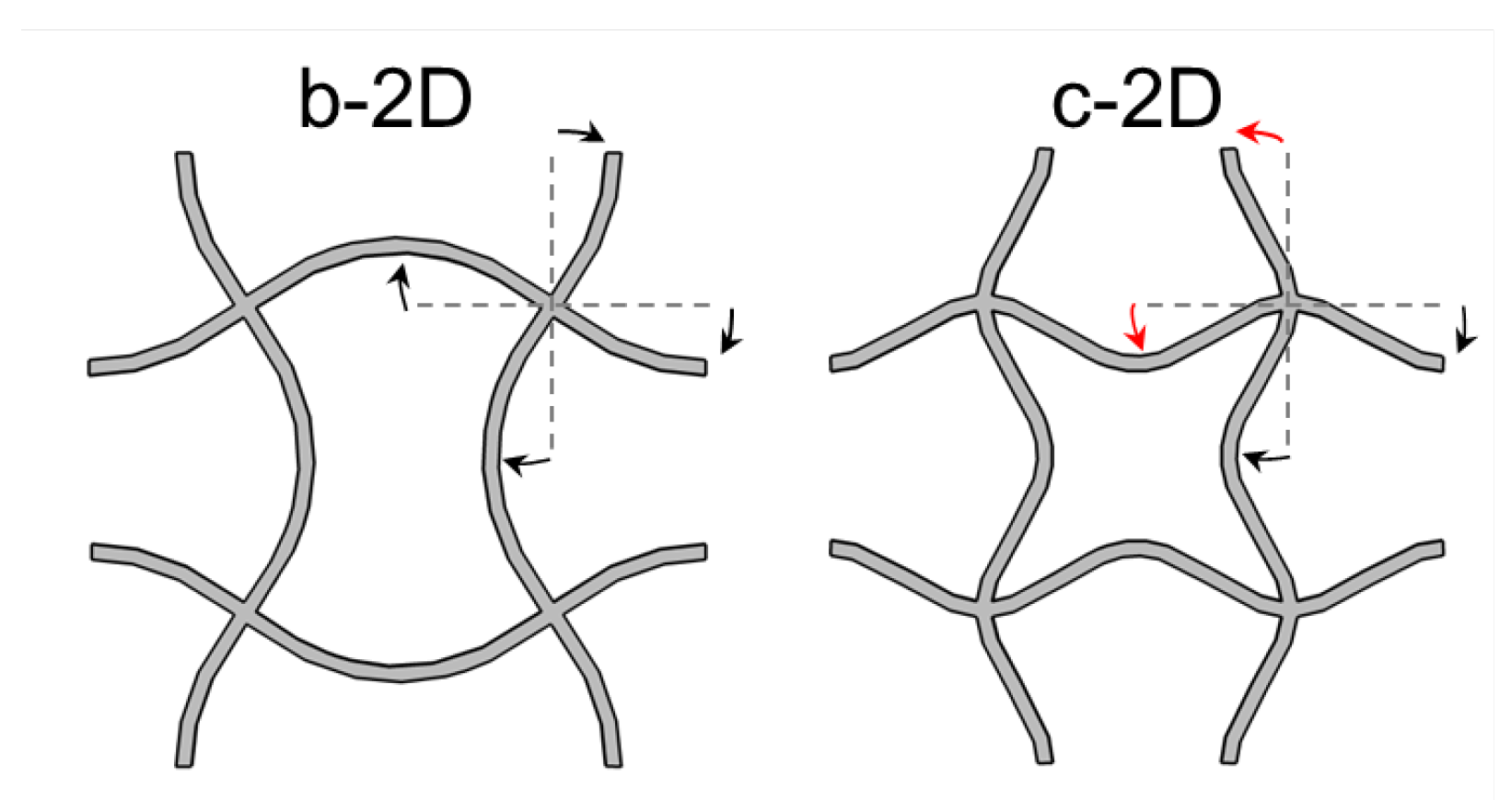
Figure 6a. The eigenmode at the lower edge of the band gap can be described by an alternating translation of the two left or the two right nodal points, respectively. One pair of points moves towards each other and bends the connecting vertical strut further while the other pair of nodal points moves away from each other and unbends the connecting vertical strut between them to a plateau-like form. The two horizontal struts follow the motion of the two nodal points they connect.
Figure 5.
Dispersion relations of structure b-2D, the eigenmode with chiral nodal points (a); and structure c-2D, the eigenmode with fixed nodal points (l = 5.0 mm, A = 1.0 mm, d = 0.25 mm) (b).
Figure 5.
Dispersion relations of structure b-2D, the eigenmode with chiral nodal points (a); and structure c-2D, the eigenmode with fixed nodal points (l = 5.0 mm, A = 1.0 mm, d = 0.25 mm) (b).
Figure 6.
Eigenmodes at the lower and upper edge of the 1st band gap of structure b-2D (a) and c-3D (b).
Figure 6.
Eigenmodes at the lower and upper edge of the 1st band gap of structure b-2D (a) and c-3D (b).
The eigenmode at the upper edge of the band gap is a collective rotation of all nodal points in the same direction. The rotation direction changes between left and right while the nodal points stay fixed at their initial position all the time. The struts have to follow the rotation of the nodal points and bend. Körner and Liebold-Ribeiro showed in [
12] that their bent shape is comparable to the first anti-symmetric mode of a single strut with hinged-hinged boundary condition.
The dispersion relation of the c-2D structure is shown in
Figure 5b. Structure c-2D is the 8th eigenmode of structure a-2D (see
Figure 4). The different clamping of the nodal points in structure b-2D and c-2D due to the different form of the bent struts leads to different eigenfrequencies of the eigenmodes depending on the direction of the incoming wave. This is reflected in the different form and density of the dispersion branches in
Figure 5a,b. Now, eight band gaps of different sizes are showing up in the same range of frequencies as in
Figure 5a. The first band gap occurs also between the 8th and 9th dispersion branch. While the lower frequency of the band gap is lower compared to structure b-2D, the size of the band gap is much larger. The corresponding mode shapes are depicted in
Figure 6.
Again, the eigenmode at the lower limit of the band gap is a translation of nodes. All four nodal points move towards each other into the middle of the unit cell. The struts follow this movement by bending. Then, all nodal points move away from each other and stretch the sines in the struts so that they get unbent. As for structure b-2D, the eigenmode at the upper edge of the band gap is a collective rotation of the fixed nodal points to the left and then to the right.
3.2. 3D Quadratic Unit Cells
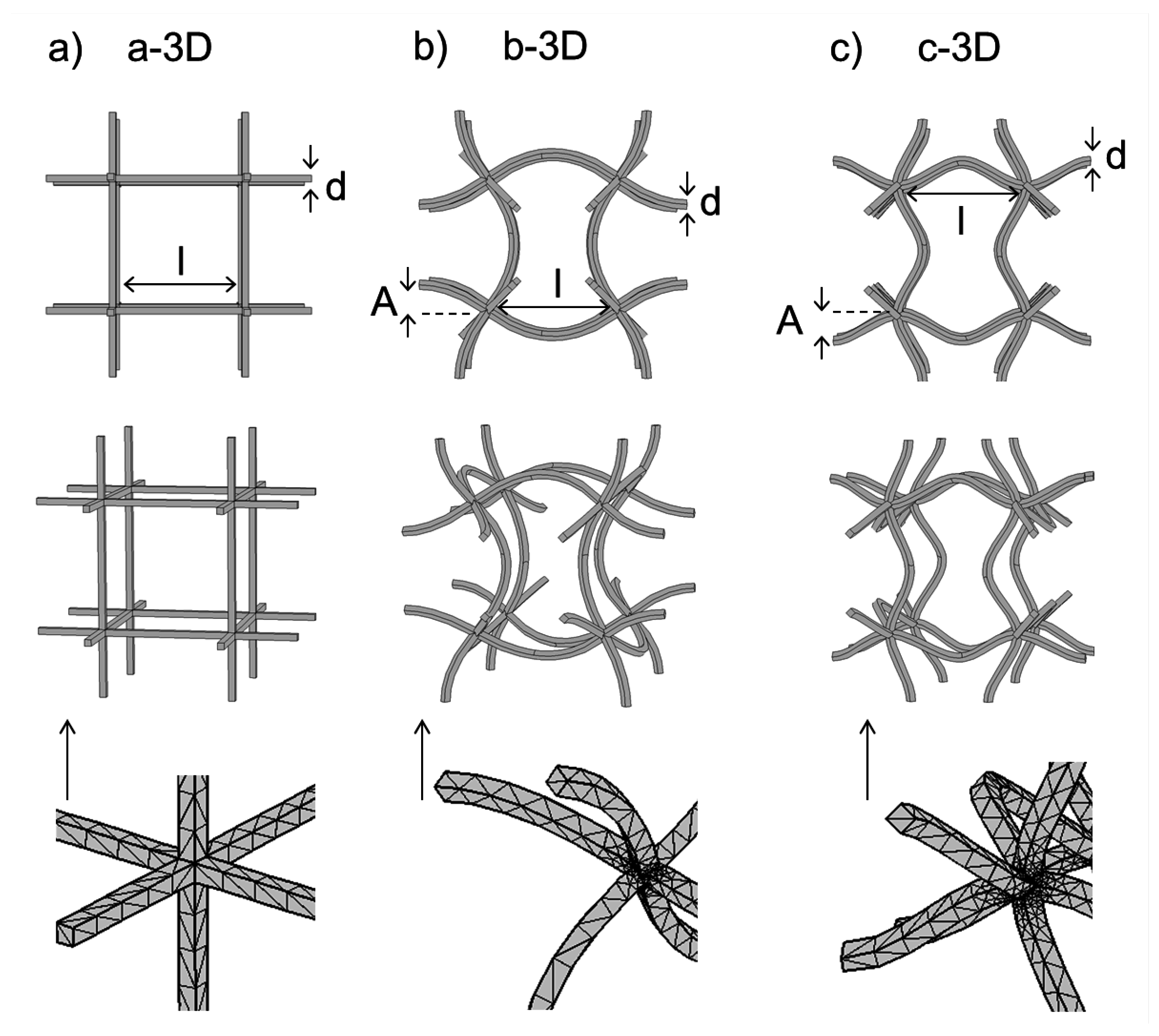
The dispersion relation for the a-3D quadratic three-dimensional unit cell is shown in
Figure 7a. The eigenfrequencies are normalized with
(see Equation
3) and plotted in dependancy of the position in
-space on the path Γ-X-M-R-Γ (see
Figure 1). No band gap is present. As movements in z-direction are now allowed, in the same range of frequencies, the number of dispersion branches strongly increases compared to the regular two-dimensional structure (see
Figure 4).
For the b-3D structure, a small band gap emerges (see
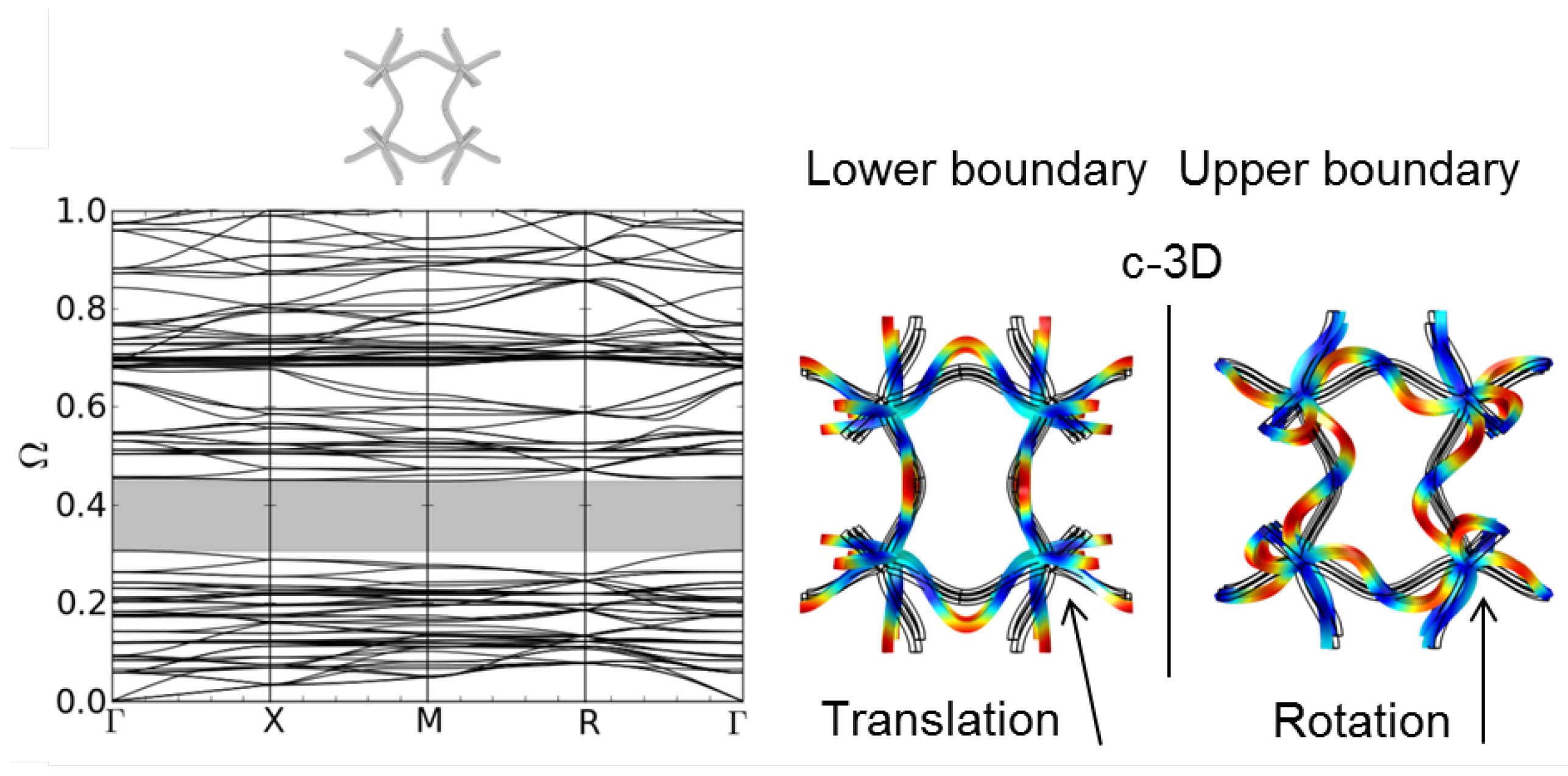
Figure 7b). Finally, the c-3D structure shows a pronounced gap at low frequencies (see
Figure 8). The corresponding mode shapes at the lower and upper edge of the band gap can be seen in
Figure 8. As in 2D, the mode shapes can be explained by a translation rotation of the nodal points, respectively. The different clamping of the nodal points in structure b-3D and c-3D due to the different form of the bent struts leads to different eigenfrequencies of the eigenmodes depending on the direction of the incoming wave. This is reflected in the different form and density of the dispersion branches in
Figure 7b and
Figure 8.
Figure 7.
Dispersion relations of structure (a) a-3D (l = 5.0 mm, d = 0.25 mm); and (b) b-3D (l = 5.0 mm, A = 1.0 mm, d = 0.25 mm).
Figure 7.
Dispersion relations of structure (a) a-3D (l = 5.0 mm, d = 0.25 mm); and (b) b-3D (l = 5.0 mm, A = 1.0 mm, d = 0.25 mm).
Figure 8.
Dispersion relations of structure c-3D (l = 5.0 mm, A = 1.0 mm, d = 0.25 mm) and corresponding mode shapes at the lower and upper boundary of the first band gap.
Figure 8.
Dispersion relations of structure c-3D (l = 5.0 mm, A = 1.0 mm, d = 0.25 mm) and corresponding mode shapes at the lower and upper boundary of the first band gap.
3.3. Variation of the 2D Unit Cell Dimensions
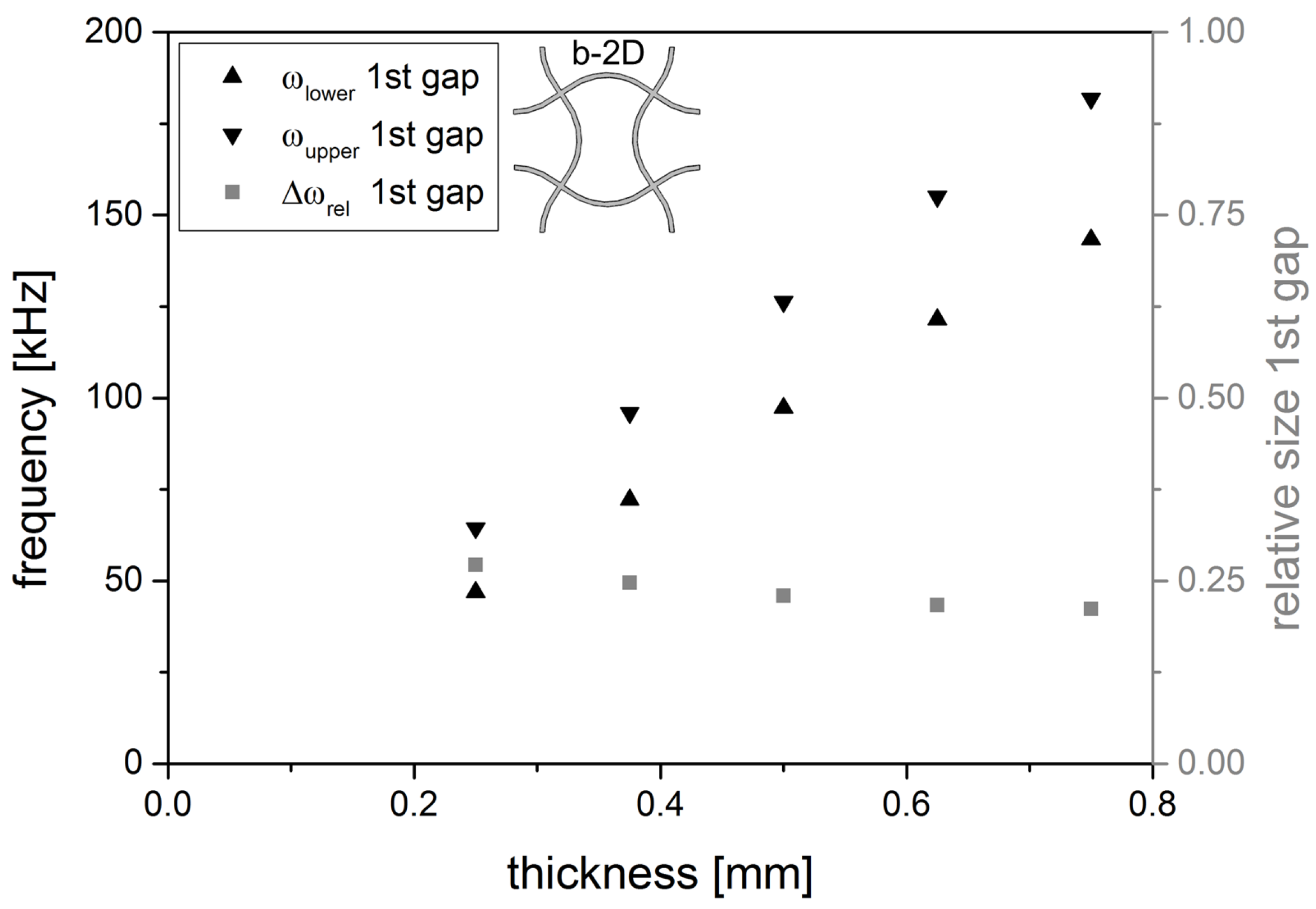
The band gap is also influenced by the dimensions of the unit cell. When changing the thickness of the struts of structure b-2D, the upper and lower frequency of the band gap is shifted to higher frequencies (see
Figure 9). The thicker the strut, the stiffer the structure, the more difficult is the excitation of natural resonances. To get a measure for the size of the band gap, the relative size
of the band gap is calculated as
with
being the lower or upper limiting frequency of the band gap respectively.
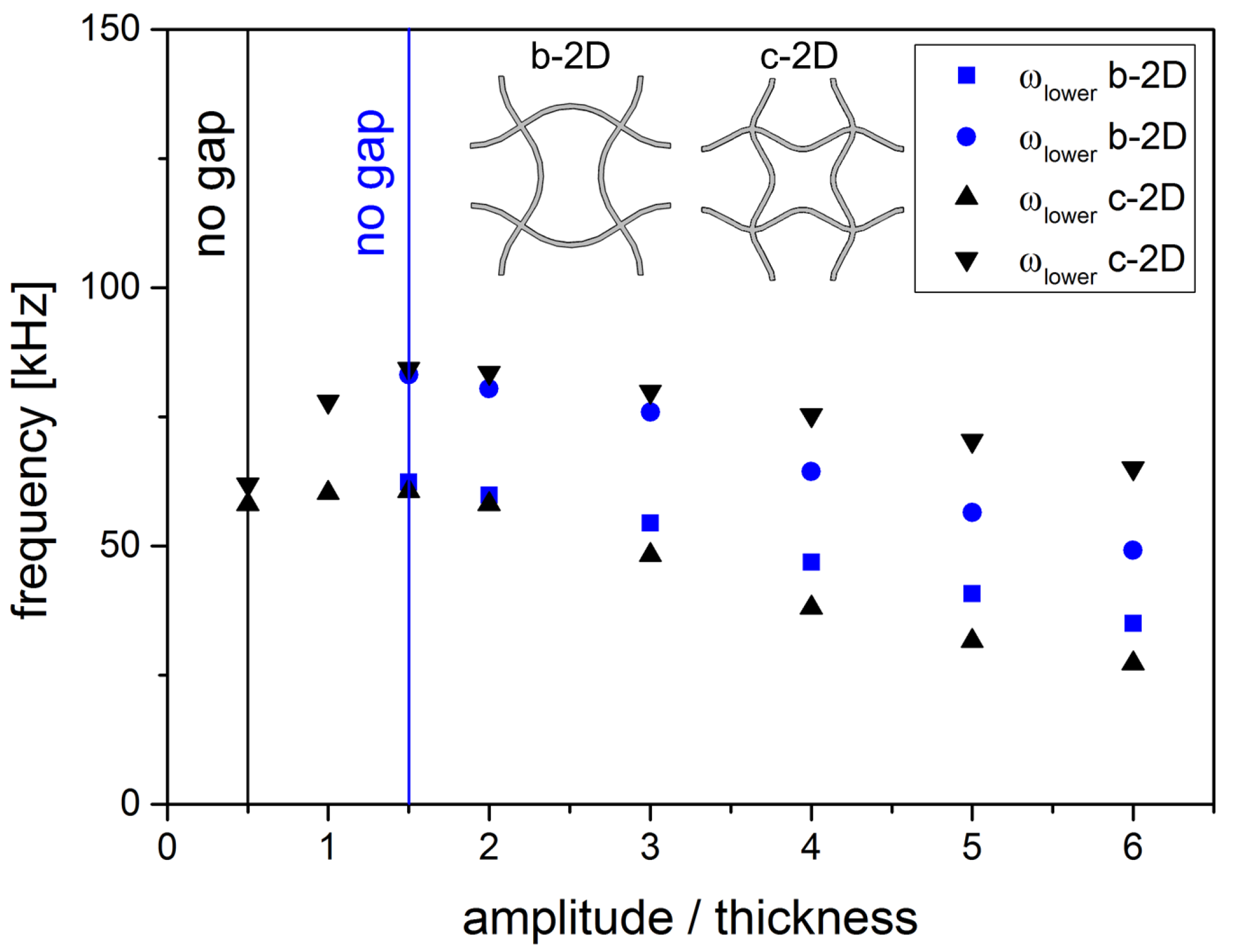
The dependancy on the second parameter of the structure, the amplitude of the sine, can be seen in
Figure 10 where the upper and lower frequency of the band gaps for structure b-2D and c-2D for increasing ratios of amplitude to thickness are shown. For both structures, a certain amplitude is needed to open the band gap. In structure b-2D, the gap emerges at a relative amplitude larger than
. Once the band gap is opened, the limits of the band gap decrease and approach each other with increasing amplitude. In structure c-2D, the relative amplitude needs to be higher than
. In the beginning, the band gap is quite small but grows with increasing amplitude while the upper and lower limits of the band gap are shifted to higher frequency values at the same time. For relative amplitudes
, the band gap width still increases, but the upper and lower limits of the band gap decrease. The frequency of the lower limit decreases faster than that of the upper limit. Thus, the width of the band gap grows with increasing amplitude A.
Figure 9.
Lower and upper frequency of the 1st gap of structure b-2D as a function of the strut thickness (l = 5.0 mm, A = 1.0 mm) as well as the relative size of the 1st band gap.
Figure 9.
Lower and upper frequency of the 1st gap of structure b-2D as a function of the strut thickness (l = 5.0 mm, A = 1.0 mm) as well as the relative size of the 1st band gap.
Figure 10.
Upper and lower frequencies of the 1st band gap for structure b-2D and c-2D in dependancy of the amplitude A (l = 5.0 mm, d = 0.25 mm).
Figure 10.
Upper and lower frequencies of the 1st band gap for structure b-2D and c-2D in dependancy of the amplitude A (l = 5.0 mm, d = 0.25 mm).
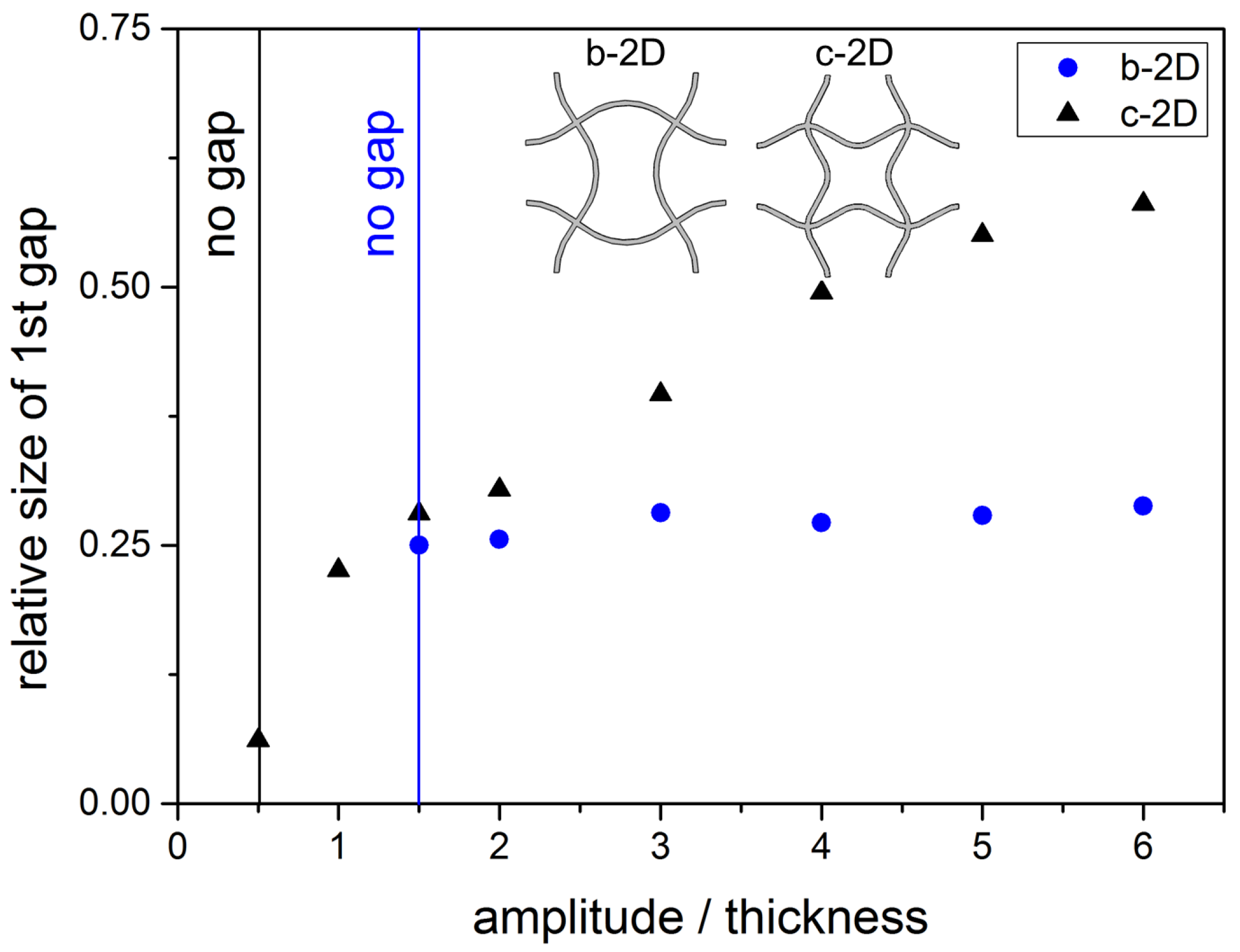
This behaviour is illustrated in
Figure 11 where the relative size of the band gap is plotted against the relative amplitude, the ratio of amplitude to thickness. The relative size is calculated according to Equation
4. For structure b-2D, once the band gap is open, the relative size stays approximately constant. For structure c-2D, two zones are visible: For A
, a steep increase of the relative size of the band gap can be seen. For A
, the growth of the relative size is less steep.
Figure 11.
Relative size of the 1st band gap for structure b-2D and c-2D in dependancy of the amplitude A of the bent struts (l = 5.0 mm, d = 0.25 mm).
Figure 11.
Relative size of the 1st band gap for structure b-2D and c-2D in dependancy of the amplitude A of the bent struts (l = 5.0 mm, d = 0.25 mm).