It has been shown that uncertainty spreads all over the sliding stability model, including geotechnical aspects related with strength parameters, but also operational, maintenance, monitoring and inspection issues related with drainage system performance and water level in the reservoir. In this context, risk analysis is an attractive option to deal with safety issues. Risk analysis uses the concept of probability as a measure of uncertainty, so reliability-based approaches are incorporated into risk analysis.
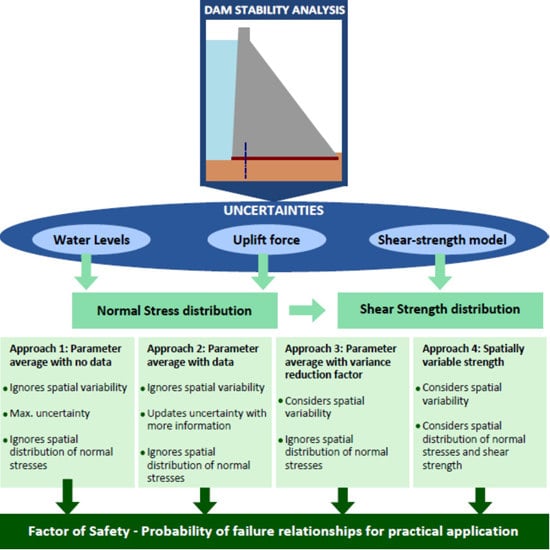
3.1. Approach I—Parameter Average with No Data
The first approach considers average values for strength parameters over the failure surface under the hypothesis of lack of on-site specific data, thus allowing for high levels of uncertainty on the probability distributions of such average parameters. This approach assumes average values of friction coefficient, tanφ
contact, and cohesion,
cohcontact, for the whole contact plane. In the absence of specific, on-site data, characteristic values of strength parameters are proposed by the engineer based on his/her own experience or published data of dams with similar characteristics and geology features. Then, a factor of safety against sliding is calculated. The characteristic values shall be selected as cautious estimates of the value affecting the occurrence of the limit state, thus the characteristic value is normally a prudent estimate of the average value on the failure surface, not a particular fractile of the test results. According to Eurocode 7 [
23], the calculated probability of a worse value governing the occurrence of the limit state under consideration should not be greater than 5% [
24].
Under a reliability perspective, we are interested in the assessment of the probability associated with such average strength parameters. Assuming probabilistic normal distributions and independence, we have Equations (5) and (6). The use of normal distributions has its limitations derived from the unbonded tails and possibility of negative values without physical meaning. Nevertheless, for the sake of simplicity and to keep the focus on the comparison of different approaches and not on the discussion of probability distributions the normal probability distribution is used.
where μ[tanφ
contact] is the mean and SD[tanφ
contact] is the standard deviation of the friction coefficient for the whole contact plane, while μ[
cohcontact] is the mean and SD[
cohcontact] is the standard deviation of cohesion for the whole contact plane.
It is assumed that at any point on the failure surface, the local strength parameters are realizations of a random field where μ[tanφlocal] is the mean and SD[tanφlocal] is the standard deviation of local friction coefficient, while μ[cohlocal] is the mean and SD[cohlocal]) is the standard deviation of local cohesion. These probabilistic parameters are the same at each point of the failure surface. If probabilistic normal distributions are assumed for local friction coefficient, tanφlocal, and for local cohesion, cohlocal, and assuming that they are statistically independent, uncorrelated random values, then we have Equations (7) and (8).
In the absence of information on spatial variability, which can be expressed in the form of correlation distances or scale of fluctuation, the approach followed in this case of no information is to let the average values to vary over the full range of variation of the local strength parameters, as shown in Equations (9)–(12).
Conceptually, this approach assumes that the average strength parameters for the whole contact plane may take any value randomly extracted from the full range of variation of the local strength parameters. This approach assumes maximum uncertainty on strength values, and it is equivalent to consider an infinite scale of fluctuation of strength parameters in relation to the extension of the failure surface. The calculation of the factor of safety is carried out selecting a cautious estimate of the value of the corresponding strength parameter. Following Eurocode 7 [
23] and in the absence of data we will use the 5% fractile as the characteristic value.
The calculation of the probability of failure is carried out using the full probability distributions defined in Equations (5) and (6), with a Monte Carlo based methodology [
25] that incorporates the limit state curve concept.
3.2. Approach II—Parameter Average with Data
The second approach uses also average values for strength parameters over the failure surface, but incorporates a reduction on uncertainty as more information is added to the analysis. Under a reliability perspective, we accept that data of local strength values represent realizations of random values from their independent, uncorrelated normal probability distributions, according to Equations (7) and (8). We are assuming that local strength parameters vary spatially over the whole contact plane so they can be described by Gaussian random fields. In this context, strength data are understood as realizations of Gaussian random fields, so they are normally distributed.
We have a number of observations, n, of friction coefficient and cohesion. The mean of the observed values for both parameters is, respectively, and . The mean of the observed values is an estimator of the expected value of the population and it is normally distributed, with parameters given by Equations (13)–(16).
Without other considerations, a first approximation relies on evaluating average strength parameter values in the contact by the mean values obtained with the n data, as shown in Equations (17)–(20).
An important underlying assumption needed is to accept that the on-site data are evenly distributed over the contact plane, being representative of different zones of similar extension, so we can express the probability distribution of average strength parameter values using the probability parameters of the n local strength values retrieved from tests. The expected value of the average is the mean of the probability distribution of local parameters and that the standard deviation of the average is reduced with respect the standard deviation of local parameters. Conceptually, this approach assumes that the average strength parameters for the whole contact plane are estimated using local strength parameters, and as more information is gained less room is left to variability. We will use the 5% fractile as the characteristic value to calculate the factor of safety. The calculation of the probability of failure is made in the same fashion described for Approach I.
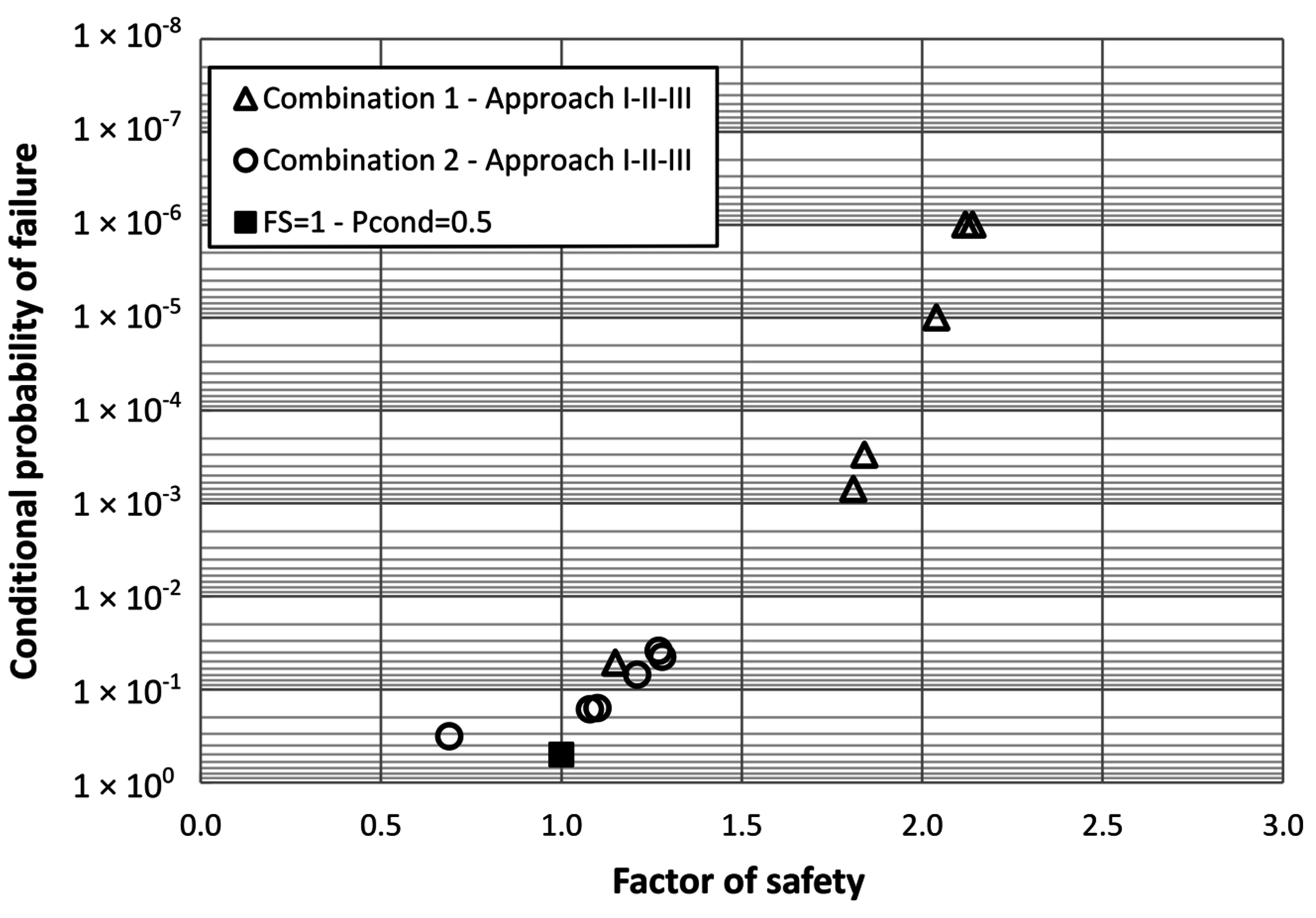
Approaches I and II applied to the analysis of the sliding problem under a reliability perspective are commonly used in risk analysis practice, and none of them takes into account the effect of spatial variability of strength parameters and strength forces.
3.3. Parameter Average with Variance Reduction Factor
The third approach considers also average values for strength parameters, but takes into account their spatial variability and relation to the extension of the failure surface using the variance reduction factor. One way to account for the spatial variability is using the approach proposed by Phoon and Kulhawy [
26], expressed by Equation (21).
where Г
S2 is the variance reduction factor, considering the spatial extent of the governing failure mechanism;
COVinher is the coefficient of variation of the parameter inherent variability;
COVmeas is the coefficient of variation of the measurement errors;
COVtrans is the coefficient of variation of the transformation errors; and
COVstat is the coefficient of variation of the statistical parameters.
The variance reduction function can be approximated by Equation (22) as proposed by Schneider and Schneider [
27].
where Г
X2 is the variance reduction factor in the horizontal direction
X, which is the upstream-downstream direction, and Г
Y2 is the variance reduction factor in the horizontal direction
Y, which the left-right direction of the failure surface. The variance reduction factor in a particular direction,
i, is calculated using Equations (23) and (24) which represent a simplification of Vanmarcke’s Equations [
28].
where
SOFi is the Scale of Fluctuation of the strength parameter in the direction i and
Li is the extent of the failure mechanism in the direction i. If
SOFi >
Li Equation (23) is used. If
Li ≤
SOFi then Equation (24) is used.
Assuming best standard practices in the testing procedure, then COVmeas ≅ 0. If a well-established model is used to transform measured test results into the required parameter, then COVtrans ≅ 0. Assuming that the probabilistic parameters that describe the statistical distribution are known, then COVstat ≅ 0.
Once the coefficient of variation has been estimated, the calculation of the new total standard deviation of strength parameters is straightforward, and the parameters of the new normal probability distributions are defined. We will use the 5% fractile as the characteristic value to calculate the factor of safety. The calculation of the probability of failure follows the same procedure as with Approaches I and II.
3.4. Spatially Variable Strength
The fourth approach does not consider average values for strength parameters, but evaluates shear strength locally taking into account parameter variability and the spatial variability of other influencing factors, such as the normal effective stress variability over the failure surface, and then sums local strengths to evaluate total strength. In this case, we assume that the local strength parameters are independent, uncorrelated random variables with spatial variation represented by random fields.
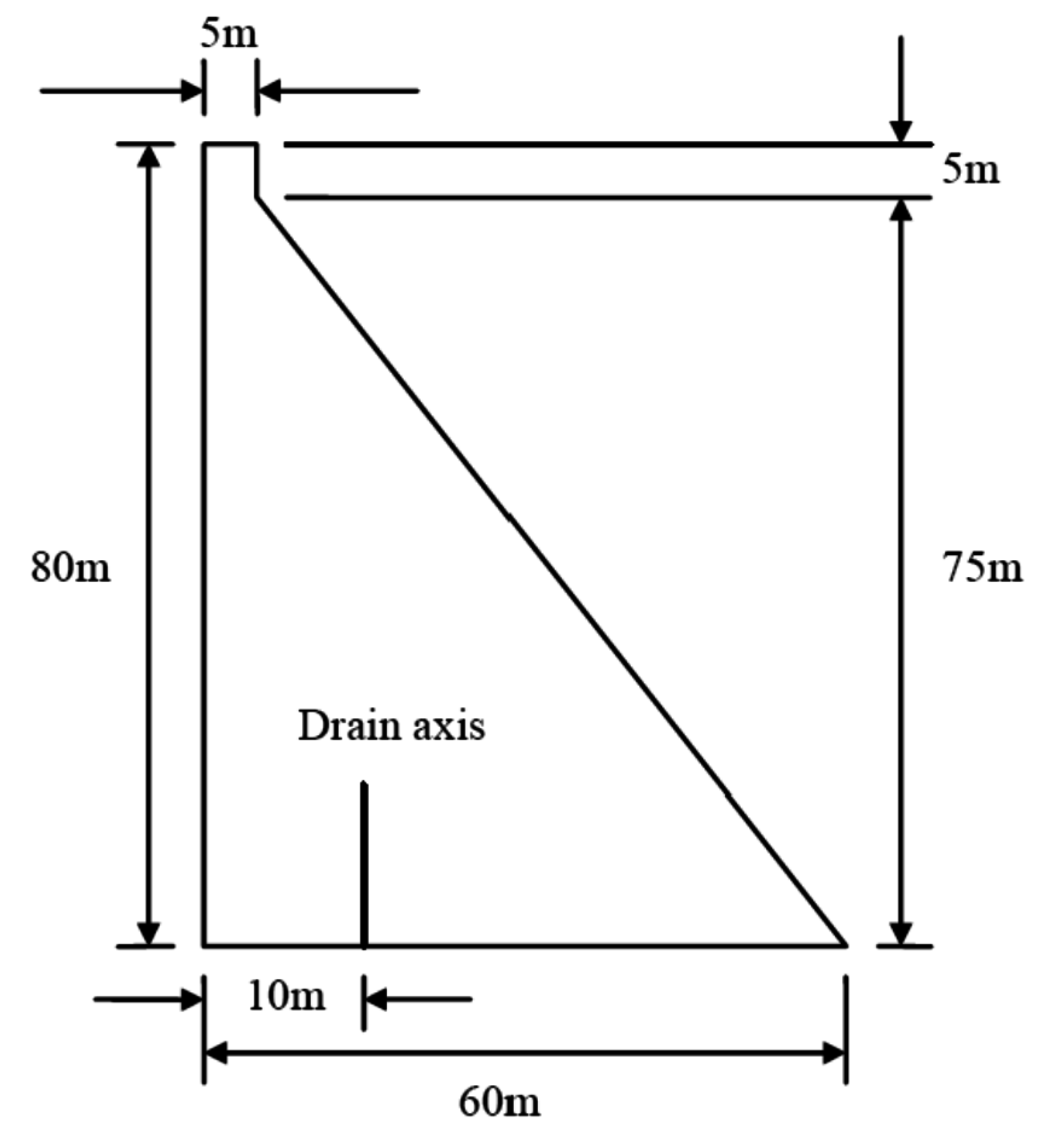
We consider the failure surface of length, L, and width, W, as a regular grid of I rows which follow the left-right direction and J columns in the upstream-downstream direction, dividing the surface into I × J = M cells. Each cell is a square, so W/J = L/I, and has an area s(i,j) = S/M, where S is the total area of the failure surface. The tensile strength that can be sustained by each cell, τ(i,j), is given by Equation (25).
where σ
′n(i,j) is the average normal effective stress acting on cell (i,j), tanφ(i,j) is the friction coefficient of cell (i,j),
coh(i,j) is the cohesion of cell (i,j) and δ(i,j) is the indicator function defined by Equation (26).
The sliding strength of each cell, r(i,j) is defined according to Equation (27).
And the total sliding strength along the failure surface, RS, is given by Equation (28).
As RS is the sum of M random variables normally distributed, it will be also normally distributed. Under the hypothesis of no spatial correlation in strength parameters, which means a null scale of fluctuation, the expected value, E[RS], and the variance, VAR[RS], can be estimated by Equations (29) and (30).
With the factor of safety defined by Equation (31) and the probability of failure, Pfail, defined by Equation (32), we can use the normal probability distribution of RS to estimate the probability of failure.
If there is spatial correlation in strength parameters, the Equations (29) and (30) cannot be applied, and a different strategy is needed. If we generate a set of i = 1, 2,.., N realizations of the random fields with a certain scale of fluctuation, SOF, for both coefficient of friction and cohesion, we will get a set of different N values of RS, and, in accordance, a set of different N values of the factor of safety, which is defined by Equation (33).
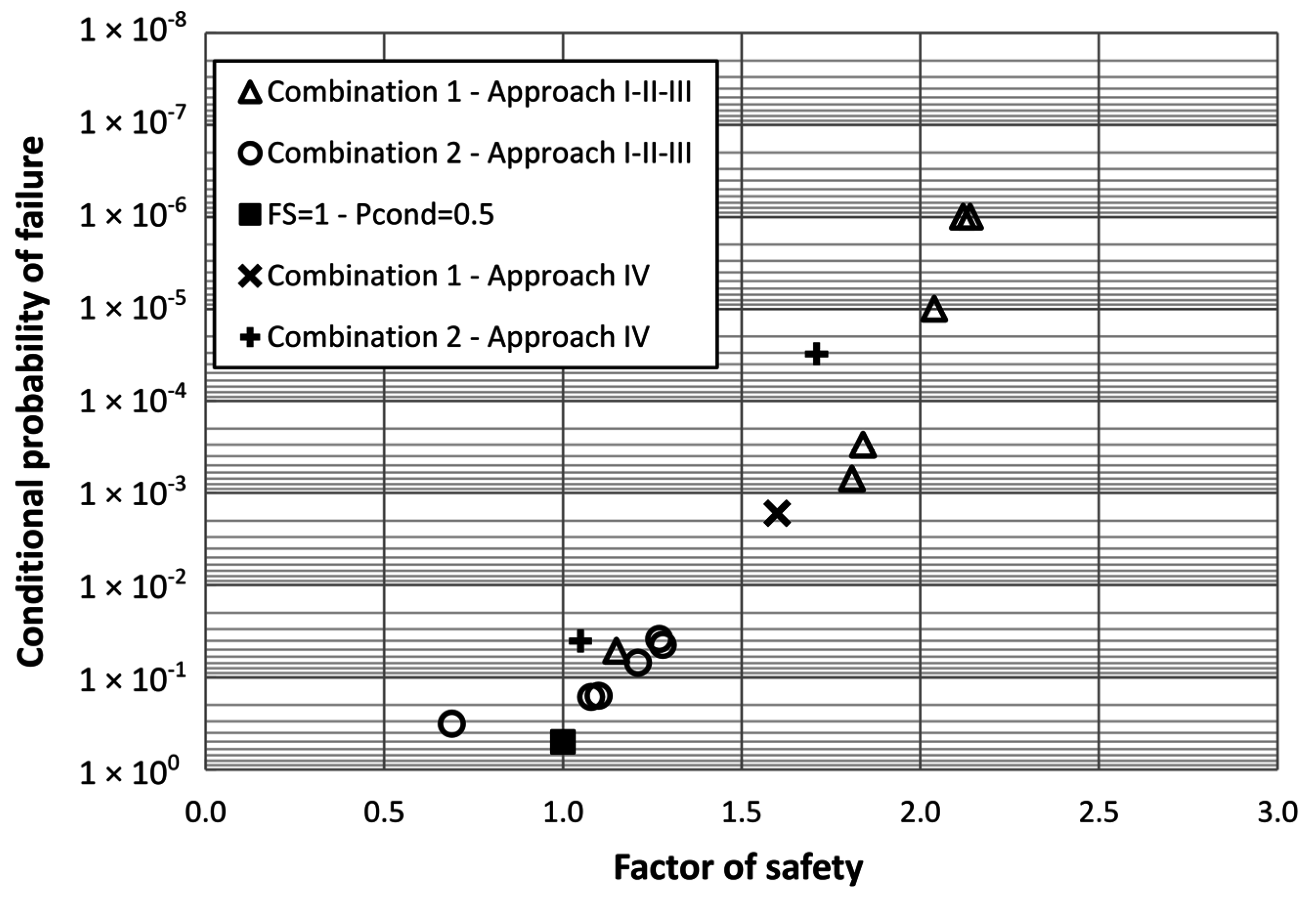
If a large number of random fields, N, is generated, then the probability of failure can be estimated as the ratio between the number of sets where FSi < 1, Nf, and the total number of sets, N. Obviously, to be able to capture low orders of magnitude of the probability of failure, a large value of N is needed. Another strategy to approximate the probability of failure is to calculate a shorter number of random fields, retrieve the FSi values, and calculate the expected value and the standard deviation of the sample of FS. Then, assuming that FS is normally distributed, the probability of failure can be calculated according to Equation (32). This latter approach is followed in this paper.
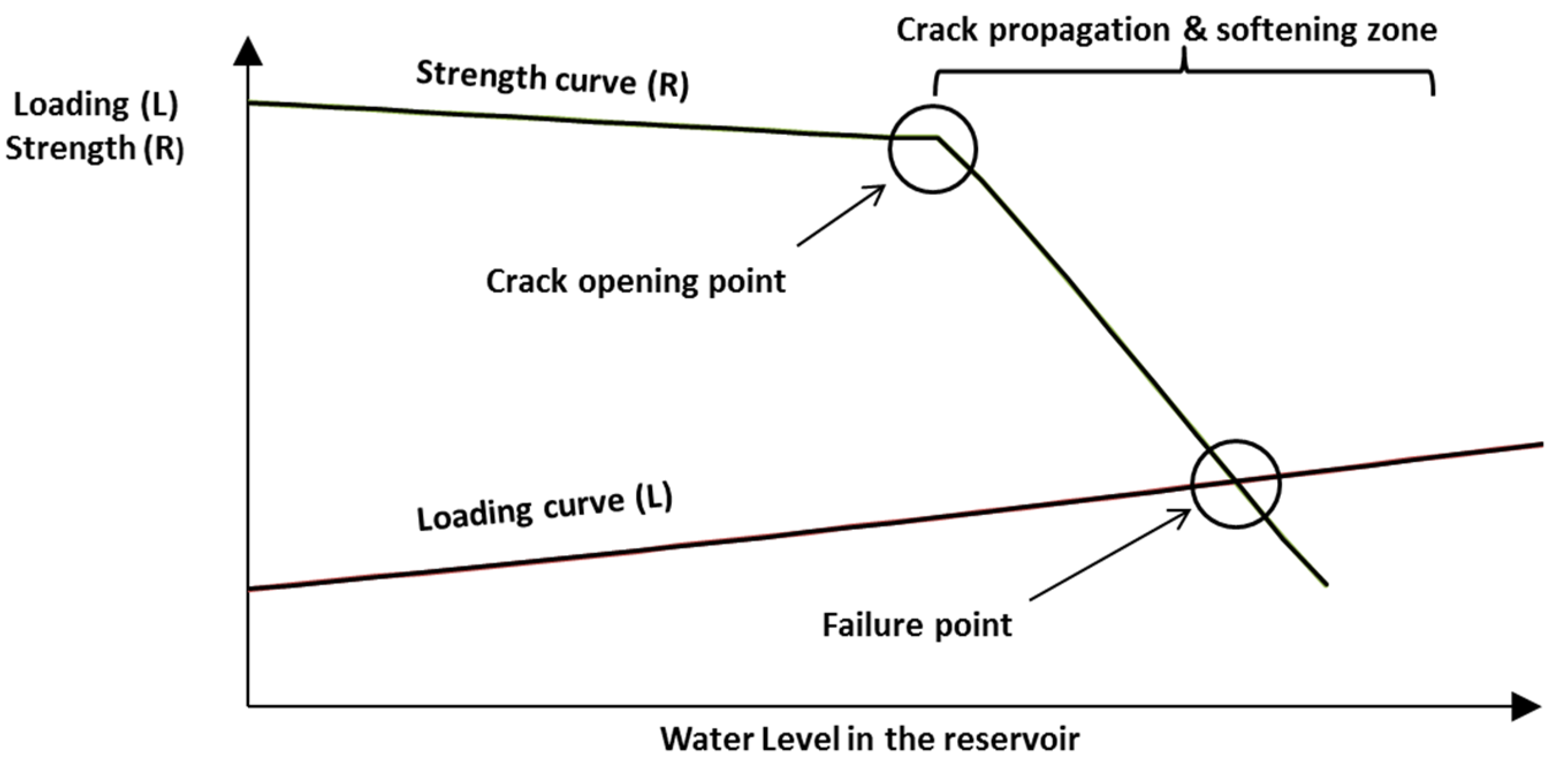
If we make the hypothesis that the distance of correlation of random fields is zero or close to zero, we are accepting that low local values will be compensated with higher local values occurring in the vicinity. If we consider a significant positive spatial correlation we get a different picture. Under this hypothesis of positive correlation distance, the cohesive part of the sliding strength still compensates lower values in some zones with higher values in other zones, but the frictional part of the sliding strength no longer exhibits such compensation effect. This is due to the asymmetrical distribution of compressive normal effective stresses along the contact plane. For typical pool water levels in the reservoir close to the maximum normal operation level or for higher levels under flood conditions the compressive normal effective stresses are higher at the downstream part of the contact plane and lower at the upstream part. Under some circumstances, even tensile effective stresses may develop at the upstream heel leading to the opening and propagation of a crack, changing the contact area under compressive stress even further.
A reliability analysis based on probability distributions of overall contact strength parameters cannot be carried out rigorously, because local effects and asymmetrical distribution of local strengths become important. A practical problem arises under this approach, which is the estimation of the correlation distance for each strength parameter. The assessment of this correlation distance or scale of fluctuation can only be gained with an extensive testing program, usually out of the scope of typical dam safety reviews.
However, the effect of the different scales of fluctuation over the factor of safety can be estimated by generating different stochastic realizations of the random fields and evaluating the variations of the factor of safety. Under a reliability perspective, a large number of realizations of the stochastic random fields are needed in order to evaluate the probability of failure in a Monte Carlo fashion.
Stationary Gaussian random fields have been generated with a tool developed at the University of Maryland [
29] for regular grids using an exponential correlation form of the covariance function.