1. Introduction
The widespread use of fasteners reflects their importance in various industries. Taiwan exported roughly 1.46 million tons of fasteners in 2013, with gross revenues reaching U.S. $4 billion to rank fifth in global fastener production. Both the quantity and the quality of fasteners from Taiwan contribute significantly to international markets. However, product innovation is increasingly difficult owing to price competitiveness from China and Southeast Asian countries and to the increasing complexity of emerging products. Fortunately, recent collaborative ventures between academia and industry allow for designers, who require 5–10 years of training, to receive knowledge, expertise and a theoretical foundation through industry-university cooperation. With comprehensive curriculum planning and the introduction and training of operating skills, the practical experiences of designers are combined with a theoretical knowledge of graphics and simulation software, which is then cross-referenced and mutually verified to improve a project. Moreover, peer involvement stimulates manufacturing skills, simplifies the product development schedule, reduces overhead costs and increases industrial competitiveness.
Wear, such as friction loss, erosion and fatigue, commonly damages machine elements. Wear appears between objects when friction causes continuous material peeling and loss. Die wear is of priority concern in manufacturing, because it lowers the quality of work pieces, reduces die life and raises processing costs. Metal forming die wear research largely adopts the Archard wear model [
1], which assumes that the wear volume generated over a sliding distance is related to the contact area in order to derive the wear equation and to study the effects of processing parameters on metal fabrication wear. Based on finite element analysis, Vardan
et al. [
2] examined die wear in rough forging and discussed friction mechanisms during metal forming. Wibom
et al. [
3] studied the rising temperature caused by friction and the effects of lubricating conditions on die wear and life. Based on finite element analysis, Lee
et al. [
4] predicted die life during bolt forming and proposed empirical formulas for fatigue failure and wear. According to their results, the fatigue failure mode should be applied to evaluate the die life of high-tensile cold forging steel, while the wear model could be used for evaluating low tensile cold forging steel. Furthermore, several studies on the simulation of cutting die wear discussed wear parameters. Yen
et al. [
5] evaluated wear with the parameters of metal cutting tools (e.g., cutting temperature, contact stress and relative sliding speed), indicating that such parameters play major roles in tool wear. Dubar
et al. [
6], Bouzakis
et al. [
7] and Filice
et al. [
8] also analyzed wear in coated cutting tools. Stavropoulos
et al. [
9] investigated the limitations of tool wear prediction on the milling of CGI 450 plates through the simultaneous detection of acceleration and spindle drive current sensor signals. Their results indicate that predictability is affected by the mean signal energy acquired from vibration acceleration signals.
It has become a common trend in recent years to use computer aided analysis software FEM (DEFORM-3D) for the development of metal forging processes. Its introduction into the design and production of fastener dies could effectively shorten product development time by reducing the number of die tests and test failures. Vazquez
et al. [
10] summarized an investigation of different alternatives for improving the life of a tungsten carbide insert used in a cold forming operation performed on an automatic cold header. Their analysis of metal flow and stress on the carbide insert used FEM software to improve insert life. Vazquez and Altan [
11] also combined computer aided engineering with physical modeling for applications with cold forging connecting rods. Modifying the forming process based on DEFORM analysis software results, production costs were effectively reduced, tolerance decreased and die life enhanced. Moreover, flow defects generated during product fabrication were predicted for further improvement. Falk
et al. [
12] applied Finite Element DEFORM software to propose a method correlated with forging volume, which easily and accurately predicted cold forging die life and was verified with experiments. Joun
et al. [
13] presented an application-oriented finite element approach to forging die structural analysis. The die set structural analysis problem was formulated as a contact problem considering both shrink fit and preloaded clamping, solved iteratively by a varying penalty method. Hsia [
14] used FEM DERORM-3D software to simulate the 3C micro-pin forward extrusion and forging process. His study simulated the forward micro-extrusion of a workpiece, discussed the differences between the simulated stage process and the experimental process and determined effective stress-strain and material flow properties after extrusion, as well as the upper punch reaction when the material was formed. This was used as the evaluation standard for designing an upper punch and determining the strength of a die structure. Hsia and Chou [
15] used computer simulations to analyze the fabrication of hexagonal nuts, and experimental metallography and hardness values were used to understand the cold forging characteristics of hexagonal nuts. Their research provided the information needed to understand forging loads and forming conditions at various stages before fastener formation. Han and Lin [
16] utilized finite element (FE) methods to predict die and workpiece wear during cold rotary forging by systematically investigating contact pressure and contact slip distance. Consequently, new insight into the wear that occurs at the surfaces of dies and workpieces was gained based on Archard’s wear law.
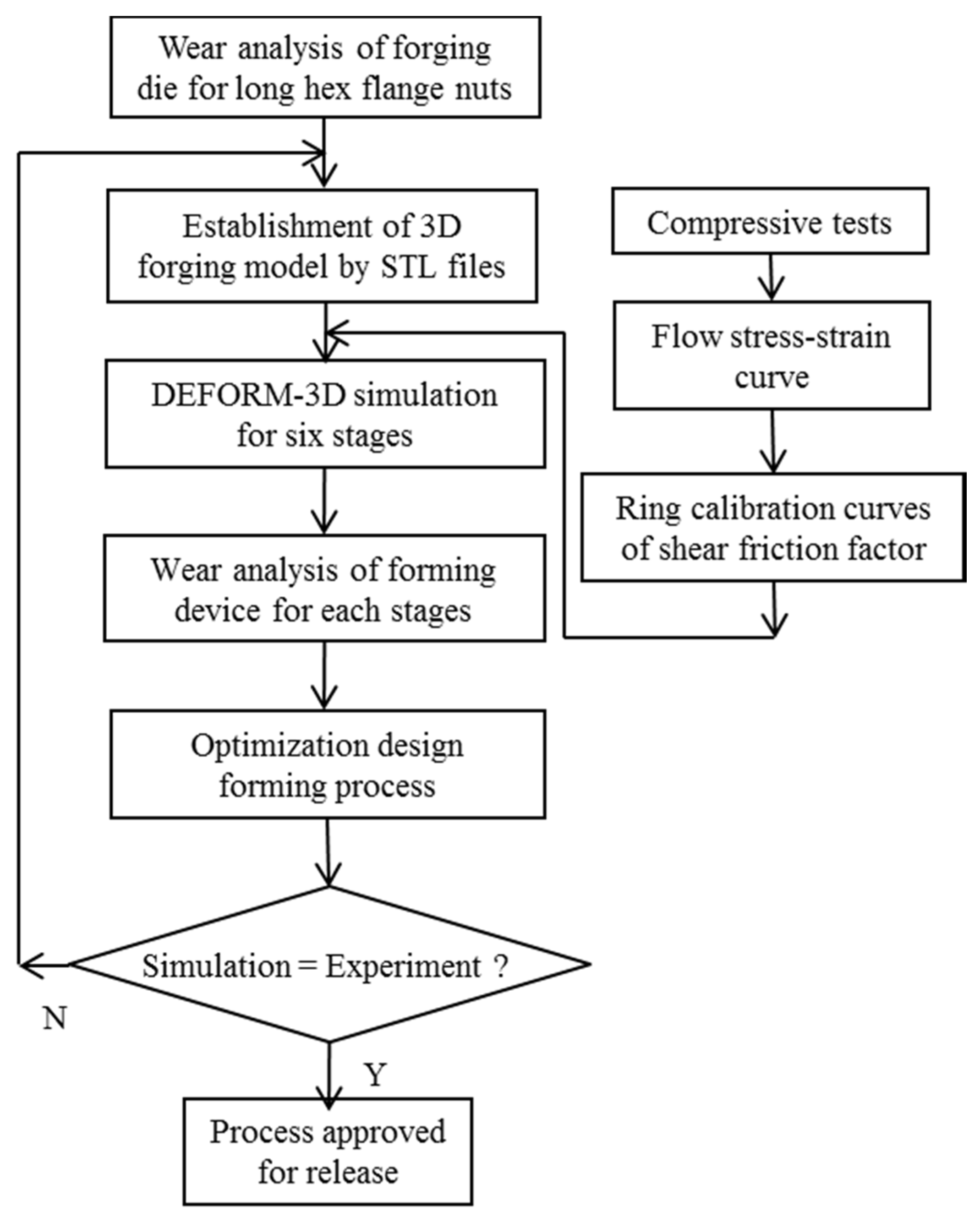
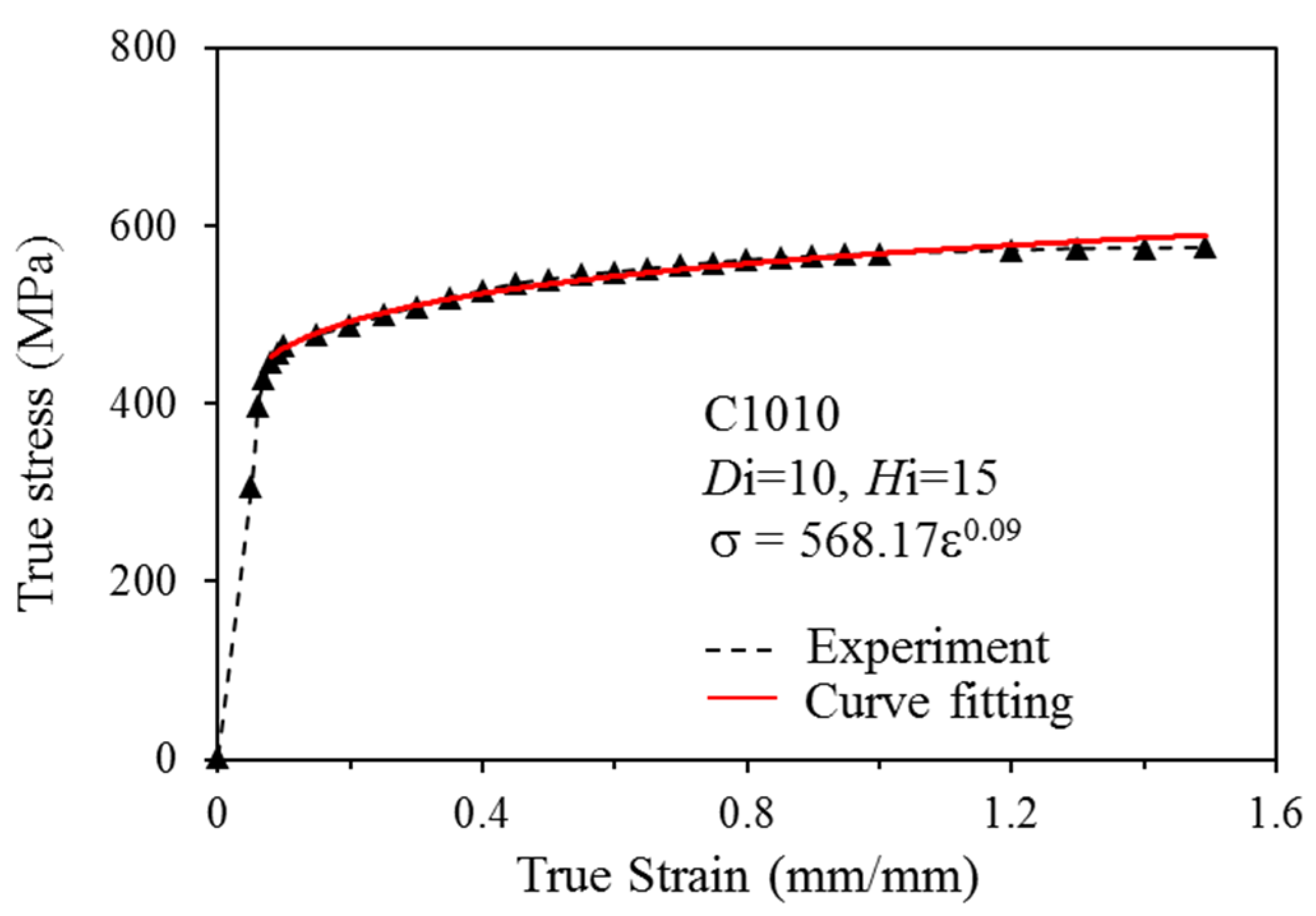
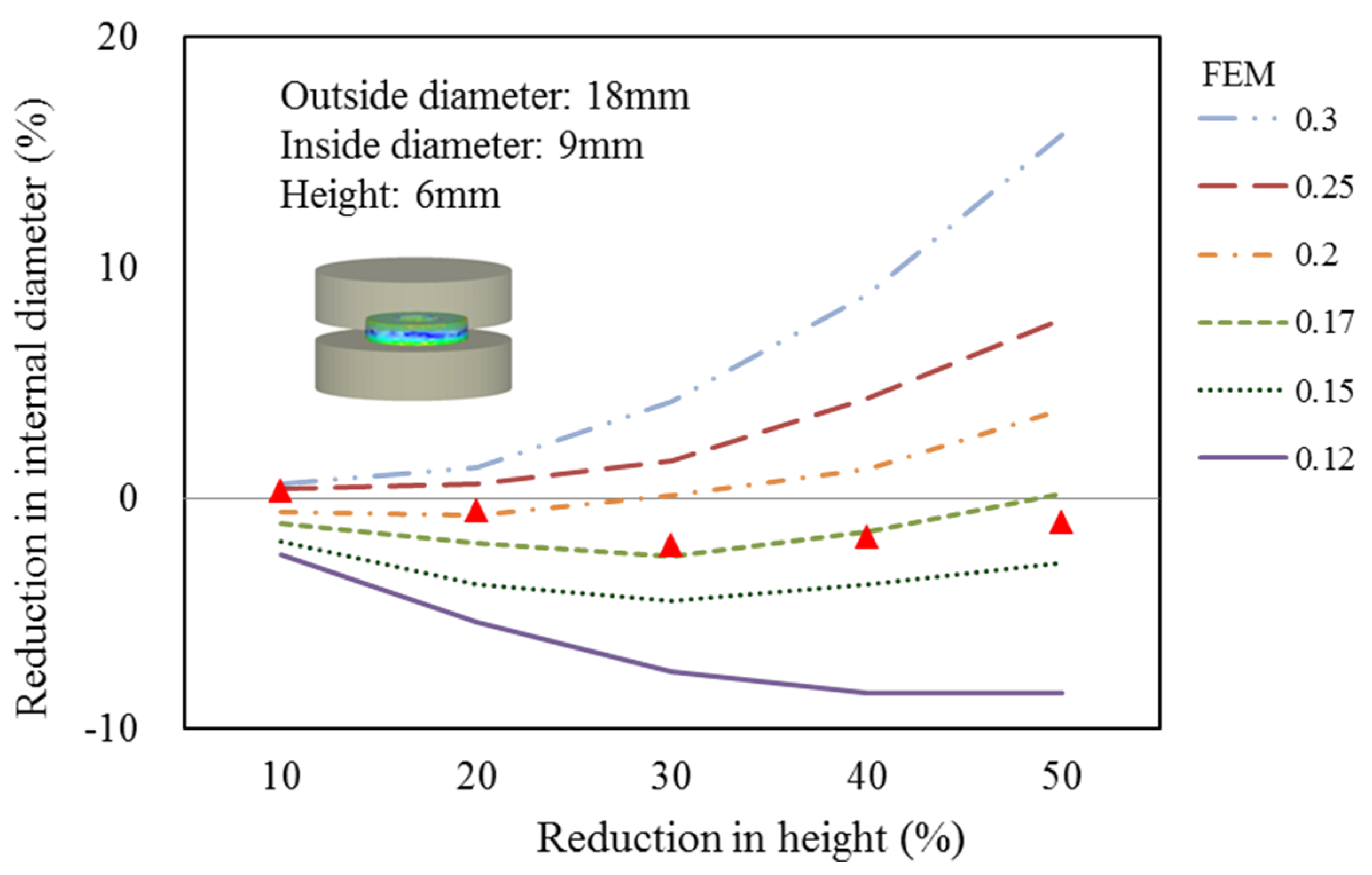
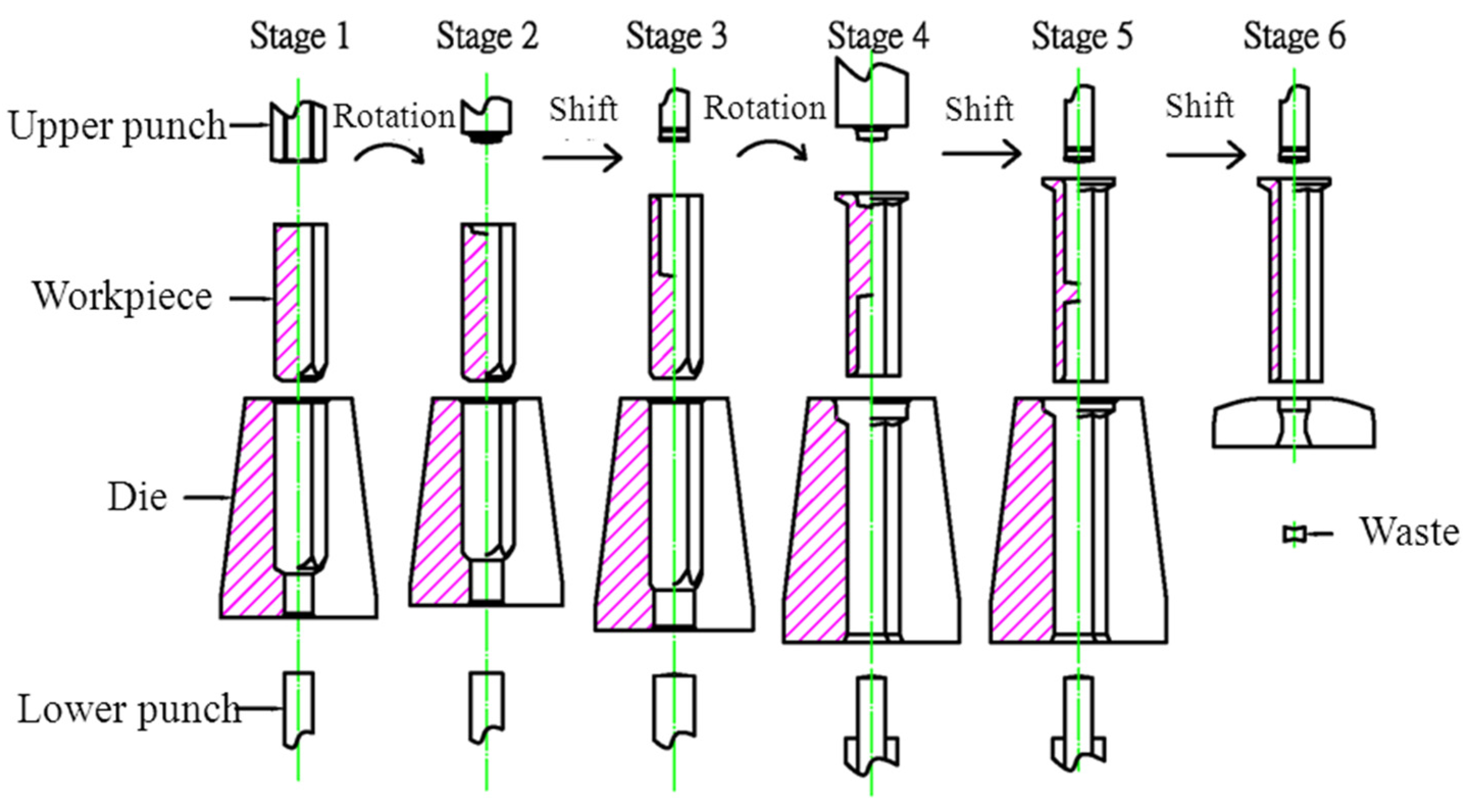
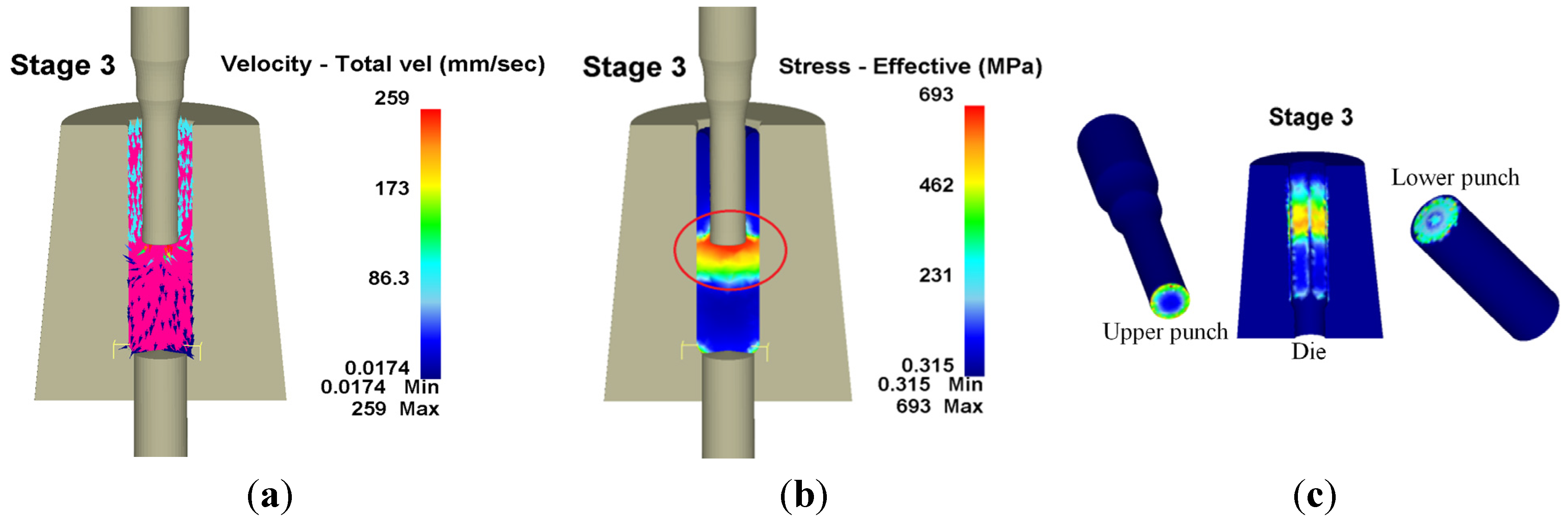
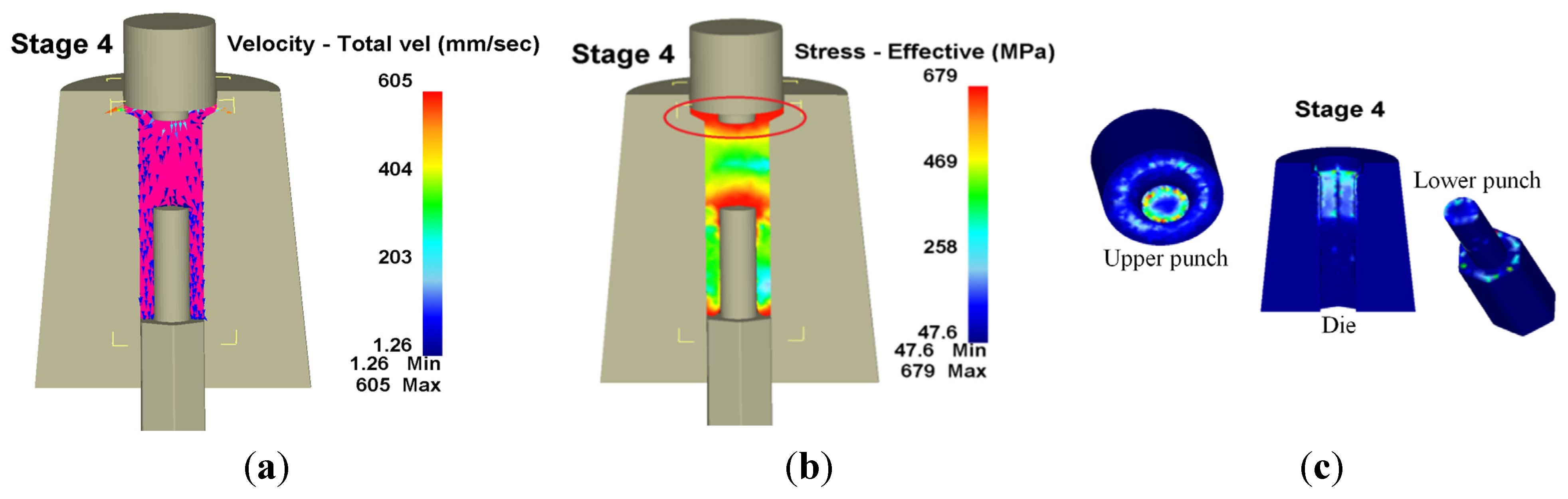
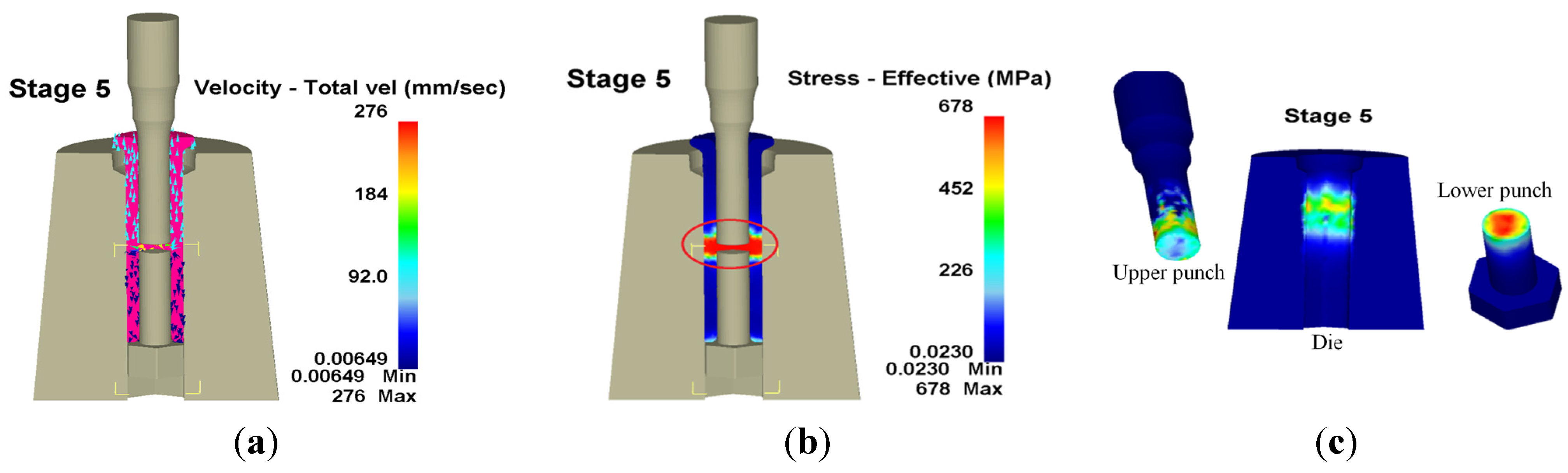
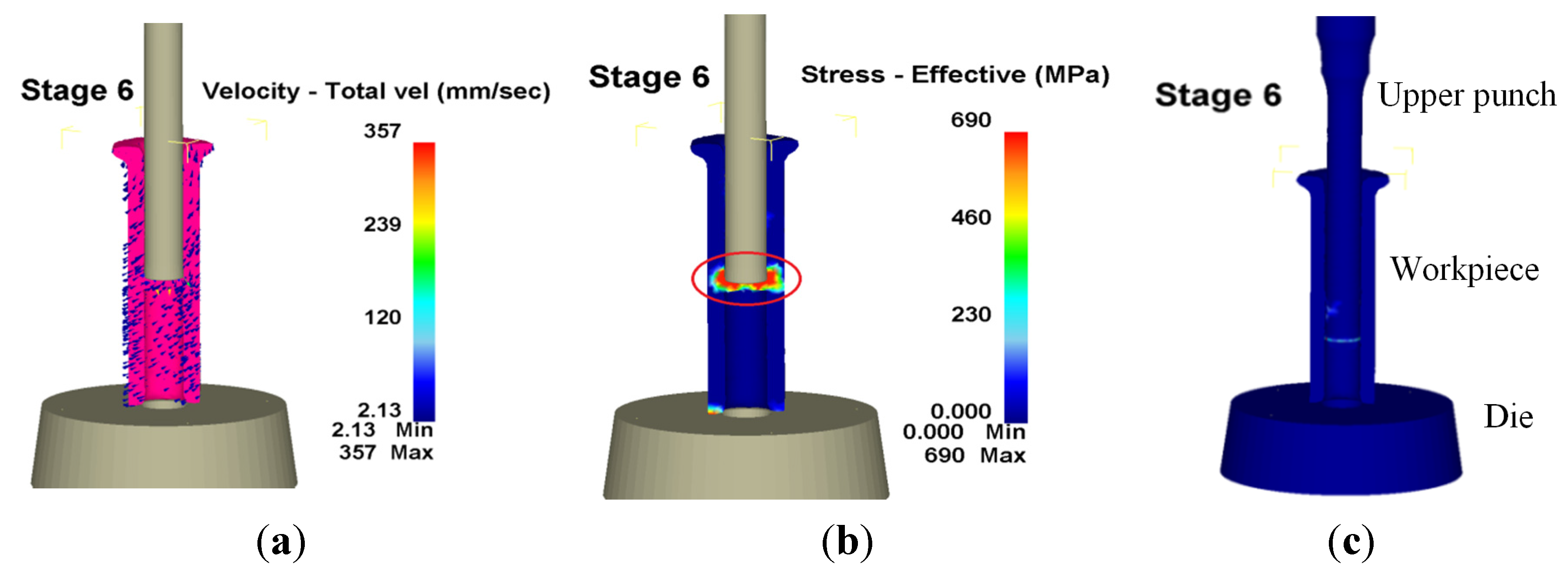
Many studies have focused on the wear model used in tool design and computer software utilized in the analysis of metal forming processes. However, since the operative wear regime cannot be accurately predicted in a manufacturing process, few scholars have explored wear mechanisms at the interface between tool and workpiece. This results in operator experience and trial and error being subjective and unreliable in the fastener industry. By using computer-assisted product design software and computer-assisted metal forming software in the analysis of long hex flange nuts, this study investigated the major parameters required for die design and stress distribution in a workpiece. Different specimens were used in experiments to evaluate the flow stress-strain curve and friction coefficient. Moreover, based on DEFORM-3D finite element analysis, the production of long hex flange nuts was simulated to determine metal flow, stress distribution, load conditions and optimal wear conditions in order to select optimal die materials and relevant equipment during the primary stage of product development. Finally, multistage serial forged products were used to verify the accuracy of our numerical analyses, and SEM micrographs of the worn surfaces on the upper punch indicate that the primary wear mechanism on the cold forging die for long hex flange nuts was adhesive wear. Consequently, simulations verified by actual fabrication can simplify the development schedule for the entire process, reduce the number of trials and further enhance production quality and die life.