3.1. Material Constitutive Models
The damage plasticity model from the ABAQUS software was applied to simulate the concrete constitutive law. The stress-logarithmic strain relationship of concrete in code GB50010-2010 [
30] was used here. The test values were obtained by the concrete cylinder compression test, and Poisson’s ratio was taken as 0.2.
The stress-strain curve of a standard concrete cylinder subjected to a uniaxial compression is solved mathematically by Equation (5):
where α
c is the coefficient at the descent stage of the uniaxial compression stress-strain curve of concrete,
fc,r is the representative value of uniaxial compressive strength of concrete,
εc,r is the peak compressive strain of concrete corresponding to
fc,r and
Ec is the elastic modulus of concrete. In the numerical simulation, α
c = 0.74,
fc,r = 13.4 MPa, ε
c,r = 0.00133 and
Ec = 2.55 × 10
4 MPa are based on the test concrete compressive strength and elastic modulus. The compressive stress-strain curve of concrete is plotted in
Figure 12a.
The compression damage factor
dc can be calculated by Equation (6):
where is
![Materials 07 05934 i006]()
the elastic compression strain,
![Materials 07 05934 i007]()
is the inelastic compression strain and
![Materials 07 05934 i008]()
is the plastic compression strain. In this paper,
bc = 0.7.
The “σ-ε” formula for tension is given in the Equation (7):
where
αt is the coefficient at the descent stage of the uniaxial tension stress-strain curve of concrete,
ft,r is the representative value of uniaxial tension strength of concrete and ε
t,r is the peak tension strain of concrete corresponding to
ft,r. In the numerical simulation, α
t = 0.7399,
fc,r = 1.54 MPa and ε
c,r = 0.000604 are based on the test concrete tensile strength and elastic modulus. The tensile stress-strain curve of concrete is plotted in
Figure 12b.
The calculation of tension damage factor
dt is given in Equation (8):
where,
![Materials 07 05934 i011]()
is the elastic compression strain,
![Materials 07 05934 i012]()
is the inelastic tension strain and
![Materials 07 05934 i013]()
is the plastic tension strain. In this paper,
bt = 0.1.
Figure 12.
Constitutive law of concrete under uniaxial compression: (a) Compressive stress-strain curve; (b) Tensile stress-strain curve.
Figure 12.
Constitutive law of concrete under uniaxial compression: (a) Compressive stress-strain curve; (b) Tensile stress-strain curve.
The constitutive law of the RCB wall: Integrated modeling by the plastic-damage model was based on ABAQUS. The compressive strain-stress curve of RCB masonry obtained was based on Yang’s model [
31]. The true values were obtained by the compression test on the RCB masonry and Poisson’s ratio was taken as 0.15.
The “σ
cm-ε
cm” formula for the compression of RCB masonry is given in Equation (9):
where
fcm is the representative value of the uniaxial compressive strength of RCB masonry, ε
cm is the peak compressive strain corresponding to
fcm and
Em is the elastic modulus of RCB masonry. In the numerical simulation,
fcm = 2.49 MPa, ε
cm = 0.003 and
Em = 2400 MPa are based on the test masonry strength and elastic modulus. The constitutive low of RCB masonry under uniaxial compression is shown in
Figure 13.
Figure 13.
Constitutive law of RCB masonry under uniaxial compression.
Figure 13.
Constitutive law of RCB masonry under uniaxial compression.
The tensile softening uses the method based on fracture energy; where
![Materials 07 05934 i015]()
,
ftm is the uniaxial tension strength of the RCB masonry,
![Materials 07 05934 i016]()
[
16] and
f2 is the compressive strength of the mortar. The fracture energy
![Materials 07 05934 i017]()
was taken as 20 N·m
−1 [
32]. The post-failure stress-fracture energy curve in the descent stage is shown in
Figure 14.
Figure 14.
Post-failure stress-fracture energy curve in the descent stage for RCB masonry.
Figure 14.
Post-failure stress-fracture energy curve in the descent stage for RCB masonry.
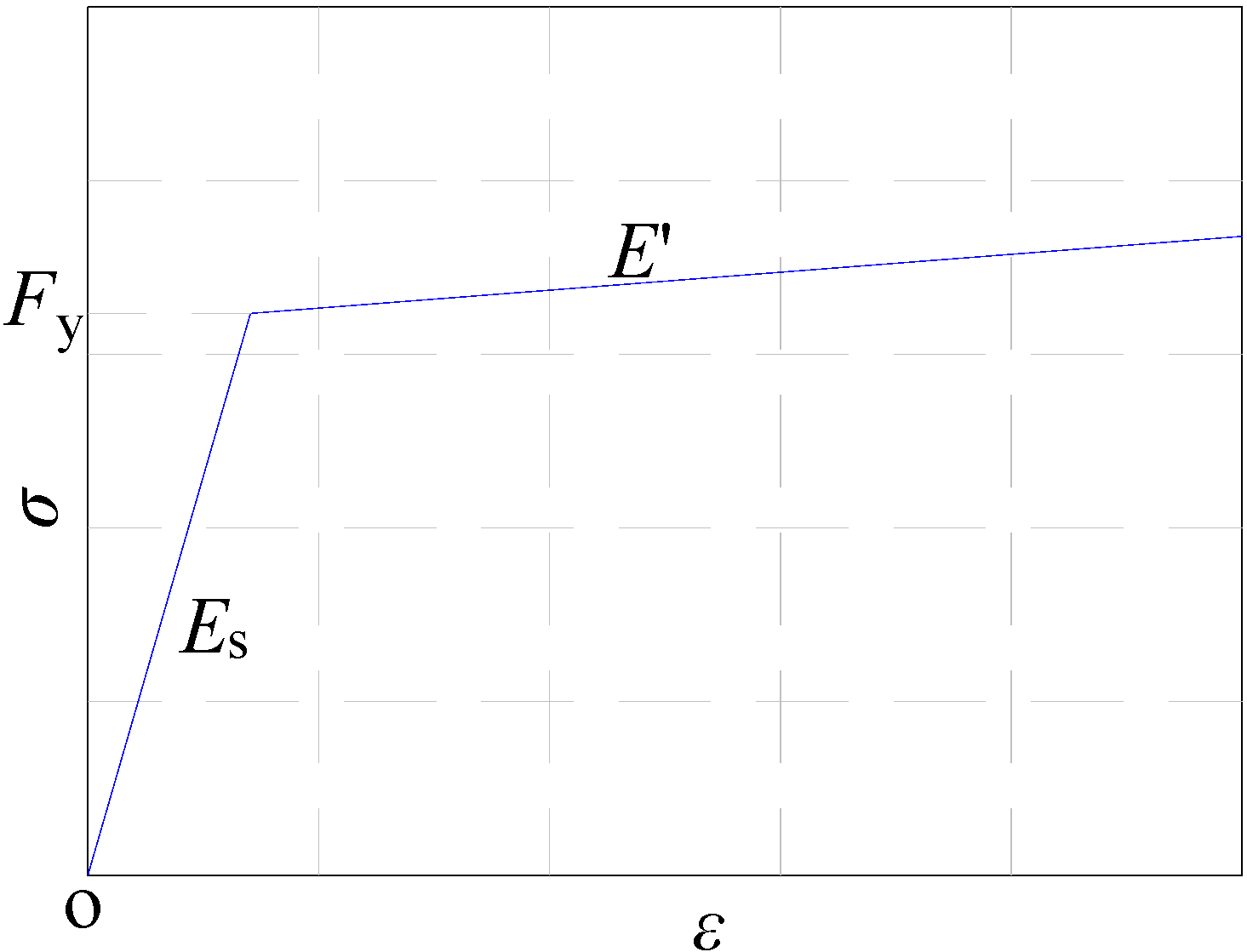
The “plasticity” model from ABAQUS software was adopted to simulate the reinforcement law. The stress-strain curve is plotted in
Figure 15. Each stress-strain curve, made up of two linear portions, represents the character of a bare mild steel bar; where the modulus
Es is the elastic modulus of the reinforcement and the modulus
E′ is the deformation modulus at the strain hardening stage,
E′ = 0.01
Es. The test yield strength and elastic modulus of the reinforcement were adopted in the paper, and Poisson’s ratio was taken as 0.3.
Figure 15.
Stress-strain curve of reinforcement.
Figure 15.
Stress-strain curve of reinforcement.
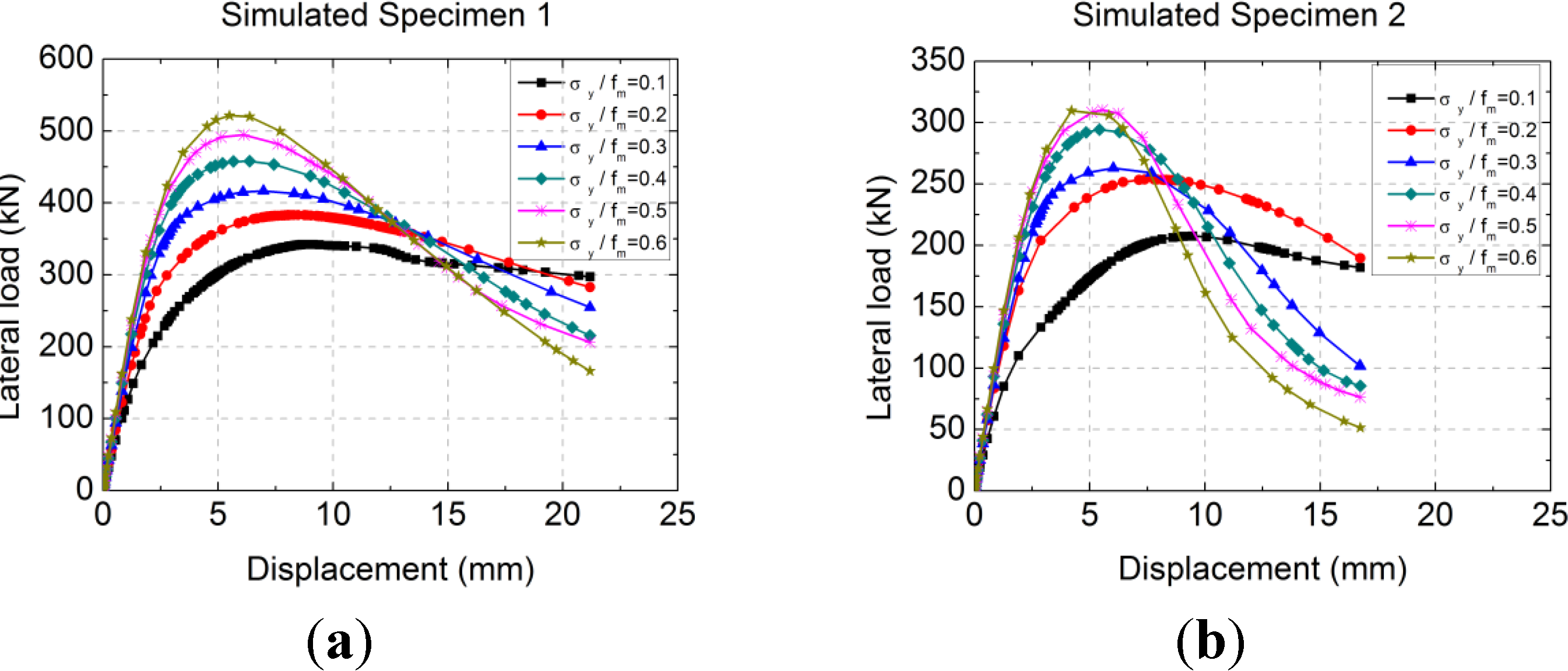
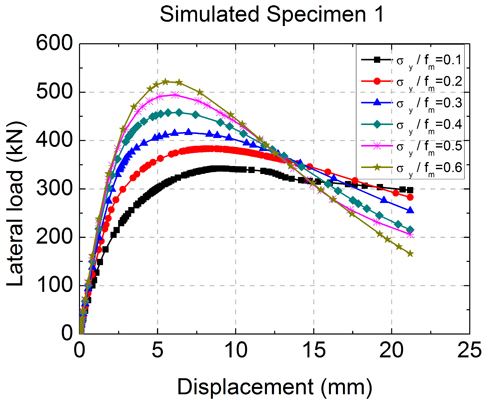
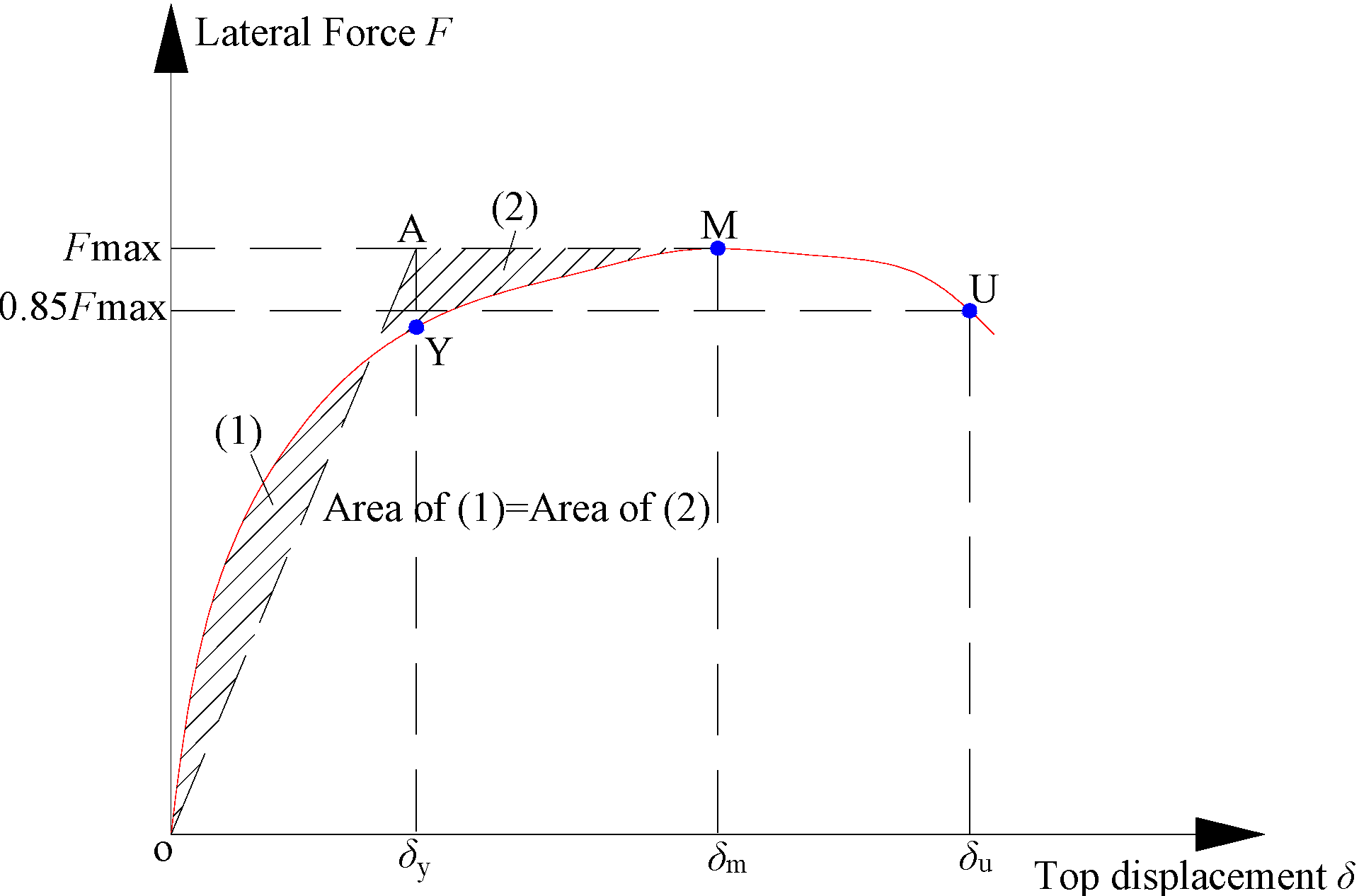
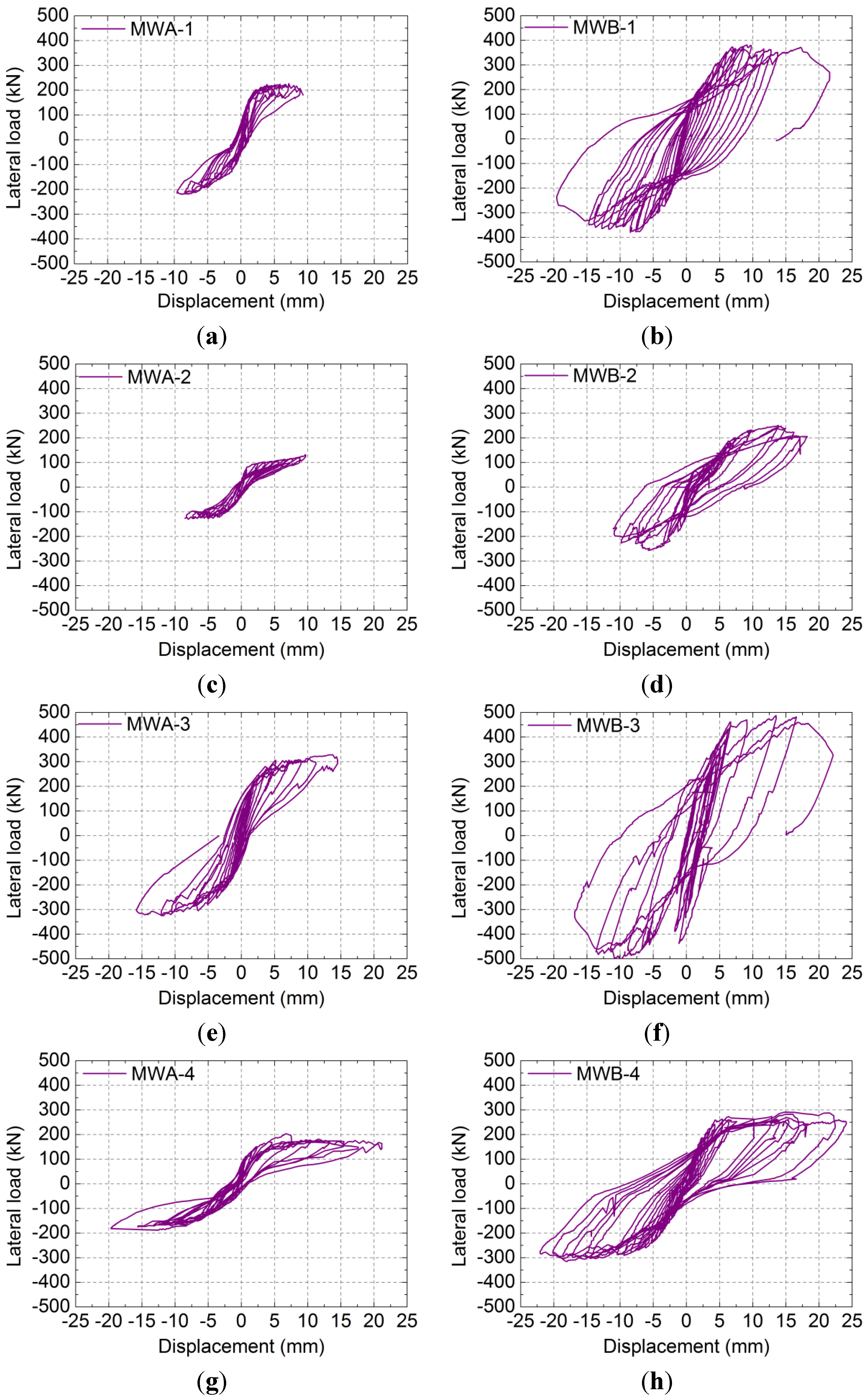
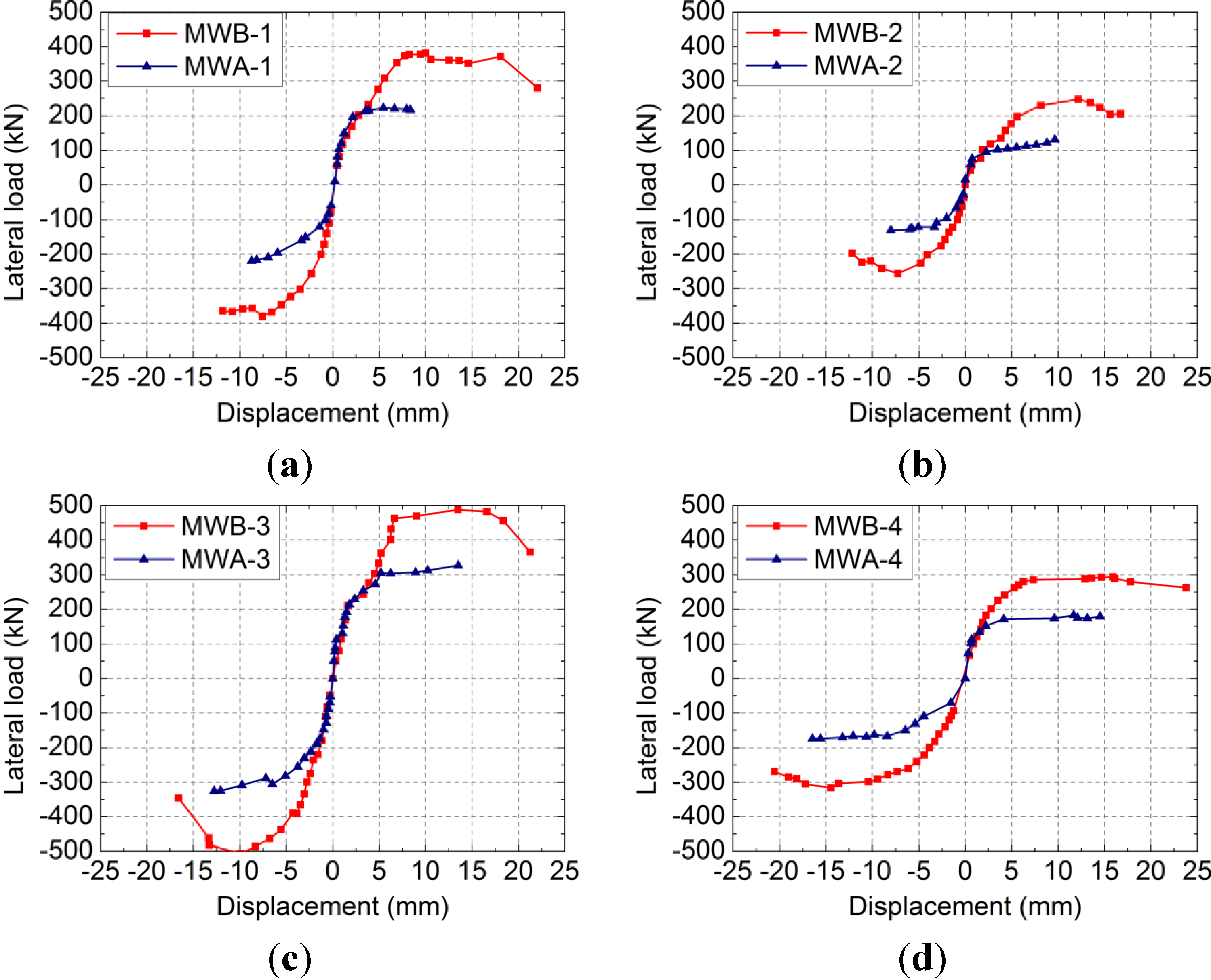
3.4. Effect of Axial Compressive Stress Σy on Lateral Load-Displacement Curves and Lateral Ultimate Strength
The mechanical performances of two simulated specimens, namely simulated Specimen 1 and simulated Specimen 2, were analyzed under six compressive stress ratios by ABAQUS. The parameter of the simulated Specimen 1 was the same as the test specimen MWB-1 with an aspect ratio of 0.6, and the simulated Specimen 2 was the same as the test specimen MWB-2 with an aspect ratio of 1.0. The change rules of lateral load-displacement curves to axial compressive stress ratio σ
y/
fm are analyzed, where σ
y is the axial compressive stress of the wall section and
fm is the average compressive strength of RCB masonry. The calculated lateral load-displacement curves of the two simulation specimens under six compressive stress ratios are shown in
Figure 18.
Figure 18.
The calculated lateral load-displacement curves under different σy/fm: (a) Simulated Specimen 1; (b) Simulated Specimen 2.
Figure 18.
The calculated lateral load-displacement curves under different σy/fm: (a) Simulated Specimen 1; (b) Simulated Specimen 2.
Figure 18 shows that under a certain limit of compressive stress ratio, the lateral ultimate strength (
Fmax) of the RCB masonry walls with vertical reinforcement grows with the increase of the compressive stress ratio by a slow growth rate. However, the ductility declines with the increase of the compressive stress ratio by a fast degradation rate. The compressive stress ratio has little effect on the initial elastic stiffness, but affects the stiffness degradation speed gradually during the elastic stage to the elastic-plastic stage. The concluded ultimate strength (
Fmax)-compressive stress ratio (σ
y/
fm) curves of the two simulation specimens under nine compressive stress ratios are shown in
Figure 19.
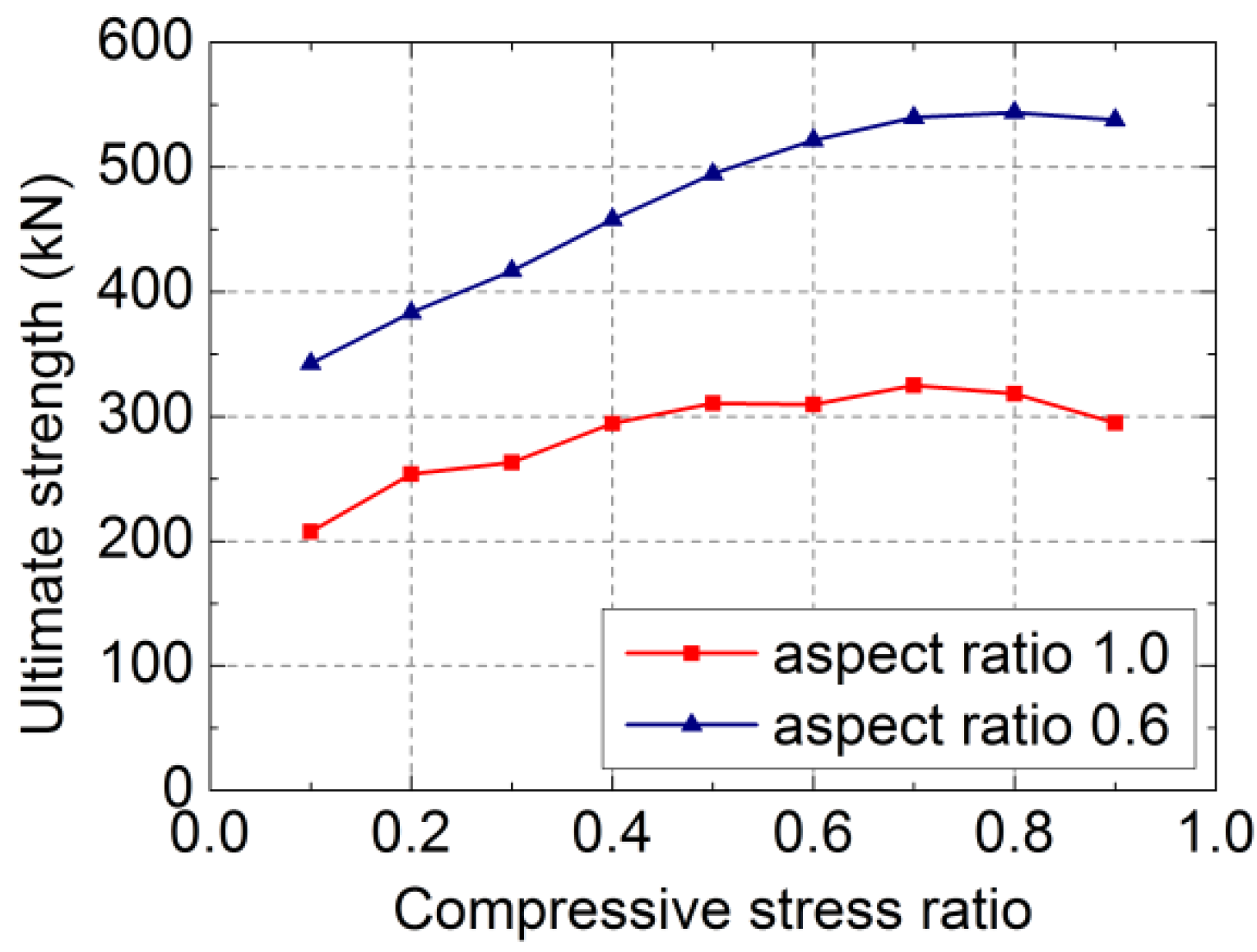
Figure 19.
The concluded ultimate strength (Fmax)-compressive stress ratio (σy/fm) curves.
Figure 19.
The concluded ultimate strength (Fmax)-compressive stress ratio (σy/fm) curves.
Figure 19 shows that the lateral ultimate strength of the RCB wall with vertical reinforcement experiences the process from the increase stage to the decrease stage with the increase of the compressive stress ratio. As for the two simulated specimens, the ultimate strength increases with the increase of the compressive stress ratio when the compressive stress ratio is less than 0.7, but declines when the compressive stress ratio exceeds 0.7.

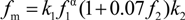


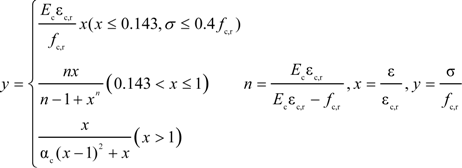
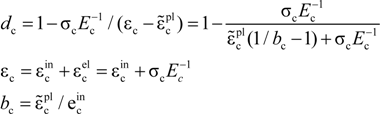
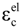 the elastic compression strain,
the elastic compression strain, 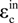 is the inelastic compression strain and
is the inelastic compression strain and 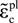 is the plastic compression strain. In this paper, bc = 0.7.
is the plastic compression strain. In this paper, bc = 0.7.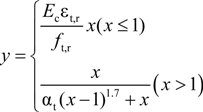
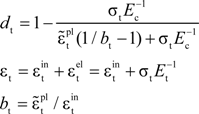
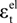 is the elastic compression strain,
is the elastic compression strain, 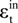 is the inelastic tension strain and
is the inelastic tension strain and 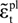 is the plastic tension strain. In this paper, bt = 0.1.
is the plastic tension strain. In this paper, bt = 0.1.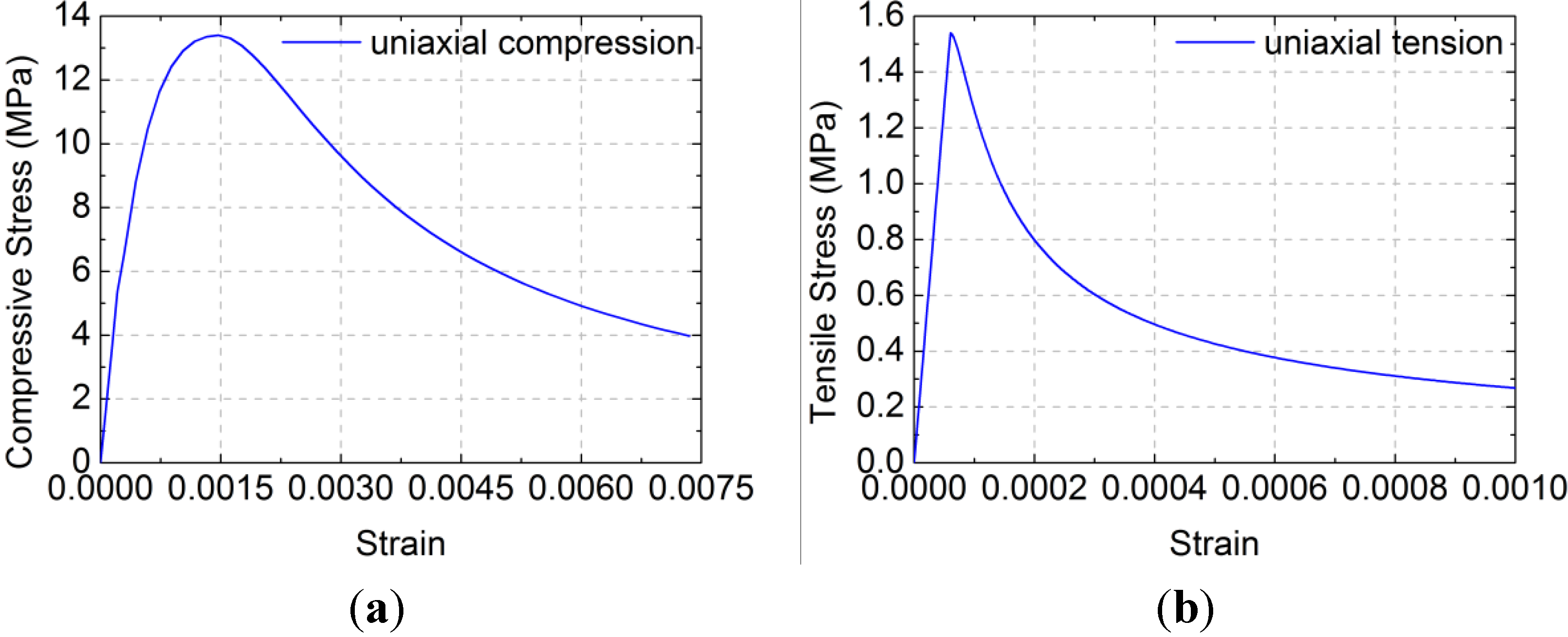
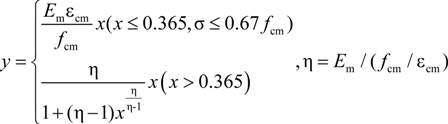
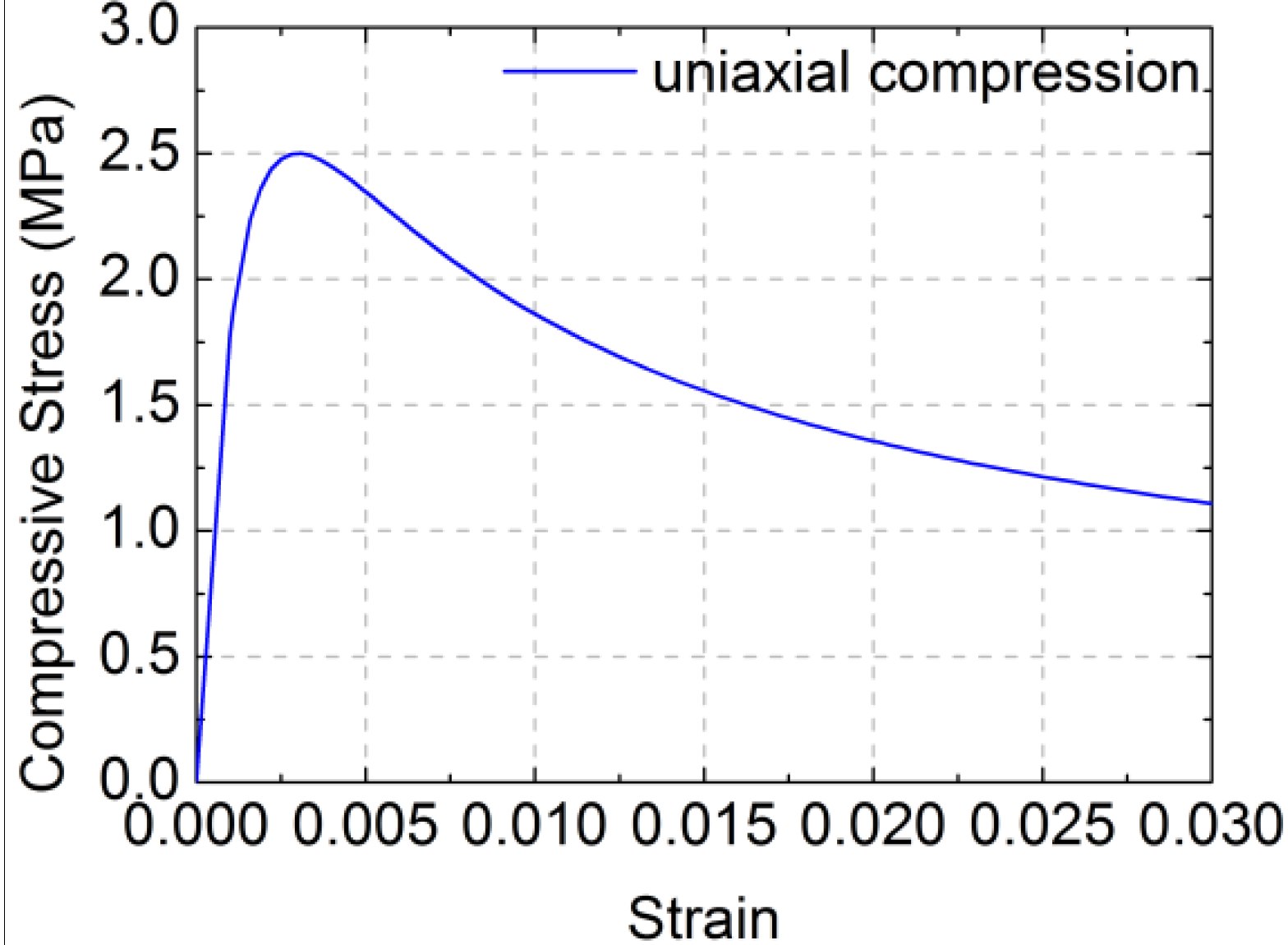
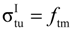 , ftm is the uniaxial tension strength of the RCB masonry,
, ftm is the uniaxial tension strength of the RCB masonry, 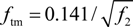 [16] and f2 is the compressive strength of the mortar. The fracture energy
[16] and f2 is the compressive strength of the mortar. The fracture energy 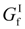 was taken as 20 N·m−1 [32]. The post-failure stress-fracture energy curve in the descent stage is shown in Figure 14.
was taken as 20 N·m−1 [32]. The post-failure stress-fracture energy curve in the descent stage is shown in Figure 14.