Constitutive Behavior and Finite Element Analysis of FRP Composite and Concrete Members
Abstract
:1. Introduction
2. Constitutive Model for FRP Composite and Concrete Circular Section
2.1. Laminate Composite for FRP Composite
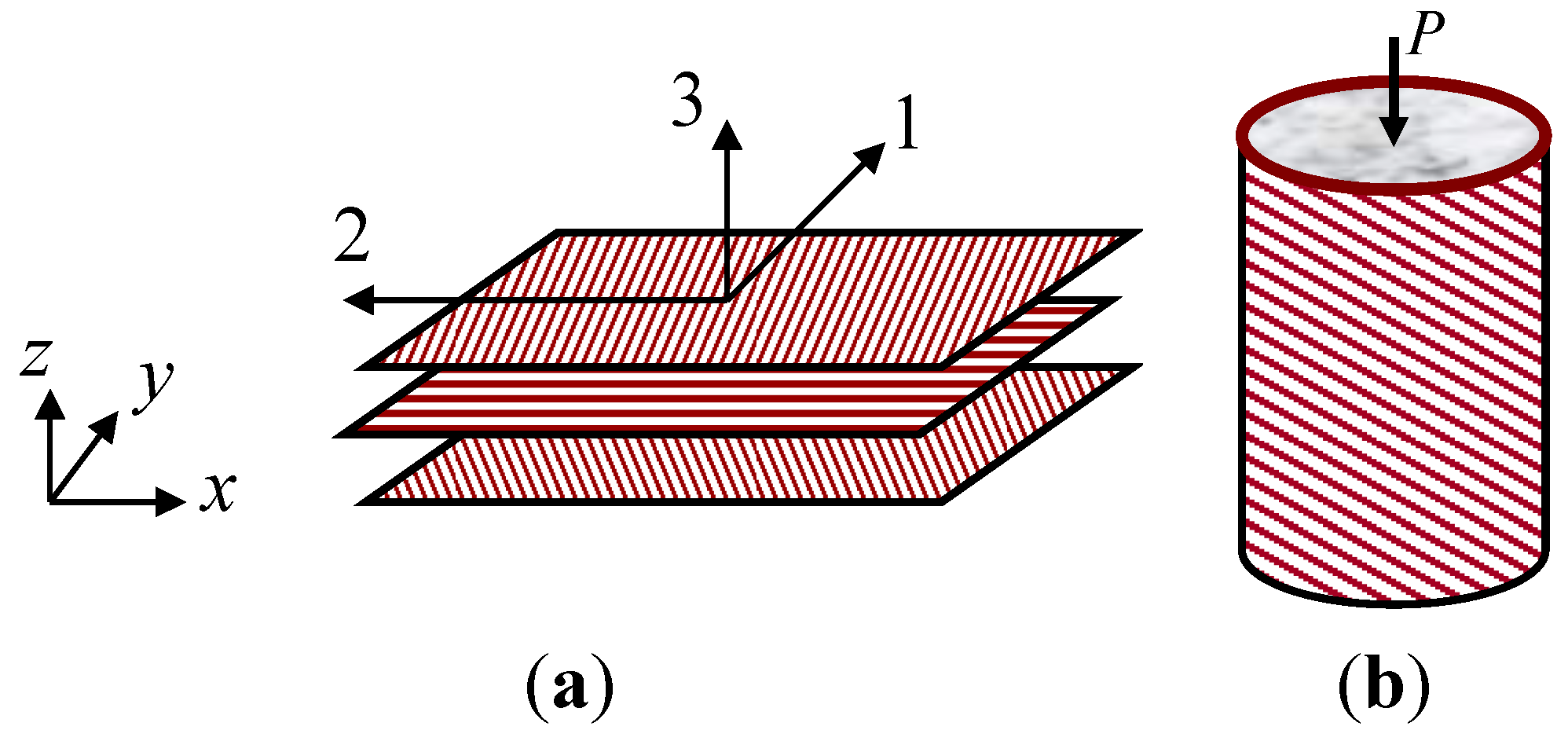
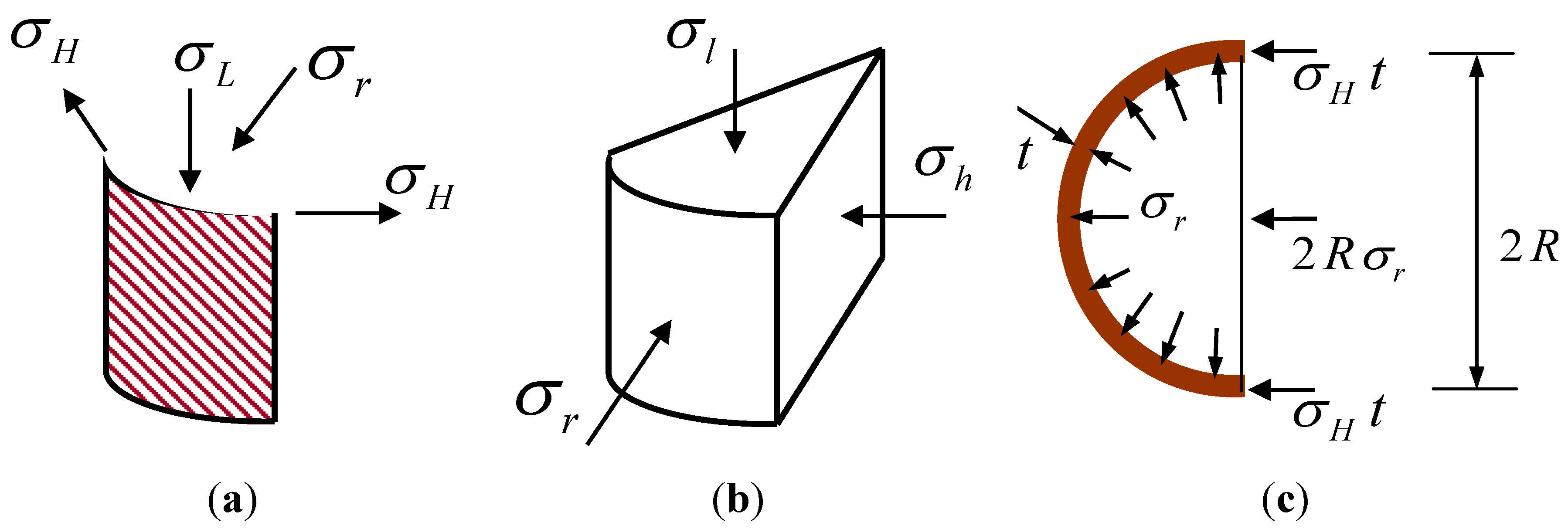
2.2. Stresses and Strains of FRP Composite and Concrete Circular Section
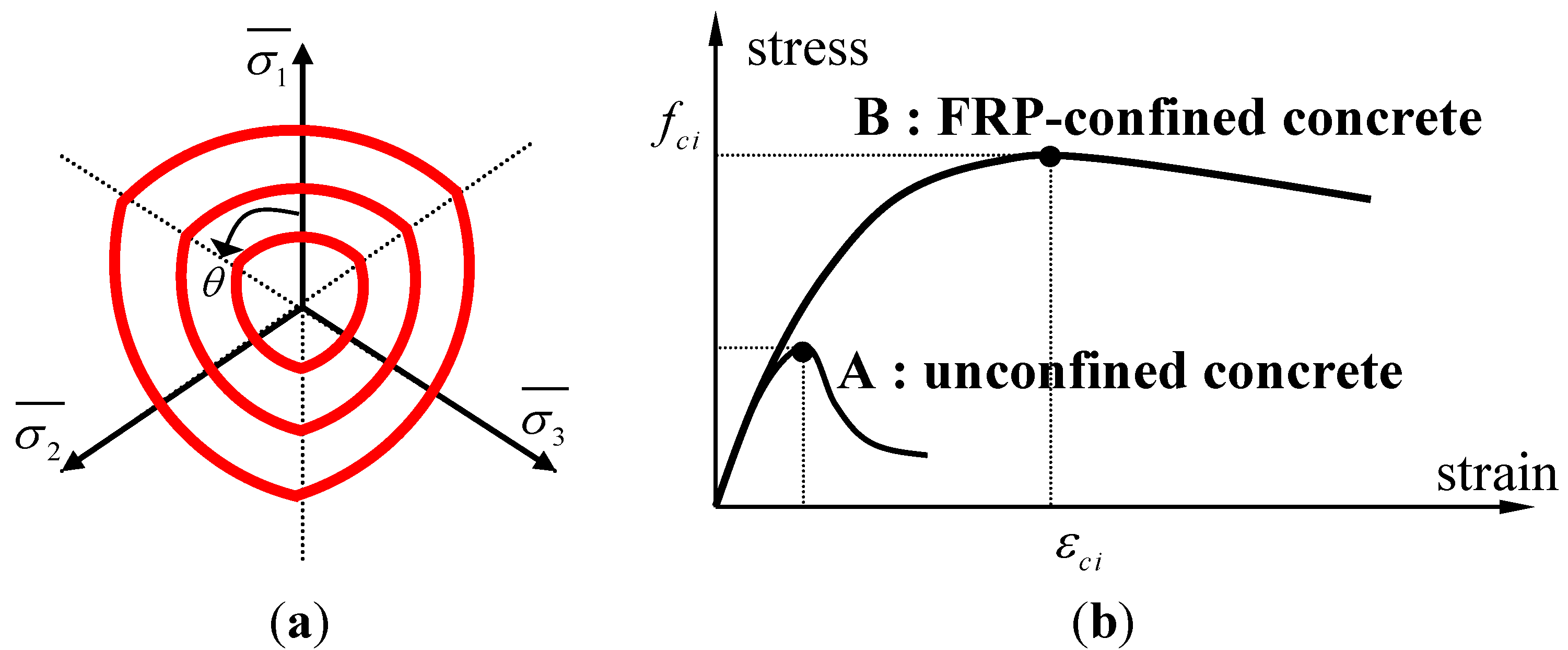
2.3. Constitutive Model of Concrete in Triaxial Stress State
3. Mixed Beam Finite Element with Layered FRP Concrete Composite Section
3.1. Finite Element Formulation
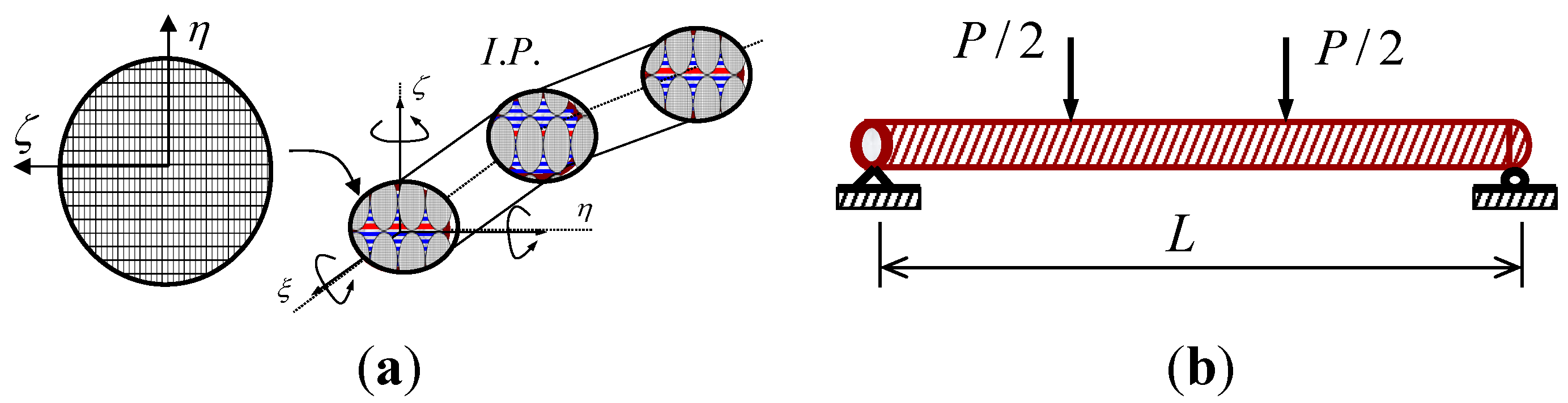
3.2. Layered Section Discretization
4. Analysis of FRP and Concrete Composite Cylinder in Compression
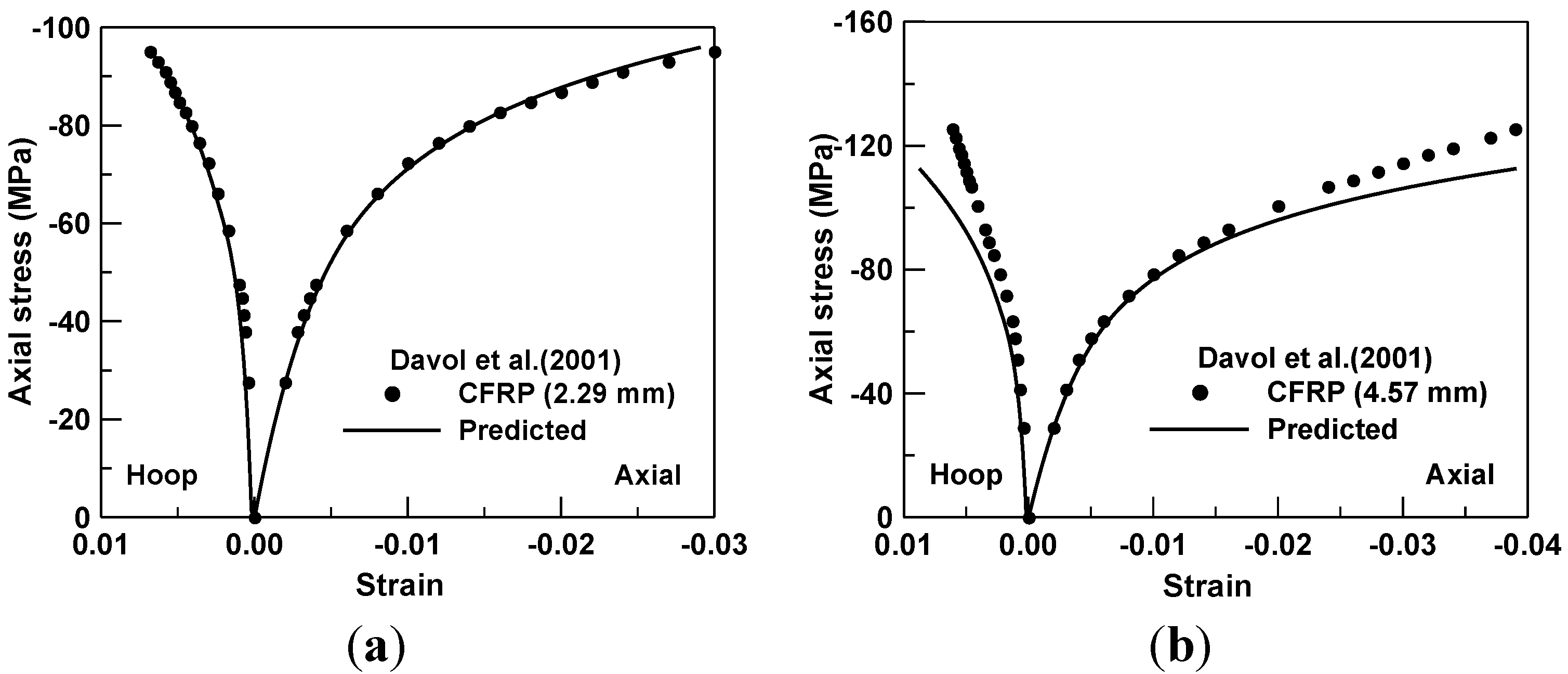
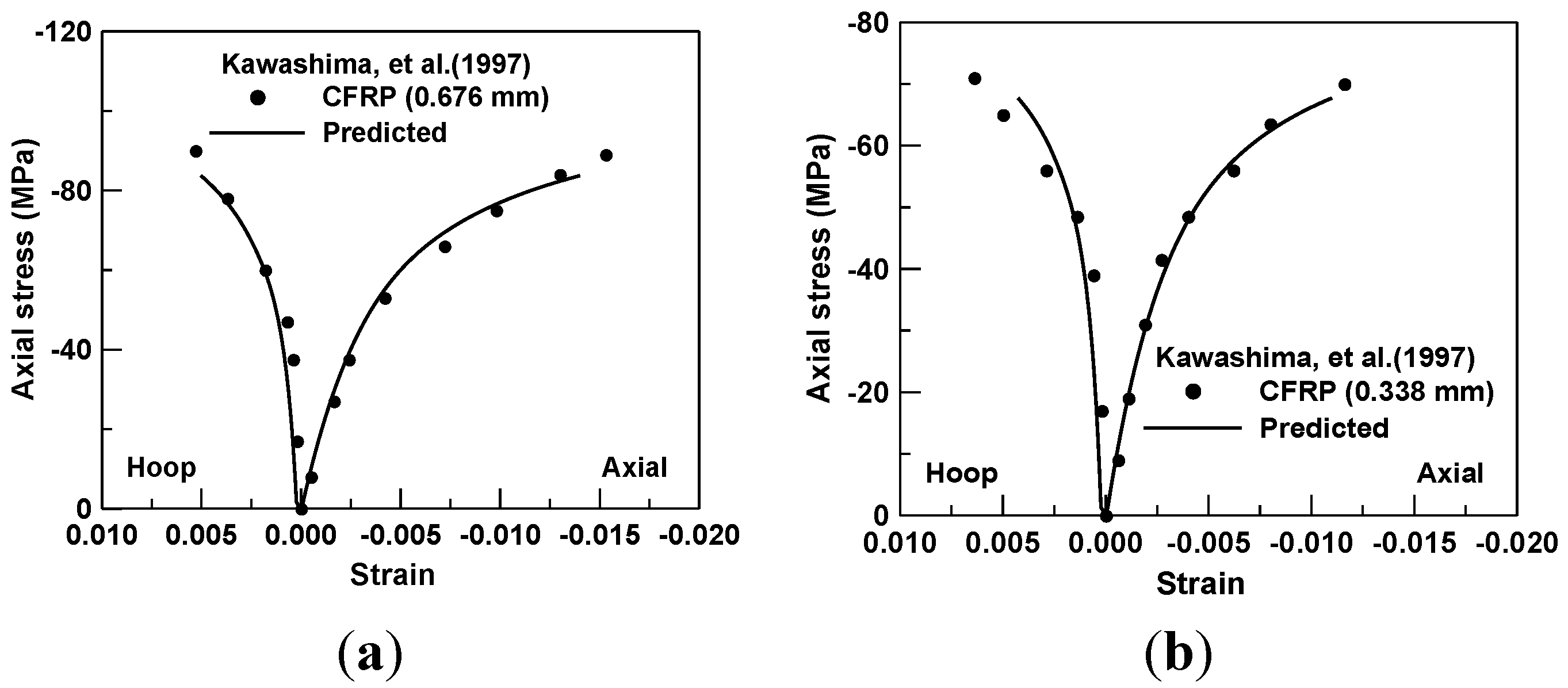
5. Finite Element Prediction of FRP and Concrete Composite Beams
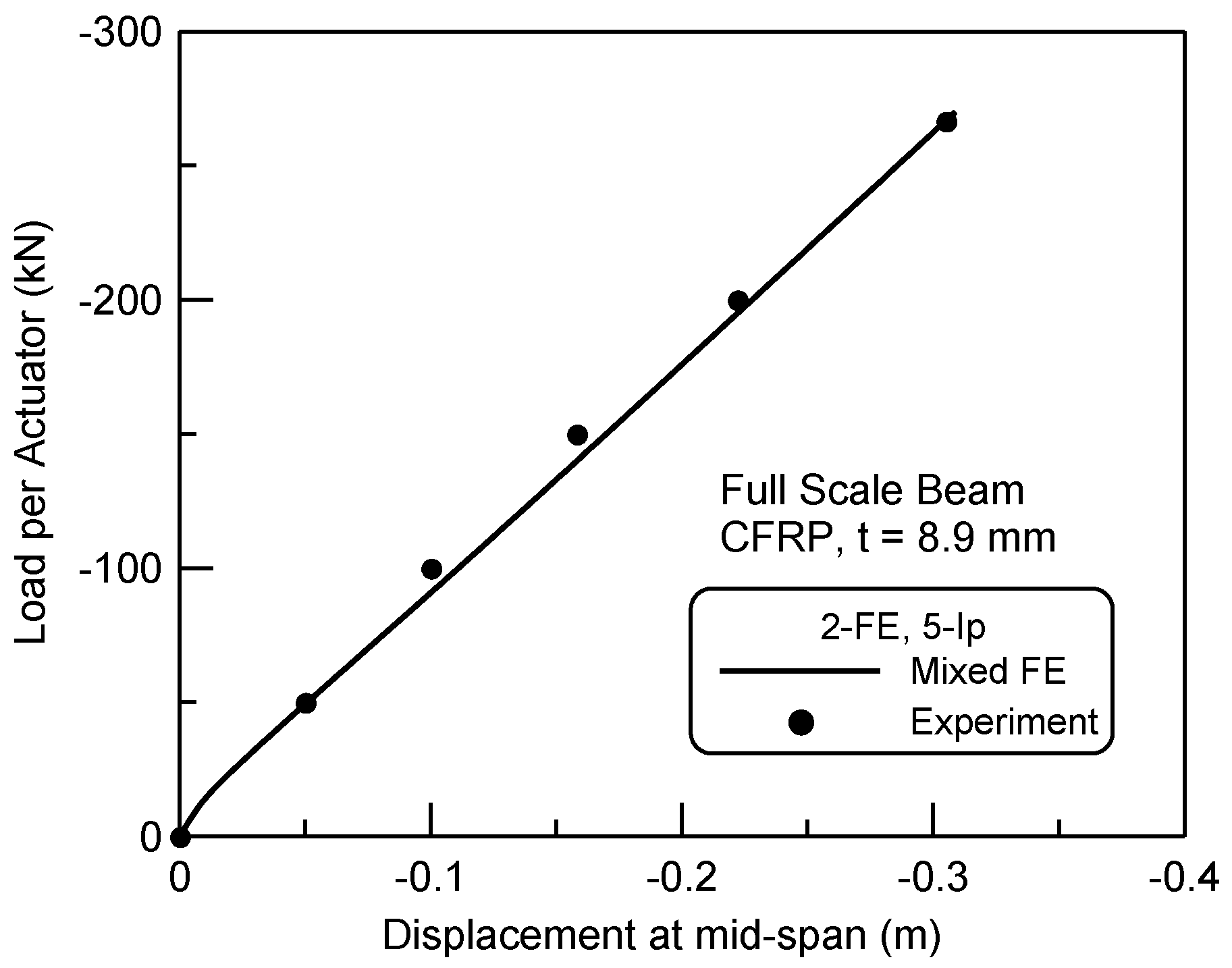
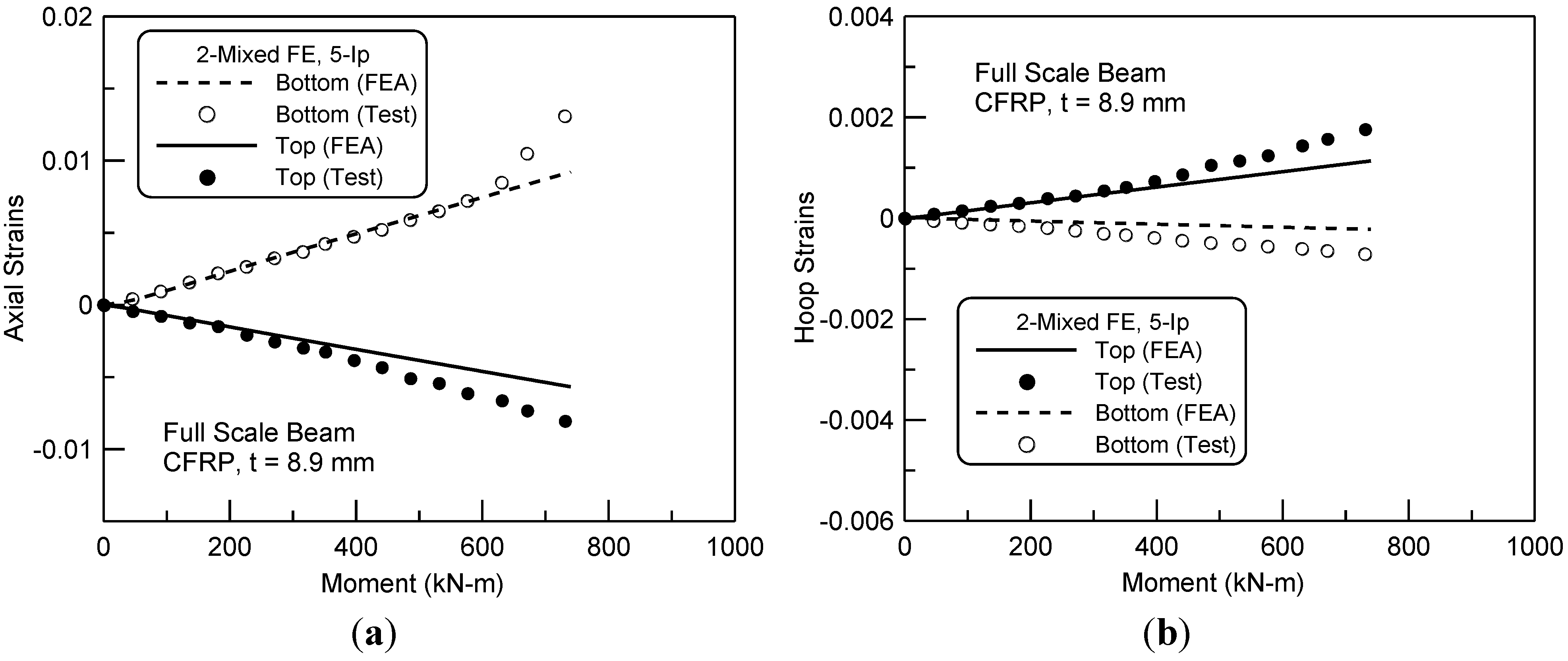
6. Conclusions
Acknowledgments
References
- Cho, C.G.; Kwon, M.; Spacone, E. Analytical model of concrete-filled fiber-reinforced polymer tubes based on multiaxial constitutive laws. J. Struct. Eng. 2005, 131, 1426–1433. [Google Scholar] [CrossRef]
- Burgueno, R. System characterization and design of modular fiber reinforced polymer (FRP) short- and medium-span bridges. Ph.D. Thesis, University of California, San Diego, CA, USA, 1999. [Google Scholar]
- Davol, A.; Burgueno, RJ.M.; Seible, F. Flexural behavior of circular concrete filled FRP shells. J. Struct. Eng. 2001, 127, 810–817. [Google Scholar] [CrossRef]
- El-Tawil, S.; Ogunc, C.; Okeil, A.; Shahawy, M. Static and fatigue analysis of RC beams strengthened with CFRP laminates. J. Compos. Constr. 2001, 5, 258–267. [Google Scholar] [CrossRef]
- Fam, A.Z.; Rizkalla, S.H. Confinement model for axially loaded concrete confined by circular fiber-reinforced polymer tubes. ACI Struct. J. 2001, 98, 451–461. [Google Scholar]
- Hosotani, M.; Kawashima, K.; Hoshikuma, J. A stress–strain model for concrete cylinders confined by carbon fiber sheets. J. Mater. Concr. Struct. Pavement JSCE 1998, 39, 37–52. [Google Scholar]
- Kawashima, K.; Hosotani, M.; Hoshikuma, J. A Model for Confinement Effect for Concrete Cylinders Confined by Carbon Fiber Sheets; Technical Report NCEER-97-0005; State University of New York: Buffalo, NY, USA, 1997; pp. 405–430. [Google Scholar]
- Mimiran, A.; Shahawy, M. Behavior of concrete columns confined by fiber composites. J. Struct. Eng. 1997, 123, 583–590. [Google Scholar] [CrossRef]
- Spoelstra, M.R.; Monti, G. FRP-confined concrete model. J. Compos. Constr. 1999, 3, 143–150. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress–strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Pantazopoulou, S.J.; Mills, R.H. Microstructural aspects of the mechanical response of plaine concrete. ACI Mater. J. 1995, 92, 605–616. [Google Scholar]
- Kupfer, H.B.; Hildorf, H.K.; Rusch, H. Behavior of concrete under biaxial stresses. ACI J. 1969, 66, 656–666. [Google Scholar]
- Darwin, D.; Pecknold, D.A. Nonlinear biaxial law for concrete. J. Eng. Mech. Div. 1977, 103, 229–241. [Google Scholar]
- Willam, K.J.; Warnke, E.P. Constitutive model for the triaxial behavior of concrete. In Proceedings of International Association for Bridge and Structural Engineering, Bergamo, Italy, 17–19 May, 1974; IABSE: Zurich, Switzerland, 1975; Volume 19, pp. 1–30. [Google Scholar]
- Cho, C.G.; Park, M.H. Finite element prediction of the influence of confinement on RC beam-columns under single or double curvature bending. Eng. Struct. 2002, 13, 313–328. [Google Scholar]
- Saenz, L.P. Discussion of equation for the stress–strain curve of concrete by Desayi and Krishman. ACI J. 1994, 61, 1229–1235. [Google Scholar]
- Tsai, S.W.; Wu, E.M. A general theory of strength for anisotropic materials. J. Compos. Mater. 1971, 5, 58–80. [Google Scholar] [CrossRef]
- Spacone, E.; Filippou, F.C.; Taucer, F.F. Fibre beam-column model for nonlinear analysis of R/C frames: Part I. Formulation. Earthq. Eng. Struct. Dyn. 1996, 25, 711–725. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ann, K.Y.; Cho, C.-G. Constitutive Behavior and Finite Element Analysis of FRP Composite and Concrete Members. Materials 2013, 6, 3978-3988. https://doi.org/10.3390/ma6093978
Ann KY, Cho C-G. Constitutive Behavior and Finite Element Analysis of FRP Composite and Concrete Members. Materials. 2013; 6(9):3978-3988. https://doi.org/10.3390/ma6093978
Chicago/Turabian StyleAnn, Ki Yong, and Chang-Geun Cho. 2013. "Constitutive Behavior and Finite Element Analysis of FRP Composite and Concrete Members" Materials 6, no. 9: 3978-3988. https://doi.org/10.3390/ma6093978
APA StyleAnn, K. Y., & Cho, C.-G. (2013). Constitutive Behavior and Finite Element Analysis of FRP Composite and Concrete Members. Materials, 6(9), 3978-3988. https://doi.org/10.3390/ma6093978



