Theory-Guided Materials Design of Multi-Phase Ti-Nb Alloys with Bone-Matching Elastic Properties
Abstract
:1. Introduction
Theory-Guided Materials Design
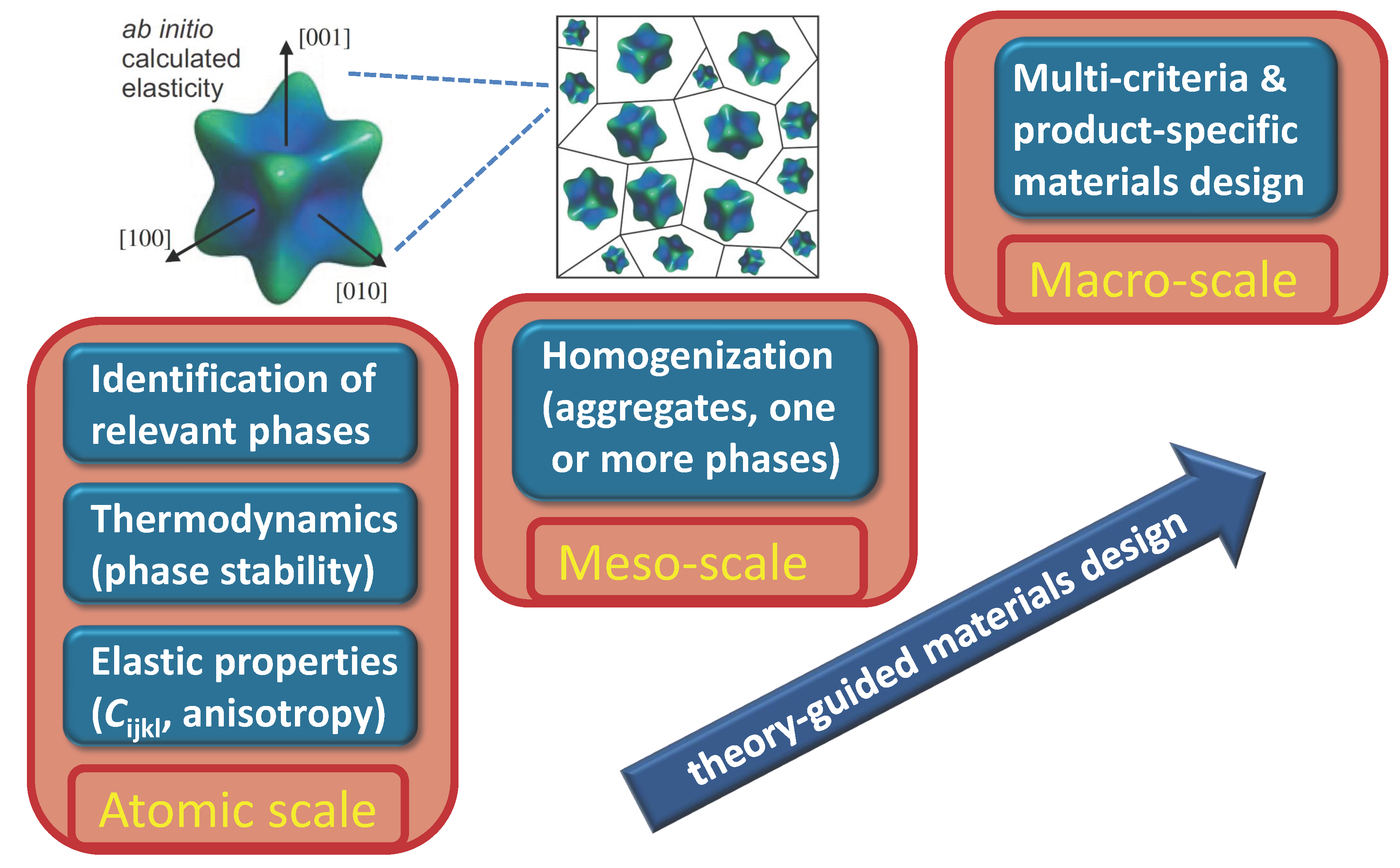
2. Methodology
2.1. Ab Initio Calculations
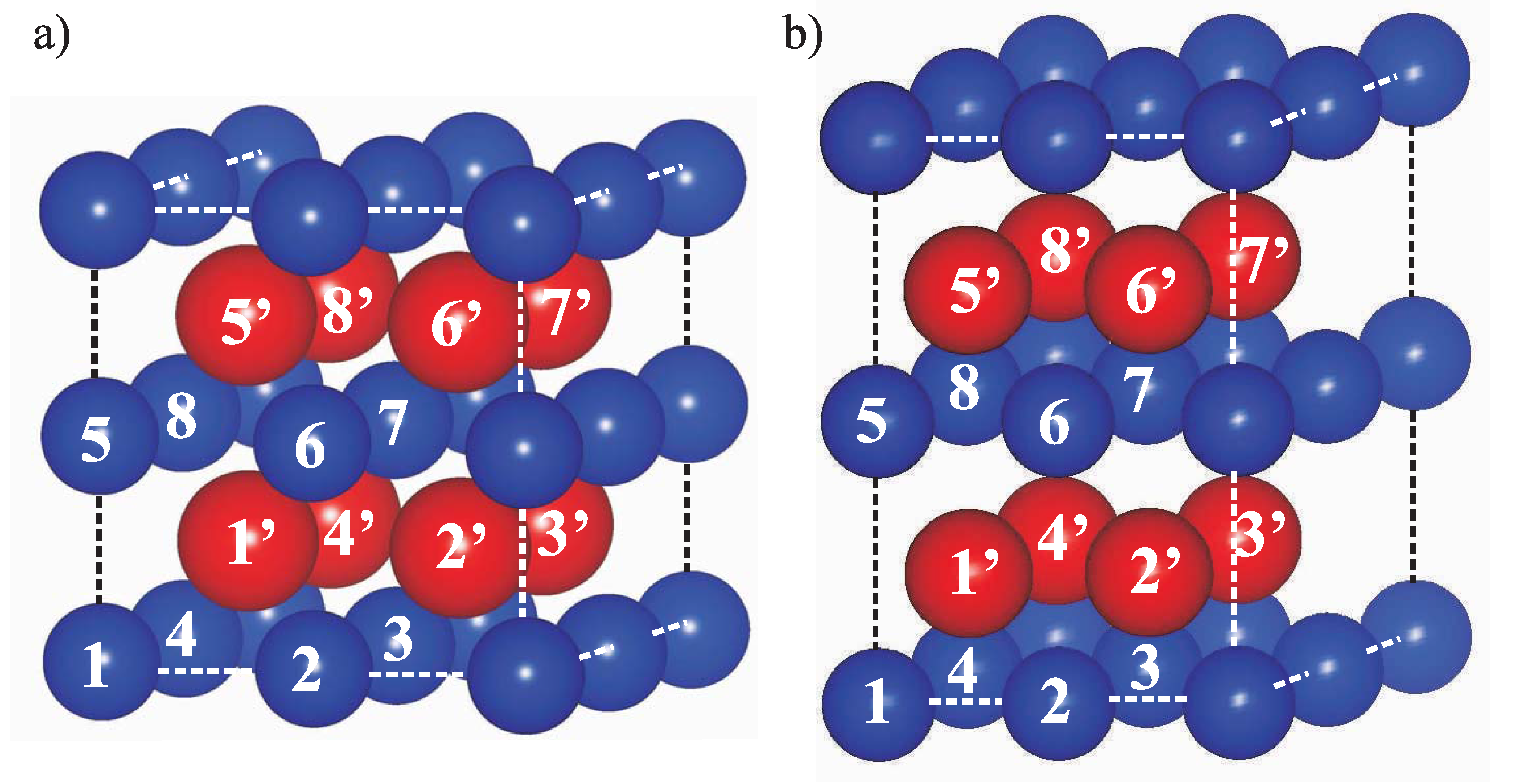
2.2. Analytic Homogenization Scheme
2.3. Single-Phase Aggregate
2.4. Multi-Phase Composite
2.5. Homogenized Young’s Modulus and Poisson’s Ratio
2.6. Experimental Methods
3. Results and Discussion
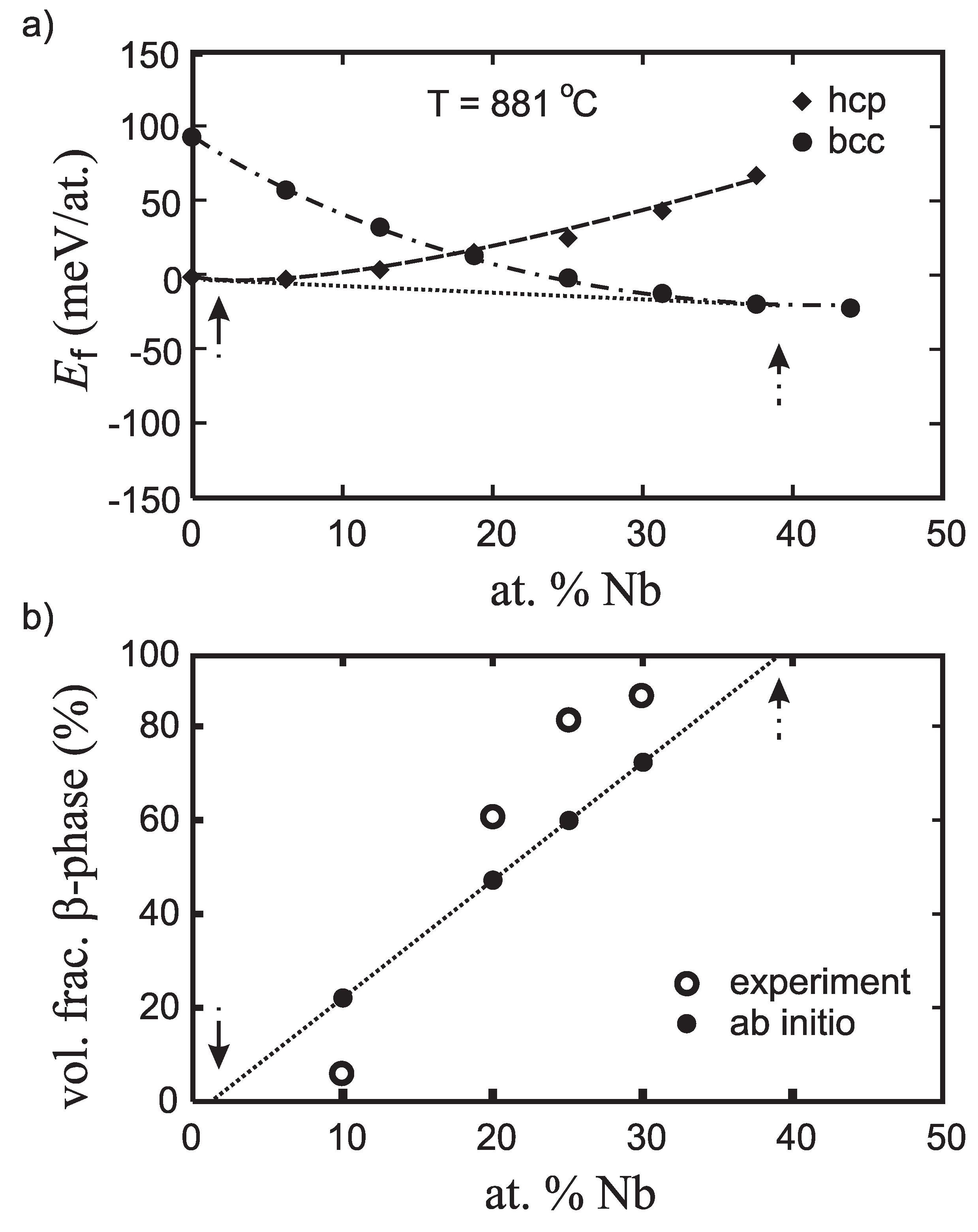
| Material | a | ||||||
|---|---|---|---|---|---|---|---|
| Ti theory | 2.921 | 1.585 | 200 | 72 | 90 | 191 | 40 |
| Ti theory[49] | 2.946 | 1.584 | 172 | 87 | 73 | 191 | 41 |
| Ti experiment[52] | 2.951 | 1.587 | 162 | 92 | 69 | 181 | 47 |
| Nb theory | 3.335 | - | 227 | 129 | - | - | 22 |
| Nb theory[49] | 3.325 | - | 247 | 134 | - | - | 15.6 |
| Nb experiment[53] | 3.301 | - | 246 | 133 | - | - | 28 |
| β-Ti-37.5%Nb theory | 3.261 | - | 156 | 121 | - | - | 10 |
| β-Ti-37.5%Nb theory | 3.264 | - | 168 | 118 | - | - | 29 |
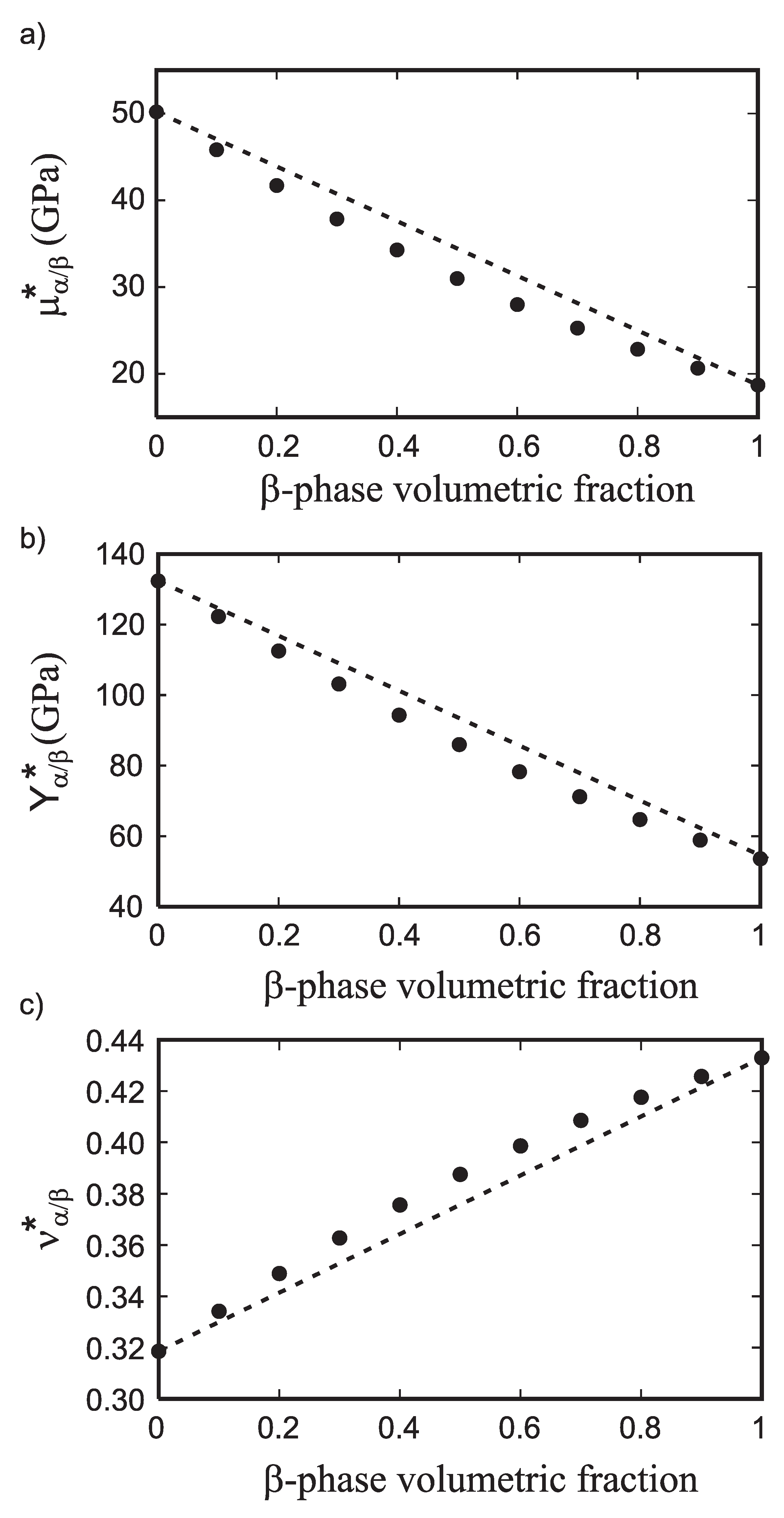
| Material | ||||||
|---|---|---|---|---|---|---|
| α-Ti | 0 | 0 | 122 | 115 | 132 | - |
| Ti-10at.% Nb | 0.17 | 0.06 | 124 | 0.43 | 115 | 91 |
| Ti-20at.% Nb | 0.49 | 0.60 | 127 | 0.32 | 89 | 75 |
| Ti-25at.% Nb | 0.60 | 0.81 | 129 | 0.28 | 78 | 74 |
| Ti-30at.% Nb | 0.75 | 0.90 | 130 | 0.24 | 69 | 72 |
| β-Ti-37.5at.%Nb | 1 | 1 | 133 | 19 | 54 | - |

4. Summary and Conclusions
Acknowledgment
5. Appendix
References
- De Gelas, B.; Molinier, R.; Seraphin, L.; Armand, M.; Tricot, R. Titanium and Titanium Alloys; Plenum Press: New York, NY, USA, 1982. [Google Scholar]
- Breme, J. Titanium and titanium alloys, biomaterials of preference. Mem. Etud. Sci. Rev. Met. 1989, 86, 625–637. [Google Scholar]
- Long, M.J.; Rack, H.J. Review: Titanium alloys in total joint replacement—A materials science perspective. Biomaterials 1998, 19, 1621–1639. [Google Scholar] [CrossRef]
- Niinomi, M. Recent metallic materials for biomedical applications. Metall. Mater. Trans. A 2002, 33A, 477–486. [Google Scholar] [CrossRef]
- Wang, K. The use of titanium for medical applications in the USA. Mater. Sci. Eng. A 1996, 213, 134–137. [Google Scholar] [CrossRef]
- Niinomi, M. Mechanical properties of biomedical titanium alloys. Mater. Sci. Eng. A 1998, 243, 231–236. [Google Scholar] [CrossRef]
- Goldberg, A.J.; Burstone, C.J. Evaluation of beta titanium-alloys for use in orthodontic appliances. Dent. Res. 1979, 58, 593–599. [Google Scholar] [CrossRef]
- Burstone, C.J.; Goldberg, A.J. Beta-titanium—New orthodontic alloy. Am. J. Orthod. 1980, 77, 121–132. [Google Scholar] [CrossRef]
- Nelson, K.R.; Burstone, C.J.; Goldberg, A.J. Optimal welding of beta titanium orthodontic wires. Am. J. Orthod. Dentofac. Orthop. 1987, 92, 213–219. [Google Scholar] [CrossRef]
- Boyer, R.R.; Rosenberg, H.W. Beta Titanium Alloys in the 1980s; AIME: New York, NY, USA, 1984. [Google Scholar]
- Lee, C.M.; Ho, W.F.; Ju, C.P.; Chern-Lin, J.H. Structure and properties of Titanium-25 Niobium-x iron alloys. J. Mater. Sci. Mater. Med. 2002, 13, 695–700. [Google Scholar] [CrossRef] [PubMed]
- Ho, W.F.; Ju, C.P.; Chern-Lin, J.H. Structure and properties of cast binary Ti-Mo alloys. Biomaterials 1999, 20, 2115–2122. [Google Scholar] [CrossRef]
- Ou, S.F.; Chou, H.H.; Lin, C.S.; Shih, C.J.; Wang, K.K.; Pan, Y.N. Effects of anodic oxidation and hydrothermal treatment on surface characteristics and biocompatibility of Ti-30Nb-1Fe-1Hf alloy. Appl. Surf. Sci. 2012, 258, 6190–6198. [Google Scholar] [CrossRef]
- Malek, J.; Hnilica, F.; Vesely, J.; Smola, B.; Bartakova, S.; Vanek, J. The influence of chemical composition and thermo-mechanical treatment on Ti-Nb-Ta-Zr alloys. Mater. Des. 2012, 35, 731–740. [Google Scholar] [CrossRef]
- Kuroda, D.; Niinomi, M.; Morinaga, M.; Kato, Y.; Yashiro, T. Design and mechanical properties of new beta type titanium alloys for implant materials. Mater. Sci. Eng. A 1998, 243, 244–249. [Google Scholar] [CrossRef]
- Niinomi, M.; Hattori, T.; Morkawa, K.; Kasuga, T. Development of low rigidity beta-type titanium alloy for biomedical applications. Mater. Trans. 2002, 43, 2970–2977. [Google Scholar] [CrossRef]
- Niinomi, M. Fatigue performance and cyto-toxicity of low rigidity titanium alloy, Ti-29Nb-13Ta-4.6Zr. Biomaterials 2003, 24, 2673–2683. [Google Scholar] [CrossRef]
- Ankem, S.; Greene, C.A. Recent developments in microstructure/property relationships of beta titanium alloys. Mater. Sci. Eng. A 1999, 263, 127–131. [Google Scholar] [CrossRef]
- Prima, F.; Vermaut, P.; Ansel, D.; Debuigne, J. Omega precipitation in a beta metastable titanium alloy, resistometric study. Mater. Trans. 2000, 41, 1092–1097. [Google Scholar] [CrossRef]
- Weiss, I.; Semiatin, S.L. Thermomechanical processing of beta titanium alloys—An overview. Mater. Sci. Eng. A 1998, 243, 46–65. [Google Scholar] [CrossRef]
- Ikeda, M.; Komatsu, S.Y.; Sowa, I.; Niimoni, M. Aging behavior of the Ti-29Nb-13Ta-4.6Zr new beta alloy for medical implants. Metall. Mater. Trans. 2002, 33A, 487–493. [Google Scholar] [CrossRef]
- Geetha, M.; Singh, A.K.; Muraleedharan, K.; Gogia, A.K. Effect of thermomechanical processing on microstructure of a Ti-13Nb-13Zr alloy. J. Alloys Comp. 2001, 329, 264–271. [Google Scholar] [CrossRef]
- Hao, Y.L.; Niimoni, M.; Kuroda, D.; Fukunaga, K.; Zhou, Y.L.; Yang, R.; Suzuki, A. Aging response of the Young’s modulus and mechanical properties of Ti-29Nb-13Ta-4.6Zr for biomedical applications. Metall. Mater. Trans. A 2003, 34A, 1007–1012. [Google Scholar] [CrossRef]
- Banerjee, R.; Nag, S.; Fraser, H.L. A novel combinatorial approach to the development of beta titanium alloys for orthopaedic implants. Mater. Sci. Eng. C 2005, 25, 282–289. [Google Scholar] [CrossRef]
- Nag, S.; Banerjee, R.; Fraser, H.L. Microstructural evolution and strengthening mechanisms in Ti-Nb-Zr-Ta, Ti-Mo-Zr-Fe and Ti-15Mo biocompatible alloys. Mater. Sci. Eng. C 2005, 25, 357–362. [Google Scholar] [CrossRef]
- Banerjee, R.; Collins, P.C.; Bhattacharyya, D.; Banerjee, S.; Fraser, H.L. Microstructural evolution in laser deposited compositionally graded alpha/beta titanium-vanadium alloys. Acta Mater. 2003, 51, 3277–3292. [Google Scholar] [CrossRef]
- Banerjee, R.; Nag, S.; Stechschulte, J.; Fraser, H.L. Strengthening mechanisms in Ti-Nb-Zr-Ta and Ti-Mo-Zr-Fe orthopaedic alloys. Biomaterials 2004, 25, 3413–3419. [Google Scholar] [CrossRef] [PubMed]
- Miura, K.; Yamada, N.; Hanada, S.; Jung, T.K.; Itoi, E. The bone tissue compatibility of a new Ti-Nb-Sn alloy with a low Young modulus. Acta Biomater. 2011, 7, 2320–2326. [Google Scholar] [CrossRef] [PubMed]
- Aziz-Kerrzo, M.; Conroy, K.G.; Fenelon, A.M.; Farrell, S.T.; Breslin, C.B. Electrochemical studies on the stability and corrosion resistance of titanium-based implant materials. Biomaterials 2001, 22, 1531–1539. [Google Scholar] [CrossRef]
- Yu, S.Y.; Scully, J.R. Corrosion and passivity of Ti-13% Nb-13% Zr in comparison to other biomedical implant alloys. Corrosion 1997, 53, 965–976. [Google Scholar] [CrossRef]
- Godley, R.; Starosvetsky, D.; Gotman, I. Corrosion behavior of a low modulus beta-Ti-45%Nb alloy for use in medical implants. J. Mater. Sci. Mater. Med. 2006, 17, 63–67. [Google Scholar] [CrossRef] [PubMed]
- Li, S.J.; Yang, R.; Li, S.; Hao, Y.L.; Cui, Y.Y.; Niinomi, M.; Guo, Z.X. Wear characteristics of Ti-Nb-Ta-Zr and Ti-6Al-4V alloys for biomedical applications. Wear 2004, 257, 869–876. [Google Scholar] [CrossRef]
- Counts, W.A.; Friák, M.; Raabe, D.; Neugebauer, J. Using ab initio calculations in designing bcc Mg-Li alloys for ultra light-weight Applications. Acta Mater. 2009, 57, 69–76. [Google Scholar] [CrossRef]
- Counts, W.A.; Friák, M.; Raabe, D.; Neugebauer, J. Ab initio guided design of bcc ternary Mg-Li-X (X = Ca, Al, Si, Zn, Cu) alloys for ultra-lightweight applications. Adv. Eng. Mat. 2010, 12, 572–576. [Google Scholar] [CrossRef]
- Counts, W.A.; Friák, M.; Raabe, D.; Neugebauer, J. Using ab initio calculations in designing bcc MgLi-X alloys for ultra-lightweight applications. Adv. Eng. Mat. 2010, 12, 1198–1205. [Google Scholar] [CrossRef]
- Nikolov, S.; Petrov, M.; Lymperakis, L.; Friák, M.; Sachs, C.; Fabritius, H.O.; Raabe, D.; Neugebauer, J. Revealing the design principles of high-performance biological composites using ab initio and multiscale simulations, the example of lobster cuticle. Adv. Mater. 2010, 22, 519–526. [Google Scholar] [CrossRef] [PubMed]
- Nikolov, S.; Fabritius, H.; Petrov, M.; Friák, M.; Lymperakis, L.; Sachs, C.; Raabe, D.; Neugebauer, J. Robustness and optimal use of design principles of arthropod exoskeletons studied by ab initio-based multiscale simulations. J. Mech. Behav. Biomed. Mater. 2011, 4, 129–145. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864–B871. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Raabe, D.; Sander, B.; Friák, M.; Ma, D.; Neugebauer, J. Theory-guided bottom-up design of beta-titanium alloys as biomaterials based on first principles calculations: Theory and experiments. Acta Mater. 2007, 55, 4475–4487. [Google Scholar] [CrossRef]
- Chen, K.; Zhao, L.R.; Tse, J.S. Ab initio study of elastic properties of Ir and Ir3X compounds. J. Appl. Phys. 2003, 93, 2414–2417. [Google Scholar] [CrossRef]
- Middya, T.R.; Basu, A.N. Self-consistent T-matrix solution for the effective elastic properties of noncubic polycrystals. J. Appl. Phys. 1986, 59, 2368–2375. [Google Scholar] [CrossRef]
- Middya, T.R.; Paul, M.; Basu, A.N. Multiple-scaterring theoretical and computer-simulated dynamic-model approaches to effective elastic properties of randomly disordered composites. J. Appl. Phys. 1986, 59, 2376–2381. [Google Scholar] [CrossRef]
- Zeller, R.; Dederichs, P.H. Elastic constants of polycrystals. Phys. Stat. Solid. B 1973, 55, 831–842. [Google Scholar] [CrossRef]
- Ikehata, H.; Nagasako, N.; Furuta, T.; Fukumoto, A.; Miwa, K.; Saito, T. First-principles calculations for development of low elastic modulus Ti alloys. Phys. Rev. B 2004, 70, 174113:1–174113:8. [Google Scholar] [CrossRef]
- Ikehata, H.; Nagasako, N.; Kuramoto, S.; Saito, T. Designing new structural materials using density functional theory: The example of gum metal. MRS Bull. 2006, 31, 688–692. [Google Scholar] [CrossRef]
- Reid, C.N.; Routbort, J.L.; Maynard, R.A. Elastic Modulus of Ti-40 at.% Nb at 298 K. J. Appl. Phys. 1973, 44, 1398–1399. [Google Scholar] [CrossRef]
- Allard, S. Metals, thermal and mechanical data. In International Tables of Selected Constants; Pergamon Press: New York, NY, USA, 1969. [Google Scholar]
- Magerl, A.; Berre, B.; Alefeld, G. Cjanges of elastic-constants of V, Nb, and Ta by hydogen and deuterium. Phys. Status Solidi A 1976, 36, 161–171. [Google Scholar] [CrossRef]
- Ghosh, G.; Delsante, S.; Borzone, G.; Asta, M.; Ferro, R. Phase stability and cohesive properties of Ti-Zn intermetallics: First-principles calculations and experimental results. Acta Mater. 2006, 54, 4977–4977. [Google Scholar] [CrossRef]
- Grabowski, B.; Hickel, T.; Neugebauer, J. Ab initio study of the thermodynamic properties of nonmagnetic elementary fcc metals: Exchange-correlation-related error bars and chemical trends. Phys. Rev. B 2007, 76, 024309:1–024309:16. [Google Scholar] [CrossRef]
- Da Silva, L.M.; Rosifini-Alves-Claro, A.P.; Rabelo-Buzalaf, M.A.; Grandini, C.R. Influence of the substitutional solute on the mechanical properties of Ti-Nb binary alloys for biomedical use. Mater. Res.-Ibero-Am. J. Mater. 2012, 15, 355–358. [Google Scholar] [CrossRef]
- Zhukova, Y.S.; Pustov, Y.A.; Filonov, M.R. Kinetic regularities and mechanism of formation of nanosize passive films on titanium alloys for medical application and their electrochemical behavior in simulated physiological media. Prot. Met. Phys. Chem. Surf. 2012, 48, 315–321. [Google Scholar] [CrossRef]
- Huang, J.; Xing, H.; Sun, J. Structural stability and generalized stacking fault energies in beta Ti-Nb alloys, relation to dislocation properties. Scr. Mater. 2012, 66, 682–685. [Google Scholar] [CrossRef]
- Lopes, E.S.N.; Cremasco, A.; Afonso, C.R.M.; Caram, R. Effects of double aging heat treatment on the microstructure, Vickers hardness and elastic modulus of Ti-Nb alloys. Mater. Charact. 2011, 62, 673–680. [Google Scholar] [CrossRef]
- You, L.; Song, X. First principles study of low Young modulus Ti-Nb-Zr alloy system. Mater. Lett. 2012, 80, 165–167. [Google Scholar] [CrossRef]
- You, L.; Song, X. A study of low Young modulus Ti-Nb-Zr alloys using d electrons alloy theory. Scr. Mater. 2012, 67, 57–60. [Google Scholar] [CrossRef]
- Ye, W.; Mi, X.; Song, X. Martensitic transformation of Ti-18Nb alloy with zirconium. Rare Met. 2012, 31, 227–230. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, X.; Xu, L.; Liu, Z.; Woo, K.D. Tribological behavior study on Ti-Nb-Sn hydroxyapatite composites in simulated body fluid solution. J. Mech. Behav. Biomed. Mater. 2012, 10, 97–107. [Google Scholar] [CrossRef] [PubMed]
- Malek, J.; Hnilica, F.; Vesely, J.; Smola, B.; Bartakova, S.; Vanek, J. Microstructure and mechanical properties of Ti-35Nb-6Ta alloy after thermomechanical treatment. Mater. Charact. 2012, 66, 75–82. [Google Scholar] [CrossRef]
- Rosalbino, F.; Maccio, D.; Scavino, G.; Saccone, A. In vitro corrosion behaviour of Ti-Nb-Sn shape memory alloys in Ringer physiological solution. J. Mater. Sci. Mater. Med. 2012, 23, 865–871. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Niinomi, M.; Nakai, M.; Cui, Z.; Zhu, S.; Yang, X. Effect of Zr on super-elasticity and mechanical properties of Ti-24 at% Nb-(0,2,4) at% Zr alloy subjected to aging treatment. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2012, 536, 197–206. [Google Scholar] [CrossRef]
- Da Silva, L.M.; Rosifini Alves-Claro, A.P.; Goto-Donato, T.A.; Arana-Chavez, V.E.; Silos-Moraes, J.C.; Rabelo-Buzalaf, M.A.; Grandini, C.R. Influence of heat treatment and oxygen doping on the mechanical properties and biocompatibility of titanium-niobium binary alloys. Artif. Org. 2011, 35, 516–521. [Google Scholar] [CrossRef] [PubMed]
- Okazaki, Y.; Rao, S.; Tateishi, T.; Ito, Y. Cytocompatibility of various metal and development of new titanium alloys for medical implants. Mat. Sci. Eng. A Struc. Mat. Prop. Microstruct. Process. 1998, 243, 250–256. [Google Scholar] [CrossRef]
- Lo, W.J.; Grant, D.M. Hydroxyapatite thin films deposited onto uncoated and (Ti,Al,V)N-coated Ti alloys. J. Biomed. Mat. Res. 1999, 46, 408–417. [Google Scholar] [CrossRef]
- Berberich, F.; Matz, W.; Richter, E.; Schell, N.; Kreissig, U.; Moller, W. Structural mechanisms of the mechanical degradation of Ti-Al-V alloys: In situ study during annealing. Surf. Coat. Tech. 2000, 128, 450–454. [Google Scholar] [CrossRef]
- Jia, C.C.; Ishida, K.; Nishizawa, T. Partition of alloying elements between gamma-(A1), gamma′-(L12), and beta-(B2) phases in Ni-Al based systems. Metall. Mat. Trans. A Phys. Metall. Mat. Sci. 1994, 25, 473–485. [Google Scholar] [CrossRef]
- Bannykh, O.A.; Sheftel, E.N.; Usmanova, G.S.; Sharapov, A.A.; Filipeva, O.A.; Terekhin, A.E. Study of heat resistance of the alloy based on intermetallic compounds of Nb-Ti-Al system. Rus. Metall. 1996, 1, 30–36. [Google Scholar]
- Xu, Y.F.; Yi, D.Q.; Liu, H.Q.; Wu, X.Y.; Wang, B.; Yang, F.L. Effects of cold deformation on microstructure, texture evolution and mechanical properties of Ti-Nb-Ta-Zr-Fe alloy for biomedical applications. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruct. Process. 2012, 547, 64–71. [Google Scholar] [CrossRef]
- Narita, K.; Niinomi, M.; Nakai, M.; Hieda, J.; Oribe, K. Development of thermo-mechanical processing for fabricating highly durable beta-type Ti-Nb-Ta-Zr rod for use in spinal fixation devices. J. Mech. Behav. Biomed. Mater. 2012, 9, 207–216. [Google Scholar] [CrossRef] [PubMed]
- Nagasako, N.; Asahi, R.; Hafner, J. Ideal tensile and shear strength of a gum metal approximant, Ab initio density functional calculations. Phys. Rev. B 2012, 85, 024122–024138. [Google Scholar] [CrossRef]
- Woo, K.D.; Kim, S.H.; Kim, J.Y.; Park, S.H. Fabrication and biomaterial characteristics of HA added Ti-Nb-HA composite fabricated by rapid sintering. Korean J. Met. Mater. 2012, 50, 86–91. [Google Scholar] [CrossRef]
- Nakai, M.; Niinomi, M.; Oneda, T. Improvement in fatigue strength of biomedical beta-type Ti-Nb-Ta-Zr alloy while maintaining low Young modulus through optimizing omega-phase precipitation. Metall. Mater. Trans. A 2012, 43A, 294–302. [Google Scholar] [CrossRef]
- Xu, Y.F.; Yi, D.Q.; Liu, H.Q.; Wang, B.; Yang, F.L. Age-hardening behavior, microstructural evolution and grain growth kinetics of isothermal omega phase of Ti-Nb-Ta-Zr-Fe alloy for biomedical applications. Mater. Sci. Eng. A Struct. Mater. Prop. Microstruc. Process. 2011, 529, 326–334. [Google Scholar] [CrossRef]
- Sun, F.; Hao, Y.L.; Nowak, S.; Gloriant, T.; Laheurte, P.; Prima, F. A thermo-mechanical treatment to improve the superelastic performances of biomedical Ti-26Nb and Ti-20Nb-6Zr (at.%) alloys. J. Mech. Behav. Biomed. Mater. 2011, 4, 1864–1872. [Google Scholar] [CrossRef] [PubMed]
- Tane, M.; Nakano, T.; Kuramoto, S.; Hara, M.; Niinomi, M.; Takesue, N.; Yano, T.; Nakajima, H. Low Young modulus in Ti-Nb-Ta-Zr-O alloys, cold working and oxygen effects. Acta Mater. 2011, 59, 6975–6988. [Google Scholar] [CrossRef]
- Lazar, P.; Jahnatek, M.; Hafner, J.; Nagasako, N.; Asahi, R.; Blaas-Schenner, C.; Stoehr, M.; Podloucky, R. Temperature-induced martensitic phase transitions in gum-metal approximants, First-principles investigations for Ti3Nb. Phys. Rev. B 2011, 84, 054202:1–054202:17. [Google Scholar] [CrossRef]
- Wei, Q.; Wang, L.; Fu, Y.; Qin, J.; Lu, W.; Zhang, D. Influence of oxygen content on microstructure and mechanical properties of Ti-Nb-Ta-Zr alloy. Mater. Des. 2011, 32, 2934–2939. [Google Scholar] [CrossRef]
- Aguilar-Maya, A.E.; Grana, D.R.; Hazarabedian, A.; Kokubu, G.A.; Luppo, M.I.; Vigna, G. Zr-Ti-Nb porous alloys for biomedical application. Mater. Sci. Eng. C Mater. Biol. Appl. 2012, 32, 321–329. [Google Scholar] [CrossRef]
- Song, X.P.; You, L.; Zhang, B.; Song, A. Design of low elastic modulus Ti-Nb-Zr alloys for implant materials. Mater. Technol. 2012, 27, 55–57. [Google Scholar] [CrossRef]
- Brailovski, V.; Prokoshkin, S.; Gauthier, M.; Inaekyan, K.; Dubinskiy, S.; Petrzhik, M.; Filonov, M. Bulk and porous metastable beta Ti-Nb-Zr(Ta) alloys for biomedical applications. Mater. Sci. Eng. C Mater. Biol. Appl. 2011, 31, 643–657. [Google Scholar] [CrossRef]
- Bai, Y.J.; Wang, Y.B.; Cheng, Y.; Deng, F.; Zheng, Y.F.; Wei, S.C. Comparative study on the corrosion behavior of Ti-Nb and TMA alloys for dental application in various artificial solutions. Mater. Sci. Eng. C Mater. Biol. Appl. 2011, 31, 702–711. [Google Scholar] [CrossRef]
- Narita, K.; Niinomi, M.; Nakai, M.; Oribe, K. Heterogeneous alpha phase precipitation and peculiar aging strengthening in biomedical beta-type Ti-Nb-Ta-Zr alloy having vortical structure. J. Jpn. Inst. Met. 2011, 75, 198–206. [Google Scholar] [CrossRef]
- Elmay, W.; Patoor, E.; Bolle, B.; Gloriant, T.; Prima, F.; Eberhardt, A.; Laheurte, P. Optimisation of mechanical properties of Ti-Nb binary alloys for biomedical applications. Comput. Methods Biomech. Biomed. Eng. 2011, 14, 119–120. [Google Scholar] [CrossRef]
© 2012 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Friák, M.; Counts, W.A.; Ma, D.; Sander, B.; Holec, D.; Raabe, D.; Neugebauer, J. Theory-Guided Materials Design of Multi-Phase Ti-Nb Alloys with Bone-Matching Elastic Properties. Materials 2012, 5, 1853-1872. https://doi.org/10.3390/ma5101853
Friák M, Counts WA, Ma D, Sander B, Holec D, Raabe D, Neugebauer J. Theory-Guided Materials Design of Multi-Phase Ti-Nb Alloys with Bone-Matching Elastic Properties. Materials. 2012; 5(10):1853-1872. https://doi.org/10.3390/ma5101853
Chicago/Turabian StyleFriák, Martin, William Art Counts, Duancheng Ma, Benedikt Sander, David Holec, Dierk Raabe, and Jörg Neugebauer. 2012. "Theory-Guided Materials Design of Multi-Phase Ti-Nb Alloys with Bone-Matching Elastic Properties" Materials 5, no. 10: 1853-1872. https://doi.org/10.3390/ma5101853
APA StyleFriák, M., Counts, W. A., Ma, D., Sander, B., Holec, D., Raabe, D., & Neugebauer, J. (2012). Theory-Guided Materials Design of Multi-Phase Ti-Nb Alloys with Bone-Matching Elastic Properties. Materials, 5(10), 1853-1872. https://doi.org/10.3390/ma5101853






