1. Introduction
Suspension thermal spraying is, together with solution thermal spraying, a new process that enables production of finely grained nanometric or sub-micrometric coatings [
1]. The suspensions are formulated usually with the use of fine powder particles in water or alcohol with some additives. Subsequently, the suspension can be injected as a continuous stream or atomized liquid into the plasma jet and the liquid additives evaporate. The microstructure of coatings depends strongly on the mode of suspension injection. The coatings sprayed using atomizing injectors are generally finely grained such as ZrO
2, stabilized with 8 wt % Y
2O
3 coatings as described in [
2], or TiO
2 coatings as described in [
3] and shown in
Figure 1.
Similar microstructure is exhibited by the coatings plasma sprayed using a continuous-stream external injector (see e.g., Al
2O
3 coatings described in [
4]). On the other hand, the processing with the use of plasma torches having internal injection results in coatings that have different microstructure. The axial internal suspension injection enabled Waldbillig and Kesler [
5] to obtain ZrO
2 + 20 wt % Y
2O
3 coatings having large, well molten grains with the pores characteristic for conventional coarse powder plasma spraying. An intermediate microstructure was observed when processing with internal radial injection [
6,
7,
8]. The previous experimental studies carried out in our laboratory using the
SG 100 plasma spray torch from
Praxair to spray Ca
5(PO
4)
3OH (HA, hydroxyapatite) and TiO
2 coatings with a continuous-stream, internal radial injection, enabled us to find out two zones of microstructure, which correspond to two groups of particles. These groups are: (i) well molten particles forming a dense zone, and (ii) fine solid particles that arrive on the substrate in a solid state, forming an agglomerated zone. The typical two zones microstructure is shown in
Figure 2a and b.
Figure 1.
SEM (secondary electrons) micrograph of titanium oxide (TiO2) coatings suspension plasma sprayed using an external atomizing injector.
Figure 1.
SEM (secondary electrons) micrograph of titanium oxide (TiO2) coatings suspension plasma sprayed using an external atomizing injector.
The microstructure of the thermal spray coating results directly from the status of the grains when they arrive on the substrate or on the previously deposited coating. The large and well-deformed grains, having the form of splats, are visible in coatings sprayed using internal injectors. They agglomerate from fine initial particles in the plasma jet and are, later on, molten. These grains have their trajectory close to the hottest and fastest part of the plasma jet axis. They arrive on the substrate or on the previously deposited coating with a velocity that is sufficient for their deformation. On the contrary, the fine grains are close to the size of the solids used to formulate the suspension. They are sometimes spherical, which indicates that they were molten in the plasma jet. The ones with an irregular shape should have had their trajectory in the outer part the plasma jet. As the fine grains are not deformed, it is possible to deduce that they arrived on the substrate with low velocity.
The present study focuses on the analysis of the part of coatings’ microstructure formed by fine grains during suspension plasma spraying with the use of continuous stream injections. In particular, the thermophysical factors influencing their cohesion are analyzed. Firstly, the convective and radiative heat fluxes transferred to the growing coating is experimentally determined. The fluxes may cause the sintering of fine grains during the coating’s growth, which enhances the coating’s cohesion. On the other hand, the flux may generate residual stresses in the coatings, which can result in the formation of cracks. Different models of sintering are reviewed to determine which model is applicable for the time and temperature occurring during suspension plasma spraying. Finally, the calculations of the neck size between fine particles of Ca5(PO4)3OH and TiO2 are made for different temperatures and the results obtained are discussed in view of the microstructures observed in suspension sprayed deposits.
Figure 2.
SEM (secondary electrons) micrographs of the coatings suspension plasma sprayed using internal, radial continuous-stream injector (a) hydroxyapatite (b) titanium oxide.
Figure 2.
SEM (secondary electrons) micrographs of the coatings suspension plasma sprayed using internal, radial continuous-stream injector (a) hydroxyapatite (b) titanium oxide.
2. Experimental Methods
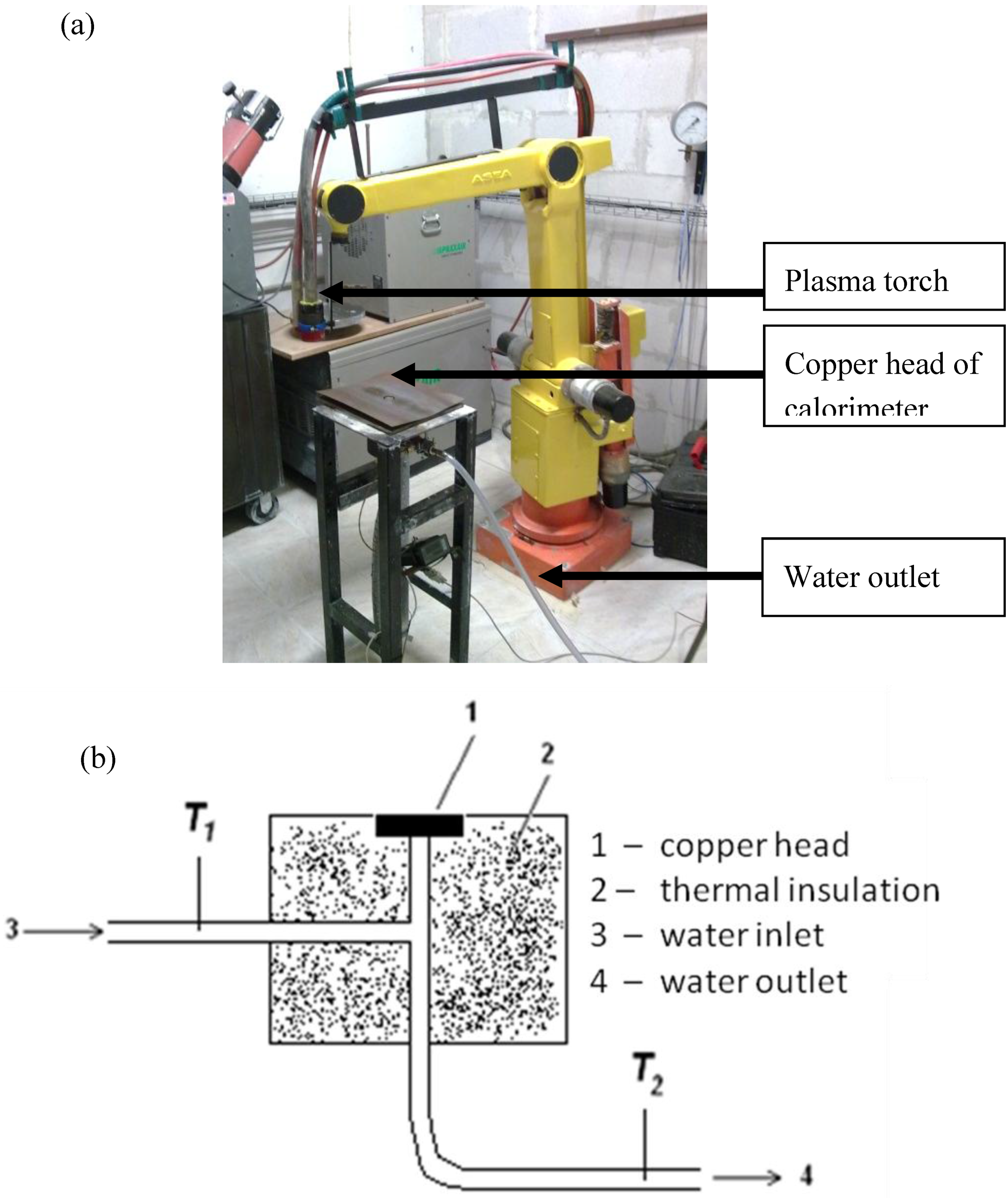
The calorimetric measurements of heat flux simulated the experimental conditions during suspension plasma spraying of hydroxyapatite and titania coatings. The experimental setup for the calorimetric measurement of heat flux is shown in
Figure 3. The copper head with a diameter of 25 mm was cooled down by water. The temperature of the water cooling the head was measured with a thermocouple. The heat flux was calculated with the use of the following equation:
In the experiments, two values of water flow rate,
Q, were applied (
Q = 0.5 and 1 L/min). The value of the copper head surface of
S = 4.91 cm
2 and the physical data for water
cp = 4.187259 J/(g K) and
ρ = 998999.7 g/m
3 were taken for calculations. The
SG-100 torch with the anode 03083-175 and the cathode 03083-129 and the gas injector 03083-112, mounted on a 5-axis
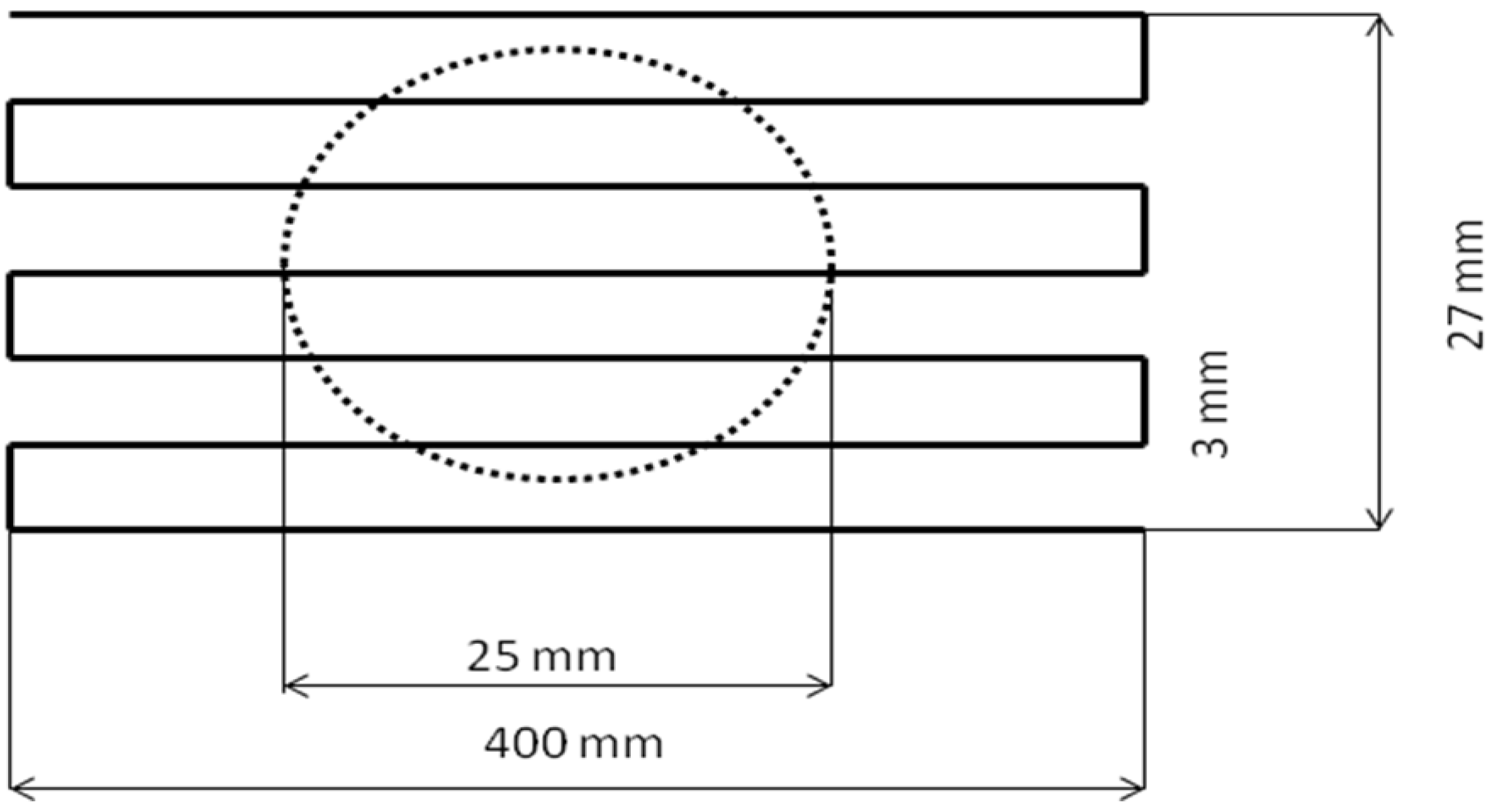
ABB IRB-6 industrial robot was used throughout the experiments. The torch trajectory is shown in
Figure 4. The trajectories were repeated three times in the experiments simulating the deposition of HA coatings and once in the experiments simulating the deposition of TiO
2 coating. The suspension liquid (no solid charge was used), with a flow rate of 20 g/min and composed of H
2O + 50 wt % C
2H
5OH, was introduced by an internal injector through a nozzle of 0.5 mm of internal diameter. The heat flux was determined in the experiments simulating the spray condition of HA as described in [
6] as a fifth set of parameters and titanium oxide as described in [
8] with the exception of spray distance, which was taken as 85 mm instead of 57 mm, which is used effectively to spray real coatings.
These spray variables are collected in
Table 1. The working gas used throughout all the experiments was a mixture of 45 Standard liter per minute (slpm) of Ar and 5 slpm of H
2. The investigations were made varying the following operational processing parameters: the power of the plasma torch, the spraying distance and the speed of the robot (to which the plasma torch was attached).
Table 1.
Plan of experiments for determining the heat flux input to the substrate.
Table 1.
Plan of experiments for determining the heat flux input to the substrate.
| Experiment number | Power input to plasma, kW | Distance between torch and substrate, mm | Linear speed of robot, mm/s | Cooling water flow rate, L/min | Suspension liquid used | Parameters simulating deposition of: |
| 1 | 33 | 70 | 500 | 0.5 | No | HA |
| 2 | 1.0 |
| 3 | 0.5 | Yes |
| 4 | 1.0 |
| 5 | 40 | 85 | 250 | 0.5 | No | TiO2 |
| 6 | 1.0 |
| 7 | 0.5 | Yes |
| 8 | 1.0 |
The temperature of incoming water (
T1 in
Figure 3b) was measured before each experiment. The temperature of outcoming water was measured continuously during the experiments. The temperature of the copper head was measured during the experiments with the use of an
IN 5 pyrometer from
Impac.
Figure 3.
Experimental setup to determine the heat flux at suspension plasma spraying (a) a general overview (b) details of the calorimetric head.
Figure 3.
Experimental setup to determine the heat flux at suspension plasma spraying (a) a general overview (b) details of the calorimetric head.
Figure 4.
The trajectory of the torch in the calorimetric experiments.
Figure 4.
The trajectory of the torch in the calorimetric experiments.
3. Modeling of the Sintering of Fine Grains in the Coating during Deposition
The small grains deposited on the substrate during the coating’s build-up are heated mainly by convective heat flux coming from the plasma jet. However, their temperature at impact may vary: a part of the small grains may remain at the periphery of the plasma jet and, independent of their thermal history (heating up, melting…), contact the substrate as a solid. Let us consider in detail the process of sintering of the particles adhering to the surface. According to the classical theory of sintering [
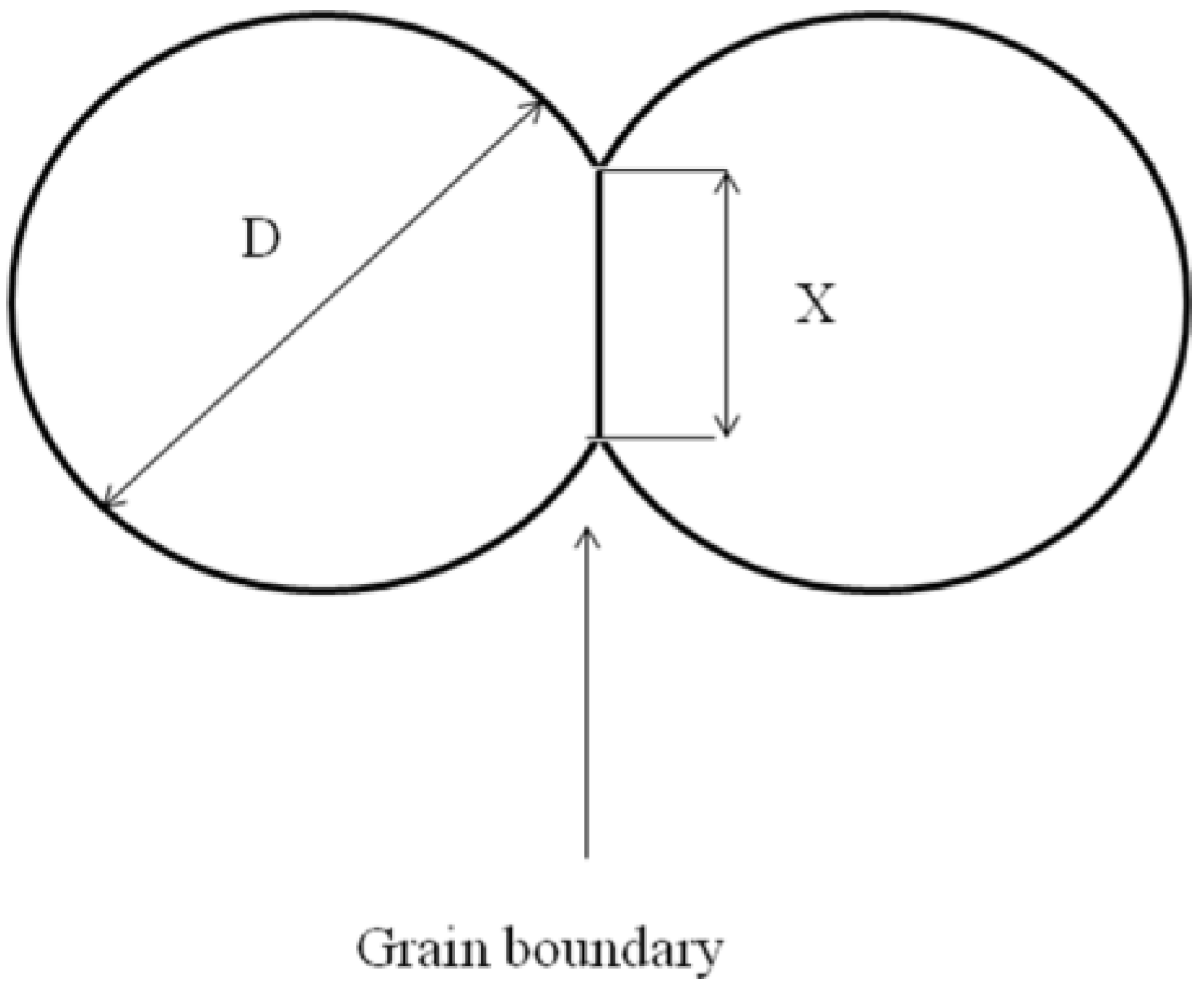
9], one can distinguish four stages of this process: adhesion, initial stage, intermediate stage and final stage. Adhesion occurs almost immediately after mechanical contact between particles. So the starting point is an assembly of contacting particles. The initial stage of sintering corresponds to the period during which the inter-particle contact area increases from 0 to 0.2 of the cross-sectional area of the particle and neck size ratio
X/
D increases from 0 to 0.1 (
Figure 5). The main driving force for sintering is the reduction of surface energy of the particles.
Figure 5.
Sketch of a model of the sintering of two particles. D = cross-sectional area of the particle; X = neck size.
Figure 5.
Sketch of a model of the sintering of two particles. D = cross-sectional area of the particle; X = neck size.
A few sintering models are available to provide an estimation of the neck’s growth rate for different mechanisms of matter transport: plastic flow, evaporation-condensation, volume diffusion, grain boundary diffusion and surface diffusion. The result can be summarized by the following expression of the neck size
vs. sintering time
t under isothermal conditions:
The mechanisms and corresponding values of the coefficients are summarized in
Table 2. This equation can be reformulated to show the time required for the growth of neck diameter up to the value
X:
In temperatures below half of the melting point, only the three mechanisms listed in
Table 2 contribute significantly to the sintering time, while others are negligible. The material data needed to calculate the sintering time are collected in
Table 3.
Table 2.
Initial-stage sintering equations [
9].
Table 2.
Initial-stage sintering equations [9].
| No | Mechanism of matter transport | The values of coefficients in equations (2) and (3) |
| n | m | C(T) |
| 1 | Volume diffusion | 5 | 3 | |
| 2 | Grain boundary diffusion | 6 | 4 | |
| 3 | Surface diffusion | 7 | 4 | |
Table 3.
Numerical data used for calculation of sintering time.
Table 3.
Numerical data used for calculation of sintering time.
| Parameters | HA | TiO2 |
| Numerical data | Commentary and reference | Numerical data | Commentary and reference |
| θ, K/s | 0.17 | [18] | - | - |
| D, m | 6 × 10-8 | [18] | - | - |
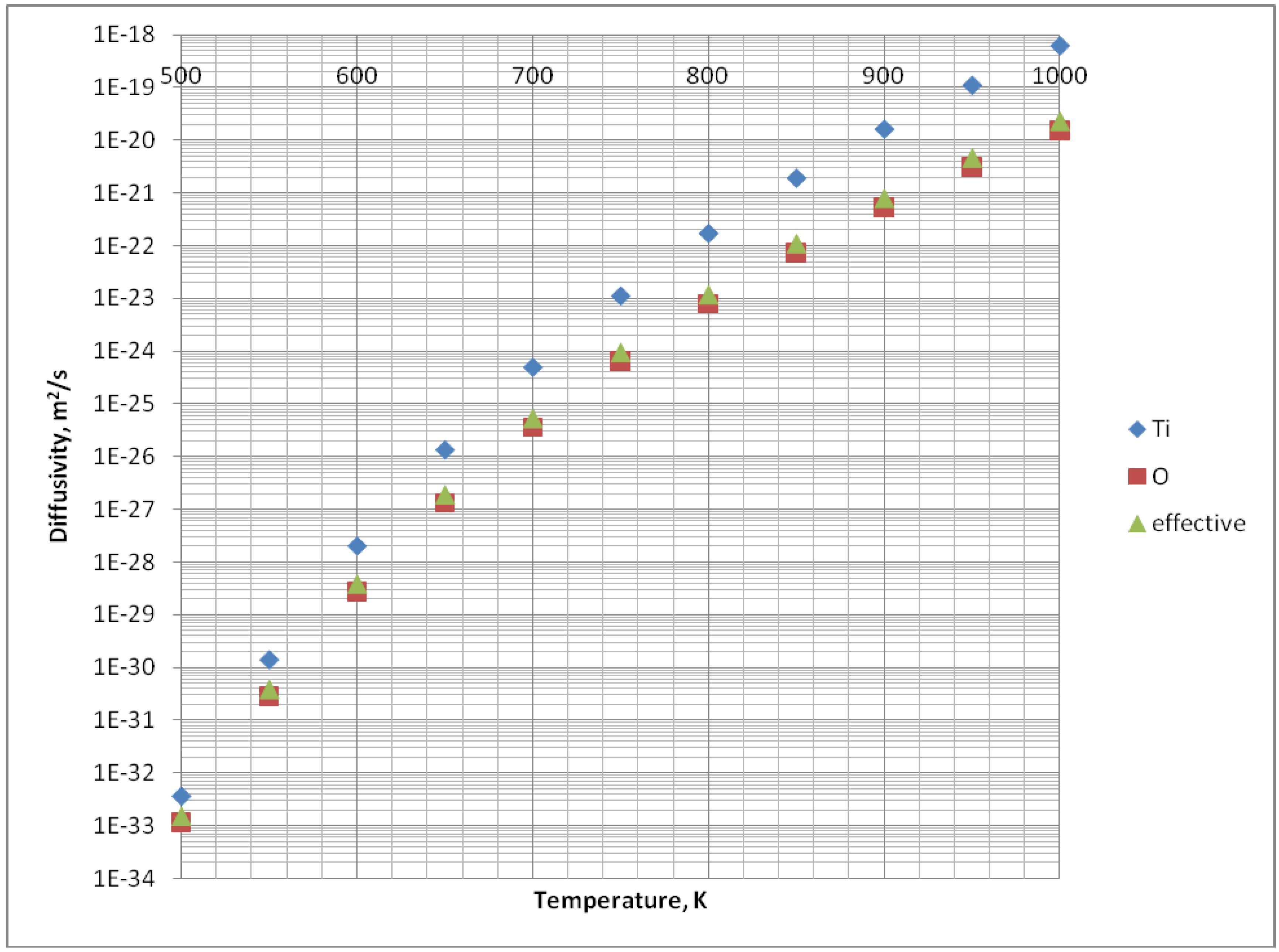
| Dv0, m2/s | 5 × 10-11 | Estimated from fitting, [18] | 2 × 10-7 | Oxygen diffusivity was taken, [14] |
| δbDb0, m3/s | 4 × 10-21 | Calculated, [10] | 6.3 × 10-18 | Calculated, [10] |
| δsDs0, m3/s |
| Qv, J/mol | 1.4 × 105 | Estimated from fitting, [18] | 2.51 × 105 | Oxygen diffusivity was taken, [14] |
| Qb, J/mol | 8.4 × 104 | Calculated, [10] | 1.51 × 105 | Calculated, [10] |
| Qs, J/mol |
| γ, J/m2 | 4.67 × 10-2 | [12] | 0.7 | [15] |
| Ω, m3 | 5.28 × 10-28 | [11] | 6.24 × 10-29 | [16] |
There were many available data concerning TiO2, but much less for HA. Some coefficients, for this material, were approximated. These approximations are described in more detail in the Results section.
5. Discussion
The microstructure of thermally sprayed deposits results mainly from the state of the particles arriving on the substrate or on the previously deposited coating. The conventional thermal spray process generally uses powders as the feedstock, and the particles arriving on the substrate can be molten, partly molten or unmolten, depending on their trajectory in flame or jet [
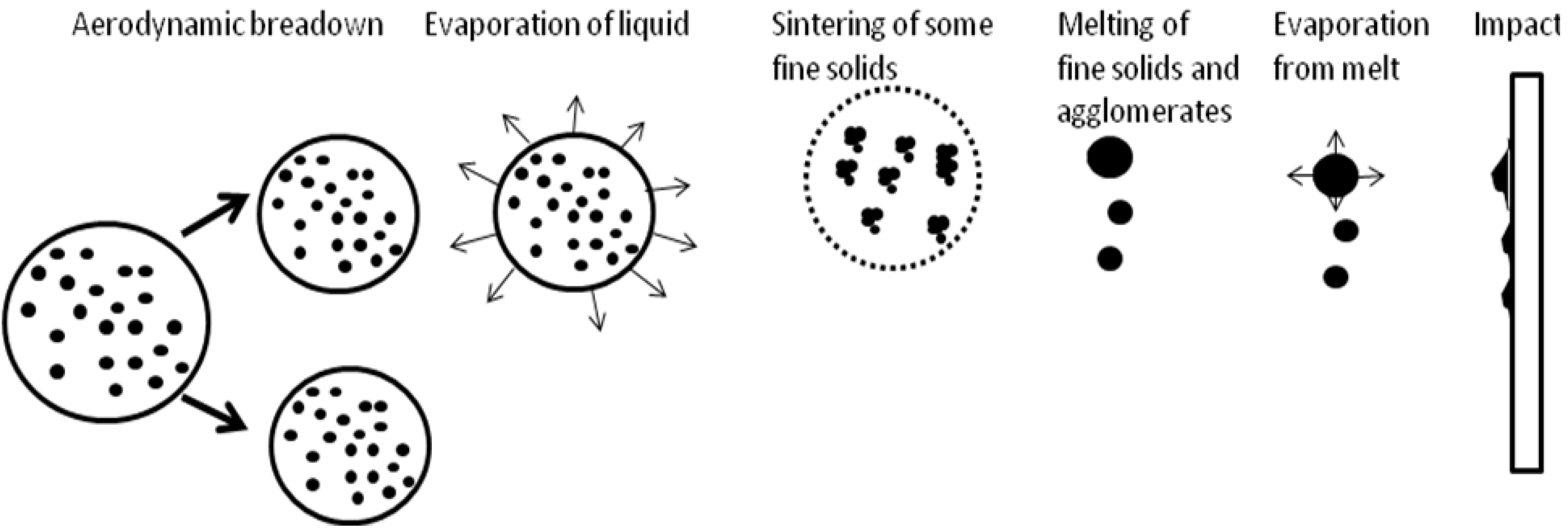
19]. The use of suspension as the feedstock to spray renders the phenomena in-flight more complicated. The droplets of suspension, depending on their trajectory in flame or jet, can be submitted to the primary and secondary break-up, liquid evaporation, fine solids agglomeration, melting (see
Figure 16).
Figure 16.
Evolution of a suspension droplet in the high temperature plasma or flame [
1].
Figure 16.
Evolution of a suspension droplet in the high temperature plasma or flame [
1].
Supposing radial injection of suspension, the trajectory of droplets can be [
1,
20]: (i) outside of the jet or flame, and the solids contained in such droplets (which do not penetrate into plasma jet) arrive unmolten on the substrate and correspond to the solids used to formulate the suspension visualized in
Figure 1 (as the irregular particles) or in
Figure 2 a and b (as agglomerated zones); (ii) in the center of the jet or flame, and these particles will be, at internal continuous-stream injection of suspension, agglomerated and well molten on impact with the substrate as shown in the dense areas in
Figure 2a and b; (iii) traversing the jet or flame, and the particles having such trajectory are re-solidified on arriving on the substrate, such as the round grains shown in
Figure 1. The sketch of possible trajectories is shown in
Figure 17. The energy flux arriving to the substrate heats up the growing coating. The resulting temperature depends on the operational conditions of spraying (
Table 3). Among the spray parameters, the spray distance most influences the coating’s temperature. The heat flux values found in the present study are slightly lower than that of the convective flux equal to
q = 1.1 MW/m
2 found by Marynowski
et al. [
21] for the spray distance of 75 mm and Ar+H
2 plasma supplied with 30 kW of electric power. The flux estimated by Tingaud
et al. [24] was even greater,
q = 30 MW/m
2, for Ar+H
2 plasma. The data of the latter study were originally obtained in the PhD thesis of Etchart-Salas [
23], who used the spray distance of 40 mm and torch in rest with regard to substrate. The values, being in the range of
q = 0.1 – 0.5 MW/m
2, were obtained in the present study with the torch being in movement and the experiment was designed to simulate the flux obtained at the coating deposition.
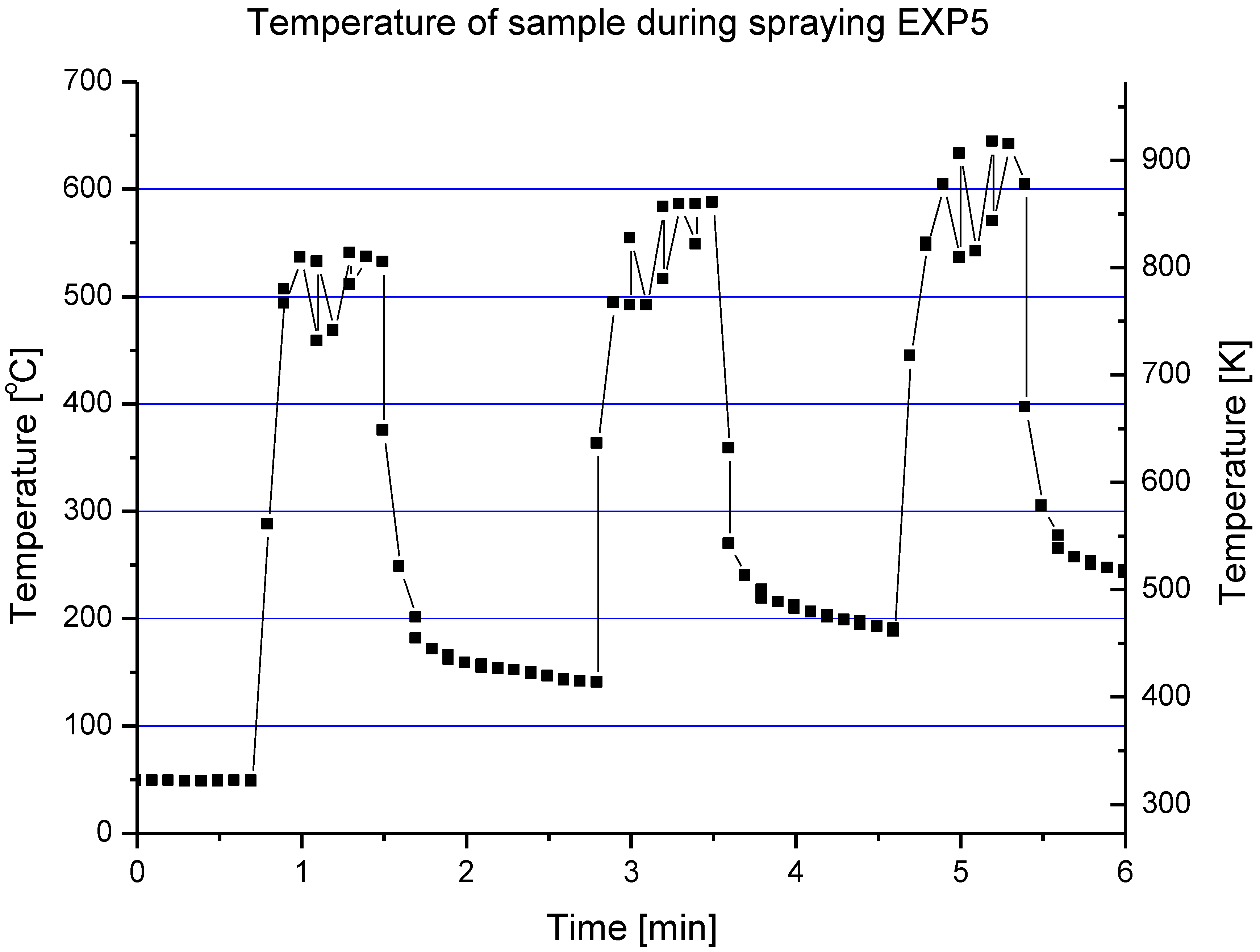
The processes of the spraying of TiO
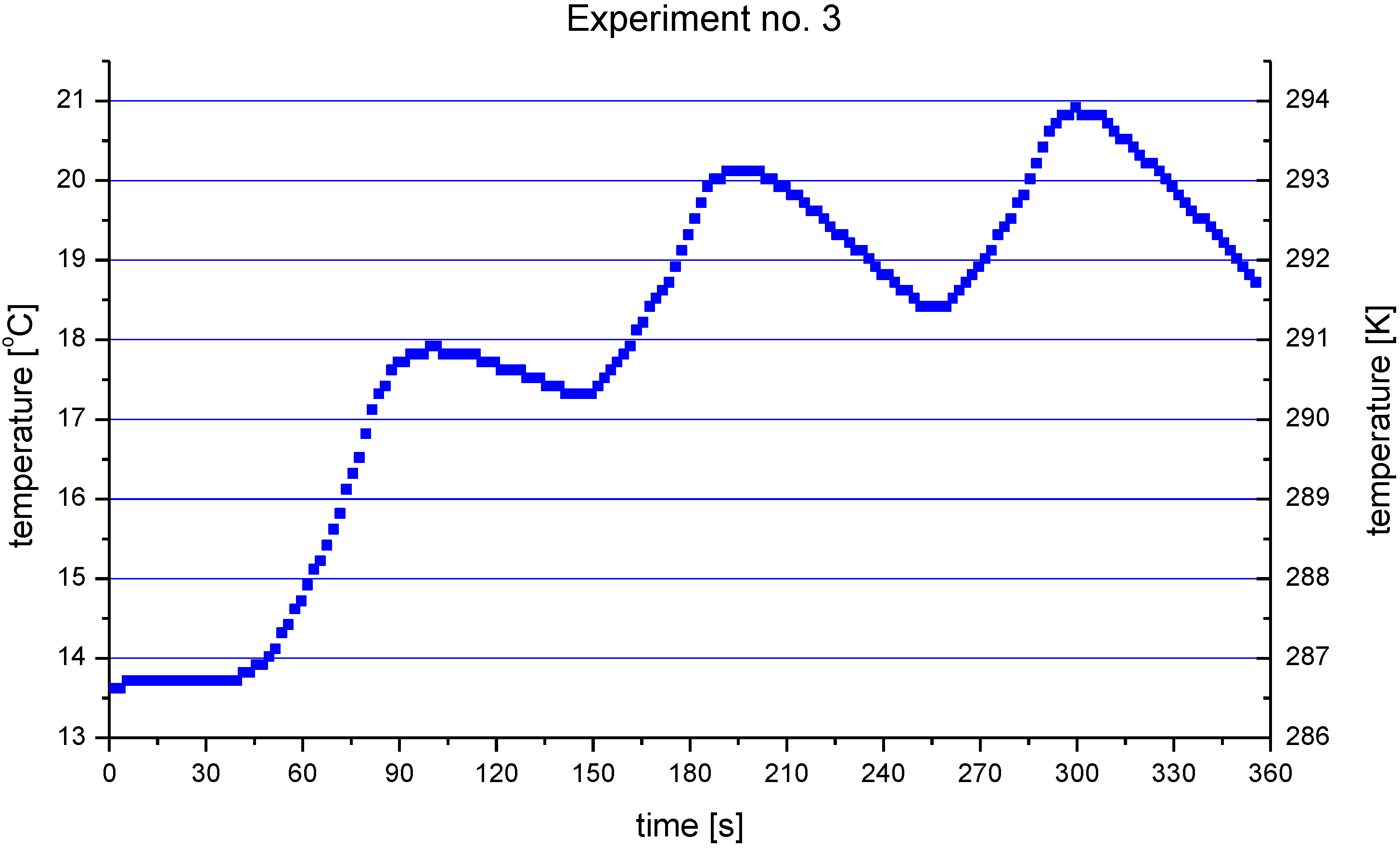
2 and HA coatings, described in this paper, were carried out in such a way that the torch realized the scans over the substrate. One trajectory over a substrate lasted about 10 s. After five such trajectories the torch was put in rest until the coating cools down to the temperature of about
T = 303 K. The resulting temperature cycles had a duration of about 1 min and minimum temperatures of about 303 K and maximum temperatures reached 663 K for TiO
2 (sprayed using internal continuous-stream injector) and about 873 K for HA as shown in
Figure 18. Among the different sintering mechanisms, only the surface diffusion method seems to be able to result in the sintering of TiO
2 or HA grains in such temperature-time conditions as show it
Figure 9 and
Figure 13, respectively.
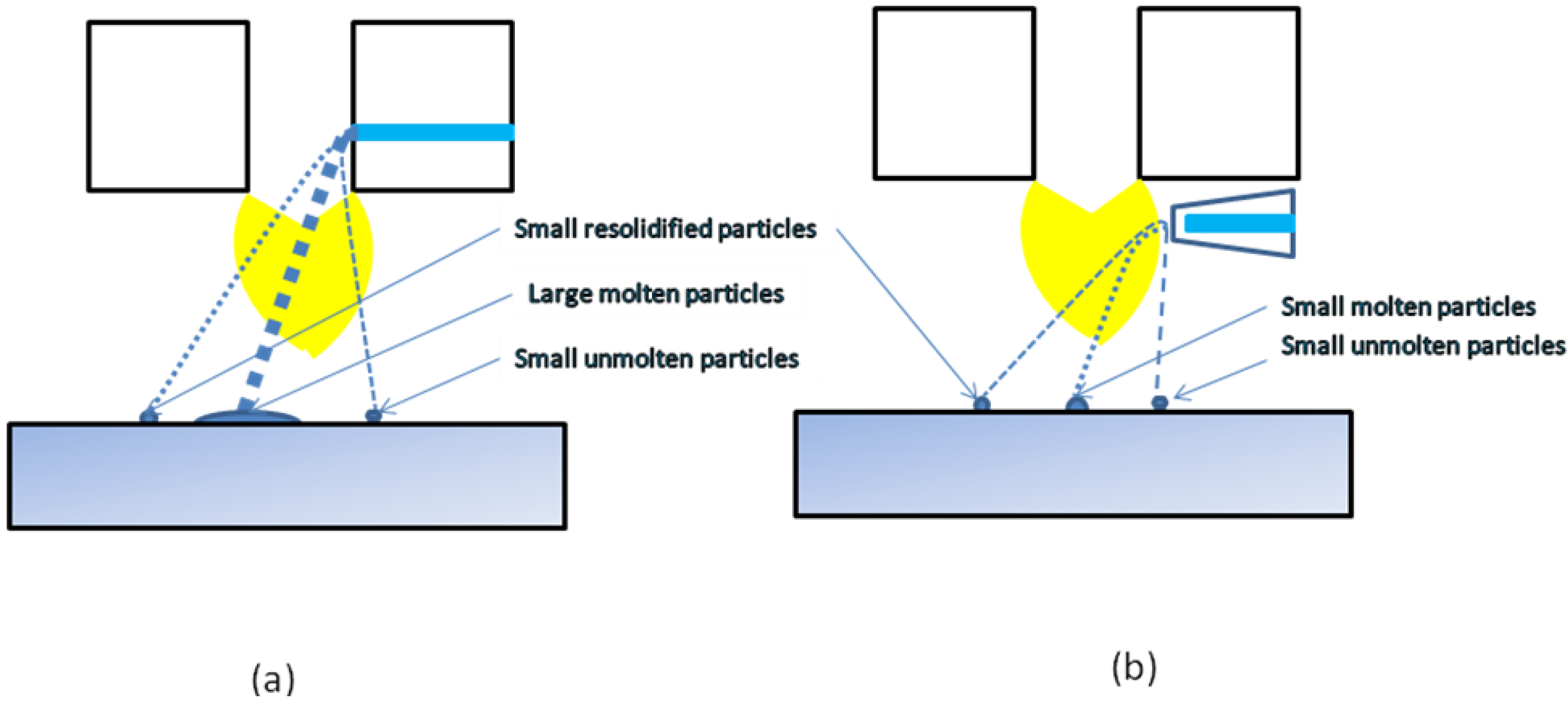
Figure 17.
Possible trajectories of droplets/particles during plasma spraying with the use of internal, continuous-stream injection (a) and external, atomizing injection (b).
Figure 17.
Possible trajectories of droplets/particles during plasma spraying with the use of internal, continuous-stream injection (a) and external, atomizing injection (b).
Figure 18.
Evolution of a typical surface temperature during HA coating deposition [
7].
Figure 18.
Evolution of a typical surface temperature during HA coating deposition [
7].
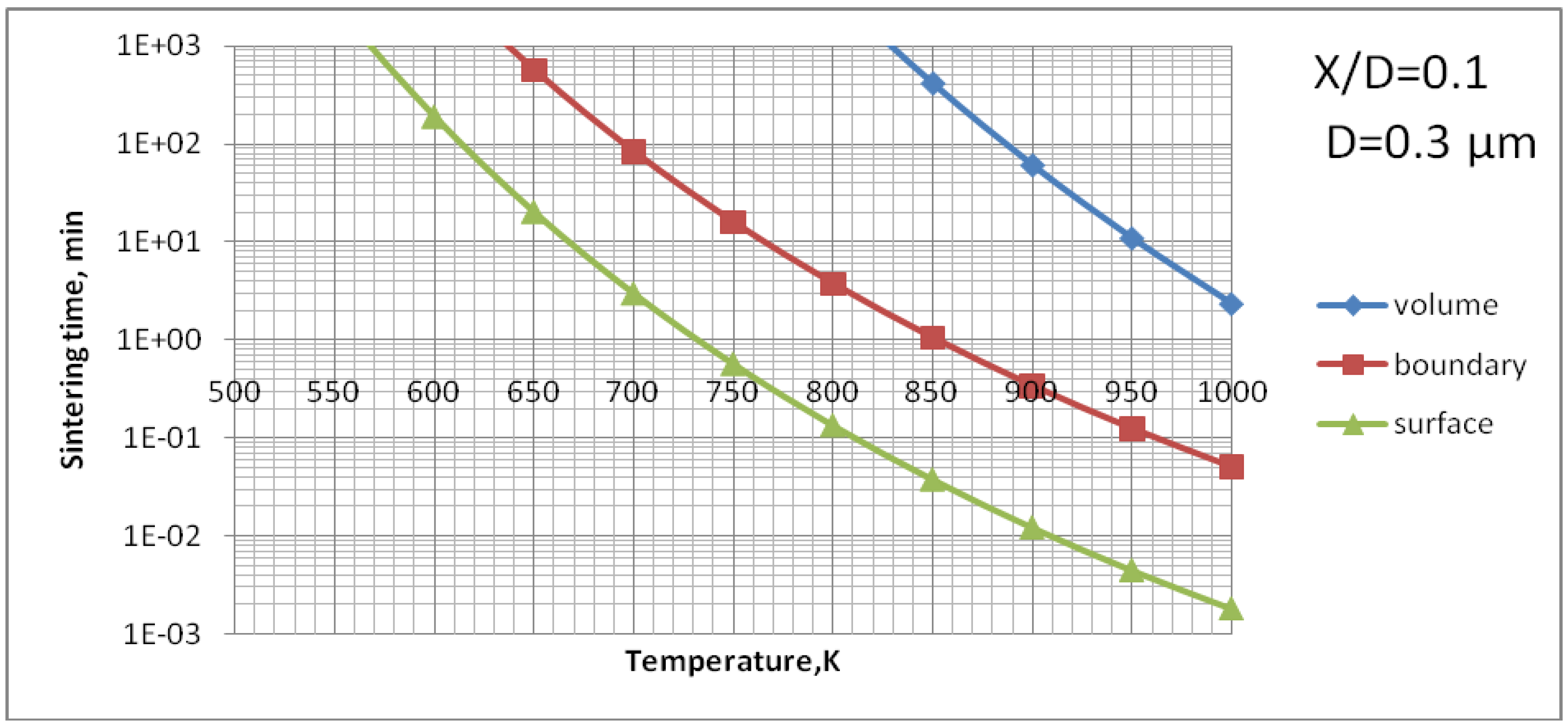
The sintering of TiO
2 grains having a size of 0.3 µm would result in formation of a neck having a size of about
X/
D = 0.1 (
Figure 10) for the experimental conditions characterized by temperature cycle of 650 K during one minute. Necks of greater size would need much longer times to grow. The cycle for HA (873 K during 1 min) would enable a neck of the size of about
X/
D = 0.2 to develop (
Figure 14). The heat flux coming from plasma jet and burning suspension, and resulting thereof coating temperature, would result in the sintering of hydroxyapatite grains. Finally, the start of the sintering processes,
i.e. the development of the neck of
X/
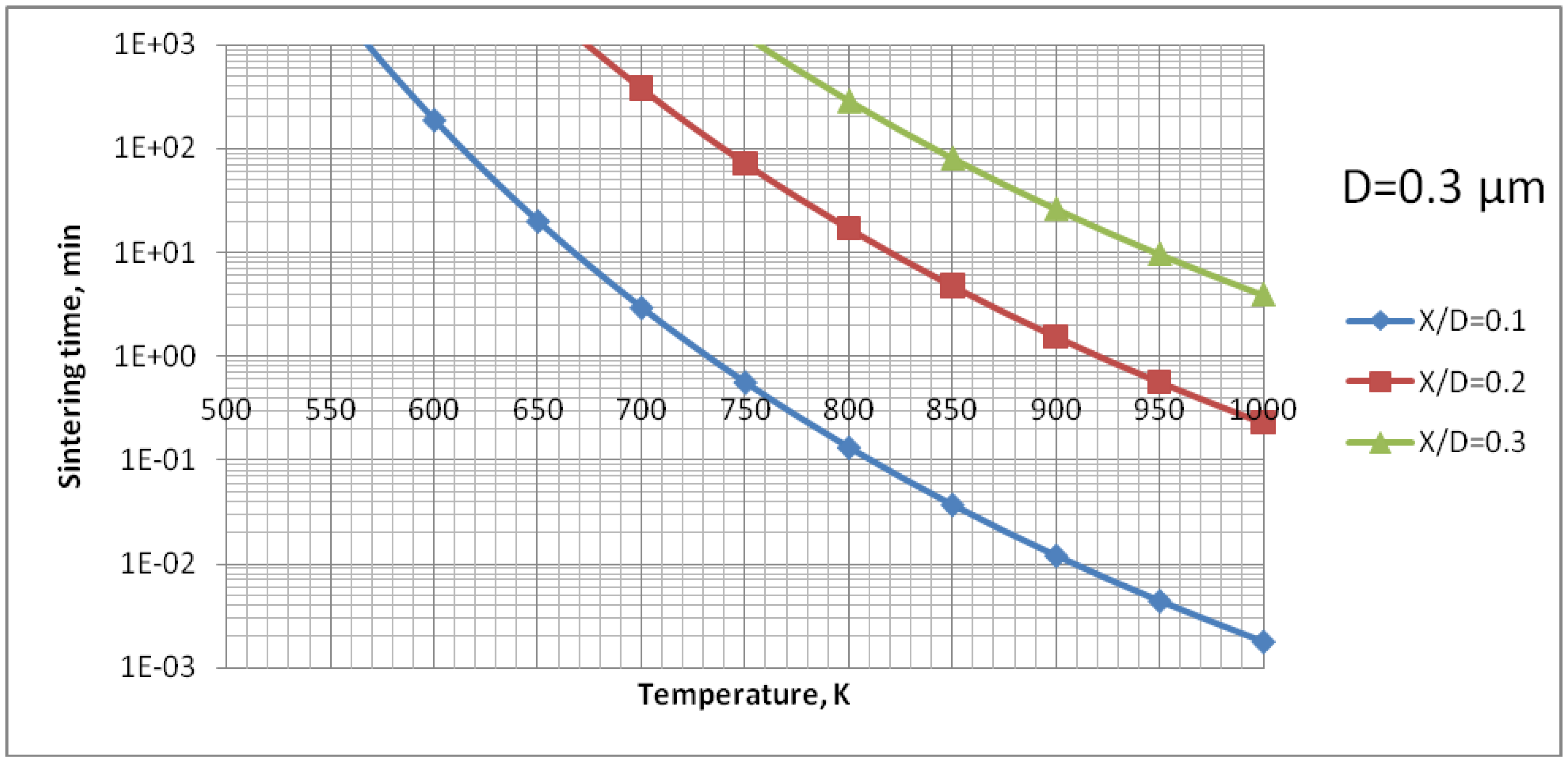
D = 0.1, depends very strongly on the size of the particles. Two TiO
2 particles having diameter of 0.1 µm would sinter such a neck at the temperature of
T = 650 K in a time as short as 12 s (
Figure 11). A HA particle of such size would develop such a neck at the experimental temperature of
T = 873 K within milliseconds (see
Figure 15). Such sintering seems to be confirmed by the transmission electron microscope observations of suspension plasma sprayed HA coatings observed by Podlesak
et al. [
7] and shown in
Figure 19.
The last point that should be stressed is the presence of vapors of water and of ethanol (the part of ethanol which did not burn out) from the suspension spraying atmosphere around the growing coating. Such atmosphere would rather promote sintering.
Figure 19.
Transmission electron micrograph of an agglomerated zone of HA coating obtained by suspension plasma spraying [
7].
Figure 19.
Transmission electron micrograph of an agglomerated zone of HA coating obtained by suspension plasma spraying [
7].
6. Conclusions
Suspension plasma spraying is a process which enables the production of finely grained nanometric or submicrometric coatings. The suspensions are formulated with the use of fine powder particles in water or alcohol. Subsequently, the suspension is injected into the plasma jet and the liquid additives evaporate. The remaining fine solids are molten and agglomerate with other molten particles or remain solid, depending on their trajectory in the plasma jet. The coating’s microstructure results from these two groups of particles arriving on a substrate. The previous experimental studies carried out for plasma sprayed titanium oxide and hydroxyapatite coatings enabled us to find out, depending on the suspension injection mode, a microstructure composed of fine grains or a microstructure characterized by two zones: (i) a dense zone formed by well molten particles, and, (ii) an agglomerated zone formed by fine solid particles that arrived on the substrate in a solid state.
The present paper concentrates on the theoretical analysis of the process of formation of finely grained microstructure, which corresponds also to the agglomerated zone. The experimental section deals with the calorimetric measurements of the convective heat flux input to the substrate in the experimental conditions simulating the coating deposition. The heat flux was found to be in the range from 0.08 to 0.5 MW/m2, depending on experimental conditions. The theoretical section of the paper deals with the calculation of possible sintering of fine particles arriving on the substrate in the solid state. The models of volume, grain boundary and surface diffusion sintering were analyzed and adapted to the size and chemical composition of particles, temperature and time scales corresponding to suspension plasma spraying conditions. The model of surface diffusion was the most appropriate to describe the sintering at suspension plasma spraying. It was found that it is possible to develop necks having the relative size of 10% of particle diameter during the thermal cycles occurring at the processing of sprayed coatings. Consequently, the sintering of the fine grains deposited on the substrate was proved to occur in the experimental conditions of suspension plasma sprayed TiO2 and HA coatings’ growth. The transmission electron microscopic observations of the agglomerated zone in the HA coating obtained by using such a technique confirms this conclusion. Further research should characterize the local mechanical properties of agglomerate zones by means of nanoindentation tests and compare the properties of such agglomerate zones to those of dense zones.