Carrier States in Ferromagnetic Semiconductors and Diluted Magnetic Semiconductors—Coherent Potential Approach—
Abstract
:1. Introduction
2. Conduction-electron States in a Ferromagnetic Semiconductor (FMS)
2.1. Coherent Potential Approach to the s-f Model
2.2. t-Matrix Elements and Their Thermal Average
2.3. Results for the Conduction-electron States in an FMS
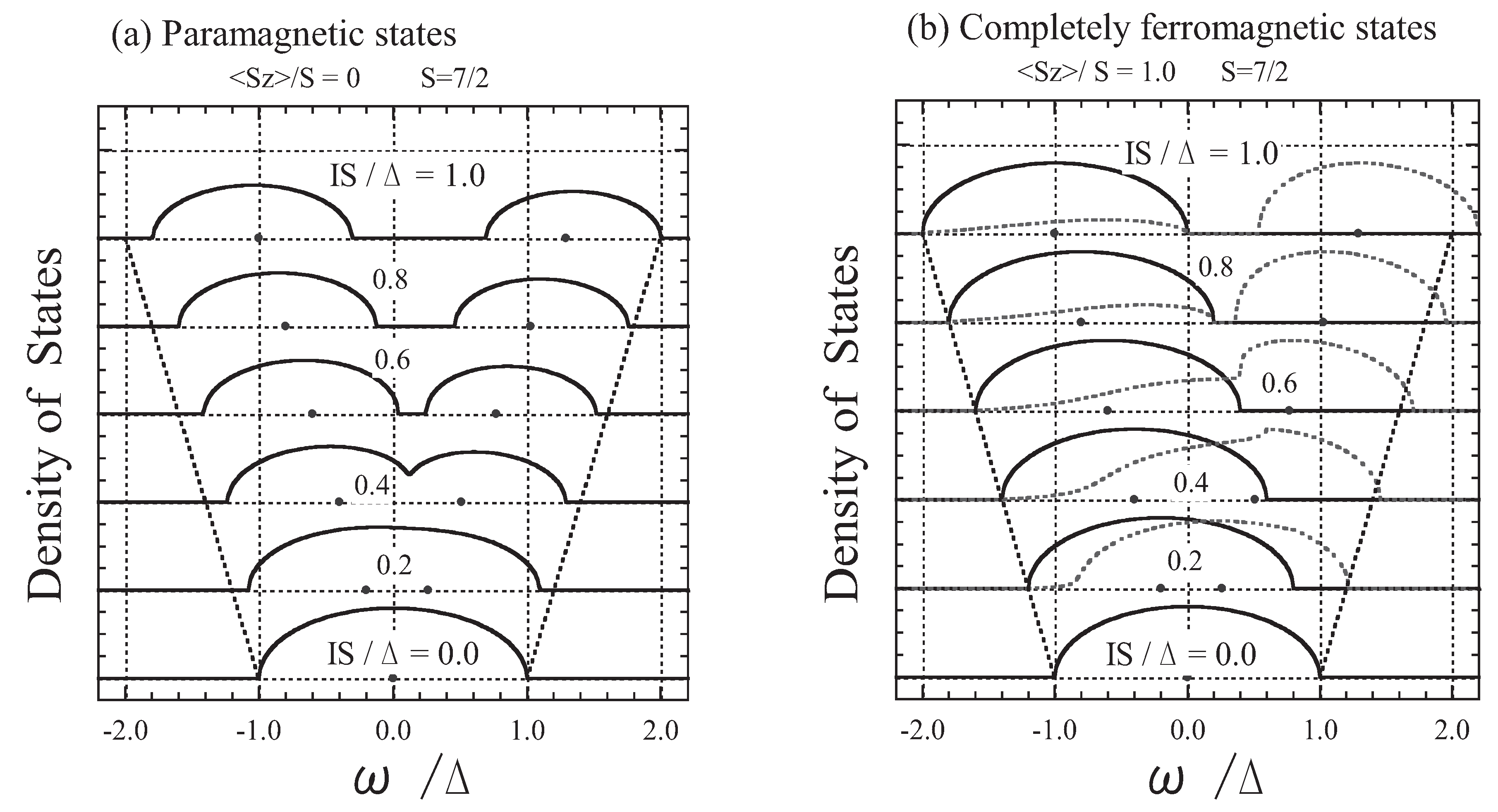

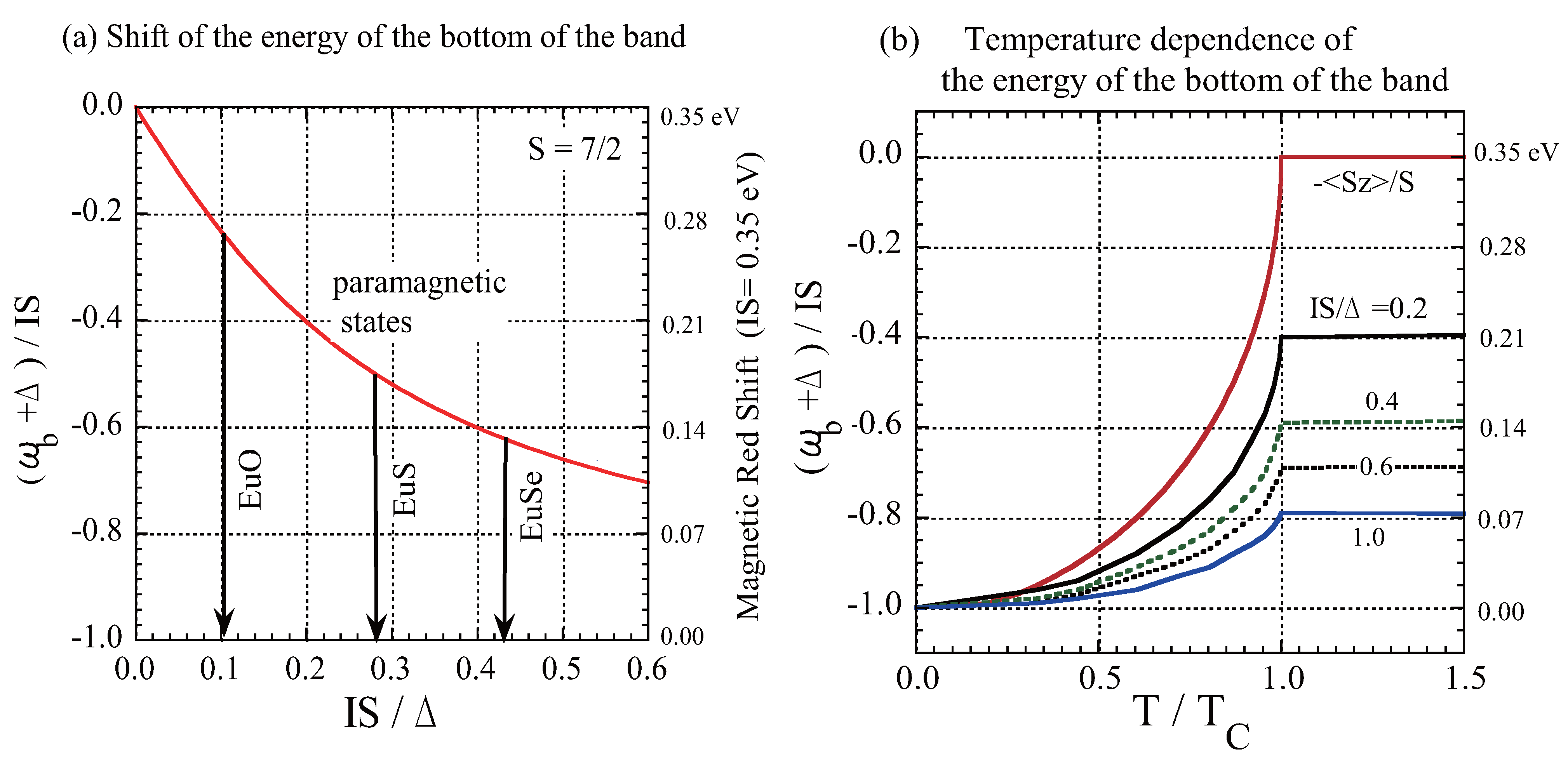
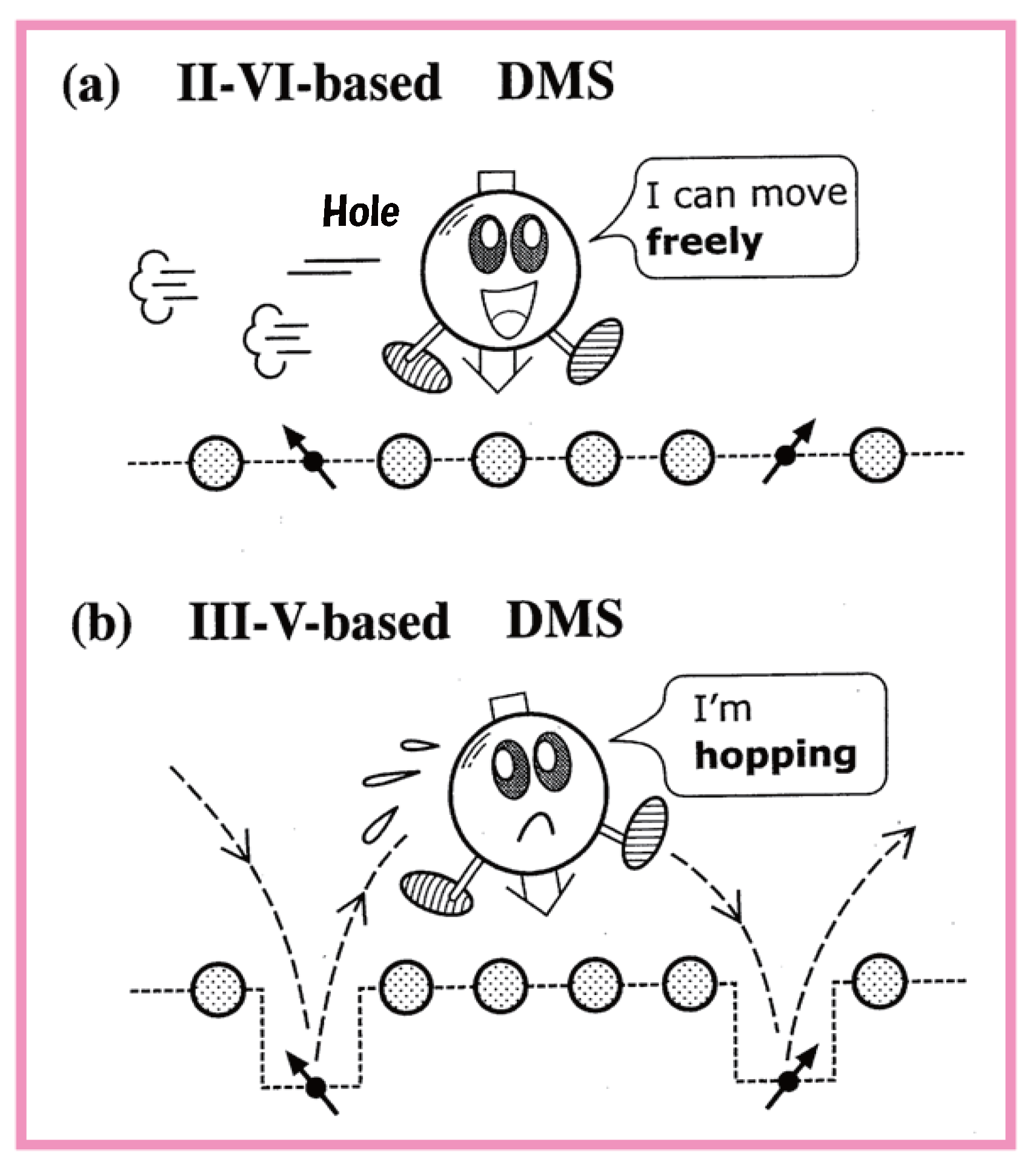
3. Carrier States in Diluted Magnetic Semiconductors (DMSs)
3.1. Model Hamiltonian for a Carrier in a DMS and the Application of the Dynamical CPA
3.2. General Consideration for the Carrier States in a DMS
3.3. The Case of Strong Exchange Interaction
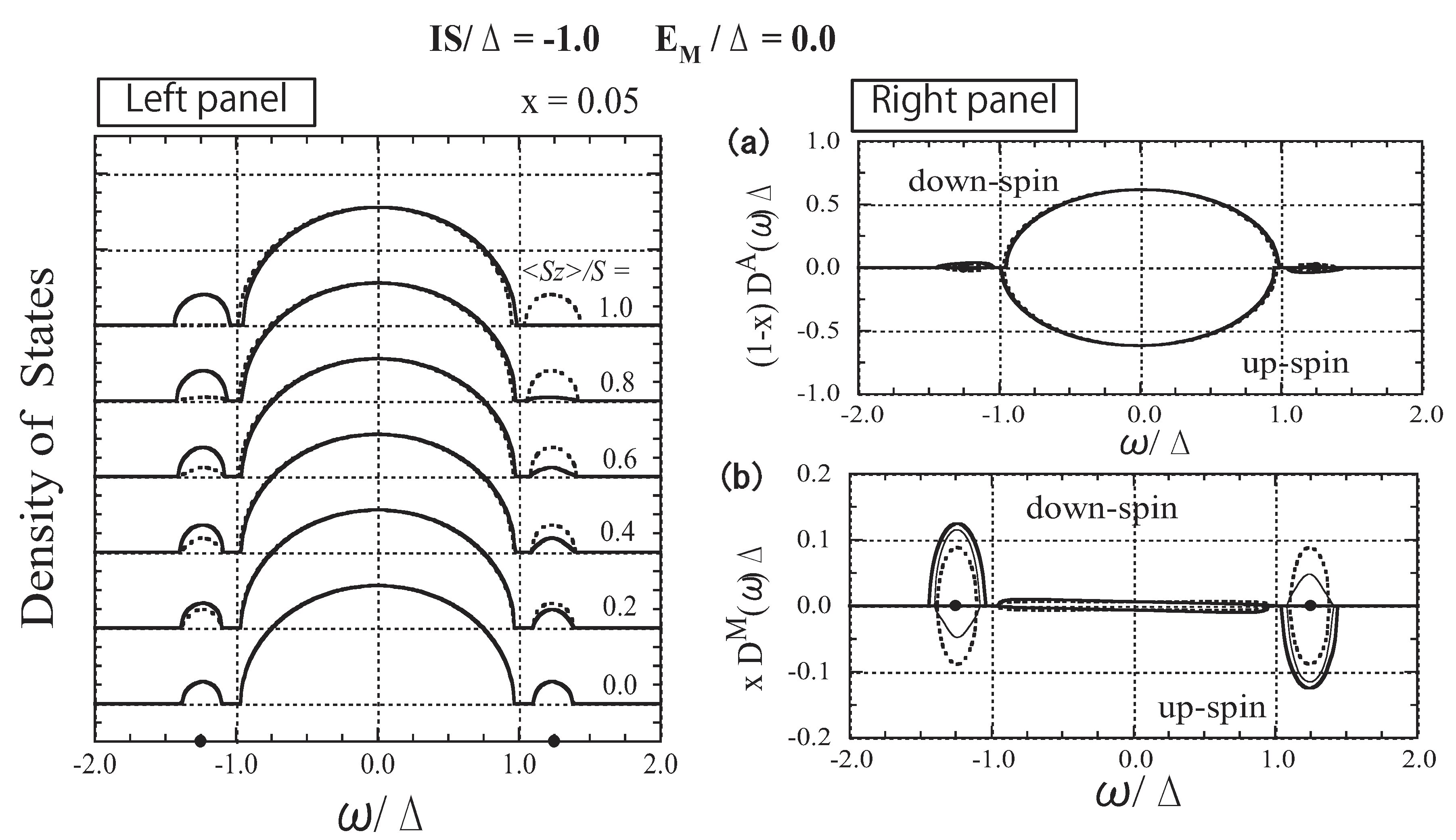
3.4. The Case of Moderate Exchange Strength (II-VI-based DMSs)
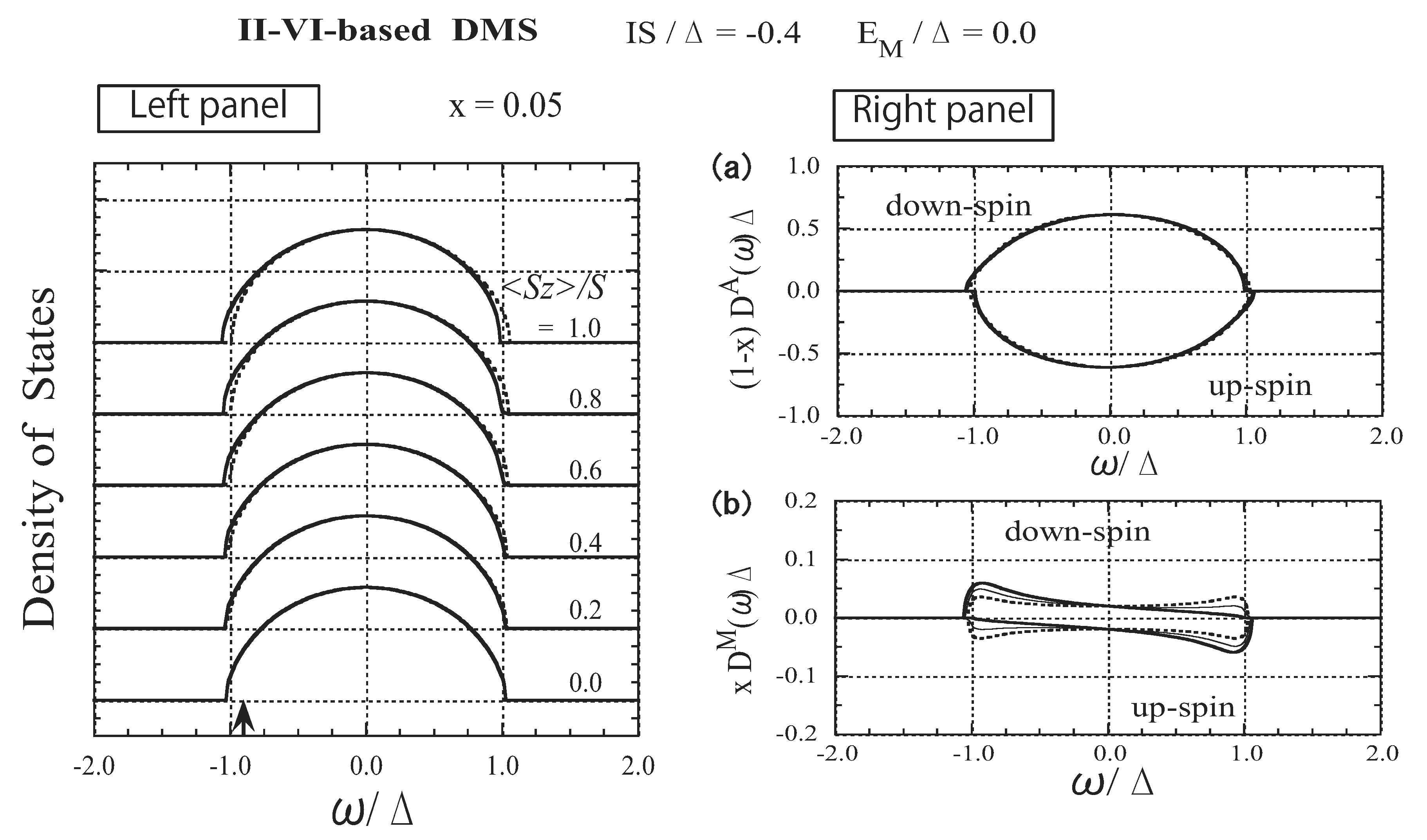
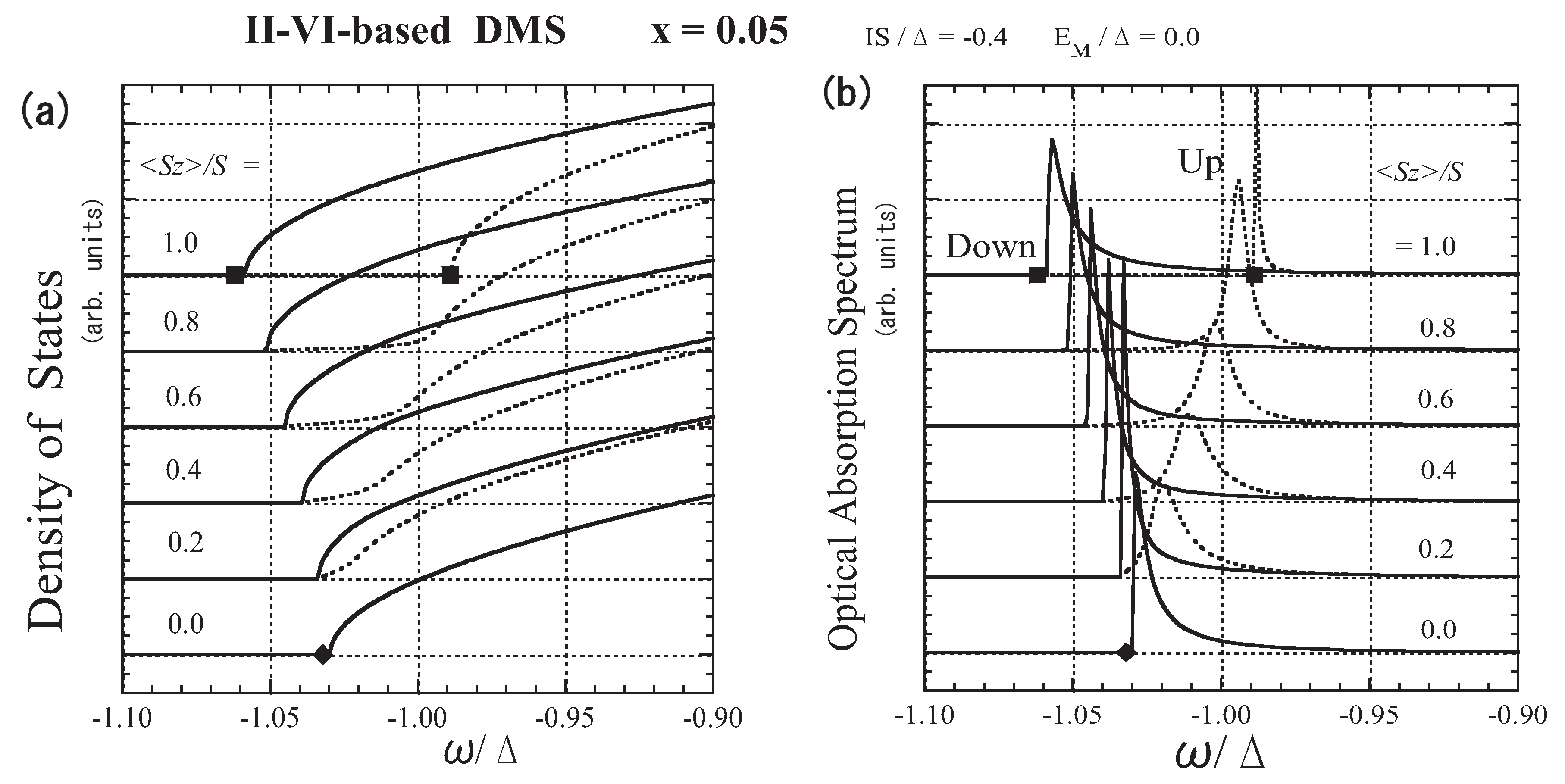
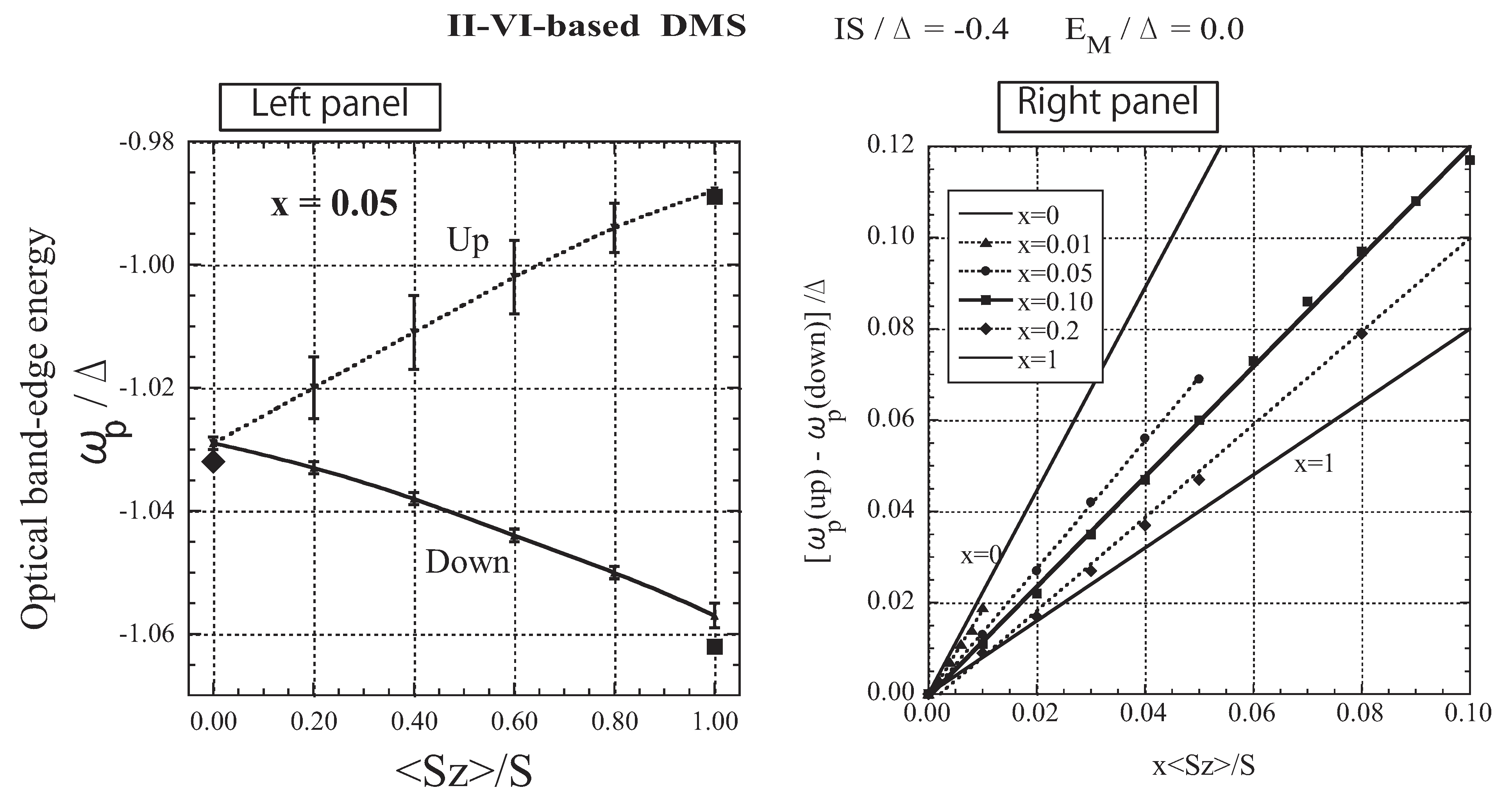
3.5. The Case of Strong Attractive Potential
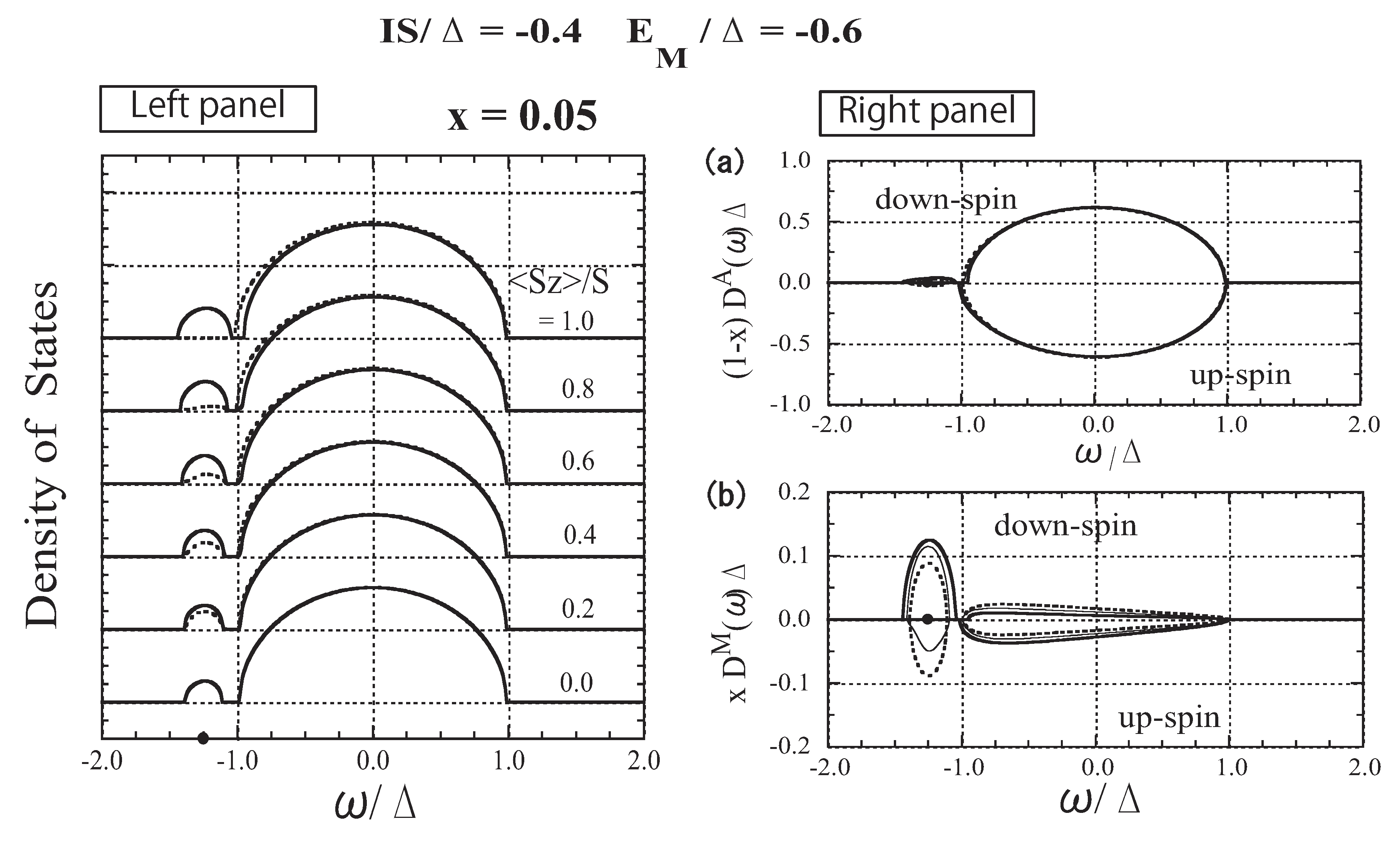
3.6. Mechanism of Carrier-induced Ferromagnetism in DMSs
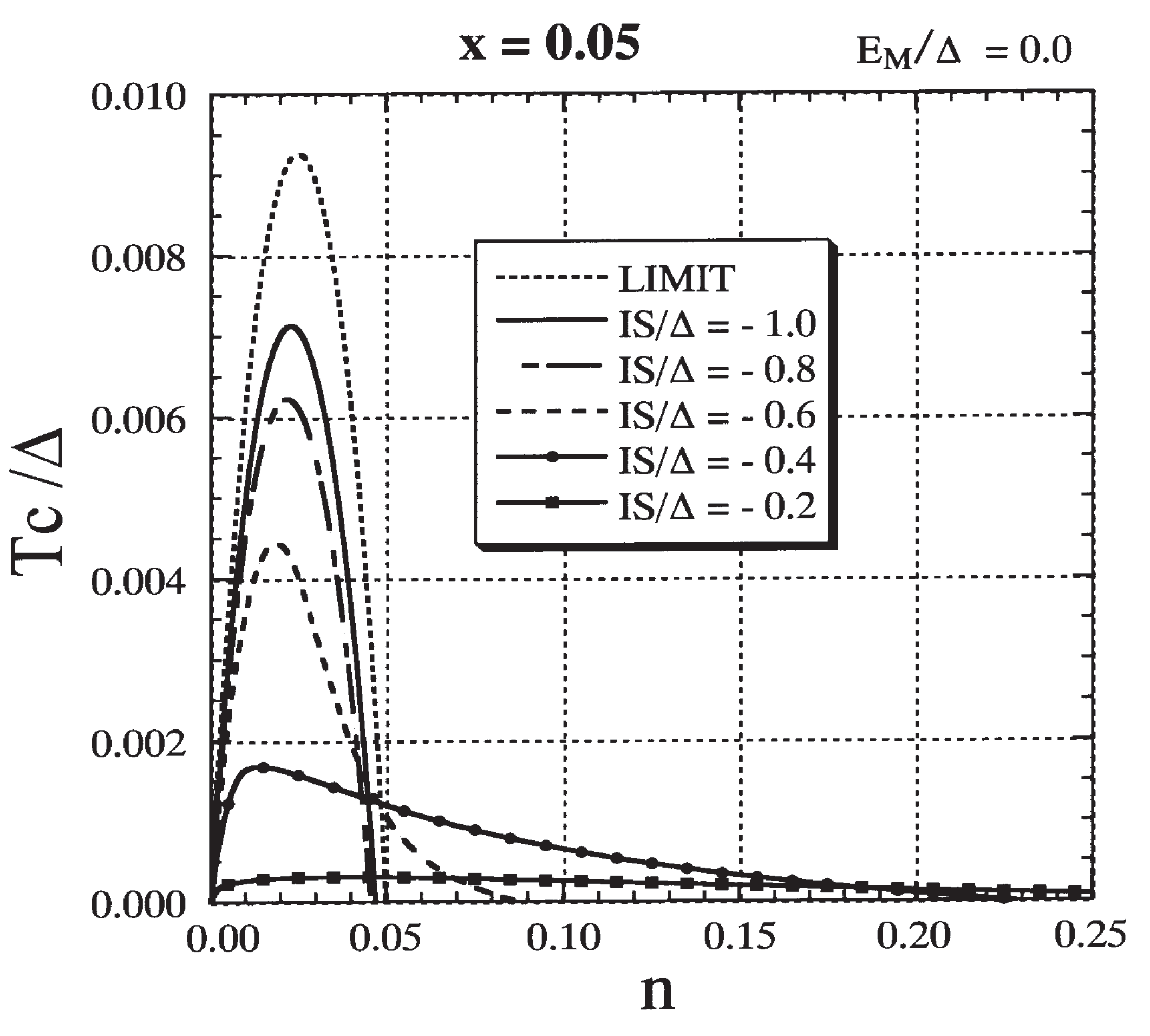
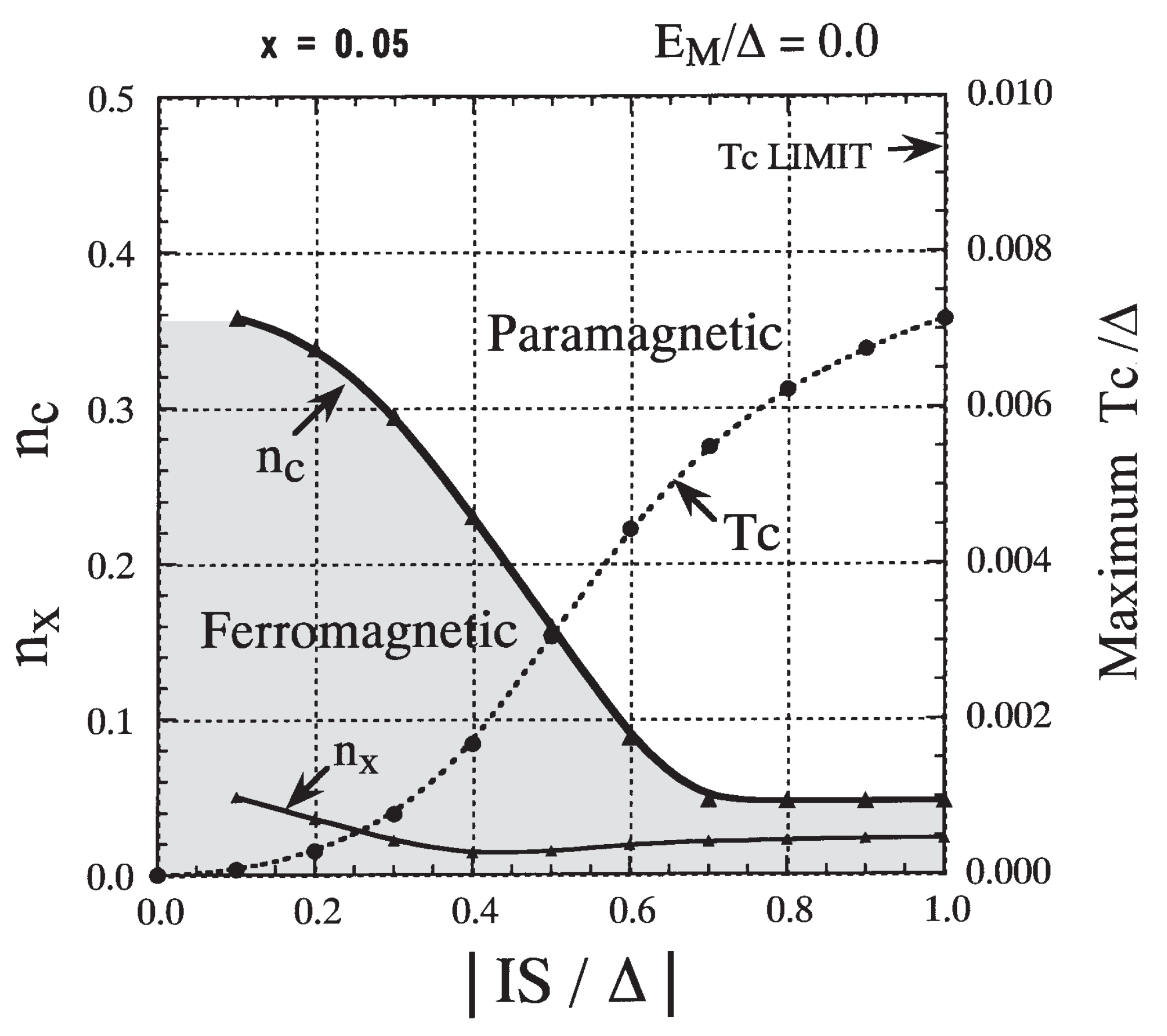
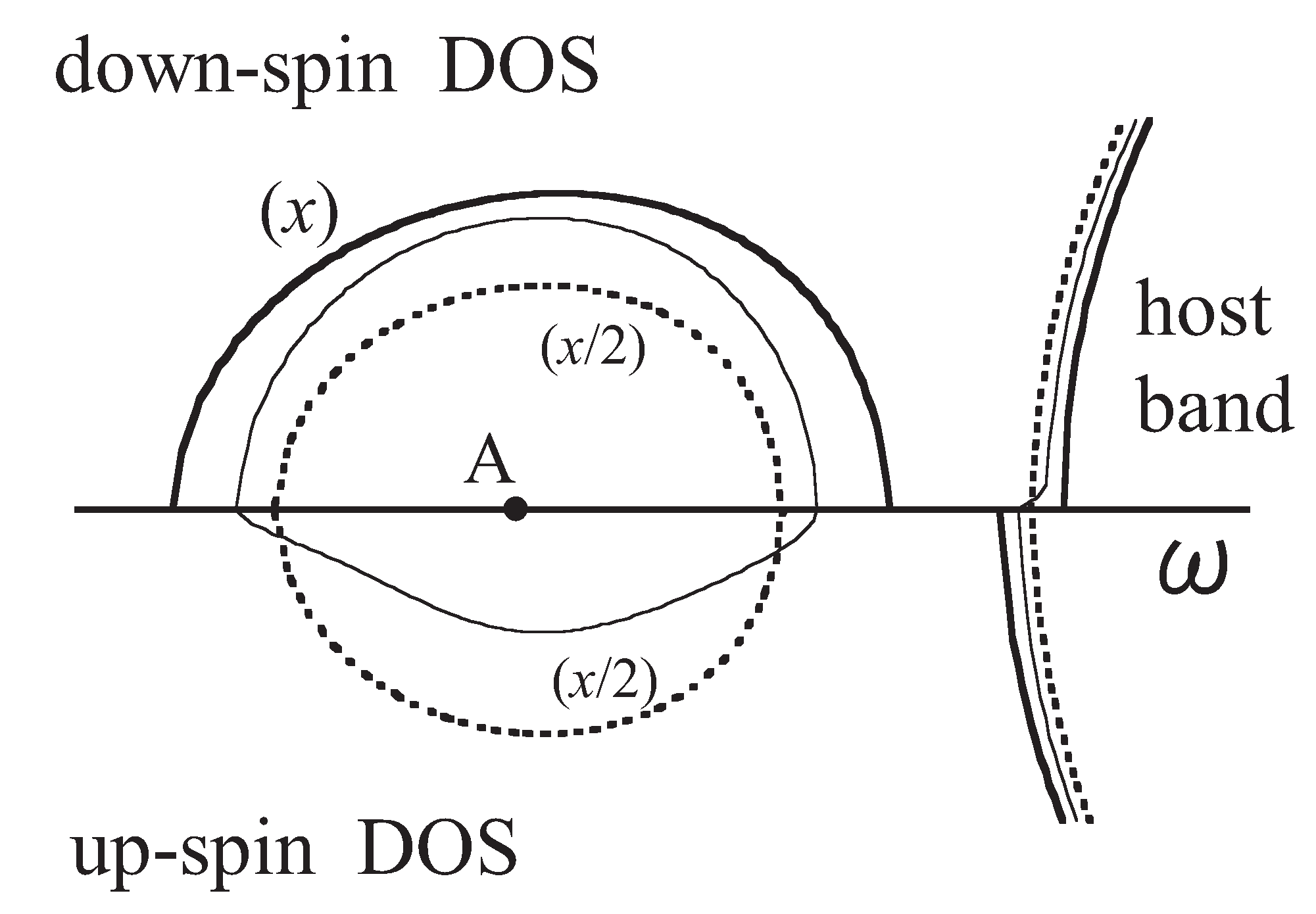
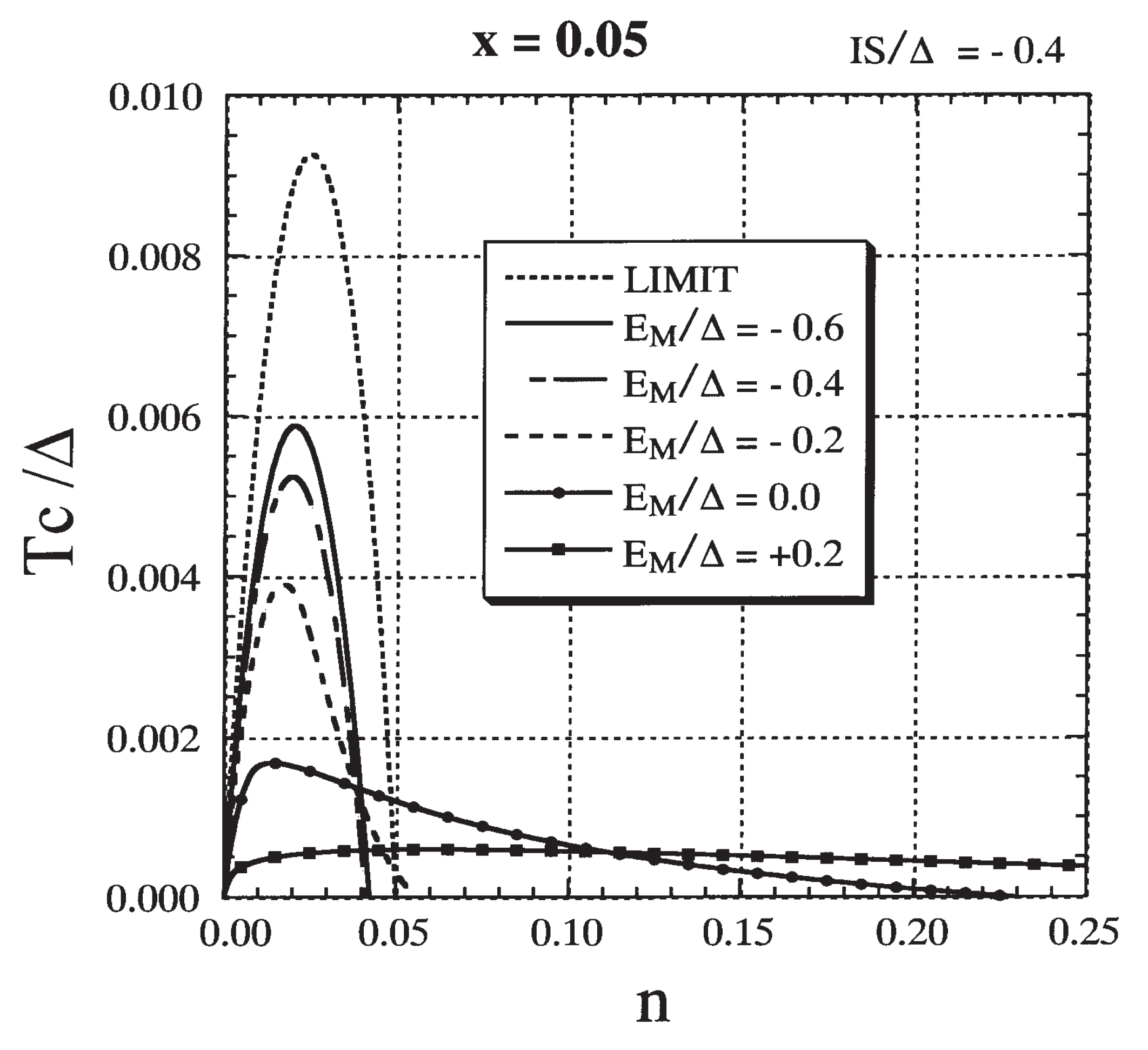
3.7. Specific Results for (Ga,Mn)As
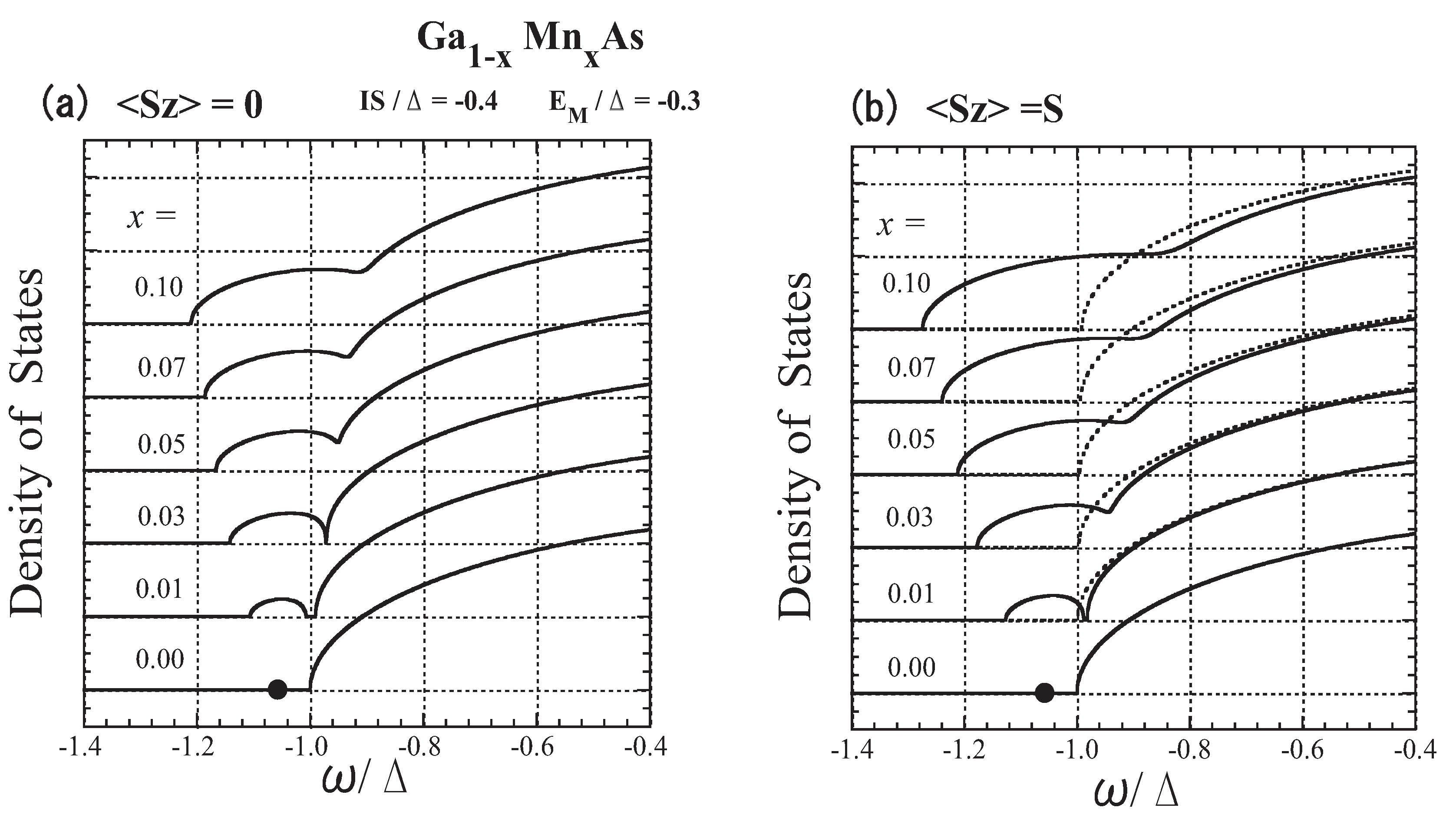
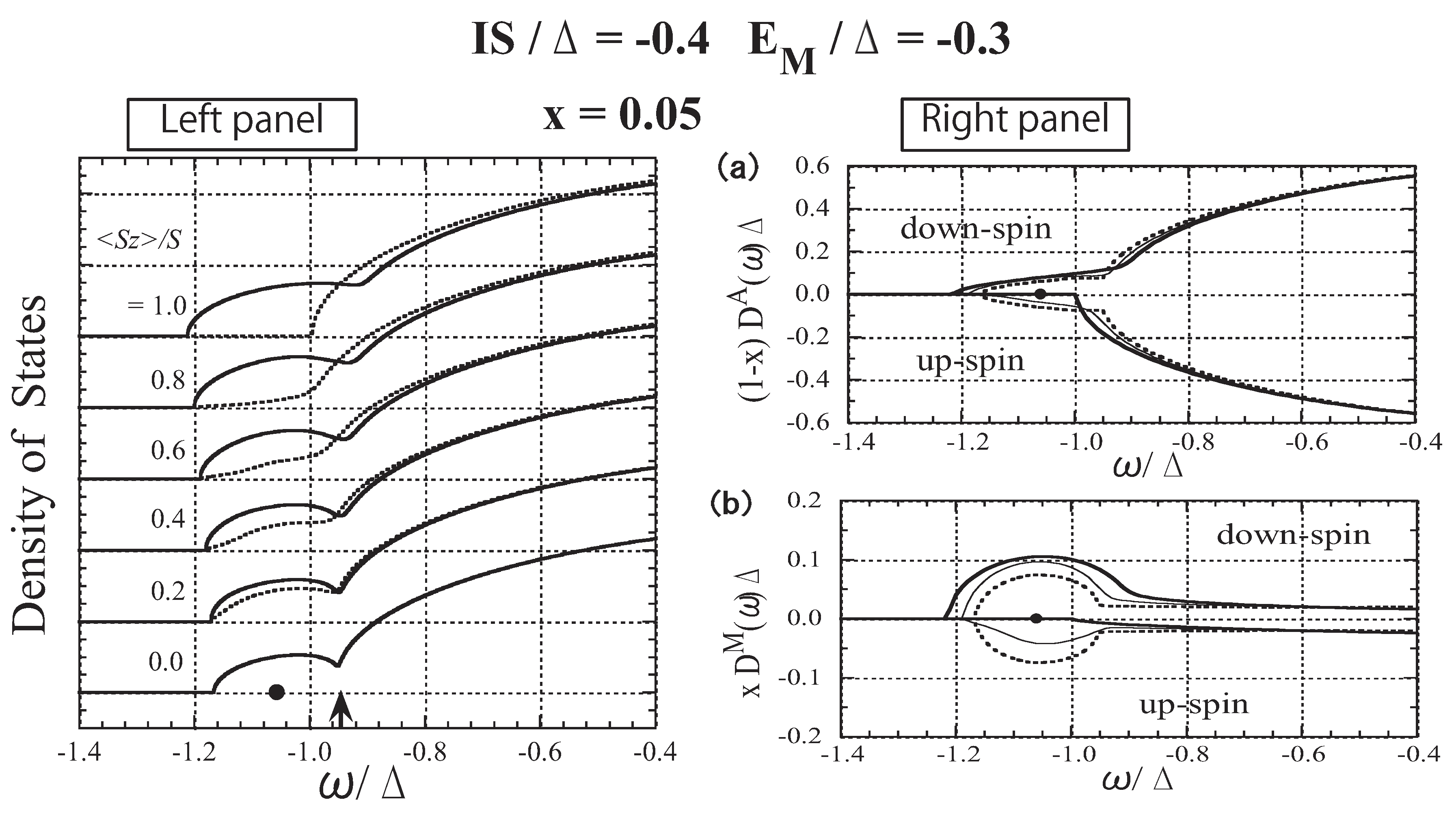
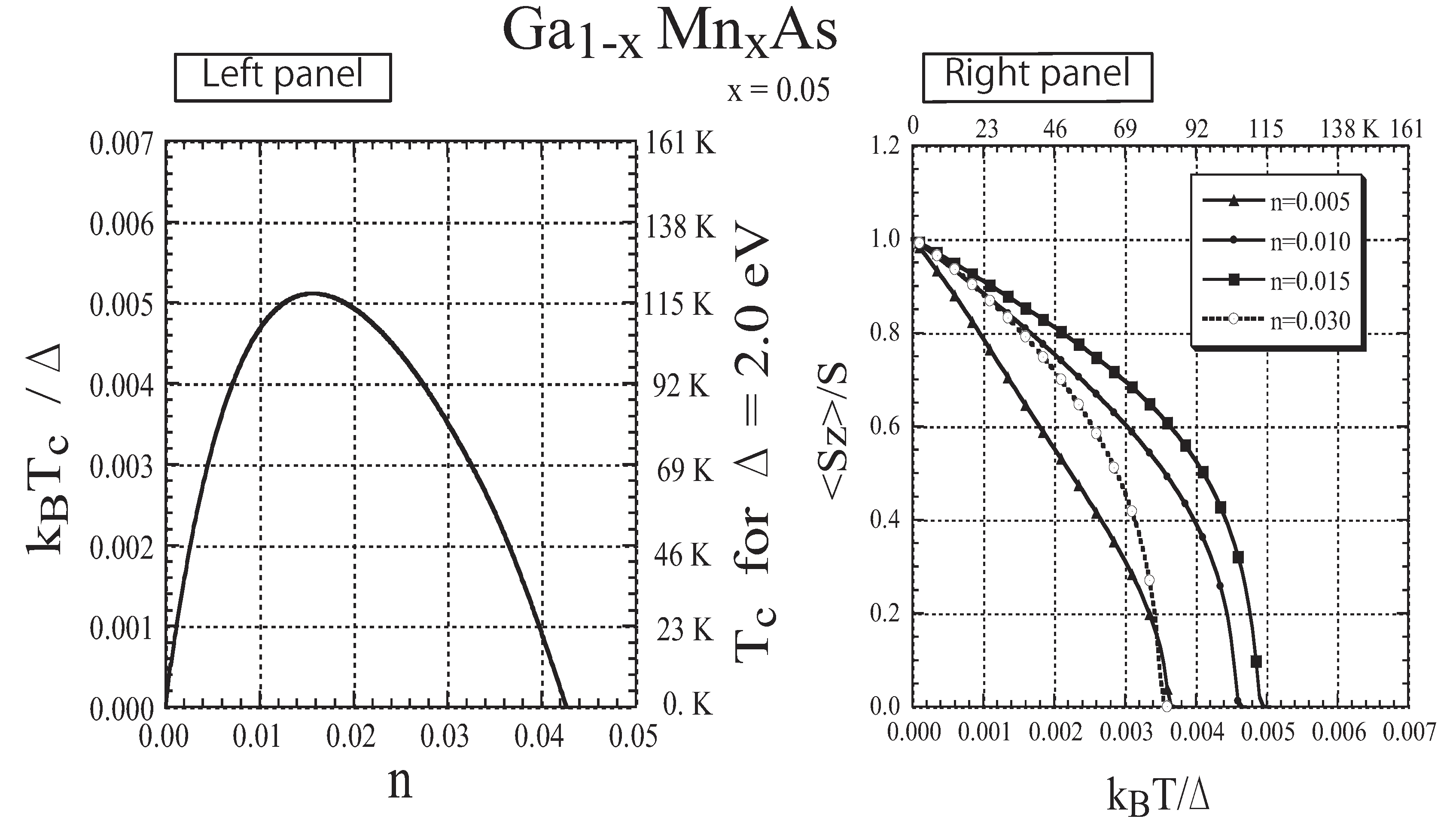
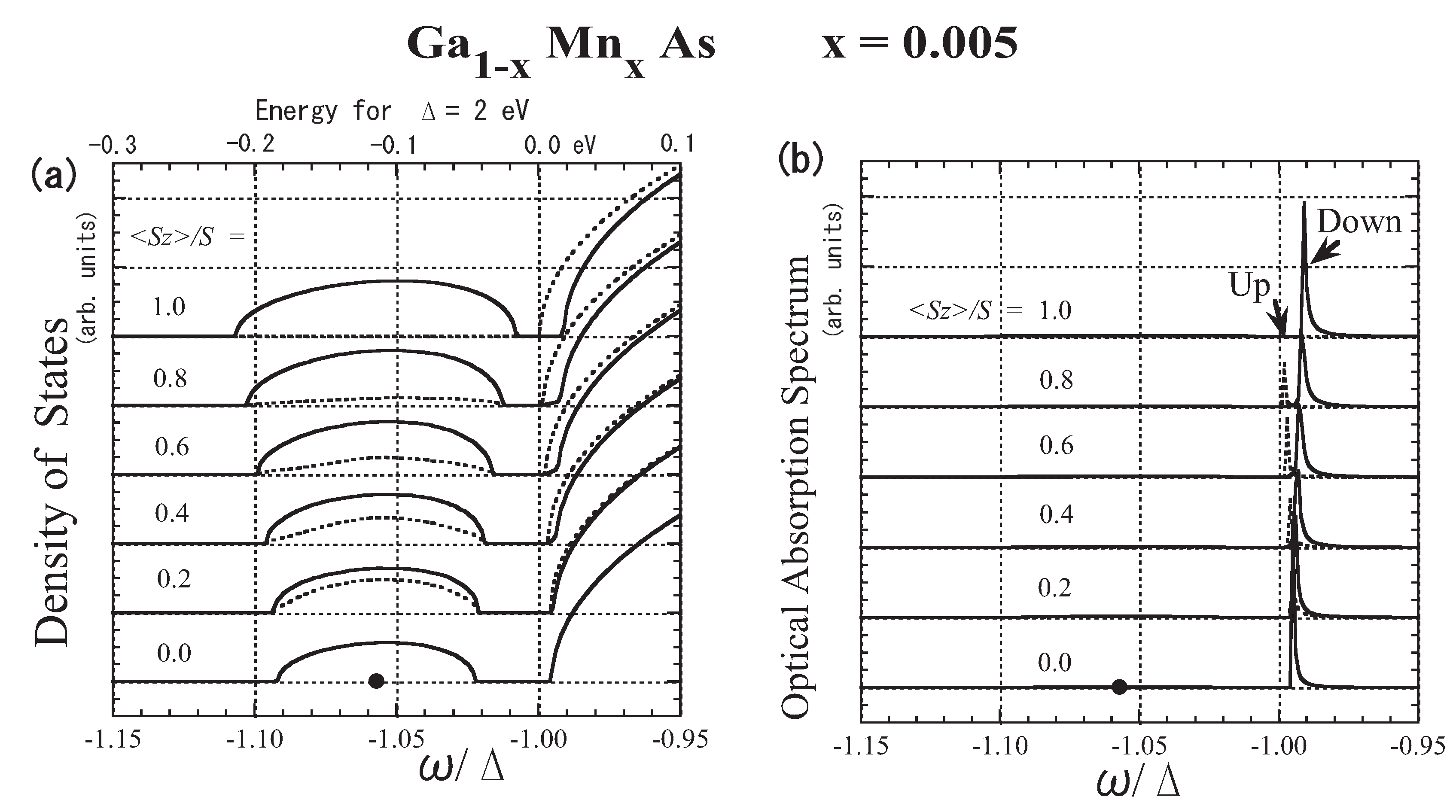
4. Summary and Concluding Comments
Acknowledgement
References
- Wacter, P. Europium chalcogenides: EuO, EuS, EuSe and EuTe. In Handbook on Physics and Chemistry of Rare Earths; Gschneidner, K.A., Eyring, L., Eds.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1979; pp. 507–576. [Google Scholar]
- Mauger, A.; Godart, C. The magnetic, optical, and transport properties of representatives of a class of magnetic semiconductors: The europium chalcogenides. Phys. Rep. 1986, 141, 51–176. [Google Scholar] [CrossRef]
- von Molnar, S.; Kasuya, T. Evidence of band conduction and critical scattering in dilute Eu-chalcogenide alloys. Phys. Rev. Lett. 1968, 21, 1757–1761. [Google Scholar] [CrossRef]
- Oliver, M.R.; Dimmock, J.O.; McWhorter, A.L.; Reed, T.B. Conductivity studies in europium oxide. Phys. Rev. B 1971, 5, 1078–1098. [Google Scholar] [CrossRef]
- Matsumoto, T.; Yamaguchi, K.; Yuri, M.; Kawaguchi, K.; Koshizaki, N.; Yamada, K. Preparation of Gd-doped EuO1−x thin films and the magnetic and magneto-transport properties. J. Phys-Condens. Matter 2004, 16, 6017–6028. [Google Scholar] [CrossRef]
- Ott, H.; Heise, S.J.; Sutarto, R.; Hu, Z.; Chang, C.F.; Hsieh, H.H.; Lin, H.-J.; Chen, C.T.; Tjeng, L.H. Soft x-ray magnetic circular dichroism study on Gd-doped EuO thin films. Phys. Rev. B 2006, 73, 094407. [Google Scholar] [CrossRef]
- Santos, T.S.; Moodera, J.S.; Raman, K.V.; Negusse, E.; Holroyd, J.; Dvorak, J.; Liberati, M.; Idzerda, Y.U.; Arenholz, E. Determining exchange splitting in a magnetic semiconductor by spin-filter tunneling. Phys. Rev. Lett. 2008, 101, 147201. [Google Scholar] [CrossRef] [PubMed]
- Sutarto, R.; Altendorf, S.G.; Coloru, B.; Moretti Sala, M.; Haupricht, T.; Chang, C.F.; Hu, Z.; Schusler-Langeheine, C.; Hollmann, N.; Kierspel, H.; Mydosh, J.A.; Hsieh, H.H.; Lin, H.-J.; Chen, C.T.; Tjeng, L.H. Epitaxy, stoichiometry, and magnetic properties of Gd-doped EuO films on YSZ (001). Phys. Rev. B 2009, 80, 085308. [Google Scholar] [CrossRef]
- Kimura, S.; Ito, T.; Miyazaki, H.; Mizuno, T.; Iizuka, T.; Takahashi, T. Electronic inhomogeneity EuO: Possibility of magnetic polaron states. Phys. Rev. B 2008, 78, 052409. [Google Scholar] [CrossRef]
- Comment, A.; Ansermet, J.-P.; Slichter, C.P.; Rho, H.; Snow, C.S.; Cooper, S.L. Magnetic properties of pure and Gd-doped EuO probed by NMR. Phys. Rev. B 2005, 72, 014428. [Google Scholar] [CrossRef]
- Miyazaki, H.; Ito, T.; Im, H.J.; Yagi, S.; Kato, M.; Soda, K.; Kimura, S. Direct observation of momentum-dependent exchange interaction in a Heisenberg ferromagnet. Phys. Rev. Lett. 2009, 102, 227203. [Google Scholar] [CrossRef] [PubMed]
- Steeneken, P.G.; Tjeng, L.H.; Elfimov, I.; Sawatzky, G.A.; Ghiringhelli, G.; Brookes, N.B.; Huang, D.-J. Exchange splitting and charge carrier spin polarization in EuO. Phys. Rev. Lett. 2002, 88, 047201. [Google Scholar] [CrossRef] [PubMed]
- Souza-Neto, N.M.; Haskel, D.; Tseng, Y.-C.; Lapertot, G. Pressure-induced electronic mixing and enhancement of ferromagnetic ordering in EuX (X=Te, Se, S, O) magnetic semiconductors. Phys. Rev. Lett. 2009, 102, 057206. [Google Scholar] [CrossRef] [PubMed]
- Schiller, R.; Müller, W.; Nolting, W. Kondo-lattice model: Application to the temperature-dependent electronic structure of EuO(100) films. Phys. Rev. B 2001, 64, 134409. [Google Scholar] [CrossRef]
- Sinjukow, P.; Nolting, W. Fully self-consistent determination of transport properties in Eu-rich EuO. Phys. Rev. B 2004, 69, 214432. [Google Scholar] [CrossRef]
- Ghosh, D.B.; De, M.; De, S.K. Electronic structure and magneto-optical properties of magnetic semiconductors: Europium monochalcogenides. Phys. Rev. B 2004, 70, 115211. [Google Scholar] [CrossRef]
- Ingle, N.J.C.; Elfimov, I.S. Influence of epitaxial strain on the ferromagnetic semiconductor EuO: First-principles calculations. Phys. Rev. B 2008, 77, 121202. [Google Scholar] [CrossRef]
- Arnold, M.; Kroha, J. Simultaneous ferromagnetic metal-semiconductor transition in electron-doped EuO. Phys. Rev. Lett. 2008, 100, 046404. [Google Scholar] [CrossRef] [PubMed]
- Nolting, W.; Java, M.S.; Rex, S. Magnetic polaron in ferro- and antiferromagnetic semiconductors. Phys. Rev. B 1996, 54, 14455–14466. [Google Scholar] [CrossRef]
- Nolting, W.; Rex, S.; Java, M.S. Magnetism and electronic structure of local moment ferromagnet. J. Phys-Condens. Matter 1997, 9, 1301–1330. [Google Scholar] [CrossRef]
- Bryksa, V.; Nolting, W. Disordered Kondo-lattice model: Extension of coherent potential approximation. Phys. Rev. B 2008, 78, 064417. [Google Scholar] [CrossRef]
- Tang, G.; Nolting, W. Carrier-induced ferromagnetism in diluted local moment systems. Phys. Rev. B 2007, 75, 024426. [Google Scholar] [CrossRef]
- Furdya, J.K. Diluted magnetic semiconductors. J. Appl. Phys. 1988, 64, R29–R64. [Google Scholar] [CrossRef]
- Haas, K.C. Band structure and theory of magnetic interactions. In Semimagnetic Semiconductors and Diluted Magnetic Semiconductors; Averous, M., Balkanski, M., Eds.; Plenum: New York, NY, USA, 1991; pp. 59–82. [Google Scholar]
- Lascaray, J.P. II1−xMnxVI semimagnetic semiconductors. In Semimagnetic Semiconductors and Diluted Magnetic Semiconductors; Averous, M., Balkanski, M., Eds.; Plenum: New York, NY, USA, 1991; pp. 169–190. [Google Scholar]
- Ohno, H. Properties of ferromagnetic III-V semiconductors. J. Magn. Magn. Mater. 1999, 200, 110–129. [Google Scholar] [CrossRef]
- Jungwirth, T.; Masek, J.; Kucera, J.; MacDonald, H. Theory of ferromagnetic (III,Mn)V semiconductors. Rev. Mod. Phys. 2006, 78, 809–864. [Google Scholar] [CrossRef]
- Ehrenreich, H.; Schwartz, L.M. The electronic structure of alloys. In Solid State Physics, Advances in Research and Application; Ehrenreich, H., Seitz, F., Turnbull, D., Eds.; Academic Press: New York, NY, USA, 1976; Volume 31, pp. 149–286. [Google Scholar]
- Gonis, A. Green functions for ordered and disordered systems. In Studies in Mathematical Physics; van Groesen, E., de Jager, E.M., Eds.; North-Holland: Amsterdam, The Netherlands, 1992; Volume 4. [Google Scholar]
- Onodera, Y.; Toyozawa, Y. Persistence and amalgamation types in the electronic structure of mixed crystals. J. Phys. Soc. Jpn. 1968, 24, 341–355. [Google Scholar] [CrossRef]
- Rangette, A.; Yanase, A.; Kübker, J. CPA treatment of the s-d model at high temperatures. Solid State Commun. 1973, 12, 171–174. [Google Scholar] [CrossRef]
- Kubo, K. Electronic states in magnetic semiconductors–An extension of CPA to random spin systems–. J. Phys. Soc. Jpn. 1974, 36, 32–38. [Google Scholar] [CrossRef]
- Takahashi, M.; Mitsui, K. Single-site approximation for the s-f model in ferromagnetic semiconductors. Phys. Rev. B 1996, 54, 11298–11304. [Google Scholar] [CrossRef]
- Takahashi, M. Electron-spin polarization in ferromagnetic semiconductors. Phys. Rev. B 1997, 56, 7389–7394. [Google Scholar] [CrossRef]
- Takahashi, M.; Mitsui, K. Electron scattering due to fluctuating localized spins in degenerate ferromagnetic semiconductors. J. Magn. Magn. Mater. 1998, 182, 329–334. [Google Scholar] [CrossRef]
- Takahashi, M. Conduction electron band in antiferromagnetic semiconductors. Phys. Rev. B 1997, 55, 6950–6956. [Google Scholar] [CrossRef]
- Takahashi, M.; Nolting, W. Single-site approximation for the s-f model of antiferromagnetic semiconductors. J. Magn. Magn. Mater. 2001, 237, 225–230. [Google Scholar] [CrossRef]
- Takahashi, M. Coherent-potential approach to magnetic and chemical disorder in diluted magnetic semiconductors. Phys. Rev. B 1999, 60, 15858–15865. [Google Scholar] [CrossRef]
- Takahashi, M. Coherent potential approach to exchange-induced band splitting in diluted magnetic semiconductors under a saturating magnetic field. J. Phys-Condens. Matter 2001, 13, 3433–3442. [Google Scholar] [CrossRef]
- Takahashi, M. Asymmetric splitting of exciton states in diluted magnetic semiconductor Cd1−xMnxS. J. Phys. Soc. Jpn. 2001, 70, 2224–2225. [Google Scholar] [CrossRef]
- Takahashi, M.; Kubo, K. Mechanism of carrier-induced ferromagnetism in magnetic semiconductors. Phys. Rev. B 2002, 66, 153202. [Google Scholar] [CrossRef]
- Takahashi, M.; Kubo, K. Carrier states and ferromagnetism in diluted magnetic semiconductors. J. Phys. Soc. Jpn. 2003, 72, 2866–2879. [Google Scholar] [CrossRef]
- Takahashi, M. Optical band edge of diluted magnetic semiconductors. Phys. Rev. B 2004, 70, 035207. [Google Scholar] [CrossRef]
- Takahashi, M.; Furukawa, N.; Kubo, K. Mechanism of carrier-induced ferromagnetism in diluted magnetic semiconductors. J. Magn. Magn. Mater. 2003, 272, 2021–2022. [Google Scholar] [CrossRef]
- Popescu, F.; Şen, C.; Dagotto, E.; Moreo, A. Crossover from impurity to valence band in diluted magnetic semiconductors: Role of Coulomb attraction by acceptors. Phys. Rev. B 2007, 76, 085206. [Google Scholar] [CrossRef]
- Hoang, A.T. Optical properties of diluted magnetic semiconductors in coherent potential approximation. Physica B 2008, 403, 1803–1807. [Google Scholar] [CrossRef]
- Nolting, W.; Oreś, A.M. Conduction-band structure of a ferromagnetic semiconductor. Phys. Rev. B 1980, 22, 6184–6195. [Google Scholar] [CrossRef]
- Lascaray, J.P.; Deruelle, M.C.D.; Coquillat, D. Magnetization and magnetoreflectivity measurements in Zn1−xMnxTe with 0.25 ≤ x ≤ 0.71. Phys. Rev. B 1987, 35, 675–677. [Google Scholar] [CrossRef]
- Lascaray, J.P.; Coquillat, D.; Deportes, J.; Bhattacharjee, A.K. Zeeman splitting of exciton and magnetization in Cd1−xMnxTe: Anomalous behavior at high x. Phys. Rev. B 1988, 38, 7602–7606. [Google Scholar] [CrossRef]
- Takahashi, M.; Kubo, K. Limitation of mean field approximation for carrier states and ferromagnetism in diluted magnetic semiconductors. J. Phys. Soc. Jpn. 2005, 74, 1642–1643. [Google Scholar] [CrossRef]
- Chattopadhyay, A.; Das Sarma, S.; Millis, A.J. Transition temperature of ferromagnetic semiconductors: A dynamical mean field study. Phys. Rev. Lett. 2001, 87, 227202. [Google Scholar] [CrossRef] [PubMed]
- Yagi, M.; Kayanuma, Y. Theory for carrier-induced ferromagnetism in diluted magnetic semiconductors. J. Phys. Soc. Jpn. 2002, 71, 2010–2018. [Google Scholar] [CrossRef]
- Calderón, M.J.; Gomez-Santos, G.; Brey, L. Impurity-semiconductor band hybridization effects on the critical temperature of diluted magnetic semiconductors. Phys. Rev. B 2002, 66, 075218. [Google Scholar] [CrossRef]
- Zener, C. Interaction between the d-shells in the transition metals. II. Ferromagnetic compounds of manganese with perovskite structure. Phys. Rev. 1951, 82, 403–405. [Google Scholar] [CrossRef]
- Linnarsson, M.; Janzen, E.; Monemar, B.; Kleverman, M.; Thilderkvist, A. Electronic structure of the GaAs:MnGa center. Phys. Rev. B 1997, 55, 6938–6944. [Google Scholar] [CrossRef]
- Iye, Y.; Oiwa, A.; Endo, A.; Katsumoto, S.; Matsukura, F.; Shen, A.; Ohno, H.; Munekata, H. Metal-insulator transition and magnetotransport in III-V compound diluted magnetic semiconductors. Mater. Sci. Eng. B 1999, 63, 88–95. [Google Scholar] [CrossRef]
- Ohldag, H.; Solinus, V.; Hillebrecht, F.U.; Goedkoop, J.B.; Finazzi, M.; Matsukura, F.; Ohno, H. Magnetic moment of Mn in the ferromagnetic semiconductor (Ga0.98Mn0.02)As. Appl. Phys. Lett. 2000, 76, 2928–2930. [Google Scholar] [CrossRef]
- Okabayashi, J.; Kimura, A.; Mizokawa, T.; Fujimori, A.; Hayashi, T.; Tanaka, M. Mn 3d partial density of states in Ga1−xMnxAs studied by resonant photoemission spectroscopy. Phys. Rev. B 1999, 59, R2486–R2489. [Google Scholar] [CrossRef]
- Okabayashi, J.; Kimura, A.; Rader, O.; Mizokawa, T.; Fujimori, A.; Hayashi, T.; Tanaka, M. Angle-resolved photoemission study of Ga1−xMnxAs. Phys. Rev. B 2001, 64, 125304. [Google Scholar] [CrossRef]
- Okabayashi, J.; Kimura, A.; Rader, O.; Mizokawa, T.; Fujimori, A.; Hayashi, T.; Tanaka, M. Core-level photoemission study of Ga1−xMnxAs. Phys. Rev. B 1998, 58, R4211–R4214. [Google Scholar] [CrossRef]
- Ishiwata, Y.; Watanabe, M.; Eguchi, R.; Takeuchi, T.; Harada, Y.; Chainani, A.; Shin, S.; Hayashi, T.; Hashimoto, Y.; Katsumoto, S.; Iye, Y. Manganese concentration and low-temperature annealing dependence of Ga1−xMnxAs by x-ray absorption spectroscopy. Phys. Rev. B 2002, 65, 233201. [Google Scholar] [CrossRef]
- Park, J.H.; Kwon, S.K.; Min, B.I. Electronic structures of III-V based ferromagnetic semiconductors: half-metallic phase. Physica B 2001, 281, 703–704. [Google Scholar] [CrossRef]
- Shirai, M.; Ogawa, T.; Kitagawa, I.; Suzuki, N. Band structures of zinc-blende-type MnAs and (MnAs)1(GaAs)1 superlattice. J. Magn. Magn. Mater. 1998, 177, 1383–1384. [Google Scholar] [CrossRef]
- Szczytko, J.; Mac, W.; Twardowski, A.; Matsukura, F.; Ohno, H. Antiferromagnetic p-d exchange in ferromagnetic Ga1−xMnxAs epilayers. Phys. Rev. B 1999, 59, 12935–12939. [Google Scholar] [CrossRef]
- Ando, K.; Hayashi, T.; Tanaka, M.; Twardowski, A. Magneto-optic effect of the ferromagnetic diluted magnetic semiconductor Ga1−xMnxAs. J. Appl. Phys. 1998, 83, 6548–6550. [Google Scholar] [CrossRef]
- Okabayashi, J.; Mizokawa, T.; Sarma, D.D.; Fujimori, A.; Slupinski, T.; Oiwa, A.; Munekata, H. Electronic structure of In1−xMnxAs studied by photoemission spectroscopy: Comparison with Ga1−xMnxAs. Phys. Rev. B 2002, 65, 161203. [Google Scholar] [CrossRef]
- Hayashi, T.; Hashimoto, Y.; Katsumoto, S.; Iye, Y. Effect of low-temperature annealing on transport and magnetism of diluted magnetic semiconductor (Ga,Mn)As. Appl. Phys. Lett. 2001, 78, 1691–1693. [Google Scholar] [CrossRef]
- Yu, K.M.; Walukiewicz, W.; Wojtowicz, T.; Kuryliszyn, I.; Liu, X.; Sasaki, Y.; Furdyna, J.K. Effect of the location of Mn sites in ferromagnetic Ga1−xMnxAs on its Curie temperature. Phys. Rev. B 2002, 65, 201303. [Google Scholar] [CrossRef]
- Korzhavyi, P.A.; Abrikosov, I.A.; Smirnova, E.A.; Bergqvist, L.; Mohn, P.; Mathieu, R.; Svedlindh, P.; Sadowski, J.; Isaev, E.I.; Vekilov, Yu.Kh.; Eriksson, O. Defect-induced magnetic structure in (Ga1−xMnx)As. Phys. Rev. Lett. 2002, 88, 187202. [Google Scholar] [CrossRef] [PubMed]
- Timm, C. Disorder effects in diluted magnetic semiconductors. J. Phys-Condens. Matter 2003, 15, R1865–R1896. [Google Scholar] [CrossRef]
- Okabayashi, J.; Kimura, A.; Rader, O.; Mizokawa, T.; Fujimori, A.; Hayashi, T.; Tanaka, M. Electronic structure of GaMnAs studied by angle-resolved photoemission spectroscopy. Physica E 2001, 10, 192–195. [Google Scholar] [CrossRef]
- Oiwa, A.; Katsumoto, S.; Endo, A.; Hirakawa, M.; Iye, M.; Ohno, H.; Matsukura, F.; Shen, A.; Sugawara, Y. Nonmetal-metal-nonmetal transition and large negative magnetoresistance in (Ga,Mn)As/GaAs. Solid State Commun. 1997, 103, 209–213. [Google Scholar] [CrossRef]
- Oiwa, A.; Katsumoto, S.; Endo, A.; Hirakawa, M.; Iye, M.; Matsukura, F.; Shen, A.; Sugawara, Y.; Ohno, H. Low-temperature conduction and giant negative magnetoresistance in III-V-based diluted magnetic semiconductor. Physica B 1998, 249, 775–779. [Google Scholar] [CrossRef]
- Matsukura, F.; Ohno, H.; Shen, A.; Sugawara, Y. Transport properties and origin of ferromagnetism in (Ga,Mn)As. Phys. Rev. B 1998, 57, R2037–R2040. [Google Scholar] [CrossRef]
- Hirakawa, K.; Katsumoto, S.; Hayashi, T.; Hashimoto, Y.; Iye, Y. Double-exchange-like interaction in Ga1−xMnxAs investigated by infrared absorption spectroscopy. Phys. Rev. B 2002, 65, 193312. [Google Scholar] [CrossRef]
- Katsumoto, S.; Hayashi, T.; Hashimoto, Y.; Iye, Y.; Ishiwata, Y.; Watanabe, M.; Eguchi, R.; Takeuchi, T.; Harada, Y.; Shin, S.; Hirakawa, K. Magnetism and metal-insulator transition in III-V based diluted magnetic semiconductors. Mater. Sci. Eng. 2001, 84, 88–95. [Google Scholar] [CrossRef]
- Akai, H. Ferromagnetism and its stability in the diluted magnetic semiconductor (In, Mn)As. Phys. Rev. Lett. 1998, 81, 3002–3005. [Google Scholar] [CrossRef]
- Szczytko, J.; Twardowski, A.; Świa̧tek, K.; Palczewska, M.; Tanaka, M.; Hayashi, T.; Ando, K. Mn impurity in Ga1−xMnxAs epilayers. Phys. Rev. B 1999, 60, 8304–8308. [Google Scholar] [CrossRef]
- Szczytko, J.; Mac, M.; Stachow, A.; Twardowski, A.; Becla, P.; Tworzydlo, J. The s,p-d exchange interaction in GaAs heavily doped with Mn. Solid State Commun. 1996, 99, 927–931. [Google Scholar] [CrossRef]
- Kagami, K.; Takahashi, M.; Yasuda, C.; Kubo, K. Theory of diluted magnetic semiconductors: A minimum model. Sci. Technol. Adv. Mater. 2006, 7, 31–41. [Google Scholar] [CrossRef]
- Nazir, S.; Ikram, N.; Tanveer, M.; Shaukat, A.; Saeed, Y.; Reshak, A.H. Spin-polarized structural, electronic, and magnetic properties of diluted magnetic semiconductors Cd1−xMnxS and Cd1−xMnxSe in zinc blende phase. J. Phys. Chem. A 2009, 113, 6022–6027. [Google Scholar] [CrossRef] [PubMed]
- Sato, K.; Katayama-Yoshida, H. First-principles materials design for semiconductor spintronics. Semicond. Sci. Technol. 2002, 17, 367–376. [Google Scholar] [CrossRef]
- Sakai, O.; Suzuki, S.; Nishizawa, K. Study on the magnetic and transport properties of low density carrier ferromagnetic semiconductors. J. Phys. Soc. Jpn. 2001, 70, 1105–1116. [Google Scholar] [CrossRef]
- Ohe, J.; Tomoda, Y.; Bulut, N.; Arita, R.; Nakamura, K.; Maekawa, S. Combined approach of density function theory and quantum Monte Carlo method to electron correlation in diluted magnetic semiconductors. J. Phys. Soc. Jpn. 2009, 78, 083703. [Google Scholar] [CrossRef]
- Takahashi, M.; Mitsui, K.; Umehara, M. Conduction-electron states in ferromagnetic semiconductors above the Curie temperature. Phys. Rev. B 1993, 48, 17053–17063, Erratum: Phys. Rev. B 1994, 50, 17759–17760. [Google Scholar] [CrossRef]
- Takahashi, M.; Mitsui, K.; Umehara, M. Multiple-scattering approach to the s-f model in ferromagnetic semiconductors above the Curie temperature. Phys. Rev. B 1995, 52, 16313–16316. [Google Scholar] [CrossRef]
- Takahashi, M.; Kasuya, T. A theory for a self-trapped molecular magnetic polaron in ferromagnetic semiconductor. J. Phys. Soc. Jpn. 1983, 52, 3127–3137. [Google Scholar] [CrossRef]
- Takahashi, M.; Kasuya, T. Effect of electron-phonon interaction in the magnetic polaron. J. Phys. Soc. Jpn. 1983, 52, 3138–3143. [Google Scholar] [CrossRef]
- Edwards, D.M.; Green, A.C.M.; Kubo, K. Electronic structure and resistivity of the double exchange model. J. Phys-Condens. Matter 1999, 11, 2791. [Google Scholar] [CrossRef]
- Matsunaka, D.; Kasai, H.; Dino, W.A.; Nakanishi, H. Dynamical cluster approximation in disordered systems with magnetic impurities. J. Phys. Soc. Jpn. 2004, 73, 3448–3452. [Google Scholar] [CrossRef]
Appendix
Dynamical CPA–Locator Formalism
© 2010 by the author; licensee MDPI, Basel, Switzerland. This article is an Open Access article distributed under the terms and conditions of the Creative Commons Attribution license http://creativecommons.org/licenses/by/3.0/.
Share and Cite
Takahashi, M. Carrier States in Ferromagnetic Semiconductors and Diluted Magnetic Semiconductors—Coherent Potential Approach—. Materials 2010, 3, 3740-3776. https://doi.org/10.3390/ma3063740
Takahashi M. Carrier States in Ferromagnetic Semiconductors and Diluted Magnetic Semiconductors—Coherent Potential Approach—. Materials. 2010; 3(6):3740-3776. https://doi.org/10.3390/ma3063740
Chicago/Turabian StyleTakahashi, Masao. 2010. "Carrier States in Ferromagnetic Semiconductors and Diluted Magnetic Semiconductors—Coherent Potential Approach—" Materials 3, no. 6: 3740-3776. https://doi.org/10.3390/ma3063740
APA StyleTakahashi, M. (2010). Carrier States in Ferromagnetic Semiconductors and Diluted Magnetic Semiconductors—Coherent Potential Approach—. Materials, 3(6), 3740-3776. https://doi.org/10.3390/ma3063740



