Bond Strength—Coordination Number Fluctuation Model of Viscosity: An Alternative Model for the Vogel-Fulcher-Tammann Equation and an Application to Bulk Metallic Glass Forming Liquids
Abstract
:1. Introduction
2. The BSCNF Model and the VFT Equation
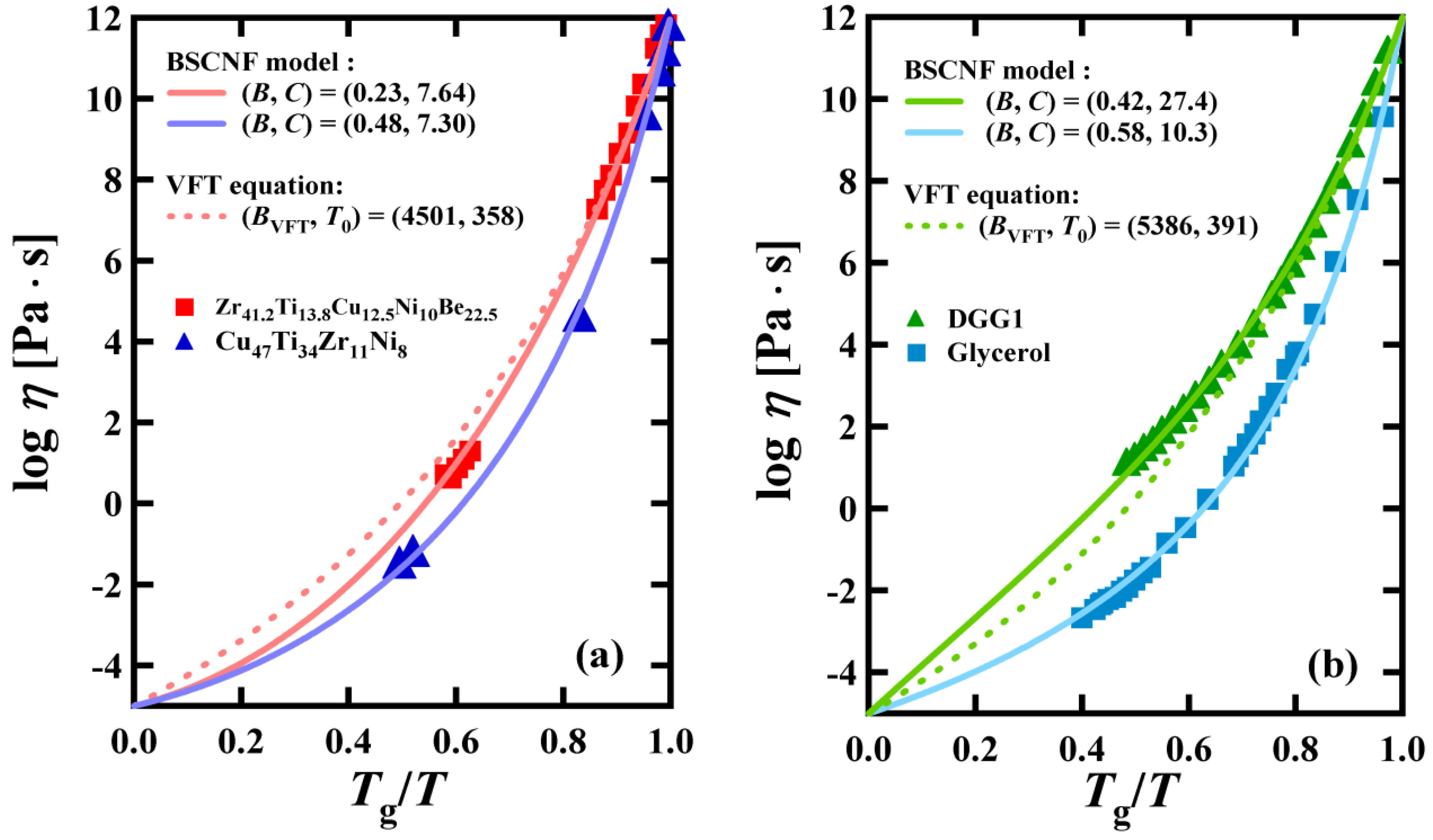
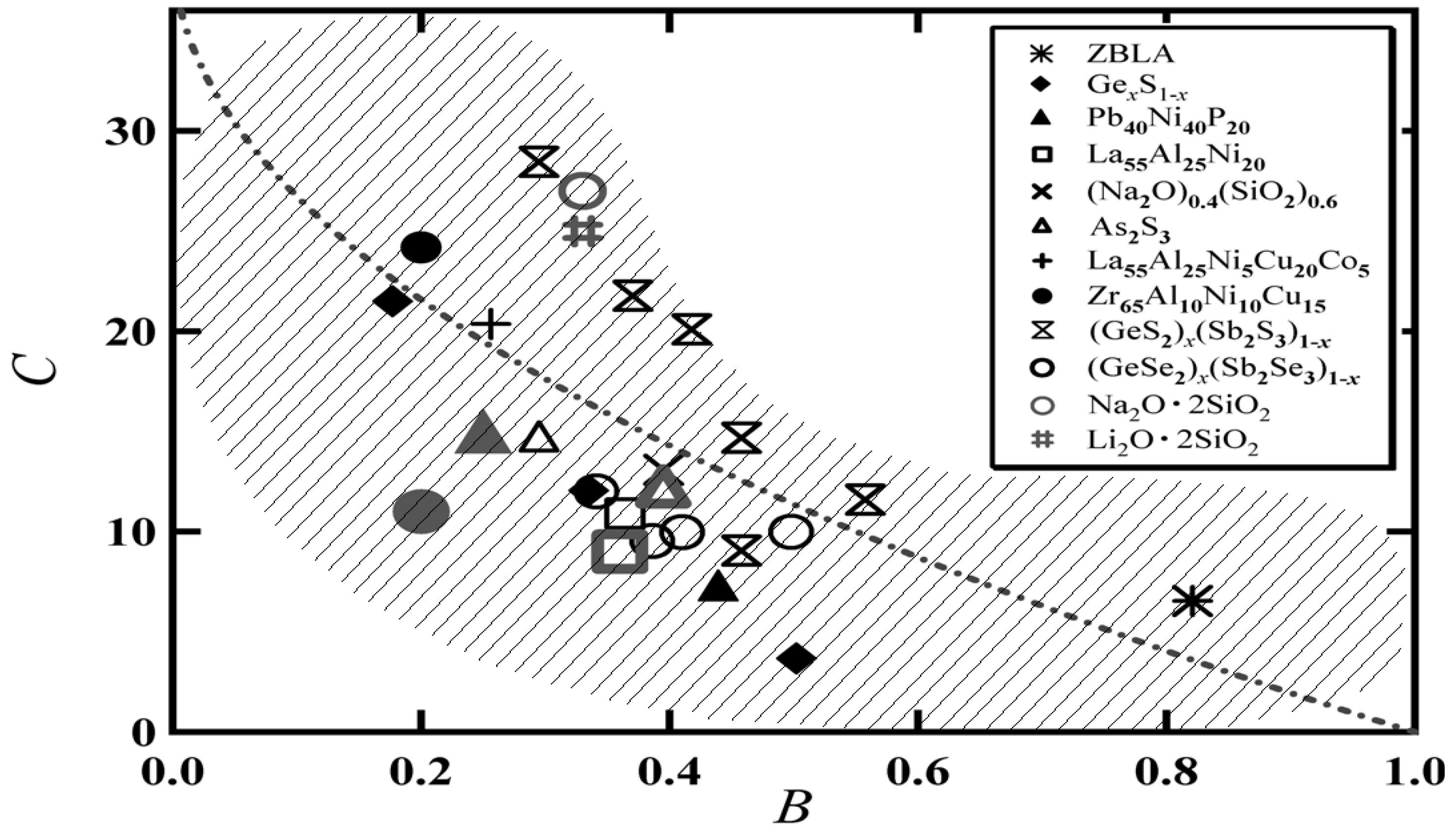
| No. Material | BVFT (K) | T0 (K) | Tg (K) | m | ln(ηTg/η0) | (B*, C*) |
|---|---|---|---|---|---|---|
| 1. SiO2 | 21,254 | 139 | 1,450 | 17.9 | 37.3 | (0.01, 3.8) |
| 2. Li2O·SiO2 | 5,744 | 276 | 593 | 33.9 | 41.7 | (0.22, 2.3) |
| 3. Li2O·2SiO2 | 5,752 | 380 | 727 | 34.7 | 38.2 | (0.27, 18.2) |
| 4. Li2O·3SiO2 | 8,218 | 255 | 734 | 26.3 | 39.5 | (0.12, 25.7) |
| 5. Na2O·SiO2 | 4,999 | 395 | 687 | 40.3 | 39.4 | (0.33, 16.7) |
| 6. Na2O·2SiO2 | 5,538 | 393 | 728 | 35.9 | 38.1 | (0.23, 17.5) |
| 7. Na2O·3SiO2 | 7,484 | 287 | 743 | 26.7 | 37.8 | (0.15, 23.2) |
| 8. Na2O·4SiO2 | 7,618 | 323 | 765 | 29.8 | 39.7 | (0.18, 22.9) |
| 9. K2O·SiO2 | 4,395 | 416 | 675 | 44.2 | 39.1 | (0.38, 14.9) |
| 10. K2O·2SiO2 | 7,461 | 333 | 768 | 30.3 | 39.5 | (0.19, 22.3) |
| 11. K2O·3SiO2 | 8,334 | 253 | 760 | 24.6 | 37.9 | (0.11, 25.3) |
| 12. K2O·4SiO2 | 8,471 | 255 | 766 | 24.8 | 38.2 | (0.11, 25.5) |
| 13. Na2O·Al2O3·6SiO2 | 12,281 | 347 | 1,087 | 24.4 | 38.2 | (0.10, 26.0) |
| 14. CaO·MgO·2SiO2 | 4,826 | 710 | 995 | 59.1 | 39.0 | (0.51, 11.1) |
| 15. CaO·Al2O3·2SiO2 | 5,802 | 785 | 1,113 | 60.0 | 40.7 | (0.50, 11.9) |
| 16. 2MgO·2Al2O3·5SiO2 | 8,244 | 583 | 1,088 | 35.2 | 37.6 | (0.29, 17.4) |
| 17. 15.45Na2O·12.81CaO·71.74SiO2 | 6,785 | 421 | 819 | 35.1 | 39.3 | (0.26, 19.0) |
| 18. 2BaO·TiO2·2SiO2 | 3,896 | 750 | 983 | 70.5 | 38.5 | (0.58, 9.0) |
| 19. PbO·SiO2 | 3,690 | 454 | 673 | 51.8 | 38.8 | (0.46, 12.5) |
| 20. PbO·2SiO2 | 6,001 | 390 | 749 | 34.9 | 38.5 | (0.27, 18.4) |
| 21. 2PbO·SiO2 | 2,496 | 473 | 613 | 78.1 | 41.1 | (0.60, 9.2) |
| 22. B2O3 | 4,695 | 252 | 540 | 30.6 | 37.5 | (0.22, 20.0) |
| 23. Li2O·B2O3 | 2,557 | 542 | 693 | 77.7 | 39.0 | (0.61, 8.4) |
| 24. Li2O·2B2O3 | 2,497 | 616 | 763 | 88.2 | 39.1 | (0.65, 7.4) |
| 25. Li2O·3B2O3 | 2,850 | 598 | 768 | 76.6 | 38.8 | (0.61, 8.4) |
| 26. Li2O·4B2O3 | 2,908 | 579 | 751 | 73.8 | 38.9 | (0.60, 8.8) |
| 27. Na2O·2B2O3 | 2,405 | 600 | 748 | 82.1 | 37.4 | (0.65, 7.3) |
| 28. Na2O·3B2O3 | 3,121 | 557 | 746 | 65.2 | 38.0 | (0.56, 9.5) |
| 29. Na2O·4B2O3 | 3,172 | 539 | 727 | 65.2 | 38.9 | (0.55, 9.9) |
| 30. K2O·2B2O3 | 2,888 | 520 | 705 | 59.5 | 36.0 | (0.55, 9.3) |
| 31. K2O·3B2O3 | 3,403 | 512 | 709 | 62.2 | 39.8 | (0.52, 10.9) |
| 32. K2O·4B2O3 | 3,588 | 463 | 691 | 47.7 | 36.2 | (0.45, 11.9) |
| 33. Cs2O·3B2O3 | 3,363 | 491 | 693 | 57.1 | 38.3 | (0.50, 11.1) |
| 34. BaO·2B2O3 | 3,262 | 619 | 810 | 72.4 | 39.3 | (0.59, 9.2) |
| 35. SrO·2B2O3 | 2,592 | 755 | 911 | 97.0 | 38.3 | (0.69, 6.4) |
| 36. PbO·B2O3 | 2,171 | 525 | 658 | 80.8 | 37.6 | (0.64, 7.5) |
| 37. PbO·2B2O3 | 3,020 | 545 | 738 | 59.8 | 36.0 | (0.55, 9.3) |
| 38. PbO·3B2O3 | 2,656 | 569 | 728 | 76.5 | 38.5 | (0.61, 8.3) |
3. Comparison between the BSCNF Model and the VFT Equation
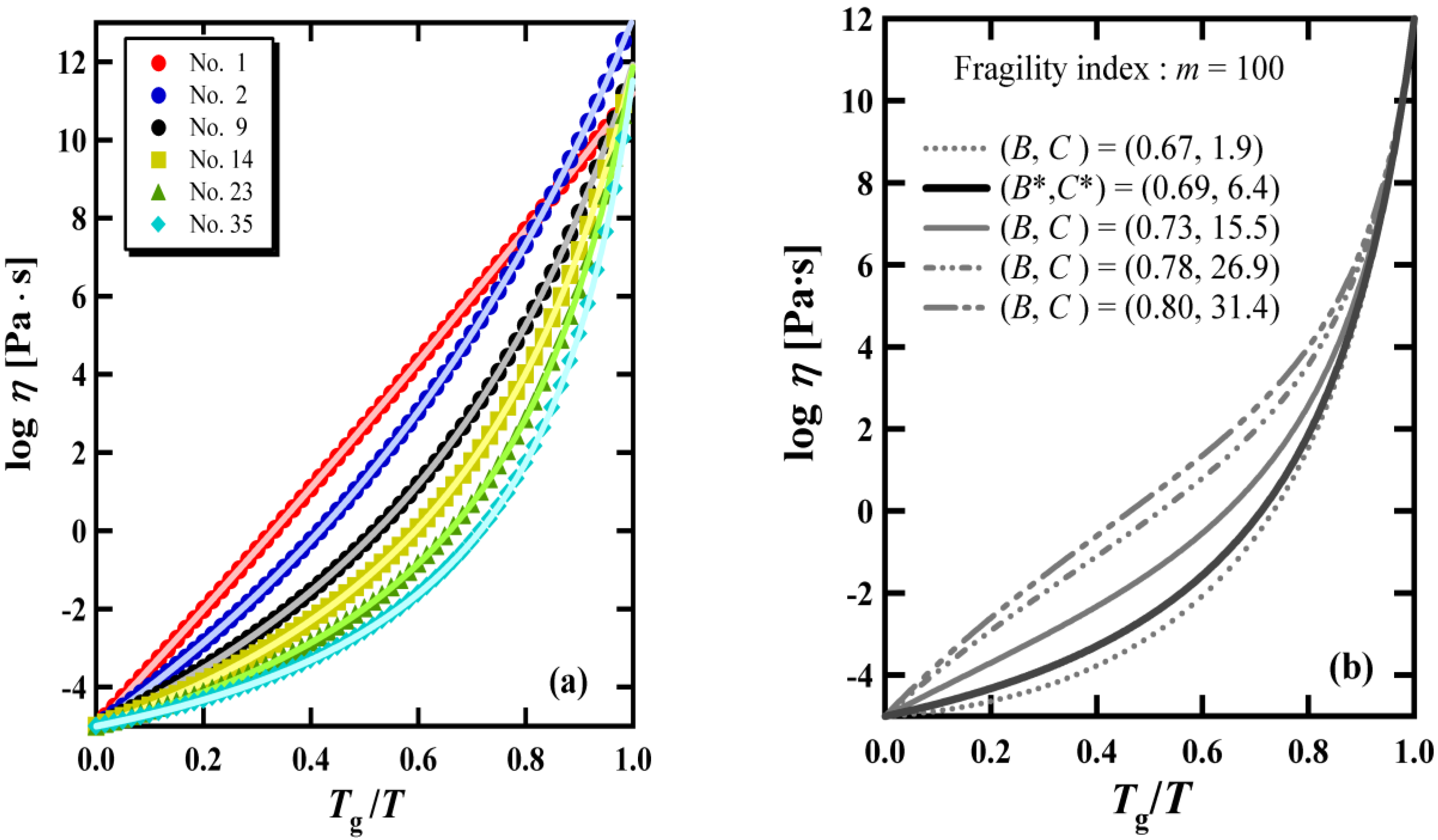
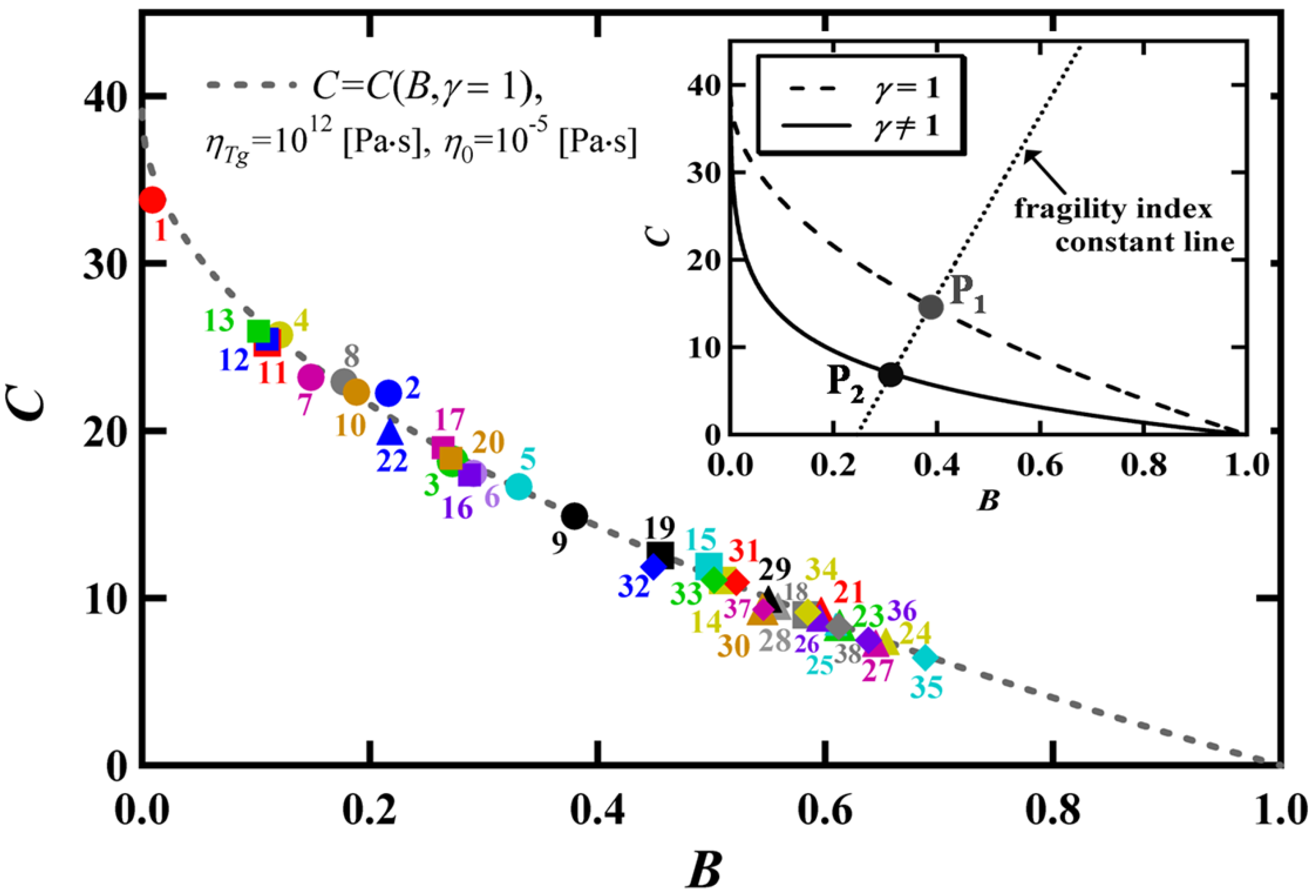
4. Correlation between the Exponent of the KWW Function and the Fragility
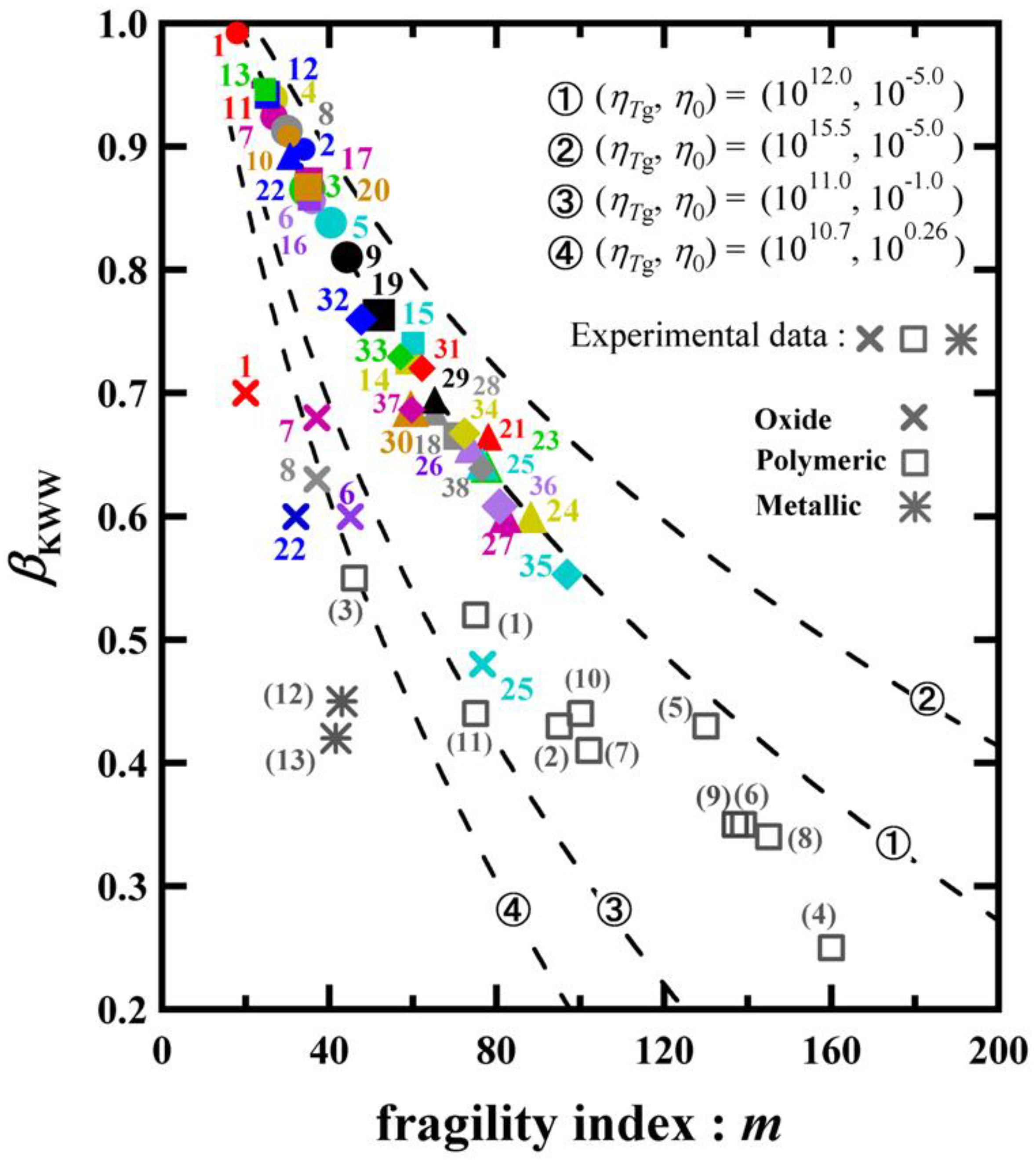
| Materials | m | βKWW | Reference | |
|---|---|---|---|---|
| 1. | SiO2 | 20 | 0.70 | [21] |
| 6. | Na2O·2SiO2 | 45 | 0.60 | |
| 7. | Na2O·3SiO2 | 37 | 0.68 | |
| 8. | Na2O·4SiO2 | 37 | 0.63 | |
| 22. | B2O3 | 32 | 0.60 | |
| 25. | Li2O·3 B2O3 | 77 | 0.48 | [47] |
| (1) | Poly(propylene glycol) | 75 | 0.52 | [17] |
| (2) | Poly(vinyl acetate) | 95 | 0.43 | |
| (3) | Polyisobutylene | 46 | 0.55 | [57] |
| (4) | Polyvinyle chloride | 160 | 0.25 | |
| (5) | Polyvinyl acetate | 130 | 0.43 | |
| (6) | Polystyrene | 139 | 0.35 | |
| (7) | Polymethyl acrylate | 102 | 0.41 | |
| (8) | Poly(methylmethacrylate) | 145 | 0.34 | [21] |
| (9) | Polypropylene | 137 | 0.35 | |
| (10) | Poly(methylphenysiloxane) | 100 | 0.44 | |
| (11) | Poly(vinylmethylether) | 75 | 0.44 | |
| (12) | Zr65Al7.5Cu17.5 Ni10 | 43 | 0.45 | [48] |
| (13) | Pd40Ni40P40 | 42 | 0.42 |
5. Conclusions
Acknowledgements
References
- Vogel, H. The law of relation between the viscosity of liquids and the temperature. Phys. Z 1921, 22, 645–646. [Google Scholar]
- Fulcher, G.S. Analysis of recent measurements of viscosity of glasses. J. Amer. Ceram. Soc. 1925, 8, 339–355. [Google Scholar] [CrossRef]
- Tammann, G.; Hesse, W. The dependence of viscosity upon the temperature of supercooled liquids. Z. Anorg. Allg. Chem. 1926, 156, 245–257. [Google Scholar] [CrossRef]
- Nascimento, M.L.F.; Aparicio, C. Viscosity of strong and fragile glass-forming liquids investigated by means of principal component analysis. J. Phys. Chem. Solids 2007, 68, 104–110. [Google Scholar] [CrossRef]
- Stickel, F.; Fischer, E.W.; Richert, R. Dynamics of glass-forming liquids. II. Detailed comparison of dielectric relaxation, dc-conductivity, and viscosity data. J. Chem. Phys. 1996, 104, 2043–2055. [Google Scholar] [CrossRef]
- Noda, A.; Hayamizu, K.; Watanabe, M. Pulsed-Gradient Spin-Echo 1H and 19F NMR ionic diffusion coefficient, viscosity, and ionic conductivity of non-chloroaluminate room-temperature ionic liquids. J. Phys. Chem. B 2001, 105, 4603–4610. [Google Scholar] [CrossRef]
- Tokuda, H.; Hayamizu, K.; Ishii, K.; Susan, M.A.B.H.; Watanabe, M. Physicochemical properties and structures of room temperature ionic liquids. 1. Variation of anionic species. J. Phys. Chem. B 2004, 108, 16593–16600. [Google Scholar] [CrossRef]
- Stickel, F.; Fischer, E.W.; Richert, R. Dynamics of glass-forming liquids. I. Temperature-derivative analysis of dielectric relaxation data. J. Chem. Phys. 1995, 102, 6251–6257. [Google Scholar] [CrossRef]
- Rössler, E. Indications for a change of diffusion mechanism in supercooled liquids. Phys. Rev. Lett. 1990, 65, 1595–1598. [Google Scholar] [CrossRef] [PubMed]
- Park, I.-S.; Saruta, K.; Kojima, S. Dielectric relaxation and calorimetric measurements of glass transition in the glass-forming dyhydroxyl alcohols. J. Phys. Soc. Jpn. 1998, 67, 4131–4138. [Google Scholar] [CrossRef]
- Nozaki, R.; Zenitani, H.; Minoguchi, A.; Kitai, K. Dielectric relaxation processes in water-in-sorbitol mixtures. J. Non-Cryst. Solids 2002, 307-310, 349–355. [Google Scholar] [CrossRef]
- Liu, H.; Jiang, B.; Liu, M.; Mao, M.; Mao, X. The first application of the Vogel-Fulcher-Tammann equation to biological problem: A new interpretation of the temperature dependent hydrogen exchanges rates of the thrombin-binding DNA. Phys. Lett. A 2007, 361, 248–251. [Google Scholar] [CrossRef]
- Angell, C.A.; Ngai, K.L.; McKenna, G.B.; McMillan, P.F.; Martin, S.W. Relaxation in glassforming liquids and amorphous solids. J. Appl. Phys. 2000, 88, 3113–3157. [Google Scholar] [CrossRef]
- Kokshenev, V.B. Characteristic temperatures of liquid-glass transition. Physica A Stat. Mech. Appl. 1999, 262, 88–97. [Google Scholar] [CrossRef]
- Takagi, Y.; Hosokawa, T.; Hoshikawa, K.; Kobayashi, H.; Hiki, Y. Relaxation of polystyrene near the glass transition temperature studied by acoustic measurements. J. Phys. Soc. Jpn. 2007, 76, 024604–024611. [Google Scholar] [CrossRef]
- Kivelson, D.; Tarjus, G.; Zhao, X.; Kivelson, S.A. Fitting of viscosity: Distinguishing the temperature dependences predicted by various models of supercooled liquids. Phys. Rev. E 1996, 53, 751–758. [Google Scholar] [CrossRef]
- Kivelson, D.; Tarjus, G. SuperArrhenius character of supercooled glass-forming liquids. J. Non-Cryst. Solids 1998, 235-237, 86–100. [Google Scholar] [CrossRef]
- Hecksher, T.; Nielsen, A.I.; Olsen, N.B.; Dyre, J.C. Little evidence for dynamic divergences in ultraviscous molecular liquids. Nature Phys. 2008, 4, 737–741. [Google Scholar] [CrossRef]
- Bässler, H. Viscous flow in supercooled liquids analyzed in terms of transport theory for random media with energetic disorder. Phys. Rev. Lett. 1987, 58, 767–770. [Google Scholar] [CrossRef] [PubMed]
- Angell, C.A. Relaxation in liquids, polymers and plastic crystals—Strong/fragile patterns and problems. J. Non-Cryst. Solids 1991, 131-133, 13–31. [Google Scholar] [CrossRef]
- Böhmer, R.; Ngai, K.L.; Angell, C.A.; Plazek, D.J. Nonexponential relaxations in strong and fragile glass formers. J. Chem. Phys. 1993, 99, 4201–4209. [Google Scholar] [CrossRef]
- Matsuoka, S. Entropy, free volume, and cooperative relaxation. J. Res. Nat. Ins. Stand. Technol. 1997, 102, 213–228. [Google Scholar] [CrossRef]
- Aniya, M. A model for the fragility of the melts. J. Therm. Anal. Calorim. 2002, 69, 971–978. [Google Scholar] [CrossRef]
- Aniya, M.; Shinkawa, T. A model for the fragility of metallic glass forming liquids. Mater. Trans. 2007, 48, 1793–1796. [Google Scholar] [CrossRef]
- Ndeugueu, J.L.; Ikeda, M.; Aniya, M. A comparison between the Bond Strength—Coordination Number Fluctuation model and the Random Walk model of viscosity. J. Therm. Anal. Calorim. 2010, 99, 33–38. [Google Scholar] [CrossRef]
- Aniya, M.; Ikeda, M. Viscosity of metallic glass forming liquids: Analysis based on Bond Strength-Coordination Number Fluctuations. Mater. Sci. Forum 2010, 638-642, 1621–1626. [Google Scholar] [CrossRef]
- Ikeda, M.; Aniya, M. Correlation between fragility and cooperativity in bulk metallic glass-forming liquids. Intermetallics 2010, 18, 1796–1799. [Google Scholar] [CrossRef]
- Ikeda, M.; Aniya, M. A model for the temperature dependence of the viscosity in Cu-As-Se system. Solid State Ionics 2009, 180, 522–526. [Google Scholar] [CrossRef]
- Adam, G.; Gibbs, J.H. On the temperature dependence of cooperative relaxation properties in glass-forming liquids. J. Chem. Phys. 1965, 43, 139–146. [Google Scholar] [CrossRef]
- Park, I.-S.; Saruta, K.; Kojima, S. Calorimetric and dielectric investigations of glass transition in intermediate glass-forming liquid. J. Therm. Anal. Calorim. 1999, 57, 687–693. [Google Scholar] [CrossRef]
- Yamamuro, O.; Ishikawa, M.; Kishimoto, I.; Pinvidic, J.-J.; Matsuo, T. Thermodynamic approach to glass transitions of plastically crystalline cyanoadamantane and isocyanocyclohexane. J. Phys. Soc. Jpn. 1999, 68, 2969–2976. [Google Scholar] [CrossRef]
- Cohen, M.H.; Grest, G.S. Liquid-glass transition, a free-volume approach. Phys. Rev. B 1979, 20, 1077–1098. [Google Scholar] [CrossRef]
- Haruyama, O.; Sakagami, H.; Nishiyama, N.; Inoue, A. The free volume kinetics during structural relaxation in bulk Pd-P based metallic glasses. Mater. Sci. Eng. A 2007, 449-451, 497–500. [Google Scholar] [CrossRef]
- Leyser, H.; Schulte, A.; Doster, W.; Petry, W. High-pressure specific-heat spectroscopy at the glass transition in o-terphenyl. Phys. Rev. E 1995, 51, 5899–5904. [Google Scholar] [CrossRef]
- Aniya, M.; Ikeda, M. Bond Strength—Coordination Number Fluctuations and the fragility of some ion conducting oxide and chalcogenide glass forming liquids. Ionics 2010, 16, 7–11. [Google Scholar] [CrossRef]
- Kohlrausch, R. Theorie des elektrischen Rüekstander in der Leidener Flasche. Pogg. Ann. Phys. 1854, 91, 56–82. [Google Scholar] [CrossRef]
- Williams, G.; Watts, D.C. Non-symmetrical dielectric relaxation behavior arising from a simple empirical decay function. Trans. Faraday Soc. 1970, 66, 80–85. [Google Scholar] [CrossRef]
- Tanaka, H. Relationship among glass-forming ability, fragility, and short-range bond ordering of liquids. J. Non-Cryst. Solids 2005, 351, 678–690. [Google Scholar] [CrossRef]
- Novikov, V.N.; Sokolov, A.P. Poisson’s ratio and the fragility of glass-forming liquids. Nature 2004, 431, 961–963. [Google Scholar] [CrossRef] [PubMed]
- Ngai, K.L. Dynamic and thermodynamic properties of glass-forming substances. J. Non-Cryst. Solids 2000, 275, 7–51. [Google Scholar] [CrossRef]
- Plazek, D.L.; Magill, J.H. Physical properties of aromatic hydrocarbons. IV. An analysis of the temperature dependence of the viscosity and the compliance of 1,3,5 tri-α-naphthylbenzene. J. Chem. Phys. 1968, 49, 3678–3682. [Google Scholar] [CrossRef]
- Kawamura, Y.; Inoue, A. Newtonian viscosity of supercooled liquid in a Pd40Ni20P20 metallic glass. Appl. Phys. Lett. 2000, 77, 1114–1116. [Google Scholar] [CrossRef]
- Patkowski, A.; Paluch, M.; Gapiński, J. Relationship between T0, Tg, and their pressure dependence for supercooled liquids. J. Non-Cryst. Solids 2003, 330, 259–263. [Google Scholar] [CrossRef]
- Zhao, Y.; Bian, X.; Yin, K.; Zhou, J.; Zhang, J.; Hou, X. Relations of the characteristic temperatures and fragility parameters in glass-forming metallic system. Physica B Cond. Mat. 2004, 349, 327–332. [Google Scholar] [CrossRef]
- Privalko, V.P. Glass transition in polymers: Dependence of the Kohlrausch-stretching exponent on the kinetic free volume fraction. J. Non-Cryst. Solids 1999, 255, 259–263. [Google Scholar] [CrossRef]
- Hodge, I.M. Strong and fragile liquids—A brief critique. J. Non-Cryst. Solids 1996, 202, 164–172. [Google Scholar] [CrossRef]
- Sidebottom, D.L.; Green, P.F.; Brow, R.K. Comparison of KWW and power law analyses of an ion-conducting glass. J. Non-Cryst. Solids 1995, 183, 151–160. [Google Scholar] [CrossRef]
- Schröter, K.; Donth, E. Comparison of shear response with other properties at the dynamic glass transition of different glassformers. J. Non-Cryst. Solids 2002, 307-310, 270–280. [Google Scholar] [CrossRef]
- Putz, K.; Green, P.F. Fragility in mixed alkali tellurites. J. Non-Cryst. Solids 2004, 337, 254–260. [Google Scholar] [CrossRef]
- Ngai, K.L.; Jonscher, A.K.; White, C.T. On the origin of the universal dielectric response in condensed matter. Nature 1979, 277, 185–189. [Google Scholar] [CrossRef]
- Vilgis, T.A. Strong and fragile glasses: A powerful classification and its consequences. Phys. Rev. B 1993, 47, 2882–2885. [Google Scholar] [CrossRef]
- Busch, R.; Bakke, E.; Johnson, W.L. Viscosity of the supercooled liquid and relaxation at the glass transition of the Zr46.75Ti8.25Cu7.5Ni10Be27.5 bulk metallic glass forming alloy. Acta Mater. 1998, 46, 4725–4732. [Google Scholar] [CrossRef]
- Rault, J. Remarks on the Kohlrausch exponent and the Vogel-Fulcher-Tammann law in glass-forming materials. J. Non-Cryst. Solids 1999, 260, 164–166. [Google Scholar] [CrossRef]
- Wang, L.W.; Fecht, H.-J. A kinetic model for liquids: Relaxation in liquids, origin of the Vogel-Tammann-Fulcher equation, and the essence of fragility. J. Appl. Phys. 2008, 104, 113538–113547. [Google Scholar] [CrossRef]
- Trachenko, K. Slow dynamics and stress relaxation in a liquid as an elastic medium. Phys. Rev. B 2007, 75, 212201–212204. [Google Scholar] [CrossRef]
- Trachenko, K. The Vogel-Fulcher-Tammann law in the elastic theory of glass transition. J. Non-Cryst. Solids 2008, 354, 3903–3906. [Google Scholar] [CrossRef]
- Niss, K.; Dalle-Ferrier, C.; Tarjus, G.; Alba-Simionesco, C. On the correlation between fragility and stretching in glass-forming liquids. J. Phys Cond. Matt. 2007, 19, 076102–076126. [Google Scholar] [CrossRef]
© 2010 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ikeda, M.; Aniya, M. Bond Strength—Coordination Number Fluctuation Model of Viscosity: An Alternative Model for the Vogel-Fulcher-Tammann Equation and an Application to Bulk Metallic Glass Forming Liquids. Materials 2010, 3, 5246-5262. https://doi.org/10.3390/ma3125246
Ikeda M, Aniya M. Bond Strength—Coordination Number Fluctuation Model of Viscosity: An Alternative Model for the Vogel-Fulcher-Tammann Equation and an Application to Bulk Metallic Glass Forming Liquids. Materials. 2010; 3(12):5246-5262. https://doi.org/10.3390/ma3125246
Chicago/Turabian StyleIkeda, Masahiro, and Masaru Aniya. 2010. "Bond Strength—Coordination Number Fluctuation Model of Viscosity: An Alternative Model for the Vogel-Fulcher-Tammann Equation and an Application to Bulk Metallic Glass Forming Liquids" Materials 3, no. 12: 5246-5262. https://doi.org/10.3390/ma3125246
APA StyleIkeda, M., & Aniya, M. (2010). Bond Strength—Coordination Number Fluctuation Model of Viscosity: An Alternative Model for the Vogel-Fulcher-Tammann Equation and an Application to Bulk Metallic Glass Forming Liquids. Materials, 3(12), 5246-5262. https://doi.org/10.3390/ma3125246




