Focal Conic Stacking in Smectic A Liquid Crystals: Smectic Flower and Apollonius Tiling
Abstract
:1. Introduction

2. Materials and Experimental Setup
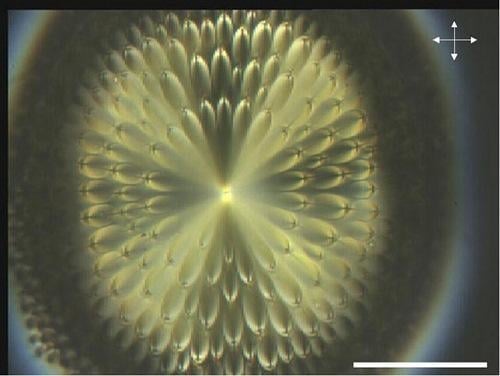
2.1. Flower texture
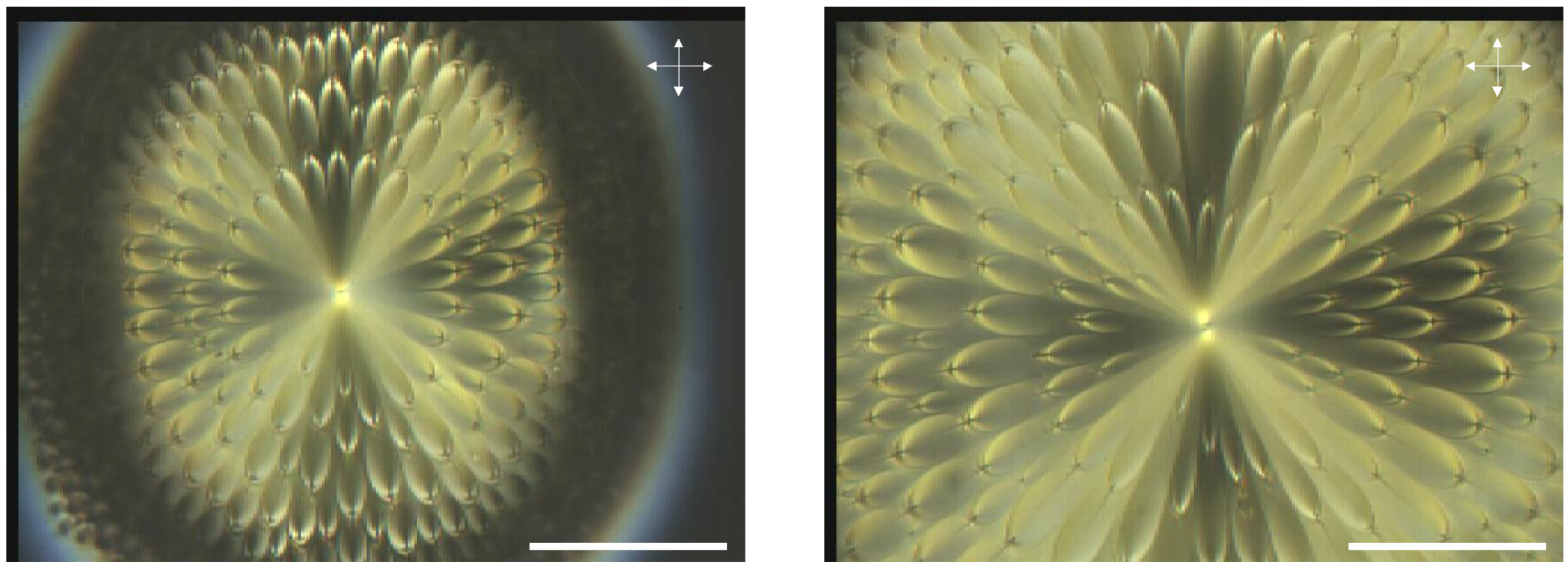
2.2. Generation texture
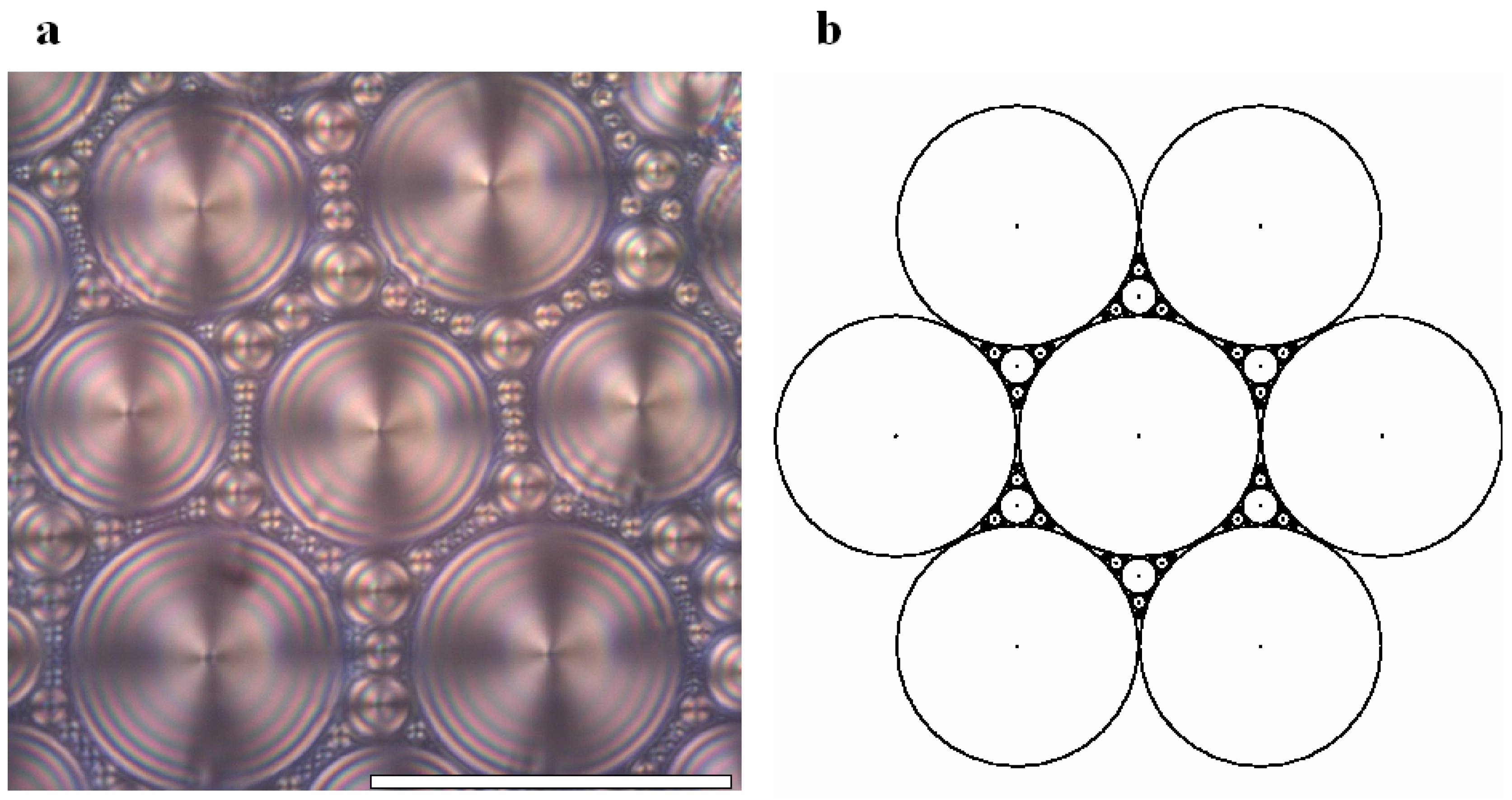
3. The smectic layers
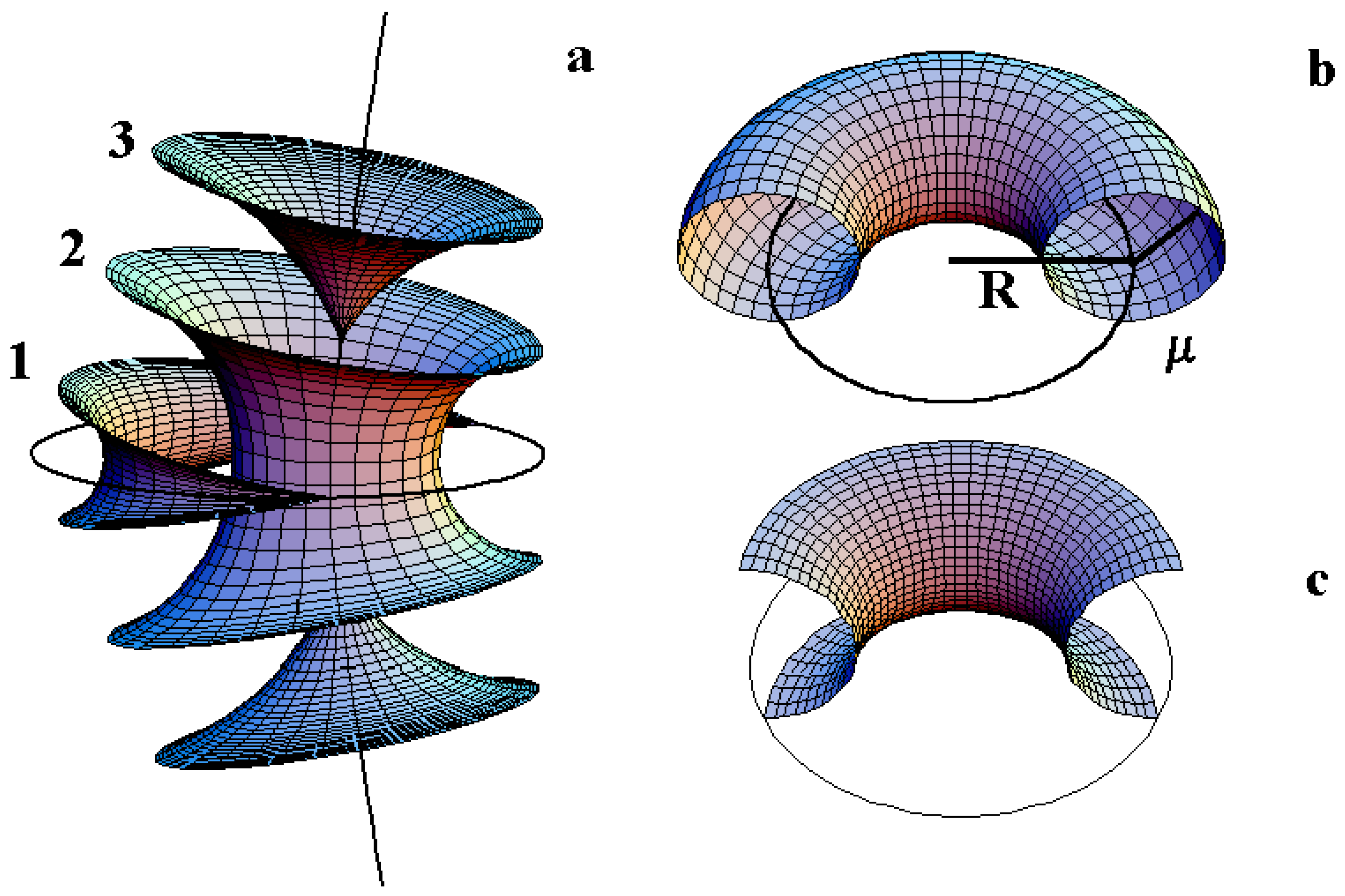
4. The Law of Corresponding Cones
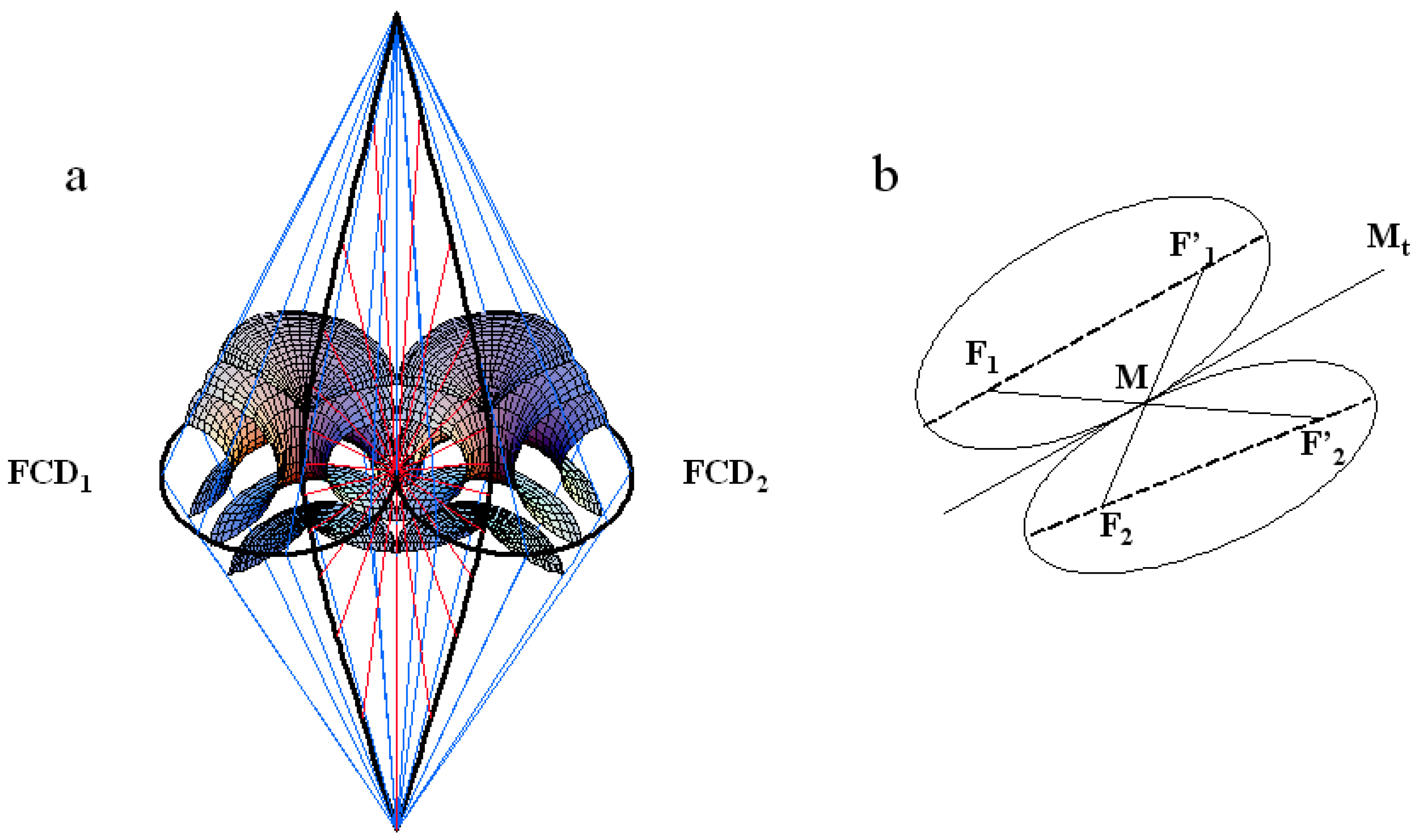
5. Results and Discussion
5.1. Flower texture
Model of the experimental texture.
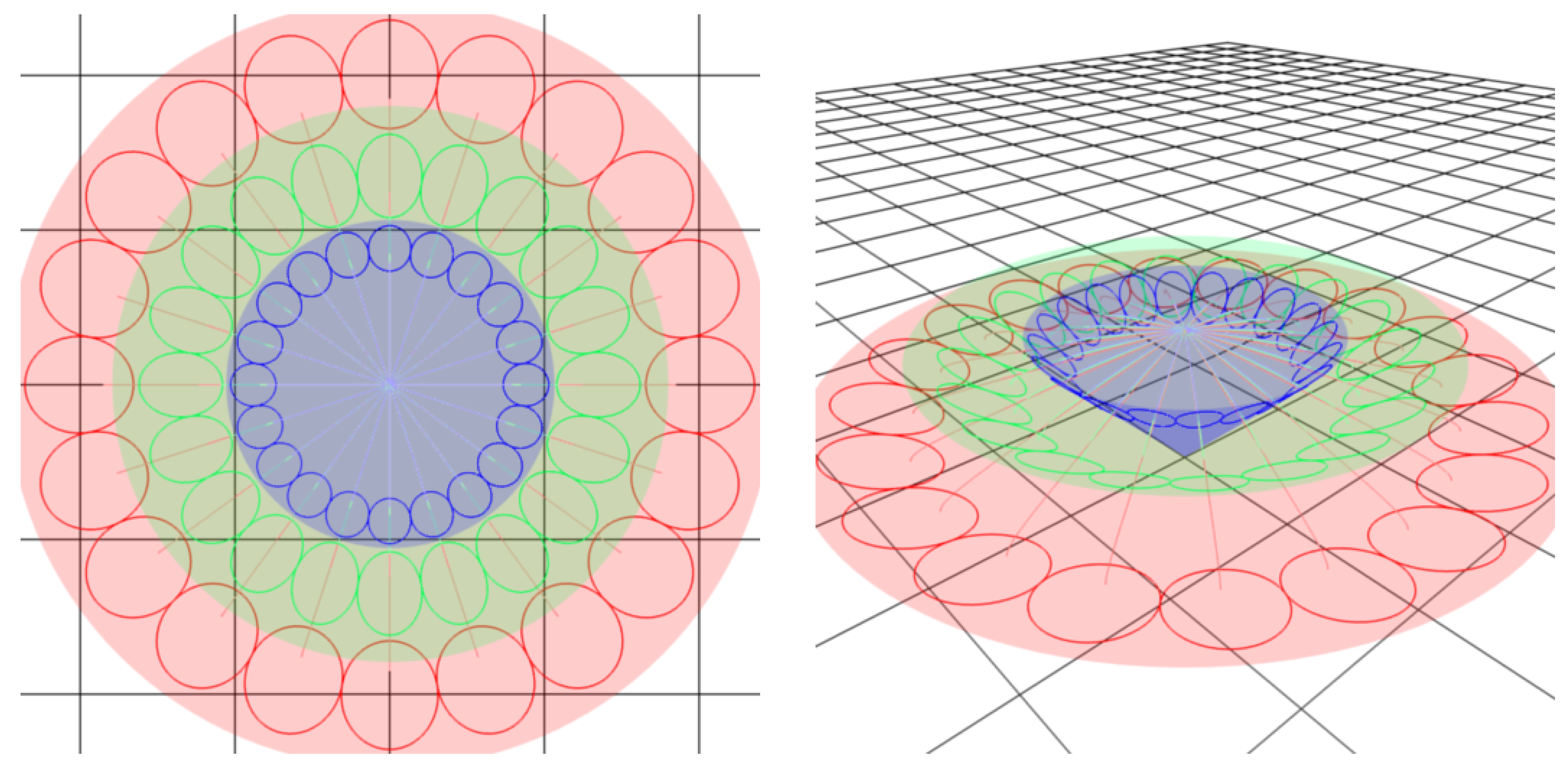
5.2. Generation texture
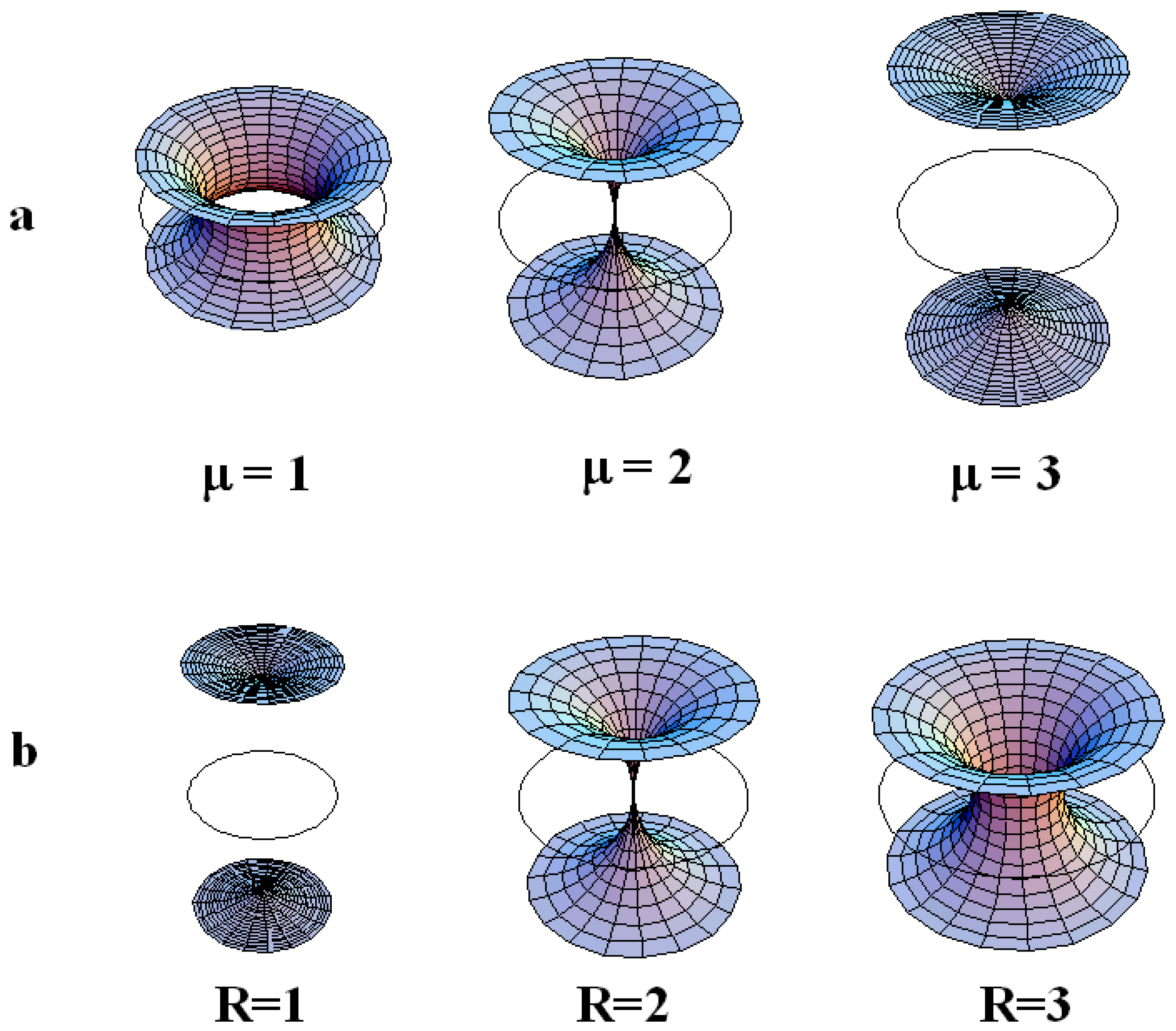
The variation of μ at fixed R.
The variation of R at fixed μ.
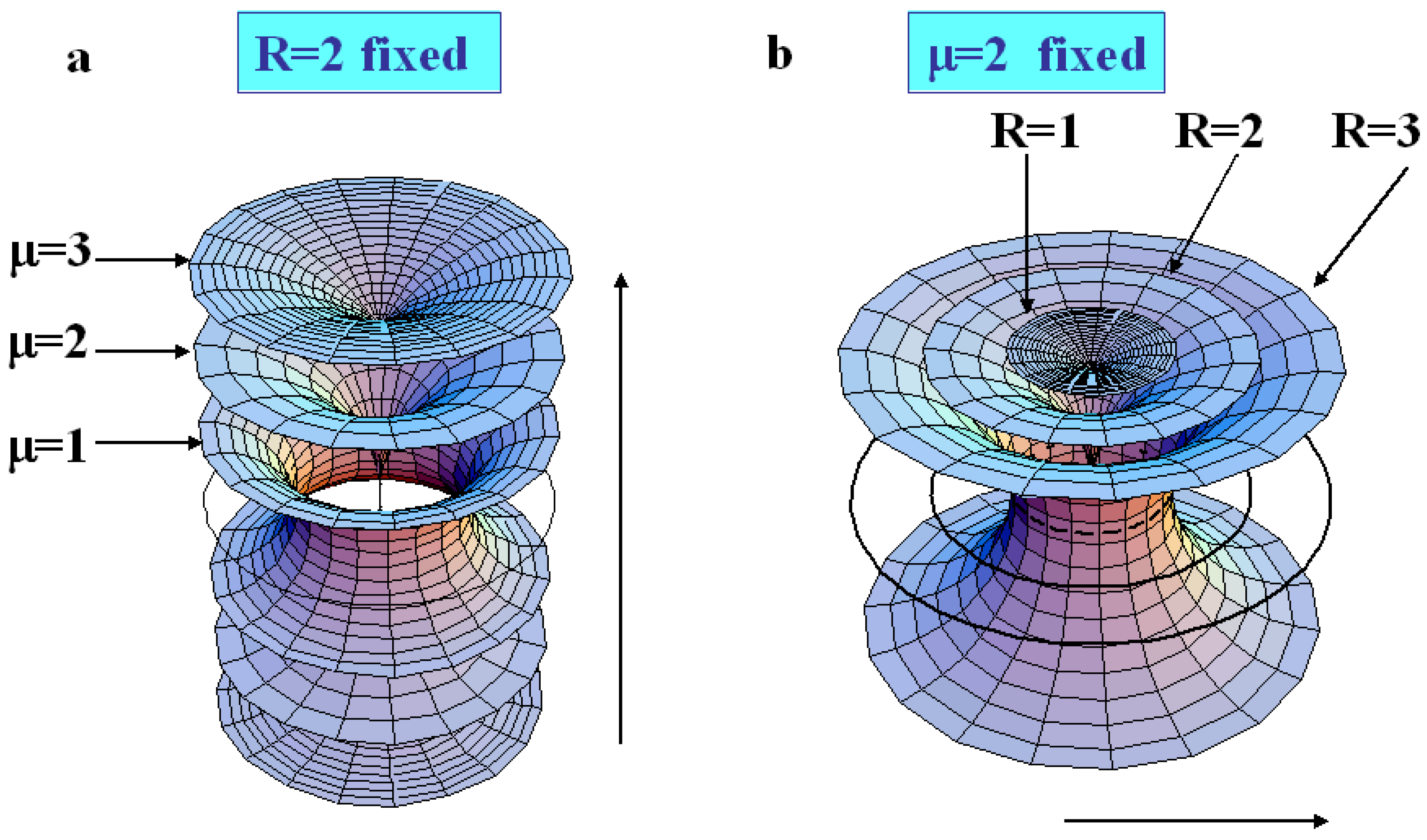
The simulation of the smectic layers.
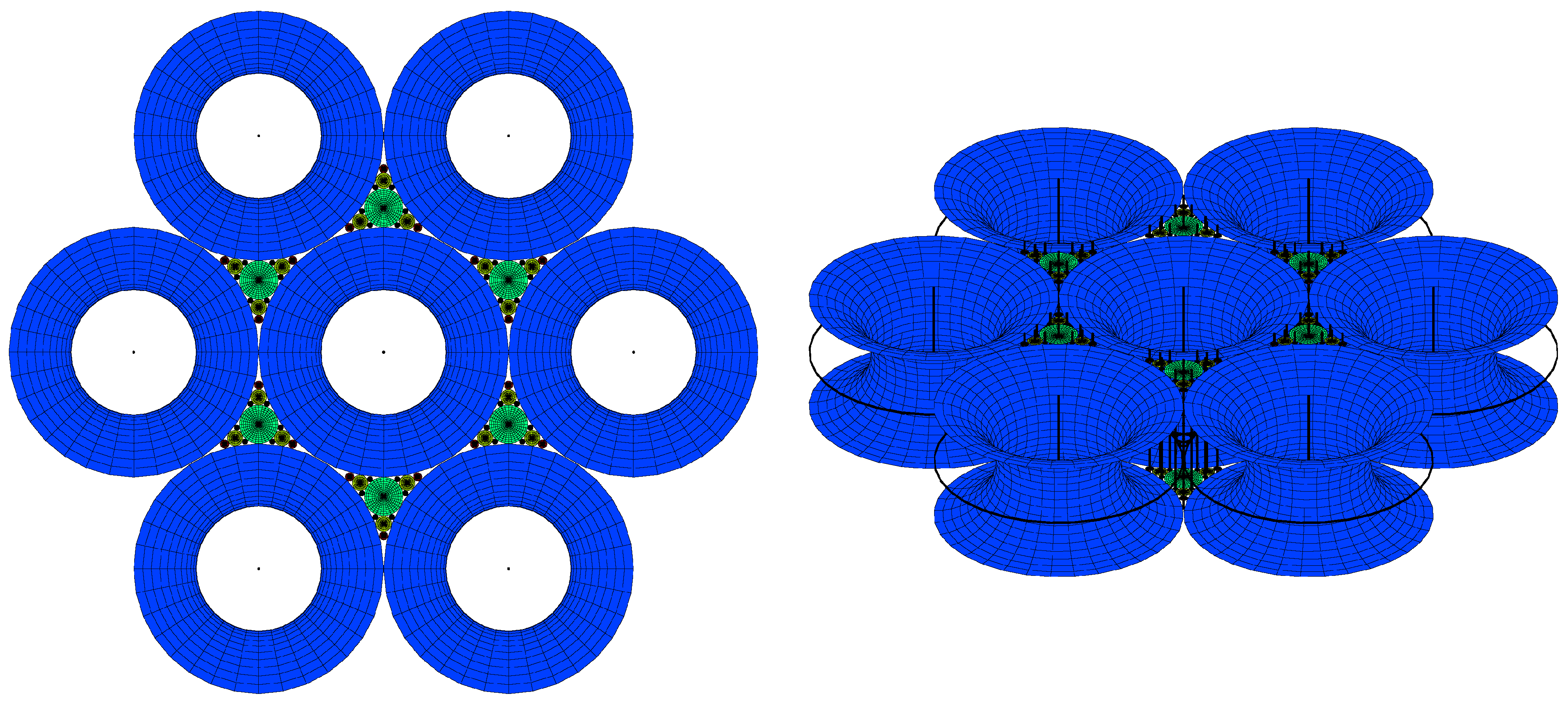
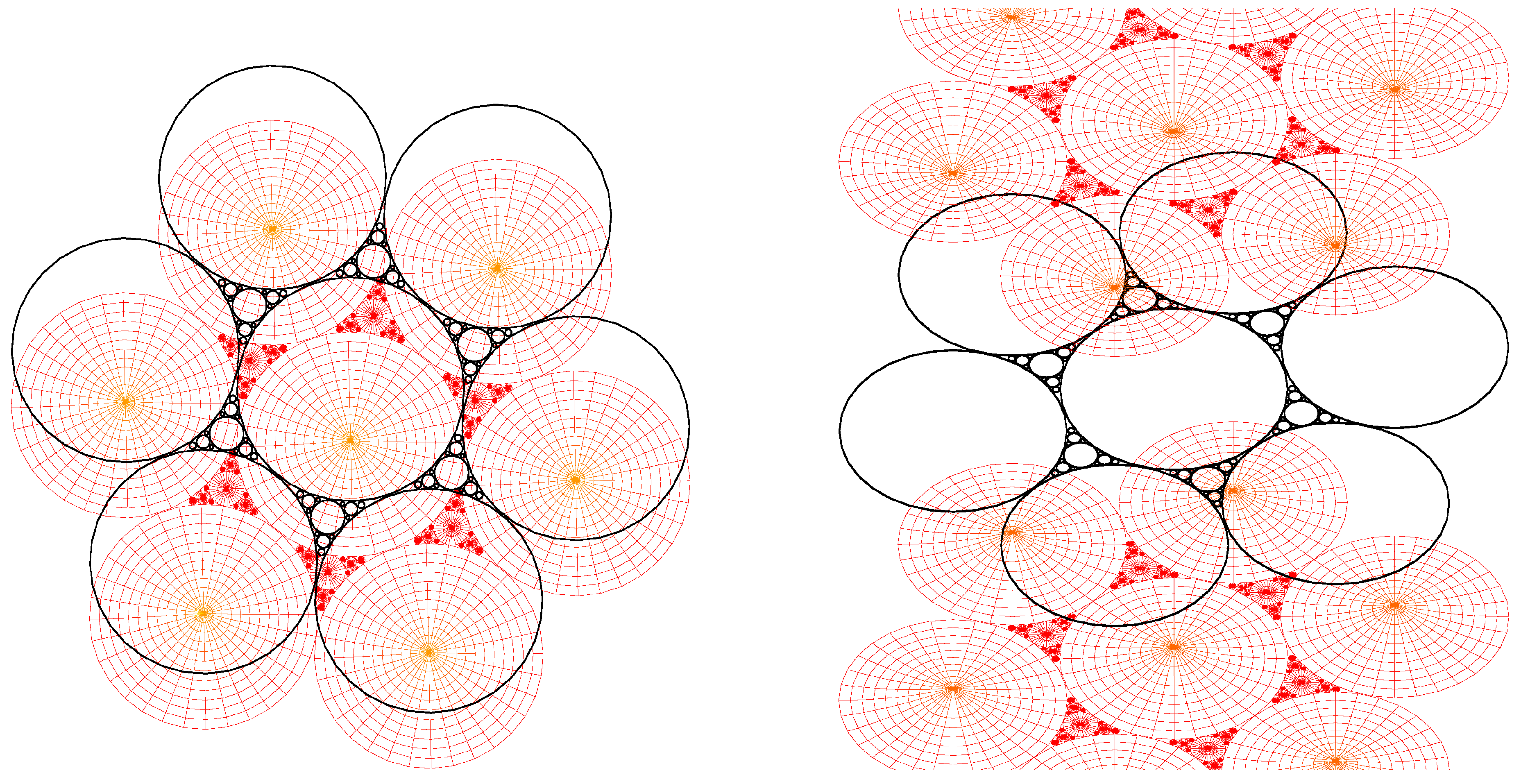
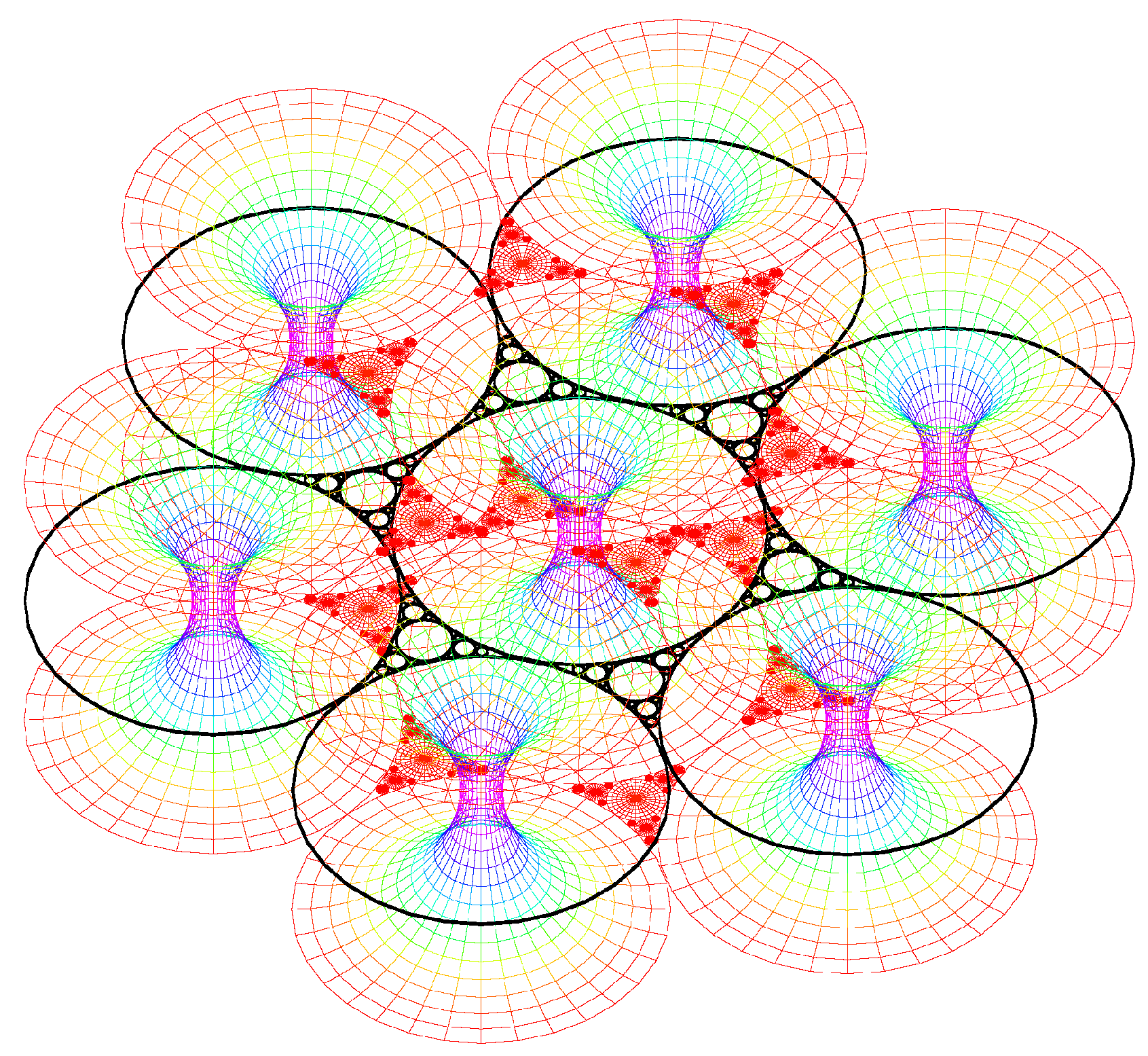
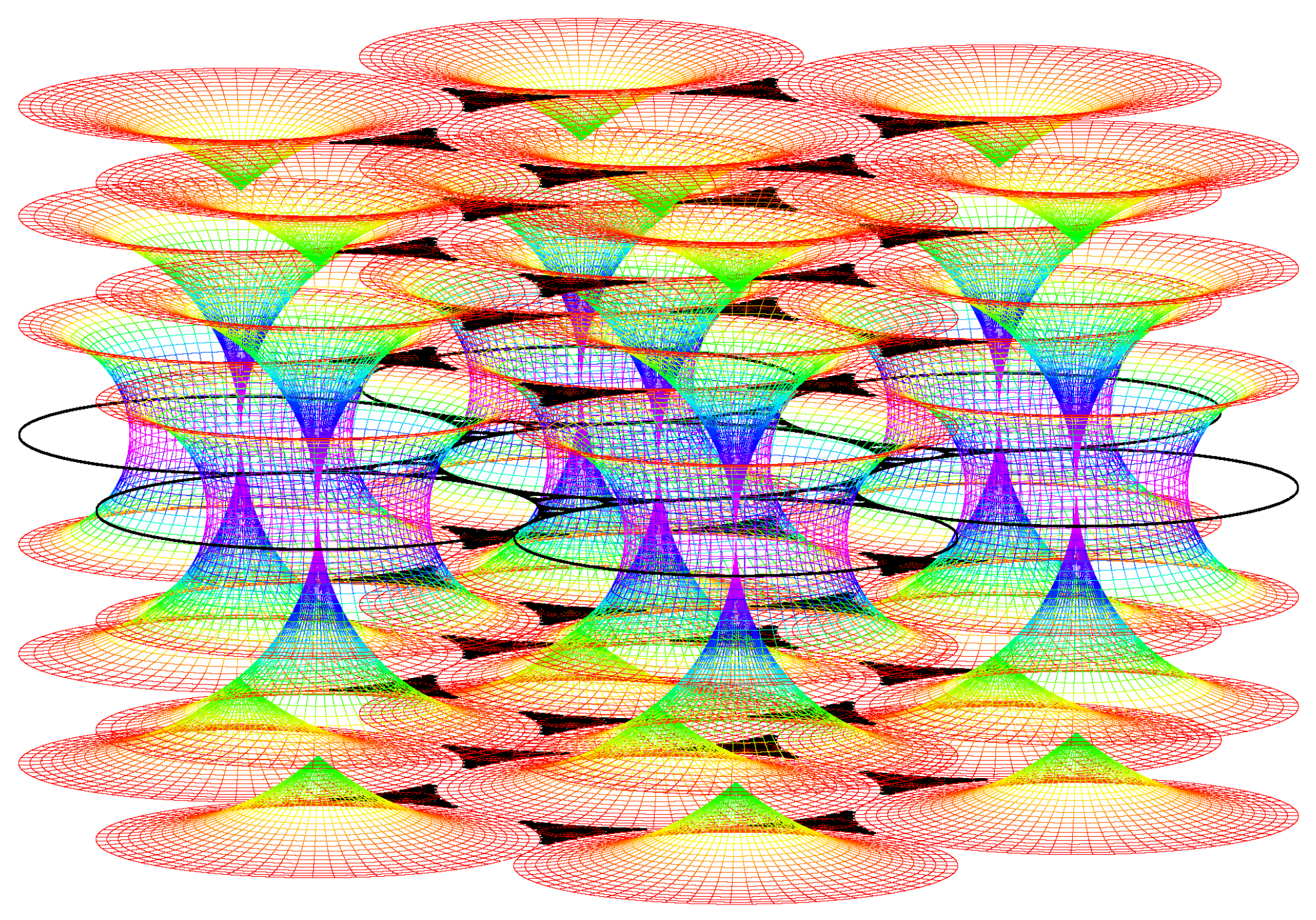
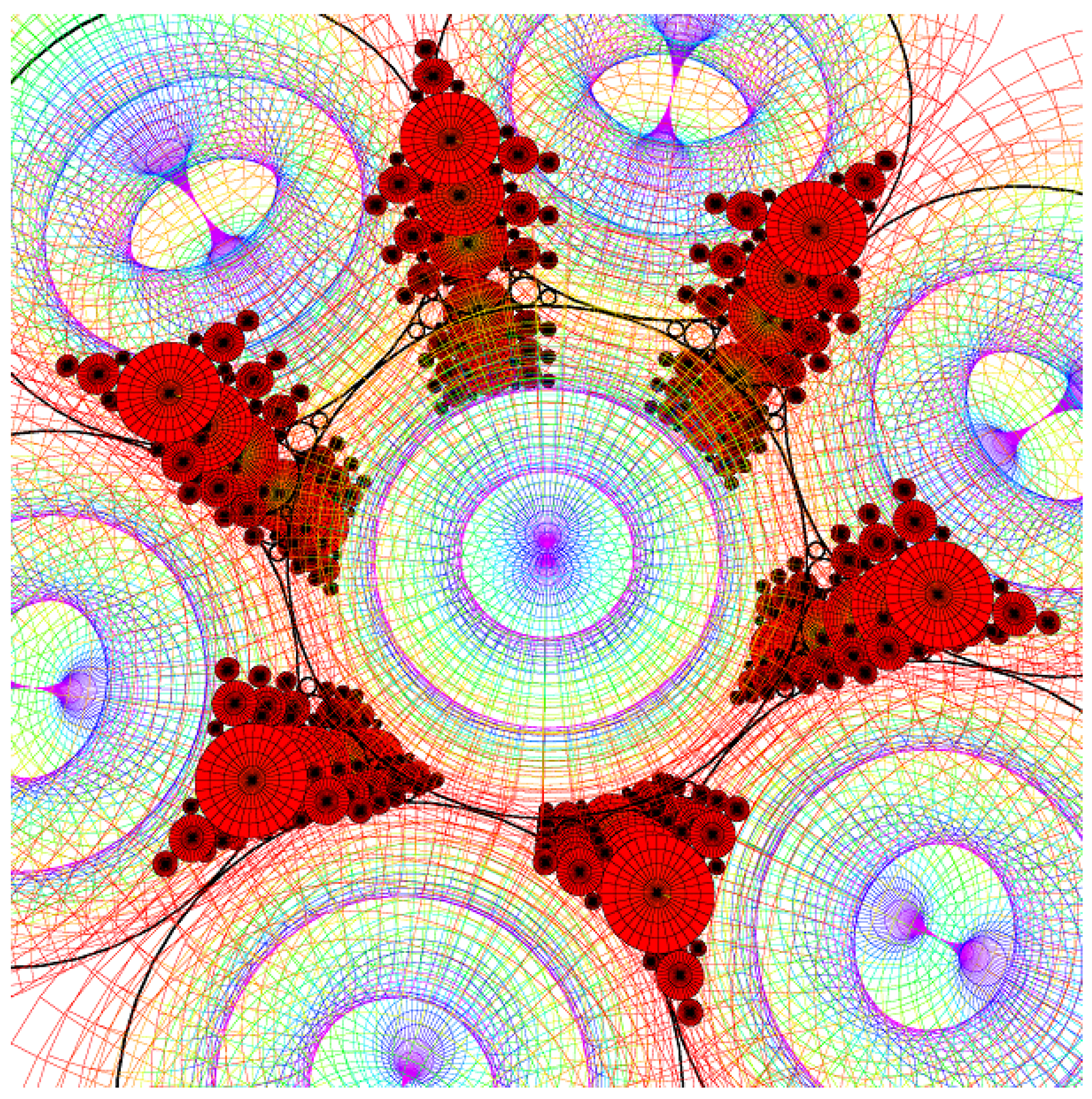
6. Conclusions
Acknowledgements
References and Notes
- Bragg, W.L. Focal Conic Structures. Trans. Faraday Soc. 1933, 29, 1056–1060. [Google Scholar] [CrossRef]
- Söddy, F. The Kiss Precise. Nature 1936, 137, 1021–1021. [Google Scholar] [CrossRef]
- Coxeter, H.S.M. The Problem of Apollonius. Amer. Math. Monthly 1968, 75, 5–15. [Google Scholar] [CrossRef]
- Descartes, R. Oeuvres de Descartes, Correspondance IV; Adam, C., Tannery, P., Eds.; Leopold Cerf: Paris, 1901. [Google Scholar]
- Beecroft, P. Properties of Circles in Mutual Contact. Lady’s and Gentleman’s Diary 1842, 139, 91–96. [Google Scholar]
- Bidaux, R.; Boccara, N.; Sarma, G.; De Seze, L.; De Gennes, P.G.; Parodi, O. Statistical Properties of Focal Conic Textures in Smectic Liquid Crystals. Journal de Physique 1973, 34, 661–672. [Google Scholar] [CrossRef]
- Berger, M. Géométrie: Espaces euclidiens, triangles, cercles et sphères volume 2. Cedic/Fernand Nathan, Ed.; Publisher: Paris, 1977. [Google Scholar]
- Zhang, Z.; Comellas, F.; Fertin, G.; Rong, L. High Dimensional Apollonian Networks. J. Phys. A: Math Gen. 2006, 39, 1811–1818. [Google Scholar] [CrossRef]
- Fournier, J.-B.; Durand, G. Focal Conic Faceting in Smectic-A Liquid Crystals. J. Phys. II France 1991, 1, 845–870. [Google Scholar] [CrossRef]
- Lavrentovich, O.D.; Pergamenshchik, V.M. Patterns in thin liquid crystal films and the divergence ("surfacelike") elasticity. Intern. Journ. Modern Phys. B 1995, 9, 2389–2437. [Google Scholar] [CrossRef]
- Bouligand, Y. Recherches sur les Textures des États Mésomorphes 1. Les Arrangements dans les Smectiques: Rappels et Considérations Théoriques. Journal de Physique 1972, 33, 525–547. [Google Scholar] [CrossRef]
- Blanc, C. Étude de l’interface lamellaire-éponge des systèmes lyotropes gonflés: du facettage volumique et des formes de croissance aux modèles microscopiques. PhD thesis, Université Paris VI, Paris, France, 2000. [Google Scholar]
- Blanc, C.; Kleman, M. Tiling the Plane with Noncongruent Toric Focal Conic Domains. Phys. Rev. E 2000, 62, 6739–6748. [Google Scholar] [CrossRef]
- Lavrentovich, O.D.; Kleman, M. Grain Boundaries and The Law of Corresponding Cones. Eur. Phys. J. E 2000, 2, 47–57. [Google Scholar]
- Kim, Ho Yun; Yoon, Dong, Ki; Choi, M.C.; Jeong, Hyeon Su; Kim, Mahn Won; Lavrentovich, O. D.; Jung, Hee-Tae. Confined Self-Assembly of Toric Focal Conic Domains (The effects of Confined Geometry on the Feature Size of Toric Focal Conic Domains). Langmuir 2009, 25, 1685–1691. [Google Scholar]
- Designole, V.; Herminghaus, S.; Pfohl, T.; Bahr, Ch. AFM Study of Defect-Induced Depressions of the Smectic-A/ Air Interface. Langmuir 2006, 22, 363–368. [Google Scholar] [CrossRef] [PubMed]
- Michel, J.P.; Lacaze, E.; Goldmann, M.; Gailhanou, M.; de Boissieu, M.; Alba, M. Structure of Smectic Defect Cores: X-Ray Study of 8CB Liquid Crystal Ultrathin Films. Phys. Rev. Lett. 2006, 96, 027803-1-4. [Google Scholar] [CrossRef] [PubMed]
- Lacaze, E.; Michel, J.-P.; Alba, M.; Goldmann, M. Planar anchoring and surface melting in the smectic-A phase. Phys. Rev. E 2007, 76, 041702-1-6. [Google Scholar] [CrossRef] [PubMed]
- Zappone, B.; Lacaze, E. Surface-frustrated periodic textures of smectic-A liquid crystals on crystalline surfaces. Phys. Rev. E 2008, 78, 061704-1-9. [Google Scholar] [CrossRef] [PubMed]
- Garnier, L. Mathématiques pour la modélisation géométrique, la représentation 3D et la synthèse d’images. Ellipses, Paris, France, 2007. [Google Scholar]
- Friedel, G. Les Etats Mésomorphes de la Matière. Ann. Phys. 1922, 18, 273–474. [Google Scholar]
- Sethna, J.-P.; Kleman, M. Spheric Domains in Smectic Liquid Crystals. Phys. Rev. A 1982, 26(5), 3037–3040. [Google Scholar] [CrossRef]
- De Gennes, P.G.; Prost, J. The Physics of Liquid Crystals, Second editionClarendon Press: Oxford, Paris, 1993. [Google Scholar]
- Kleman, M.; Meyer, C.; Nastishin, Yu. A. Imperfections in Focal Conic Domains: The Role of Dislocations. Philos. Mag. 2006, 86, 4439–4458. [Google Scholar] [CrossRef]
- Yoon, Dong Ki; Choi, M. C.; Kim, Ho Yun; Kim, Mahn Won; Lavrentovich, O. D.; Jung, Hee-tae. Internal Structure Visualization and Lithographic Use of Periodic Toroidal Holes in Liquid Crystals. Nature Materials 2007, 6, 866–870. [Google Scholar]
© 2009 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Meyer, C.; Le Cunff, L.; Belloul, M.; Foyart, G. Focal Conic Stacking in Smectic A Liquid Crystals: Smectic Flower and Apollonius Tiling. Materials 2009, 2, 499-513. https://doi.org/10.3390/ma2020499
Meyer C, Le Cunff L, Belloul M, Foyart G. Focal Conic Stacking in Smectic A Liquid Crystals: Smectic Flower and Apollonius Tiling. Materials. 2009; 2(2):499-513. https://doi.org/10.3390/ma2020499
Chicago/Turabian StyleMeyer, Claire, Loic Le Cunff, Malika Belloul, and Guillaume Foyart. 2009. "Focal Conic Stacking in Smectic A Liquid Crystals: Smectic Flower and Apollonius Tiling" Materials 2, no. 2: 499-513. https://doi.org/10.3390/ma2020499
APA StyleMeyer, C., Le Cunff, L., Belloul, M., & Foyart, G. (2009). Focal Conic Stacking in Smectic A Liquid Crystals: Smectic Flower and Apollonius Tiling. Materials, 2(2), 499-513. https://doi.org/10.3390/ma2020499