Parameter Estimation for the Basic Zirka-Moroz History-Dependent Hysteresis Model for Electrical Steels
Abstract
1. Introduction
2. Theoretical Background
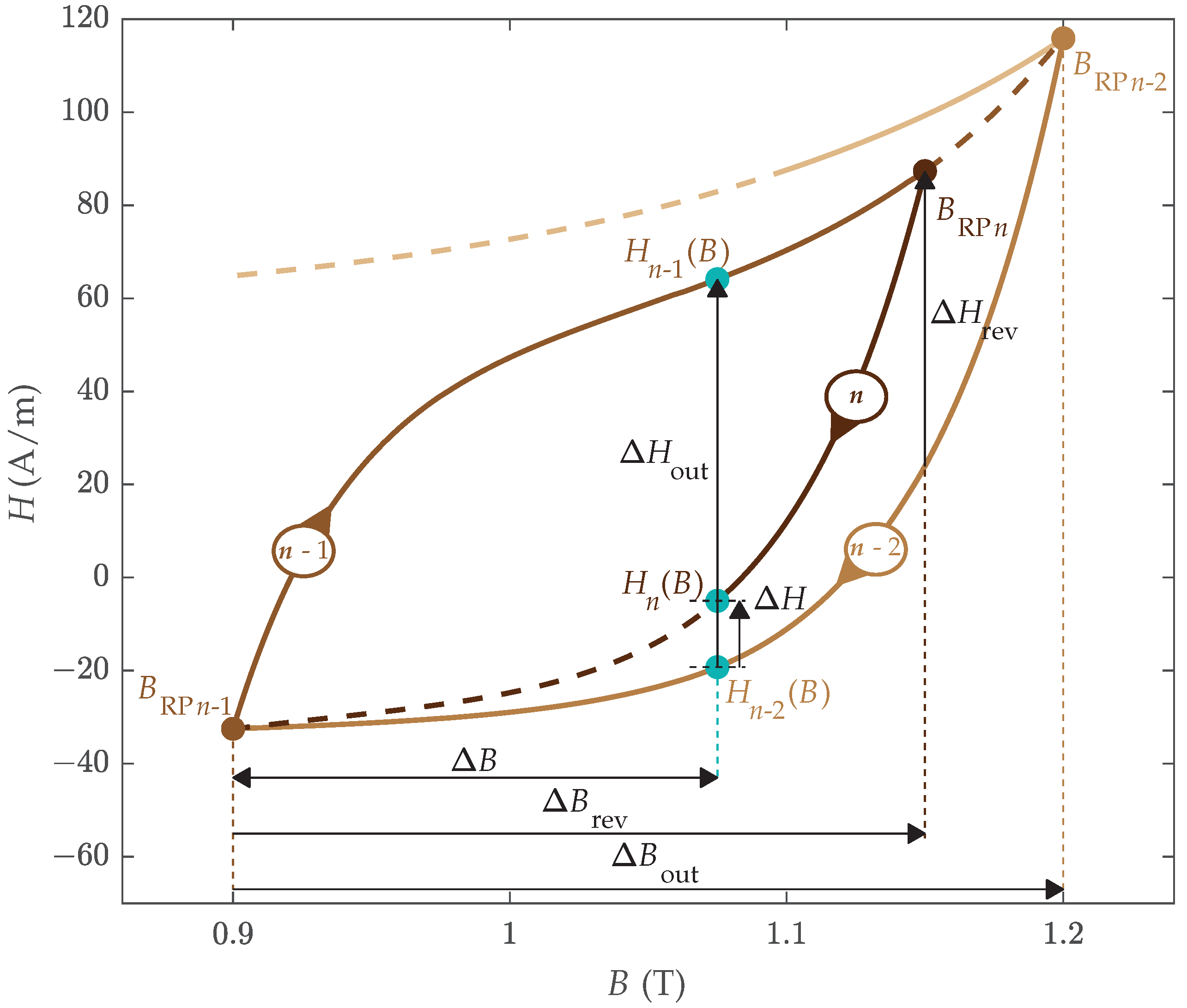
2.1. Branching off from the Previous Magnetization Trajectory
- 1.
- In this case, RC was descending, where B decreased from to . After the RP at , B is increasing, and magnetization evolves according to RC , as presented in Figure 1a.
- 2.
- In this case, RC was ascending, where B increased from to . After the RP at , B is decreasing, and magnetization evolves according to RC , as presented in Figure 1b.
2.2. Merging of Consecutive Trajectories into a Hysteresis Loop
2.3. History-Independent Magnetization
2.4. Modeling of HD Magnetization Trajectories
2.5. Considering the Position-Based Shape Variations of Reversal Curves
2.6. Initialization of the HD Model, First Magnetization Curve, and Symmetric Minor Loops
3. Estimation of ZM Model’s Parameters
3.1. Estimation of Parameters Based on Symmetric Minor Loops
3.2. Estimation of Parameters Based on the Measured FORCs
3.3. A Two-Step Estimation Approach
4. Results
- (a)
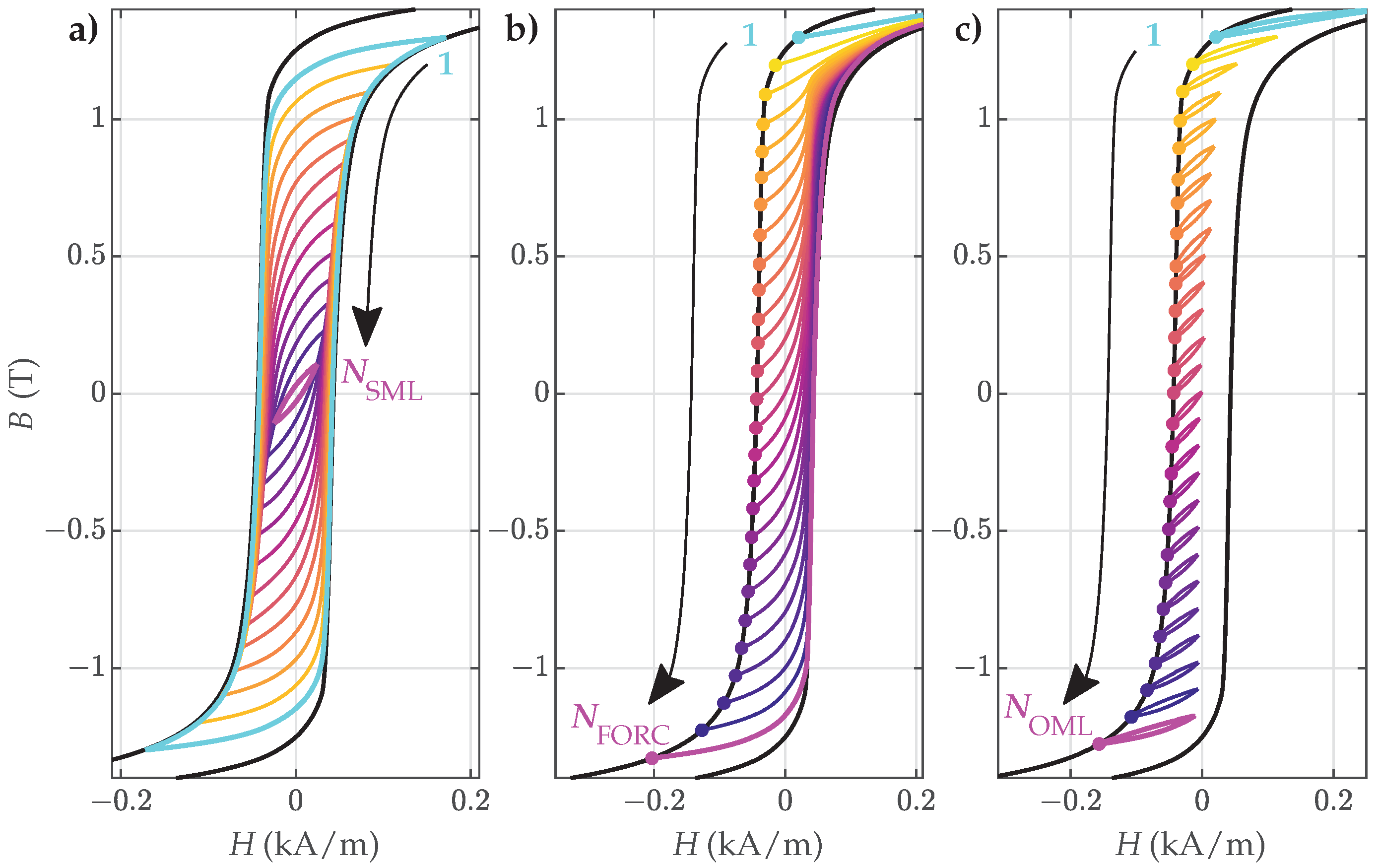
- Symmetric hysteresis loops, presented schematically in Figure 3a: The biggest symmetric loop for individual material samples was assumed as the major loop (i.e., the loop tips were assumed ) and was used as the model input. The remaining SMLs were used for the validation of the estimated parameters.
- (b)
- First-order reversal curves (FORCs), presented schematically in Figure 3b: A family of FORCs was measured within the assumed major loop. These represented the basis for the proposed two-step estimation of the parameters.
- (c)
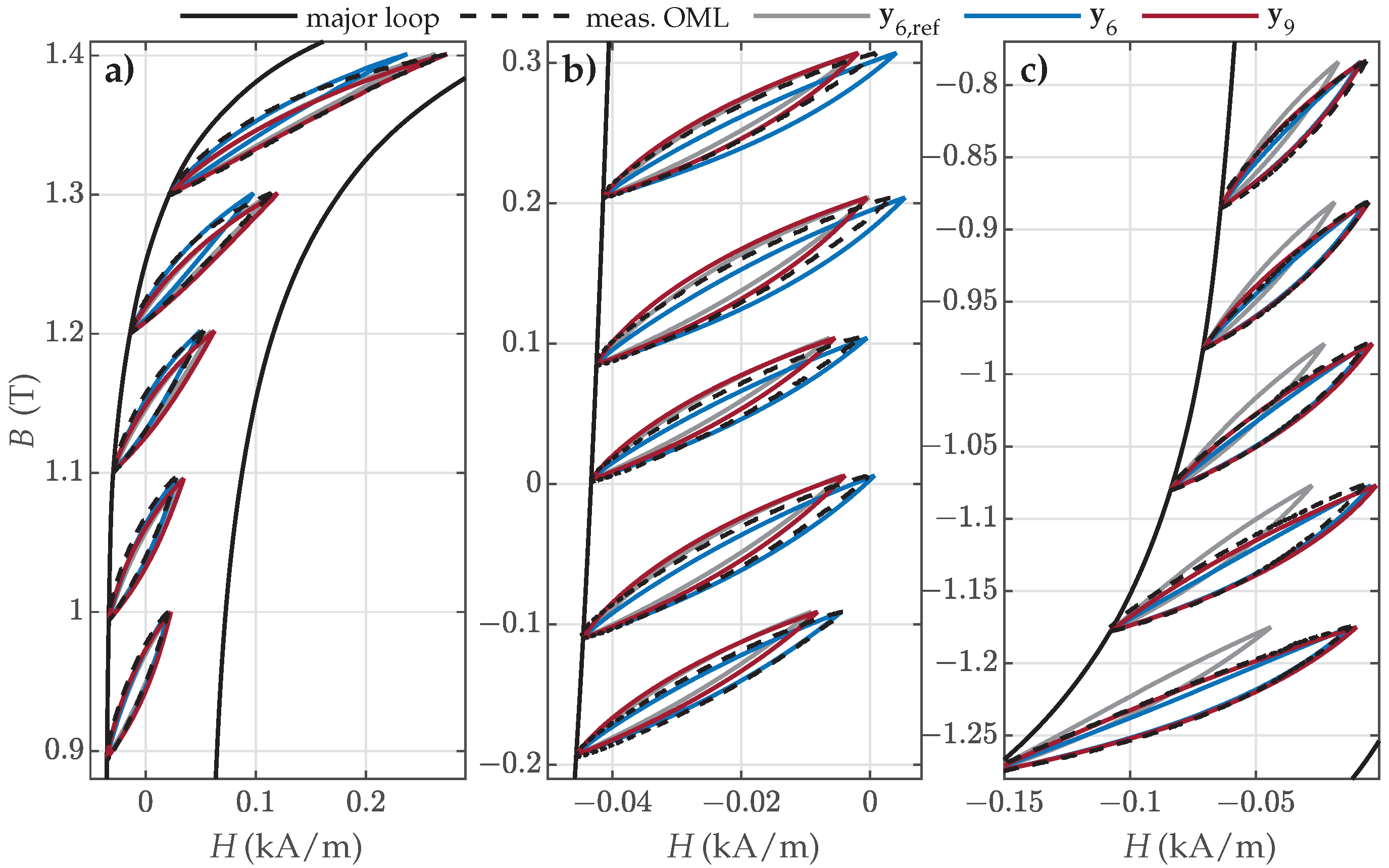
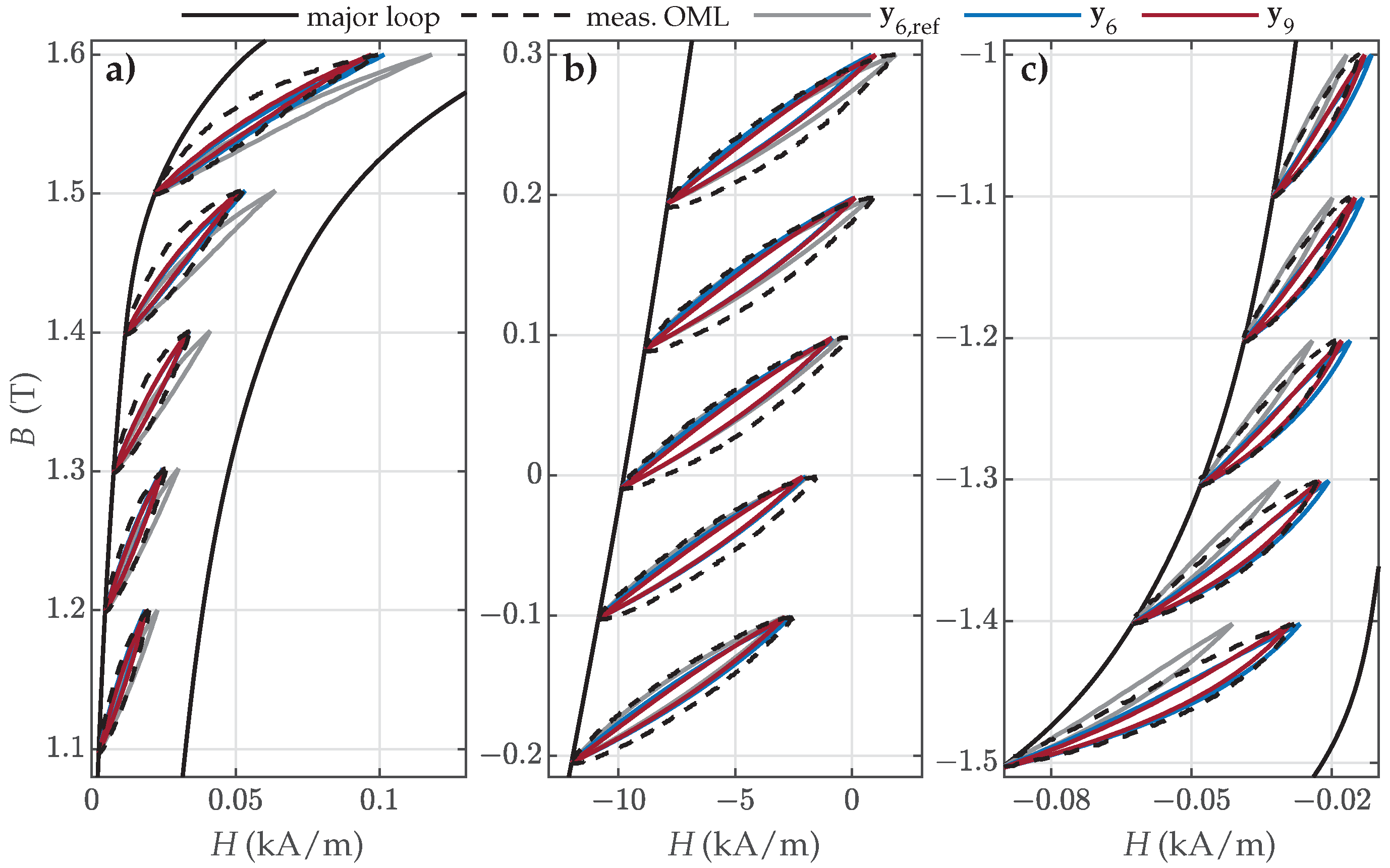
- Offset minor loops (OMLs) along the assumed major loop, presented schematically in Figure 3c: These were used for the validation of the estimated parameters.
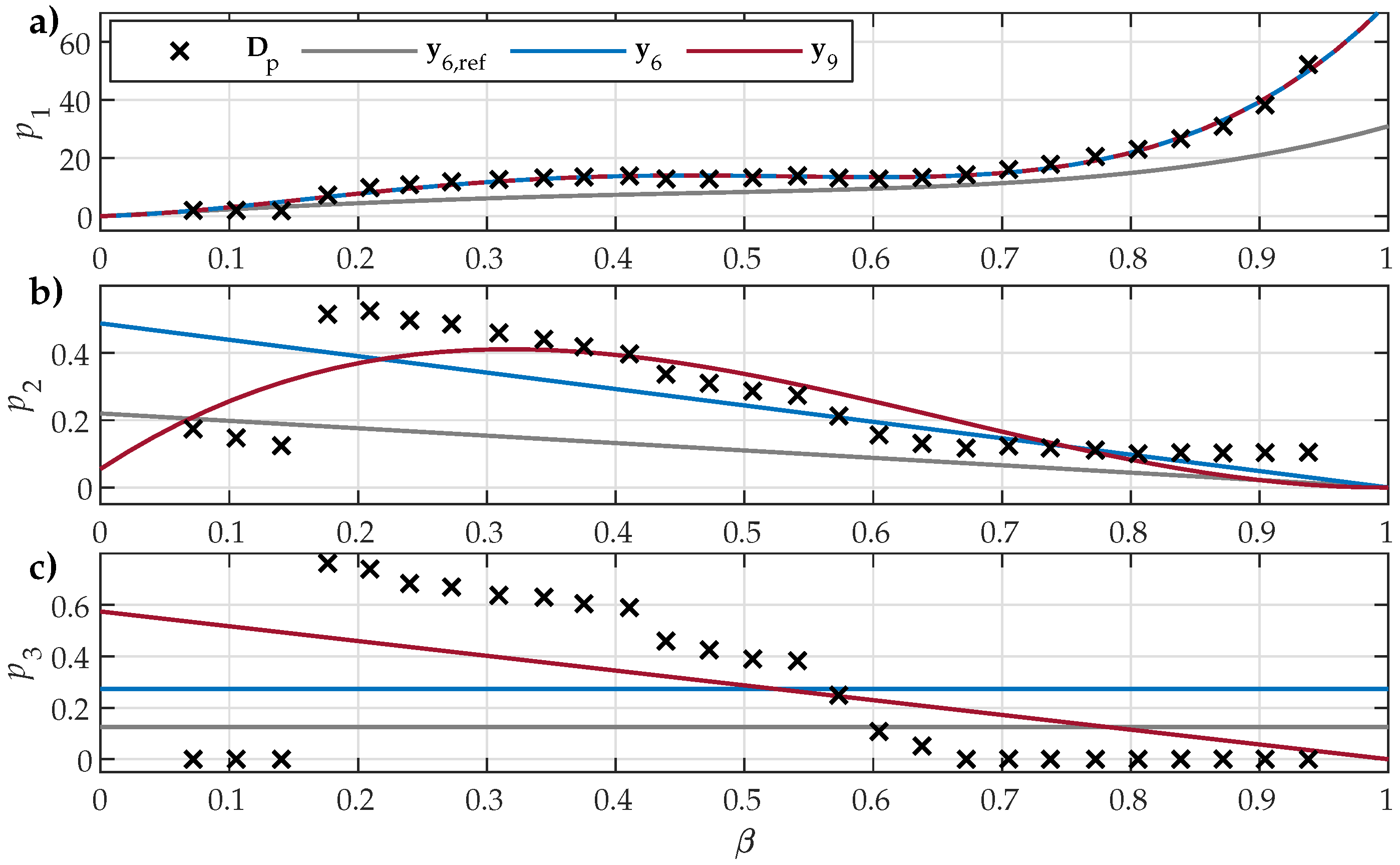
4.1. First Step of the Estimation Approach
4.2. Second Step of the Estimation Approach
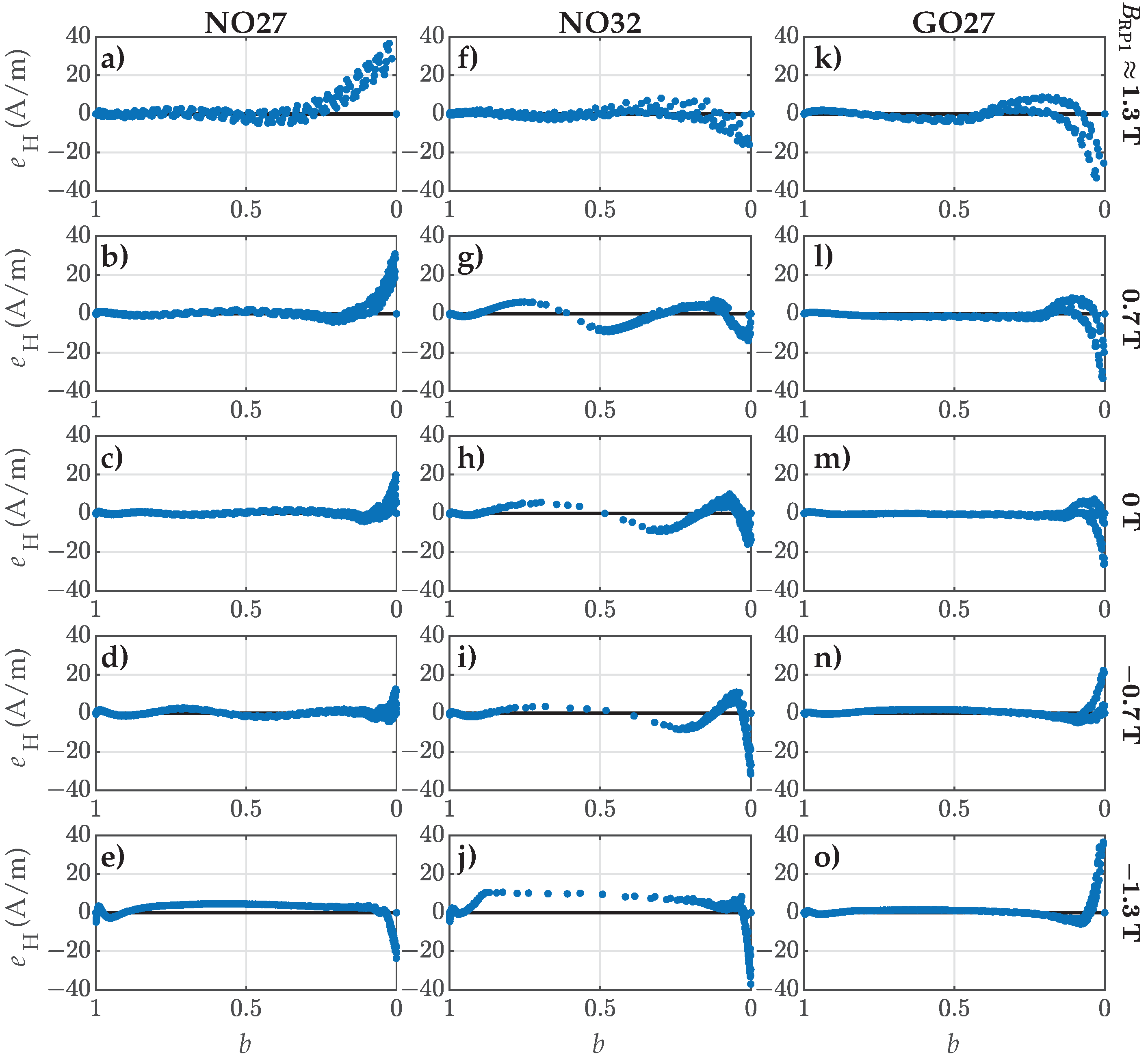
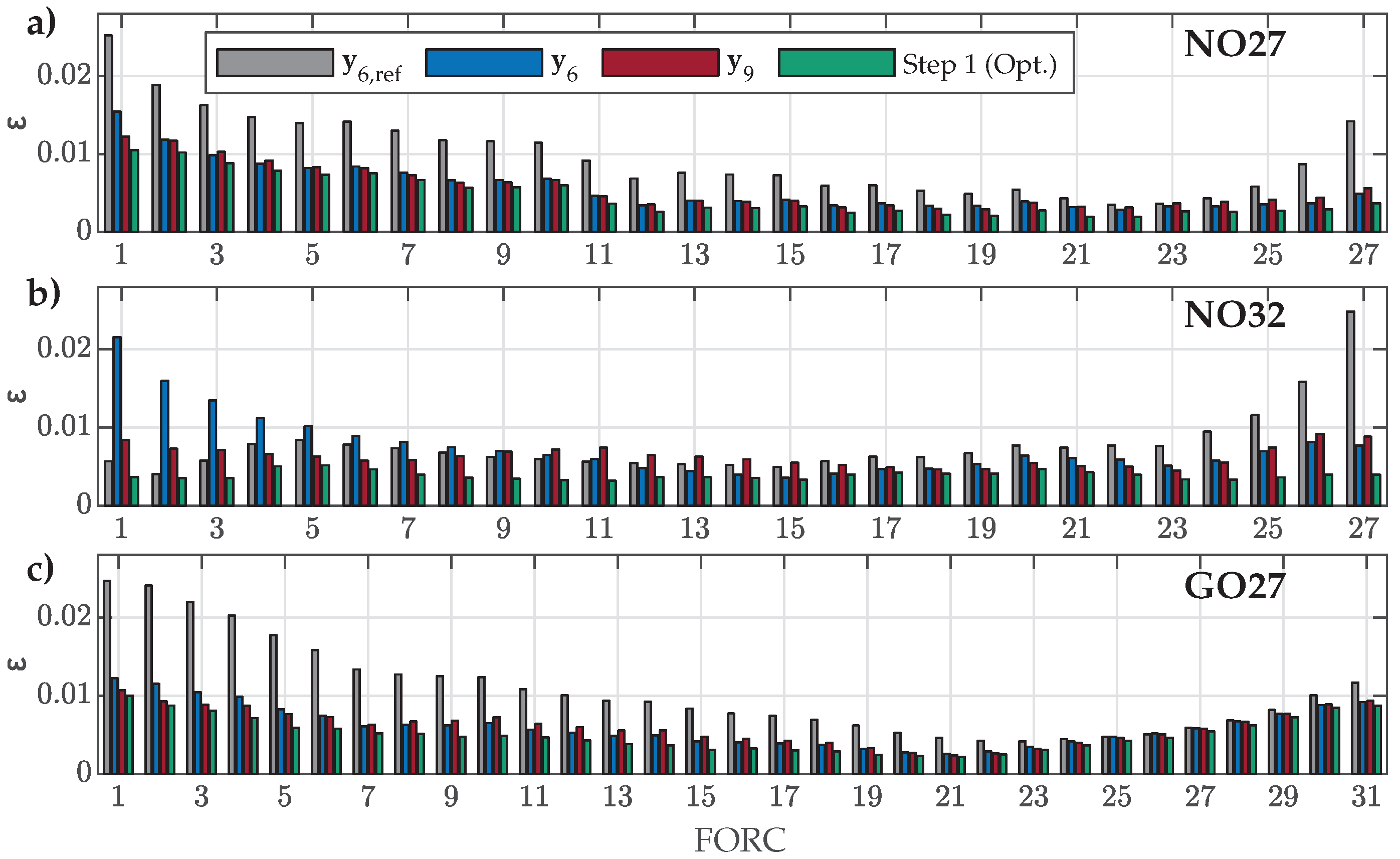
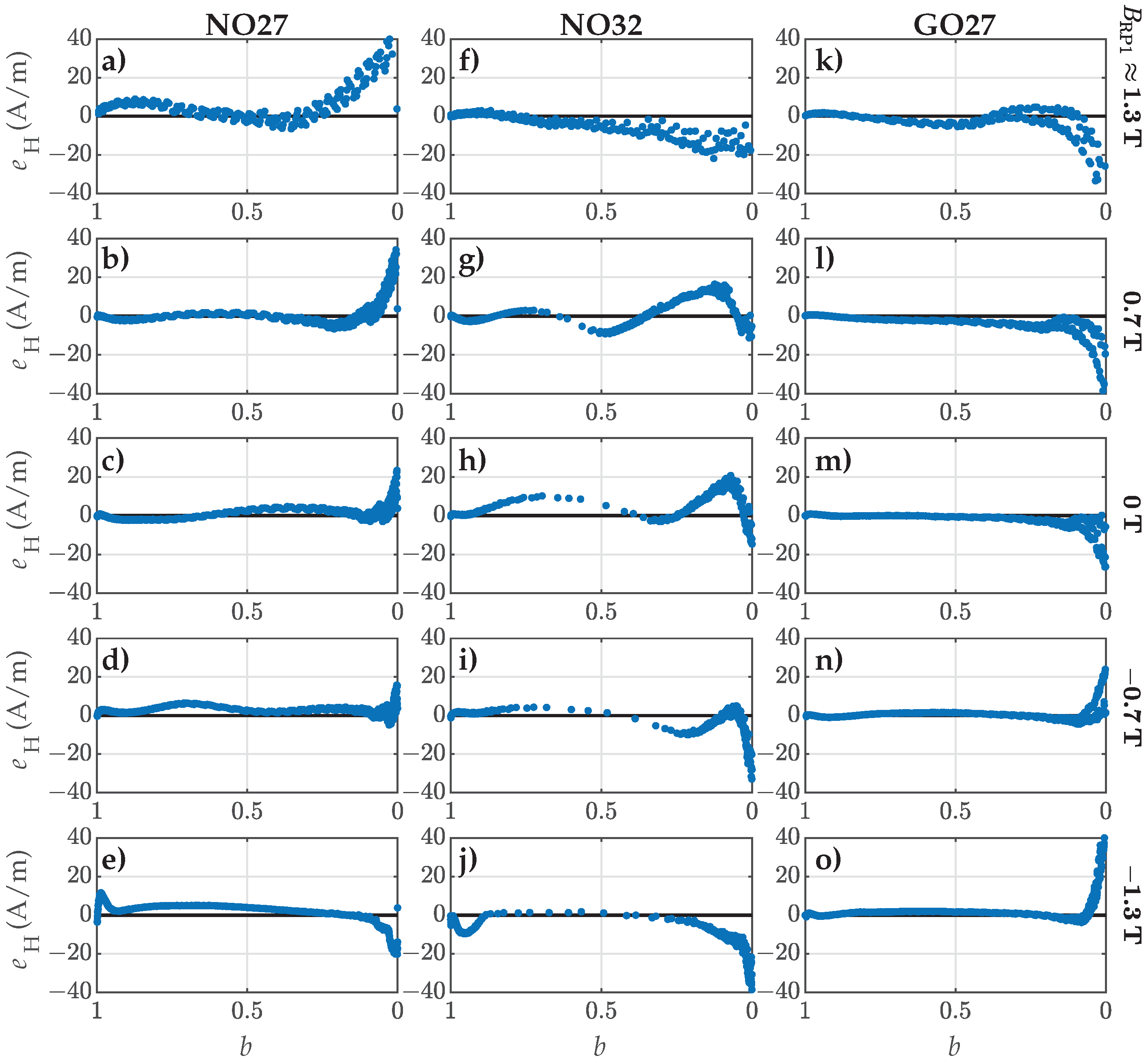
4.3. Validation Versus Measured FORCs
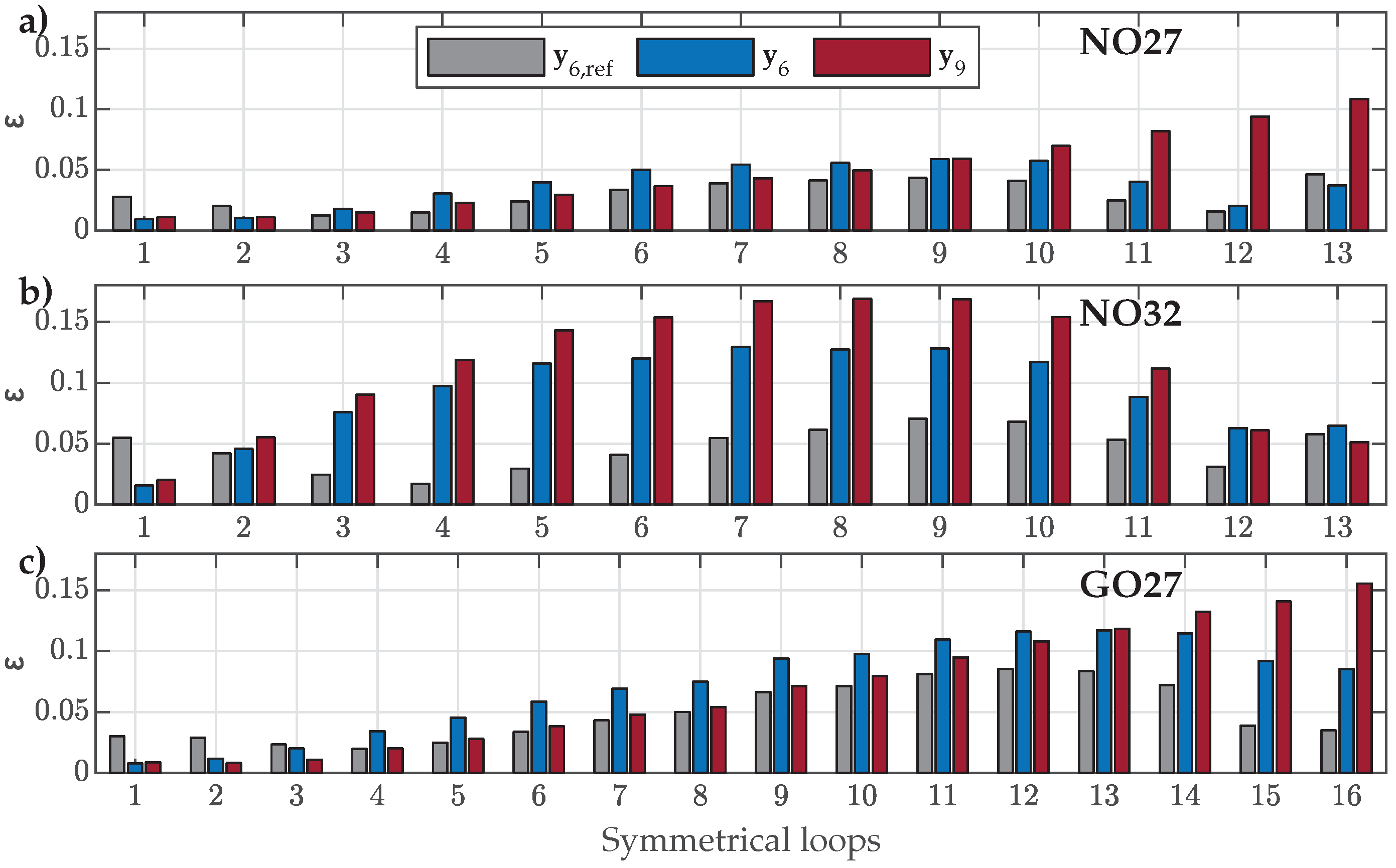
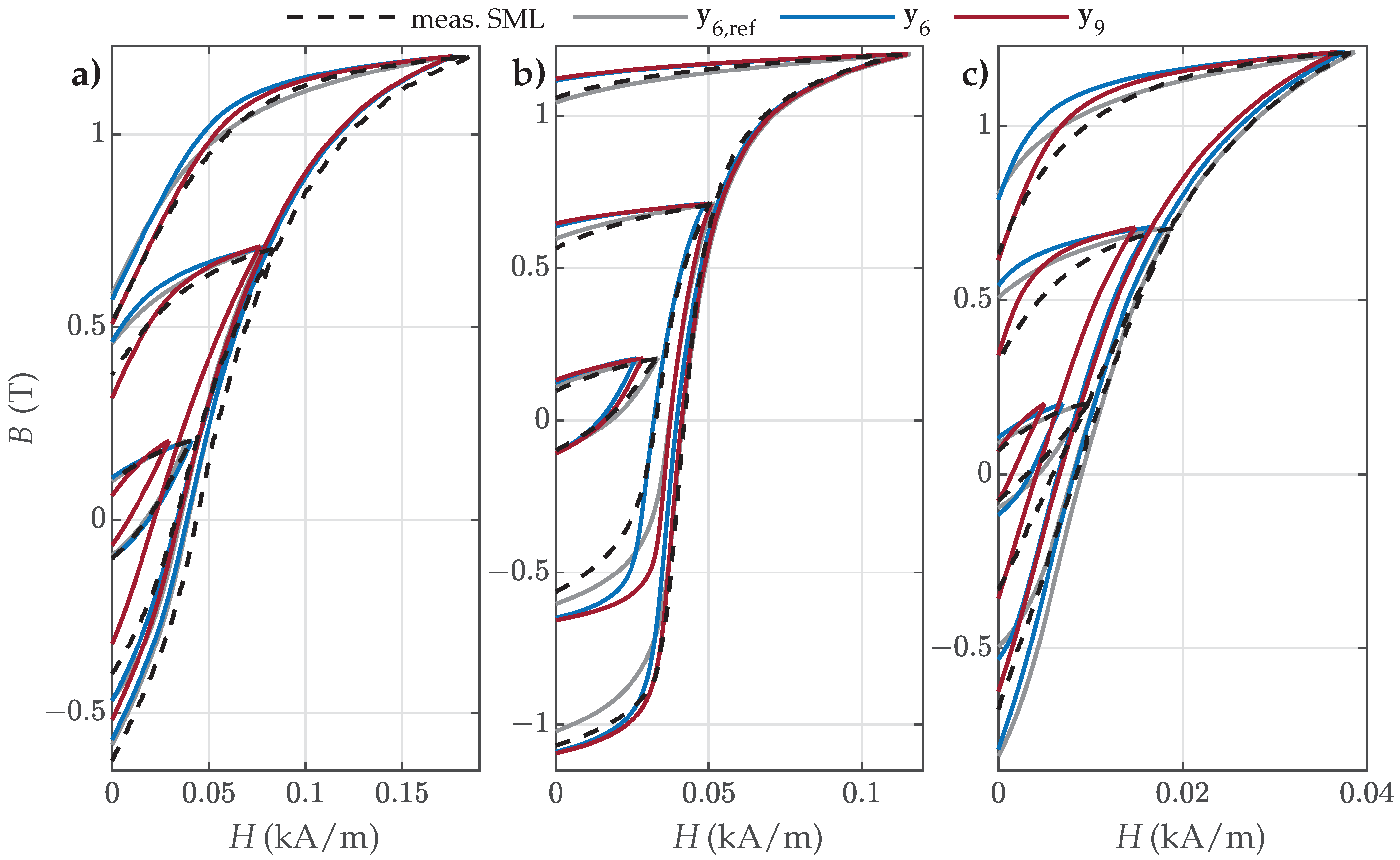
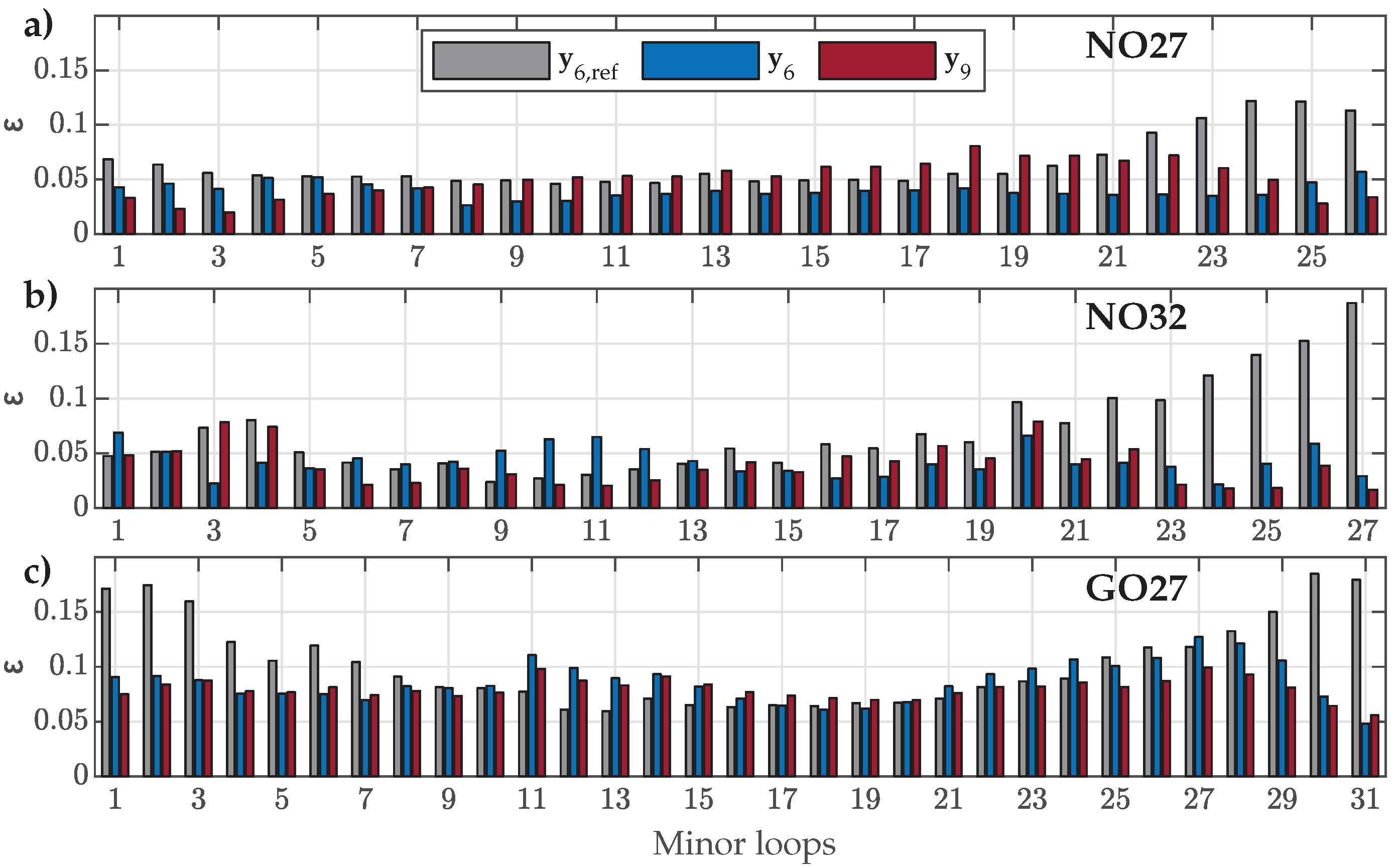
4.4. Validation Versus Measured Symmetric and Offset Minor Loops
- For NO27 ES, all three parameter sets performed comparably well, except that applying resulted in a bigger deviation for SMLs with small amplitudes, where the predicted SMLs were significantly narrower and steeper.
- For NO32 ES, all three parameter sets exhibited comparable performance. However, applying led to greater deviations for SMLs with medium amplitudes, where the predicted SMLs were wider.
- For GO27 ES, all three parameter sets performed comparably well, except that applying resulted in a bigger deviation for SMLs with small amplitudes, where the predicted SMLs were significantly steeper.
5. Discussion
5.1. Accuracy
5.2. Computational Complexity
5.3. Physical Interpretation of the Parameters
5.4. Multiphysics Extension
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ES | Electrical steel; |
| FORC | First-order reversal curve; |
| GO | Grain oriented; |
| HD | History dependent; |
| HI | History independent; |
| JA | Jiles–Atherton; |
| NO | Non-oriented; |
| NRMS | Normalized root mean square; |
| OML | Offset minor loop; |
| RC | Reversal curve; |
| RP | Reversal point; |
| SML | Symmetric minor loop; |
| SORC | Second-order reversal curve; |
| ZM | Zirka–Moroz. |
References
- Mörée, G.; Leijon, M. Review of Hysteresis Models for Magnetic Materials. Energies 2023, 16, 3908. [Google Scholar] [CrossRef]
- Mörée, G.; Leijon, M. Review of Play and Preisach Models for Hysteresis in Magnetic Materials. Materials 2023, 16, 2422. [Google Scholar] [CrossRef] [PubMed]
- Taurines, J.; Martin, F.; Rasilo, P.; Belahcen, A. Thermodynamically Consistent Magnetic Hysteresis Model—Application to Soft and Hard Magnetic Materials Including Minor Loops. IEEE Trans. Magn. 2024, 60, 7300809. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Harrison, R.G.; Chiesa, N. Inverse Hysteresis Models for Transient Simulation. IEEE Trans. Power Deliv. 2014, 29, 552–559. [Google Scholar] [CrossRef]
- Messal, O.; Vo, A.T.; Fassenet, M.; Mas, P.; Buffat, S.; Kedous-Lebouc, A. Advanced approach for static part of loss-surface iron loss model. J. Magn. Magn. Mater. 2020, 502, 166401. [Google Scholar] [CrossRef]
- Mikula, L.; Ramdane, B.; Blattner Martinho, L.; Kedous-Lebouc, A.; Meunier, G. Numerical Modeling of Static Hysteresis Phenomena Using a Vector Extension of the Loss Surface Model. IEEE Trans. Magn. 2023, 59, 7300404. [Google Scholar] [CrossRef]
- Harrison, R.G. Positive-Feedback Theory of Hysteretic Recoil Loops in Hard Ferromagnetic Materials. IEEE Trans. Magn. 2011, 47, 175–191. [Google Scholar] [CrossRef]
- Vo, A.T.; Fassenet, M.; Préault, V.; Espanet, C.; Kedous-Lebouc, A. New formulation of Loss-Surface Model for accurate iron loss modeling at extreme flux density and flux variation: Experimental analysis and test on a high-speed PMSM. J. Magn. Magn. Mater. 2022, 563, 169935. [Google Scholar] [CrossRef]
- Chwastek, K.R.; Jabłoński, P.; Kusiak, D.; Szczegielniak, T.; Kotlan, V.; Karban, P. The Effective Field in the T(x) Hysteresis Model. Energies 2023, 16, 2237. [Google Scholar] [CrossRef]
- Quondam Antonio, S.; Bonaiuto, V.; Sargeni, F.; Salvini, A. Neural Network Modeling of Arbitrary Hysteresis Processes: Application to GO Ferromagnetic Steel. Magnetochemistry 2022, 8, 18. [Google Scholar] [CrossRef]
- Licciardi, S.; Ala, G.; Francomano, E.; Viola, F.; Lo Giudice, M.; Salvini, A.; Sargeni, F.; Bertolini, V.; Di Schino, A.; Faba, A. Neural Network Architectures and Magnetic Hysteresis: Overview and Comparisons. Mathematics 2024, 12, 3363. [Google Scholar] [CrossRef]
- Duan, N.; Gao, X.; Zhang, L.; Xu, W.; Huang, S.; Lu, M.; Wang, S. An Improved Preisach Model for Magnetic Hysteresis of Grain-Oriented Silicon Steel under PWM Excitation. Appl. Sci. 2024, 14, 321. [Google Scholar] [CrossRef]
- Zhang, C.; Li, H.; Tian, Y.; Li, Y.; Yang, Q. Harmonic and DC Bias Hysteresis Characteristics Simulation Based on an Improved Preisach Model. Materials 2023, 16, 4385. [Google Scholar] [CrossRef]
- Harrison, R.G. Modeling High-Order Ferromagnetic Hysteretic Minor Loops and Spirals Using a Generalized Positive-Feedback Theory. IEEE Trans. Magn. 2012, 48, 1115–1129. [Google Scholar] [CrossRef]
- Harrison, R.G.; Steentjes, S. Simplification and inversion of the mean-field positive-feedback model: Application to constricted major and minor hysteresis loops in electrical steels. J. Magn. Magn. Mater. 2019, 491, 165552. [Google Scholar] [CrossRef]
- Cui, R.; Li, S.; Wang, Z.; Wang, X. A modified residual stress dependent Jile-Atherton hysteresis model. J. Magn. Magn. Mater. 2018, 465, 578–584. [Google Scholar] [CrossRef]
- Hussain, S.; Benabou, A.; Clénet, S.; Lowther, D.A. Temperature Dependence in the Jiles–Atherton Model for Non-Oriented Electrical Steels: An Engineering Approach. IEEE Trans. Magn. 2018, 54, 7301205. [Google Scholar] [CrossRef]
- Fulginei, F.; Salvini, A. Softcomputing for the identification of the Jiles-Atherton model parameters. IEEE Trans. Magn. 2005, 41, 1100–1108. [Google Scholar] [CrossRef]
- Benabou, A.; Leite, J.; Clénet, S.; Simão, C.; Sadowski, N. Minor loops modelling with a modified Jiles–Atherton model and comparison with the Preisach model. J. Magn. Magn. Mater. 2008, 320, e1034–e1038. [Google Scholar] [CrossRef]
- Steentjes, S.; Hameyer, K.; Dolinar, D.; Petrun, M. Iron-Loss and Magnetic Hysteresis Under Arbitrary Waveforms in NO Electrical Steel: A Comparative Study of Hysteresis Models. IEEE Trans. Ind. Electron. 2017, 64, 2511–2521. [Google Scholar] [CrossRef]
- Atyia, A.; Ghanim, A. Limitations of Jiles–Atherton models to study the effect of hysteresis in electrical steels under different excitation regimes. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2024, 43, 66–79. [Google Scholar] [CrossRef]
- Rasilo, P.; Martinez, W.; Fujisaki, K.; Kyyrä, J.; Ruderman, A. Simulink Model for PWM-Supplied Laminated Magnetic Cores Including Hysteresis, Eddy-Current, and Excess Losses. IEEE Trans. Power Electron. 2019, 34, 1683–1695. [Google Scholar] [CrossRef]
- Zou, L.; Xin, S.; Li, Z.; Wang, Y.; Han, Z. The Critical Saturation Magnetization Properties of Nanocrystalline Alloy Under Rectangular Wave Excitation with Adjustable Duty Cycle. Materials 2025, 18, 735. [Google Scholar] [CrossRef] [PubMed]
- Petrun, M.; Steentjes, S.; Hameyer, K.; Dolinar, D. Magnetization Dynamics and Power Loss Calculation in NO Soft Magnetic Steel Sheets Under Arbitrary Excitation. IEEE Trans. Magn. 2015, 51, 7300104. [Google Scholar] [CrossRef]
- Zhu, Q.; Wu, Q.; Li, W.; Pham, M.T.; Zhu, L. A General and Accurate Iron Loss Calculation Method Considering Harmonics Based on Loss Surface Hysteresis Model and Finite-Element Method. IEEE Trans. Ind. Appl. 2021, 57, 374–381. [Google Scholar] [CrossRef]
- Huang, Q.; Li, Y.; Dou, Y.; Li, Y.; Zhu, J.; Li, S. History-Dependent Prandtl-Ishlinskii Neural Network for Quasi-Static Core Loss Prediction Under Arbitrary Excitation Waveforms. IEEE Trans. Power Electron. 2025, 40, 9625–9637. [Google Scholar] [CrossRef]
- Orosz, T.; Horváth, T.; Tóth, B.; Kuczmann, M.; Kocsis, B. Iron Loss Calculation Methods for Numerical Analysis of 3D-Printed Rotating Machines: A Review. Energies 2023, 16, 6547. [Google Scholar] [CrossRef]
- Jesenik, M.; Mernik, M.; Trlep, M. Determination of a Hysteresis Model Parameters with the Use of Different Evolutionary Methods for an Innovative Hysteresis Model. Mathematics 2020, 8, 201. [Google Scholar] [CrossRef]
- Rahmanović, E.; Petrun, M. Modelling of unit differential reversal curves in the G2E hysteresis model. Phys.B Condens. Matter 2024, 677, 415694. [Google Scholar] [CrossRef]
- Zirka, S.E.; Moroz, Y.I.; Chiesa, N.; Harrison, R.G.; Høidalen, H.K. Implementation of Inverse Hysteresis Model Into EMTP—Part I: Static Model. IEEE Trans. Power Deliv. 2015, 30, 2224–2232. [Google Scholar] [CrossRef]
- Um, D.Y.; Kim, M.J.; Park, G.S. Numerical Analysis of DC-Biased Eddy Current Sensor Considering Hysteresis Effects. IEEE Trans. Magn. 2022, 58, 6201504. [Google Scholar] [CrossRef]
- Egorov, D.; Petrov, I.; Pyrhönen, J.J.; Link, J.; Stern, R.; Sergeant, P.; Sarlioglu, B. Hysteresis Loss in NdFeB Permanent Magnets in a Permanent Magnet Synchronous Machine. IEEE Trans. Ind. Electron. 2022, 69, 121–129. [Google Scholar] [CrossRef]
- Egorov, D.; Petrov, I.; Link, J.; Stern, R.; Pyrhönen, J.J. Model-Based Hysteresis Loss Assessment in PMSMs With Ferrite Magnets. IEEE Trans. Ind. Electron. 2018, 65, 179–188. [Google Scholar] [CrossRef]
- Liu, R.; Lu, Y. Inverse Rheological Hysteresis Model and its Efficient Parameter Identification Method. IEEE Trans. Magn. 2024, 60, 7300204. [Google Scholar] [CrossRef]
- Zirka, S.; Moroz, Y.; Marketos, P.; Moses, A. Congruency-based hysteresis models for transient simulation. IEEE Trans. Magn. 2004, 40, 390–399. [Google Scholar] [CrossRef]
- Pierce, M.S.; Buechler, C.R.; Sorensen, L.B.; Kevan, S.D.; Jagla, E.A.; Deutsch, J.M.; Mai, T.; Narayan, O.; Davies, J.E.; Liu, K.; et al. Disorder-induced magnetic memory: Experiments and theories. Phys. Rev. B 2007, 75, 144406. [Google Scholar] [CrossRef]
- Wulf, M.D.; Dupré, L.; Melkebeek, J. Quasistatic measurements for hysteresis modeling. J. Appl. Phys. 2000, 87, 5239–5241. [Google Scholar] [CrossRef]
- Harrison, R.G. Physical Theory of Ferromagnetic First-Order Return Curves. IEEE Trans. Magn. 2009, 45, 1922–1939. [Google Scholar] [CrossRef]
- Cao, Y.; Xu, K.; Jiang, W.; Droubay, T.; Ramuhalli, P.; Edwards, D.; Johnson, B.R.; McCloy, J. Hysteresis in single and polycrystalline iron thin films: Major and minor loops, first order reversal curves, and Preisach modeling. J. Magn. Magn. Mater. 2015, 395, 361–375. [Google Scholar] [CrossRef]
- Franco, V.; Dodrill, B. (Eds.) Magnetic Measurement Techniques for Materials Characterization; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Fiorillo, F. Chapter 7—Characterization of Soft Magnetic Materials. In Characterization and Measurement of Magnetic Materials; Fiorillo, F., Ed.; Elsevier Series in Electromagnetism; Academic Press: San Diego, CA, USA, 2004; pp. 307–474. [Google Scholar] [CrossRef]





| (T) | () | ||||
|---|---|---|---|---|---|
| NO27 ES | 1.469 | 1010.1 | 13 | 27 | 26 |
| NO32 ES | 1.516 | 1013.4 | 13 | 27 | 27 |
| GO27 ES | 1.807 | 1001.8 | 16 | 31 | 31 |
| NO27 ES | NO32 ES | GO27 ES | ||||
|---|---|---|---|---|---|---|
| 15.81 | 15.81 | 3.794 | 3.794 | 10.54 | 10.54 | |
| 18.2 | 18.2 | 84.8 | 84.8 | −17.65 | −17.65 | |
| −112.9 | −112.9 | −231.8 | −231.8 | 11.73 | 11.73 | |
| 102.3 | 102.3 | 167.5 | 167.5 | 14.77 | 14.77 | |
| 0.6946 | 1.926 | 0.4877 | −0.027 | 0.4869 | 1.38 | |
| / | −3.714 | / | 2.727 | / | −2.786 | |
| / | 2.613 | / | −2.645 | / | 2.024 | |
| 1.4 | 1.993 | 0.2733 | 0.5743 | 0.129 | 1.9 × 10−7 | |
| / | −1.171 | / | −0.5743 | / | 0.3355 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Petrun, M.; Rahmanović, E. Parameter Estimation for the Basic Zirka-Moroz History-Dependent Hysteresis Model for Electrical Steels. Materials 2025, 18, 2104. https://doi.org/10.3390/ma18092104
Petrun M, Rahmanović E. Parameter Estimation for the Basic Zirka-Moroz History-Dependent Hysteresis Model for Electrical Steels. Materials. 2025; 18(9):2104. https://doi.org/10.3390/ma18092104
Chicago/Turabian StylePetrun, Martin, and Ermin Rahmanović. 2025. "Parameter Estimation for the Basic Zirka-Moroz History-Dependent Hysteresis Model for Electrical Steels" Materials 18, no. 9: 2104. https://doi.org/10.3390/ma18092104
APA StylePetrun, M., & Rahmanović, E. (2025). Parameter Estimation for the Basic Zirka-Moroz History-Dependent Hysteresis Model for Electrical Steels. Materials, 18(9), 2104. https://doi.org/10.3390/ma18092104






