Digitally Controlled Piezoelectric Metamaterial for Low-Frequency and High-Efficiency Sound Absorption
Abstract
1. Introduction
2. Physical Model and Theory
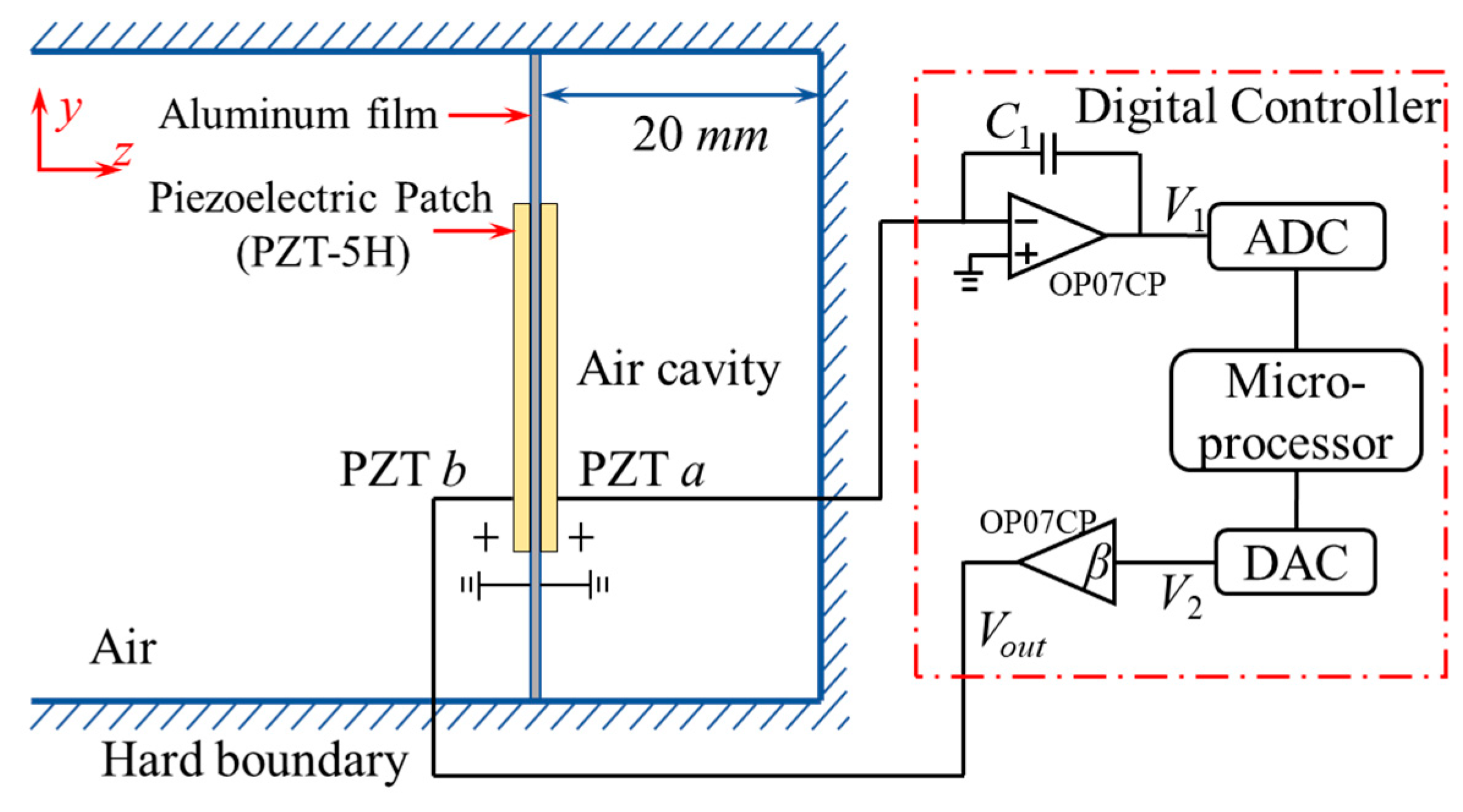
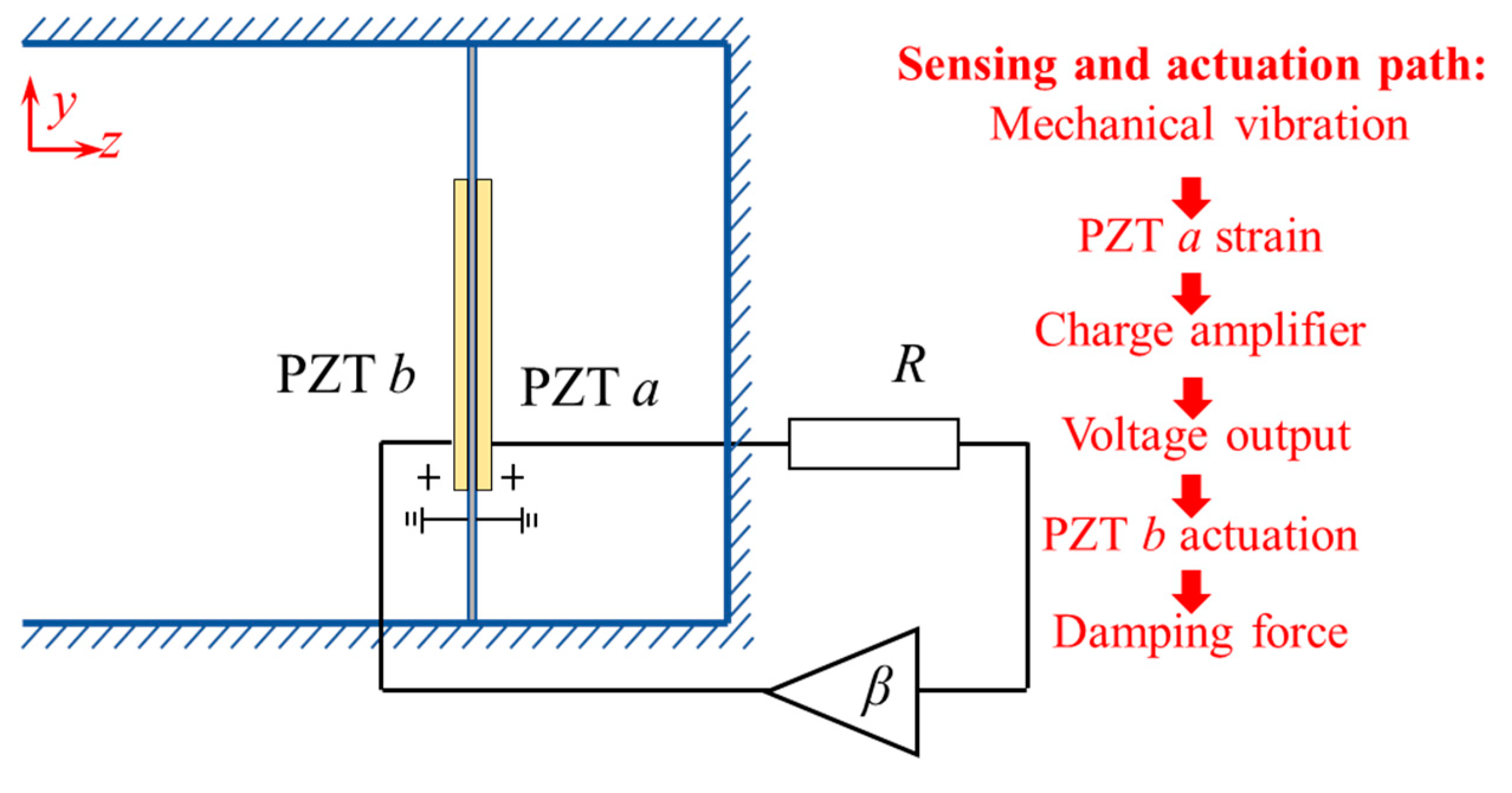
2.1. Design of the Metamaterial
2.2. Design of the Transfer Function
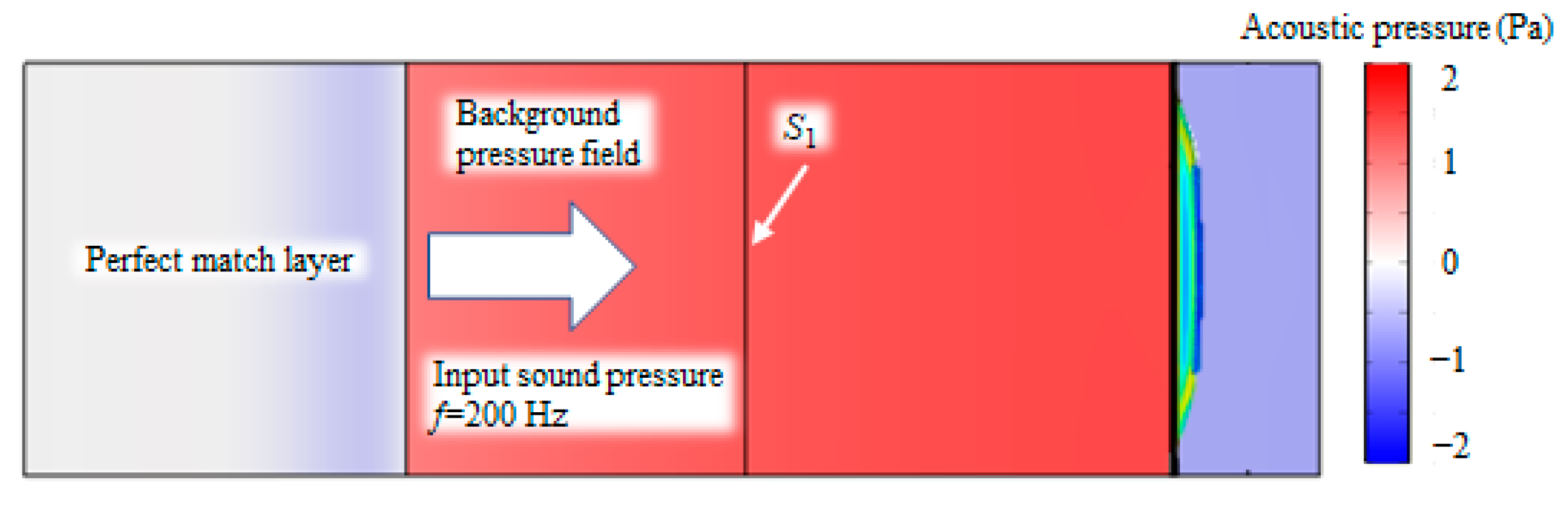
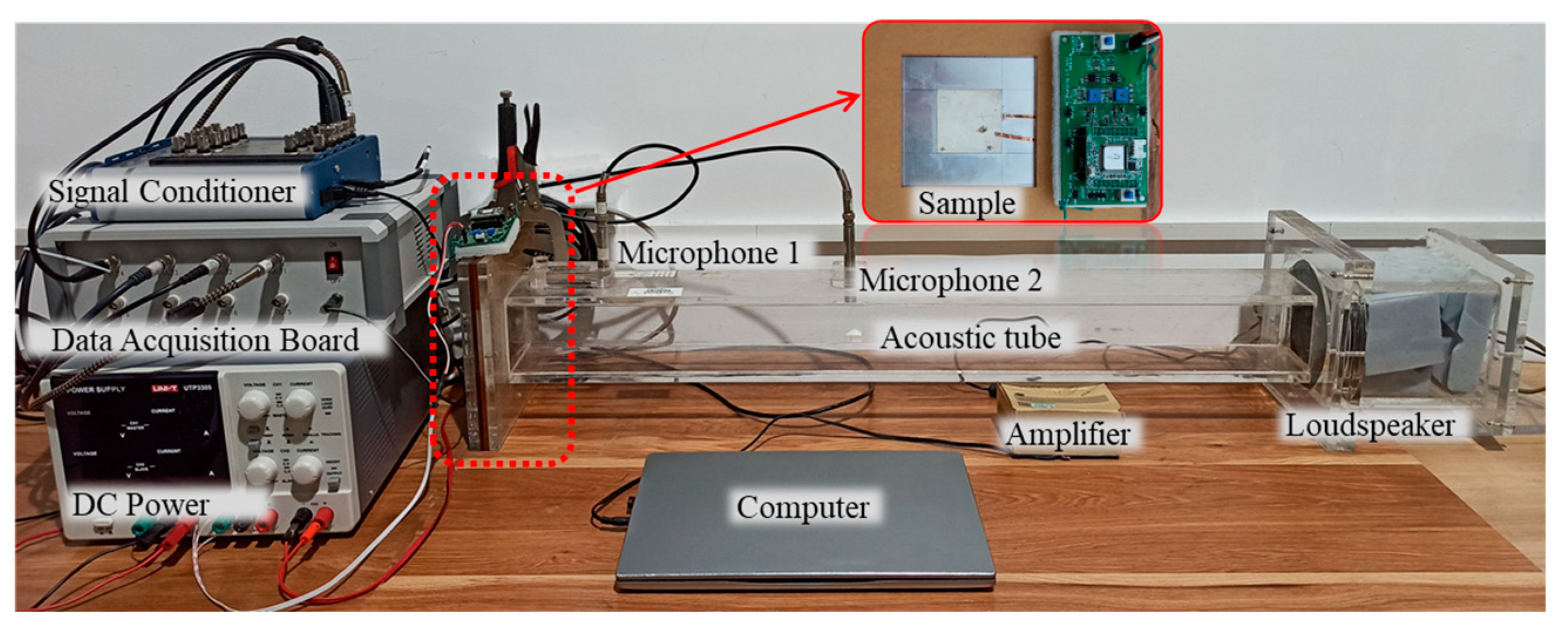
3. Finite Element Modeling and Experimental Setup
4. Results and Discussion
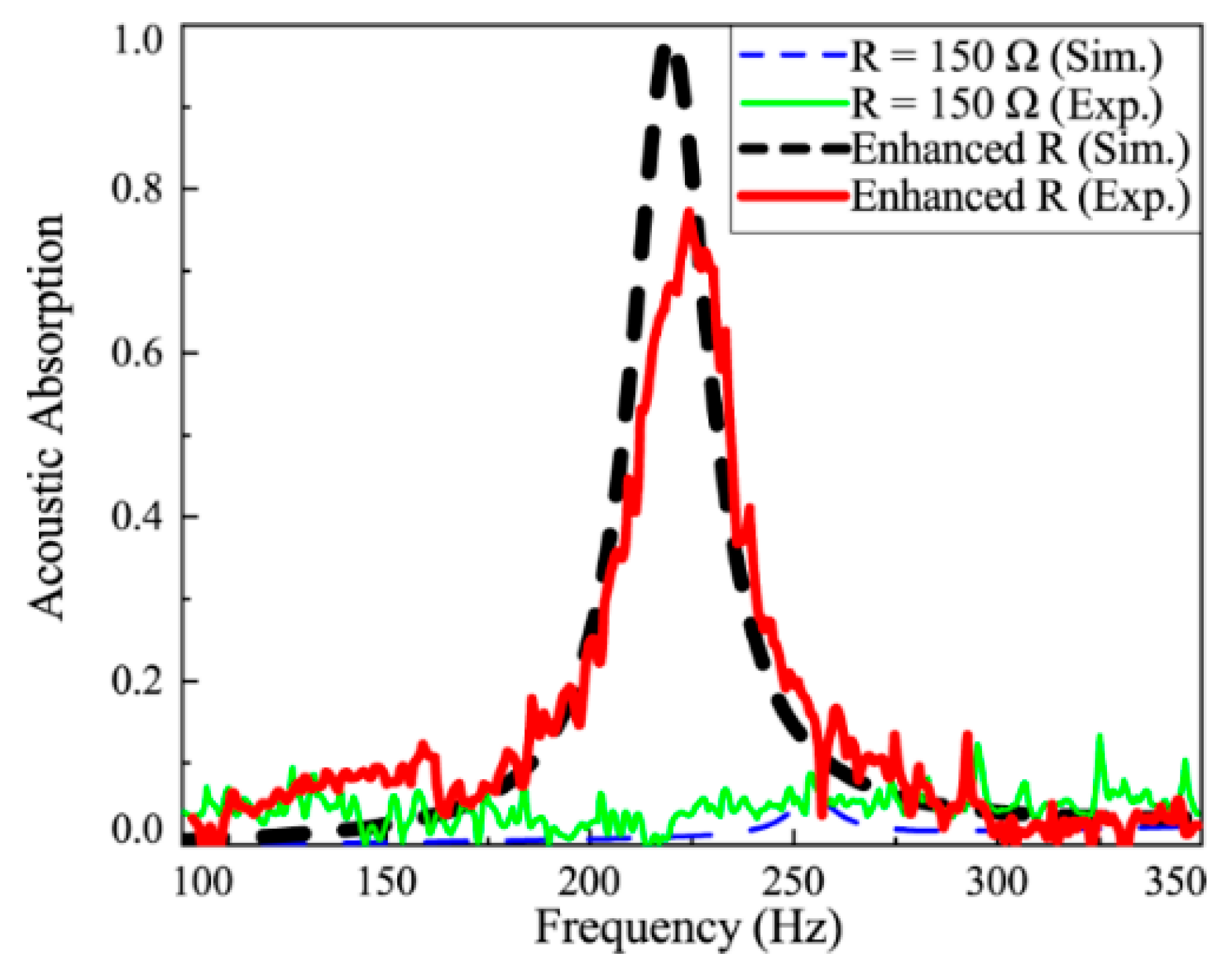
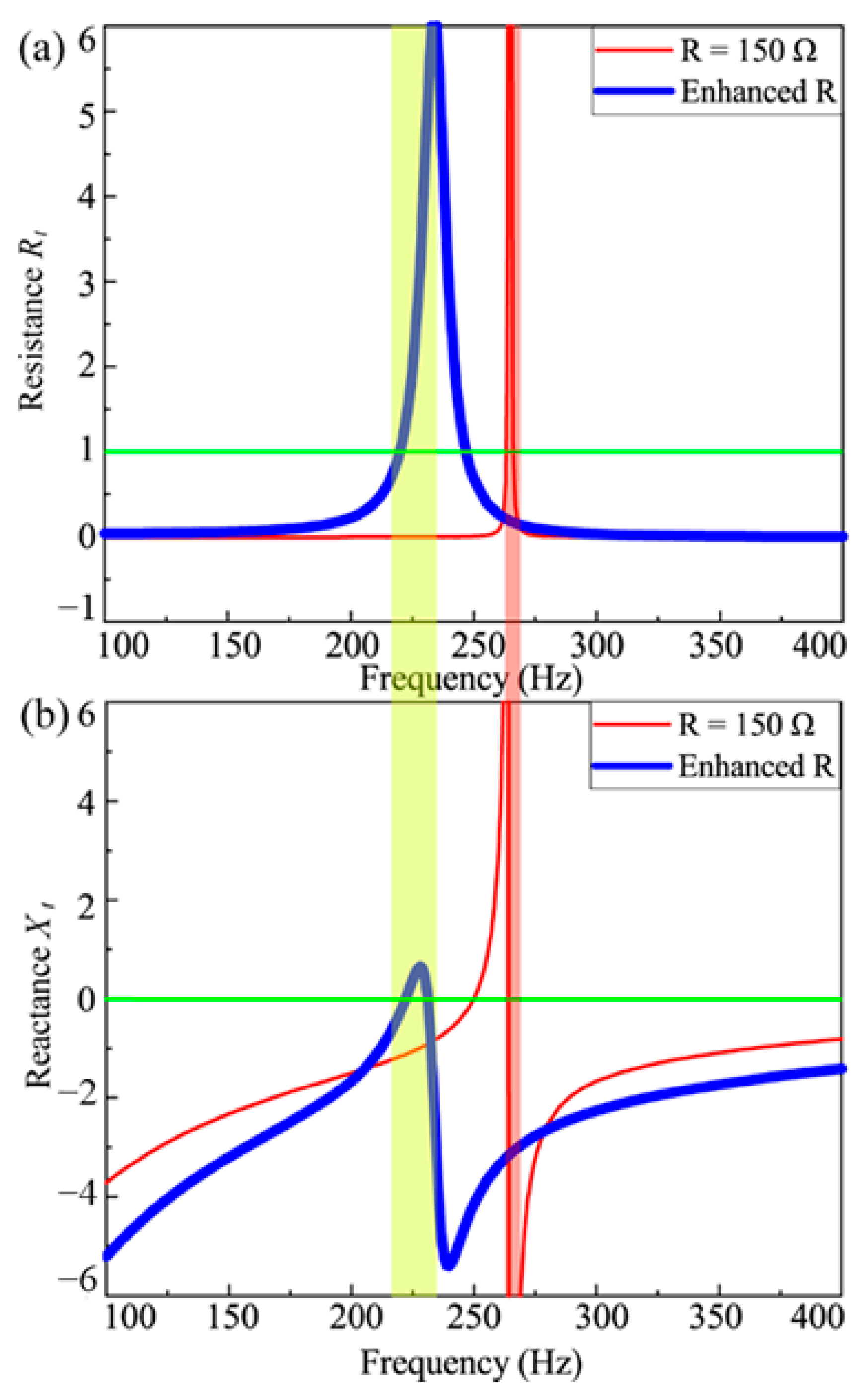
4.1. “Resistance-Enhancement” Control
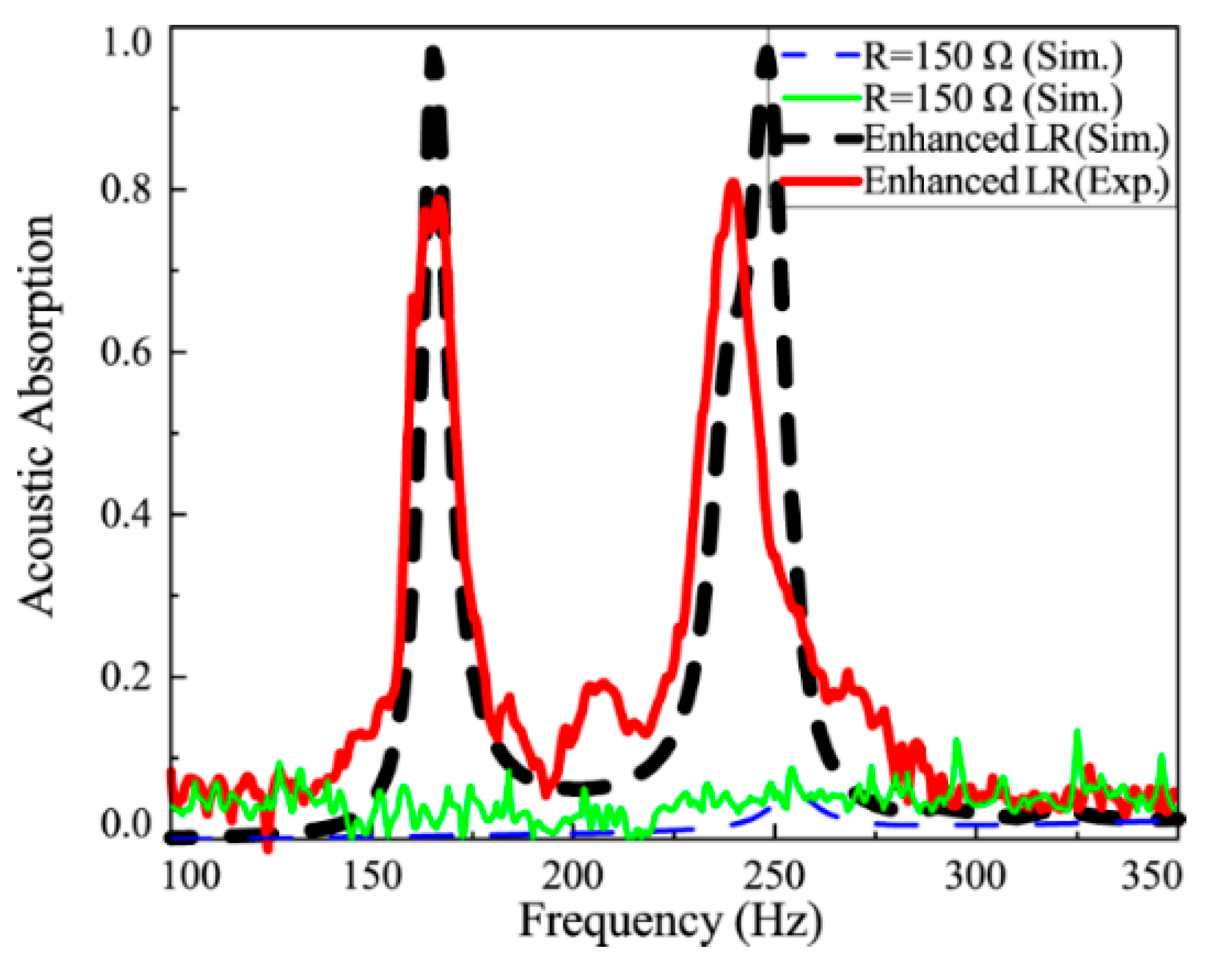
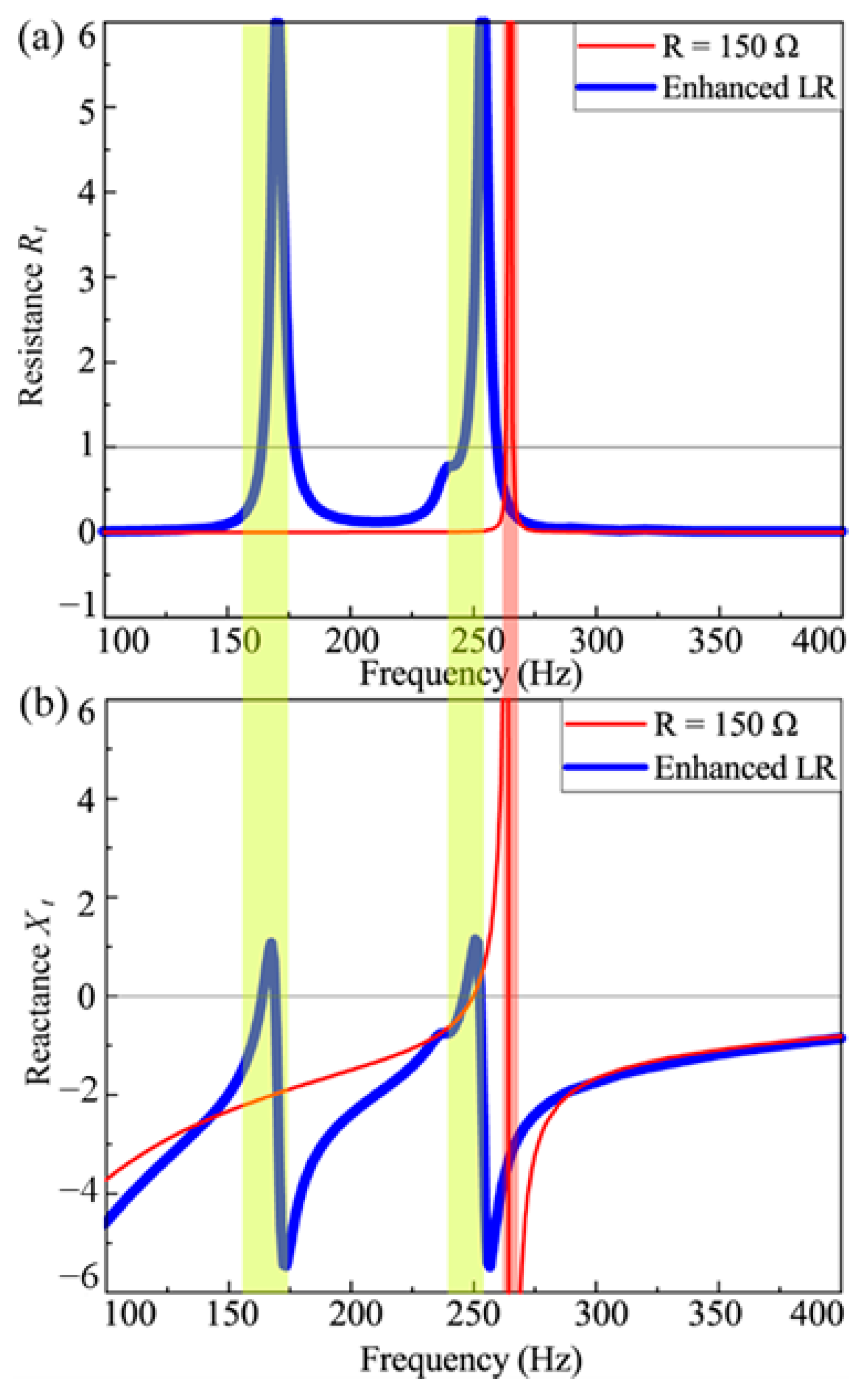
4.2. “Resonance-Enhancement” Control
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tao, Y.; Ren, M.; Zhang, H.; Peijs, T. Recent Progress in Acoustic Materials and Noise Control Strategies—A Review. Appl. Mater. Today 2021, 24, 101141. [Google Scholar] [CrossRef]
- Yang, M.; Sheng, P. Sound Absorption Structures: From Porous Media to Acoustic Metamaterials. Annu. Rev. Mater. Res. 2017, 47, 83–114. [Google Scholar] [CrossRef]
- Zhang, X.; Qu, Z.; Wang, H. Engineering Acoustic Metamaterials for Sound Absorption: From Uniform to Gradient Structures. iScience 2020, 23, 101110. [Google Scholar] [CrossRef] [PubMed]
- Ji, G.; Huber, J. Recent Progress in Acoustic Metamaterials and Active Piezoelectric Acoustic Metamaterials—A Review. Appl. Mater. Today 2022, 26, 101260. [Google Scholar] [CrossRef]
- Qu, S.; Sheng, P. Microwave and Acoustic Absorption Metamaterials. Phys. Rev. Appl. 2022, 17, 047001. [Google Scholar] [CrossRef]
- Cheng, Y.; Zhou, C.; Yuan, B.G.; Wu, D.J.; Wei, Q.; Liu, X.J. Ultra-Sparse Metasurface for High Reflection of Low-Frequency Sound Based on Artificial Mie Resonances. Nat. Mater. 2015, 14, 1013–1019. [Google Scholar] [CrossRef]
- Li, Y.; Assouar, B.M. Acoustic Metasurface-Based Perfect Absorber with Deep Subwavelength Thickness. Appl. Phys. Lett. 2016, 108, 063502. [Google Scholar] [CrossRef]
- Long, H.; Shao, C.; Cheng, Y.; Tao, J.; Liu, X. High Absorption Asymmetry Enabled by a Deep-Subwavelength Ventilated Sound Absorber. Appl. Phys. Lett. 2021, 118, 263502. [Google Scholar] [CrossRef]
- Liu, X.; Duan, M.; Liu, M.; Xin, F.; Zhang, C. Acoustic Labyrinthine Porous Metamaterials for Subwavelength Low-Frequency Sound Absorption. J. Appl. Phys. 2021, 129, 195103. [Google Scholar] [CrossRef]
- Lemkalli, B.; Fellah, Z.E.A.; Guenneau, S.; Lamzoud, K.; Mir, A.; Achaoui, Y. Bi-Functional Metamaterial Based on Helmholtz Resonators for Sound and Heat Insulation. arXiv 2023, arXiv:2310.05098. [Google Scholar]
- Ma, K.; Tan, T.; Yan, Z.; Liu, F.; Liao, W.-H.; Zhang, W. Metamaterial and Helmholtz Coupled Resonator for High-Density Acoustic Energy Harvesting. Nano Energy 2021, 82, 105693. [Google Scholar] [CrossRef]
- Ramos, D.; Godinho, L.; Amado-Mendes, P.; Mareze, P. Experimental and Numerical Investigations of Ventilated Acoustic Metamaterial Based In-Parallel Arrangement of Helmholtz Resonator for Façade Screen. INTER-NOISE NOISE-CON Congr. Conf. Proc. 2021, 263, 5382–5390. [Google Scholar] [CrossRef]
- Romero-García, V.; Jiménez, N.; Theocharis, G.; Achilleos, V.; Merkel, A.; Richoux, O.; Tournat, V.; Groby, J.-P.; Pagneux, V. Design of Acoustic Metamaterials Made of Helmholtz Resonators for Perfect Absorption by Using the Complex Frequency Plane. Comptes Rendus Phys. 2020, 21, 713–749. [Google Scholar] [CrossRef]
- Papadakis, N.M.; Stavroulakis, G.E. Tunable Helmholtz Resonators Using Multiple Necks. Micromachines 2023, 14, 1932. [Google Scholar] [CrossRef]
- Chen, A.; Yang, Z.; Zhao, X.; Anderson, S.; Zhang, X. Composite Acoustic Metamaterial for Broadband Low-Frequency Acoustic Attenuation. Phys. Rev. Appl. 2023, 20, 014011. [Google Scholar] [CrossRef]
- Jung, J.; Park, H.; Park, J.; Chang, T.; Shin, J. Broadband Metamaterials and Metasurfaces: A Review from the Perspectives of Materials and Devices. Nanophotonics 2020, 9, 3165–3196. [Google Scholar] [CrossRef]
- Ma, G.; Sheng, P. Acoustic Metamaterials: From Local Resonances to Broad Horizons. Sci. Adv. 2016, 2, e1501595. [Google Scholar] [CrossRef]
- Mei, J.; Ma, G.; Yang, M.; Yang, Z.; Wen, W.; Sheng, P. Dark Acoustic Metamaterials as Super Absorbers for Low-Frequency Sound. Nat. Commun. 2012, 3, 756. [Google Scholar] [CrossRef]
- Huang, H.; Cao, E.; Zhao, M.; Alamri, S.; Li, B. Spider Web-Inspired Lightweight Membrane-Type Acoustic Metamaterials for Broadband Low-Frequency Sound Isolation. Polymers 2021, 13, 1146. [Google Scholar] [CrossRef]
- Xu, J.; Yang, R.; Fan, Y.; Fu, Q.; Zhang, F. A Review of Tunable Electromagnetic Metamaterials With Anisotropic Liquid Crystals. Front. Phys. 2021, 9, 67. [Google Scholar] [CrossRef]
- Wang, Y.-F.; Wang, Y.-Z.; Wu, B.; Chen, W.; Wang, Y.-S. Tunable and Active Phononic Crystals and Metamaterials. Appl. Mech. Rev. 2020, 72, 040801. [Google Scholar] [CrossRef]
- Cheer, J.; Hook, K.; Daley, S. Active Feedforward Control of Flexural Waves in an Acoustic Black Hole Terminated Beam. Smart Mater. Struct. 2021, 30, 035003. [Google Scholar] [CrossRef]
- Danawe, H.; Tol, S. Electro-Momentum Coupling Tailored in Piezoelectric Metamaterials with Resonant Shunts. APL Mater. 2023, 11, 091118. [Google Scholar] [CrossRef]
- Jian, Y.; Hu, G.; Tang, L.; Shen, Y.; Zhan, Y.; Aw, K. Adaptive Piezoelectric Metamaterial Beam: Autonomous Attenuation Zone Adjustment in Complex Vibration Environments. Smart Mater. Struct. 2023, 32, 105023. [Google Scholar] [CrossRef]
- Liao, Y.; Chen, Y.; Huang, G.; Zhou, X. Broadband Low-Frequency Sound Isolation by Lightweight Adaptive Metamaterials. J. Appl. Phys. 2017, 123, 091705. [Google Scholar] [CrossRef]
- Zhang, H.; Wen, J.; Xiao, Y.; Wang, G.; Wen, X. Sound Transmission Loss of Metamaterial Thin Plates with Periodic Subwavelength Arrays of Shunted Piezoelectric Patches. J. Sound Vib. 2015, 343, 104–120. [Google Scholar] [CrossRef]
- Zhang, H.; Xiao, Y.; Wen, J.; Yu, D.; Wen, X. Ultra-Thin Smart Acoustic Metasurface for Low-Frequency Sound Insulation. Appl. Phys. Lett. 2016, 108, 141902. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, F.; Chen, Z.; Wang, G. Membrane-Type Smart Metamaterials for Multi-Modal Sound Insulation. J. Acoust. Soc. Am. 2018, 144, 3514–3524. [Google Scholar] [CrossRef]
- Liao, Y.; Zhou, X.; Chen, Y.; Huang, G. Adaptive Metamaterials for Broadband Sound Absorption at Low Frequencies. Smart Mater. Struct. 2018, 28, 025005. [Google Scholar] [CrossRef]
- Berardengo, M.; Manzoni, S.; Thomas, O.; Vanali, M. Piezoelectric Resonant Shunt Enhancement by Negative Capacitances: Optimisation, Performance and Resonance Cancellation. J. Intell. Mater. Syst. Struct. 2018, 29, 2581–2606. [Google Scholar] [CrossRef]
- Chen, Y.Y.; Huang, G.L.; Sun, C.T. Band Gap Control in an Active Elastic Metamaterial With Negative Capacitance Piezoelectric Shunting. J. Vib. Acoust 2014, 136, 061008. [Google Scholar] [CrossRef]
- Chen, S.; Wang, G.; Song, Y. Low-Frequency Vibration Isolation in Sandwich Plates by Piezoelectric Shunting Arrays. Smart Mater. Struct. 2016, 25, 125024. [Google Scholar] [CrossRef]
- Wang, G.; Chen, S. Large Low-Frequency Vibration Attenuation Induced by Arrays of Piezoelectric Patches Shunted with Amplifier–Resonator Feedback Circuits. Smart Mater. Struct. 2016, 25, 015004. [Google Scholar] [CrossRef]
- Wang, G.; Cheng, J.; Chen, J. Multi-Resonant Piezoelectric Shunting Induced by Digital Controllers for Subwavelength Elastic Wave Attenuation in Smart Metamaterial. Smart Mater. Struct. 2017, 26, 025031. [Google Scholar] [CrossRef]
- Alshaqaq, M.; Sugino, C.; Erturk, A. Digital Programming of Reciprocity Breaking in Resonant Piezoelectric Metamaterials. Phys. Rev. Res. 2023, 5, 043003. [Google Scholar] [CrossRef]
- Li, X.; Chen, Y.; Hu, G.; Huang, G. A Self-Adaptive Metamaterial Beam with Digitally Controlled Resonators for Subwavelength Broadband Flexural Wave Attenuation. Smart Mater. Struct. 2018, 27, 045015. [Google Scholar] [CrossRef]
- Zhang, X.; Yu, H.; He, Z.; Huang, G.; Chen, Y.; Wang, G. A Metamaterial Beam with Inverse Nonlinearity for Broadband Micro-Vibration Attenuation. Mech. Syst. Signal Process. 2021, 159, 107826. [Google Scholar] [CrossRef]
- Luo, Z.; Chen, M.Z.; Wang, Z.X.; Zhou, L.; Li, Y.B.; Cheng, Q.; Ma, H.F.; Cui, T.J. Digital Nonlinear Metasurface with Customizable Nonreciprocity. Adv. Funct. Mater. 2019, 29, 1906635. [Google Scholar] [CrossRef]
- Yi, K.; Matten, G.; Ouisse, M.; Sadoulet-Reboul, E.; Collet, M.; Chevallier, G. Programmable Metamaterials with Digital Synthetic Impedance Circuits for Vibration Control. Smart Mater. Struct. 2020, 29, 035005. [Google Scholar] [CrossRef]
- Yan, B.; Wang, K.; Hu, Z.; Wu, C.; Zhang, X. Shunt Damping Vibration Control Technology: A Review. Appl. Sci. 2017, 7, 494. [Google Scholar] [CrossRef]
- Marakakis, K.; Tairidis, G.K.; Koutsianitis, P.; Stavroulakis, G.E. Shunt Piezoelectric Systems for Noise and Vibration Control: A Review. Front. Built Environ. 2019, 5, 64. [Google Scholar] [CrossRef]
- Zheng, Y.; Qu, Y.; Dai, S.; Chen, B.; Mao, J. Mitigating Vibration and Sound Radiation with a Digital Piezoelectric Meta-Shell in Heavy Fluids. J. Sound Vib. 2024, 573, 118221. [Google Scholar] [CrossRef]


| Parameters | Value |
|---|---|
| Length | |
| Thickness | |
| Density | |
| Young’s modulus | |
| Poisson’s ratio |
| Parameters | Value |
|---|---|
| Length | |
| Thickness | |
| Density | |
| Compliance coefficient | |
| Piezoelectric strain constant | |
| Dielectric constant |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Nie, J.; He, J.; Lin, F.; Liu, Y. Digitally Controlled Piezoelectric Metamaterial for Low-Frequency and High-Efficiency Sound Absorption. Materials 2025, 18, 2102. https://doi.org/10.3390/ma18092102
Zhang X, Nie J, He J, Lin F, Liu Y. Digitally Controlled Piezoelectric Metamaterial for Low-Frequency and High-Efficiency Sound Absorption. Materials. 2025; 18(9):2102. https://doi.org/10.3390/ma18092102
Chicago/Turabian StyleZhang, Xiaodong, Jing Nie, Jinhong He, Fengbin Lin, and Yang Liu. 2025. "Digitally Controlled Piezoelectric Metamaterial for Low-Frequency and High-Efficiency Sound Absorption" Materials 18, no. 9: 2102. https://doi.org/10.3390/ma18092102
APA StyleZhang, X., Nie, J., He, J., Lin, F., & Liu, Y. (2025). Digitally Controlled Piezoelectric Metamaterial for Low-Frequency and High-Efficiency Sound Absorption. Materials, 18(9), 2102. https://doi.org/10.3390/ma18092102






