Effect of Workwear Fit on Thermal Insulation: Assessment Using 3D Scanning Technology
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Parameters and Methods
2.2.1. Test Variants
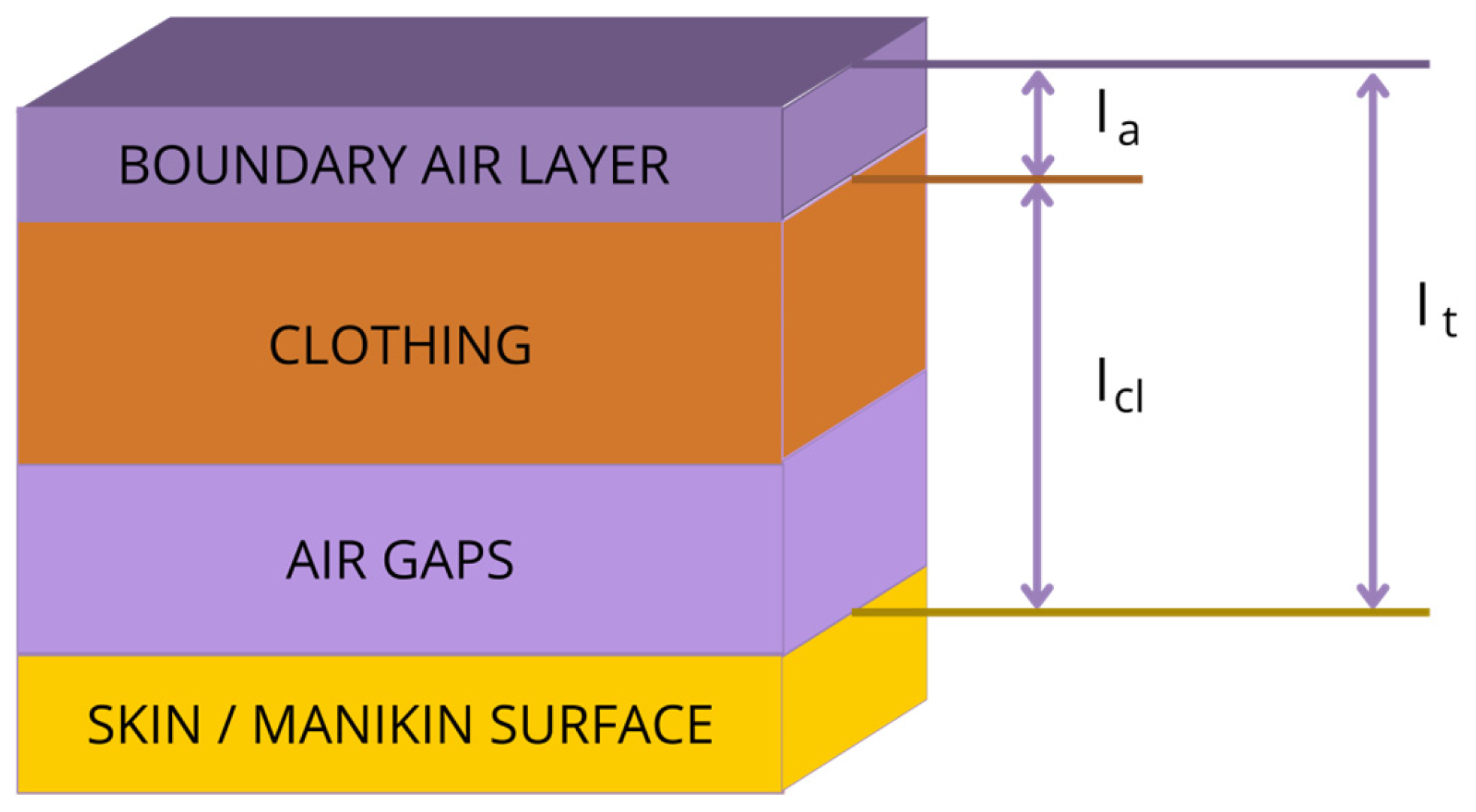
2.2.2. Thermal Insulation
2.2.3. Evaporative Resistance
2.2.4. Air Gap Size—3D Scanning Technique
2.3. Equipment
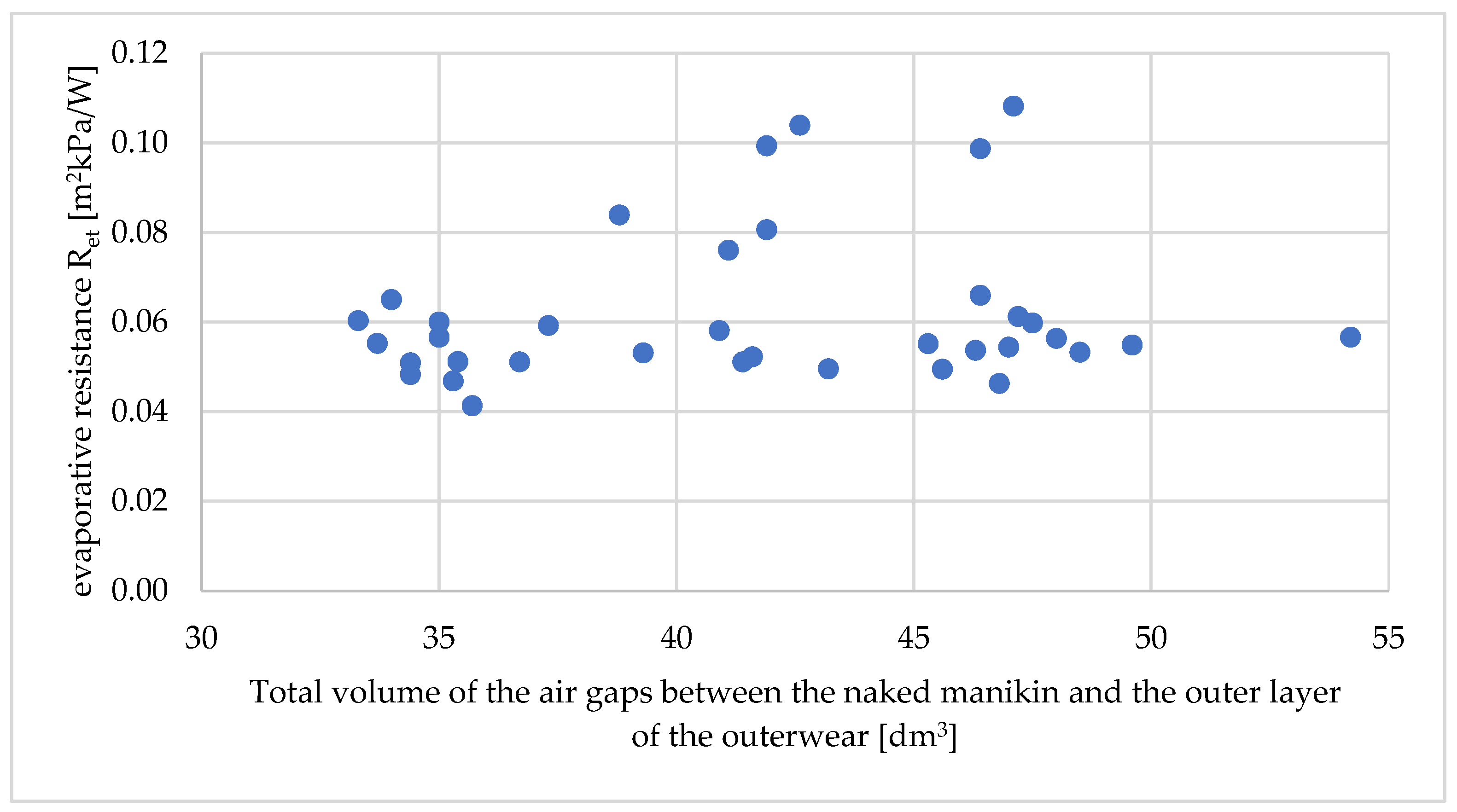
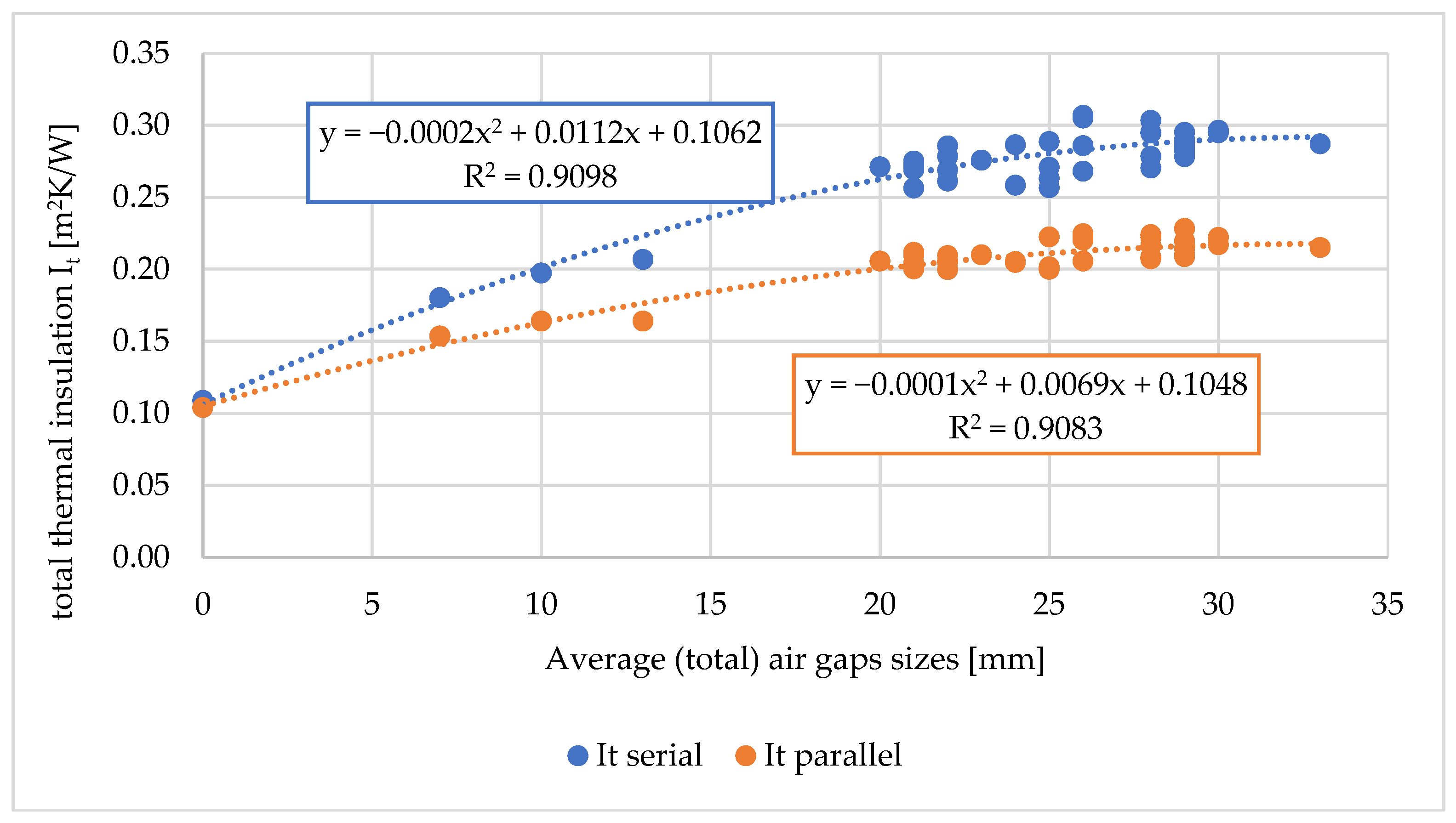
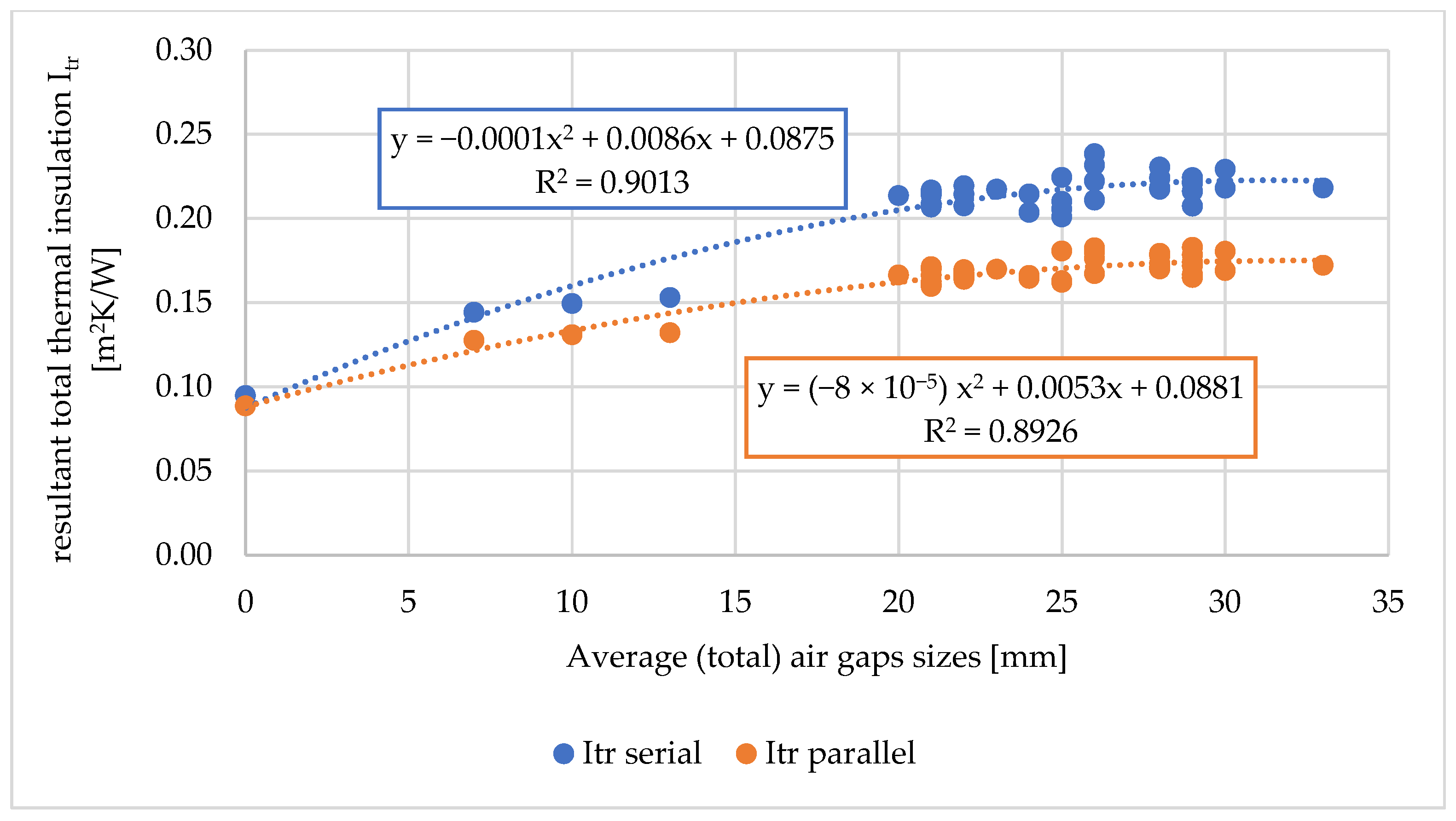
3. Results
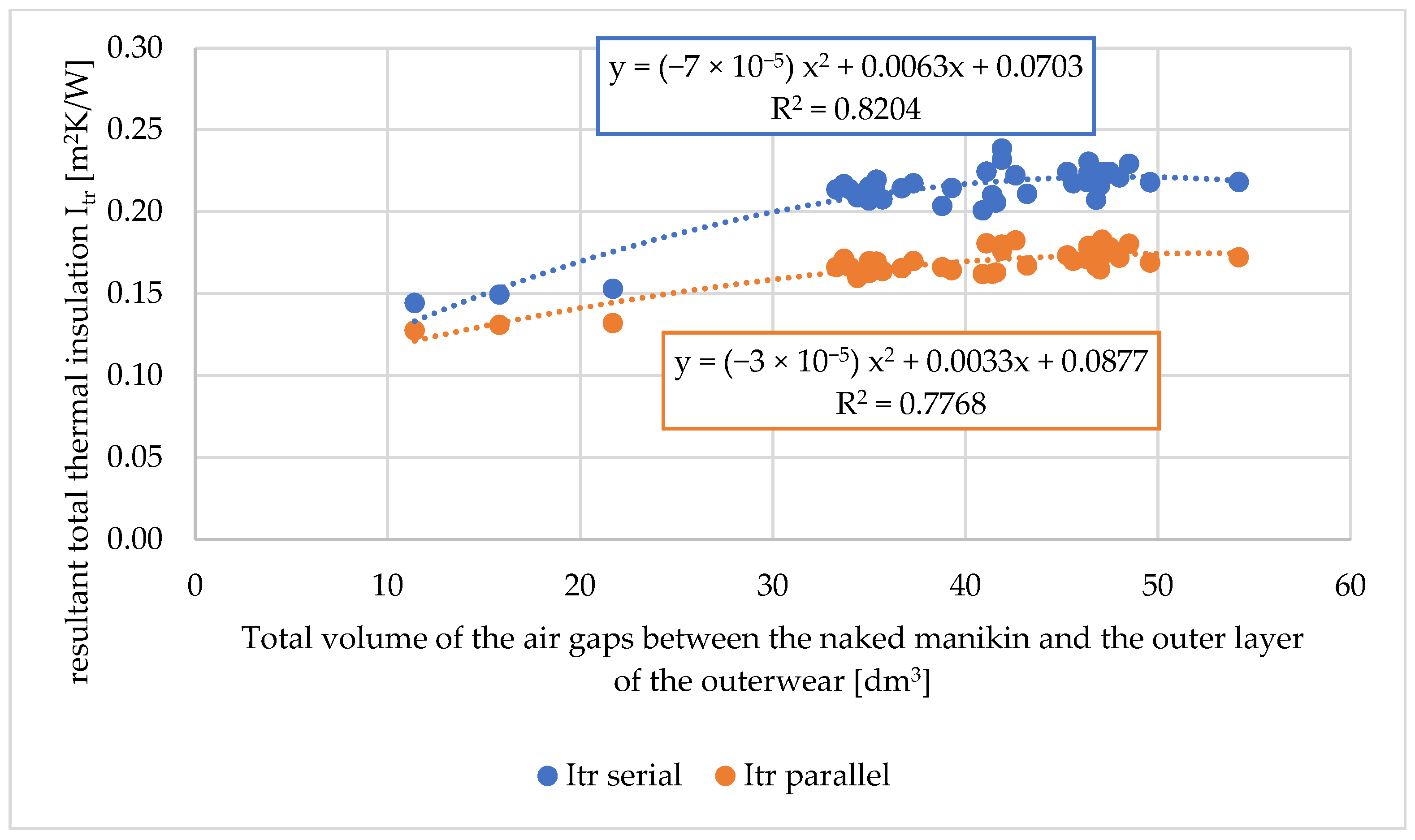
Total Volume and Average Total Size of Air Gaps
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Młynarczyk, M.; Orysiak, J. Przestrzenie powietrzne pod odzieżą—Ich pomiar i wpływ na poziom ciepłochronności. Occup. Saf.—Sci. Pract. 2021, 595, 22–24. [Google Scholar] [CrossRef]
- EN ISO 9920:2009; Ergonomics of the Thermal Environment-Estimation of the Thermal Insulation and Evaporative Resistance of Clothing. International Standard Organization for Standardization (ISO): Brussels, Belgium, 2009.
- Psikuta, A.; Frackiewicz-Kaczmarek, J.; Frydrych, I.; Rossi, R. Quantitative evaluation of air gap thickness and contact area between body and garments. Text. Res. J. 2012, 82, 1405–1413. [Google Scholar] [CrossRef]
- Bogdan, A.; Zwolińska, M. Wpływ odzieży na wymianę ciepła między człowiekiem a otoczeniem. Ciepłownictwo Ogrzew. Went. 2010, 41, 27–31. [Google Scholar]
- Havenith, G. Heat balance when wearing protective clothing. Ann. Occup. Hyg. 1999, 43, 289–296. [Google Scholar] [CrossRef] [PubMed]
- Kenney, W.L.; Wilmore, J.H.; Costill, D.L. Physiology of Sport and Exercise; Human kinetics: Champaign, IL, USA, 2021; ISBN 9781718201736. [Google Scholar]
- Song, G. Clothing air gap layers and thermal protective performance in single layer garments. J. Ind. Text. 2007, 36, 193–205. [Google Scholar] [CrossRef]
- Zhang, Y.; Jia, J. Numerical investigation of heat transfer in garment air gap. Autex Res. J. 2020, 22, 89–95. [Google Scholar] [CrossRef]
- Stoll, A.M.; Chianta, M.A.; Munroe, L.R. Flame-Contact Studies. J. Heat Transf. 1964, 86, 449–456. [Google Scholar] [CrossRef]
- Deng, M.; Wang, Y.; Li, P. Effect of air gaps characteristics on thermal protective performance of firefighters’ clothing. Int. J. Cloth. Sci. Technol. 2018, 30, 246–267. [Google Scholar] [CrossRef]
- Mert, E.; Böhnisch, S.; Psikuta, A.; Bueno, M.A.; Rossi, R.M. Determination of the Air Gap Thickness underneath the Garments for Lower Body Using 3D Body Scanning. In Proceedings of the 6th International Conference on 3D Body Scanning Technologies, Lugano, Switzerland, 27–28 October 2015; pp. 114–119. [Google Scholar] [CrossRef][Green Version]
- Benisek, L.; Phillips, W.A. Protective clothing fabrics: Part II. Against convective heat (open-flame) hazards. Text. Res. J. 1981, 51, 191–196. [Google Scholar] [CrossRef]
- Ke, Y.; Wang, F. An Exploration of Relationships among Thermal Insulation, Area Factor and Air Gap of Male Chinese Ethnic Costumes. Polymers 2020, 12, 1302. [Google Scholar] [CrossRef]
- Rathour, R.; Islam, A.; Das, A.; Alagirusamy, R. Review of heat and Moisture transfer Models of Fire-Protective Clothing. Tekstilec 2024, 67, 292–307. [Google Scholar] [CrossRef]
- Zhu, F.; Zhang, W.; Chen, M. Investigation of material combinations for fire-fighter’s protective clothing on radiant protective and heat-moisture transfer performance. Fibres Text. East. Eur. 2007, 15, 72–75. [Google Scholar]
- Lu, Y.; Li, J.; Li, X.; Song, G. The effect of air gaps in moist protective clothing on protection from heat and flame. J. Fire Sci. 2012, 31, 99–111. [Google Scholar] [CrossRef]
- Torvi, D.A.; Dale, J.D.; Faulkner, B. Influence of air gaps on Bench-Top test results of flame resistant fabrics. J. Fire Prot. Eng. 1999, 10, 1–12. [Google Scholar] [CrossRef]
- Sawcyn, C.M.J. Heat Transfer Model of Horizontal Air Gaps in Bench Top Testing of Thermal Protective Fabrics. Master’s Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2003. Available online: https://researchers.usask.ca/david-torvi/documents/cmj-sawcyn-msc-thesis-2003.pdf (accessed on 1 April 2025).
- Talukdar, P.; Torvi, D.A.; Simonson, C.J.; Sawcyn, C.M.J. Coupled CFD and radiation simulation of air gaps in bench top protective fabric tests. Int. J. Heat Mass Transf. 2009, 53, 526–539. [Google Scholar] [CrossRef]
- Sawcyn, C.M.J.; Torvi, D.A. Improving heat transfer models of air gaps in bench top tests of thermal protective fabrics. Text. Res. J. 2009, 79, 632–644. [Google Scholar] [CrossRef]
- Song, G.; Chitrphiromsri, P.; Ding, D. Numerical simulations of heat and moisture transport in thermal protective clothing under flash fire conditions. Int. J. Occup. Saf. Ergon. 2008, 14, 89–106. [Google Scholar] [CrossRef]
- Torvi, D.A.; Eng, P.; Threlfall, T.G. Heat transfer model of flame resistant fabrics during cooling after exposure to fire. Fire Technol. 2005, 42, 27–48. [Google Scholar] [CrossRef]
- de Dear, R.J.; Arens, E.; Hui, Z.; Oguro, M. Convective and radiative heat transfer coefficients for individual human body segments. Int. J. Biometeorol. 1997, 40, 141–156. [Google Scholar] [CrossRef]
- Quintela, D.; Gaspar, A.; Borges, C. Analysis of sensible heat exchanges from a thermal manikin. Eur. J. Appl. Physiol. 2004, 92, 663–668. [Google Scholar] [CrossRef]
- Islam, M.R.; Golovin, K.; Dolez, P.I. Clothing Thermophysiological Comfort: A Textile Science Perspective. Textiles 2023, 3, 353–407. [Google Scholar] [CrossRef]
- Joshi, A. Comprehensive Model for Heat and Mass Transfer in Human Skin-Clothing-Environment System. Ph.D. Thesis, Université de Haute-Alsace, Mulhouse, France, 2019. [Google Scholar]
- Mert, E.; Psikuta, A.; Bueno, M.A.; Rossi, R.M. Effect of heterogenous and homogenous air gaps on dry heat loss through the garments. Int. J. Biometeorol. 2015, 59, 1701–1710. [Google Scholar] [CrossRef] [PubMed]
- Ding, D.; Tian Tang, T.; Song, G.; McDonald, A. Characterizing the Performance of a Single-Layer Fabric System through a Heat and Mass Transfer Model—Part II: Thermal and Evaporative Resistances. Text. Res. J. 2011, 81, 945–958. [Google Scholar] [CrossRef]
- Psikuta, A.; Allegrini, J.; Koelblen, B.; Bogdan, A.; Annaheim, S.; Martínez, N.; Derome, D.; Carmeliet, J.; Rossi, R.M. Thermal manikins controlled by human thermoregulation models for energy efficiency and thermal comfort research—A review. Renew. Sustain. Energy Rev. 2017, 78, 1315–1330. [Google Scholar] [CrossRef]
- Joshi, A.; Psikuta, A.; Bueno, M.; Annaheim, S.; Rossi, R.M. Analytical clothing model for sensible heat transfer considering spatial heterogeneity. Int. J. Therm. Sci. 2019, 145, 105949. [Google Scholar] [CrossRef]
- EN ISO 13688:2013; Protective clothing—General requirements. CEN: Brussels, Belgium, 2013.
- EN ISO 11612:2015; Protective clothing—Clothing to protect against heat and flame—Minimum performance requirements. CEN: Brussels, Belgium, 2015.
- EN 1149-5:2018; Protective clothing—Electrostatic properties—Part 5: Material performance and design requirements. CEN: Brussels, Belgium, 2018.
- EN ISO 20471:2013; High visibility clothing—Test methods and requirements. CEN: Brussels, Belgium, 2013.
- EN ISO 11611:2024; Protective clothing for use in welding and allied processes. CEN: Brussels, Belgium, 2024.
- EN 13034:2005+A1:2009; Protective clothing against liquid chemicals—Performance requirements for chemical protective clothing offering limited protective performance against liquid chemicals (Type 6 and Type PB [6] equipment). CEN: Brussels, Belgium, 2009.
- EN ISO 14116:2015; Protective clothing—Protection against flame—Limited flame spread materials, material assemblies and clothing. CEN: Brussels, Belgium, 2015.
- IEC 61482-2:2018; Live working—Protective clothing against the thermal hazards of an electric arc—Part 2: Requirements. International Electrotechnical Commission: Geneva, Switzerland, 2018.
- EN 342:2017; Protective Clothing—Ensembles and Garments for Protection Against Cold. CEN: Brussels, Belgium, 2017.
- EN ISO 15831:2004; Clothing—Physiological Effects—Measurement of Thermal Insulation by Means of a Thermal Manikin. CEN: Brussels, Belgium, 2004.
- ASTM F2370-15; Standard Test Method for Measuring the Evaporative Resistance of Clothing Using a Sweating Manikin. ASTM International: West Conshohocken, PA, USA, 2015.
- Młynarczyk, M.; Havenith, G.; Léonard, J.; Martins, R.; Hodder, S. Inter-laboratory proficiency tests in measuring thermal insulation and evaporative resistance of clothing using the Newton-type thermal manikin. Text. Res. J. 2016, 88, 453–466. [Google Scholar] [CrossRef]
- Młynarczyk, M. Characteristics of specialised firefighter clothing used in Poland—The thermal parameters. Fibres Text. East. Eur. 2020, 28, 65–70. [Google Scholar] [CrossRef]
- Rogale, D.; Firšt Rogale, S.; Knezić, Ž.; Jukl, N.; Majstorović, G. Measurement Methods of the Thermal Resistance of Materials Used in Clothing. Materials 2023, 16, 3842. [Google Scholar] [CrossRef]
- EN ISO 20685-1:2018; 3-D Scanning Methodologies for Internationally Compatible Anthropometric Databases—Part 1: Evaluation Protocol for Body Dimensions Extracted from 3-D Body Scans. CEN: Brussels, Belgium, 2018.
- McQuerry, M.; DenHartog, E.; Barker, R. Analysis of air gap volume in structural firefighter turnout suit constructions in relation to heat loss. Text. Res. J. 2017, 88, 2475–2484. [Google Scholar] [CrossRef]
- Młynarczyk, M.; Bartkowiak, G.; Dąbrowska, A. Cooling Effect of Phase Change Materials Applied in Undergarments of Mine Rescuers in Simulated Utility Conditions on Thermal Manikin. Materials 2022, 15, 1999. [Google Scholar] [CrossRef]
- Młynarczyk, M.; Jankowski, J.; Orysiak, J. Określanie objętości przestrzeni powietrznych pod odzieżą z wykorzystaniem techniki skanowania 3D—Studium przypadku. Occup. Saf.—Sci. Pract. 2022, 611, 17–21. [Google Scholar] [CrossRef]
- Młynarczyk, M.; Orysiak, J.; Jankowski, J.; Prus, P. Impact of clothing size on thermal insulation—A pilot study. Fibres Text. East. Eur. 2023, 31, 1–8. [Google Scholar] [CrossRef]
- Kuklane, K.; Gao, C.; Wang, F.; Holmér, I. Parallel and Serial Methods of Calculating Thermal Insulation in European Manikin Standards. Int. J. Occup. Saf. Ergon. 2012, 18, 171–179. [Google Scholar] [CrossRef] [PubMed]
- Frackiewicz-Kaczmarek, J.; Psikuta, A.; Rossi, R. Quantitative Analysis of the Air Gap between the Skin and the Clothing. In Proceedings of the 1st International Conference on 3D Body Scanning Technologies, Lugano, Switzerland, 19–20 October 2010; pp. 107–112. [Google Scholar] [CrossRef]
- Wissler, E.H.; Havenith, G. A simple theoretical model of heat and moisture transport in multi-layer garments in cool ambient air. Eur. J. Appl. Physiol. 2009, 105, 797–808. [Google Scholar] [CrossRef]
- He, H.; Yu, Z. Effect of air gap entrapped in firefighter protective clothing on thermal resistance and evaporative resistance. Autex Res. J. 2017, 18, 28–34. [Google Scholar] [CrossRef]
- Špelić, I.; Rogale, D.; Bogdanić, A.M. The laboratory investigation of the clothing microclimatic layers in accordance with the volume quantification and qualification. J. Text. Inst. 2018, 110, 26–36. [Google Scholar] [CrossRef]
- Psikuta, A.; Sherif, F.; Mert, E.; Mandal, S.; Annaheim, S. Clothing air gaps in various postures in firefighters’ work. Int. J. Biometeorol. 2022, 67, 121–131. [Google Scholar] [CrossRef]
- Chen, Y.S.; Fan, J.; Qian, X.; Zhang, W. Effect of garments fit on thermal insulation and evaporative resistance. Text. Res. J. 2004, 74, 742–748. [Google Scholar] [CrossRef]
- Li, J. Volume of Air Gaps under Clothing and Its Related Thermal Effects. J. Fiber Bioeng. Inform. 2011, 4, 137–144. [Google Scholar] [CrossRef]
- Lu, Y.; Song, G.; Li, J. A novel approach for fit analysis of thermal protective clothing using three-dimensional body scanning. Appl. Ergon. 2014, 45, 1439–1446. [Google Scholar] [CrossRef]
- Frackiewicz-Kaczmarek, J.; Psikuta, A.; Bueno, M.-A.; Rossi, R.M. Effect of garments properties on air gap thickness and the contact area distribution. Text. Res. J. 2015, 85, 1907–1918. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Z.; Wang, Y. The relationship between air gap sizes and clothing heat transfer performance. J. Text. Inst. 2013, 104, 1327–1336. [Google Scholar] [CrossRef]
- Epps, H.H.; Song, N.M.K. Thermal transmittance and air permeability of plain weave fabrics. Cloth. Text. Res. J. 1992, 11, 10–17. [Google Scholar] [CrossRef]
- Wilson, C.A.; Laing, R.M.; Carr, D.J. Air and Air Spaces—The Invisible Addition to Thermal Resistance. J. Hum.-Environ. Syst. 2002, 5, 69–77. [Google Scholar] [CrossRef][Green Version]
- Frackiewicz-Kaczmarek, J.; Psikuta, A.; Bueno, M.-A.; Rossi, R.M. Air gap thickness and contact area in undershirts with various moisture contents: Influence of garments fit, fabric structure and fiber composition. Text. Res. J. 2015, 85, 2196–2207. [Google Scholar] [CrossRef]
- Mert, E.; Böhnisch, S.; Psikuta, A.; Bueno, M.A.; Rossi, R.M. Contribution of garments fit and style to thermal comfort at the lower body. Int. J. Biometeorol. 2016, 60, 1995–2004. [Google Scholar] [CrossRef]
- Mert, E.; Psikuta, A.; Arévalo, M.; Charbonnier, C.; Luible-Bär, C.; Bueno, M.; Rossi, R.M. A validation methodology and application of 3D garment simulation software to determine the distribution of air layers in garments during walking. Measurement 2017, 117, 153–164. [Google Scholar] [CrossRef]
- Lee, Y.; Hong, K.; Hong, S.A. 3D quantification of microclimate volume in layered clothing for the prediction of clothing insulation. Appl. Ergon. 2007, 38, 349–355. [Google Scholar] [CrossRef]




| Name | Photos of Garments | Materials Composition 1 | Surface Mass 1 [gm−2] | Normative Requirements 1 |
|---|---|---|---|---|
| U (underwear) |  | 59% protex, 39% cotton, 2% negastat | 205 | EN ISO 13688 [31], EN ISO 11612 A1,A2,B1,C1,F1 [32], EN 1149-5 [33] |
| W1 (jacket and waist-length pants) |  | Main fabric: 80% polyester, 20% cotton Contrast fabric: 65% polyester, 35% cotton | 225 245 | EN ISO 13688 [31] EN ISO 20471 cl.1 [34] |
| W2 (jacket and waist-length pants) |  | 79% cotton, 20% polyester, 1% anti-electrostatic fiber; finish Hydro-Tec | 260 | EN ISO 13688 [31] EN ISO 11611 cl.1 A1 + A2 [35] EN 11612 A1,A2,B1,C1,E2,F1 [32] EN 1149-5 [33] EN 13034 [36] EN ISO 14116 [37] IEC 61482-2 cl.1 [38] |
| W3 (flame retardant jacket and flame retardant pants (waist-length) |  | 100% cotton with proban finish | 335 | EN ISO 13688 [31] EN ISO 11611 cl.1 A1 + A2 [35] EN ISO 11612 A1,A2,B1,C1,E2,F1 [32] EN ISO 14116 [37] IEC 61482-2 cl.1 [38] |
| W4 (acid-proof jacket and acid-proof dungarees) |  | 80% polyester, 20% cotton | 225 | EN ISO 13688 [31] EN 13034 [36] |
| Study Variants | Total Volume of the Manikin V [dm3] (Scan 3D) | Total Volume of Air Gaps Between the Naked Manikin and the Outer Layer of the Outerwear V0 [dm3] | Total Air Gaps Volume Between the Underwear Manikin and the Outer Garments VP [dm3] |
|---|---|---|---|
| naked manikin | 71 | - | - |
| U_S | 82.3 | 11.4 | - |
| U_S_W1_50 | 105.9 | 35.0 | 23.6 |
| U_S_W1_54 | 114.2 | 43.2 | 31.8 |
| U_S_W1_56 | 117.7 | 46.8 | 35.4 |
| U_S_W2_50 | 106.2 | 35.3 | 23.9 |
| U_S_W2_54 | 117.3 | 46.3 | 34.9 |
| U_S_W2_56 | 116.5 | 45.6 | 34.2 |
| U_S_W3_50 | 106.6 | 35.7 | 24.3 |
| U_S_W3_54 | 111.9 | 40.9 | 29.5 |
| U_S_W3_56 | 112.6 | 41.6 | 30.2 |
| U_S_W4_50 | 105.4 | 34.4 | 23.0 |
| U_S_W4_54 | 112.4 | 41.4 | 30.0 |
| U_S_W4_56 | 107.6 | 36.7 | 25.3 |
| U_M | 86.8 | 15.8 | - |
| U_M_W1_50 | 104.2 | 33.3 | 17.4 |
| U_M_W1_54 | 118.1 | 47.2 | 31.4 |
| U_M_W1_56 | 125.2 | 54.2 | 38.4 |
| U_M_W2_50 | 104.9 | 34.0 | 18.1 |
| U_M_W2_54 | 118.9 | 48.0 | 32.1 |
| U_M_W2_56 | 120.6 | 49.6 | 33.8 |
| U_M_W3_50 | 106.0 | 35.0 | 19.2 |
| U_M_W3_54 | 119.4 | 48.5 | 32.6 |
| U_M_W3_56 | 116.2 | 45.3 | 29.5 |
| U_M_W4_50 | 105.4 | 34.4 | 18.6 |
| U_M_W4_54 | 110.3 | 39.3 | 23.5 |
| U_M_W4_56 | 118.0 | 47.0 | 31.2 |
| U_L | 92.6 | 21.7 | - |
| U_L_W1_50 | 109.7 | 38.8 | 17.1 |
| U_L_W1_54 | 113.6 | 42.6 | 21.0 |
| U_L_W1_56 | 118.1 | 47.1 | 25.4 |
| U_L_W2_50 | 108.3 | 37.3 | 15.6 |
| U_L_W2_54 | 118.5 | 47.5 | 25.8 |
| U_L_W2_56 | 117.3 | 46.4 | 24.7 |
| U_L_W3_50 | 104.6 | 33.7 | 12.0 |
| U_L_W3_54 | 112.0 | 41.1 | 19.4 |
| U_L_W3_56 | 117.3 | 46.4 | 24.7 |
| U_L_W4_50 | 106.4 | 35.4 | 13.7 |
| U_L_W4_54 | 112.8 | 41.9 | 20.2 |
| U_L_W4_56 | 112.8 | 41.9 | 20.2 |
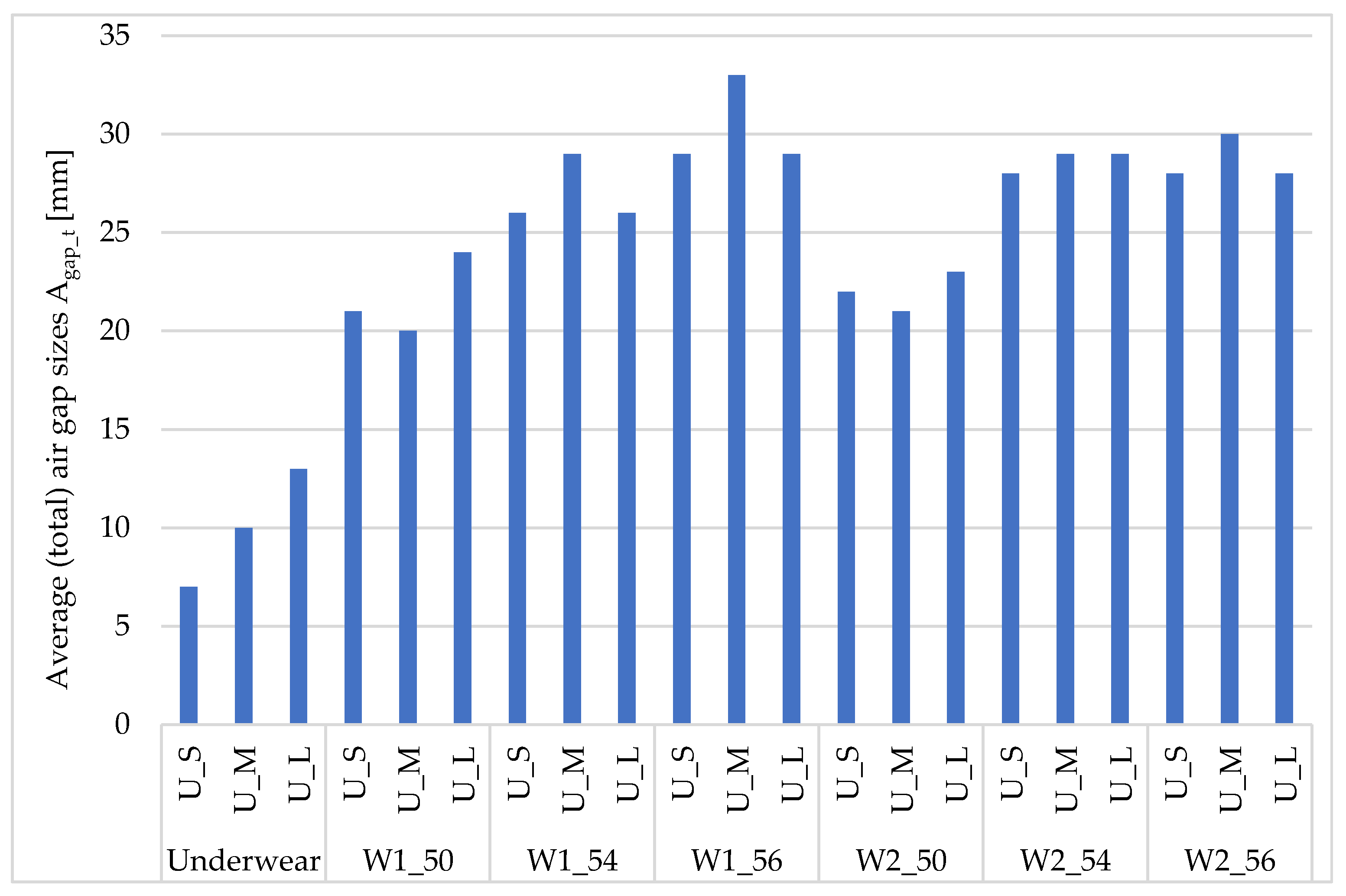
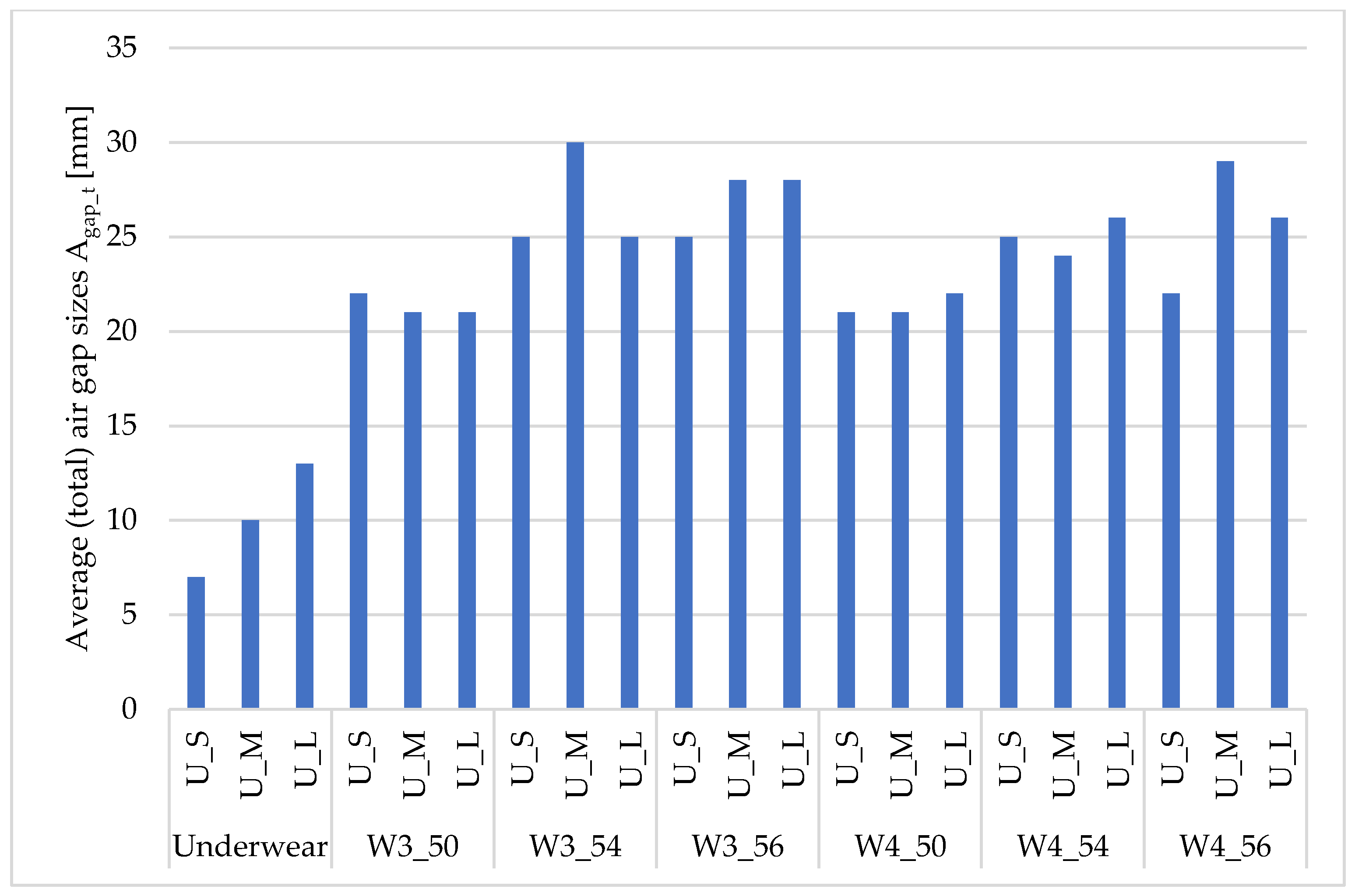
| Study Variants | Average (Total) Air Gap Sizes Agap_t [mm] | Average Size of Air Gaps Between Underwear and Outer Garmentss Agap_P [mm] |
|---|---|---|
| naked manikin | 0 | - |
| U_S | 7 | - |
| U_S_W1_50 | 21 | 14 |
| U_S_W1_54 | 26 | 19 |
| U_S_W1_56 | 29 | 22 |
| U_S_W2_50 | 22 | 15 |
| U_S_W2_54 | 28 | 21 |
| U_S_W2_56 | 28 | 21 |
| U_S_W3_50 | 22 | 15 |
| U_S_W3_54 | 25 | 18 |
| U_S_W3_56 | 25 | 18 |
| U_S_W4_50 | 21 | 14 |
| U_S_W4_54 | 25 | 18 |
| U_S_W4_56 | 22 | 15 |
| U_M | 10 | - |
| U_M_W1_50 | 20 | 11 |
| U_M_W1_54 | 29 | 19 |
| U_M_W1_56 | 33 | 23 |
| U_M_W2_50 | 21 | 11 |
| U_M_W2_54 | 29 | 20 |
| U_M_W2_56 | 30 | 21 |
| U_M_W3_50 | 21 | 12 |
| U_M_W3_54 | 30 | 20 |
| U_M_W3_56 | 28 | 18 |
| U_M_W4_50 | 21 | 11 |
| U_M_W4_54 | 24 | 14 |
| U_M_W4_56 | 29 | 19 |
| U_L | 13 | - |
| U_L_W1_50 | 24 | 10 |
| U_L_W1_54 | 26 | 13 |
| U_L_W1_56 | 29 | 16 |
| U_L_W2_50 | 23 | 10 |
| U_L_W2_54 | 29 | 16 |
| U_L_W2_56 | 28 | 15 |
| U_L_W3_50 | 21 | 7 |
| U_L_W3_54 | 25 | 12 |
| U_L_W3_56 | 28 | 15 |
| U_L_W4_50 | 22 | 8 |
| U_L_W4_54 | 26 | 12 |
| U_L_W4_56 | 26 | 12 |
| Study Variants | Total Air Gaps Volume [dm3] | Average (Total) Sizes of Air Gaps [mm] |
|---|---|---|
| It (serial) | 51 | 28 |
| It (parallel) | 50 | 34–35 |
| Itr (serial) | 45 | 43 |
| Itr (parallel) | 55 | 33 |
| It (serial) | 51 | 28 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Młynarczyk, M.; Orysiak, J.; Jankowski, J. Effect of Workwear Fit on Thermal Insulation: Assessment Using 3D Scanning Technology. Materials 2025, 18, 2098. https://doi.org/10.3390/ma18092098
Młynarczyk M, Orysiak J, Jankowski J. Effect of Workwear Fit on Thermal Insulation: Assessment Using 3D Scanning Technology. Materials. 2025; 18(9):2098. https://doi.org/10.3390/ma18092098
Chicago/Turabian StyleMłynarczyk, Magdalena, Joanna Orysiak, and Jarosław Jankowski. 2025. "Effect of Workwear Fit on Thermal Insulation: Assessment Using 3D Scanning Technology" Materials 18, no. 9: 2098. https://doi.org/10.3390/ma18092098
APA StyleMłynarczyk, M., Orysiak, J., & Jankowski, J. (2025). Effect of Workwear Fit on Thermal Insulation: Assessment Using 3D Scanning Technology. Materials, 18(9), 2098. https://doi.org/10.3390/ma18092098







