Discrete Element Method (DEM) Studies on Correcting the Particle Size Effect on the Shear Behaviors of Gravelly Soils
Abstract
1. Introduction
2. Scaling Relations for Correcting the Particle Size Effect
3. DEM Model and Simulation Arrangement
3.1. DEM Model Preparation and Parameters
3.2. Loading Procedures
3.3. Simulation Arrangement
4. Simulation Results and Analysis
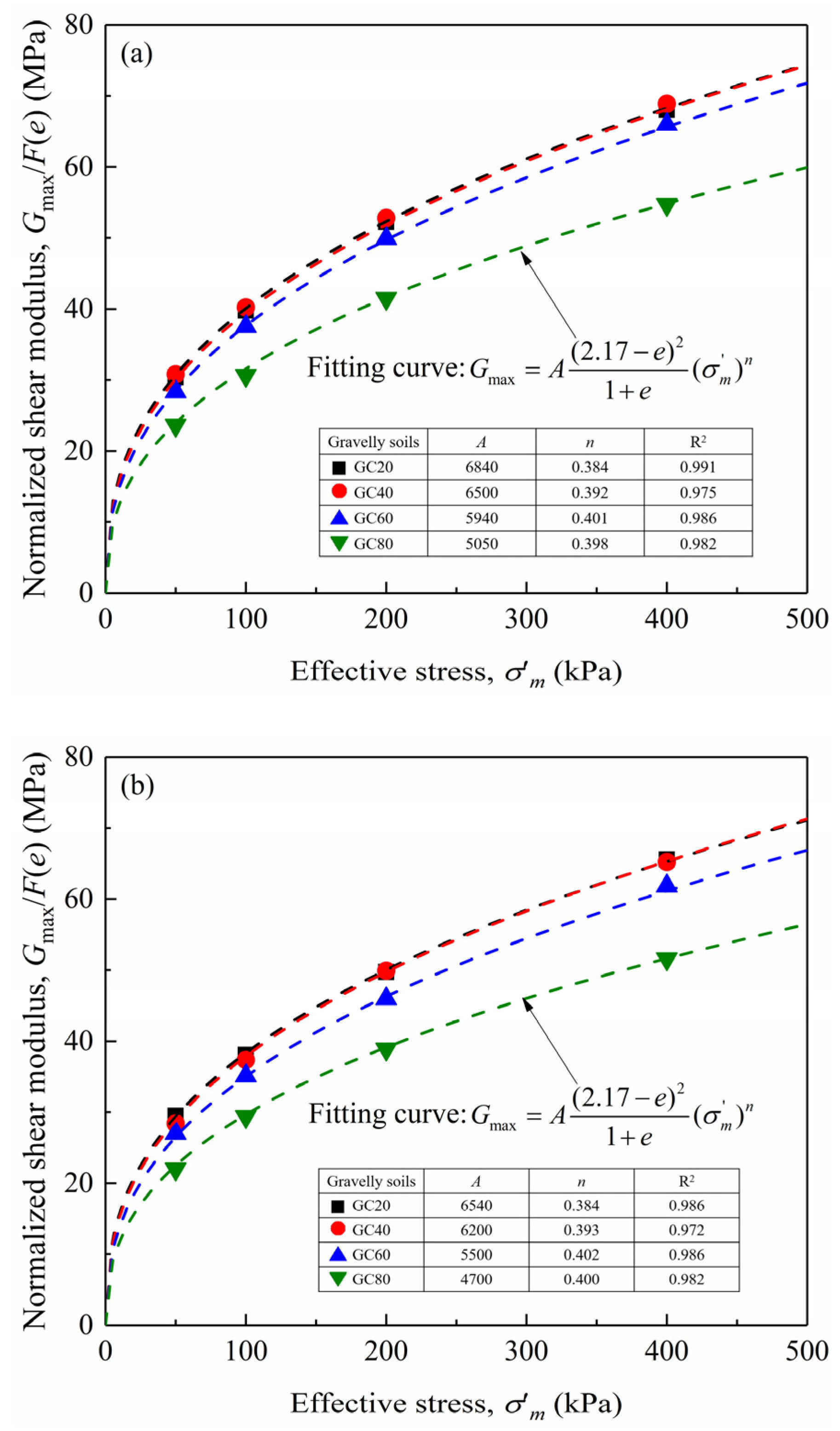
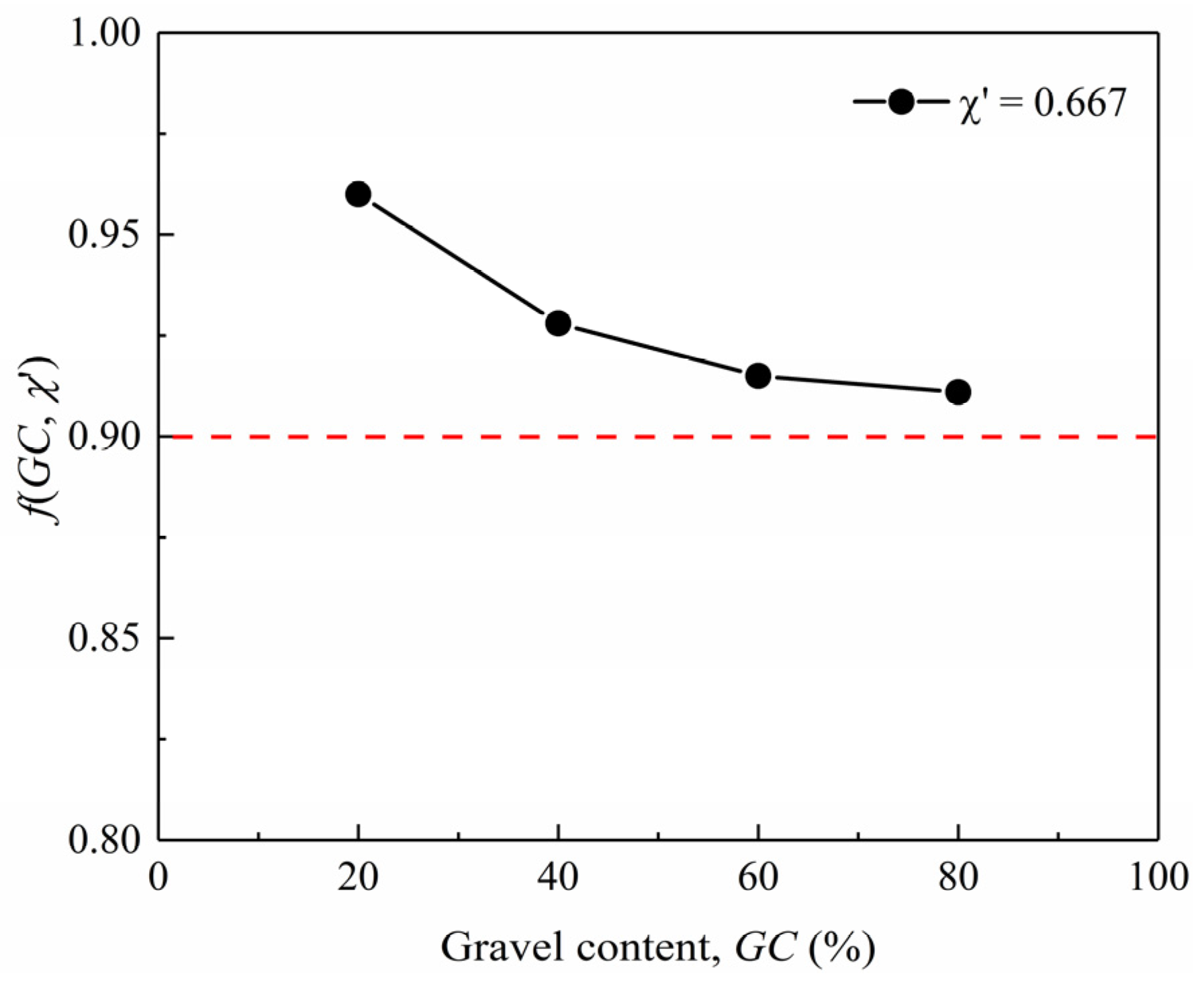
4.1. Determining the Scaling Relation for Stiffness
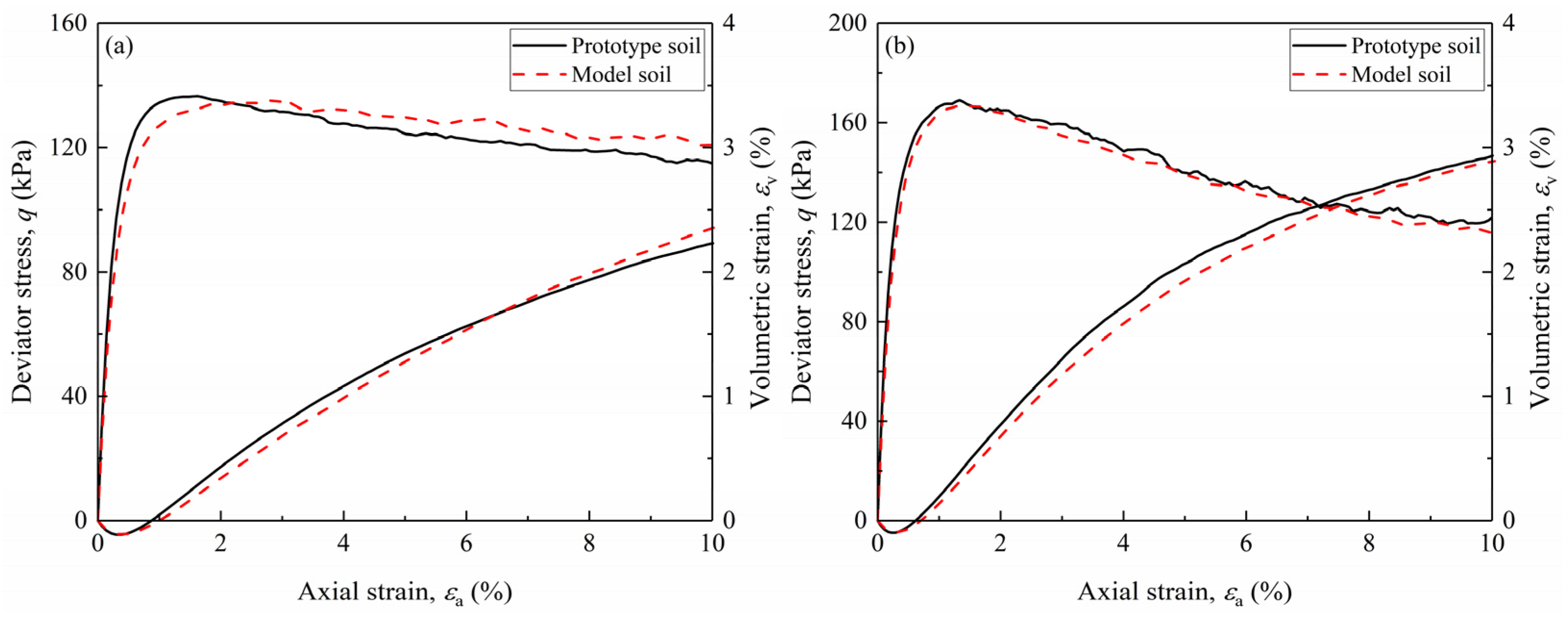
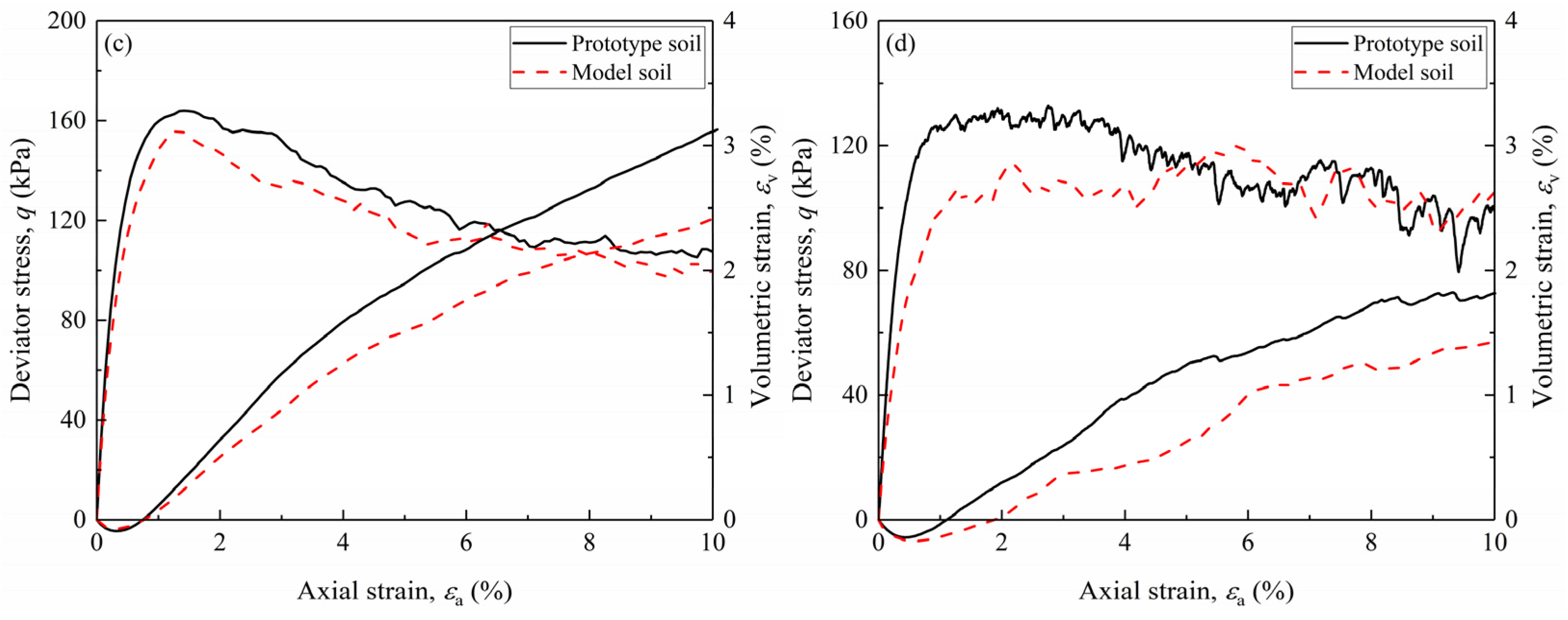
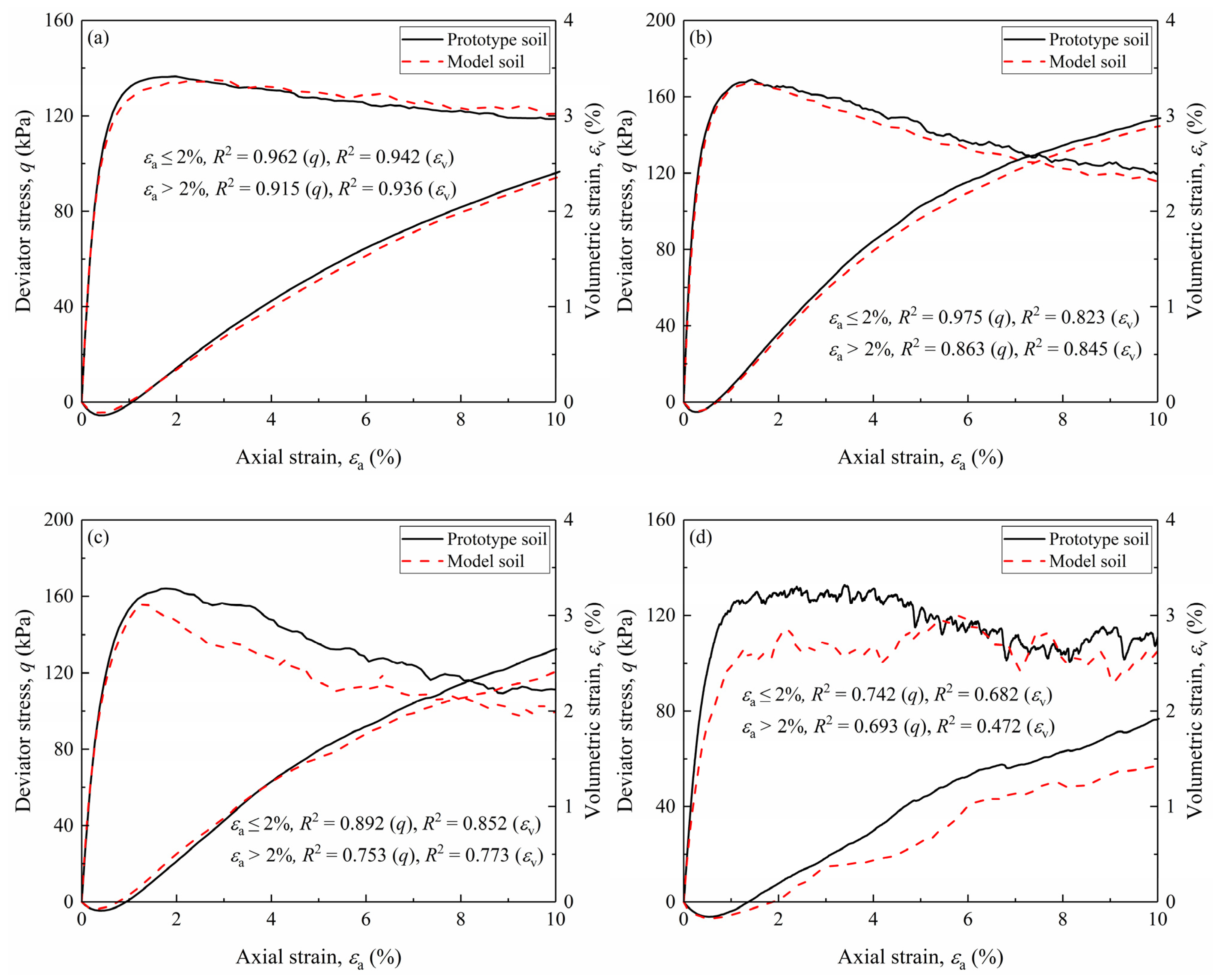
4.2. Drained Triaxial Test Simulation Results and Analysis
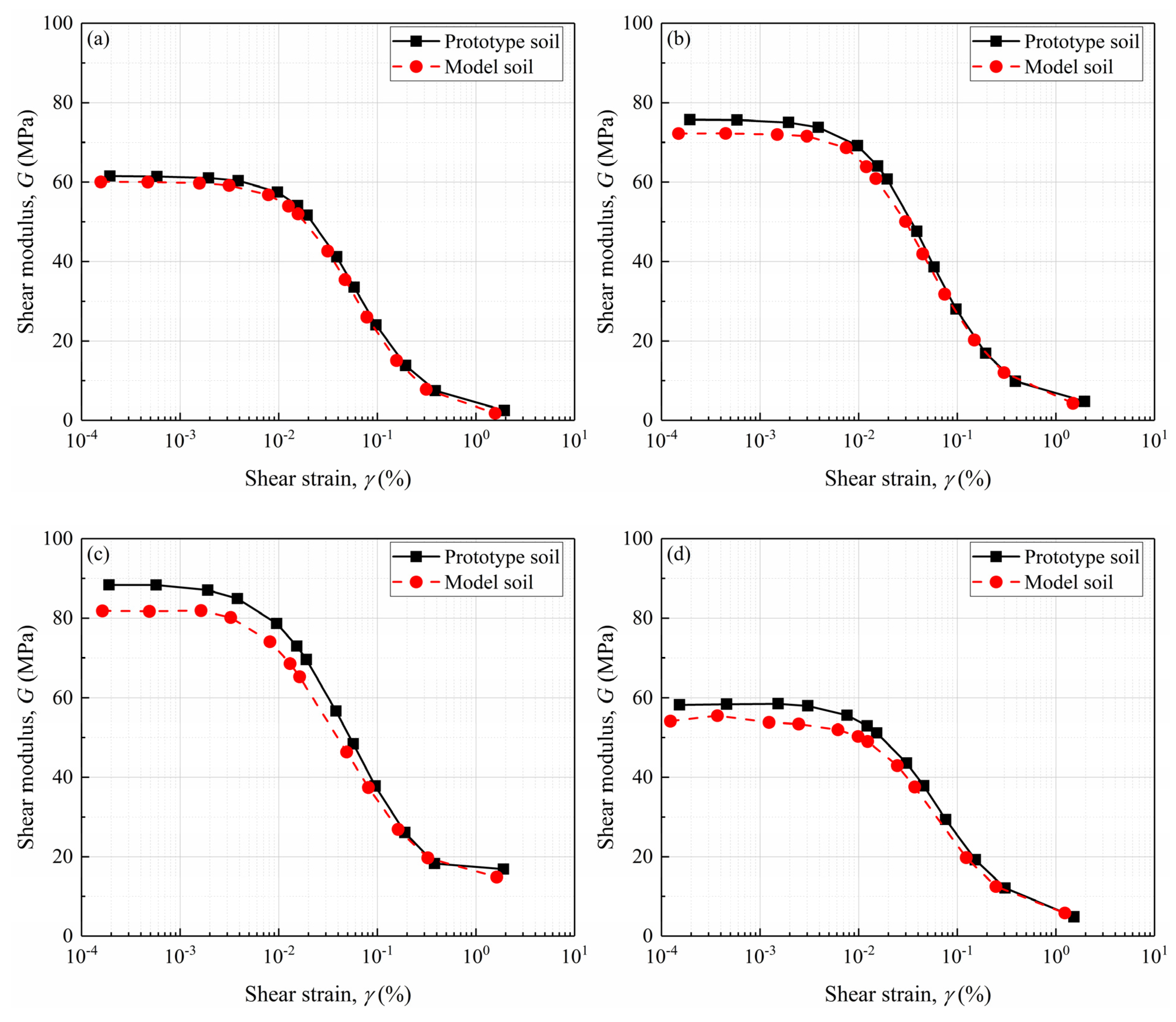
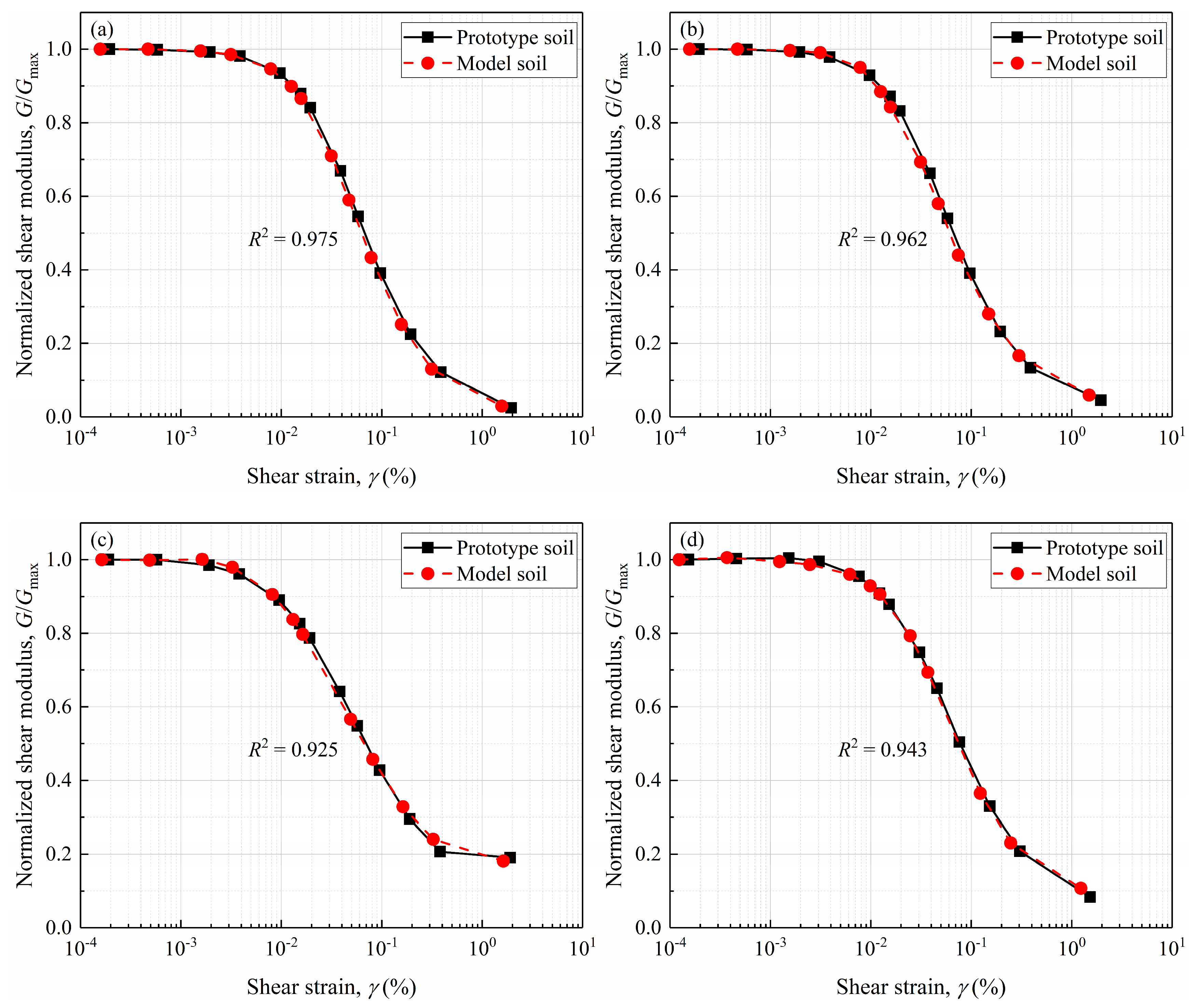
4.3. Shear Modulus Test Simulation Results and Analysis
5. Conclusions
- (1)
- The simulation results demonstrate that larger gravel particles significantly enhance soil stiffness, while the gravel replacement technique, which substitutes overlarge particles with finer ones, leads to a reduction in soil stiffness from small to large shear strains. This effect is more pronounced in soils with high GCs (e.g., GC > 60%), although the impact on peak shear strength remains minimal.
- (2)
- The scaling relations for correcting the particle size effect for gravelly soils are proposed based on the well-known Iai’s GSR. The scaling relations for stiffness and strain were successfully applied to predict the mechanical responses of prototype soils from model tests, particularly for small to medium strain levels. This validation confirms the reliability of the updated scaling relations in predicting the shear responses of gravelly soils with overlarge particles.
- (3)
- Rocha’s assumption, which relates stress and strain similarities between model and prototype soils, is validated to be highly applicable for correcting particle size effects in deformation problems. However, for gravel-dominant soils with high GCs, this assumption shows moderate applicability, indicating some limitations in accurately predicting shear behavior, especially at large strains.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, Y.G.; Xia, P.; Ling, D.S.; Chen, Y.M. A liquefaction case study of gently sloping gravelly soil deposits in the near-fault region of the 2008 Mw7.9 Wenchuan earthquake. Bull. Earthq. Eng. 2020, 18, 6181–6201. [Google Scholar] [CrossRef]
- Shi, X.S.; Zhao, J.; Gao, Y. A homogenization-based state-dependent model for gap-graded granular materials with fine-dominated structure. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 1007–1028. [Google Scholar] [CrossRef]
- Xia, P.; Zhou, Y.G.; Chen, Y.M. An Improved CRR-Vs1 Characterization Model for Sand-Like Gravelly Soils Validated by Dynamic Centrifuge Tests. J. Geotech. Geoenviron. Eng. 2025, 151, 04025015. [Google Scholar] [CrossRef]
- Shi, X.; Miao, X.; Xiong, H.; Bian, X. Estimation of bearing capacity of bimsoils under shallow foundations. J. Rock Mech. Geotech. Eng. 2024, 16, 4335–4814. [Google Scholar] [CrossRef]
- Xia, P.; Zhou, Y.G.; Chen, Y.M. Gravel content effect on site response of sand-like gravelly soil deposits by centrifuge model tests. Soil Dyn. Earthq. Eng. 2025, 190, 109169. [Google Scholar] [CrossRef]
- ASTM D2487-17; Standard Practice for Classification of Soils for Engineering Purposes (Unified Soil Classification System). ASTM International: West Conshohocken, PA, USA, 2017.
- Shi, X.; He, Z.; Zhao, J.; Liu, J. Determination of the size of representative volume element for gap-graded granular materials. Powder Technol. 2024, 437, 119578. [Google Scholar] [CrossRef]
- Hassan, N.A.; Nguyen, N.S.; Marot, D.; Bendahmane, F. Consequences of scalping and scalping/replacement procedures on strength properties of coarse-grained gap-graded soils. Can. Geotech. J. 2022, 59, 1819–1832. [Google Scholar] [CrossRef]
- Chang, W.J.; Phantachang, T. Effects of gravel content on shear resistance of gravelly soils. Eng. Geol. 2016, 207, 78–90. [Google Scholar] [CrossRef]
- Xia, P.; Yu, D.G.; Luo, H.D.; Li, Z.F.; Ma, Q.; Gao, Y.F. Scaling law for correcting the gravel content effect due to scalping techniques by DEM investigations. Comput. Geotech. 2025, 178, 106954. [Google Scholar] [CrossRef]
- Fragaszy, R.J.; Su, J.; Siddiqi, F.H.; Ho, C.L. Modeling strength of sandy gravel. J. Geotech. Eng. 1992, 118, 920–935. [Google Scholar] [CrossRef]
- Lin, P.S.; Chang, C.W.; Chang, W.J. Characterization of liquefaction resistance in gravelly soil: Large hammer penetration test and shear wave velocity approach. Soil Dyn. Earthq. Eng. 2004, 24, 675–687. [Google Scholar] [CrossRef]
- Fannin, R.J.; Eliadorani, A.; Wilkinson, J.M.T. Shear strength of cohesionless soils at low stress. Géotechnique 2005, 55, 467–478. [Google Scholar] [CrossRef]
- Chen, G.X.; Wu, Q.; Sun, T.; Zhao, K.; Zhou, E.Q.; Xu, L.Y.; Zhou, Y.G. Cyclic behaviors of saturated sand-gravel mixtures under undrained cyclic triaxial loading. J. Earthq. Eng. 2018, 25, 756–789. [Google Scholar] [CrossRef]
- Zeng, Y.W.; Shi, X.S.; Zhao, J.D.; Bian, X.; Liu, J.Y. Estimation of compression behavior of granular soils considering initial density effect based on equivalent concept. Acta Geotech. 2024, 20, 1035–1048. [Google Scholar] [CrossRef]
- Zuo, K.; Gu, X.; Zhang, J.; Wang, R. Exploring packing density, critical state, and liquefaction resistance of sand-fines mixture using DEM. Comput. Geotech. 2023, 156, 105278. [Google Scholar] [CrossRef]
- Chen, G.; Zhou, Z.; Sun, T.; Wu, Q.; Xu, L.; Khoshnevisan, S.; Ling, D. Shear modulus and damping ratio of sand–gravel mixtures over a wide strain range. J. Earthq. Eng. 2018, 23, 1407–1440. [Google Scholar] [CrossRef]
- Zhou, Y.G.; Xia, P.; Ling, D.S.; Chen, Y.M. Liquefaction case studies of gravelly soils during the 2008 Wenchuan earthquake. Eng. Geol. 2020, 274, 105691. [Google Scholar] [CrossRef]
- Hu, W.; Dano, C.; Hicher, P.Y.; Le Touzo, J.Y.; Derkx, F.; Merliot, E. Effect of sample size on the behavior of granular materials. Geotech. Test. J. 2011, 34, 186–197. [Google Scholar] [CrossRef]
- Ning, F.; Liu, J.; Kong, X.; Zou, D. Critical state and grading evolution of rockfill material under different triaxial compression tests. Int. J. Geomech. 2020, 20, 04019154. [Google Scholar] [CrossRef]
- Cundall, P.A. A Discrete numerical model for granular assemblies Geotechnique. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Xia, P.; Dai, D.; Hang, L.; Li, Z. DEM study on the dynamic behaviors of binary mixtures with the same equivalent skeleton void ratio. Comput. Geotech. 2024, 168, 106160. [Google Scholar] [CrossRef]
- Xia, P.; Zhou, Y.G.; Chen, Y.M. An improved characterization model of liquefaction resistance by shear wave velocity for binary mixtures with consideration of coarse content. Eng. Geol. 2024, 332, 107459. [Google Scholar] [CrossRef]
- Shi, X.; Xu, J.; Guo, N.; Bian, X.; Zeng, Y. A novel approach for describing gradation curves of rockfill materials based on the mixture concept. Comput. Geotech. 2025, 177, 106911. [Google Scholar] [CrossRef]
- Iai, S. Similitude for shaking table tests on soil-structure-fluid model in 1g gravitational field. Soils Found. 1989, 29, 105–118. [Google Scholar] [CrossRef]
- Rocha, M. The possibility of solving soil mechanics problems by the use of models. In Proceedings of the 4th ICSMFE International Conference on Doil Mechanics and Foundation Engineering, London, UK, 12–24 August 1957; pp. 183–188. [Google Scholar]
- Zhou, Y.G.; Ma, Q.; Liu, K.; Chen, Y.M. Centrifuge model tests at Zhejiang University for LEAP-Asia-2019 and validation of the generalized scaling law. Soil Dyn. Earthq. Eng. 2021, 144, 106660. [Google Scholar] [CrossRef]
- Shi, X.S.; Zhao, J.D. Practical estimation of compression behavior of clayey/silty sands using equivalent void-ratio concept. J. Geotech. Geoenviron. Eng. 2020, 146, 04020046. [Google Scholar] [CrossRef]
- Shi, X.S.; Liu, K.; Yin, J.H. Effect of initial density, particle shape, and confining stress on the critical state behavior of weathered gap-graded granular soils. J. Geotech. Geoenviron. Eng. 2021, 147, 04020160. [Google Scholar] [CrossRef]
- Shi, X.S.; Nie, J.; Zhao, J.; Gao, Y. A homogenization equation for the small strain stiffness of gap-graded granular materials. Comput. Geotech. 2020, 121, 103440. [Google Scholar] [CrossRef]
- Menq, F.Y. Dynamic Properties of Sandy and Gravelly Soils. Ph.D. Thesis, The University of Texas at Austin, Austin, TX, USA, 2003. [Google Scholar]
- Oztoprak, S.A.D.I.K.; Bolton, M.D. Stiffness of sands through a laboratory test database. Géotechnique 2013, 63, 54–70. [Google Scholar] [CrossRef]
- Liu, X.; Zou, D.; Ning, F.; Liu, J. Investigating the effect of gravel content on the small-strain shear modulus of sand-gravel mixtures. Granul. Matter 2023, 25, 22. [Google Scholar] [CrossRef]
- Itasca. User’s Manual for PFC3D Version PFC5.0; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2015. [Google Scholar]
- Xu, X.M.; Ling, D.S.; Cheng, Y.P.; Chen, Y.M. Correlation between liquefaction resistance and shear wave velocity of granular soils: A micromechanical perspective. Geotechnique 2015, 65, 337–348. [Google Scholar] [CrossRef]
- Shire, T.; O’Sullivan, C.; Hanley, K.J. The influence of fines content and size-ratio on the micro-scale properties of dense bimodal materials. Granul. Matter 2016, 18, 52. [Google Scholar] [CrossRef]
- Gu, X.Q.; Lu, L.T.; Qian, J.G. Discrete element modeling of the effect of particle size distribution on the small strain stiffness of granular soils. Particuology 2017, 32, 21–29. [Google Scholar] [CrossRef]
- Zhu, Y.; Gong, J.; Nie, Z. Numerical investigation of the elastic properties of binary mixtures as a function of the size ratio and fines content. Int. J. Geomech. 2020, 20, 04020155. [Google Scholar] [CrossRef]
- Gong, J.; Liu, J. Mechanical transitional behavior of binary mixtures via DEM: Effect of differences in contact-type friction coefficients. Comput. Geotech. 2017, 85, 1–14. [Google Scholar] [CrossRef]
- Baziar, M.H.; Salemi, S.H.; Merrifield, C.M. Dynamic centrifuge model tests on asphalt-concrete core dams. Geotechnique 2009, 59, 763–771. [Google Scholar] [CrossRef]
- Da Cruz, F.; Emam, S.; Prochnow, M.; Roux, J.N.; Chevoir, F. Rheophysics of dense granular materials: Discrete simulation of plane shear flows. Phys. Rev. E-Stat. Nonlinear Soft Matter Phys. 2005, 72, 021309. [Google Scholar] [CrossRef]
- Krievans, M.; Burlakovs, J.; Krope, D.; Zekker, I.; Vincevica-Gaile, Z.; Vilnitis, M. Correlation of Unconsolidated Undrained Shear Strength of Clay Soils Between Uniaxial and Triaxial Test Results. In Proceedings of the EAGE Workshop on Naturally Fractured Rocks (NFR), Muscat, Oman, 6–8 October 2024; European Association of Geoscientists & Engineers: Utrecht, The Netherlands; Volume 1, pp. 1–3. [Google Scholar]
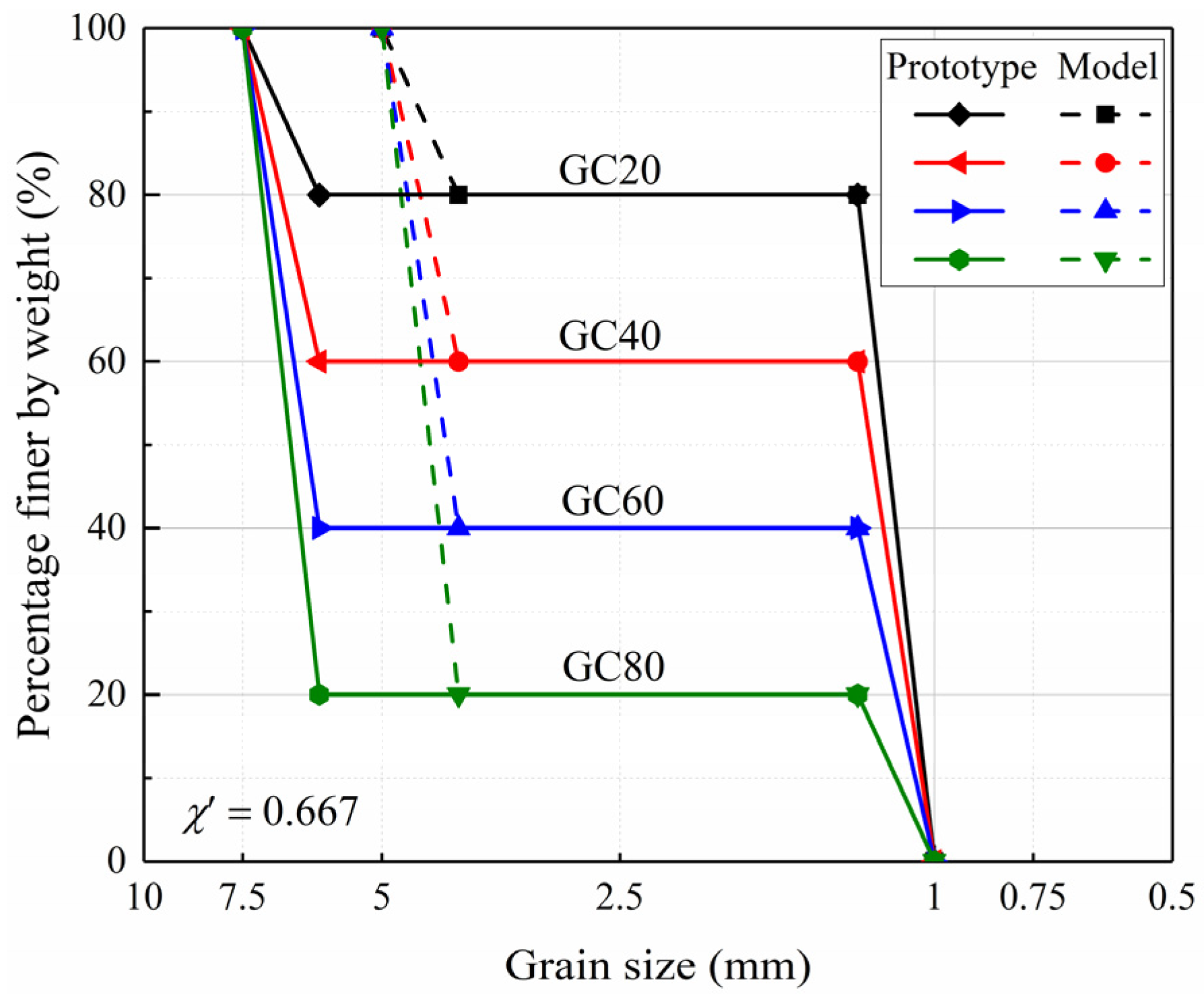
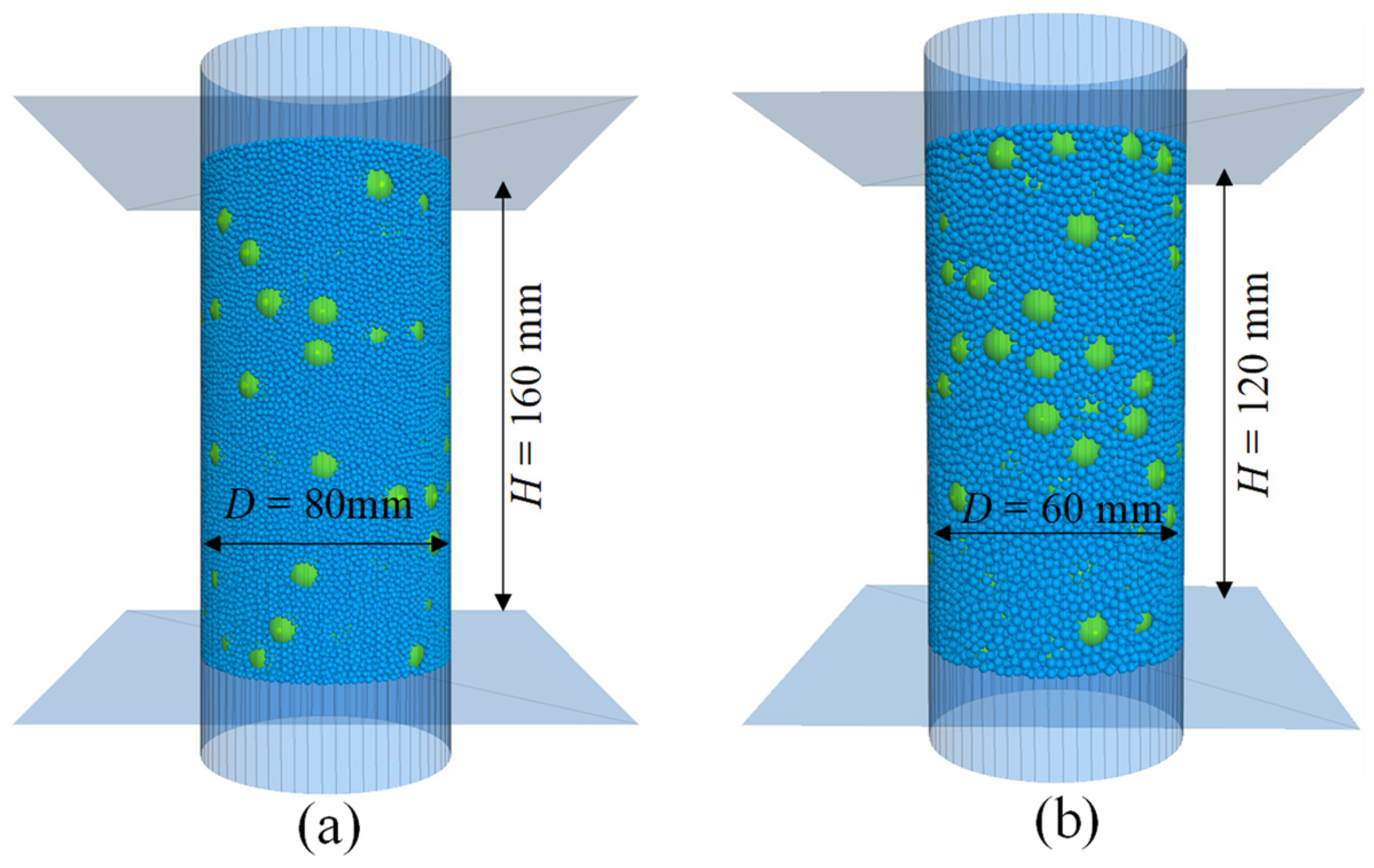
| Mechanical Properties | Scaling Relations of the Type I GSR by Iai [25] | The Developed Scaling Relations for Correcting the Particle Size Effect |
|---|---|---|
| Length | λ | 1 |
| Density | λρ | 1 |
| Time | (λλε)0.5 | (1/f(GC, χ′))0.5 |
| Frequency | (λλε)−0.5 | (1/f(GC, χ′))−0.5 |
| Acceleration | 1 | 1 |
| Velocity | (λλε)0.5 | (1/f(GC, χ′))0.5 |
| Displacement | λλε | 1/f(GC, χ′) |
| Stress | λλρ | 1 |
| Strain | λε | 1/f(GC, χ′) |
| Stiffness | λλρ/λε | f(GC, χ′) |
| Permeability | (λλε)0.5/λρ | (1/f(GC, χ′))0.5 |
| Pore pressure | λλρ | 1 |
| Parameters | Value | References |
|---|---|---|
| Particle density, ρ (g/cm3) | 2.63 | Xia et al. (2024) [22] |
| Particle shear modulus, G (kPa) | 107 | Xia et al. (2024) [23] |
| Normal stiffness for wall-particle contacts, kn (kN/m) | 105 | Xu et al. (2015) [35] |
| Wall-particle frictional coefficient, μwp | 0 | Xia et al. (2024) [22] |
| Particle frictional coefficient, μ | 0.5 | Gong and Liu (2017) [39] |
| Particle Poisson’s ratio, ν | 0.2 | Xia et al. (2024) [22] |
| Damping factor, α | 0.7 | Xu et al. (2015) [35] |
| GC | Ap | Am | np | nm |
|---|---|---|---|---|
| 20% | 6840 | 6540 | 0.384 | 0.384 |
| 40% | 6500 | 6200 | 0.392 | 0.393 |
| 60% | 5940 | 5500 | 0.401 | 0.402 |
| 80% | 5050 | 4700 | 0.398 | 0.400 |
| GC | Soil Type | Void Ratio | Shear Modulus (MPa) | λ | λρ | λε |
|---|---|---|---|---|---|---|
| 20% | Prototype | 0.558 | 62.51 | 1 | 1 | 0.960 |
| Model | 0.559 | 60.03 | ||||
| 40% | Prototype | 0.463 | 76.71 | 1 | 1 | 0.928 |
| Model | 0.457 | 71.22 | ||||
| 60% | Prototype | 0.419 | 89.36 | 1 | 1 | 0.915 |
| Model | 0.420 | 81.81 | ||||
| 80% | Prototype | 0.521 | 58.24 | 1 | 1 | 0.911 |
| Model | 0.436 | 53.11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Wu, Z.; Han, H.; Gao, Y.; Li, Z.; Xia, P. Discrete Element Method (DEM) Studies on Correcting the Particle Size Effect on the Shear Behaviors of Gravelly Soils. Materials 2025, 18, 2024. https://doi.org/10.3390/ma18092024
Zhang X, Wu Z, Han H, Gao Y, Li Z, Xia P. Discrete Element Method (DEM) Studies on Correcting the Particle Size Effect on the Shear Behaviors of Gravelly Soils. Materials. 2025; 18(9):2024. https://doi.org/10.3390/ma18092024
Chicago/Turabian StyleZhang, Xiaolei, Zhenping Wu, Houyun Han, Yifeng Gao, Zhuofeng Li, and Peng Xia. 2025. "Discrete Element Method (DEM) Studies on Correcting the Particle Size Effect on the Shear Behaviors of Gravelly Soils" Materials 18, no. 9: 2024. https://doi.org/10.3390/ma18092024
APA StyleZhang, X., Wu, Z., Han, H., Gao, Y., Li, Z., & Xia, P. (2025). Discrete Element Method (DEM) Studies on Correcting the Particle Size Effect on the Shear Behaviors of Gravelly Soils. Materials, 18(9), 2024. https://doi.org/10.3390/ma18092024






