Development of an Improved Stiffness Ellipsoid Method for Precise Robot-Positioner Collaborative Control in Friction Stir Welding
Abstract
1. Introduction
2. Materials and Methods
2.1. Robot Joint and End-Effector Stiffness Modeling
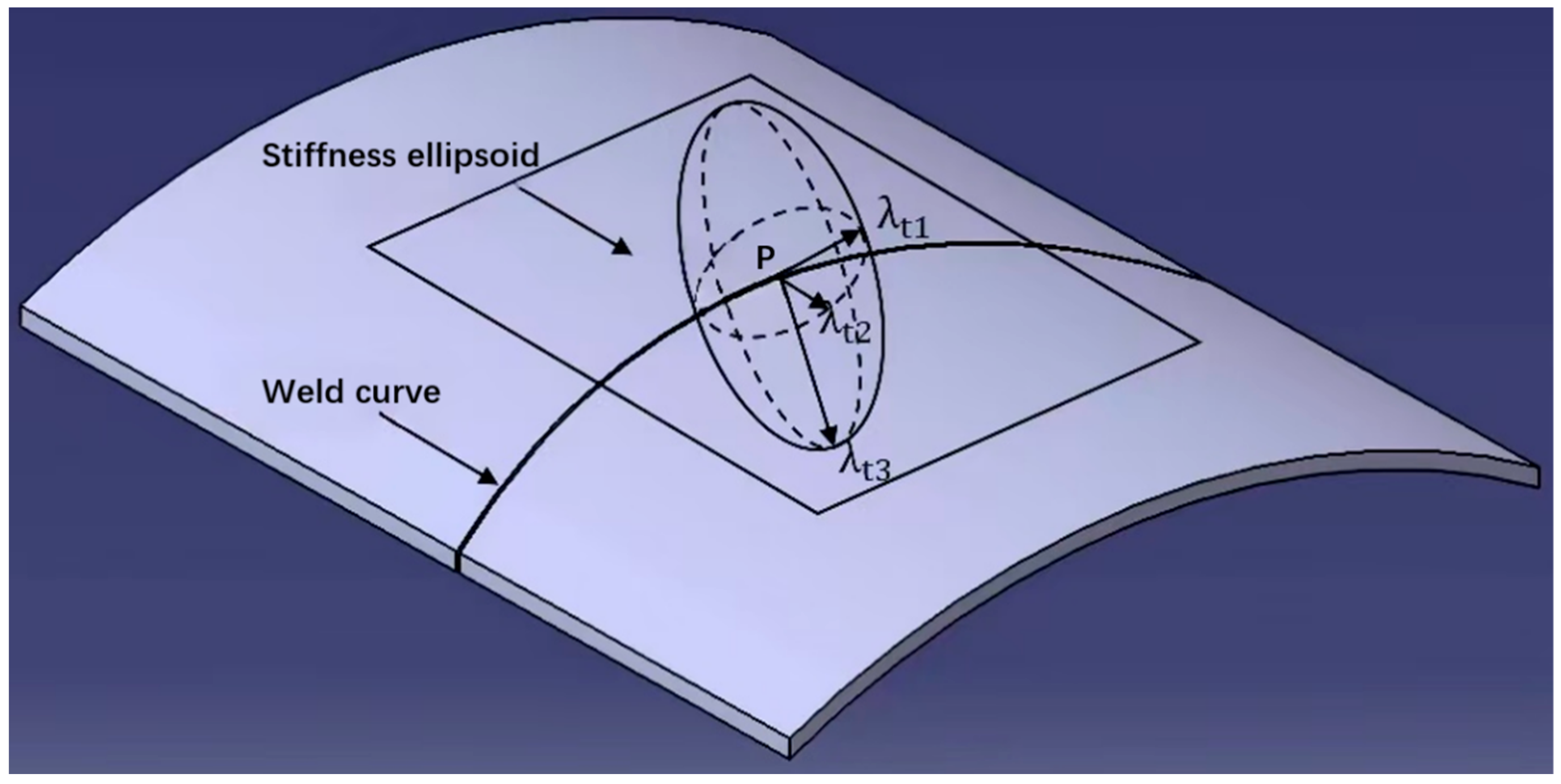
2.2. Enhancing Robotic Friction Stir Welding Through Stiffness Ellipsoid Modeling
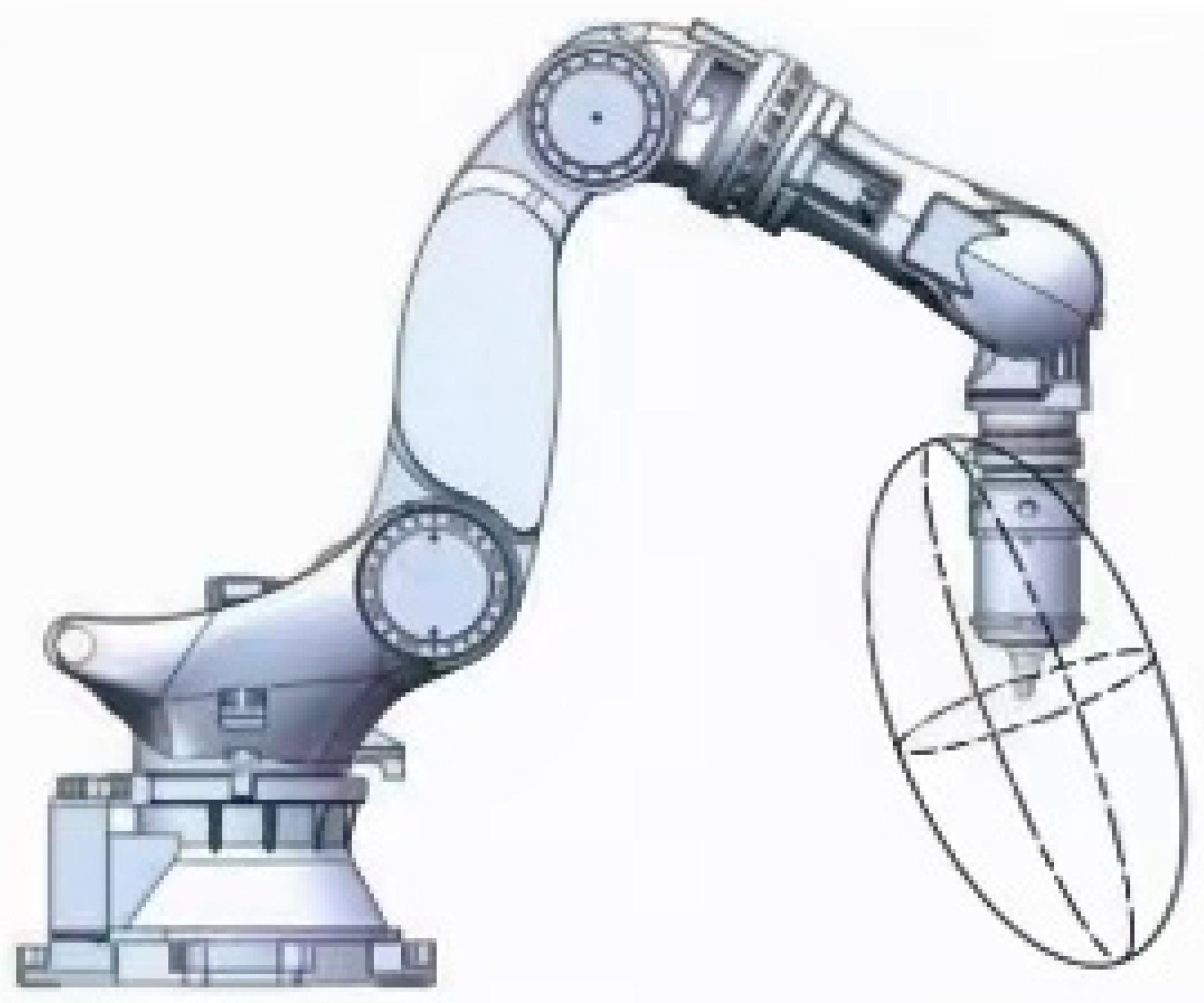
2.3. Analysis of Robot Stiffness Characteristics
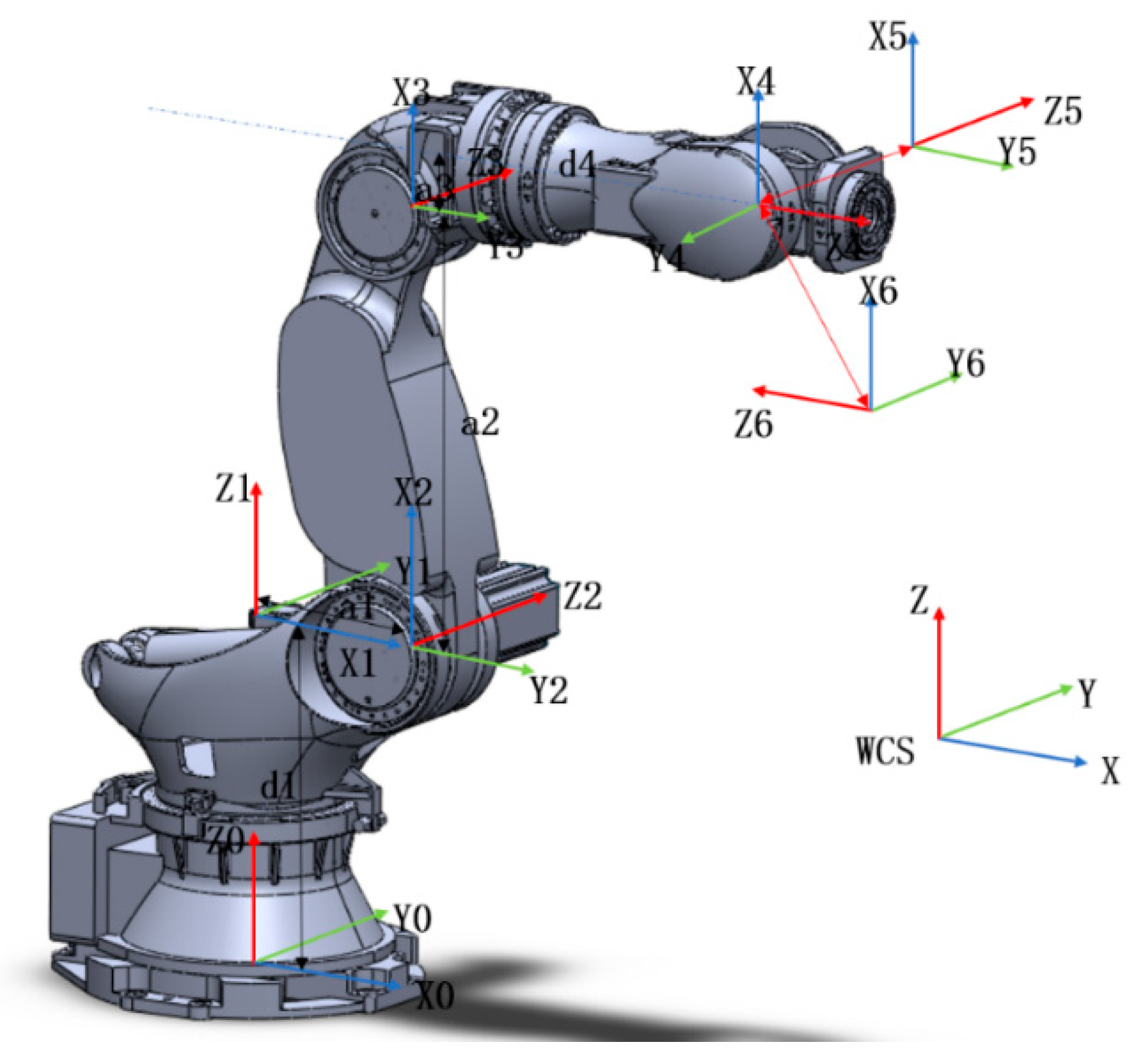
2.4. Composition and Kinematic Modeling of the Robot Friction Stir Welding System
2.5. Collaborative Motion Control Algorithm for Robot and Positioner Based on the Stiffness Index
2.5.1. Collaborative Motion Control Model of Robot and Positioner
- (1)
- Objective function
- (2)
- Decision variables
- (3)
- Constraints
2.5.2. Solution of Collaborative Motion Control Model
- (1)
- Genetic algorithm for solving the model
- a.
- Fitness function settings
- b.
- Design variables
- c.
- Boundary condition settings
- d.
- Initial population generation
- e.
- Selection method and crossover operator
- f.
- Algorithm termination condition
- (2)
- Improvement of the Genetic Algorithm
3. Discussion
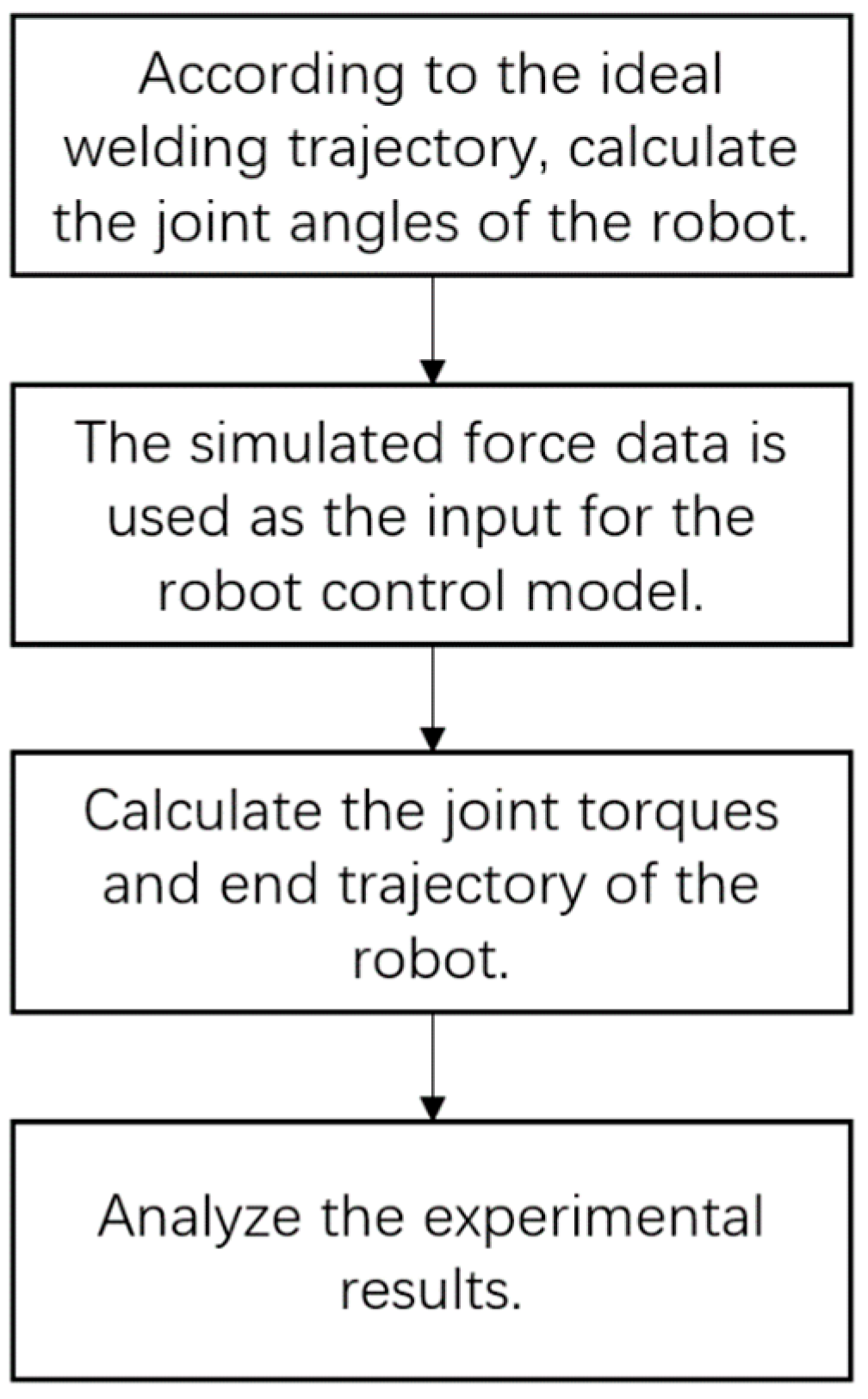
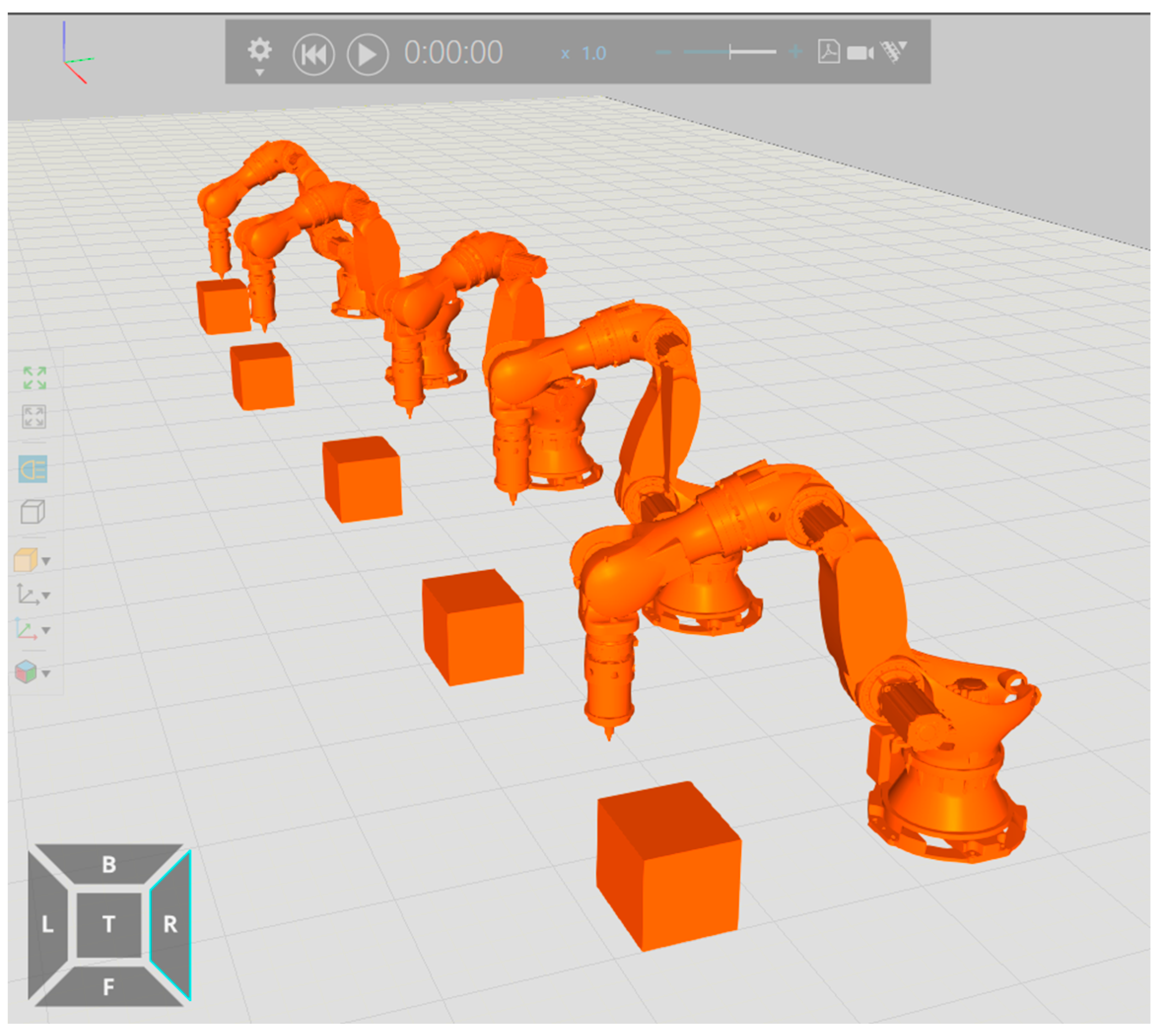
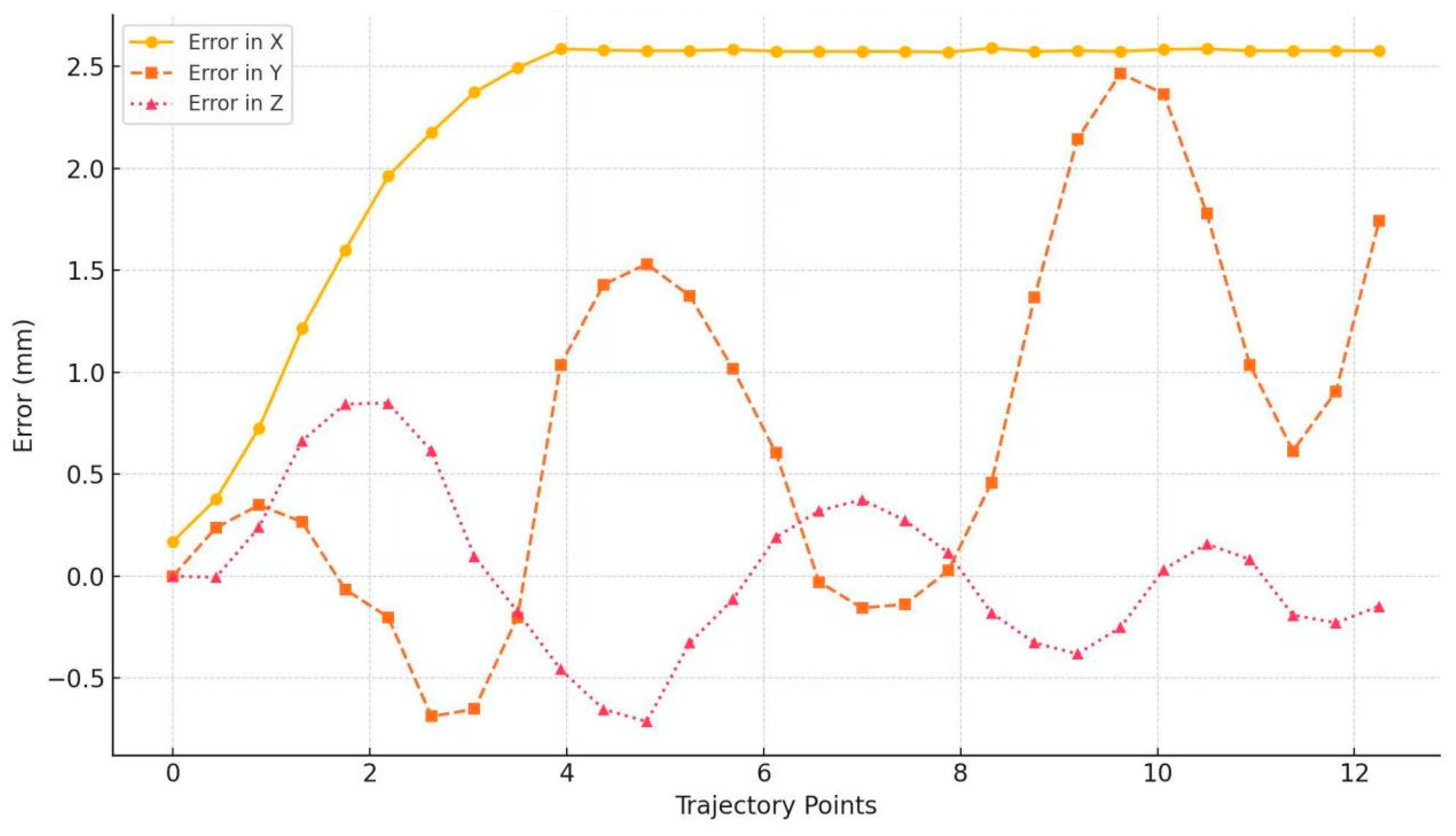
3.1. Collaborative Motion Control Simulation Experiment
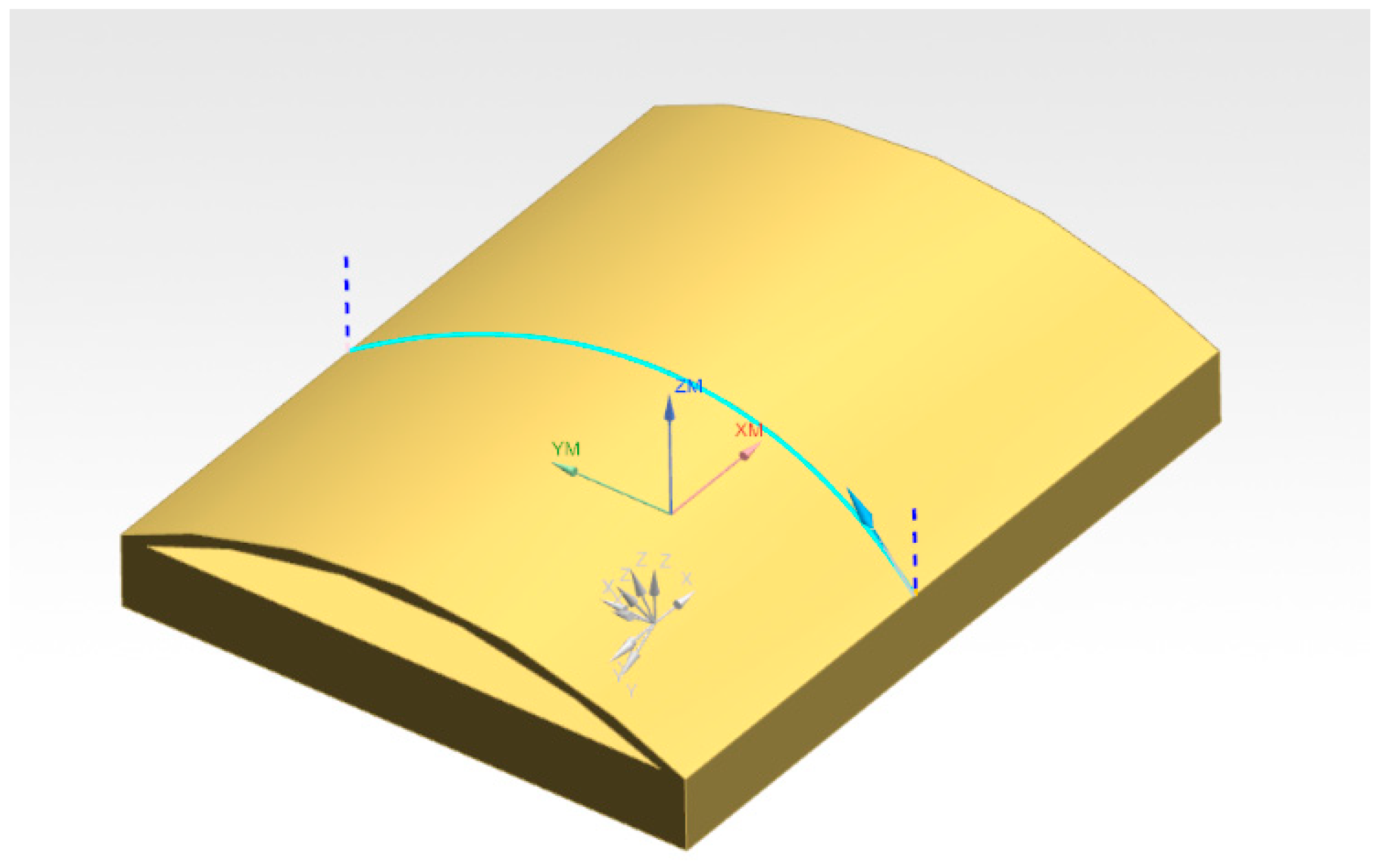
3.2. Welding Pose Optimization Calculation Example
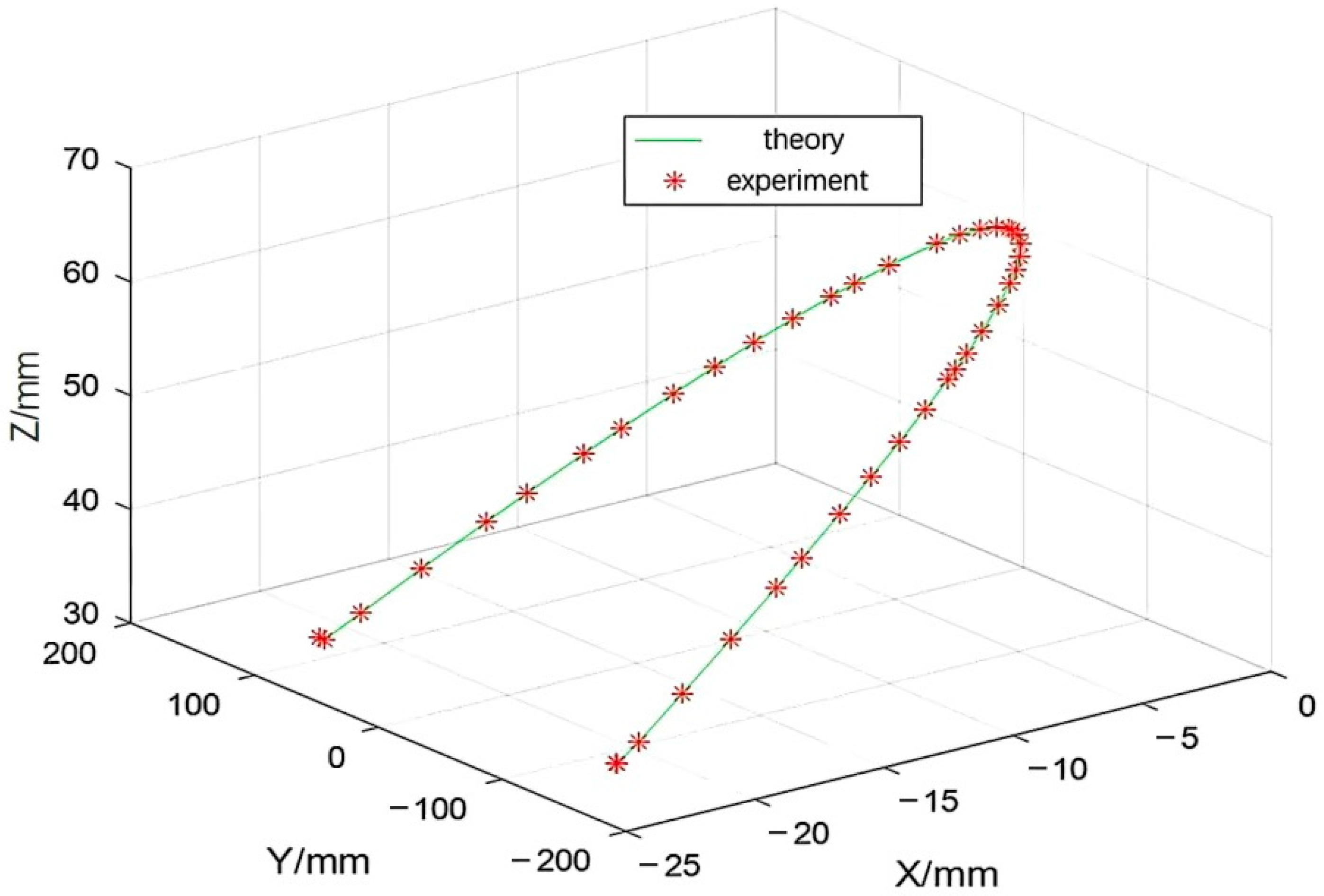
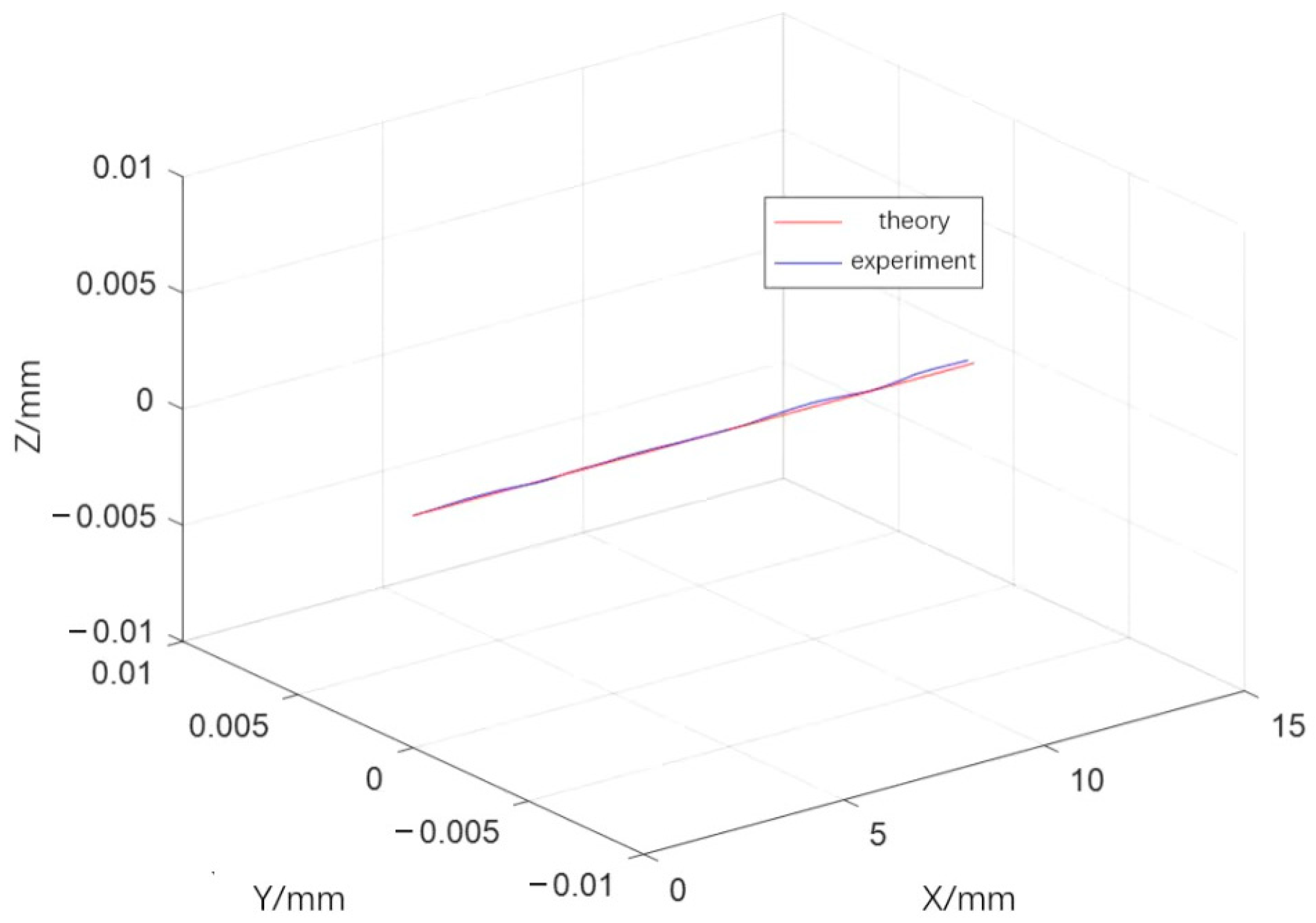
3.3. Welding Simulation Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Meng, X.; Huang, Y.; Cao, J.; Shen, J.; dos Santos, J.F. Recent progress on control strategies for inherent issues in friction stir welding. Prog. Mater. Sci. 2021, 115, 100706. [Google Scholar] [CrossRef]
- Guillo, M.; Dubourg, L. Impact & improvement of tool deviation in friction stir welding: Weld quality & real-time compensation on an industrial robot. Robot. Comput. Integr. Manuf. 2016, 39, 22–31. [Google Scholar] [CrossRef]
- Lin, J.; Ye, C.; Yang, J.; Zhao, H.; Ding, H.; Luo, M. Contour error-based optimization of the end-effector pose of a 6 degree-of-freedom serial robot in milling operation. Robot. Comput. Manuf. 2022, 73, 102257. [Google Scholar] [CrossRef]
- Chen, L.; Tan, J.; Wu, T.; Tan, Z.; Yuan, G.; Yang, Y.; Liu, C.; Zhou, H.; Xie, W.; Xiu, Y.; et al. An Optimization Method for Multi-Robot Automatic Welding Control Based on Particle Swarm Genetic Algorithm. Machines 2024, 12, 763. [Google Scholar] [CrossRef]
- Zong, G.; Kang, C.; Chen, S.; Jiang, X. Optimization of installation position for complex space curve weldments in robotic friction stir welding based on dynamic dual particle swarm optimization. Processes 2024, 12, 536. [Google Scholar] [CrossRef]
- Lukić, B.; Knežević, N.; Jovanović, K. Robot’s Cartesian Stiffness Adjustment Through the Stiffness Ellipsoid Shaping. In Advances in Service and Industrial Robotics; Petrič, T., Ude, A., Žlajpah, L., Eds.; RAAD 2023; Mechanisms and Machine Science; Springer: Cham, Switzerland, 2023; Volume 135. [Google Scholar]
- Lemos, G.V.B.; Hanke, S.; Dos Santos, J.F.; Bergmann, L.; Reguly, A.; Strohaecker, T.R. Progress in friction stir welding of Ni alloys. Sci. Technol. Weld. Join. 2017, 22, 643–657. [Google Scholar] [CrossRef]
- Abbasi, M.; Bagheri, B.; Sharifi, F. Simulation and experimental study of dynamic recrystallization process during friction stir vibration welding of magnesium alloys. Trans. Nonferrous Met. Soc. China 2021, 31, 2626–2650. [Google Scholar] [CrossRef]
- De Backer, J.; Christiansson, A.; Oqueka, J.; Bolmsjö, G. Investigation of path compensation methods for robotic friction stir welding. Ind. Robot. Int. J. Robot. Res. Appl. 2012, 39, 601–608. [Google Scholar] [CrossRef]
- Ni, H.P.; Ji, S.; Ye, Y.X. Redundant Posture Optimization for 6R Robotic Milling Based on Piecewise-Global-Optimization-Strategy Considering Stiffness, Singularity and Joint-Limit. Symmetry 2022, 14, 2066. [Google Scholar] [CrossRef]
- Yue, W.; Liu, H.; Huang, T. An Approach for Predicting Stiffness of a 5-DOF Hybrid Robot for Friction Stir Welding. Mech. Mach. Theory 2022, 175, 104941. [Google Scholar] [CrossRef]
- Zhang, Y.M.; Yang, Y.-P.; Zhang, W.; Na, S.-J. Advanced welding manufacturing: A brief analysis and review of challenges and solutions. J. Manuf. Sci. Eng. 2020, 142, 110816. [Google Scholar] [CrossRef]
- Dumas, C.; Caro, S.; Garnier, S.; Furet, B. Joint stiffness identification of six-revolute industrial serial robots. Robot. Comput. Manuf. 2011, 27, 881–888. [Google Scholar] [CrossRef]
- Lukić, B.; Jovanović, K. Maximizing the End-Effector Cartesian Stiffness Range for Kinematic Redundant Robot with Compliance. In Advances in Service and Industrial Robotics; Petrič, T., Ude, A., Žlajpah, L., Eds.; RAAD 2023; Mechanisms and Machine Science; Springer: Cham, Switzerland, 2023; Volume 135. [Google Scholar]
- Sun, L.; Fang, L. An approximation method for stiffness calculation of robotic arms with hybrid open- and closed-loop kinematic chains. Adv. Mech. Eng. 2018, 10, 1–12. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, H.Y.; Chen, Y.H.; Chen, B.-G. Effect of Ni interlayer on microstructure and properties of TC4/2A14 dissimilar metal joints welded by friction stir welding. J. Netshape Form. Eng. 2023, 15, 140–146. [Google Scholar]
- Han, Y.; Chen, S.; Jiang, X.; Bai, Y.; Yuan, T.; Wang, X. Effect of microstructure, texture and deformation behavior on tensile properties of electrically assisted friction stir welded Ti-6Al-4V joints. Mater. Charact. 2021, 176, 111141. [Google Scholar] [CrossRef]
- Zhao, J.; Duan, Y.; Xie, B.; Zhang, Z. FSW robot system dimensional optimization and trajectory planning based on soft stiffness indices. J. Manuf. Process. 2021, 63, 88–97. [Google Scholar] [CrossRef]
- Xiao, J.; Wang, N.; Liu, H.; Yue, W.; Wang, J.; Zhao, H.; Gao, J. Optimization method of position of robot friction stir welding parts based on optimal stiffness interval. Aeronaut. Manuf. Technol. 2023, 66, 22–31. [Google Scholar]
- Li, Z.; Zhao, H.; Zhang, X.; Dong, J.; Hu, L.; Gao, H. Multi-parameter sensing of robotic friction stir welding based on laser circular scanning. J. Manuf. Process. 2023, 89, 92–104. [Google Scholar] [CrossRef]
- Knežević, N.; Lukić, B.; Petrič, T.; Jovanovič, K. A Geometric Approach to Task-Specific Cartesian Stiffness Shaping. J. Intell. Robot. Syst. 2024, 110, 14. [Google Scholar] [CrossRef]
- GholamiOmali, A.; Alizadeh, M.; Sadedel, M. Simulation and kinematic analysis of a 3-DOF marine antenna pedestal focusing on singularity avoidance and its effects on angular velocity and angular acceleration. Sci. Rep. 2024, 14, 28373. [Google Scholar] [CrossRef] [PubMed]
| Joint | Joint Stiffness (N·m/rad) |
|---|---|
| 1 | 1.14 × 107 |
| 2 | 8.89 × 106 |
| 3 | 8.21 × 106 |
| 4 | 7.44 × 106 |
| 5 | 3.67 × 106 |
| 6 | 2.35 × 106 |
| Variable Symbol | Variable Meaning | Relevant Formulas and Explanations |
|---|---|---|
| Cartesian stiffness matrix of the robot end-effector | (Formula (1)). It is used to describe the stiffness characteristics of the robot end-effector in the Cartesian coordinate system. The elements represent the relationships between forces and displacements in different directions. | |
| Robot joint stiffness matrix | Involved in establishing the robot joint stiffness model, it is the matrix representation of the robot joint stiffness. It is constructed by obtaining joint stiffness values through static identification experiments. | |
| Robot Jacobian matrix | When calculating the Cartesian stiffness matrix, it is used to describe the mapping relationship between the robot joint space and the Cartesian space and is an important part of the formula . | |
| Force–displacement stiffness sub-matrix | It is a sub-matrix of the Cartesian stiffness matrix (Formula (2)), composed of the first 3 rows and 3 columns of . It is used to describe the stiffness relationship between forces and linear displacements and is mainly considered when establishing the stiffness ellipsoid. | |
| Force–angular displacement stiffness sub-matrix | A sub-matrix of the Cartesian stiffness matrix (Formula (2)), which describes the stiffness relationship between forces and angular displacements. | |
| Torque–displacement stiffness sub-matrix | A sub-matrix of the Cartesian stiffness matrix (Formula (2)), reflecting the stiffness relationship between torques and linear displacements. | |
| Torque–angular displacement stiffness sub-matrix | A sub-matrix of the Cartesian stiffness matrix (Formula (2)), representing the stiffness relationship between torques and angular displacements. | |
| Linear displacement of the robot end-effector along the , , and axes | In the formula (Formula (3)), it is used to describe the relationship between the linear displacement of the robot end-effector in the Cartesian coordinate system and the force–displacement stiffness sub-matrix. | |
| Angular displacement of the robot end-effector around the , , and axes | In the definitions and formulas of relevant stiffness sub-matrices, it is used to describe the relationship between the angular displacement of the robot end-effector and the stiffness sub-matrices. For example, in Formula (2), it reflects its connection with the torque–angular displacement stiffness sub-matrix, etc. | |
| , , | Semi-axis lengths of the stiffness ellipsoid along the , , and axes | In the formula (Formula (4)), they are used to determine the shape and size of the stiffness ellipsoid. Their values are obtained from the eigenvalues of the real-symmetric matrix , reflecting the stiffness characteristics of the robot end-effector in different directions. |
| , , | Eigenvectors corresponding to the eigenvalues of the real-symmetric matrix | They represent the vector directions of the semi-axes of the stiffness ellipsoid, corresponding to , , and , and determine the orientation of the stiffness ellipsoid in space. |
| , , | Direction cosines of the unit normal vector of the tangent plane of the welding surface | They are used to map the stiffness ellipsoid to the tangent plane of the welding surface to analyze the actual stiffness characteristics of the robot during the welding process. |
| , , | Stiffness direction quantities related to the new stiffness index | In the formula for constructing the new stiffness index |
| New stiffness index based on the improved stiffness ellipsoid | Used to evaluate the performance of the robot during the friction stir welding process. The formula | |
| Objective function of the collaborative motion control model | In the collaborative motion control model, (Formula (7)). The maximum value of the new stiffness index is taken as the goal, and the optimal collaborative motion of the robot and the positioner is determined by solving this objective function. | |
| Robot joint angle | In the collaborative motion control model, it is one of the decision variables. It is related to the joint angles of the positioner. For example, (Formula (8)) indicates that the robot joint angle is a function of the positioner joint angles, reflecting the relationship of their collaborative motion. | |
| , | Positioner joint angles | They are the decision variables of the collaborative motion control model, used to describe the motion state of the positioner. The robot joint angle is a function of them, jointly determining the collaborative motion of the robot and the positioner. |
| Pose information of the weld joint in the robot base coordinate system | In the formula (Formula (8)), it is used to determine the relationship between the robot joint angle and the pose of the weld joint, playing a key role in the collaborative motion control of the robot and the positioner. | |
| Fitness function of the genetic algorithm | When the genetic algorithm is used to solve the collaborative motion control model, (Formula (10)). Based on the new stiffness index , it is used to evaluate the quality of individuals and guide the genetic algorithm to find the optimal solution. | |
| Positioner joint angle vector | (Formula (11)). The two joint angles of the positioner are combined into a vector form for convenient calculation and processing in the genetic algorithm and the collaborative motion control model. |
| Welding Spots | Optimization | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | before | 45.00 | 0 | −1.75 | −15.77 | 48.52 | −4.09 | 37.36 | 8.13 | 2476.6 |
| after | 42.46 | 0.75 | −3.01 | −14.82 | 55.02 | 6.32 | 37.81 | −15.77 | 2902.4 | |
| 2 | before | 45.00 | 0 | −3.24 | −25.76 | 60.05 | −10.37 | 27.21 | 4.86 | 2231.7 |
| after | 24.89 | 6.52 | −2.31 | −14.49 | 52.43 | −0.53 | 35.61 | −10.51 | 2792.4 | |
| 3 | before | 45.00 | 0 | −11.35 | −22.33 | 65.51 | −50.67 | 25.73 | 13.27 | 1847.1 |
| after | 6.67 | 10.29 | −1.21 | −14.21 | 50.15 | −5.48 | 34.41 | 15.64 | 3215.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, C.; Jia, H.; Zhao, E.; Ma, C. Development of an Improved Stiffness Ellipsoid Method for Precise Robot-Positioner Collaborative Control in Friction Stir Welding. Materials 2025, 18, 1852. https://doi.org/10.3390/ma18081852
Kang C, Jia H, Zhao E, Ma C. Development of an Improved Stiffness Ellipsoid Method for Precise Robot-Positioner Collaborative Control in Friction Stir Welding. Materials. 2025; 18(8):1852. https://doi.org/10.3390/ma18081852
Chicago/Turabian StyleKang, Cunfeng, Haonan Jia, Eryang Zhao, and Chunmin Ma. 2025. "Development of an Improved Stiffness Ellipsoid Method for Precise Robot-Positioner Collaborative Control in Friction Stir Welding" Materials 18, no. 8: 1852. https://doi.org/10.3390/ma18081852
APA StyleKang, C., Jia, H., Zhao, E., & Ma, C. (2025). Development of an Improved Stiffness Ellipsoid Method for Precise Robot-Positioner Collaborative Control in Friction Stir Welding. Materials, 18(8), 1852. https://doi.org/10.3390/ma18081852






