Mesoscopic Perspective into the High-Temperature Triaxial Dilation of Asphalt Mixtures via PFC–FLAC Coupled Simulation
Abstract
1. Introduction
2. Materials and Experimental Method
2.1. Materials
2.2. Triaxial Testing
3. Discrete and Finite Element Modeling
3.1. Virtual Specimen
3.2. Boundary Condition and the Coupled Model
3.3. Contact Model and Parameters
3.4. Loading Conditions
4. Results and Discussion
4.1. Test Results and Model Verification
4.2. Aggregate Movement Characteristics
4.3. Crack Analysis
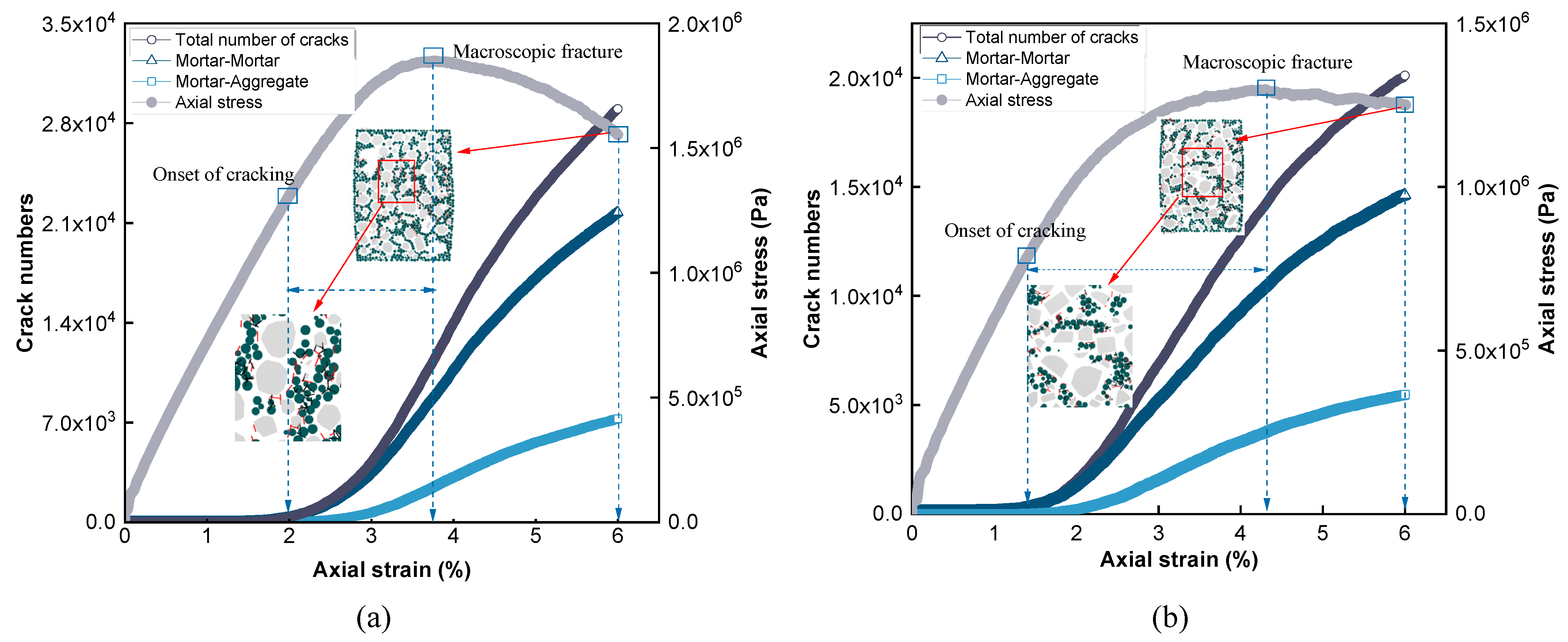
4.3.1. Crack Development
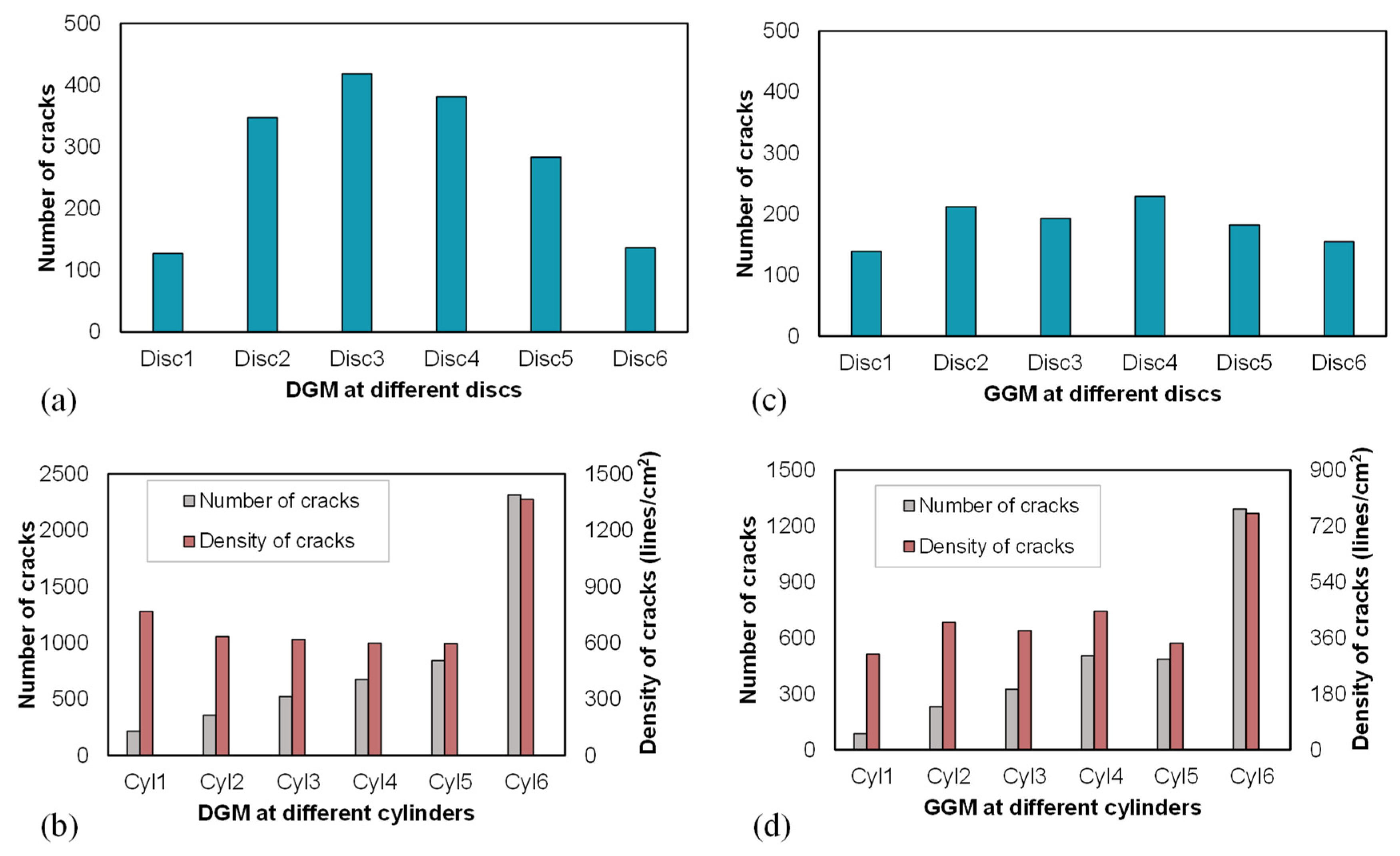
4.3.2. Crack Distribution
4.4. Contact Analysis
4.4.1. Tensile and Compressive Contacts
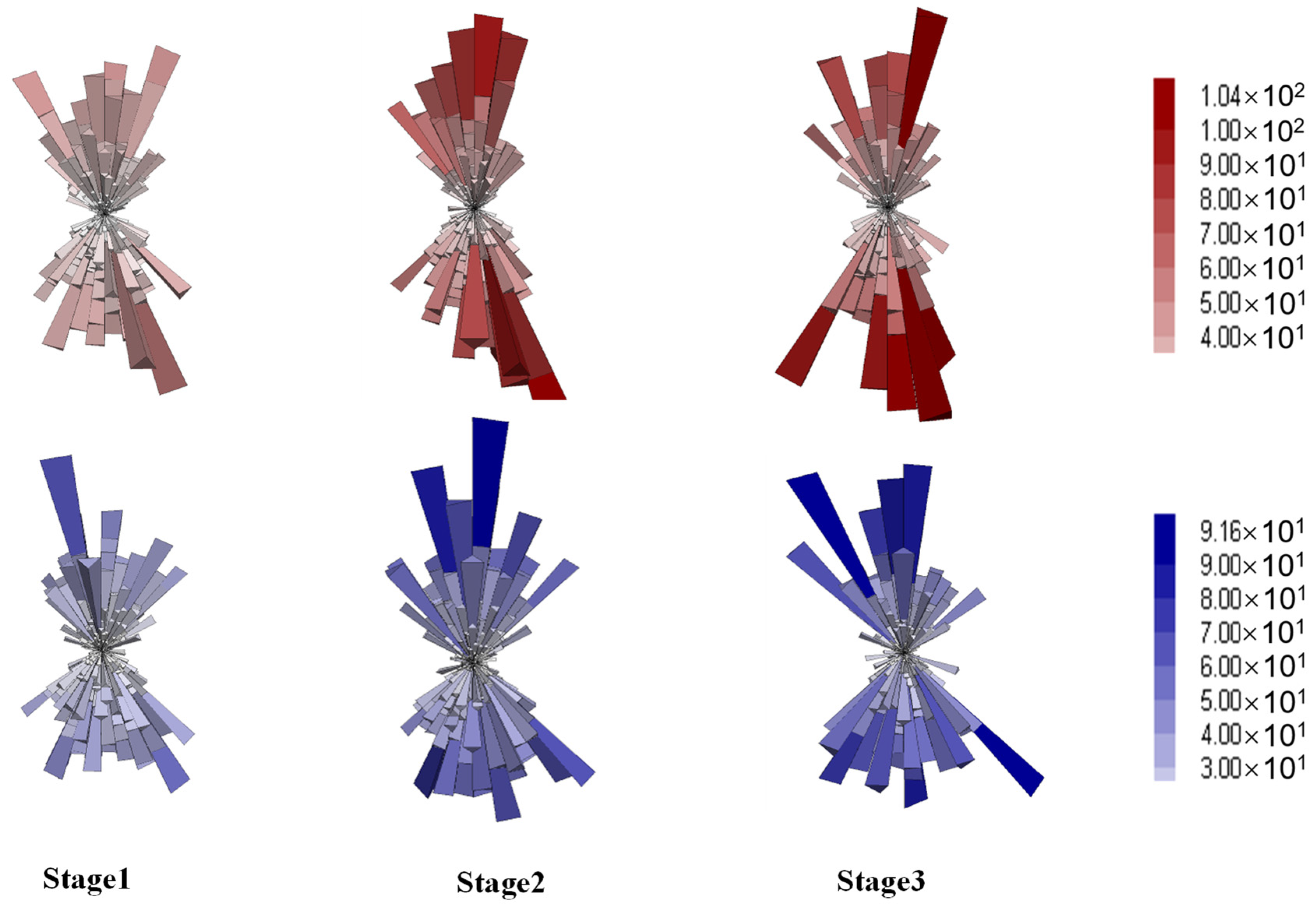
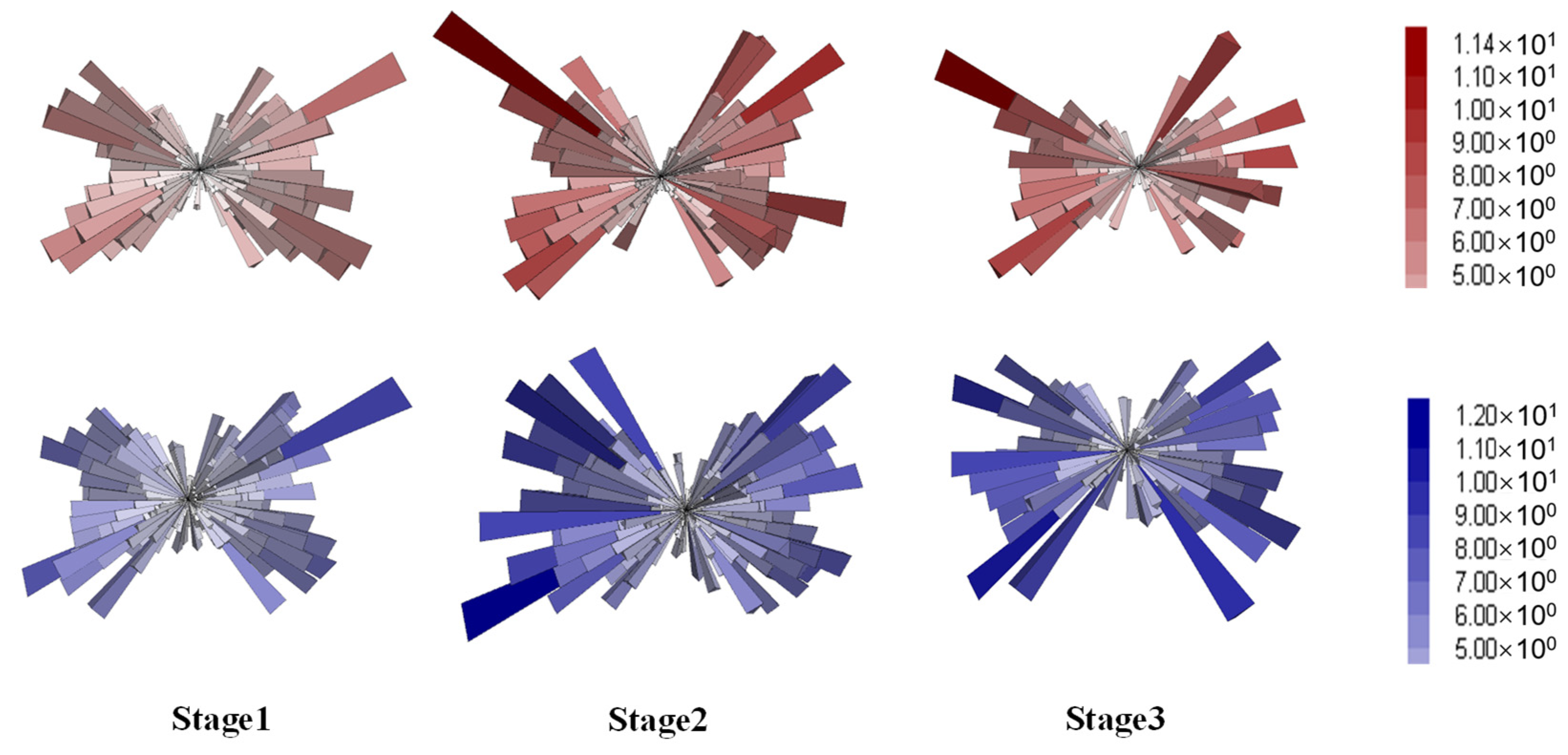
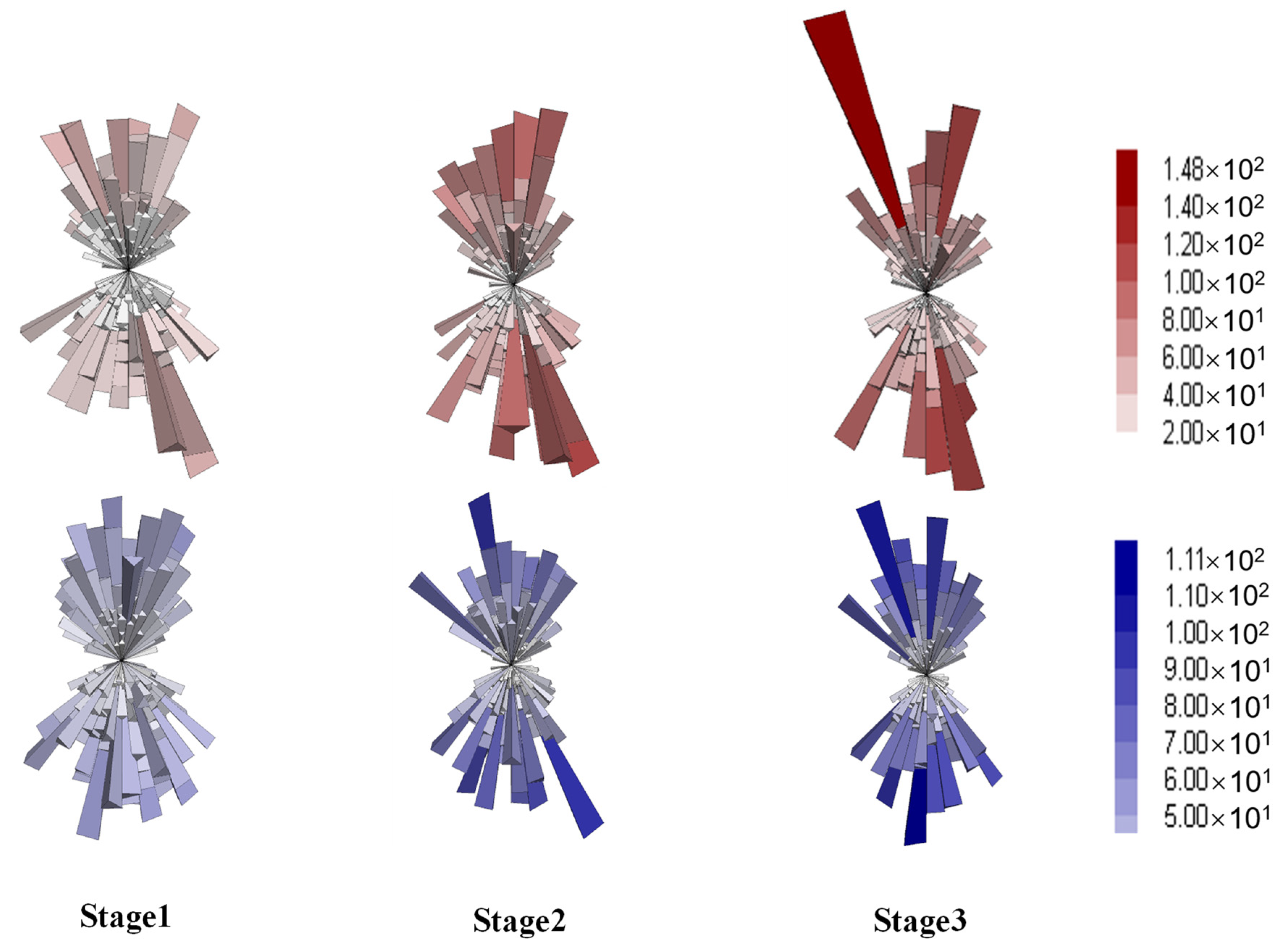
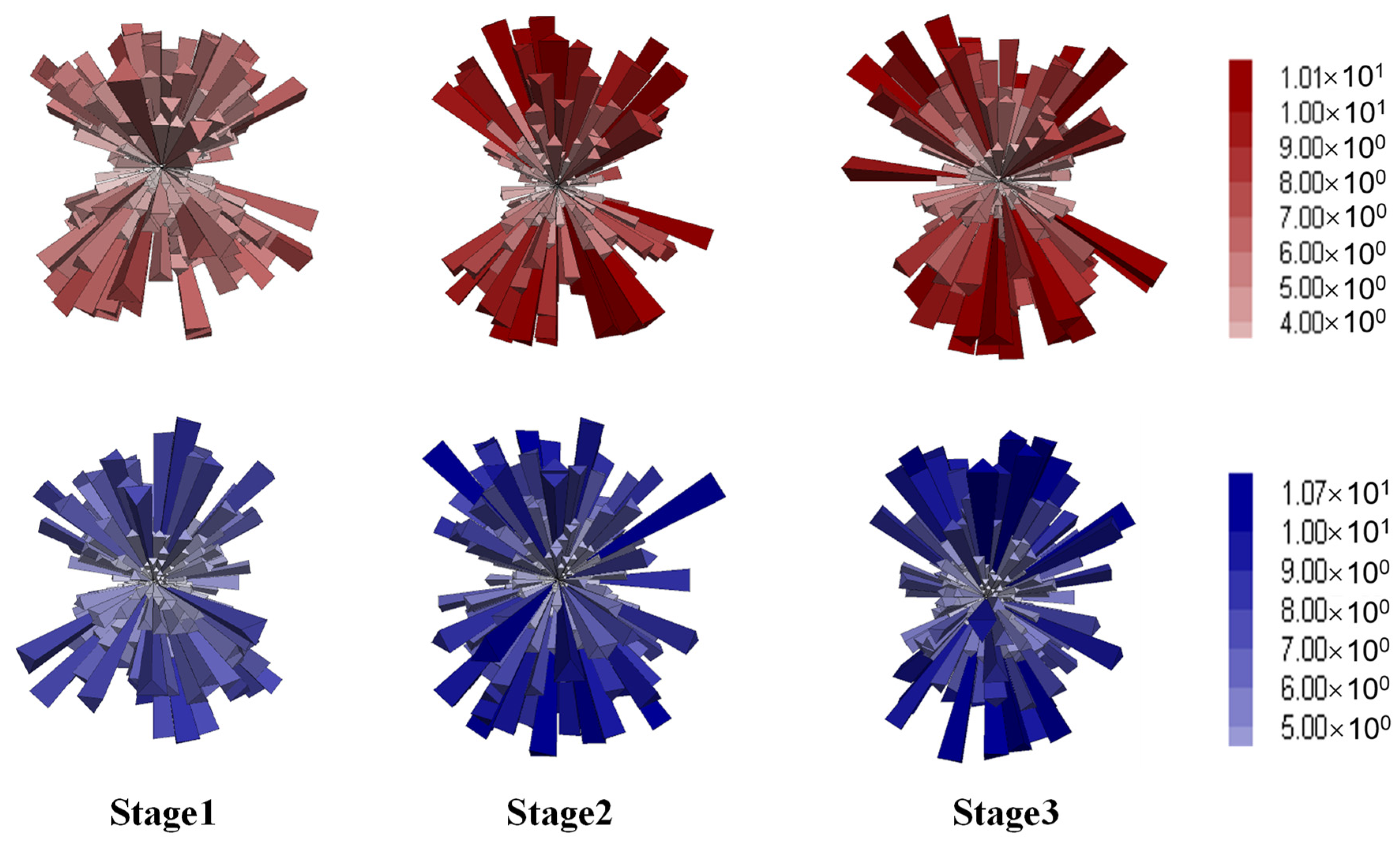
4.4.2. Anisotropy of Contact Forces
5. Conclusions
- With the same asphalt binder, the gap-graded mixture yielded lower strengths in the experiment at all confining pressures considered, which was attributed to its higher binder content (as required by the gap gradation) not being compensated for by enhanced viscosity.
- Compared to the dense-graded mixture, GGM entered the post-peak softening phase at a larger strain level; it softened at a much lower rate and exhibited lower volumetric expansion, suggesting a higher structural stability at high temperatures.
- The specimen bulging, which was most prominent around the middle height, was driven by the dominant in-plane or horizontal components of particle rotation and translation. The structural stability of the gap-graded mixture was attributed to its lower magnitudes in both components of particle movements and also to its inclusion of less interfering particles in the size range of 2.36–4.75 mm.
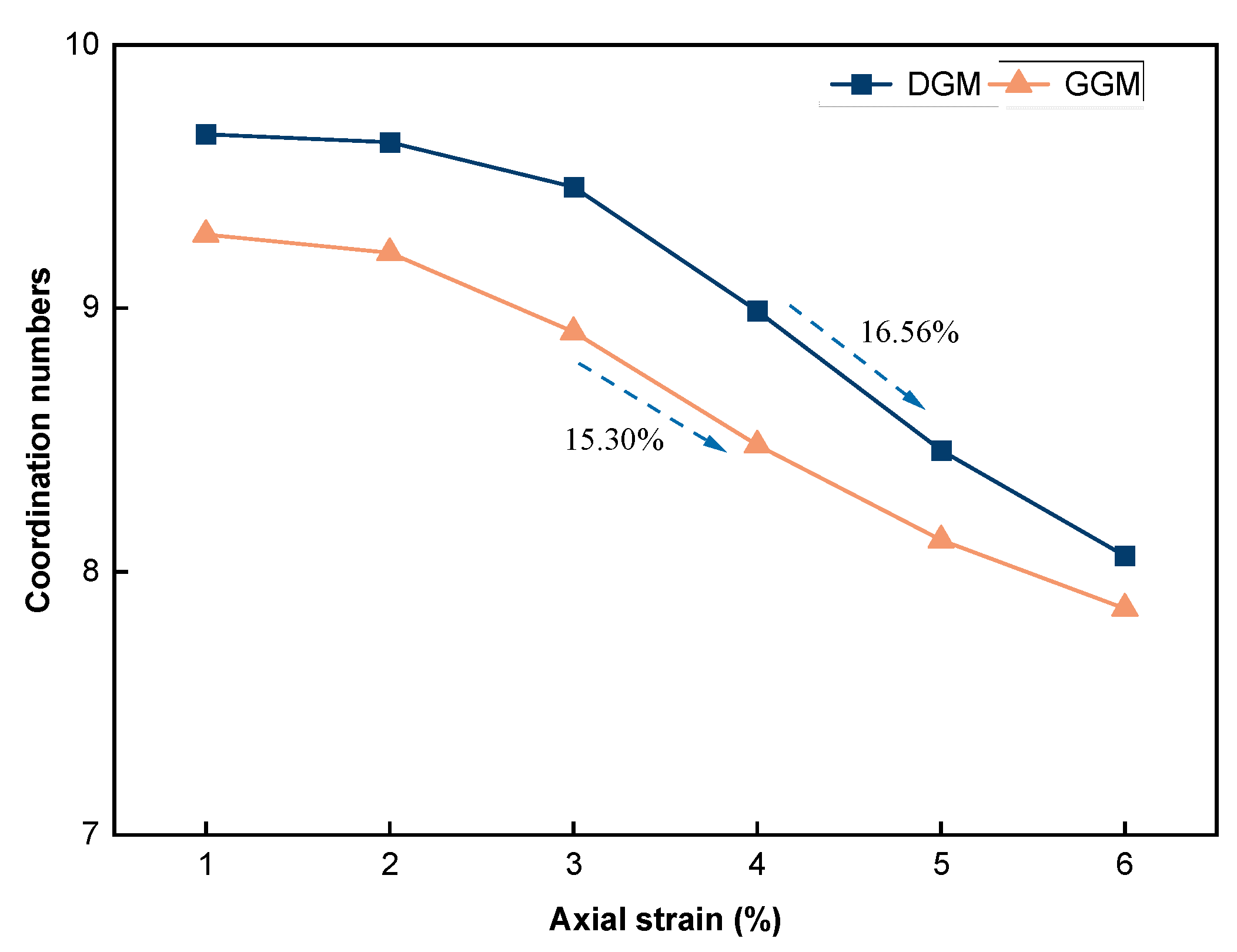
- Contact failure-induced cracks primarily occurred within the mortar phase. The accumulation of cracks and the reduction in coordination number due to contact failures were both faster in the DGM, suggesting a more rapid loss of internal cohesion in agreement with the quicker drop in the axial stress after the peak. The cracks were more concentrated at the middle height and towards the perimeter of the virtual specimens; lower numbers or densities of cracks were noted within the gap-graded mixture.
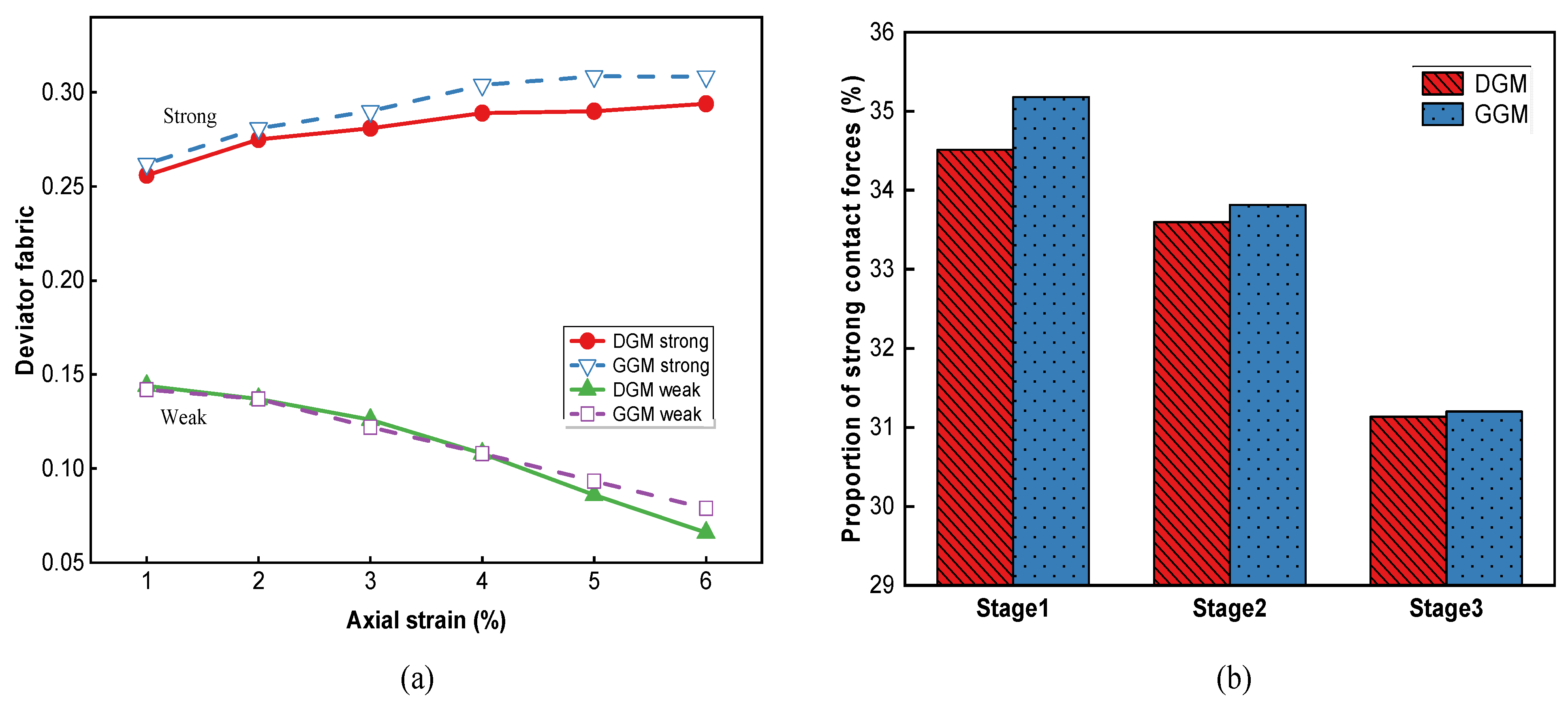
- In both mixtures, the mortar–aggregate interfaces were the major bearer of tensile contact forces, but the average forces and the accumulation of cracks at the interfaces were considerably higher in the DGM. The compressive contact forces were dominated by the inter-aggregate contacts, especially in the case of the GGM; the gap gradation yielded lower and yet more steadily varying compressive forces.
- Anisotropy analysis on the contact forces suggested that the distribution of strong forces was more pertinent to resisting the axial loading, while that of the weak forces was more relevant to the volumetric expansion. It was inferred from the contact anisotropy that the aggregate skeleton played a more significant role in the strength and stability of gap-graded mixtures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lv, J.; Zhang, X. Prediction models of shear parameters and dynamic creep instability for asphalt mixture under different high temperatures. Polymers 2021, 13, 2542. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zhang, Z.; Luo, Y. Inspection method and evaluation standard based on cylindrical core sample for rutting resistance of asphalt pavement. Measurement 2018, 117, 241–251. [Google Scholar] [CrossRef]
- Song, J.; Pellinen, T. Dilation behavior of hot mix asphalt under triaxial loading—A mechanism of permanent deformation generation. Road Mater. Pavement Des. 2007, 8, 103–125. [Google Scholar]
- Chen, X.; Huang, B.; Xu, Z. Uniaxial penetration testing for shear resistance of Hot-Mix asphalt mixtures. Transp. Res. Rec. 2006, 1970, 116–125. [Google Scholar] [CrossRef]
- Walubita, L.; Faruk, A.; Fuentes, L.; Prakoso, A.; Dessouky, S.; Naik, B.; Nyamuhokya, T. Using the Simple Punching Shear Test (SPST) for evaluating the HMA shear properties and predicting field rutting performance. Constr. Build. Mater. 2019, 224, 920–929. [Google Scholar] [CrossRef]
- Huang, T.; Qi, S.; Liu, H.; Yu, H.; Li, S. Shear properties of asphalt mixtures under triaxial compression. Appl. Sci. 2019, 9, 1489. [Google Scholar] [CrossRef]
- Ji, J.; Chen, M.; Suo, Z.; Wei, J.; Wang, J.; Chen, L. Rutting prediction model of asphalt mixture based on the triaxial repeated load test. Adv. Civ. Eng. 2021, 2021, 5238680. [Google Scholar] [CrossRef]
- Orosa, P.; Perez, I.; Pasandin, A. Evaluation of the shear and permanent deformation properties of cold in-place recycled mixtures with bitumen emulsion using triaxial tests. Constr. Build. Mater. 2022, 328, 127054. [Google Scholar] [CrossRef]
- Zhou, F.; Chen, D.; Scullion, T.; Bilyeu, J. Case study: Evaluation of laboratory test methods to characterize permanent deformation properties of asphalt mixes. Int. J. Pavement Eng. 2003, 4, 155–164. [Google Scholar] [CrossRef]
- Gu, X.; Zhang, X.; Lv, J. Establishment and verification of prediction models of creep instability points of asphalt mixtures at high temperatures. Constr. Build. Mater. 2018, 171, 303–311. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, J. Experimental and numerical Investigation of dilation behavior of asphalt mixture. Int. J. Geomech. 2017, 17, 04016062. [Google Scholar] [CrossRef]
- Gu, X.; Dong, Q.; Yuan, Q. Development of an innovative uniaxial compression test to evaluate permanent deformation of asphalt mixtures. J. Mater. Civ. Eng. 2015, 27, 04014104. [Google Scholar] [CrossRef]
- Liu, Z.; Gu, X.; Ren, H. Rutting prediction of asphalt pavement with semi-rigid base: Numerical modeling on laboratory to accelerated pavement testing. Constr. Build. Mater. 2023, 375, 130903. [Google Scholar] [CrossRef]
- Jiang, Y.; Zhang, Y.; Yi, Y.; Tian, T.; Fan, J.; Xue, J. Study of shear strength and gradation optimization of asphalt mixture based on uniaxial penetration numerical test. Constr. Build. Mater. 2023, 397, 132398. [Google Scholar] [CrossRef]
- Dan, H.; Zhang, Z.; Chen, J.; Cao, W. Low-temperature fracture characteristics of asphalt mixtures using the eccentric single-edge notched bend test: A 3D discrete element study. Constr. Build. Mater. 2022, 344, 128182. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, E.; Li, N.; Wang, L.; Si, C.; Wang, C. Micromechanical analysis of the rutting evolution of asphalt pavement under temperature-stress coupling based on the discrete element method. Constr. Build. Mater. 2022, 325, 126800. [Google Scholar] [CrossRef]
- Xue, B.; Xu, J.; Pei, J.; Zhang, J.; Li, R. Investigation on the micromechanical response of asphalt mixture during permanent deformation based on 3D virtual wheel tracking test. Constr. Build. Mater. 2021, 267, 121031. [Google Scholar] [CrossRef]
- Wang, H.; Zhou, Z.; Huang, W.; Dong, X. Investigation of asphalt mixture permanent deformation based on three-dimensional discrete element method. Constr. Build. Mater. 2021, 272, 121808. [Google Scholar] [CrossRef]
- Peng, Y.; Xu, Y.; Zhang, X.; Meng, H.; Lu, X. Investigation on the effects of asphalt mixes and their combinations on asphalt mix shear strength by 3D discrete element method. Int. J. Pavement Eng. 2023, 24, 2251078. [Google Scholar] [CrossRef]
- Zou, X.; Xie, Y.; Bi, Y.; Li, B.; Wang, W.; Ye, X. Study on the shear strength of asphalt mixture by discrete element modeling with coarse aggregate morphology. Constr. Build. Mater. 2023, 409, 134058. [Google Scholar] [CrossRef]
- Zhou, C.; Zhang, M.; Li, Y.; Lu, J.; Chen, J. Influence of particle shape on aggregate mixture’s performance: DEM results. Road Mater. Pavement Des. 2019, 20, 399–413. [Google Scholar] [CrossRef]
- Collop, A.; McDowell, G.; Lee, Y. Modelling dilation in an idealised asphalt mixture using discrete element modelling. Granul. Matter 2006, 8, 175–184. [Google Scholar] [CrossRef]
- Fan, J.; Jiang, Y.; Yi, Y.; Tian, T.; Yuan, K.; Deng, C. Investigation on triaxial numerical test method and dilatancy behavior of asphalt mixture. Constr. Build. Mater. 2022, 316, 125815. [Google Scholar] [CrossRef]
- Li, S.; Smith, A. Acoustic emission and energy dissipation in soils during triaxial shearing. Comput. Geotech. 2023, 162, 105639. [Google Scholar] [CrossRef]
- Ge, H.; Quezada, J.C.; Le Houerou, V.; Chazallon, C. Three-dimensional FEM-DEM coupling simulation for analysis of asphalt mixture responses under rolling tire loads. Constr. Build. Mater. 2023, 369, 130615. [Google Scholar] [CrossRef]
- Liu, P.; Wang, C.; Lu, W.; Moharekpour, M.; Oeser, M.; Wang, D. Development of an FEM-DEM model to investigate preliminary compaction of asphalt pavements. Buildings 2022, 12, 932. [Google Scholar] [CrossRef]
- Hu, S.; Jin, X.; Sun, G.; Li, H.; Nie, Z. Triaxial test and PFC-FLAC coupling simulation study on material parameters and deformation characteristics of soil-rock mixture. Chin. J. Rock Mech. Eng. 2021, 40 (Suppl. 2), 3344–3356. [Google Scholar]
- Xiao, Y.; Wang, X.; Yu, Q.; Hua, W.; Chen, X. Discrete element modeling of shear strength evolution characteristics of unbound permeable aggregate base material. China J. Highw. Transp. 2023, 36, 52–68. [Google Scholar]
- JTG E20-2011; Standard Test Methods of Bitumen and Bituminous Mixtures for Highway Engineering. Ministry of Transport of the People’s Republic of China and China Communications Press: Beijing, China, 2011; pp. 189–194.
- JTG F40-2004; Technical Specification for Construction of Highway Asphalt Pavement. Ministry of Transport of the People’s Republic of China and China Communications Press: Beijing, China, 2004; pp. 17–18.
- Itasca Consulting Group. PFC 6.0 Documentation; Itasca Consulting Group: Minneaplois, MN, USA, 2019; Available online: https://docs.itascacg.com/pfc600/pfc/docproject/index.html (accessed on 1 August 2024).
- Zhao, L.; Zhang, S.; Huang, D.; Wang, X.; Zhang, Y. 3D shape quantification and random packing simulation of rock aggregates using photogrammetry-based reconstruction and discrete element method. Constr. Build. Mater. 2020, 262, 119986. [Google Scholar] [CrossRef]
- Khattak, M.; Khattab, A.; Rizvi, H.; Bhuyan, M. Imaged-based discrete element modeling of hot mix asphalt mixtures. Mater Struct 2015, 48, 2417–2430. [Google Scholar] [CrossRef]
- Pouranian, M.; Shishehbor, M.; Haddock, J. Impact of the coarse aggregate shape parameters on compaction characteristics of asphalt mixtures. Powder Technol. 2020, 363, 369–386. [Google Scholar] [CrossRef]
- Zhu, X.; Yu, H.; Qian, G.; Yao, D.; Dai, W.; Zhang, H.; Li, J.; Zhong, H. Evaluation of asphalt mixture micromechanical behavior evolution in the failure process based on discrete element method. Case Stud. Constr. Mater. 2023, 18, e01773. [Google Scholar] [CrossRef]
- Ma, T.; Zhang, D.; Zhang, Y.; Hong, J. Micromechanical response of aggregate skeleton within asphalt mixture based on virtual simulation of wheel tracking test. Constr. Build. Mater. 2016, 111, 153–163. [Google Scholar] [CrossRef]
- Liu, Y.; You, Z. Visualization and simulation of asphalt concrete with randomly generated three-dimensional models. J. Comput. Civ. Eng. 2009, 23, 340–347. [Google Scholar] [CrossRef]
- Meng, X.; Liu, Y.; Ning, Z.; Dong, J.; Liang, G. Experimental Investigation of the Size Effect on Roller-Compacted Hydraulic Asphalt Concrete under Different Strain Rates of Loading. Materials 2024, 17, 353. [Google Scholar] [CrossRef]
- Zhao, P.; Shi, S.; Lu, W.; Lv, S.; Chen, Q.; Duan, H.; Yang, Y. Analysis of strength size effect and failure mechanism of asphalt mixtures based on discrete element method. Case Stud. Constr. Mater. 2024, 21, e03482. [Google Scholar] [CrossRef]
- Le, J.; Hendrickson, R.; Marasteanu, M.; Turos, M. Use of fine aggregate matrix for computational modeling of low temperature fracture of asphalt concrete. Mater Struct 2018, 51, 152. [Google Scholar] [CrossRef]
- Xia, C.; Liu, Z.; Zhou, C. Burger’s bonded model for distinct element simulation of the multi-factor full creep process of soft rock. J. Mar. Sci. Eng. 2021, 9, 945. [Google Scholar] [CrossRef]
- Si, C.; Zhou, X.; You, Z.; He, Y.; Chen, E.; Zhang, R. Micro-mechanical analysis of high modulus asphalt concrete pavement. Constr. Build. Mater. 2019, 220, 128–141. [Google Scholar] [CrossRef]
- Yi, X.; Chen, H.; Wang, H.; Tang, Z.; Yang, J.; Wang, H. Cross-Functional test to explore the determination method of meso-parameters in the discrete element model of asphalt mixtures. Materials 2021, 14, 5786. [Google Scholar] [CrossRef]
- Huan, F.; Matteo, P.; Bernhard, H.; Henrik, S. Study of normal and shear material properties for viscoelastic model of asphalt mixture by discrete element method. Constr. Build. Mater. 2015, 98, 366–375. [Google Scholar]
- Liu, Y.; Dai, Q.; You, Z. Viscoelastic model for discrete element simulation of asphalt mixtures. J. Eng. Mech. 2009, 135, 324–333. [Google Scholar] [CrossRef]
- Cao, W.; Kim, Y.R. A triaxial viscoplastic model with temperature dependence for asphalt concrete permanent deformation. Int. J. Appl. Mech. 2022, 14, 2250023. [Google Scholar] [CrossRef]
- Cao, W. Experimental and Analytical Investigations of Permanent Deformation Behavior of Asphalt Mixtures Under Confining Pressure. Ph.D. Thesis, North Carolina State University, Raleigh, NC, USA, 2015. [Google Scholar]
- Wu, W.; Lu, J.; Tu, Z. Influence of gradation segregation on mechanical properties of asphalt mixture skeleton structure based on X-ray CT and discrete element method. Highw. Eng. 2020, 45, 55–61,97. [Google Scholar]
- Tan, Y.; Xing, C.; Ren, J.; Zhang, l. Research on mesostructured characteristics of asphalt mixture based on particle packing theory. China J. Highw. Transp. 2017, 30, 1–8. [Google Scholar]
- Pouranian, M.; Haddock, J. A new framework for understanding aggregate structure in asphalt mixtures. Int. J. Pavement Eng. 2019, 22, 1090–1106. [Google Scholar] [CrossRef]
- Kim, S.; Guarin, A.; Roque, R.; Birgisson, B. Laboratory evaluation for rutting performance based on the DASR porosity of asphalt mixture. Road Mater. Pavement Des. 2008, 9, 421–440. [Google Scholar] [CrossRef]
- Ding, X.; Rath, P.; Giraldo-Londono, O.; Buttlar, W.; Ma, T. Fracture modeling of rubber-modified binder based on Discrete Element Method. J. Clean. Prod. 2022, 380, 135017. [Google Scholar] [CrossRef]
- Song, W.; Xu, F.; Wu, H.; Xu, Z. Investigating the skeleton behaviors of open-graded friction course using discrete element method. Powder Technol. 2021, 385, 528–536. [Google Scholar] [CrossRef]
- Oda, M. Co-ordination number and its relation to shear strength of granular material. Soils Found. 1977, 17, 29–42. [Google Scholar] [CrossRef]
- Liu, G.; Han, D.; Jia, Y.; Zhao, Y. Asphalt mixture skeleton main force chains composition criteria and characteristics evaluation based on discrete element methods. Constr. Build. Mater. 2022, 323, 126313. [Google Scholar] [CrossRef]
- Zhao, S.; Evans, T.; Zhou, X. Three-dimensional Voronoi analysis of monodisperse ellipsoids during triaxial shear. Powder Technol. 2018, 323, 323–336. [Google Scholar] [CrossRef]
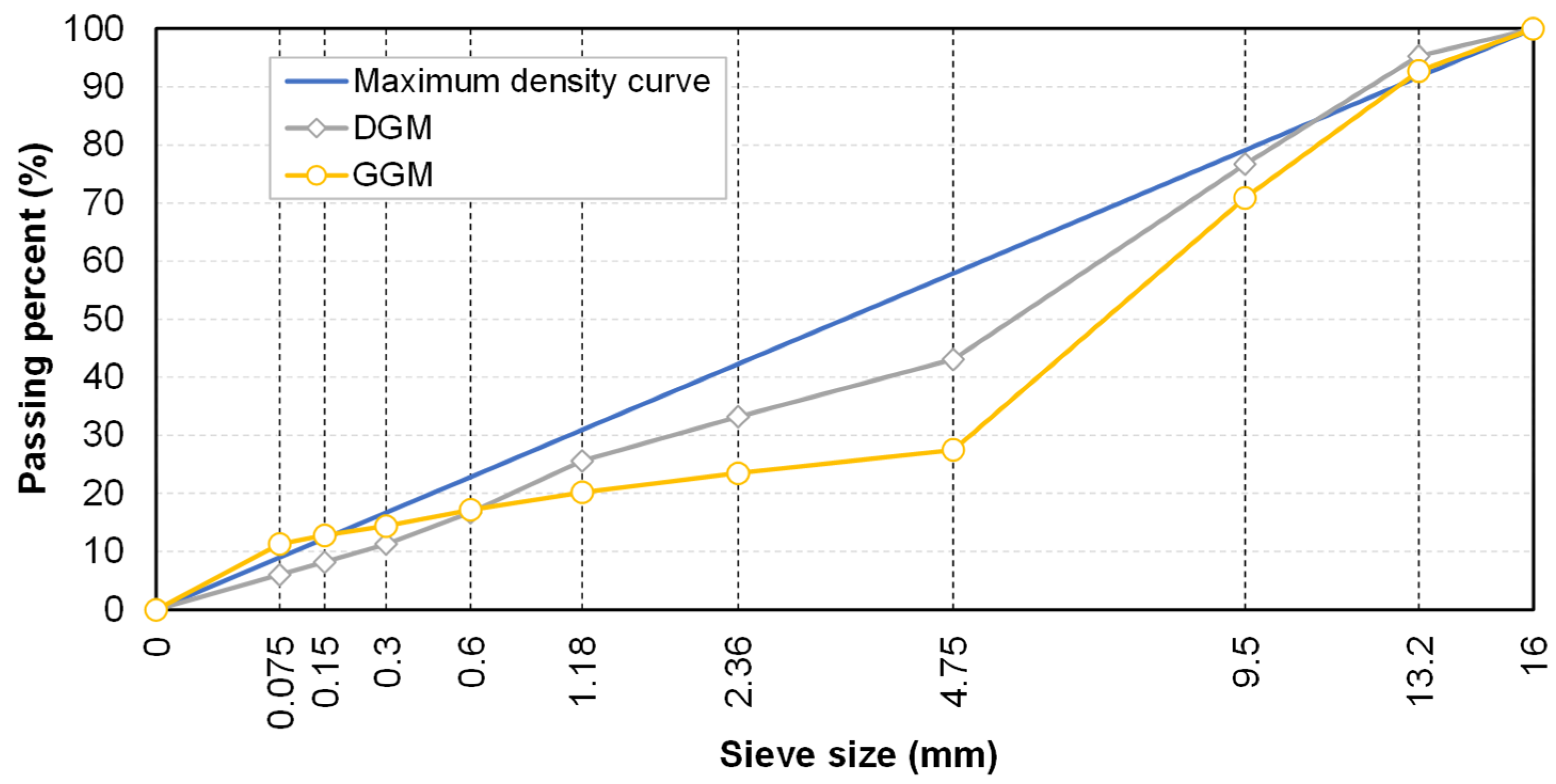
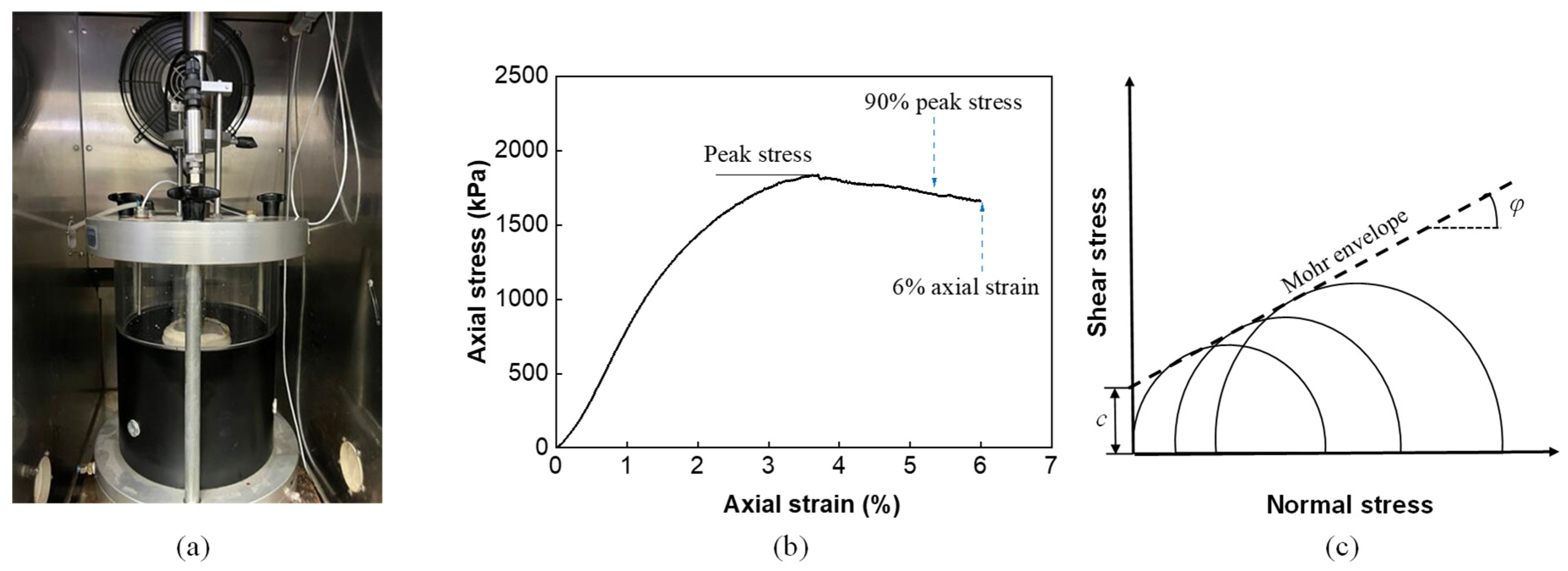
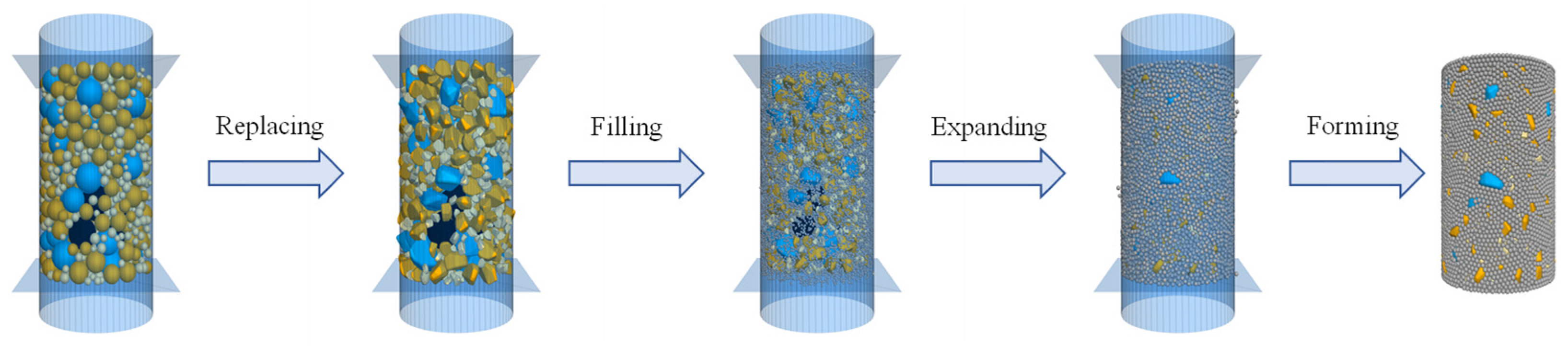
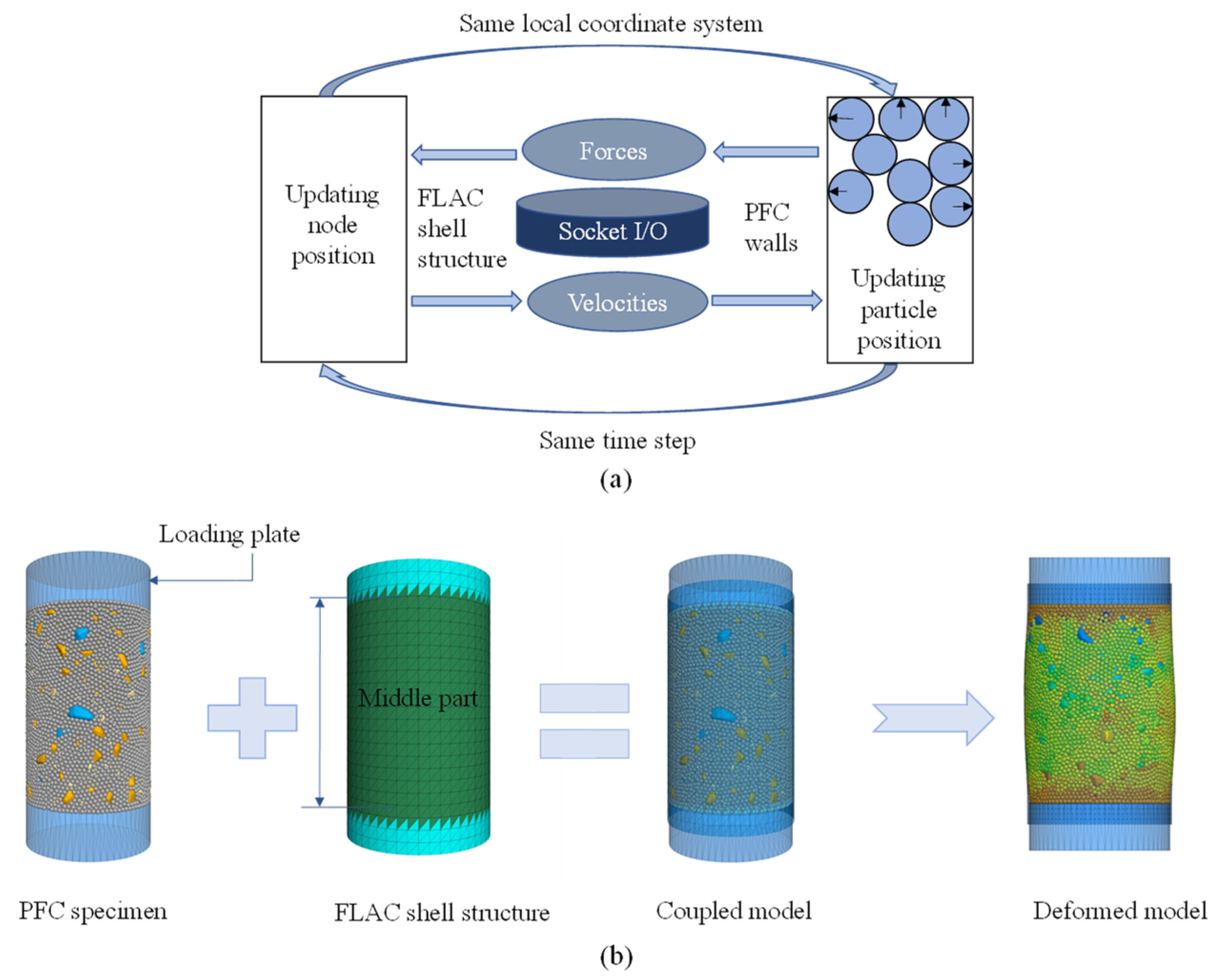
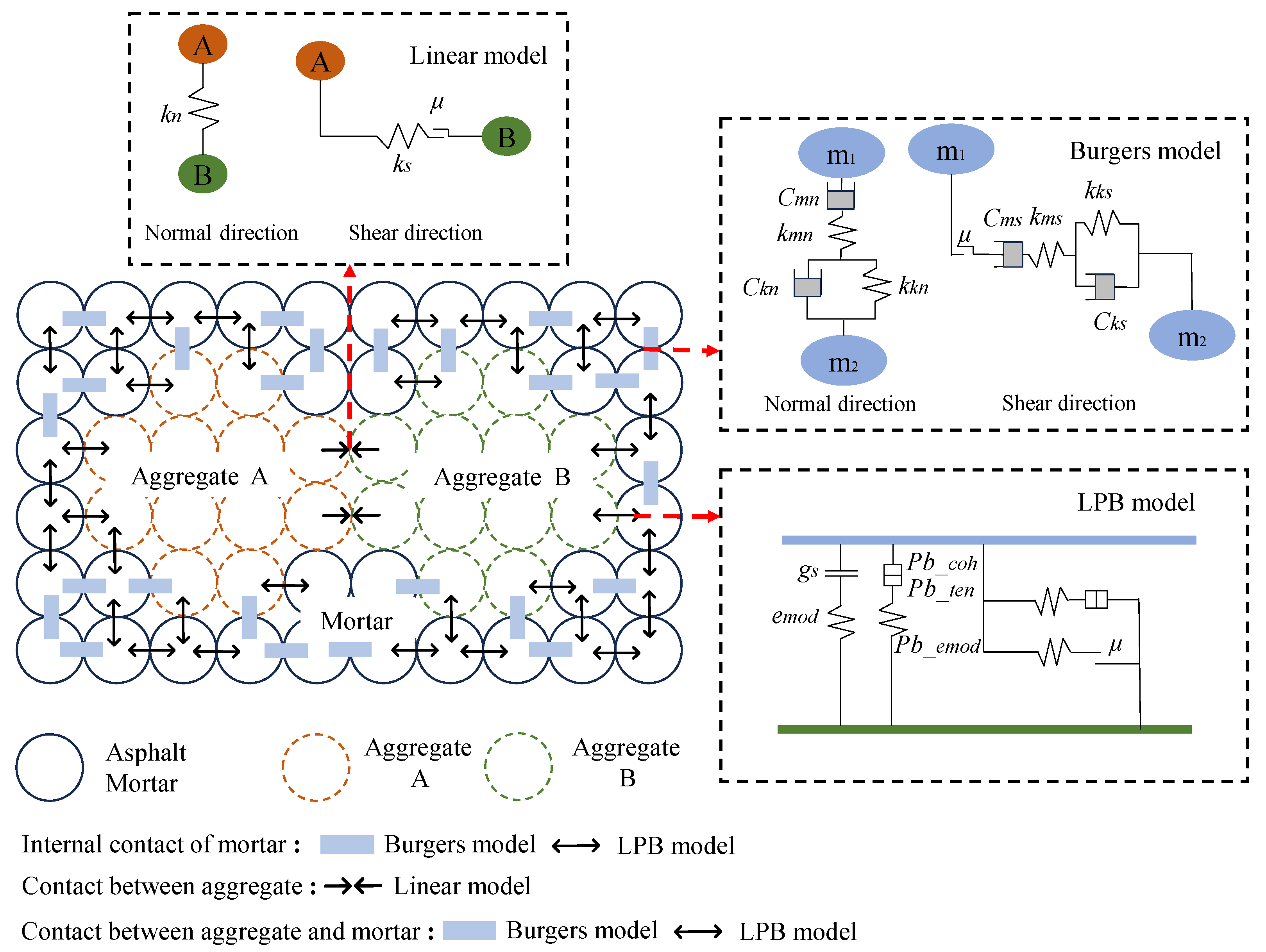
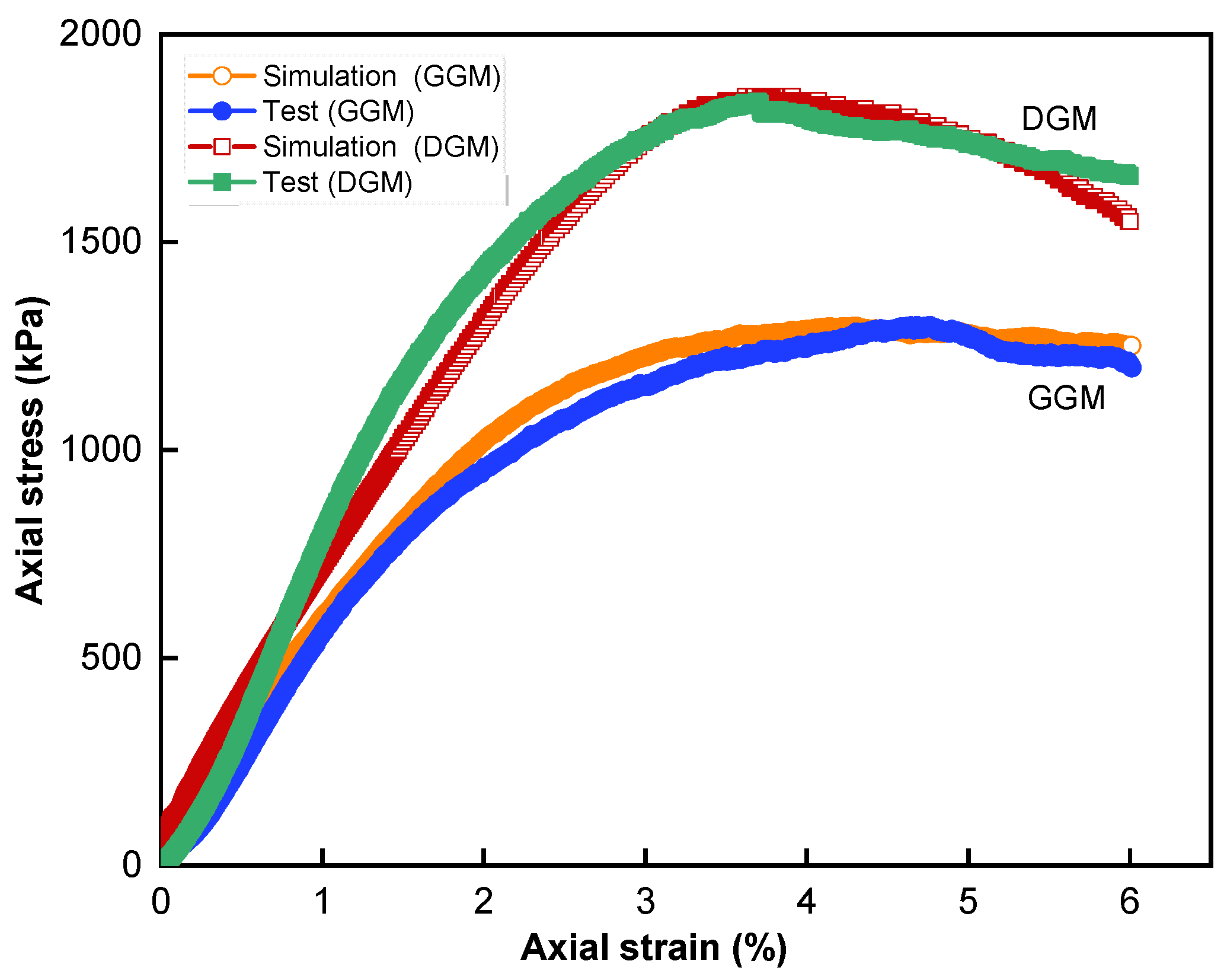
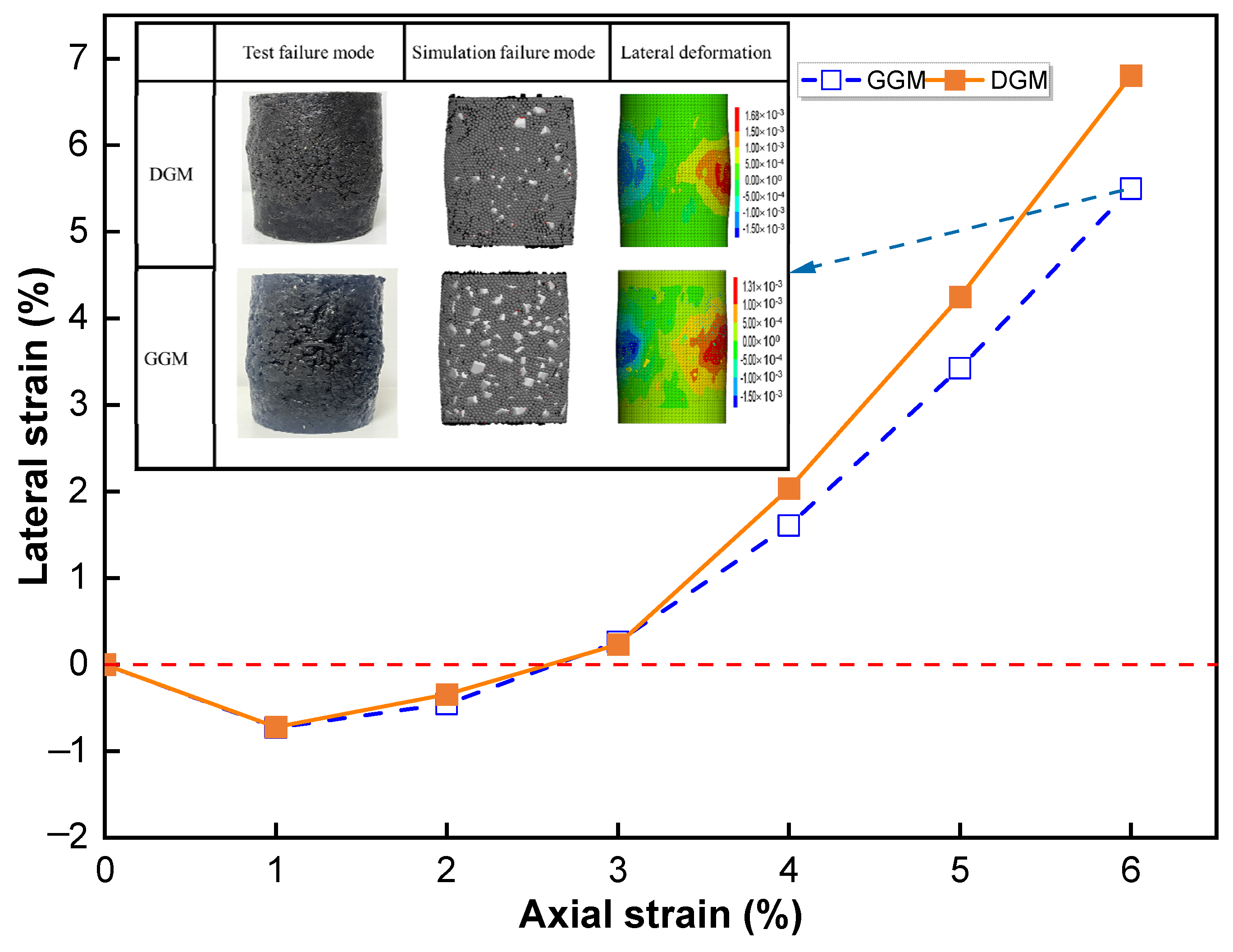

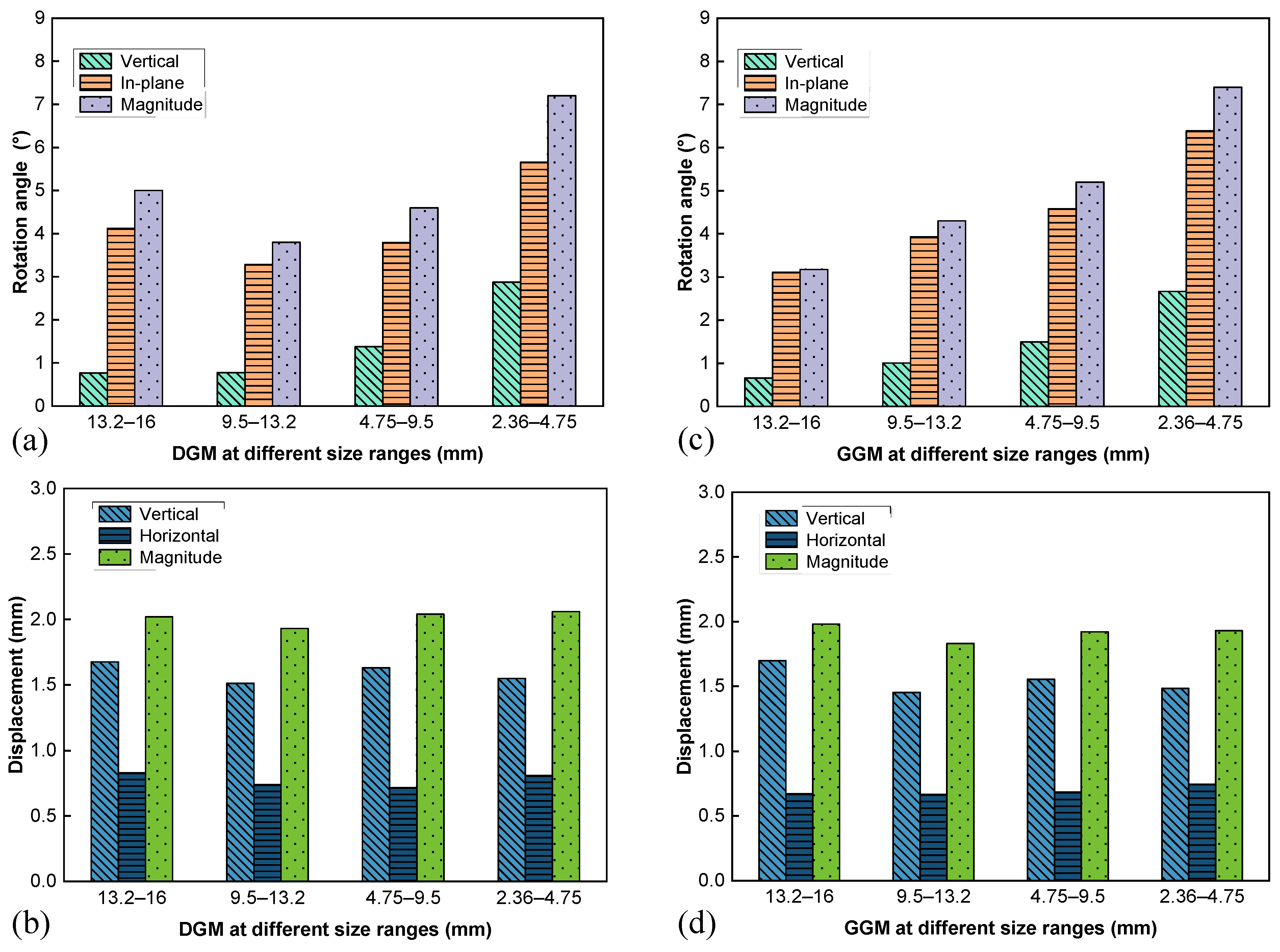


| Properties | Test Methods | Requirements | Measurements |
|---|---|---|---|
| Penetration (0.1 mm) | T0604/JTG E20-2011 [29] | 60–80 | 67.8 |
| Softening point (°C) | T0606/JTG E20-2011 | ≥46 | 47 |
| Ductility (cm) | T0605/JTG E20-2011 | ≥100 | 150 |
| Dynamic viscosity (Pa⋅s) | T0620/JTG E20-2011 | ≥180 | 224 |
| Density (g/cm3) | T0603/JTG E20-2011 | As measured | 1.035 |
| Properties | Sieve Size Ranges (mm) | Requirements | ||
|---|---|---|---|---|
| 0~5 | 5~10 | 10~15 | ||
| Apparent density (g/cm3) | 2.73 | 2.74 | 2.84 | ≥2.6 |
| Crushing value (%) | / | / | 11.1 | ≤26 |
| Water absorption rate (%) | 1.6 | 1.2 | 0.9 | ≤2 |
| Flat and elongated particles (%) | / | 14.6 | 12.8 | ≤18 |
| Model Parameters | Sieve Size Ranges (mm) | |||
|---|---|---|---|---|
| 2.36~4.75 | 4.75~9.5 | 9.5~13.2 | 13.2~16 | |
| Volume fraction (%) | 8.28 | 28.12 | 15.56 | 3.93 |
| Total volume (mm3) | 21,091.64 | 71,549.81 | 39,607.85 | 10,008.47 |
| Average diameter (mm) | 3.56 | 7.13 | 11.35 | 14.60 |
| Volume of each ball (mm3) | 23.52 | 189.38 | 765.57 | 1629.51 |
| Number of balls | 896 | 378 | 51 | 6 |
| Mesoscopic Parameters | Units | DGM | GGM |
|---|---|---|---|
| Kkn | Pa·m | 4.93 × 103 | 3.67 × 103 |
| Ckn | Pa·m·s | 8.83 × 105 | 6.58 × 105 |
| Kmn | Pa·m | 2.60 × 104 | 1.93 × 104 |
| Cmn | Pa·m·s | 1.52 × 107 | 1.13 × 107 |
| Kks | Pa·m | 1.97 × 103 | 1.47 × 103 |
| Cks | Pa·m·s | 3.53 × 105 | 2.63 × 105 |
| Kms | Pa·m | 1.03 × 104 | 7.73 × 103 |
| Cms | Pa·m·s | 6.09 × 106 | 4.54 × 106 |
| Pb_coh (MPa) | Pb_ten (MPa) | Pb_fa (°) | Pb_emod (GPa) | Emod (GPa) | μ |
|---|---|---|---|---|---|
| 0.53 | 1.43 | 40 | 0.0225 | 0.15 | 0.35 |
| Mixture Types | Average Strengths at Different Pressures (kPa) | Mohr–Coulomb Parameters | |||
|---|---|---|---|---|---|
| 0 | 138 | 276 | c (kPa) | j (°) | |
| DGM | 1047 | 1696 | 2341 | 242.2 | 40.4 |
| GGM | 572 | 1442 | 1783 | 146.3 | 40.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, B.; Cao, W.; Zhou, L. Mesoscopic Perspective into the High-Temperature Triaxial Dilation of Asphalt Mixtures via PFC–FLAC Coupled Simulation. Materials 2025, 18, 1722. https://doi.org/10.3390/ma18081722
Xiao B, Cao W, Zhou L. Mesoscopic Perspective into the High-Temperature Triaxial Dilation of Asphalt Mixtures via PFC–FLAC Coupled Simulation. Materials. 2025; 18(8):1722. https://doi.org/10.3390/ma18081722
Chicago/Turabian StyleXiao, Bin, Wei Cao, and Liang Zhou. 2025. "Mesoscopic Perspective into the High-Temperature Triaxial Dilation of Asphalt Mixtures via PFC–FLAC Coupled Simulation" Materials 18, no. 8: 1722. https://doi.org/10.3390/ma18081722
APA StyleXiao, B., Cao, W., & Zhou, L. (2025). Mesoscopic Perspective into the High-Temperature Triaxial Dilation of Asphalt Mixtures via PFC–FLAC Coupled Simulation. Materials, 18(8), 1722. https://doi.org/10.3390/ma18081722







