Straight Disclinations in Fractional Nonlocal Medium
Abstract
1. Introduction
2. Fractional Nonlocal Elasticity
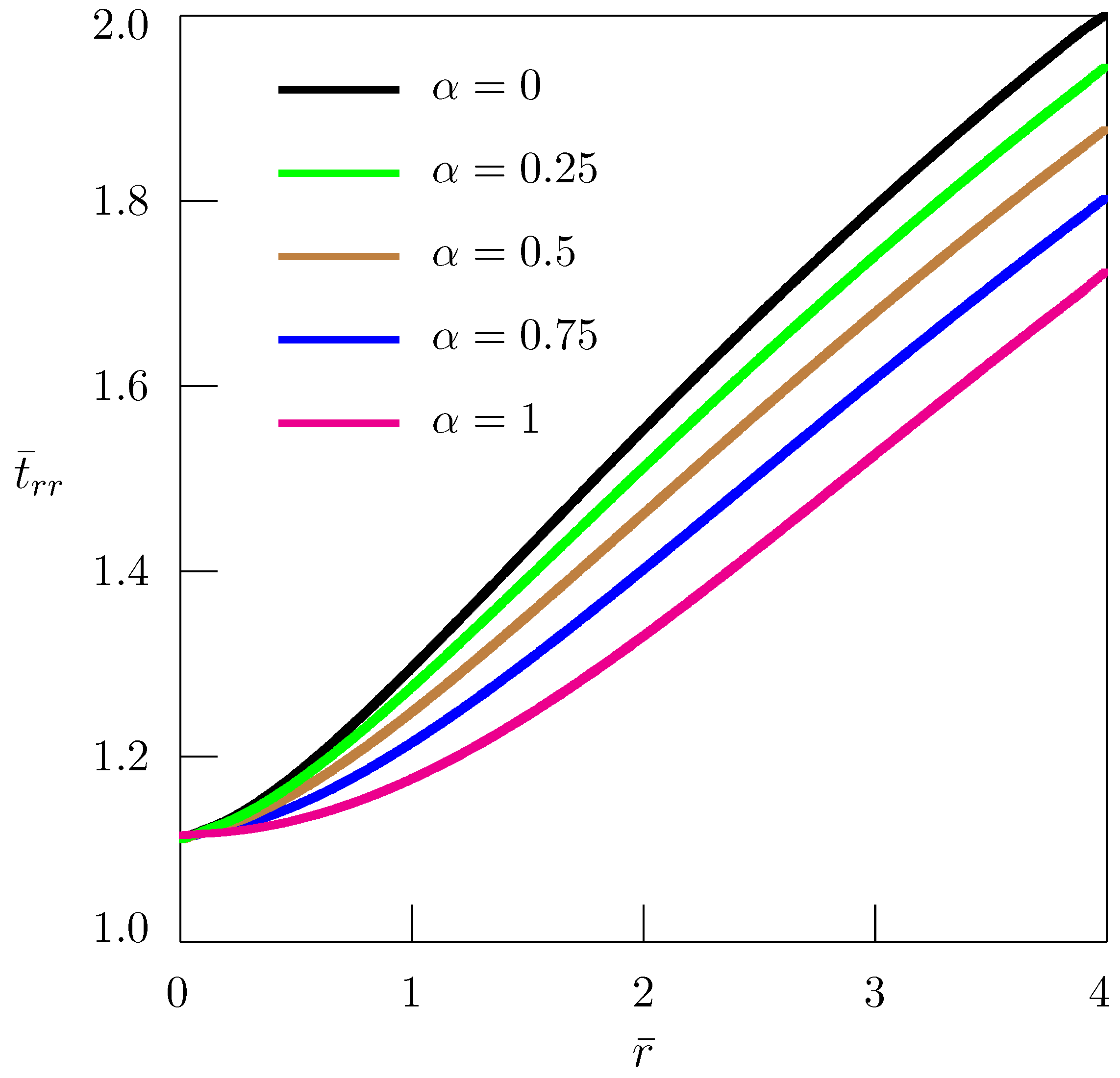
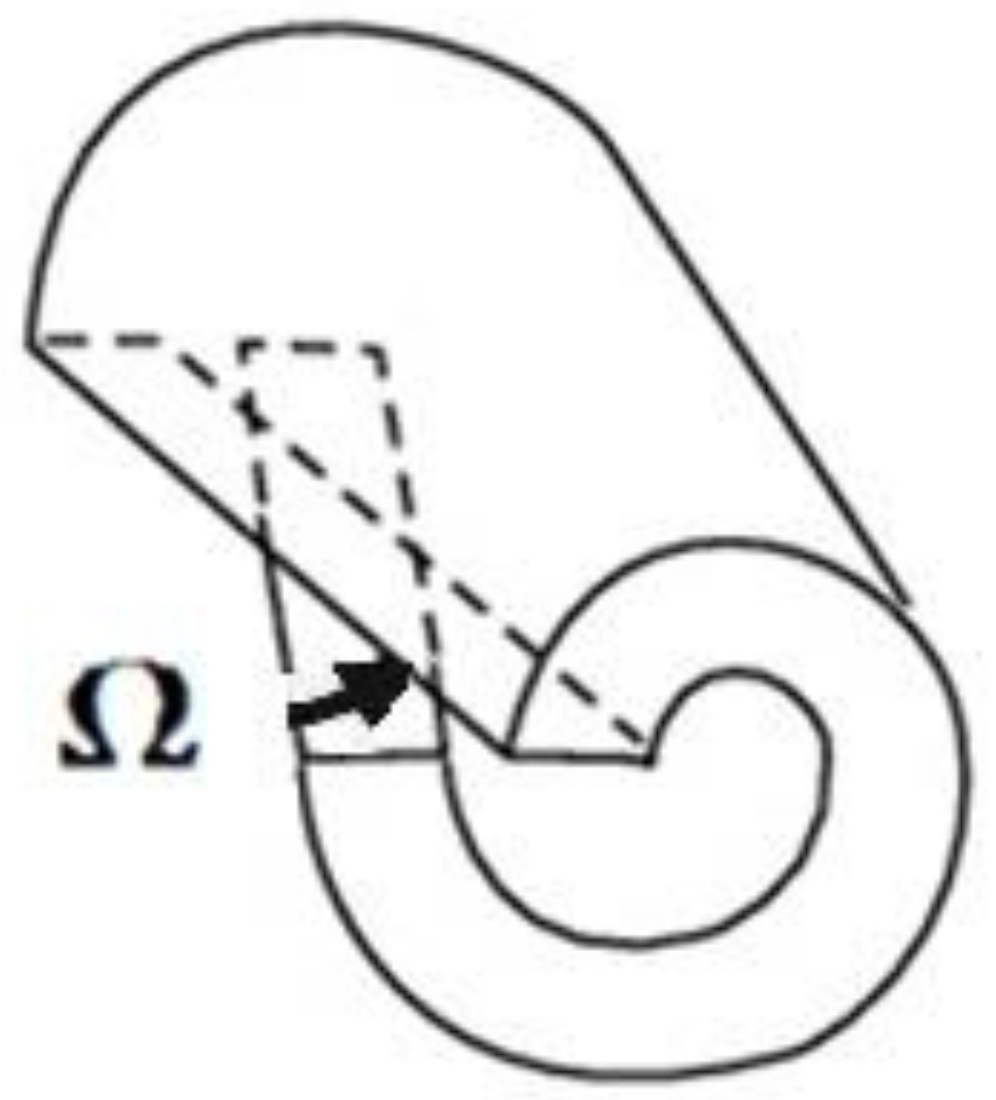
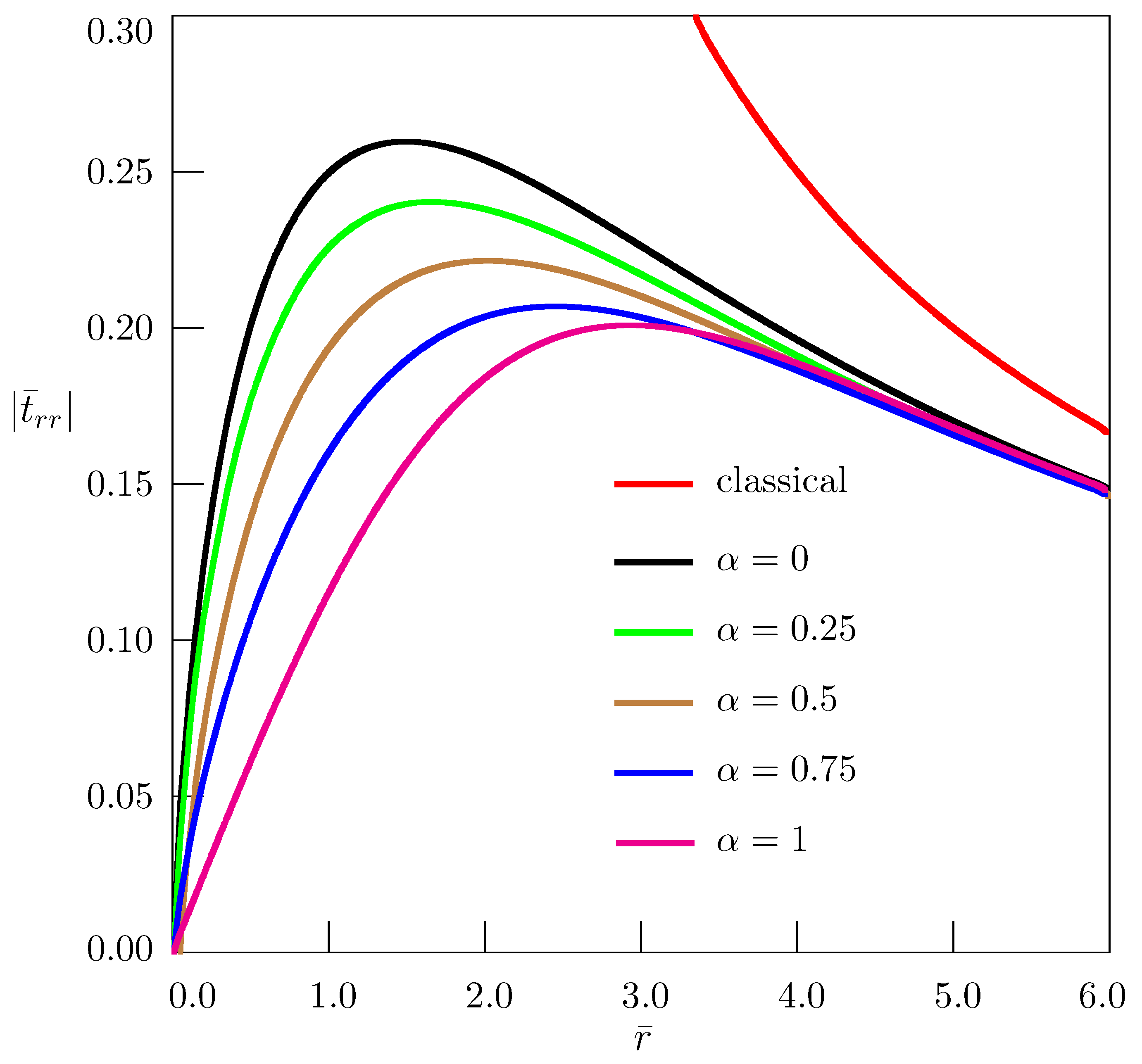
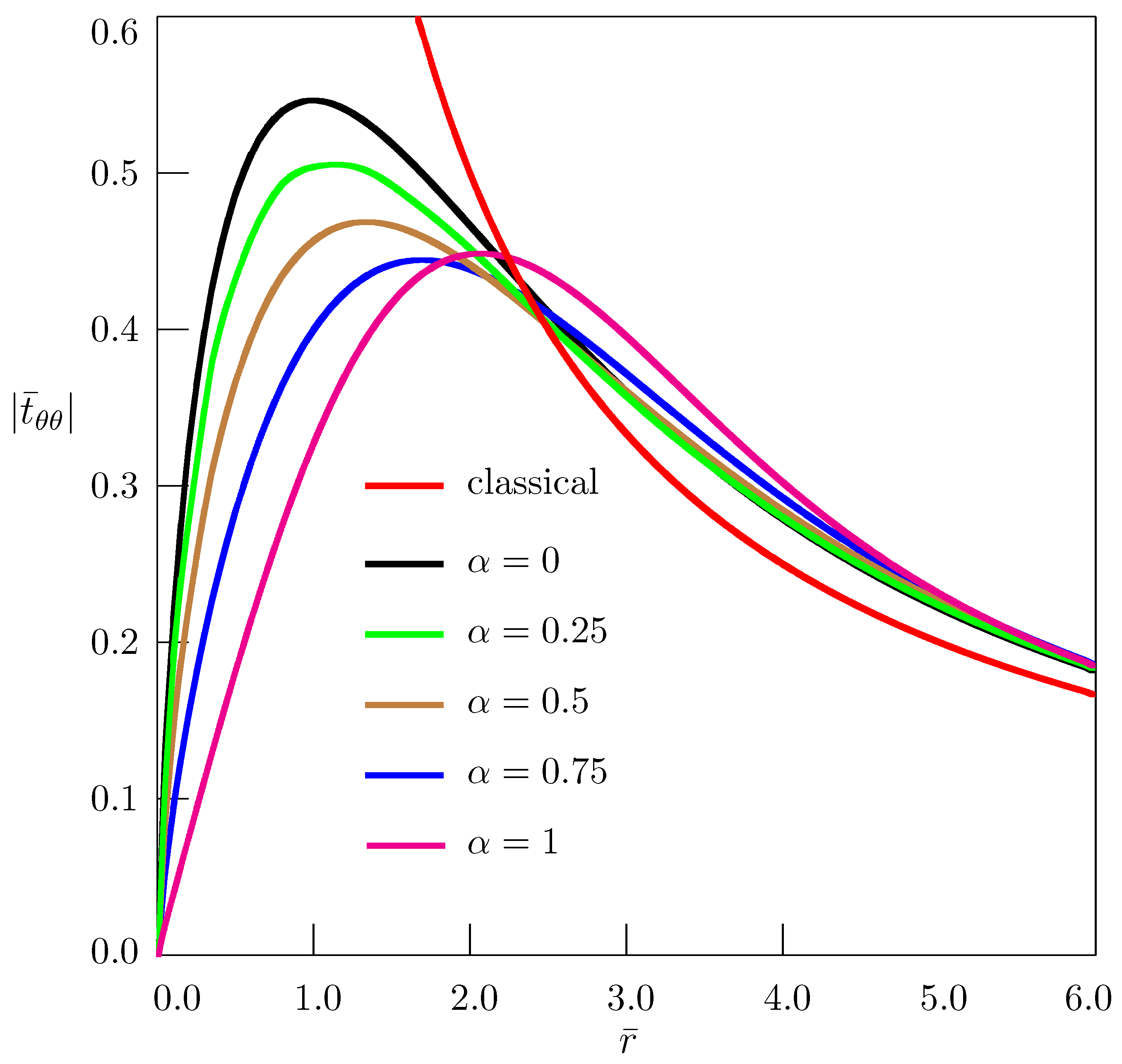
3. Straight Wedge Disclination
4. Straight Twist Disclination
5. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | proportionality coefficient for wedge disclination stresses |
| a | coefficient in the diffusion equation for the nonlocal kernel |
| B | proportionality coefficient for twist disclination stresses |
| Mittag–Leffler function | |
| exponential integral | |
| linear strain tensor | |
| f | auxiliary function |
| g | auxiliary function |
| h | auxiliary function |
| unit tensor | |
| modified Bessel function | |
| Bessel function | |
| K | nonlocality kernel |
| modified Bessel function | |
| l | characteristic length |
| p | auxiliary function |
| q | auxiliary function |
| r | cylindrical coordinate |
| s | Laplace transform variable |
| coefficients of expressions for components of nonlocal stress tensor | |
| nonlocal stress tensor | |
| reference point | |
| running point | |
| z | cylindrical coordinate |
| order of fractional derivative with respect to nonlocality parameter | |
| gamma function | |
| Euler constant | |
| Laplace operator | |
| Dirac’s delta function | |
| cylindrical coordinate | |
| Lamé constant | |
| Lamé constant | |
| Poisson ratio | |
| Hankel transform variable | |
| local stress tensor | |
| nonlocality parameter | |
| Frank vector |
Appendix A
Appendix B
References
- Volterra, V. Sur l’équilibre des corps élastiques multiplement connexes. Ann. Sci. Éc. Norm. Supér. 1907, 24, 401–517. [Google Scholar] [CrossRef]
- Love, A.E.H. Treatise on the Mathematical Theory of Elasticity, 3rd ed.; Cambridge University Press: Cambridge, UK, 1920. [Google Scholar]
- Frank, F.C. I. Liquid crystals. On the theory of liquid crystals. Disc. Faraday Soc. 1958, 25, 19–28. [Google Scholar] [CrossRef]
- Taylor, G.L. The mechanism of plastic deformation of crystals. I–II. Proc. Roy. Soc. A 1934, 145, 362–388. [Google Scholar]
- Orowan, E. Zur Kristallplastizität. III. Über die Mechanismus des Gleitvorganges. Z. Phys. 1934, 89, 634–659. [Google Scholar] [CrossRef]
- Polanyi, M. Über eine Art Gitterstörung, die einem Kristall plastisch machen könnte. Z. Phys. 1934, 89, 660–664. [Google Scholar] [CrossRef]
- Friedel, J. Dislocations; Pergamon Press: New York, NY, USA, 1964. [Google Scholar]
- Nabarro, F.R.N. Theory of Crystal Dislocations; Clarendon Press: Oxford, UK, 1967. [Google Scholar]
- Teodosiu, C. Elastic Models of Crystal Defects; Springer: Berlin, Germany, 1982. [Google Scholar]
- Weertman, J.; Weertman, J.R. Elementary Dislocation Theory; Oxford University Press: Oxford, UK, 1992. [Google Scholar]
- Cai, W.; Nix, W.D. Imperfections in Crystalline Solids; Cambridge University Press: Cambridge, UK, 2016. [Google Scholar]
- Anderson, P.M.; Hirth, J.P.; Lothe, J. Theory of Dislocations, 3rd ed.; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Saka, H. Classical Theory of Crystal Dislocations; World Scientific: Singapore, 2017. [Google Scholar]
- deWit, R. Linear theory of static disclinations. In Fundamental Aspects of Dislocation Theory; National Bureau of Standards Special Publ. 317; U.S. Government Publishing Office: Washington, DC, USA, 1970; Volume 1, pp. 651–680. [Google Scholar]
- deWit, R. Theory of disclinations: IV. Straight disclinations. J. Res. Nat. Bureau Stand.—A. Phys. Chem. 1973, 77, 607–658. [Google Scholar] [CrossRef]
- Likhachev, V.A.; Khairov, R.Y. Introduction to the Theory of Disclinations; Leningrad University Press: Leningrad, Russia, 1975. (In Russian) [Google Scholar]
- Romanov, A.E.; Vladimirov, V.I. Disclinations in solids. Phys. Stat. Sol. 1983, 78, 11–34. [Google Scholar] [CrossRef]
- Vladimirov, V.I.; Romanov, A.E. Disclinations in Crystals; Nauka: Leningrad, Russia, 1986. (In Russian) [Google Scholar]
- Romanov, A.E. Mechanics and physics of disclinations in solids. Eur. J. Mech. A/Solids 2003, 22, 727–741. [Google Scholar] [CrossRef]
- Romanov, A.E.; Kolesnikova, A.L. Application of disclination concept to solid structures. Prog. Mater. Sci. 2009, 54, 740–769. [Google Scholar] [CrossRef]
- Kolesnikova, A.L.; Gutkin, M.Y.; Proskura, A.V.; Morozov, N.F.; Romanov, A.E. Elastic fields of straight wedge disclinations axially piercing bodies with spherical free surfaces. Int. J. Solids Struct. 2016, 99, 82–96. [Google Scholar] [CrossRef]
- Fressengeas, C.; Sun, X. On the theory of dislocation and generalized disclination fields and its application to straight and stepped symmetrical tilt boundaries. J. Mech. Phys. Solids 2020, 143, 104092. [Google Scholar] [CrossRef]
- Bamney, D.; Reyes, R.; Capolungo, L.; Spearot, D.E. Disclination-dislocation based model for grain boundary stress field evolution due to slip transmission history and influence on subsequent dislocation transmission. J. Mech. Phys. Solids 2022, 165, 104920. [Google Scholar] [CrossRef]
- Zhang, C.; Acharya, A. On the relevance of generalized disclinations in defect mechanics. J. Mech. Phys. Solids 2018, 119, 188–223. [Google Scholar] [CrossRef]
- Fressengeas, C.; Taupin, V. Revisiting the application of field dislocation and disclination mechanics to grain boundaries. Metals 2020, 10, 1517. [Google Scholar] [CrossRef]
- Hirth, J.P.; Hirth, G.; Wang, J. Disclinations and disconnections in minerals and metals. Proc. Nat. Acad. Sci. USA 2020, 117, 196–204. [Google Scholar] [CrossRef]
- Geier, M.; Fulga, I.C.; Lau, A. Bulk-boundary-defect correspondence at disclinations in rotation-symmetric topological insulators and superconductors. SciPost Phys. 2021, 10, 92. [Google Scholar] [CrossRef]
- Demouchy, S.; Thieme, M.; Barou, F.; Beausir, B.; Taupin, V.; Cordier, P. Dislocation and disclination densities in experimentally deformed polycrystalline olivine. Eur. J. Mineral. 2023, 35, 219–242. [Google Scholar] [CrossRef]
- deWit, R. Relation between dislocations and disclinations. J. Appl. Phys. 1971, 42, 3304–3308. [Google Scholar] [CrossRef]
- Marcinkowski, M.J. Dislocations and disclinations in a new light. Arch. Mech. 1990, 42, 279–289. [Google Scholar]
- Kontorova, T.A.; Frenkel, J.I. Theory of plastic deformation and twinning. J. Exp. Theor. Phys. 1938, 8, 89–95. (In Russian) [Google Scholar]
- Braun, O.M.; Kivshar, Y.S. Nonlinear dynamics of the Frenkel–Kontorova model. Phys. Rep. 1998, 306, 1–108. [Google Scholar] [CrossRef]
- Braun, O.M.; Kivshar, Y.S. The Frenkel–Kontorova Model: Concepts, Methods and Applications; Springer: Berlin, Germany, 2004. [Google Scholar]
- Peierls, R.E. The size of a dislocation. Proc. Phys. Soc. Lond. 1940, 52, 34–37. [Google Scholar] [CrossRef]
- Nabarro, F.R.N. Dislocations in a simple cubic lattice. Proc. Phys. Soc. Lond. 1947, 59, 256–272. [Google Scholar] [CrossRef]
- Bullough, R.; Tewary, V.K. Lattice theory of dislocations. In Dislocations in Solids, Vol. 2. Dislocations in Crystals; Nabarro, F.R.N., Ed.; North-Holland: Amsterdam, The Netherlands, 1979; pp. 1–66. [Google Scholar]
- Duesbery, M.S. Modeling of the dislocation core. In Dislocations in Solids, Vol. 8. Basic Problems and Applications; Nabarro, F.R.N., Ed.; North-Holland: Amsterdam, The Netherlands, 1989; pp. 67–173. [Google Scholar]
- Raabe, D. Computational Materials Science. The Simulation of Materials Microstructures and Properties; Wiley: Weinheim, Germany, 1998. [Google Scholar]
- Tewary, V.K. Lattice-statics model for edge dislocations in crystal. Phil. Mag. A 2000, 80, 1445–1452. [Google Scholar] [CrossRef]
- Eringen, A.C. Edge dislocation in nonlocal elasticity. Int. J. Eng. Sci. 1977, 15, 177–183. [Google Scholar] [CrossRef]
- Eringen, A.C. Screw dislocation in nonlocal elasticity. J. Phys. D Appl. Phys. 1977, 10, 671–678. [Google Scholar] [CrossRef]
- Eringen, A.C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C. Vistas on nonlocal continuum physics. Int. J. Eng. Sci. 1992, 30, 1551–1565. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer: New York, NY, USA, 2002. [Google Scholar]
- Lazar, M.; Agiasofitou, E. Screw dislocation in nonlocal anisotropic elasticity. Int. J. Eng. Sci. 2011, 49, 1404–1414. [Google Scholar] [CrossRef]
- Povstenko, Y. Straight disclinations in nonlocal elasticity. Int. J. Eng. Sci. 1995, 33, 575–582. [Google Scholar] [CrossRef]
- Gutkin, M.Y.; Aifantis, E.C. Screw dislocation in gradient elasticity. Scr. Mater. 1996, 35, 1353–1358. [Google Scholar] [CrossRef]
- Gutkin, M.Y.; Aifantis, E.C. Edge dislocation in gradient elasticity. Scr. Mater. 1997, 36, 129–135. [Google Scholar] [CrossRef]
- Lazar, M. The fundamentals of non-singular dislocations in the theory of gradient elasticity: Dislocation loops and straight dislocations. Int. J. Solids Struct. 2013, 50, 352–362. [Google Scholar] [CrossRef]
- Lazar, M. Non-singular dislocation continuum theories: Strain gradient elasticity versus Peierls-Nabarro model. Phil. Mag. 2017, 97, 3246–3275. [Google Scholar] [CrossRef]
- Tsagrakis, I.; Yasnikov, I.S.; Aifantis, E.C. Gradient elasticity for disclinated micro crystals. Mech. Res. Commun. 2018, 93, 159–162. [Google Scholar] [CrossRef]
- Lazar, M.; Po, G. Non-singular straight dislocations in anisotropic crystals. J. Mater. Sci. Mater. Theory 2024, 8, 5. [Google Scholar] [CrossRef]
- Wu, M.S. A revisit of the elastic fields of straight disclinations with new solutions for a rigid core. Acta Mech. 2019, 230, 2505–2520. [Google Scholar] [CrossRef]
- Wu, M.S. A wedge disclination in a nonlinear elastic cylinder. Math. Mech. Solids 2019, 24, 2030–2046. [Google Scholar] [CrossRef]
- Wu, M.S. Elastic fields of a wedge disclination in a functionally graded cylinder. Mech. Mater. 2021, 157, 103835. [Google Scholar] [CrossRef]
- Lazar, M.; Maugin, G.A.; Aifantis, E.C. On a theory of nonlocal elasticity of bi-Helmholtz type and some applications. Int. J. Solids Struct. 2006, 43, 1404–1421. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Nonlocal elasticity in nanobeams: The stress-driven integral model. Int. J. Eng. Sci. 2017, 115, 14–27. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Stress-driven versus strain-driven nonlocal integral model for elastic nano-beams. Compos. Part B 2017, 114, 184–188. [Google Scholar] [CrossRef]
- Apuzzo, A.; Barretta, R.; Faghidian, S.A.; Luciano, R.; Marotti de Sciarra, F. Free vibrations of elastic beams by modified nonlocal strain gradient theory. Int. J. Eng. Sci. 2018, 133, 99–108. [Google Scholar] [CrossRef]
- Di Paola, M.; Zingales, M. Long-range cohesive interactions of non-local continuum faced by fractional calculus. Int. J. Solids Struct. 2008, 45, 5642–5659. [Google Scholar] [CrossRef]
- Challamel, N.; Zorica, D.; Atanacković, T.M.; Spasić, D.T. On the fractional generalization of Eringen’s nonlocal elasticity for wave propagation. Comptes Rendus Mécanique 2013, 341, 298–303. [Google Scholar] [CrossRef]
- Carpinteri, A.; Cornetti, P.; Sapora, A. Nonlocal elasticity: An approach based on fractional calculus. Meccanica 2014, 49, 2551–2569. [Google Scholar] [CrossRef]
- Tarasov, V.E. Lattice model of fractional gradient and integral elasticity: Long-range interaction of Grünwald–Letnikov–Riesz type. Mech. Mater. 2014, 70, 106–114. [Google Scholar] [CrossRef]
- Tarasov, V.E. Fractional nonlocal continuum mechanics and microstructural models. In Handbook of Nonlocal Continuum Mechanics for Materials and Structures; Voyiadjis, G.Z., Ed.; Springer: Cham, Switzerland, 2019; pp. 839–849. [Google Scholar]
- Povstenko, Y. Generalized theory of diffusive stresses associated with the time-fractional diffusion equation and nonlocal constitutive equations for the stress tensor. Comput. Math. Appl. 2019, 78, 1819–1825. [Google Scholar] [CrossRef]
- Povstenko, Y. Fractional nonlocal elasticity and solutions for straight screw and edge dislocations. Phys. Mesomech. 2020, 23, 547–555. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Kunin, I.A. Elastic Media with Microstructure I. One-Dimensional Models; Springer: Berlin, Germany, 1982. [Google Scholar]
- Kunin, I.A. Elastic Media with Microstructure II. Three-Dimensional Models; Springer: Berlin, Germany, 1983. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables; Dover: New York, NY, USA, 1972. [Google Scholar]
- Doetsch, G. Anleitung zum Praktischer Gebrauch der Laplace-Transformation und der Z-Transformation; Springer: München, Germany, 1967. [Google Scholar]
- Lawn, B.R.; Wilshaw, T.R. Fracture of Brittle Solids; Cambridge University Press: Cambridge, UK, 1975. [Google Scholar]
- Kelly, A. Strong Solids, 2nd ed.; Clarendon Press: Oxford, UK, 1973. [Google Scholar]
- Kelly, A.; Knowles, K.M. Crystallography and Crystal Defects, 2nd ed.; John Wiley & Sons: Chichester, UK, 2012. [Google Scholar]
- Povstenko, Y. The mathematical theory of defects in a Cosserat continuum. J. Math. Sci. 1992, 62, 2524–2530. [Google Scholar] [CrossRef]
- Povstenko, Y. Stress functions for continua with couple stresses. J. Elast. 1994, 36, 99–116. [Google Scholar] [CrossRef]
- Ghavanloo, E.; Rafii-Tabar, H.; Fazelzadeh, S.A. Computational Continuum Mechanics of Nanoscopic Structures: Nonlocal Elasticity Approaches; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Povstenko, Y. Fractional Thermoelasticity, 2nd ed.; Springer: Cham, Switzerland, 2024. [Google Scholar]
- Prudnikov, A.P.; Brychkov, Y.A.; Marichev, O.I. Integrals and Series, Vol. 2: Special Functions; Gordon & Breach Science Publishers: Amsterdam, The Netherlands, 1983. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kyrylych, T.; Povstenko, Y. Straight Disclinations in Fractional Nonlocal Medium. Materials 2025, 18, 1717. https://doi.org/10.3390/ma18081717
Kyrylych T, Povstenko Y. Straight Disclinations in Fractional Nonlocal Medium. Materials. 2025; 18(8):1717. https://doi.org/10.3390/ma18081717
Chicago/Turabian StyleKyrylych, Tamara, and Yuriy Povstenko. 2025. "Straight Disclinations in Fractional Nonlocal Medium" Materials 18, no. 8: 1717. https://doi.org/10.3390/ma18081717
APA StyleKyrylych, T., & Povstenko, Y. (2025). Straight Disclinations in Fractional Nonlocal Medium. Materials, 18(8), 1717. https://doi.org/10.3390/ma18081717







