1.5 GPa Grade High-Strength Steel Sheet Flattening by Roll Gap Adjustment Considering Pattern Roll Effects
Abstract
1. Introduction
2. Experimental Procedure
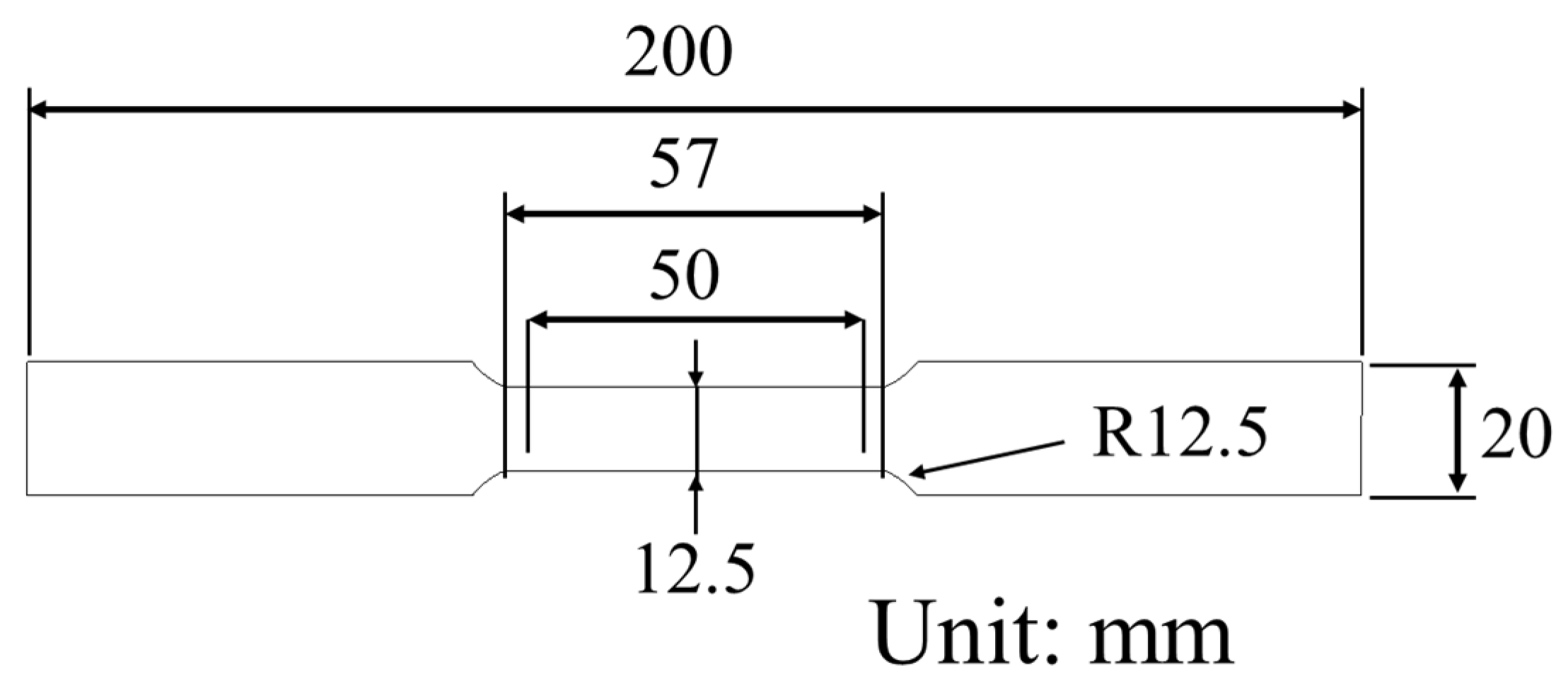
2.1. Materials
2.2. Experimental Setup
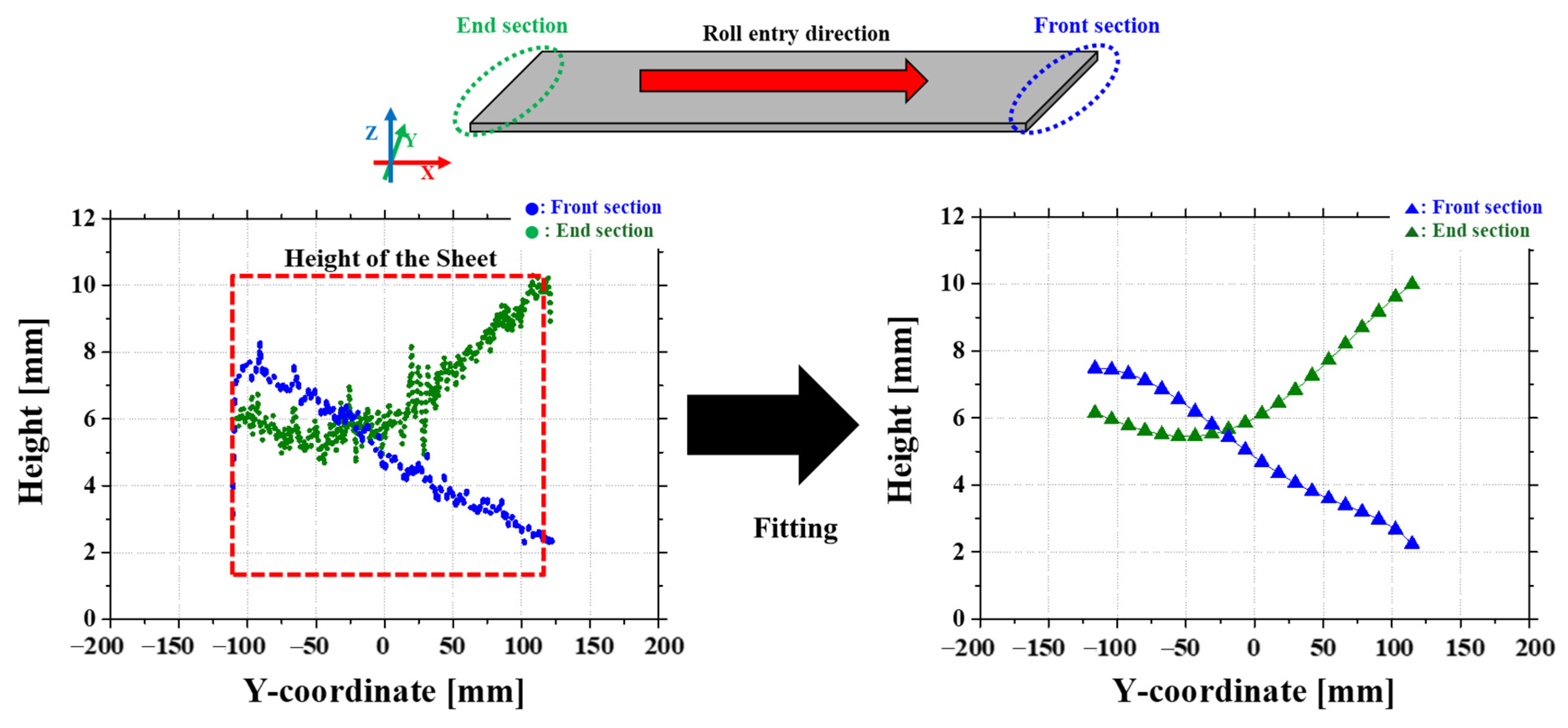
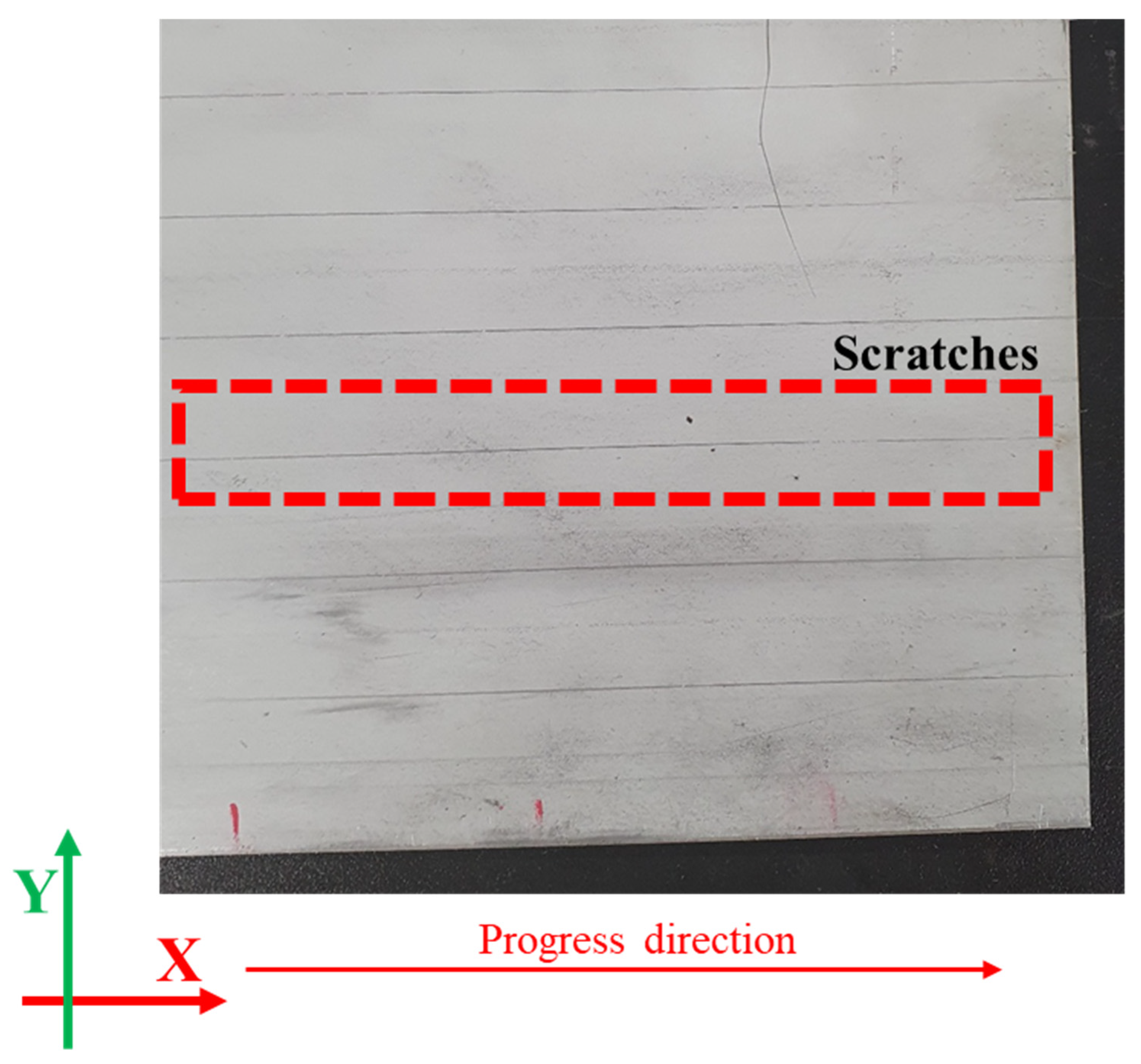
2.3. Measurement Method
3. Methods
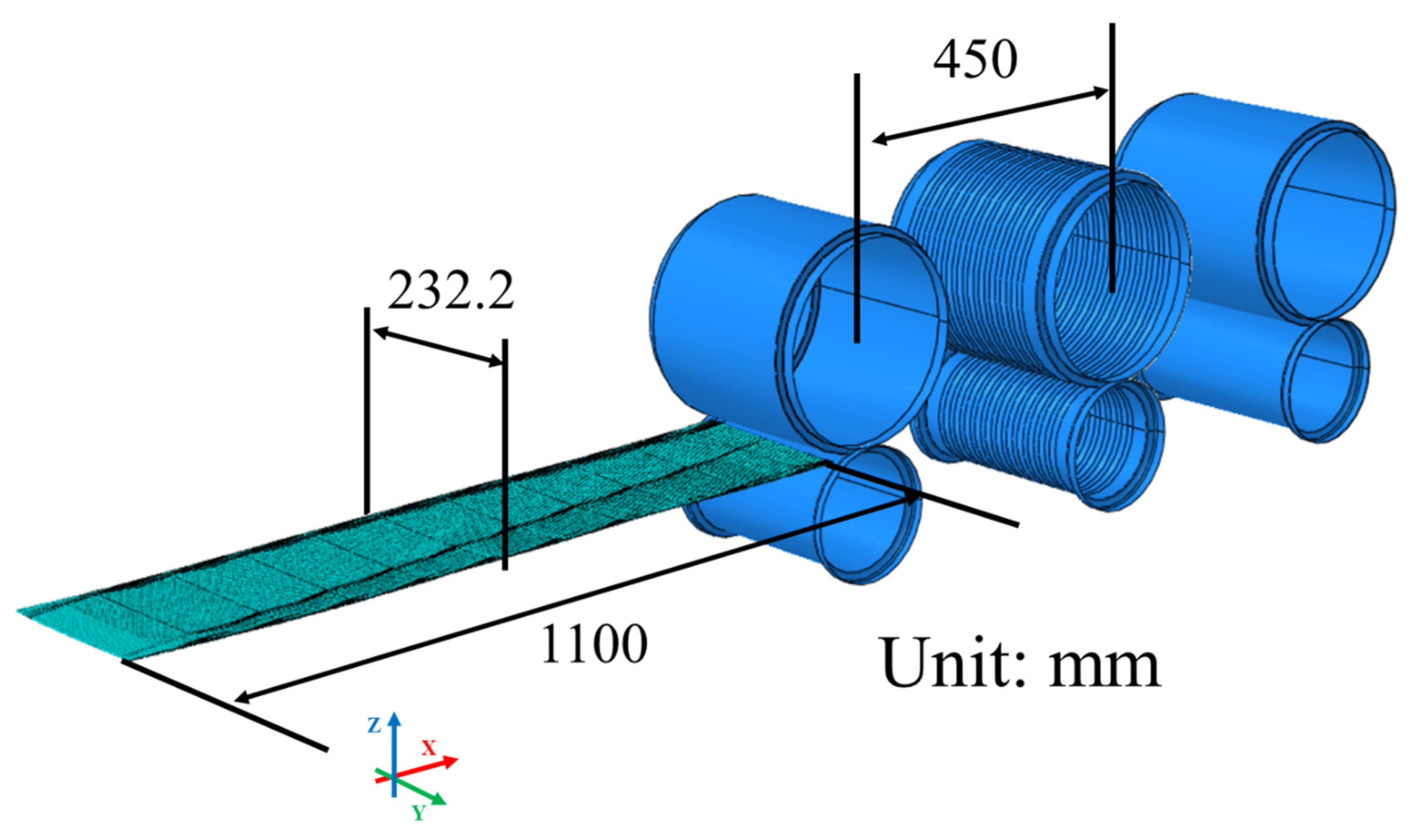
3.1. Analysis Model
3.2. Analysis Conditions
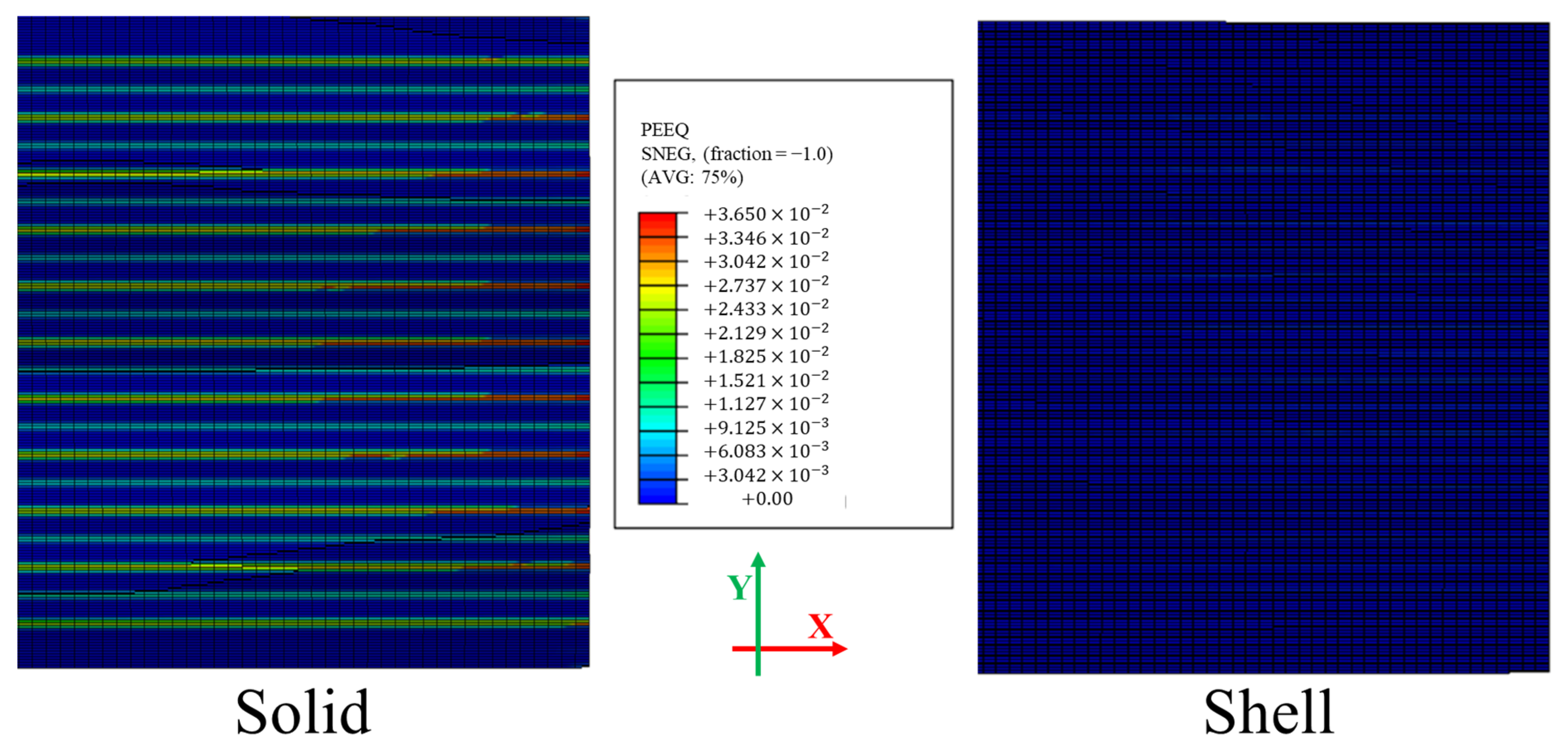
3.2.1. Comparison Between Solid and Shell Elements
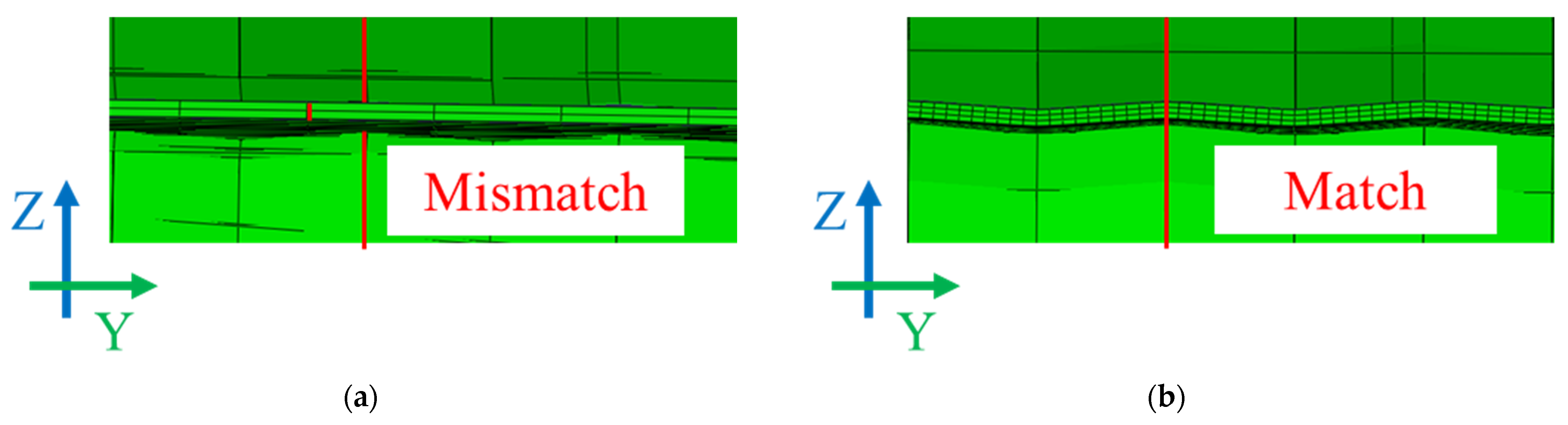
3.2.2. Number of Elements
3.2.3. Spring Stiffness
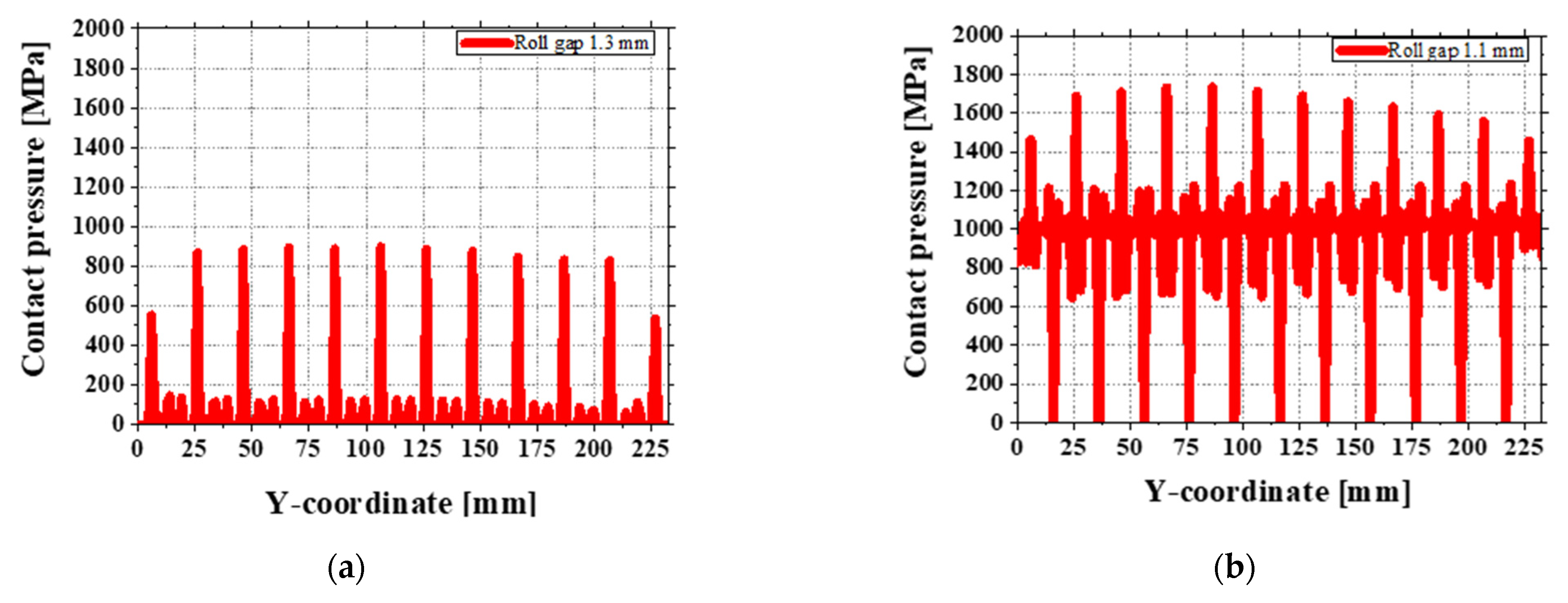
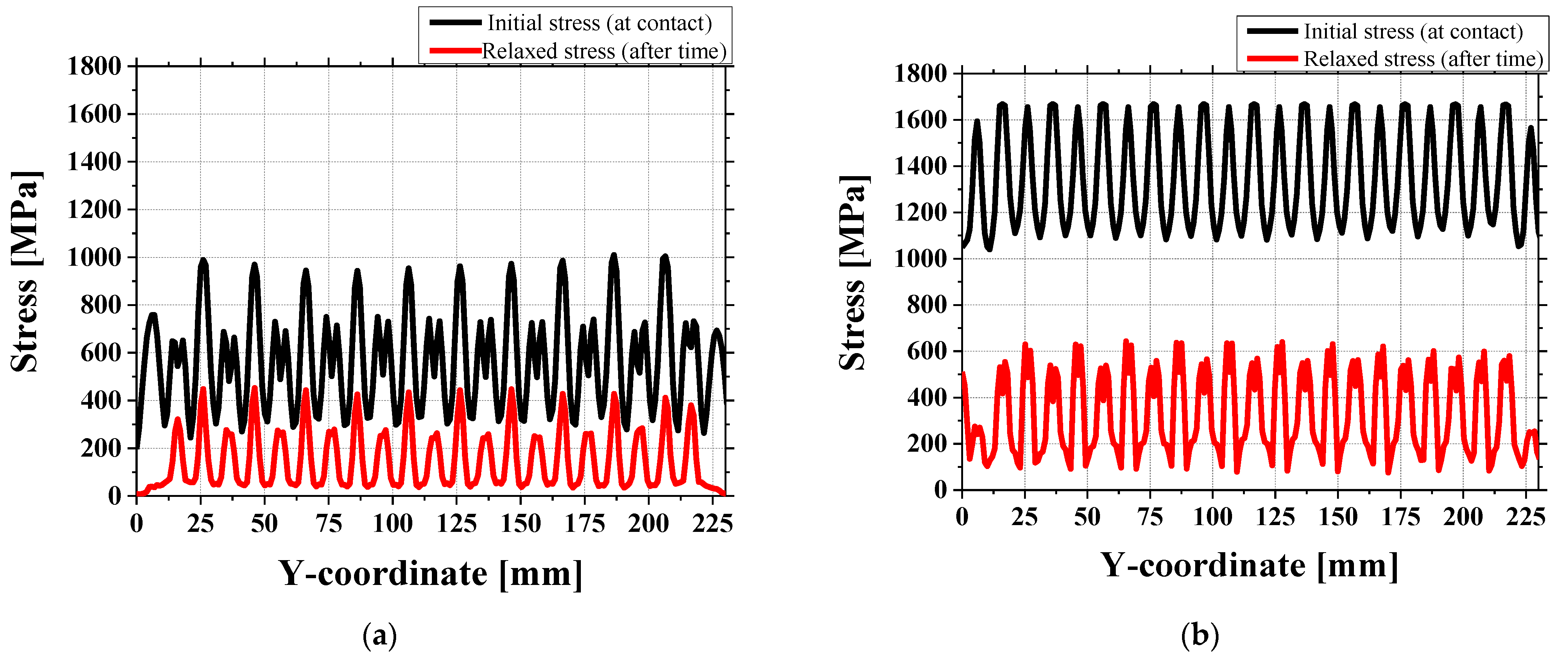
3.2.4. Contact and Dynamic Influences
4. Results and Discussion
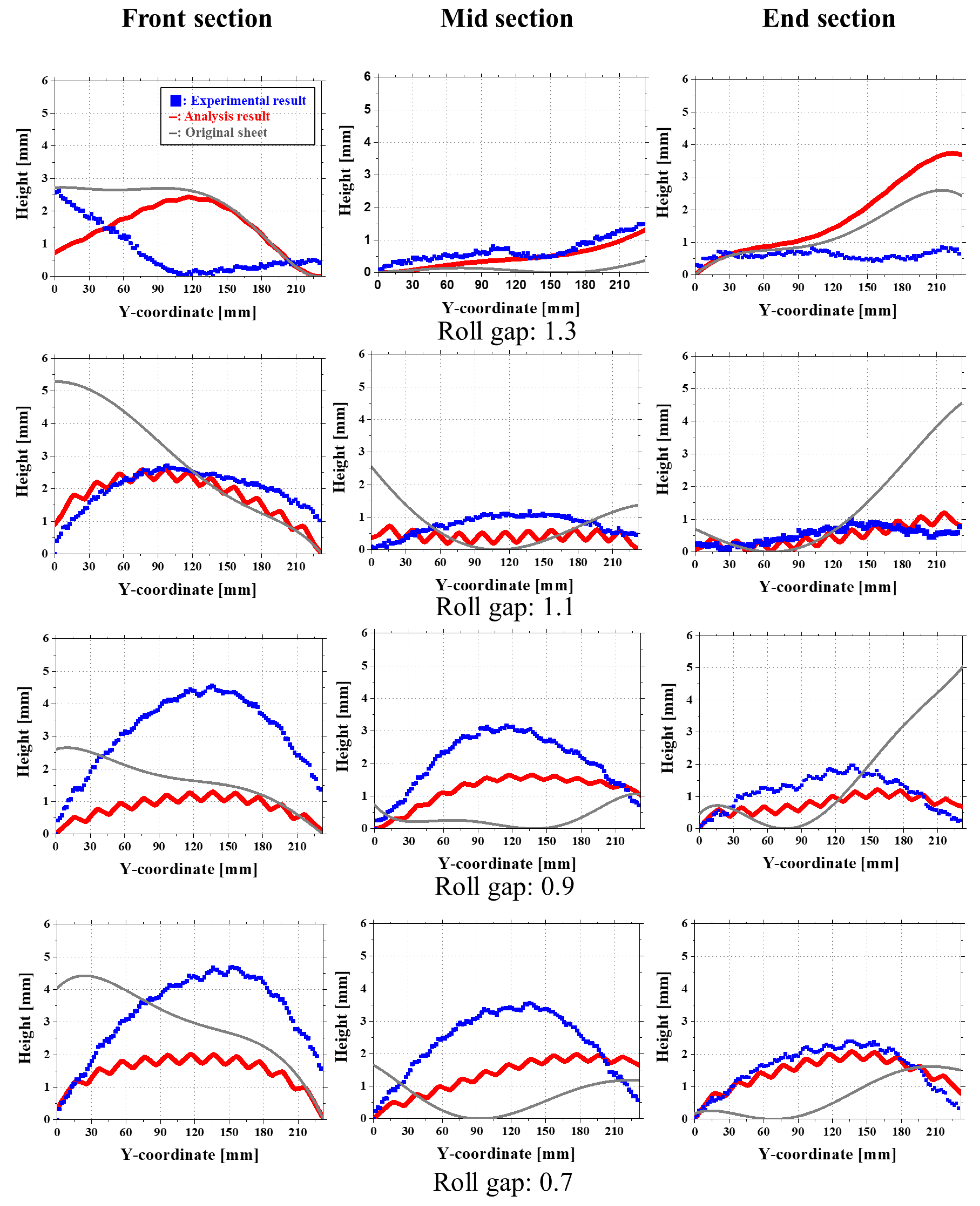
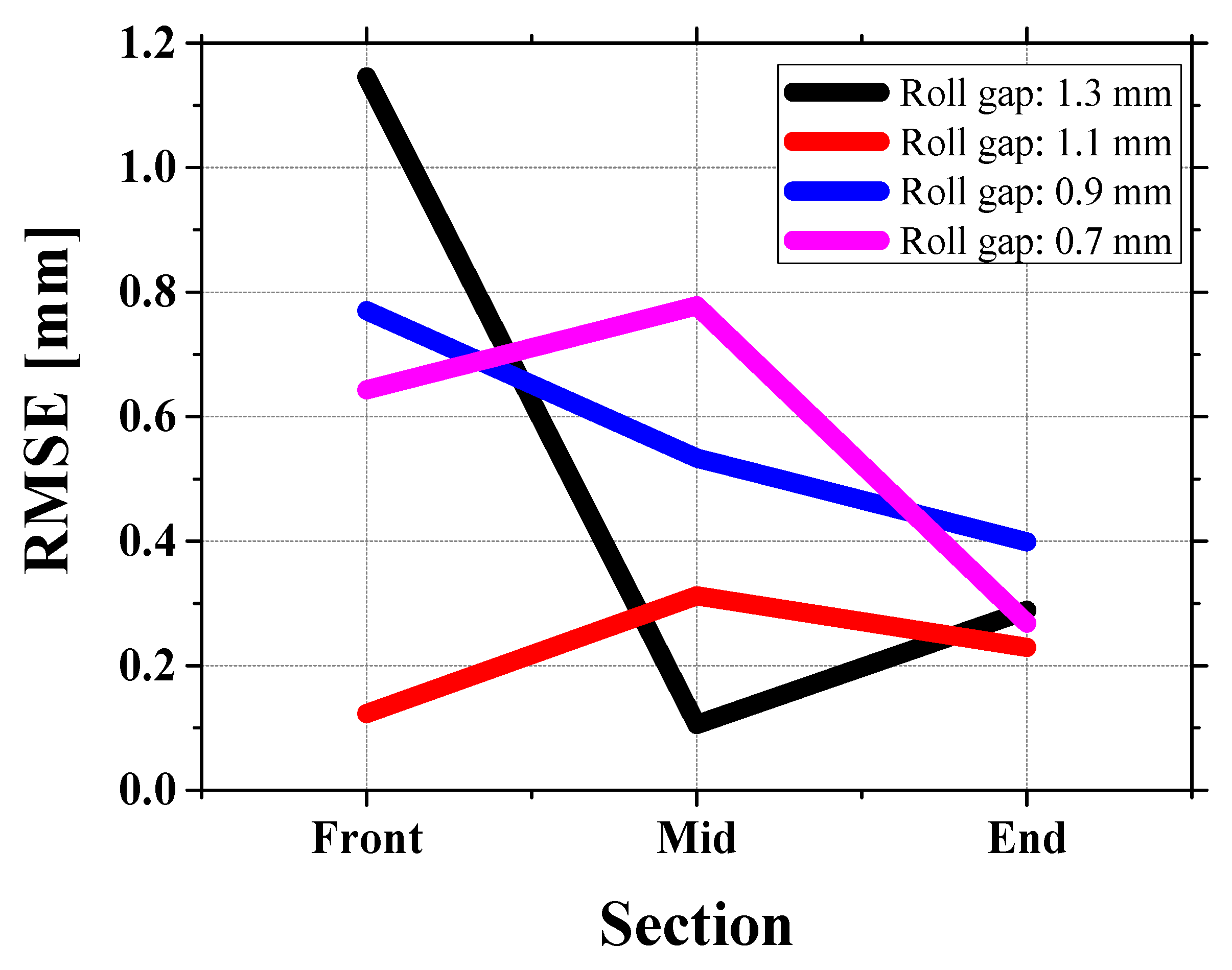
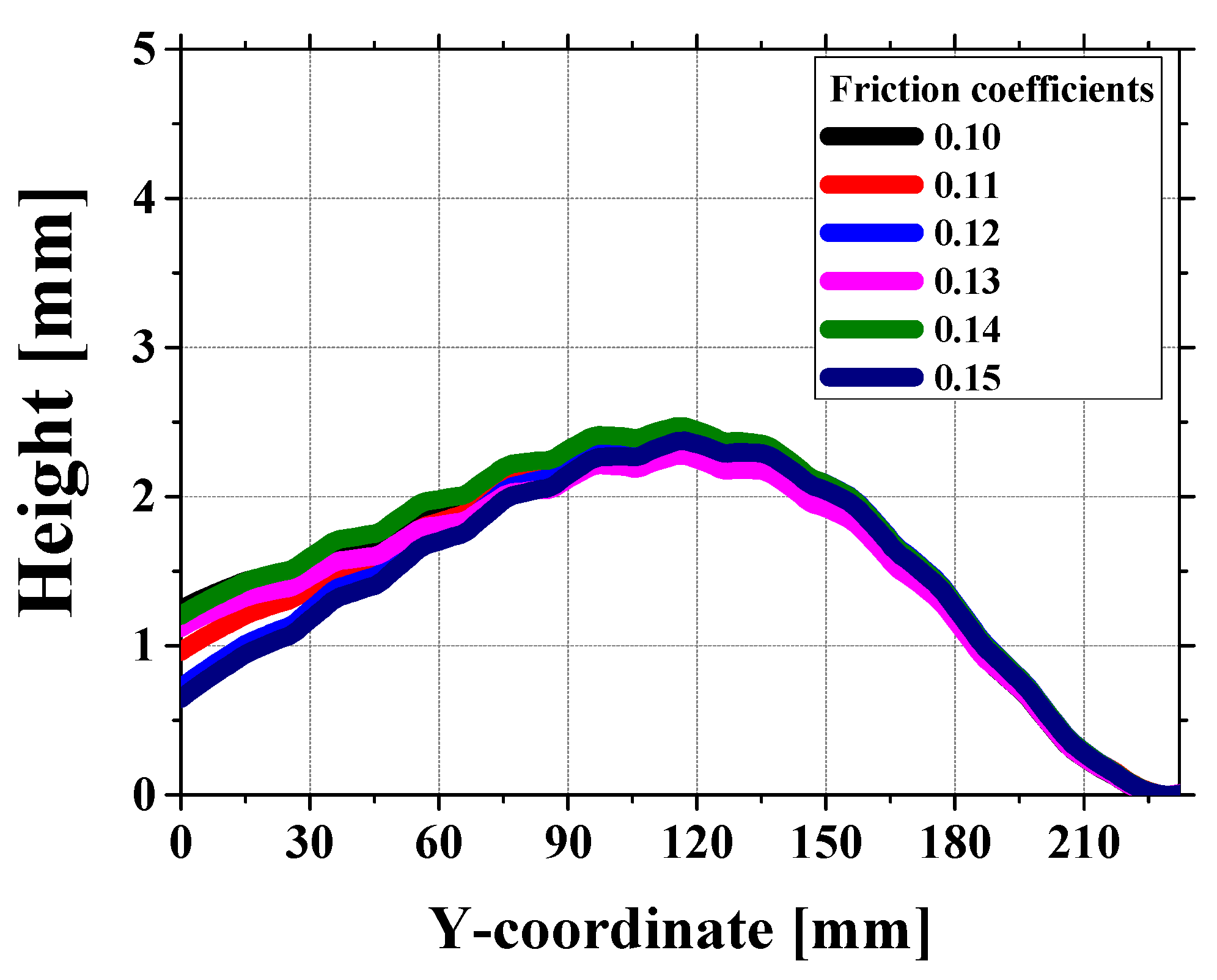
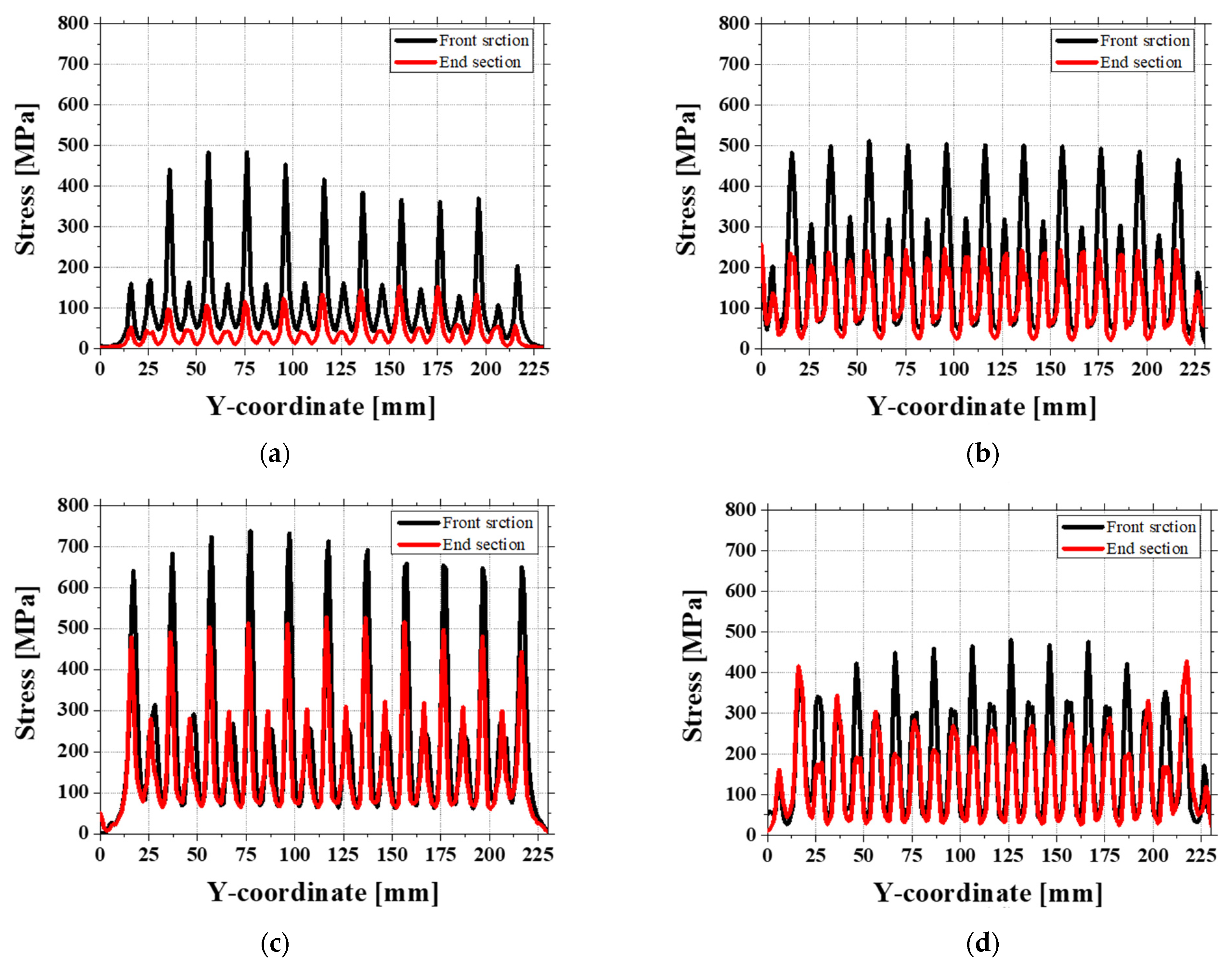
4.1. Comparison of Sheet Geometry and RMSE for Different Gaps
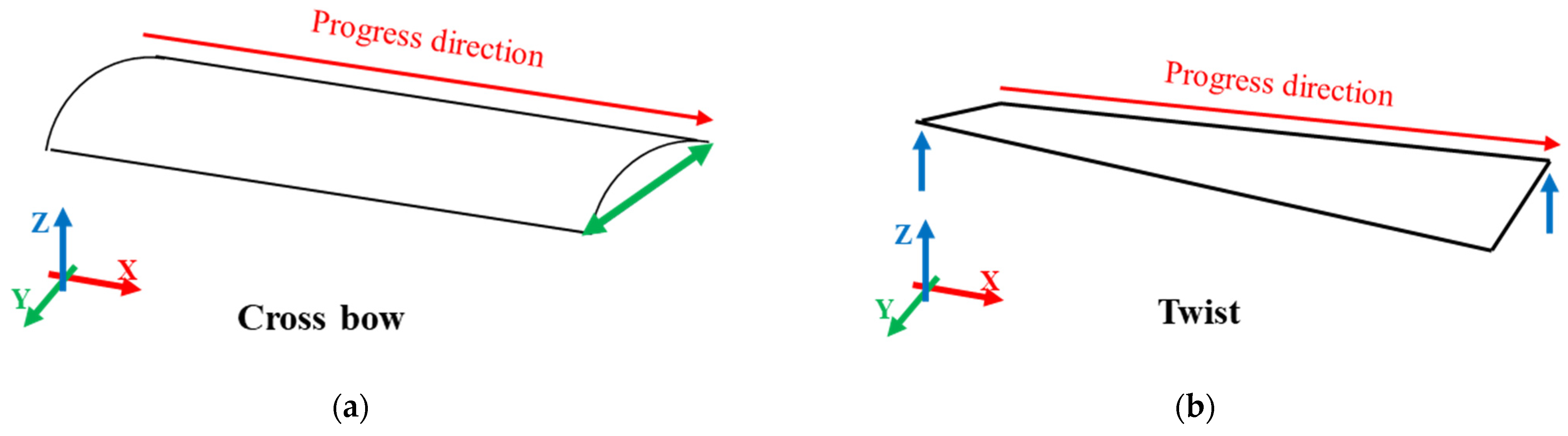
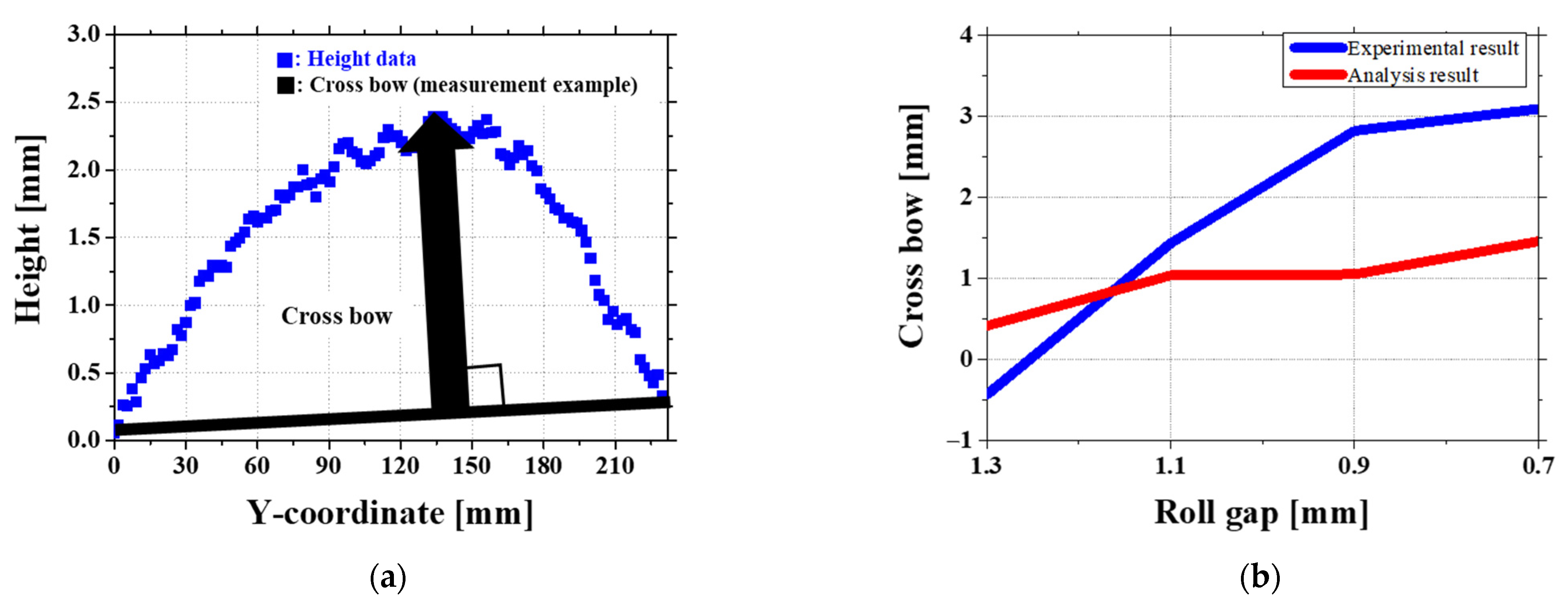
4.2. Crossbow Defect
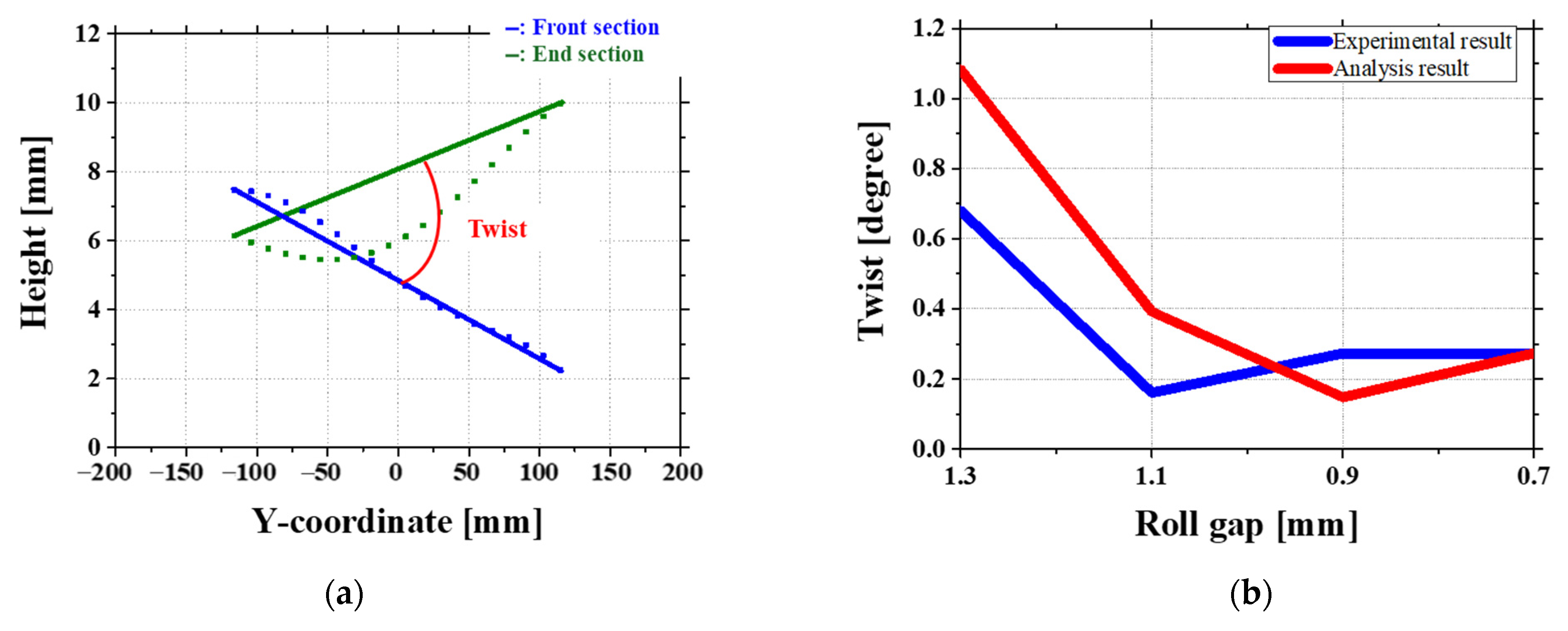
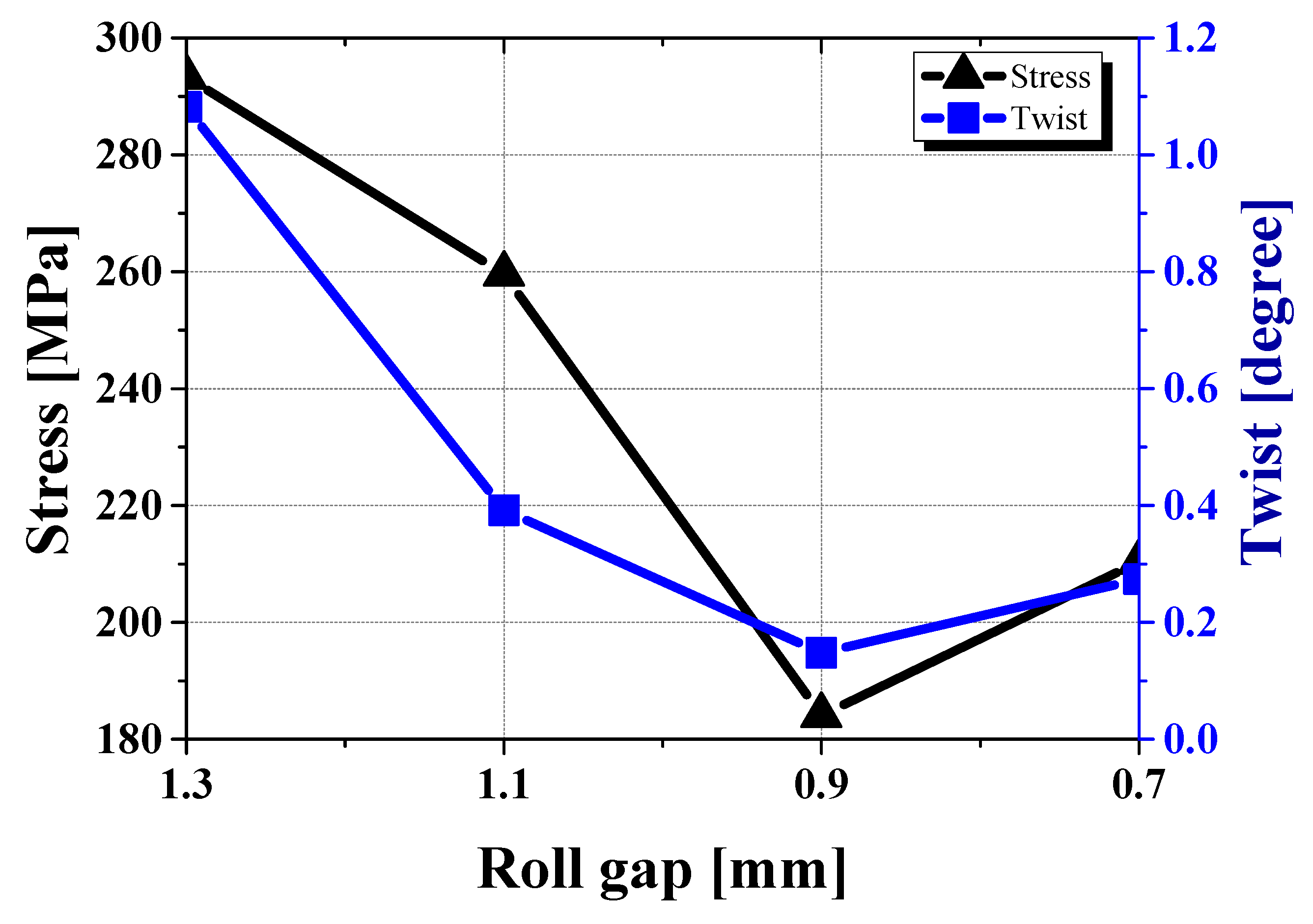
4.3. Twist Defect
5. Conclusions
- A 1.1 mm roll gap was found to be the most effective condition, reducing twist defects by more than 80% and minimizing crossbow deformation (RMSE ≈ 0.22 mm).
- At a 1.3 mm gap, simulations overestimated the effect of the second roll, leading to a reversed crossbow pattern in the front section, which was not observed in experiments.
- When the roll gap was reduced to 0.9 mm and 0.7 mm, the experiment showed a significant increase in crossbow deformation, while the simulation underestimated this effect due to limitations in considering friction changes and local stress accumulation. In experimental, the end of the roll is fixed by a shaft, limiting the edge movement, resulting in a more bent center, resulting in a disproportionate force distribution and stronger crossbow deformation. On the other hand, the simulation lowers the crossbow prediction by evenly applying force throughout the sheet. Due to this difference in roll fixation, the experiment consistently shows a larger crossbow than the simulation, and this effect becomes more pronounced as the roll gap decreases.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Sun, Y.; Luzin, V.; Khan, S.; Vajragupta, N.; Meehan, P.; Daniel, B.; Yanagimoto, J.; Xiong, Z.; Ding, S. Understanding of residual stresses in chain-die-formed dual-phase (DP) metallic components: Predictive modelling and experimental validation. Int. J. Adv. Manuf. Technol. 2019, 103, 3337–3360. [Google Scholar] [CrossRef]
- Yesane, D.P.; Bhortake, R.V. Analytical Modeling and Validation of Residual Stresses in the Coiling and Uncoiling Process of Advanced High Strength Steel. Nanotechnol. Percept. 2024, 20, 533–548. [Google Scholar] [CrossRef]
- Quach, W.M.; Teng, J.G.; Chung, K.F. Residual stresses in steel sheets due to coiling and uncoiling: A closed-form analytical solution. Eng. Struct. 2004, 26, 1249–1259. [Google Scholar] [CrossRef]
- Richard, P.; Smith, J. Modeling Plastic Strain During Cold Leveling of Steel Plates. In Proceedings of the AISE Annual Conference, Pittsburgh, PA, USA, May 1999. [Google Scholar]
- Silvestre, E.; Sáenz de Argandoña, E.; Galdos, L.; Mendiguren, J. Testing and modeling of roll levelling process. Key Eng. Mater. 2014, 611, 1753–1762. [Google Scholar] [CrossRef]
- Perzynski, K.; Pyzynsk, K.; Swierczynski, S.; Pidvysots’kyy, V.; Klis, J.; Madej, L. Influence of the roll leveler setup parameters on the quality of high-strength steel leveling operation. Int. J. Adv. Manuf. Technol. 2022, 120, 1203–1217. [Google Scholar] [CrossRef]
- Yi, G.; Wang, Y.; Liu, X.; Wang, C. Multi-roll levelling for wave defects of metal sheets based on the beam-membrane method. Int. J. Adv. Manuf. Technol. 2019, 105, 4783–4795. [Google Scholar] [CrossRef]
- Argandoña, S.d.; Silvestre, E.; Garcia, D.; Mendiguren, J.; Galdos, L. Energy Efficient Servo Controlled Roll Levelling Machines. Key Eng. Mater. 2016, 716, 413–419. [Google Scholar] [CrossRef]
- Lee, J.-B.; Kang, S.-S. Numerical modeling of roller leveler for thick plate leveling. Int. J. Precis. Eng. Manuf. 2018, 19, 425–430. [Google Scholar] [CrossRef]
- Soares, J.P. Design and Pre-Dimensioning of the Upper Cassette of an Intelligent Roller Leveler. Master’s Thesis, Faculty of Engineering, University of Porto, Porto, Portugal, 2022. [Google Scholar]
- ZhaoDong, L.; XinJun, S.; WenQuan, C.; QiLong, Y.; ZhiGang, Y.; Han, D.; YuQing, W. Ausforming effects on anisotropy of mechanical properties in HSLA martensitic steel. Sci. China Technol. Sci. 2012, 55, 1806–1813. [Google Scholar] [CrossRef]
- Atreya, V.; Dokkum, J.S.V.; Bos, C.; Santofimia, M.J. Effect of the anisotropy of martensitic transformation on ferrite deformation in Dual-Phase steels. Mater. Des. 2022, 219, 110805. [Google Scholar] [CrossRef]
- Heibel, S.; Dettinger, T.; Nester, W.; Clausmeyer, T.; Tekkaya, A.E. Damage Mechanisms and Mechanical Properties of High-Strength Multiphase Steels. Materials 2018, 11, 761. [Google Scholar] [CrossRef] [PubMed]
- Manopulo, N.; Barlat, F.; Hora, P. Isotropic to distortional hardening transition in metal plasticity. Int. J. Solids Struct. 2015, 56–57, 11–19. [Google Scholar] [CrossRef]
- Liu, S.; Kouadri-Henni, A.; Gavrus, A. Numerical simulation and experimental investigation on the residual stresses in a laser beam welded dual phase DP600 steel plate: Thermomechanical material plasticity model. Int. J. Mech. Sci. 2017, 122, 235–243. [Google Scholar] [CrossRef]
- Dratz, B.; Nalewajk, V.; Bikard, J.; Chastel, Y. Testing and modelling the behaviour of steel sheets for roll levelling applications. Int. J. Mater. Form. 2009, 2, 519–522. [Google Scholar] [CrossRef]
- Doege, E.; Menz, R.; Huinink, S. Analysis of the levelling process based upon an analytic forming model. Cirp Ann.-Manuf. Technol. 2002, 51, 191–194. [Google Scholar] [CrossRef]
- Abeyrathna, B.; Rolfe, B.; Hodgson, P.; Weiss, M. A first step towards a simple in-line shape compensation routine for the roll forming of high strength steel. Int. J. Mater. Form. 2016, 9, 426–434. [Google Scholar] [CrossRef]
- Tsang, K.S.; Ion, W.; Blackwell, P.; English, M. Industrial validation of strain in cold roll forming of UHSS. Procedia Manuf. 2018, 15, 788–795. [Google Scholar] [CrossRef]
- Kang, W.; Zhao, Y.; Yu, W.; Wang, S.; Ma, Y.; Yan, P. Numerical simulation and parameters analysis for roll forming of martensitic steel MS980. Procedia Eng. 2014, 81, 251–256. [Google Scholar] [CrossRef][Green Version]
- Li, Q.-M.; Yi, Z.-W.; Liu, Y.-Q.; Tang, X.-F.; Jiang, W.; Li, H.-J. Explicit Analysis of Sheet Metal Forming Processes Using Solid-Shell Elements. Metals 2021, 12, 52. [Google Scholar] [CrossRef]
- Moneke, M.; Groche, P. Control of residual stresses in roll forming through targeted adaptation of the roll gap. Int. J. Solids Struct. 2021, 294, 117129. [Google Scholar] [CrossRef]
- Mathieu, N.; Potier-Ferry, M.; Zahrouni, H. Reduction of flatness defects in thin metal sheets by a pure tension leveler. Int. J. Mech. Sci. 2017, 122, 267–276. [Google Scholar] [CrossRef]
- Lenard, J.G. Measurements of Friction in Cold Flat Rolling. J. Mater. Shap. Technol. 1991, 9, 171–180. [Google Scholar] [CrossRef]
- Tieu, A.K.; Liu, Y.J. Friction variation in the cold-rolling process. Tribol. Int. 2004, 37, 177–183. [Google Scholar] [CrossRef]
- Huo, T.; Nakamachi, E. Evaluation of the dynamic explicit/elastoviscoplastic finite-element method in sheet-forming simulation. J. Mater. Process. Technol. 1995, 50, 180–196. [Google Scholar] [CrossRef]
- Chang, Z.; Chen, J. Mechanism of the twisting in incremental sheet forming process. J. Mater. Process. Tech. 2020, 276, 116396. [Google Scholar] [CrossRef]
- Wang, T.; Huang, Q.X.; Xiao, H.; Qi, X.D. Modification of Roll Flattening Analytical Model Based on the Plane Assumption. Chin. J. Mech. Eng. 2018, 31, 46. [Google Scholar] [CrossRef]
- Abeyrathna, B.; Rolfe, B.; Hodgson, P.; Weiss, M. Local deformation in roll forming. Int. J. Adv. Manuf. Technol. 2017, 88, 2405–2415. [Google Scholar] [CrossRef]
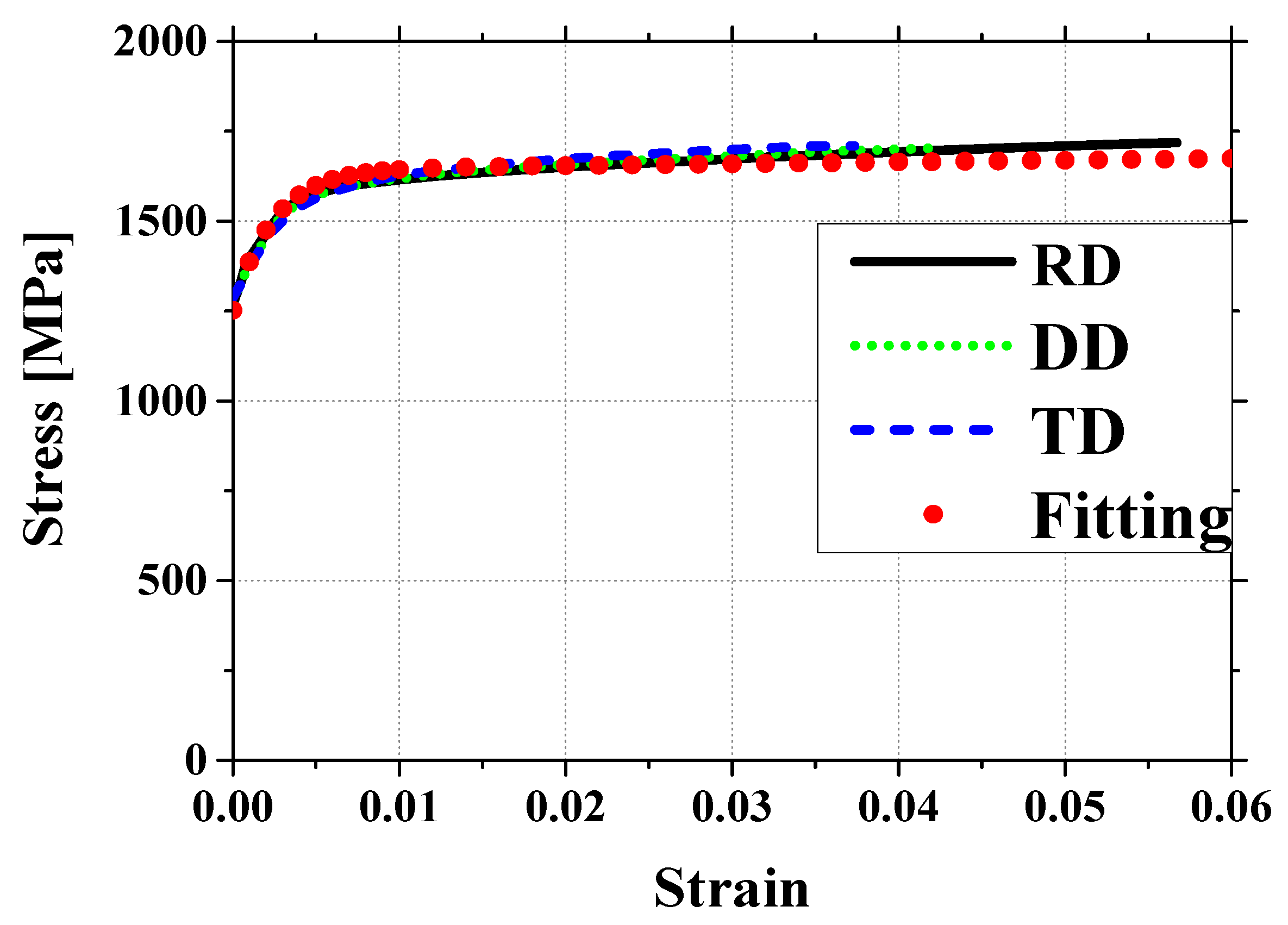




| Parameter | Value |
|---|---|
| Young’s modulus | 217,000 |
| Poisson’s ratio | 0.33 |
| 1251.73 | |
| 392.74 | |
| 419.64 | |
| 500 |
| Roll Gap (Unit: mm) | Twist (Unit: Degree) | Crossbow (Unit: mm) |
|---|---|---|
| 1.3 | 0.532 | 0.138 |
| 1.1 | 0.356 | 0.002 |
| 0.9 | 0.481 | 0.326 |
| 0.7 | 0.730 | 0.245 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, Y.; Jeong, K.; Kim, G.-h.; Yoon, J. 1.5 GPa Grade High-Strength Steel Sheet Flattening by Roll Gap Adjustment Considering Pattern Roll Effects. Materials 2025, 18, 1702. https://doi.org/10.3390/ma18081702
Jeon Y, Jeong K, Kim G-h, Yoon J. 1.5 GPa Grade High-Strength Steel Sheet Flattening by Roll Gap Adjustment Considering Pattern Roll Effects. Materials. 2025; 18(8):1702. https://doi.org/10.3390/ma18081702
Chicago/Turabian StyleJeon, Youngjin, Kyucheol Jeong, Geun-ho Kim, and Jonghun Yoon. 2025. "1.5 GPa Grade High-Strength Steel Sheet Flattening by Roll Gap Adjustment Considering Pattern Roll Effects" Materials 18, no. 8: 1702. https://doi.org/10.3390/ma18081702
APA StyleJeon, Y., Jeong, K., Kim, G.-h., & Yoon, J. (2025). 1.5 GPa Grade High-Strength Steel Sheet Flattening by Roll Gap Adjustment Considering Pattern Roll Effects. Materials, 18(8), 1702. https://doi.org/10.3390/ma18081702






