Micromagnetic and Quantitative Prediction of Hardness and Impact Energy in Martensitic Stainless Steels Using Mutual Information Parameter Screening and Random Forest Modeling Methods
Abstract
1. Introduction
2. Experimental
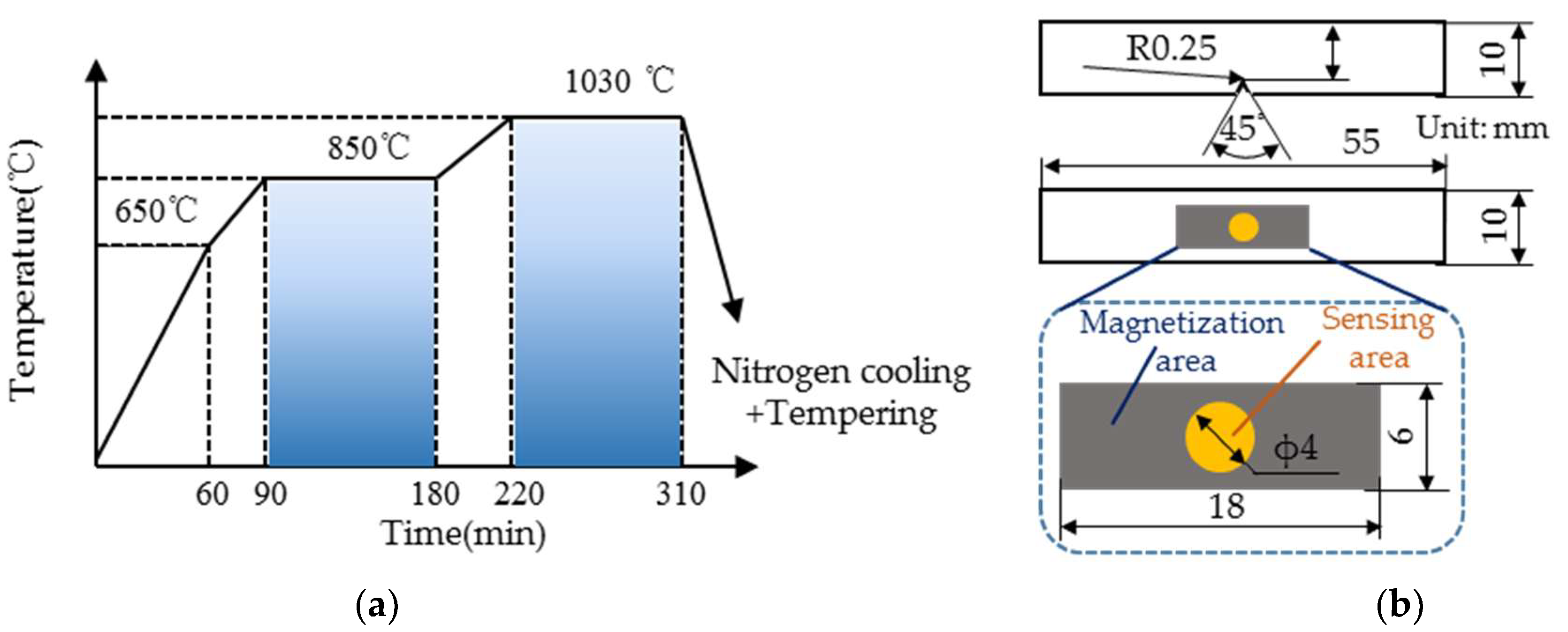
2.1. Specimen Preparation
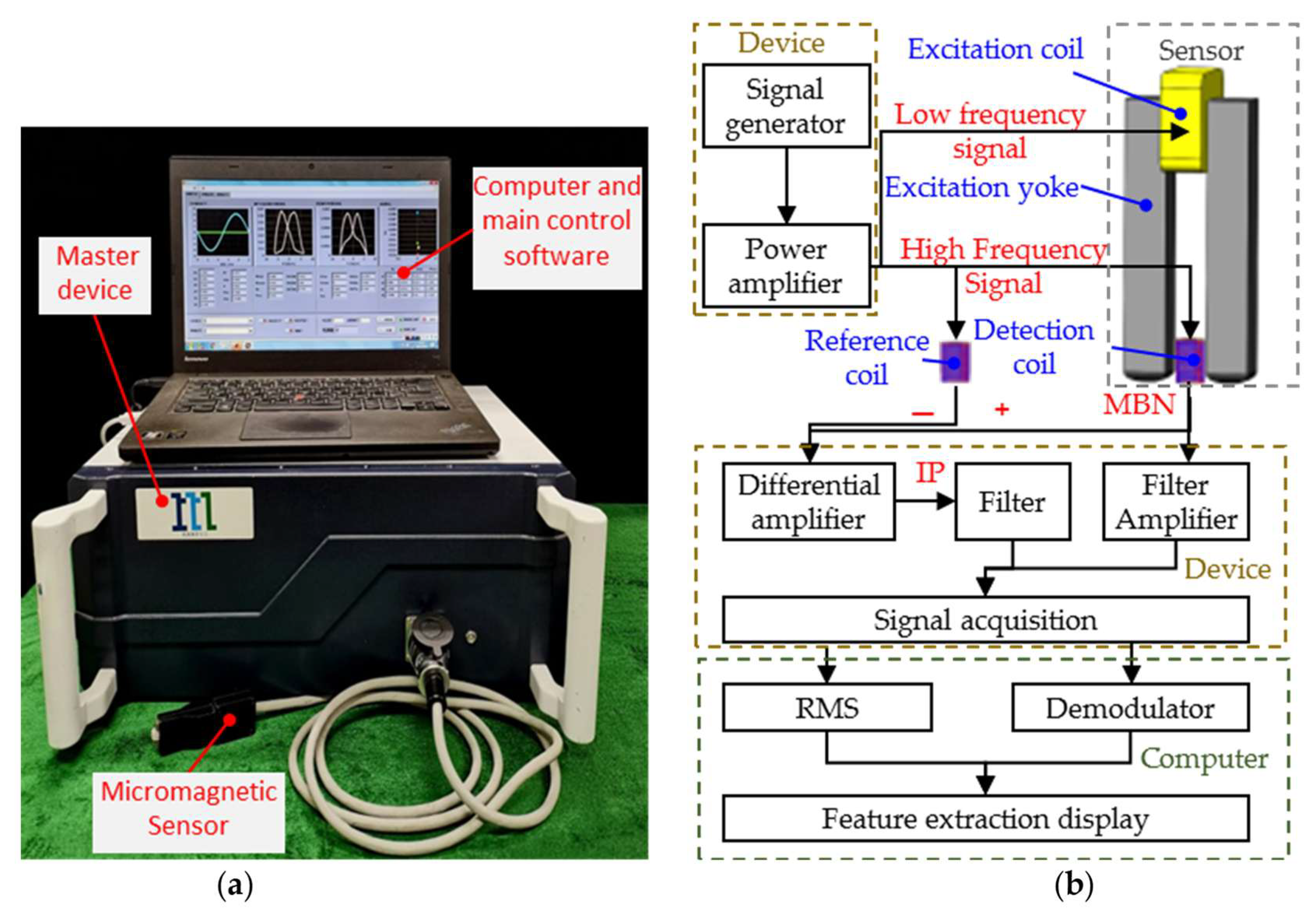
2.2. Micromagnetic Testing
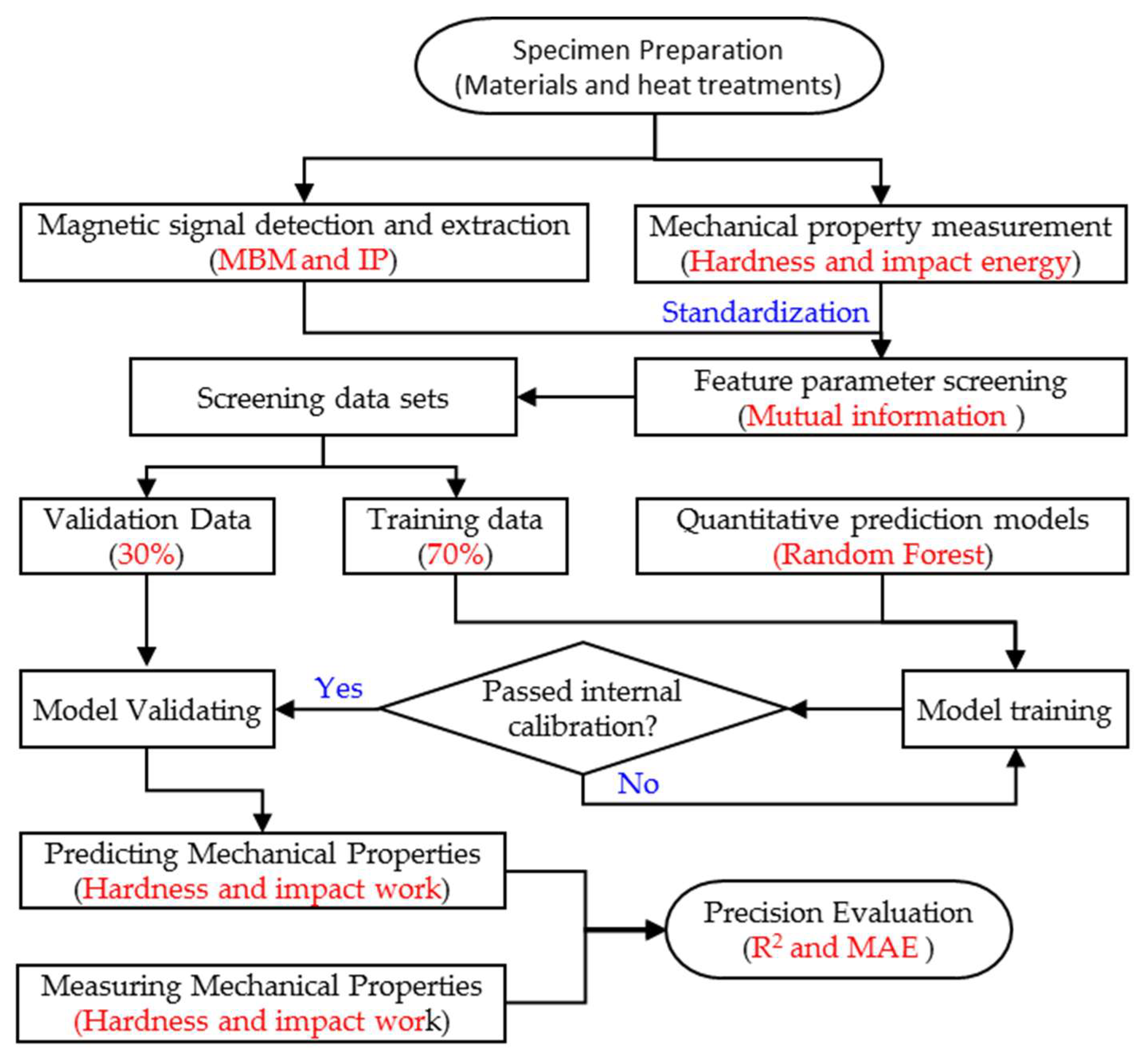
3. Modeling
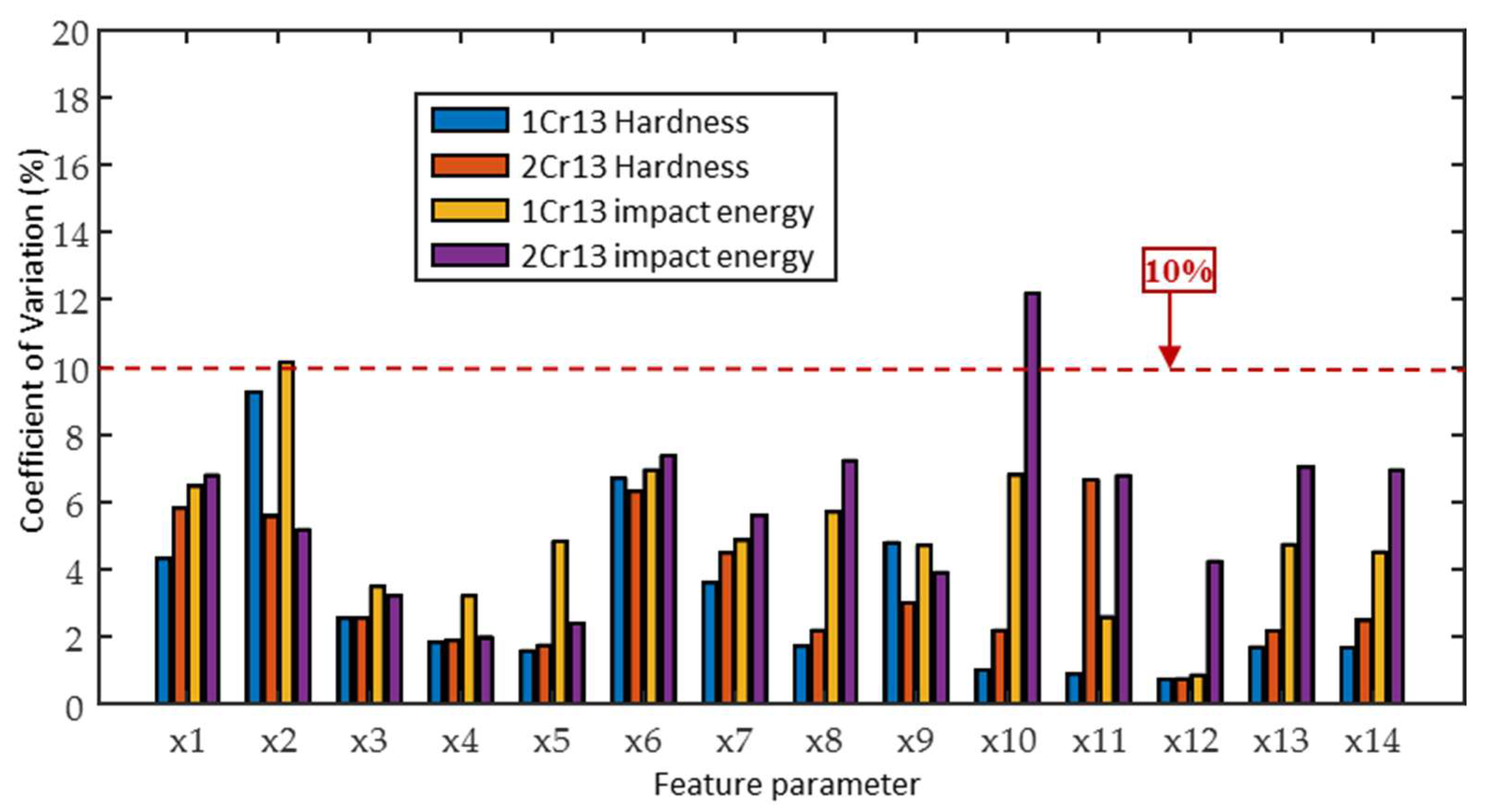
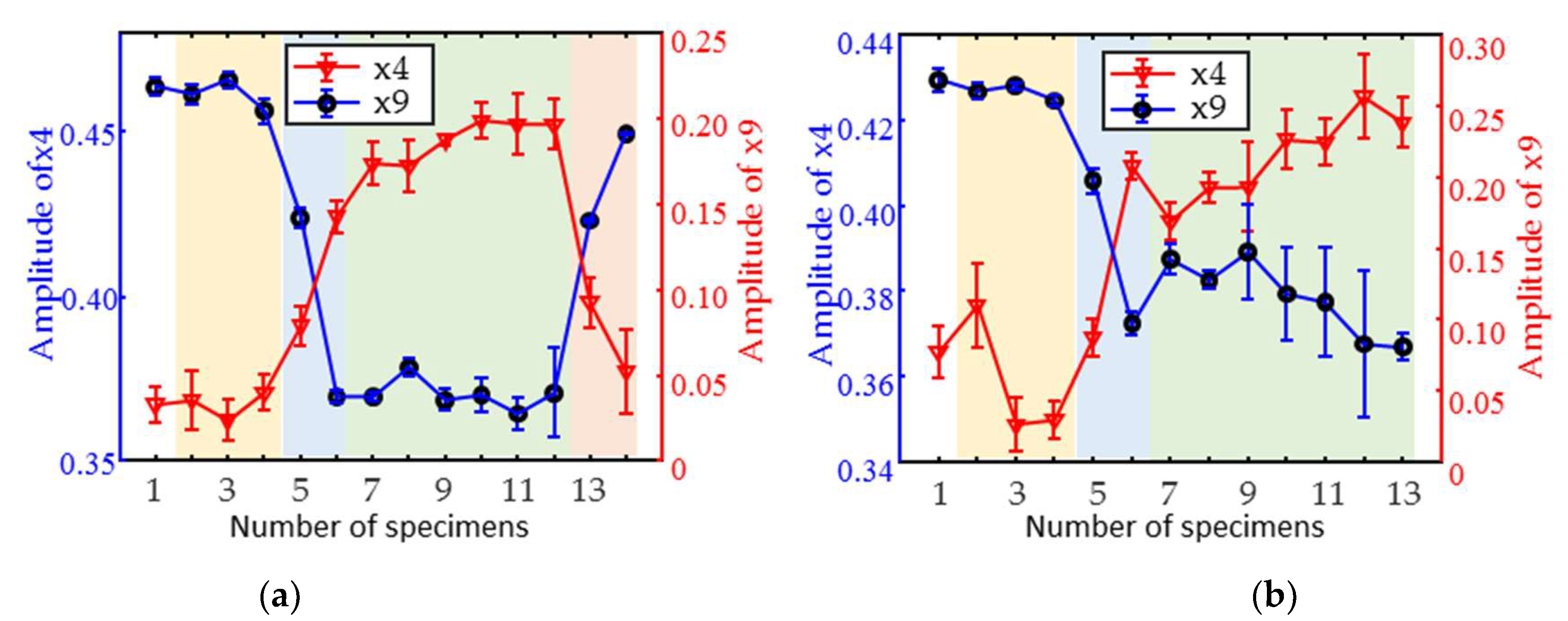
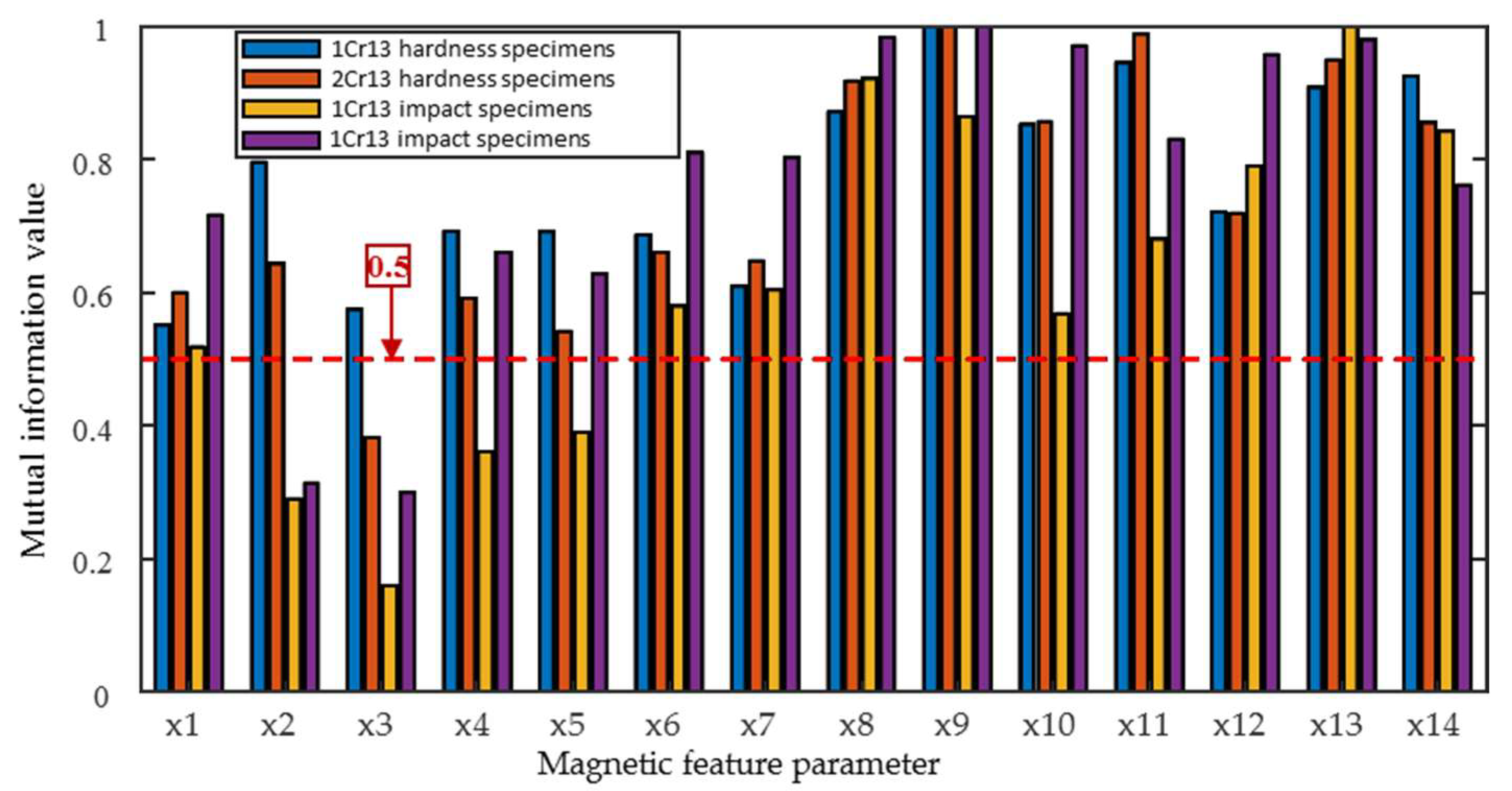
3.1. Feature Parameters Screening
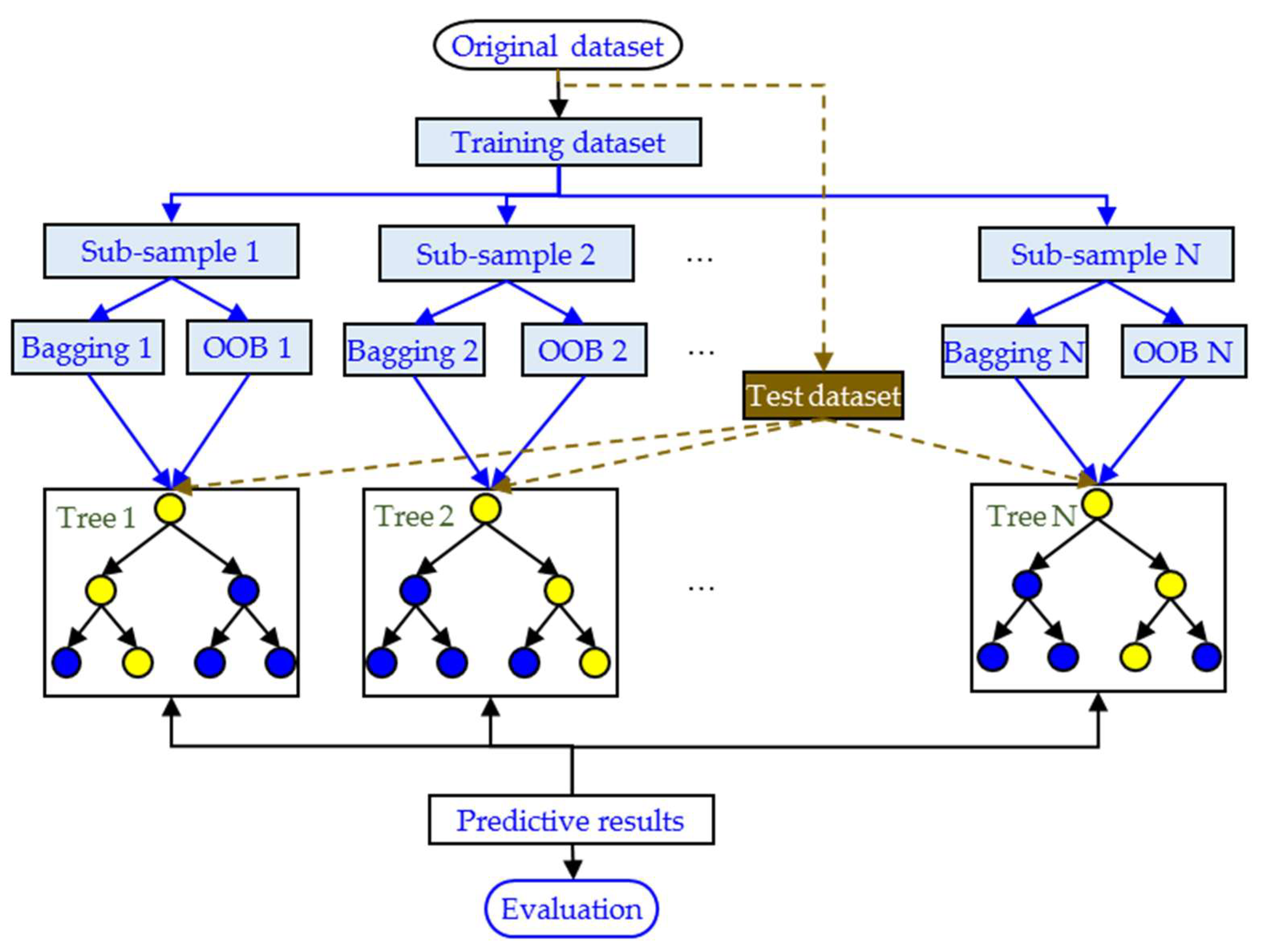
3.2. Random Forest Modeling
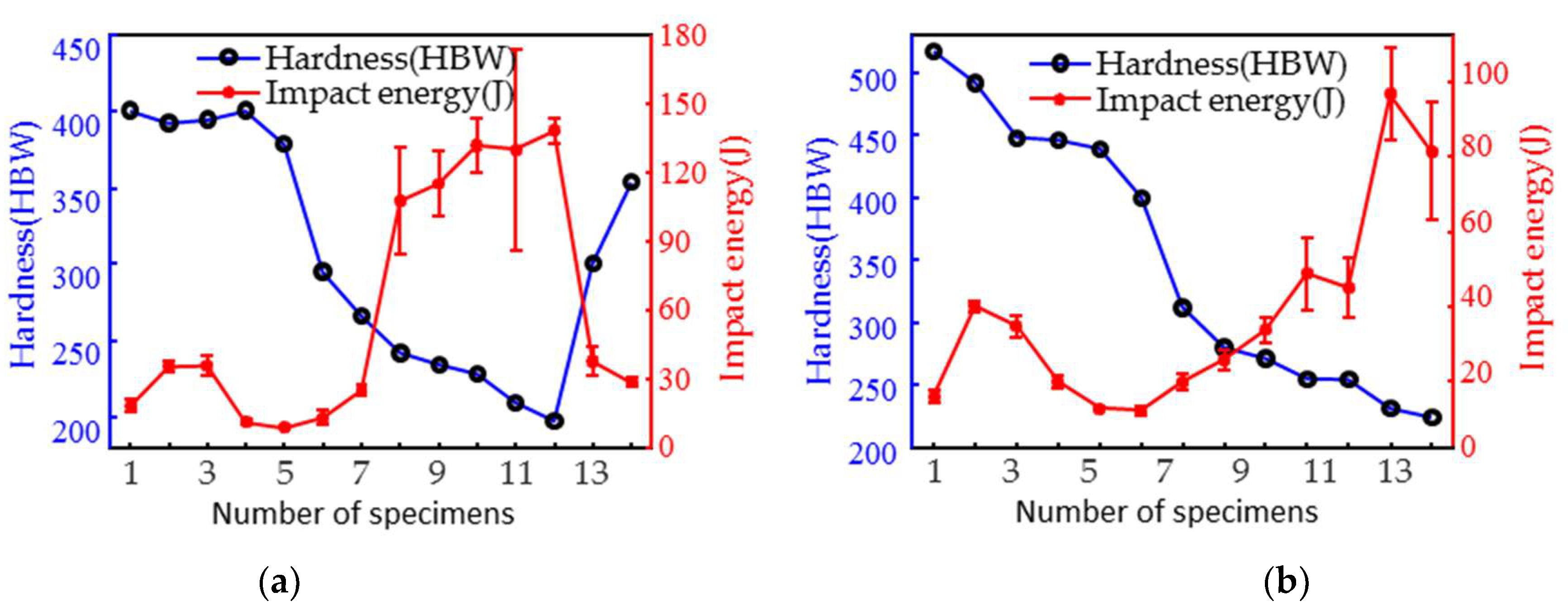
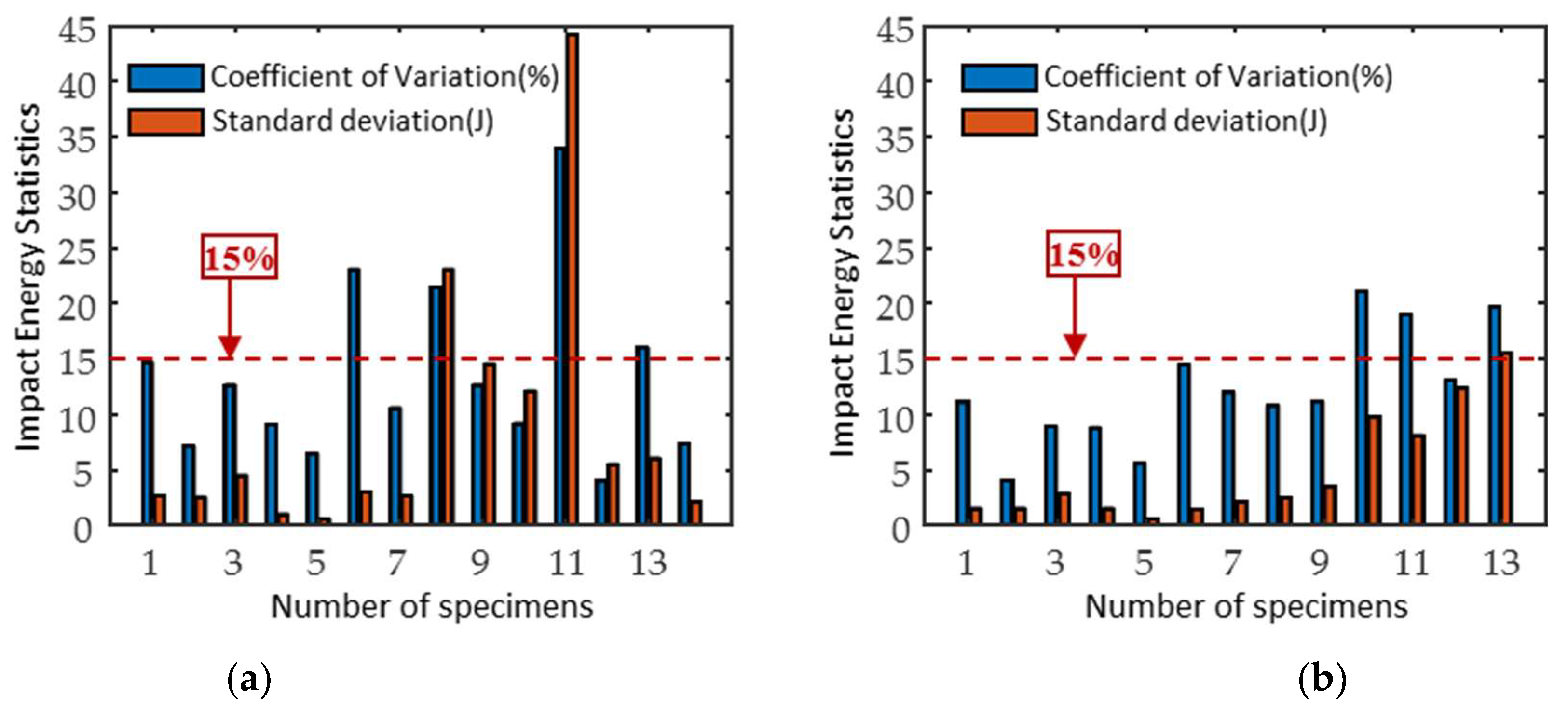
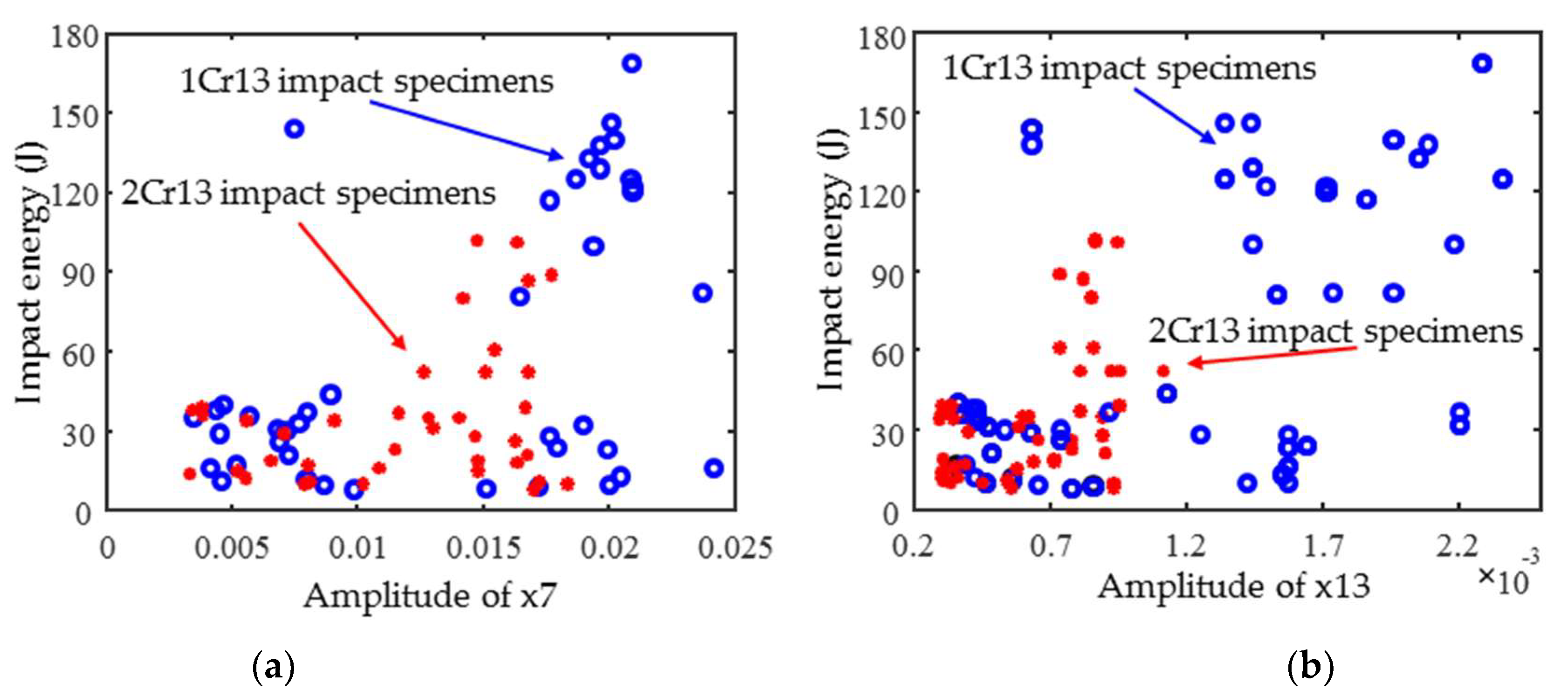
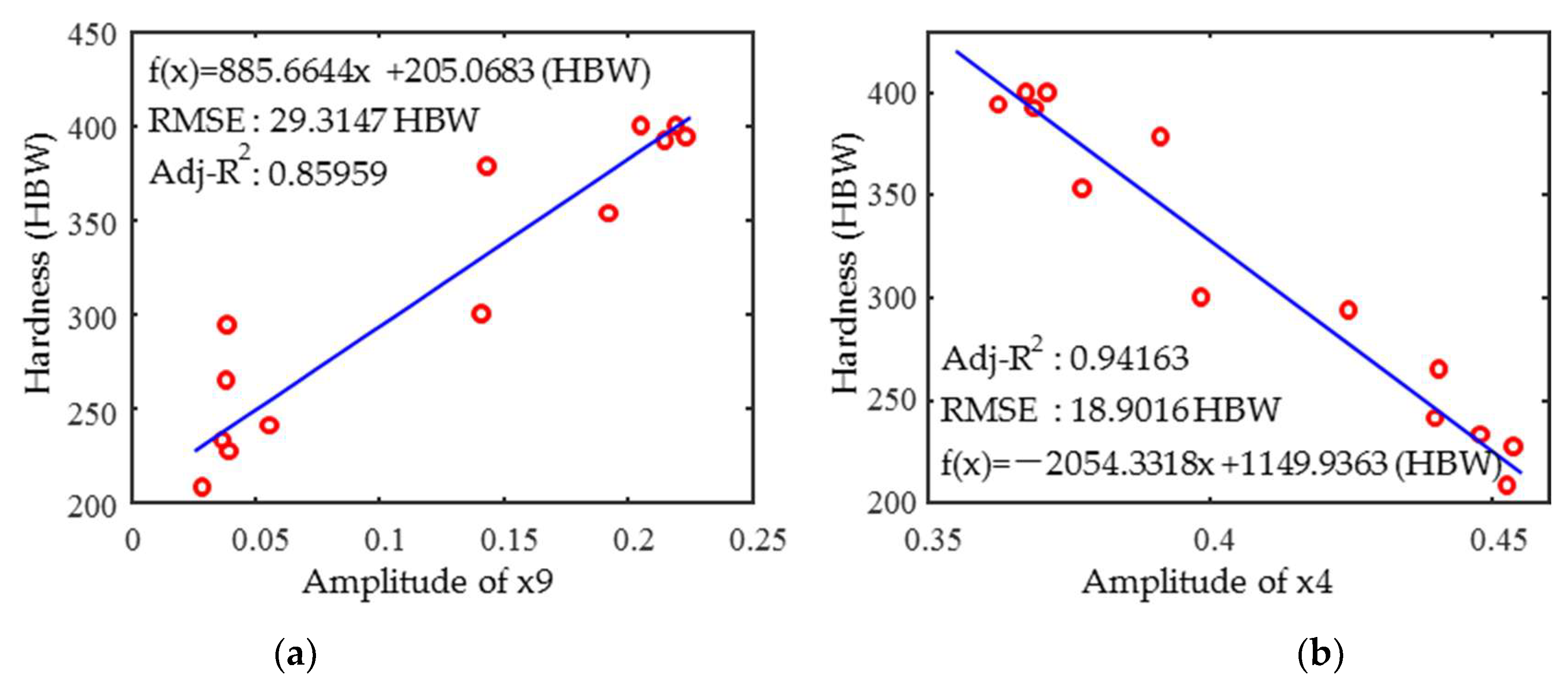
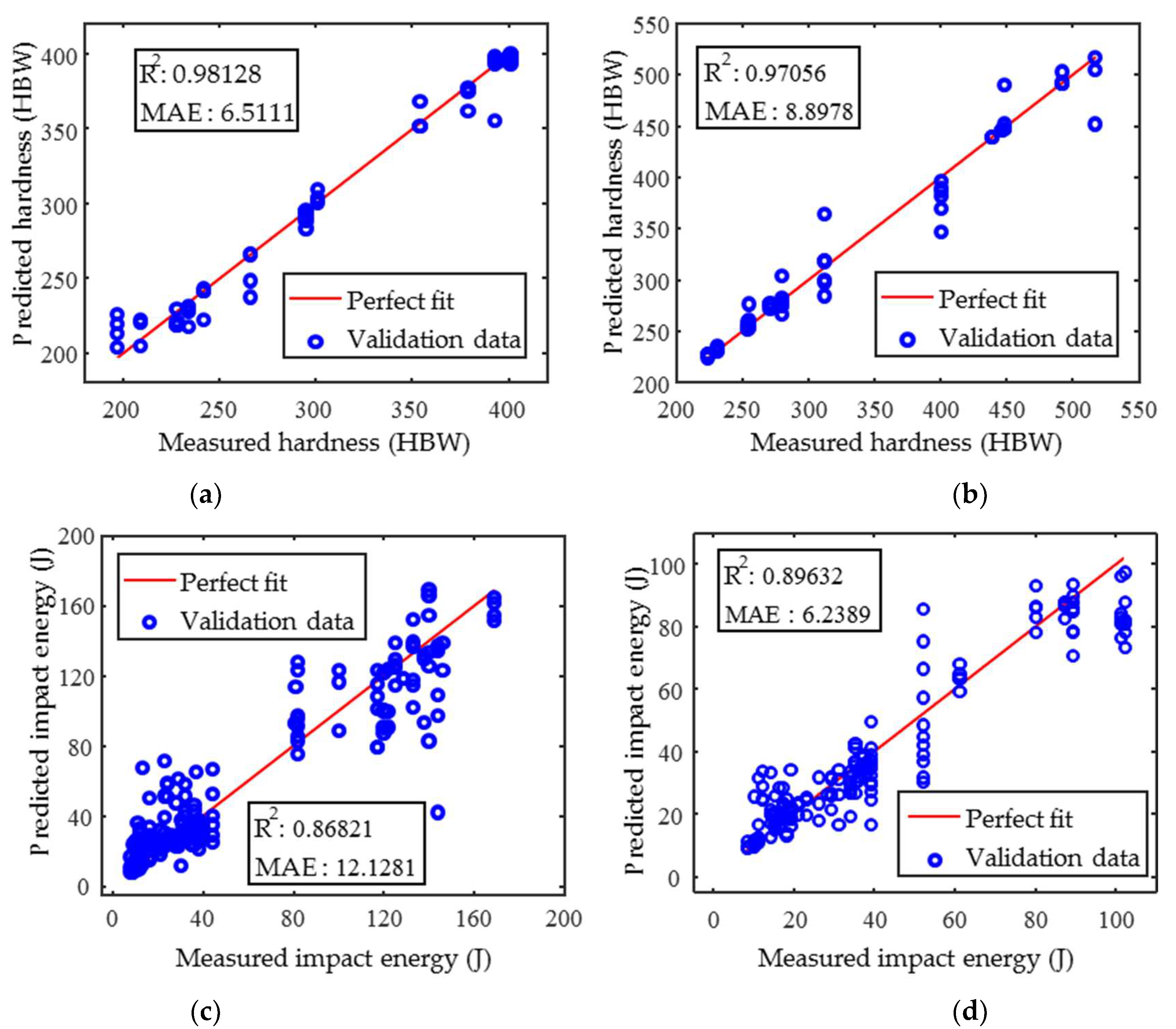
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Soutis, C.; Goutas, A.; Smith, P.A. Advances in ultrasonic evaluation of impact damage in carbon fiber-reinforced polymer composites. Compos. Part B Eng 2021, 215, 108776. [Google Scholar]
- Prakash, R.; Bhattacharya, D.; Sharma, S.K. Correlation between ultrasonic velocity and impact toughness in metallic materials: A review. NDTE Int. 2019, 107, 102145. [Google Scholar]
- He, J.; Yang, F.; Wang, H.; Sun, X.; Zhu, Y.; Wang, Y.; Guan, X. A physics-based acoustic emission energy method for mixed-mode impact damage prediction of composite laminates. Ultrasonics 2024, 145, 107490. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Zhao, J.; Qiao, H.; Liu, X. Real-time monitoring of laser shock peening surface hardness using acoustic emission keyframes. Appl. Opt. 2021, 60, 3114–3121. [Google Scholar] [PubMed]
- Baak, N.; Hajavifard, R.; Lücker, L.; Rozo Vasquez, J.; Strodick, S.; Teschke, M.; Walther, F. Micromagnetic approaches for microstructure analysis and capability assessment. Mater. Charact. 2021, 175, 111189. [Google Scholar]
- Wolter, B.; Dobmann, G. Micromagnetic Testing for Rolled Steel. Steel Res. Int. 2023, 94, 2200145. [Google Scholar]
- Szielasko, K.; Wolter, B.; Tschuncky, R.; Youssef, S. Micromagnetic materials characterization using machine learning. Tm-Tech. Mess. 2023, 197, 112158. [Google Scholar]
- Wolter, B.; Gabi, Y.; Conrad, C. Nondestructive Testing with 3MA—An Overview of Principles and Applications. Appl. Sci. 2019, 9, 1068. [Google Scholar] [CrossRef]
- Hanke, R. Expanding the potential of NDT across the entire product life cycle. In Proceedings of the 55th Annual Conference of the British Institute of Non-Destructive Testing, Nottingham, UK, 12–14 September 2016; pp. 305–308. [Google Scholar]
- Franco, F.A.; González, M.F.R. Relation Between Magnetic Barkhausen Noise and Hardness for Jominy Quench Tests in SAE 4140 and 6150 Steels. J. Nondestruct. Eval. 2013, 32, 93–103. [Google Scholar]
- Luo, X.; Wang, Y.; Wang, L. Non-destructive hardness measurement of hot-stamped high strength steel sheets based on magnetic Barkhausen noise. Procedia Eng. 2014, 81, 1768–1773. [Google Scholar]
- Vértesy, G.; Rabung, M.; Gasparics, A.; Uytdenhouwen, I.; Griffin, J.; Algernon, D. Evaluation of the embrittlement in reactor pressure-vessel steels using a hybrid nondestructive electromagnetic testing and evaluation approach. Materials 2024, 17, 1106. [Google Scholar] [CrossRef]
- Deng, Y.; Li, Z.; Chen, J. The Effects of the Structure Characteristics on Magnetic Barkhausen Noise in Commercial Steels. J. Magn. Magn. Mater. 2018, 451, 276–282. [Google Scholar]
- Gupta, B.; Uchimoto, T.; Ducharne, B. Magnetic Incremental Permeability Non-destructive Evaluation of 12 Cr-Mo-W-V Steel Creep Test Samples with Varied Ageing Levels and Thermal Treatments. NDT E Int. 2019, 104, 42–50. [Google Scholar]
- Ghanei, S.; Alam, A.S.; Kashefi, M. Nondestructive characterization of microstructure and mechanical properties of intercritically annealed dual-phase steel by magnetic Barkhausen noise technique. Mater. Sci. Eng. A 2014, 607, 253–260. [Google Scholar]
- Nahak, B.; Srivastava, A. Non-destructive monitoring of electro-discharge machined die steel. Arab. J. Sci. Eng. 2022, 47, 15153–15160. [Google Scholar]
- Akhlaghi, I.A.; Haghighi, M.S.; Kahrobaee, S. Prediction of chemical composition and mechanical properties in powder metallurgical steels using multi-electromagnetic nondestructive methods and a data fusion system. J. Magn. Magn. Mater. 2020, 498, 166095. [Google Scholar]
- Sorsa, A.; Leivisk, K.; Santa-Aho, S. Quantitative prediction of residual stress and hardness in case-hardened steel based on the Barkhausen noise measurement. NDT E Int. 2012, 46, 100–106. [Google Scholar]
- Kahrobaee, S.; Hejazi, T.H.; Akhlaghi, I.A. Electromagnetic methods to improve the nondestructive characterization of induction hardened steels: A statistical modeling approach. Surf. Coat. Technol. 2019, 380, 125074. [Google Scholar]
- Jedamski, R.; Epp, J. Non-destructive micromagnetic determination of hardness and case hardening depth using linear regression analysis and artificial neural networks. Metals 2021, 11, 18. [Google Scholar]
- Yan, Z.X.; Sun, G.M.; Liu, X.C. Filternet: A deep convolutional neural network for measuring plastic deformation from raw Barkhausen noise waveform. J. Magn. Magn. Mater. 2022, 555, 169330. [Google Scholar]
- Akhlaghi, I.A.; Kahrobaee, S.; Nezhad, K.K. An accurate non-destructive method for determining mechanical properties of plain carbon steel parts using MHL and GRNN. Nondestruct. Test. Eval. 2020, 36, 278–296. [Google Scholar] [CrossRef]
- Sheng, H.; Wang, P.; Tang, C. Predicting mechanical properties of cold-rolled steel strips using micro-magnetic NDT technologies. Materials 2022, 15, 2151. [Google Scholar] [CrossRef] [PubMed]
- Xing, Z.; Wang, X.; Ning, M.; He, C.; Liu, X. Micromagnetic and Robust Evaluation of Surface Hardness in Cr12MoV Steel Considering Repeatability of the Instrument. Sensors 2023, 23, 1273. [Google Scholar] [CrossRef]
- Wang, X.; Cai, Y.; Liu, X.; He, C. Quantitative prediction of surface hardness in Cr12MoV steel and S136 steel with two magnetic Barkhausen noise feature extraction methods. Sensors 2024, 24, 2051. [Google Scholar] [CrossRef] [PubMed]
- Dong, H.J.; Liu, X.C.; Song, Y.H. Quantitative evaluation of residual stress and surface hardness in deep drawn parts based on magnetic Barkhausen noise technology. Measurement 2021, 168, 108473. [Google Scholar] [CrossRef]
- Wang, X.X.; He, C.F.; Li, P. Micromagnetic and quantitative prediction of surface hardness in carbon steels based on a joint classification-regression method. J. Nondestruct. Eval. 2022, 41, 62. [Google Scholar] [CrossRef]
- Al-Qutayri, M.; Al-Ani, A.; Abu-Rub, H. Yield Strength Estimation Using Eddy Current Signals and Random Forest Algorithm. J. Magn. Magn. Mater. 2023, 573, 170068. [Google Scholar]
- Wang, L.; Liu, Y.; Zhao, J. Hardness Prediction via Incremental Permeability and Support Vector Regression. Mater. Sci. Eng. A 2023, 831, 142528. [Google Scholar]
- Qiu, F.; Fu, W.; Wu, W.; Zhang, H.; Shi, W.; Zhang, Y.; Li, D. Electromagnetic-Acoustic Sensing-Based Multi-Feature Fusion Method for Stress Assessment and Prediction. J. Nondestruct. Eval. 2024, 43, 66. [Google Scholar] [CrossRef]
- GB/T 229-2007; Metallic Materials—Charpy Pendulum Impact Test Method. Standardization Administration of China: Beijing, China, 2007.


| Elements | C | Mn | Si | P | Cr | Mo | Ni | V | Cu | S | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Alloy | |||||||||||
| 1Cr13 | 0.133 | 0.487 | 0.352 | 0.020 | 12.00 | 0.029 | 0.488 | 0.050 | 0.043 | <0.005 | |
| 2Cr13 | 0.189 | 0.504 | 0.330 | 0.023 | 13.18 | 0.041 | 0.384 | 0.060 | 0.058 | <0.005 | |
| Signal Type | Indicators | Descriptions |
|---|---|---|
| Barkhausen Noise | x1 | Peak height of the MBN butterfly curve |
| x2 | Peak position of the MBN butterfly curve | |
| x3 | Full width at 75% of maxima of the MBN butterfly curve | |
| x4 | Full width at half maxima of the MBN butterfly curve | |
| x5 | Full width at 25% of maxima of the MBN butterfly curve | |
| x6 | Intercept of the MBN envelope at the vertical axis | |
| x7 | Mean value of the MBN envelope for a single magnetization cycle | |
| Incremental magnetic permeability | x8 | Peak height of the IP butterfly curve |
| x9 | Peak position of the IP butterfly curve | |
| x10 | Full width at 75% of maxima of the IP butterfly curve | |
| x11 | Full width at half maxima of the IP butterfly curve | |
| x12 | Full width at 25% of maxima of the IP butterfly curve | |
| x13 | Intercept of the IP envelope at the vertical axis | |
| x14 | Mean value of the IP envelope for a single magnetization cycle |
| Operational conditions | Properties | Units |
|---|---|---|
| Low frequency excitation | Frequency | 200 Hz |
| Amplitude | 1 App | |
| Cycle | 5 | |
| High Frequency excitation | Frequency | 100 kHz |
| Amplitude | 0.5 Vpp | |
| Sampling | Rate | 2 MS/s |
| Point | 50,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, C.; Dong, H.; Yan, Z.; Wang, L.; Ning, M.; Liu, X.; He, C. Micromagnetic and Quantitative Prediction of Hardness and Impact Energy in Martensitic Stainless Steels Using Mutual Information Parameter Screening and Random Forest Modeling Methods. Materials 2025, 18, 1685. https://doi.org/10.3390/ma18071685
Xu C, Dong H, Yan Z, Wang L, Ning M, Liu X, He C. Micromagnetic and Quantitative Prediction of Hardness and Impact Energy in Martensitic Stainless Steels Using Mutual Information Parameter Screening and Random Forest Modeling Methods. Materials. 2025; 18(7):1685. https://doi.org/10.3390/ma18071685
Chicago/Turabian StyleXu, Changjie, Haijiang Dong, Zhengxiang Yan, Liting Wang, Mengshuai Ning, Xiucheng Liu, and Cunfu He. 2025. "Micromagnetic and Quantitative Prediction of Hardness and Impact Energy in Martensitic Stainless Steels Using Mutual Information Parameter Screening and Random Forest Modeling Methods" Materials 18, no. 7: 1685. https://doi.org/10.3390/ma18071685
APA StyleXu, C., Dong, H., Yan, Z., Wang, L., Ning, M., Liu, X., & He, C. (2025). Micromagnetic and Quantitative Prediction of Hardness and Impact Energy in Martensitic Stainless Steels Using Mutual Information Parameter Screening and Random Forest Modeling Methods. Materials, 18(7), 1685. https://doi.org/10.3390/ma18071685








