A Deformational Analysis of a Titanium Alloy Supported by the Mathematical Modelling of the Sheet Metal Forming Process via Numerical Simulation
Abstract
1. Introduction
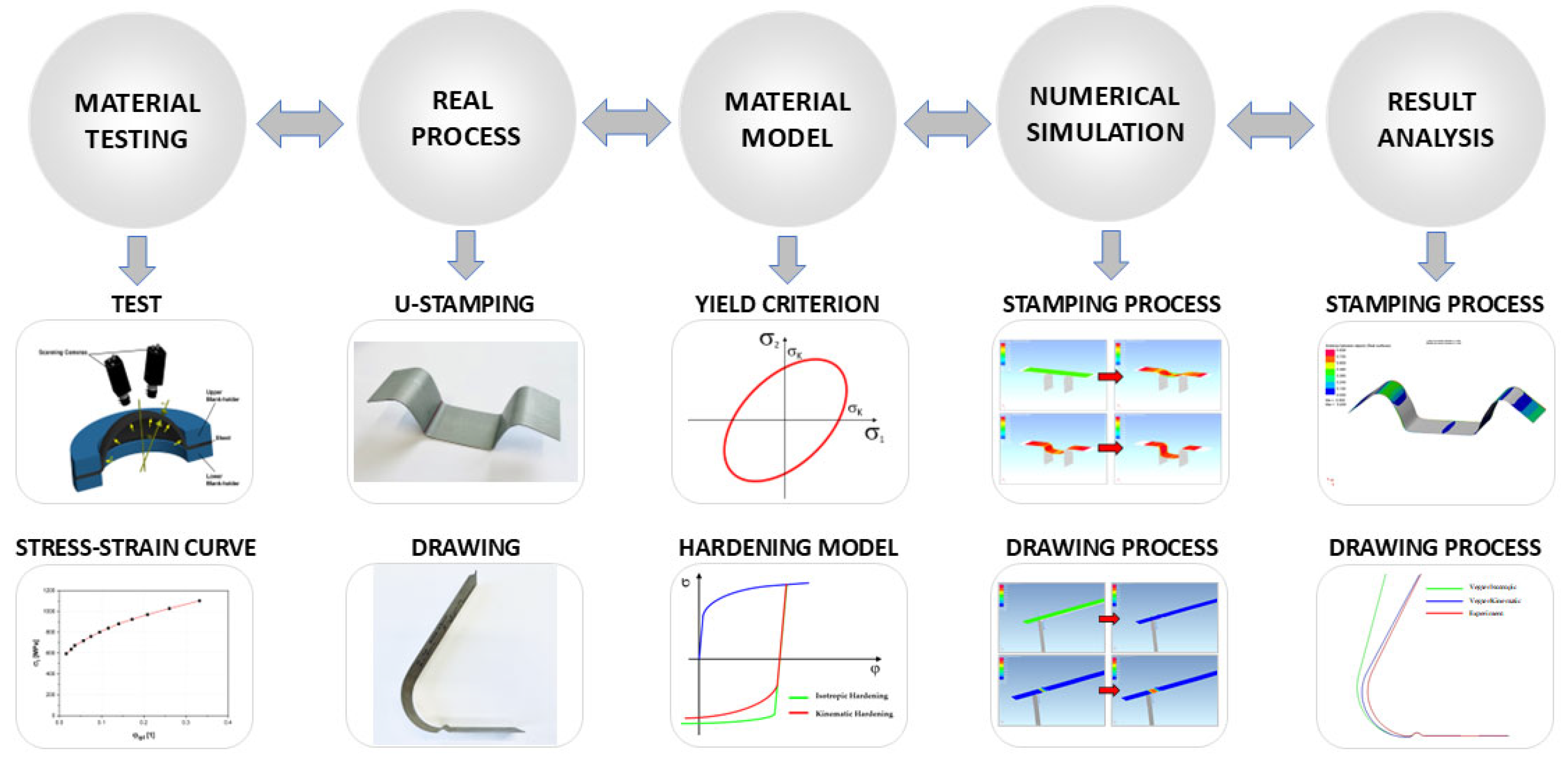
2. Materials and Methods
2.1. Material
Titanium Grade 3 AMS4900
2.2. Mechanical Testing of Material
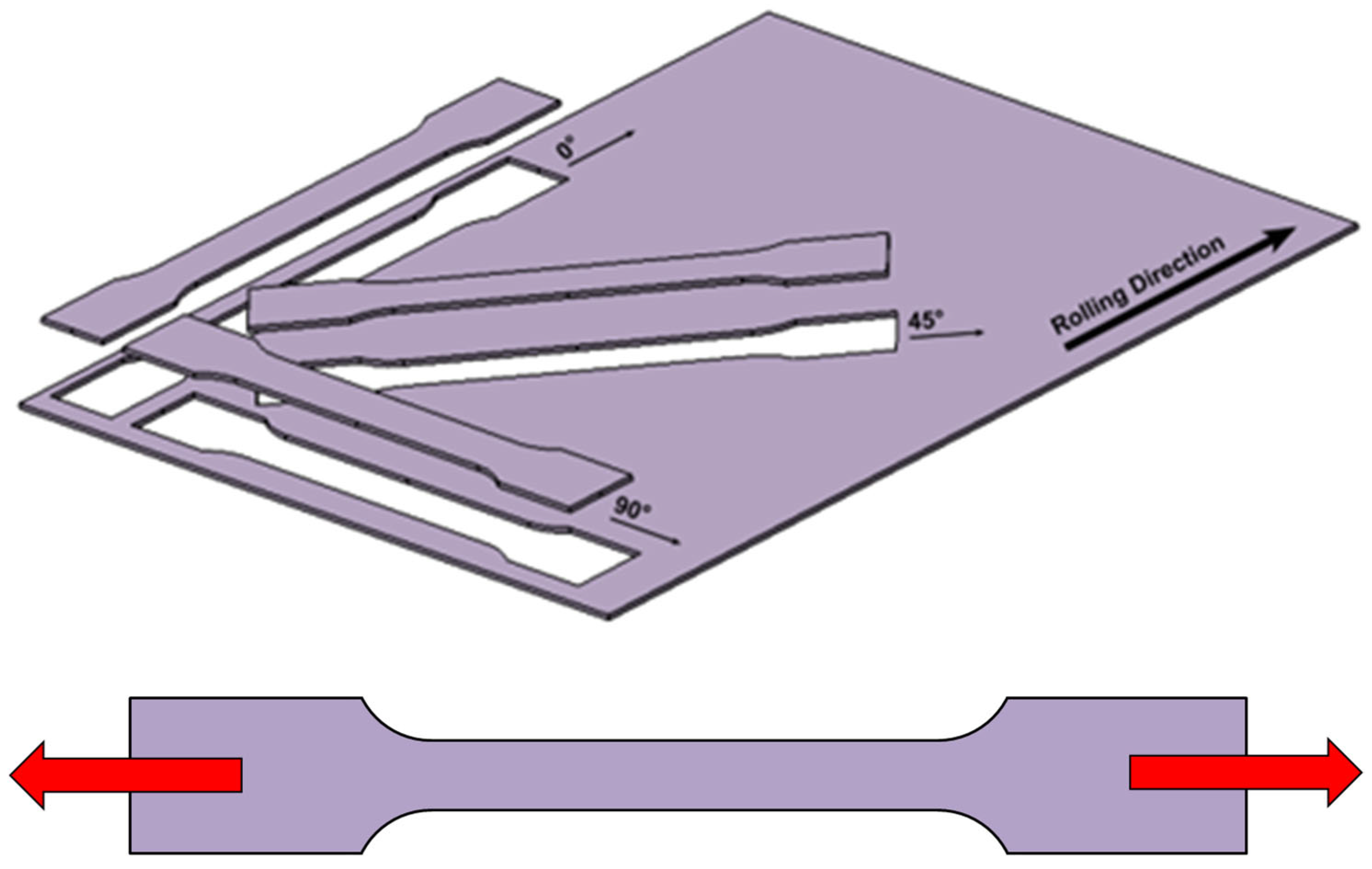
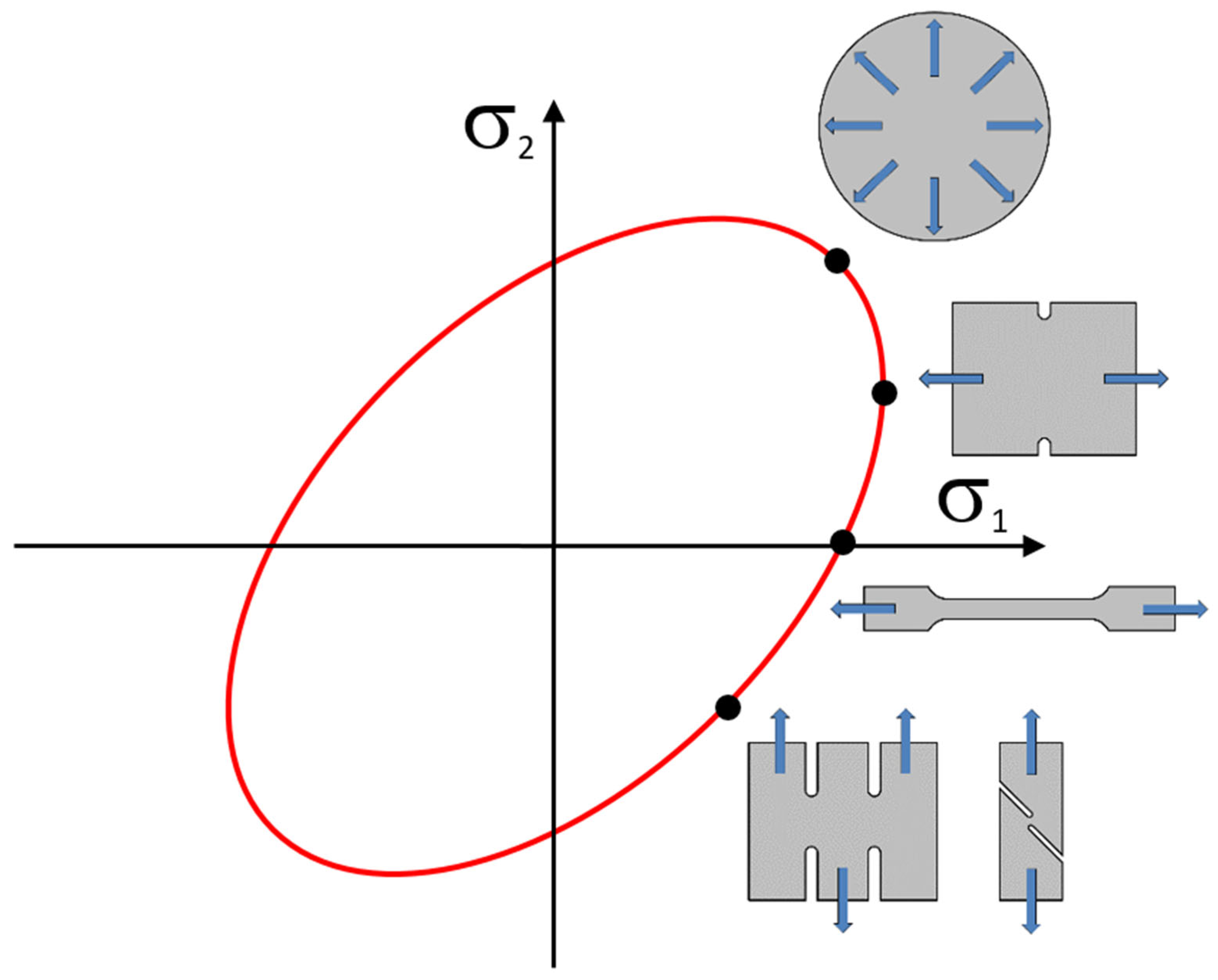
2.2.1. Static Tensile Test
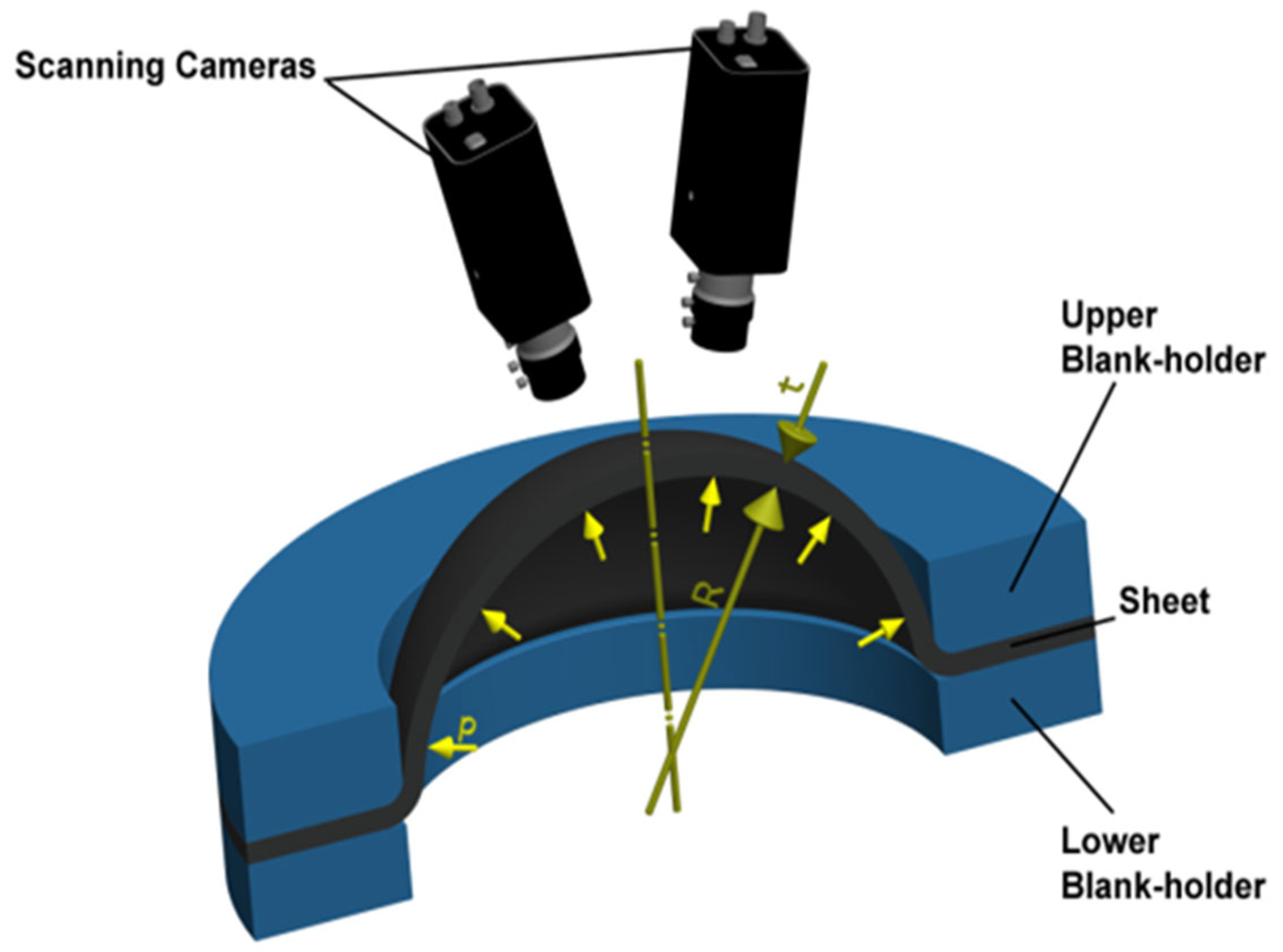
2.2.2. Hydraulic Bulge Test
2.2.3. Plane Strain Tensile Test
2.2.4. Shear Test
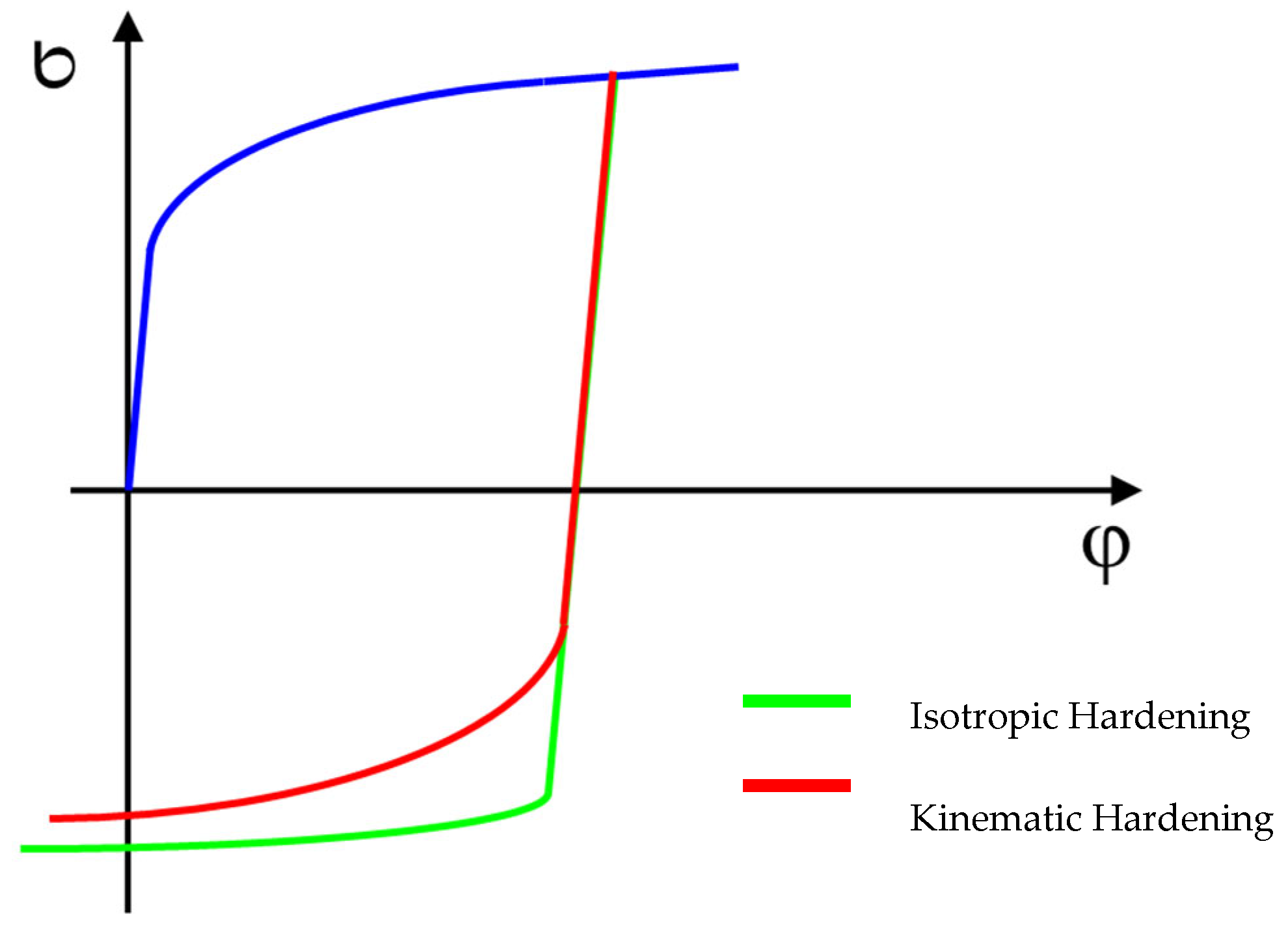
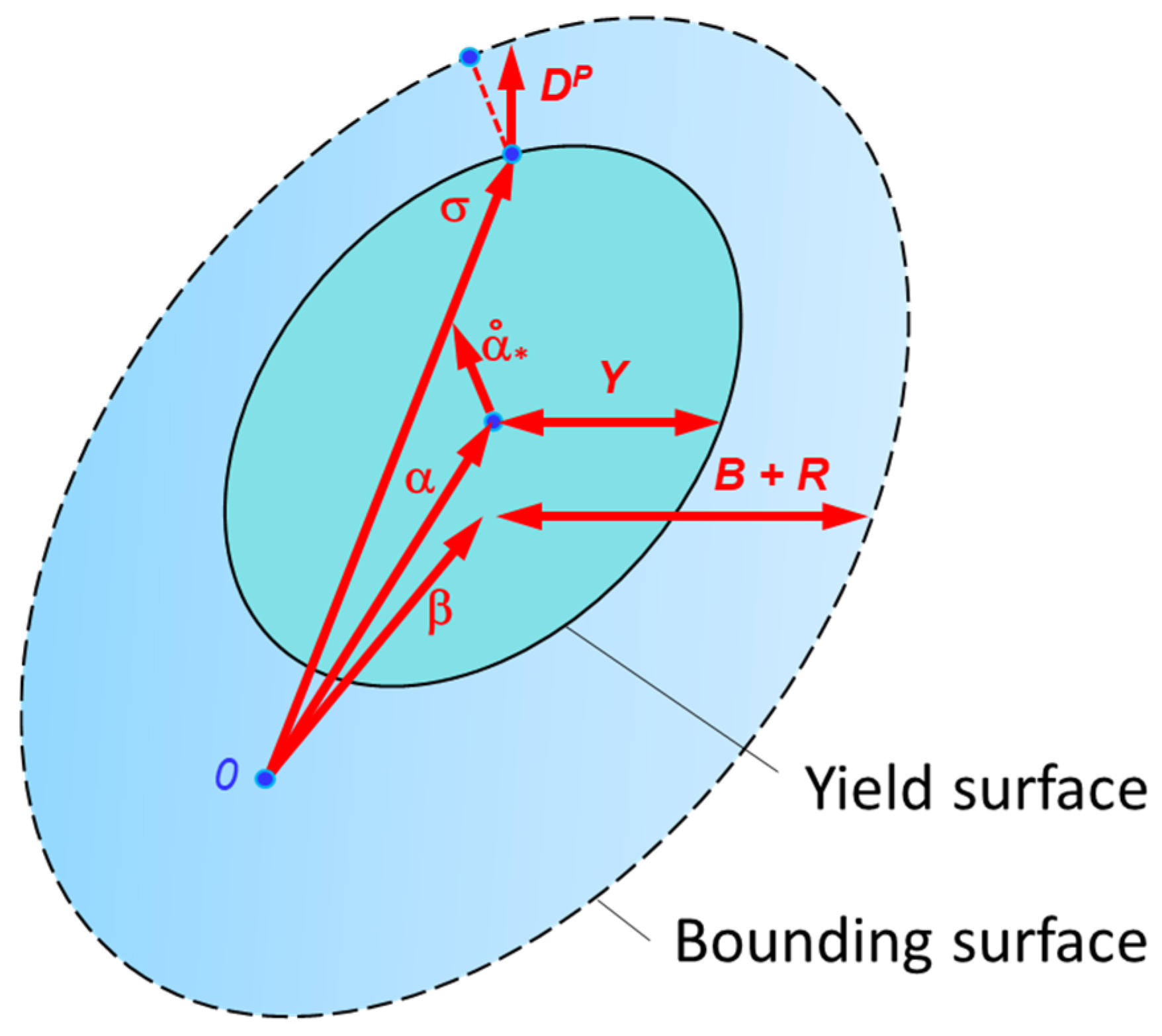
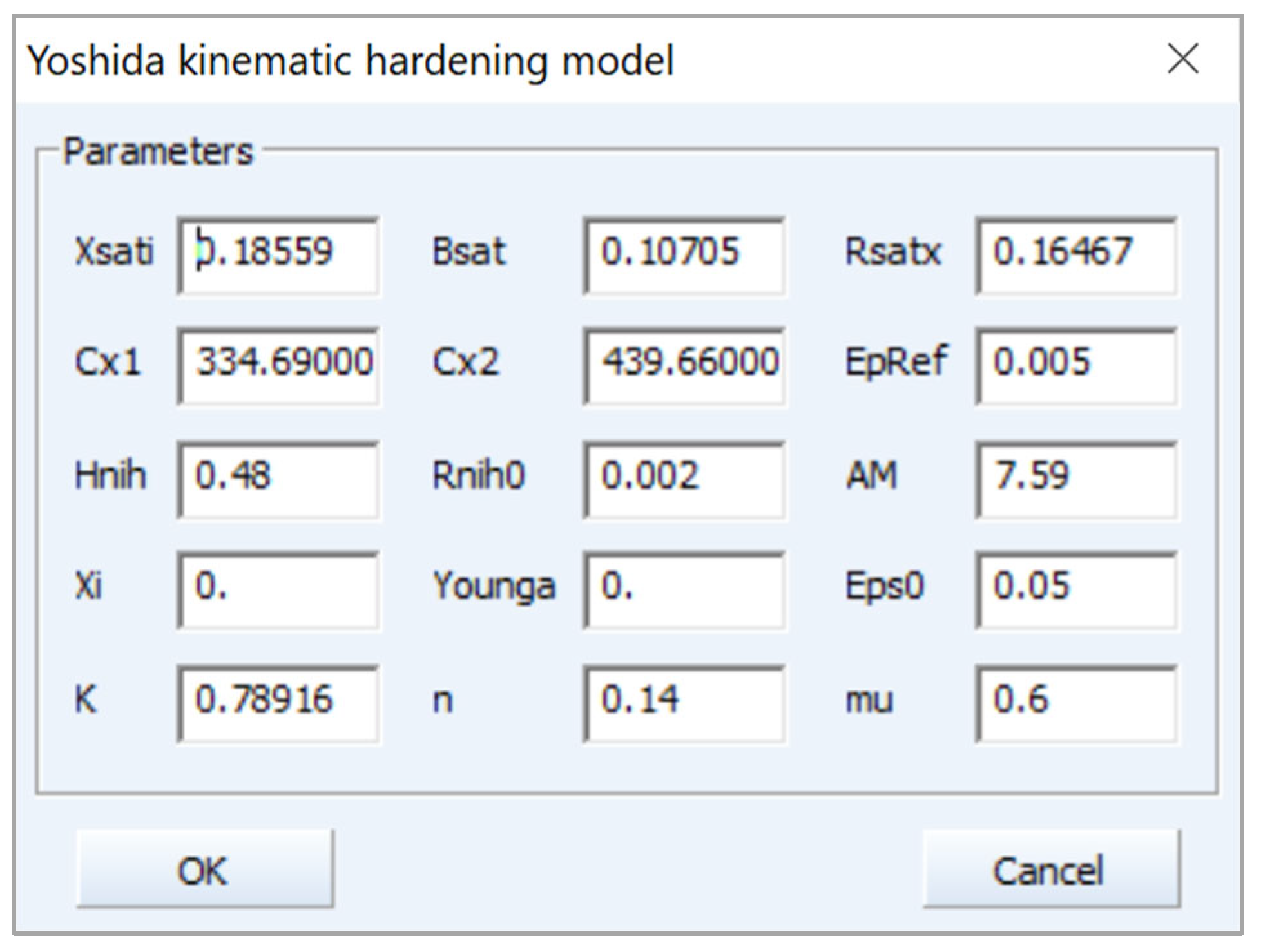
2.2.5. Cyclic Test
2.3. The Fabrication of the Real Stampings
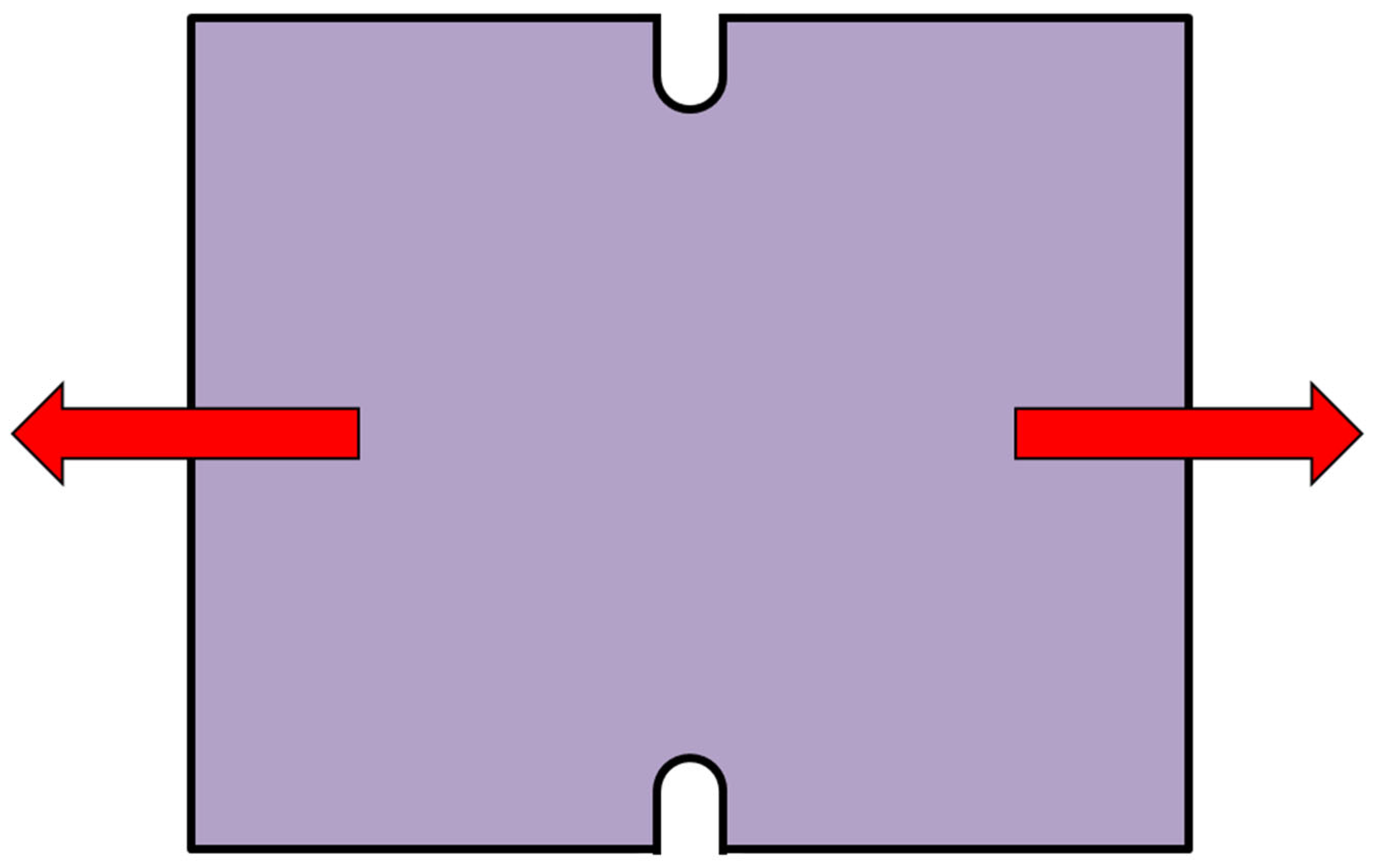
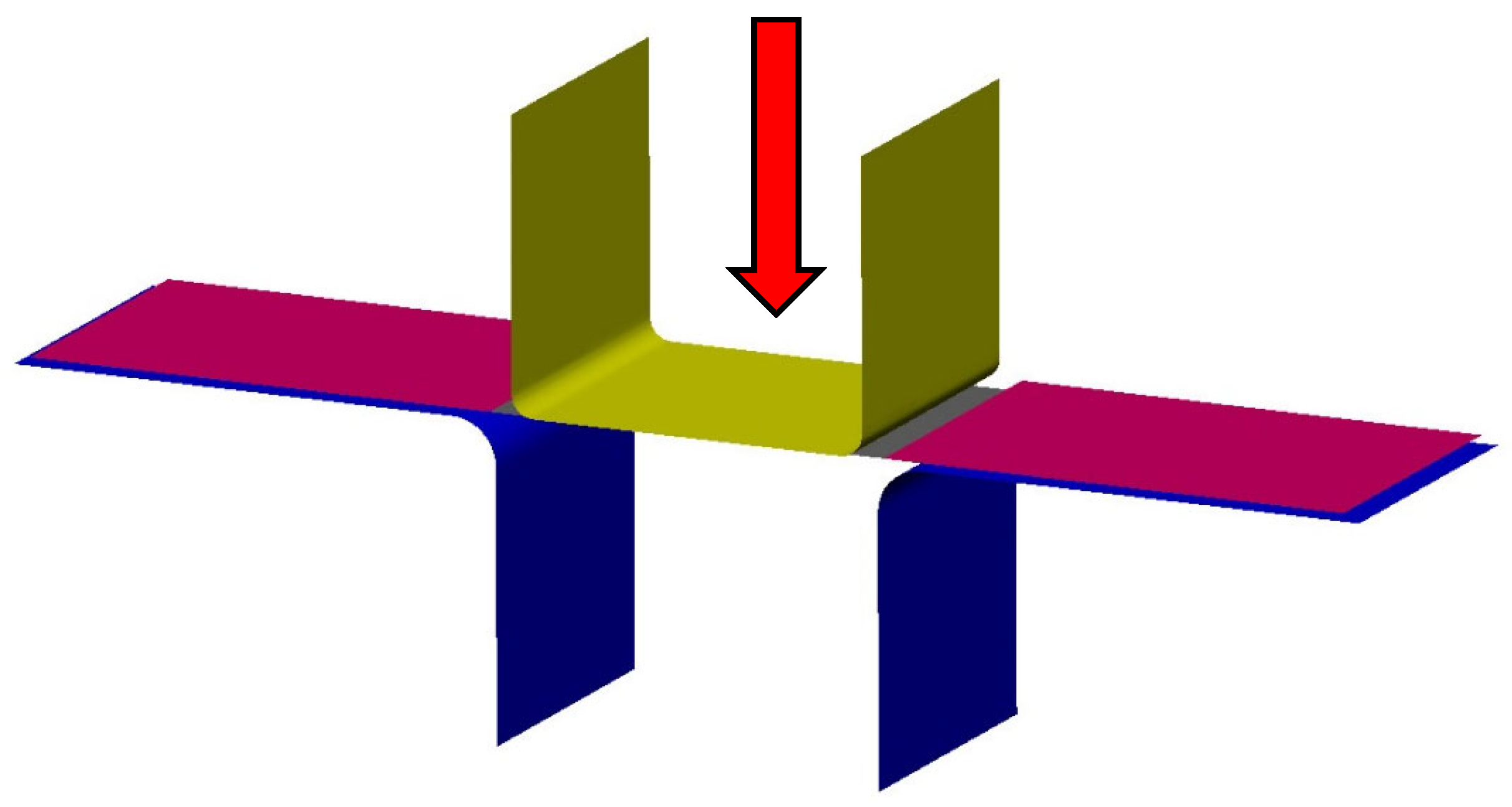
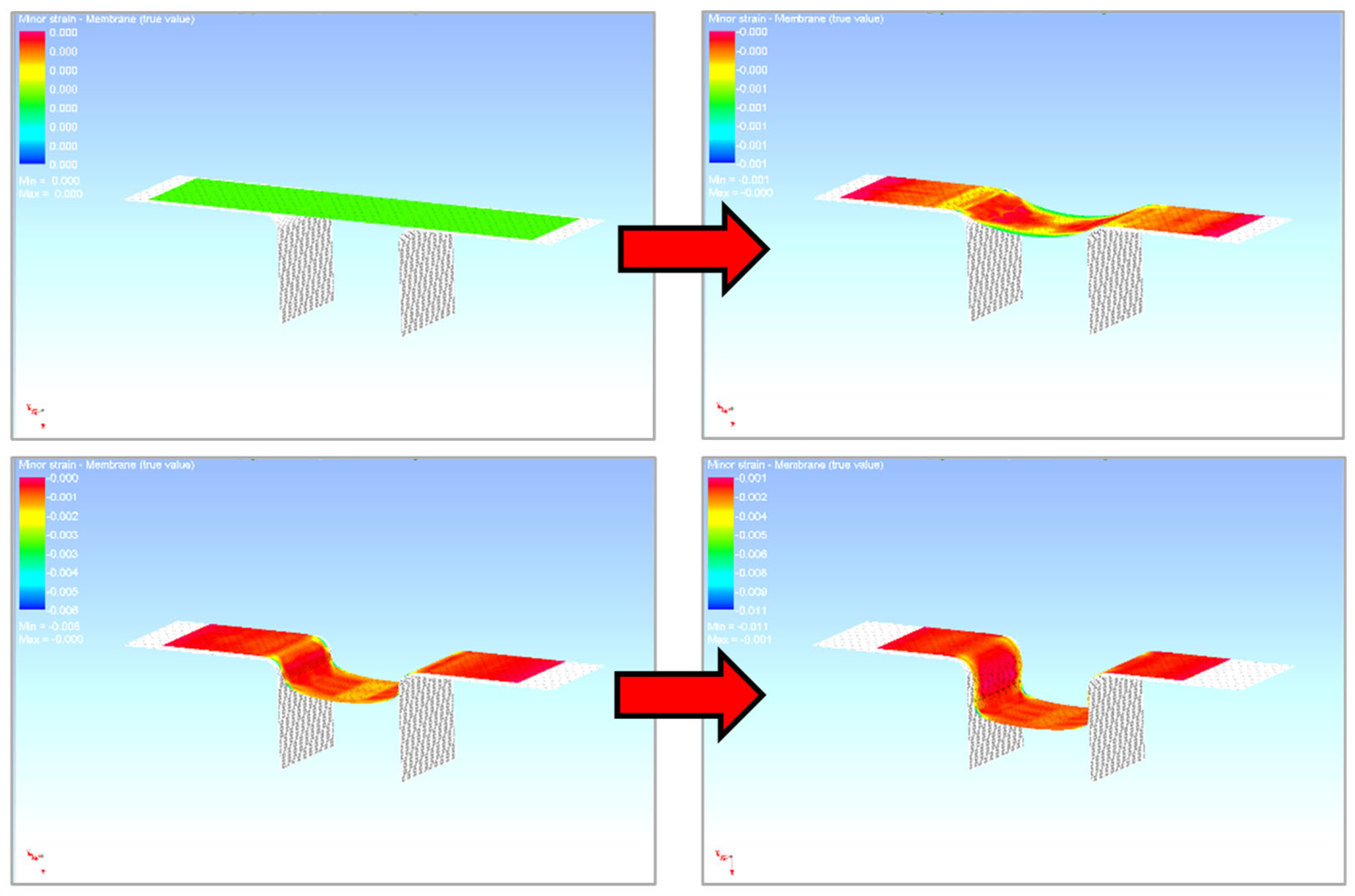
2.3.1. U-Shaped Drawing
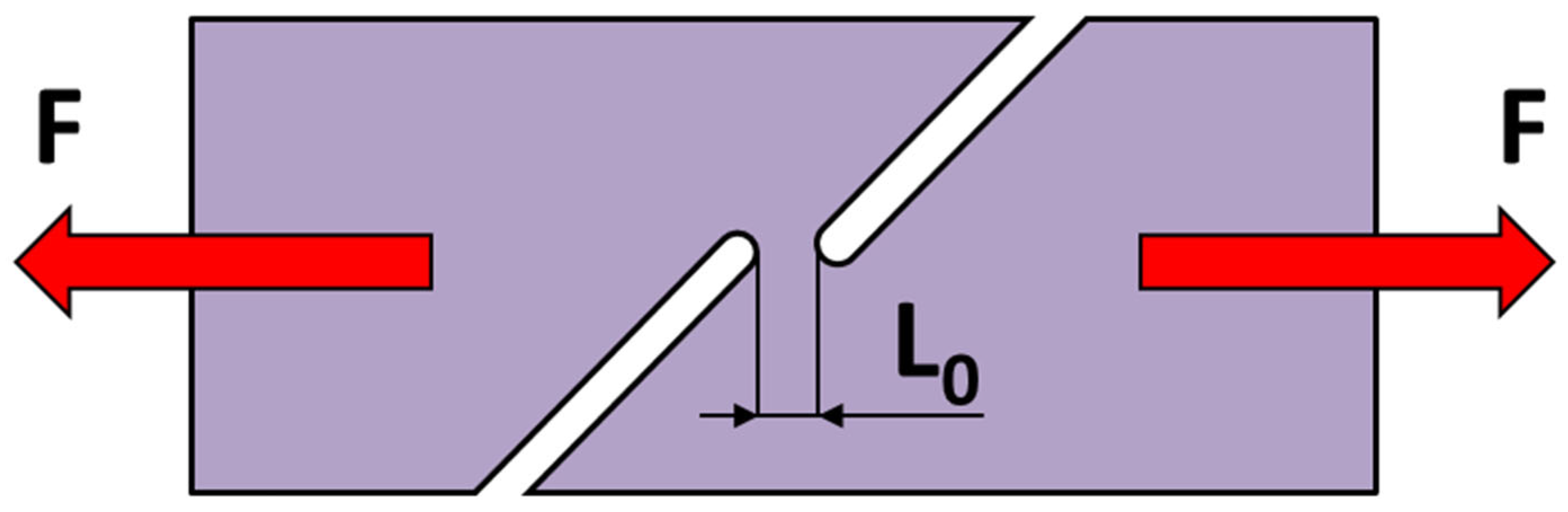
2.3.2. Drawing over the Draw-Bead
2.4. Numerical Simulation
2.4.1. The Finite Element Method (FEM) in the Sheet Metal Forming Process
2.4.2. Computational Material Models in PAM STAMP 2G Software
- C—strength coefficient (MPa);
- n—strain hardening exponent (-);
- φ0—offset true strain (-).
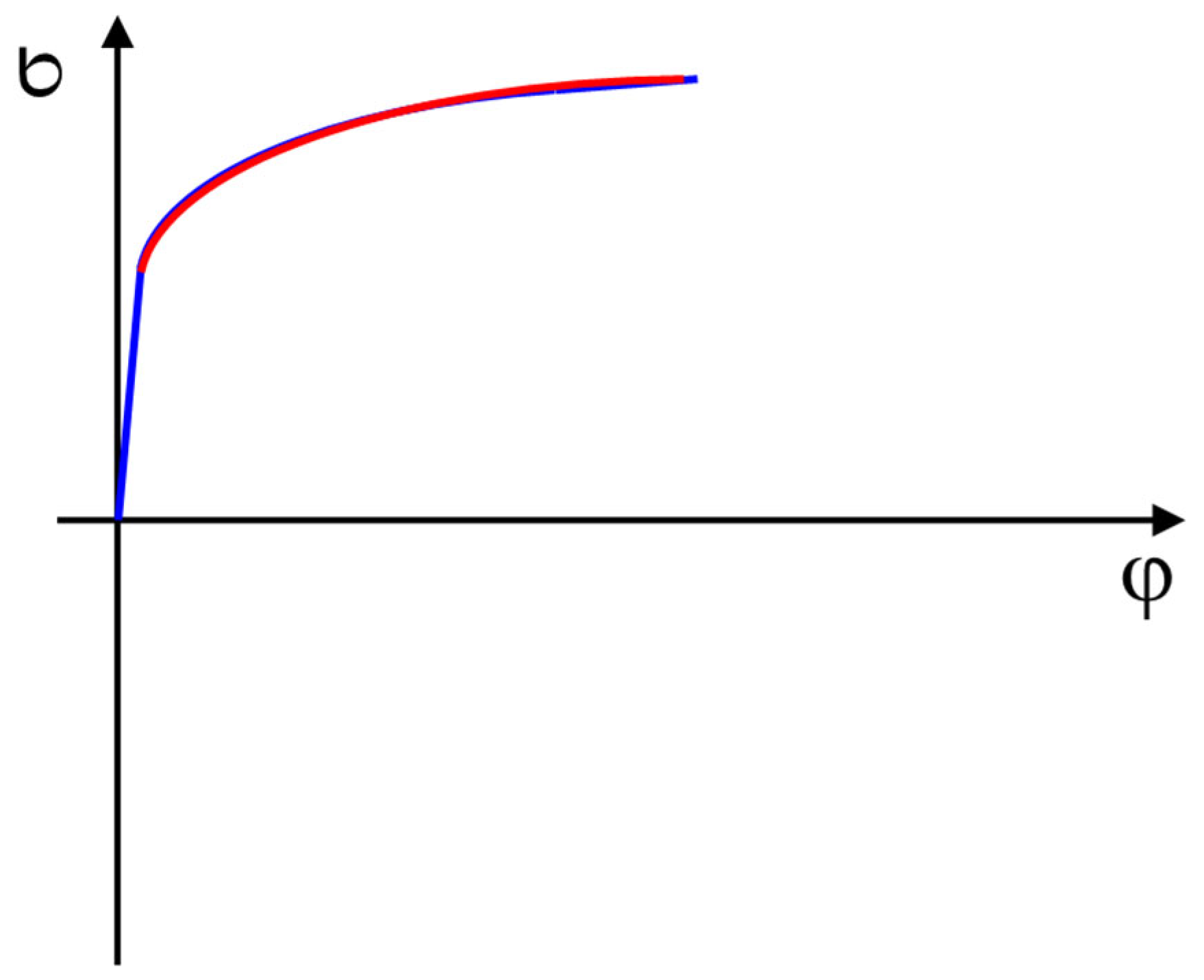
- σ1—principal stress (direction 1) (MPa);
- σ2—principal stress (direction 2) (MPa);
- σxx—stress in the direction 0° (MPa);
- σyy—stress in the direction 90° (MPa);
- σxy—shear stress (MPa);
- ϴ—angle of the coordination system rotation (°).
- Young’s modulus E;
- Poisson’s ratio μ;
- Density ρ;
- Normal anisotropy coefficients r0, r45 and r90;
- Uniaxial stress σun(0°) and σun(90°);
- Bi-axial anisotropy coefficient rbi;
- Bi-axial stress σbi;
- Plain strain–stress σps(0°), σps(45°) and σps(90°);
- Shear strain–stress σsh(0°), σsh(45°) and σsh(90°).
3. Results
3.1. A Metallographic Evaluation of the Structure of the Tested Material
3.2. Mechanical Tests of Titanium AMS4900
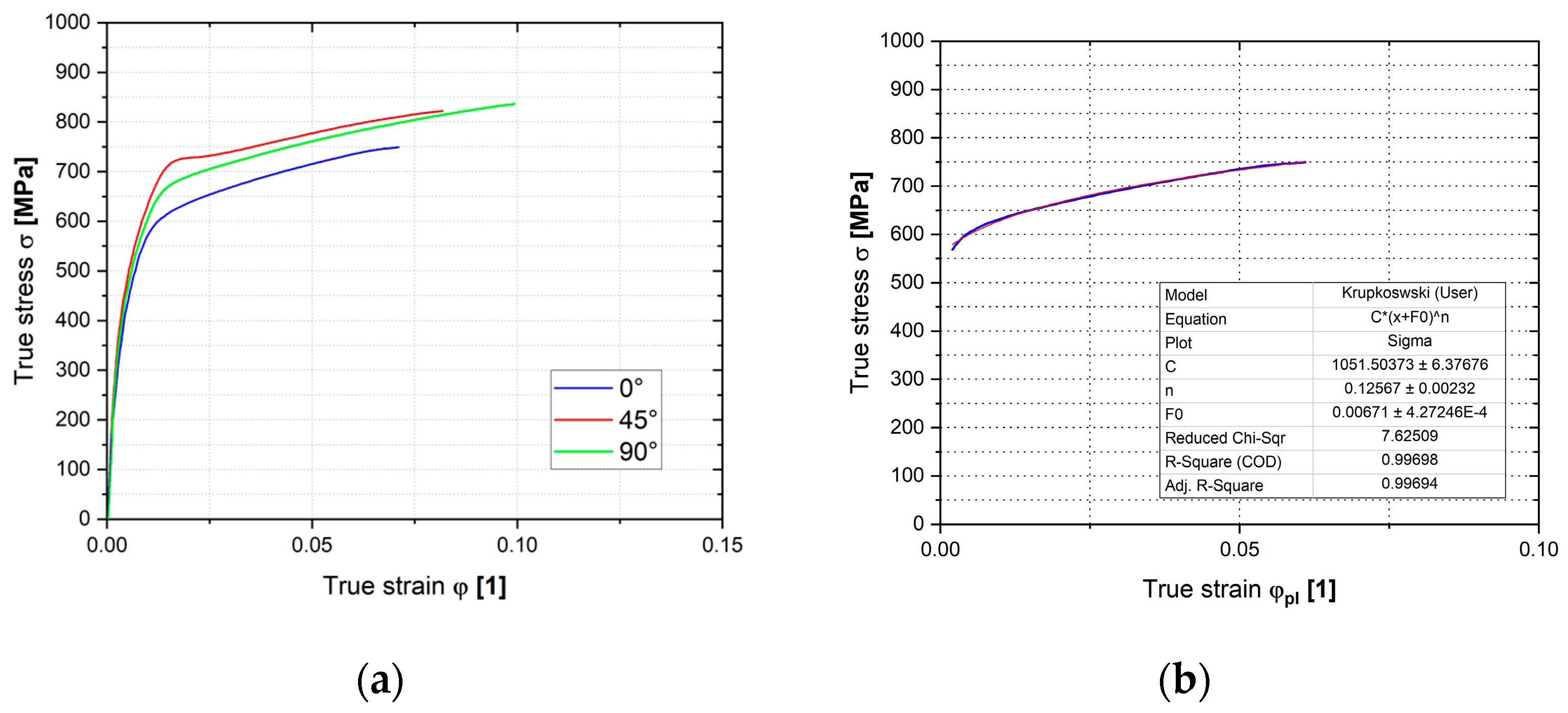
3.2.1. Static Tensile Test
3.2.2. Hydraulic Bulge Test
3.2.3. Plane Strain Tensile Test
3.2.4. Shear Test
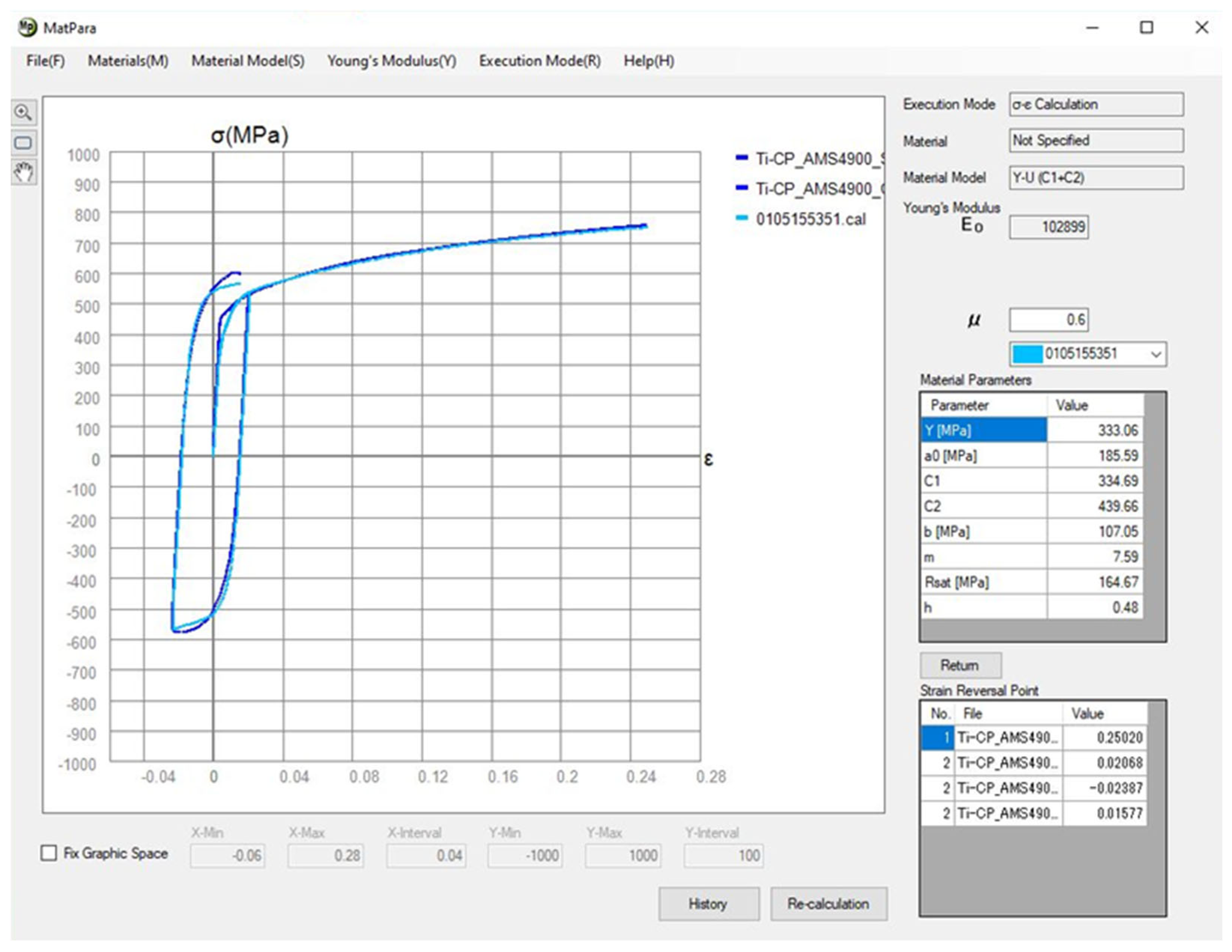
3.2.5. Cyclic Test
3.3. Numerical Simulation
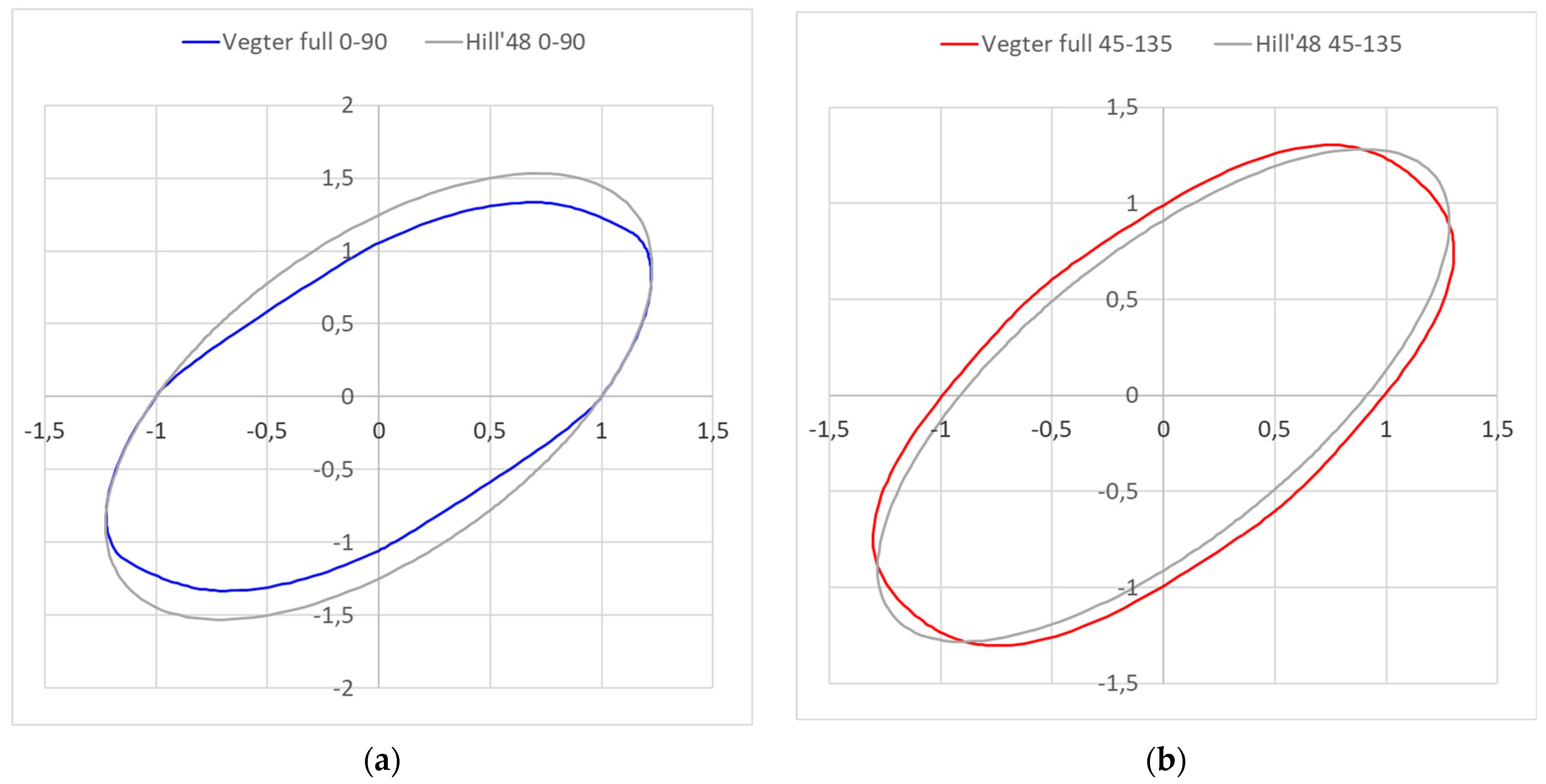
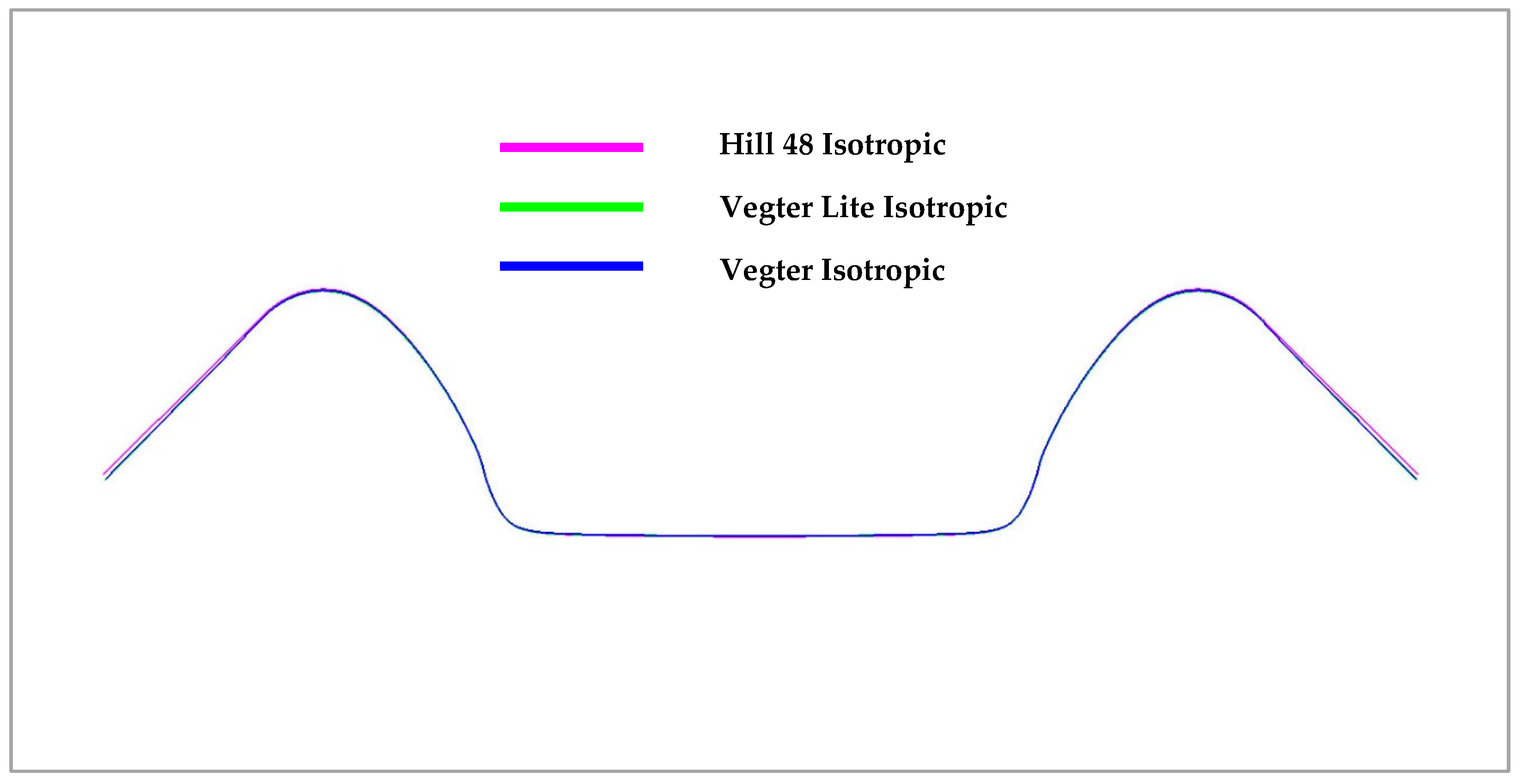
3.3.1. Material Model Definition in Software PAM STAMP 2G
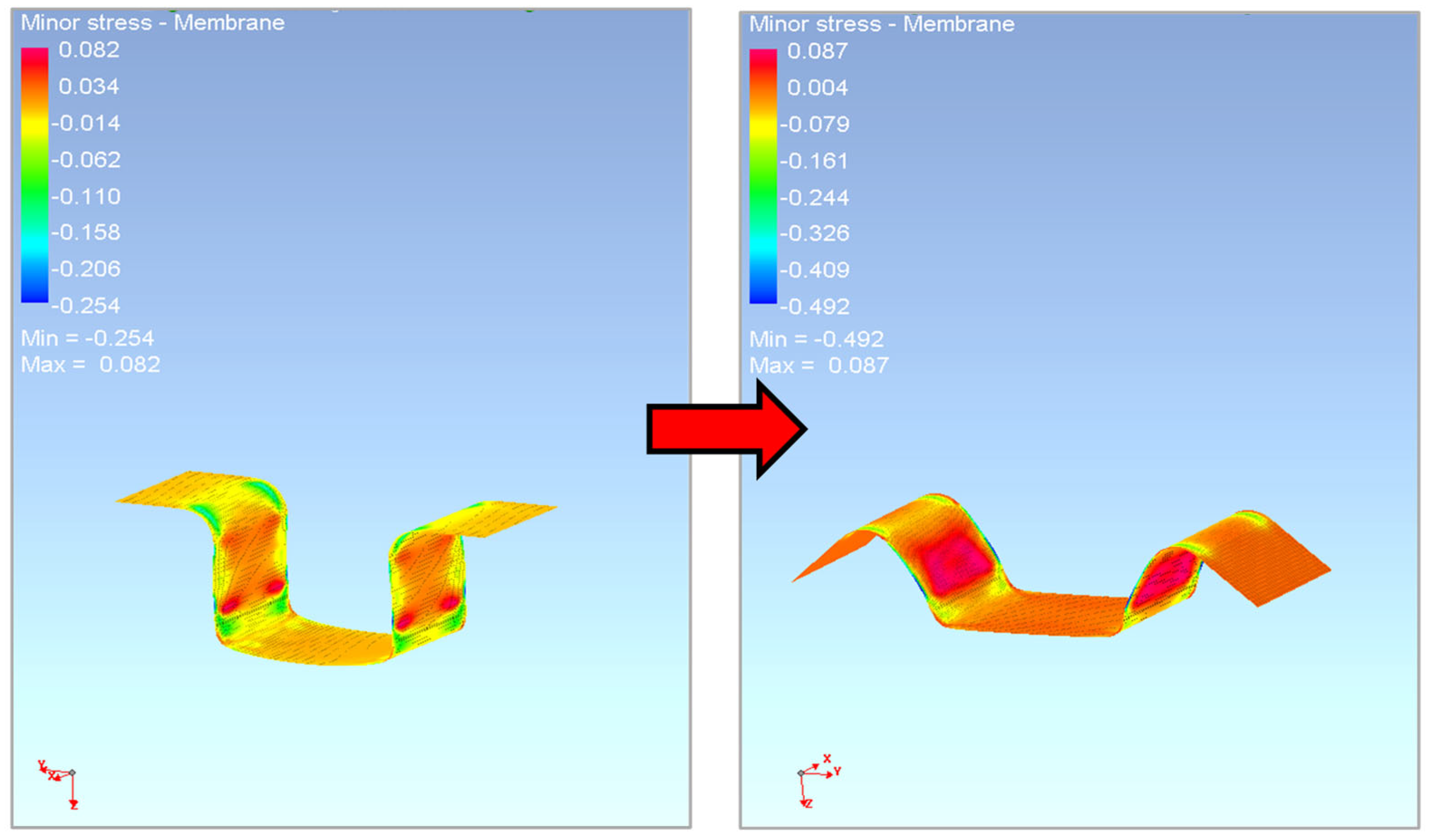
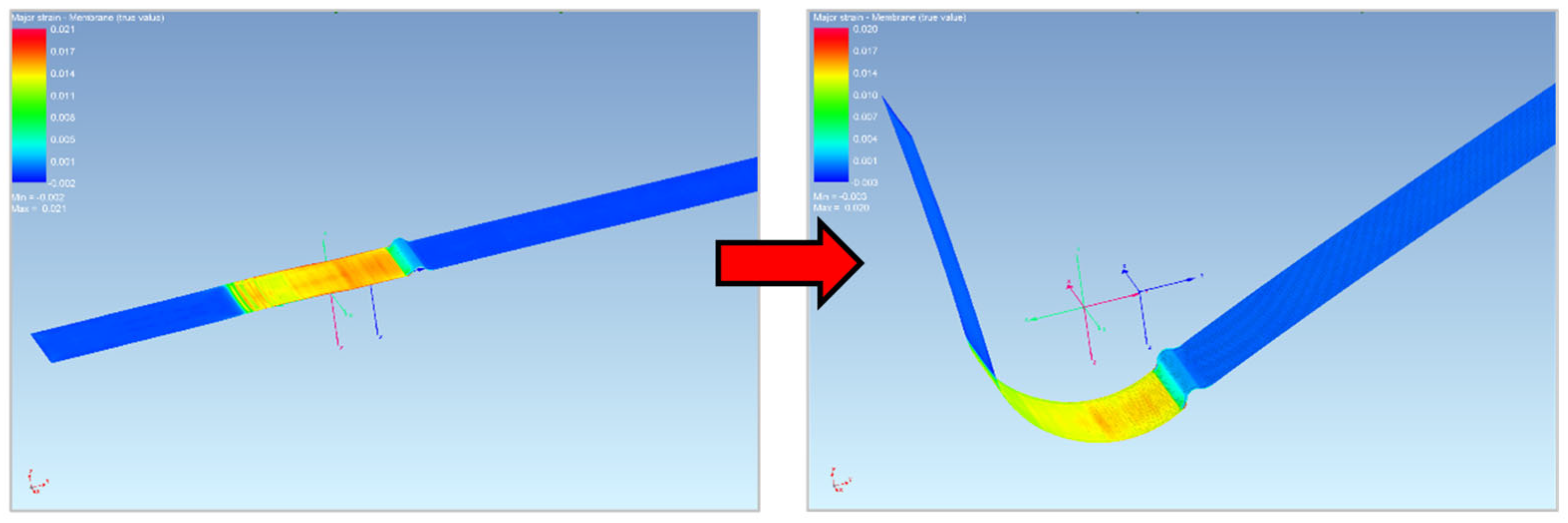
3.3.2. Numerical Simulation of the Sheet Metal Process in PAM STAMP 2G Software
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rana, R.; Singh, S.B. Automotive Steels: Design, Metallurgy, Processing and Applications; Woodhead Publishing: Sawston, UK, 2016; ISBN 978-0-08-100653-5. [Google Scholar]
- Vegter, H.; Mulder, H.; van Liempt, P.; Heijne, J. Work Hardening Descriptions in Simulation of Sheet Metal Forming Tailored to Material Type and Processing. Int. J. Plast. 2016, 80, 204–221. [Google Scholar] [CrossRef]
- An, Y.G.; Vegter, H. Analytical and Experimental Study of Frictional Behavior in Through-Thickness Compression Test. J. Mater. Process. Technol. 2005, 160, 148–155. [Google Scholar] [CrossRef]
- Vegter, H.; ten Horn, C.; Abspoel, M. The Vegter Lite Material Model: Simplifying Advanced Material Modelling. Int. J. Mater. Form. 2011, 4, 85–92. [Google Scholar] [CrossRef]
- An, Y.G.; Vegter, H.; Elliott, L. A Novel and Simple Method for the Measurement of Plane Strain Work Hardening. J. Mater. Process. Technol. 2004, 155, 1616–1622. [Google Scholar] [CrossRef]
- Kok, P.J.J.; Spanjer, W.; Vegter, H. A Microstructure Based Model for the Mechanical Behavior of Multiphase Steels. Key Eng. Mater. 2015, 651–653, 975–980. [Google Scholar] [CrossRef]
- Abspoel, M.; Scholting, M.E.; Lansbergen, M.; An, Y.; Vegter, H. A New Method for Predicting Advanced Yield Criteria Input Parameters from Mechanical Properties. J. Mater. Process. Technol. 2017, 248, 161–177. [Google Scholar] [CrossRef]
- Raemy, C.; Manopulo, N.; Hora, P. On the Modelling of Plastic Anisotropy, Asymmetry and Directional Hardening of Commercially Pure Titanium: A Planar Fourier Series Based Approach. Int. J. Plast. 2017, 91, 182–204. [Google Scholar] [CrossRef]
- Hu, Q.; Yoon, J.W.; Manopulo, N.; Hora, P. A Coupled Yield Criterion for Anisotropic Hardening with Analytical Description under Associated Flow Rule: Modeling and Validation. Int. J. Plast. 2021, 136, 102882. [Google Scholar] [CrossRef]
- Komischke, T.; Hora, P.; Domani, G. A New Experimental Method for the Evaluation of Fracture Criteria in Bulk Forming Operations. In Proceedings of the Experimental and Numerical Methods in the FEM Based Crack Prediction, Zurich, Switzerland, 2–3 July 2018; Institute of Virtual Manufacturing, ETH Zurich: Zurich, Switzerland, 2018; pp. 65–69. [Google Scholar]
- Harsch, D.; Heingärtner, J.; Hortig, D.; Hora, P. Process Windows for Sheet Metal Parts Based on Metamodels. J. Phys. Conf. Ser. 2016, 734, 032014. [Google Scholar] [CrossRef]
- Hora, P.; Tong, L.; Gorji, M.; Manopulo, N.; Berisha, B. Significance of the Local Sheet Curvature in the Prediction of Sheet Metal Forming Limits by Necking Instabilities and Cracks. In Proceedings of the NUMIFORM 2016: The 12th International Conference on Numerical Methods in Industrial Forming Processes, Troyes, France, 4–7 July 2016; EDP Sciences: Les Ulis, France, 2016; Volume 80, p. 11003. [Google Scholar]
- Hippke, H.; Hirsiger, S.; Rudow, F.; Berisha, B.; Hora, P. Optimized Prediction of Strain Distribution with Crystal Plasticity Supported Definition of Yielding Direction; ETH Zurich, Institute of Virtual Manufacturing: Zurich, Switzerland, 2019. [Google Scholar]
- Uemori, T.; Sumikawa, S.; Naka, T.; Ma, N.; Yoshida, F. Influence of Bauschinger Effect and Anisotropy on Springback of Aluminum Alloy Sheets. Keikinzoku/J. Jpn. Inst. Light Met. 2015, 65, 582–587. [Google Scholar] [CrossRef][Green Version]
- Yoshida, F.; Hamasaki, H.; Uemori, T. A Model of Anisotropy Evolution of Sheet Metals. Procedia Eng. 2014, 81, 1216–1221. [Google Scholar] [CrossRef]
- Yoshida, F.; Uemori, T. Cyclic Plasticity Model for Accurate Simulation of Springback of Sheet Metals. In 60 Excellent Inventions in Metal Forming; Tekkaya, A.E., Homberg, W., Brosius, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2015; pp. 61–66. ISBN 978-3-662-46312-3. [Google Scholar]
- Tada, N.; Uemori, T. Microscopic Elastic and Plastic Inhomogeneous Deformations and Height Changes on the Surface of a Polycrystalline Pure-Titanium Plate Specimen under Cyclic Tension. Appl. Sci. 2018, 8, 1907. [Google Scholar] [CrossRef]
- Uemori, T.; Naka, T.; Tada, N.; Yoshimura, H.; Katahira, T.; Yoshida, F. Theoretical Predictions of Fracture and Springback for High Tensile Strength Steel Sheets under Stretch Bending. Procedia Eng. 2017, 207, 1594–1598. [Google Scholar] [CrossRef]
- Yoshida, F.; Hamasaki, H.; Uemori, T. Modeling of Anisotropic Hardening of Sheet Metals Including Description of the Bauschinger Effect. Int. J. Plast. 2015, 75, 170–188. [Google Scholar] [CrossRef]
- Yoshida, F. Description of Elastic–Plastic Stress–Strain Transition in Cyclic Plasticity and Its Effect on Springback Prediction. Int. J. Mater. Form. 2022, 15, 12. [Google Scholar] [CrossRef]
- Xia, X.; Gong, M.; Wang, T.; Liu, Y.; Zhang, H.; Zhang, Z. Parameter Identification of the Yoshida-Uemori Hardening Model for Remanufacturing. Metals 2021, 11, 1859. [Google Scholar] [CrossRef]
- Chang, C.-Y.; Ho, M.-H.; Shen, P.-C. Yoshida–Uemori Material Models in Cyclic Tension–Compression Tests and Shear Tests. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2014, 228, 245–254. [Google Scholar] [CrossRef]
- Yoshida, F. Elasto-Plasticity Models for Accurate Metal Forming Simulation III: Anisotropic Yield Function and Anisotropic Hardening Model. Zair./J. Soc. Mater. Sci. Jpn. 2023, 72, 262–267. [Google Scholar] [CrossRef]
- Yoshida, F. Elasto-Plasticity Models for Accurate Metal Forming Simulation II: Role of Accurate Material Model in Springback Simulation. Zair./J. Soc. Mater. Sci. Jpn. 2023, 72, 144–149. [Google Scholar] [CrossRef]
- Uemori, T.; Fujii, K.; Nakata, T.; Narita, S.; Tada, N.; Naka, T.; Yoshida, F. Springback Analysis of Aluminum Alloy Sheet Metals by Yoshida-Uemori Model. Key Eng. Mater. 2017, 725, 566–571. [Google Scholar] [CrossRef]
- Eyckens, P.; Mulder, H.; Gawad, J.; Vegter, H.; Roose, D.; van den Boogaard, T.; Van Bael, A.; Van Houtte, P. The Prediction of Differential Hardening Behaviour of Steels by Multi-Scale Crystal Plasticity Modelling. Int. J. Plast. 2015, 73, 119–141. [Google Scholar] [CrossRef]
- An, Y.; Vegter, H.; Carless, L.; Lambriks, M. A Novel Yield Locus Description by Combining the Taylor and the Relaxed Taylor Theory for Sheet Steels. Int. J. Plast. 2011, 27, 1758–1780. [Google Scholar] [CrossRef]
- Yoshida, F.; Uemori, T. A Model of Large-Strain Cyclic Plasticity Describing the Bauschinger Effect and Workhardening Stagnation. Int. J. Plast. 2002, 18, 661–686. [Google Scholar] [CrossRef]
- Yoshida, F.; Uemori, T.; Fujiwara, K. Elastic–Plastic Behavior of Steel Sheets under in-Plane Cyclic Tension–Compression at Large Strain. Int. J. Plast. 2002, 18, 633–659. [Google Scholar] [CrossRef]
- Barlat, F.; Ha, J.; Grácio, J.J.; Lee, M.-G.; Rauch, E.F.; Vincze, G. Extension of Homogeneous Anisotropic Hardening Model to Cross-Loading with Latent Effects. Int. J. Plast. 2013, 46, 130–142. [Google Scholar] [CrossRef]
- Feigenbaum, H.P.; Dugdale, J.; Dafalias, Y.F.; Kourousis, K.I.; Plesek, J. Multiaxial Ratcheting with Advanced Kinematic and Directional Distortional Hardening Rules. Int. J. Solids Struct. 2012, 49, 3063–3076. [Google Scholar] [CrossRef]
- Freund, M.; Shutov, A.V.; Ihlemann, J. Simulation of Distortional Hardening by Generalizing a Uniaxial Model of Finite Strain Viscoplasticity. Int. J. Plast. 2012, 36, 113–129. [Google Scholar] [CrossRef]
- Korecek, D.; Solfronk, P.; Sobotka, J. Numerical Simulation as a Tool to Predict Sheet Metal Forming Process of TRIP Steel HCT690. Manuf. Technol. 2020, 20, 625–631. [Google Scholar] [CrossRef]
- Li, Y.; Gao, P.; Yu, J.; Jin, S.; Chen, S.; Zhan, M. Mesoscale Deformation Mechanisms in Relation with Slip and Grain Boundary Sliding in TA15 Titanium Alloy during Tensile Deformation. J. Mater. Sci. Technol. 2022, 98, 72–86. [Google Scholar] [CrossRef]
- Salvador, C.A.F.; Maia, E.L.; Costa, F.H.; Escobar, J.D.; Oliveira, J.P. A Compilation of Experimental Data on the Mechanical Properties and Microstructural Features of Ti-Alloys. Sci. Data 2022, 9, 188. [Google Scholar] [CrossRef]
- Danard, Y.; Martin, G.; Lilensten, L.; Sun, F.; Seret, A.; Poulain, R.; Mantri, S.; Guillou, R.; Thiaudière, D.; Freiherr von Thüngen, I.; et al. Accommodation Mechanisms in Strain-Transformable Titanium Alloys. Mater. Sci. Eng. A 2021, 819, 141437. [Google Scholar] [CrossRef]
- Hosseini, R.; Morakabati, M.; Abbasi, S.M.; Hajari, A. Development of a Trimodal Microstructure with Superior Combined Strength, Ductility and Creep-Rupture Properties in a near Alpha Titanium Alloy. Mater. Sci. Eng. A 2017, 696, 155–165. [Google Scholar] [CrossRef]
- Brozek, C.; Sun, F.; Vermaut, P.; Millet, Y.; Lenain, A.; Embury, D.; Jacques, P.J.; Prima, F. A β-Titanium Alloy with Extra High Strain-Hardening Rate: Design and Mechanical Properties. Scr. Mater. 2016, 114, 60–64. [Google Scholar] [CrossRef]
- Zang, M.C.; Niu, H.Z.; Yu, J.S.; Zhang, H.R.; Zhang, T.B.; Zhang, D.L. Cryogenic Tensile Properties and Deformation Behavior of a Fine-Grained near Alpha Titanium Alloy with an Equiaxed Microstructure. Mater. Sci. Eng. A 2022, 840, 142952. [Google Scholar] [CrossRef]
- Liu, Z.; Li, R.; Chen, D.; Sun, Y.; He, B.; Zou, Y. Enhanced Tensile Ductility of an Additively Manufactured Near-α Titanium Alloy by Microscale Shear Banding. Int. J. Plast. 2022, 157, 103387. [Google Scholar] [CrossRef]
- Adamus, J. Stamping of Titanium Sheets. Key Eng. Mater. 2009, 410–411, 279–288. [Google Scholar] [CrossRef]
- Titanium Material History: Titanium Alloy, Pure Titanium—Supra Alloys. Available online: https://supraalloys.com/titanium-2/ (accessed on 10 August 2021).
- Titanium Processing|Technology, Methods, & Facts. Available online: https://www.britannica.com/technology/titanium-processing (accessed on 10 August 2021).
- Ptáček, L. Nauka o Materiálu II; CERM: Brno, Czech Republic, 1999; ISBN 978-80-7204-130-5. [Google Scholar]
- Veiga, C.; Davim, J.; Loureiro, A. Properties and Applications of Titanium Alloys: A Brief Review. Rev. Adv. Mater. Sci. 2012, 32, 133–148. [Google Scholar]
- Vývoj a Aplikace Titanu a Slitiny Titanu v Automobilovém Průmyslu–Nový Projekt–Novinky—Baoji ChuangXin Metal Materials Co., Ltd. (CXMET). Available online: https://cz.cxmetti.com/news/development-and-application-of-titanium-and-ti-31550303.html (accessed on 18 March 2025).
- Tvarování Titanových Plechů. WOLFTEN 2020. Available online: https://wolften.pl/cs/tvarovani-titanovych-plechu/ (accessed on 25 March 2025).
- Gheorghe, D.; Pop, D.; Ciocoiu, R.; Trante, O.; Milea, C.; Mohan, A.G.; Benea, H.; Saceleanu, V. Microstructure Development in Titanium and Its Alloys Used for Medical Applications. UPB Sci. Bull. Ser. B Chem. Mater. Sci. 2019, 81, 244–258. [Google Scholar]
- Welsch, G.; Boyer, R.; Collings, E.W. Materials Properties Handbook: Titanium Alloys; ASM International: Almere, The Netherlands, 1993; ISBN 978-0-87170-481-8. [Google Scholar]
- Liu, X.; Chu, P.K.; Ding, C. Surface Modification of Titanium, Titanium Alloys, and Related Materials for Biomedical Applications. Mater. Sci. Eng. R Rep. 2004, 47, 49–121. [Google Scholar] [CrossRef]
- Motyka, M.; Kubiak, K.; Sieniawski, J.; Ziaja, W. 2.02—Phase Transformations and Characterization of α + β Titanium Alloys. In Comprehensive Materials Processing; Hashmi, S., Batalha, G.F., Van Tyne, C.J., Yilbas, B., Eds.; Elsevier: Oxford, UK, 2014; pp. 7–36. ISBN 978-0-08-096533-8. [Google Scholar]
- Ezugwu, E.O.; Wang, Z.M. Titanium Alloys and Their Machinability—A Review. J. Mater. Process. Technol. 1997, 68, 262–274. [Google Scholar] [CrossRef]
- Ahmed, W.; Elhissi, A.; Jackson, M.J.; Ahmed, E. 2—Precision Machining of Medical Devices. In The Design and Manufacture of Medical Devices; Davim, J.P., Ed.; Woodhead Publishing Reviews: Mechanical Engineering Series; Woodhead Publishing: Sawston, UK, 2012; pp. 59–113. ISBN 978-1-907568-72-5. [Google Scholar]
- Titanium Allotropes: Definition & Examples. Available online: https://study.com/academy/lesson/titanium-allotropes-definition-examples.html (accessed on 13 August 2021).
- Kánocz, A.; Španiel, M. Metoda Konečných Prvků v Mechanice Poddajných Těles; České vysoké učení technické: Prague, Czech Republic, 1995; ISBN 80-01-01283-2. [Google Scholar]
- Kanócz, A.; Španiel, M.; České vysoké učení technické v Praze. Strojní fakulta. In Metoda Konečných Prvků v Mechanice Poddajných těles; Nakladatelství ČVUT: Praha, Czech Republic, 2007; ISBN 978-80-01-03590-0. [Google Scholar]
- Machálek, I.J.; Radek, I.; Frodlová, I.B. Simulace Procesů Plošného Tváření v Softwaru Pam-Stamp 2G; Vysoká škola báňská—Technická univerzita Ostrava: Ostrava-Poruba, Czech Republic, 2012; ISBN 978-80-248-2715-5. [Google Scholar]
- ESI Group. PAM-STAMP 2G 2018 User’s Guide; ESI Group: Tokyo, Japan, 2018. [Google Scholar]
- Hill, R.; Orowan, E. A Theory of the Yielding and Plastic Flow of Anisotropic Metals. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1997, 193, 281–297. [Google Scholar] [CrossRef]
- Tomáš, M.; Evin, E.; Kepič, J.; Hudák, J. Physical Modelling and Numerical Simulation of the Deep Drawing Process of a Box-Shaped Product Focused on Material Limits Determination. Metals 2019, 9, 1058. [Google Scholar] [CrossRef]








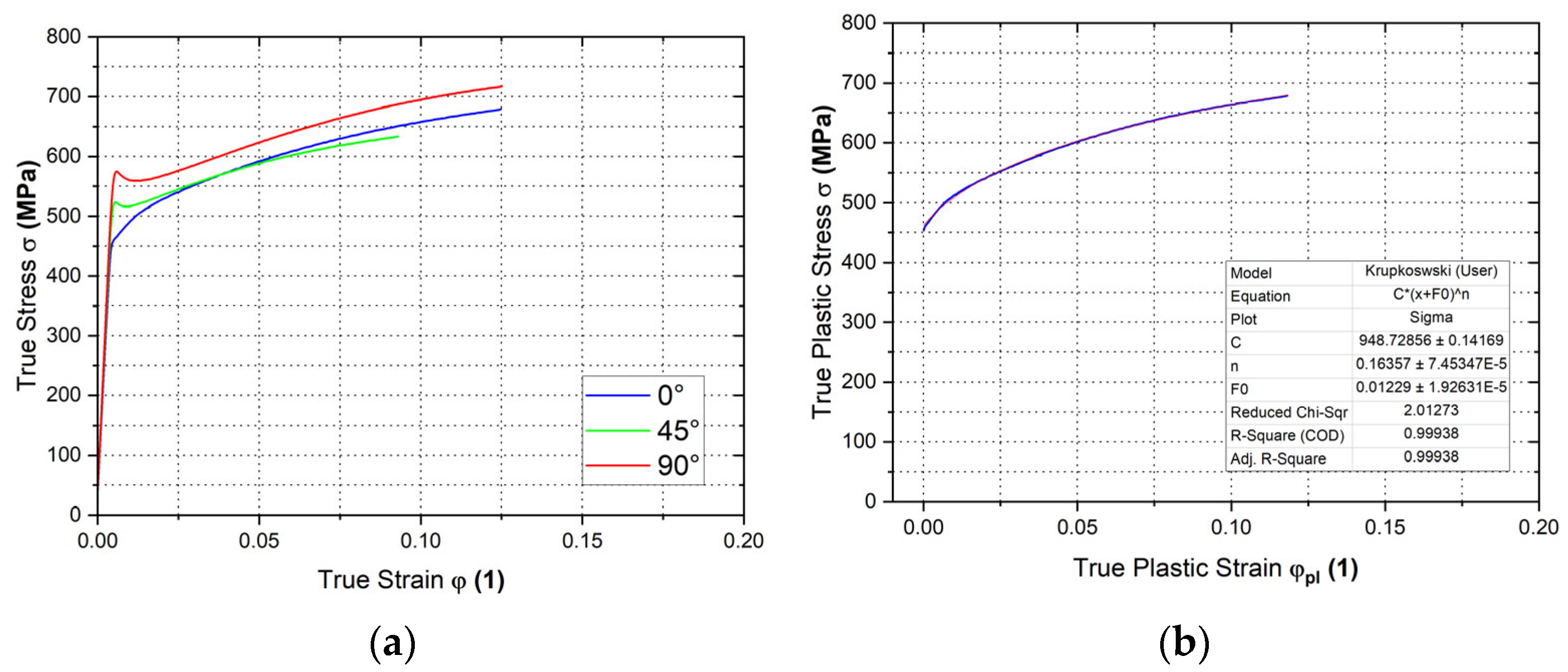
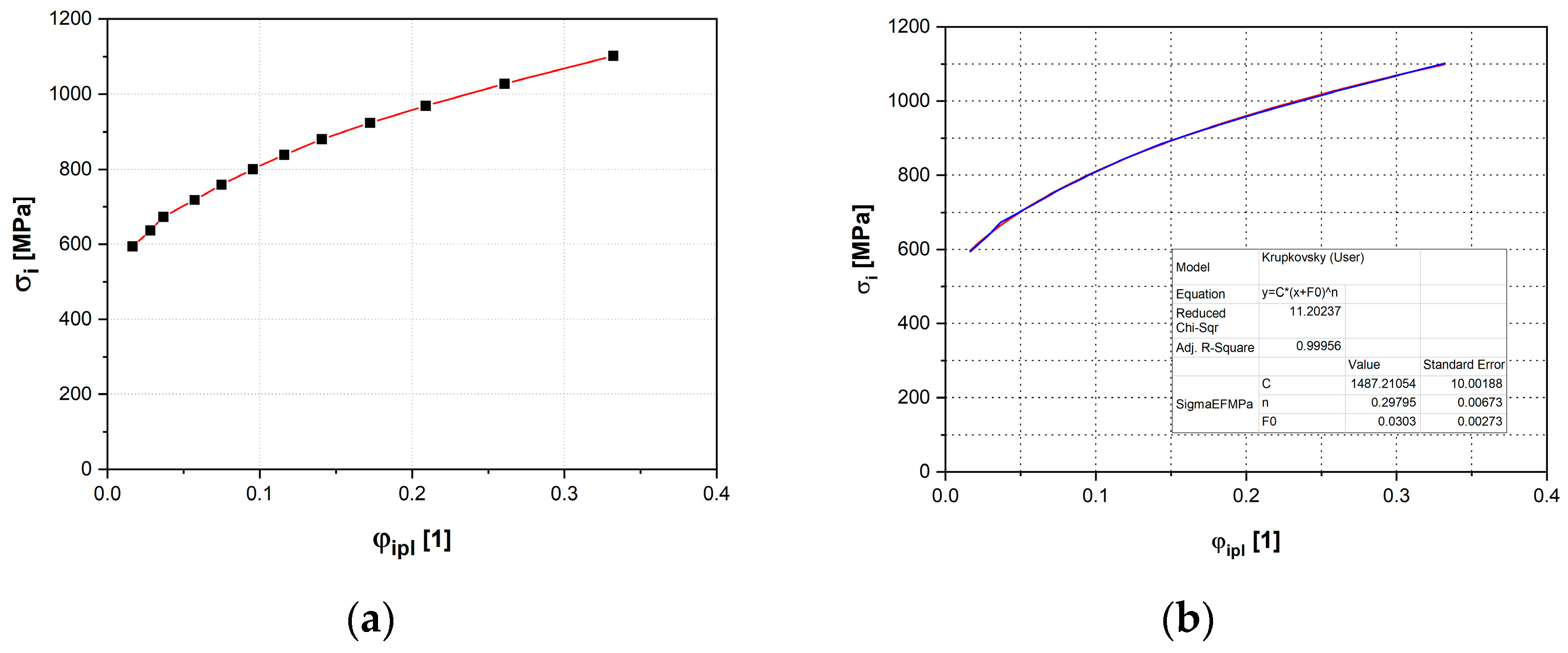






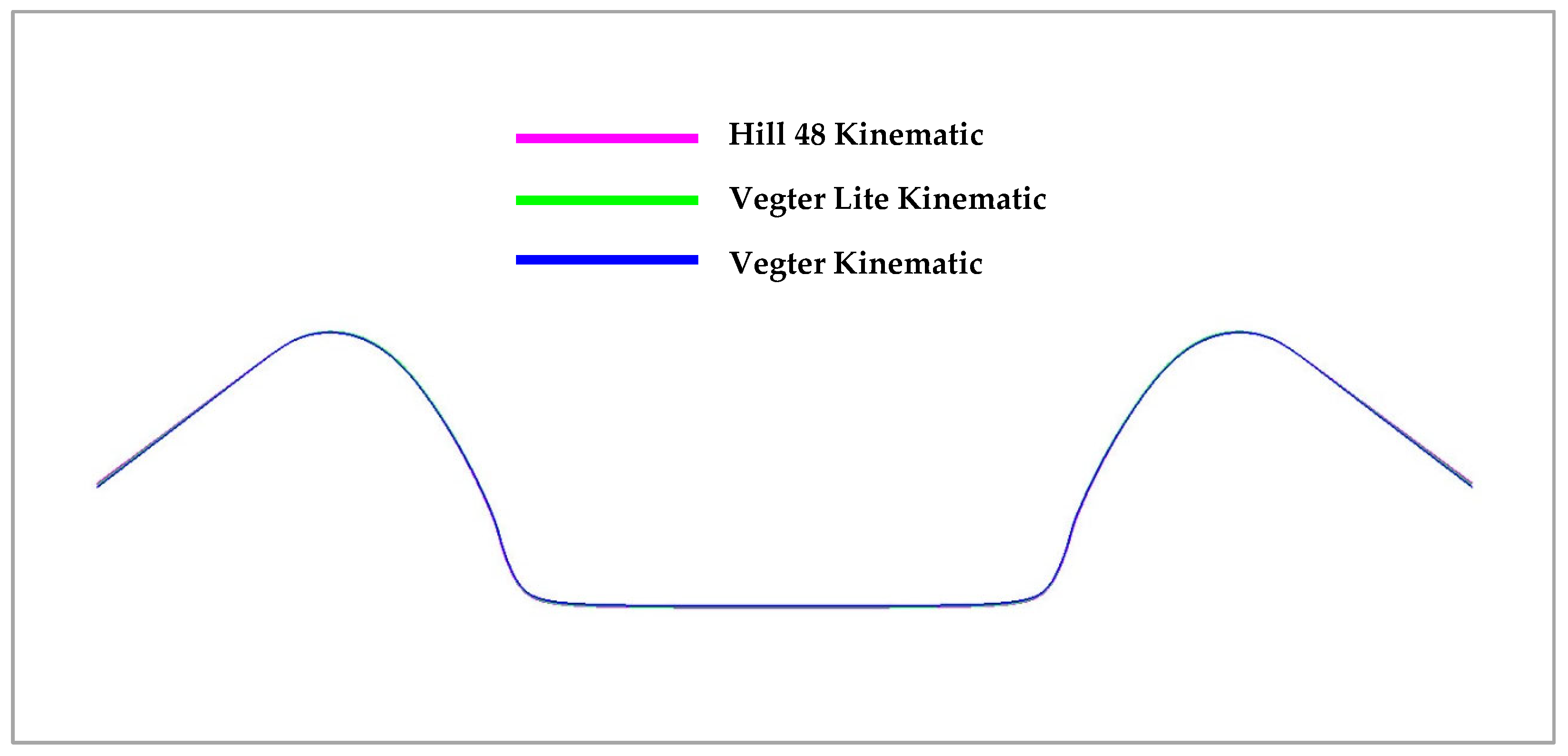
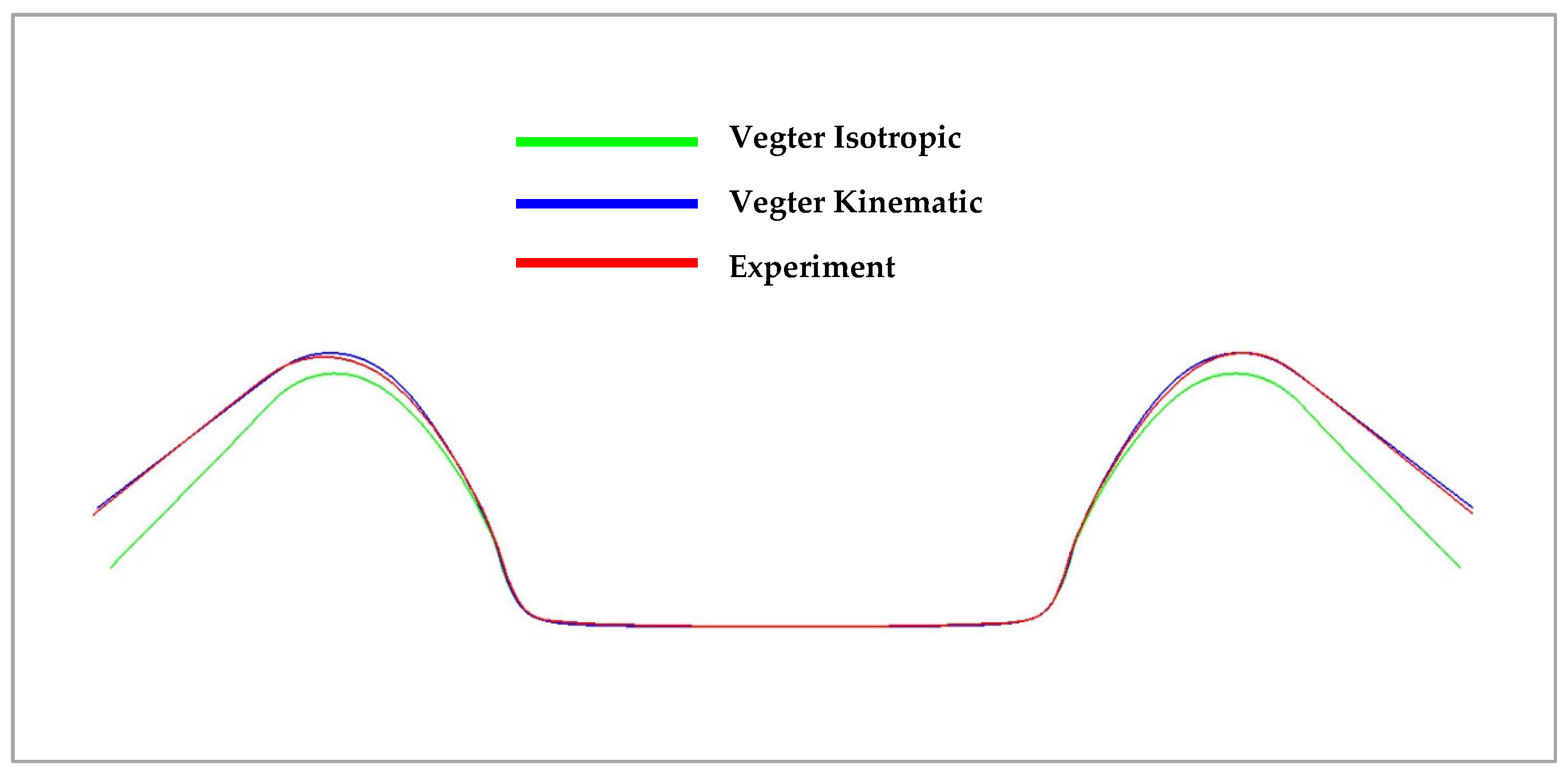
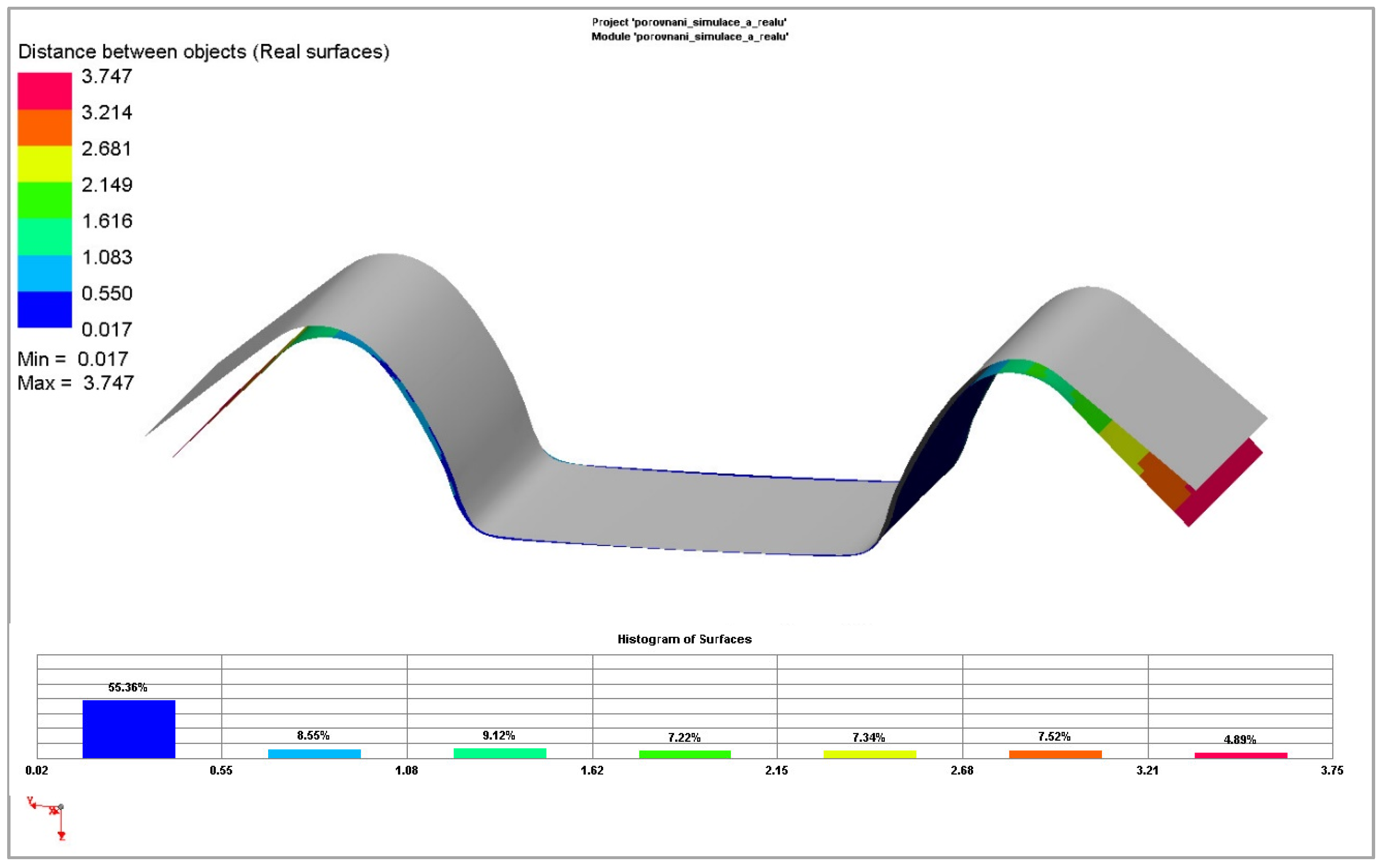

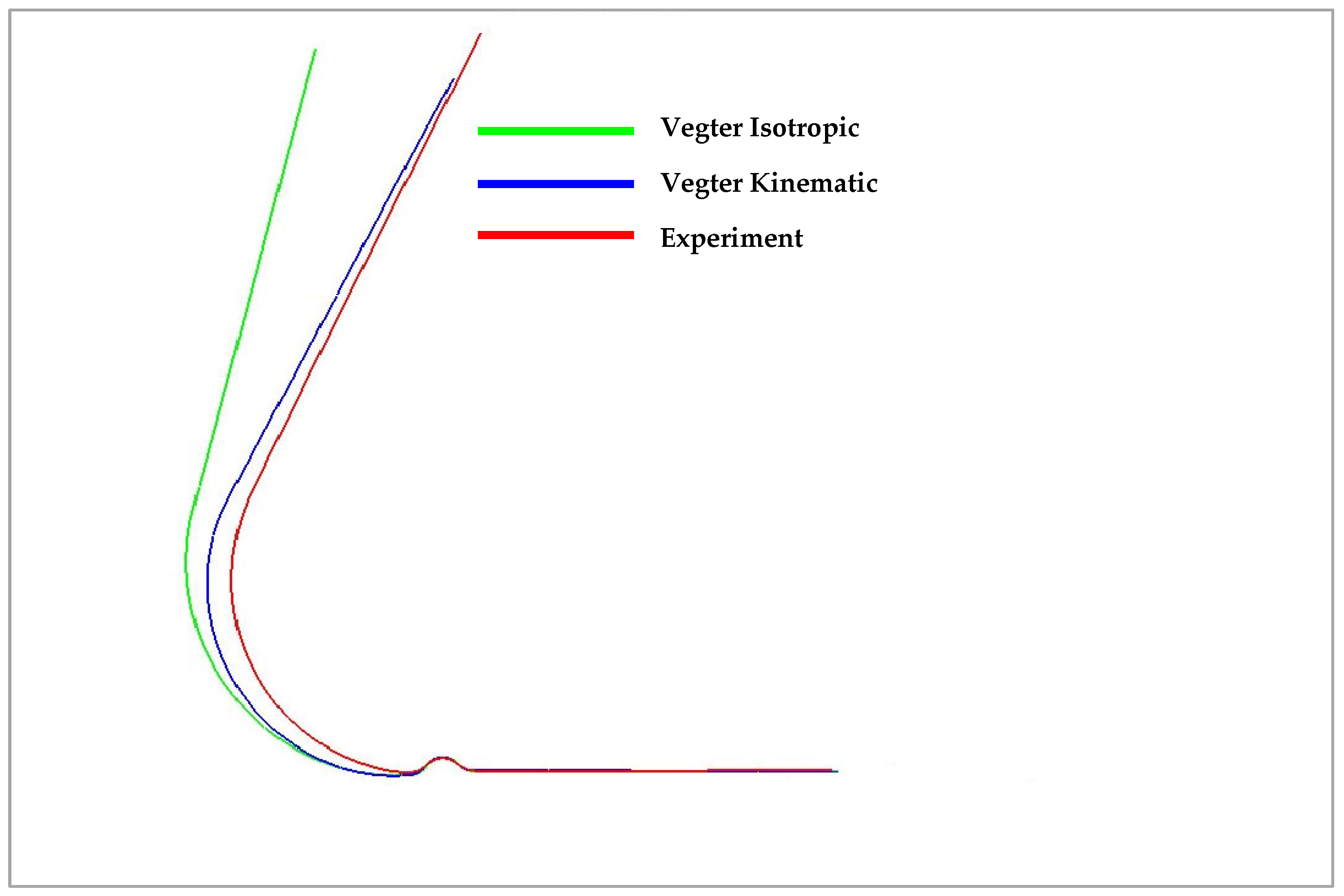
| Rolling Direction (°) | Rp0.2 (MPa) | Rm (MPa) | Ag (-) | A80mm (-) | E (MPa) |
|---|---|---|---|---|---|
| 0 | 464.0 ± 1.2 | 599.5 ± 1.1 | 0.1329 ± 0.0018 | 0.2513 ± 0.0021 | 102,899 ± 118 |
| 45 | 521.0 ± 1.0 | 577.5 ± 1.1 | 0.0973 ± 0.0021 | 0.2551 ± 0.0028 | 109,420 ± 124 |
| 90 | 573.0 ± 1.1 | 624.0 ± 1.0 | 0.1294 ± 0.0012 | 0.2530 ± 0.0019 | 116,215 ± 115 |
| Rolling Direction (°) | C (MPa) | n (-) | φ0 (-) | R (-) |
|---|---|---|---|---|
| 0 | 948.7 ± 0.1 | 0.1636 ± 0.0001 | 0.01229 ± 0.00002 | 0.87 ± 0.01 |
| 45 | 887.1 ± 0.3 | 0.1482 ± 0.0002 | 0.01779 ± 0.00007 | 2.36 ± 0.01 |
| 90 | 1089.9 ± 0.6 | 0.2226 ± 0.0004 | 0.03746 ± 0.00014 | 2.61 ± 0.01 |
| Rolling Direction (°) | C (MPa) | n (-) | φ0 (-) | R (-) |
|---|---|---|---|---|
| - | 1487.2 ± 10.0 | 0.2980 ± 0.0067 | 0.03030 ± 0.00273 | 1.15 ± 0.01 |
| Rolling Direction (°) | C (MPa) | n (-) | φ0 (-) |
|---|---|---|---|
| 0 | 1051.5 ± 6.4 | 0.1257 ± 0.0023 | 0.00671 ± 0.00043 |
| 45 | 1163.1 ± 7.1 | 0.1466 ± 0.0030 | 0.01773 ± 0.00090 |
| 90 | 1242.7 ± 16.8 | 0.1912 ± 0.0093 | 0.04621 ± 0.00415 |
| Rolling Direction (°) | C (MPa) | n (-) | φ0 (-) |
|---|---|---|---|
| 0 | 448.1 ± 0.6 | 0.1033 ± 0.0012 | 0.00093 ± 0.00098 |
| 45 | 509.0 ± 0.3 | 0.1668 ± 0.0014 | 0.02833 ± 0.00176 |
| 90 | 491.2 ± 0.2 | 0.5935 ± 0.0007 | 0.03008 ± 0.00086 |
| Rolling Direction (°) | Rp0.2 (MPa) | RCp0.2 (MPa) | Difference Rp0.2 (%) |
|---|---|---|---|
| 0° | 464.0 ± 0.1 | −304.9 ± 0.2 | 34.3 ± 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koreček, D.; Solfronk, P.; Sobotka, J. A Deformational Analysis of a Titanium Alloy Supported by the Mathematical Modelling of the Sheet Metal Forming Process via Numerical Simulation. Materials 2025, 18, 1598. https://doi.org/10.3390/ma18071598
Koreček D, Solfronk P, Sobotka J. A Deformational Analysis of a Titanium Alloy Supported by the Mathematical Modelling of the Sheet Metal Forming Process via Numerical Simulation. Materials. 2025; 18(7):1598. https://doi.org/10.3390/ma18071598
Chicago/Turabian StyleKoreček, David, Pavel Solfronk, and Jiří Sobotka. 2025. "A Deformational Analysis of a Titanium Alloy Supported by the Mathematical Modelling of the Sheet Metal Forming Process via Numerical Simulation" Materials 18, no. 7: 1598. https://doi.org/10.3390/ma18071598
APA StyleKoreček, D., Solfronk, P., & Sobotka, J. (2025). A Deformational Analysis of a Titanium Alloy Supported by the Mathematical Modelling of the Sheet Metal Forming Process via Numerical Simulation. Materials, 18(7), 1598. https://doi.org/10.3390/ma18071598






