Mixed-Mode Crack Growth Behavior of Compact Tension Shear (CTS) Specimens: A Study on the Impact of the Fatigue Stress Ratio, Loading Angle, and Geometry Thickness
Abstract
1. Introduction
2. Numerical Analysis Procedure
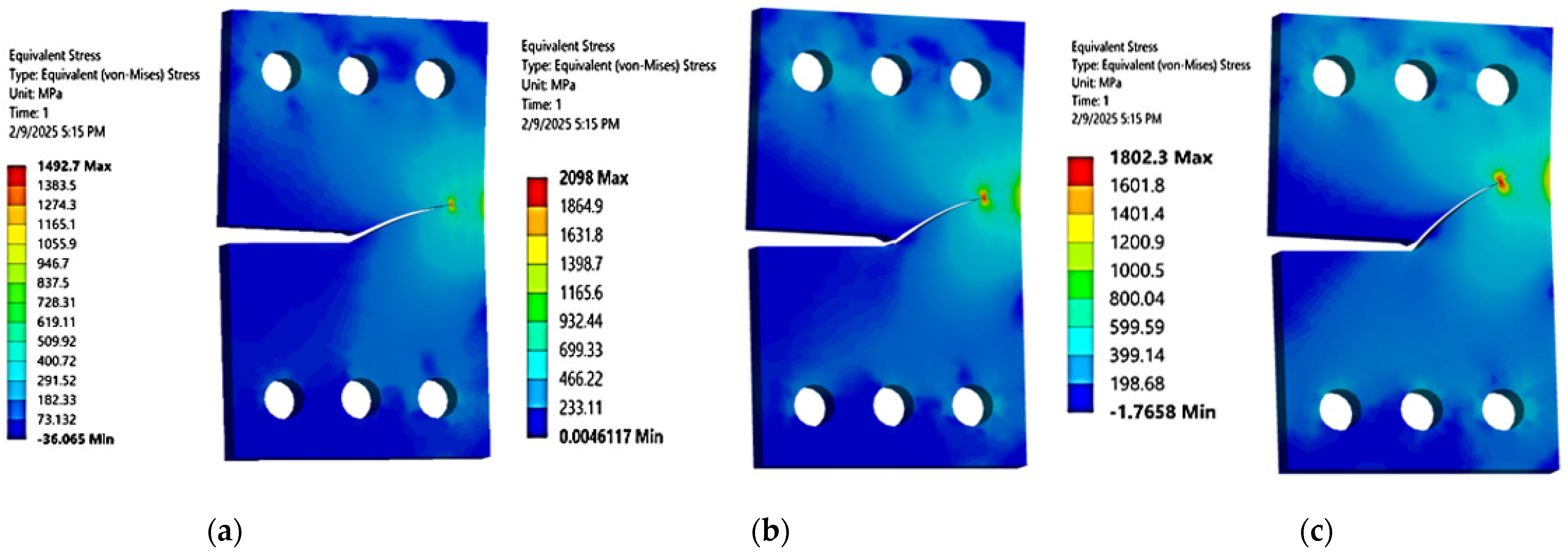
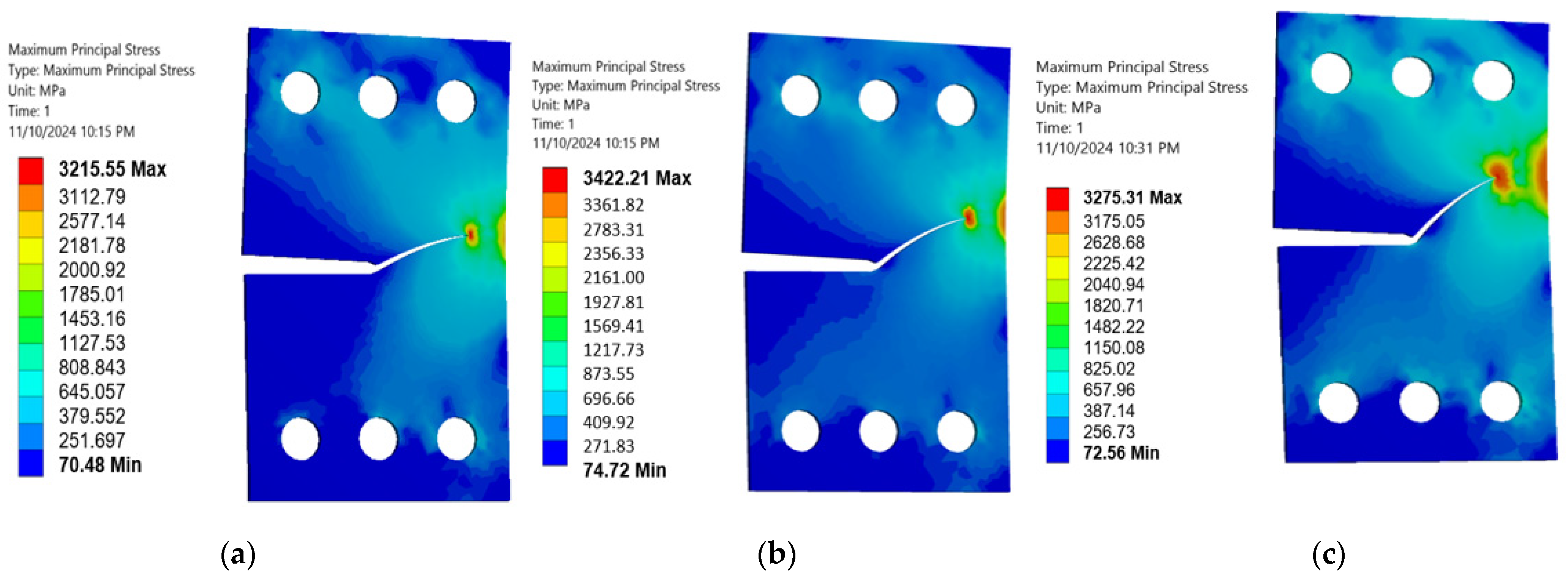
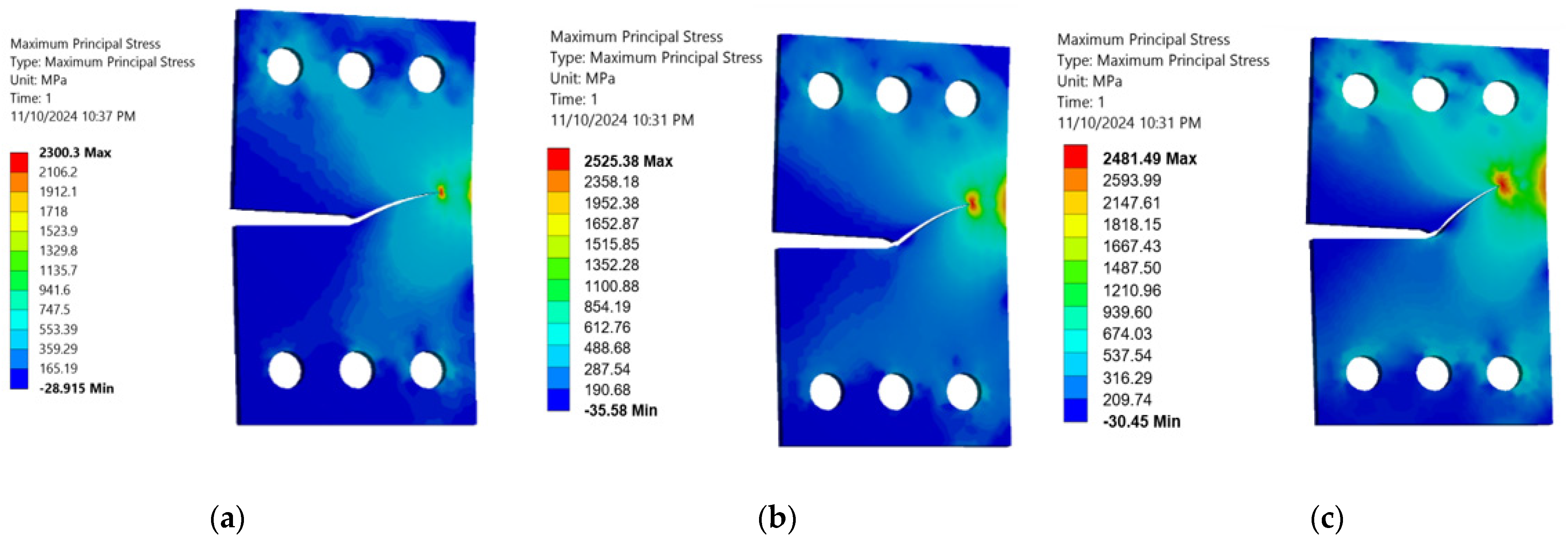
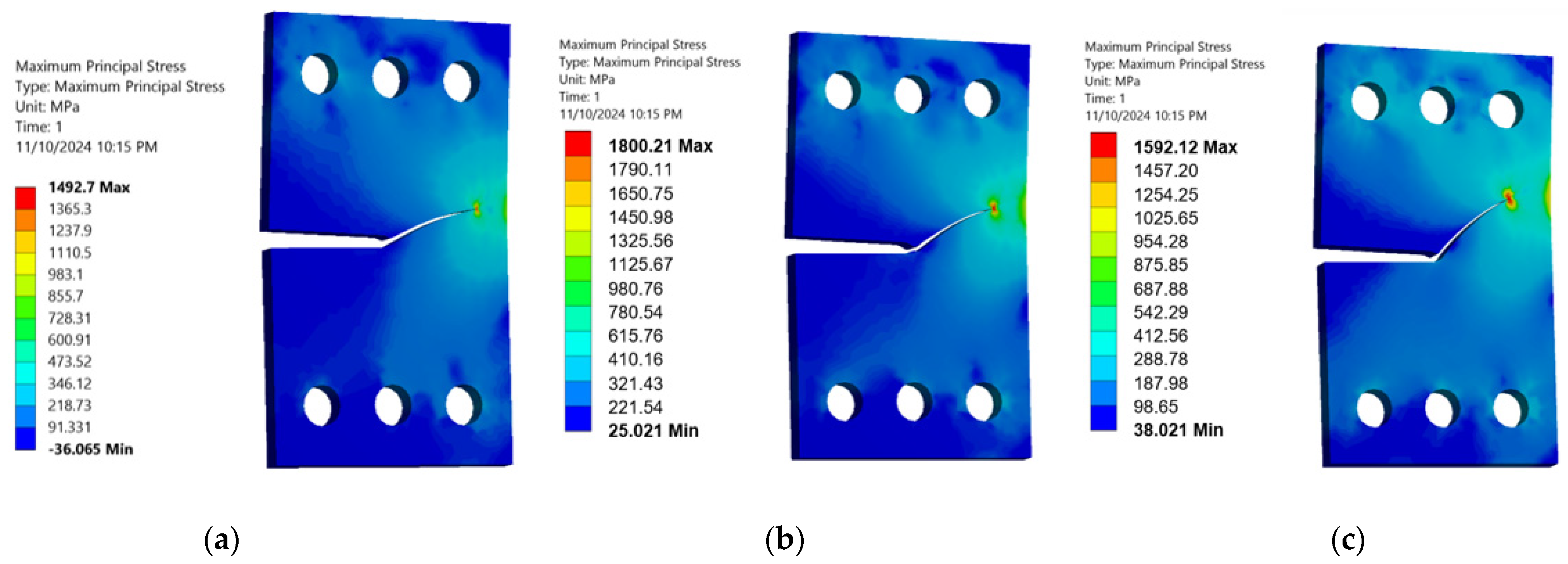
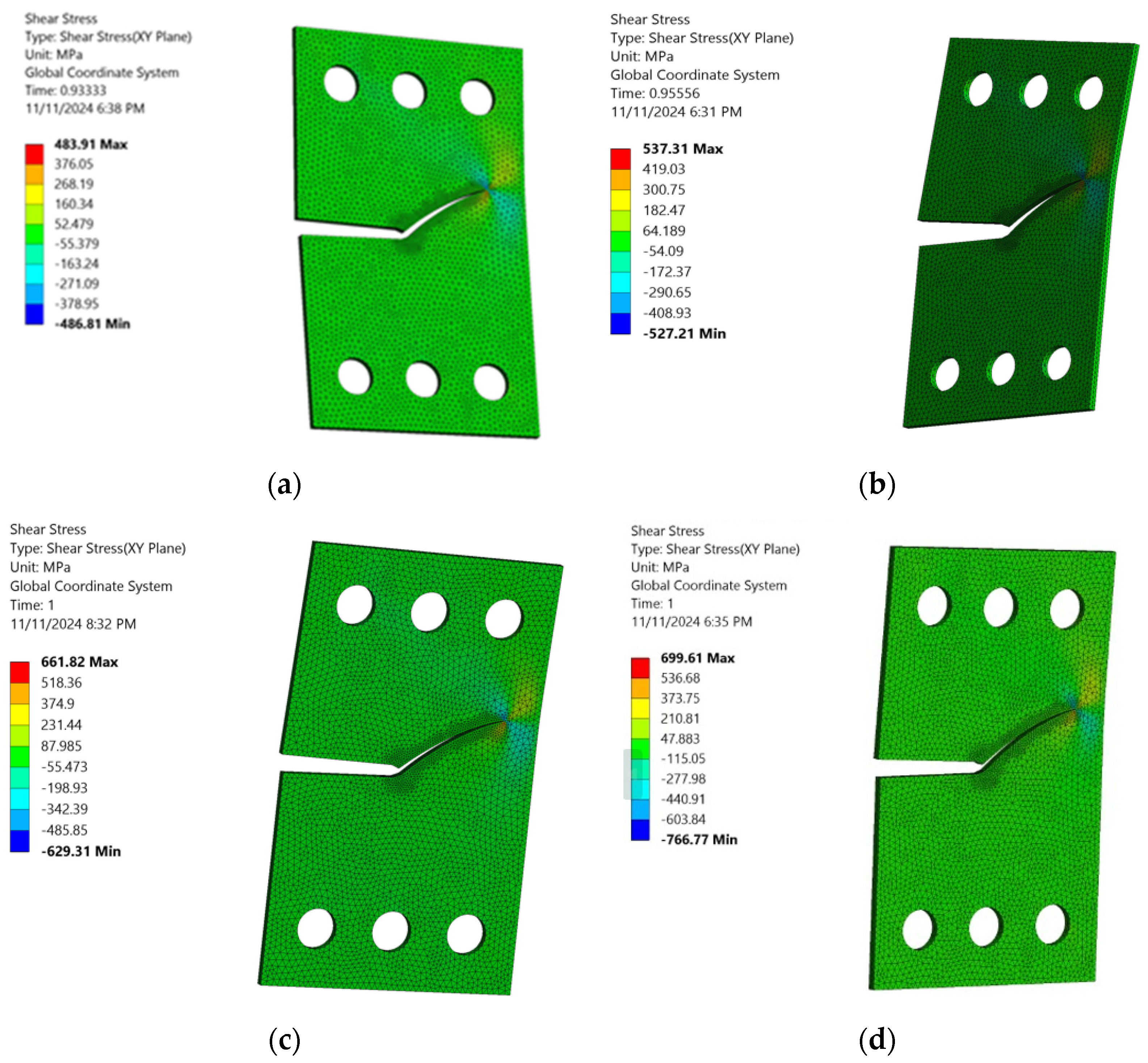
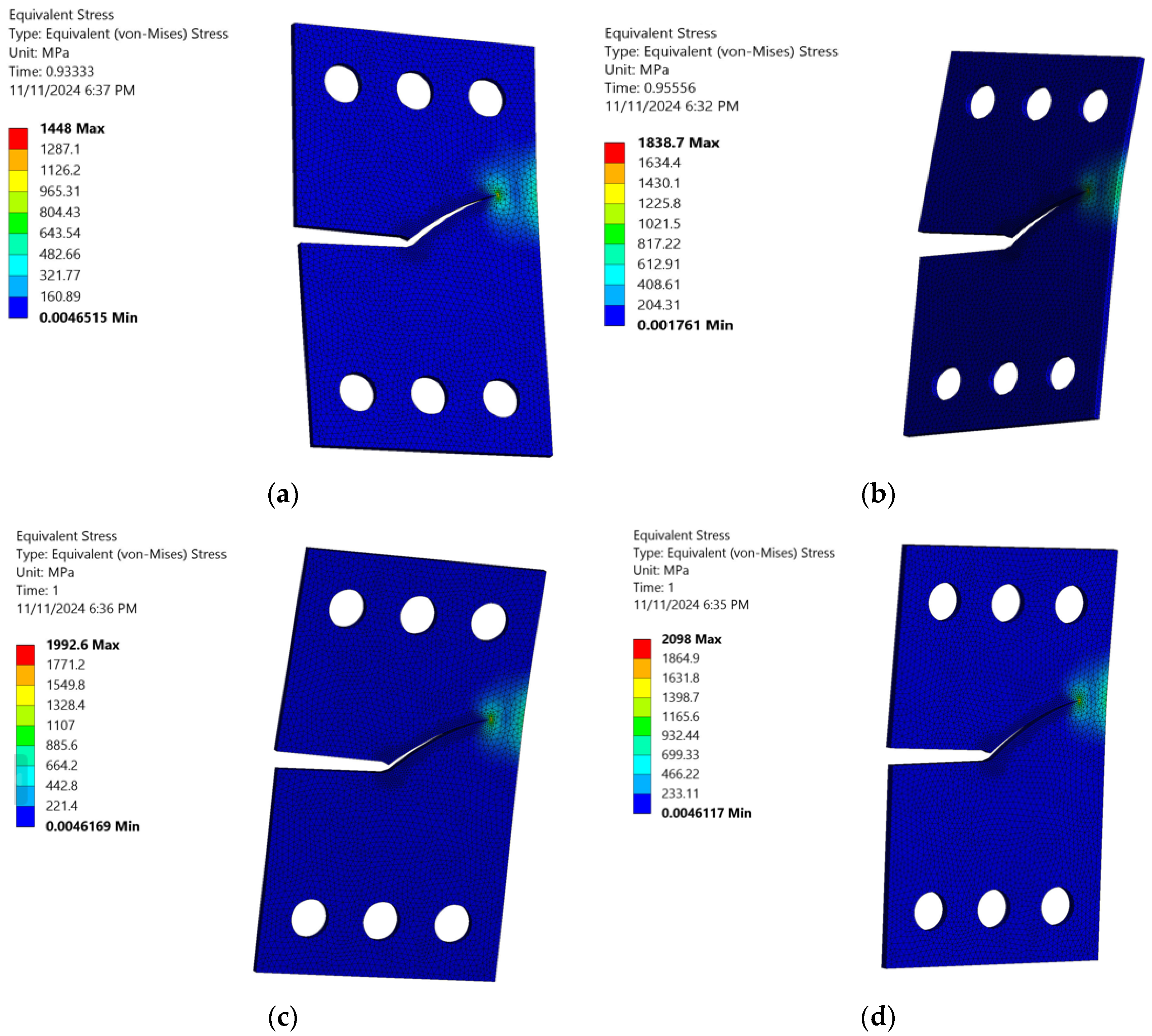
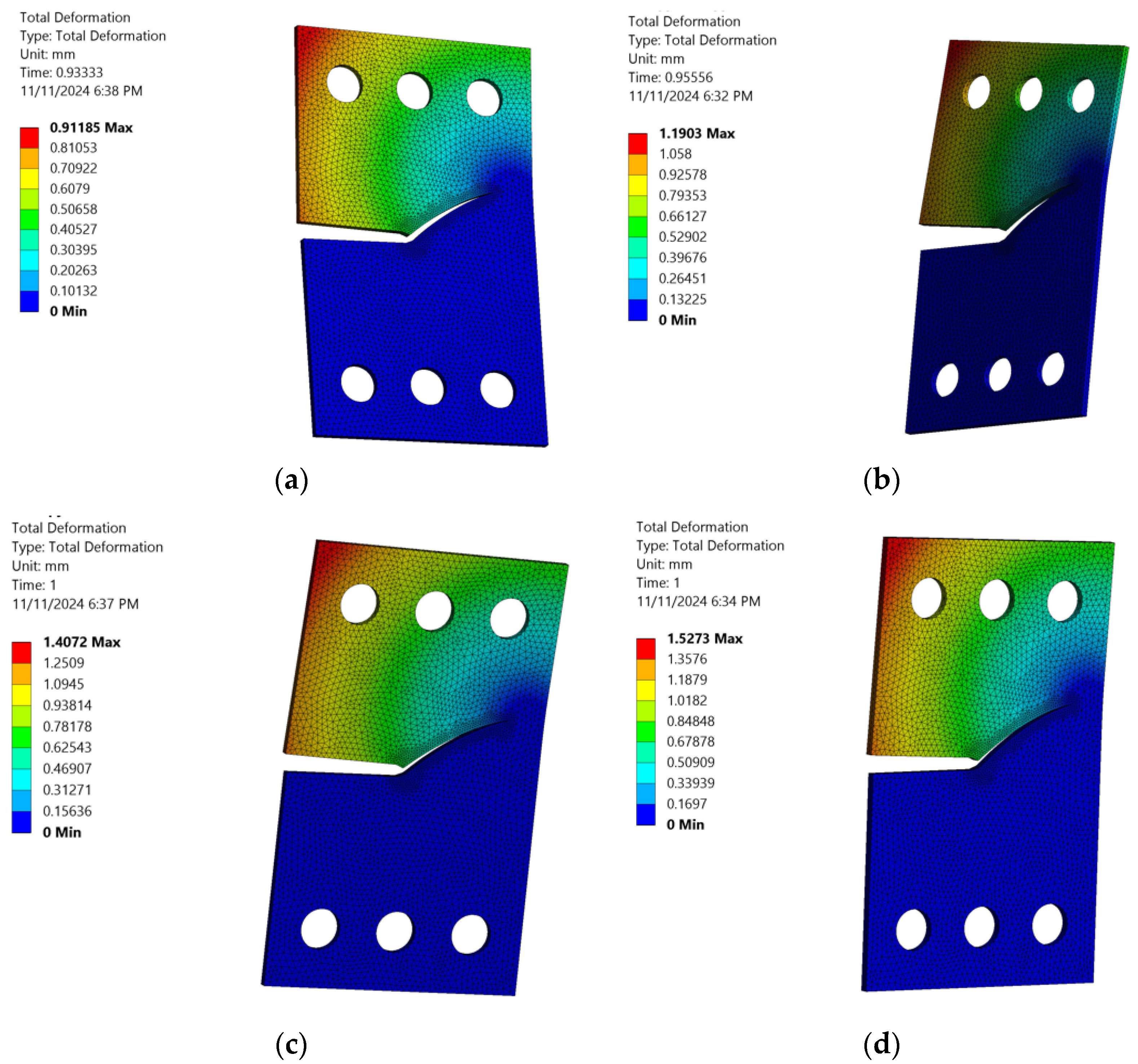
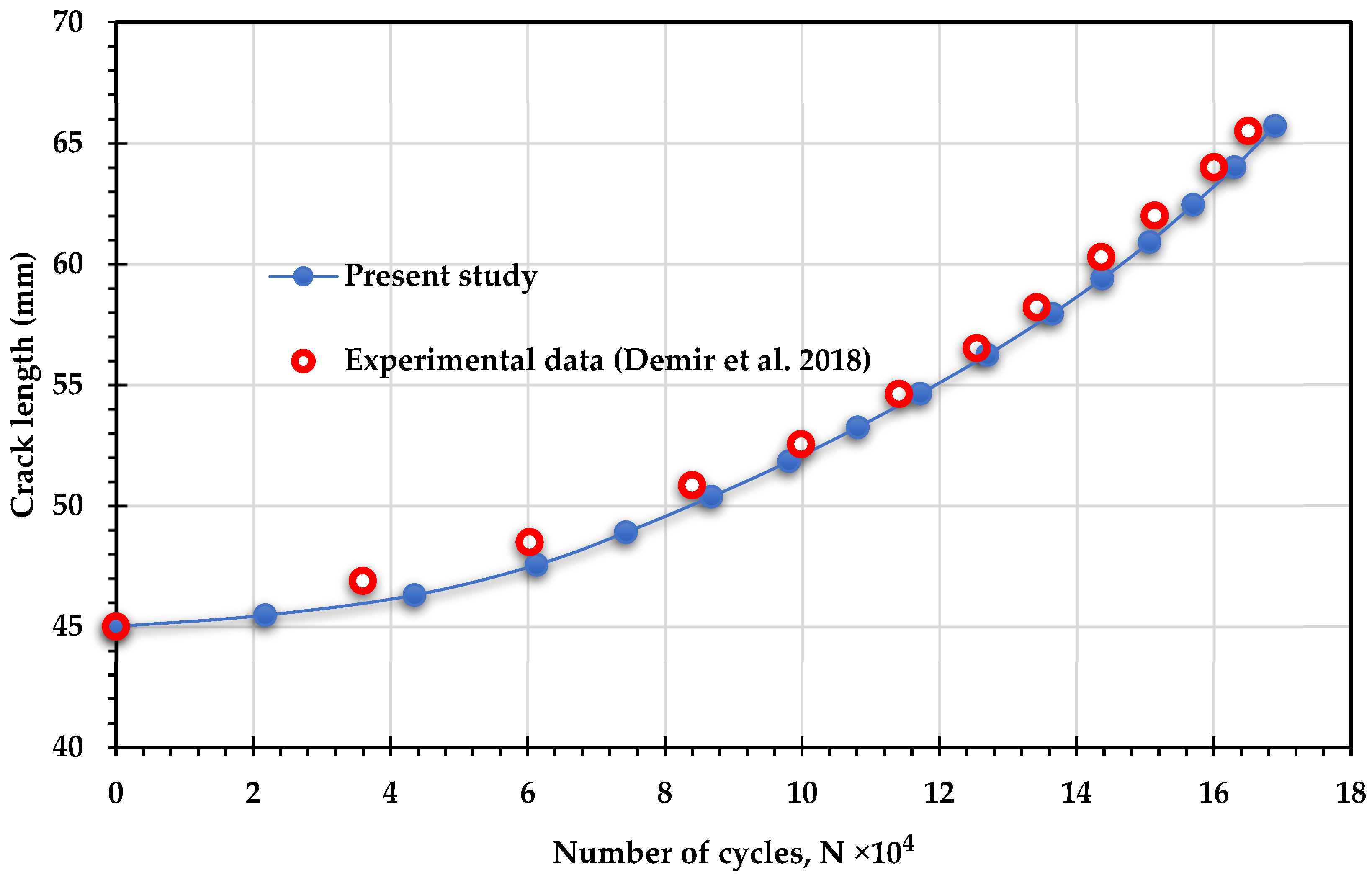
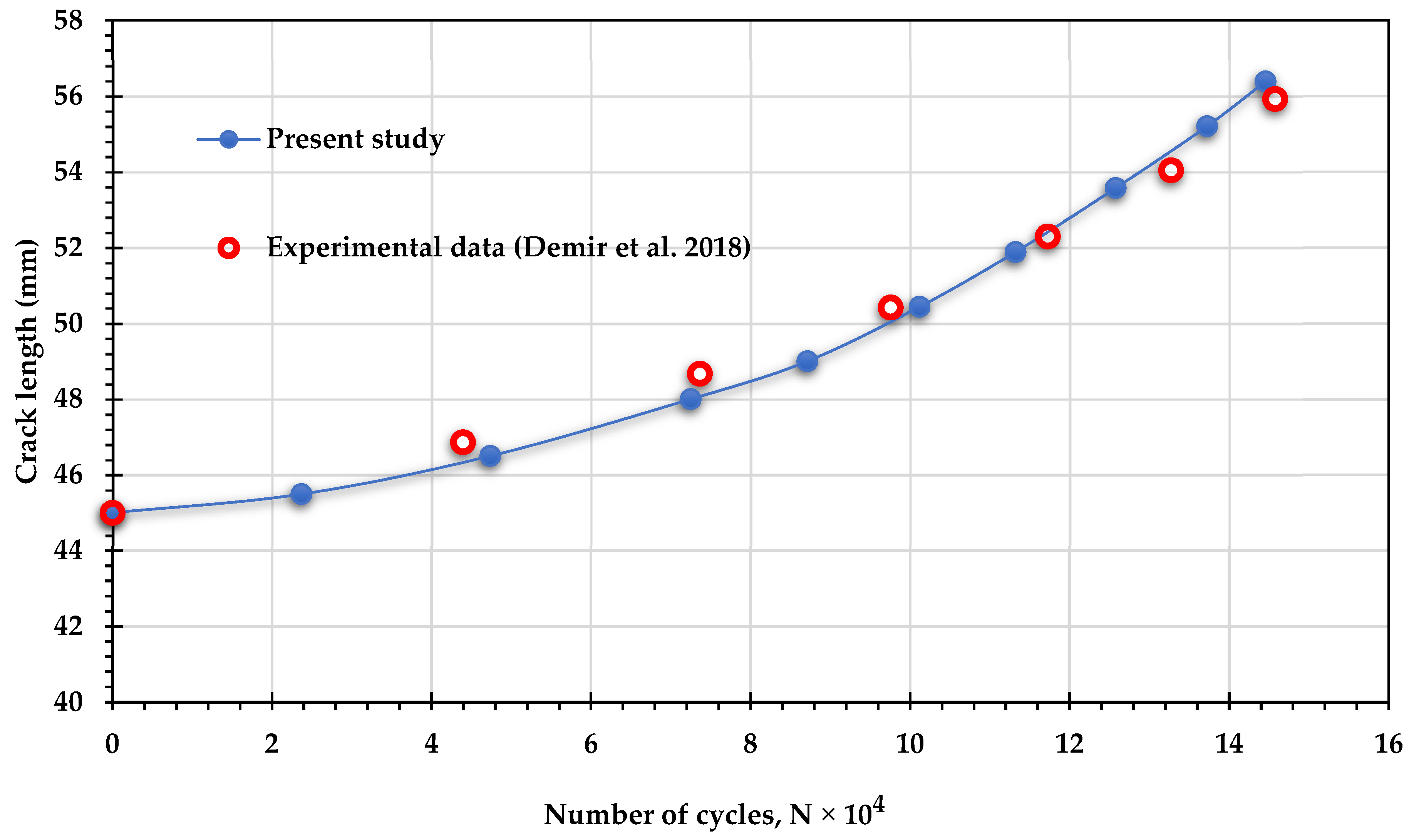
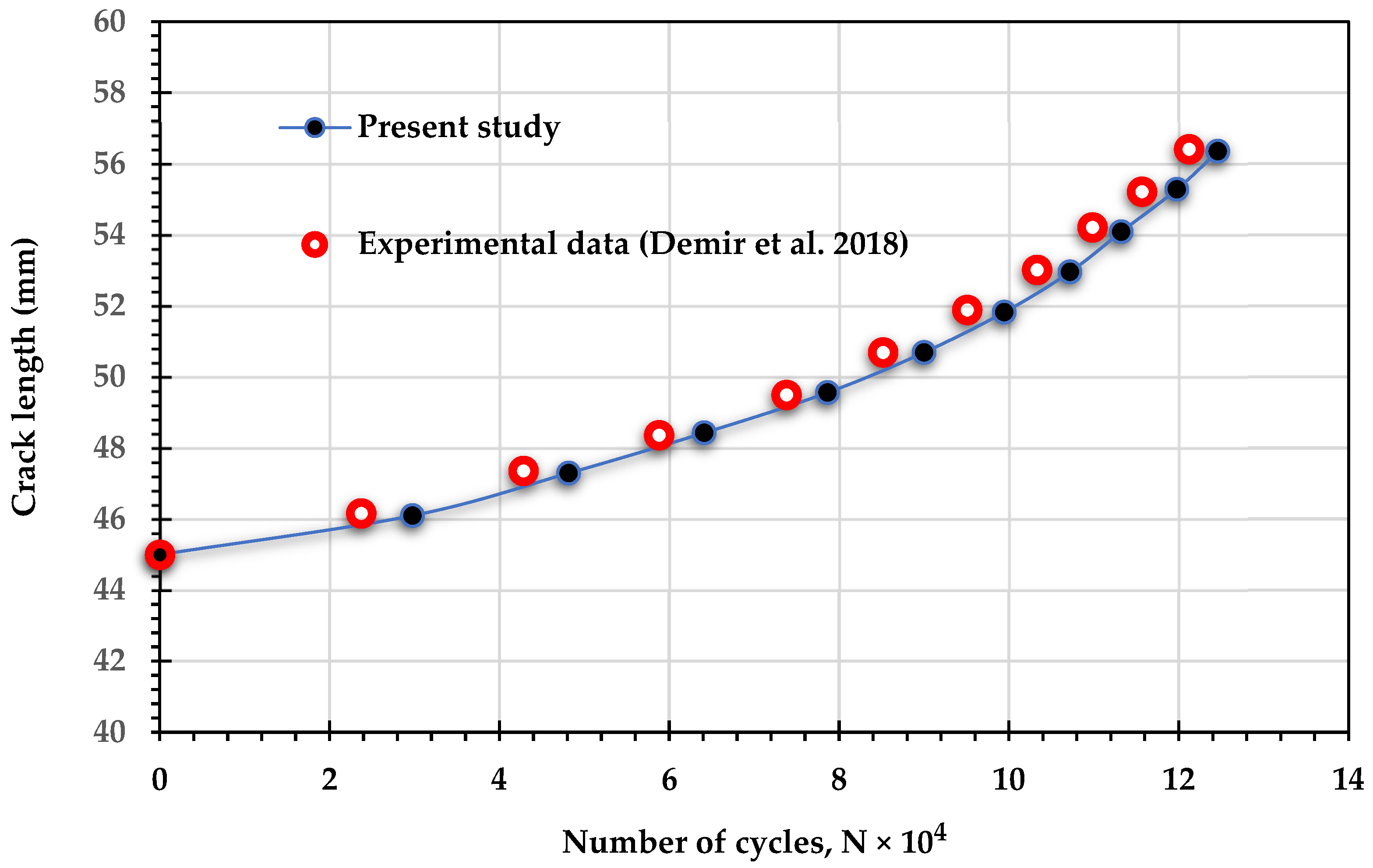
3. Numerical Results and Discussions
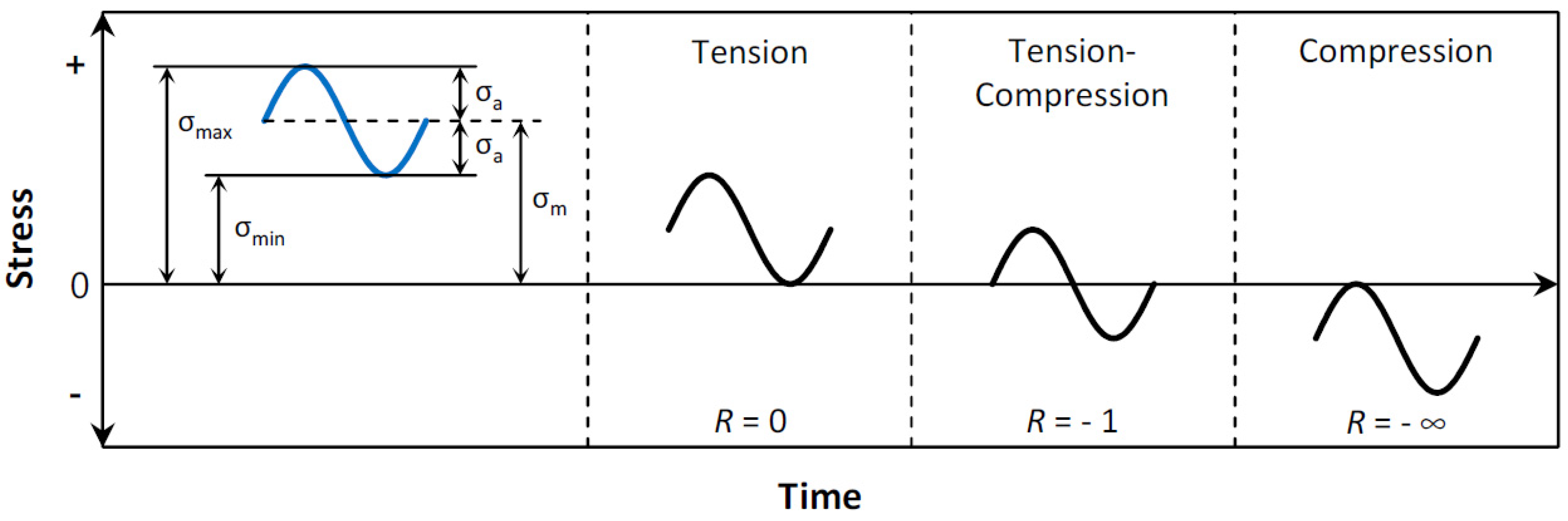
- Reduced Maximum Stress: A higher stress ratio results in a lower maximum stress during each loading cycle, which alleviates the overall stress experienced by the specimen. This reduction contributes significantly to prolonging the material’s fatigue life.
- Increased Compressive Cycles: A higher stress ratio leads to a larger proportion of compressive loads in each cycle, which can close existing cracks and suppress their growth, thereby increasing fatigue resistance.
- Lower Strain Rates: An increased stress ratio often leads to decreased strain rates, which can mitigate crack propagation rates, thereby extending the fatigue life.
- Minimized Plastic Deformation: Higher stress ratios tend to limit the extent of plastic deformation during loading cycles. Since plastic deformation can trigger and accelerate crack growth, reducing it plays a crucial role in enhancing fatigue life.
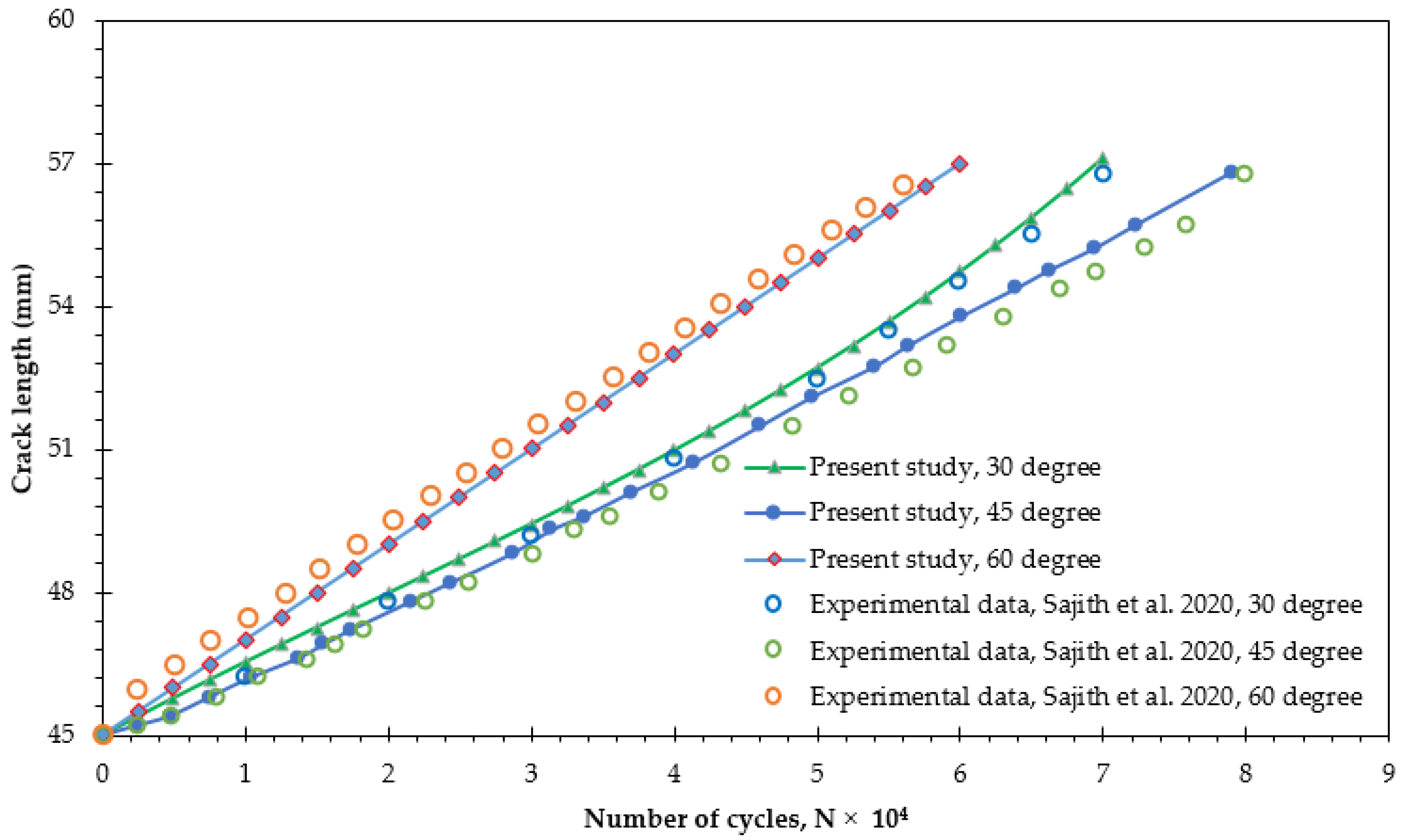
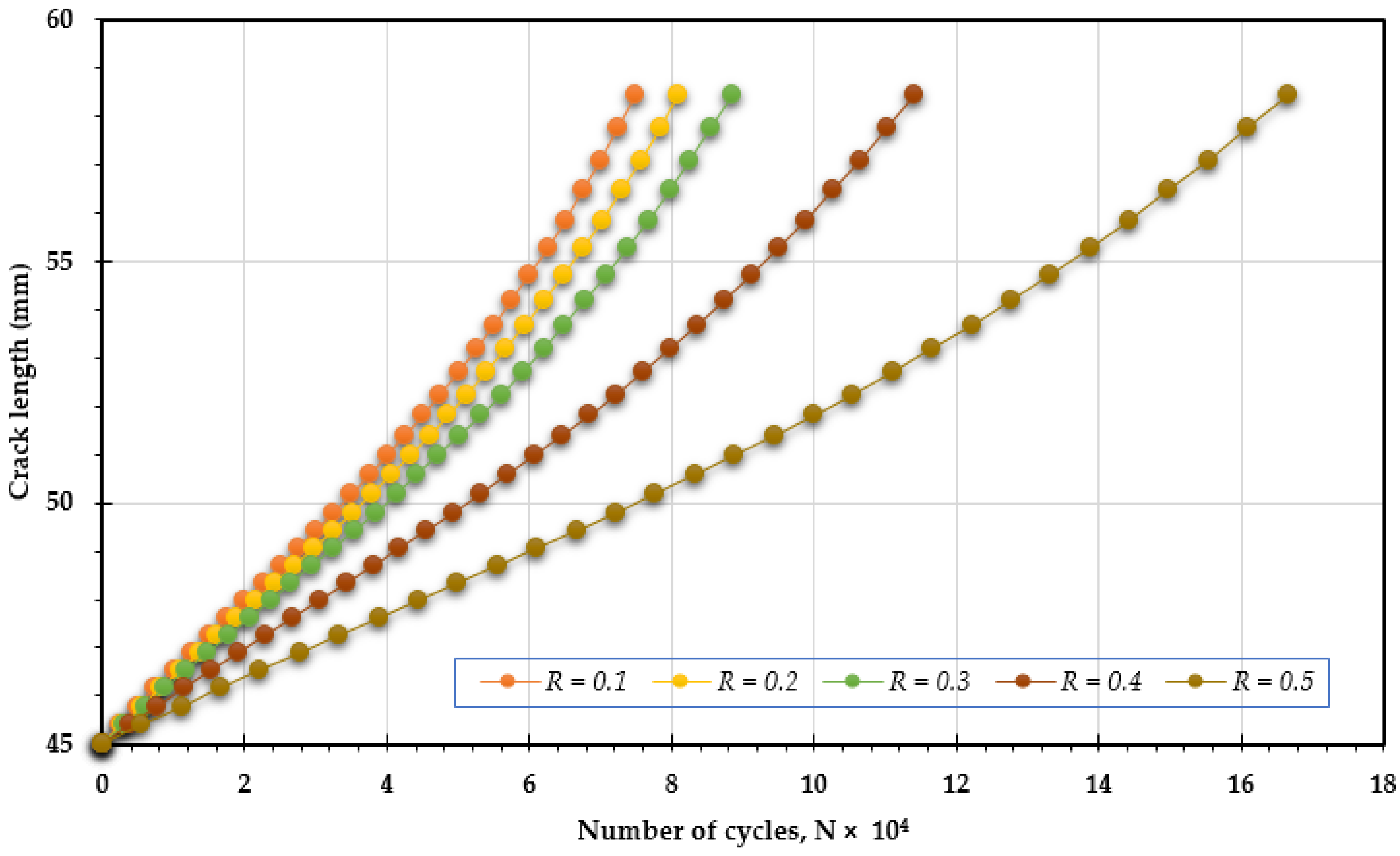
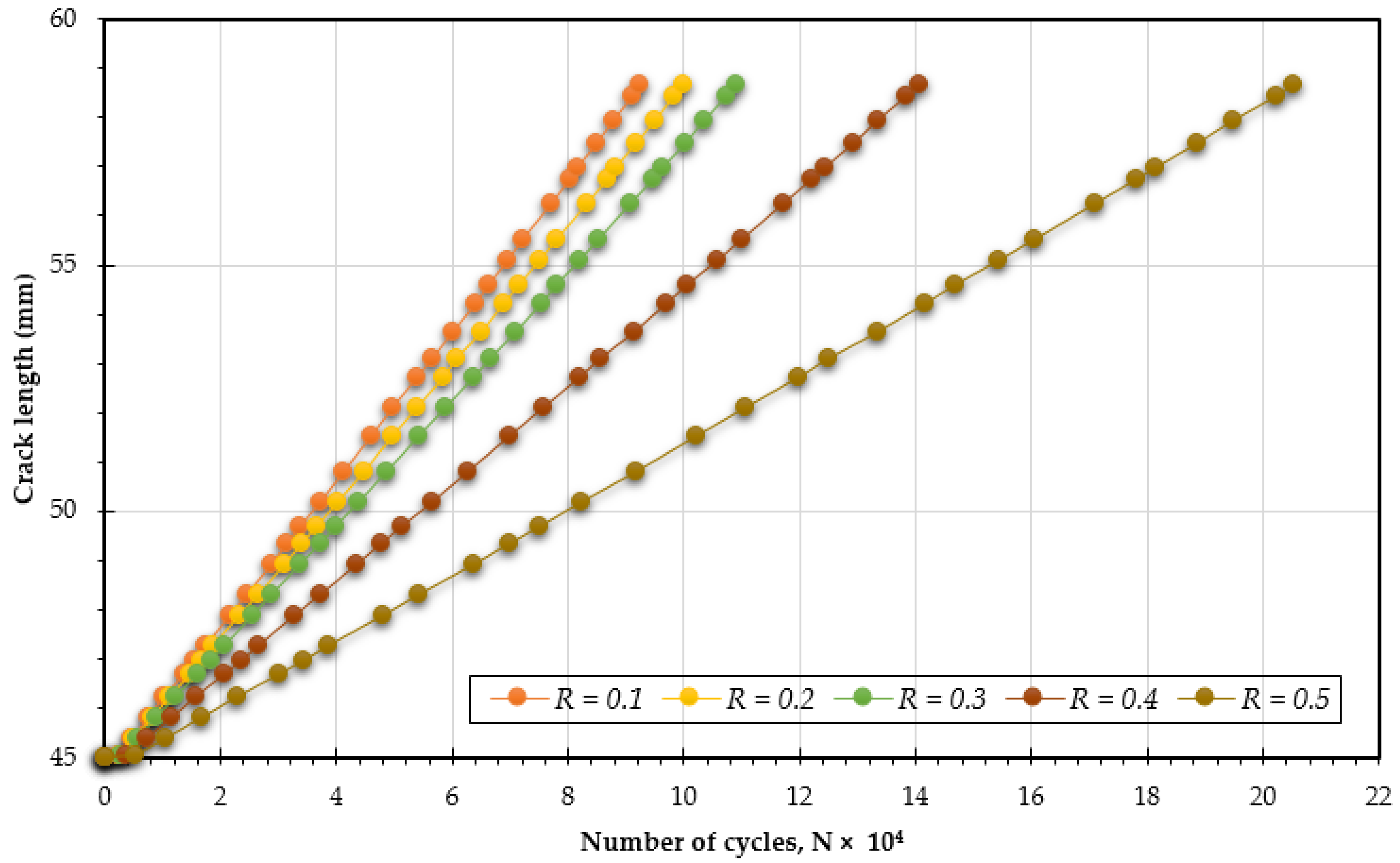
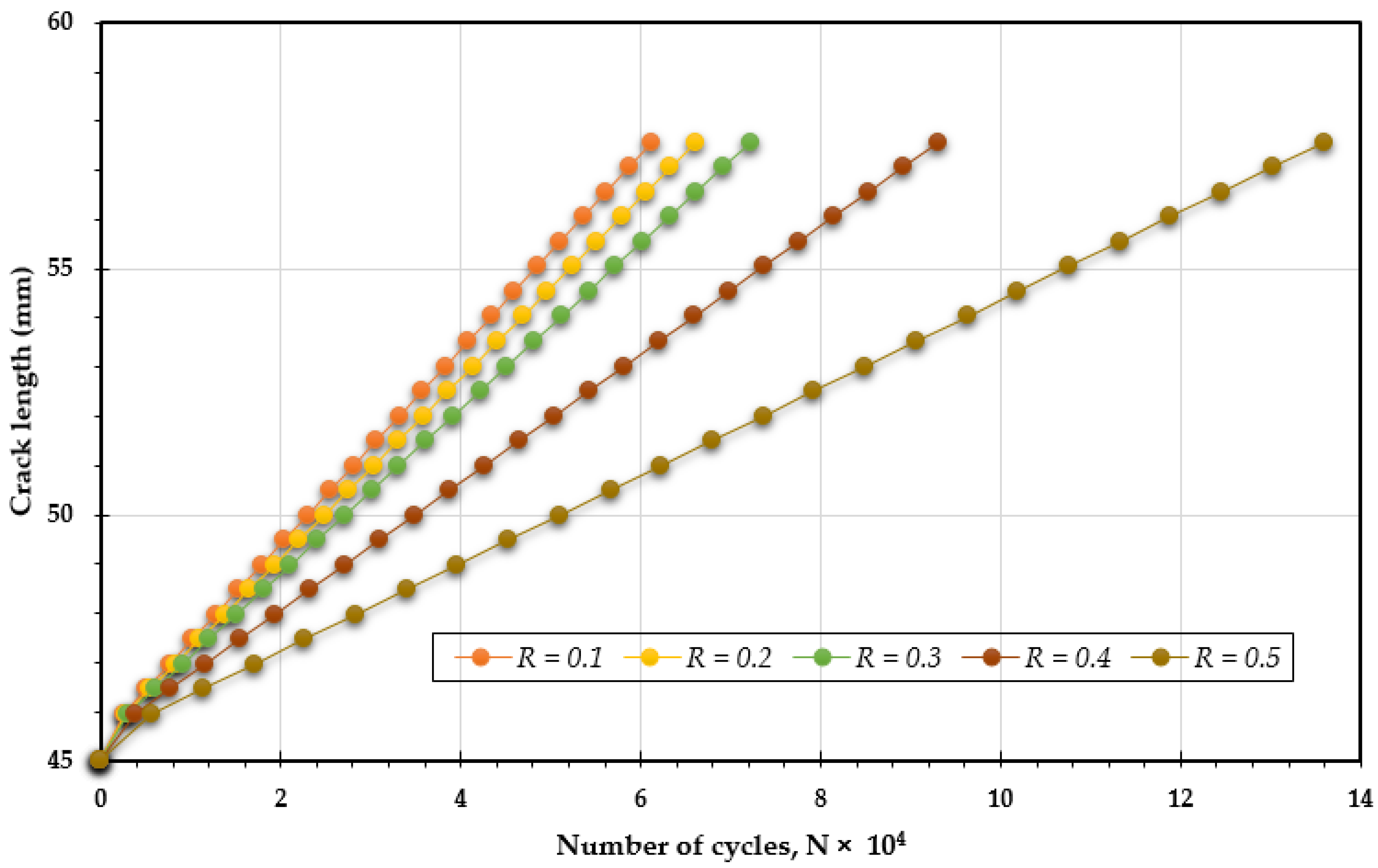
4. Conclusions
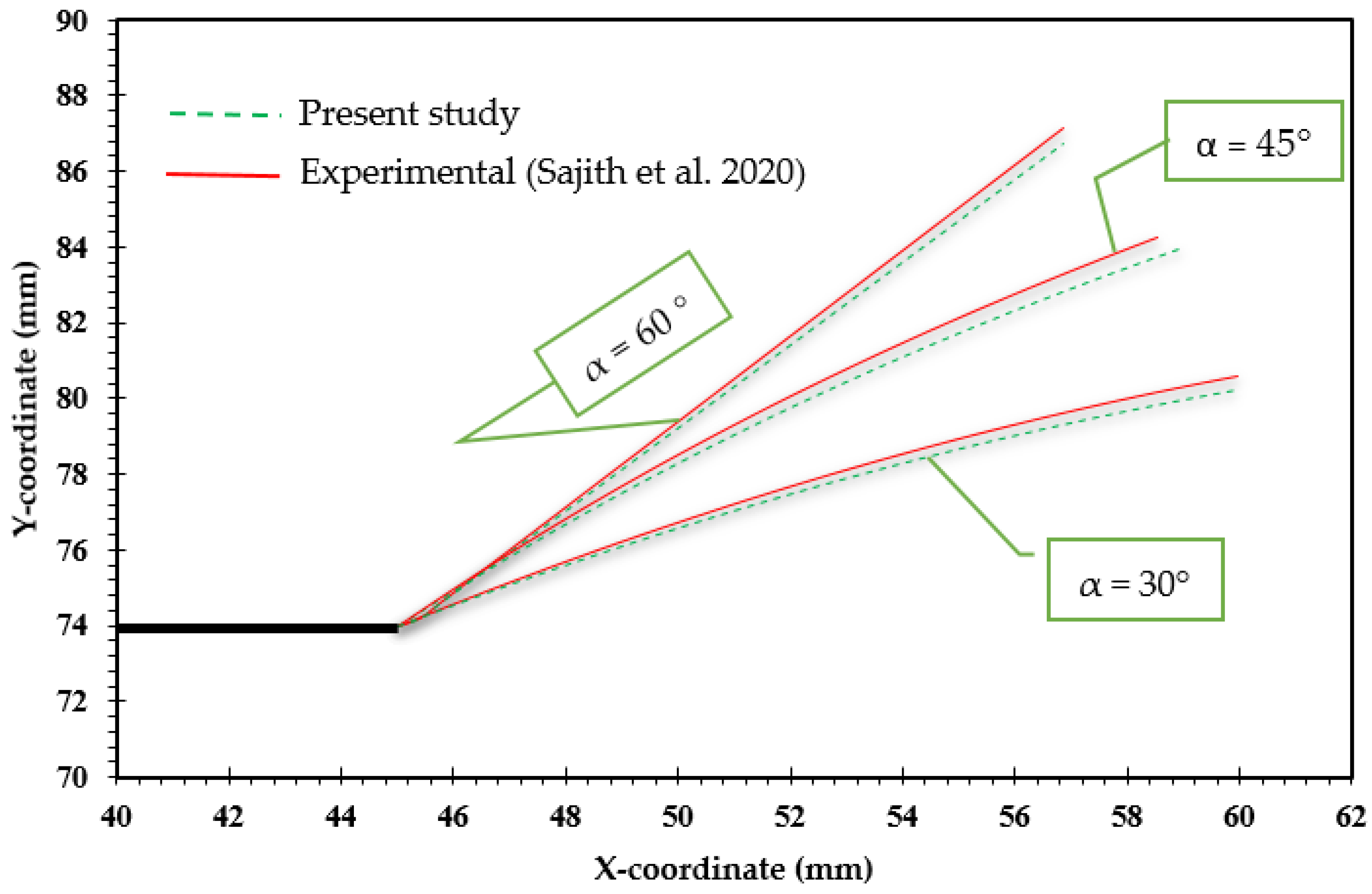
- The findings reveal that the loading angle has a significant effect on the trajectory of FCG and the number of fatigue life cycles.
- This research elucidates the critical role of the fatigue stress ratio in the mechanical response of materials, demonstrating that an increased stress ratio markedly enhances fatigue life cycles. This finding provides new insights into how stress conditions affect material durability. The results demonstrate that increasing the fatigue stress ratio in CTS specimens results in higher mean stress levels and a decrease in stress variation. Consequently, this leads to greater accumulated deformation over time.
- By examining the intricate interactions among the fatigue stress ratio, loading angle, and geometry thickness, this research offers valuable guidance for optimizing component performance and safety under cyclic loading. These findings are essential for advancing design strategies, improving material selection, and enhancing life cycle assessments of fatigue-sensitive components, ultimately contributing to greater reliability and safety across various industries.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ma, S.; Zhang, X.; Recho, N.; Li, J. The mixed-mode investigation of the fatigue crack in CTS metallic specimen. Int. J. Fatigue 2006, 28, 1780–1790. [Google Scholar] [CrossRef]
- Jin, P.; Wang, X.; Chen, H.; Liu, Z.; Chen, X. Analysis of mixed-mode Compact-Tension-Shear (CTS) specimens with slanted propagating cracks. Theor. Appl. Fract. Mech. 2023, 127, 104037. [Google Scholar] [CrossRef]
- Li, G.; Ke, L.; Ren, X.; Sun, C. High cycle and very high cycle fatigue of TC17 titanium alloy: Stress ratio effect and fatigue strength modeling. Int. J. Fatigue 2023, 166, 107299. [Google Scholar] [CrossRef]
- Gao, C.; Pang, J.; Hu, D.; Li, S.; Qi, K.; Wang, B.; Zhang, Y.; Nie, L.; Yang, M.; Zhang, Z. A new method for predicting the fatigue strength at various stress ratios based on damage of metallic materials. Fatigue Fract. Eng. Mater. Struct. 2024, 47, 2103–2126. [Google Scholar] [CrossRef]
- Alshoaibi, A.M. Fatigue Crack Growth Analysis in Modified Compact Tension Specimen with Varying Stress Ratios: A Finite Element Study. Appl. Sci. 2023, 13, 13160. [Google Scholar] [CrossRef]
- Xin, H.; Liu, J.; Correia, J.A.; Berto, F.; Veljkovic, M.; Qian, G. Mixed-mode fatigue crack propagation simulation by means of Geq and walker models of the structural steel S355. Theor. Appl. Fract. Mech. 2023, 123, 103717. [Google Scholar] [CrossRef]
- White, P.; Barter, S.; Medhekar, N. Comparison of fatigue crack growth stress ratio effects under simple variable amplitude loading using fractographic and strain measurements. Int. J. Fatigue 2018, 112, 240–252. [Google Scholar] [CrossRef]
- Richard, H.A.; Sander, M. Fatigue Crack Growth; Springer: Berlin/Heidelberg, Germany, 2016; Volume 18. [Google Scholar]
- Li, H.; Yang, S.; Zhang, P.; Liu, Y.; Wang, B.; Zhang, Z. Material-independent stress ratio effect on the fatigue crack growth behavior. Eng. Fract. Mech. 2022, 259, 108116. [Google Scholar] [CrossRef]
- Malipatil, S.G.; Majila, A.N.; Fernando, D.C.; Manjunatha, C. Influence of crack driving force on correlating stress ratio effects in fatigue crack growth rate of a nickel base super alloy IN720. Int. J. Adv. Eng. Sci. Appl. Math. 2020, 12, 19–26. [Google Scholar] [CrossRef]
- Newman, J., Jr.; Kota, K.; Lacy, T. Fatigue and crack-growth behavior in a titanium alloy under constant-amplitude and spectrum loading. Eng. Fract. Mech. 2018, 187, 211–224. [Google Scholar] [CrossRef]
- Arifin, A.; Abdullah, S.; Ariffin, A.; Jamaludin, N.; Singh, S. Characterising the stress ratio effect for fatigue crack propagation parameters of SAE 1045 steel based on magnetic flux leakage. Theor. Appl. Fract. Mech. 2022, 121, 103514. [Google Scholar]
- Bian, J.; Yu, P.; Zhao, Y.; Yao, L.; Wei, P.; Zhao, J. Fatigue crack growth of marine 980 high-strength steel: From standard specimen testing to three-dimensional curved crack life prediction. Ocean Eng. 2024, 296, 116950. [Google Scholar]
- Garcia, C.; Lotz, T.; Martinez, M.; Artemev, A.; Alderliesten, R.; Benedictus, R. Fatigue crack growth in residual stress fields. Int. J. Fatigue 2016, 87, 326–338. [Google Scholar]
- Boyce, B.; Ritchie, R. Effect of load ratio and maximum stress intensity on the fatigue threshold in Ti–6Al–4V. Eng. Fract. Mech. 2001, 68, 129–147. [Google Scholar]
- Richard, H.; Benitz, K. A loading device for the creation of mixed mode in fracture mechanics. Int. J. Fract. 1983, 22, R55–R58. [Google Scholar]
- Sajith, S.; Shukla, S.; Murthy, K.; Robi, P. Mixed mode fatigue crack growth studies in AISI 316 stainless steel. Eur. J. Mech.-A/Solids 2020, 80, 103898. [Google Scholar]
- Zhang, P.; Zhou, C.-Y.; Xie, L.-Q.; He, X.-H. Numerical investigation of mechanical behavior of crack tip under mode I and mixed-mode I-II fatigue loading at negative load ratios. Theor. Appl. Fract. Mech. 2020, 108, 102673. [Google Scholar]
- Shakeri, I.; Shahani, A.R.; Rans, C.D. Fatigue crack growth of butt welded joints subjected to mixed mode loading and overloading. Eng. Fract. Mech. 2021, 241, 107376. [Google Scholar]
- Xie, Q.; Qi, H.; Li, S.; Yang, X.; Shi, D. Experimental and numerical investigation of mixed-mode fatigue crack growth in nickel-based superalloy at high temperature. Eng. Fract. Mech. 2022, 273, 108736. [Google Scholar]
- Salehnasab, B.; Marzbanrad, J.; Poursaeidi, E. Conventional shot peening treatment effects on thermal fatigue crack growth and failure mechanisms of a solid solution alloy. Eng. Fail. Anal. 2024, 155, 107740. [Google Scholar]
- Shahani, A.; Farrahi, A. Experimental investigation and numerical modeling of the fatigue crack growth in friction stir spot welding of lap-shear specimen. Int. J. Fatigue 2019, 125, 520–529. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Fageehi, Y.A. Numerical Analysis on Fatigue Crack Growth at Negative and Positive Stress Ratios. Materials 2023, 16, 3669. [Google Scholar] [CrossRef] [PubMed]
- Alshoaibi, A.M.; Fageehi, Y.A. Finite Element Simulation of a Crack Growth in the Presence of a Hole in the Vicinity of the Crack Trajectory. Materials 2022, 15, 363. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Fageehi, Y.A. Numerical Analysis of Fatigue Crack Growth Path and Life Predictions for Linear Elastic Material. Materials 2020, 13, 3380. [Google Scholar] [CrossRef]
- Alshoaibi, A.M. Comprehensive comparisons of two and three dimensional numerical estimation of stress intensity factors and crack propagation in linear elastic analysis. Int. J. Integr. Eng. 2019, 11, 45–52. [Google Scholar]
- Alshoaibi, A.M. Computational Simulation of 3D Fatigue Crack Growth under Mixed-Mode Loading. Appl. Sci. 2021, 11, 5953. [Google Scholar] [CrossRef]
- Fageehi, Y.A.; Alshoaibi, A.M. Investigating the Influence of Holes as Crack Arrestors in Simulating Crack Growth Behavior Using Finite Element Method. Appl. Sci. 2024, 14, 897. [Google Scholar] [CrossRef]
- Alshoaibi, A.M.; Bashiri, A.H. Fatigue Crack Growth Studies under Mixed-Mode Loading in AISI 316 Stainless Steel. Appl. Sci. 2023, 13, 9446. [Google Scholar] [CrossRef]
- Malekan, M.; Khosravi, A.; St-Pierre, L. An Abaqus plug-in to simulate fatigue crack growth. Eng. Comput. 2021, 38, 2991–3005. [Google Scholar]
- Rocha, A.; Akhavan-Safar, A.; Carbas, R.; Marques, E.; Goyal, R.; El-zein, M.; da Silva, L. Numerical analysis of mixed-mode fatigue crack growth of adhesive joints using CZM. Theor. Appl. Fract. Mech. 2020, 106, 102493. [Google Scholar]
- Alshoaibi, A.M.; Fageehi, Y.A. A Comparative Analysis of 3D Software for Modeling Fatigue Crack Growth: A Review. Appl. Sci. 2024, 14, 1848. [Google Scholar] [CrossRef]
- Martins, R.F.; Xavier, J.; Caldeira, J. Numerical Fatigue Crack Growth on Compact Tension Specimens under Mode I and Mixed-Mode (I + II) Loading. Materials 2024, 17, 4570. [Google Scholar] [CrossRef] [PubMed]
- Jafari, A.; Broumand, P.; Vahab, M.; Khalili, N. An eXtended Finite Element Method Implementation in COMSOL Multiphysics: Solid Mechanics. Finite Elem. Anal. Des. 2022, 202, 103707. [Google Scholar]
- Zhang, S.; Liu, Y.; Yuan, S. Enhanced fatigue crack detection in complex structure with large cutout using nonlinear Lamb wave. Sensors 2024, 24, 6872. [Google Scholar] [CrossRef]
- Carter, B.; Wawrzynek, P.; Ingraffea, A. Automated 3-D crack growth simulation. Int. J. Numer. Methods Eng. 2000, 47, 229–253. [Google Scholar]
- Nagarajappa, N.; Malipatil, S.G.; Majila, A.N.; Fernando, D.C.; Manjuprasad, M.; Manjunatha, C. Fatigue Crack Growth Prediction in a Nickel-Base Superalloy Under Spectrum Loads Using FRANC3D. Trans. Indian Natl. Acad. Eng. 2022, 7, 533–540. [Google Scholar]
- Kuang, Y.; Wang, Y.; Xiang, P.; Tao, L.; Wang, K.; Fan, F.; Yang, J. Experimental and Theoretical Study on the Fatigue Crack Propagation in Stud Shear Connectors. Materials 2023, 16, 701. [Google Scholar] [CrossRef]
- Teh, S.; Andriyana, A.; Ramesh, S.; Putra, I.; Kadarno, P.; Purbolaksono, J. Tetrahedral meshing for a slanted semi-elliptical surface crack at a solid cylinder. Eng. Fract. Mech. 2021, 241, 107400. [Google Scholar]
- Bjørheim, F. Practical Comparison of Crack Meshing in ANSYS Mechanical APDL 19.2. Master’s Thesis, University of Stavanger, Stavanger, Norway, 2019. [Google Scholar]
- ANSYS. Academic Research Mechanical, Release 19.2, Help System. In Coupled-Field Analysis Guide; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Albuquerque, C.; Silva, A.L.; de Jesus, A.M.; Calçada, R. An efficient methodology for fatigue damage assessment of bridge details using modal superposition of stress intensity factors. Int. J. Fatigue 2015, 81, 61–77. [Google Scholar]
- Sajith, S.; Murthy, K.K.; Robi, P. Prediction of Accurate mixed mode fatigue crack growth curves using the paris’ law. J. Inst. Eng. India Ser. C 2019, 100, 165–174. [Google Scholar]
- Yan, X.; Du, S.; Zhang, Z. Mixed-mode fatigue crack growth prediction in biaxially stretched sheets. Eng. Fract. Mech. 1992, 43, 471–475. [Google Scholar]
- Richard, H. Fracture Predictions for Cracks Exposed to Superimposed Normal and Shear Stresses; VDI Verlag: Duesseldorf, Germany, 1985. [Google Scholar]
- Sander, M.; Richard, H. Experimental and numerical investigations on the influence of the loading direction on the fatigue crack growth. Int. J. Fatigue 2006, 28, 583–591. [Google Scholar]
- Sajjadi, S.; Ostad Ahmad Ghorabi, M.; Salimi-Majd, D. A novel mixed-mode brittle fracture criterion for crack growth path prediction under static and fatigue loading. Fatigue Fract. Eng. Mater. Struct. 2015, 38, 1372–1382. [Google Scholar]
- Sajith, S.; Murthy, K.; Robi, P. Experimental and numerical investigation of mixed mode fatigue crack growth models in aluminum 6061-T6. Int. J. Fatigue 2020, 130, 105285. [Google Scholar]
- Rozumek, D.; Marciniak, Z.; Lesiuk, G.; Correia, J. Mixed mode I/II/III fatigue crack growth in S355 steel. Procedia Struct. Integr. 2017, 5, 896–903. [Google Scholar]
- Demir, O.; Ayhan, A.O.; Sedat, I.; Lekesiz, H. Evaluation of mixed mode-I/II criteria for fatigue crack propagation using experiments and modeling. Chin. J. Aeronaut. 2018, 31, 1525–1534. [Google Scholar]
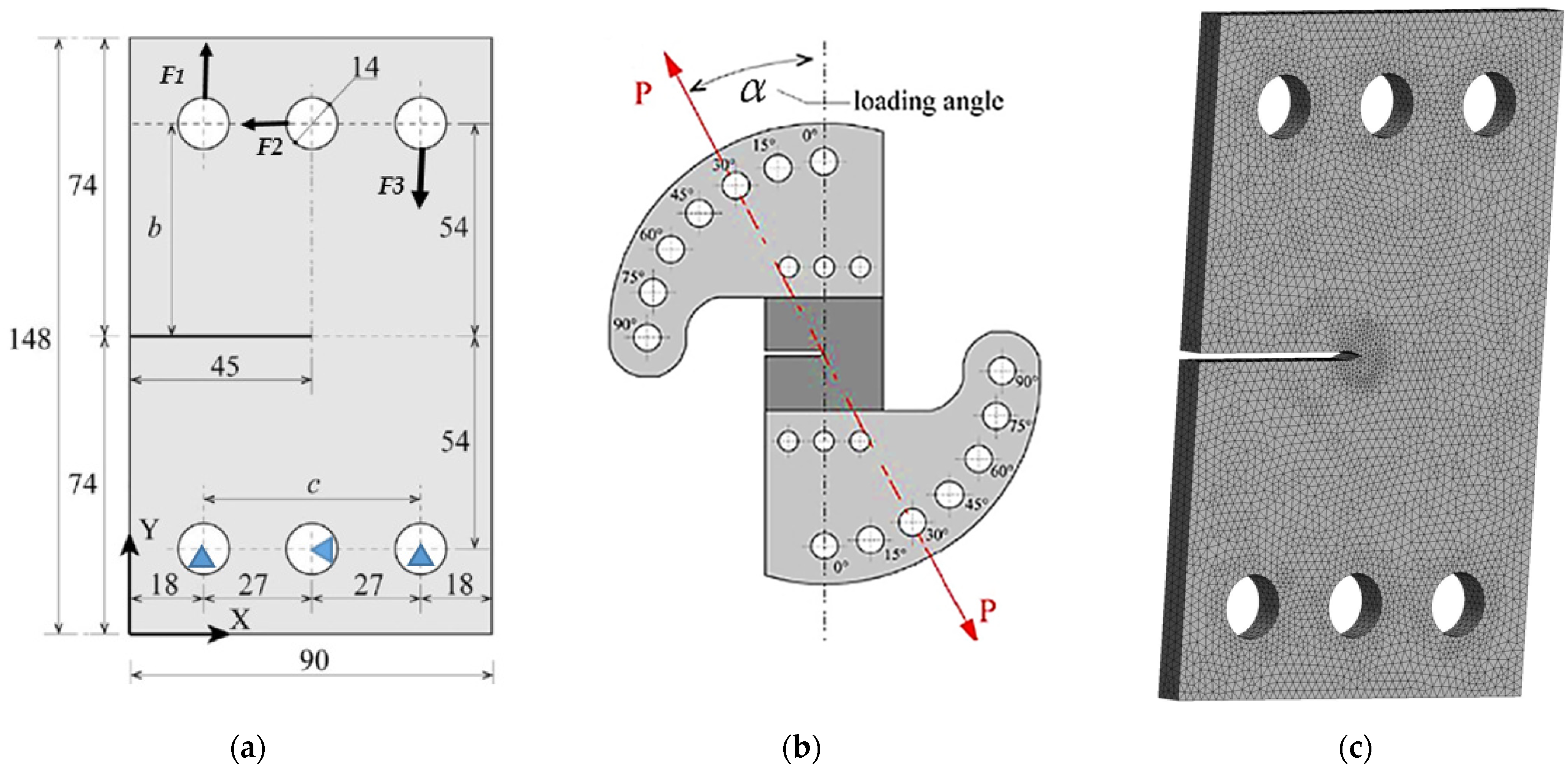

| α | F2 | F1 | F3 |
|---|---|---|---|
| 30 | 0.5 F | 0.933 F | −0.067 F |
| 45 | 0.707 F | 1.061 F | −0.354 F |
| 60 | 0.866 F | 1.116 F | −0.616 F |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fageehi, Y.A.; Alshoaibi, A.M. Mixed-Mode Crack Growth Behavior of Compact Tension Shear (CTS) Specimens: A Study on the Impact of the Fatigue Stress Ratio, Loading Angle, and Geometry Thickness. Materials 2025, 18, 1484. https://doi.org/10.3390/ma18071484
Fageehi YA, Alshoaibi AM. Mixed-Mode Crack Growth Behavior of Compact Tension Shear (CTS) Specimens: A Study on the Impact of the Fatigue Stress Ratio, Loading Angle, and Geometry Thickness. Materials. 2025; 18(7):1484. https://doi.org/10.3390/ma18071484
Chicago/Turabian StyleFageehi, Yahya Ali, and Abdulnaser M. Alshoaibi. 2025. "Mixed-Mode Crack Growth Behavior of Compact Tension Shear (CTS) Specimens: A Study on the Impact of the Fatigue Stress Ratio, Loading Angle, and Geometry Thickness" Materials 18, no. 7: 1484. https://doi.org/10.3390/ma18071484
APA StyleFageehi, Y. A., & Alshoaibi, A. M. (2025). Mixed-Mode Crack Growth Behavior of Compact Tension Shear (CTS) Specimens: A Study on the Impact of the Fatigue Stress Ratio, Loading Angle, and Geometry Thickness. Materials, 18(7), 1484. https://doi.org/10.3390/ma18071484








