Three-Dimensional Printing of Rigid–Flexible Ceramic–Epoxy Composites with Excellent Mechanical Properties
Highlights
- A bio-inspired gradient structure model with rigid–flexible coupling characteristics was developed.
- An accretive helicogradient architecture (AHA) was fabricated via direct ink writing (DIW) 3D printing technology using a programmable material deposition strategy.
- The inherent brittle fracture behavior of conventional ceramics was effectively ameliorated.
- The microscopic toughening mechanisms within the ceramic/epoxy composite were systematically elucidated, along with silica's reinforcing effects on the matrix ceramic
Abstract
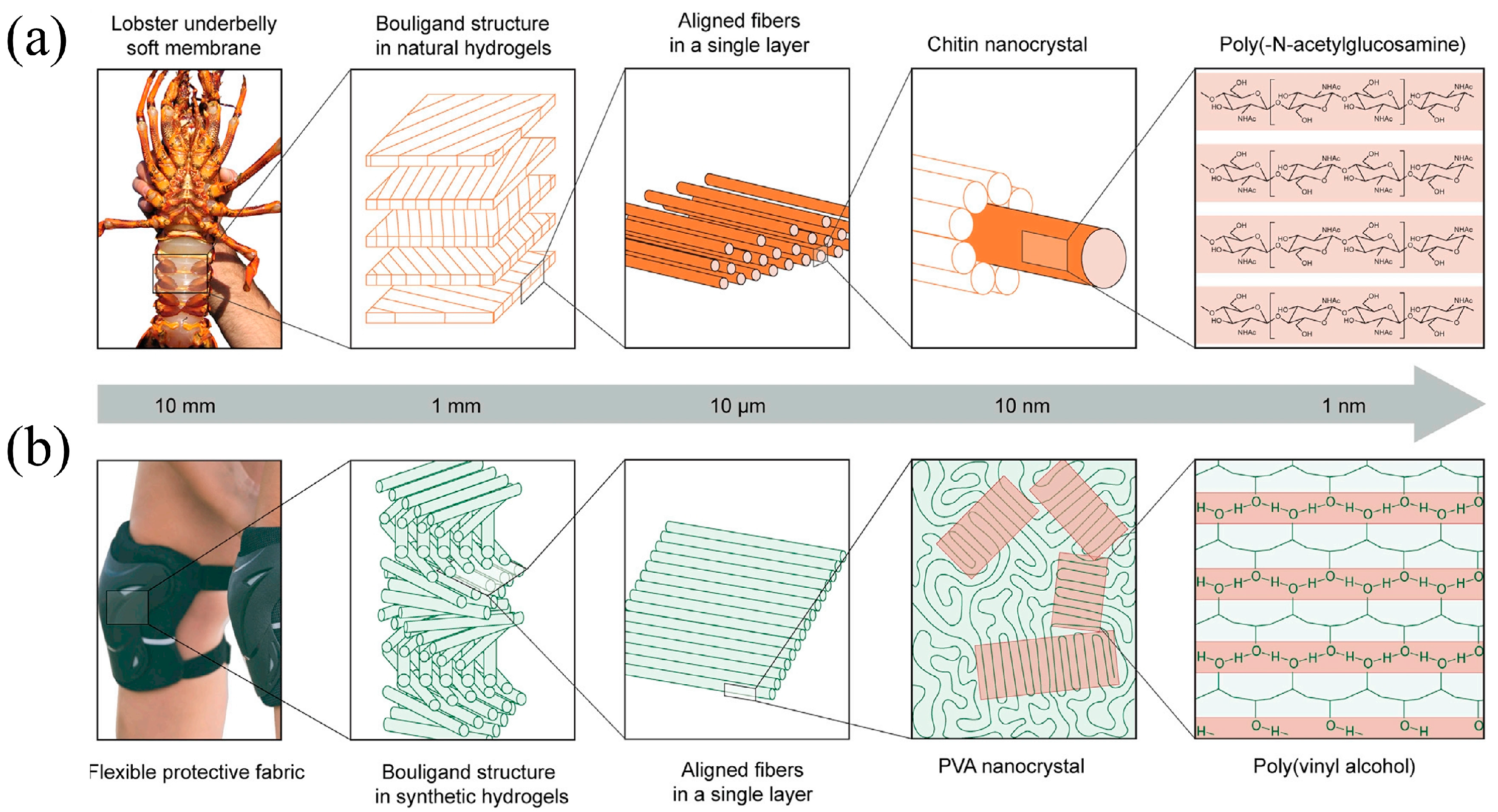
1. Introduction
2. Materials and Methods
2.1. Raw Materials
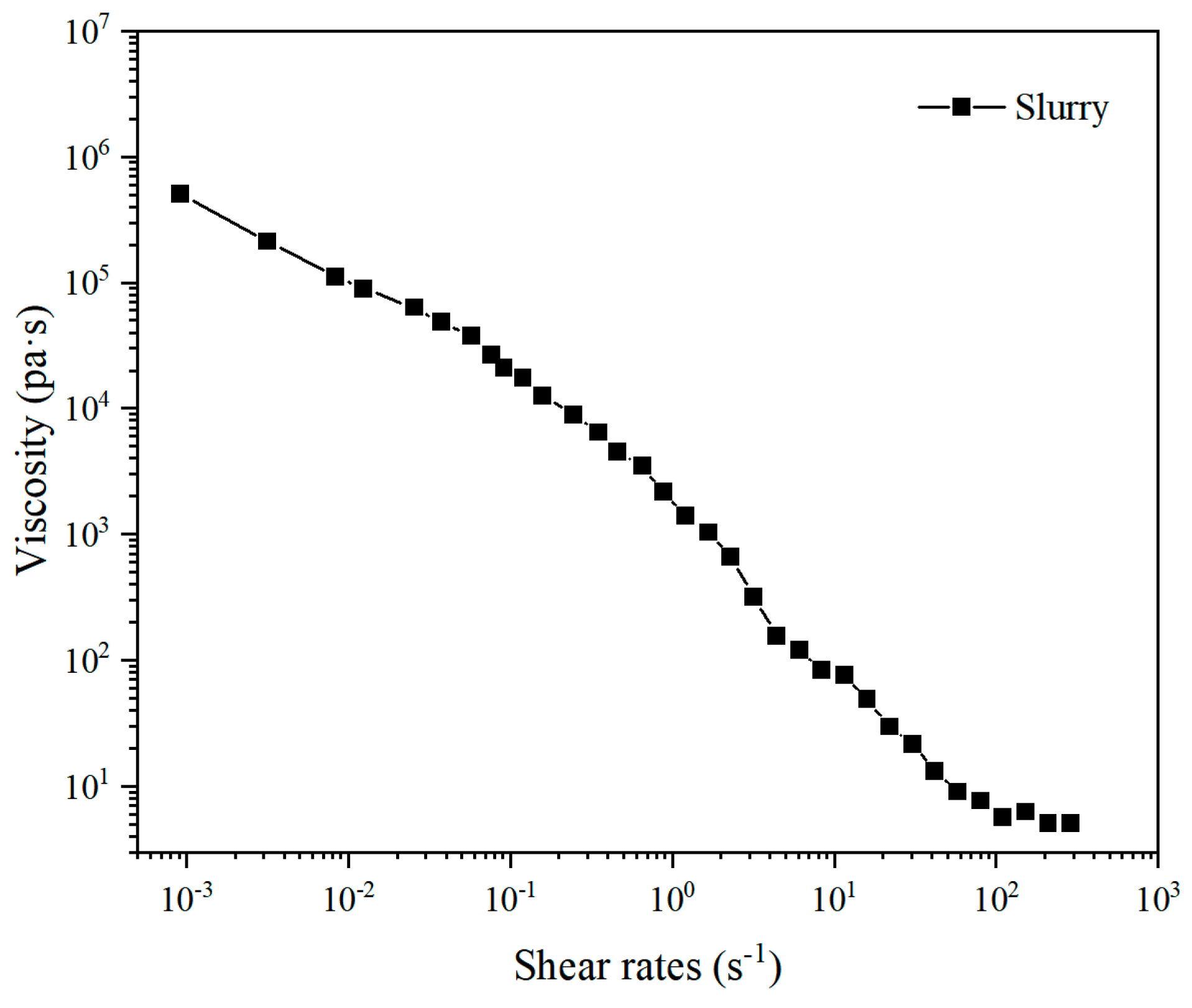
2.2. Slurry Preparation for 3D Printing
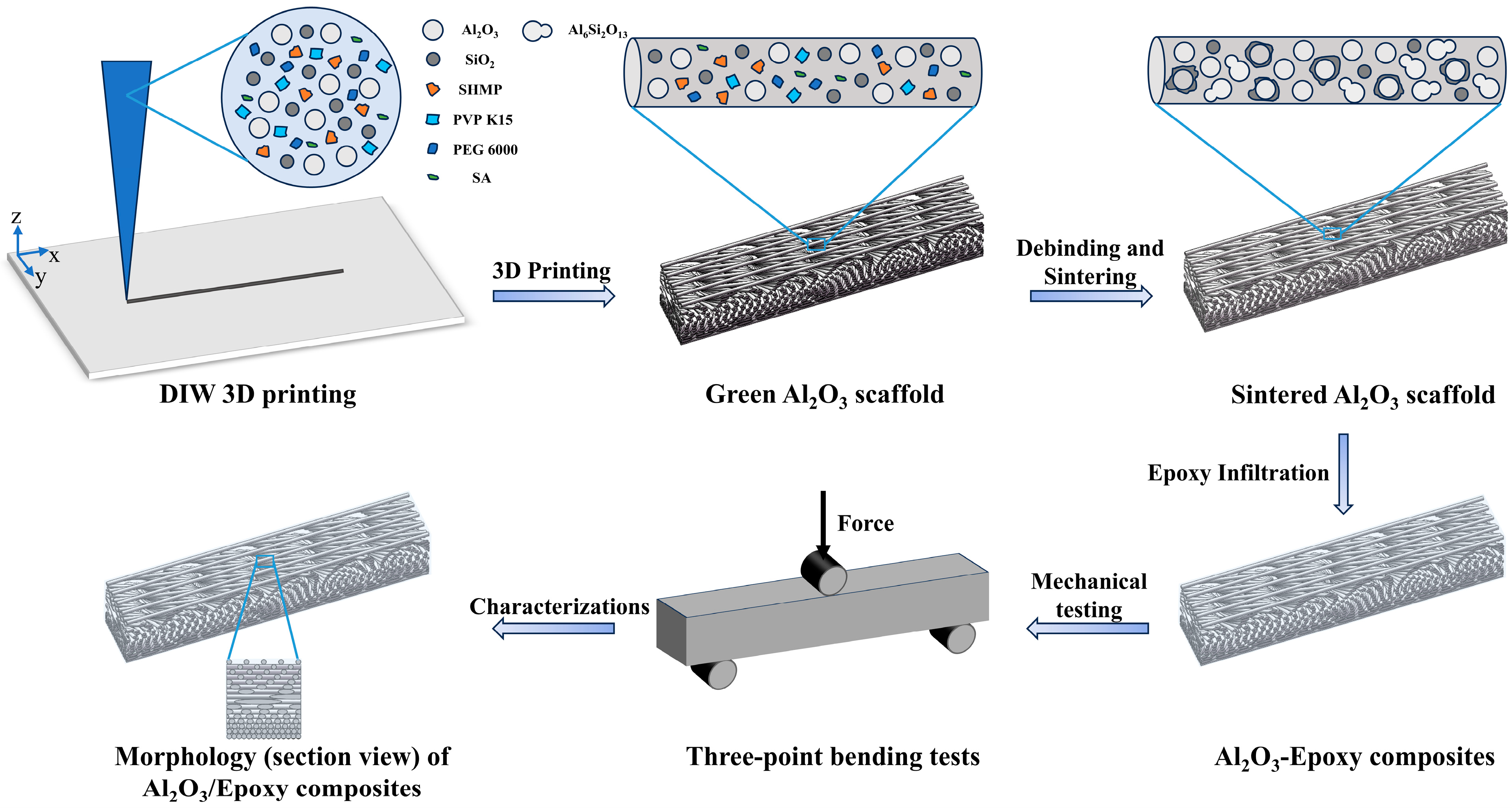
2.3. Direct Ink Writing 3D Printing of Gradient Bouligand Structure
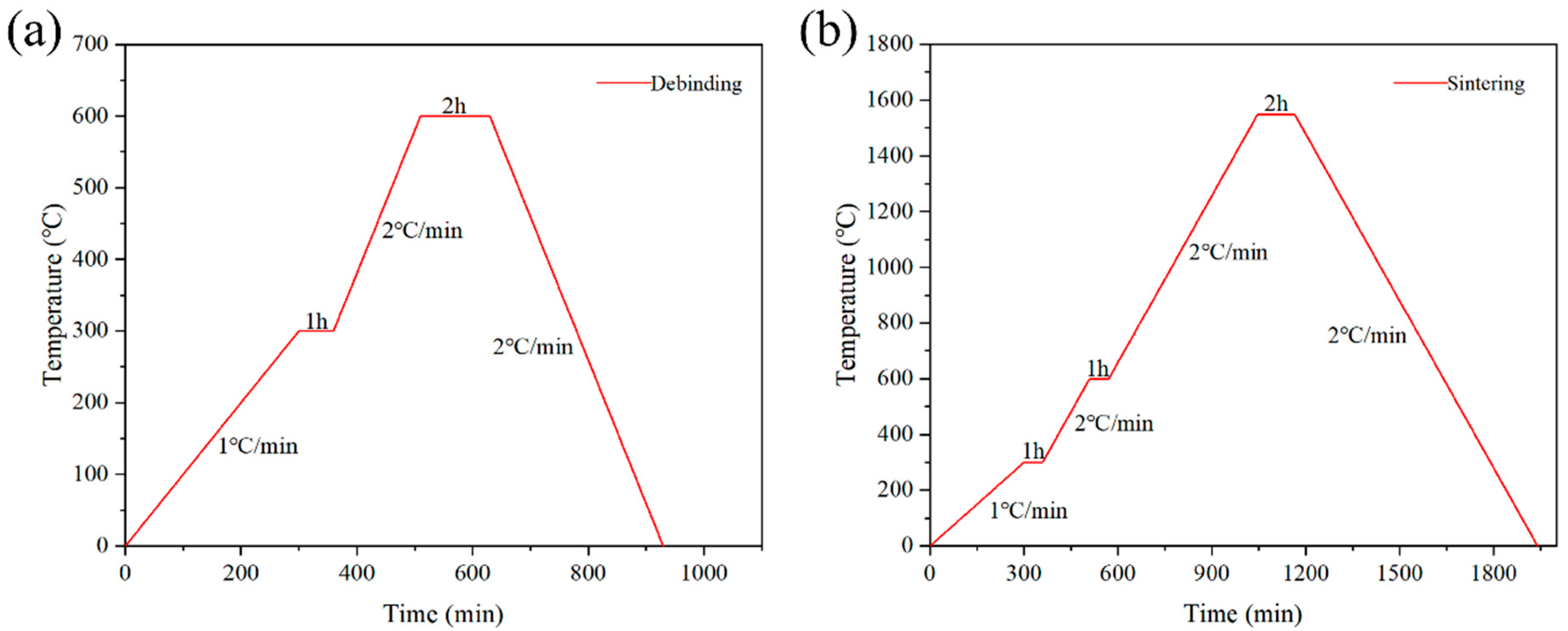
2.4. Debinding and Sintering
2.5. Fabrication of Bioinspired Composites
2.6. Structural Characterization
2.7. Mechanical Testing
3. Results and Discussion
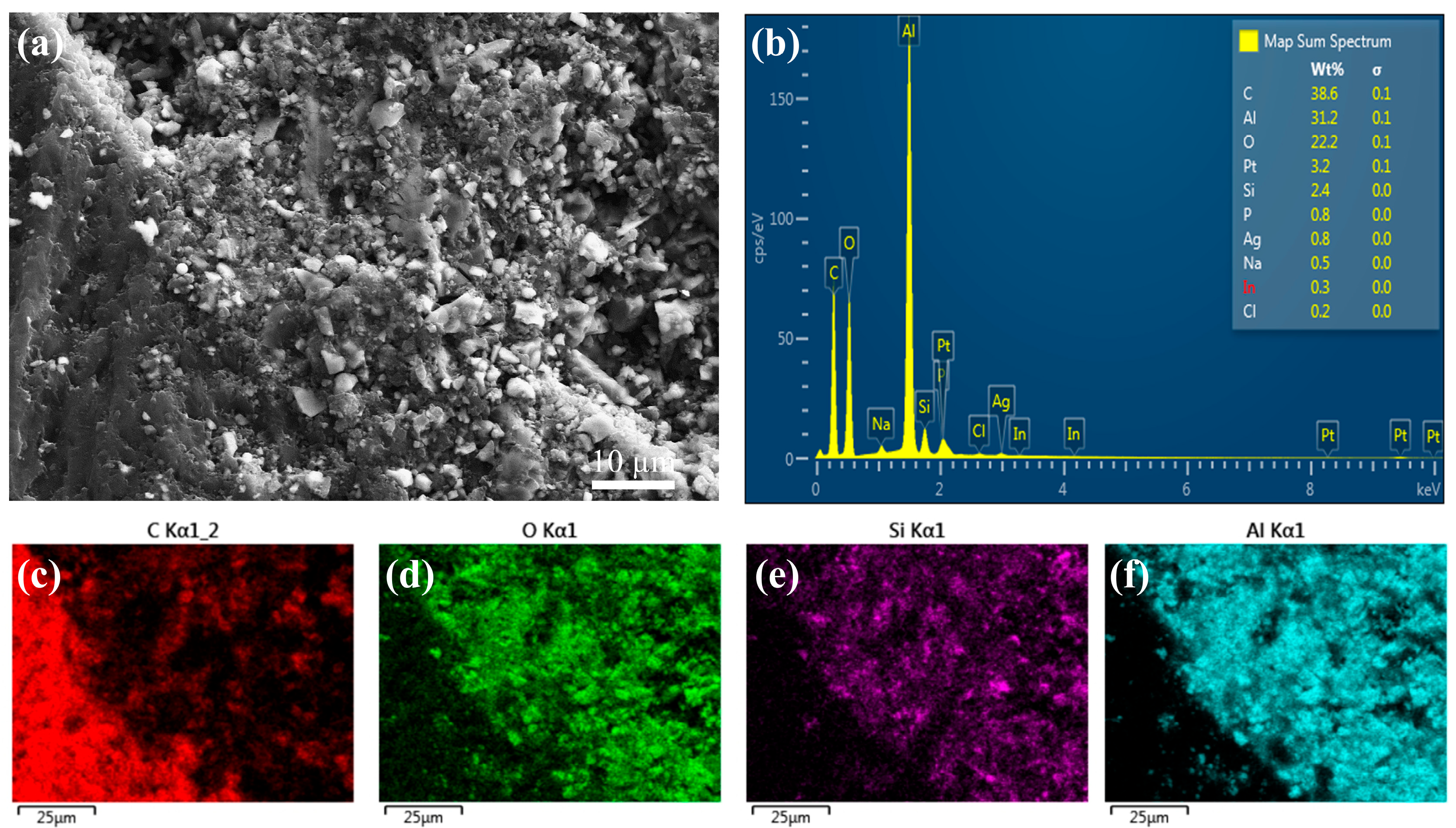
3.1. Morphologies of Al2O3 Scaffolds and Al2O3–Epoxy Composite Structures
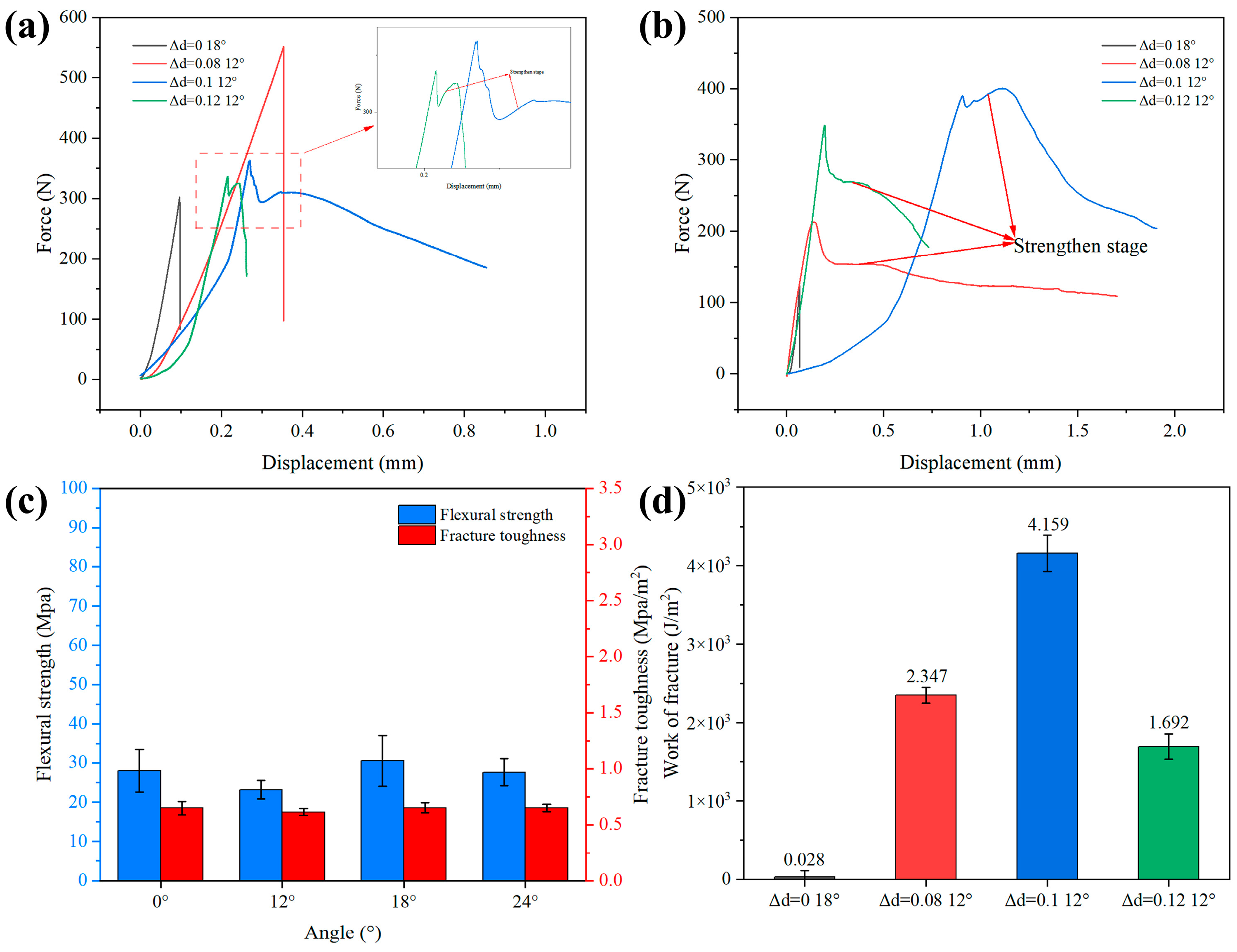
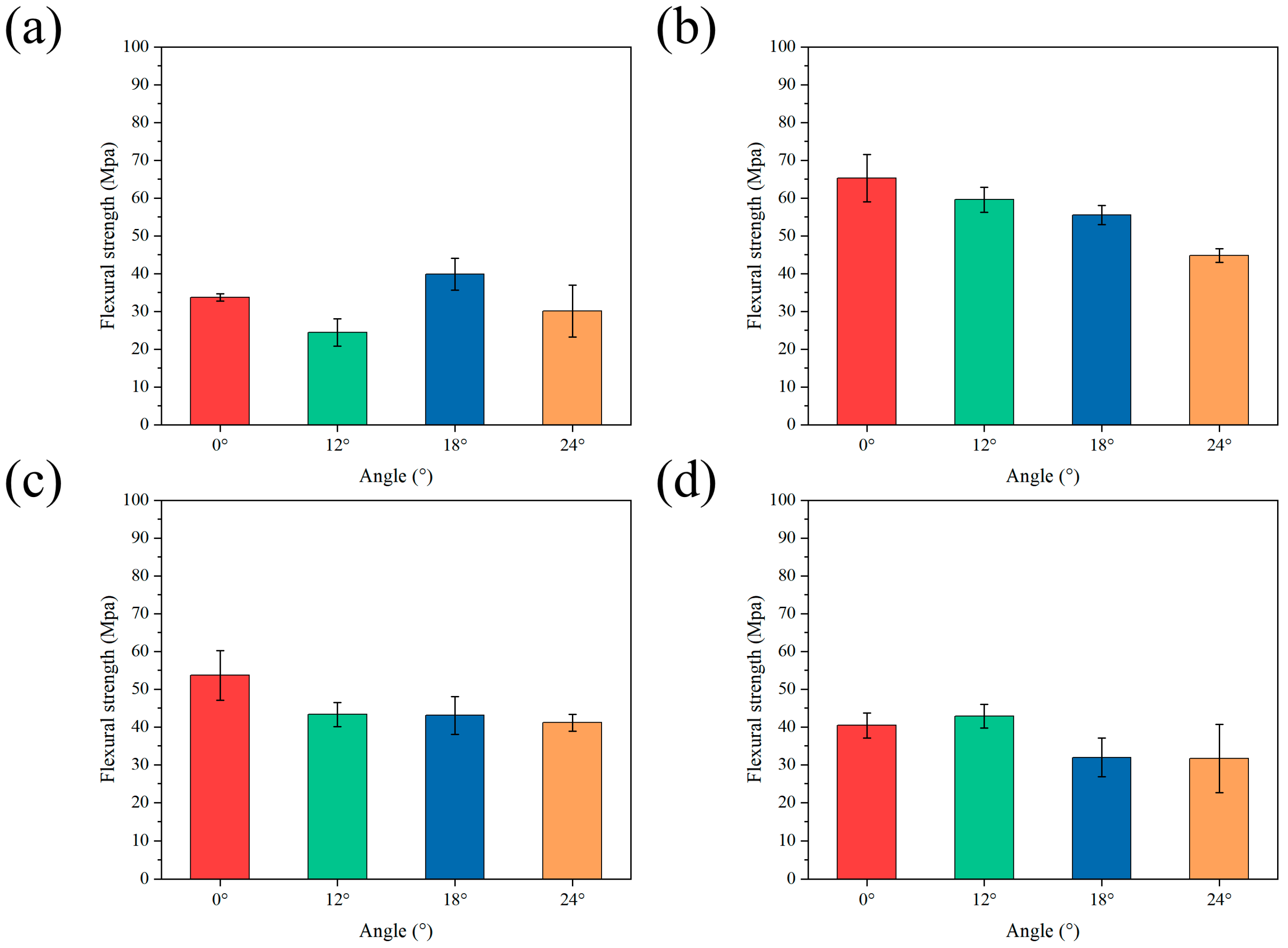
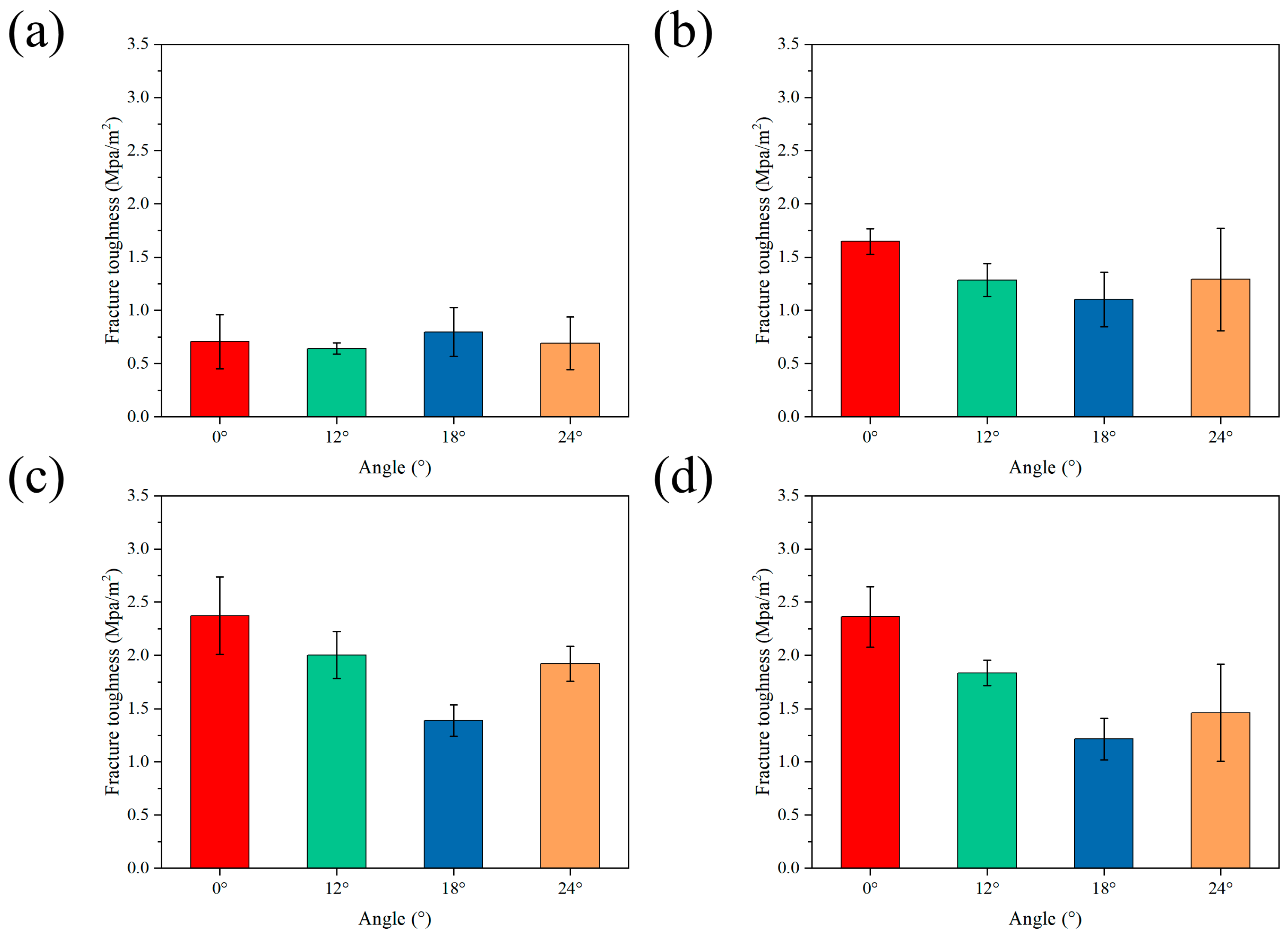
3.2. Mechanical Properties
3.3. Microstructure Analysis
3.4. Analysis of Toughening Mechanisms
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Shi, S.; Si, Y.; Han, Y.; Wu, T.; Iqbal, M.I.; Fei, B.; Li, R.K.Y.; Hu, J.; Qu, J. Recent Progress in Protective Membranes Fabricated via Electrospinning: Advanced Materials, Biomimetic Structures, and Functional Applications. Adv. Mater. 2022, 34, 2107938. [Google Scholar] [CrossRef]
- Zhang, C.; Li, X.; Jiang, L.; Tang, D.; Xu, H.; Zhao, P.; Fu, J.; Zhou, Q.; Chen, Y. 3D Printing of Functional Magnetic Materials: From Design to Applications. Adv. Funct. Mater. 2021, 31, 2102777. [Google Scholar] [CrossRef]
- Ni, D.; Cheng, Y.; Zhang, J.; Liu, J.-X.; Zou, J.; Chen, B.; Wu, H.; Li, H.; Dong, S.; Han, J.; et al. Advances in Ultra-High Temperature Ceramics, Composites, and Coatings. J. Adv. Ceram. 2022, 11, 1–56. [Google Scholar] [CrossRef]
- Eckel, Z.C.; Zhou, C.; Martin, J.H.; Jacobsen, A.J.; Carter, W.B.; Schaedler, T.A. Additive Manufacturing of Polymer-Derived Ceramics. Science 2016, 351, 58–62. [Google Scholar] [CrossRef]
- Wegst, U.G.K.; Bai, H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Bioinspired Structural Materials. Nat. Mater. 2015, 14, 23–36. [Google Scholar] [CrossRef]
- Saleem, I.A.; Ahmed, P.S.; Abed, M.S. Experimental and Numerical Investigation of Kevlar and UHMWPE Multi-Layered Armors against Ballistic Impact. Mater. Today Proc. 2022, 56, 2516–2524. [Google Scholar] [CrossRef]
- Benyamina, A.B.; Bouderba, B.; Saoula, A. Bending Response of Composite Material Plates with Specific Properties, Case of a Typical FGM “Ceramic/Metal” in Thermal Environments. Period. Polytech. Civ. Eng. 2018, 62, 930–938. [Google Scholar] [CrossRef]
- Ulianitsky, V.Y.; Shtertser, A.A.; Batraev, I.S.; Rybin, D.K. Fabrication of Layered Ceramic-Metal Composites by Detonation Spraying. Ceram. Int. 2020, 46, 27903–27908. [Google Scholar] [CrossRef]
- Kolli, M.; Aruri, D.; Gadakary, S.; Kosaraju, S. Electrical Discharge Machining of SiC Reinforced 6061-T6 Aluminum Alloy Surface Composite Fabricated by Friction Stir Processing. E3S Web Conf. 2021, 309, 1044. [Google Scholar] [CrossRef]
- Dilip Kumar, K.; Shantharaja, M.; Kumar, N.; Manjunatha, G. Morphological and Mechanical Properties of Short Fibres Reinforced Hybrid Composites for Automotive Applications. Mater. Today Proc. 2022, 52, 957–962. [Google Scholar] [CrossRef]
- Rogachev, A.S.; Vadchenko, S.G.; Kochetov, N.A.; Kovalev, D.Y.; Kovalev, I.D.; Shchukin, A.S.; Gryadunov, A.N.; Baras, F.; Politano, O. Combustion Synthesis of TiC-Based Ceramic-Metal Composites with High Entropy Alloy Binder. J. Eur. Ceram. Soc. 2020, 40, 2527–2532. [Google Scholar] [CrossRef]
- Chen, Q.; Pugno, N.M. Bio-Mimetic Mechanisms of Natural Hierarchical Materials: A Review. J. Mech. Behav. Biomed. Mater. 2013, 19, 3–33. [Google Scholar] [CrossRef]
- Liu, Z.; Meyers, M.A.; Zhang, Z.; Ritchie, R.O. Functional Gradients and Heterogeneities in Biological Materials: Design Principles, Functions, and Bioinspired Applications. Prog. Mater. Sci. 2017, 88, 467–498. [Google Scholar] [CrossRef]
- Meyers, M.A.; Chen, P.-Y.; Lin, A.Y.-M.; Seki, Y. Biological Materials: Structure and Mechanical Properties. Prog. Mater. Sci. 2008, 53, 1–206. [Google Scholar] [CrossRef]
- Chen, P.-Y.; Stokes, A.G.; McKittrick, J. Comparison of the Structure and Mechanical Properties of Bovine Femur Bone and Antler of the North American Elk (Cervus Elaphus Canadensis). Acta Biomater. 2009, 5, 693–706. [Google Scholar] [CrossRef]
- Fratzl, P.; Weinkamer, R. Nature’s Hierarchical Materials. Prog. Mater. Sci. 2007, 52, 1263–1334. [Google Scholar] [CrossRef]
- Wen, S.; Chen, S.; Gao, W.; Zheng, Z.; Bao, J.; Cui, C.; Liu, S.; Gao, H.; Yu, S. Biomimetic Gradient Bouligand Structure Enhances Impact Resistance of Ceramic-polymer Composites. Adv. Mater. 2023, 35, 2211175. [Google Scholar] [CrossRef]
- Yang, F.; Xie, W.; Meng, S. Analysis and Simulation of Fracture Behavior in Naturally Occurring Bouligand Structures. Acta Biomater. 2021, 135, 473–482. [Google Scholar] [CrossRef]
- Sun, J.; Yu, S.; Wade-Zhu, J.; Wang, Y.; Qu, H.; Zhao, S.; Zhang, R.; Yang, J.; Binner, J.; Bai, J. 3D Printing of Ceramic Composite with Biomimetic Toughening Design. Addit. Manuf. 2022, 58, 103027. [Google Scholar] [CrossRef]
- Yang, W.; Sherman, V.R.; Gludovatz, B.; Mackey, M.; Zimmermann, E.A.; Chang, E.H.; Schaible, E.; Qin, Z.; Buehler, M.J.; Ritchie, R.O.; et al. Protective Role of Arapaima Gigas Fish Scales: Structure and Mechanical Behavior. Acta Biomater. 2014, 10, 3599–3614. [Google Scholar] [CrossRef]
- Chen, P.-Y.; Lin, A.Y.-M.; McKittrick, J.; Meyers, M.A. Structure and Mechanical Properties of Crab Exoskeletons. Acta Biomater. 2008, 4, 587–596. [Google Scholar] [CrossRef] [PubMed]
- Greenfeld, I.; Kellersztein, I.; Wagner, H.D. Nested Helicoids in Biological Microstructures. Nat. Commun. 2020, 11, 224. [Google Scholar] [CrossRef] [PubMed]
- Ni, J.; Lin, S.; Qin, Z.; Veysset, D.; Liu, X.; Sun, Y.; Hsieh, A.J.; Radovitzky, R.; Nelson, K.A.; Zhao, X. Strong Fatigue-Resistant Nanofibrous Hydrogels Inspired by Lobster Underbelly. Matter 2021, 4, 1919–1934. [Google Scholar] [CrossRef]
- Mencattelli, L.; Pinho, S.T. Ultra-Thin-Ply CFRP Bouligand Bio-Inspired Structures with Enhanced Load-Bearing Capacity, Delayed Catastrophic Failure and High Energy Dissipation Capability. Compos. Part A 2020, 129, 105655. [Google Scholar] [CrossRef]
- Jiao, D.; Zhang, J.; Liu, Y.Y.; Liu, X.G.; Zhang, Q.; Tang, S.F.; Liu, Z.Q.; Zhang, Z.F. Hierarchical Toughening of Bioinspired Nacre-like Hybrid Carbon Composite. Carbon 2021, 171, 409–416. [Google Scholar] [CrossRef]
- Li, D.; Peng, E.; Shen, Y.; Li, Y.; Liu, L.; Huang, Y.; Hu, Z. Nacre-Inspired Hierarchical Framework Enables Tough and Impact-Monitoring Epoxy Nanocomposites. Compos. Part B 2024, 111246. [Google Scholar] [CrossRef]
- Su, R.; Chen, J.; Zhang, X.; Wang, W.; Li, Y.; He, R.; Fang, D. 3D-printed Micro/Nano-scaled Mechanical Metamaterials: Fundamentals, Technologies, Progress, Applications, and Challenges. Small 2023, 19, 2206391. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, K.; Zhang, B.; Li, Y.; He, R. Mechanical Properties of Additively-Manufactured Cellular Ceramic Structures: A Comprehensive Study. J. Adv. Ceram. 2022, 11, 1918–1931. [Google Scholar] [CrossRef]
- Chen, Y.; Ma, Y.; Yin, Q.; Pan, F.; Cui, C.; Zhang, Z.; Liu, B. Advances in Mechanics of Hierarchical Composite Materials. Compos. Sci. Technol. 2021, 214, 108970. [Google Scholar] [CrossRef]
- Li, X.; Kim, M.; Zhai, W. Ceramic Microlattice and Epoxy Interpenetrating Phase Composites with Simultaneous High Specific Strength and Specific Energy Absorption. Mater. Des. 2022, 223, 111206. [Google Scholar] [CrossRef]
- Sun, L.; Gibson, R.F.; Gordaninejad, F.; Suhr, J. Energy Absorption Capability of Nanocomposites: A Review. Compos. Sci. Technol. 2009, 69, 2392–2409. [Google Scholar] [CrossRef]
- Manh, N.T.; Triet, L.N.D.; Choi, Y.; Cho, Y.; Ahn, W.; Lee, K.J.; Cho, N. Fabrication of Polymer Infiltrated Zirconia Ceramic Composite Materials. Mol. Cryst. Liq. Cryst. 2020, 707, 118–125. [Google Scholar] [CrossRef]
- Launey, M.E.; Ritchie, R.O. On the Fracture Toughness of Advanced Materials. Adv. Mater. 2009, 21, 2103–2110. [Google Scholar] [CrossRef]
- Hyde, A.R. Ceramic Matrix Composites. Mater. Des. 1990, 11, 30–36. [Google Scholar] [CrossRef]
- Zhao, Y.; Yap, X.Y.; Ye, P.; Seetoh, I.; Guo, H.; Lai, C.; Du, Z.; Gan, C.L. Enhanced Mechanical and Thermal Properties in 3D Printed Al2O3 Lattice/Epoxy Interpenetrating Phase Composites. Mech. Mater. 2024, 190, 104930. [Google Scholar] [CrossRef]
- Liu, Q.; Hong, L.; Dong, X.; Zhai, W. 3D Printed Hierarchical Interpenetrating Phase Composites with Multi-Scale Mechanical Energy Absorption Mechanisms. Compos. Part B 2023, 264, 110911. [Google Scholar] [CrossRef]
- Wu, K.; Song, Z.; Zhang, S.; Ni, Y.; Cai, S.; Gong, X.; He, L.; Yu, S.-H. Discontinuous Fibrous Bouligand Architecture Enabling Formidable Fracture Resistance with Crack Orientation Insensitivity. Proc. Natl. Acad. Sci. USA 2020, 117, 15465–15472. [Google Scholar] [CrossRef]
- Behera, R.P.; Le Ferrand, H. Impact-Resistant Materials Inspired by the Mantis Shrimp’s Dactyl Club. Matter 2021, 4, 2831–2849. [Google Scholar] [CrossRef]
- Tang, S.; Fan, Z.; Zhao, H.; Yang, L.; Liu, F.; Liu, X. Layered Extrusion Forming—A Simple and Green Method for Additive Manufacturing Ceramic Core. Int. J. Adv. Manuf. Technol. 2018, 96, 3809–3819. [Google Scholar] [CrossRef]
- Wei, C.; Liu, Z.; Zhang, Z.; Ma, X.; Wang, P.; Li, S.; Liu, L. High Toughness and R-Curve Behaviour of Laminated SiC/Graphite Ceramics. Ceram. Int. 2020, 46, 22973–22979. [Google Scholar] [CrossRef]
- Craig, B.D.; Francis, L.F. Alumina/Epoxy Interpenetrating Phase Composite Coatings: I, Processing and Microstructural Development. J. Am. Ceram. Soc. 1998, 81, 3109–3116. [Google Scholar] [CrossRef]
- Kim, E.-H.; Jung, Y.-G.; Jo, C.-Y. Microstructure and Mechanical Properties of Heterogeneous Ceramic-Polymer Composite Using Interpenetrating Network. J. Nanomater. 2012, 2012, 932059. [Google Scholar] [CrossRef]
- Sperling, L.H.; Mishra, V. The Current Status of Interpenetrating Polymer Networks. Polym. Adv. Technol. 1996, 7, 197–208. [Google Scholar] [CrossRef]
- Li, H.; Liu, Y.; Liu, Y.; Zeng, Q.; Liang, J. Silica Strengthened Alumina Ceramic Cores Prepared by 3D Printing. J. Eur. Ceram. Soc. 2021, 41, 2938–2947. [Google Scholar] [CrossRef]
- Sajadi, S.M.; Vásárhelyi, L.; Mousavi, R.; Rahmati, A.H.; Kónya, Z.; Kukovecz, Á.; Arif, T.; Filleter, T.; Vajtai, R.; Boul, P.; et al. Damage-Tolerant 3D-Printed Ceramics via Conformal Coating. Sci. Adv. 2021, 7, eabc5028. [Google Scholar] [CrossRef]
- Zhang, X.; Luan, Y.; Li, Y.; Wang, Z.; Li, Z.; Xu, F.; Guo, Z. Bioinspired Design of Lightweight Laminated Structural Materials and the Intralayer/Interlayer Strengthening and Toughening Mechanisms Induced by the Helical Structure. Compos. Struct. 2021, 276, 114575. [Google Scholar] [CrossRef]
- Zhang, X.; Wen, Z.; Li, Y.; Luan, Y.; Zhang, Q. Improved Strength and Toughness of Bioinspired Bouligand Architecture Composite by Discontinuous Carbon Fiber. J. Phys. Conf. Ser. 2021, 1906, 12030. [Google Scholar] [CrossRef]






| Ceramic Powder | Sintering Aid | Dispersant | Stabilizer | Lubricant | Thickener | Solvent |
| α-Al2O3 (g) | SiO2 (g) | (NaPO3)6 (wt%) | K15 (wt%) | PEG 6000 (wt%) | SA (wt%) | Deionized water (g) |
| 13 | 1 | 3 | 3 | 1 | 0.36 | 9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Jiang, B.; Liu, Y.; Xin, Z.; Jiao, Z. Three-Dimensional Printing of Rigid–Flexible Ceramic–Epoxy Composites with Excellent Mechanical Properties. Materials 2025, 18, 1479. https://doi.org/10.3390/ma18071479
Wang Z, Jiang B, Liu Y, Xin Z, Jiao Z. Three-Dimensional Printing of Rigid–Flexible Ceramic–Epoxy Composites with Excellent Mechanical Properties. Materials. 2025; 18(7):1479. https://doi.org/10.3390/ma18071479
Chicago/Turabian StyleWang, Zhaozhi, Biao Jiang, Yajie Liu, Zhiheng Xin, and Zhibin Jiao. 2025. "Three-Dimensional Printing of Rigid–Flexible Ceramic–Epoxy Composites with Excellent Mechanical Properties" Materials 18, no. 7: 1479. https://doi.org/10.3390/ma18071479
APA StyleWang, Z., Jiang, B., Liu, Y., Xin, Z., & Jiao, Z. (2025). Three-Dimensional Printing of Rigid–Flexible Ceramic–Epoxy Composites with Excellent Mechanical Properties. Materials, 18(7), 1479. https://doi.org/10.3390/ma18071479






