Strategy to Enhance the Collapse Capacity of Composite Cylindrical Tubes: Experiments and Simulations
Abstract
1. Introduction
2. Materials, Experimental Procedures, and Modeling
2.1. Specimen Manufacturing and Material Properties
2.2. Experimental Setup
2.3. Numerical Modeling
3. Results and Discussion
3.1. Experimental Results
3.1.1. Deformation Behavior
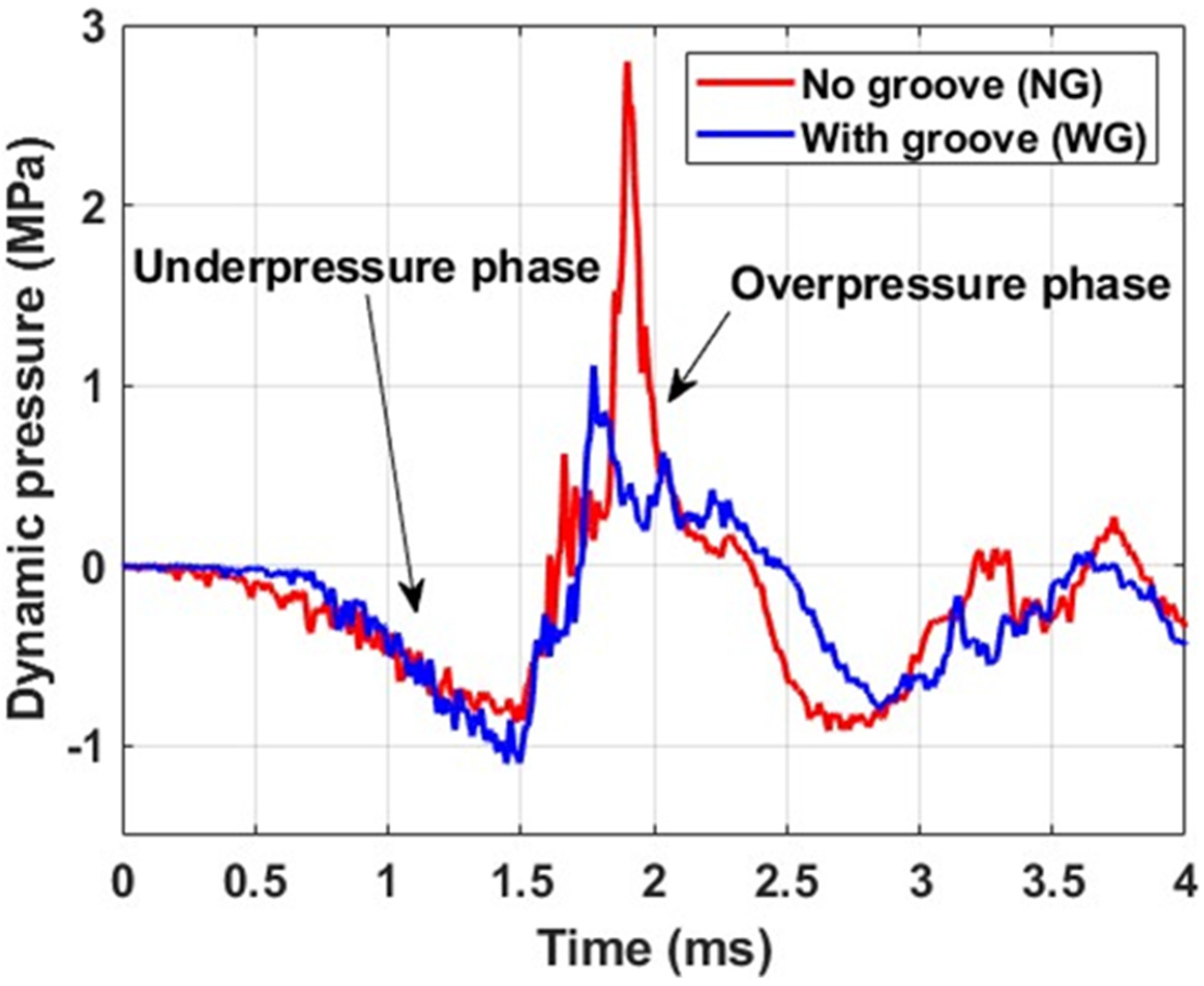
3.1.2. Dynamic Pressure History
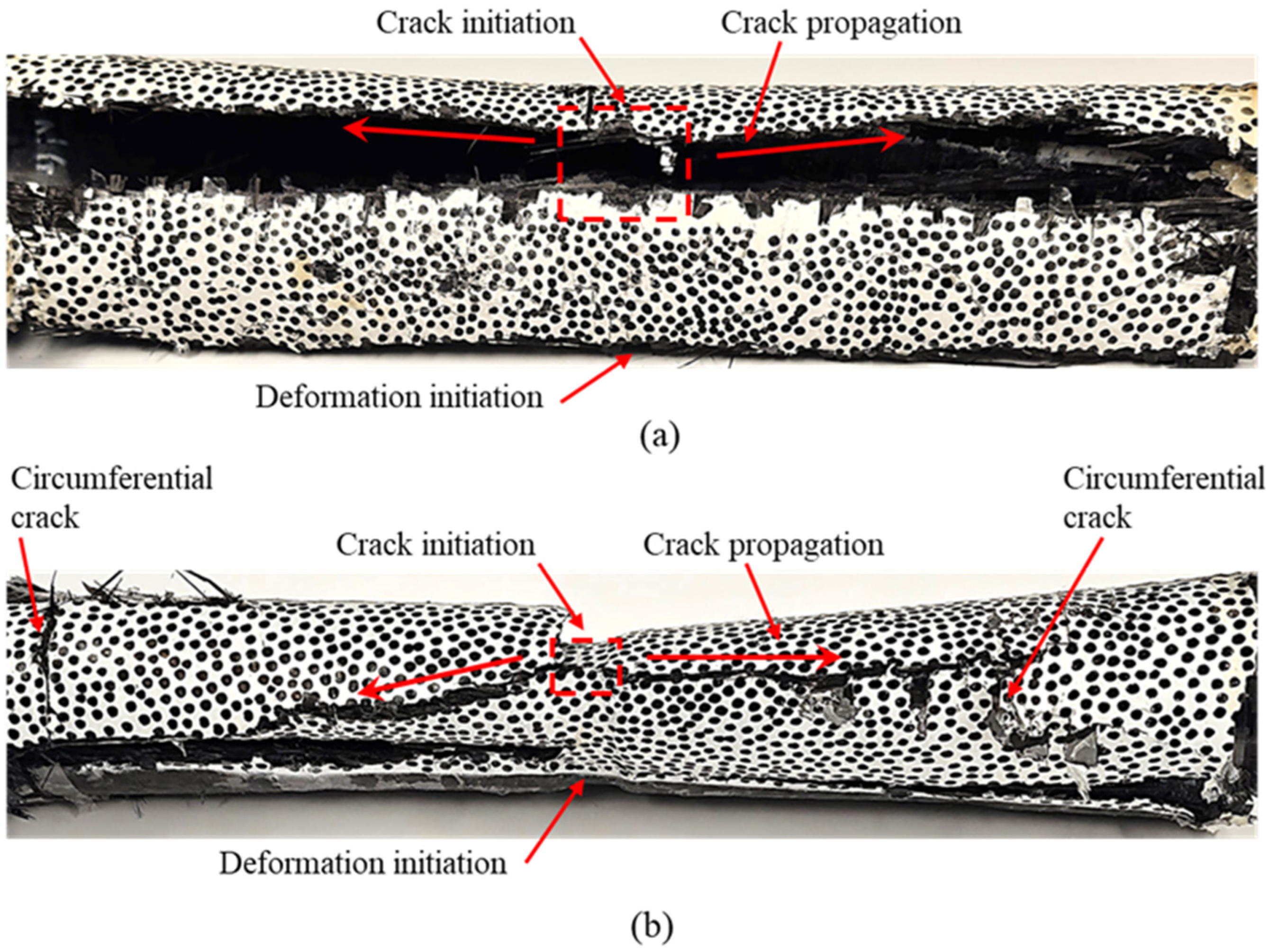
3.1.3. Postmortem Inspection
3.2. Numerical Study Results
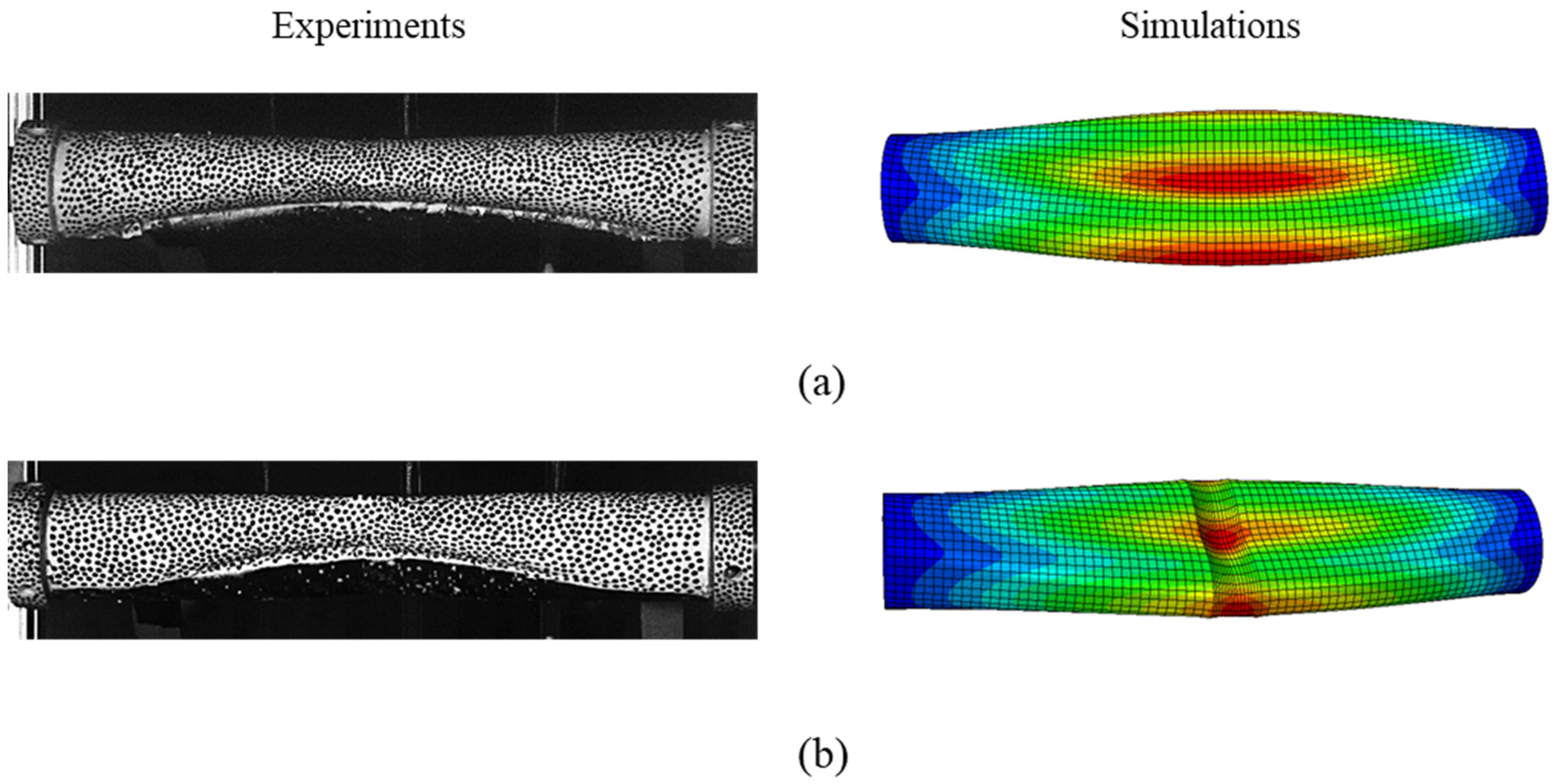
3.2.1. Validation of Numerical Model
3.2.2. Parametric Study
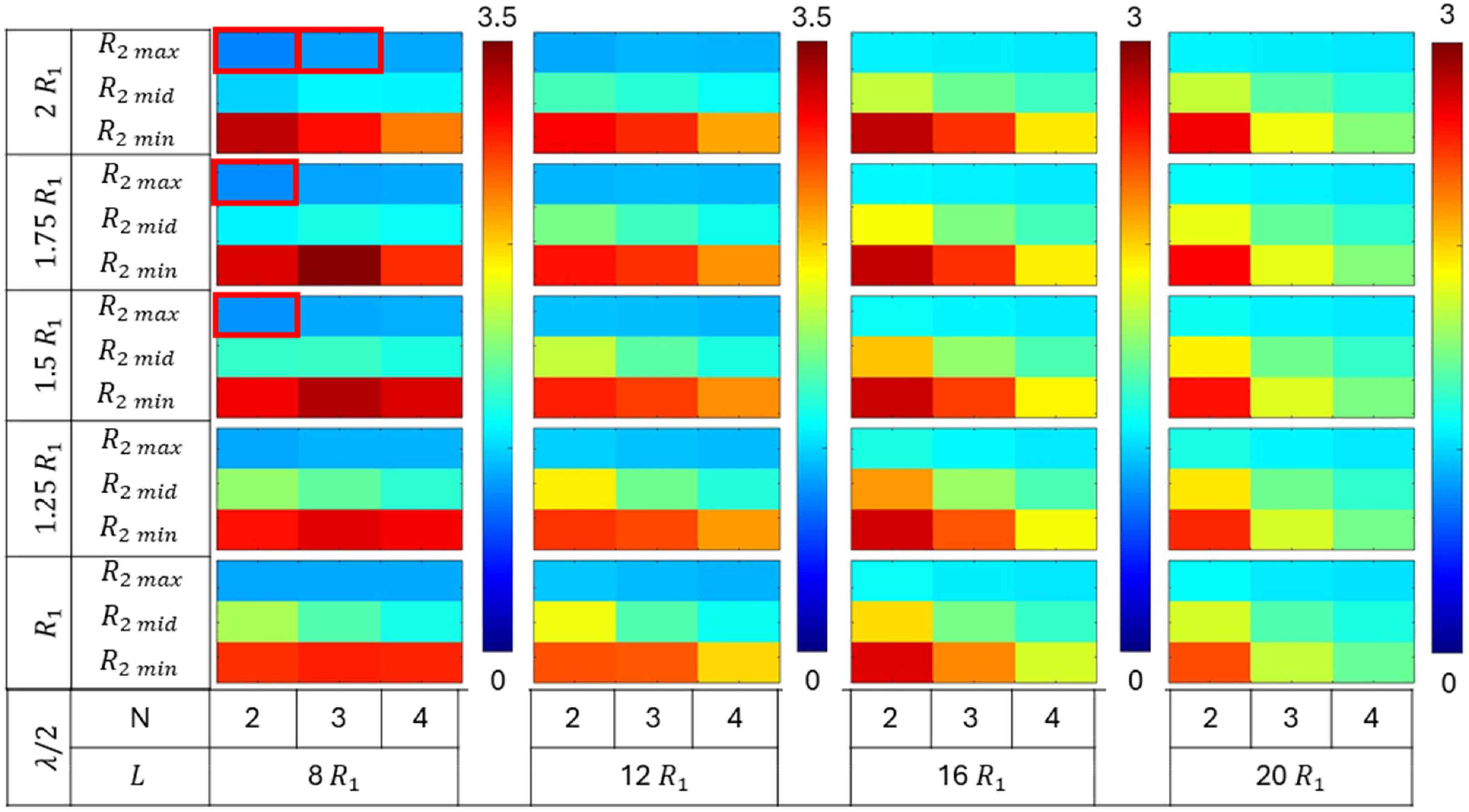
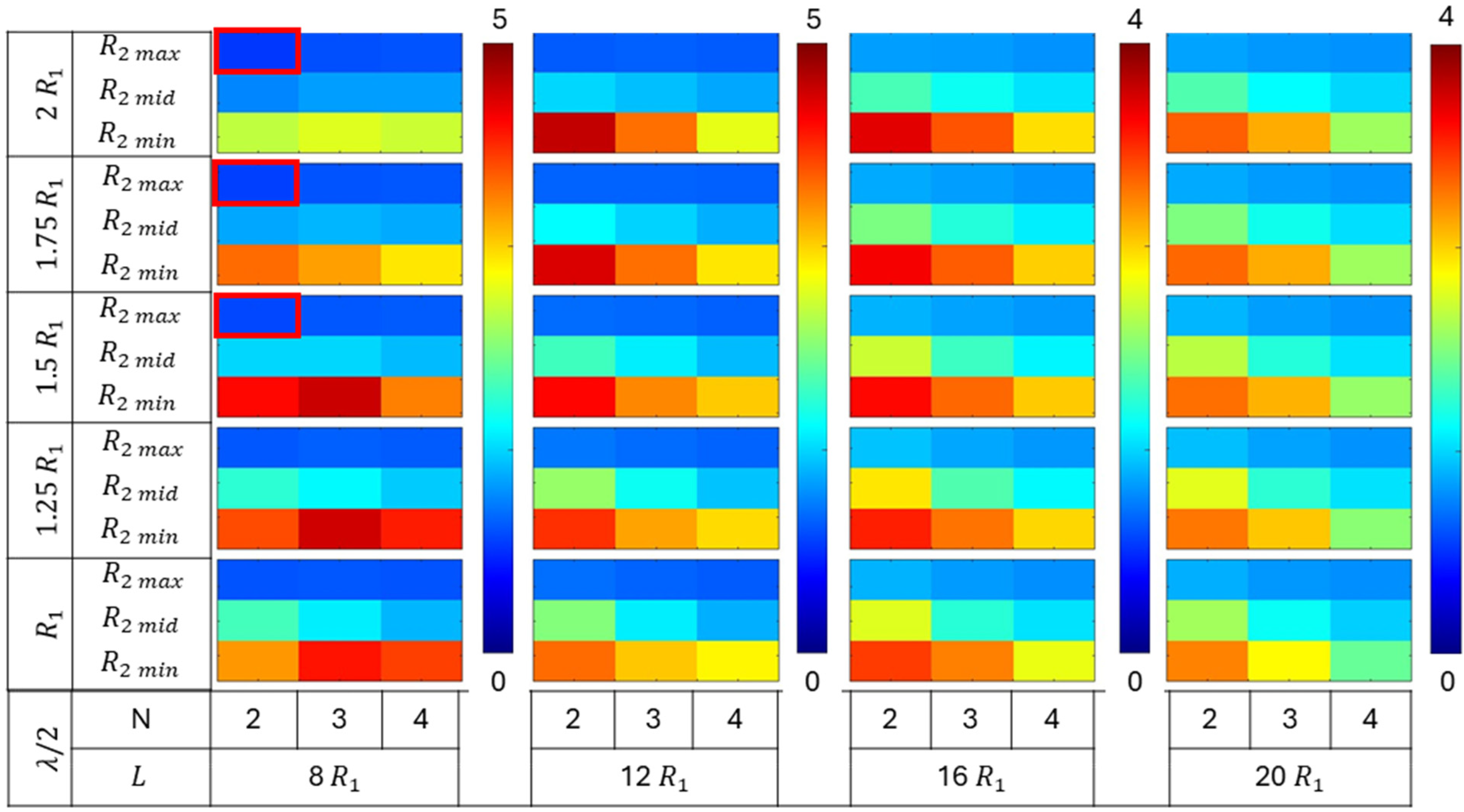
Results from Parametric Study
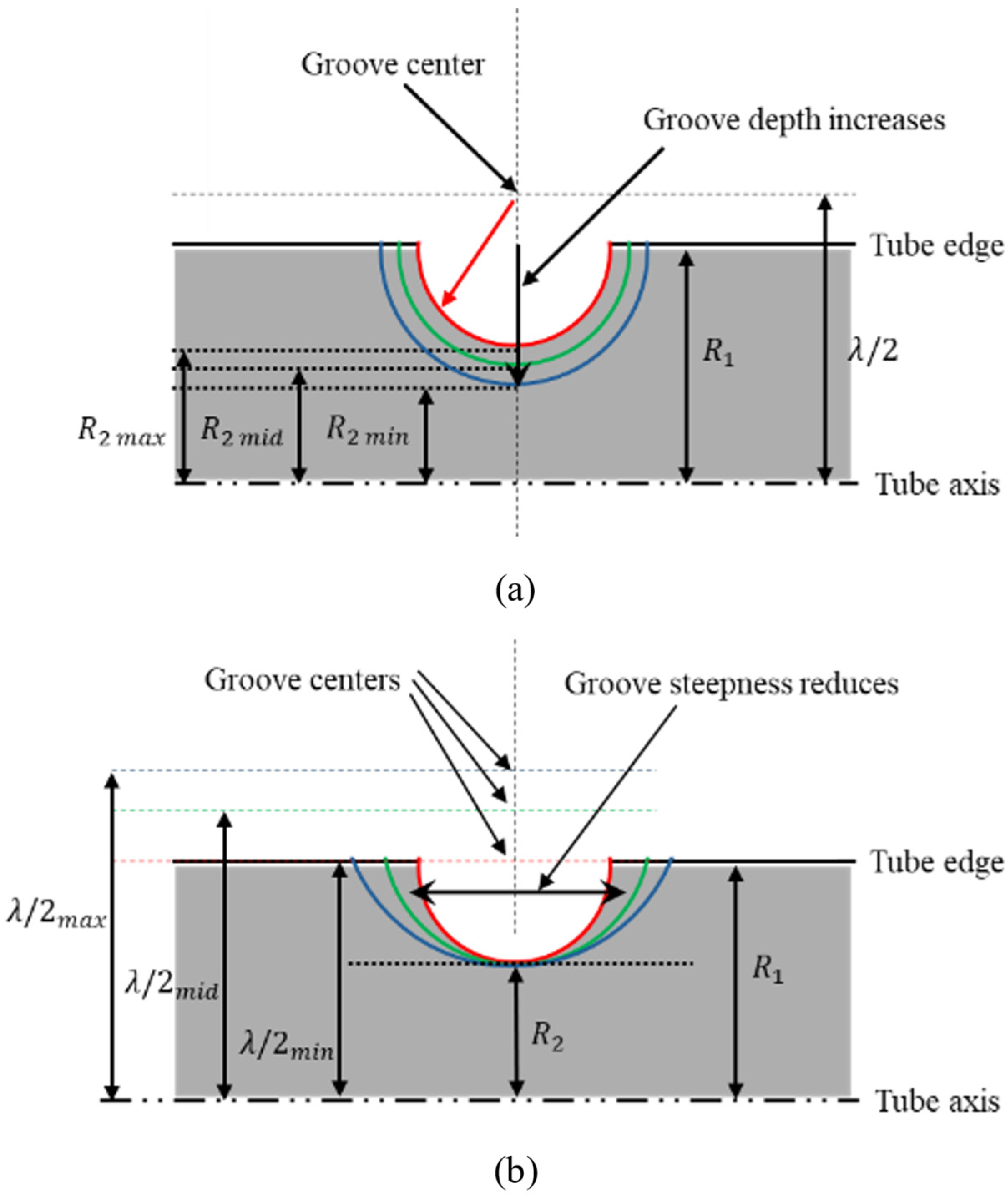
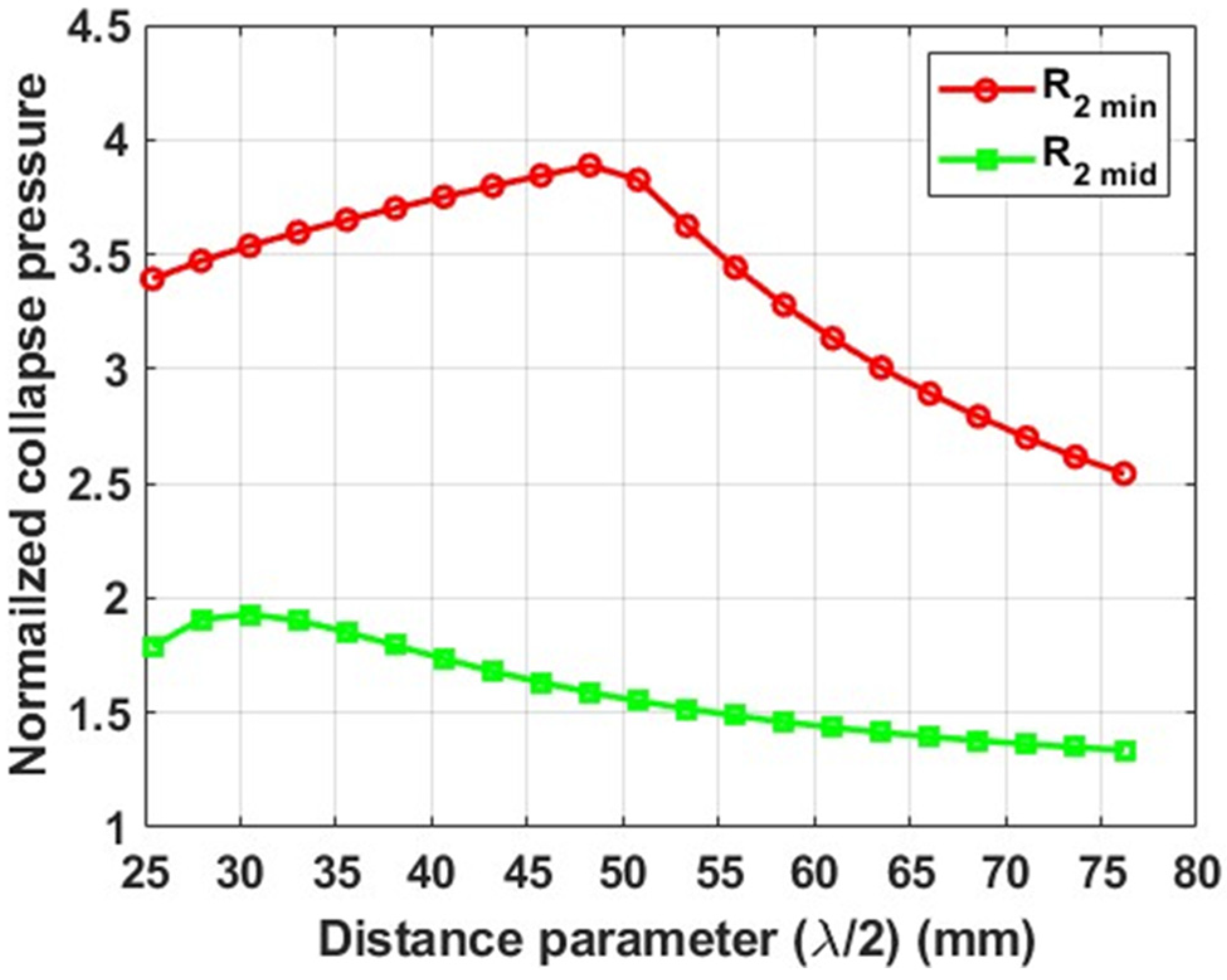
Effect of Root Radius
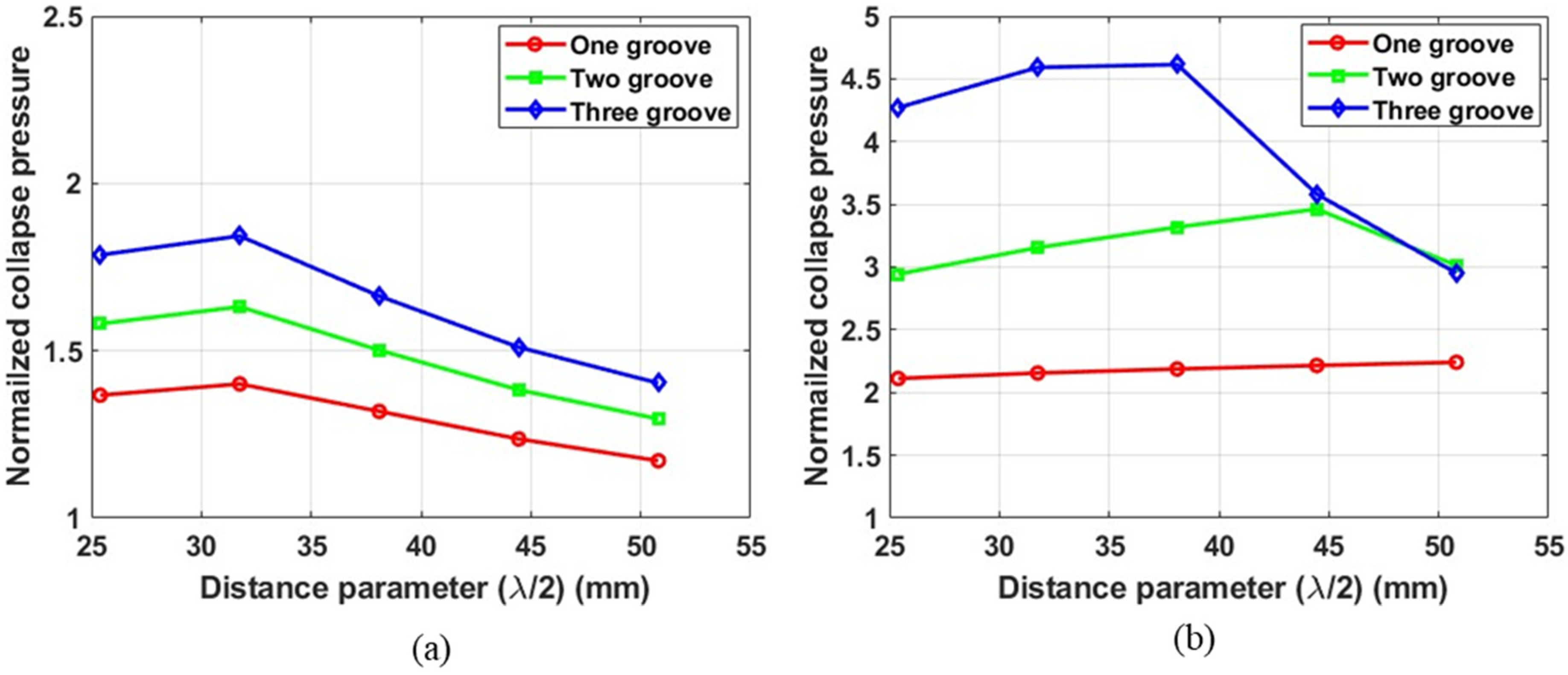
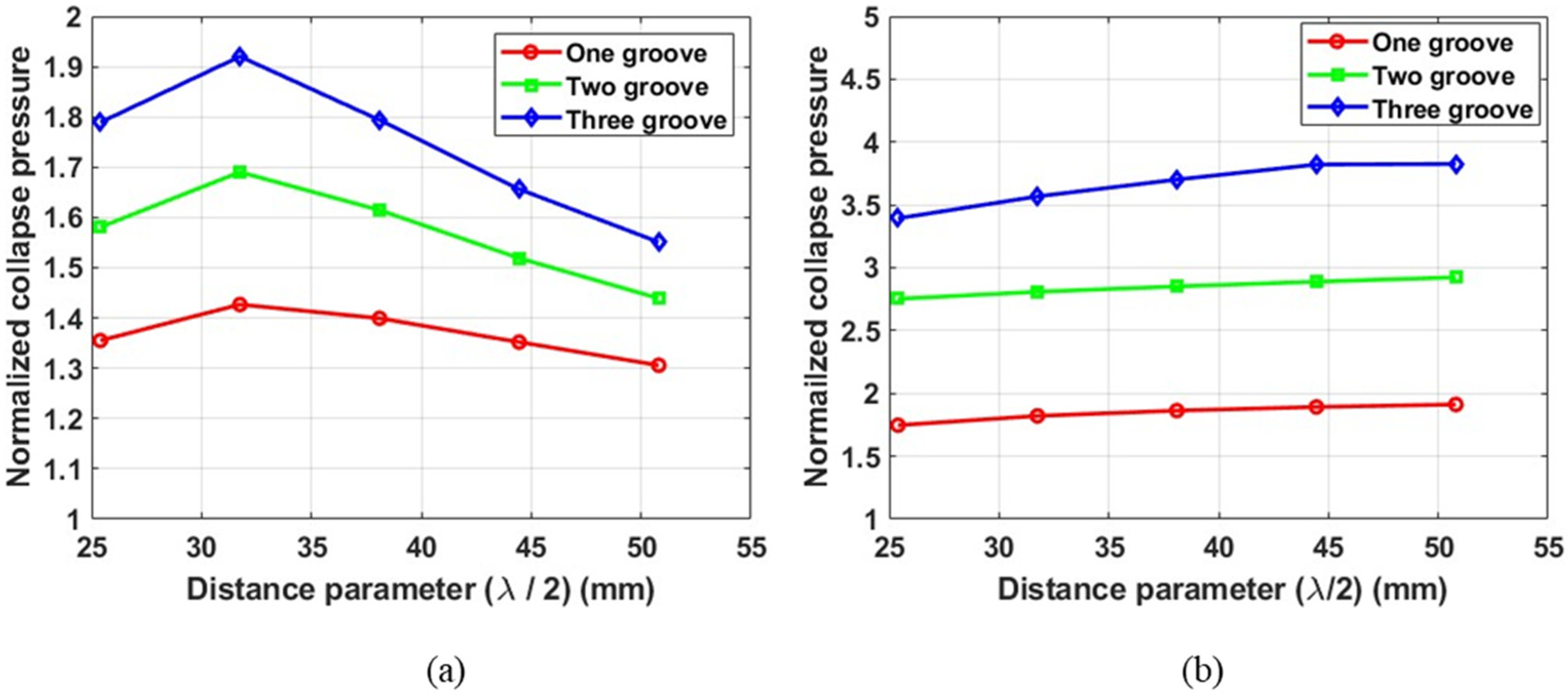
Effect of Distance Parameter
4. Conclusions
- The experimental results indicated a 20% increase in collapse pressures for tubes with a groove geometry;
- The parametric study shows that groove geometries with a smaller root radius exhibit a higher stiffness. Tubes with grooves featuring a minimum root radius (R2min) collapsed locally at the subsections, resulting in higher collapse pressures. In contrast, tubes with grooves featuring a maximum root radius (R2max) collapsed globally, with collapse pressures like those of tubes without grooves;
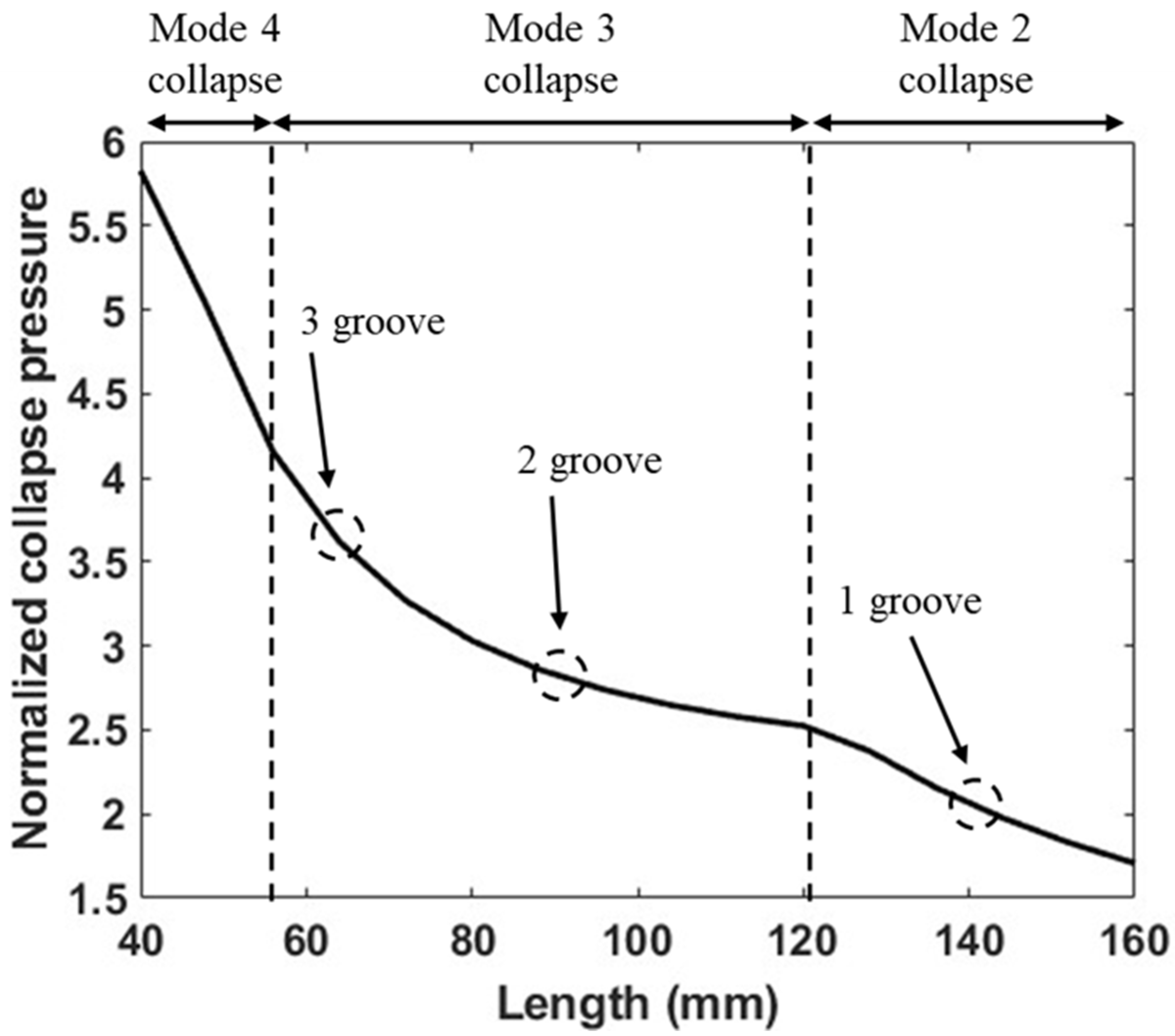
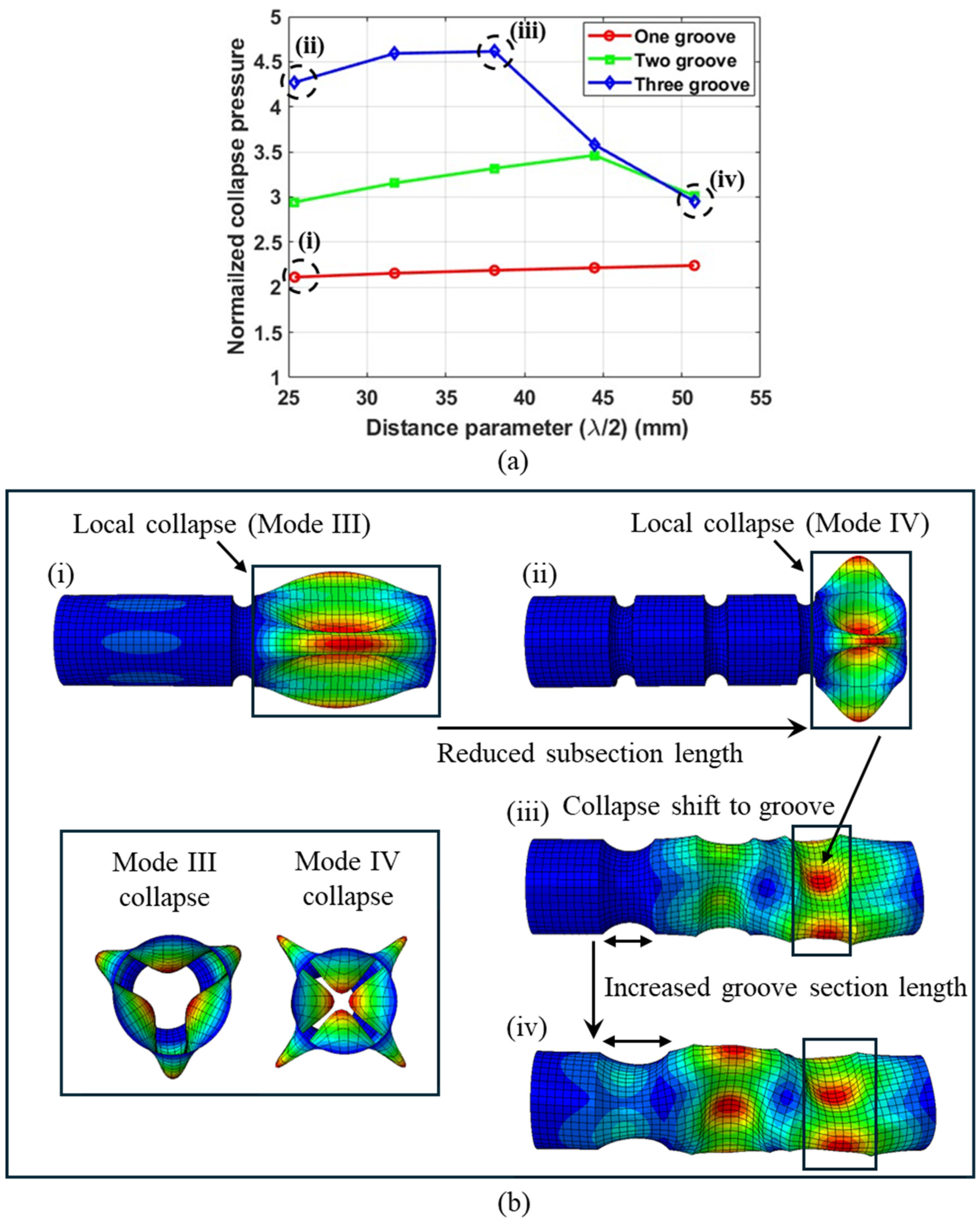
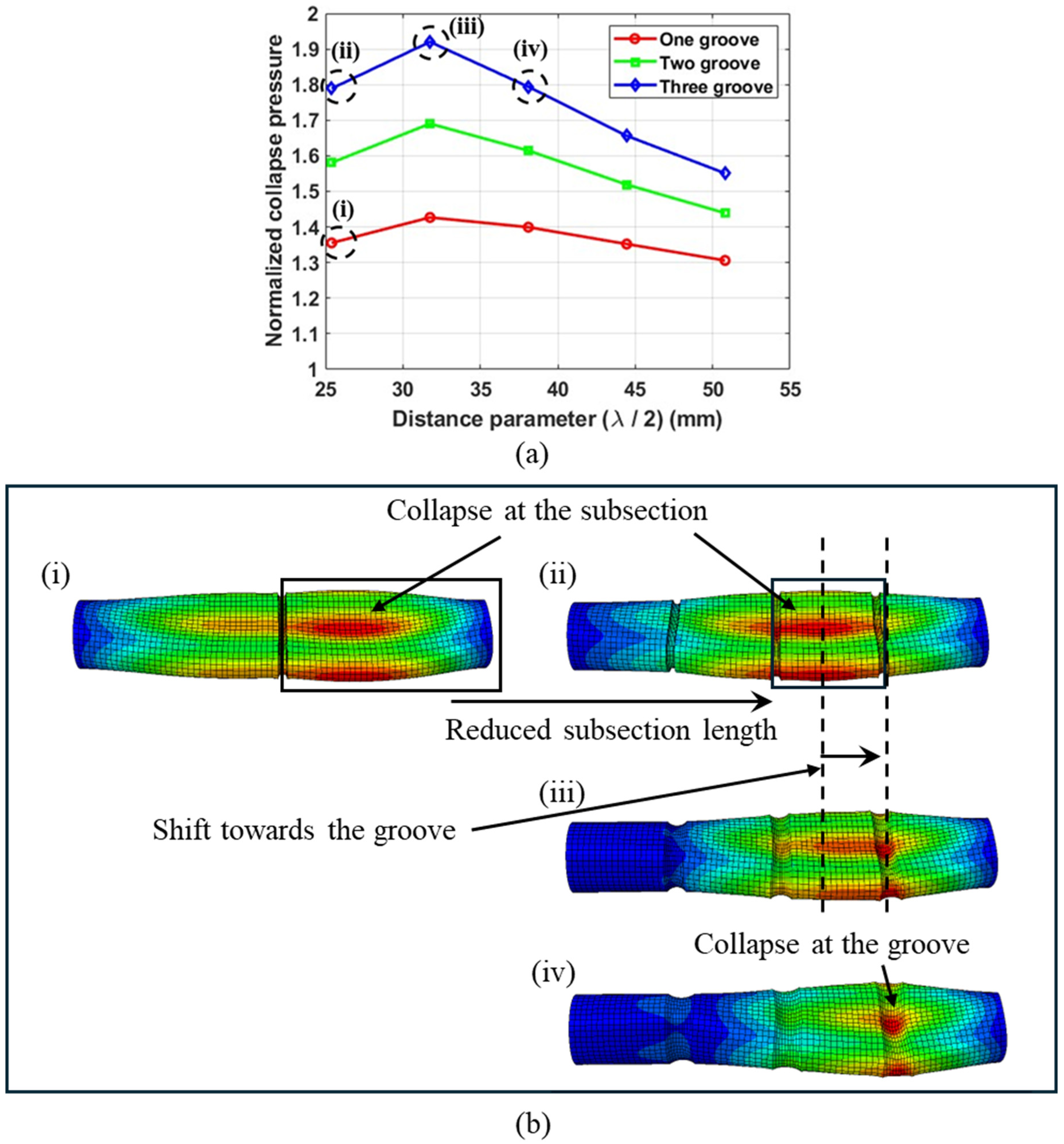
- In cases where the tubes collapsed locally, the collapse pressures showed dependence on the subsection geometry. Shorter subsection lengths resulted in higher-mode collapses, leading to an increase in collapse pressure;
- A higher number of grooves leads to shorter subsection lengths. Shorter subsections exhibit greater stiffness, leading to higher-mode collapse and an increased collapse capacity. Consequently, tubes with three grooves demonstrated the highest collapse pressures. This suggests that the pitch distance of the grooves can be varied to achieve the desired collapse mode and collapse capacity;
- The groove geometry with the smallest distance parameter (λ/2) results in the steepest groove, which exhibits the highest stiffness. An increase in the distance parameter leads to a decrease in groove stiffness and an increase in subsection stiffness. The highest collapse pressures were achieved at intermediate values of the distance parameter. The transition from collapse at the subsection to collapse at the groove section occurs at this intermediate value of the distance parameter, resulting in the highest collapse pressure. This indicates that, when designing tubes with grooves, this transitional value of the distance parameter must be considered;
- The transitional value of the distance parameter depends on the following parameters:
- Root radius of the groove: Grooves with a smaller root radius exhibit a higher stiffness. Therefore, tubes with smaller root radii will have a higher transition value of the distance parameter, and vice versa;
- Tube length: Longer tubes correspond to longer subsections, which have a lower stiffness. Therefore, longer tubes will have a higher transition value of the distance parameter for the same groove geometry and vice versa;
- Number of grooves: A higher number of grooves results in smaller subsections in tubes of the same length. Smaller subsections exhibit a higher stiffness. Therefore, tubes of the same length with a higher number of grooves will have a lower transition value of the distance parameter for the same groove geometry and vice versa.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- von Mises, R.; Basin, U. The Critical External Pressure of Cylindrical Tubes. 2017. Available online: https://api.semanticscholar.org/CorpusID:136286273 (accessed on 21 March 2025).
- Palmer, A.C.; Martin, J.H. Buckle propagation in submarine pipelines. Nature 1975, 254, 46–48. [Google Scholar] [CrossRef]
- Urick, R.J. Implosions as Sources of Underwater Sound. J. Acoust. Soc. Am. 1963, 35, 2026–2027. [Google Scholar] [CrossRef]
- Orr, M.; Schoenberg, M. Acoustic signatures from deep water implosions of spherical cavities. J. Acoust. Soc. Am. 1976, 59, 1155–1159. [Google Scholar] [CrossRef]
- Matos, H.; Ngwa, A.N.; Chaudhary, B.; Shukla, A. Review of Implosion Design Considerations for Underwater Composite Pressure Vessels. J. Mar. Sci. Eng. 2024, 12, 1468. [Google Scholar] [CrossRef]
- Yeh, M.K.; Kyriakides, S. Collapse of Deepwater Pipelines. J. Energy Resour. Technol. 1988, 110, 1–11. [Google Scholar] [CrossRef]
- Park, T.-D.; Kyriakides, S. On the collapse of dented cylinders under external pressure. Int. J. Mech. Sci. 1996, 38, 557–578. [Google Scholar] [CrossRef]
- Weijermars, R. Comprehensive assessment of deep-water vessel implosion mechanisms: OceanGate’s Titan submersible failure sequence explained. Int. J. Press. Vessel. Pip. 2025, 213, 105340. [Google Scholar] [CrossRef]
- DiLisi, G.A.; Eppell, S.J.; Rarick, R.A. The Implosion of the Titan Submersible: A Stress–Strain Experiment. Phys. Teach. 2025, 63, 156–160. [Google Scholar] [CrossRef]
- Mouritz, A.P.; Gellert, E.; Burchill, P.; Challis, K. Review of advanced composite structures for naval ships and submarines. Compos. Struct. 2001, 53, 21–42. [Google Scholar] [CrossRef]
- Li, Y.; Yu, C.; Wang, W.; Li, H.; Jiang, X. A Review on Structural Failure of Composite Pressure Hulls in Deep Sea. J. Mar. Sci. Eng. 2022, 10, 1456. [Google Scholar] [CrossRef]
- Awad, Z.K.; Aravinthan, T.; Zhuge, Y.; Gonzalez, F. A review of optimization techniques used in the design of fibre composite structures for civil engineering applications. Mater. Des. 2012, 33, 534–544. [Google Scholar] [CrossRef]
- Turner, S.E.; Ambrico, J.M. Underwater Implosion of Cylindrical Metal Tubes. J. Appl. Mech. 2013, 80, 011013. [Google Scholar] [CrossRef]
- Guzas, E.L.; Gupta, S.; Ambrico, J.M.; LeBlanc, J.M.; Shukla, A. Computational Modeling of Dynamically Initiated Instabilities and Implosion of Underwater Cylindrical Structures in a Confined Environment. J. Appl. Mech. 2019, 86, 021008. [Google Scholar] [CrossRef]
- Chamberlin, R.E.; Guzas, E.L.; Ambrico, J.M. Energy balance during underwater implosion of ductile metallic cylinders. J. Acoust. Soc. Am. 2014, 136, 2489–2496. [Google Scholar] [CrossRef]
- Matos, H.; Kishore, S.; Salazar, C.; Shukla, A. Buckling, vibration, and energy solutions for underwater composite cylinders. Compos. Struct. 2020, 244, 112282. [Google Scholar] [CrossRef]
- Koudela, K.L.; Strait, L.H. Simplified Methodology for Prediction of Critical Buckling Pressure for Smooth-Bore Composite Cylindrical Shells. J. Reinf. Plast. Compos. 1993, 12, 570–583. [Google Scholar] [CrossRef]
- Messager, T.; Pyrz, M.; Gineste, B.; Chauchot, P. Optimal laminations of thin underwater composite cylindrical vessels. Compos. Struct. 2002, 58, 529–537. [Google Scholar] [CrossRef]
- Farhat, C.; Wang, K.G.; Main, A.; Kyriakides, S.; Lee, L.H.; Ravi-Chandar, K.; Belytschko, T. Dynamic implosion of underwater cylindrical shells: Experiments and Computations. Int. J. Solids Struct. 2013, 50, 2943–2961. [Google Scholar] [CrossRef]
- Ikeda, C.M.; Wilkerling, J.; Duncan, J.H. The implosion of cylindrical shell structures in a high-pressure water environment. Proc. R. Soc. A Math. Phys. Eng. Sci. 2013, 469, 20130443. [Google Scholar] [CrossRef]
- Moon, C.-J.; Kim, I.-H.; Choi, B.-H.; Kweon, J.-H.; Choi, J.-H. Buckling of filament-wound composite cylinders subjected to hydrostatic pressure for underwater vehicle applications. Compos. Struct. 2010, 92, 2241–2251. [Google Scholar] [CrossRef]
- Pinto, M.; Shukla, A. Shock-Initiated Buckling of Carbon/Epoxy Composite Tubes at Sub-Critical Pressures. Exp. Mech. 2016, 56, 583–594. [Google Scholar] [CrossRef]
- Kishore, S.; Parrikar, P.N.; Shukla, A. Response of an underwater cylindrical composite shell to a proximal implosion. J. Mech. Phys. Solids 2021, 152, 104414. [Google Scholar] [CrossRef]
- Yang, C.; Pang, S.-S.; Zhao, Y. Buckling Analysis of Thick-Walled Composite Pipe under External Pressure. J. Compos. Mater. 1997, 31, 409–426. [Google Scholar] [CrossRef]
- Hernández-Moreno, H.; Douchin, B.; Collombet, F.; Choqueuse, D.; Davies, P. Influence of winding pattern on the mechanical behavior of filament wound composite cylinders under external pressure. Compos. Sci. Technol. 2008, 68, 1015–1024. [Google Scholar] [CrossRef]
- Ross, C.T.F.; Little, A.P.F.; Haidar, Y.; Waheeb, A.A. Buckling of Carbon/Glass Composite Tubes Under Uniform External Hydrostatic Pressure. Strain 2011, 47, e156–e174. [Google Scholar] [CrossRef]
- Matos, H.; Chaudhary, B.; Ngwa, A.N. Optimization of Composite Cylindrical Shell Structures for Hydrostatic Pressure Loading. J. Press. Vessel. Technol. 2023, 145, 011504. [Google Scholar] [CrossRef]
- Ngwa, A.N.; Chaudhary, B.; Matos, H.; Shukla, A. Design Optimization for Hydrostatic Pressure in Hybrid Composite Cylinders. Appl. Compos. Mater. 2024, 32, 1–22. [Google Scholar] [CrossRef]
- Kyriakides, S.; Youn, S.-K. On the collapse of circular confined rings under external pressure. Int. J. Solids Struct. 1984, 20, 699–713. [Google Scholar] [CrossRef]
- Singer, J.; Haftka, R.T. Buckling of Discretely Stringer-Stiffened Cylindrical Shells and Elastically Restrained Panels. AIAA J. 1975, 13, 849–850. [Google Scholar] [CrossRef]
- Pegg, N.G. A numerical study of dynamic pulse buckling of ring-stiffened cylinders. Comput. Struct. 1992, 44, 1205–1214. [Google Scholar] [CrossRef]
- Park, T.-D.; Kyriakides, S. On the performance of integral buckle arrestors for offshore pipelines. Int. J. Mech. Sci. 1997, 39, 643–669. [Google Scholar] [CrossRef]
- Ngwa, A.; Rossell, V.; Matos, H.; Shukla, A. Effects of ring stiffeners on the underwater collapse behavior of carbon/epoxy composite tubes. J. Compos. Mater. 2023, 57, 1755–1767. [Google Scholar] [CrossRef]
- Tian, J.; Wang, C.M.; Swaddiwudhipong, S. Elastic buckling analysis of ring-stiffened cylindrical shells under general pressure loading via the Ritz method. Thin-Walled Struct. 1999, 35, 1–24. [Google Scholar] [CrossRef]
- Foryś, P. Optimization of cylindrical shells stiffened by rings under external pressure including their post-buckling behaviour. Thin-Walled Struct. 2015, 95, 231–243. [Google Scholar] [CrossRef]
- Smith, M. ABAQUS/Standard User’s Manual, Version 6.9; Dassault Systèmes Simulia Corp: Johnston, RI, USA, 2009. [Google Scholar]
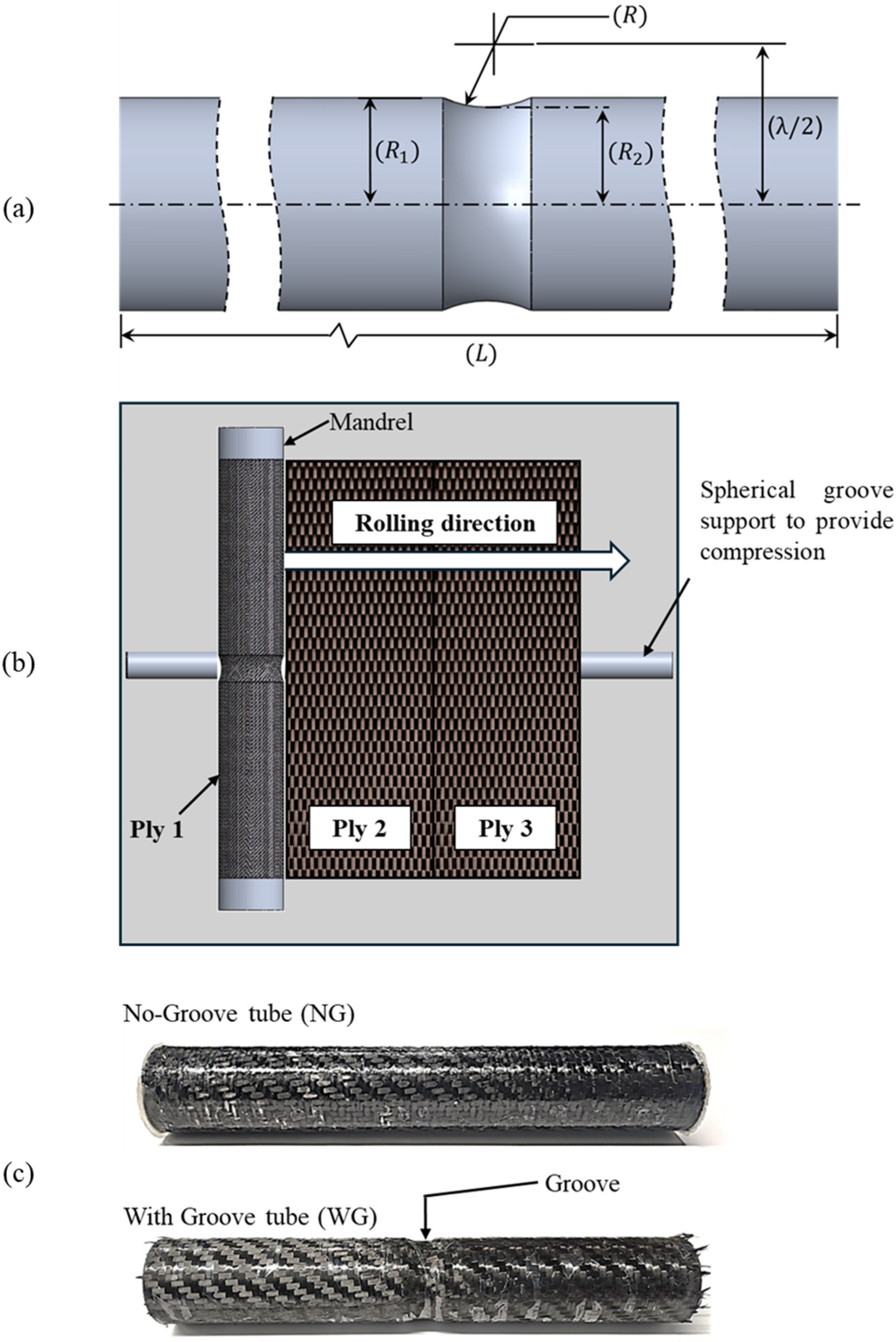
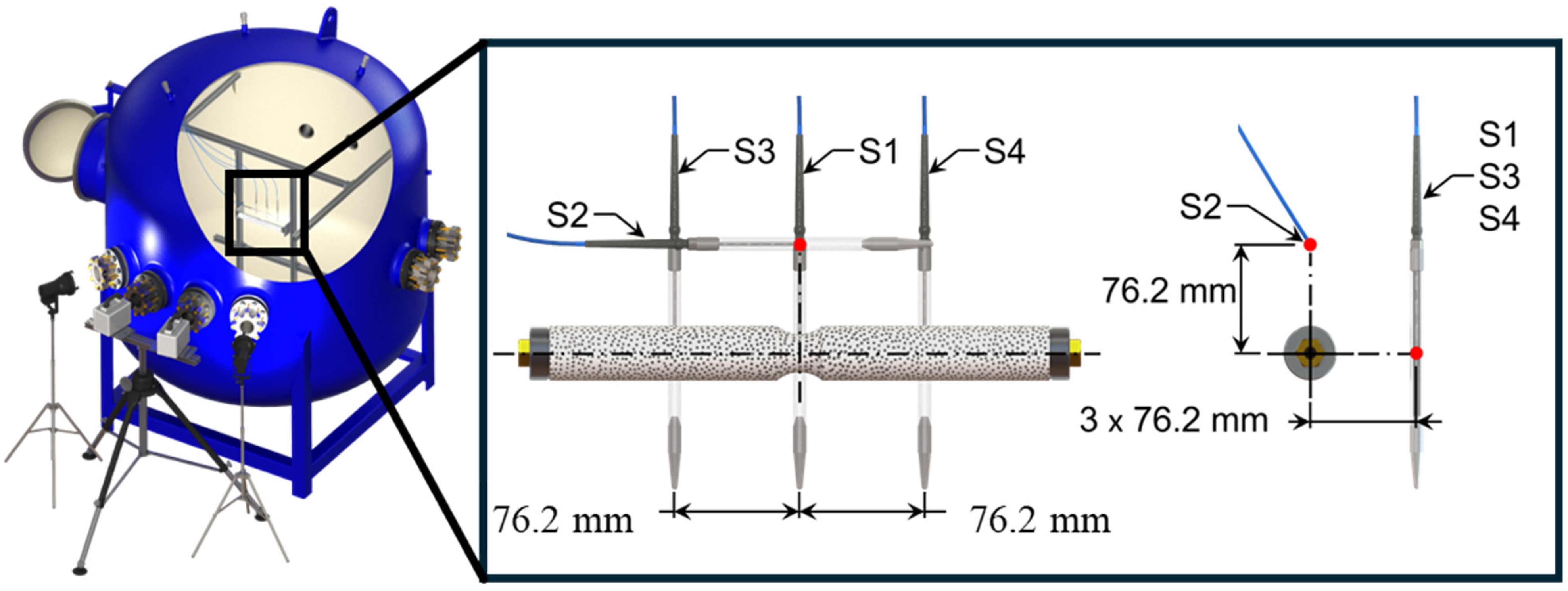
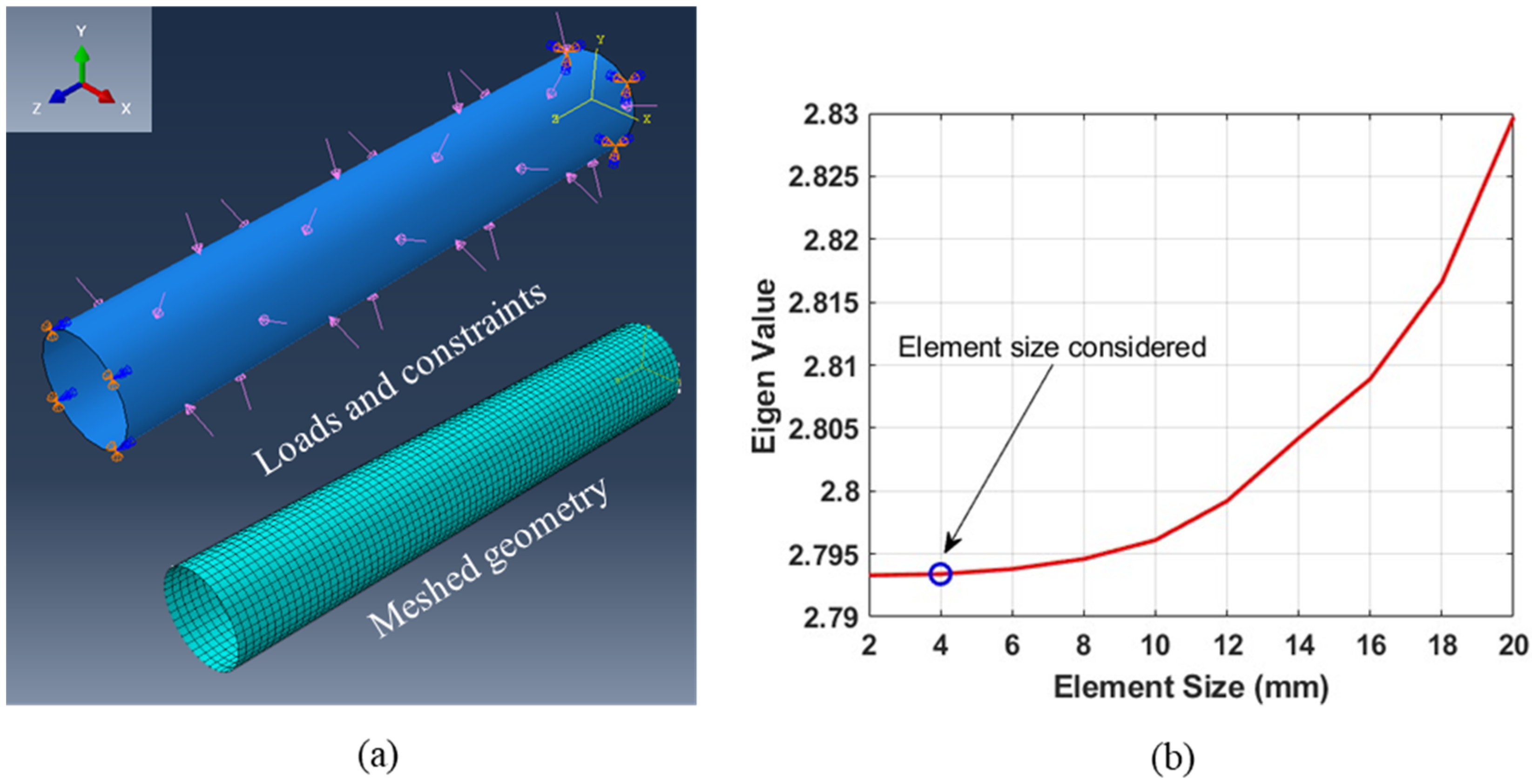


| Type | (mm) | (mm) | (mm) | (mm) |
|---|---|---|---|---|
| No groove (NG) | 330 | 25.4 | - | - |
| With groove (WG) | 330 | 25.4 | 23 | 48.5 |
| Mechanical Property | Values | Reference |
|---|---|---|
| and [GPa] | 38.0 ± 0.5 | ASTM D3039 |
| and | 0.1 | ASTM D3039 |
| [GPa] | 3.0 ± 0.4 | ASTM D5379 |
| and [GPa] | 2.8 ± 0.2 | ASTM D5379 |
| Specimen ID | Configuration | (MPa) |
|---|---|---|
| NG1 | No groove | 2.7 |
| NG2 | No groove | 2.6 |
| WG1 | With groove | 3.2 |
| WG2 | With groove | 3.2 |
| Specimen ID | Configuration | (MPa) (Simulations) | (MPa) (Experiments) | Error |
|---|---|---|---|---|
| NG | No groove | 2.7 | 2.65 | 1.8% |
| WG | With groove | 3 | 3.2 | 6% |
| Parameter | Variation |
|---|---|
| (mm) | |
| (mm) | |
| No. of plies (N) | |
| (mm) | |
| (mm) | |
| Parameter | Effect |
|---|---|
| Root radius |
|
| Tube length |
|
| No. of grooves |
|
| Distance parameter ) |
|
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jain, S.; Pandey, A.; Shukla, A. Strategy to Enhance the Collapse Capacity of Composite Cylindrical Tubes: Experiments and Simulations. Materials 2025, 18, 1458. https://doi.org/10.3390/ma18071458
Jain S, Pandey A, Shukla A. Strategy to Enhance the Collapse Capacity of Composite Cylindrical Tubes: Experiments and Simulations. Materials. 2025; 18(7):1458. https://doi.org/10.3390/ma18071458
Chicago/Turabian StyleJain, Siddharth, Akash Pandey, and Arun Shukla. 2025. "Strategy to Enhance the Collapse Capacity of Composite Cylindrical Tubes: Experiments and Simulations" Materials 18, no. 7: 1458. https://doi.org/10.3390/ma18071458
APA StyleJain, S., Pandey, A., & Shukla, A. (2025). Strategy to Enhance the Collapse Capacity of Composite Cylindrical Tubes: Experiments and Simulations. Materials, 18(7), 1458. https://doi.org/10.3390/ma18071458








