Dynamic Performance of a Steel Road Sign with Multi-Material Electronic Signboard Under Mining-Induced Tremors from Different Mining Areas: Experimental and Numerical Research
Abstract
1. Introduction
- Investigate how variations in the dominant frequency range of different mining activity areas influence the sign’s dynamic behavior;
- Conduct a preliminary assessment of whether standard prefabricated road signs, particularly those with multi-material electronic signboards, provide a safe and effective material solution in mining areas.
- Comparing the dynamic performance of a road sign in two distinct mining regions, highlighting how regional variations in seismic excitation characteristics affect the dynamic response of a steel road sign;
- Utilizing an experimentally validated numerical model of a road sign to improve the accuracy of vibration predictions;
- Providing new insights into the dynamic performance of multi-material electronic signboards under mining tremors, enhancing their safety assessment in mining areas.
- ▪
- Presentation of the geometric and material details of a typical road sign structure, the description of its numerical model, and theoretical background along with the experimental set-up for estimating modal properties (Section 2);
- ▪
- Experimental and numerical modal analysis to determine the natural frequencies and mode shapes of the typical road sign structure (Section 3.1 and Section 3.2);
- ▪
- Verification and calibration of the numerical model of the sign (Section 3.3);
- ▪
- Evaluation of the dynamic response of the road sign subjected to seismic shocks from two different mining regions (Section 4.1);
- ▪
- Prediction of the potential plastic behavior of the multi-material electronic signboard under mining-induced tremors with anticipated maximum PGA (Section 4.2);
- ▪
- Conclusions (Section 5).
2. Materials and Methods
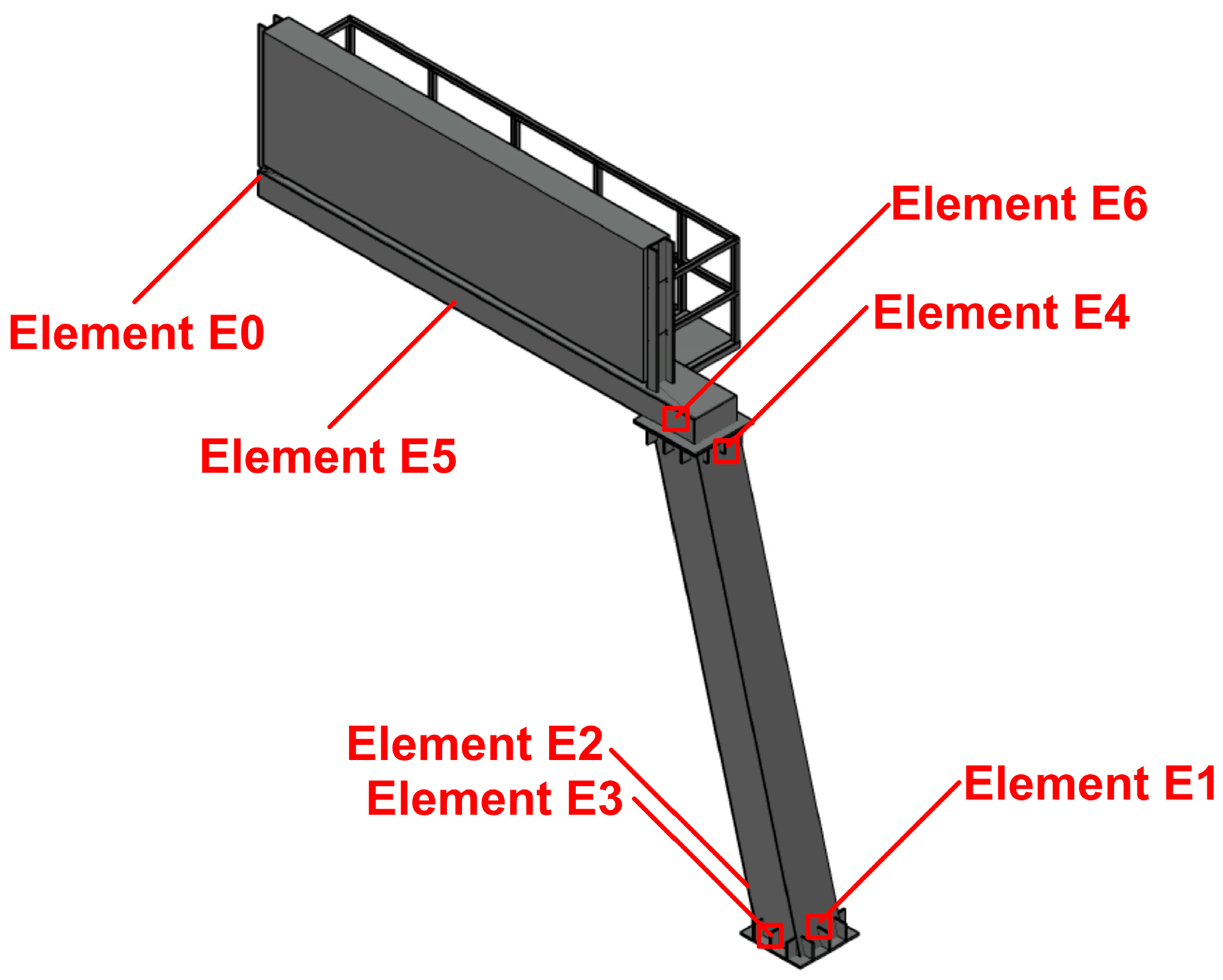
2.1. Structural Morphology of the Analysed Steel Road Sign
2.2. In-Field Tests and Experimental Set-Up
2.3. Theoretical Background
2.4. The Numerical Model of the Road Sign
- —the coefficient for various ground stiffness, recommended in [47] for different types of subsoil [Mpa/m];
- p—the on-ground static pressure [Mpa];
- —the reference on-ground static pressure;
- —the dimensional coefficient;
- L, B—the dimensions of the contact area [m].
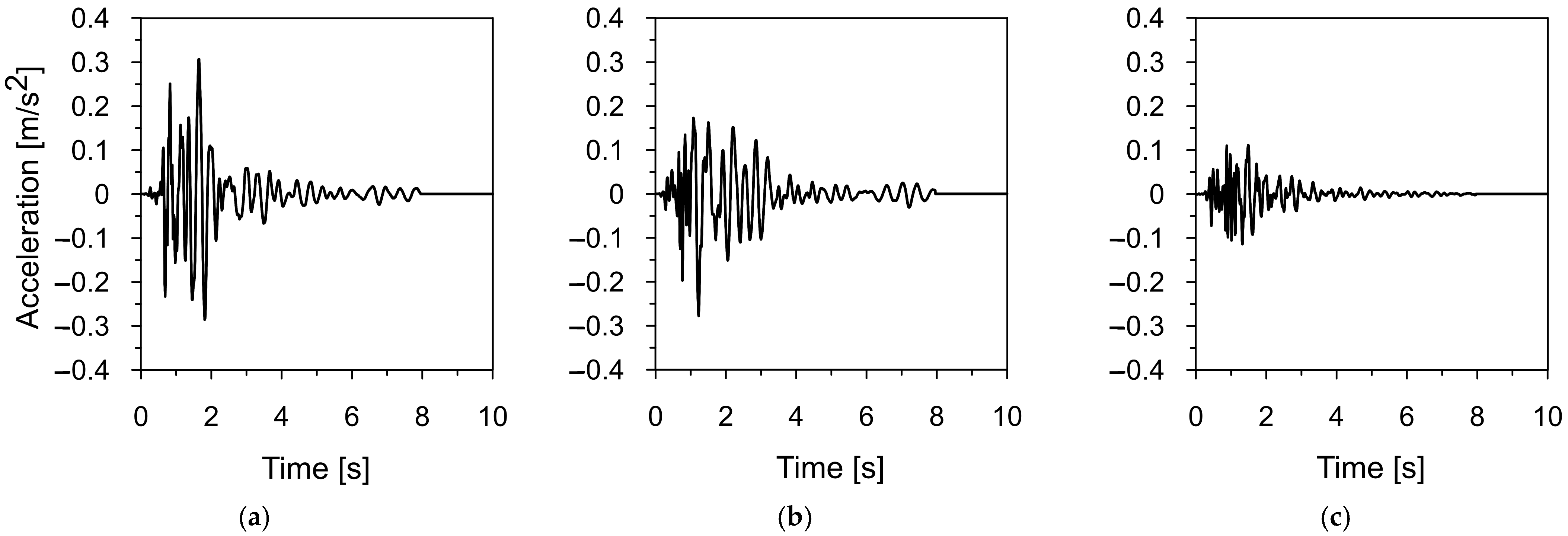
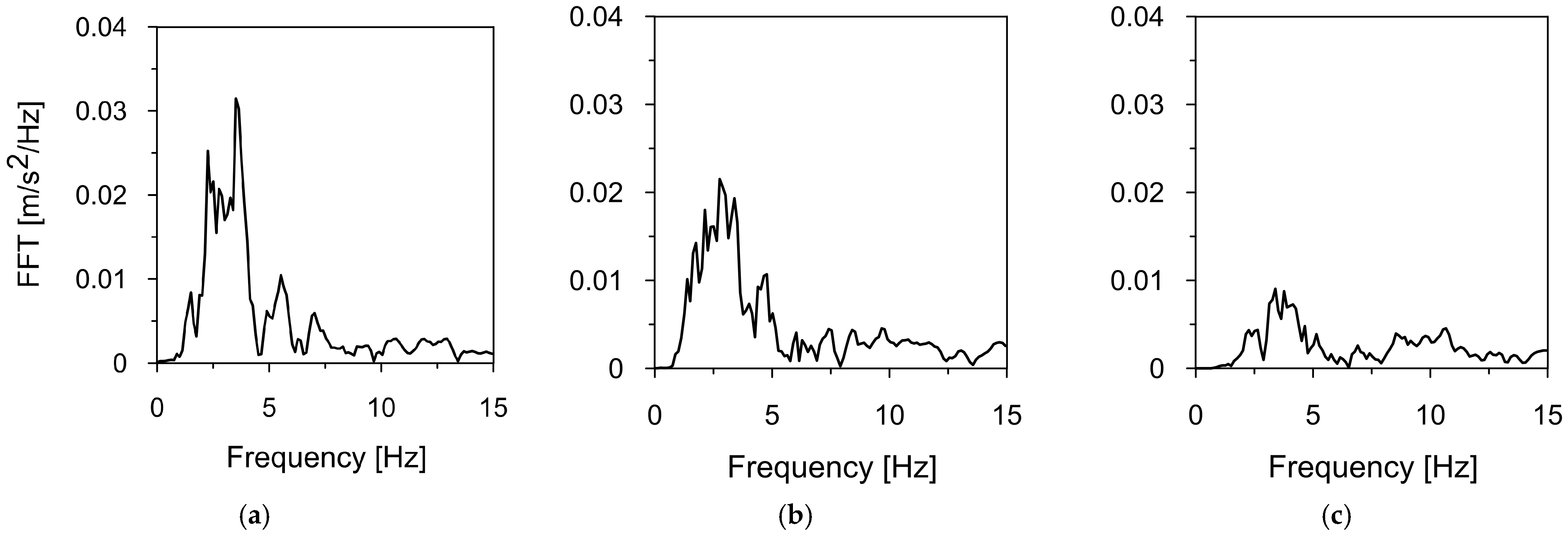
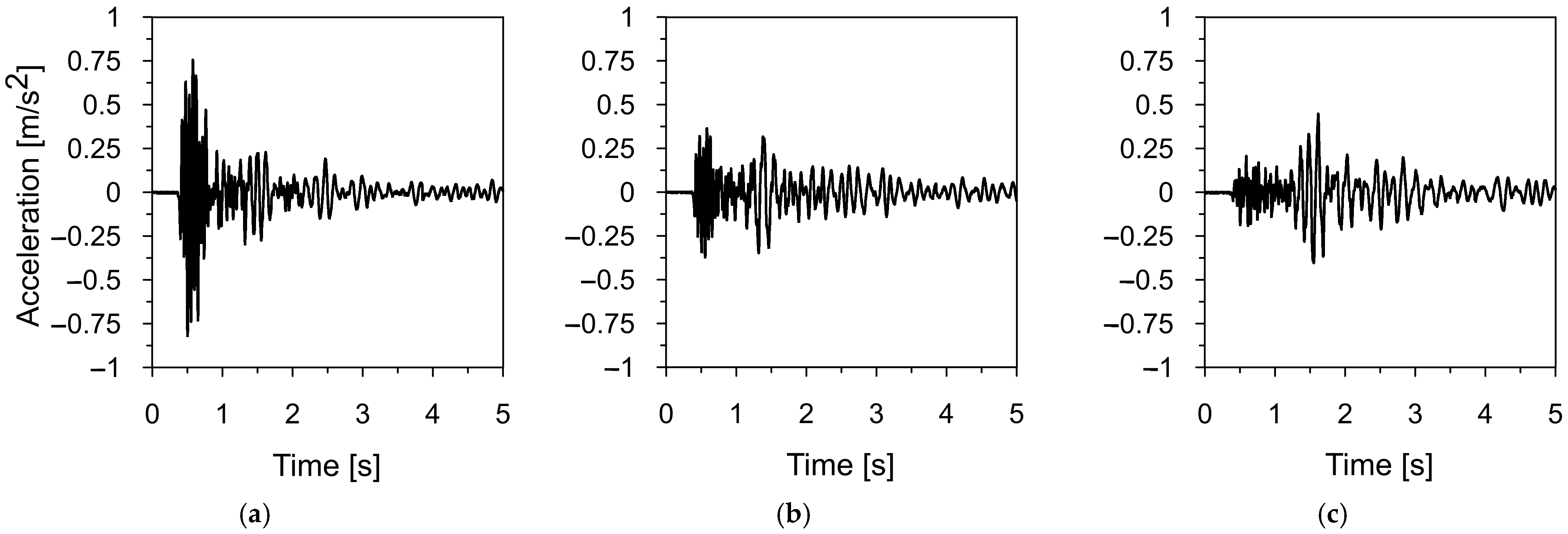
2.5. Characteristics of Mining-Induced Tremors Used for Dynamic Analysis
3. Results of Numerical Assessment and Field Experiments on Dynamic Properties of the Road Sign
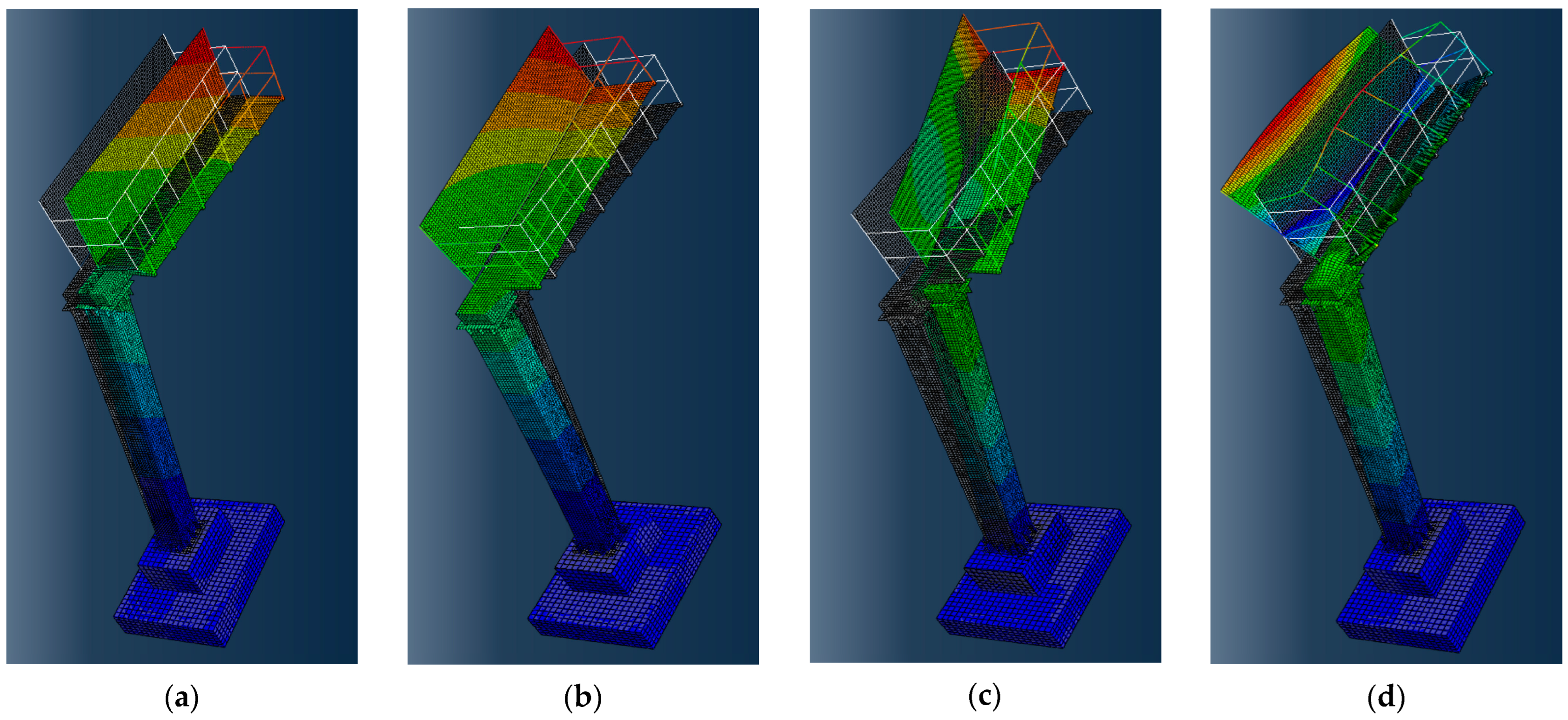
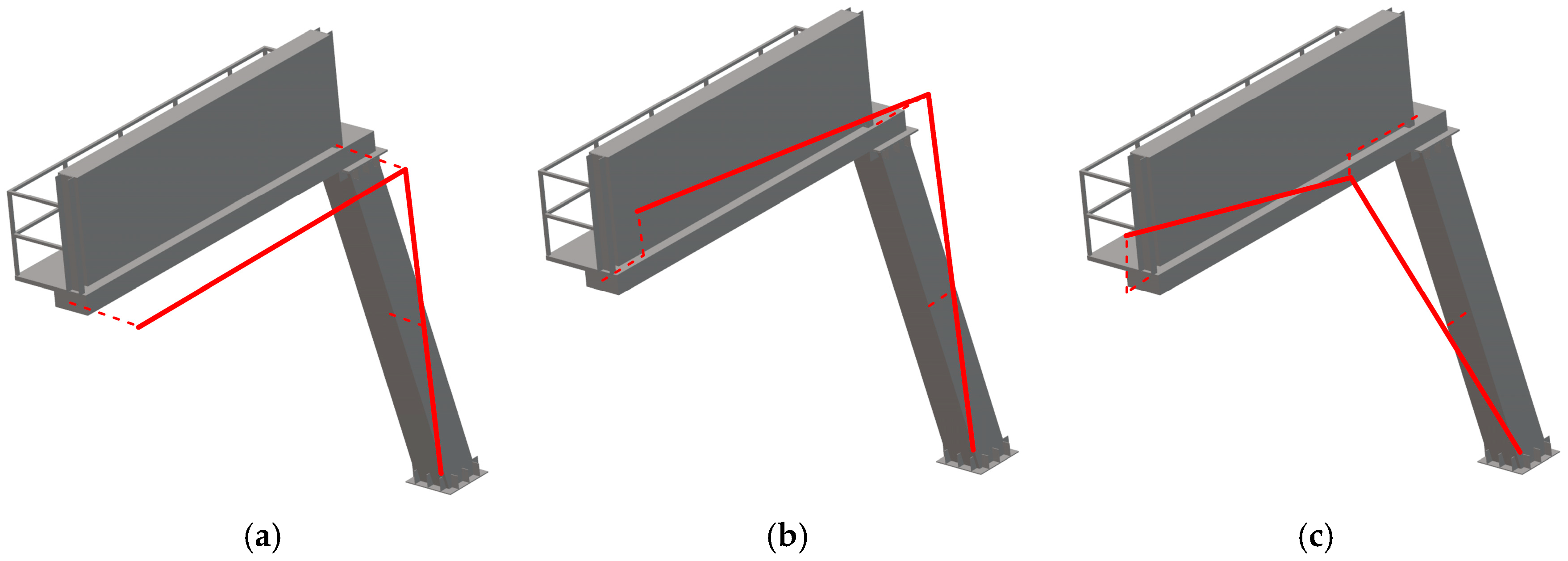
3.1. Numerical Estimation of Natural Frequencies and Modes of Vibration
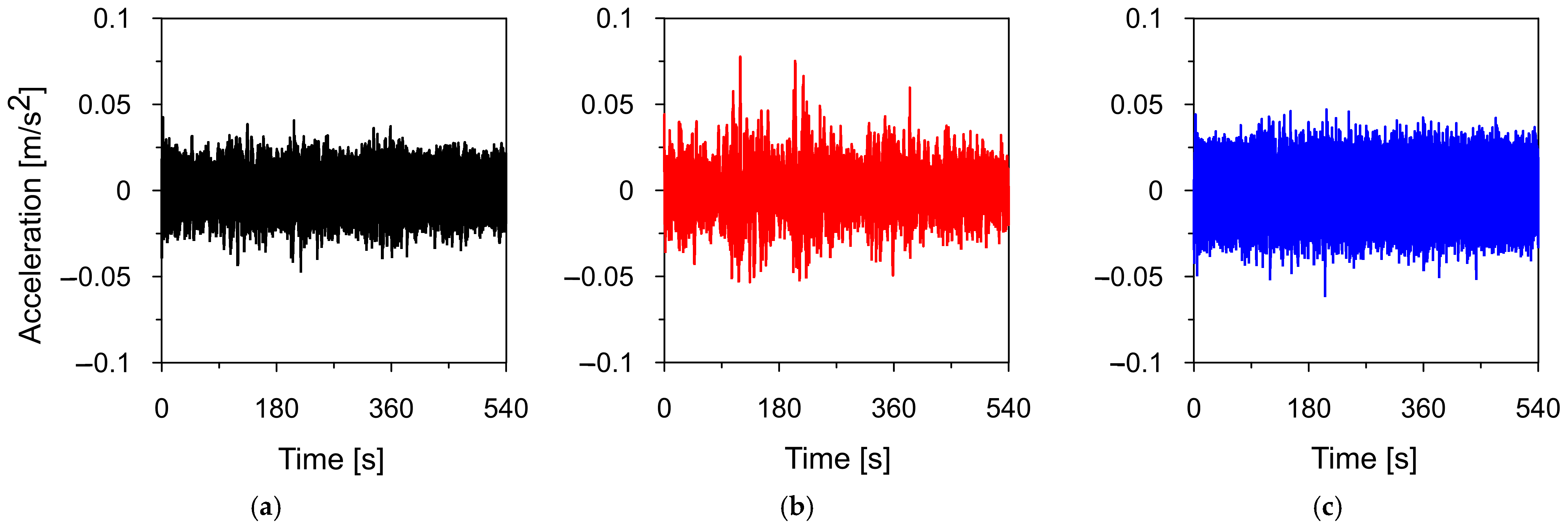
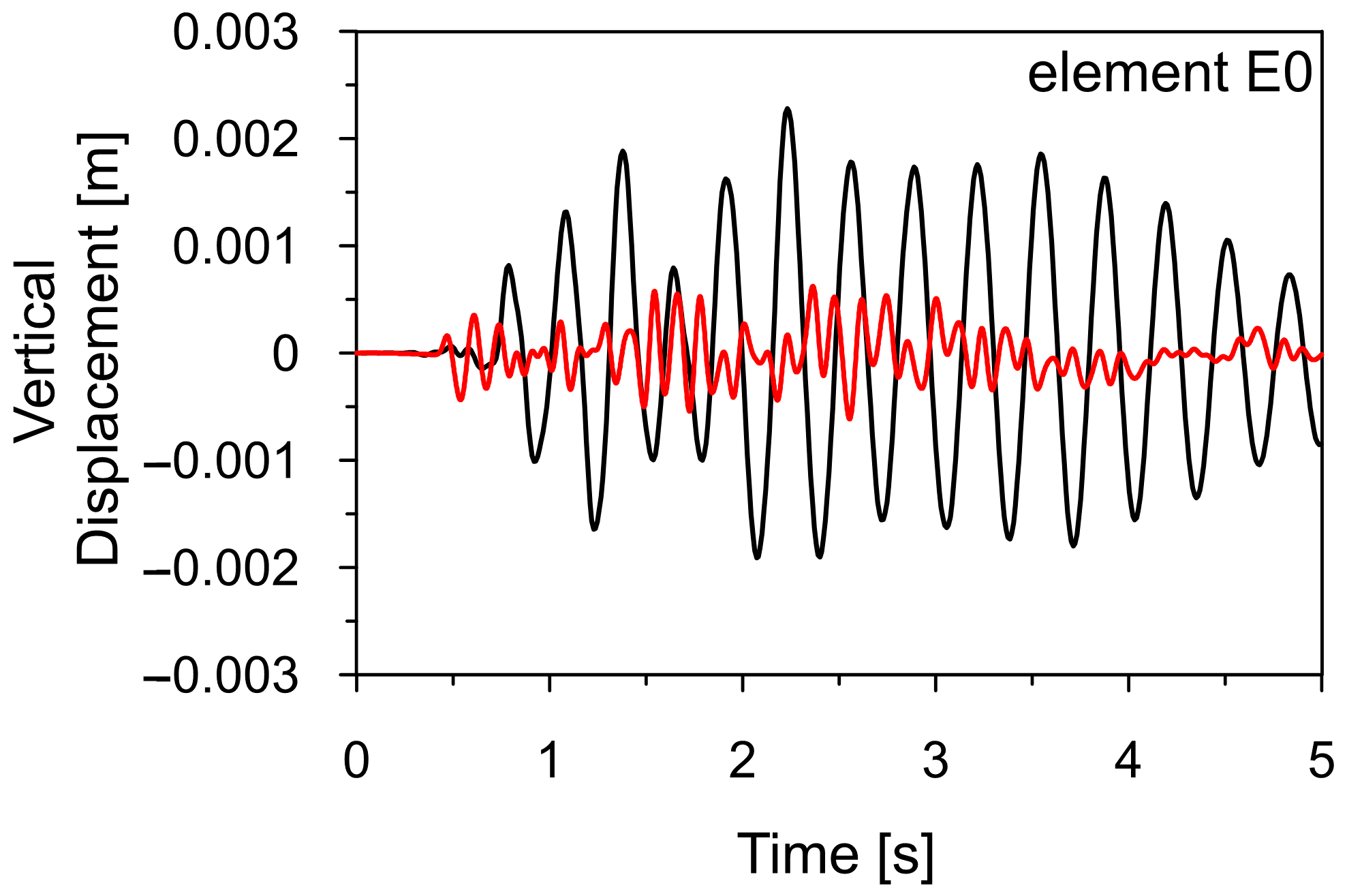
3.2. Experimental Estimation of Natural Frequencies and Modes of Vibration
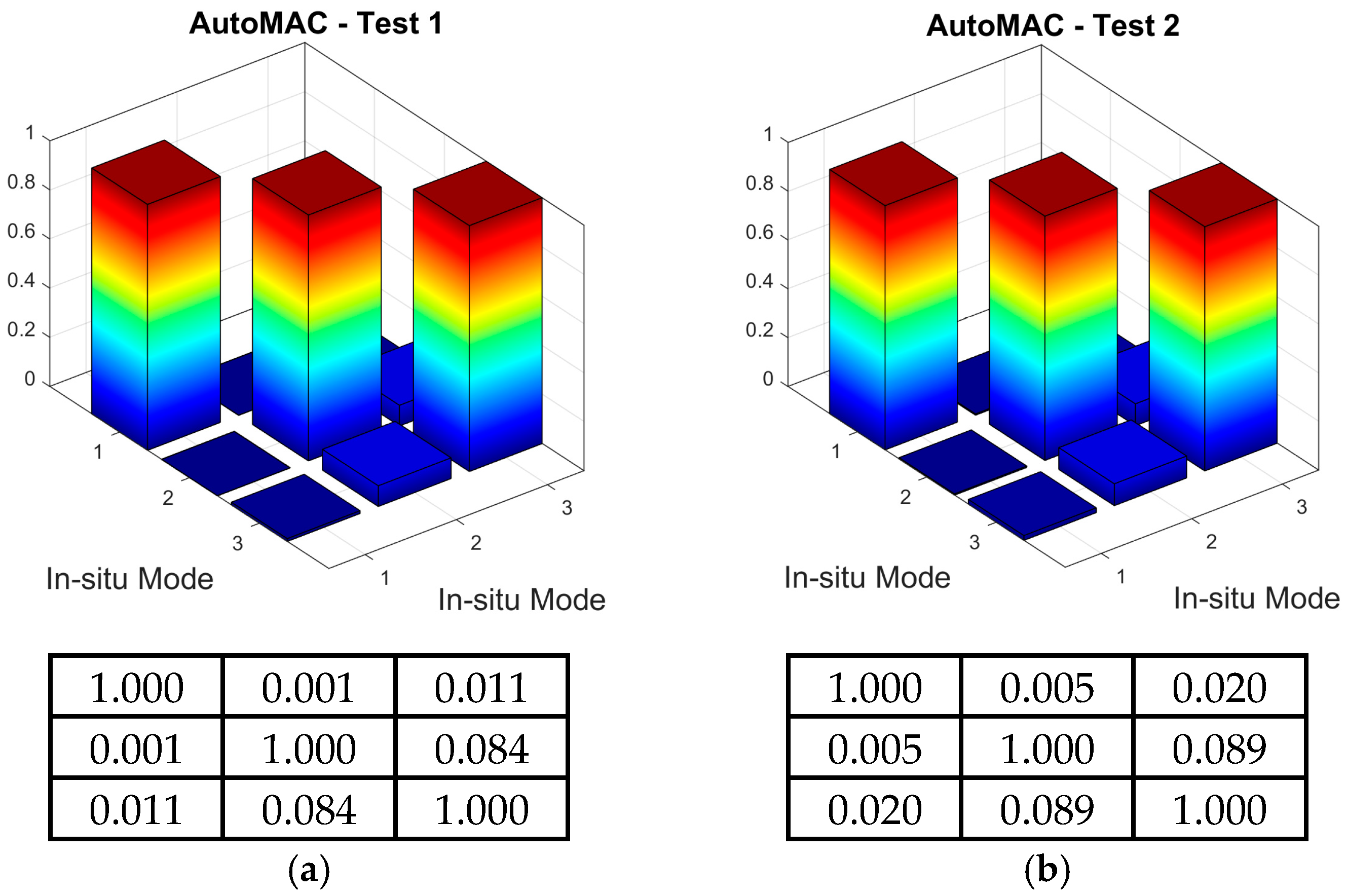
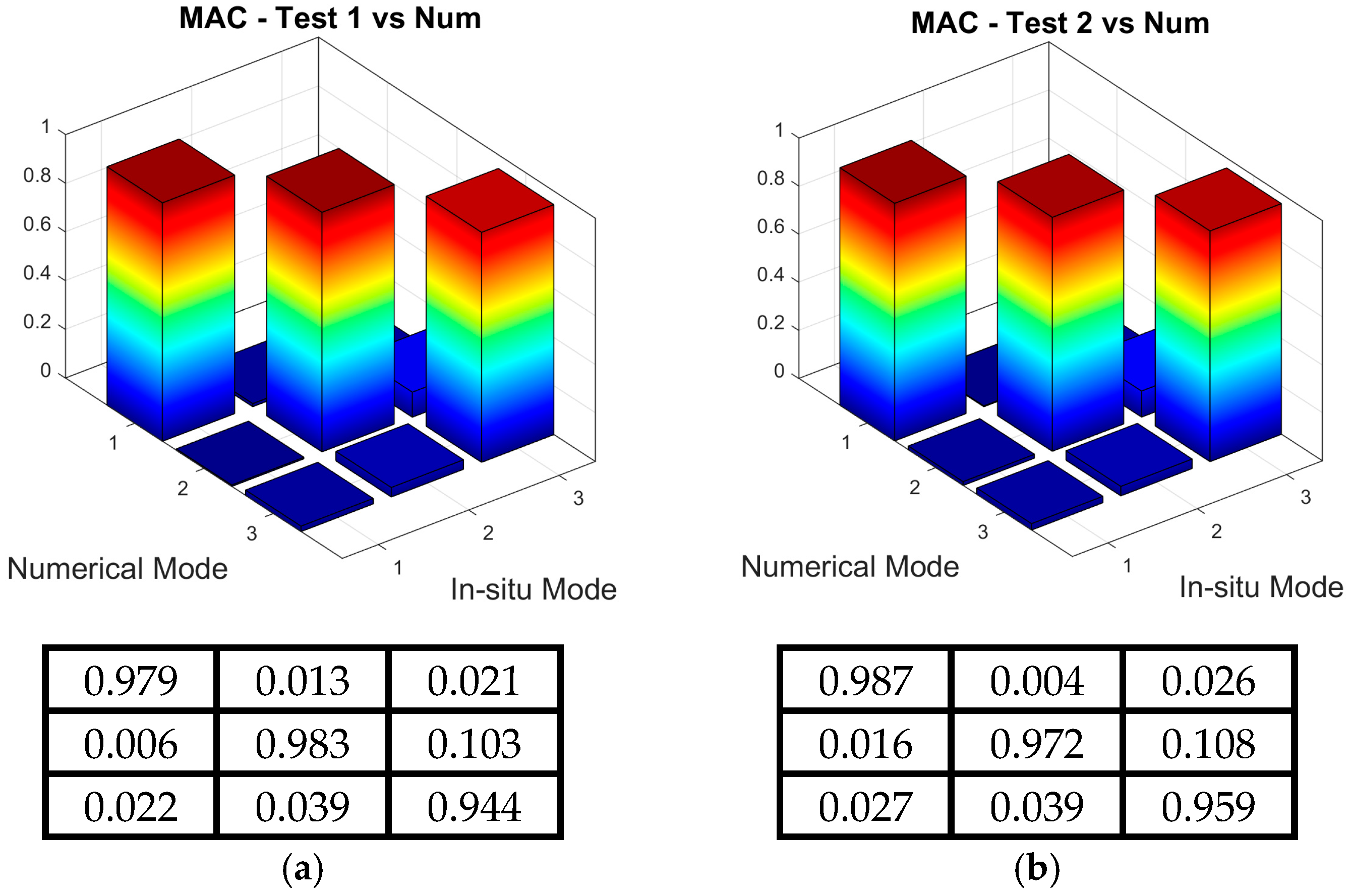
3.3. Validation of the Experimentally Obtained Natural Frequencies and Modes of Vibration
3.4. The Numerical Modal Model Validation
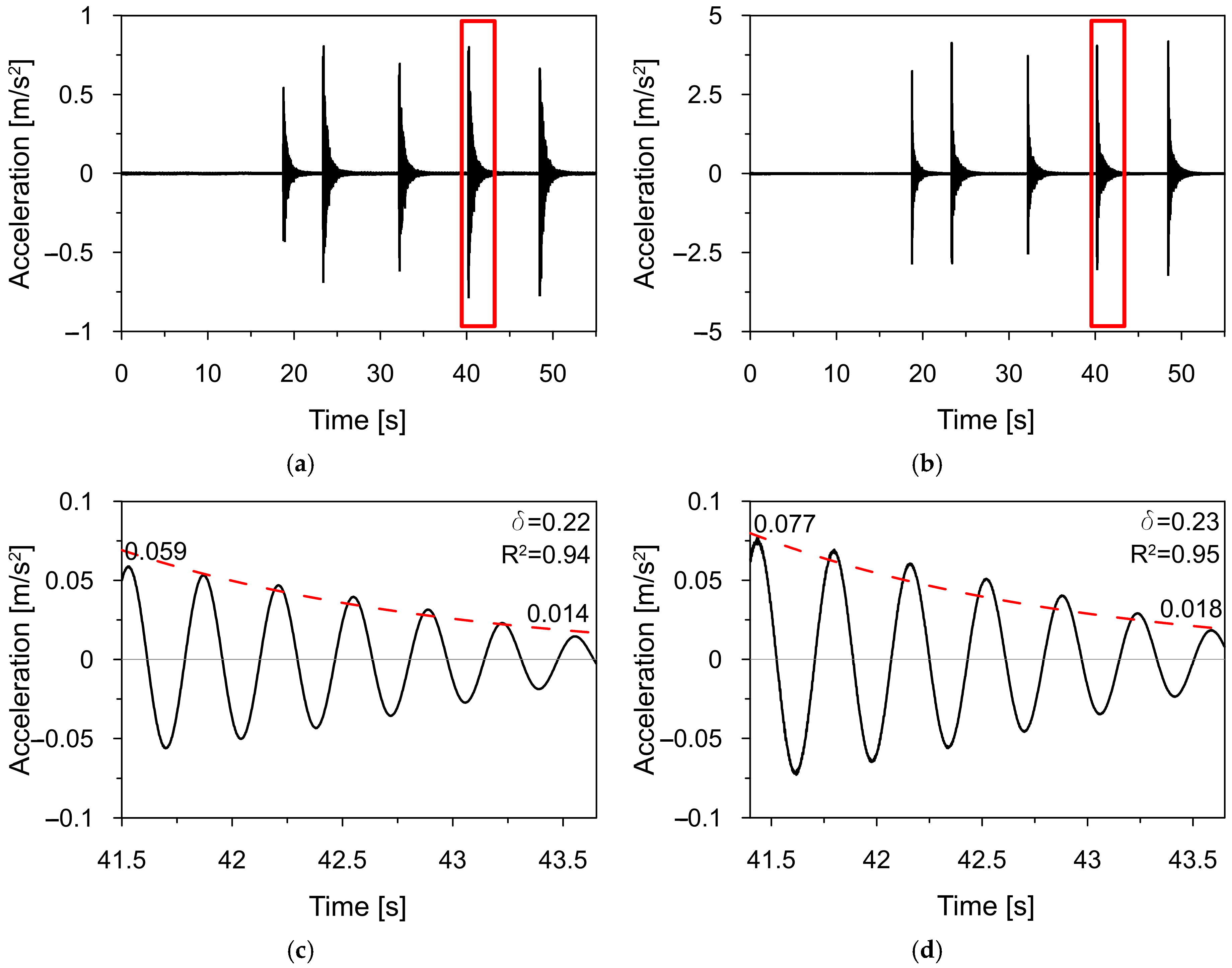
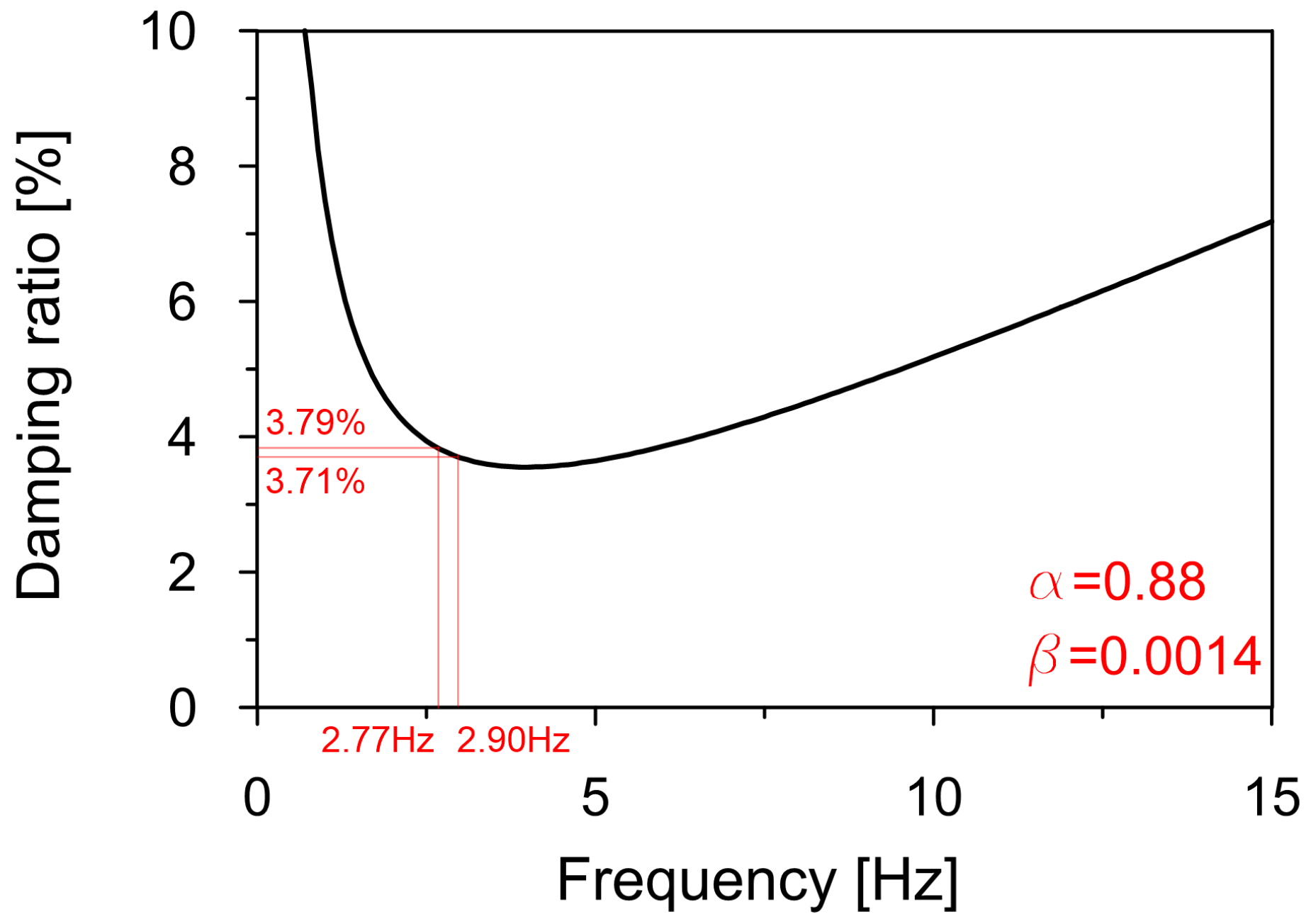
3.5. Experimental Evaluation of Damping Properties
4. Results and Discussion on the Dynamic Performance of the Steel Road Sign with Multi-Material Electronic Signboard Under Mining-Induced Seismicity
4.1. Dynamic Response of the Road Sign to the Shocks from Different Mining Activity Regions
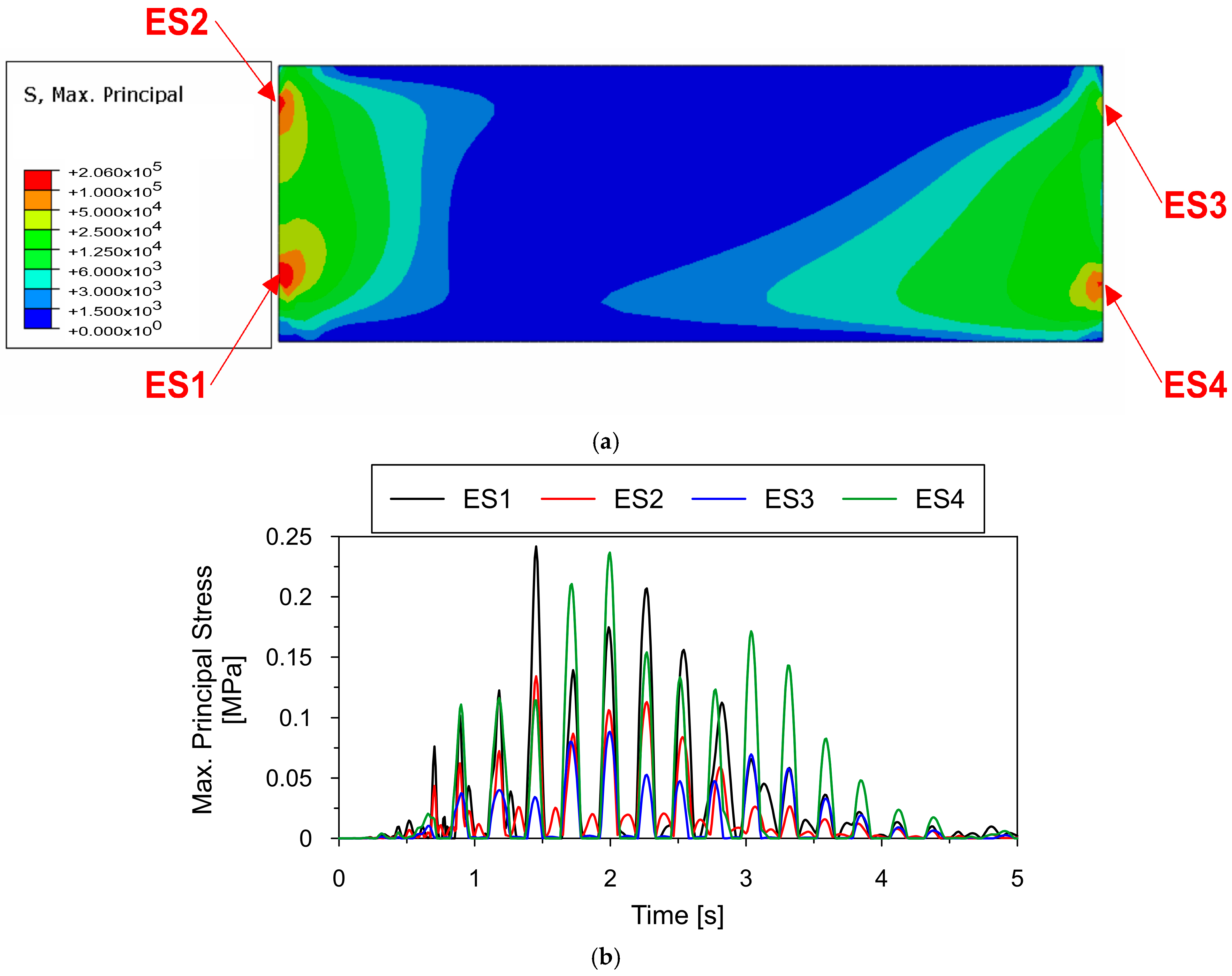
4.2. Prediction of the Potential Plastic Behavior of the Multi-Material Electronic Signboard Under Mining-Induced Tremors with the Anticipated Maximum PGA
5. Conclusions
- The comparison between the numerically and experimentally obtained natural frequencies showed good agreement. Additionally, the numerical modal analysis, validated through MAC methods, confirmed a close match between the numerical and experimental mode shapes, indicating proper calibration of the FE model;
- The damping properties of the road sign, measured through hammer tests, showed consistent results with similar studies, confirming the reliability of the damping estimation;
- A strong correlation between the numerical simulations and experimental results validated the FE model, enabling further assessment of dynamic performance under mining-induced shocks and ensuring the accuracy of vibration predictions;
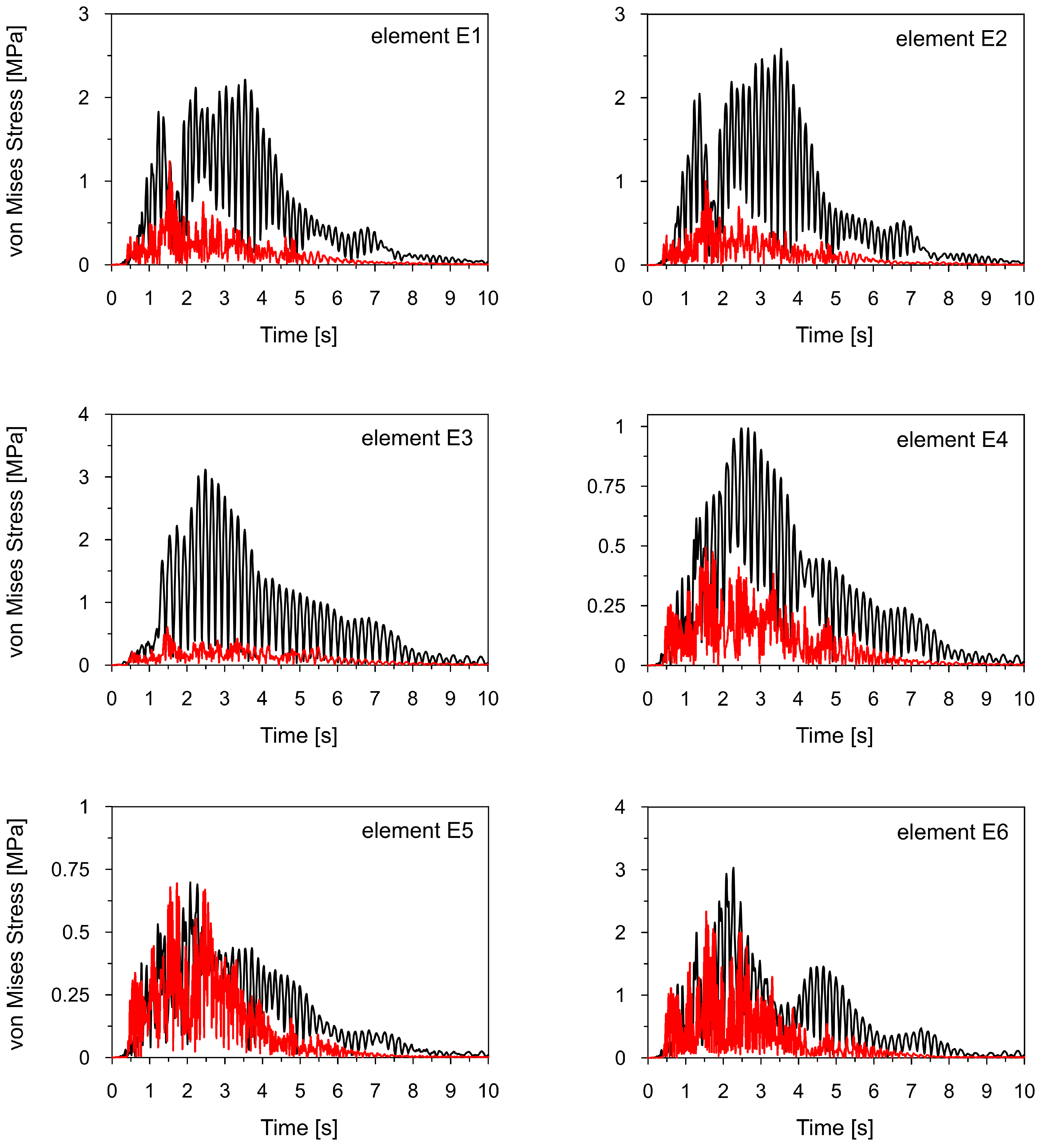
- The Moskorzyn tremor had twice the peak ground acceleration (PGA) of the Szombierki tremor; however, it caused five-times lower response stress and displacements. The Szombierki tremor, with a frequency range of 1.6–4.8 Hz, which is closer to the natural frequencies of the sign, led to a significantly higher response level than the Moskorzyn tremor, which had a frequency range of 5–10 Hz. This indicates that frequency matching had a greater impact on the road sign’s response than the PGA;
- The stress levels resulting from both tremors remain well below the permissible limits for the steel structure. In the case of the Szombierki tremor, with a PGA of 0.35 m/s2, the maximum von Mises stress observed in the steel structure of the sign reached 5 MPa, while the displacement at the end of the arm was 2 mm. However, the predicted maximum PGA values in this region reach 1.8 m/s2—approximately six times higher than the analyzed tremor. Consequently, stresses may increase sixfold, reaching around 30 MPa, with displacements of approximately 1.2 cm. At this level, the stress reaches about 20% of that induced by the dead load;
- The preliminary assessment of the road sign’s dynamic performance showed that the multi-material electronic signboard remained intact, with no plastic deformation or damage. This suggests that such signboards are suitable for use in mining activity areas.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Worlanyo, A.; Li, J. Evaluating the environmental and economic impact of mining for post-mined land restoration and land-use: A review. J. Environ. Manag. 2021, 279, 111623. [Google Scholar] [CrossRef]
- Xiao, W.; Zhang, W.; Ye, Y.; Lv, X.; Yang, W. Is underground coal mining causing land degradationand significantly damaging ecosystems in semi-arid areas? A study from an Ecological Capital perspective. Land Degrad. Dev. 2020, 31, 1969–1989. [Google Scholar] [CrossRef]
- Zembaty, Z.; Kokot, S.; Bozzoni, F.; Scandella, L.; Lai, C.G.; Kuś, J.; Bobra, P. A system to mitigate deep mine tremor effects in the design of civil infrastructure. Int. J. Rock Mech. Min. Sci. 2015, 74, 81–90. [Google Scholar] [CrossRef]
- He, Y.; Yan, H.; Yang, W.; Yao, S.; Zhang, L.; Chen, Y. Time-Series Analysis and Prediction of Surface Deformation in the Jinchuan Mining Area, Gansu Province, by Using InSAR and CNN–PhLSTM Network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6732–6751. [Google Scholar] [CrossRef]
- Huang, C.; Xia, J.; Hu, J. Surface Deformation Monitoring in Coal Mine Area Based on PSI. IEEE Access 2019, 7, 29672–29678. [Google Scholar] [CrossRef]
- Hradil, P.; Kaláb, Z.; Knejzlík, J.; Kořínek, R.; Salajka, V.; Kanický, V. Response of a panel building to mining induced seismicity in Karvina area (Czech Republic). Acta Montan. Slovaca 2009, 14, 143–151. [Google Scholar]
- Boroń, P.; Dulińska, J.M.; Jasińska, D. Impact of High Energy Mining-Induced Seismic Shocks from Different Mining Activity Regions on a Multiple-Support Road Viaduct. Energies 2020, 13, 4045. [Google Scholar] [CrossRef]
- Pachla, F.; Kowalska-Koczwara, A.; Tatara, T.; Stypuła, K. The influence of vibration duration on the structure of irregular RC buildings. Bull. Earthq. Eng. 2019, 17, 3119–3138. [Google Scholar] [CrossRef]
- Bal, I.; Dais, D.; Smyrou, E. “Differences” between induced and natural seismic events. In Proceedings of the 16th European Conference on Earthquake Engineering, (16ECEE), Thessaloniki, Greece, 18–21 June 2018. [Google Scholar]
- Li, N.; Li, B.; Chen, D.; Wang, E.; Tan, Y.; Qian, Y.; Jia, H. Waveform characteristics of earthquakes induced by hydraulic fracturing and mining activities: Comparison with those of natural earthquakes. Nat. Resour. Res. 2020, 29, 3653–3674. [Google Scholar] [CrossRef]
- Liu, D.; Lu, W.; Liu, Y.; Chen, M.; Yan, P.; Sun, P. Analysis of the Main Factors Influencing the Dominant Frequency of Blast Vibration. Shock. Vib. 2019, 17, 8480905. [Google Scholar] [CrossRef]
- Tatara, T. Dynamic Resistance of Building Under Mining Tremors; Cracow University of Technology Press: Krakow, Poland, 2012. (In Polish) [Google Scholar]
- Tatara, T.; Pachla, F. Analysis of the Dynamic Response of Masonry Buildings with Irregularities of Localization of Bearing Elements Due to Mining Shocks. In Seismic Behaviour and Design of Irregular and Complex Civil Structures II; Geotechnical, Geological and Earthquake Engineering; Zembaty, Z., De Stefano, M., Eds.; Springer: Cham, Switzerland, 2016; Volume 40. [Google Scholar] [CrossRef]
- Gad, E.F.; Wilson, J.L.; Moore, A.J.; Richards, A.B. Effects of Mine Blasting on Residential Structures. J. Perform. Constr. Fac. 2005, 19, 222–228. [Google Scholar] [CrossRef]
- Kumar, S.; Dutta, S.; Goswami, K.; Mandal, P. Vulnerability assessment of building structures due to underground blasts using ANN and non-linear dynamic analysis. J. Build. Eng. 2021, 44, 102674. [Google Scholar] [CrossRef]
- Hajali, M.; Abishdid, C. Finite Element Evaluation of Modal Stresses in Cantilever Highway Sign Structures. In Advances in Hurricane Engineering: Learning from Our Past; Jones, C.P., Lawrence, P.E., Griffis, G., Eds.; Advances in Hurricane Engineering; ASCE: Reston, VA, USA, 2012. [Google Scholar] [CrossRef]
- Barle, J.; Grubisic, V.; Vlak, F. Failure analysis of the highway sign structure and the design improvement. Eng. Fail. Anal. 2011, 18, 1076–1084. [Google Scholar] [CrossRef]
- Rice, J.A.; Foutch, D.A.; LaFave, J.M.; Valdovinos, S. Field testing and analysis of aluminum highway sign trusses. Eng. Struct. 2012, 34, 173–186. [Google Scholar] [CrossRef]
- Ngamkhanong, C.; Kaewunruen, S. The effect of ground borne vibrations from high speed train on overhead line equipment (OHLE) structure considering soil-structure interaction. Sci. Total Environ. 2018, 627, 934–941. [Google Scholar] [CrossRef]
- Zalewski, B.; Huckelbridge, A. Dynamic Load Environment of Bridge-Mounted Sign Support Structures. Report No. ST/SS/05-002 for the Ohio Department of Transportation Office of Research and Development, State Job Number 134153. September 2005. Available online: https://rosap.ntl.bts.gov/view/dot/17527 (accessed on 1 March 2025).
- Alic, D.D.; Miklos, I.Z.; Miklos, C.C. Numerical Investigation on the Modal Analysis of Truss Type Highway Sign Support Structures. In Machine and Industrial Design in Mechanical Engineering. KOD 2024; Rackov, M., Miltenović, A., Banić, M., Eds.; Mechanisms and Machine Science; Springer: Cham, Switzerland, 2025; Volume 174. [Google Scholar] [CrossRef]
- Kim, T.; Hong, S.; Oh, J.; Roh, H. Investigation of Seismic Responses of Single- and Bi-Directional Traffic Light Poles EESK. J. Earthq. Eng. 2022, 26, 219–226. [Google Scholar] [CrossRef]
- Siringoringo, D.M.; Fujino, Y.; Nagasaki, A.; Matsubara, T. Seismic performance evaluation of existing light poles on elevated highway bridges. Struct. Infrastruct. E 2020, 17, 649–663. [Google Scholar] [CrossRef]
- Zhang, R.; Liu, C.; Gou, W.; Liu, Q. Comprehensive performance analysis and optimal design of smart light pole for cooperative vehicle infrastructure system. Nanotechnol. Rev. 2021, 10, 904–918. [Google Scholar] [CrossRef]
- Barros, R.C.; Paiva, M.F. Seismic Response Control of a Cantilevered Highway Sign Support, Using a TMD. Int. J. Civ. Eng. 2017, 6, 51–60. [Google Scholar]
- Li, R.S. A Methodology for Fatigue Prediction of Electronic Components Under Random Vibration Load. ASME J. Electron. Packag. 2001, 123, 394–400. [Google Scholar] [CrossRef]
- Pitarresi, J.M.; Caletka, D.V.; Caldwell, R.; Smith, D.E. The “Smeared” Property Technique for the FE Vibration Analysis of Printed Circuit Cards. ASME J. Electron. Packag. 1991, 113, 250–257. [Google Scholar] [CrossRef]
- Kim, Y.J.; Koo, J.C.; Moon, S.I.; Kim, Y.J. An effective method for measuring elastic modulus of large TFT-LCD panels. Key Eng. Mat. 2004, 270–273, 1767–1772. [Google Scholar] [CrossRef]
- Reynders, E. System Identification Methods for (Operational) Modal Analysis: Review and Comparison. Arch. Computat. Methods Eng. 2012, 19, 51–124. [Google Scholar] [CrossRef]
- Zahid, F.B.; Ong, Z.C.; Khoo, S.Y. A review of operational modal analysis techniques for in-service modal identification. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 398. [Google Scholar] [CrossRef]
- Van Overschee, P.; De Moor, B. Subspace Identification for Linear Systems: Theory—Implementation—Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1996. [Google Scholar]
- Pan, H.; Li, Y.; Deng, T.; Fu, J. An improved stochastic subspace identification approach for automated operational modal analysis of high-rise buildings. J. Build. Eng. 2024, 89, 109267. [Google Scholar] [CrossRef]
- Kim, B.; Stubbs, N.; Park, T. A new method to extract modal parameters using output-only responses. J. Sound. Vib. 2005, 282, 215–230. [Google Scholar] [CrossRef]
- De Moor, B.; van Overshee, P.; Suykens, J. Subspace algorithms for system identification and stochastic realization. ESAT—SISTA Report 1990-28. In Proceedings of the MTNS, Kobe, Japan, 17–21 June 1991; pp. 17–21. [Google Scholar]
- Allemang, R.J.; Brown, D.L. A Complete review of the Complex Mode Indicator Function (CMIF) with applications. In Proceedings of the ISMA2006: International Conference on Noise and Vibration Engineering, Leuven, Belgium, 18–20 September 2006. [Google Scholar]
- Lin, C.S. System Identification of Structures with Severe Closely Spaced Modes Using Parametric Estimation Algorithms Based on Complex Mode Indicator Function with Singular Value Decomposition. KSCE J. Civ. Eng. 2020, 24, 2716–2730. [Google Scholar] [CrossRef]
- Rainieri, C.; Fabbrocino, G. Operational Modal Analysis of Civil Engineering Structures. An Introduction and Guide for Applications; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Hasani, H.; Freddi, F. Operational Modal Analysis on Bridges: A Comprehensive Review. Infrastructures 2023, 8, 172. [Google Scholar] [CrossRef]
- Greś, S.Z.; Döhler, M.; Mevel, L. Uncertainty quantification of the Modal Assurance Criterion in operational modal analysis. Mech. Syst. Signal Process. 2021, 152, 107457. [Google Scholar] [CrossRef]
- Allemang, R.J. The Modal Assurance Criterion–Twenty Years of Use And Abuse. Sound. Vib. 2003, 37, 14–23. [Google Scholar]
- Casiano, M.J.; George, C.M. Extracting Damping Ratio from Dynamic Data and Numerical Solutions; National Aeronautics and Space Administration, Marshall Space Flight Center: Huntsville, AL, USA, 2016.
- Abaqus/Standard User’s Manual; Dassault Systèmes Simulia Corp.: Johnston, RI, USA, 2020.
- EN 1998-2; Eurocode 8: Design of Structures for Earthquake Resistance—Part 2: Bridges. CEN: Brussels, Belgium, 2005.
- Cruz, C.; Miranda, E. A Critical Review of the Rayleigh Damping Model, In Proceedings of the 16th World Conference on Earthquake, (16WCEE), Santiago, Chile, 9–13 January 2017.
- Savinov, O. Modern Foundations Structure for Machines and Their Calculations; Stroyizdat Press: Leningrad, Russia, 1979. [Google Scholar]
- Drygala, I.J.; Dulińska, J.M.; Nisticò, N.; Tatara, T. Impact of Dynamic Soil-Structure Interaction on Performance of a Single Span Footbridge with Overhangs Subjected to Mining-Induced Shocks. Materials 2022, 15, 9084. [Google Scholar] [CrossRef] [PubMed]
- PN-80/B-03040; Machine Foundations and Supporting Structures. Calculation and Design; Polish Committee for Standardization: Warsaw, Poland, 1980.
- Stec, K. Causes of the occurrence of high-energy seismic events based on focal mechanism parameters. Zesz. Nauk. Inst. Gospod. Surowcami Miner. Energ. PAN 2017, 101, 19–32. [Google Scholar]
- Asnaashari, E.; Morris, A.; Andrew, I.; Hahn, W.; Sinha, J.K. Finite Element Modelling and In Situ Modal Testing of an Offshore Wind Turbine. J. Vib. Eng. Technol. 2018, 6, 101–106. [Google Scholar] [CrossRef]
- Bautista-De Castro, A.; Sánchez-Aparicio, L.H.; Ramos, L.F.; Sena-Cruz, J.; González-Aguilera, D. Integrating geomatic approaches, Operational Modal Analysis, advanced numerical and updating methods to evaluate the current safety conditions of the historical Bôco Bridge. Constr. Build. Mater. 2018, 158, 961–984. [Google Scholar] [CrossRef]
- Kaczinski, M.; Dexter, R.; Van Dien, J. Fatigue-Resistant Design of Cantilevered Signal, Sign, and Light Supports; National Cooperative Highway Research Program, National Research Council (U.S.); Transportation Research Board: Washington, DC, USA, 1998. [Google Scholar]
- Hamilton, H.R., III; Riggs, G.S.; Puckett, J.A. Increased Damping in Cantilevered Traffic Signal Structures. J. Struct. Eng. 2000, 126, 530–537. [Google Scholar] [CrossRef]
- Cook, R.A.; Bloomquist, D.; Richard, D.S.; Kalajian, M.A. Damping of Cantilevered Traffic Signal Structures. J. Struct. Eng. 2001, 127, 1476–1483. [Google Scholar] [CrossRef]
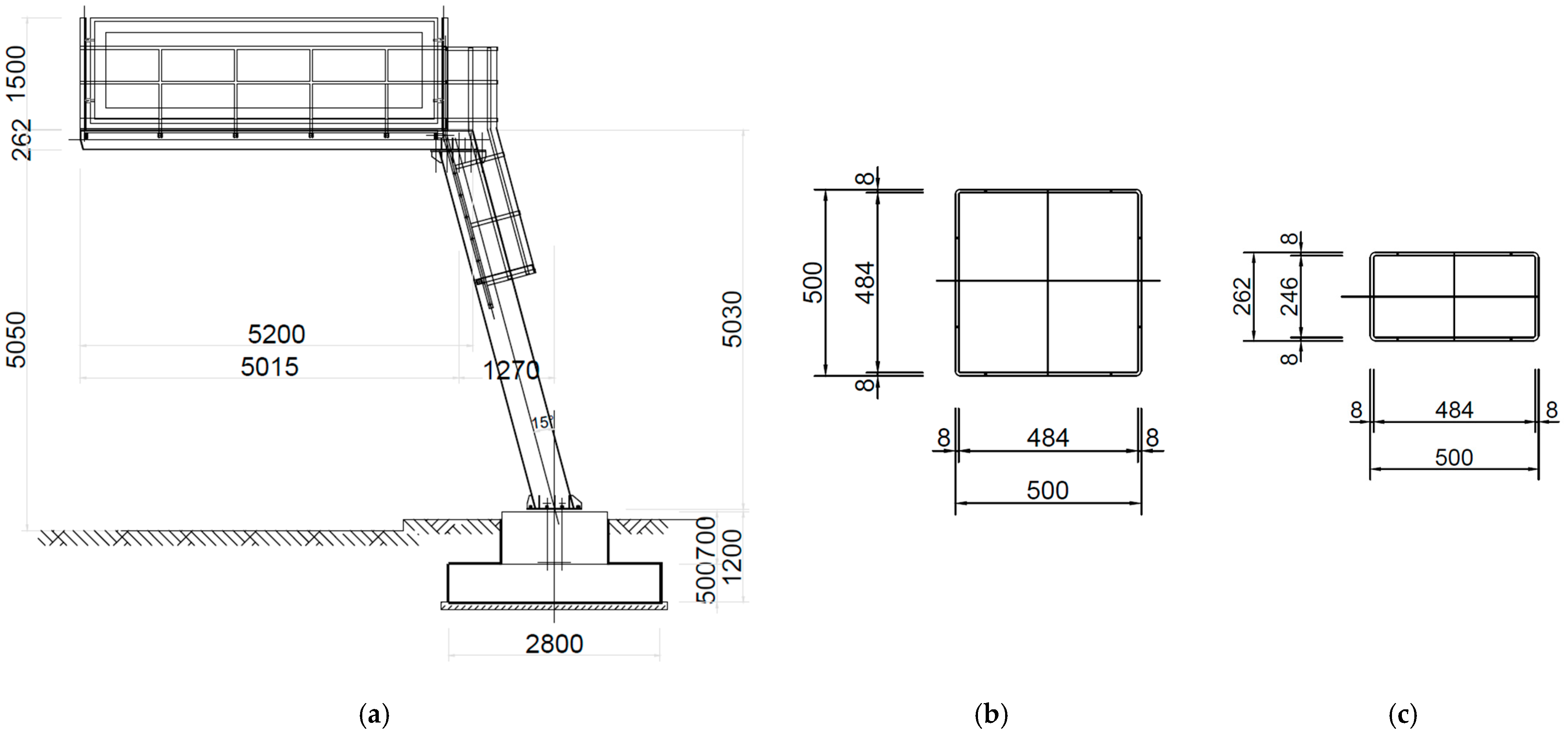


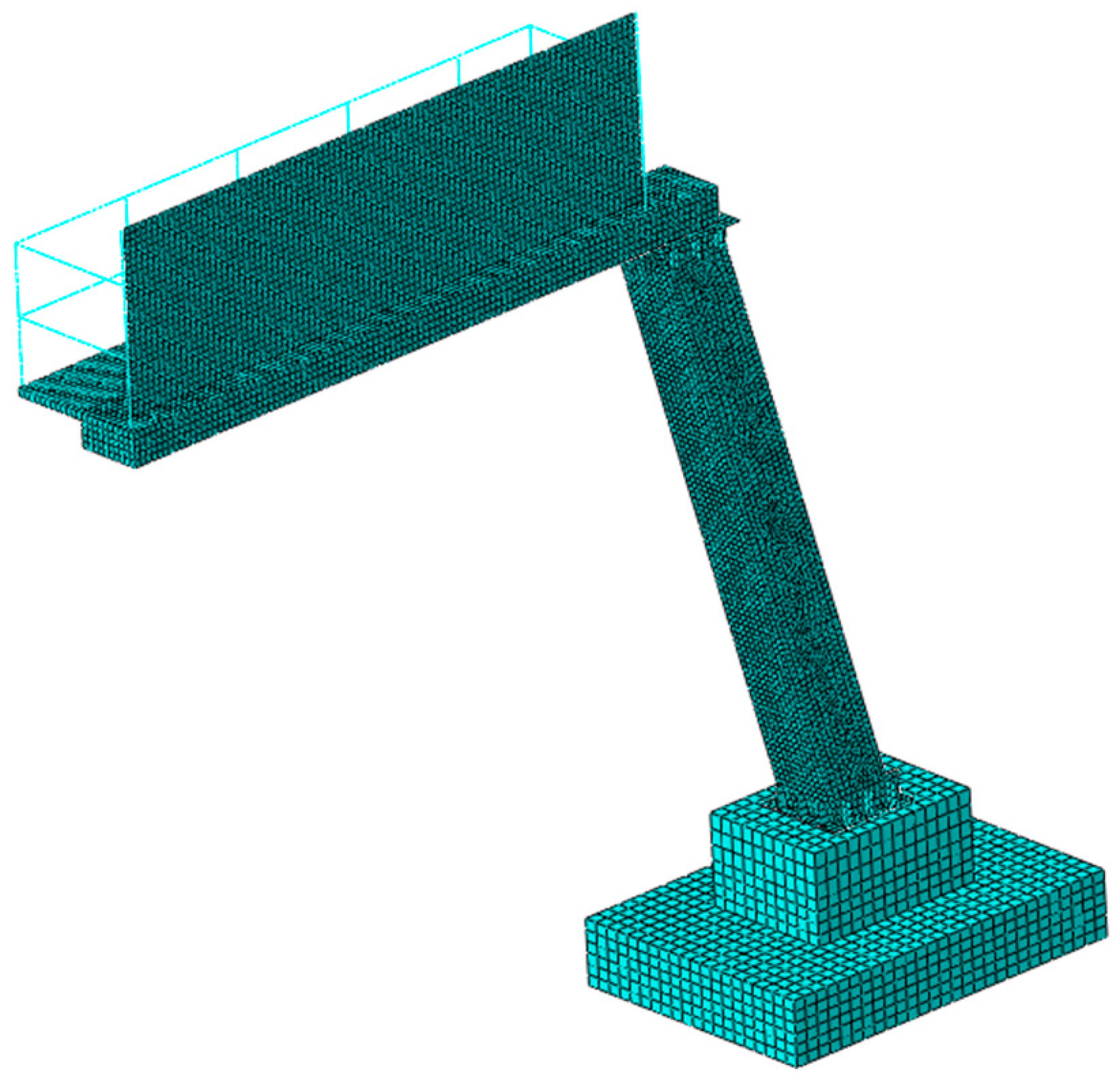
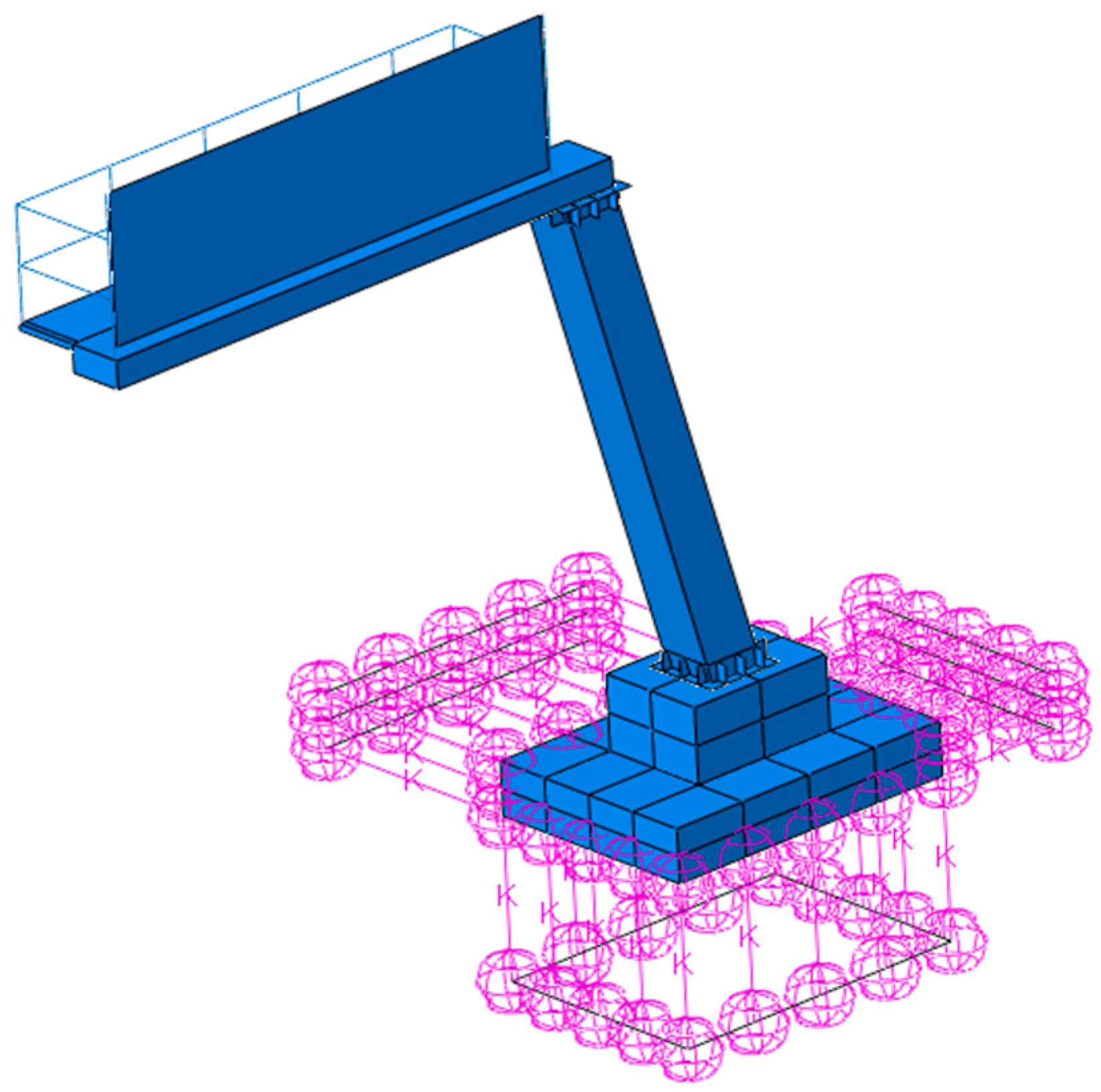



| Structural Element | Material Type | Density [kg/m3] | Young Modulus [GPa] | Poisson Ratio [-] | Yield Stress [MPa] |
|---|---|---|---|---|---|
| Foundation block | Concrete C20/25 | 2500 | 25 | 0.15 | 8 |
| Load-bearing structure | Steel St3SX | 7850 | 190 | 0.3 | 235 |
| Electronic signboard | Multi-material | 260 | 25 | 0.3 | 50 |
| Test Label | Test Purpose | Description | Mathematical Tools Used in Analyses |
|---|---|---|---|
| T1_OMA | Natural frequencies and mode shapes identification | Ambient vibrations caused by vehicle movements in heavy traffic, lasting for 10 min | Stochastic Subspace Identification (SSI) Complex Mode Indicator Function (CMIF) Time Domain Decomposition (TDD) Modal Assurance Criterion (MAC) |
| T2_OMA | Natural frequencies and mode shapes identification | Ambient vibrations caused by vehicle movements in light traffic, lasting for 10 min | |
| T3_HAM | Damping properties evaluation | Modal hammer impacts parallel to the road axis (Y-direction) | ) ) |
| T4_HAM | Damping properties evaluation | Modal hammer impacts perpendicular to the road axis (X-direction) |
| Parameter | The Szombierki Shock | The Moskorzyn Shock |
|---|---|---|
| Location | Upper Silesian Coal Basin | Legnica-Glogow Copper District |
| Duration | 6 s | 5 s |
| Strong intensity phase | 3 s | 2 s |
| Shock energy | 1 × 107 J | 5 × 107 J |
| PGA (WE) | 0.35 m/s2 | 0.8 m/s2 |
| PGA (NS) | 0.28 m/s2 | 0.37 m/s2 |
| PGA (vertical) | 0.12 m/s2 | 0.45 m/s2 |
| Dominant frequency range | 1.6–4.8 Hz (all directions) with a peak at 3.5 Hz | 5–10 Hz (all directions) with a peak at 7 Hz |
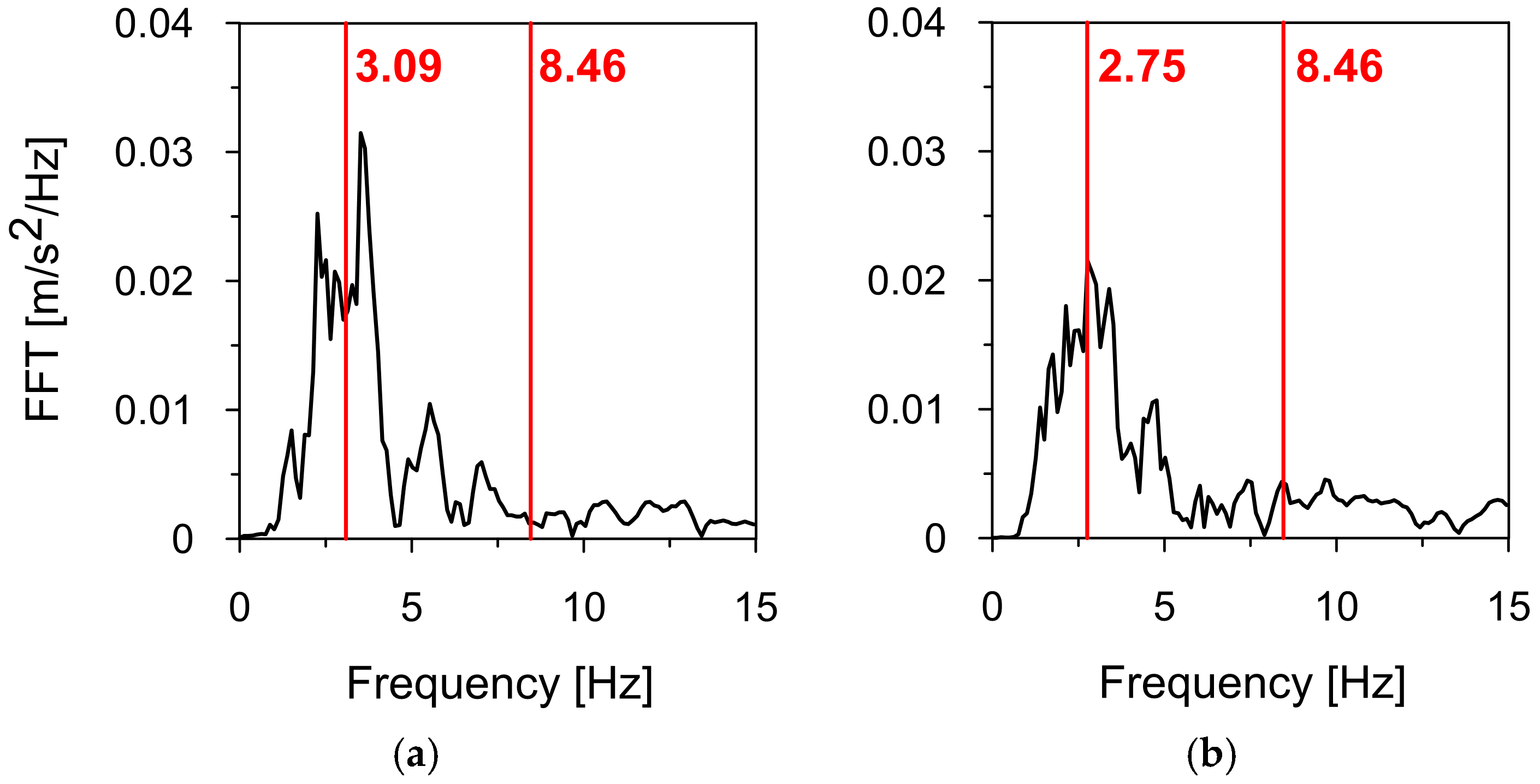
| Natural Frequency (Hz) Estimated Numerically for: | |||
|---|---|---|---|
| 1st Mode | 2nd Mode | 3rd Mode | 4th Mode |
| 2.75 | 3.09 | 8.46 | 13.50 |
| Experimental Test | Natural Frequency (Hz) Related to: | |||
|---|---|---|---|---|
| 1st Mode | 2nd Mode | 3rd Mode | 4th Mode | |
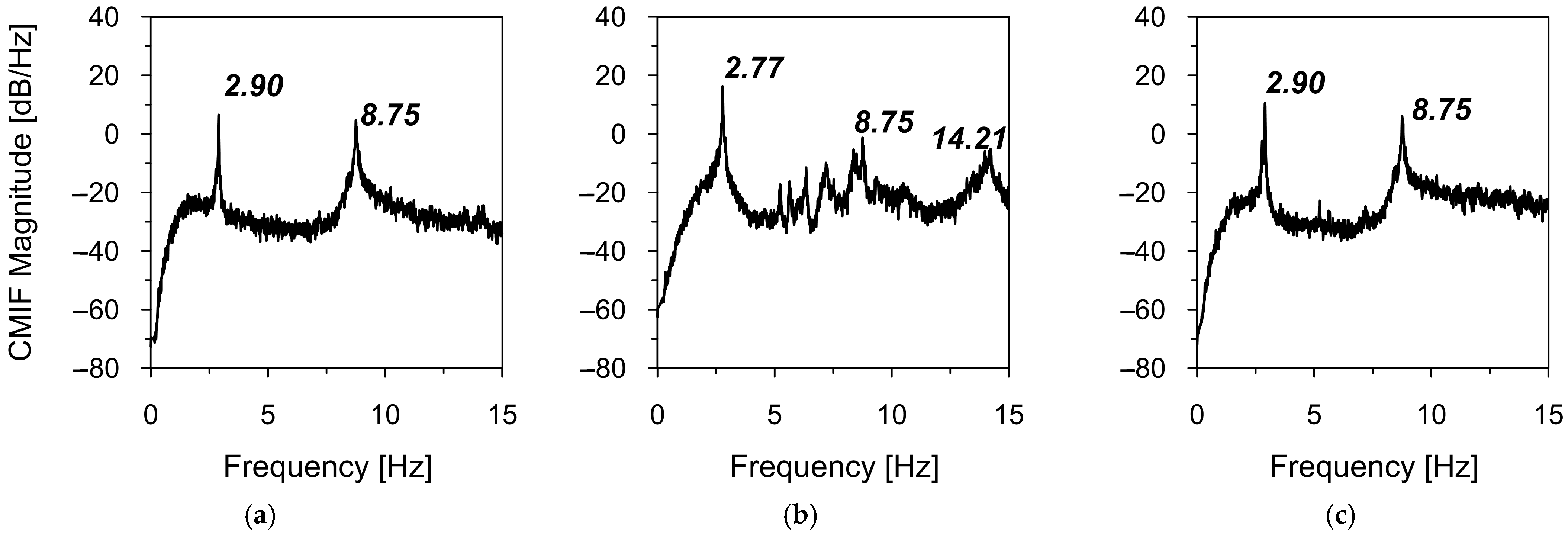
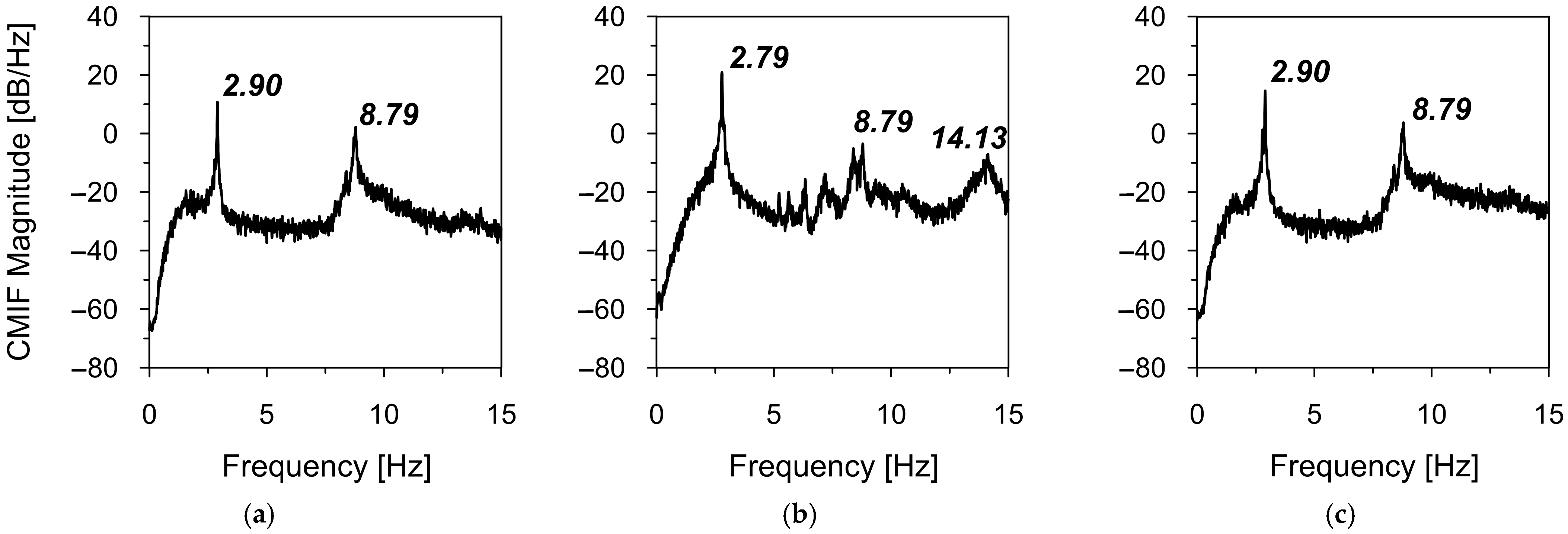
| T1_OMA | 2.77 | 2.90 | 8.75 | 14.21 |
| T2_OMA | 2.79 | 2.90 | 8.78 | 14.13 |
| Mode No. | Numerical Frequency [Hz] | Experimental Frequency [Hz] | Error [%] |
|---|---|---|---|
| 1 | 2.75 | 2.77 | 0.7 |
| 2 | 3.08 | 2.90 | 6.2 |
| 2 | 8.46 | 8.75 | 3.3 |
| 4 | 13.50 | 14.21 | 4.9 |
| Test | Strike No. | Damping Properties for the First Mode Shape | Damping Properties for the Second Mode Shape | ||
|---|---|---|---|---|---|
| [-] | Damping [-] | [-] | Damping [-] | ||
| T3_HAM | 1 | 0.254 | 0.0405 | 0.272 | 0.0432 |
| 2 | 0.223 | 0.0355 | 0.261 | 0.0416 | |
| 3 | 0.232 | 0.0369 | 0.236 | 0.0376 | |
| 4 | 0.230 | 0.0366 | 0.224 | 0.0357 | |
| 5 | 0.243 | 0.0387 | 0.221 | 0.0351 | |
| T4_HAM | 1 | 0.271 | 0.0432 | 0.230 | 0.0367 |
| 2 | 0.243 | 0.0387 | 0.225 | 0.0358 | |
| 3 | 0.218 | 0.0347 | 0.195 | 0.0311 | |
| 4 | 0.251 | 0.0400 | 0.231 | 0.0368 | |
| 5 | 0.217 | 0.0346 | 0.236 | 0.0376 | |
| Average value | 0.238 | 0.0379 | 0.233 | 0.0371 | |
| Element | Maximal Von Mises Stress [MPa] | Ratio | |
|---|---|---|---|
| Moskorzyn | Szombierki | Szombierki/ Moskorzyn | |
| E1 | 1.24 | 2.21 | 1.79 |
| E2 | 1.00 | 2.59 | 2.58 |
| E3 | 0.61 | 3.12 | 5.14 |
| E4 | 0.49 | 0.99 | 2.01 |
| E5 | 0.69 | 0.70 | 1.01 |
| E6 | 2.33 | 3.03 | 1.30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boroń, P.; Dulińska, J.M. Dynamic Performance of a Steel Road Sign with Multi-Material Electronic Signboard Under Mining-Induced Tremors from Different Mining Areas: Experimental and Numerical Research. Materials 2025, 18, 1451. https://doi.org/10.3390/ma18071451
Boroń P, Dulińska JM. Dynamic Performance of a Steel Road Sign with Multi-Material Electronic Signboard Under Mining-Induced Tremors from Different Mining Areas: Experimental and Numerical Research. Materials. 2025; 18(7):1451. https://doi.org/10.3390/ma18071451
Chicago/Turabian StyleBoroń, Paweł, and Joanna Maria Dulińska. 2025. "Dynamic Performance of a Steel Road Sign with Multi-Material Electronic Signboard Under Mining-Induced Tremors from Different Mining Areas: Experimental and Numerical Research" Materials 18, no. 7: 1451. https://doi.org/10.3390/ma18071451
APA StyleBoroń, P., & Dulińska, J. M. (2025). Dynamic Performance of a Steel Road Sign with Multi-Material Electronic Signboard Under Mining-Induced Tremors from Different Mining Areas: Experimental and Numerical Research. Materials, 18(7), 1451. https://doi.org/10.3390/ma18071451






