Thermal Insulation Efficiency and Mechanisms of Flexible Sandwich Structure
Abstract
1. Introduction
2. Experimental Procedure
2.1. Materials and Characterization
2.2. The Designing of Sandwich Structure Composite
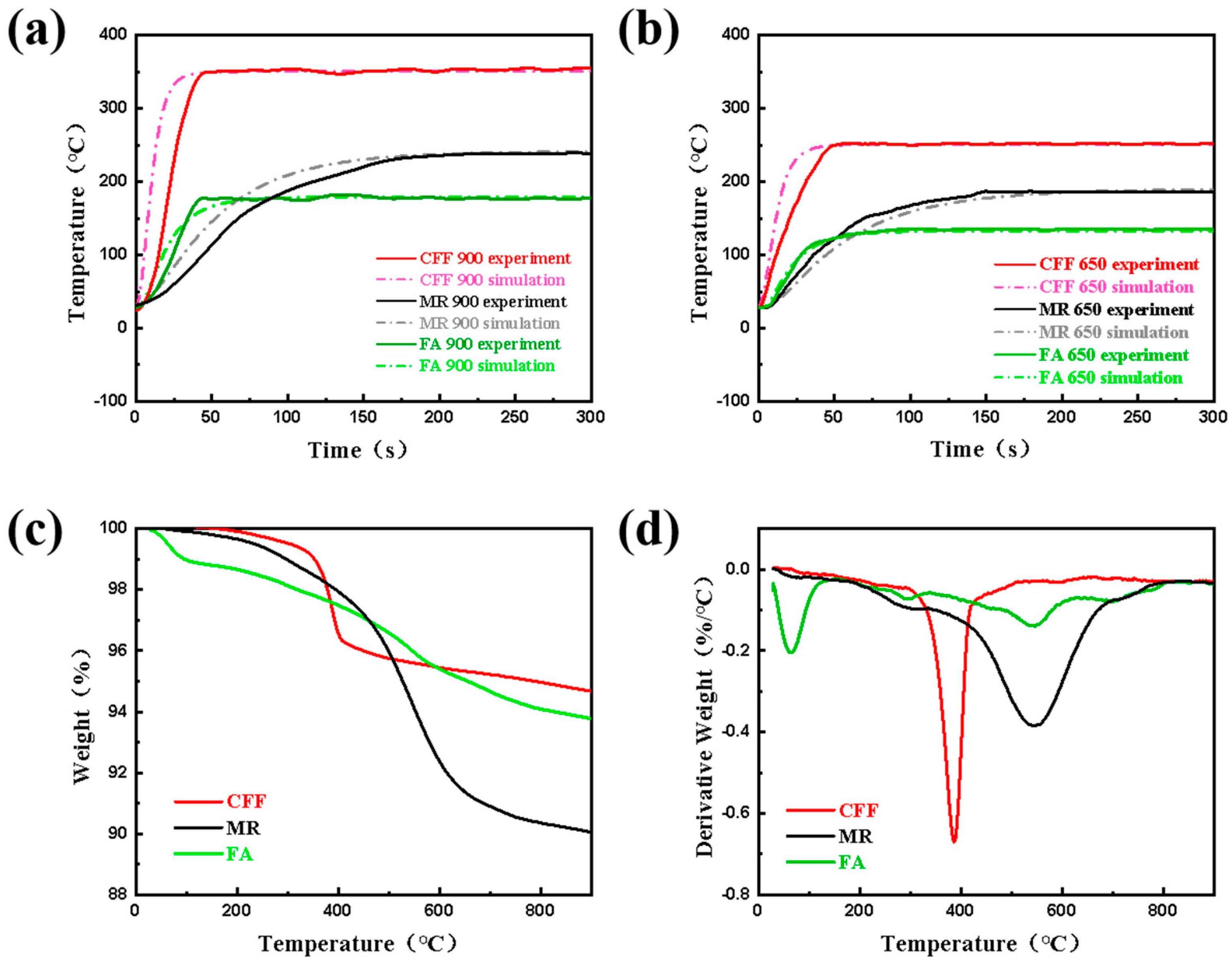
3. Numerical Simulation of Temperature Variations on the Cold Side Surface
4. Results and Discussion
4.1. Thermal Stability and Flame Retardancy
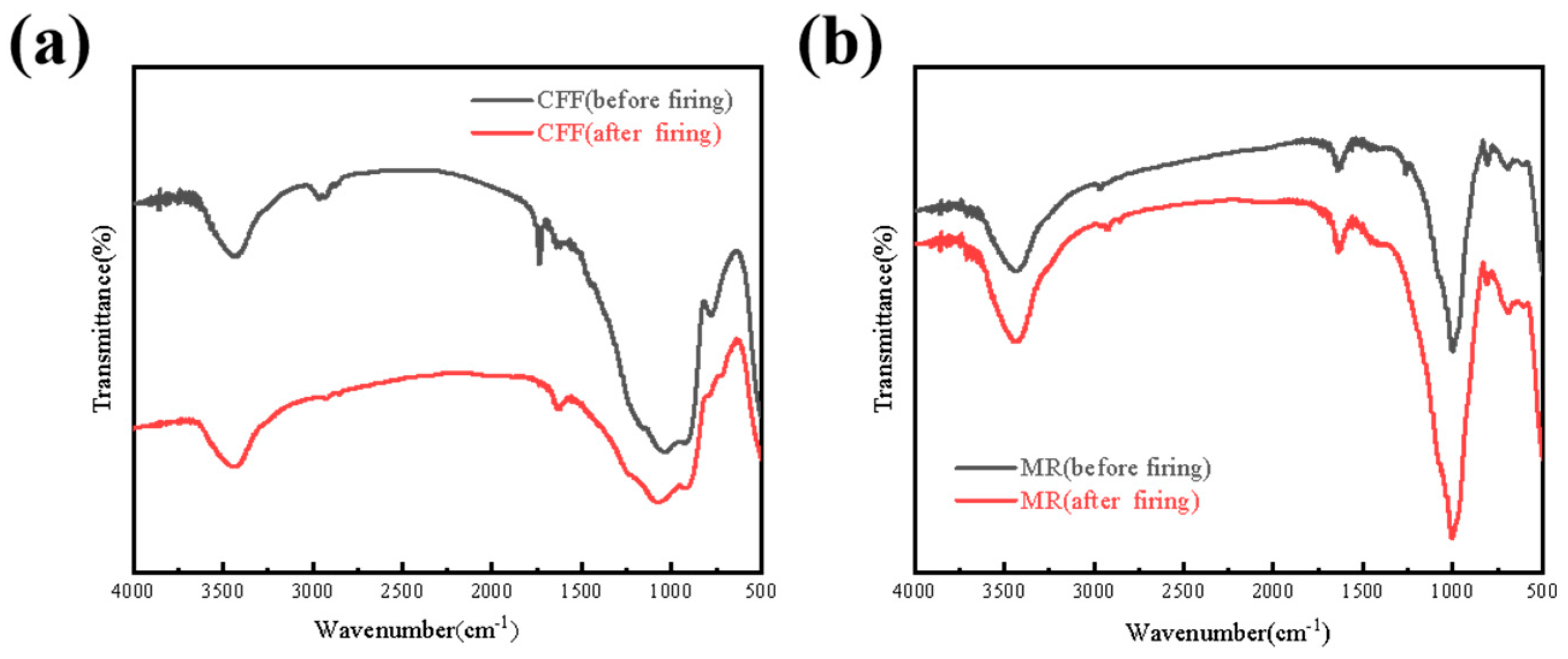
4.2. Analysis of the Heat Insulation Mechanisms
4.2.1. Structure Variations in Ceramic Fiber Felts
4.2.2. Microscopic Morphology of Ceramic Fiber Felts
4.2.3. FT-IR of CFF and MR
4.3. Heat Transfer Mechanism of Sandwich Structures
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Al-Zareer, M.; Dincer, I.; Rosen, M.A. A review of novel thermal management systems for batteries. Int. J. Energy Res. 2018, 42, 3182–3205. [Google Scholar] [CrossRef]
- Yu, H.; Mu, X.; Zhu, Y.; Liao, C.; Han, L.; Wang, J.; Cai, W.; Kan, Y.; Song, L.; Hu, Y. Sandwich structured ultra-strong-heat-shielding aerogel/copper composite insulation board for safe lithium-ion batteries modules. J. Energy Chem. 2023, 76, 438–447. [Google Scholar] [CrossRef]
- Li, H.; Song, L.; Sun, C.; Li, R.; Fu, Y.; Zhang, H.; Yang, A.; Liu, H. Thermal insulation of silica aerogel/PMMA composites with amino-capped polydivinylsiloxane phase interfaces. Sci. Eng. Compos. Mater. 2018, 25, 1107–1114. [Google Scholar] [CrossRef]
- Lin, W.-Q.; Zhang, Y.-X.; Wang, H. Thermal conductivity of unidirectional composites consisting of randomly dispersed glass fibers and temperature-dependent polyethylene matrix. Sci. Eng. Compos. Mater. 2019, 26, 412–422. [Google Scholar] [CrossRef]
- Park, K.-J.; Kim, J.-H.; Kim, S.-K.; Heo, H.-S.; Bae, J.-H.; Lee, J.-M. Material characteristics of random glass-mat-reinforced thermoplastic under cryogenic thermal cycles. Sci. Eng. Compos. Mater. 2019, 26, 270–281. [Google Scholar] [CrossRef]
- Li, Z.; Zhang, X.; Ren, J.; Zhang, M.; Pei, C. Flame-retardant cellulose composites from multilayer bacterial cellulose hydrogels stitched by interfacial gelation. Prog. Org. Coat. 2025, 200, 109088. [Google Scholar] [CrossRef]
- Yuan, C.; Wang, Q.; Wang, Y.; Zhao, Y. Inhibition effect of different interstitial materials on thermal runaway propagation in the cylindrical lithium-ion battery module. Appl. Therm. Eng. 2019, 153, 39–50. [Google Scholar] [CrossRef]
- Sun, X.; Dong, Y.; Sun, P.; Zheng, B. Effects of thermal insulation layer material on thermal runaway of energy storage lithium battery pack. J. Energy Storage 2024, 76, 109812. [Google Scholar] [CrossRef]
- Liu, F.; Wang, J.; Yang, N.; Wang, F.; Chen, Y.; Lu, D.; Liu, H.; Du, Q.; Ren, X.; Shi, M. Experimental study on the alleviation of thermal runaway propagation from an overcharged lithium-ion battery module using different thermal insulation layers. Energy 2022, 257, 124768. [Google Scholar] [CrossRef]
- Kovács, Z.; Csík, A.; Lakatos, Á. Thermal stability investigations of different aerogel insulation materials at elevated temperature. Therm. Sci. Eng. Prog. 2023, 42, 101906. [Google Scholar] [CrossRef]
- Yu, Y.; Li, Z.; Wei, Z.; Chen, S.; Huang, Z.; Fang, Z.; Li, Y.; Wang, J.; Mei, W.; Wang, Q. Enhancing battery module safety with insulation material: Hollow glass microspheres incorporating aerogel of varying particle sizes. Chem. Eng. J. 2023, 478, 147400. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Z.; Yu, S.; Awuye, D.E.; Li, B.; Liao, J.; Luo, R. Improved sandwich structured ceramic matrix composites with excellent thermal insulation. Compos. Part B Eng. 2017, 129, 180–186. [Google Scholar] [CrossRef]
- Du, F.; Jin, Z.; Yang, R.; Hao, M.; Wang, J.; Xu, G.; Zuo, W.; Geng, Z.; Pan, H.; Li, T.; et al. Thermally insulating and fire-retardant bio-mimic structural composites with a negative Poisson’s ratio for battery protection. Carbon Energy 2023, 5, e353. [Google Scholar] [CrossRef]
- Kim, R.H.; Lee, D.H.; Kim, Y.K.; Chu, C.H.; Lee, Y.G.; Kim, D.K. Numerical analysis of thermal runaway process of lithium-ion batteries considering combustion. J. Energy Storage 2024, 78, 110041. [Google Scholar] [CrossRef]
- Srinivasan, R.; Thomas, M.E.; Airola, M.B.; Carkhuff, B.G.; Frizzell-Makowski, L.J.; Alkandry, H.; Reuster, J.G.; Oguz, H.N.; Green, P.W.; La Favors, J.; et al. Preventing Cell-to-Cell Propagation of Thermal Runaway in Lithium-Ion Batteries. J. Electrochem. Soc. 2020, 167, 020559. [Google Scholar] [CrossRef]
- Yan, J.; Wang, Q.; Li, K.; Sun, J. Numerical study on the thermal performance of a composite board in battery thermal management system. Appl. Therm. Eng. 2016, 106, 131–140. [Google Scholar] [CrossRef]
- Meng, J.-H.; Gao, D.-Y.; Liu, Y.; Zhang, K.; Lu, G. Heat transfer mechanism and structure design of phase change materials to improve thermoelectric device performance. Energy 2022, 245, 123332. [Google Scholar] [CrossRef]
- Martias, C.; Joliff, Y.; Favotto, C. Effects of the addition of glass fibers, mica and vermiculite on the mechanical properties of a gypsum-based composite at room temperature and during a fire test. Compos. Part B Eng. 2014, 62, 37–53. [Google Scholar] [CrossRef]
- Feng, J.; Wang, Y.; Feng, X.; Huang, Q.; Ma, S.; Mo, W.; Yang, J.; Su, X.; Lin, M. Radiative heat attenuation mechanisms for nanoporous thermal insulating composites. Appl. Therm. Eng. 2016, 105, 39–45. [Google Scholar] [CrossRef]
- Guo, Z.; Zhu, Z.; Zhang, X.; Peng, Y.; Huang, Z.; Wang, X.; Zhu, L.; Xie, Y.; Zhang, G.; Liu, B.; et al. Ultra-flexible TiO2/SiO2 nanofiber membranes with layered structure for thermal insulation. J. Mater. 2025, 11, 100856. [Google Scholar] [CrossRef]
- Wan, X.; Fan, J. Heat transfer through fibrous assemblies incorporating reflective interlayers. Int. J. Heat Mass Transf. 2012, 55, 8032–8037. [Google Scholar] [CrossRef]
- Mirzaei, A.; Shokrieh, M. Evolution of the temperature rise and damage in laminated composites with stress concentration under fatigue loading. Compos. Part B Eng. 2023, 254, 110607. [Google Scholar] [CrossRef]
- Lakatos, Á.; Kovács, Z. Comparison of thermal insulation performance of vacuum insulation panels with EPS protection layers measured with different methods. Energy Build. 2021, 236, 110771. [Google Scholar] [CrossRef]
- Pan, X.-F.; Gao, H.-L.; Lu, Y.; Wu, C.-Y.; Wu, Y.-D.; Wang, X.-Y.; Pan, Z.-Q.; Dong, L.; Song, Y.-H.; Cong, H.-P.; et al. Transforming ground mica into high-performance biomimetic polymeric mica film. Nat. Commun. 2018, 9, 2974. [Google Scholar] [CrossRef]
- Ren, Y.; Liang, X.; Li, Q.; Hu, H.; Tang, A.; Yang, H. Significantly Enhanced the Energy Density of Dielectric Composites by Sandwich Structure with Highly Insulating Mica Nanosheets. Small 2023, 20, e2308276. [Google Scholar] [CrossRef]
- Imjai, T.; Kefyalew, F.; Garcia, R.; Kim, B.; Bras, A.; Sukontasukkul, P. Performance of a novel structural insulated panel in tropical climates: Experimental and numerical studies. Constr. Build. Mater. 2024, 421, 135568. [Google Scholar] [CrossRef]
- Zhang, T.; Yuan, J.; Pang, H.; Huang, Z.; Guo, Y.; Wei, J.; Yu, Q. UHPC-XPS insulation composite board reinforced by glass fiber mesh: Effect of structural design on the heat transfer, mechanical properties and impact resistance. J. Build. Eng. 2023, 75, 106935. [Google Scholar] [CrossRef]
- Huang, L.; Geng, X.; Li, H.; Jia, K.; Liu, J.; Xue, Z.; Aydeng, A.; Xi, W.; Liang, H. Thermal Response of Carbon Fiber Reinforced Polyimide Composite Laminate Coated with Highly Oriented Graphite Film Under Heating on Single Side. Appl. Compos. Mater. 2023, 30, 857–870. [Google Scholar] [CrossRef]
- Yang, S.; Zheng, Y.; Xue, L.; He, Z.; Wang, R.; Li, N.; Zheng, K.; Ren, Y. Numerical Simulation of the Thermal Response of the Composite Layer of Type III Gas Cylinders Under Local Thermal Impacts. Appl. Compos. Mater. 2024, 1–20. [Google Scholar] [CrossRef]
- Badshah, H.; Kumar, R.; Kumar, P.; Zafar, S. Cure Kinetic Modelling and Experimental Analysis to Predict Temperature Distribution during Microwave Curing of Carbon Fiber Composites. Appl. Compos. Mater. 2024, 31, 1741–1766. [Google Scholar] [CrossRef]
- Marszałek, J.; Stadnicki, J.; Danielczyk, P. Finite element model of laminate construction element with multi-phase microstructure. Sci. Eng. Compos. Mater. 2020, 27, 405–414. [Google Scholar] [CrossRef]
- Yang, J.; Wang, D.; Li, M.; Ji, C.; Wang, B. Thermal response and pyrolysis behavior of carbon fiber/phthalonitrile composites under one-sided butane flame heating: Experimental and numerical analysis. Compos. Part A Appl. Sci. Manuf. 2023, 175, 107788. [Google Scholar] [CrossRef]
- Bifulco, A.; Climaco, I.; Casciello, A.; Passaro, J.; Battegazzore, D.; Nebbioso, V.; Russo, P.; Imparato, C.; Aronne, A.; Malucelli, G. Prediction and validation of fire parameters for a self-extinguishing and smoke suppressant electrospun PVP-based multilayer material through machine learning models. J. Mater. Sci. 2024, 60, 1019–1040. [Google Scholar] [CrossRef]
- Lakatos, Á.; Lucchi, E. Thermal performances of Super Insulation Materials (SIMs): A comprehensive analysis of characteristics, heat transfer mechanisms, laboratory tests, and experimental comparisons. Int. Commun. Heat Mass Transf. 2024, 152, 107293. [Google Scholar] [CrossRef]
- Chen, M.; Zhu, M.; Zhao, L.; Chen, Y. Study on thermal runaway propagation inhibition of battery module by flame-retardant phase change material combined with aerogel felt. Appl. Energy 2024, 367, 123394. [Google Scholar] [CrossRef]
- Gu, W.; Sheng, J.; Huang, Q.; Wang, G.; Chen, J.; Ji, G. Environmentally Friendly and Multifunctional Shaddock Peel-Based Carbon Aerogel for Thermal-Insulation and Microwave Absorption. Nano-Micro Lett. 2021, 13, 102. [Google Scholar] [CrossRef]
- Iswar, S.; Galmarini, S.; Bonanomi, L.; Wernery, J.; Roumeli, E.; Nimalshantha, S.; Ben Ishai, A.M.; Lattuada, M.; Koebel, M.M.; Malfait, W.J. Dense and strong, but superinsulating silica aerogel. Acta Mater. 2021, 213, 116959. [Google Scholar] [CrossRef]
- Liu, Z.-H.; Ding, Y.-D.; Wang, F.; Deng, Z.-P. Thermal insulation material based on SiO2 aerogel. Constr. Build. Mater. 2016, 122, 548–555. [Google Scholar] [CrossRef]
- Qin, H.; Pei, Q.-X.; Liu, Y.; Zhang, Y.-W. Thermal transport in graphene-based layered materials: An analytical model validated with extensive molecular dynamics simulations. Carbon 2019, 155, 114–121. [Google Scholar] [CrossRef]
- Zhang, Z.; Feng, Y.; Wang, D.; Liang, L.; Wang, Z.; Yang, K.; Chen, X.; Chen, Q. Thermal conductive network construction and enhanced thermal conductivity in mica tape composites for large generator insulation. Compos. Sci. Technol. 2024, 254, 110671. [Google Scholar] [CrossRef]
- Zhuge, Y.; Liu, F. Recent Progress of Bionic Hierarchical Structure in the Field of Thermal Insulation Protection. J. Bionic Eng. 2023, 21, 1–18. [Google Scholar] [CrossRef]
- Guo, J.Y.; Su, L.J.; Wu, C.J.; Li, W.J.; Yang, J.Y.; Zhang, L.J. Performance Comparison of Aerospace High-Temperature Resistant Ceramic Fiber Felt. Mater. Sci. Forum 2021, 1036, 168–174. [Google Scholar] [CrossRef]
- Li, Y.; Guo, A.; Xu, X.; Xue, Y.; Yan, L.; Hou, F.; Liu, J. Preparation and Properties of Highly Elastic, Lightweight, and Thermally Insulating SiO2 Fibrous Porous Materials. Materials 2022, 15, 3069. [Google Scholar] [CrossRef] [PubMed]
- Guangwu, F.; Long, L.; Xiguang, G.; Yingdong, S. Finite Element Analysis of the Crack Deflection in Fiber Reinforced Ceramic Matrix Composites with Multilayer Interphase Using Virtual Crack Closure Technique. Appl. Compos. Mater. 2020, 27, 307–320. [Google Scholar] [CrossRef]
- Wei, K.; Wang, X.; Yang, X.; Qu, Z.; Tao, Y.; Fang, D. Heat transfer mechanism and characteristics of lightweight high temperature ceramic cellular sandwich. Appl. Therm. Eng. 2019, 154, 562–572. [Google Scholar] [CrossRef]
- Zhang, B.; Zhang, X.; Qiu, Y.; Han, J.; Hu, P.; Hong, C.; Peng, Z.; Han, W.; Chen, G. Enhanced thermal shock resistance of ultra-high temperature ceramic by biomimetic surface modification. J. Mater. Chem. A 2015, 3, 2199–2206. [Google Scholar] [CrossRef]







| Material | Density (g·cm−3) | Thermal Conductivity (W·m−1·k−1) | Heat Capacity (J·kg−1·K−1) |
|---|---|---|---|
| MR | 1.80 | 0.220 | 836 |
| FA | 0.20 | 0.023 | 970 |
| CFF | 0.19 | 0.036 | 1000 |
| Samples | MR (mm) | CFF (mm) | MR (mm) | Total Thickness (mm) |
|---|---|---|---|---|
| FSS A | 0.3 | 2.5 | 0.3 | 3.1 |
| FSS B | 0.3 | 3 | 0.3 | 3.6 |
| FSS C | 0.15 | 3 | 0.15 | 3.3 |
| FSS D | 0.12 | 3 | 0.12 | 3.24 |
| FSS E | 0.9 | 1.5 | 0.9 | 3.3 |
| CFF | MR | FA | ||||
|---|---|---|---|---|---|---|
| t (s) | T (°C) | t (s) | T (°C) | t (s) | T (°C) | |
| EXP | 50 | 357 | 177 | 223 | 47 | 183 |
| SIM | 31 | 350 | 150 | 220 | 73 | 185 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Chen, J.; Li, S.; Guo, M.; Jing, N. Thermal Insulation Efficiency and Mechanisms of Flexible Sandwich Structure. Materials 2025, 18, 1426. https://doi.org/10.3390/ma18071426
Xie Y, Chen J, Li S, Guo M, Jing N. Thermal Insulation Efficiency and Mechanisms of Flexible Sandwich Structure. Materials. 2025; 18(7):1426. https://doi.org/10.3390/ma18071426
Chicago/Turabian StyleXie, Yuanzhe, Juan Chen, Shuo Li, Mengxiao Guo, and Niansu Jing. 2025. "Thermal Insulation Efficiency and Mechanisms of Flexible Sandwich Structure" Materials 18, no. 7: 1426. https://doi.org/10.3390/ma18071426
APA StyleXie, Y., Chen, J., Li, S., Guo, M., & Jing, N. (2025). Thermal Insulation Efficiency and Mechanisms of Flexible Sandwich Structure. Materials, 18(7), 1426. https://doi.org/10.3390/ma18071426




