Influence of Optimization Algorithms and Computational Complexity on Concrete Compressive Strength Prediction Machine Learning Models for Concrete Mix Design
Abstract
1. Introduction
2. AI-Driven Approach in Concrete Mix Design
2.1. Optimal Concrete Properties and Traditional Concrete Mix Design
2.2. Predictive Modelling of Concrete Properties Using Machine Learning
3. Materials and Methods
3.1. Key Elements
3.2. Data Preparation and Processing
3.3. Model Training, Testing, and Selection Methodology
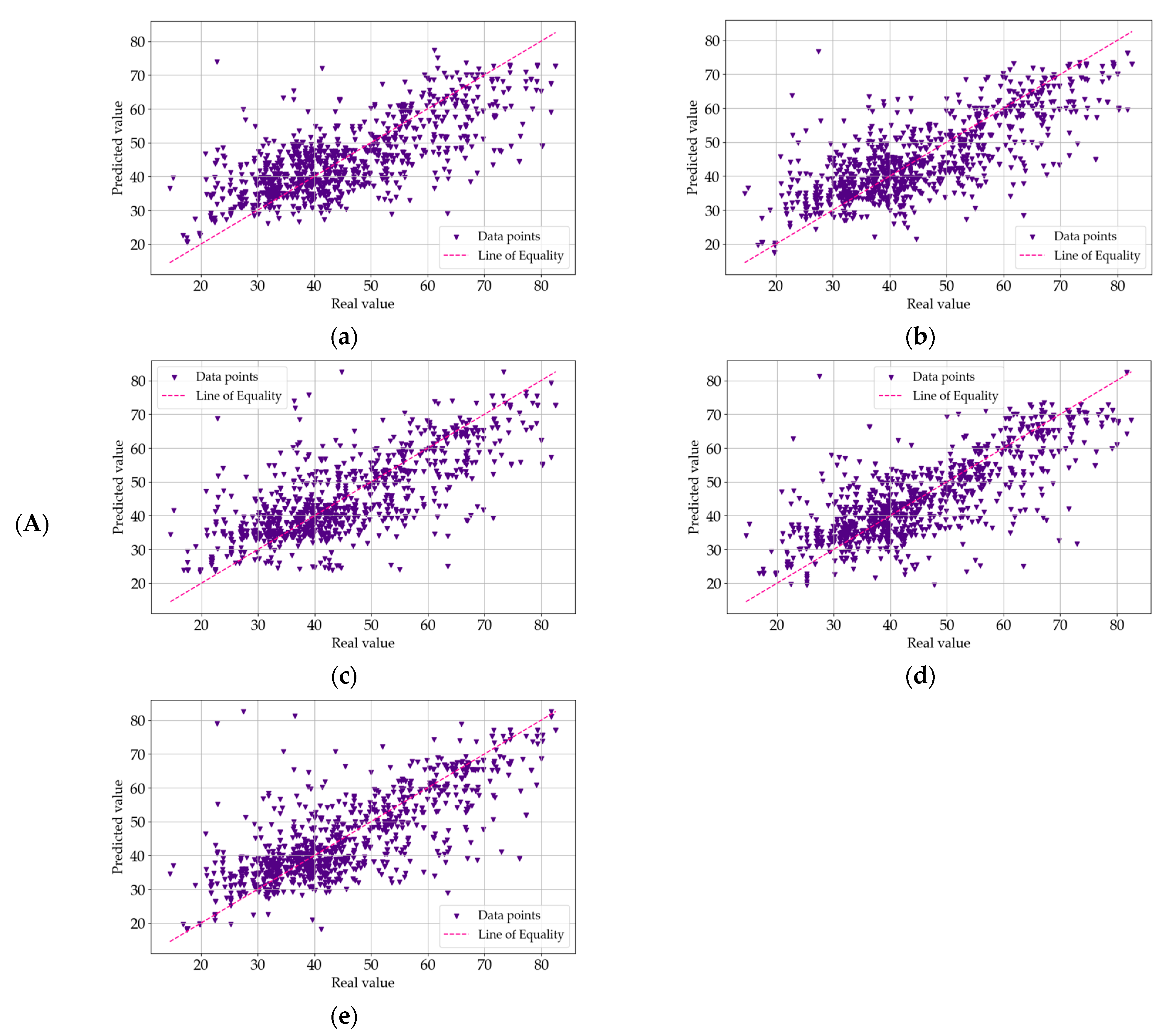
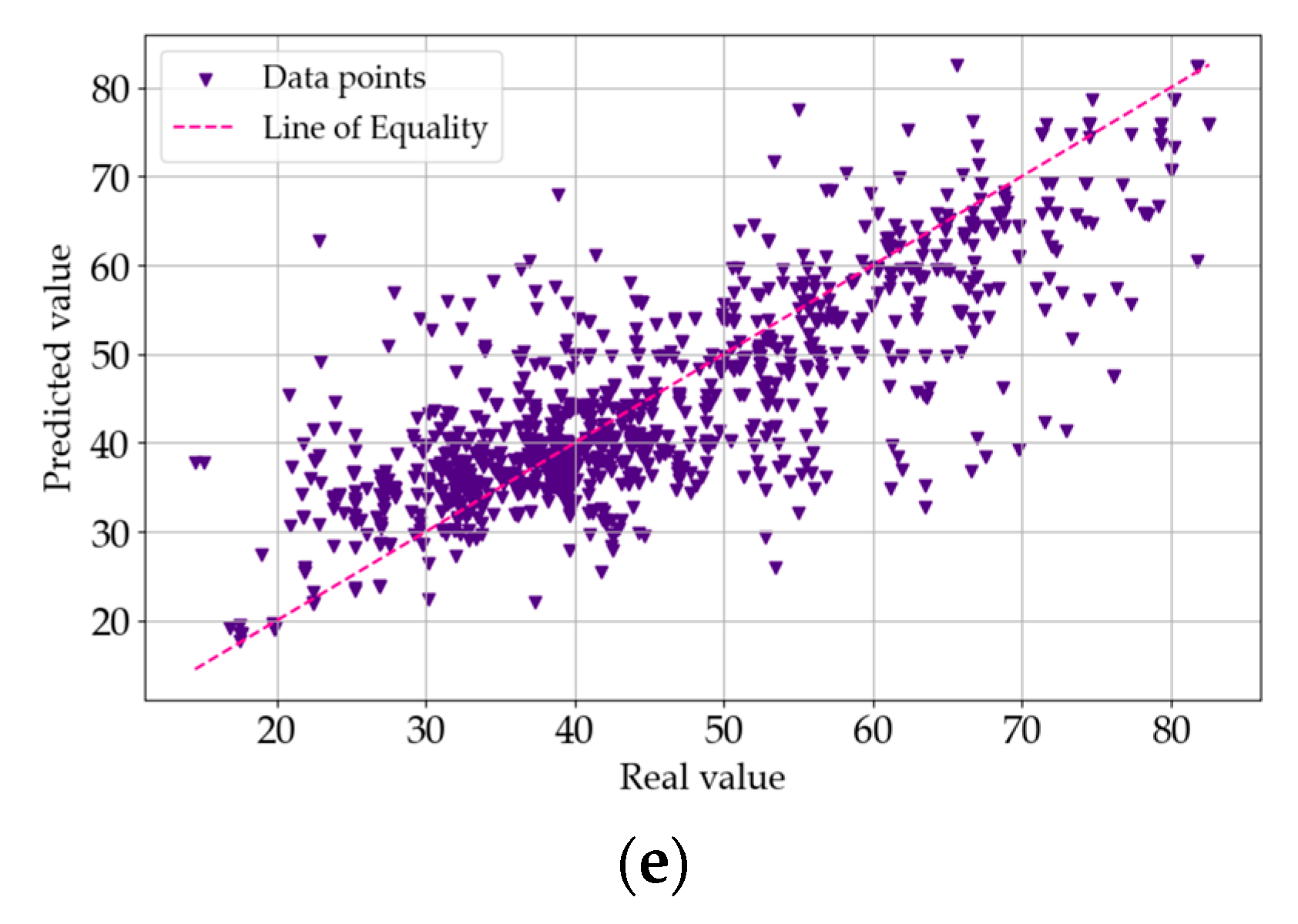
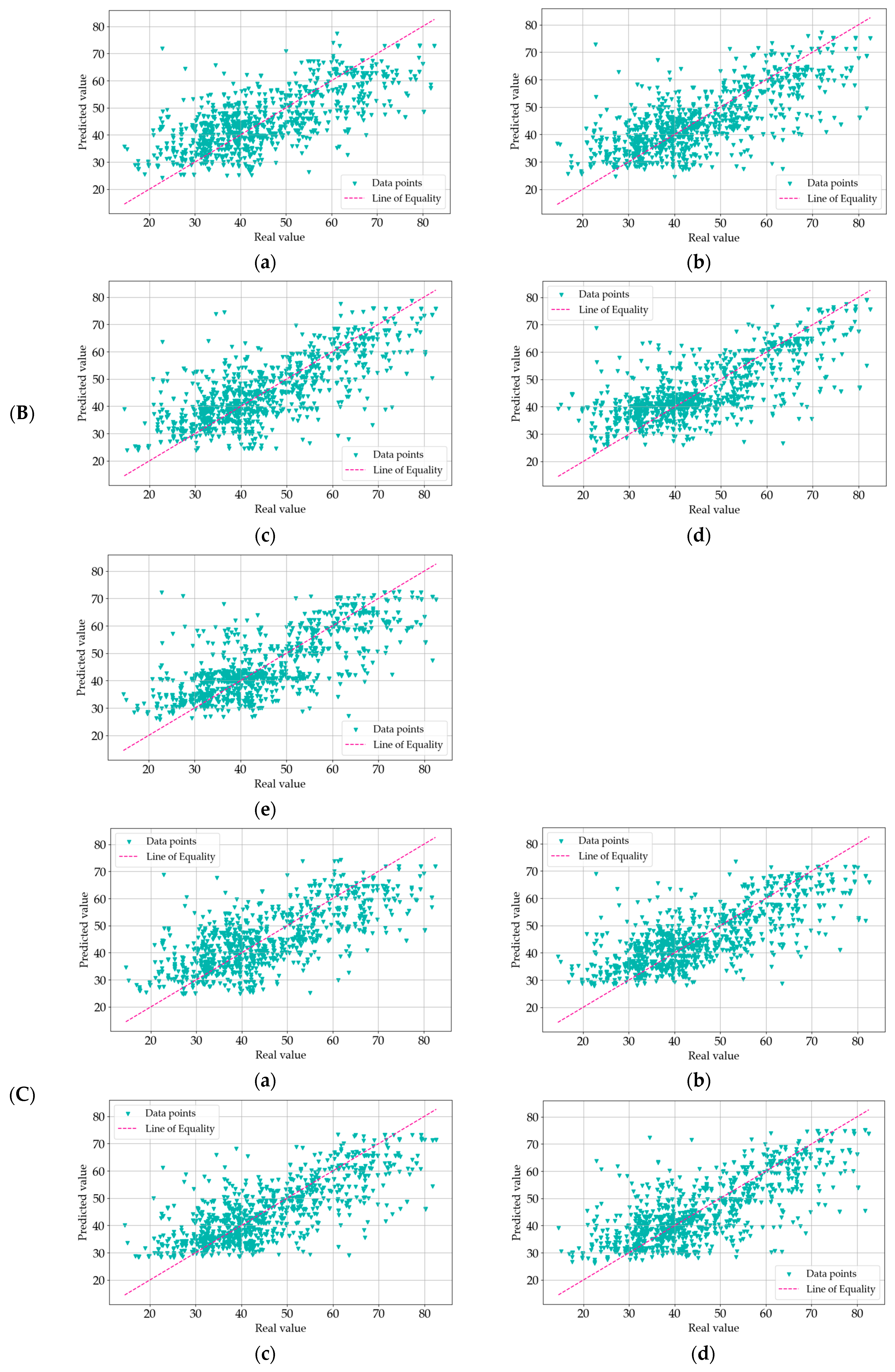
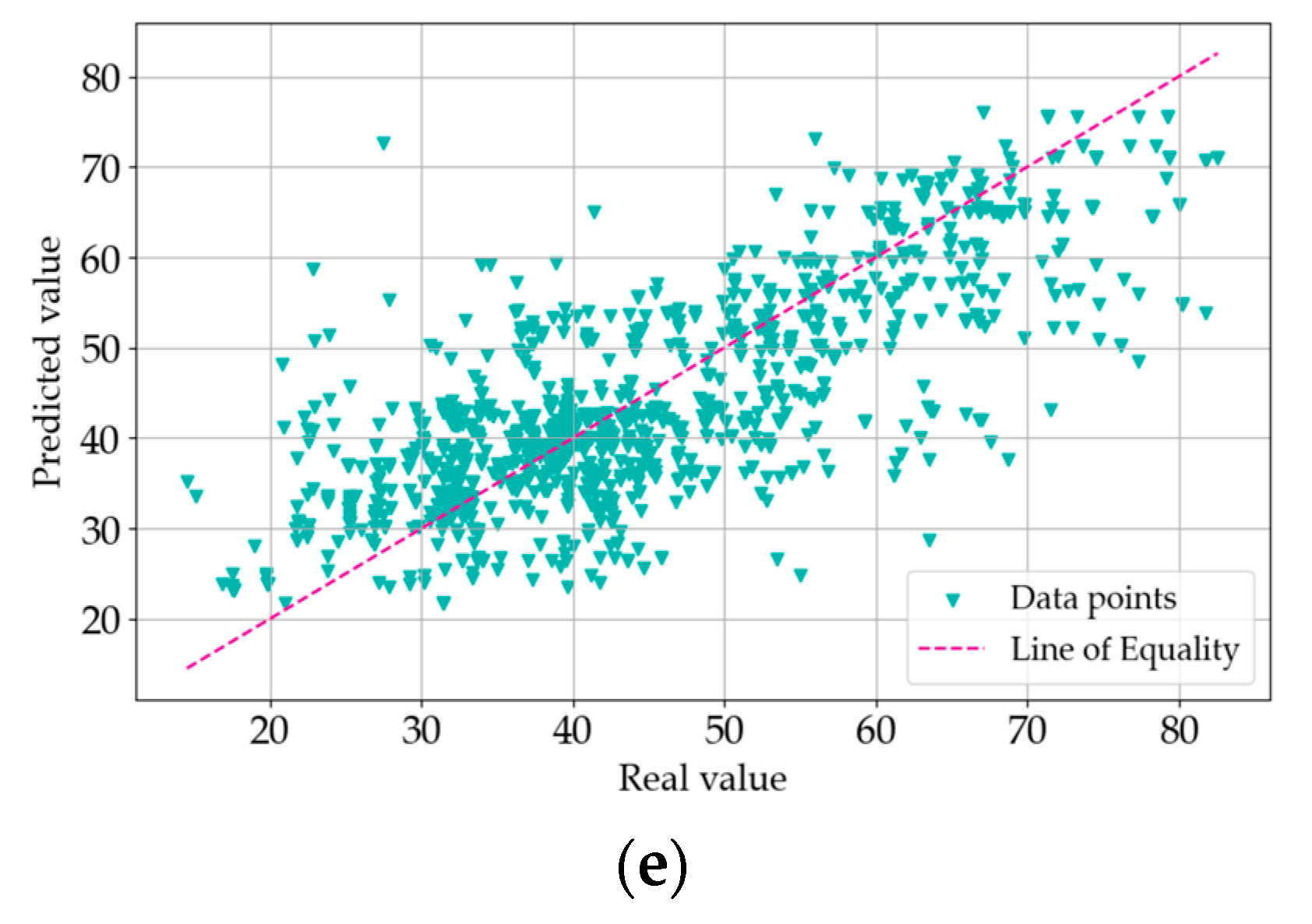
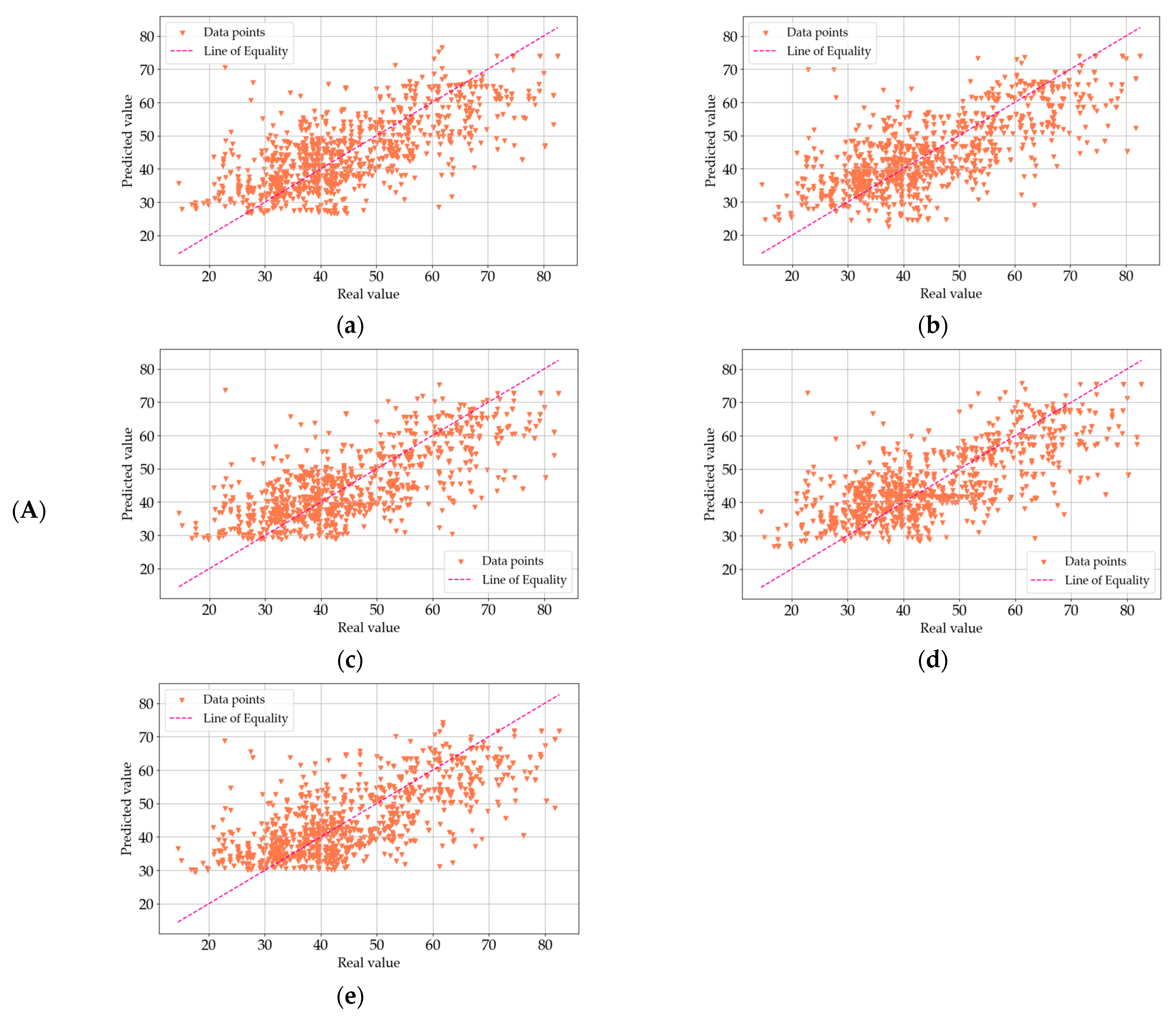
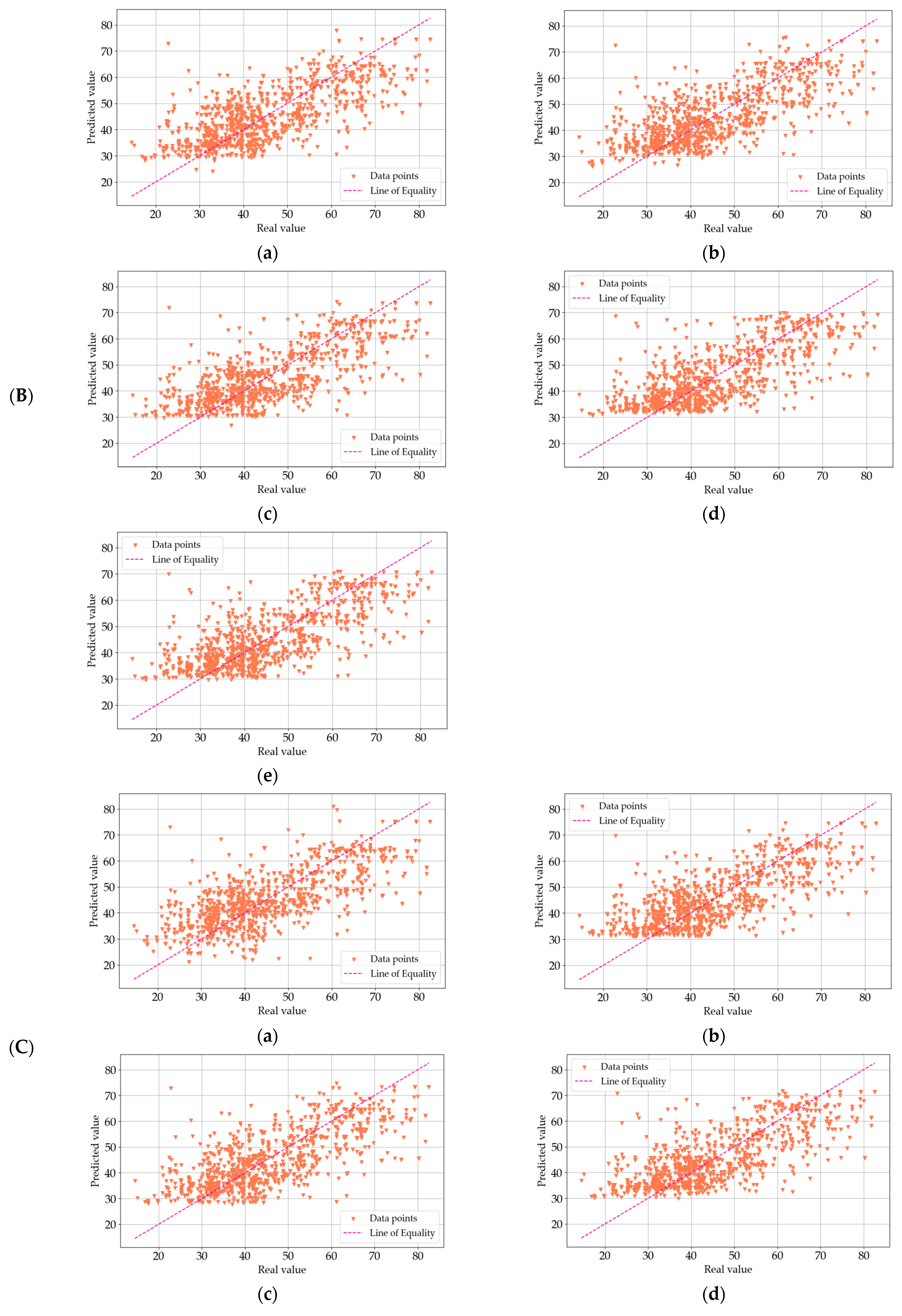
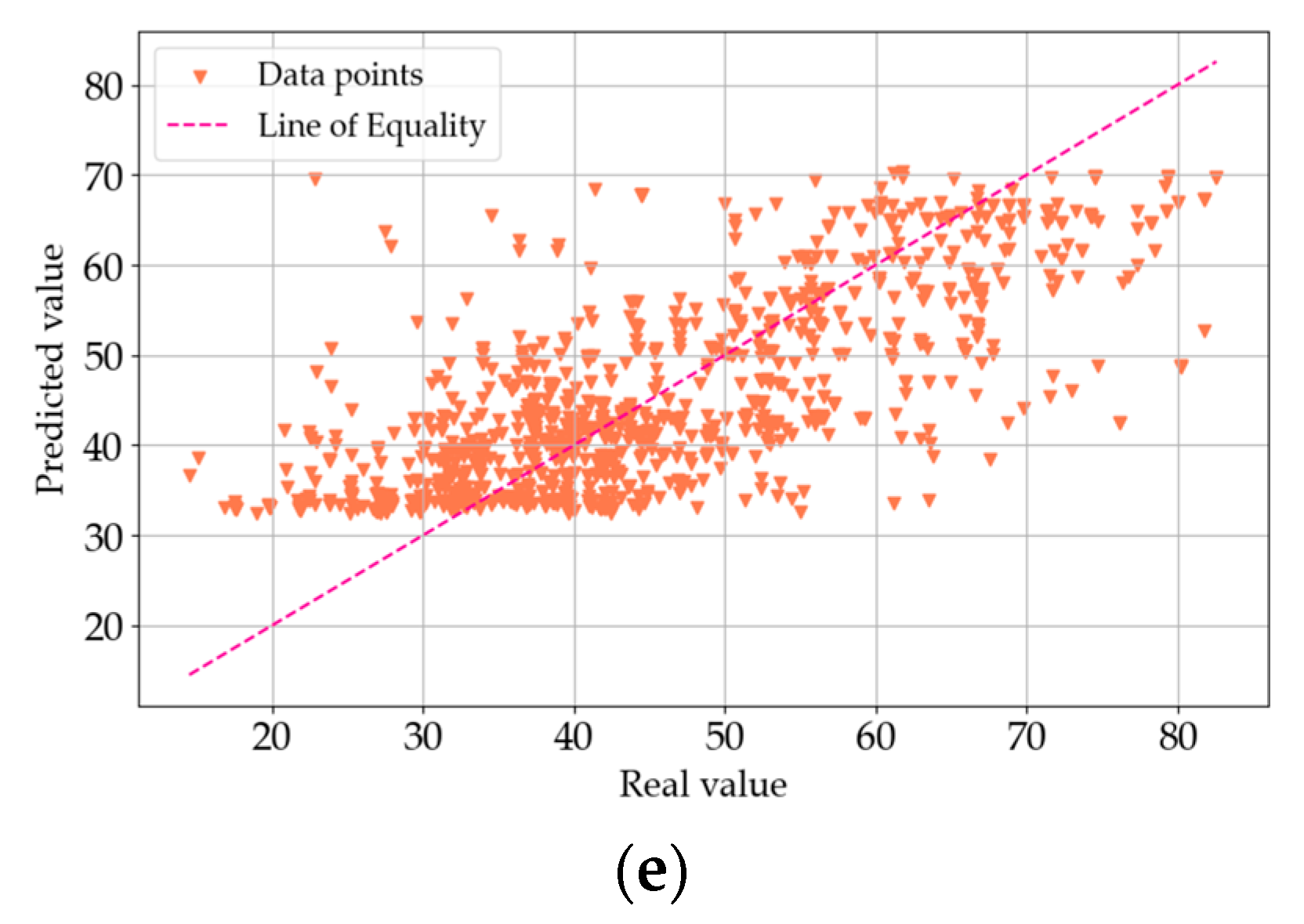
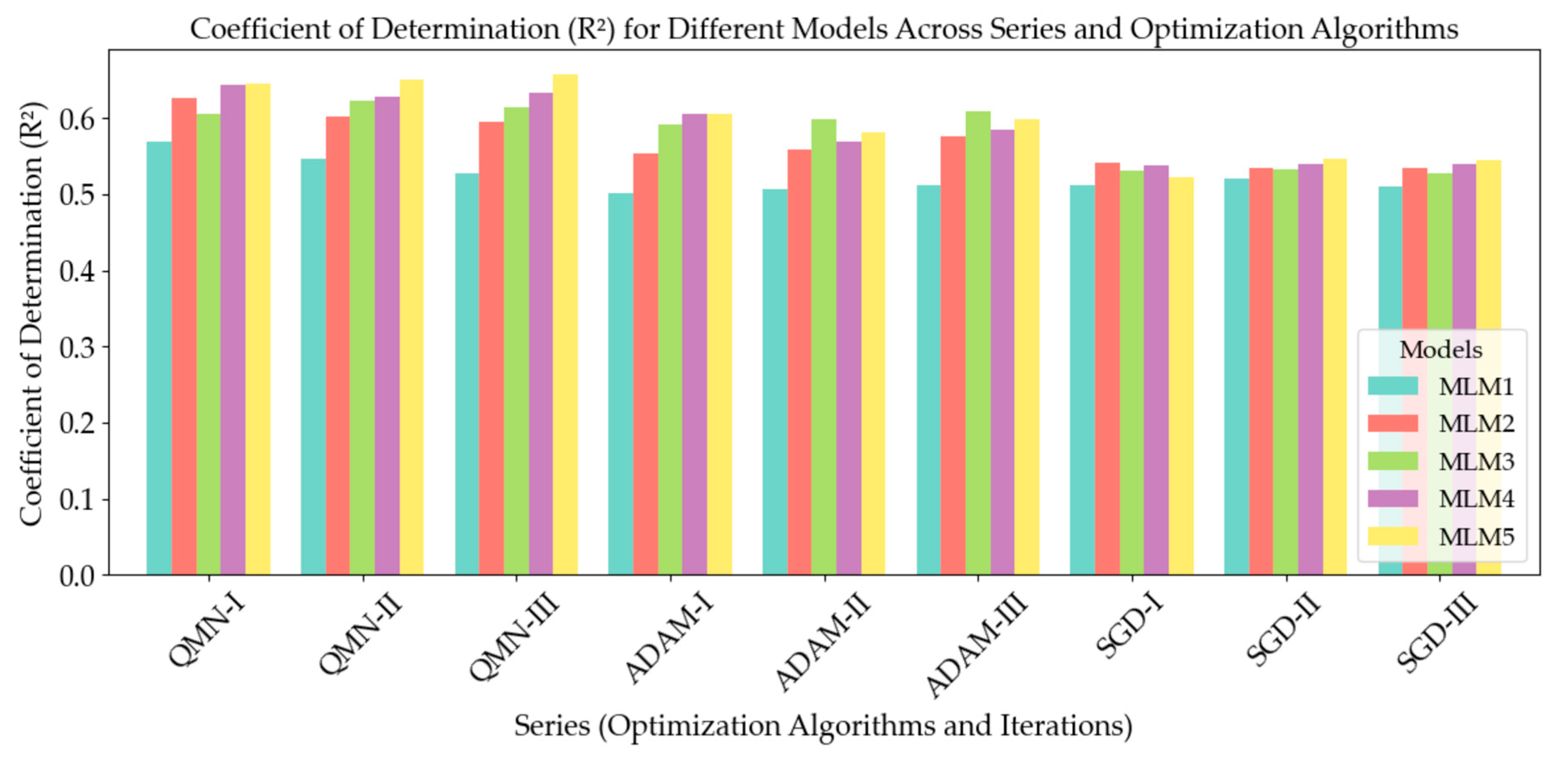
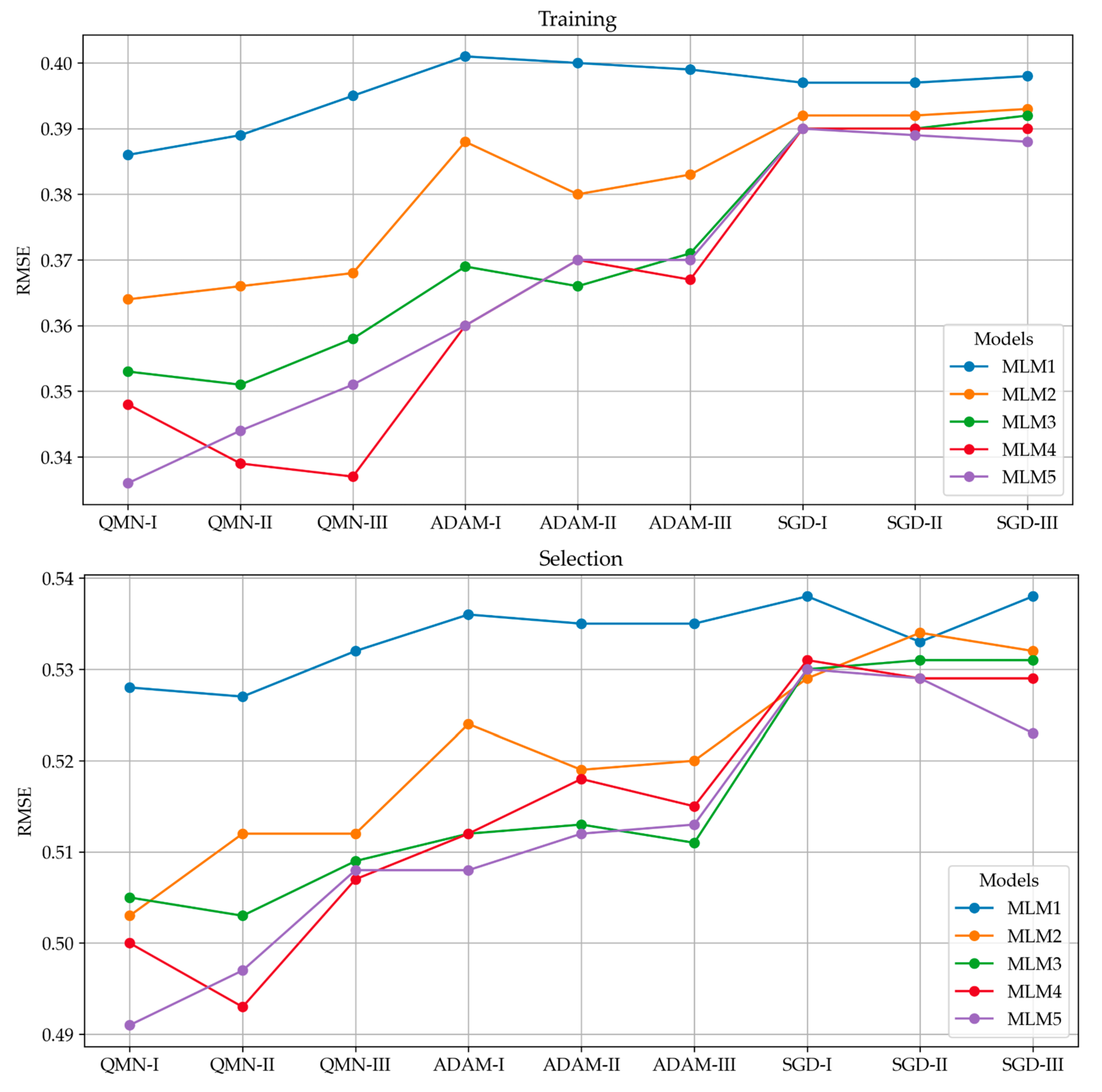
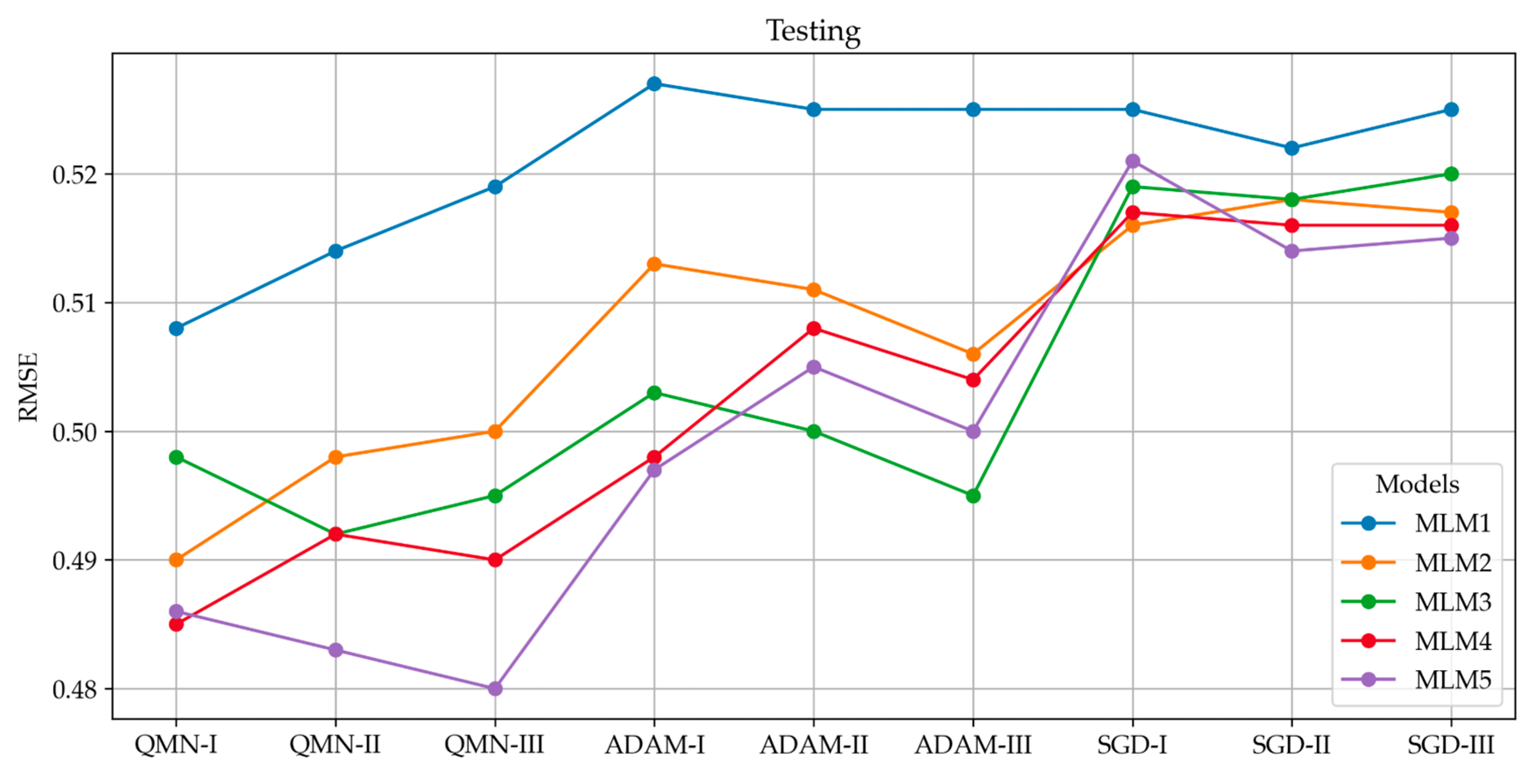
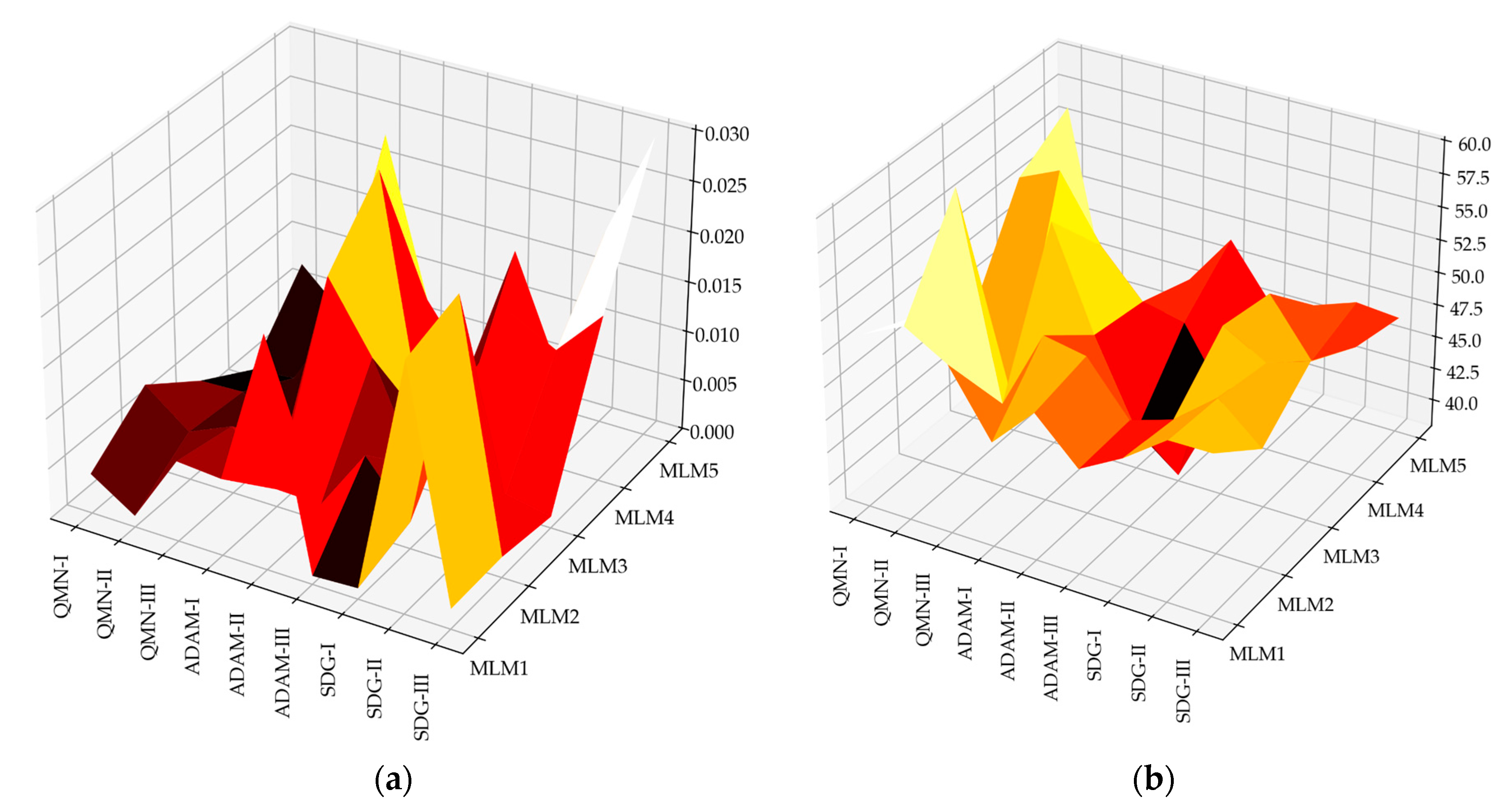
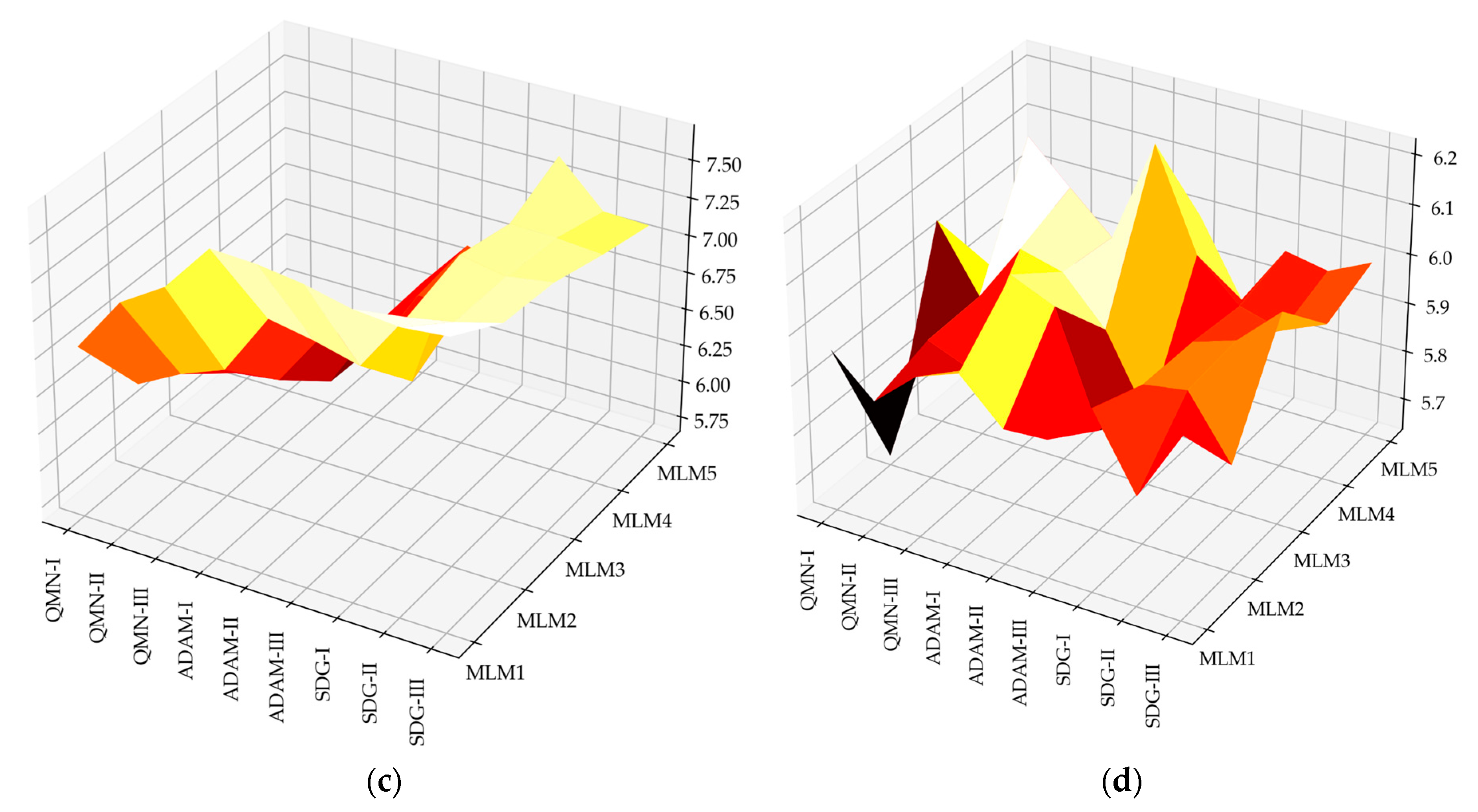
4. Results and Analysis
4.1. Data Processing Results
4.2. Analysis of R2 Trends
4.3. Analysis of Model Errors
5. Summary and Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Suchorzewski, J.; Prieto, M.; Mueller, U. An Experimental Study of Self-Sensing Concrete Enhanced with Multi-Wall Carbon Nanotubes in Wedge Splitting Test and DIC. Constr. Build. Mater. 2020, 262, 120871. [Google Scholar] [CrossRef]
- Nowek, A.; Kaszubski, P.; Abdelgader, H.S.; Górski, J. Effect of Admixtures on Fresh Grout and Two-Stage (Pre-Placed Aggregate) Concrete. Struct. Concr. 2007, 8, 17–23. [Google Scholar] [CrossRef]
- Suchorzewski, J.; Chitvoranund, N.; Srivastava, S.; Prieto, M.; Malaga, K. Recycling Potential of Cellular Lightweight Concrete Insulation as Supplementary Cementitious Material. In International RILEM Conference on Synergising Expertise Towards Sustainability and Robustness of Cement-Based Materials and Concrete Structures; RILEM Bookseries; Springer: Cham, Switzerland, 2023; Volume 44, pp. 133–141. [Google Scholar]
- Kujawa, W.; Olewnik-Kruszkowska, E.; Nowaczyk, J. Concrete Strengthening by Introducing Polymer-Based Additives into the Cement Matrix-a Mini Review. Materials 2021, 14, 6071. [Google Scholar] [CrossRef] [PubMed]
- McNamee, R.; Sjöström, J.; Boström, L. Reduction of Fire Spalling of Concrete with Small Doses of Polypropylene Fibres. Fire Mater. 2021, 45, 943–951. [Google Scholar] [CrossRef]
- García, G.; Cabrera, R.; Rolón, J.; Pichardo, R.; Thomas, C. Natural Fibers as Reinforcement of Mortar and Concrete: A Systematic Review from Central and South American Regions. J. Build. Eng. 2024, 98, 111267. [Google Scholar] [CrossRef]
- Guo, B.; Chu, J.; Zhang, Z.; Wang, Y.; Niu, D. Effect of External Loads on Chloride Ingress into Concrete: A State-of-the-Art Review. Constr. Build. Mater. 2024, 450, 138657. [Google Scholar]
- Yoon, Y.-S.; Kwon, S.-J.; Kim, K.-C.; Kim, Y.; Koh, K.-T.; Choi, W.-Y.; Lim, K.-M. Evaluation of Durability Performance for Chloride Ingress Considering Long-Term Aged GGBFS and FA Concrete and Analysis of the Relationship Between Concrete Mixture Characteristic and Passed Charge Using Machine Learning Algorithm. Materials 2023, 16, 7459. [Google Scholar] [CrossRef]
- Dimov, D.; Amit, I.; Gorrie, O.; Barnes, M.D.; Townsend, N.J.; Neves, A.I.S.; Withers, F.; Russo, S.; Craciun, M.F. Ultrahigh Performance Nanoengineered Graphene–Concrete Composites for Multifunctional Applications. Adv. Funct. Mater. 2018, 28, 1705183. [Google Scholar]
- Dimov, D. Fundamental Physical Properties of Graphene Reinforced Concrete; University of Exeter: Exeter, UK, 2018; ISBN 9798379627454. [Google Scholar]
- Marchon, D.; Flatt, R.J. Mechanisms of Cement Hydration. In Science and Technology of Concrete Admixtures; Woodhead Publishing: Cambridge, UK, 2016; pp. 129–145. [Google Scholar] [CrossRef]
- Liu, Y.; Kumar, D.; Lim, K.H.; Lai, Y.L.; Hu, Z.; Sanalkumar, K.U.A.; Yang, E.H. Efficient Utilization of Municipal Solid Waste Incinerator Bottom Ash for Autoclaved Aerated Concrete Formulation. J. Build. Eng. 2023, 71, 106463. [Google Scholar] [CrossRef]
- Moreno de los Reyes, A.M.; Suárez-Navarro, J.A.; Alonso, M.D.M.; Gascó, C.; Sobrados, I.; Puertas, F. Hybrid Cements: Mechanical Properties, Microstructure and Radiological Behavior. Molecules 2022, 27, 498. [Google Scholar] [CrossRef]
- Kasperkiewicz, J. A Review of Concrete Mix Design Methods. In Optimization Methods for Material Design of Cement-based Composites; CRC Press: Boca Raton, FL, USA, 1998; pp. 60–114. [Google Scholar]
- Day, K.W. Concrete Mix Design, Quality Control and Specification; CRC Press: Boca Raton, FL, USA, 2006; ISBN 0429224524. [Google Scholar]
- Thai, H.-T. Machine Learning for Structural Engineering: A State-of-the-Art Review. In Structures; Elsevier: Amsterdam, The Netherlands, 2022; Volume 38, pp. 448–491. [Google Scholar]
- Zhou, L.; Koehler, F.; Sutherland, D.J.; Srebro, N. Optimistic Rates: A Unifying Theory for Interpolation Learning and Regularization in Linear Regression. ACM JMS J. Data Sci. 2024, 1, 1–51. [Google Scholar]
- Pałczyński, K.; Czyżewska, M.; Talaśka, T. Fuzzy Gaussian Decision Tree. J. Comput. Appl. Math. 2023, 425, 115038. [Google Scholar]
- Zhou, J.; Su, Z.; Hosseini, S.; Tian, Q.; Lu, Y.; Luo, H.; Xu, X.; Chen, C.; Huang, J. Decision Tree Models for the Estimation of Geo-Polymer Concrete Compressive Strength. Math. Biosci. Eng. 2024, 21, 1413–1444. [Google Scholar] [PubMed]
- Fan, Z.; Gou, J.; Weng, S. An Unbiased Fuzzy Weighted Relative Error Support Vector Machine for Reverse Prediction of Concrete Components. IEEE Trans. Artif. Intell. 2024, 5, 4574–4584. [Google Scholar]
- Janowski, A.; Renigier-Bilozor, M. HELIOS Approach: Utilizing AI and LLM for Enhanced Homogeneity Identification in Real Estate Market Analysis. Appl. Sci. 2024, 14, 6135. [Google Scholar] [CrossRef]
- Janowski, A.; Hüsrevoğlu, M.; Renigier-Bilozor, M. Sustainable Parking Space Management Using Machine Learning and Swarm Theory—The SPARK System. Appl. Sci. 2024, 14, 12076. [Google Scholar] [CrossRef]
- Ghosh, S.; Ghosh, K. Reinforced Concrete Design; CRC Press: Boca Raton, FL, USA, 2024; ISBN 1040261949. [Google Scholar]
- Ambroziak, A.; Ziolkowski, P. Concrete Compressive Strength Under Changing Environmental Conditions During Placement Processes. Materials 2020, 13, 4577. [Google Scholar] [CrossRef]
- Tam, C.T.; Babu, D.S.; Li, W. EN 206 Conformity Testing for Concrete Strength in Compression. Procedia Eng. 2017, 171, 227–237. [Google Scholar] [CrossRef]
- DIN EN 206-1:2001-07; Beton—Teil 1: Festlegung, Eigenschaften, Herstellung und Konformität. DIN: Berlin, Germany, 2001.
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures. General Rules and Rules for Buildings. European Committee for Standardization: Brussels, Belgium, 1992; Volume 3.
- Blazy, J.; Drobiec, Ł. Wpływ Włókien Polimerowych Na Wytrzymałość Na Ściskanie i Rozciąganie Betonu w Świetle Norm PN-EN 206 i PN-EN 14651. Inż. Bud. 2021, 77, 391–396. [Google Scholar]
- Kareem, A.I.; Nikraz, H.; Asadi, H. Performance of Hot-Mix Asphalt Produced with Double Coated Recycled Concrete Aggregates. Constr. Build. Mater. 2019, 205, 425–433. [Google Scholar]
- Quiroga, P.N.; Fowler, D.W. Guidelines for Proportioning Optimized Concrete Mixtures with High Microfines. 2004. Available online: https://repositories.lib.utexas.edu/items/d150499e-5fb7-4fef-9a7c-f93c16970661 (accessed on 12 February 2025).
- Ashraf, W.B.; Noor, M.A. Laboratory-Scale Investigation on Band Gradations of Aggregate for Concrete. J. Mater. Civ. Eng. 2013, 25, 1776–1782. [Google Scholar] [CrossRef]
- Chaubey, A. Practical Concrete Mix Design; CRC Press: Boca Raton, FL, USA, 2020; ISBN 0429285191. [Google Scholar]
- Kovler, K.; Roussel, N. Properties of Fresh and Hardened Concrete. Cem. Concr. Res. 2011, 41, 775–792. [Google Scholar] [CrossRef]
- Bartos, P. Fresh Concrete: Properties and Tests; Elsevier: Amsterdam, The Netherlands, 2013; Volume 38, ISBN 1483290840. [Google Scholar]
- Van-Loc, T.A.; Kiesse, T.S.; Bonnet, S.; Ventura, A. Application of Sensitivity Analysis in the Life Cycle Design for the Durability of Reinforced Concrete Structures in the Case of XC4 Exposure Class. Cem. Concr. Compos. 2018, 87, 53–62. [Google Scholar] [CrossRef]
- Müller, C. How Standards Support Sustainability of Cement and Concrete in Europe. Cem. Concr. Res. 2023, 173, 107288. [Google Scholar] [CrossRef]
- Ukpata, J.O.; Ewa, D.E.; Success, N.G.; Alaneme, G.U.; Otu, O.N.; Olaiya, B.C. Effects of Aggregate Sizes on the Performance of Laterized Concrete. Sci. Rep. 2024, 14, 448. [Google Scholar] [CrossRef]
- Tam, V.W.Y.; Soomro, M.; Evangelista, A.C.J.; Haddad, A. Deformation and Permeability of Recycled Aggregate Concrete—A Comprehensive Review. J. Build. Eng. 2021, 44, 103393. [Google Scholar] [CrossRef]
- Yeh, I.C. Modeling of Strength of High-Performance Concrete Using Artificial Neural Networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Lee, S.C. Prediction of Concrete Strength Using Artificial Neural Networks. Eng. Struct. 2003, 25, 849–857. [Google Scholar] [CrossRef]
- Hola, J.; Schabowicz, K. Application of Artificial Neural Networks to Determine Concrete Compressive Strength Based on Non-Destructive Tests. J. Civ. Eng. Manag. 2005, 11, 23–32. [Google Scholar] [CrossRef]
- Hoła, J.; Schabowicz, K. New Technique of Nondestructive Assessment of Concrete Strength Using Artificial Intelligence. NDT E Int. 2005, 38, 251–259. [Google Scholar] [CrossRef]
- Gupta, R.; Kewalramani, M.A.; Goel, A. Prediction of Concrete Strength Using Neural-Expert System. J. Mater. Civ. Eng. 2006, 18, 462–466. [Google Scholar] [CrossRef]
- Deng, F.; He, Y.; Zhou, S.; Yu, Y.; Cheng, H.; Wu, X. Compressive Strength Prediction of Recycled Concrete Based on Deep Learning. Constr. Build. Mater. 2018, 175, 562–569. [Google Scholar] [CrossRef]
- Ziolkowski, P.; Niedostatkiewicz, M. Machine Learning Techniques in Concrete Mix Design. Materials 2019, 12, 1256. [Google Scholar] [CrossRef] [PubMed]
- Nunez, I.; Marani, A.; Nehdi, M.L. Mixture Optimization of Recycled Aggregate Concrete Using Hybrid Machine Learning Model. Materials 2020, 13, 4331. [Google Scholar] [CrossRef] [PubMed]
- Marani, A.; Jamali, A.; Nehdi, M.L. Predicting Ultra-High-Performance Concrete Compressive Strength Using Tabular Generative Adversarial Networks. Materials 2020, 13, 4757. [Google Scholar] [CrossRef]
- Ziolkowski, P.; Niedostatkiewicz, M.; Kang, S.B. Model-Based Adaptive Machine Learning Approach in Concrete Mix Design. Materials 2021, 14, 1661. [Google Scholar] [CrossRef]
- Adil, M.; Ullah, R.; Noor, S.; Gohar, N. Effect of Number of Neurons and Layers in an Artificial Neural Network for Generalized Concrete Mix Design. Neural Comput. Appl. 2022, 34, 8355–8363. [Google Scholar] [CrossRef]
- Feng, W.; Wang, Y.; Sun, J.; Tang, Y.; Wu, D.; Jiang, Z.; Wang, J.; Wang, X. Prediction of Thermo-Mechanical Properties of Rubber-Modified Recycled Aggregate Concrete. Constr. Build. Mater. 2022, 318, 125970. [Google Scholar] [CrossRef]
- Tavares, C.; Wang, X.; Saha, S.; Grasley, Z. Machine Learning-Based Mix Design Tools to Minimize Carbon Footprint and Cost of UHPC. Part 1: Efficient Data Collection and Modeling. Clean. Mater. 2022, 4, 100082. [Google Scholar] [CrossRef]
- Tavares, C.; Grasley, Z. Machine Learning-Based Mix Design Tools to Minimize Carbon Footprint and Cost of UHPC. Part 2: Cost and Eco-Efficiency Density Diagrams. Clean. Mater. 2022, 4, 100094. [Google Scholar] [CrossRef]
- Endzhievskaya, I.G.; Endzhievskiy, A.S.; Galkin, M.A.; Molokeev, M.S. Machine Learning Methods in Assessing the Effect of Mixture Composition on the Physical and Mechanical Characteristics of Road Concrete. J. Build. Eng. 2023, 76, 107248. [Google Scholar] [CrossRef]
- Ziolkowski, P. Computational Complexity and Its Influence on Predictive Capabilities of Machine Learning Models for Concrete Mix Design. Materials 2023, 16, 5956. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Li, T.; Yao, Y.; Hu, X.; Zuo, Y.; Du, H.; Yang, J. Optimization of Mix Proportion and Strength Prediction of Magnesium Phosphate Cement-Based Composites Based on Machine Learning. Constr. Build. Mater. 2024, 411, 134738. [Google Scholar]
- Golafshani, E.M.; Kim, T.; Behnood, A.; Ngo, T.; Kashani, A. Sustainable Mix Design of Recycled Aggregate Concrete Using Artificial Intelligence. J. Clean. Prod. 2024, 442, 140994. [Google Scholar]
- Okewu, E.; Misra, S.; Lius, F.-S. Parameter Tuning Using Adaptive Moment Estimation in Deep Learning Neural Networks. In Proceedings of the Computational Science and Its Applications–ICCSA 2020: 20th International Conference, Cagliari, Italy, 1–4 July 2020; Proceedings, Part VI 20. Springer: Berlin/Heidelberg, Germany, 2020; pp. 261–272. [Google Scholar]
- Kingma, D.P. Adam: A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Singarimbun, R.N.; Nababan, E.B.; Sitompul, O.S. Adaptive Moment Estimation to Minimize Square Error in Backpropagation Algorithm. In Proceedings of the 2019 International Conference of Computer Science and Information Technology (ICoSNIKOM), Medan, Indonesia, 28–29 November 2019; pp. 1–7. [Google Scholar]
- Tian, Y.; Zhang, Y.; Zhang, H. Recent Advances in Stochastic Gradient Descent in Deep Learning. Mathematics 2023, 11, 682. [Google Scholar] [CrossRef]
- Dohare, S.; Sutton, R.S.; Mahmood, A.R. Continual Backprop: Stochastic Gradient Descent with Persistent Randomness. arXiv 2021, arXiv:2108.06325. [Google Scholar]
- Sclocchi, A.; Wyart, M. On the Different Regimes of Stochastic Gradient Descent. Proc. Natl. Acad. Sci. USA 2024, 121, e2316301121. [Google Scholar]
- Guo, T.-D.; Liu, Y.; Han, C.-Y. An Overview of Stochastic Quasi-Newton Methods for Large-Scale Machine Learning. J. Oper. Res. Soc. China 2023, 11, 245–275. [Google Scholar]
- Rafati, J.; Marica, R.F. Quasi-Newton Optimization Methods for Deep Learning Applications. In Deep Learning Applications; Springer: Berlin/Heidelberg, Germany, 2020; pp. 9–38. [Google Scholar]
- Goldfarb, D.; Ren, Y.; Bahamou, A. Practical Quasi-Newton Methods for Training Deep Neural Networks. Adv. Neural Inf. Process. Syst. 2020, 33, 2386–2396. [Google Scholar]
- Gulli, A.; Pal, S. Deep Learning with Keras: Beginners Guide to Deep Learning with Keras; Packt Publishing Ltd.: Birmingham, UK, 2017; ISBN 9781787128422. [Google Scholar]
- Cichy, R.M.; Kaiser, D. Deep Neural Networks as Scientific Models. Trends Cogn. Sci. 2019, 23, 305–317. [Google Scholar] [CrossRef] [PubMed]
- Liu, M.; Chen, L.; Du, X.; Jin, L.; Shang, M. Activated Gradients for Deep Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2023, 34, 2156–2168. [Google Scholar] [CrossRef]
- Rehmer, A.; Kroll, A. On the Vanishing and Exploding Gradient Problem in Gated Recurrent Units. IFAC-Pap. 2020, 53, 1243–1248. [Google Scholar] [CrossRef]
- Tjoa, E.; Cuntai, G. Quantifying Explainability of Saliency Methods in Deep Neural Networks With a Synthetic Dataset. IEEE Trans. Artif. Intell. 2022, 4, 858–870. [Google Scholar] [CrossRef]
- Hernandez, M.; Epelde, G.; Alberdi, A.; Cilla, R.; Rankin, D. Synthetic Data Generation for Tabular Health Records: A Systematic Review. Neurocomputing 2022, 493, 28–45. [Google Scholar] [CrossRef]
- Juneja, T.; Bajaj, S.B.; Sethi, N. Synthetic Time Series Data Generation Using Time GAN with Synthetic and Real-Time Data Analysis. In Proceedings of the Lecture Notes in Electrical Engineering (LNEE); Springer: Berlin/Heidelberg, Germany, 2023; Volume 1011, pp. 657–667. [Google Scholar]
- Ravikumar, D.; Zhang, D.; Keoleian, G.; Miller, S.; Sick, V.; Li, V. Carbon Dioxide Utilization in Concrete Curing or Mixing Might Not Produce a Net Climate Benefit. Nat. Commun. 2021, 12, 855. [Google Scholar] [CrossRef]
- Shi, J.; Liu, B.; Wu, X.; Qin, J.; Jiang, J.; He, Z. Evolution of Mechanical Properties and Permeability of Concrete during Steam Curing Process. J. Build. Eng. 2020, 32, 101796. [Google Scholar] [CrossRef]
- Li, Y.; Nie, L.; Wang, B. A Numerical Simulation of the Temperature Cracking Propagation Process When Pouring Mass Concrete. Autom. Constr. 2014, 37, 203–210. [Google Scholar] [CrossRef]
- Patel, S.K.; Parmar, J.; Katkar, V. Graphene-Based Multilayer Metasurface Solar Absorber with Parameter Optimization and Behavior Prediction Using Long Short-Term Memory Model. Renew. Energy 2022, 191, 47–58. [Google Scholar] [CrossRef]
- Zhou, X.; Lin, W.; Kumar, R.; Cui, P.; Ma, Z. A Data-Driven Strategy Using Long Short Term Memory Models and Reinforcement Learning to Predict Building Electricity Consumption. Appl. Energy 2022, 306, 118078. [Google Scholar] [CrossRef]
- Wold, S.; Esbensen, K.; Geladi, P. Principal Component Analysis. In Chemometrics and Intelligent Laboratory Systems; Elsevier: Amsterdam, The Netherlands, 2002; Volume 2, pp. 37–52. [Google Scholar]
- Kurita, T. Principal Component Analysis (PCA) In Computer Vison; Springer International Publishing: Cham, The Switzerland, 2021; pp. 1013–1016. ISBN 978-3-03-063415-5. [Google Scholar]
- Thiyagalingam, J.; Shankar, M.; Fox, G.; Hey, T. Scientific Machine Learning Benchmarks. Nat. Rev. Phys. 2022, 4, 413–420. [Google Scholar] [CrossRef]
- Menéndez, M.L.; Pardo, J.A.; Pardo, L.; Pardo, M.C. The Jensen-Shannon Divergence. J. Frankl. Inst. 1997, 334, 307–318. [Google Scholar] [CrossRef]
- Nielsen, F. On a Generalization of the Jensen-Shannon Divergence and the Jensen-Shannon Centroid. Entropy 2020, 22, 221. [Google Scholar] [CrossRef]
- Fuglede, B.; Topsoe, F. Jensen-Shannon Divergence and Hilbert Space Embedding. In Proceedings of the International Symposium Oninformation Theory, Chicago, IL, USA, 27 June–2 July 2004; ISIT 2004. Proceedings. p. 31. [Google Scholar]
- Toniolo, G.; Di Prisco, M. Reinforced Concrete Design to Eurocode 2; Springer Tracts in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2017; pp. 1–836. [Google Scholar] [CrossRef]
- Bonaccorso, G. Machine Learning Algorithms: Popular Algorithms for Data Science and Machine Learning; Packt Publishing Ltd.: Birmingham, UK, 2018; ISBN 1789345480. [Google Scholar]
- Murphy, K.P. Probabilistic Machine Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2022; ISBN 0262046822. [Google Scholar]
- Zheng, A.; Casari, A. Feature Engineering for Machine Learning: Principles and Techniques for Data Scientists; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2018; ISBN 1491953195. [Google Scholar]
- Demir-Kavuk, O.; Kamada, M.; Akutsu, T.; Knapp, E.-W. Prediction Using Step-Wise L1, L2 Regularization and Feature Selection for Small Data Sets with Large Number of Features. BMC Bioinform. 2011, 12, 412. [Google Scholar] [CrossRef] [PubMed]
- Formentin, S.; Karimi, A. Enhancing Statistical Performance of Data-Driven Controller Tuning via L2-Regularization. Automatica 2014, 50, 1514–1520. [Google Scholar] [CrossRef]
- Naser, M.Z.; Alavi, A.H. Error Metrics and Performance Fitness Indicators for Artificial Intelligence and Machine Learning in Engineering and Sciences. Archit. Struct. Constr. 2023, 3, 499–517. [Google Scholar] [CrossRef]
- Rainio, O.; Teuho, J.; Klén, R. Evaluation Metrics and Statistical Tests for Machine Learning. Sci. Rep. 2024, 14, 6086. [Google Scholar] [CrossRef]
- Huyen, C. Designing Machine Learning Systems; O’Reilly Media, Inc.: Newton, MA, USA, 2022; ISBN 1098107934. [Google Scholar]
- Jo, T. Machine Learning Foundations. Machine Learning Foundations; Springer Nature: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Sanjuán, M.Á.; Estévez, E.; Argiz, C.; del Barrio, D. Effect of Curing Time on Granulated Blast-Furnace Slag Cement Mortars Carbonation. Cem. Concr. Compos. 2018, 90, 257–265. [Google Scholar] [CrossRef]
- Poloju, K.K.; Anil, V.; Manchiryal, R.K. Properties of Concrete as Influenced by Shape and Texture of Fine Aggregate. Am. J. Appl. Sci. Res. 2017, 3, 28–36. [Google Scholar]
- Chinchillas-Chinchillas, M.J.; Corral-Higuera, R.; Gómez-Soberón, J.M.; Arredondo-Rea, S.P.; Alamaral-Sánchez, J.L.; Acuña-Aguero, O.H.; Rosas-Casarez, C.A. Influence of the Shape of the Natural Aggregates, Recycled and Silica Fume on the Mechanical Properties of Pervious Concrete. Int. J. Adv. Comput. Sci. Its Appl.-IJCSIA 2014, 4, 216–220. [Google Scholar]
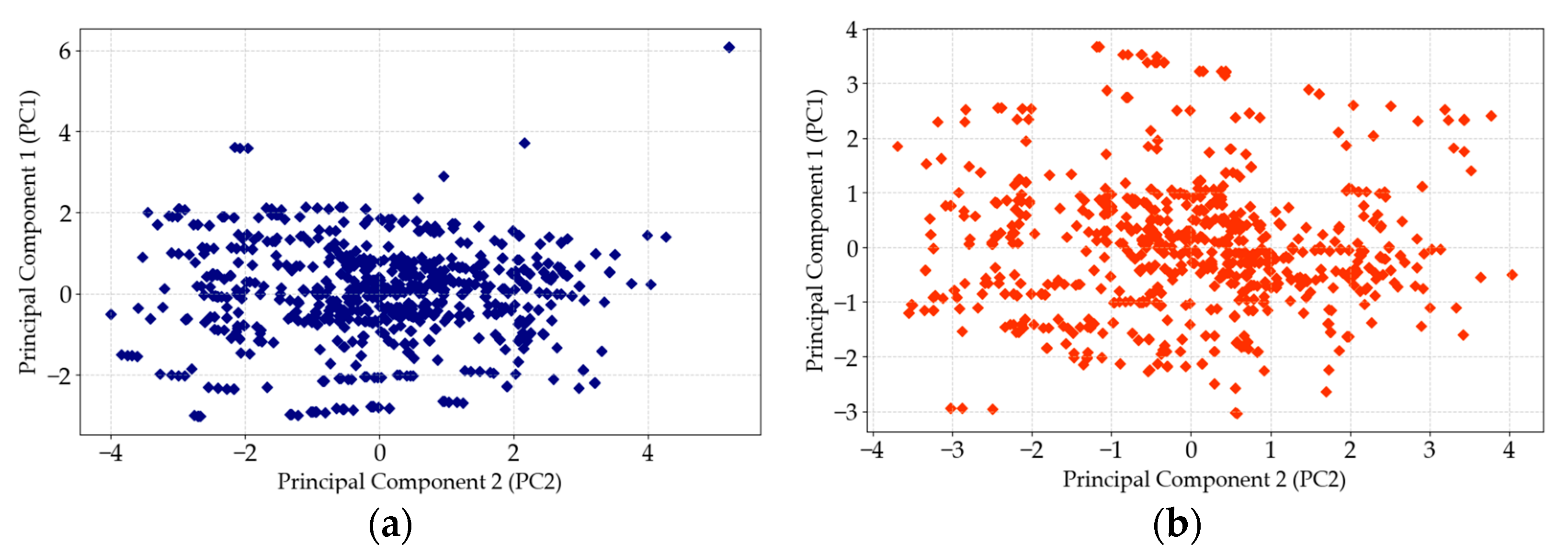
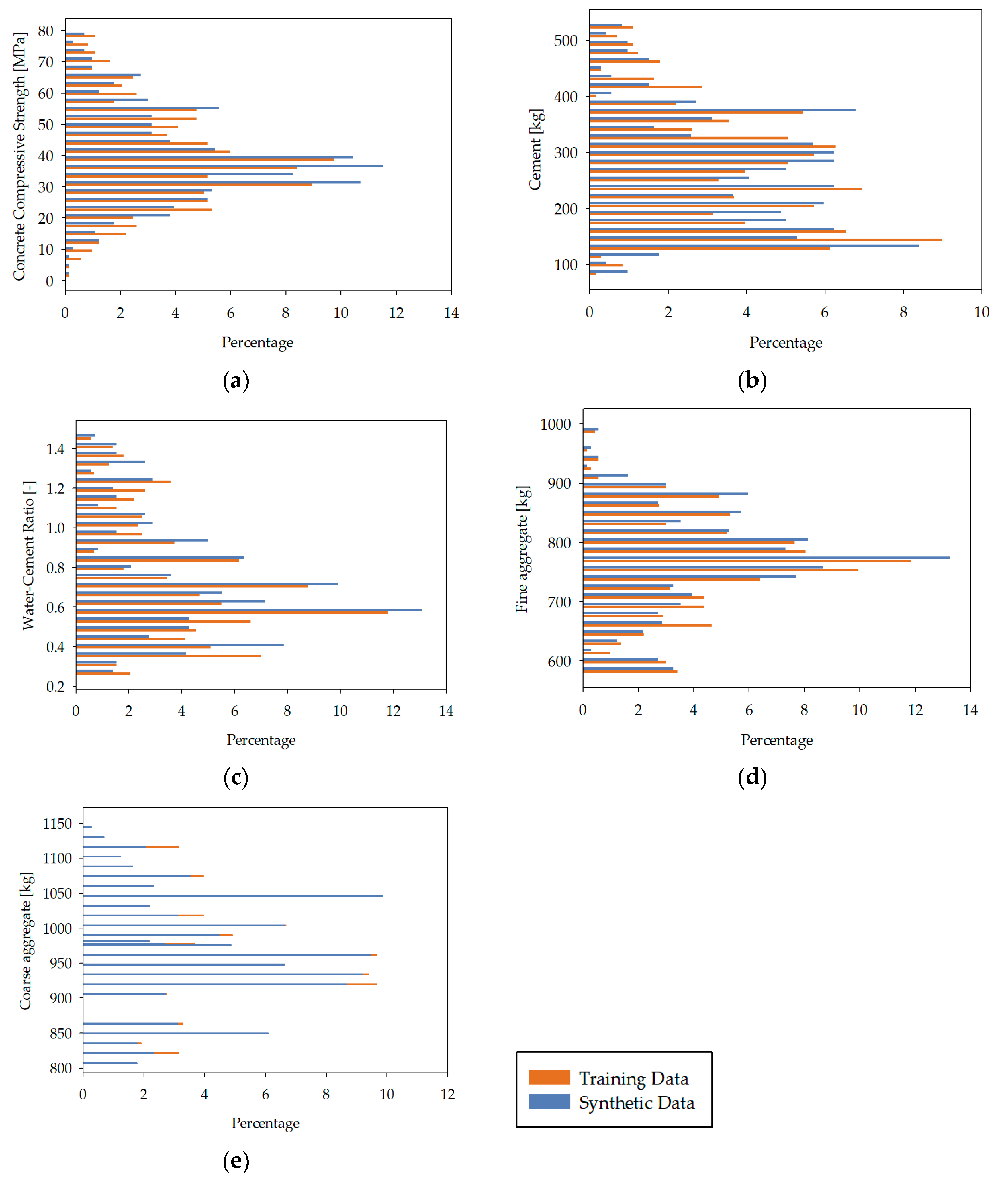

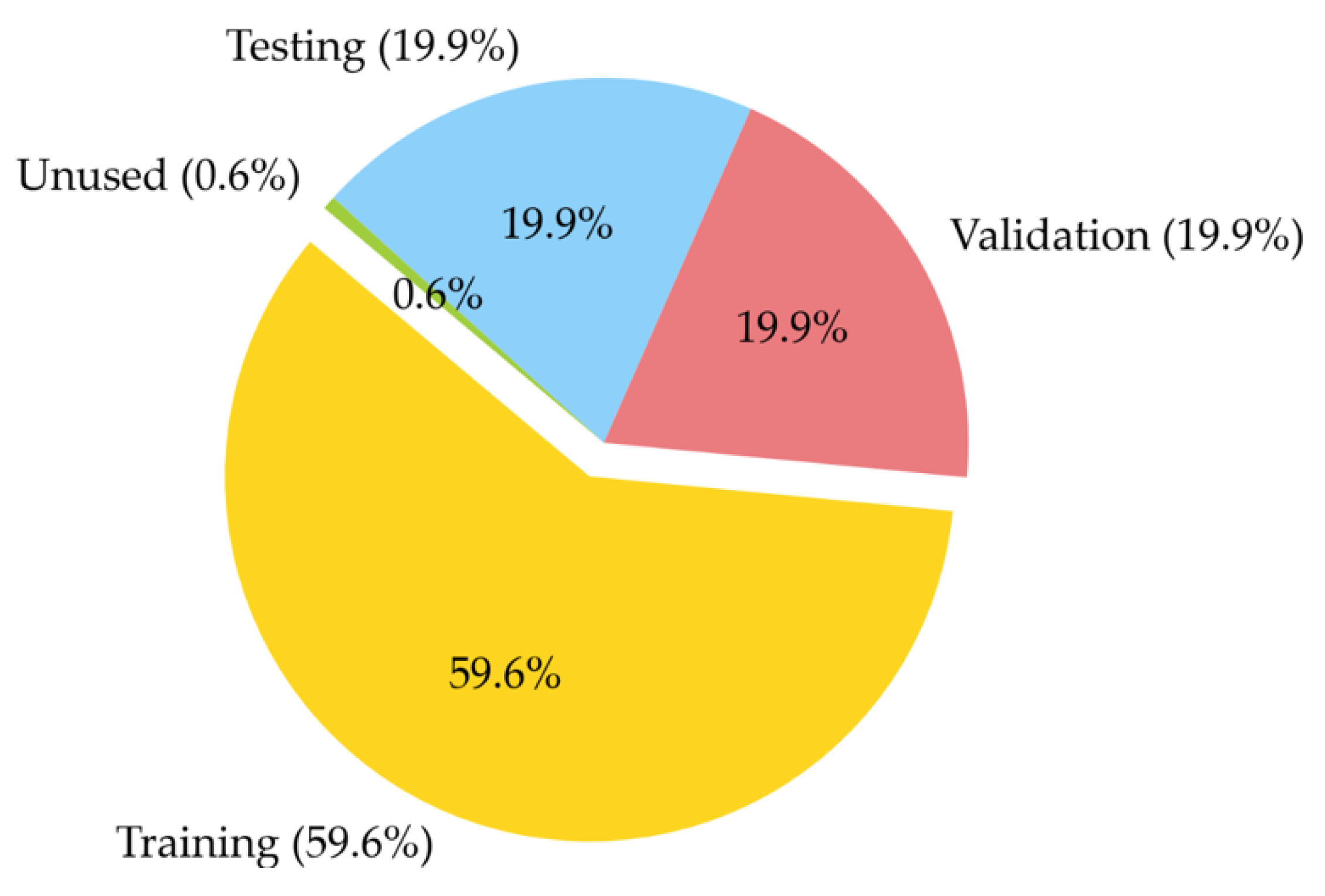
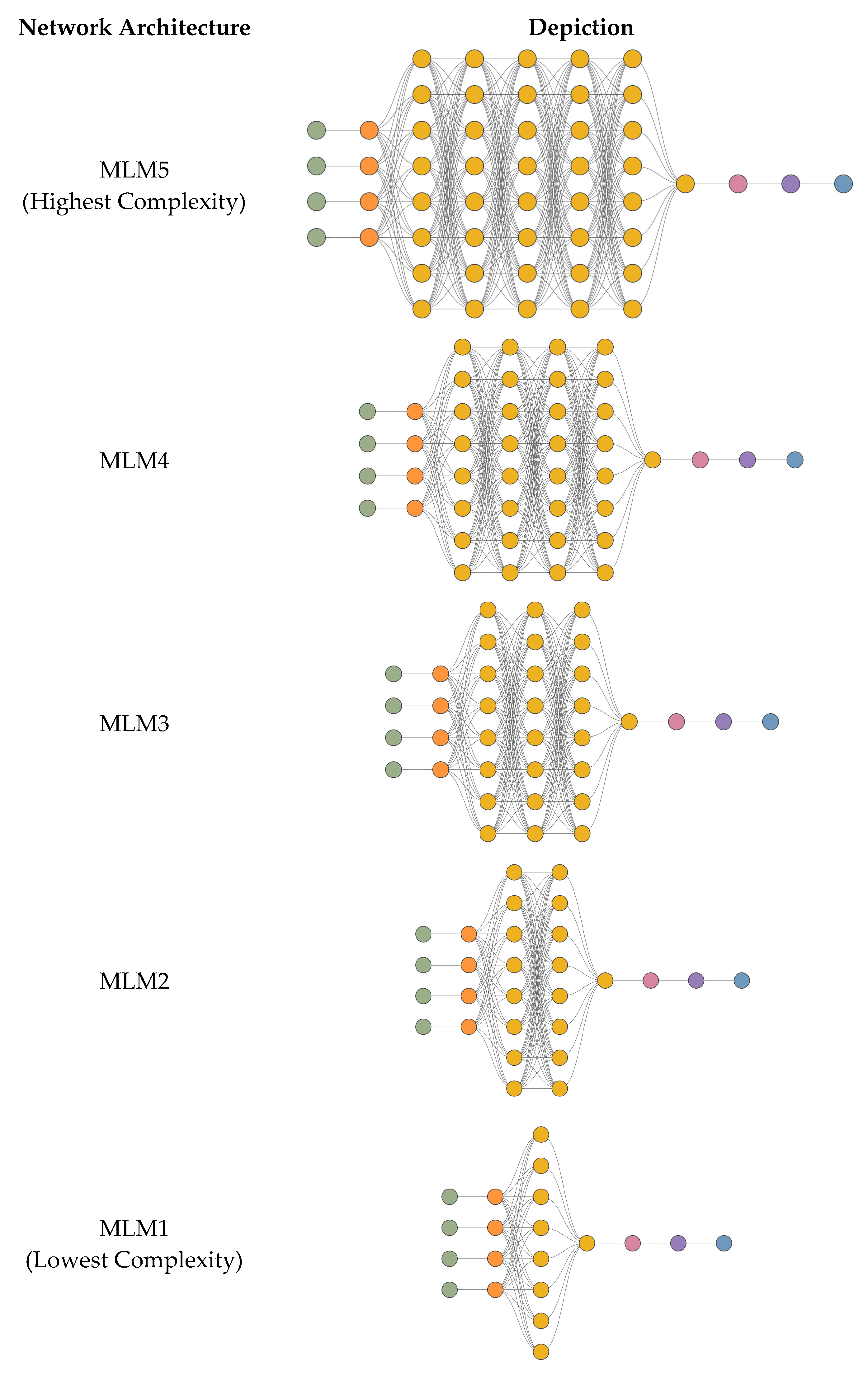





| Parameter | Compressive Strength | Cement | Water–Cement Ratio | Sand 0–2 mm | Aggregate Above 2 mm |
|---|---|---|---|---|---|
| Type | Target | Input | Input | Input | Input |
| Description | The 28-day compressive strength of concrete that is considered to have most of its strength (MPa). | Content of cement added to the mixture, expressed in (kg/m3). | Water-to-cement ratio (−). | Content of fine-grained aggregate added to the mixture, expressed in (kg/m3). | Content of coarse-grained aggregate with a size more than 2 mm, added to the mixture, expressed in (kg/m3). |
| Input Variable | Minimum | Maximum | Mean | Median | Dominant |
|---|---|---|---|---|---|
| Cement | 87.00 kg/m3 | 540.00 kg/m3 | 322.15 kg/m3 | 312.45 kg/m3 | 380.00 kg/m3 |
| Water–cement ratio | 0.30 | 0.80 | 0.58 | 0.58 | 0.58 |
| Fine-grained aggregate (sand 0–2 mm) | 472.00 kg/m3 | 995.60 kg/m3 | 767.96 kg/m3 | 774.00 kg/m3 | 594.00 kg/m3 |
| Coarse aggregate (aggregate above 2 mm) | 687.80 kg/m3 | 1198.00 kg/m3 | 969.92 kg/m3 | 963.00 kg/m3 | 932.00 kg/m3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ziolkowski, P. Influence of Optimization Algorithms and Computational Complexity on Concrete Compressive Strength Prediction Machine Learning Models for Concrete Mix Design. Materials 2025, 18, 1386. https://doi.org/10.3390/ma18061386
Ziolkowski P. Influence of Optimization Algorithms and Computational Complexity on Concrete Compressive Strength Prediction Machine Learning Models for Concrete Mix Design. Materials. 2025; 18(6):1386. https://doi.org/10.3390/ma18061386
Chicago/Turabian StyleZiolkowski, Patryk. 2025. "Influence of Optimization Algorithms and Computational Complexity on Concrete Compressive Strength Prediction Machine Learning Models for Concrete Mix Design" Materials 18, no. 6: 1386. https://doi.org/10.3390/ma18061386
APA StyleZiolkowski, P. (2025). Influence of Optimization Algorithms and Computational Complexity on Concrete Compressive Strength Prediction Machine Learning Models for Concrete Mix Design. Materials, 18(6), 1386. https://doi.org/10.3390/ma18061386






