Numerical Analysis of Inertia Forces in the Connecting Rod and Their Impact on Stress Formation
Abstract
1. Introduction
2. Materials and Methods
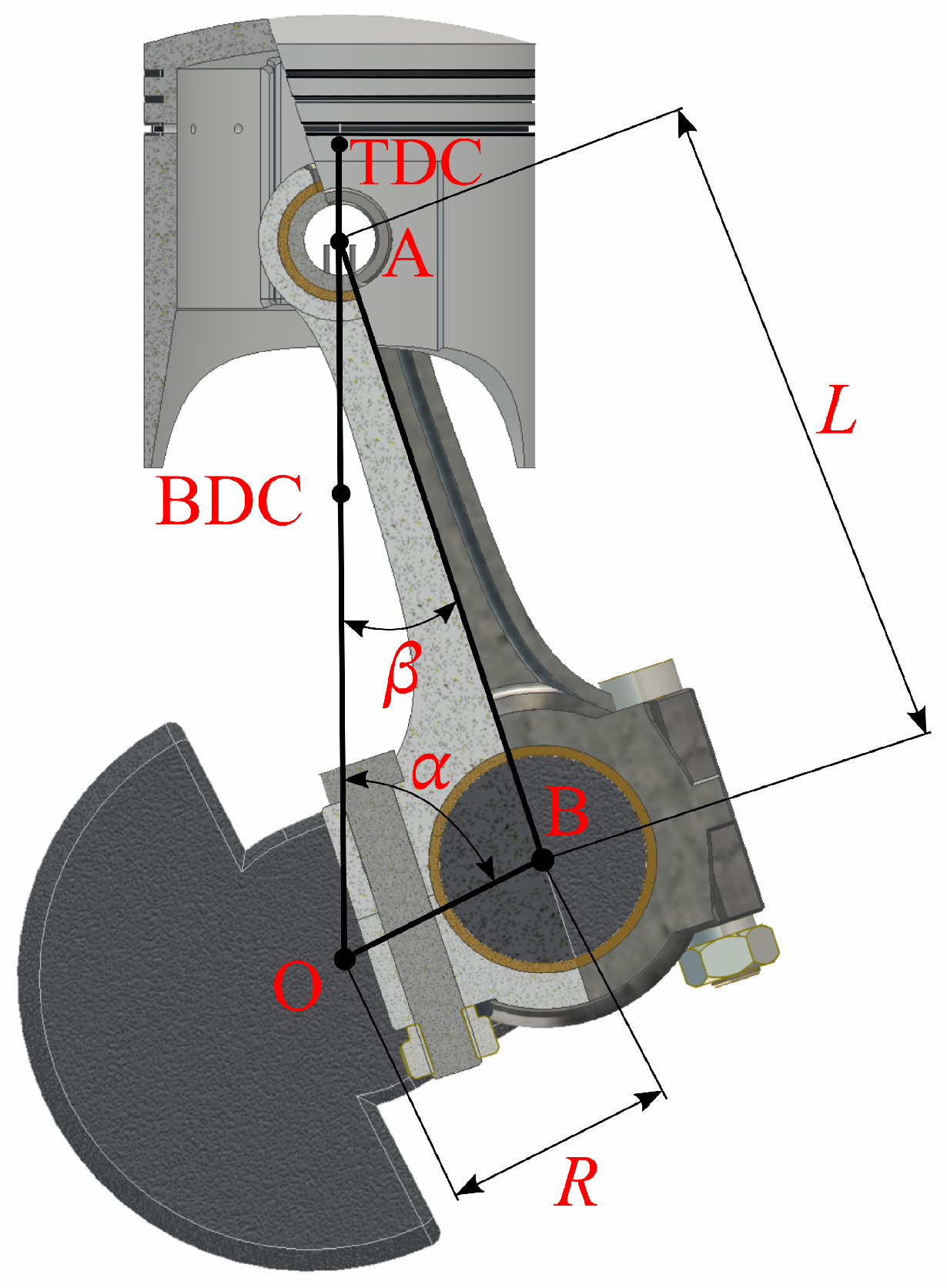
| O | point at which the crankshaft axis of rotation crosses perpendicularly the drawing plane; |
| A | point at which the connecting rod’s small-end axis of rotation crosses perpendicularly the drawing plane; |
| B | point at which the connecting rod’s big-end axis of rotation crosses perpendicularly the drawing plane; |
| TDC | top dead center; |
| BDC | bottom dead center; |
| R | crank radius (equal to the distance between O and B); |
| L | distance between the axis of the connecting rod’s small-end hole and the axis of the big-end hole (equal to the distance between A and B); |
| connecting rod’s length-to-crank’s length ratio, ; | |
| crankshaft torsion angle; | |
| connecting rod’s torsion angle; | |
| crankshaft angular speed; | |
| connecting rod’s mass. |
2.1. Determination of Inertia Force by Weighing the Connecting Rod
2.2. Numerical Analysis Tools and Material Parameters
3. Theory and Calculations
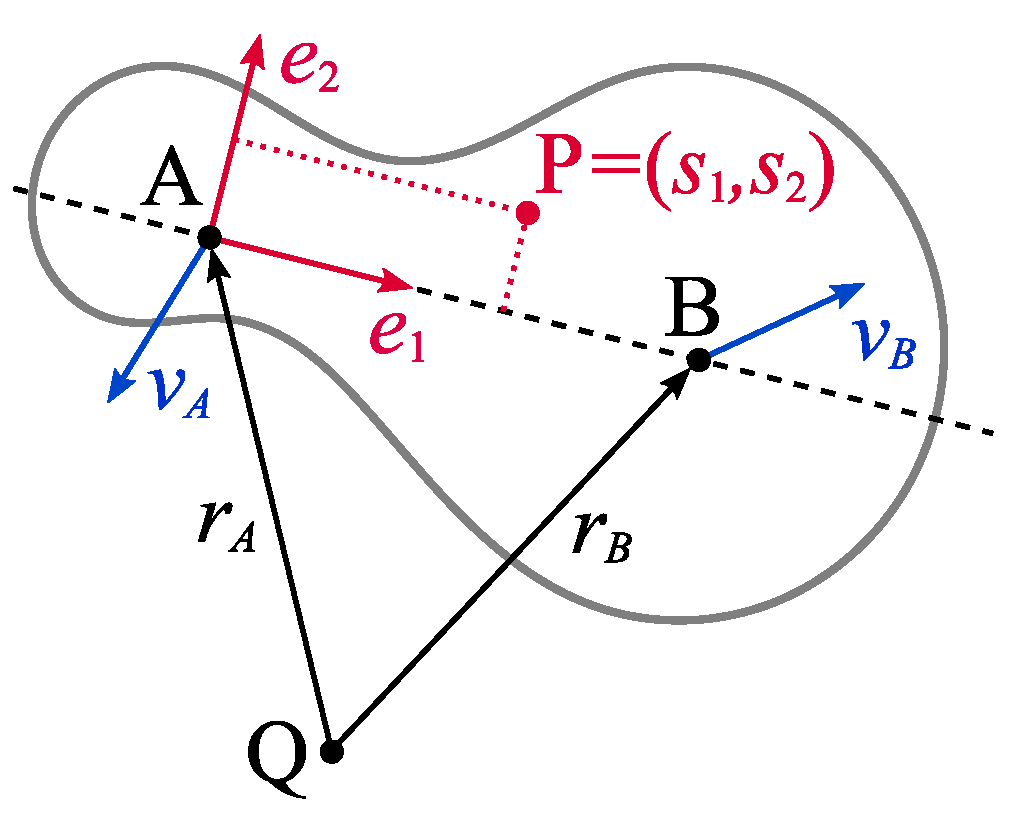
3.1. Equations of Motion
3.2. The One-Dimensional Case
3.3. The Two-Dimensional Case
3.4. The Three-Dimensional Case
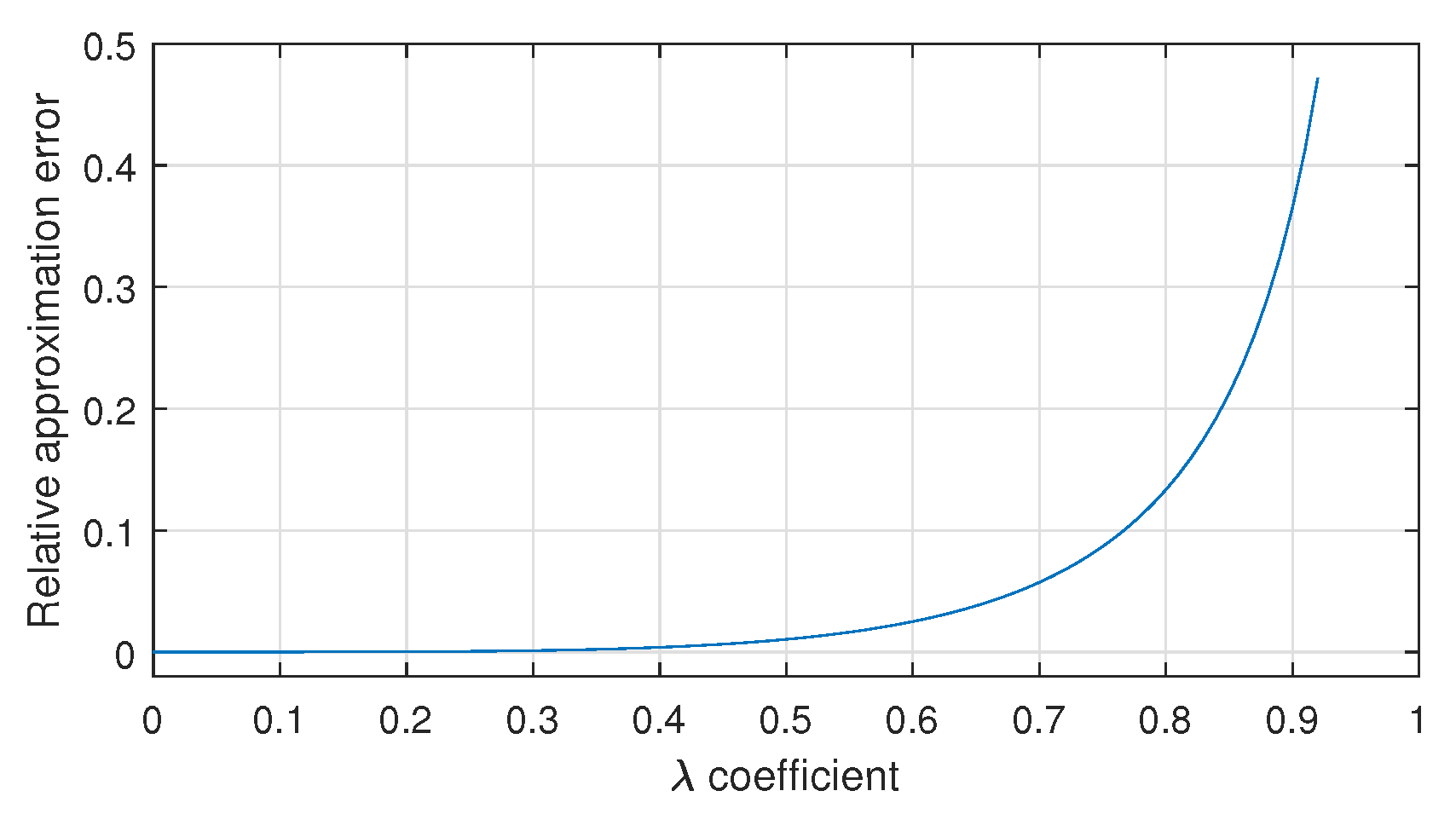
4. Results
4.1. Numerical Determination of the Inertia Force Acting on the Connecting Rod
- –
- Length of connecting rod ;
- –
- Crank radius ;
- –
- Coefficient ;
- –
- Density of connecting rod material kg/m3 for 42CrMo4, kg/m3 for aluminum 2618 and kg/m3 for Ti6Al4V;
- –
- Shaft rotational speed ;
- –
- Shaft angular speed .
- –
- Length of connecting rod ;
- –
- Crank radius ;
- –
- Coefficient ;
- –
- Weight of connecting rod ;
- –
- Shaft rotational speed ;
- –
- Shaft angular speed ;
- –
- Part of connecting rod weight in rotational motion ;
- –
- Part of the connecting rod mass unbalanced with respect to the axis connecting the center of the small end and the center of the big end .
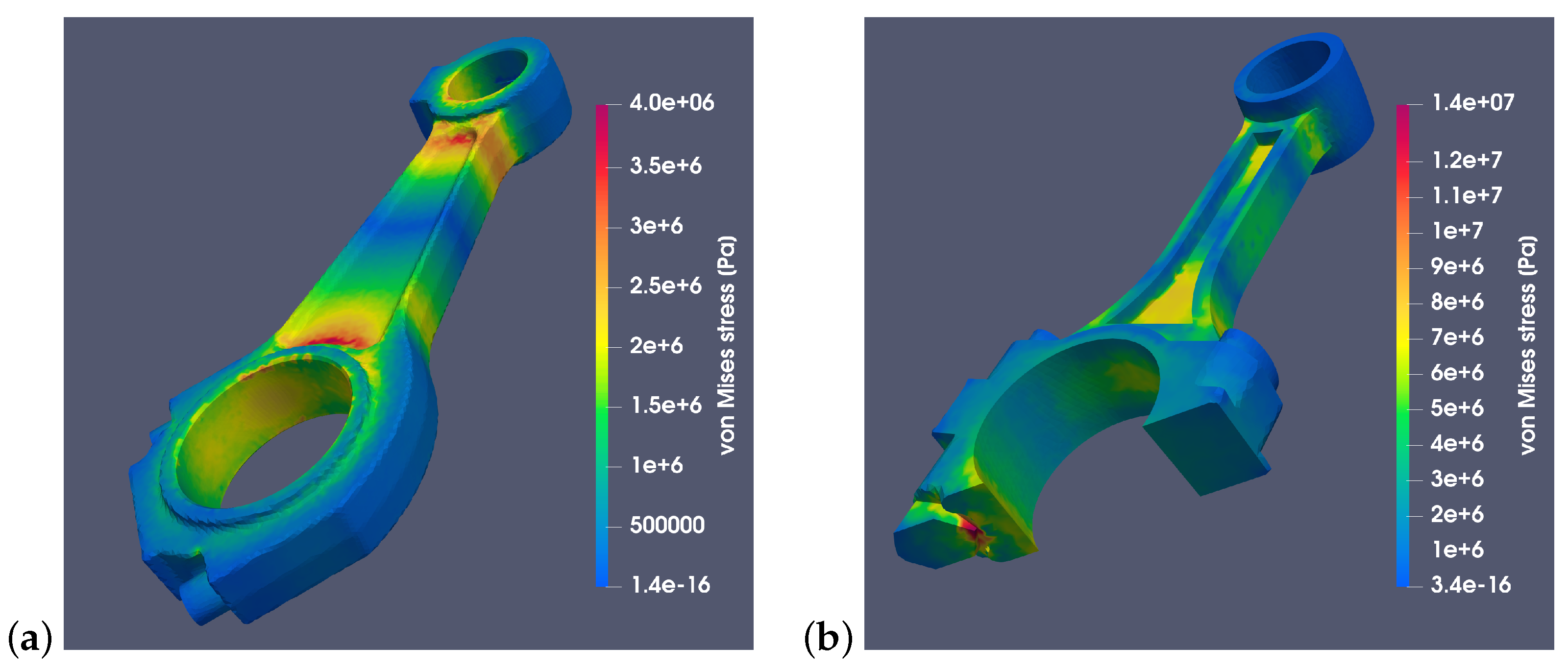
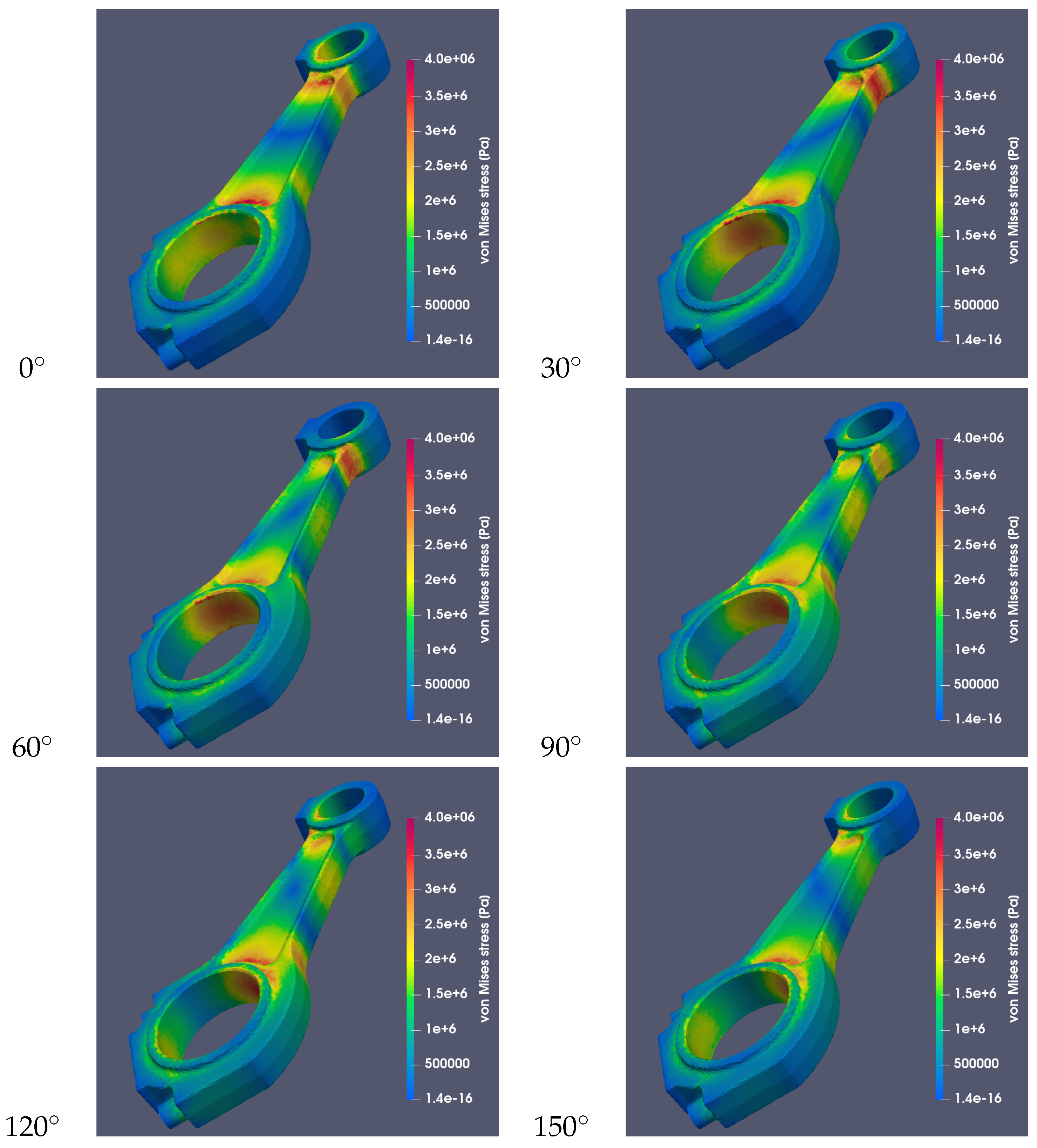
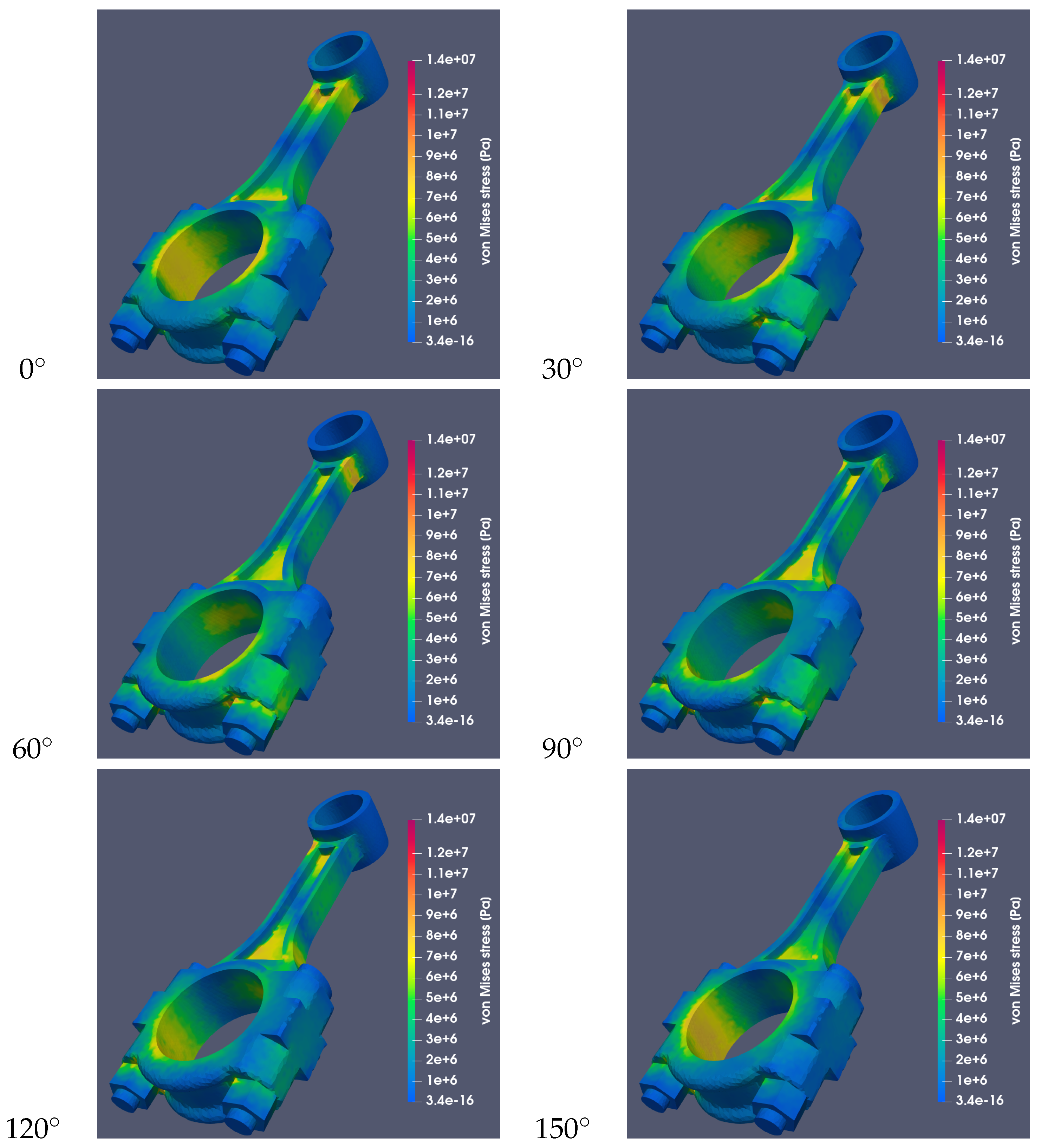
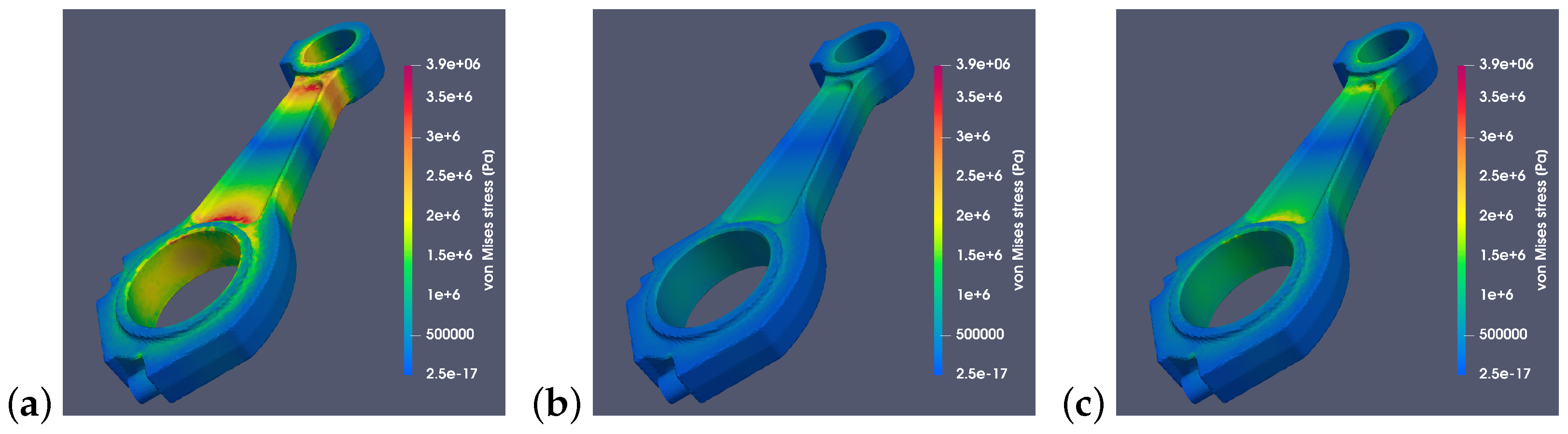
4.2. Using FEM to Analyze Inertial Stresses
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
# Load the~mesh from STL file
mesh = meshio.read("conrod_suzuki_si.msh")
#mesh = meshio.read("conrod_rabaman_si.msh")
# Extract points and cells (tetrahedrons) points = np.array(mesh.points) cells = mesh.cells_dict["tetra"]
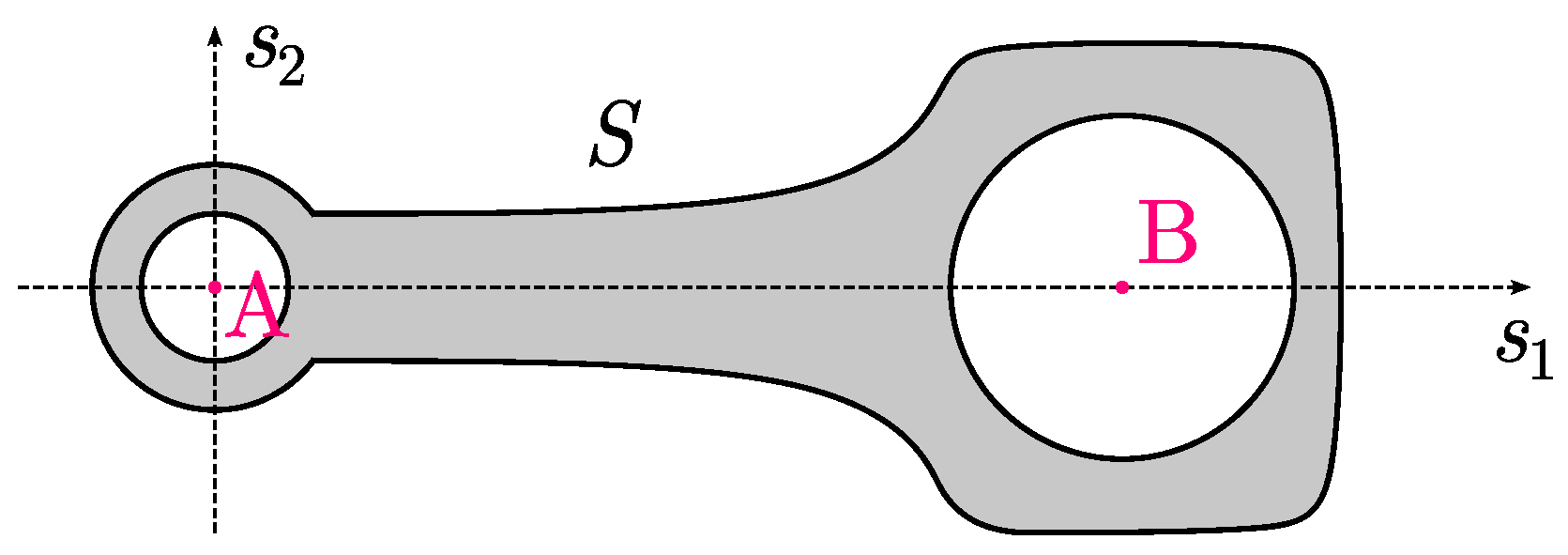
- After loading the tetrahedral mesh, the total volume of the connecting rod V, its mass , and the moments and are determined based on the model geometry and material density. The following code fragment performs these calculations.
# Numerical integration - summation by tetrahedrons
for i in range(len(cells)):
# Take tetrahedron vertices indices
ti = cells[i]
# Convert vertices indices to (x,y,z) coordinates:
pi = points[ti, :].T
# Convert vertices A,B,C,D to 3 vectors with origin at A
wi = pi[:, 1:4] - pi[:, 0:1]
# Volume of tetrahedron ABCD as 1/6 of vectors volume
Vi = abs(np.linalg.det(wi)) / 6
V += Vi
# Compute tetrahedron mass
mci = rho * Vi
mc += mci
# Tetrahedron ABCD centroid
d = np.sum(pi, axis=1) / 4
# Integration by s1*dm and s2*dm
mc1 += d[0] * mci
mc2 += d[1] * mci
Appendix B
// Macro, epsilon(ux,uy,uz)’ * epsilon(vx,vy,vz) = \ epsilon(u) : epsilon(v) macro epsilon(ux,uy,uz) [ dx(ux), (dy(ux)+dx(uy))/2, \ (dz(ux)+dx(uz))/2, (dx(uy)+dy(ux))/2, dy(uy), \ (dz(uy)+dy(uz))/2, (dx(uz)+dz(ux))/2, (dy(uz)+dz(uy))/2, \ dz(uz) ] //
// Macro, div(ux,uy,uz) = \nabla \cdot [ux,uy,uz] macro div(ux,uy,uz) ( dx(ux) + dy(uy) + dz(uz) ) //
// ...
// Body force (density * acceleration) func fx = rho*omega*omega*R*(l*cos(2*alpha) - (1/L)*x*l*cos(2*alpha) + (1/L)*y*sin(alpha) + cos(alpha)); func fy = rho*omega*omega*R*(-(1/L)*y*l*cos(2*alpha) - (1/L)*x*sin(alpha)); func fz = 0;
// Equilibrium state (weak formulation)
solve ConRod3D([ux,uy,uz], [vx,vy,vz])
= int3d(Th)(
lambda * div(ux, uy, uz) * div(vx, vy, vz)
+ 2.*mu * ( epsilon(ux, uy, uz)’ * epsilon(vx, vy, vz) )
)
- int3d(Th)(
[fx,fy,fz]’ * [vx,vy,vz]
)
+ on(212, ux=0, uy=0, uz=0)
+ on(213, ux=0, uy=0, uz=0);
References
- Ou, S.; Yu, Y.; Yang, J. Identification and reconstruction of anomalous sensing data for combustion analysis of marine diesel engines. Measurement 2022, 193, 110960. [Google Scholar] [CrossRef]
- Gutiérrez León, P.; García-Morales, J.; Escobar-Jiménez, R.; Gómez-Aguilar, J.; López-López, G.; Torres, L. Implementation of a fault tolerant system for the internal combustion engine’s MAF sensor. Measurement 2018, 122, 91–99. [Google Scholar] [CrossRef]
- Manjhi, S.; Kumar, R. Transient surface heat flux measurement for short duration using K-type, E-type and J-type of coaxial thermocouples for internal combustion engine. Measurement 2019, 136, 256–268. [Google Scholar] [CrossRef]
- Vladov, S.; Bulakh, M.; Baranovskyi, D.; Sokurenko, V.; Muzychuk, O.; Vysotska, V. Helicopter turboshaft engines combustion chamber monitoring neural network method. Measurement 2025, 242, 116267. [Google Scholar] [CrossRef]
- Razavykia, A.; Delprete, C.; Baldissera, P. Numerical study of power loss and lubrication of connecting rod big-end. Lubricants 2019, 7, 47. [Google Scholar] [CrossRef]
- He, Z.; Sun, Y.; Zhang, G.; Hong, Z.; Xie, W.; Lu, X.; Zhang, J. Tribilogical performances of connecting rod and by using orthogonal experiment, regression method and response surface methodology. Appl. Soft Comput. 2015, 29, 436–449. [Google Scholar] [CrossRef]
- Mangeruga, V.; Barbieri, S.; Giacopini, M.; Bianco, L.; Ferretti, A.; Mazziotta, M. Analysis of the tribological behaviour of the lubricated contacts of a connecting rod equipped with a direct pin oiling gallery. Tribol. Int. 2024, 198, 109851. [Google Scholar] [CrossRef]
- Sun, J.; Li, B.; Zhu, S.; Miao, E.; Wang, H.; Zhao, X.; Teng, Q. Lubrication performance of connecting-rod and main bearing in different engine operating conditions. Chin. J. Mech. Eng. 2019, 32, 23. [Google Scholar] [CrossRef]
- Yin, J.; Liu, R.; Zhang, R.; Lv, B.; Meng, X. A new tribo-dynamics model for engine connecting rod small-end bearing considering elastic deformation and thermal effects. Tribol. Int. 2023, 188, 108831. [Google Scholar] [CrossRef]
- Morris, N.; Mohammadpour, M.; Rahmani, R.; Johns-Rahnejat, P.; Rahnejat, H.; Dowson, D. Effect of cylinder deactivation on tribological performance of piston compression ring and connecting rod bearing. Tribol. Int. 2018, 120, 243–254. [Google Scholar] [CrossRef]
- Chao, J. Fretting-fatigue induced failure of a connecting rod. Eng. Fail. Anal. 2019, 96, 186–201. [Google Scholar] [CrossRef]
- Zhu, J.; Zhu, H.; Fan, S.; Xue, L.; Li, Y. A study on the influence of oil film lubrication to the strength of engine connecting rod components. Eng. Fail. Anal. 2016, 63, 94–105. [Google Scholar] [CrossRef]
- Pan, Z.; Zhang, Y. Numerical investigation into high cycle fatigue of aero kerosene piston engine connecting rod. Eng. Fail. Anal. 2021, 120, 105028. [Google Scholar] [CrossRef]
- Croccolo, D.; De Agostinis, M.; Fini, S.; Olmi, G.; Paiardini, L.; Robusto, F. Tribological properties of connecting rod high strength screws improved by surface peening treatments. Metals 2020, 10, 344. [Google Scholar] [CrossRef]
- Jiang, T.; Zhou, J.; Cao, Y.; Wang, M.; Zhang, S. A connecting rod assembly deformation cognition method based on quality characteristics probability network. Adv. Eng. Inform. 2024, 62, 102580. [Google Scholar] [CrossRef]
- Francisco, A.; Lavie, T.; Fatu, A.; Villechaise, B. Metamodel-assisted optimization of connecting rod big-end bearings. J. Tribol. 2013, 135, 041704. [Google Scholar] [CrossRef]
- Witek, L.; Zelek, P. Stress and failure analysis of the connecting rod of diesel engine. Eng. Fail. Anal. 2019, 97, 374–382. [Google Scholar] [CrossRef]
- Lee, M.; Lee, H.; Lee, T.; Jang, H. Buckling sensitivity of a connecting rod to the shank sectional area reduction. Mater. Des. 2010, 31, 2796–2803. [Google Scholar] [CrossRef]
- Seyedzavvar, M.; Seyedzavvar, M. Design of high duty diesel engine connecting rod based on finite element analysis. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 59. [Google Scholar] [CrossRef]
- Shenoy, P.; Fatemi, A. Connecting Rod Optimization for Weight and Cost Reduction. SAE Trans. 2005, 114, 523–530. [Google Scholar] [CrossRef]
- Mekonen, A.; Yosiph, B.; Dawit, J. Finite Element Analysis of Fatigue Life Prediction for Connecting Rod Using Aluminum and Steel Alloy Materials. IJISET-Int. J. Innov. Sci. Eng. Technol. 2019, 6, 417–428. [Google Scholar]
- Cheng, G.; Li, J.; Sun, J.; Liu, Y. Finite Element Analysis of the Fatigue Life for the Connecting Rod Remanufacturing. J. Appl. Sci. 2013, 13, 1436–1442. [Google Scholar] [CrossRef]
- Ranjbarkohan, M.; Asadi, M.; Mohammadi, M.; Heidar, A. Fatigue analysis of connecting rod of samand engine by Finite Element Method. Aust. J. Basic Appl. Sci. 2011, 5, 841–845. [Google Scholar]
- Muhammad, A.; Mohammed, A.; Shanono, I. Finite Element Analysis of a connecting rod in ANSYS: An overview. IOP Conf. Ser. Mater. Sci. Eng. 2020, 736, 022119. [Google Scholar] [CrossRef]
- Gopinath, D.; Sushma, C. Design and Optimization of Four Wheeler Connecting Rod Using Finite Element Analysis. Mater. Today Proc. 2015, 2, 2291–2299. [Google Scholar] [CrossRef]
- Zheng, Q.; Yang, B.; Yang, H.; Hu, M. Finite Element Analysis and Research of Engine Connecting Rod. Adv. Mater. Res. 2014, 915–916, 142–145. [Google Scholar] [CrossRef]
- Li, R.; Meng, X.; Liu, R.; Muhammad, R.; Li, W.; Dong, J. Crosshead Bearing Analysis for Low-Speed Marine Diesel Engines Based on a Multi-Body Tribo-Dynamic Model. Int. J. Engine Res. 2020, 9, 1–22. [Google Scholar] [CrossRef]
- Meng, X.; Xiea, Y. A New Numerical Analysis for Piston Skirt–Liner System Lubrication Considering the Effects of Connecting Rod Inertia. Tribol. Int. 2012, 47, 235–243. [Google Scholar] [CrossRef]
- Harrison, M. Sources of vibration and their control. In Vehicle Refinement; Butterworth-Heinemann: Oxford, UK, 2004; pp. 269–340. [Google Scholar] [CrossRef]
- Xie, Z.; Xu, Q.; Guan, N.; Zhou, M. A new closed-form method for inertia force and moment calculation in reciprocating piston engine design. Sci. China Technol. Sci. 2018, 61, 879–885. [Google Scholar] [CrossRef]
- Chmielowiec, A.; Michajłyszyn, A.; Homik, W. Behaviour of a Torsional Vibration Viscous Damper in the Event of a Damper Fluid Shortage. Pol. Marit. Res. 2023, 30, 105–113. [Google Scholar] [CrossRef]
- Chmielowiec, A.; Woś, W.; Gumieniak, J. Viscosity Approximation of PDMS Using Weibull Function. Materials 2021, 14, 6060. [Google Scholar] [CrossRef] [PubMed]
- Vladov, S.; Bulakh, M.; Baranovskyi, D.; Kisiliuk, E.; Vysotska, V.; Romanov, M.; Czyżewski, J. Application of the Integral Energy Criterion and Neural Network Model for Helicopter Turboshaft Engine’s Vibration Characteristics Analysis. Energies 2024, 17, 5776. [Google Scholar] [CrossRef]
- Lakshminarayanan, P.; Avinash, K. Design and Development of Heavy Duty Diesel Engines; Springer: Singapore, 2020. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.F. Gmsh: A 3-D finite element mesh generator with built-in pre-and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Hecht, F. New development in freefem++. J. Numer. Math. 2012, 20, 251–266. [Google Scholar] [CrossRef]
- Gao, W.; Wang, G.; Zhu, J.; Fan, Z.; Li, X.; Wu, W. Structural Optimization Design and Strength Test Research of Connecting Rod Assembly of High-Power Low-Speed Diesel Engine. Machines 2022, 10, 815. [Google Scholar] [CrossRef]
- Gopal, G.; Kumar, L.; Reddy, K.; Rao, M.; Srinivasulu, G. Analysis of Piston, Connecting rod and Crank shaft assembly. Mater. Today Proc. 2017, 4, 7810–7819. [Google Scholar] [CrossRef]
- Saxena, S.; Ambikesh, R. Design and finite element analysis of connecting rod of different materials. In Proceedings of the AIP Conference Proceedings; AIP Publishing: Jamshedpur, India, 2021; Volume 2341. [Google Scholar] [CrossRef]
- Cecchel, S.; Razavi, N.; Mega, F.; Cornacchia, G.; Avanzini, A.; Battini, D.; Berto, F. Fatigue testing and end of life investigation of a topology optimized connecting rod fabricated via selective laser melting. Int. J. Fatigue 2022, 164, 107134. [Google Scholar] [CrossRef]
- Hmida, A.; Hammami, A.; Chaari, F.; Amar, M.; Haddar, M. Effects of Misfire on the Dynamic Behavior of Gasoline Engine Crankshafts. Eng. Fail. Anal. 2021, 121, 105149. [Google Scholar] [CrossRef]
- Mendes, A.; Meirelles, P.; Zampieri, D. Analysis of Torsional Vibration in Internal Combustion Engines: Modelling and Experimental Validation. Proc. Inst. Mech. Eng. Part K J. Multi-Body Dyn. 2008, 222, 155–178. [Google Scholar] [CrossRef]
- Ali, M.; Alshalal, I.; Mohmmed, J. Effect of the Torsional Vibration Depending on the Number of Cylinders in Reciprocating Engines. Int. J. Dyn. Control. 2021, 9, 901–909. [Google Scholar] [CrossRef]
- Alkalla, M.; Helal, M.; Fouly, A. Revolutionary Superposition Layout Method for Topology Optimization of Nonconcurrent Multiload Models: Connecting-Rod Case Study. Int. J. Numer. Methods Eng. 2021, 122, 1378–1400. [Google Scholar] [CrossRef]
- Berbatov, K.; Lazarov, B.; Jivkov, A. A guide to the finite and virtual element methods for elasticity. Appl. Numer. Math. 2021, 169, 351–395. [Google Scholar] [CrossRef]
- Lamichhane, B.; McBride, A.; Reddy, B. A finite element method for a three-field formulation of linear elasticity based on biorthogonal systems. Comput. Methods Appl. Mech. Eng. 2013, 258, 109–117. [Google Scholar] [CrossRef]
- Renso, F.; Barbieri, S.; Mangeruga, V.; Giacopini, M. Finite Element Analysis of the Influence of the Assembly Parameters on the Fretting Phenomena at the Bearing/Big End Interface in High-Performance Connecting Rods. Lubricants 2023, 11, 375. [Google Scholar] [CrossRef]
- Trovato, M.; Perquoti, F.; Cicconi, P. Topological optimization for the redesigning of components in additive manufacturing: The case study of the connecting rod. Eng. Proc. 2023, 56, 131. [Google Scholar] [CrossRef]
- Andoko, D. Elastic Linear Analysis of Connecting Rods for Single Cylinder Four Stroke Petrol Engines Using Finite Element Method. J. Mech. Eng. Sci. Technol. 2019, 3, 42–50. [Google Scholar] [CrossRef]


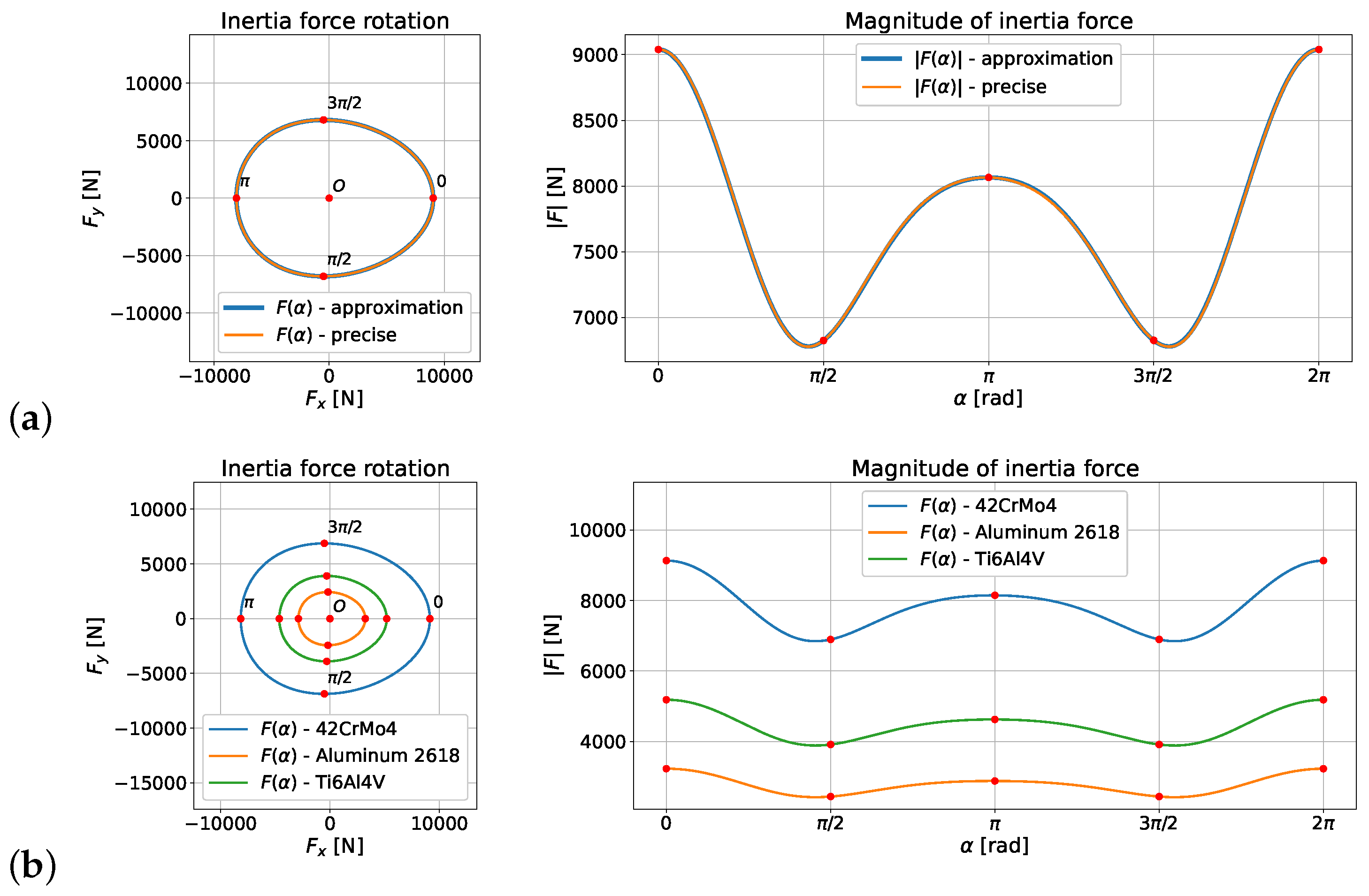
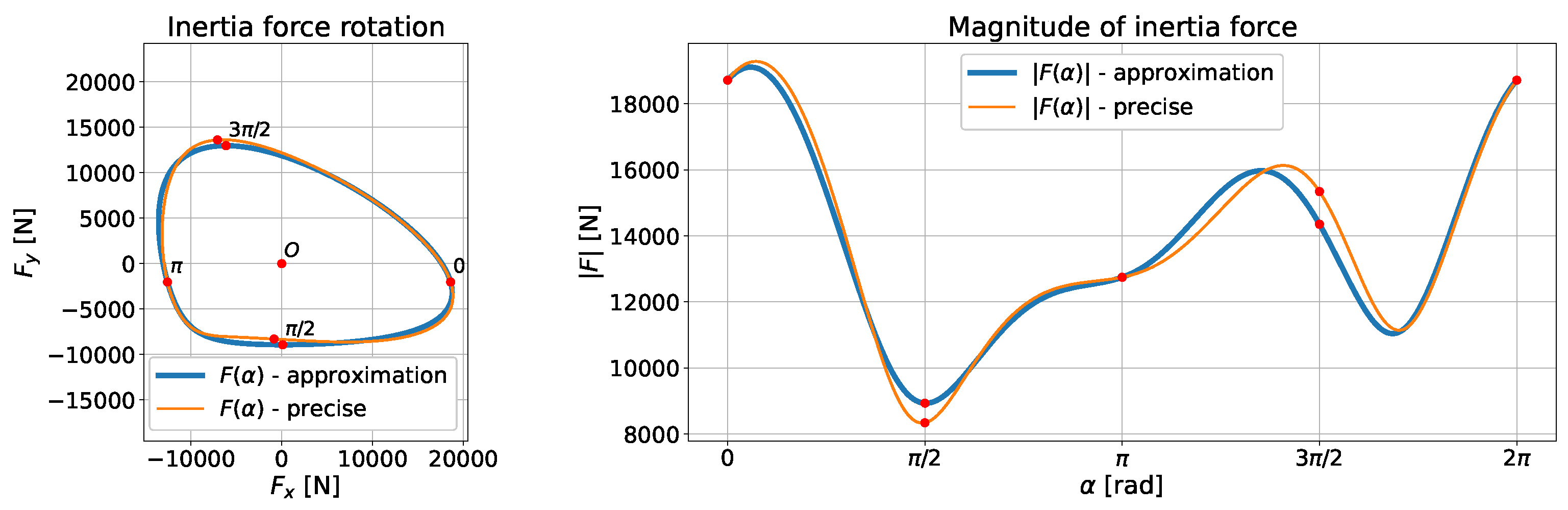

| RÁBA-MAN D2356 HM6U | Suzuki GS650 | |
|---|---|---|
| Displacement [cm3] | 10,690 | 650 |
| Maximum power [kW] | ||
| Cylinder diameter [mm] | 121 | 62 |
| Shaft’s rotational speed [rpm] | 2100 | 9500 |
| [rad/s] | ||
| R [mm] | 75 | |
| L [mm] | 275 | 100 |
| [-] | ||
| [g] |
| 42CrMo4 | Aluminum 2618 | Ti6Al4V | |
|---|---|---|---|
| Young’s modulus [Pa] | 210 × | 74 × | 114 × |
| Poisson’s ratio | 0.29 | 0.33 | 0.34 |
| Density [kg·m−3] | 7800 | 2760 | 4430 |
| RÁBA-MAN D2356 HM6U | Suzuki GS650 | ||
|---|---|---|---|
| Mesh Size [mm] | Maximum [MPa] | Mesh Size [mm] | Maximum [MPa] |
| 1.20 | 5.634 | 0.360 | 15.063 |
| 1.40 | 5.494 | 0.420 | 15.007 |
| 1.70 | 5.203 | 0.540 | 13.094 |
| 2.00 | 4.347 | 0.720 | 12.469 |
| 2.50 | 3.874 | 0.900 | 12.666 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chmielowiec, A.; Woś, W.; Czyżewski, J. Numerical Analysis of Inertia Forces in the Connecting Rod and Their Impact on Stress Formation. Materials 2025, 18, 1385. https://doi.org/10.3390/ma18061385
Chmielowiec A, Woś W, Czyżewski J. Numerical Analysis of Inertia Forces in the Connecting Rod and Their Impact on Stress Formation. Materials. 2025; 18(6):1385. https://doi.org/10.3390/ma18061385
Chicago/Turabian StyleChmielowiec, Andrzej, Weronika Woś, and Jan Czyżewski. 2025. "Numerical Analysis of Inertia Forces in the Connecting Rod and Their Impact on Stress Formation" Materials 18, no. 6: 1385. https://doi.org/10.3390/ma18061385
APA StyleChmielowiec, A., Woś, W., & Czyżewski, J. (2025). Numerical Analysis of Inertia Forces in the Connecting Rod and Their Impact on Stress Formation. Materials, 18(6), 1385. https://doi.org/10.3390/ma18061385







