Predictive Modelling of Alkali-Slag Cemented Tailings Backfill Using a Novel Machine Learning Approach
Abstract
1. Introduction
2. Methods
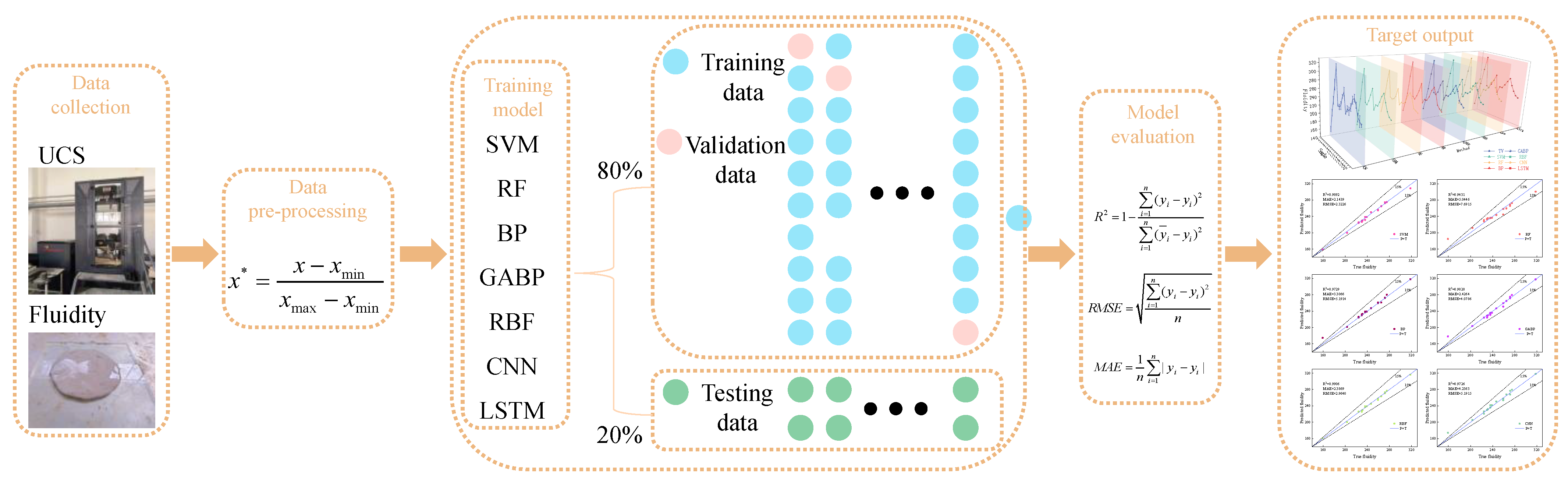
2.1. Data Collection
2.2. Overview of Learning Algorithms
2.2.1. Support Vector Machine
2.2.2. Random Forest
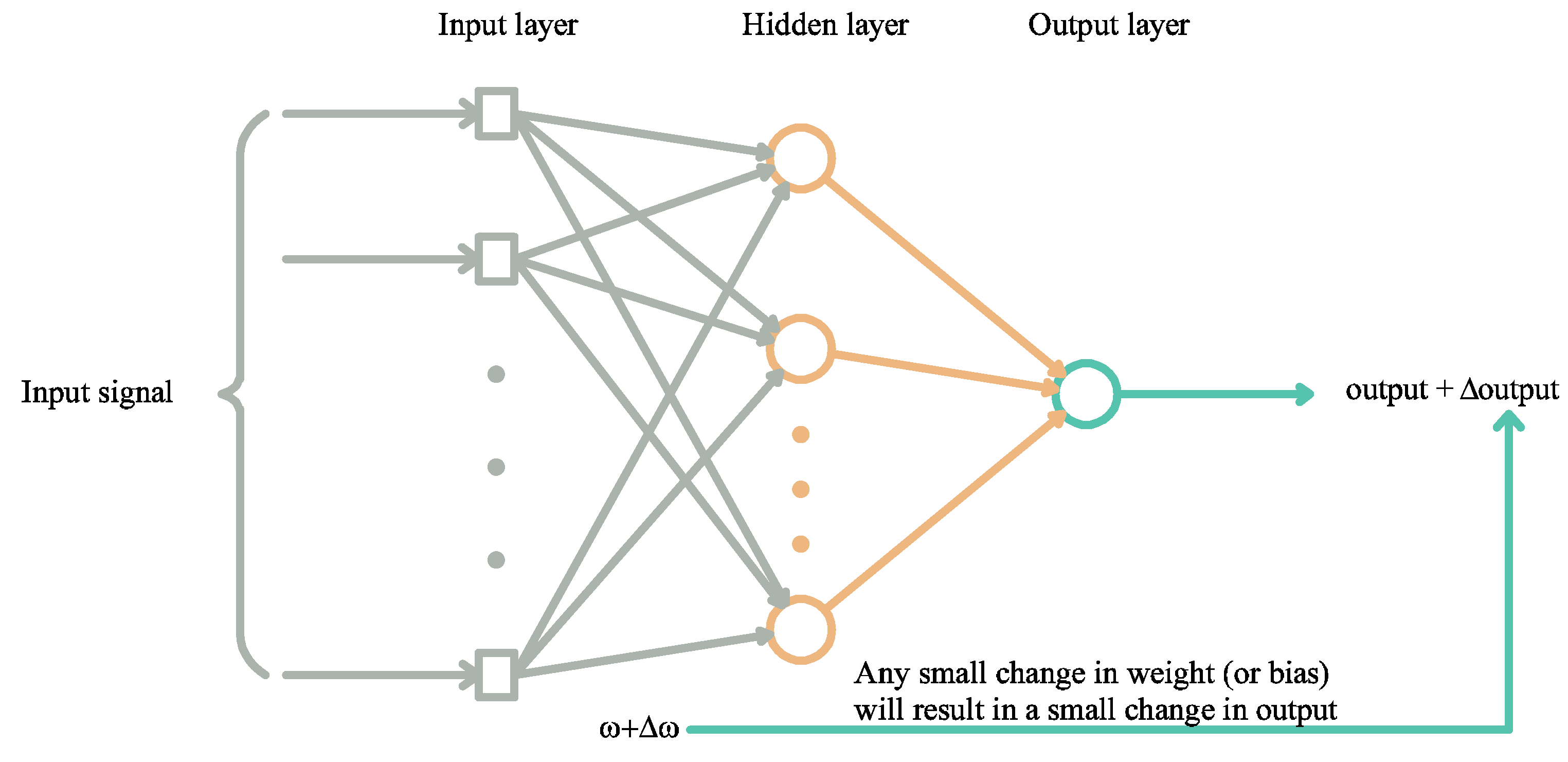
2.2.3. Artificial Neural Network
- (a)
- Backpropagation
- (b)
- Genetic algorithm optimization of BP
- (c)
- Radial basis function neural network
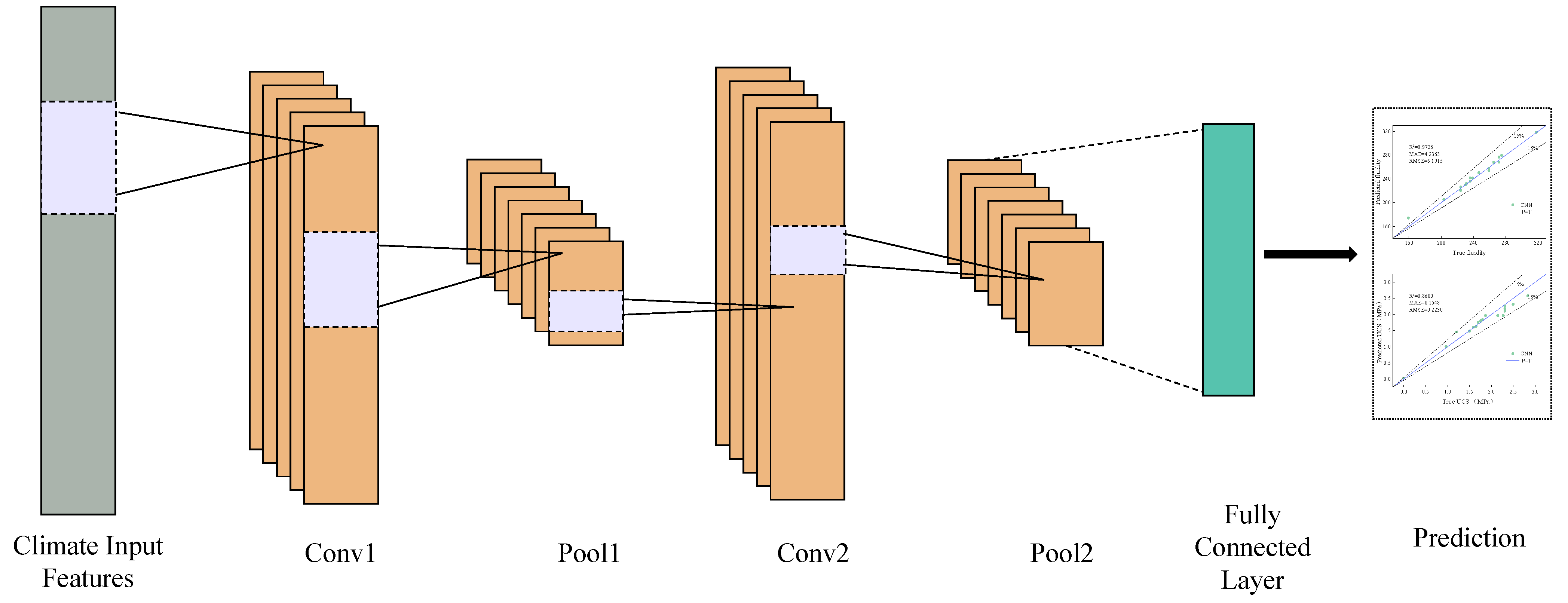
2.2.4. Convolutional Neural Network
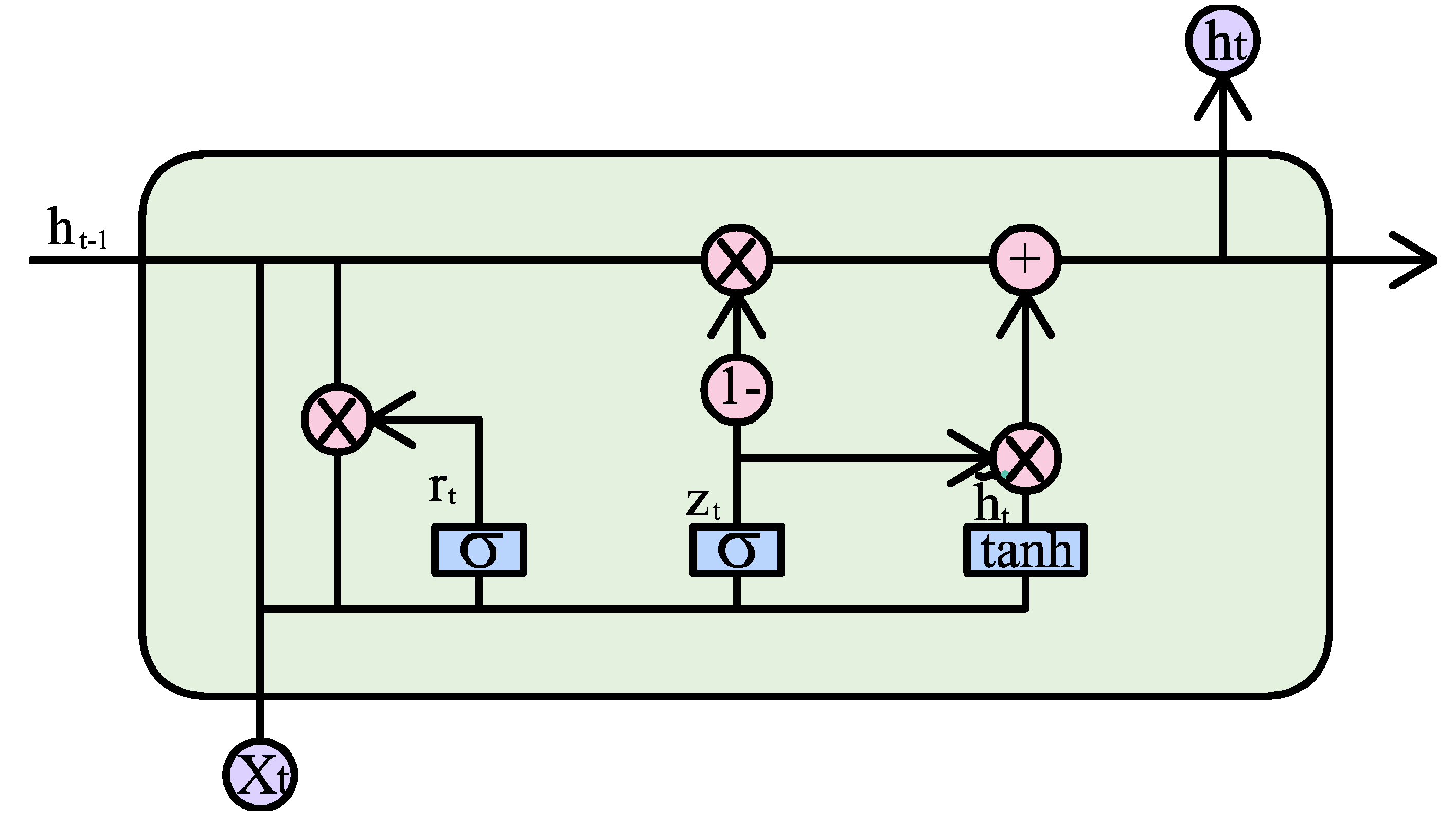
2.2.5. Recurrent Neural Network
2.3. Dataset Preprocessing and Analysis
2.3.1. Data Preprocessing
2.3.2. Data Analysis
2.4. Model Construction
2.4.1. Tuning of Hyperparameters
2.4.2. K-Fold Cross-Validation
3. Discussion
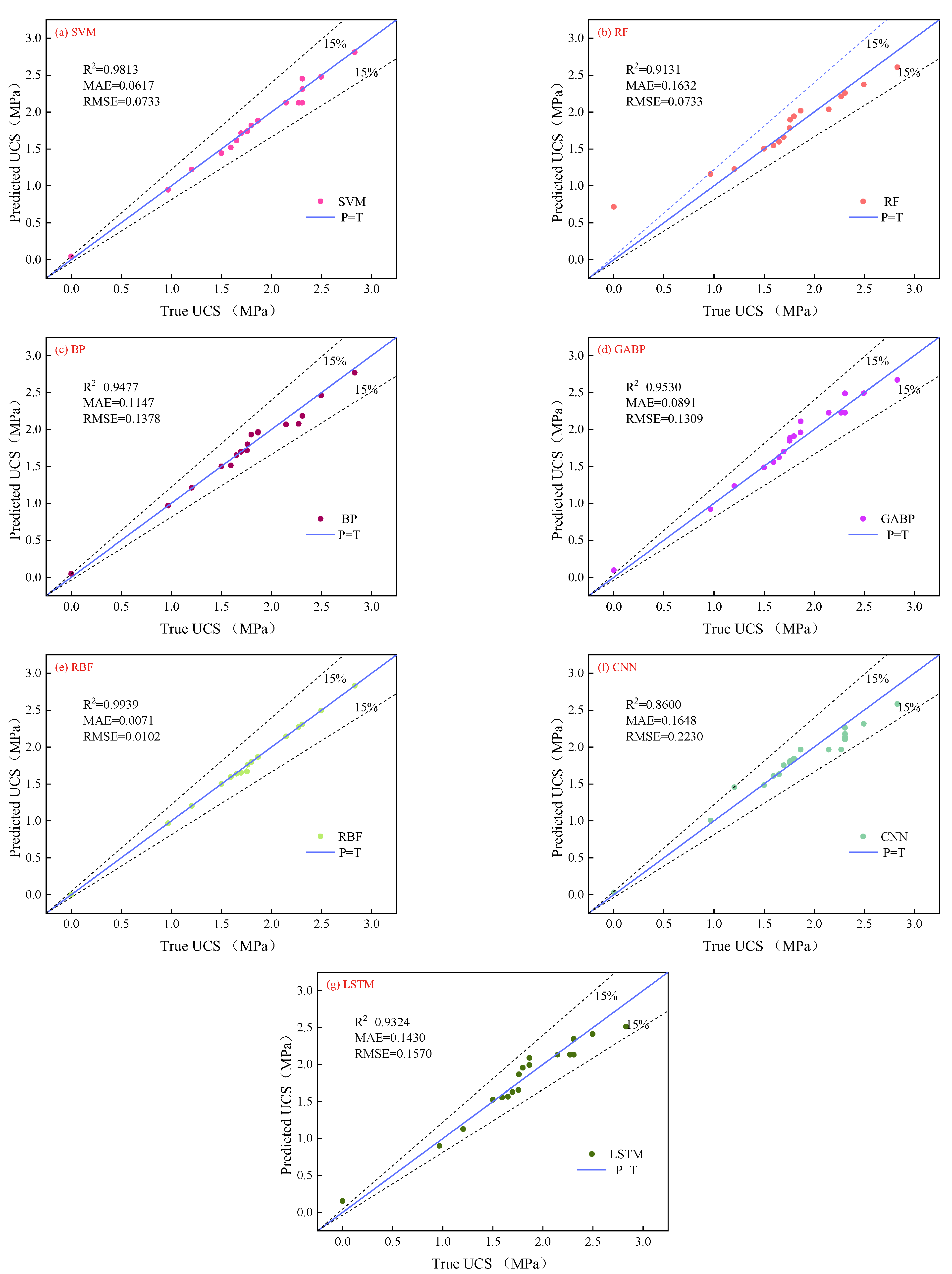
3.1. Model Evaluation
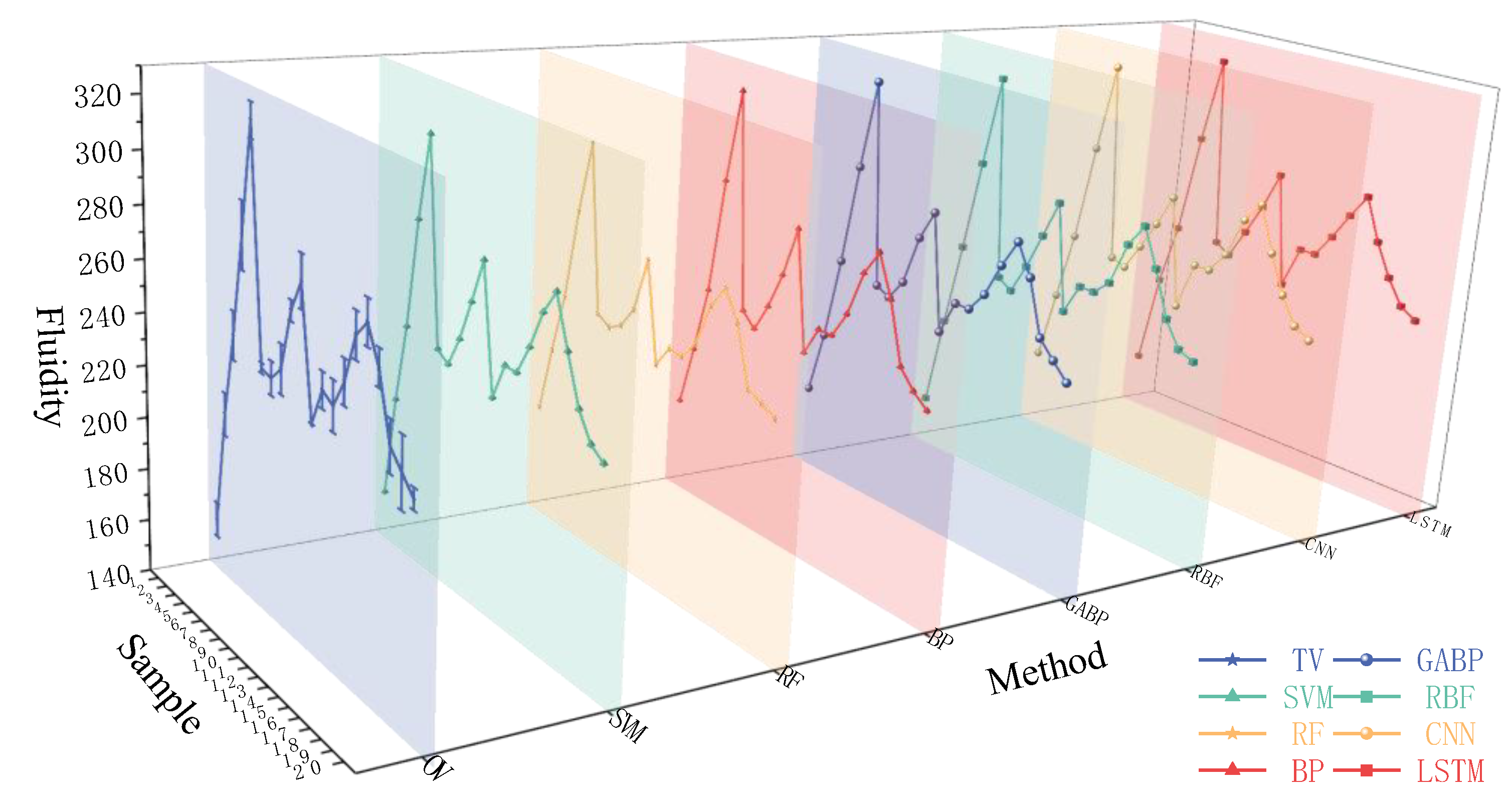
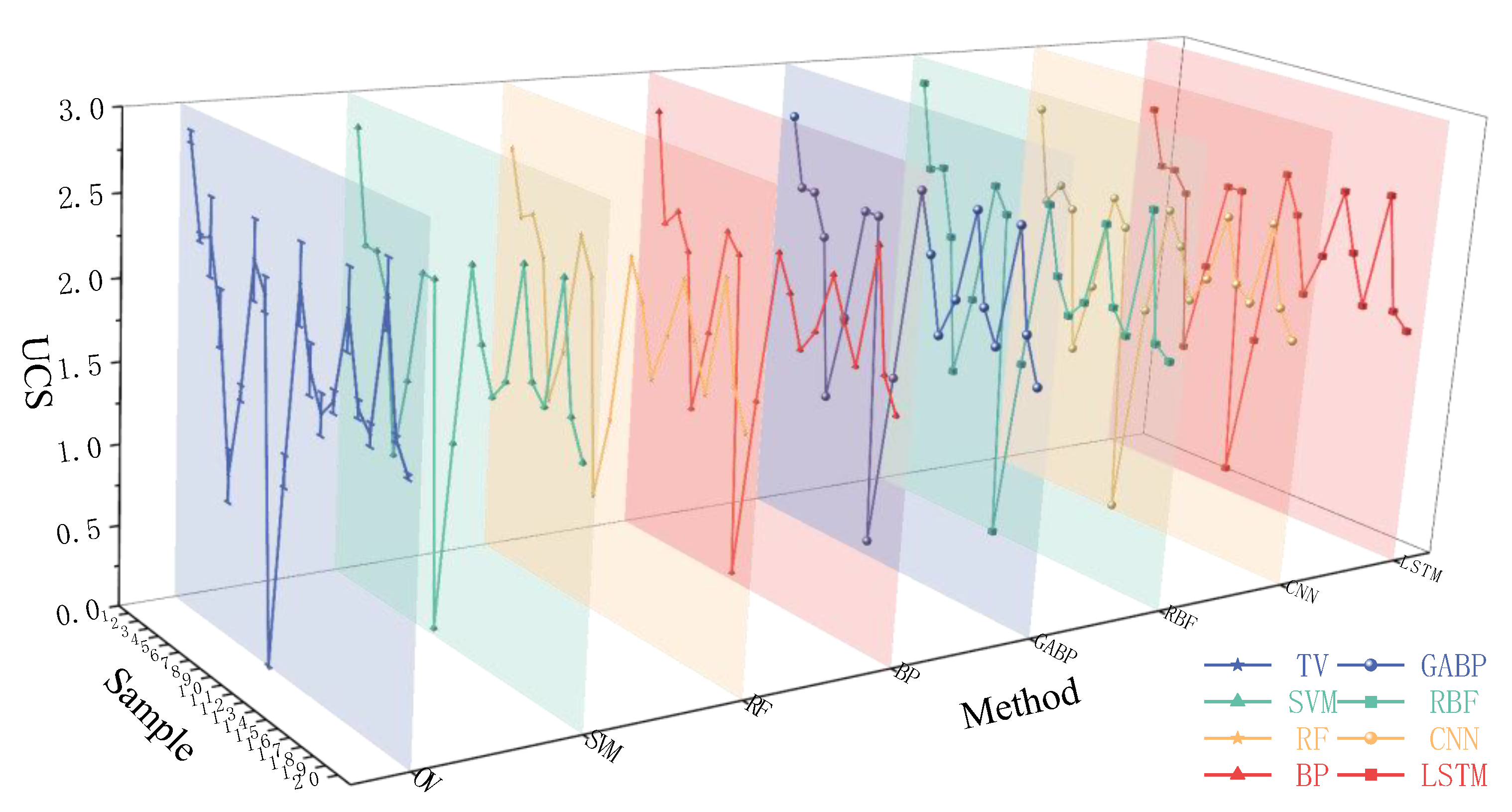
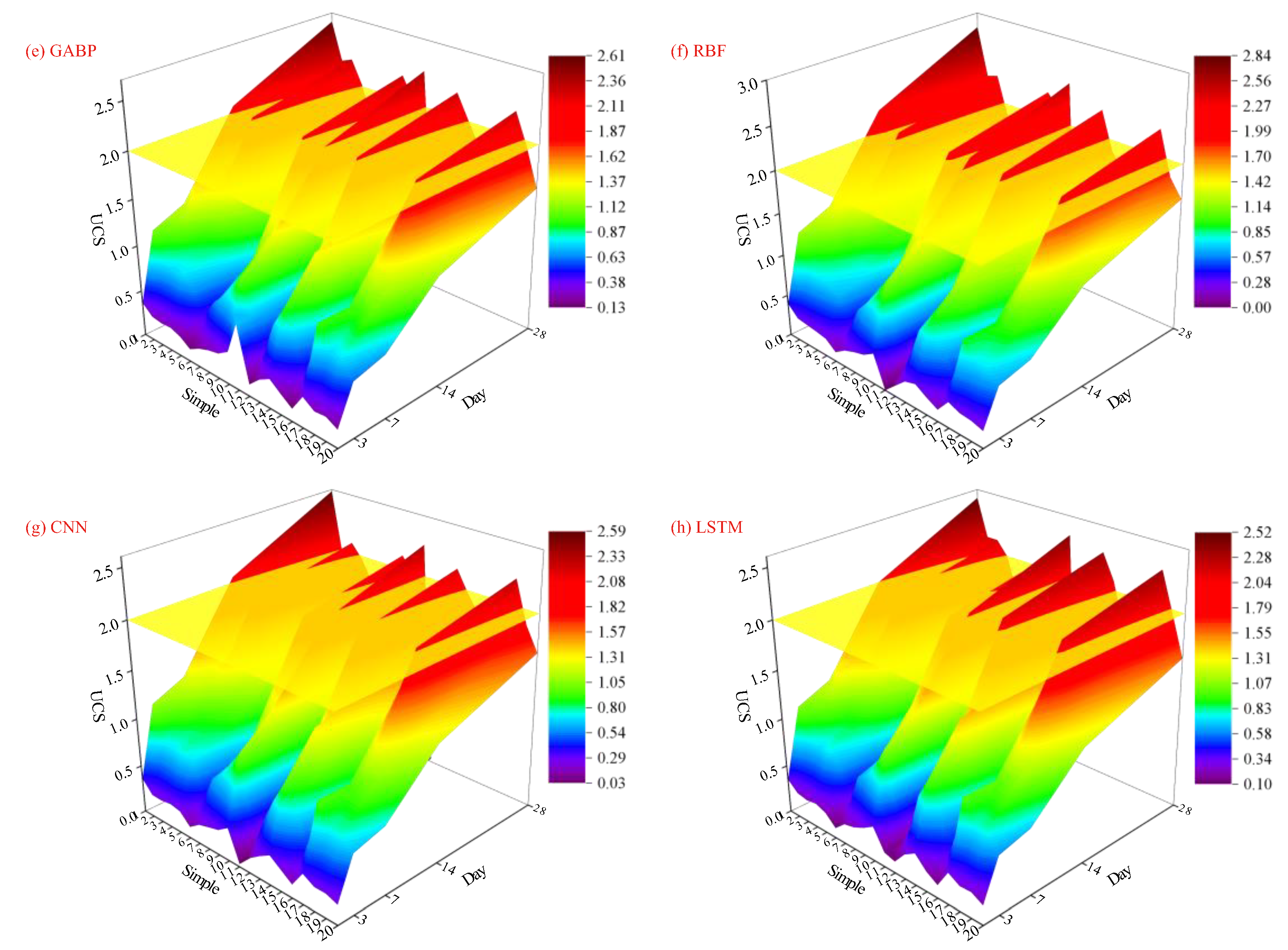
3.2. Prediction Comparison of Models
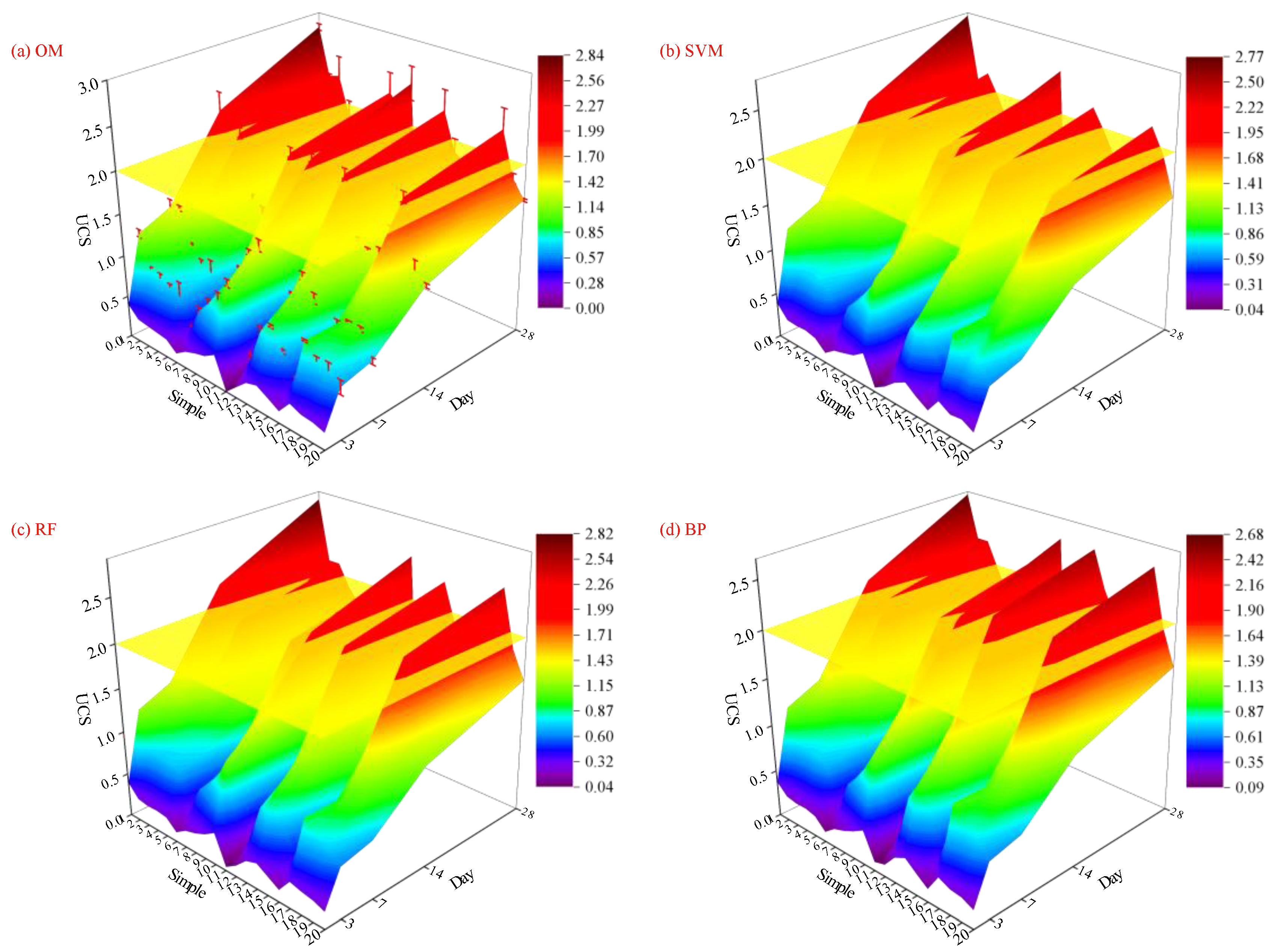
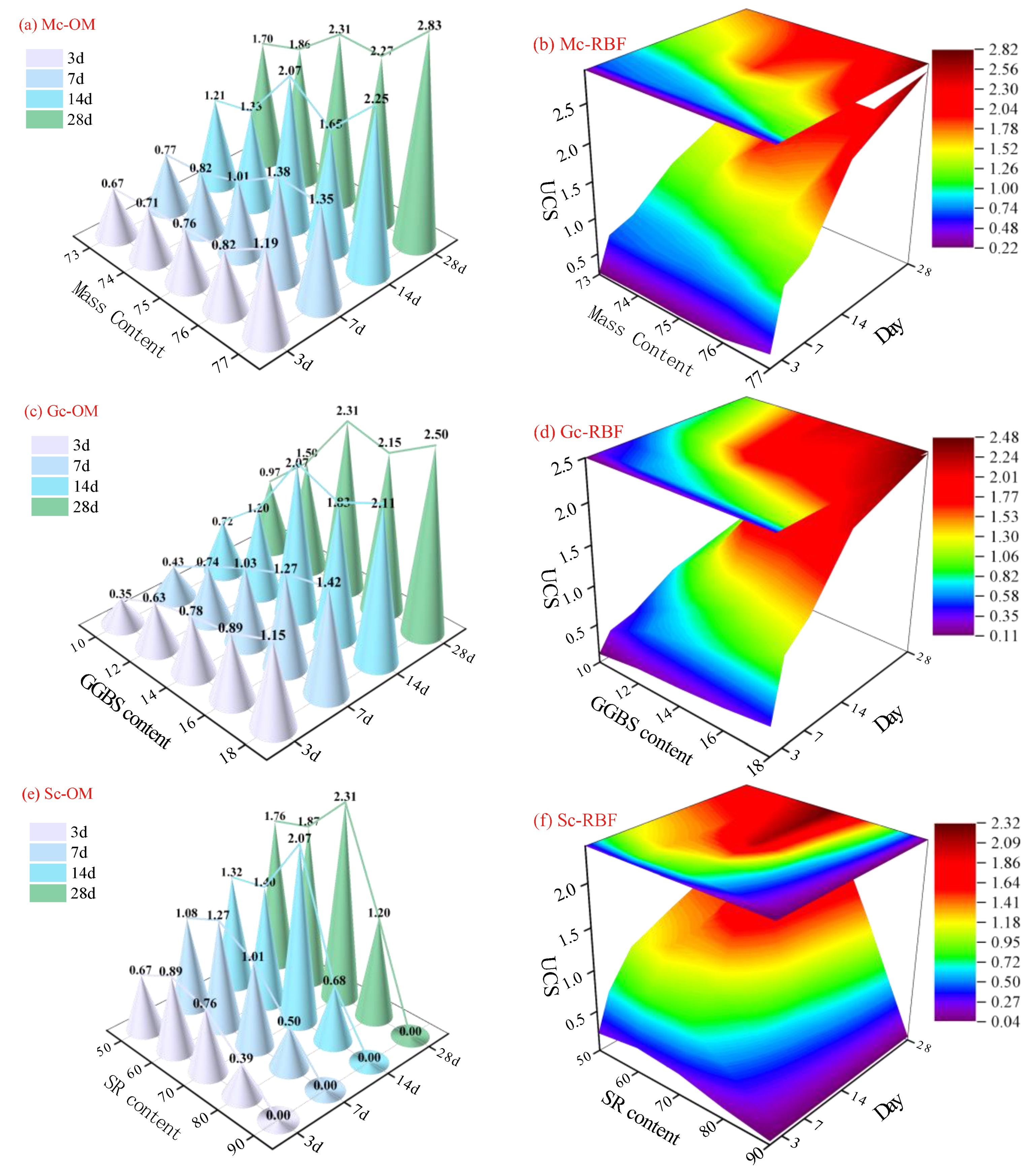
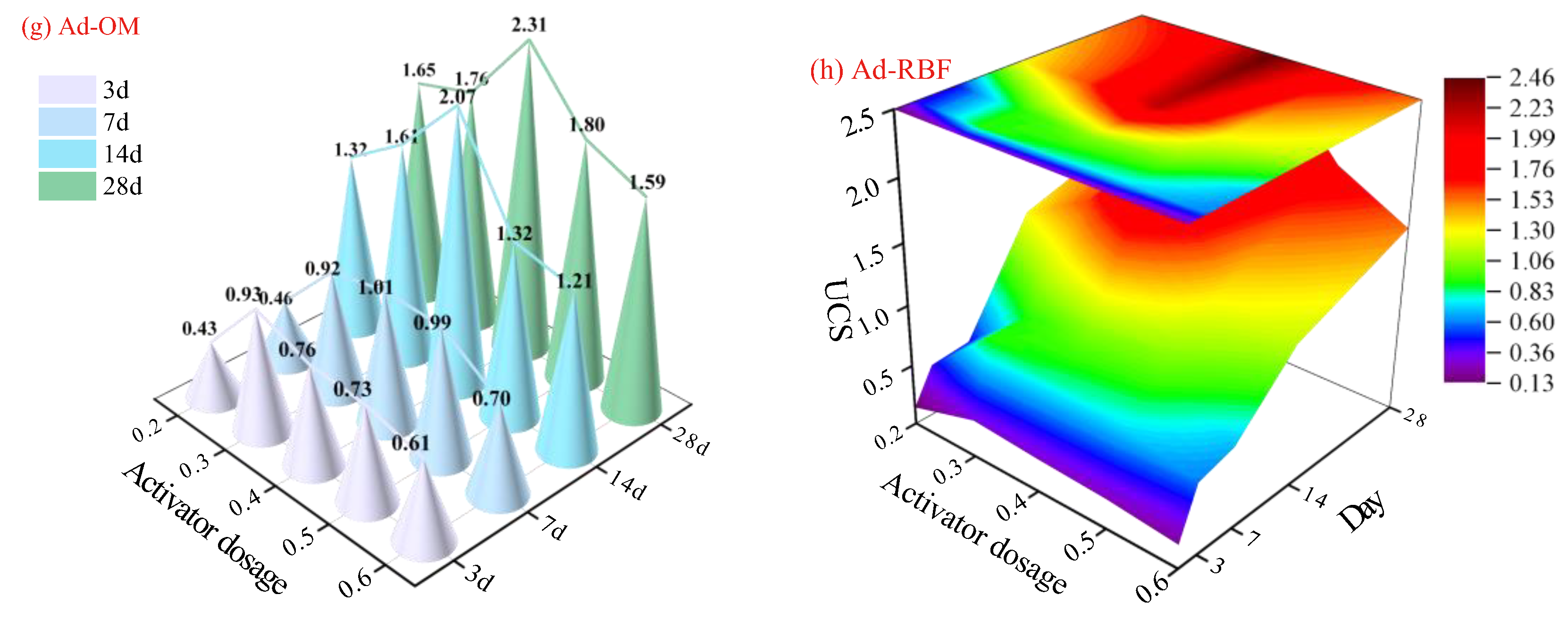
4. Dynamic Prediction on UCS
4.1. Strength Growth Prediction: Combination and Feedback
4.2. RBF-Based Coupling Process of Mix Ratio and Curing Age
5. Conclusions
- (1)
- Since the database established by the research institute contains a significant amount of data with a broad range, the ML model can learn more complex relationships and patterns within the data. This capability enhances its predictive performance and generalization ability.
- (2)
- By comparing the predictive performance of seven ML models, it was found that the RBF model achieved the best prediction for the strength of the filling material, with all R2 values being 0.99. This was followed by SVM, with R2 values close to 0.99. The R2 values for RF, BP, GABP, CNN, and LSTM, except for the CNN prediction on UCS (R2 is 0.86), were all greater than 0.90. The performance of RF in predicting the maximum mechanical properties was poor.
- (3)
- The RBF model can accurately predict the curing age at which the filling material reaches the specified strength. The BP, SVM, and CNN models exhibit delays in predicting the curing age, while the RF, GABP, and LSTM models show advances in predicting the curing age of filling materials to be close to 2 MPa.
- (4)
- The ML technique has taken a meaningful step towards tailings management for the preparation of cemented paste fillers. The effect of material proportioning was mainly considered in this study using the ML technique, and therefore, further validation in other areas is warranted in the future. For example, further studies under different activators and multi-field coupling environments could be considered.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, T.; Sun, W.; Liu, Z.; Cheng, H. Investigation on fracture characteristics and failure pattern of inclined layered cemented tailings backfill. Constr. Build. Mater. 2022, 343, 128110. [Google Scholar] [CrossRef]
- Zheng, D.; Song, W.; Cao, S.; Li, J. Dynamical mechanical properties and microstructure characteristics of cemented tailings backfill considering coupled strain rates and confining pressures effects. Constr. Build. Mater. 2022, 320, 126321. [Google Scholar] [CrossRef]
- Yin, S.; Shao, Y.; Wu, A.; Wang, H.; Liu, X.; Wang, Y. A systematic review of paste technology in metal mines for cleaner production in China. J. Clean. Prod. 2020, 247, 119590. [Google Scholar] [CrossRef]
- Xue, G.; Yilmaz, E.; Song, W.; Cao, S. Mechanical, flexural and microstructural properties of cement-tailings matrix composites: Effects of fiber type and dosage. Compos. Part B Eng. 2019, 172, 131–142. [Google Scholar] [CrossRef]
- Fall, M.; Benzaazoua, M.; Saa, E.G. Mix proportioning of underground cemented tailings backfill. Tunn. Undergr. Space Technol. 2008, 23, 80–90. [Google Scholar] [CrossRef]
- Yılmaz, T.; Ercikdi, B.; Karaman, K.; Külekçi, G. Assessment of strength properties of cemented paste backfill by ultrasonic pulse velocity test. Ultrasonics 2014, 54, 1386–1394. [Google Scholar] [CrossRef]
- Prasad, B.K.R.; Eskandari, H.; Reddy, B.V.V. Prediction of compressive strength of SCC and HPC with high volume fly ash using ANN. Constr. Build. Mater. 2009, 23, 117–128. [Google Scholar] [CrossRef]
- Qi, C.; Chen, Q.; Dong, X.; Zhang, Q.; Yaseen, Z.M. Pressure drops of fresh cemented paste backfills through coupled test loop experiments and machine learning techniques. Powder Technol. 2020, 361, 748–758. [Google Scholar] [CrossRef]
- Yang, L.; Hou, C.; Zhu, W.; Liu, X.; Yan, B.; Li, L. Monitoring the failure process of cemented paste backfill at different curing times by using a digital image correlation technique. Constr. Build. Mater. 2022, 346, 128487. [Google Scholar] [CrossRef]
- Huang, G.; Wang, M.; Liu, Q.; Zhao, S.; Liu, H.; Liu, F.; Feng, L.; Song, J. Simultaneous utilization of mine tailings and steel slag for producing geopolymers: Alkali-hydrothermal activation, workability, strength, and hydration mechanism. Constr. Build. Mater. 2024, 414, 135029. [Google Scholar] [CrossRef]
- Asadizadeh, M.; Hedayat, A.; Tunstall, L.; Gonzalez, J.A.V.; Alvarado, J.W.V.; Neira, M.T. The impact of slag on the process of geopolymerization and the mechanical performance of mine-tailings-based alkali-activated lightweight aggregates. Constr. Build. Mater. 2024, 411, 134347. [Google Scholar] [CrossRef]
- Shi, P.; Falliano, D.; Yang, Z.; Marano, G.C.; Briseghella, B. Investigation on the anti-carbonation properties of alkali-activated slag concrete: Effect of activator types and dosages. J. Build. Eng. 2024, 91, 109552. [Google Scholar] [CrossRef]
- Yang, Z.; Shi, P.; Zhang, Y.; Li, Z. Influence of liquid-binder ratio on the performance of alkali-activated slag mortar with superabsorbent polymer. J. Build. Eng. 2022, 48, 103934. [Google Scholar] [CrossRef]
- Xiao, B.; Miao, S.; Gao, Q. Quantifying particle size and size distribution of mine tailings through deep learning approach of autoencoders. Powder Technol. 2022, 397, 117088. [Google Scholar] [CrossRef]
- Qi, C.; Fourie, A. Cemented paste backfill for mineral tailings management: Review and future perspectives. Miner. Eng. 2019, 144, 106025. [Google Scholar] [CrossRef]
- Fang, K.; Zhang, J.; Cui, L.; Haruna, S.; Li, M. Cost optimization of cemented paste backfill: State-of-the-art review and future perspectives. Miner. Eng. 2023, 204, 108414. [Google Scholar] [CrossRef]
- Shi, L.; Lin, S.T.K.; Lu, Y.; Ye, L.; Zhang, Y.X. Artificial neural network based mechanical and electrical property prediction of engineered cementitious composites. Constr. Build. Mater. 2018, 174, 667–674. [Google Scholar] [CrossRef]
- Shanmugasundaram, N.; Praveenkumar, S. Influence of supplementary cementitious materials, curing conditions and mixing ratios on fresh and mechanical properties of engineered cementitious composites—A review. Constr. Build. Mater. 2021, 309, 125038. [Google Scholar] [CrossRef]
- Adel, H.; Palizban, S.M.M.; Sharifi, S.S.; Ghazaan, M.I.; Korayem, A.H. Predicting mechanical properties of carbon nanotube-reinforced cementitious nanocomposites using interpretable ensemble learning models. Constr. Build. Mater. 2022, 354, 129209. [Google Scholar] [CrossRef]
- Min, C.; Xiong, S.; Shi, Y.; Liu, Z.; Lu, X. Early-age compressive strength prediction of cemented phosphogypsum backfill using lab experiments and ensemble learning models. Case Stud. Constr. Mater. 2023, 18, e02107. [Google Scholar] [CrossRef]
- Arachchilage, C.B.; Fan, C.; Zhao, J.; Huang, G.; Liu, W.V. A machine learning model to predict unconfined compressive strength of alkali-activated slag-based cemented paste backfill. J. Rock Mech. Geotech. Eng. 2023, 15, 2803–2815. [Google Scholar] [CrossRef]
- Hu, Y.; Li, K.; Zhang, B.; Han, B. Strength investigation of the cemented paste backfill in alpine regions using lab experiments and machine learning. Constr. Build. Mater. 2022, 323, 126583. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Z.; Xiong, S.; Wang, M. Comparative prediction performance of the strength of a new type of Ti tailings cemented backfilling body using PSO-RF, SSA-RF, and WOA-RF models. Case Stud. Constr. Mater. 2024, 20, e02766. [Google Scholar] [CrossRef]
- GB/T 2419-2005; Test Method for Fluidity of Cement Mortar. China Standards Press: Beijing, China, 2005.
- GB/T 50081-2002; Standard for Test Method of Mechanical Properties on Ordinary Concrete. China Building Industry Press: Beijing, China, 2002.
- Chandra, A.; Yao, X. Evolving hybrid ensembles of learning machines for better generalisation. Neurocomputing 2006, 69, 686–700. [Google Scholar] [CrossRef]
- Szita, I.; Lőrincz, A. PIRANHA: Policy iteration for recurrent artificial neural networks with hidden activities. Neurocomputing 2006, 70, 577–591. [Google Scholar] [CrossRef]
- Guo, Y.; He, Y.; Song, H.; He, W.; Yuan, K. Correlational examples for convolutional neural networks to detect small impurities. Neurocomputing 2018, 295, 127–141. [Google Scholar] [CrossRef]
- Li, J.; Hu, M.; Guo, L. Exponential stability of stochastic memristor-based recurrent neural networks with time-varying delays. Neurocomputing 2014, 138, 92–98. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Du, K.; Dias, D. Stability prediction of hard rock pillar using support vector machine optimized by three metaheuristic algorithms. Int. J. Min. Sci. Technol. 2023, 33, 1019–1036. [Google Scholar] [CrossRef]
- Zhou, J.; Li, X.-B.; Shi, X.-Z.; Wei, W.; Wu, B.-B. Predicting pillar stability for underground mine using Fisher discriminant analysis and SVM methods. Trans. Nonferrous Met. Soc. China 2011, 21, 2734–2743. [Google Scholar] [CrossRef]
- Ngo, Q.T.; Ngo, C.T.; Nguyen, Q.H.; Nguyen, H.N.; Nguyen, L.Q.; Nguyen, K.Q.; Tran, V.Q. Data-driven approach in investigating and predicting unconfined compressive strength of cemented paste backfill. Mater. Today Commun. 2023, 37, 107065. [Google Scholar] [CrossRef]
- Fleury, M.P.; Kamakura, G.K.; Pitombo, C.S.; Cunha, A.L.B.N.; da Silva, J.L. Prediction of non-woven geotextiles’ reduction factors for damage caused by the drop of backfill materials. Geotext. Geomembr. 2023, 51, 120–130. [Google Scholar] [CrossRef]
- Xu, Y.; Yao, Z.; Huang, X.; Fang, Y.; Shu, S.; Zhu, H. Heat transfer characteristics and heat conductivity prediction model of waste steel slag–clay backfill material. Therm. Sci. Eng. Prog. 2023, 46, 102203. [Google Scholar] [CrossRef]
- Yu, Z.; Shi, X.-Z.; Chen, X.; Zhou, J.; Qi, C.-C.; Chen, Q.-S.; Rao, D.-J. Artificial intelligence model for studying unconfined compressive performance of fiber-reinforced cemented paste backfill. Trans. Nonferrous Met. Soc. China 2021, 31, 1087–1102. [Google Scholar] [CrossRef]
- Hassan, B.A.; Rashid, T.A. Operational framework for recent advances in backtracking search optimisation algorithm: A systematic review and performance evaluation. Appl. Math. Comput. 2020, 370, 124919. [Google Scholar] [CrossRef]
- Li, D.; Liu, Z.; Xiao, P.; Zhou, J.; Armaghani, D.J. Intelligent rockburst prediction model with sample category balance using feedforward neural network and Bayesian optimization. Undergr. Space 2022, 7, 833–846. [Google Scholar] [CrossRef]
- Chang, Q.-L.; Zhou, H.-Q.; Hou, C.-J. Using particle swarm optimization algorithm in an artificial neural network to forecast the strength of paste filling material. J. China Univ. Min. Technol. 2008, 18, 551–555. [Google Scholar] [CrossRef]
- Zhang, B.; Li, K.; Zhang, S.; Hu, Y.; Han, B. Strength prediction and application of cemented paste backfill based on machine learning and strength correction. Heliyon 2022, 8, e10338. [Google Scholar] [CrossRef]
- Zhang, X.; An, J. A new pre-assessment model for failure-probability-based-planning by neural network. J. Loss Prev. Process Ind. 2023, 81, 104908. [Google Scholar] [CrossRef]
- Liu, S.; Tang, X.; Li, J. Extension of ALE method in large deformation analysis of saturated soil under earthquake loading. Comput. Geotech. 2021, 133, 104056. [Google Scholar] [CrossRef]
- Liu, H.; Xu, K. Recognition of gangues from color images using convolutional neural networks with attention mechanism. Measurement 2023, 206, 112273. [Google Scholar] [CrossRef]
- Zhang, Y.; Xie, X.; Li, H.; Zhou, B.; Wang, Q.; Shahrour, I. Subway tunnel damage detection based on in-service train dynamic response, variational mode decomposition, convolutional neural networks and long short-term memory. Autom. Constr. 2022, 139, 104293. [Google Scholar] [CrossRef]
- Haidar, A.; Verma, B. Monthly Rainfall Forecasting Using One-Dimensional Deep Convolutional Neural Network. IEEE Access 2018, 6, 69053–69063. [Google Scholar] [CrossRef]
- Kim, T.-Y.; Cho, S.-B. Predicting residential energy consumption using CNN-LSTM neural networks. Energy 2019, 182, 72–81. [Google Scholar] [CrossRef]
- Momeni, E.; Yarivand, A.; Dowlatshahi, M.B.; Armaghani, D.J. An efficient optimal neural network based on gravitational search algorithm in predicting the deformation of geogrid-reinforced soil structures. Transp. Geotech. 2021, 26, 100446. [Google Scholar] [CrossRef]
- Ahmed, B.; Mangalathu, S.; Jeon, J.-S. Seismic damage state predictions of reinforced concrete structures using stacked long short-term memory neural networks. J. Build. Eng. 2022, 46, 103737. [Google Scholar] [CrossRef]
- Yin, S.; Yan, Z.; Chen, X.; Yan, R.; Chen, D.; Chen, J. Mechanical properties of cemented tailings and waste-rock backfill (CTWB) materials: Laboratory tests and deep learning modeling. Constr. Build. Mater. 2023, 369, 130610. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, Y.; Huang, G.; Liu, L.; Hao, X. A soft sensor model based on long&short-term memory dual pathways convolutional gated recurrent unit network for predicting cement specific surface area. ISA Trans. 2022, 130, 293–305. [Google Scholar] [CrossRef]
- Tanner, E.M.; Bornehag, C.-G.; Gennings, C. Repeated holdout validation for weighted quantile sum regression. MethodsX 2019, 6, 2855–2860. [Google Scholar] [CrossRef]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter Optimization for Machine Learning Models Based on Bayesian Optimizationb. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar] [CrossRef]
- Sadrossadat, E.; Basarir, H.; Luo, G.; Karrech, A.; Durham, R.; Fourie, A.; Elchalakani, M. Multi-objective mixture design of cemented paste backfill using particle swarm optimisation algorithm. Miner. Eng. 2020, 153, 106385. [Google Scholar] [CrossRef]
- Chen, B.; Liu, Q.; Chen, H.; Wang, L.; Deng, T.; Zhang, L.; Wu, X. Multiobjective optimization of building energy consumption based on BIM-DB and LSSVM-NSGA-II. J. Clean. Prod. 2021, 294, 126153. [Google Scholar] [CrossRef]
- Dong, W.; Huang, Y.; Lehane, B.; Ma, G. XGBoost algorithm-based prediction of concrete electrical resistivity for structural health monitoring. Autom. Constr. 2020, 114, 103155. [Google Scholar] [CrossRef]
- Bhatacharya, S.; Kumar, S.; Panigrahi, S.; Ayub, A.; Boratne, A.; Jahnavi, G.; Richa; Singh, D.; Venugopal, V.; Gautam, A. Financial Literacy among Health-Care Professionals in India: Challenges and Way Forward. J. Public Health Prim. Care 2023, 4, 59–62. [Google Scholar] [CrossRef]
- Wong, T.-T. Parametric methods for comparing the performance of two classification algorithms evaluated by k-fold cross validation on multiple data sets. Pattern Recognit. 2017, 65, 97–107. [Google Scholar] [CrossRef]
- Ling, H.; Qian, C.; Kang, W.; Liang, C.; Chen, H. Combination of Support Vector Machine and K-Fold cross validation to predict compressive strength of concrete in marine environment. Constr. Build. Mater. 2019, 206, 355–363. [Google Scholar] [CrossRef]
- Kang, M.-C.; Yoo, D.-Y.; Gupta, R. Machine learning-based prediction for compressive and flexural strengths of steel fiber-reinforced concrete. Constr. Build. Mater. 2021, 266, 121117. [Google Scholar] [CrossRef]
- Su, M.; Zhong, Q.; Peng, H.; Li, S. Selected machine learning approaches for predicting the interfacial bond strength between FRPs and concrete. Constr. Build. Mater. 2021, 270, 121456. [Google Scholar] [CrossRef]
- Moody, J.; Darken, C.J. Fast Learning in Networks of Locally-Tuned Processing Units. Neural Comput. 1989, 1, 281–294. [Google Scholar] [CrossRef]
- Wuxing, L.; Tse, P.W.; Guicai, Z.; Tielin, S. Classification of gear faults using cumulants and the radial basis function network. Mech. Syst. Signal Process. 2004, 18, 381–389. [Google Scholar] [CrossRef]
- Salami, B.A.; Iqbal, M.; Abdulraheem, A.; Jalal, F.E.; Alimi, W.; Jamal, A.; Tafsirojjaman, T.; Liu, Y.; Bardhan, A. Estimating compressive strength of lightweight foamed concrete using neural, genetic and ensemble machine learning approaches. Cem. Concr. Compos. 2022, 133, 104721. [Google Scholar] [CrossRef]
- Hamidian, P.; Alidoust, P.; Golafshani, E.M.; Niavol, K.P.; Behnood, A. Introduction of a novel evolutionary neural network for evaluating the compressive strength of concretes: A case of Rice Husk Ash concrete. J. Build. Eng. 2022, 61, 105293. [Google Scholar] [CrossRef]
- Minfei, L.; Yidong, G.; Ze, C.; Zhi, W.; Erik, S.; Branko, Š. Microstructure-informed deep convolutional neural network for predicting short-term creep modulus of cement paste. Cem. Concr. Res. 2022, 152, 106681. [Google Scholar] [CrossRef]

| Simple | Mass Content (%) | GGBS Content (%) | Activator Dosage | SR Content (%) | CS (%) | Fluidity | UCS |
|---|---|---|---|---|---|---|---|
| M1 | 77 | 14 | 0.4 | 70 | 30 | 159.17 | 2.83 |
| M2 | 76 | 14 | 0.4 | 70 | 30 | 203.33 | 2.27 |
| M3 | 75 | 14 | 0.4 | 70 | 30 | 235.83 | 2.31 |
| M4 | 74 | 14 | 0.4 | 70 | 30 | 275.00 | 1.86 |
| M5 | 73 | 14 | 0.4 | 70 | 30 | 317.83 | 1.70 |
| M6 | 75 | 10 | 0.4 | 70 | 30 | 231.25 | 0.97 |
| M7 | 75 | 12 | 0.4 | 70 | 30 | 230.00 | 1.50 |
| M8 | 75 | 14 | 0.4 | 70 | 30 | 235.83 | 2.31 |
| M9 | 75 | 16 | 0.4 | 70 | 30 | 259.17 | 2.15 |
| M10 | 75 | 18 | 0.4 | 70 | 30 | 271.67 | 2.50 |
| M11 | 75 | 14 | 0.4 | 90 | 10 | 224.16 | 0.00 |
| M12 | 75 | 14 | 0.4 | 80 | 20 | 238.75 | 1.20 |
| M13 | 75 | 14 | 0.4 | 70 | 30 | 235.83 | 2.31 |
| M14 | 75 | 14 | 0.4 | 60 | 40 | 246.67 | 1.87 |
| M15 | 75 | 14 | 0.4 | 50 | 50 | 265.00 | 1.76 |
| M16 | 75 | 14 | 0.2 | 70 | 30 | 271.67 | 1.65 |
| M17 | 75 | 14 | 0.3 | 70 | 30 | 259.17 | 1.76 |
| M18 | 75 | 14 | 0.4 | 70 | 30 | 235.83 | 2.31 |
| M19 | 75 | 14 | 0.5 | 70 | 30 | 230.00 | 1.80 |
| M20 | 75 | 14 | 0.6 | 70 | 30 | 224.17 | 1.59 |
| Technique | Train | Test | ||||
|---|---|---|---|---|---|---|
| RMSE | R2 | MAE | RMSE | R2 | MAE | |
| SVM | 2.1513 | 0.9964 | 1.9888 | 3.0079 | 0.9603 | 2.7643 |
| RF | 8.6368 | 0.9419 | 5.5869 | 3.9101 | 0.9478 | 2.8753 |
| BP | 4.3567 | 0.9756 | 2.5110 | 8.5301 | 0.9620 | 6.4892 |
| GABP | 2.5228 | 0.9908 | 0.9365 | 10.3016 | 0.9508 | 8.3858 |
| RBF | 2.1437 | 0.9951 | 1.5911 | 6.2450 | 0.9726 | 5.5699 |
| CNN | 5.2180 | 0.9759 | 4.0448 | 5.0857 | 0.9594 | 5.0024 |
| LSTM | 1.5624 | 0.9977 | 1.2296 | 8.2988 | 0.9286 | 7.7467 |
| Technique | Train | Test | ||||
|---|---|---|---|---|---|---|
| RMSE | R2 | MAE | RMSE | R2 | MAE | |
| SVM | 0.0313 | 0.9957 | 0.0242 | 0.2413 | 0.9236 | 0.2115 |
| RF | 0.1852 | 0.9169 | 0.1365 | 0.0750 | 0.8977 | 0.0652 |
| BP | 0.1472 | 0.9467 | 0.1212 | 0.1000 | 0.9518 | 0.0886 |
| GABP | 0.1397 | 0.9485 | 0.0911 | 0.0957 | 0.9710 | 0.0811 |
| RBF | 0.0205 | 0.9973 | 0.0168 | 0.0509 | 0.9696 | 0.0353 |
| CNN | 0.2428 | 0.8566 | 0.1822 | 0.1438 | 0.8735 | 0.0954 |
| LSTM | 0.1707 | 0.9288 | 0.1582 | 0.1024 | 0.9470 | 0.0822 |
| Study | Input Date | Output Date | Method | Achievements |
|---|---|---|---|---|
| [62] | Compressive strength of foamed concrete | Compressive strength | GBT | 0.977 (R) |
| [63] | RHA concrete | Compressive strength | ANN-LM | 0.9797 (R2) |
| [64] | Cement paste | Creep modulus | DSNN | Higher than 0.96 (R2) |
| This study | cemented tailings backfill | Fluidity and Compressive strength | SVM, RF, BP, GABP, RBF, CNN, LSTM | 0.99 (R2) |
| Simple | OM | SVM | RF | BP | GABP | RBF | CNN | LSTM |
|---|---|---|---|---|---|---|---|---|
| M1 | 13 | 13 | 14 | 13 | 14 | 13 | 14 | 15 |
| M2 | 22 | 25 | 24 | 27 | 23 | 22 | -- | 25 |
| M3 | 14 | 20 | 14 | 17 | 15 | 14 | 22 | 20 |
| M4 | -- | -- | 28 | -- | -- | -- | -- | -- |
| M8 | 14 | 20 | 14 | 17 | 15 | 14 | 20 | 20 |
| M9 | 22 | 23 | 27 | 25 | 19 | 22 | -- | 22 |
| M10 | 13 | 14 | 14 | 14 | 14 | 13 | 16 | 14 |
| M13 | 14 | 14 | 14 | 17 | 13 | 14 | 17 | 14 |
| M14 | -- | -- | 28 | -- | 26 | -- | -- | 26 |
| M18 | 14 | 14 | 14 | 17 | 14 | 14 | 14 | 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, H.; Qi, W.; Song, H.; Pang, H.; Liu, X.; Chen, J.; Chen, Z. Predictive Modelling of Alkali-Slag Cemented Tailings Backfill Using a Novel Machine Learning Approach. Materials 2025, 18, 1236. https://doi.org/10.3390/ma18061236
Pang H, Qi W, Song H, Pang H, Liu X, Chen J, Chen Z. Predictive Modelling of Alkali-Slag Cemented Tailings Backfill Using a Novel Machine Learning Approach. Materials. 2025; 18(6):1236. https://doi.org/10.3390/ma18061236
Chicago/Turabian StylePang, Haotian, Wenyue Qi, Hongqi Song, Haowei Pang, Xiaotian Liu, Junzhi Chen, and Zhiwei Chen. 2025. "Predictive Modelling of Alkali-Slag Cemented Tailings Backfill Using a Novel Machine Learning Approach" Materials 18, no. 6: 1236. https://doi.org/10.3390/ma18061236
APA StylePang, H., Qi, W., Song, H., Pang, H., Liu, X., Chen, J., & Chen, Z. (2025). Predictive Modelling of Alkali-Slag Cemented Tailings Backfill Using a Novel Machine Learning Approach. Materials, 18(6), 1236. https://doi.org/10.3390/ma18061236






