Assessing Cu3BiS3 for Thin-Film Photovoltaics: A Systematic DFT Study Comparing LCAO and PAW Across Multiple Functionals
Abstract
1. Introduction
2. Computational Details
3. Results and Discussion
3.1. Experimental Wittichenite Structure
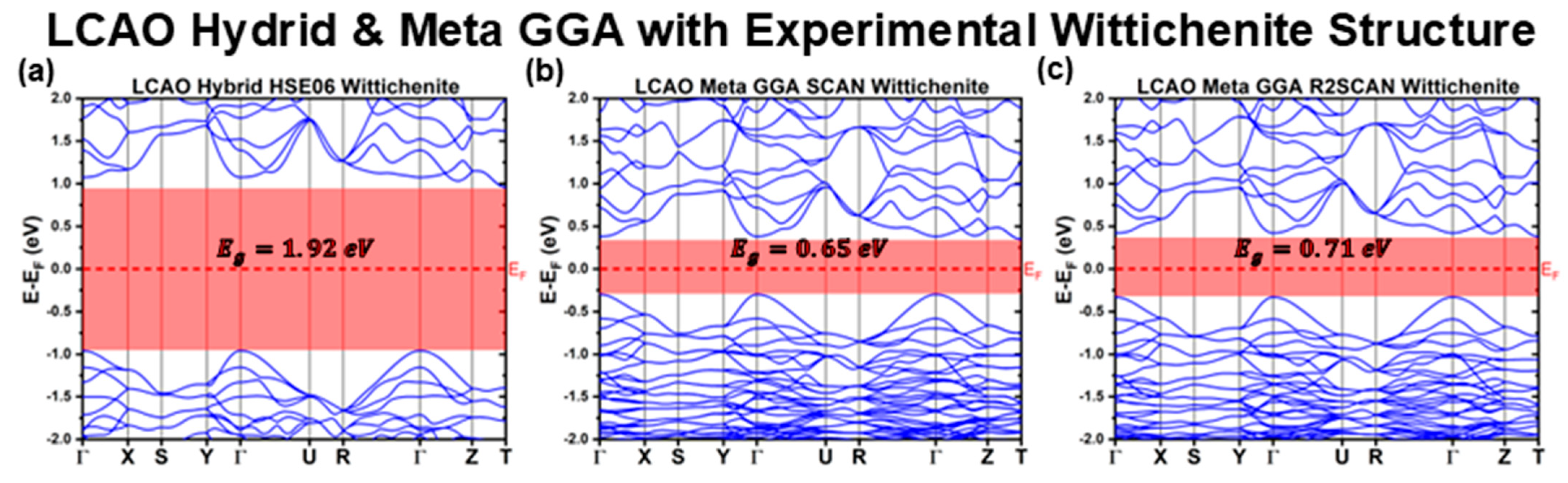
3.1.1. LCAO Calculations with Experimental Structure
3.1.2. PAW Calculations with Experimental Structure
- , for the hole charge carriers along the direction.
- , for the hole charge carriers along the direction.
- , for the hole charge carriers along the direction.
- , for the electron charge carriers.
- .
3.2. Fully Relaxed Structures
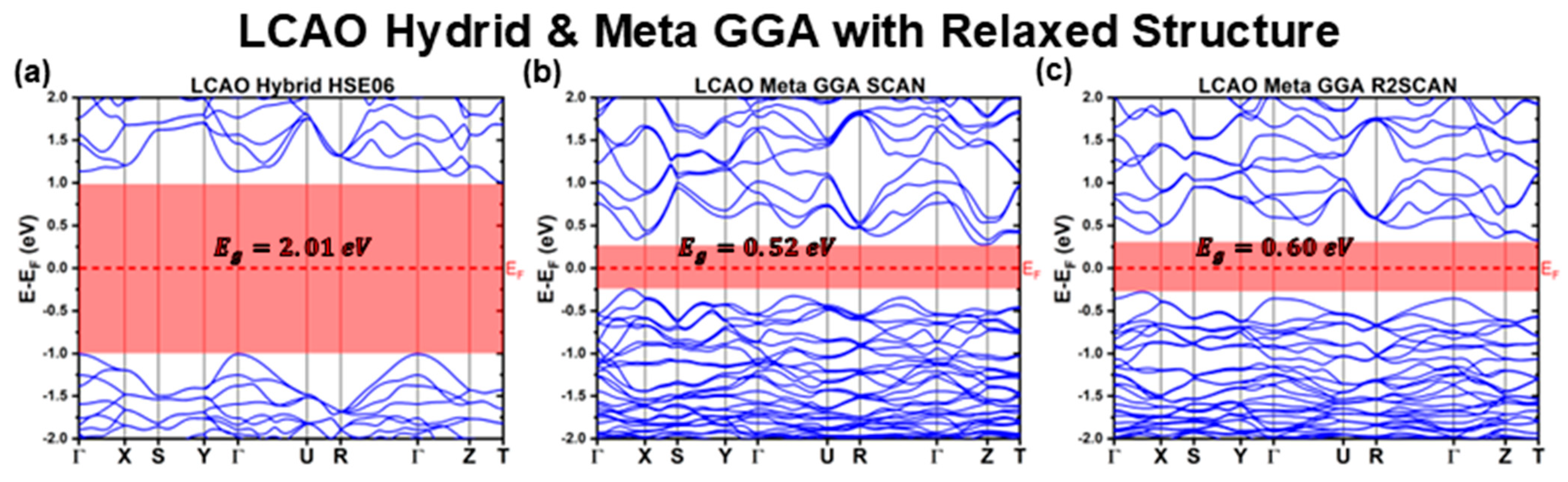
3.2.1. LCAO Calculations with Fully Relaxed Structure
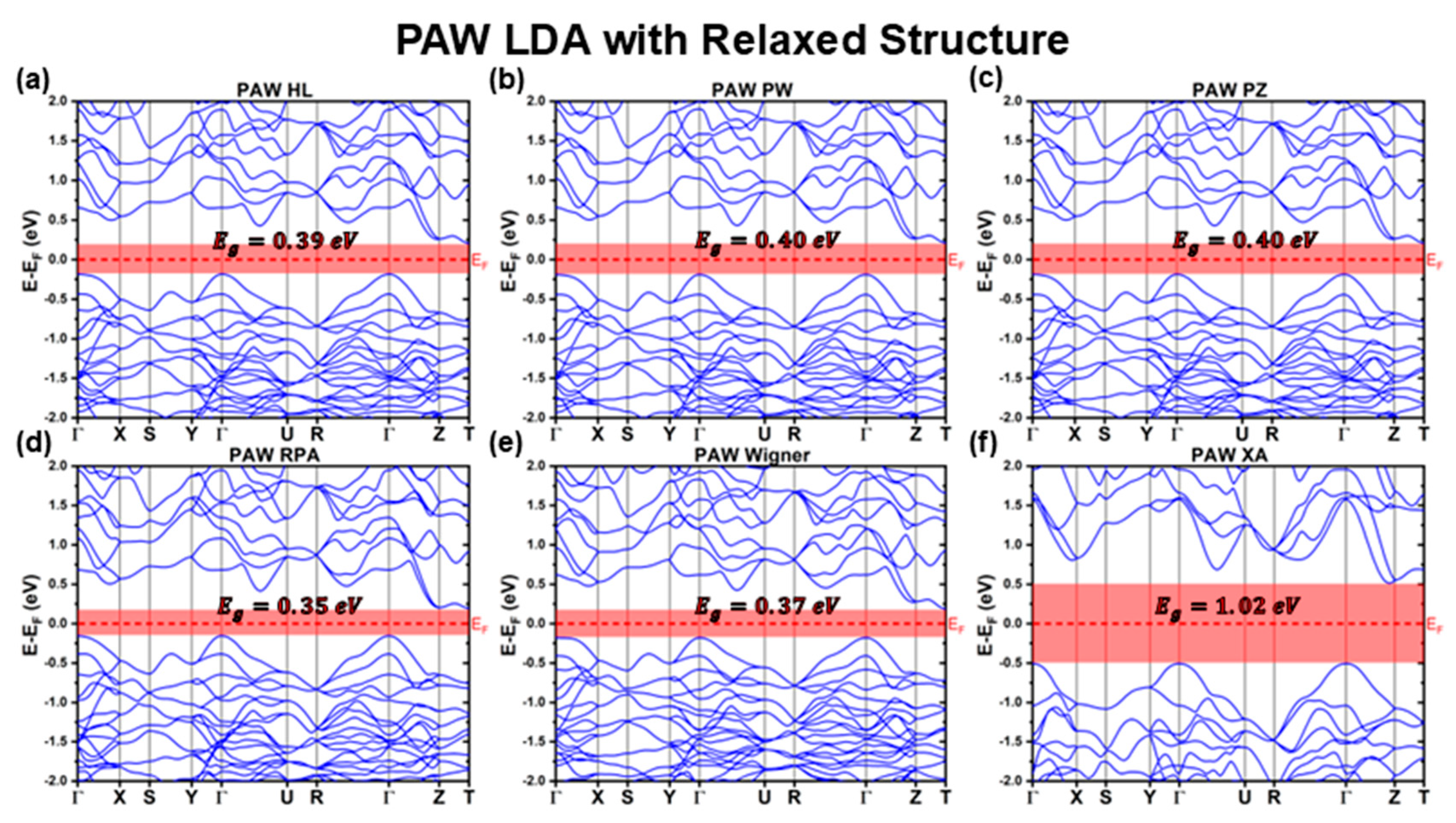
3.2.2. PAW Calculations with Fully Relaxed Structure
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Raimi, D.; Zhu, Y.; Newell, R.G.; Prest, B.C. Global Energy Outlook 2024: Peaks or Plateaus; Resources for the Future: Washington, DC, USA, 2024. [Google Scholar]
- Lewis, N.S.; Nocera, D.G. Powering the planet: Chemical challenges in solar energy utilization. Proc. Natl. Acad. Sci. USA 2006, 103, 15729–15735. [Google Scholar] [CrossRef] [PubMed]
- Oni, A.M.; Mohsin, A.S.M.; Rahman, M.M.; Bhuian, M.B.H. A comprehensive evaluation of solar cell technologies, associated loss mechanisms, and efficiency enhancement strategies for photovoltaic cells. Energy Rep. 2024, 11, 3345–3366. [Google Scholar] [CrossRef]
- Abbott, D. Keeping the energy debate clean: How do we supply the world’s energy needs? Proc. IEEE 2009, 98, 42–66. [Google Scholar] [CrossRef]
- Urishev, B. Decentralized energy systems, based on renewable energy sources. Appl. Sol. Energy 2019, 55, 207–212. [Google Scholar] [CrossRef]
- Fuchs, I.; Rajasekharan, J.; Cali, Ü. Decentralization, decarbonization and digitalization in swarm electrification. Energy Sustain. Dev. 2024, 81, 101489. [Google Scholar] [CrossRef]
- Yaqoot, M.; Diwan, P.; Kandpal, T.C. Review of barriers to the dissemination of decentralized renewable energy systems. Renew. Sustain. Energy Rev. 2016, 58, 477–490. [Google Scholar] [CrossRef]
- Khan, I. Impacts of energy decentralization viewed through the lens of the energy cultures framework: Solar home systems in the developing economies. Renew. Sustain. Energy Rev. 2020, 119, 109576. [Google Scholar] [CrossRef]
- Zisos, A.; Chatzopoulos, D.; Efstratiadis, A. The Concept of Spatial Reliability Across Renewable Energy Systems—An Application to Decentralized Solar PV Energy. Energies 2024, 17, 5900. [Google Scholar] [CrossRef]
- Biyik, E.; Araz, M.; Hepbasli, A.; Shahrestani, M.; Yao, R.; Shao, L.; Essah, E.; Oliveira, A.C.; del Caño, T.; Rico, E.; et al. A key review of building integrated photovoltaic (BIPV) systems. Eng. Sci. Technol. Int. J. 2017, 20, 833–858. [Google Scholar] [CrossRef]
- Jelle, B.P.; Breivik, C.; Røkenes, H.D. Building integrated photovoltaic products: A state-of-the-art review and future research opportunities. Sol. Energy Mater. Sol. Cells 2012, 100, 69–96. [Google Scholar] [CrossRef]
- Colberts, F.; Kingma, A.; Gómez, N.H.C.; Roosen, D.; Ahmad, S.; Vroon, Z. Feasibility study on thin-film PV laminates for road integration. Prog. Photovolt. Res. Appl. 2024, 32, 687–700. [Google Scholar] [CrossRef]
- Kingma, A.; Kirchner Sala, H.; Simeonov, L.; Aninat, R.; Villa, S.; Bakker, K.; van den Nieuwenhof, M.; Roosen, D.; de Riet, J.; Koetse, M.; et al. Post-Mortem Analysis of Building-Integrated Flexible Thin Film Modules. Prog. Photovolt. Res. Appl. 2025, 33, 276–293. [Google Scholar] [CrossRef]
- Sun, J.; Jasieniak, J.J. Semi-transparent solar cells. J. Phys. D Appl. Phys. 2017, 50, 093001. [Google Scholar] [CrossRef]
- Cannavale, A.; Martellotta, F.; Fiorito, F.; Ayr, U. The challenge for building integration of highly transparent photovoltaics and photoelectrochromic devices. Energies 2020, 13, 1929. [Google Scholar] [CrossRef]
- Ramanujam, J.; Bishop, D.M.; Todorov, T.K.; Gunawan, O.; Rath, J.; Nekovei, R.; Artegiani, E.; Romeo, A. Flexible CIGS, CdTe and a-Si: H based thin film solar cells: A review. Prog. Mater. Sci. 2020, 110, 100619. [Google Scholar] [CrossRef]
- Zohuri, B.; McDaniel, P.J. Introduction to Energy Essentials: Insight into Nuclear, Renewable, and Non-Renewable Energies; Academic Press: Cambridge, MA, USA, 2021. [Google Scholar]
- Reich, M.; Simon, A.C. Critical Minerals. Annu. Rev. Earth Planet. Sci. 2024, 53. [Google Scholar] [CrossRef]
- Deady, E.; Moon, C.; Moore, K.; Goodenough, K.M.; Shail, R.K. Bismuth: Economic geology and value chains. Ore Geol. Rev. 2022, 143, 104722. [Google Scholar] [CrossRef]
- Mohan, R. Green bismuth. Nat. Chem. 2010, 2, 336. [Google Scholar] [CrossRef]
- Libório, M.S.; de Queiroz, J.C.A.; Sivasankar, S.M.; Costa, T.H.d.C.; da Cunha, A.F.; Amorim, C.d.O. A Review of Cu3BiS3 Thin Films: A Sustainable and Cost-Effective Photovoltaic Material. Crystals 2024, 14, 524. [Google Scholar] [CrossRef]
- Amorim, C.O.; Liborio, M.S.; Queiroz, J.C.A.; Melo, B.M.G.; Sivasankar, S.M.; Costa, T.H.C.; Graça, M.P.F.; da Cunha, A.F. Cu3BiS3 film synthesis through rapid thermal processing sulfurization of electron beam evaporated precursors. Emergent Mater. 2024, 1–13. [Google Scholar] [CrossRef]
- Deshmukh, S.G.; Kheraj, V. A comprehensive review on synthesis and characterizations of Cu3BiS3 thin films for solar photovoltaics. Nanotechnol. Environ. Eng. 2017, 2, 1–12. [Google Scholar] [CrossRef]
- Mesa, F.; Dussan, A.; Gordillo, G. Study of the growth process and optoelectrical properties of nanocrystalline Cu3BiS3 thin films. Phys. Status Solidi C 2010, 7, 917–920. [Google Scholar] [CrossRef]
- Colombara, D.; Peter, L.; Hutchings, K.; Rogers, K.; Schäfer, S.; Dufton, J.; Islam, M. Formation of Cu3BiS3 thin films via sulfurization of Bi–Cu metal precursors. Thin Solid. Film. 2012, 520, 5165–5171. [Google Scholar] [CrossRef]
- Yan, C.; Gu, E.; Liu, F.; Lai, Y.; Li, J.; Liu, Y. Colloidal synthesis and characterizations of wittichenite copper bismuth sulphide nanocrystals. Nanoscale 2013, 5, 1789–1792. [Google Scholar] [CrossRef] [PubMed]
- Murali, B.; Madhuri, M.; Krupanidhi, S.B. Near-infrared photoactive Cu3BiS3 thin films by co-evaporation. J. Appl. Phys. 2014, 115, 173109. [Google Scholar] [CrossRef]
- Zhang, L.; Jin, X.; Yuan, C.; Jiang, G.; Liu, W.; Zhu, C. The effect of the sulfur concentration on the phase transformation from the mixed CuO-Bi2O3 system to Cu3BiS3 during the sulfurization process. Appl. Surf. Sci. 2016, 389, 858–864. [Google Scholar] [CrossRef]
- Estrella, V.; Nair, M.T.S.; Nair, P.K. Semiconducting Cu3BiS3 thin films formed by the solid-state reaction of CuS and bismuth thin films. Semicond. Sci. Technol. 2003, 18, 190. [Google Scholar] [CrossRef]
- Liu, S.; Wang, X.; Nie, L.; Chen, L.; Yuan, R. Spray pyrolysis deposition of Cu3BiS3 thin films. Thin Solid. Film. 2015, 585, 72–75. [Google Scholar] [CrossRef]
- Gerein, N.J.; Haber, J.A. One-step synthesis and optical and electrical properties of thin film Cu3BiS3 for use as a solar absorber in photovoltaic devices. Chem. Mater. 2006, 18, 6297–6302. [Google Scholar] [CrossRef]
- Mesa, F.; Gordillo, G. Effect of preparation conditions on the properties of Cu3BiS3 thin films grown by a two–step process. J Phys. Conf. Ser. 2009, 167, 012019. [Google Scholar] [CrossRef]
- Shockley, W.; Queisser, H. Detailed balance limit of efficiency of p–n junction solar cells. In Renew Energy; Routledge: Milton Park, UK, 2018. [Google Scholar]
- Rühle, S. Tabulated values of the Shockley–Queisser limit for single junction solar cells. Sol. Energy 2016, 130, 139–147. [Google Scholar] [CrossRef]
- Yang, Y.; Xiong, X.; Yin, H.; Zhao, M.; Han, J. Study of copper bismuth sulfide thin films for the photovoltaic application. J. Mater. Sci. Mater. Electron. 2019, 30, 1832–1837. [Google Scholar] [CrossRef]
- Lee, T.D.; Ebong, A.U. A review of thin film solar cell technologies and challenges. Renew. Sustain. Energy Rev. 2017, 70, 1286–1297. [Google Scholar] [CrossRef]
- Machkih, K.; Oubaki, R.; Makha, M. A review of CIGS thin film semiconductor deposition via sputtering and thermal evaporation for solar cell applications. Coatings 2024, 14, 1088. [Google Scholar] [CrossRef]
- Romeo, A.; Artegiani, E. CdTe-based thin film solar cells: Past, present and future. Energies 2021, 14, 1684. [Google Scholar] [CrossRef]
- Mughal, M.A.; Engelken, R.; Sharma, R. Progress in indium (III) sulfide (In2S3) buffer layer deposition techniques for CIS, CIGS, and CdTe-based thin film solar cells. Sol. Energy 2015, 120, 131–146. [Google Scholar] [CrossRef]
- Santana Liborio, M.; Amorim, C.O.; Queiroz, J.C.A.; Sivasankar, S.M.; de Costa, T.H.; da Cunha, A.F. Strategies to Enhance the Efficiency of Cu3BiS3-Based Photovoltaic Devices: Simulation Insights and Buffer Layer Engineering. ACS Appl. Opt. Mater. 2024, 3, 81–90. [Google Scholar] [CrossRef]
- Capistrán-Martínez, J.; Loeza-Díaz, D.; Mora-Herrera, D.; Pérez-Rodríguez, F.; Pal, M. Theoretical evaluation of emerging Cd-free Cu3BiS3 based solar cells using experimental data of chemically deposited Cu3BiS3 thin films. J. Alloys Compd. 2021, 867, 159156. [Google Scholar] [CrossRef]
- Mesa, F.; Ballesteros, V.; Dussan, A. Growth Analysis and Numerical Simulation of Cu3BiS3 Absorbing Layer Solar Cell through the wxAMPS and Finite Element Method. Acta Phys. Pol. A 2014, 125, 385–387. [Google Scholar] [CrossRef]
- Battaglia, C.; Cuevas, A.; De Wolf, S. High-efficiency crystalline silicon solar cells: Status and perspectives. Energy Env. Sci. 2016, 9, 1552–1576. [Google Scholar] [CrossRef]
- Schleder, G.R.; Padilha, A.C.M.; Acosta, C.M.; Costa, M.; Fazzio, A. From DFT to machine learning: Recent approaches to materials science—A review. J. Phys. Mater. 2019, 2, 032001. [Google Scholar] [CrossRef]
- Janjua, M.R.S.A. Photovoltaic properties and enhancement in near-infrared light absorption capabilities of acceptor materials for organic solar cell applications: A quantum chemical perspective via DFT. J. Phys. Chem. Solids 2022, 171, 110996. [Google Scholar] [CrossRef]
- Amorim, C.O.; Gonçalves, J.N.; Amaral, V.S.; Amaral, J.S. In-silico Thermodynamic description of Heusler compounds applied to magnetocalorics by Monte Carlo simulations starting from ab-initio. Eur. J. Inorg. Chem. 2020, 2020, 1271–1277. [Google Scholar] [CrossRef]
- Garrity, K.F.; Bennett, J.W.; Rabe, K.M.; Vanderbilt, D. Pseudopotentials for high-throughput DFT calculations. Comput. Mater. Sci. 2014, 81, 446–452. [Google Scholar] [CrossRef]
- Amorim, C.O.; Amaral, J.S.; Gonçalves, J.N.; Amaral, V.S. Electric Field Induced Room Temperature Null to High Spin State Switching: A Computational Prediction. Adv. Theory Simul. 2019, 2, 1900005. [Google Scholar] [CrossRef]
- Jain, A.; Shin, Y.; Persson, K.A. Computational predictions of energy materials using density functional theory. Nat. Rev. Mater. 2016, 1, 1–13. [Google Scholar] [CrossRef]
- Amorim, C.O.; Gonçalves, J.N.; Amaral, J.S.; Amaral, V.S. Changing the magnetic states of an Fe/BaTiO 3 interface through crystal field effects controlled by strain. Phys. Chem. Chem. Phys. 2020, 22, 18050–18059. [Google Scholar] [CrossRef]
- Amorim, C.O.; Amaral, J.S.; Amaral, V.S. Enhanced strain-induced magnetoelectric coupling in polarization-free Fe/BaTiO3 heterostructures. Phys. Chem. Chem. Phys. 2021, 23, 16053–16059. [Google Scholar] [CrossRef]
- Hussain, R.; Adnan, M.; Atiq, K.; Khan, M.U.; Farooqi, Z.H.; Iqbal, J.; Begum, R. Designing of silolothiophene-linked triphenylamine-based hole transporting materials for perovskites and donors for organic solar cells-A DFT study. Sol. Energy 2023, 253, 187–198. [Google Scholar] [CrossRef]
- Makkar, P.; Ghosh, N.N. A review on the use of DFT for the prediction of the properties of nanomaterials. RSC Adv. 2021, 11, 27897–27924. [Google Scholar] [CrossRef]
- Slater, J.C.; Koster, G.F. Simplified LCAO method for the periodic potential problem. Phys. Rev. 1954, 94, 1498. [Google Scholar] [CrossRef]
- Troullier, N.; Martins, J.L. Efficient pseudopotentials for plane-wave calculations. Phys. Rev. B 1991, 43, 1993. [Google Scholar] [CrossRef] [PubMed]
- Blöchl, P.E. Projector augmented-wave method. Phys. Rev. B 1994, 50, 17953. [Google Scholar] [CrossRef] [PubMed]
- Andersen, O.K. Linear methods in band theory. Phys. Rev. B 1975, 12, 3060. [Google Scholar] [CrossRef]
- Singh, D.J.; Nordstrom, L. Planewaves, Pseudopotentials, and the LAPW Method; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Tablero, C. Photovoltaic application of O-doped Wittichenite-Cu3BiS3: From microscopic properties to maximum efficiencies. Prog. Photovolt. Res. Appl. 2013, 21, 894–899. [Google Scholar] [CrossRef]
- Kumar, M.; Persson, C. Cu3BiS3 as a potential photovoltaic absorber with high optical efficiency. Appl. Phys. Lett. 2013, 102, 062109. [Google Scholar] [CrossRef]
- Whittles, T.J.; Veal, T.D.; Savory, C.N.; Yates, P.J.; Murgatroyd, P.A.E.; Gibbon, J.T.; Birkett, M.; Potter, R.J.; Major, J.D.; Durose, K.; et al. Band alignments, band gap, core levels, and valence band states in Cu3BiS3 for photovoltaics. ACS Appl. Mater. Interfaces 2019, 11, 27033–27047. [Google Scholar] [CrossRef]
- Morales-Gallardo, M.V.; Pascoe-Sussoni, J.E.; Delesma, C.; Mathew, X.; Paraguay-Delgado, F.; Muñiz, J.; Mathews, N.R. Surfactant free solvothermal synthesis of Cu3BiS3 nanoparticles and the study of band alignments with n-type window layers for applications in solar cells: Experimental and theoretical approach. J. Alloys Compd. 2021, 866, 158447. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, K.; Gong, S.; Mao, H.; Huang, R.; Zhu, Z. Cu3BiS3/MXenes with excellent solar–thermal conversion for continuous and efficient seawater desalination. ACS Appl. Mater. Interfaces 2021, 13, 16246–16258. [Google Scholar] [CrossRef]
- Oubakalla, M.; Bouachri, M.; Beraich, M.; Taibi, M.; Guenbour, A.; Bellaouchou, A.; Bentiss, F.; Zarrouk, A.; Fahoume, M. Potential effect on the properties of Cu3BiS3 thin film co-electrodeposited in aqueous solution enriched using DFT calculation. J. Electron. Mater. 2022, 51, 7223–7233. [Google Scholar] [CrossRef]
- Raju, N.P.; Tripathi, D.; Lahiri, S.; Thangavel, R. Heat reflux sonochemical synthesis of Cu3BiS3 quantum dots: Experimental and first-principles investigation of spin–orbit coupling on structural, electronic, and optical properties. Sol. Energy 2023, 259, 107–118. [Google Scholar] [CrossRef]
- Jia, F.; Zhao, S.; Wu, J.; Chen, L.; Liu, T.; Wu, L. Cu3BiS3: Two-Dimensional Coordination Induces Out-of-Plane Phonon Scattering Enabling Ultralow Thermal Conductivity. Angew. Chem. 2023, 135, e202315642. [Google Scholar] [CrossRef]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. 1964, 136, B864. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 1965, 140, A1133. [Google Scholar] [CrossRef]
- Smidstrup, S.; Markussen, T.; Vancraeyveld, P.; Wellendorff, J.; Schneider, J.; Gunst, T.; Verstichel, B.; Stradi, D.; A Khomyakov, P.; Vej-Hansen, U.G.; et al. QuantumATK: An integrated platform of electronic and atomic-scale modelling tools. J. Phys. Condens. Matter 2019, 32, 015901. [Google Scholar] [CrossRef]
- van Setten, M.; Giantomassi, M.; Bousquet, E.; Verstraete, M.; Hamann, D.; Gonze, X.; Rignanese, G.-M. The PseudoDojo: Training and grading a 85 element optimized norm-conserving pseudopotential table. Comput. Phys. Commun. 2018, 226, 39–54. [Google Scholar] [CrossRef]
- Hedin, L.; Lundqvist, B.I. Explicit local exchange-correlation potentials. J. Phys. C Solid. State Phys. 1971, 4, 2064. [Google Scholar] [CrossRef]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244. [Google Scholar] [CrossRef]
- Perdew, J.P.; Zunger, A. Self-interaction correction to density-functional approximations for many-electron systems. Phys. Rev. B 1981, 23, 5048. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Brueckner, K.A. Correlation energy of an electron gas at high density. Phys. Rev. 1957, 106, 364. [Google Scholar] [CrossRef]
- Carr, W.J., Jr.; Maradudin, A.A. Ground-state energy of a high-density electron gas. Phys. Rev. 1964, 133, A371. [Google Scholar] [CrossRef]
- Wigner, E. Effects of the electron interaction on the energy levels of electrons in metals. Trans. Faraday Soc. 1938, 34, 678–685. [Google Scholar] [CrossRef]
- Peter, M.W. Becke–Wigner: A simple but powerful density functional. J. Chem. Soc. Faraday Trans. 1995, 91, 4337–4341. [Google Scholar]
- Slater, J.C. A simplification of the Hartree-Fock method. Phys. Rev. 1951, 81, 385. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. [Google Scholar] [CrossRef]
- Miehlich, B.; Savin, A.; Stoll, H.; Preuss, H. Results obtained with the correlation energy density functionals of Becke and Lee, Yang and Parr. Chem. Phys. Lett. 1989, 157, 200–206. [Google Scholar] [CrossRef]
- Perdew, J.P. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys. Rev. B 1986, 33, 8822. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ziesche, P.; Eschrig, H. Electronic Structure of Solids’ 91; Akademie-Verlag: Berlin, Germany, 1991. [Google Scholar]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671. [Google Scholar] [CrossRef]
- Haoyu, S.Y.; Zhang, W.; Verma, P.; He, X.; Truhlar, D.G. Nonseparable exchange–correlation functional for molecules, including homogeneous catalysis involving transition metals. Phys. Chem. Chem. Phys. 2015, 17, 12146–12160. [Google Scholar]
- Keal, T.W.; Tozer, D.J. The exchange-correlation potential in Kohn–Sham nuclear magnetic resonance shielding calculations. J. Chem. Phys. 2003, 119, 3015–3024. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413. [Google Scholar] [CrossRef]
- Xu, X.; Goddard, W.A., III. The X3LYP extended density functional for accurate descriptions of nonbond interactions, spin states, and thermochemical properties. Proc. Natl. Acad. Sci. USA 2004, 101, 2673–2677. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly constrained and appropriately normed semilocal density functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef]
- Furness, J.W.; Kaplan, A.D.; Ning, J.; Perdew, J.P.; Sun, J. Accurate and numerically efficient r2SCAN meta-generalized gradient approximation. J. Phys. Chem. Lett. 2020, 11, 8208–8215. [Google Scholar] [CrossRef]
- Heyd, J.; Scuseria, G.E.; Ernzerhof, M. Hybrid functionals based on a screened Coulomb potential. J. Chem. Phys. 2003, 118, 8207–8215. [Google Scholar] [CrossRef]
- Krukau, A.V.; Vydrov, O.A.; Izmaylov, A.F.; Scuseria, G.E. Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 2006, 125, 224106. [Google Scholar] [CrossRef]
- Kocman, V.; Nuffield, E.W. The crystal structure of wittichenite, Cu3BiS3. Acta Crystallogr. B 1973, 29, 2528–2535. [Google Scholar] [CrossRef]
- Matzat, E. Die Kristallstruktur des Wittichenits, Cu3BiS3. Tschermaks Mineral. Petrogr. Mitteilungen 1972, 18, 312–316. [Google Scholar] [CrossRef]
- Criddle, A.J.; Stanley, C.J. New data on wittichenite. Miner. Mag. 1979, 43, 109–113. [Google Scholar] [CrossRef]
- Makovicky, E. The phase transformations and thermal expansion of the solid electrolyte Cu3BiS3 between 25 and 300 °C. J. Solid State Chem. 1983, 49, 85–92. [Google Scholar] [CrossRef]



| LCAO Experimental Wittichenite Structure | ||||||
|---|---|---|---|---|---|---|
| XC Functional | Type | |||||
| (eV) | (eV) | (eV) | (eV) | |||
| LDA | HL | 0.93 | 1.00 | Indirect | 0.49 | −0.44 |
| PW | 0.93 | 0.99 | Indirect | 0.49 | −0.44 | |
| PZ | 0.93 | 0.99 | Indirect | 0.49 | −0.44 | |
| RPA | 0.92 | 0.98 | Indirect | 0.48 | −0.43 | |
| Wigner | 0.95 | 1.01 | Indirect | 0.50 | −0.45 | |
| XA | 0.81 | 0.91 | Indirect | 0.42 | −0.39 | |
| GGA | BLYP | 1.26 | 1.35 | Indirect | 0.66 | −0.60 |
| BP86 | 1.17 | 1.25 | Indirect | 0.61 | −0.56 | |
| BPW91 | 1.10 | 1.18 | Indirect | 0.57 | −0.53 | |
| GAM | 0.93 | 1.02 | Indirect | 0.49 | −0.45 | |
| KT2 | 1.27 | 1.36 | Indirect | 0.63 | −0.63 | |
| PBE | 1.11 | 1.19 | Indirect | 0.58 | −0.53 | |
| PBEsol | 1.01 | 1.08 | Indirect | 0.53 | −0.48 | |
| PW91 | 1.12 | 1.20 | Indirect | 0.59 | −0.54 | |
| RPBE | 1.11 | 1.18 | Indirect | 0.58 | −0.53 | |
| XLYP | 1.31 | 1.40 | Indirect | 0.66 | −0.66 | |
| Meta GGA | SCAN | 0.65 | 0.68 | Indirect | 0.35 | −0.30 |
| R2SCAN | 0.71 | 0.75 | Indirect | 0.38 | −0.33 | |
| Hybrid | HSE06 | 1.92 | 2.03 | Indirect | 0.96 | −0.96 |
| LCAO Experimental Wittichenite Structure | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| XC Functional | Symmetry Point | Symmetry Point | Symmetry Point | Symmetry Point | |||||
| LDA | HL | −1.3 | −0.4 | −1.4 | 0.6 | T | |||
| PW | −1.4 | −0.5 | −1.4 | 0.6 | |||||
| PZ | −1.3 | −0.5 | −1.4 | 0.6 | |||||
| RPA | −1.3 | −0.5 | −1.4 | 0.6 | |||||
| Wigner | −1.3 | −0.4 | −1.4 | 0.6 | |||||
| XA | −1.6 | −0.8 | −1.9 | 0.6 | |||||
| GGA | BLYP | −1.4 | −0.4 | −1.5 | 0.6 | T | |||
| BP86 | −1.4 | −0.4 | −1.5 | 0.6 | |||||
| BPW91 | −1.4 | −0.5 | −1.4 | 0.6 | |||||
| GAM | −1.5 | −0.5 | −1.5 | 0.6 | |||||
| KT2 | −1.3 | −0.5 | −1.5 | 0.6 | |||||
| PBE | −1.3 | −0.4 | −1.5 | 0.6 | |||||
| PBEsol | −1.3 | −0.5 | −1.4 | 0.6 | |||||
| PW91 | −1.3 | −0.5 | −1.5 | 0.6 | |||||
| RPBE | −1.4 | −0.4 | −1.4 | 0.6 | |||||
| XLYP | −1.4 | −0.4 | −1.5 | 0.6 | |||||
| Meta GGA | SCAN | −1.3 | −0.5 | −1.4 | 0.6 | T | |||
| R2SCAN | −1.4 | −0.5 | −1.4 | 0.6 | |||||
| Hybrid | HSE06 | −1.3 | −0.4 | −1.3 | 0.5 | T | |||
| PAW Experimental Wittichenite Structure | ||||||
|---|---|---|---|---|---|---|
| XC Functional | Type | |||||
| (eV) | (eV) | (eV) | (eV) | |||
| LDA | HL | 0.77 | 0.83 | Indirect | 0.41 | −0.36 |
| PW | 0.78 | 0.83 | Indirect | 0.42 | −0.36 | |
| PZ | 0.78 | 0.83 | Indirect | 0.42 | −0.36 | |
| RPA | 0.78 | 0.83 | Indirect | 0.42 | −0.36 | |
| Wigner | 0.73 | 0.77 | Indirect | 0.39 | −0.34 | |
| XA | 1.62 | 1.77 | Indirect | 0.84 | −0.78 | |
| GGA | BLYP | 0.86 | 0.93 | Indirect | 0.45 | −0.40 |
| BP86 | 0.83 | 0.89 | Indirect | 0.44 | −0.39 | |
| BPW91 | 0.82 | 0.88 | Indirect | 0.44 | −0.38 | |
| GAM | 0.99 | 1.09 | Indirect | 0.52 | −0.47 | |
| KT2 | 0.79 | 0.85 | Indirect | 0.42 | −0.37 | |
| PBE | 0.81 | 0.87 | Indirect | 0.43 | −0.38 | |
| PBEsol | 0.77 | 0.83 | Indirect | 0.41 | −0.36 | |
| PW91 | 0.81 | 0.87 | Indirect | 0.43 | −0.38 | |
| RPBE | 0.84 | 0.90 | Indirect | 0.44 | −0.39 | |
| XLYP | 0.87 | 0.94 | Indirect | 0.46 | −0.41 | |
| PAW Experimental Wittichenite Structure | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| XC Functional | Symmetry Point | Symmetry Point | Symmetry Point | Symmetry Point | |||||
| LDA | HL | −1.3 | −0.4 | −1.4 | 0.6 | T | |||
| PW | −1.3 | −0.4 | −1.4 | 0.6 | |||||
| PZ | −1.3 | −0.4 | −1.5 | 0.6 | |||||
| RPA | −1.3 | −0.4 | −1.5 | 0.6 | |||||
| Wigner | −1.2 | −0.4 | −1.3 | 0.6 | |||||
| XA | −1.6 | −0.6 | −2.0 | 0.6 | |||||
| GGA | BLYP | −1.4 | −0.4 | −1.5 | 0.6 | T | |||
| BP86 | −1.4 | −0.4 | −1.5 | 0.6 | |||||
| BPW91 | −1.4 | −0.4 | −1.5 | 0.6 | |||||
| GAM | −1.3 | −0.5 | −1.6 | 0.6 | |||||
| KT2 | −1.3 | −0.4 | −1.5 | 0.5 | |||||
| PBE | −1.4 | −0.4 | −1.4 | 0.6 | |||||
| PBEsol | −1.3 | −0.4 | −1.4 | 0.5 | |||||
| PW91 | −1.3 | −0.4 | −1.4 | 0.6 | |||||
| RPBE | −1.4 | −0.4 | −1.4 | 0.6 | |||||
| XLYP | −1.4 | −0.4 | −1.5 | 0.6 | |||||
| Experimental Lattice Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|
| PDF # | a (Å) | b (Å) | c (Å) | ∆a | ∆b | ∆c | T (K) | Reference |
| 04-006-8325 | 7.723 | 10.395 | 6.716 | Used in this work | 298 | Kocman et al. [95] | ||
| 00-043-1479 | 7.696 | 10.388 | 6.712 | −0.3% | −0.1% | −0.1% | 298 | Kocman et al. [95] |
| 01-073-1185 | 7.700 | 10.410 | 6.740 | −0.3% | 0.1% | 0.4% | 298 | Matzat et al. [96] |
| 01-087-7691 | 7.657 | 10.308 | 6.707 | −0.9% | −0.8% | −0.1% | 298 | Criddle et al. [97] |
| 04-004-0452 | 7.696 | 10.364 | 6.729 | −0.3% | −0.3% | 0.2% | 300 | Makovicky et al. [98] |
| LCAO Relaxed Structure Lattice Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|
| XC Functional | ||||||||
| LDA | HL | 7.3503 | 10.4735 | 6.1834 | −4.8% | 0.8% | −7.9% | 4.5% |
| PW | 7.3526 | 10.4649 | 6.1793 | −4.8% | 0.7% | −8.0% | 4.5% | |
| PZ | 7.3507 | 10.4658 | 6.1794 | −4.8% | 0.7% | −8.0% | 4.5% | |
| RPA | 7.2791 | 10.4398 | 6.0903 | −5.7% | 0.4% | −9.3% | 5.2% | |
| Wigner | 7.3987 | 10.5766 | 6.2677 | −4.2% | 1.7% | −6.7% | 4.2% | |
| XA | 6.2203 | 9.4477 | 5.7470 | −19.5% | −9.1% | −14.4% | 14.3% | |
| GGA | BLYP | 8.3722 | 10.5876 | 7.0077 | 8.4% | 1.9% | 4.3% | 4.9% |
| BP86 | 7.8257 | 10.6345 | 6.8938 | 1.3% | 2.3% | 2.6% | 2.1% | |
| BPW91 * | 7.5757 | 10.6488 | 6.8786 | −1.9% | 2.4% | 2.4% | 2.3% | |
| GAM * | 8.1452 | 10.7713 | 7.0062 | 5.5% | 3.6% | 4.3% | 4.5% | |
| KT2 | 7.2425 | 10.5516 | 6.2008 | −6.2% | 1.5% | −7.7% | 5.1% | |
| PBE | 7.9564 | 10.7154 | 7.0433 | 3.0% | 3.1% | 4.9% | 3.7% | |
| PBEsol | 7.3934 | 10.5412 | 6.3001 | −4.3% | 1.4% | −6.2% | 4.0% | |
| PW91 | 7.6544 | 10.5126 | 6.8310 | −0.9% | 1.1% | 1.7% | 1.2% | |
| RPBE | 7.9153 | 10.5593 | 6.9430 | 2.5% | 1.6% | 3.4% | 2.5% | |
| XLYP | 8.1451 | 10.7715 | 7.1114 | 5.5% | 3.6% | 5.9% | 5.0% | |
| Meta GGA | SCAN | 7.1469 | 10.5251 | 6.7512 | −7.5% | 1.3% | 0.5% | 3.1% |
| R2SCAN | 7.4277 | 10.5544 | 6.7057 | −3.8% | 1.5% | −0.2% | 1.8% | |
| Hybrid | HSE06 | 7.7010 | 10.4879 | 6.8131 | −0.3% | 0.9% | 1.4% | 0.9% |
| LCAO Relaxed Structure | ||||||
|---|---|---|---|---|---|---|
| XC Functional | Type | |||||
| (eV) | (eV) | (eV) | (eV) | |||
| LDA | HL | 0.49 | 0.95 | Indirect | 0.26 | −0.23 |
| PW | 0.49 | 0.95 | Indirect | 0.26 | −0.23 | |
| PZ | 0.49 | 0.95 | Indirect | 0.26 | −0.23 | |
| RPA | 0.43 | 0.90 | Indirect | 0.23 | −0.19 | |
| Wigner | 0.52 | 0.95 | Indirect | 0.27 | −0.25 | |
| XA | 0.29 | 0.78 | Indirect | 0.17 | −0.12 | |
| GGA | BLYP | 1.23 | 1.32 | Indirect | 0.62 | −0.62 |
| BP86 | 1.11 | 1.20 | Indirect | 0.57 | −0.54 | |
| BPW91 * | 1.06 | 1.17 | Indirect | 0.54 | −0.52 | |
| GAM * | 0.89 | 0.97 | Indirect | 0.46 | −0.43 | |
| KT2 | 0.77 | 1.29 | Indirect | 0.41 | −0.36 | |
| PBE | 1.11 | 1.14 | Indirect | 0.57 | −0.53 | |
| PBEsol | 0.60 | 1.00 | Indirect | 0.31 | −0.30 | |
| PW91 | 1.03 | 1.09 | Indirect | 0.54 | −0.49 | |
| RPBE | 1.01 | 1.08 | Indirect | 0.52 | −0.49 | |
| XLYP | 1.32 | 1.38 | Indirect | 0.66 | −0.66 | |
| Meta GGA | SCAN | 0.52 | 0.60 | Indirect | 0.28 | −0.25 |
| R2SCAN | 0.60 | 0.70 | Indirect | 0.32 | −0.28 | |
| Hybrid | HSE06 | 2.01 | 2.14 | Indirect | 1.01 | −1.01 |
| LCAO Relaxed Structure | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| XC Functional | Symmetry Point | Symmetry Point | Symmetry Point | Symmetry Point | |||||
| LDA | HL | −2.0 | −0.5 | −0.7 | 0.6 | T | |||
| PW | −2.0 | −0.5 | −0.7 | 0.6 | |||||
| PZ | −2.0 | −0.5 | −0.7 | 0.6 | |||||
| RPA | −1.5 | −0.5 | −0.7 | 0.4 | Z | ||||
| Wigner | −2.5 | −0.5 | −0.8 | 0.6 | T | ||||
| XA | −15.9 | −1.0 | −0.9 | 0.4 | |||||
| GGA | BLYP | −1.6 | −0.4 | −2.0 | 0.9 | ||||
| BP86 | −1.5 | −0.5 | −1.6 | 0.6 | T | ||||
| BPW91 * | −22.9 | −0.6 | −1.5 | 0.7 | |||||
| GAM * | −2.4 | −0.5 | −2.0 | 0.6 | |||||
| KT2 | −1.0 | −0.5 | −0.7 | 0.4 | |||||
| PBE | −1.5 | −0.5 | −1.6 | 0.7 | T | ||||
| PBEsol | −3.1 | −0.6 | −0.9 | 0.6 | |||||
| PW91 | −1.6 | −0.5 | −1.5 | 0.7 | |||||
| RPBE | −1.4 | −0.5 | −1.6 | 0.6 | |||||
| XLYP | −1.4 | −0.5 | −1.8 | 0.8 | |||||
| Meta GGA | SCAN | −0.5 | N.A. | N.A. | 0.7 | ||||
| R2SCAN | −1.0 | 0.8 | T | ||||||
| Hybrid | HSE06 | −1.9 | −0.5 | −1.4 | 0.5 | T | |||
| PAW Relaxed Structure Lattice Parameters | ||||||||
|---|---|---|---|---|---|---|---|---|
| XC Functional | ||||||||
| LDA | HL | 7.3608 | 10.4337 | 6.2136 | −4.7% | 0.4% | −7.5% | 4.2% |
| PW | 7.3591 | 10.4233 | 6.2148 | −4.7% | 0.3% | −7.5% | 4.1% | |
| PZ | 7.3591 | 10.4268 | 6.2111 | −4.7% | 0.3% | −7.5% | 4.2% | |
| RPA | 7.2942 | 10.3717 | 6.1192 | −5.6% | −0.2% | −8.9% | 4.9% | |
| Wigner | 7.4516 | 10.5317 | 6.3072 | −3.5% | 1.3% | −6.1% | 3.6% | |
| XA | 6.2844 | 9.4626 | 5.7058 | −18.6% | −9.0% | −15.0% | 14.2% | |
| GGA | BLYP | 8.2990 | 10.4876 | 7.0063 | 7.5% | 0.9% | 4.3% | 4.2% |
| BP86 | 7.8733 | 10.5216 | 6.8619 | 1.9% | 1.2% | 2.2% | 1.8% | |
| BPW91 | 7.6002 | 10.5215 | 6.7696 | −1.6% | 1.2% | 0.8% | 1.2% | |
| GAM | 8.2758 | 10.4038 | 6.9232 | 7.2% | 0.1% | 3.1% | 3.4% | |
| KT2 | 7.3602 | 10.3814 | 6.1632 | −4.7% | −0.1% | −8.2% | 4.4% | |
| PBE | 7.5335 | 10.5490 | 6.7281 | −2.5% | 1.5% | 0.2% | 1.4% | |
| PBEsol | 7.4014 | 10.4420 | 6.2253 | −4.2% | 0.5% | −7.3% | 4.0% | |
| PW91 | 7.5436 | 10.5282 | 6.7515 | −2.3% | 1.3% | 0.5% | 1.4% | |
| RPBE | 7.8264 | 10.4997 | 6.8274 | 1.3% | 1.0% | 1.7% | 1.3% | |
| XLYP | 8.4712 | 10.5177 | 7.0292 | 9.7% | 1.2% | 4.7% | 5.2% | |
| PAW Relaxed Structure | ||||||
|---|---|---|---|---|---|---|
| XC Functional | Type | |||||
| (eV) | (eV) | (eV) | (eV) | |||
| LDA | HL | 0.39 | 0.81 | Indirect | 0.21 | −0.18 |
| PW | 0.40 | 0.82 | Indirect | 0.21 | −0.19 | |
| PZ | 0.40 | 0.82 | Indirect | 0.21 | −0.19 | |
| RPA | 0.35 | 0.83 | Indirect | 0.20 | −0.15 | |
| Wigner | 0.37 | 0.74 | Indirect | 0.19 | −0.18 | |
| XA | 1.02 | 1.49 | Indirect | 0.51 | −0.51 | |
| GGA | BLYP | 0.83 | 0.86 | Indirect | 0.43 | −0.40 |
| BP86 | 0.75 | 0.78 | Indirect | 0.40 | −0.35 | |
| BPW91 | 0.71 | 0.83 | Indirect | 0.37 | −0.34 | |
| GAM | 1.15 | 1.23 | Indirect | 0.59 | −0.56 | |
| KT2 | 0.39 | 0.86 | Indirect | 0.21 | −0.18 | |
| PBE | 0.71 | 0.86 | Indirect | 0.36 | −0.34 | |
| PBEsol | 0.35 | 0.77 | Indirect | 0.19 | −0.16 | |
| PW91 | 0.71 | 0.84 | Indirect | 0.37 | −0.34 | |
| RPBE | 0.72 | 0.78 | Indirect | 0.38 | −0.34 | |
| XLYP | 0.85 | 0.91 | Indirect | 0.44 | −0.41 | |
| PAW Relaxed Structure | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| XC Functional | Symmetry Point | Symmetry Point | Symmetry Point | Symmetry Point | |||||
| LDA | HL | −2.9 | −0.5 | −0.7 | 0.5 | T | |||
| PW | −3.1 | −0.5 | −0.8 | 0.5 | |||||
| PZ | −3.7 | −0.5 | −0.7 | 0.6 | |||||
| RPA | −1.8 | −0.5 | −0.6 | 0.6 | |||||
| Wigner | −8.3 | −0.6 | −0.8 | 0.5 | |||||
| XA | −1.2 | −1.3 | −1.4 | 0.3 | |||||
| GGA | BLYP | −1.3 | −0.4 | −1.9 | 1.0 | ||||
| BP86 | −1.9 | −0.4 | −1.5 | 0.6 | T | ||||
| BPW91 | −19.9 | −0.5 | −1.4 | 0.6 | |||||
| GAM | −1.5 | −0.5 | −1.9 | 1.1 | |||||
| KT2 | −2.3 | −0.6 | −0.7 | 0.6 | T | ||||
| PBE | −1.8 | N.A. | N.A. | 0.6 | |||||
| PBEsol | −3.6 | −0.5 | −0.7 | 0.5 | |||||
| PW91 | −2.5 | N.A. | N.A. | 0.6 | |||||
| RPBE | −2.1 | −0.4 | −1.5 | 0.6 | |||||
| XLYP | −1.4 | −0.4 | −2.0 | 1.0 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amorim, C.O.; Sivasankar, S.M.; Cunha, A.F.d. Assessing Cu3BiS3 for Thin-Film Photovoltaics: A Systematic DFT Study Comparing LCAO and PAW Across Multiple Functionals. Materials 2025, 18, 1213. https://doi.org/10.3390/ma18061213
Amorim CO, Sivasankar SM, Cunha AFd. Assessing Cu3BiS3 for Thin-Film Photovoltaics: A Systematic DFT Study Comparing LCAO and PAW Across Multiple Functionals. Materials. 2025; 18(6):1213. https://doi.org/10.3390/ma18061213
Chicago/Turabian StyleAmorim, Carlos O., Sivabalan M. Sivasankar, and António F. da Cunha. 2025. "Assessing Cu3BiS3 for Thin-Film Photovoltaics: A Systematic DFT Study Comparing LCAO and PAW Across Multiple Functionals" Materials 18, no. 6: 1213. https://doi.org/10.3390/ma18061213
APA StyleAmorim, C. O., Sivasankar, S. M., & Cunha, A. F. d. (2025). Assessing Cu3BiS3 for Thin-Film Photovoltaics: A Systematic DFT Study Comparing LCAO and PAW Across Multiple Functionals. Materials, 18(6), 1213. https://doi.org/10.3390/ma18061213








