Dynamic Compressive Behavior, Constitutive Modeling, and Complete Failure Criterion of 30 Vol.% B4C/2024Al Composite
Highlights
- A constitutive model incorporating strain softening was developed to describe the plastic behavior of 30vol.%B4C/2024Al.
- An ultimate failure criterion compatible with the above model for 30 vol.% B4C/2024Al was established.
- The implementation of the model and failure criterion in commercial software was successfully achieved, offering a novel approach to describing the plastic and failure behaviors of particle-reinforced metal matrix composites.
Abstract
1. Introduction
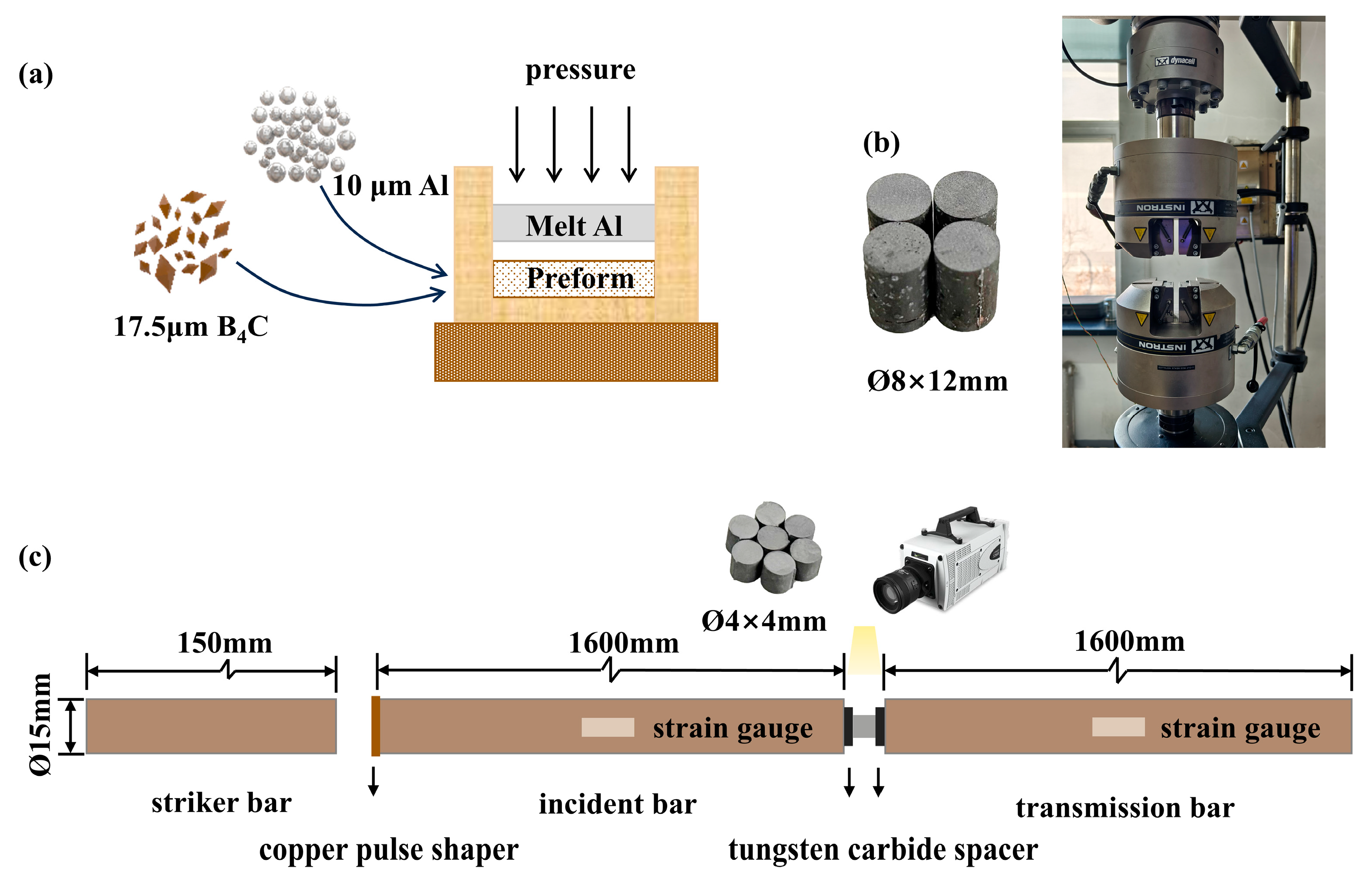
2. Materials and Methods
2.1. The 30 Vol.%B4C/2024Al Composite
2.2. Quasi-Static and Dynamic Compression Test
2.3. Microstructural Characterization
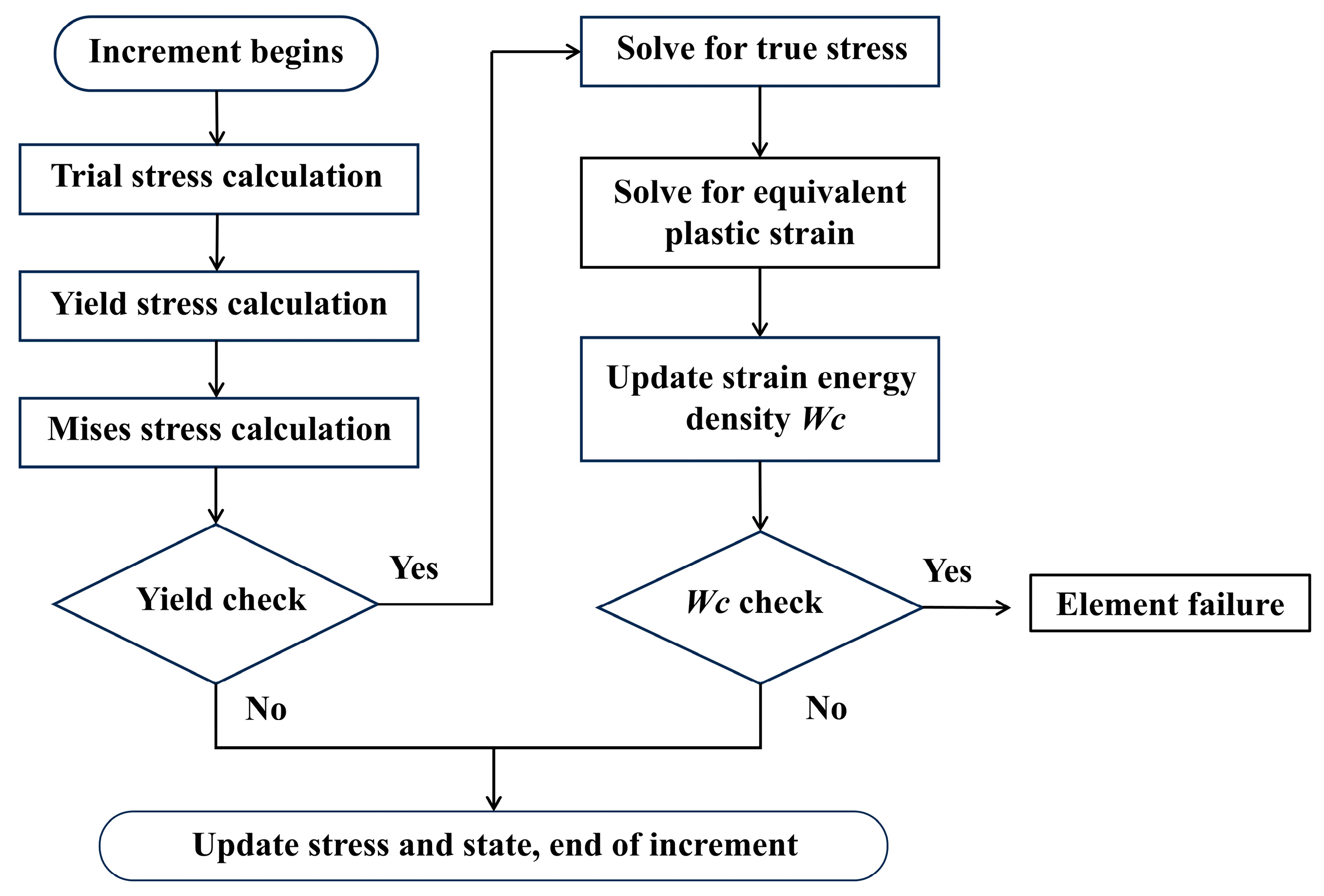
2.4. VUHARD Subroutine Implementation
2.5. Numerical Simulation
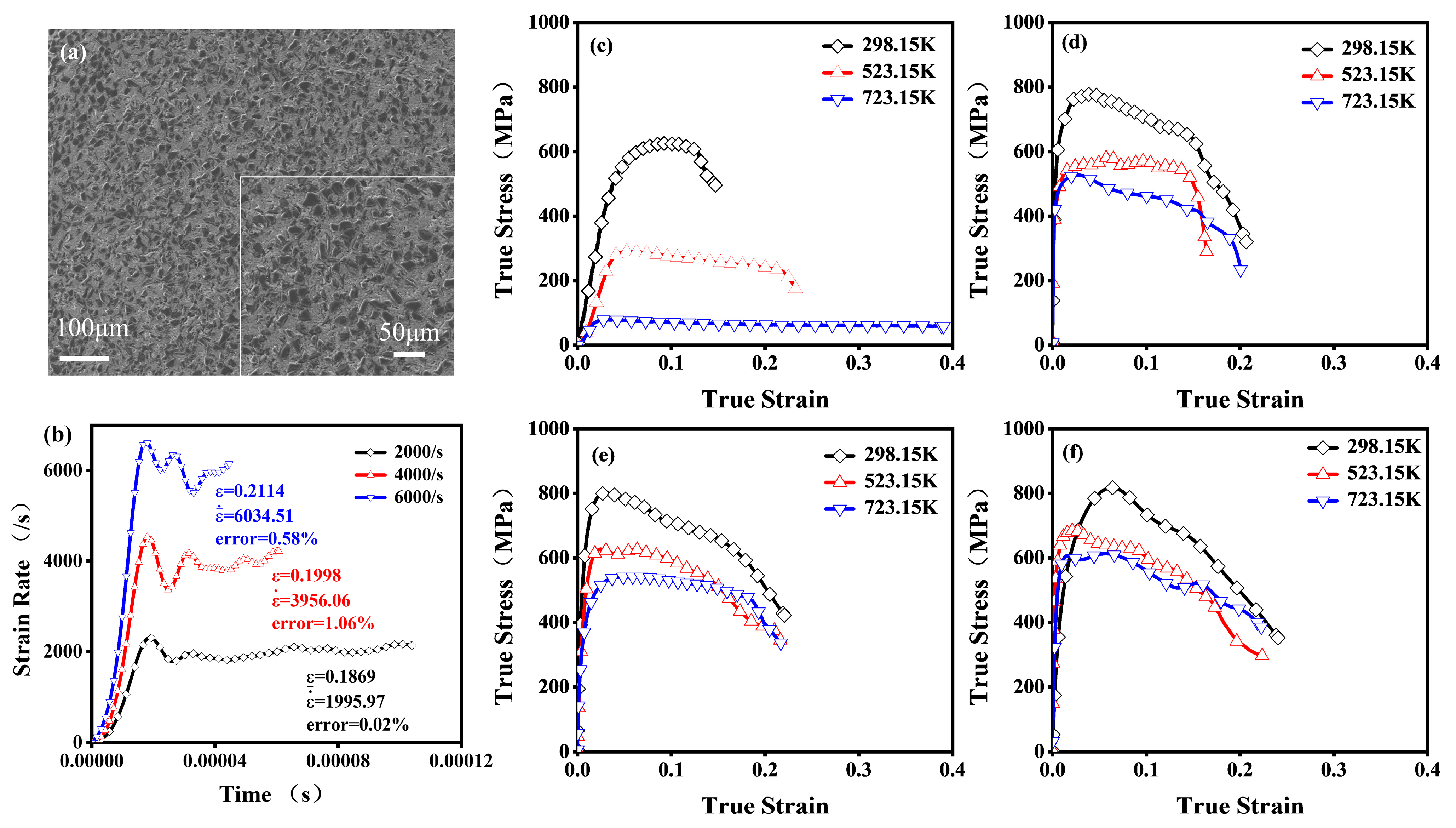
3. Experimental Results and Discussion
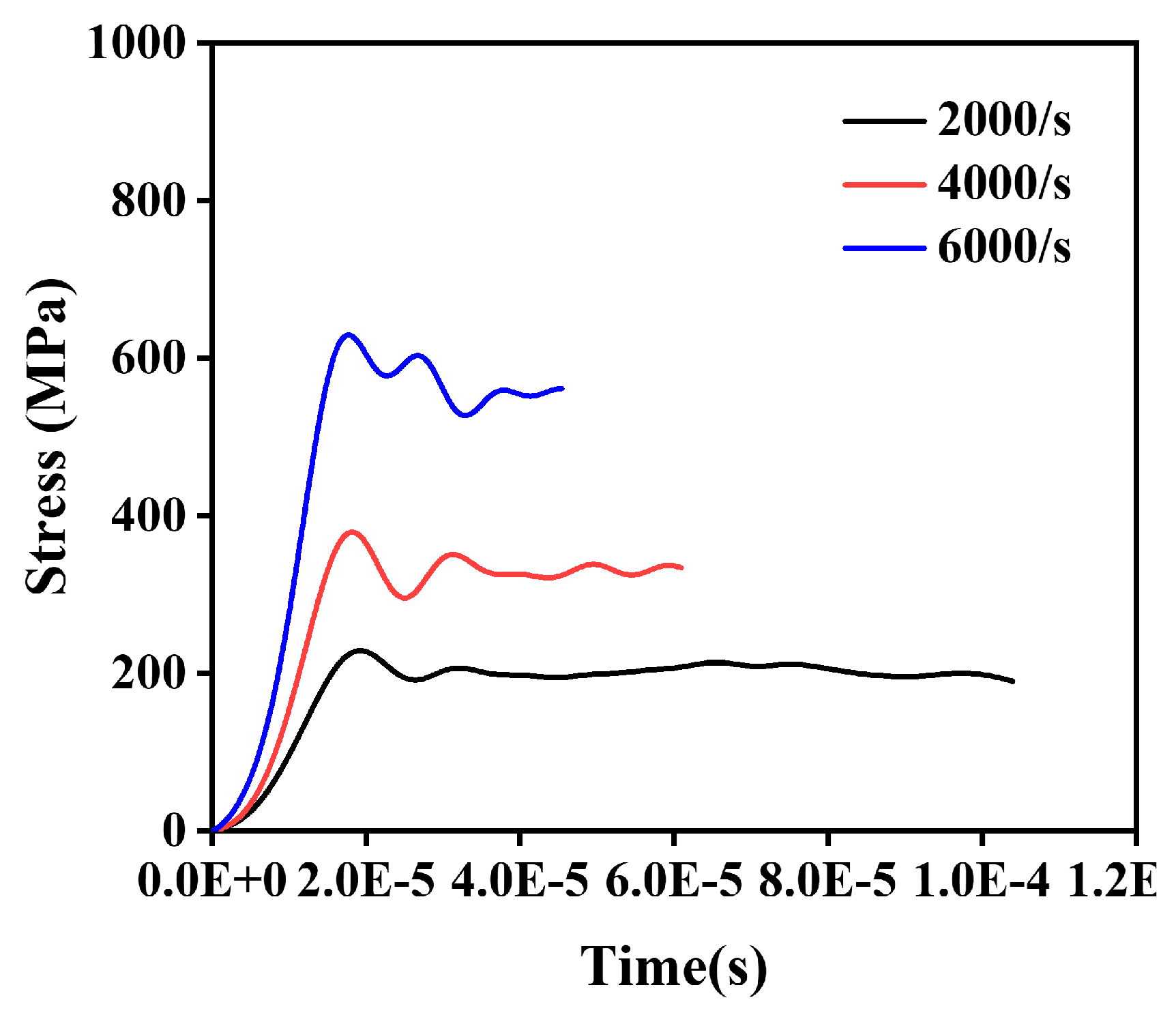
3.1. Stress–Strain Curve
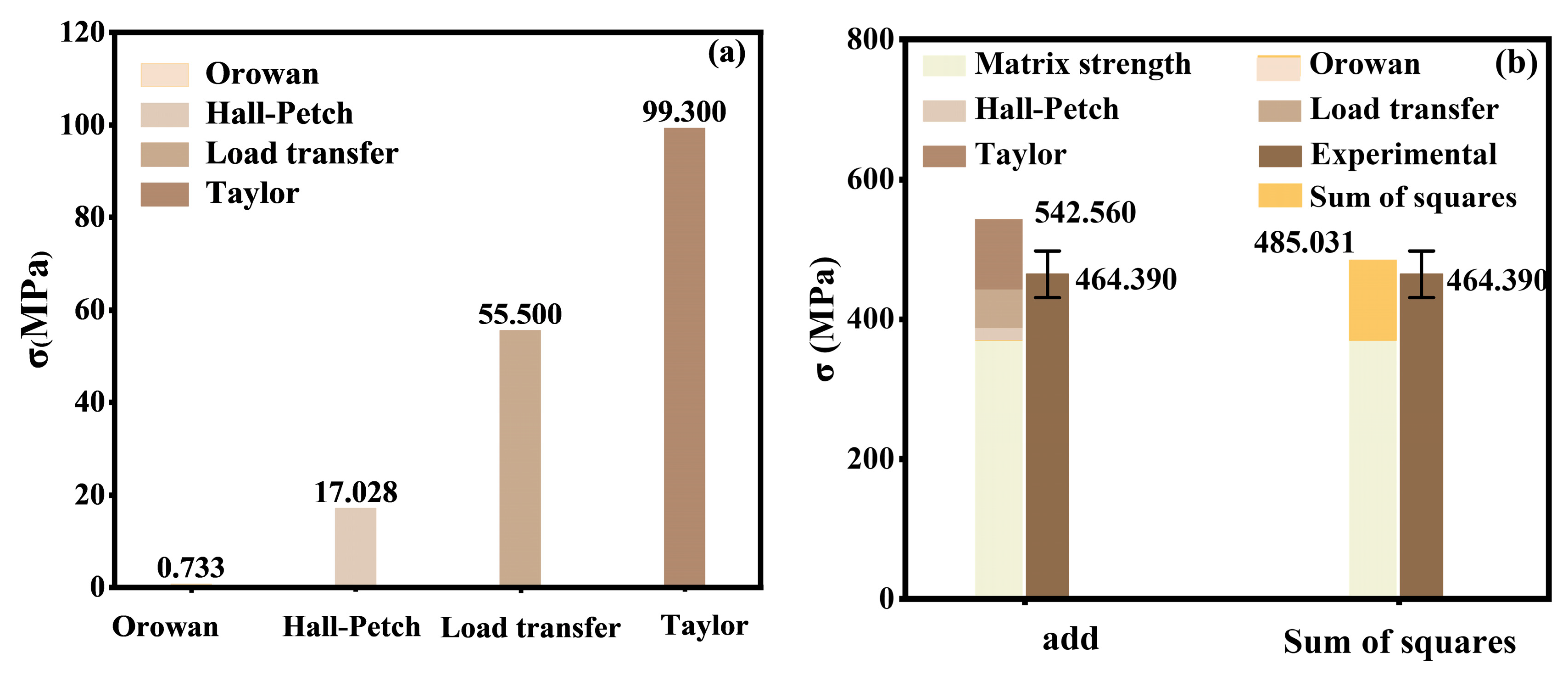
3.2. Strengthening Mechanisms
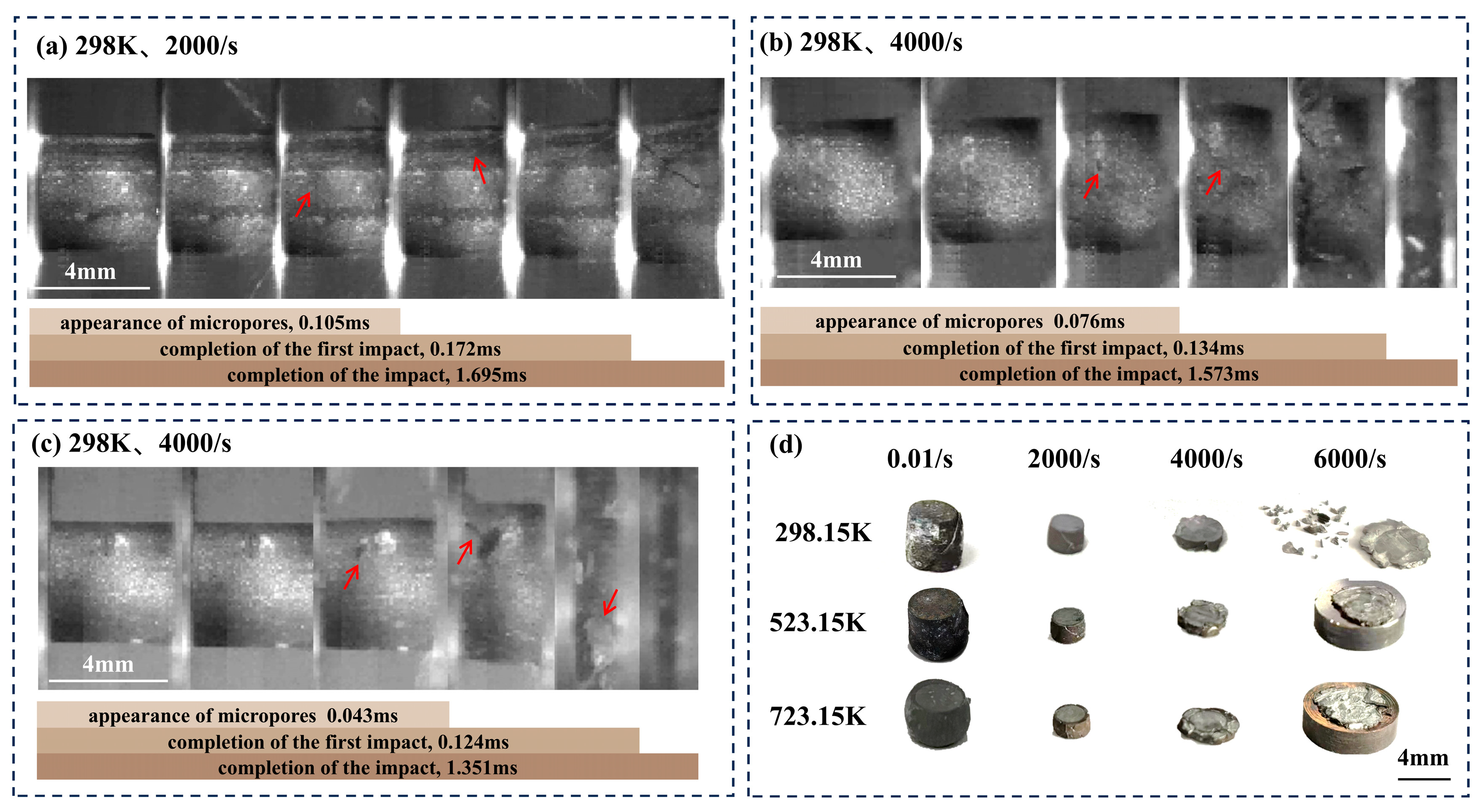
3.3. Damage Mechanisms
4. MJC Model & Complete Failure Criterion
4.1. MJC Model
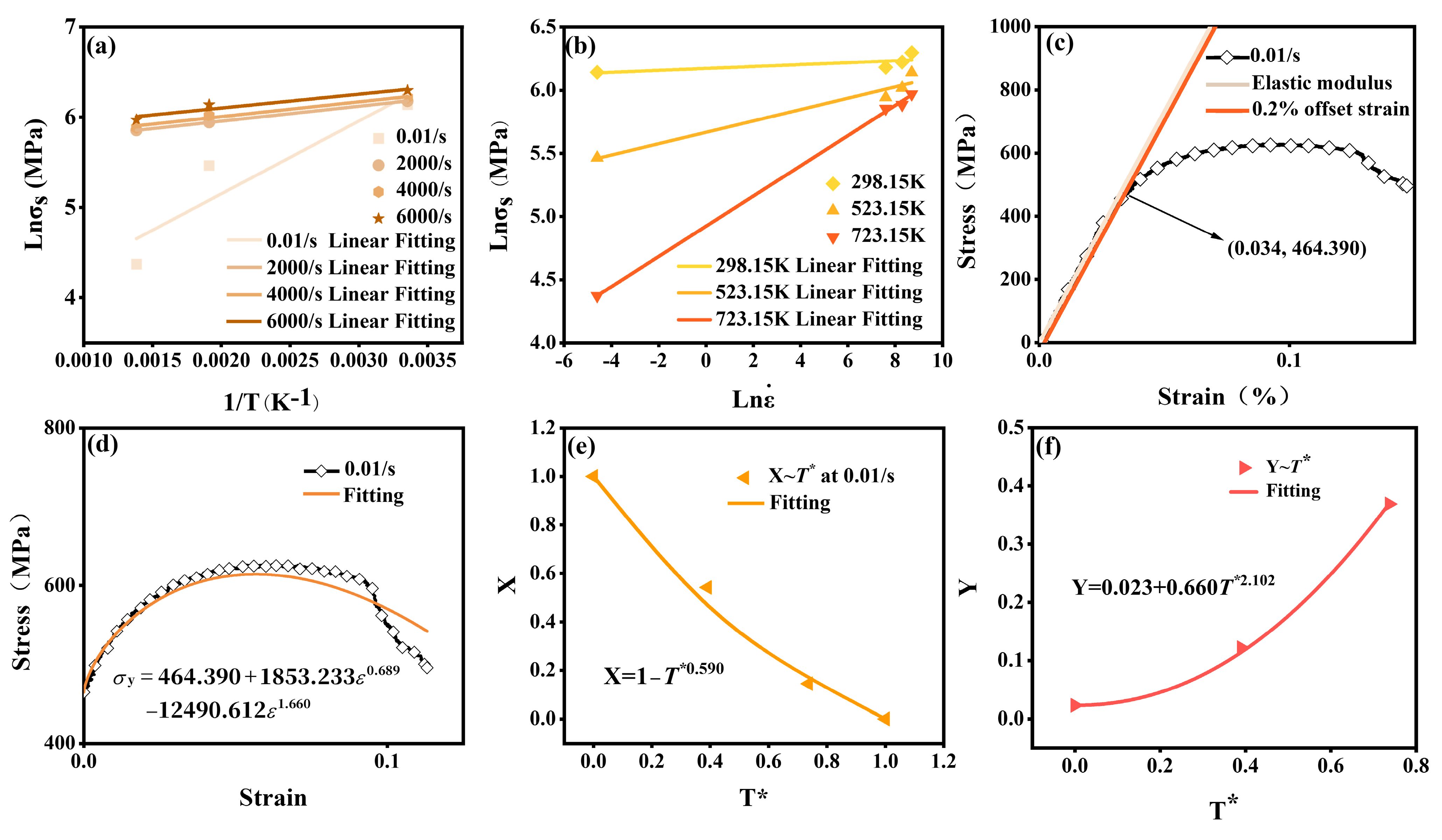
4.1.1. Determination of f and g
4.1.2. Calibration of Parameters A, B, C, p, and q
4.1.3. Calibration of Parameter n
4.1.4. Determination of Parameters C1, C2, and C3
4.2. Complete Failure Criterion
4.2.1. Calibration of Parameters D5 and D6
4.2.2. Calibration of Parameters D1, D2, D3, and D4
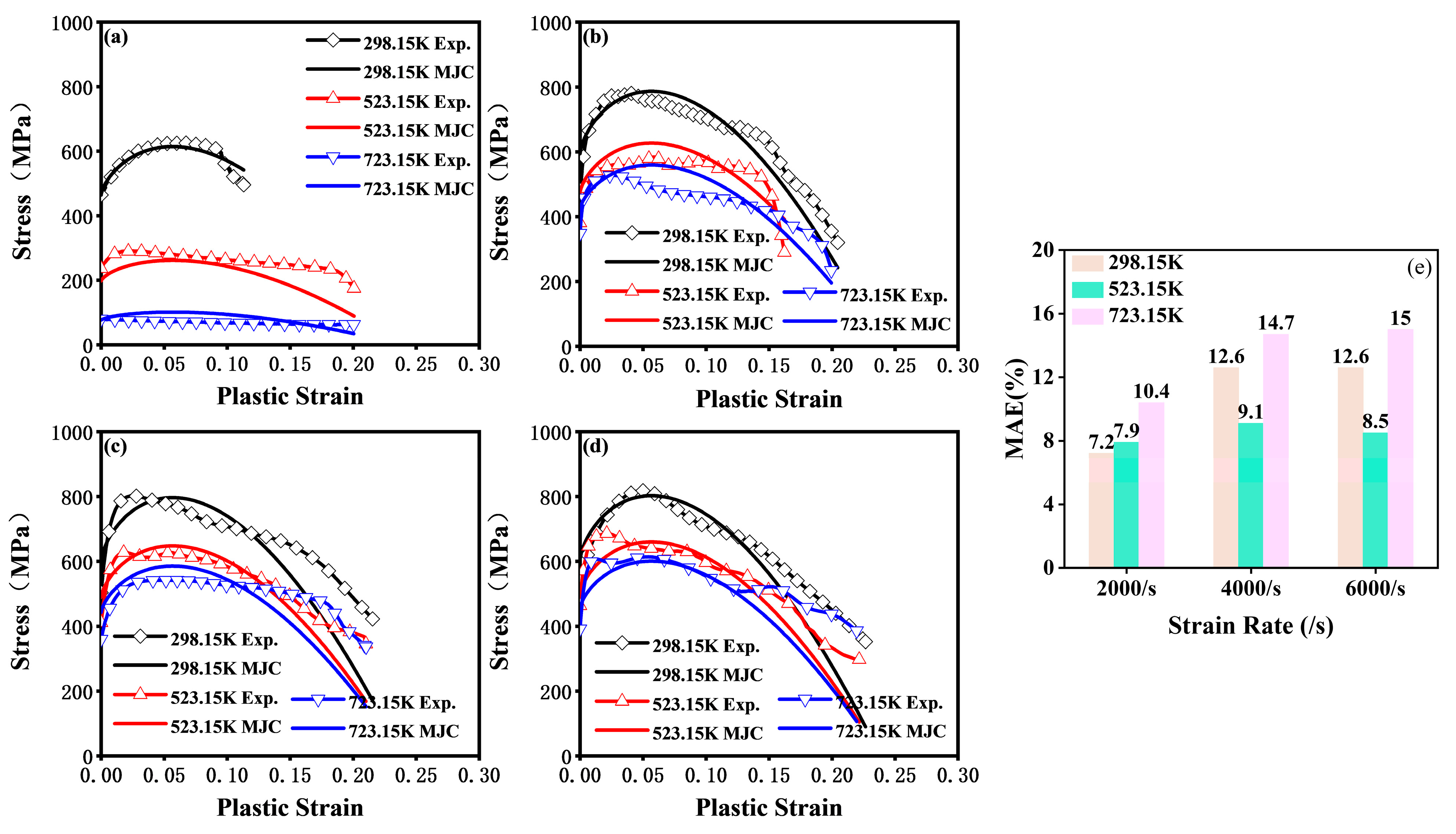
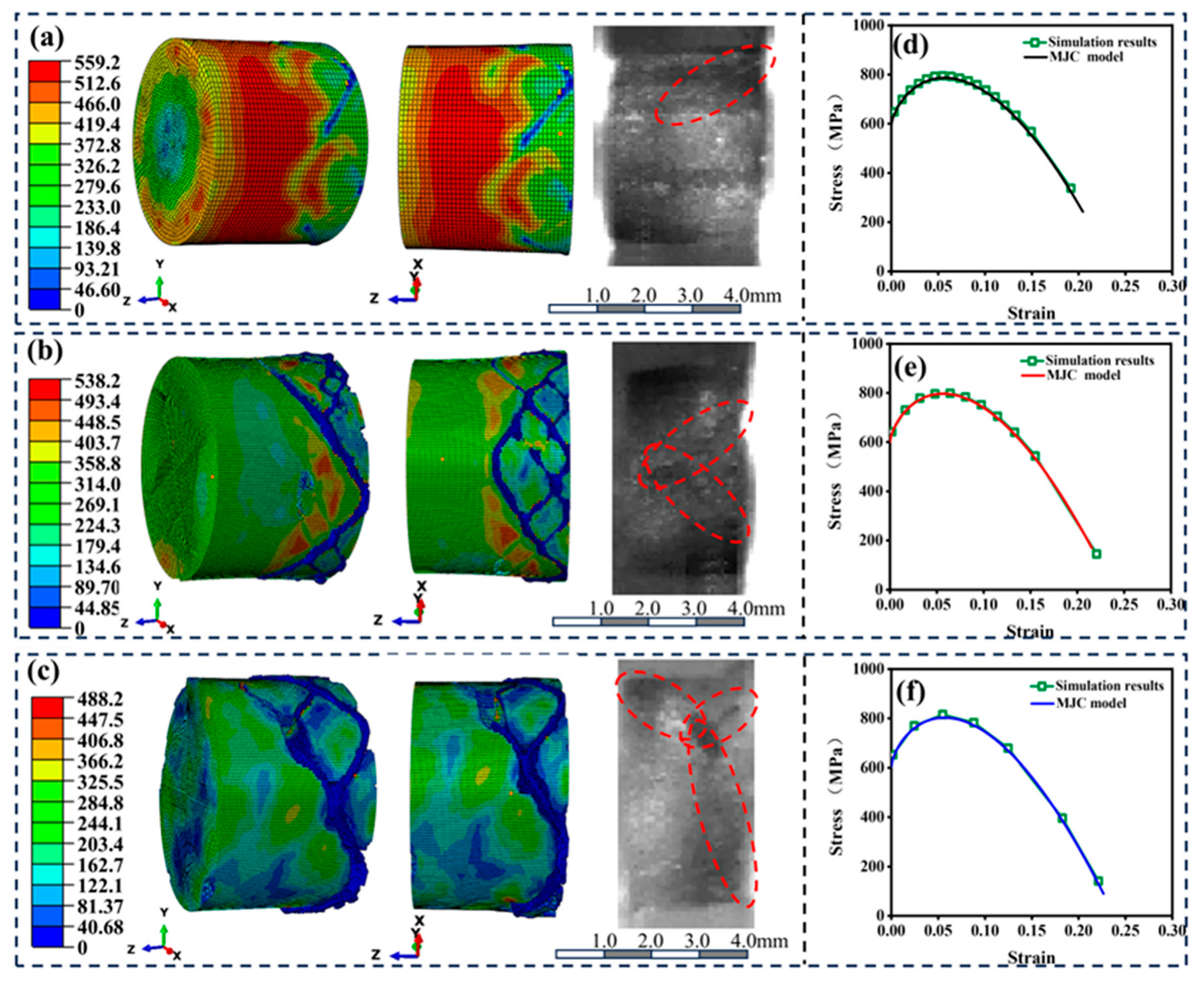
4.3. Prediction Performance of the MJC
5. Numerical Simulation Results and Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Samal, P.; Vundavilli, P.R.; Meher, A.; Mahapatra, M.M. Recent progress in aluminum metal matrix composites: A review on processing, mechanical and wear properties. J. Manuf. Process. 2020, 59, 131–152. [Google Scholar] [CrossRef]
- Deng, Y.J.; Ren, Y.F.; Liu, X.; Li, L.; Qin, M. Protection performance of aluminum matrix ceramic ball composite materials plate for hypervelocity impact based on FE-SPH adaptive method. Compos. Struct. 2024, 338, 118103. [Google Scholar] [CrossRef]
- Sharma, A.; Srinivasan, K.V.S.; Dixit, M.; Gupta, A.K.; Sujith, R. Ballistic performance of functionally graded boron carbide reinforced Al–Zn–Mg–Cu alloy. J. Mater. Res. Technol. 2022, 18, 4042–4059. [Google Scholar] [CrossRef]
- Karamis, M.B.; Nair, F.; Tasdemirci, A. Analyses of metallurgical behavior of Al–SiCp composites after ballistic impacts. Compos. Struct. 2004, 64, 219–226. [Google Scholar] [CrossRef]
- Dubey, R.; Jayaganthan, R.; Ruan, D.; Gupta, N.K.; Jones, N.; Velmurugan, R. Ballistic perforation and penetration of 6xxx-series aluminium alloys: A review. Int. J. Impact Eng. 2023, 172, 104426. [Google Scholar] [CrossRef]
- Zhang, F.; Zhu, P.; Lu, P.; Liu, S.; Wang, L. Bio-inspired Optimization of Al2O3/Al Composite Armor: Structural Design and Ballistic Simulation Based on Armadillo Shell. Sci. Rep. 2024, 14, 20216. [Google Scholar]
- Ho, E. Developing Functionally Graded Ceramic/Polymer and Ceramic/Metal Composites for Advanced Armour Materials. Ph.D. Thesis, University of Bristol, Bristol, UK, 2024. [Google Scholar]
- Wang, Y.; Liu, Q.; Zhang, B.; Wang, H.; Hazell, P.J.; Han, Z.; Li, J.; Li, B.; Li, L.; Liu, F.; et al. Ballistic performance of functionally graded B4C/Al composites without abrupt interfaces: Experiments and simulations. J. Mater. Res. Technol. 2023, 25, 1011–1029. [Google Scholar] [CrossRef]
- Luo, T.; Chao, Z.; Du, S.; Jiang, L.; Chen, S.; Zhang, R.; Han, H.; Han, B.; Wang, Z.; Chen, G.; et al. Novel Multi-Scale Ceramic-Based Array (SiCb+B4Cp)/7075Al as Promising Materials for Armor Structure. Materials 2023, 16, 5796. [Google Scholar] [CrossRef]
- Evci, C.; Gülgeç, M. An experimental investigation on the impact response of composite materials. Int. J. Impact Eng. 2012, 43, 40–51. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Q.; Zhang, B.; Zhang, H.; Jin, Y.; Zhong, Z.; Ye, J.; Ren, Y.; Ye, F.; Wang, W. Dynamic compressive response and impact resistance of bioinspired nacre-like 2024Al/B4C composites. Mater. Sci. Eng. A 2022, 831, 142261. [Google Scholar] [CrossRef]
- Liu, B.; Huang, W.; Huang, L.; Wang, H. Size-dependent compression deformation behaviors of high particle content B4C/Al composites. Mater. Sci. Eng. A 2012, 534, 530–535. [Google Scholar] [CrossRef]
- Ye, S.J.; Bie, B.X.; Zhang, Z.M.; Zhao, X.J.; Sun, T.; Fezzaa, K.; Huang, J.Y.; Yao, X.H.; Luo, S.N. Rate-dependent strength and deformation heterogeneity of B4C-reinforced Al composite: Time-resolved imaging with synchrotron X-rays. Ceram. Int. 2021, 47, 16141–16151. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Q.; Zhang, B.; Zhang, H.; Zhong, Z.; Ye, J.; Ren, Y.; Shen, L.; Ye, F.; Wang, W. Mechanical response and damage evolution of bio-inspired B4C-reinforced 2024Al composites subjected to quasi-static and dynamic loadings. Mater. Sci. Eng. A 2022, 840, 142991. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Q.; Zhang, B.; Zhang, H.; Jin, Y.; Zhong, Z.; Ye, J.; Ren, Y.; Ye, F.; Wang, W. Dynamic mechanical response and damage mechanisms of nacre-inspired 2024Al/B4C composite at elevated temperature. Mater. Sci. Eng. A 2022, 831, 142263. [Google Scholar] [CrossRef]
- Jain, R.; Soni, H.; Mahto, R.P.; Sahoo, B.N. An insight into high-temperature deformation mechanism of magnesium in-situ composite through development of Johnson-Cook and constitutive model. Int. J. Lightweight Mater. Manuf. 2023, 6, 574–588. [Google Scholar] [CrossRef]
- Li, S.; Luo, T.; Chao, Z.; Jiang, L.; Han, H.; Han, B.; Du, S.; Liu, M. A Review of Dynamic Mechanical Behavior and the Constitutive Models of Aluminum Matrix Composites. Materials 2024, 17, 1879. [Google Scholar] [CrossRef]
- Ren, L.; Zhao, K.; Gao, T.; Liu, G.; Sun, Q.; Liu, S.; Liu, X. Constitutive equation and microstructural evolution of one distinctive Al–based hybrid composite reinforced by nano–AlN and micro–TiC particles during hot compression. Mater. Sci. Eng. A 2023, 888, 145830. [Google Scholar] [CrossRef]
- Wang, J.; Liang, Q.; Li, Y. The flow stress prediction of TiB2/2024 aluminum matrix composites based on modified Arrhenius model and gene expression programming model. J. Sci. Adv. Mater. Devices 2024, 9, 100777. [Google Scholar] [CrossRef]
- Naguib, M.E.; Gad, S.I.; Megahed, M.; Agwa, M.A. Computational damage analysis of metal matrix composites to identify optimum particle characteristics in indentation process. Eng. Fract. Mech. 2024, 295, 109751. [Google Scholar] [CrossRef]
- Ban, H.; Yao, Y.; Chen, S.; Fang, D. A new constitutive model of micro-particle reinforced metal matrix composites with damage effects. Int. J. Mech. Sci. 2019, 152, 524–534. [Google Scholar] [CrossRef]
- Ghandehariun, A.; Kishawy, H.; Balazinski, M. On machining modeling of metal matrix composites: A novel comprehensive constitutive equation. Int. J. Mech. Sci. 2016, 107, 235–241. [Google Scholar] [CrossRef]
- Sun, W.; Duan, C.; Yin, W. Development of a dynamic constitutive model with particle damage and thermal softening for Al/SiCp composites. Compos. Struct. 2020, 236, 111856. [Google Scholar] [CrossRef]
- Nie, K.B.; Wang, X.J.; Deng, K.K.; Hu, X.S.; Wu, K. Magnesium matrix composite reinforced by nanoparticles—A review. J. Magnes. Alloys 2021, 9, 57–77. [Google Scholar] [CrossRef]
- De Cicco, M.; Konishi, H.; Cao, G.; Choi, H.S.; Turng, L.-S.; Perepezko, J.H.; Kou, S.; Lakes, R.; Li, X. Strong, Ductile Magnesium-Zinc Nanocomposites. Metall. Mater. Trans. A 2009, 40, 3038–3045. [Google Scholar] [CrossRef]
- Sun, J.; Ding, D.; Liu, W.; Wu, G.; Liu, H.; Wei, G.; Liu, H. Strength and elastic modulus enhancement in Mg-Li-Al matrix composites reinforced by ex situ TiB2 particles via stir casting. J. Magnes. Alloys 2024, 12, 3574–3588. [Google Scholar] [CrossRef]
- Chen, L.Y.; Xu, J.Q.; Choi, H.; Pozuelo, M.; Ma, X.; Bhowmick, S.; Yang, J.M.; Mathaudhu, S.; Li, X.C. Processing and properties of magnesium containing a dense uniform dispersion of nanoparticles. Nature 2015, 528, 539–543. [Google Scholar] [CrossRef]
- Liu, R.; Wu, C.; Zhang, J.; Luo, G.; Shen, Q.; Zhang, L. Microstructure and mechanical behaviors of the ultrafine grained AA7075/B4C composites synthesized via one-step consolidation. J. Alloys Compd. 2018, 748, 737–744. [Google Scholar] [CrossRef]
- Mu, D.K.Q.; Jiang, Z.H.; Zhang, Z.; Liang, J.M.; Wang, J.; Zhang, D.L.; Xian, Q.G. Microstructural evolution, precipitation and mechanical properties of ultrafine-grained and coarse-grained 2024 aluminum alloys fabricated by powder metallurgy. J. Mater. Res. 2022, 37, 692–704. [Google Scholar] [CrossRef]
- Sun, L.; Guo, Y.; Chen, L.; Zhao, G. Effects of solution and aging treatments on the microstructure and mechanical properties of cold rolled 2024 Al alloy sheet. J. Mater. Res. Technol. 2021, 12, 1126–1142. [Google Scholar] [CrossRef]
- Zhou, Z.; Wu, G.; Jiang, L.; Xu, Z. The deformation of B 4 C particle in the B 4 C/2024Al composites after high velocity impact. Micron 2014, 67, 107–111. [Google Scholar] [CrossRef]
- Chao, Z.; Wang, Z.; Jiang, L.; Chen, S.; Pang, B.; Zhang, R.; Du, S.; Chen, G.; Zhang, Q.; Wu, G. Microstructure and mechanical properties of B4C/2024Al functionally gradient composites. Mater. Des. 2022, 215, 110449. [Google Scholar] [CrossRef]
- Kocks, U. The relation between polycrystal deformation and single-crystal deformation. Metall. Mater. Trans. B 1970, 1, 1121–1143. [Google Scholar] [CrossRef]
- Zhang, K.; Holmedal, B.; Mánik, T.; Saai, A. Assessment of advanced Taylor models, the Taylor factor and yield-surface exponent for FCC metals. Int. J. Plast. 2019, 114, 144–160. [Google Scholar] [CrossRef]
- Hansen, N. The effect of grain size and strain on the tensile flow stress of aluminium at room temperature. Acta Metall. 1977, 25, 863–869. [Google Scholar] [CrossRef]
- Luo, K.; Liu, S.; Xiong, H.; Zhang, Y.; Kong, C.; Yu, H. Mechanical Properties and Strengthening Mechanism of Aluminum Matrix Composites Reinforced by High-entropy Alloy Particles. Met. Mater. Int. 2022, 28, 2811–2821. [Google Scholar] [CrossRef]
- Arsenault, R.; Shi, N. Dislocation generation due to differences between the coefficients of thermal expansion. Mater. Sci. Eng. 1986, 81, 175–187. [Google Scholar] [CrossRef]
- Sahoo, B.P.; Das, D.; Chaubey, A.K. Strengthening mechanisms and modelling of mechanical properties of submicron-TiB2 particulate reinforced Al 7075 metal matrix composites. Mater. Sci. Eng. A 2021, 825, 141873. [Google Scholar] [CrossRef]
- Wang, S.; Deng, X.; Gao, P.; Ren, Z.; Wang, X.; Feng, H.; Zeng, L.; Zhang, Z. Physical constitutive modelling of hot deformation of titanium matrix composites. Int. J. Mech. Sci. 2023, 262, 108712. [Google Scholar] [CrossRef]
- Yu, F.; Jar, P.Y.B.; Hendry, M.T. Constitutive analysis of pressure-insensitive metals under axisymmetric tensile loading: A stress triaxiality-dependent plasticity damage model. Int. J. Mech. Sci. 2018, 142–143, 21–32. [Google Scholar] [CrossRef]
- Peng, J.; Wang, Y.; Dai, Q.; Liu, X.; Liu, L.; Zhang, Z. Effect of Stress Triaxiality on Plastic Damage Evolution and Failure Mode for 316L Notched Specimen. Metals 2019, 9, 1067. [Google Scholar] [CrossRef]
- Zhan, J.; Yao, X.; Han, F.; Zhang, X. A rate-dependent peridynamic model for predicting the dynamic response of particle reinforced metal matrix composites. Compos. Struct. 2021, 263, 113673. [Google Scholar] [CrossRef]
- Zhan, J.M.; Yao, X.H.; Han, F. An approach of peridynamic modeling associated with molecular dynamics for fracture simulation of particle reinforced metal matrix composites. Compos. Struct. 2020, 250, 112613. [Google Scholar] [CrossRef]
- Chao, Z.; Jiang, L.; Chen, G.; Zhang, Q.; Zhang, N.; Zhao, Q.; Pang, B.; Wu, G. A modified Johnson-Cook model with damage degradation for B4Cp/Al composites. Compos. Struct. 2022, 282, 115029. [Google Scholar] [CrossRef]
- Yang, X.; Guo, H.; Yao, Z.; Yuan, S. Strain rate sensitivity, temperature sensitivity, and strain hardening during the isothermal compression of BT25y alloy. J. Mater. Res. 2016, 31, 2863–2875. [Google Scholar] [CrossRef]
- Shokry, A. A Modified Johnson–Cook Model for Flow Behavior of Alloy 800H at Intermediate Strain Rates and High Temperatures. J. Mater. Eng. Perform. 2017, 26, 5723–5730. [Google Scholar] [CrossRef]
- Rudra, A.; Ashiq, M.; Das, S.; Dasgupta, R. Constitutive Modeling for Predicting High-Temperature Flow Behavior in Aluminum 5083+10 Wt Pct SiCp Composite. Metall. Mater. Trans. B 2019, 50, 1060–1076. [Google Scholar] [CrossRef]
- Cao, Y.; Zhen, Y.; Song, M.; Yi, H.; Li, F.; Li, X. Determination of Johnson–Cook parameters and evaluation of Charpy impact test performance for X80 pipeline steel. Int. J. Mech. Sci. 2020, 179, 105627. [Google Scholar] [CrossRef]
- Qian, L.; Du, J.; Li, P.; Ma, T.; Zhou, Y.; Sun, C. Fracture prediction of high-strength steel sheet during in-plane compression-shear forming under negative stress triaxiality. Arch. Civ. Mech. Eng. 2024, 24, 60. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, Q.; Zhao, Z.; Luo, T.; Li, F.; Zhao, J.; Chao, Z.; Liu, S.; Mei, Y.; Zhou, F. Dynamic Compressive Behavior, Constitutive Modeling, and Complete Failure Criterion of 30 Vol.% B4C/2024Al Composite. Materials 2025, 18, 1170. https://doi.org/10.3390/ma18051170
Yan Q, Zhao Z, Luo T, Li F, Zhao J, Chao Z, Liu S, Mei Y, Zhou F. Dynamic Compressive Behavior, Constitutive Modeling, and Complete Failure Criterion of 30 Vol.% B4C/2024Al Composite. Materials. 2025; 18(5):1170. https://doi.org/10.3390/ma18051170
Chicago/Turabian StyleYan, Qiang, Zhihong Zhao, Tian Luo, Feng Li, Jianjun Zhao, Zhenlong Chao, Sanfeng Liu, Yong Mei, and Fengjun Zhou. 2025. "Dynamic Compressive Behavior, Constitutive Modeling, and Complete Failure Criterion of 30 Vol.% B4C/2024Al Composite" Materials 18, no. 5: 1170. https://doi.org/10.3390/ma18051170
APA StyleYan, Q., Zhao, Z., Luo, T., Li, F., Zhao, J., Chao, Z., Liu, S., Mei, Y., & Zhou, F. (2025). Dynamic Compressive Behavior, Constitutive Modeling, and Complete Failure Criterion of 30 Vol.% B4C/2024Al Composite. Materials, 18(5), 1170. https://doi.org/10.3390/ma18051170





