Influence of Pre-Strain on the Course of Energy Dissipation and Durability in Low-Cycle Fatigue
Abstract
1. Introduction
2. Materials and Methods
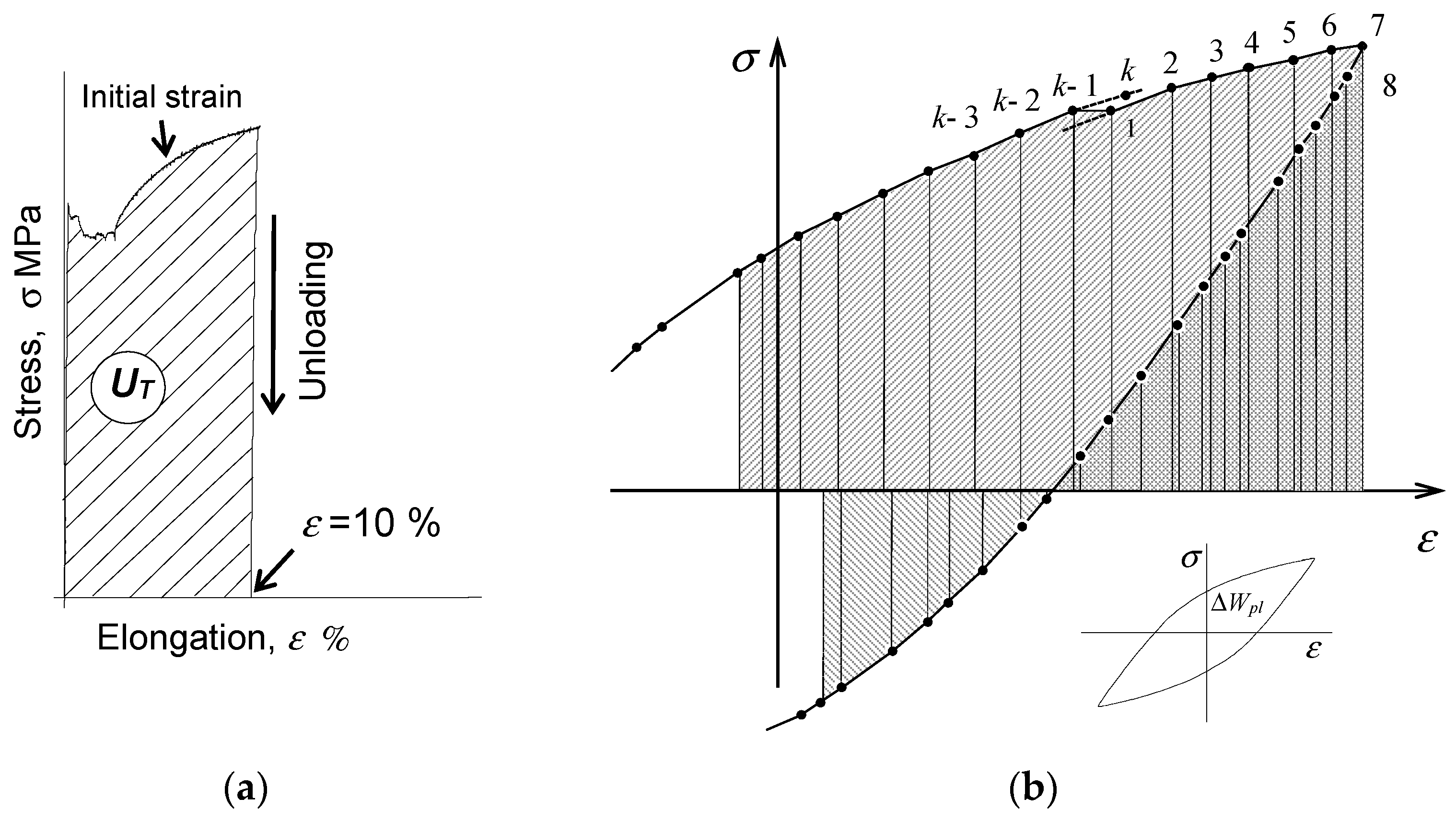
2.1. Description of Energy Accumulation
2.1.1. Basic Assumptions
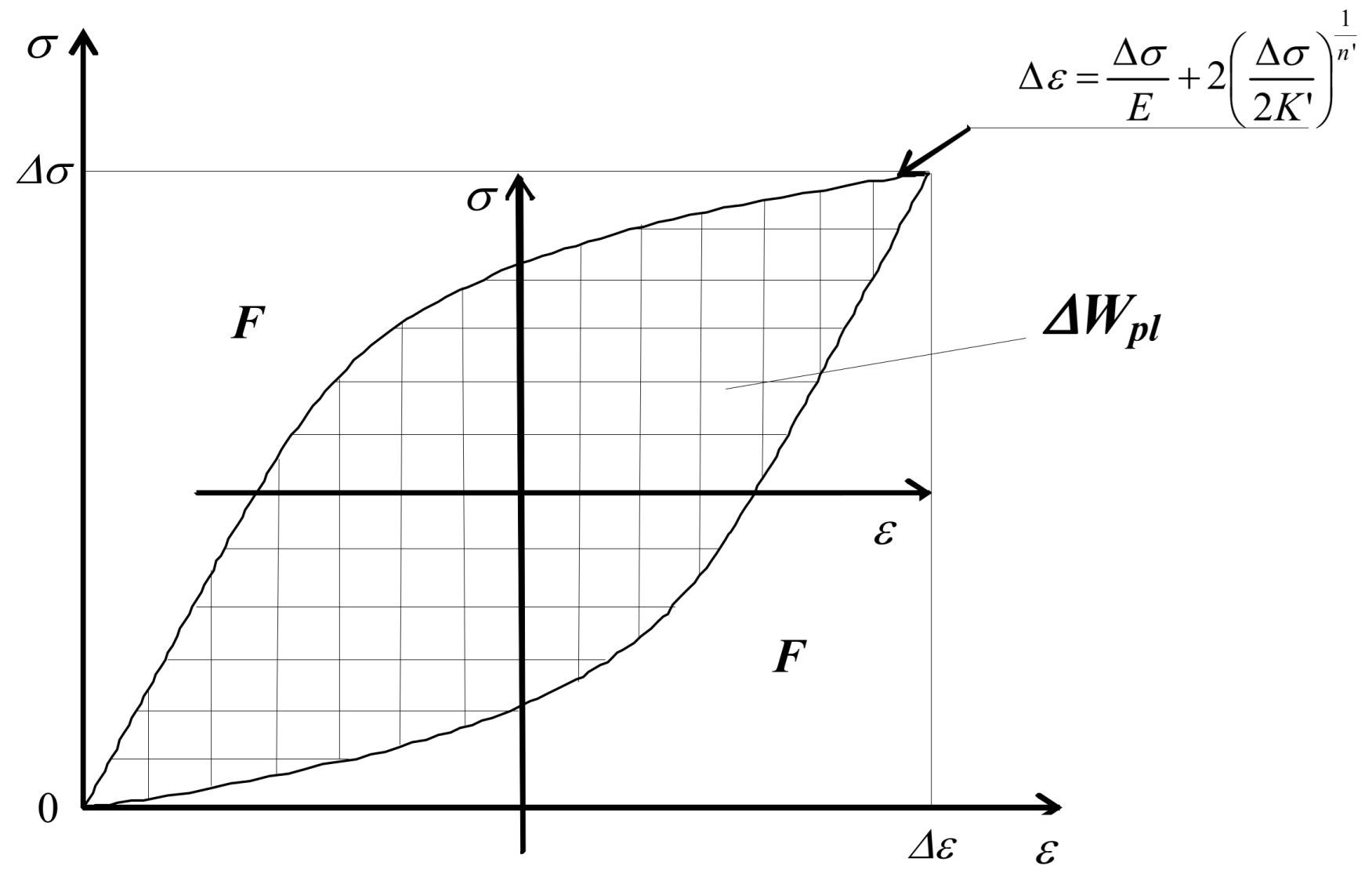
2.1.2. Analytical Description of Hysteresis Loop
2.2. Experimental Tests
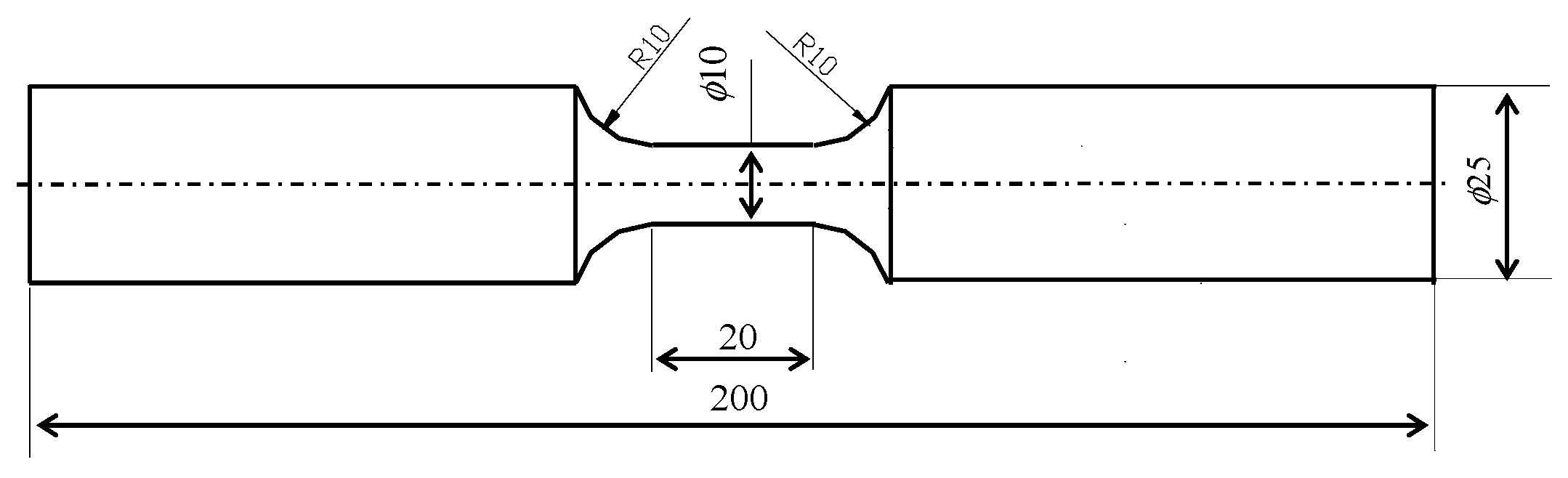
2.2.1. Static Tensile Tests
2.2.2. Fatigue Tests
2.2.3. Statistical Analysis
3. Results
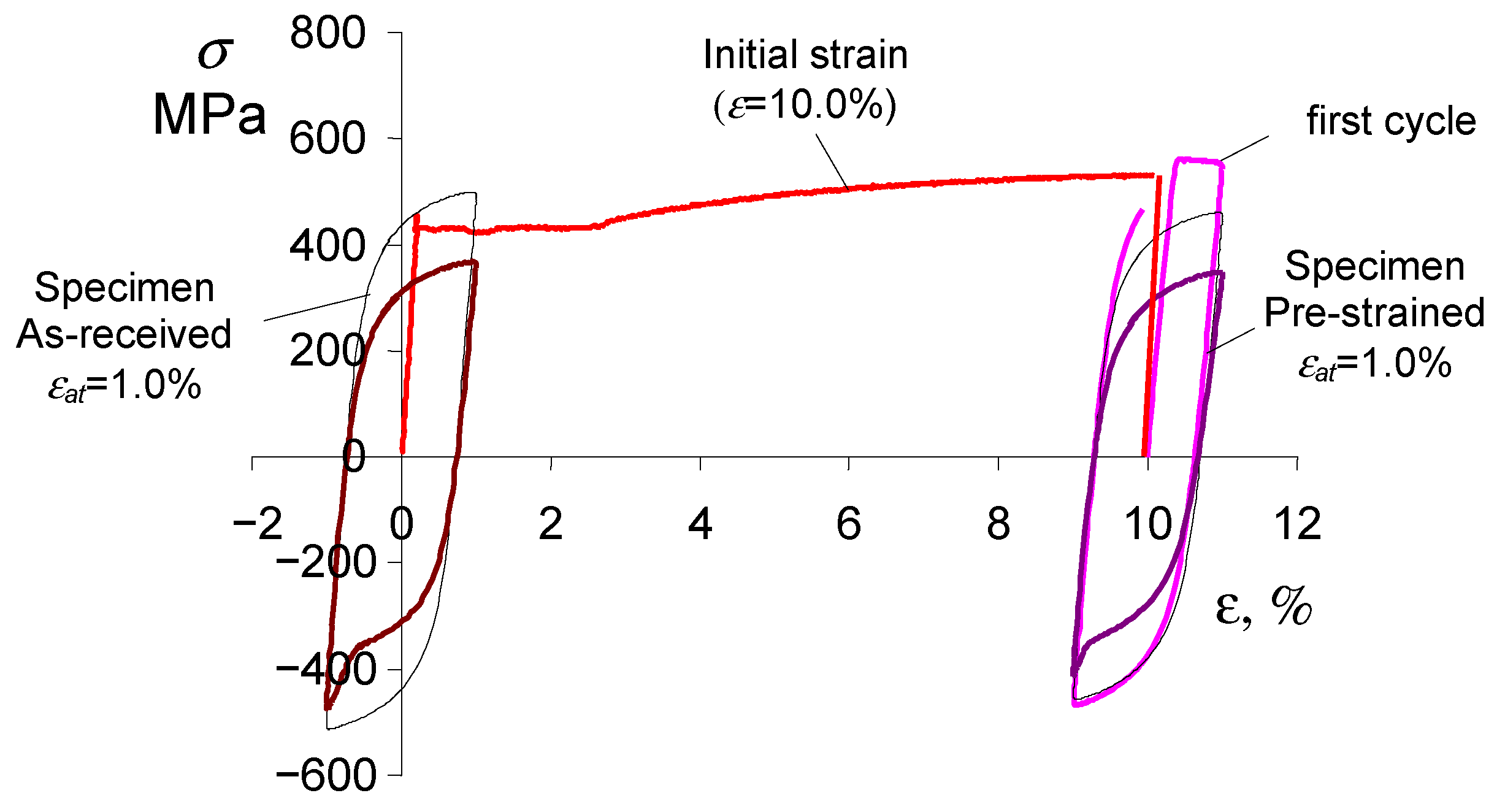
3.1. Static Tensile Tests
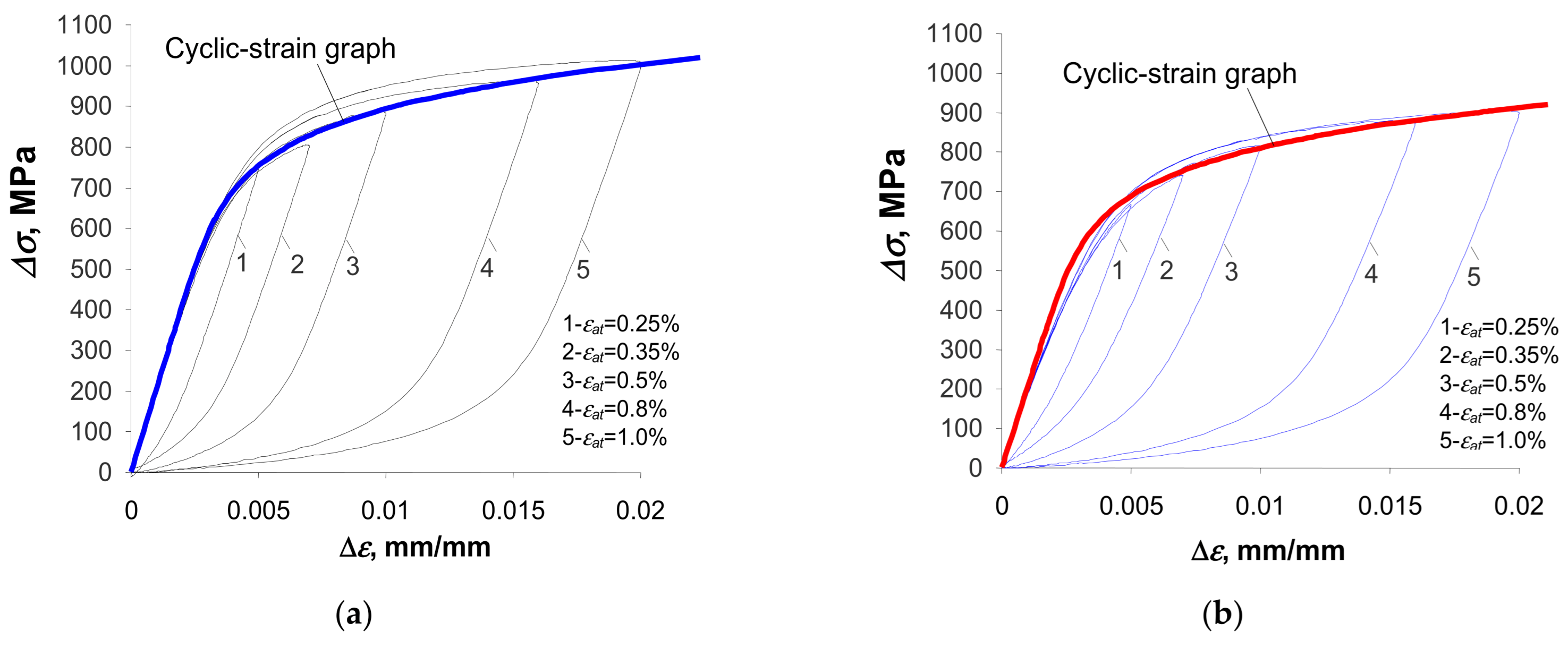
3.2. Low-Cycle Fatigue Tests—Strain-Based Description
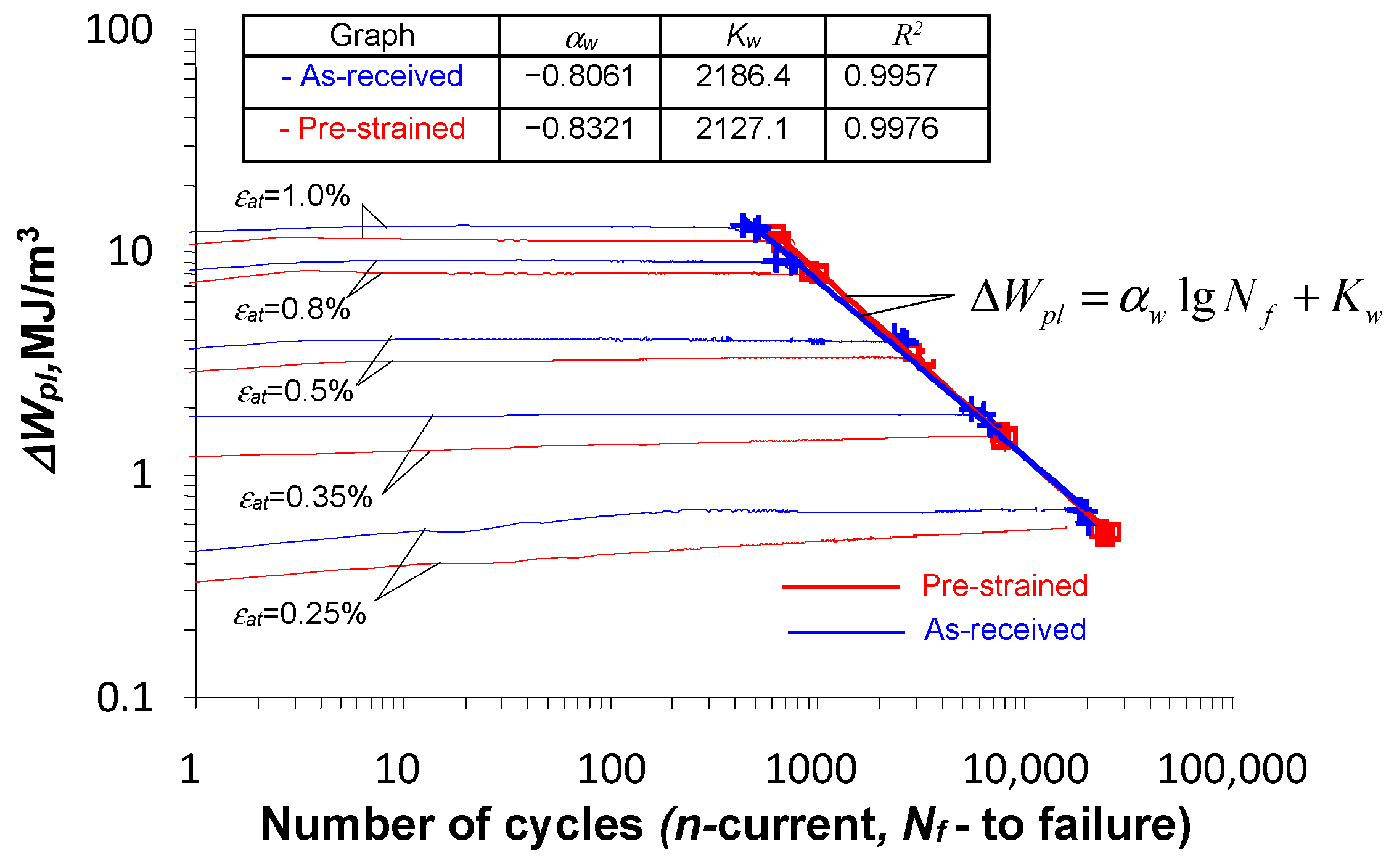
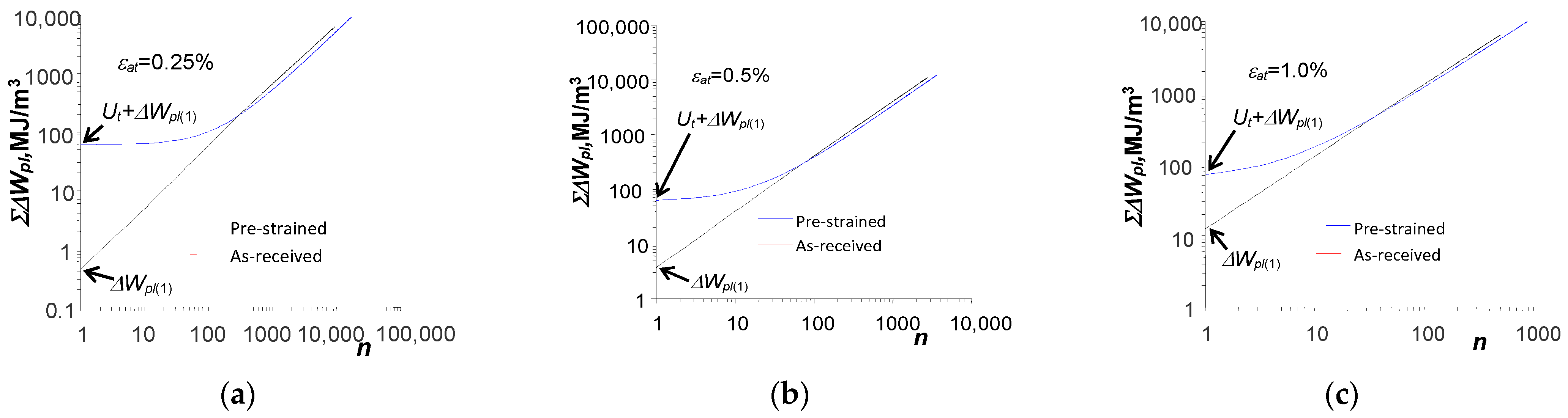
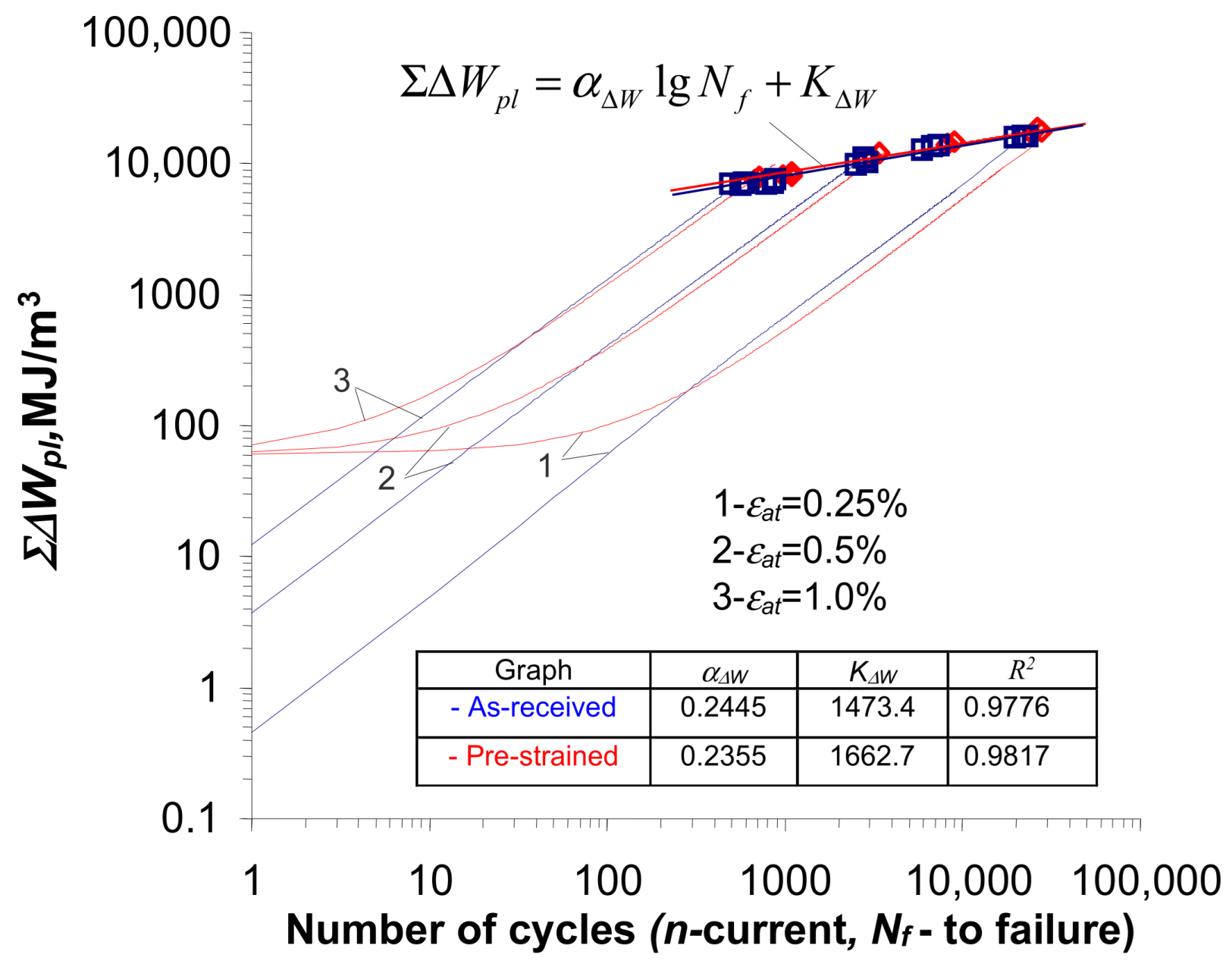
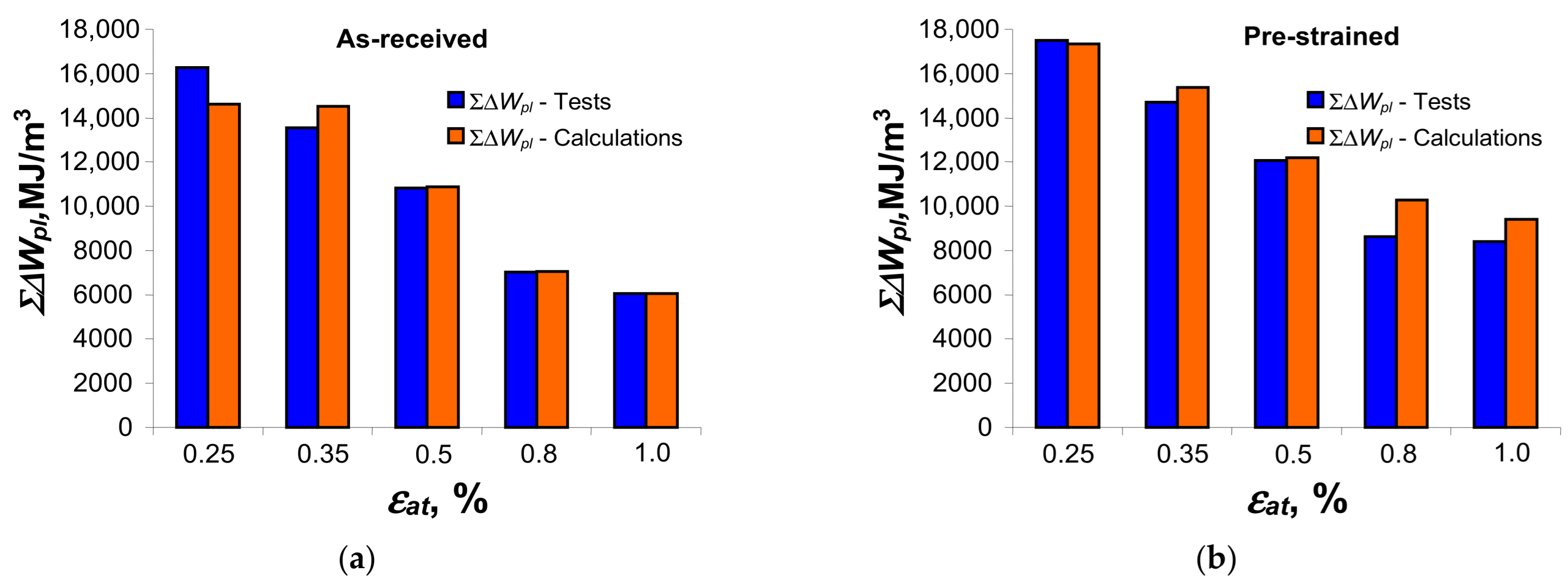
3.3. Low-Cycle Fatigue Tests—Energy-Based Description
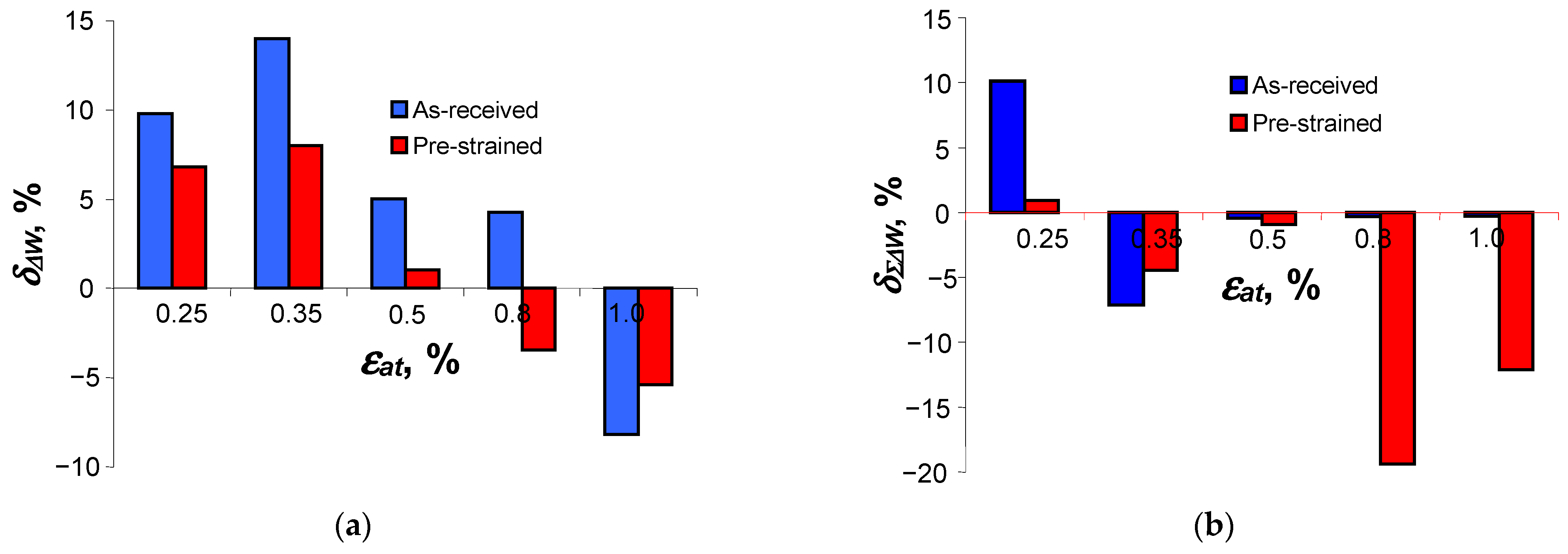
4. Discussion: Verification of Analytical Models
5. Conclusions
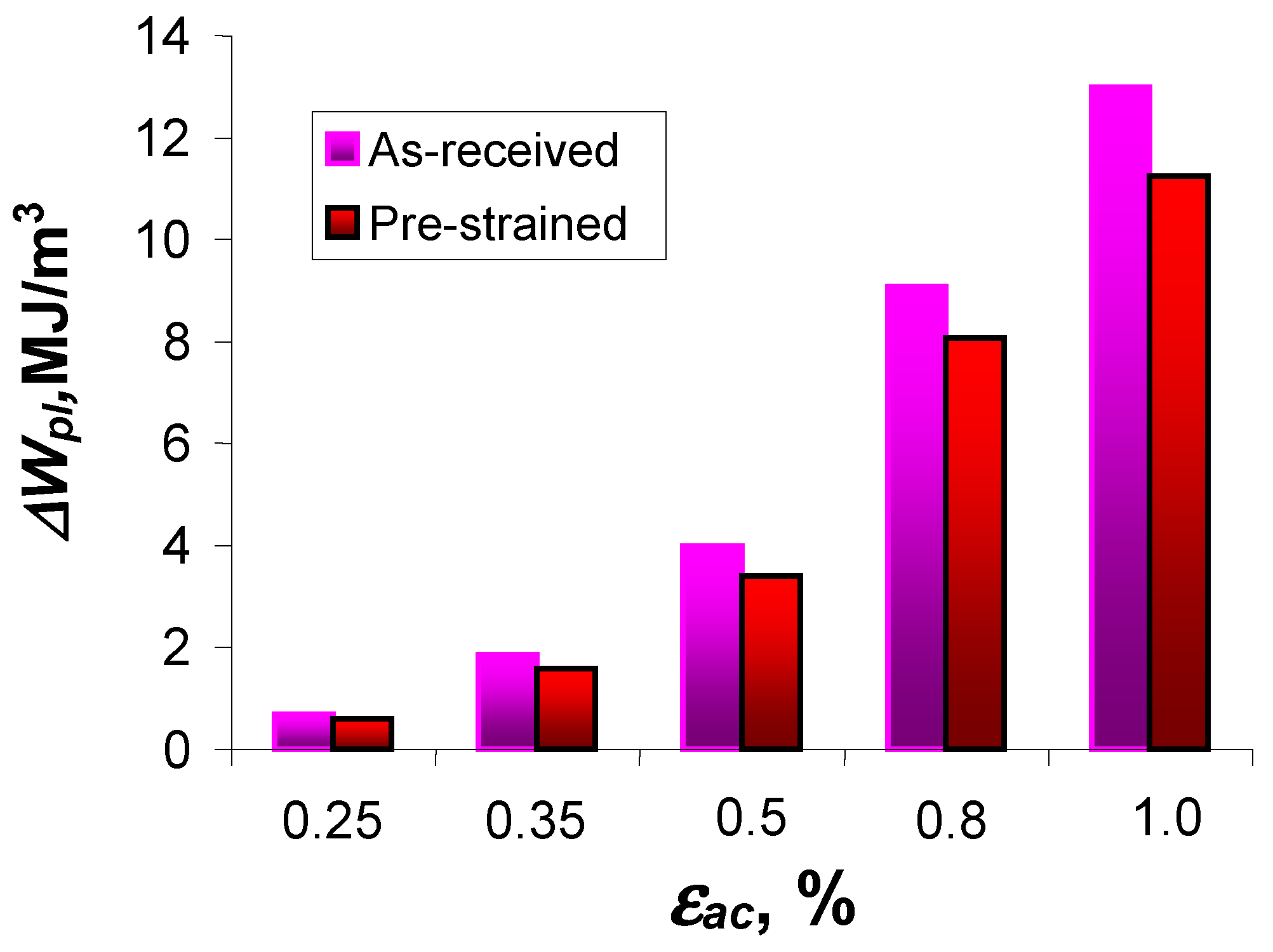
- Total dissipated energy until fracture, , depends on the level of strain amplitude . The dissipated energy increases as the strain level decreases.
- Unit loop energy, , accounts for stresses, strains and their interactions; therefore, it is not sensitive to the type of control quantities (stresses or strains) used in experimental tests. It can be classified as a parameter that is not very sensitive to changes in the cyclic properties of steel, and the classical analytical descriptions are capable of reproducing well the experimental values of the unit loop energy of both as-received and pre-strained specimens.
- The pre-straining of S420M steel specimens causes a reduction in the loop plastic strain . Thus, a decrease in the unit hysteresis loop energy is observed at all levels of strain amplitude . For this reason, a slight increase in the fatigue life of pre-strained specimens is observed compared to as-received specimens.
- Despite the different durabilities obtained at the same strain levels for the pre-strained and as-received samples, their fatigue characteristics in terms of energy, i.e., the fatigue plot and the accumulation plot are statistically the same.
- There is a close relationship between the total energy dissipated during fatigue testing and the durability . In fatigue calculations, the relationship can perform similar functions as the classical fatigue diagram of . The parameters of Equation (7), i.e., the directional coefficient and the free expression, can be material-specific quantities (cf. [8]), and Mroziński and Topoliński [13] utilized the relation in a new method of fatigue damage summation in terms of energy, pointing out the advantages of the energy-based approach in degradation modeling, cf. [1].
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
List of Symbols
| Young’s modulus | |
| tensile strength | |
| upper yield strength | |
| lower yield strength | |
| cyclic strength coefficient | |
| current number of cycles of constant-amplitude loading | |
| cyclic strain-hardening exponent | |
| number of cycles to failure | |
| number of reversals to failure | |
| transition life | |
| relative number of cycles | |
| , | energy per cycle exponent |
| , | energy per cycle coefficient |
| plastic strain energy in a unit volume of material per cycle (area of the hysteresis loop) | |
| energy dissipated during static pre-strain | |
| energy dissipated during static pre-strain until failure | |
| stress in general terms | |
| cyclic stress range | |
| amplitude of stress | |
| strain in general terms | |
| amplitude of total strain | |
| amplitude of plastic strain | |
| amplitude of elastic strain | |
| cyclic total strain range | |
| cyclic plastic strain range | |
| coefficient of cyclic plastic strain | |
| fatigue strength coefficient | |
| , | exponents of strain diagram of fatigue |
References
- Egner, W.; Sulich, P.; Mroziński, S.; Egner, H. Modelling thermo-mechanical cyclic behavior of P91 steel. Int. J. Plast. 2020, 135, 102820. [Google Scholar] [CrossRef]
- Liao, D.; Zhu, S.-P.; Gao, J.-W.; Correia, J.; Calçada, R.; Lesiuk, G. Generalized strain energy density-based fatigue indicator parameter. Int. J. Mech. Sci. 2023, 254, 108427. [Google Scholar] [CrossRef]
- Ye, D.; Wang, Z. A new approach to low-cycle fatigue damage based on exhaustion of static toughness and dissipation of cyclic plastic strain energy during fatigue. Int. J. Fatigue 2001, 23, 679–687. [Google Scholar]
- Mroziński, S.; Piotrowski, M.; Egner, H. Effects of fatigue testing on low-cycle properties of P91 steel. Int. J. Fatigue 2019, 120, 65–72. [Google Scholar] [CrossRef]
- Branco, R.; Martins, R.F.; Correia, J.; Marciniak, Z.; Macek, W.; Jesus, J. On the use of the cumulative strain energy density for fatigue life assessment in advanced high-strength steels. Int. J. Fatigue 2022, 164, 107–121. [Google Scholar] [CrossRef]
- Golański, G.; Mroziński, S. Fatigue life of GX12CrMoVNbN9-1 cast steel in the energy-based approach. Adv. Mater. Res. 2012, 396–398, 398–449. [Google Scholar] [CrossRef]
- Mroziński, S.; Golański, G. Low cycle fatigue of GX12CrMoVNbN9-1 cast steel at elevated temperature. J. Achiev. Mater. Manuf. Eng. 2011, 49, 7–16. [Google Scholar]
- Atzori, B.; Meneghetti, G.; Ricotta, M. Unified material parameters based on full compatibility for low-cycle fatigue characterisation of as-cast and austempered ductile irons. Int. J. Fatigue 2014, 68, 111–122. [Google Scholar] [CrossRef]
- Gołoś, K.; Ellyin, F. Generalisation of cumulative damage criterion to multilevel cyclic loading. Theor. Appl. Fract. Mech. 1987, 7, 169–176. [Google Scholar] [CrossRef]
- Gołoś, K.; Ellyin, F. A total strain energy theory for cumulative fatigue damage. Trans. ASME J. Press. Vessel Technol. 1988, 110, 35–41. [Google Scholar] [CrossRef]
- Morrow, J. Cyclic Plastic Strain Energy and Fatigue of Metals. In Internal Friction, Damping, and Cyclic Plasticity; Lazan, B.J., Ed.; American Society for Testing & Materials: West Conshohocken, PA, USA, 1965; Volume 45. [Google Scholar]
- Mroziński, S. Energy-based method of fatigue damage cumulation. Int. J. Fatigue 2019, 121, 73–83. [Google Scholar] [CrossRef]
- Mroziński, S.; Topoliński, T. New Energy Model of Fatigue Damage Accumulation and its verification for 45-steel. J. Theor. Appl. Mech. 1999, 2, 223–239. [Google Scholar]
- Mansson, S.S.; Halford, G.R. Re-Examination of Cumulative Fatigue Damage Analysis—An Engineering Perspective. Eng. Fract. Mech. 1986, 25, 539–571. [Google Scholar] [CrossRef]
- Fatemi, A.; Yang, L. Cumulative Fatigue Damage and Life Prediction Theories: A Survey of the State of the Art for Homogeneous Materials. Int. J. Fatigue 1998, 20, 9–34. [Google Scholar] [CrossRef]
- Mroziński, S.; Szala, J. An analysis of the influence of overloads on a fatigue life of 45-steel within the range of low–cycle fatigue. J. Theor. Appl. Mech. 1993, 4, 111–123. [Google Scholar]
- Robertson, L.T.; Hilditch, T.B.; Hodgson, P.D. The effect of prestrain and bake hardening on the low-cycle fatigue properties of TRIP steel. Int. J. Fatigue 2008, 30, 587–594. [Google Scholar] [CrossRef]
- Ly, A.L.; Findley, K.O. The effects of pre-straining conditions on fatigue behavior of a multiphase TRIP steel. Int. J. Fatigue 2016, 87, 225–234. [Google Scholar] [CrossRef]
- Branco, R.; Costa, J.D.; Borrego, L.P.; Wuc, S.C.; Long, X.Y.; Antunes, F.V. Effect of tensile pre-strain on low-cycle fatigue behaviour of 7050-T6 aluminium alloy. Eng. Fail. Anal. 2020, 114, 104592. [Google Scholar] [CrossRef]
- Mroziński, S.; Lipski, A.; Piotrowski, M.; Egner, H. Influence of Pre-Strain on Static and Fatigue Properties of S420M Steel. Materials 2023, 16, 590. [Google Scholar] [CrossRef]
- Yang, Z.A.; Wang, Z. Effect of prestrain on cyclic creep behaviour of a high strength spring steel. Mater. Sci. Eng. A 1996, 210, 83–93. [Google Scholar] [CrossRef]
- Chiou Y-Ch Jen, Y.-M.; Weng, W.-K. Experimental investigation on the effect of tensile pre-strain on ratcheting behavior of 430 Stainless Steel under fully-reversed loading conditions. Eng. Fail. Anal. 2011, 18, 766–775. [Google Scholar] [CrossRef]
- Wang, G. Effect of local plastic stretch on total fatigue life evaluation. In Proceedings of the ECF Proceedings of the 15th European Conference of Fracture, Stockholm, Sweden, 11–13 August 2004. [Google Scholar]
- Wang, Y.; Yu, D.; Chen, G.; Chen, X. Effects of pre-strain on uniaxial ratcheting and fatigue failure of Z2CN18.10 austenitic stainless steel. Int. J. Fatigue 2013, 52, 106–113. [Google Scholar] [CrossRef]
- Feltner, C.E.; Morrow, J.D. Microplastic strain hysteresis energy as a criterion for fatigue fracture. J. Fluids Eng. Trans. ASME 1961, 83, 15–22. [Google Scholar] [CrossRef]
- Mroziński, S. Energy dissipated in a material during monotonic and cyclic loading. In Proceedings of the 19th Symposium on Experimental Mechanics of Solids, Jachranka, Poland, 18–20 October 2000. [Google Scholar]
- Ramberg, W.; Osgood, W.R. Description of Stress-Strain Curves by Three Parameters; NACA, Technical Note No. 902; National Advisory Committee for Aeronautics: Washington DC, USA, 1943. [Google Scholar]
- Masing, G. Eigenspannungen und Verfestigung beim Messing. In Proceedings of the 2nd International Congress of Applied Mechanics, Zurich, Switzerland, 12–17 September 1926; pp. 332–335. [Google Scholar]
- Kujawski, D.; Ellyin, F. A Cumulative damage theory for fatigue crack initiation and propagation. Int. J. Fatigue 1984, 6, 83–88. [Google Scholar] [CrossRef]
- ASTM E606-92; Standard Practice for Strain-Controlled Fatigue Testing. ASTM: West Conshohocken, PA, USA, 1998.
- ASTM E8; Tension Testing of Metallic Material. ASTM: West Conshohocken, PA, USA, 2024.
- Muralidharan, U.; Manson, S.S. A modified universal slopes equation for estimation of fatigue characteristics of metals, Journal of Engineering Materials and Technology. Trans. ASME 1988, 110, 55–58. [Google Scholar]
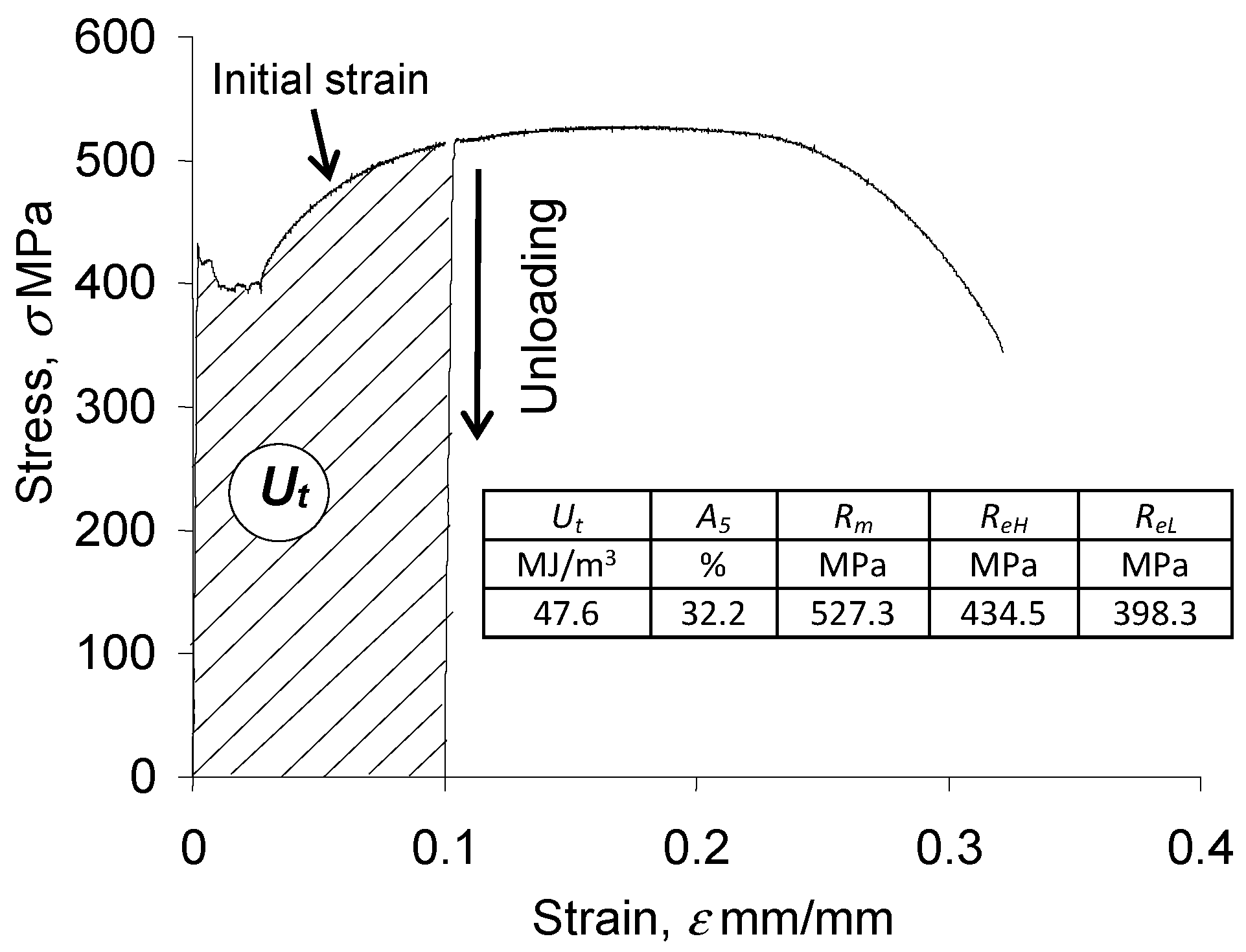
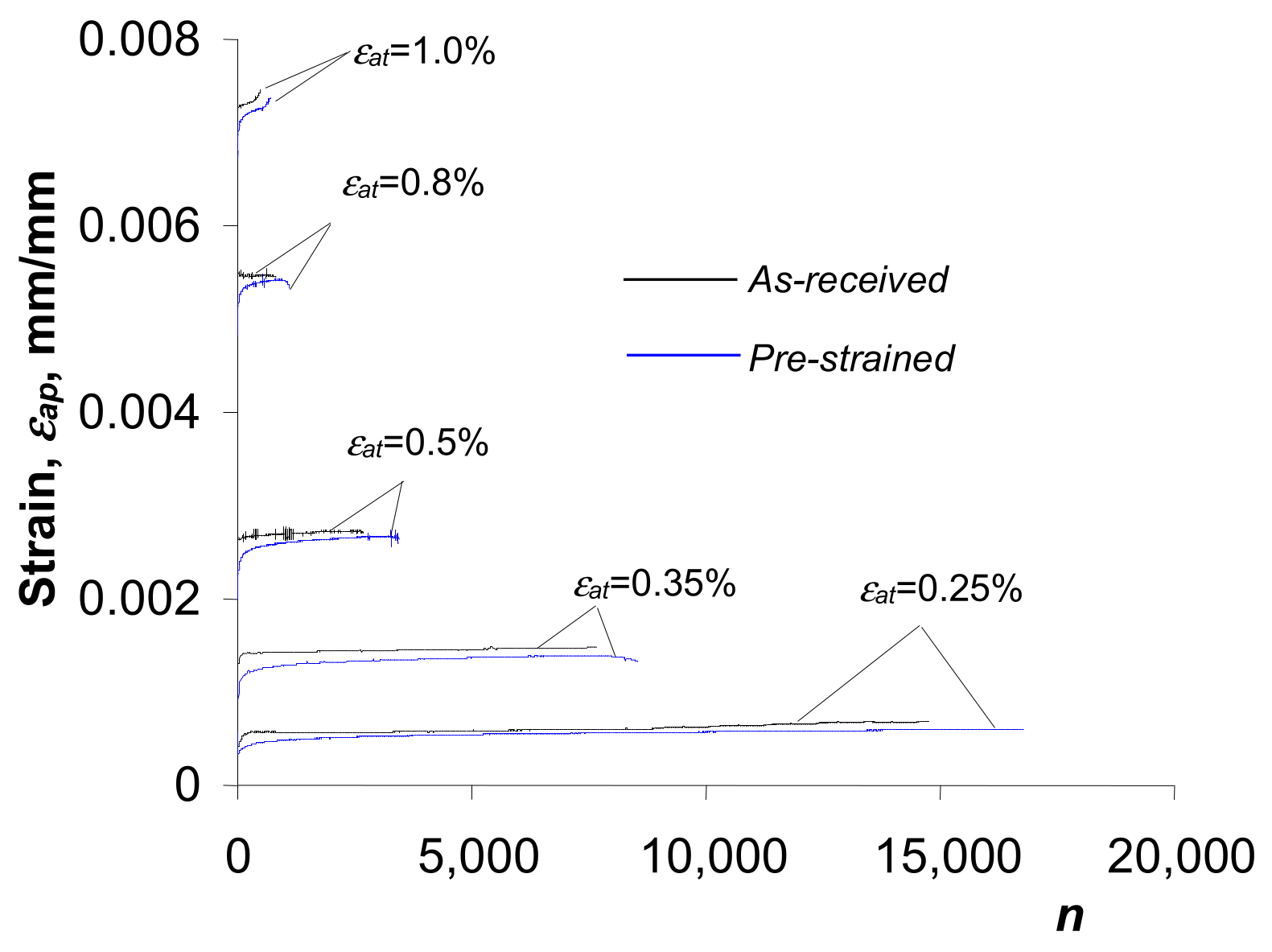
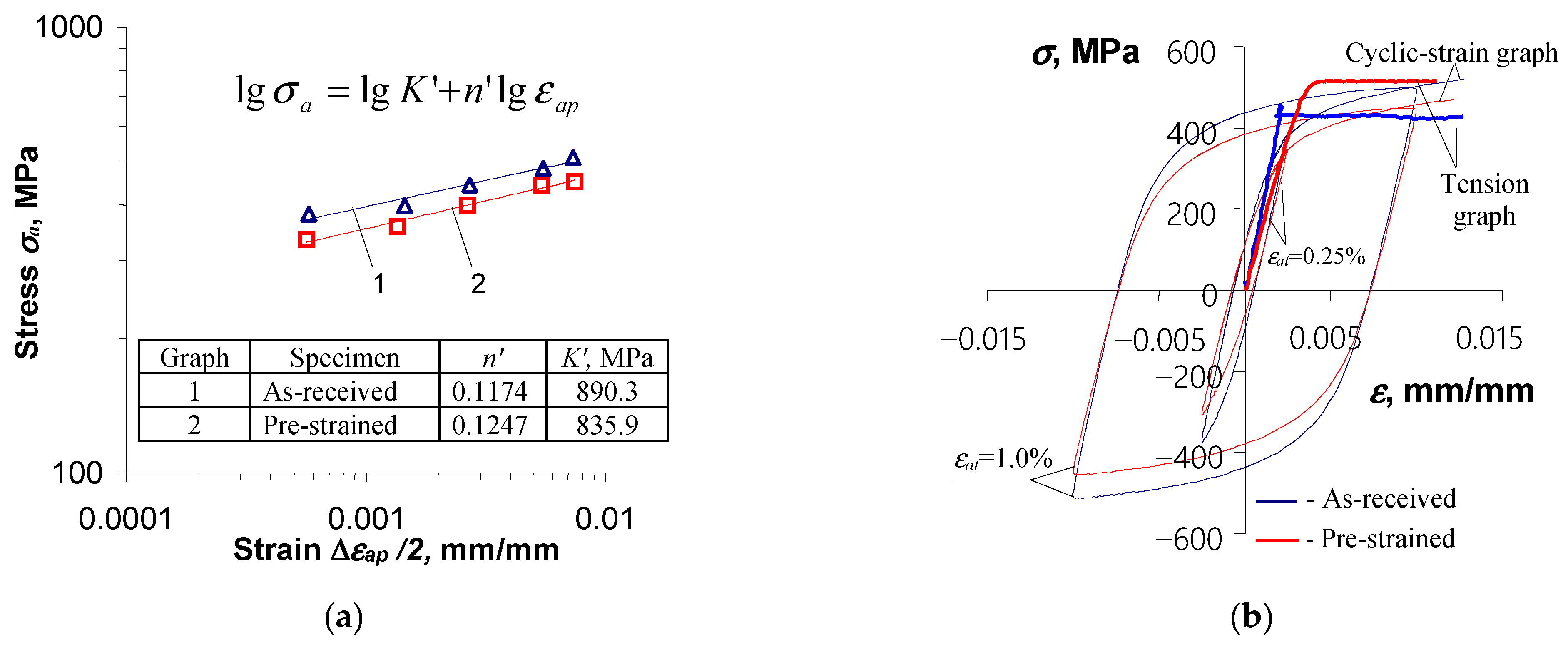

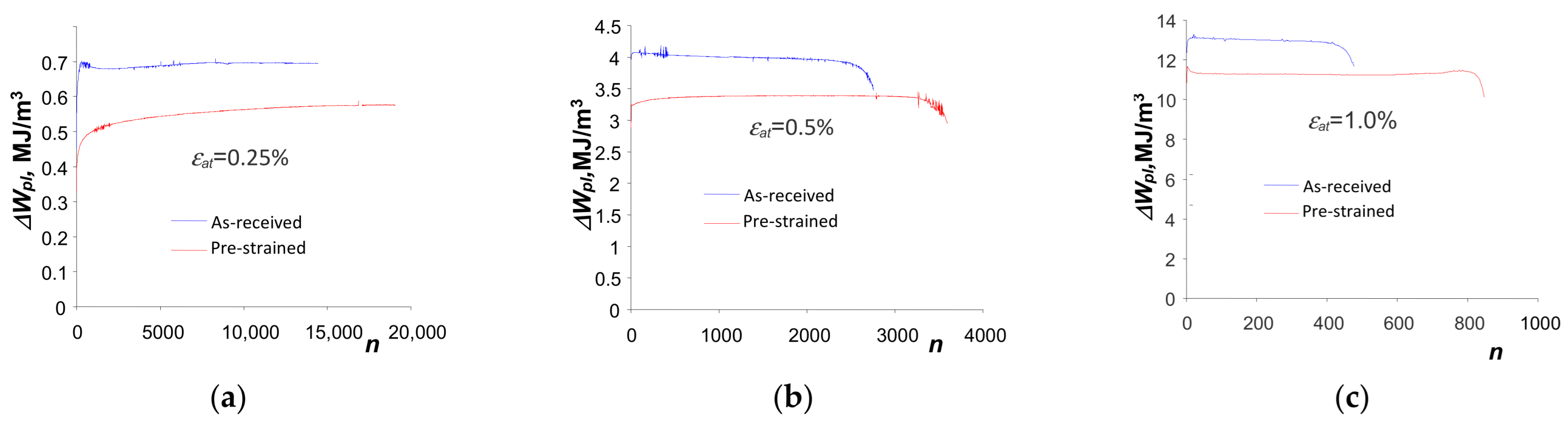



| Fe | C | Si | Mn | P | Cr | Al | Nb | Ti | V | W |
|---|---|---|---|---|---|---|---|---|---|---|
| 98.0 | 0.125 | 0.215 | 1.45 | 0.0135 | 0.0208 | 0.0268 | 0.0288 | 0.013 | 0.0519 | 0.0150 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mroziński, S.; Piotrowski, M.; Egner, W.; Egner, H. Influence of Pre-Strain on the Course of Energy Dissipation and Durability in Low-Cycle Fatigue. Materials 2025, 18, 893. https://doi.org/10.3390/ma18040893
Mroziński S, Piotrowski M, Egner W, Egner H. Influence of Pre-Strain on the Course of Energy Dissipation and Durability in Low-Cycle Fatigue. Materials. 2025; 18(4):893. https://doi.org/10.3390/ma18040893
Chicago/Turabian StyleMroziński, Stanisław, Michał Piotrowski, Władysław Egner, and Halina Egner. 2025. "Influence of Pre-Strain on the Course of Energy Dissipation and Durability in Low-Cycle Fatigue" Materials 18, no. 4: 893. https://doi.org/10.3390/ma18040893
APA StyleMroziński, S., Piotrowski, M., Egner, W., & Egner, H. (2025). Influence of Pre-Strain on the Course of Energy Dissipation and Durability in Low-Cycle Fatigue. Materials, 18(4), 893. https://doi.org/10.3390/ma18040893







