Studies of the Thermophysical Properties of Selected Hot-Working Tool Steels in a Wide Temperature Range
Abstract
1. Introduction
1.1. Thermal Diffusivity
1.2. Thermal Expansivity
- -
- Measure the thermal diffusivity and thermal expansion of hot-working tool steel WLV (1.2365) in the temperature range from (−)50 °C to 500 °C;
- -
- Investigate the methods of combining the thermal diffusivity characteristics a(T) of WLV, 38HMJ and WCL steels obtained with both devices, i.e., low-temperature LFA 467 and high-temperature LFA 427, into thermal diffusivity characteristics in the full temperature range, i.e., from (−)50 °C to 1100 °C;
- -
- Show the a(T) dependencies of selected steels as input data for calculations in the range from (−)50 °C to 1100 °C;
- -
- Propose conversion procedures in the range from (−)50 °C to 500 °C, which shift the characteristics to point 0 for RT;
- -
- Show the dependencies of selected steels as input data for calculations in the range from (−)50 °C to 1100 °C.
2. Materials and Methods
2.1. Materials
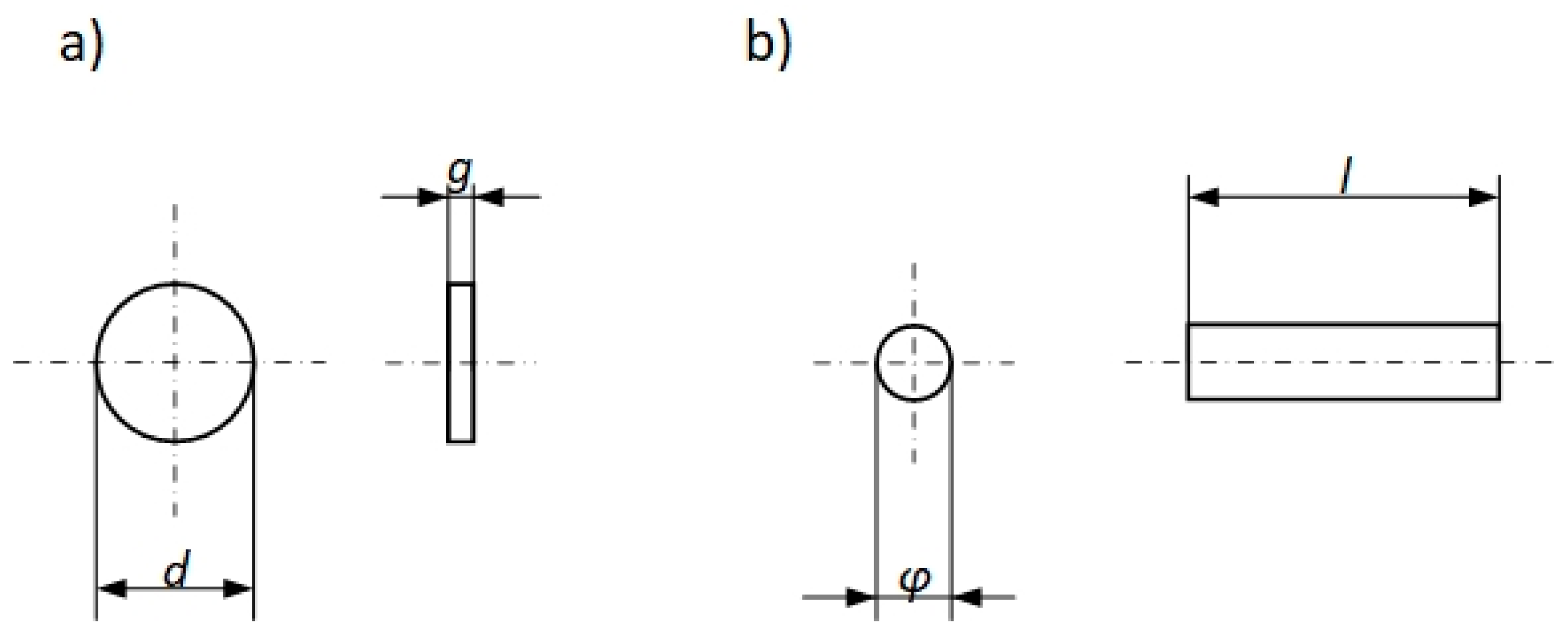
2.2. Specimen Preparation
- -
- Specimens for testing thermal diffusivity had the shape of a cylinder with a diameter of d = 12.70 mm and a thickness of g = 1.63 mm, cut from a 71.0 mm diameter bar using a water-cooled cutting disc (Figure 3a);
- -
- Specimens for testing thermal expansion had the shape of a cylinder with a diameter of = 6.0 mm and a length of l = 24.35 mm (Figure 3b); the specimens for the DIL tests were cut from the bar using a water-cooled cutting disc.
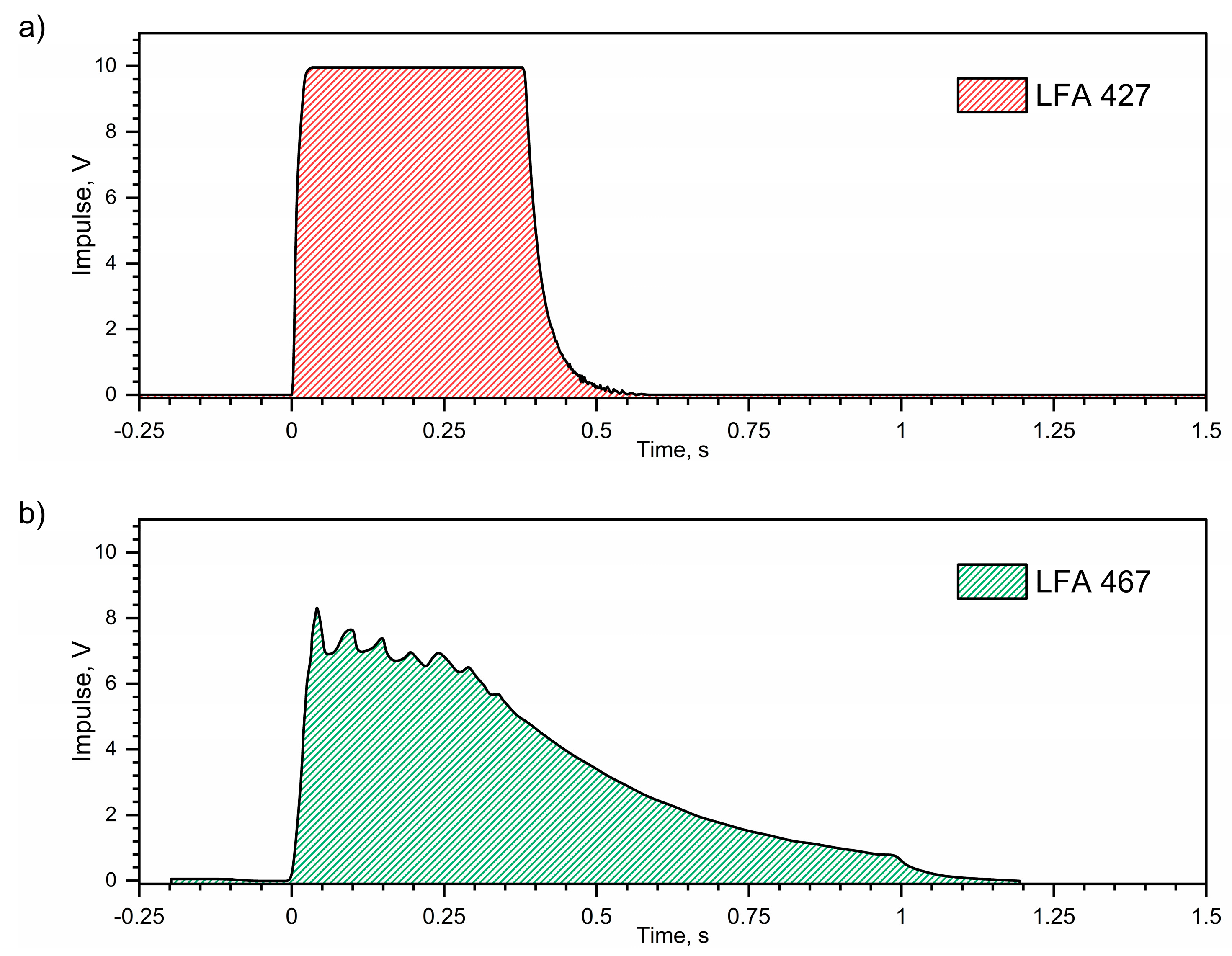
2.3. Thermal Diffusivity and Thermal Expansion Measurements
3. Results and Discussion
3.1. Thermal Diffusivity Results
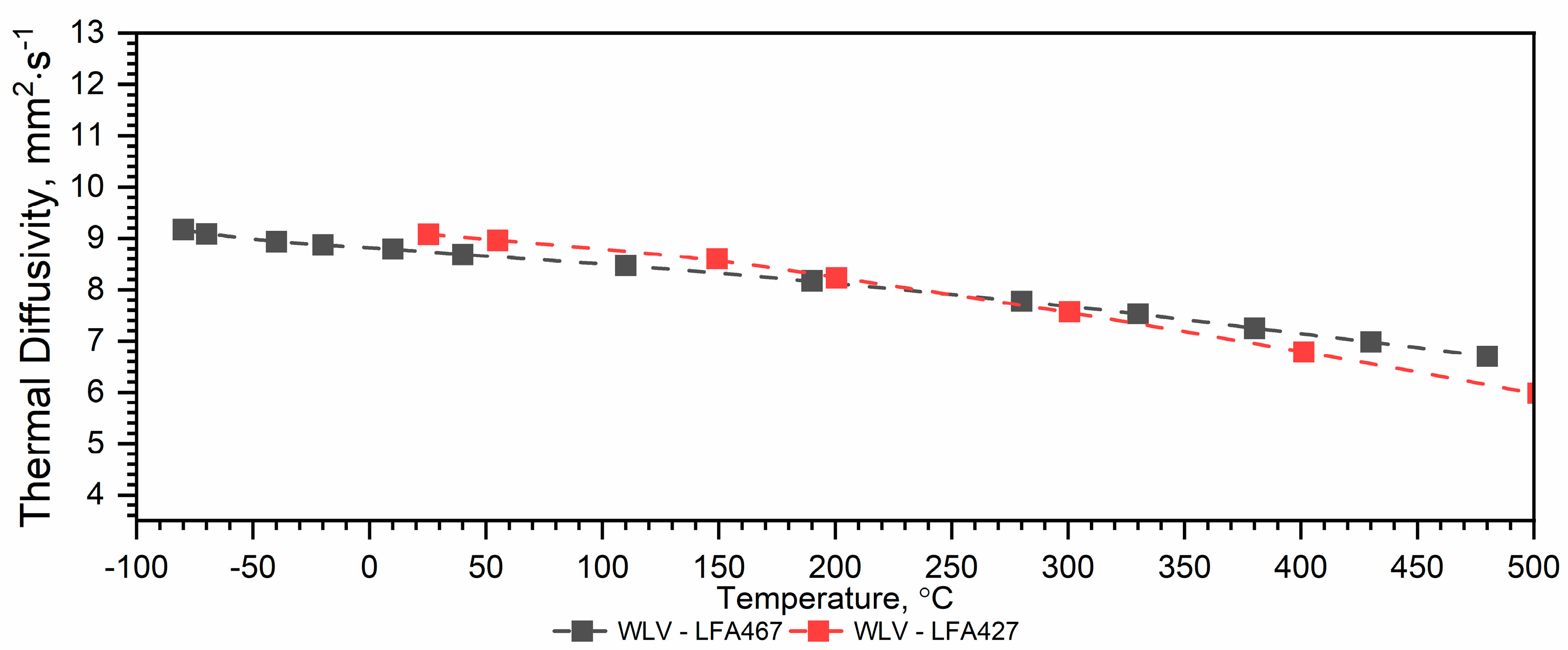
3.1.1. WLV Thermal Diffusivity Results
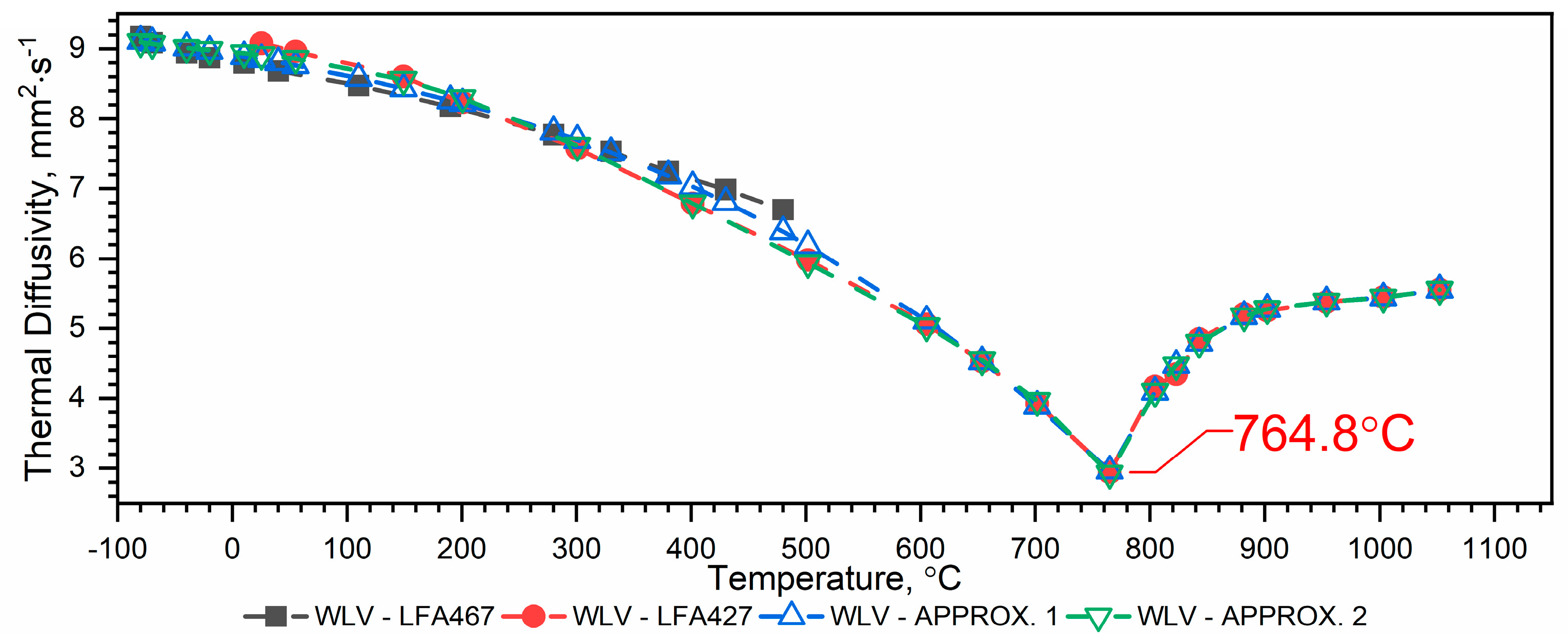
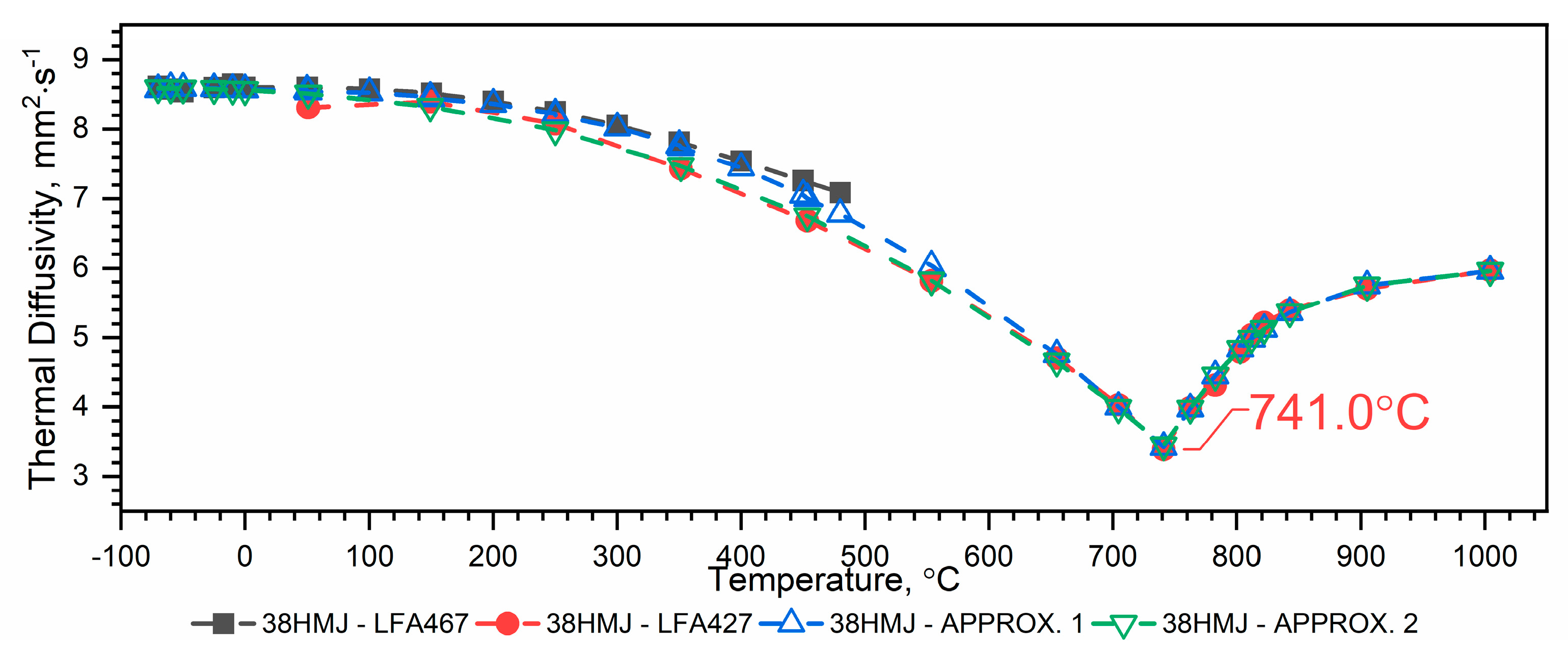
3.1.2. Thermal Diffusivity of WLV, 38HMJ and WCL Steels in the Temperature Range from −50 °C to 1100 °C
- For WLV steel—Figure 5:
- For 38HMJ steel—Figure 6:
- For WCL steel—Figure 7:
3.1.3. Discussion
- Approx. 1—takes into account all measurement data, determined in the full temperature ranges of the thermal diffusivity measurements of both devices, i.e., from (−)50 °C to about 500 °C and from RT to about 1100 °C;
- Approx. 2—takes into account measurement data determined in the temperature range from (−)50 °C to RT and from RT to about 1100 °C.
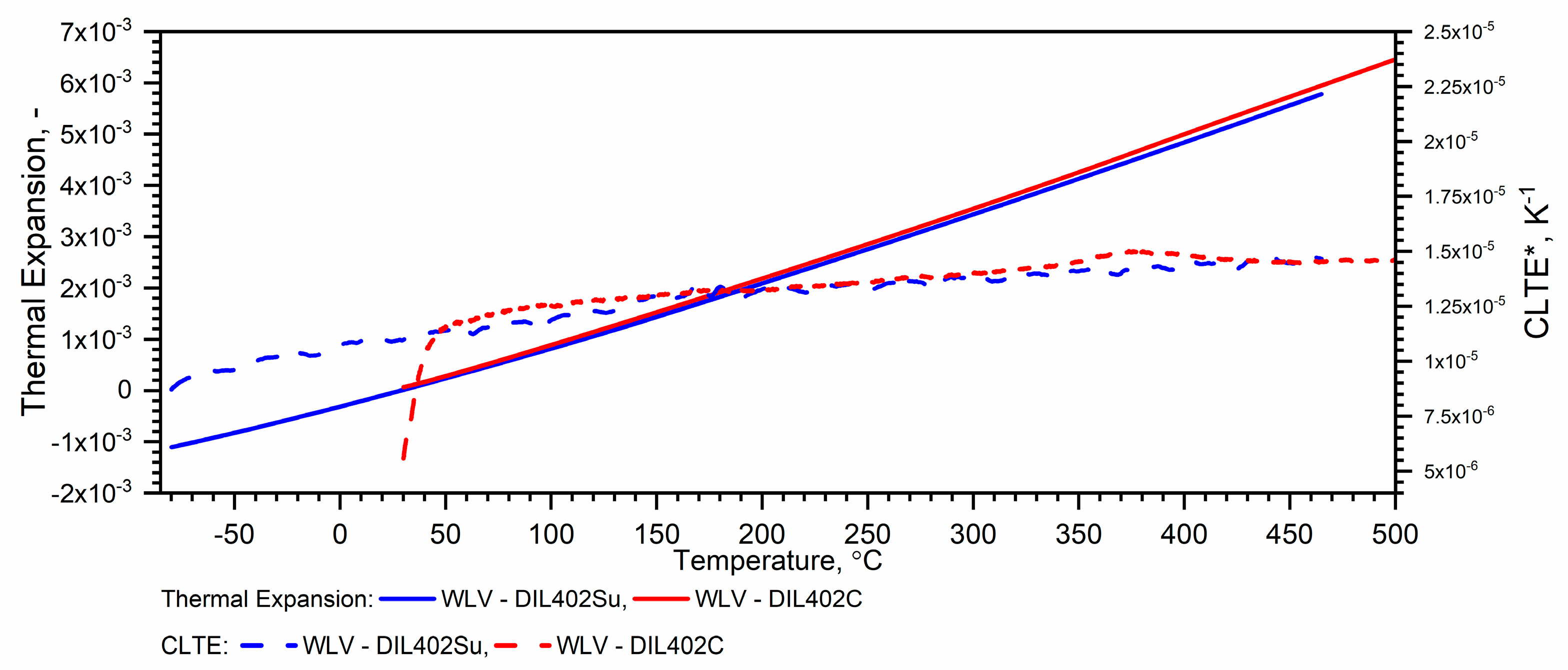
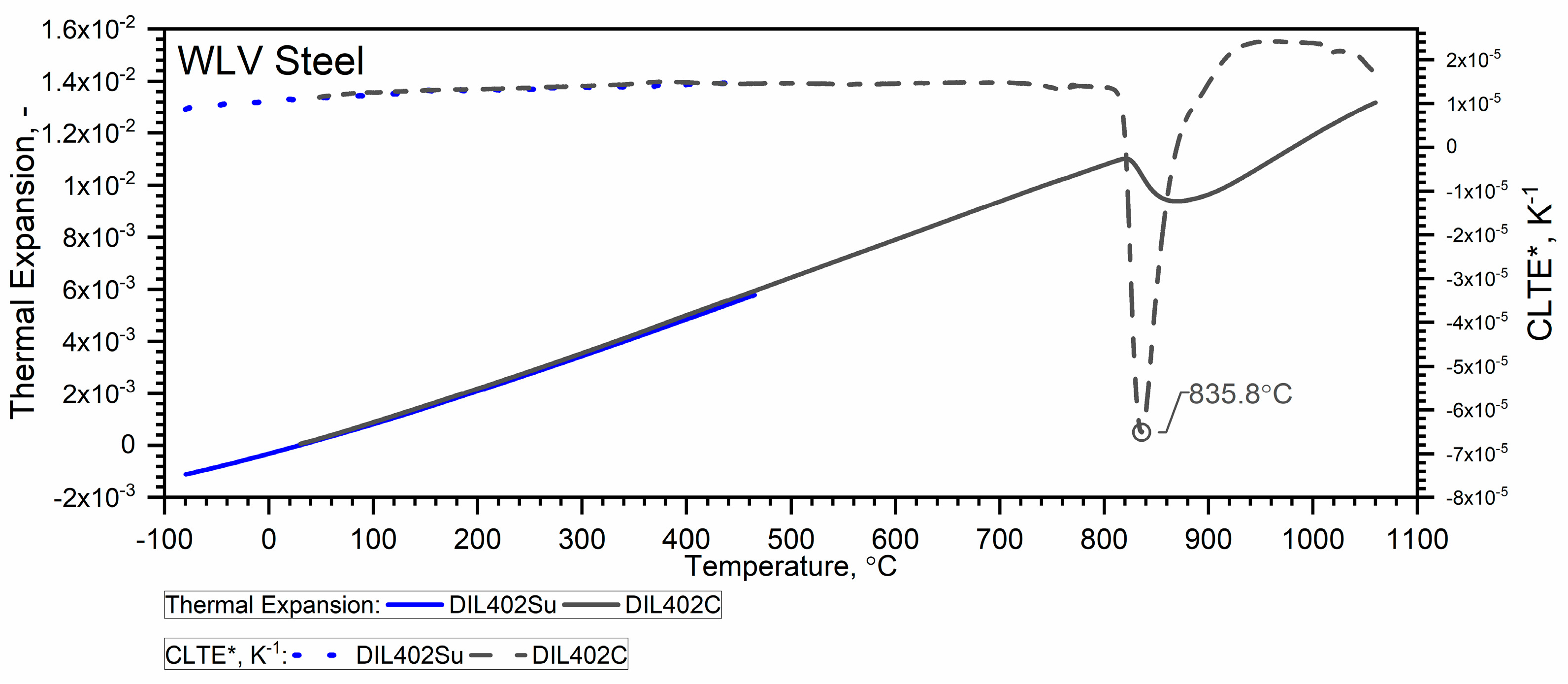
3.2. Thermal Expansion Results
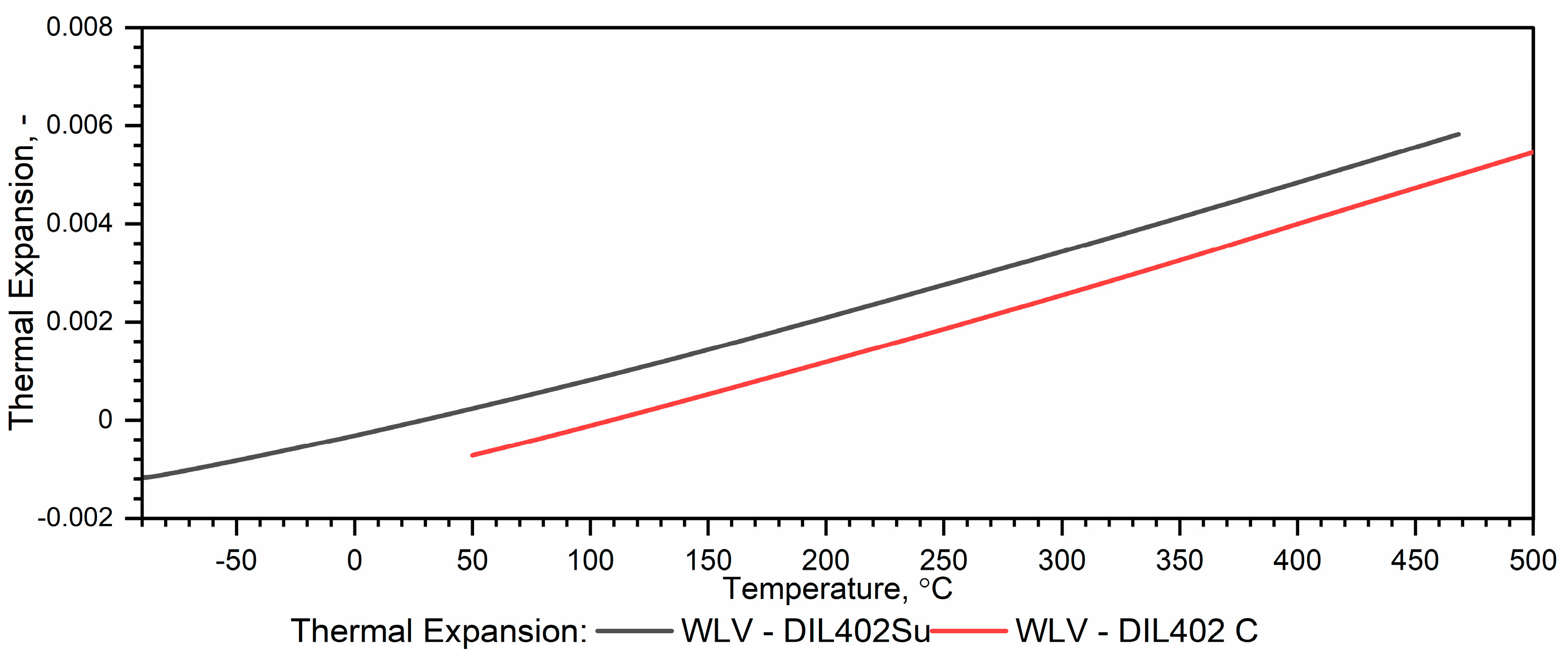
3.2.1. WLV Thermal Expansion Results
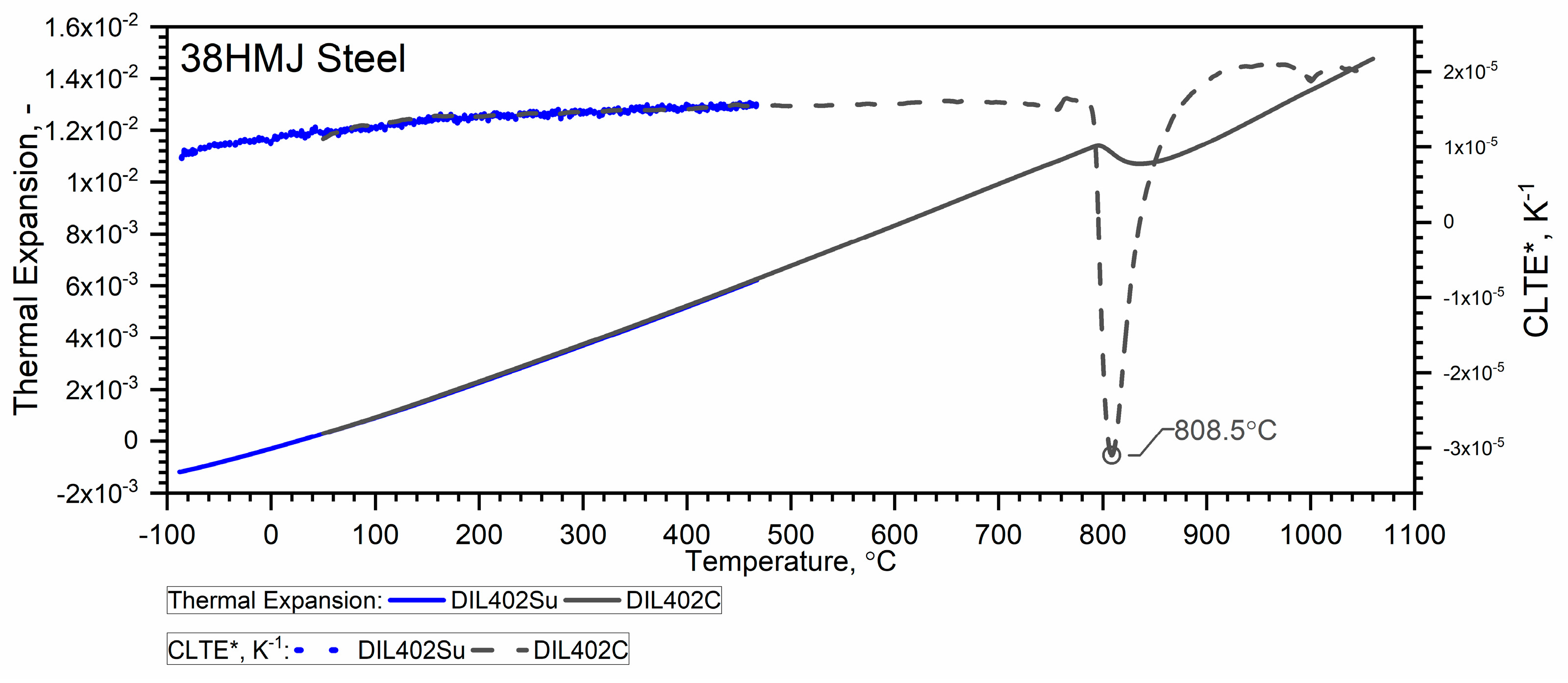
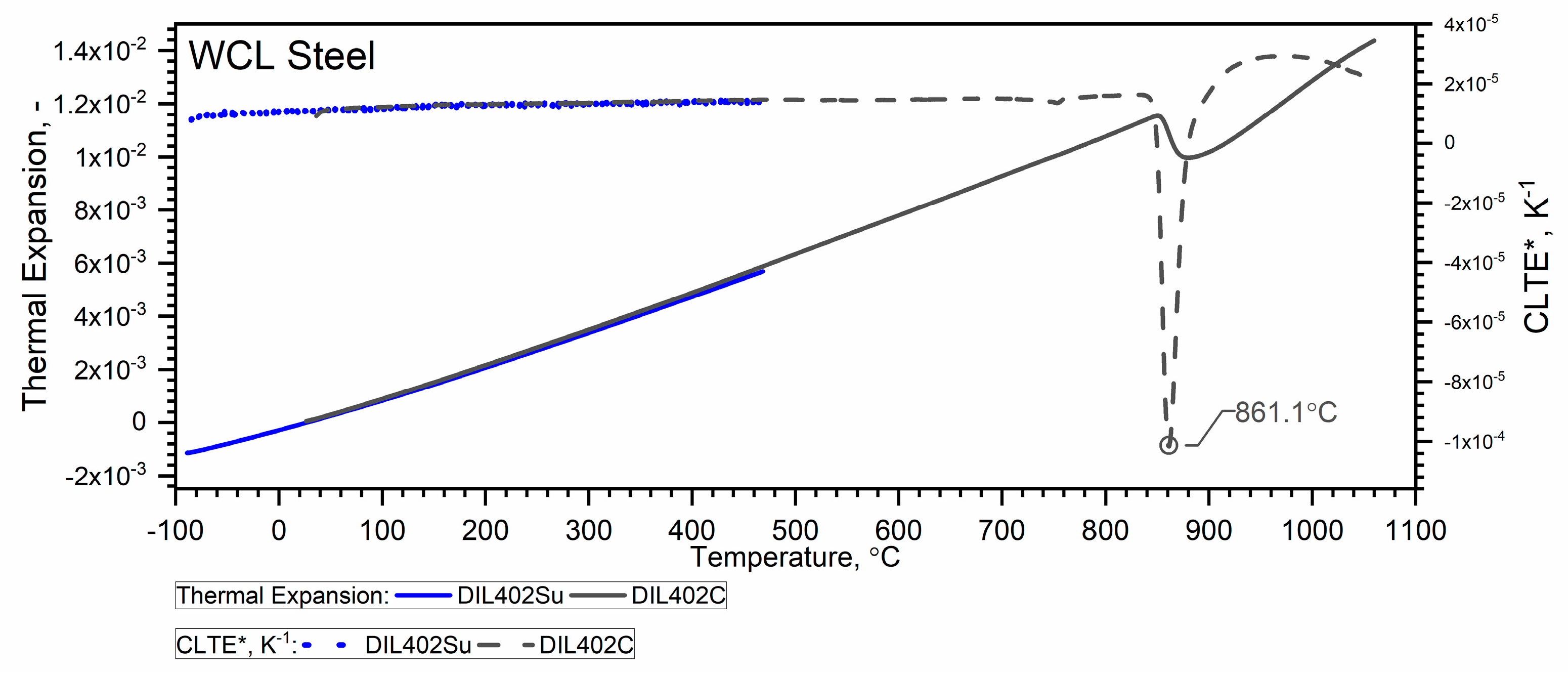
3.2.2. Thermal Expansion of WLV, 38HMJ and WCL Steels in the Temperature Range from −50 °C to 1100 °C
4. Conclusions
- (1)
- The analysis of combining thermal characteristics a(T) obtained from measurements with LFA 467—in the low temperature range, with the same results a(T) obtained from measurements with LFA 427—in the high temperature range allows us to conclude the following:
- (a)
- The thermal diffusivity characteristics of LFA 427 and LFA 467 in the range from RT to about 500 °C do not overlap. This is due to the different methods of generating a thermal pulse on the front surface of the specimen;
- (b)
- Although both methods of combining thermal diffusivity characteristics, i.e., Approx. 1 and Approx 2, can be used, the authors recommend Approx. 1 because the a(T) dependence obtained in this way is within the measurement errors for both LFA 467 and LFA 427.
- (2)
- The analysis of the DIL thermograms obtained from measurements with DIL 402 Expedis (DIL 402 Su)—in the low temperature range and DIL 402C—in the high temperature range shows the following:
- (a)
- The thermal expansion ε(T) obtained by DIL 402 Expedis is substantially consistent with the ε(T) results obtained by DIL 402 C in the range from RT to 500 °C;
- (b)
- Due to the sample shrinkage after the first heating, in the process of combining the characteristics from DIL 402 Expedis and DIL 402 C, the authors propose the calculation of the dependence ε(T) from DIL 402 C in accordance with the proposed procedure.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moynihan, M.C.; Allwood, J.M. The flow of steel into the construction sector. Resour. Conserv. Recycl. 2012, 68, 88–95. [Google Scholar] [CrossRef]
- Ajayebi, A.; Hopkinson, P.; Zhou, K.; Lam, D.; Chen, H.-M.; Wang, Y. Estimation of structural steel and concrete stocks and flows at urban scale–towards a prospective circular economy. Resour. Conserv. Recycl. 2021, 174, 105821. [Google Scholar] [CrossRef]
- Bolina, F.L.; Fachinelli, E.G.; Pachla, E.C.; Centeno, F.R. A critical analysis of the influence of architecture on the temperature field of RC structures subjected to fire using CFD and FEA models. Appl. Therm. Eng. 2024, 247, 123086. [Google Scholar] [CrossRef]
- Bolina, F.L.; Rodrigues, J.P.C. Finite element analysis criteria for composite steel decking concrete slabs subjected to fire. Fire Saf. J. 2023, 139, 103818. [Google Scholar] [CrossRef]
- Mesquita, R.A.; Michael, K.; Schneider, R. Tool Steels: Properties and Performance; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781439881729. [Google Scholar]
- Zieliński, M.; Koniorczyk, P.; Surma, Z. Influence of the Shrinkage of the Inner Layer of Steel Tubes on Permissible Thermal Load. Energies 2024, 17, 702. [Google Scholar] [CrossRef]
- Koniorczyk, P.; Zieliński, M.; Sienkiewicz, J.; Zmywaczyk, J. Thermophysical properties and microstructure of 32CrMoV12-28 hot-work tool steel. Arch. Thermodyn. 2024, 45, 269–277. [Google Scholar] [CrossRef]
- NETZSCH—Analyzing and Testing. Leading in Thermal Analysis, Rheology and Fire Testing. Light/Laser Flash Analyzer (LFA). Available online: https://analyzing-testing.netzsch.com/en/products/thermal-diffusivity-and-conductivity (accessed on 5 February 2025).
- NETZSCH—Analyzing and Testing. Leading in Thermal Analysis, Rheology and Fire Testing. The Most Advanced Instruments for Dilatometry by NETZSCH. Available online: https://analyzing-testing.netzsch.com/en/products/dilatometry-dil (accessed on 5 February 2025).
- Nishi, T.; Shibata, H.; Tsutsumi, K.; Ohta, H.; Waseda, Y. Measurement of Thermal Diffusivity of Steels at Elevated Temperature by a Laser Flash Method. ISIJ Int. 2002, 42, 498–503. [Google Scholar] [CrossRef]
- Terpiłowski, J. A Modified Flash Method for Determination of Thermal Diffusivity in Solids. Arch. Thermodyn. 2003, 24, 59–80. [Google Scholar]
- Terpiłowski, J.; Piotrowska-Woroniak, J.; Romanowska, J. A study of thermal diffusivity of carbon-epoxy and glass-epoxy composites using the modified pulse method. Arch. Thermodyn. 2014, 35, 117–128. [Google Scholar] [CrossRef]
- Terpiłowski, J.; Rudzki, R.; Szczepaniak, R.; Woroniak, G. Thermal diffusivity investigation of Fe61Ni39, Fe52Ni48 and Fe40Ni60 binary iron–nickel alloys using the modified pulse method. J. Alloys Compd. 2016, 657, 748–754. [Google Scholar] [CrossRef]
- Kaschnitz, E.; Hofer-Hauser, P.; Funk, W. Electrical resistivity measured by millisecond pulse-heating in comparison to thermal conductivity of the hot work tool steel AISI H11 (1.2343) at elevated temperature. HTHP High Temp.-High Press. 2020, 49, 75–87. [Google Scholar] [CrossRef]
- Xing, Y.; Wang, W.; Al-azzani, H. Assessment of thermal properties of various types of high-strength steels at elevated temperatures. Fire Saf. J. 2021, 122, 103348. [Google Scholar] [CrossRef]
- Technical Specifications. Available online: https://analyzing-testing.netzsch.com/en/products/thermal-diffusivity-and-conductivity/lfa-467-hyper-flash-light-flash-apparatus (accessed on 23 January 2025).
- Vozár, L.; Hohenauer, W. Flash method of measuring the thermal diffusivity. A review. HTHP High Temp.-High Press. 2003, 35/36, 253–264. [Google Scholar] [CrossRef]
- Agazhanov, A.S.; Stankus, S.V.; Samoshkin, D.A. Coefficient of thermal diffusivity of ChS-139 steel in wide temperature range. Thermophys. Aeromech. 2013, 20, 651–653. [Google Scholar] [CrossRef]
- Yamane, T.; Katayama, S.; Todoki, M. Experimental investigation of nonuniform heating and heat loss from a specimen for the measurement of thermal diffusivity by the laser pulse heating method. Int. J. Thermophys. 1997, 18, 269–290. [Google Scholar] [CrossRef]
- Baba, T.; Ono, A. Improvement of the laser flash method to reduce uncertainty in thermal diffusivity measurements. Meas. Sci. Technol. 2001, 12, 2046–2057. [Google Scholar] [CrossRef]
- Akoshima, M.; Baba, T. Thermal Diffusivity Measurements of Candidate Reference Materials by the Laser Flash Method. Int. J. Thermophys. 2005, 26, 151–163. [Google Scholar] [CrossRef]
- Lim, K.-H.; Kim, S.-K.; Chung, M.-K. Improvement of the thermal diffusivity measurement of thin samples by the flash method. Thermochim. Acta 2009, 494, 71–79. [Google Scholar] [CrossRef]
- Parker, W.J.; Jenkins, R.J.; Butler, C.P.; Abbott, G.L. Flash Method of Determining Thermal Diffusivity, Heat Capacity, and Thermal Conductivity. J. Appl. Phys. 1961, 32, 1679–1684. [Google Scholar] [CrossRef]
- Cape, J.A.; Lehman, G.W. Temperature and Finite Pulse-Time Effects in the Flash Method for Measuring Thermal Diffusivity. J. Appl. Phys. 1963, 34, 1909–1913. [Google Scholar] [CrossRef]
- Netzsch. Proteus Software Manual [Online]. Available online: https://analyzing-testing.netzsch.com/en/products/software/proteus (accessed on 22 February 2024).
- Koniorczyk, P.; Zieliński, M.; Sienkiewicz, J.; Zmywaczyk, J.; Dębski, A. Experimental Studies of Thermophysical Properties and Microstructure of X37CrMoV5-1 Hot-Work Tool Steel and Maraging 350 Steel. Materials 2023, 16, 1206. [Google Scholar] [CrossRef] [PubMed]
- Koniorczyk, P.; Zielinski, M. Some problems related to thermophysical properties of selected barrel steels. J. Phys. Conf. Ser. 2023, 2628, 012014. [Google Scholar] [CrossRef]
- Koniorczyk, P.; Sienkiewicz, J.; Zmywaczyk, J.; Dębski, A.; Zieliński, M.; Preiskorn, M. Effect of Microstructure on Thermophysical Properties of Heat-Treated Duplex Steel. Materials 2021, 14, 6043. [Google Scholar] [CrossRef] [PubMed]
- Zieliński, M.; Koniorczyk, P. Thermal diffusivity and thermal expansion investigations of WLV steel. J. Phys. Conf. Ser. 2023, 2628, 012035. [Google Scholar] [CrossRef]
- Dębski, A.; Surma, Z.; Koperski, W. Material and Technological Optimization Research in Terms of Increasing the Durability of Small Arms; Research Report; Military University of Technology: Warsaw, Poland, 2009. (In Polish) [Google Scholar]
- Blicharski, M. Materials Engineering: Steel, 2nd ed.; 1st Reprint; Publishing House WNT: Warsaw, Poland, 2017; ISBN 9788301189556. (In Polish) [Google Scholar]

| Component | Fe | C | Si | Mn | Cr | Mo | V | P |
|---|---|---|---|---|---|---|---|---|
| Concentration [wt.%] | 92.88 | 0.32 | 0.25 | 0.30 | 3.00 | 2.75 | 0.55 | 0.03 |
| WLV | 38HMJ | WCL | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| −80 | 9.17 | 0.6% | 0.8% | −70 | 8.41 | 2.0% | 2.2% | −70 | 7.45 | 2.6% | 3.1% |
| −70 | 9.14 | 0.6% | 0.8% | −60 | 8.39 | 2.5% | 2.3% | −60 | 7.44 | 2.3% | 2.8% |
| −40 | 9.07 | 0.5% | 0.6% | −50 | 8.38 | 2.5% | 2.4% | −50 | 7.43 | 2.1% | 2.5% |
| −20 | 9.02 | 0.5% | 0.4% | −25 | 8.38 | 2.4% | 2.3% | −25 | 7.41 | 1.6% | 1.6% |
| 10 | 8.94 | 0.5% | 0.0% | −10 | 8.39 | 2.2% | 2.1% | −10 | 7.40 | 1.4% | 1.1% |
| 25 | 8.90 | 0.6% | 0.2% | 0 | 8.40 | 2.0% | 1.9% | 0 | 7.39 | 1.2% | 0.8% |
| 40 | 8.86 | 0.6% | 0.5% | 50 | 8.46 | 1.2% | 0.7% | 27 | 7.36 | 0.9% | 0.0% |
| 55 | 8.81 | 0.6% | 0.5% | 51 | 8.46 | 1.0% | 0.6% | 50 | 7.33 | 0.6% | 0.4% |
| 110 | 8.62 | 0.5% | 0.7% | 100 | 8.49 | 0.4% | 0.6% | 55 | 7.33 | 0.6% | 0.7% |
| 149 | 8.45 | 0.3% | 1.2% | 149 | 8.46 | 0.1% | 1.6% | 100 | 7.26 | 0.3% | 1.1% |
| 190 | 8.26 | 0.1% | 0.7% | 150 | 8.46 | 0.2% | 1.6% | 149 | 7.17 | 0.2% | 1.7% |
| 201 | 8.20 | 0.2% | 1.2% | 200 | 8.35 | 0.2% | 2.1% | 150 | 7.17 | 0.2% | 1.6% |
| 280 | 7.75 | 0.9% | 0.3% | 250 | 8.16 | 0.7% | 2.2% | 200 | 7.05 | 0.3% | 1.8% |
| 301 | 7.62 | 1.0% | 0.1% | 250 | 8.16 | 0.4% | 2.2% | 249 | 6.91 | 0.5% | 1.8% |
| 330 | 7.43 | 1.2% | 0.3% | 300 | 7.92 | 1.3% | 2.1% | 250 | 6.91 | 0.5% | 2.0% |
| 380 | 7.11 | 1.1% | 1.2% | 350 | 7.63 | 1.8% | 2.0% | 300 | 6.74 | 0.7% | 2.2% |
| 401 | 6.96 | 0.9% | 2.5% | 351 | 7.62 | 1.6% | 2.0% | 350 | 6.53 | 0.9% | 2.5% |
| 430 | 6.77 | 0.6% | 2.7% | 400 | 7.31 | 1.8% | 2.2% | 351 | 6.53 | 0.9% | 2.3% |
| 480 | 6.43 | 0.6% | 4.7% | 450 | 6.98 | 1.0% | 3.0% | 400 | 6.30 | 0.8% | 2.9% |
| 453 | 6.96 | 0.7% | 3.0% | 450 | 6.03 | 0.5% | 3.5% | ||||
| 480 | 6.78 | 0.0% | 3.8% | 451 | 6.03 | 0.5% | 3.7% | ||||
| 480 | 5.86 | 0.1% | 4.0% | ||||||||
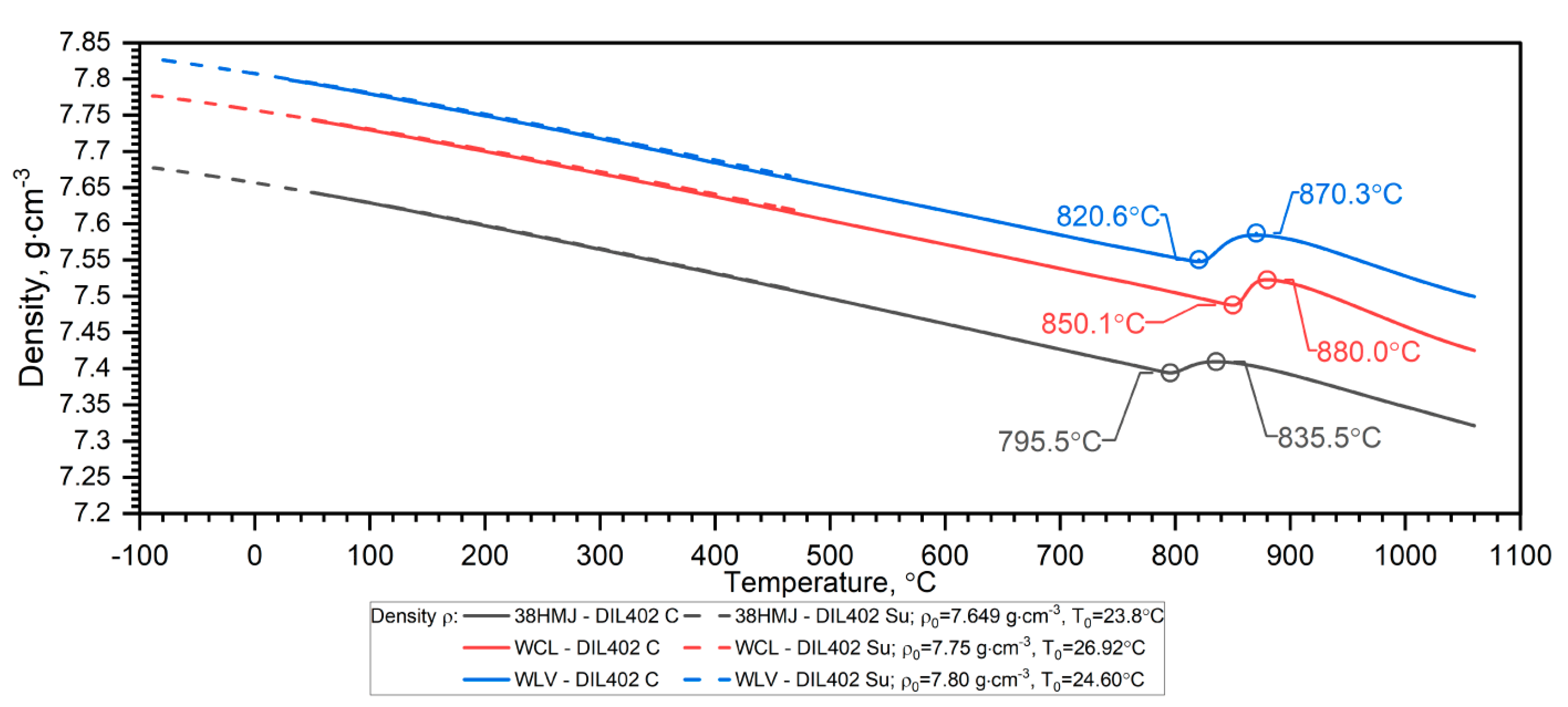
| WLV | 38HMJ | WCL | |||
|---|---|---|---|---|---|
| T, [°C] | T, [°C] | T, [°C] | |||
| −85 | 7.825 | −85 | 7.677 | −85 | 7.776 |
| −80 | 7.824 | −80 | 7.676 | −80 | 7.775 |
| −75 | 7.823 | −75 | 7.675 | −75 | 7.774 |
| −50 | 7.818 | −50 | 7.669 | −50 | 7.769 |
| −25 | 7.812 | −25 | 7.663 | −25 | 7.763 |
| 0 | 7.806 | 0 | 7.657 | 0 | 7.757 |
| 25 | 7.799 | 25 | 7.650 | 25 | 7.750 |
| 50 | 7.793 | 50 | 7.643 | 50 | 7.744 |
| 100 | 7.779 | 100 | 7.629 | 100 | 7.729 |
| 200 | 7.750 | 200 | 7.597 | 250 | 7.685 |
| 400 | 7.686 | 400 | 7.531 | 350 | 7.653 |
| 600 | 7.620 | 600 | 7.462 | 500 | 7.604 |
| 780 | 7.562 | 780 | 7.399 | 700 | 7.538 |
| 800 | 7.555 | 795 | 7.394 | 800 | 7.505 |
| 820 | 7.550 | 800 | 7.395 | 850 | 7.488 |
| 830 | 7.557 | 820 | 7.407 | 858 | 7.496 |
| 840 | 7.571 | 830 | 7.409 | 863 | 7.507 |
| 850 | 7.58 | 840 | 7.409 | 869 | 7.518 |
| 860 | 7.586 | 850 | 7.408 | 875 | 7.522 |
| 870 | 7.587 | 860 | 7.406 | 882 | 7.523 |
| 890 | 7.584 | 870 | 7.403 | 890 | 7.521 |
| 920 | 7.573 | 880 | 7.400 | 902 | 7.517 |
| 955 | 7.554 | 890 | 7.396 | 930 | 7.503 |
| 1000 | 7.531 | 900 | 7.392 | 980 | 7.471 |
| 1020 | 7.520 | 1000 | 7.347 | 1020 | 7.446 |
| 1060 | 7.502 | 1060 | 7.321 | 1056 | 7.427 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koniorczyk, P.; Zieliński, M.; Zmywaczyk, J. Studies of the Thermophysical Properties of Selected Hot-Working Tool Steels in a Wide Temperature Range. Materials 2025, 18, 852. https://doi.org/10.3390/ma18040852
Koniorczyk P, Zieliński M, Zmywaczyk J. Studies of the Thermophysical Properties of Selected Hot-Working Tool Steels in a Wide Temperature Range. Materials. 2025; 18(4):852. https://doi.org/10.3390/ma18040852
Chicago/Turabian StyleKoniorczyk, Piotr, Mateusz Zieliński, and Janusz Zmywaczyk. 2025. "Studies of the Thermophysical Properties of Selected Hot-Working Tool Steels in a Wide Temperature Range" Materials 18, no. 4: 852. https://doi.org/10.3390/ma18040852
APA StyleKoniorczyk, P., Zieliński, M., & Zmywaczyk, J. (2025). Studies of the Thermophysical Properties of Selected Hot-Working Tool Steels in a Wide Temperature Range. Materials, 18(4), 852. https://doi.org/10.3390/ma18040852









