Multi-Perspective Characterization of a Performance of a Barrel Drill Made of Tungsten Carbide Composite
Abstract
:1. Introduction
- -
- Surface roughness is highly correlated with a tool wear data [11],
- -
- The drill type, followed by drill diameter, shows a higher percentage contribution to surface roughness [12],
- -
- The internal friction angle and cohesive strength of cement-rock composites both increase with the rise in surface roughness [13],
- -
- Failure to control the flank wear occurring during the drilling process causes both the cutting tool and the workpiece to be significantly affected [14].
2. Materials and Methods
2.1. Gun Barrel Drill
- -
- A single blade (8 mm in diameter) with two asymmetric cutting edges,
- -
- An uncoated cutting edge made of monolithic sintered WC-Co composite,
- -
- A G-type guide strips with 1:800 alignment,
- -
- A whistle notch shank.
2.2. Metallographic Imaging
2.3. Hardness Measurements
2.4. X-Ray Diffraction Measurements
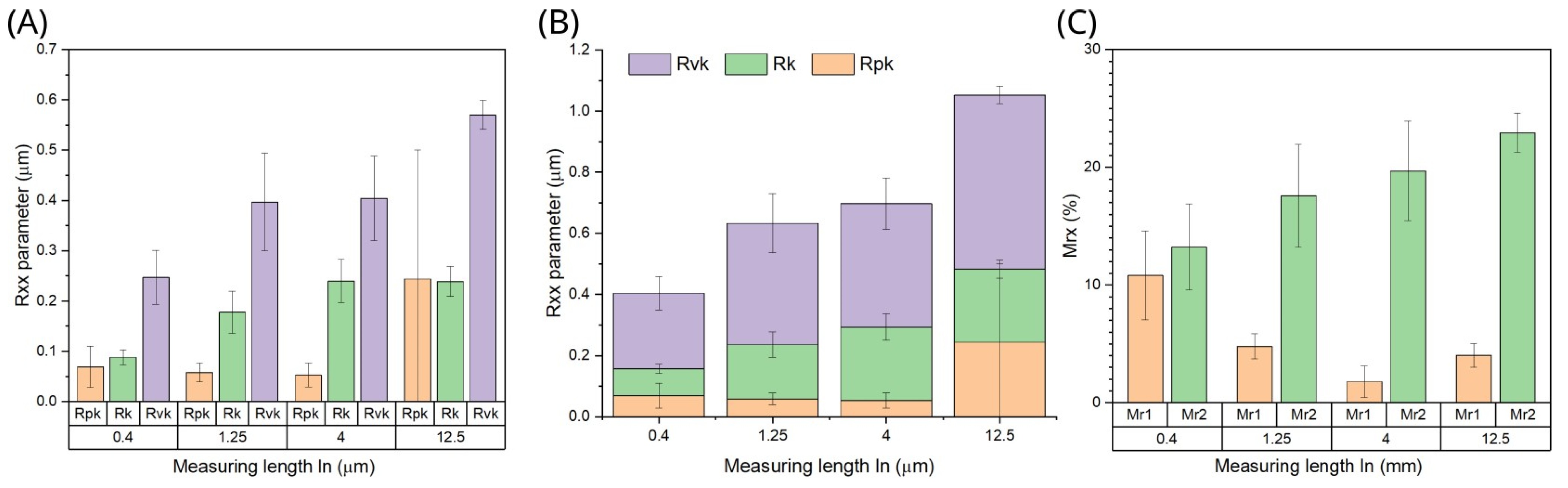
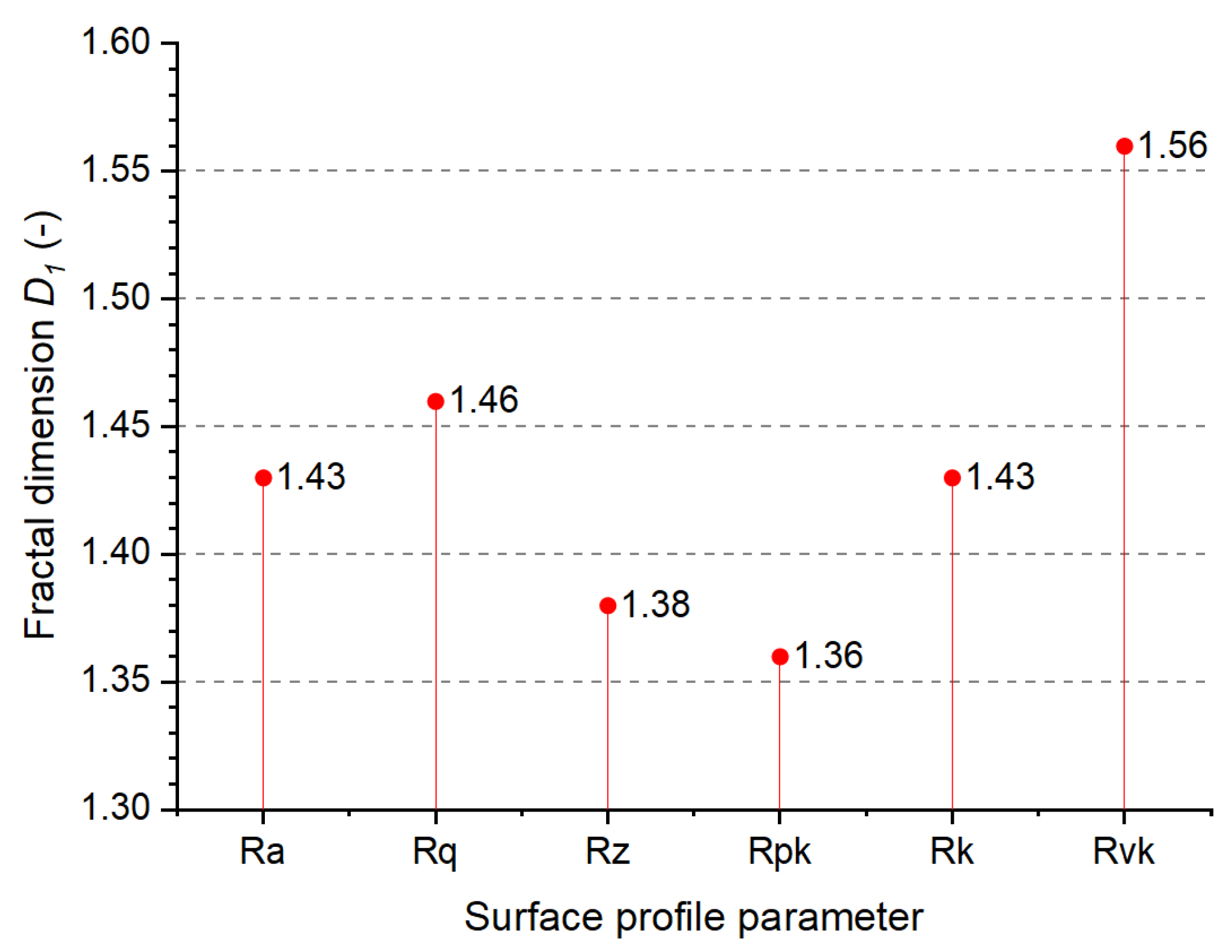
2.5. Surface Roughness Measurements
3. Results and Discussion
3.1. Metallographic Analysis
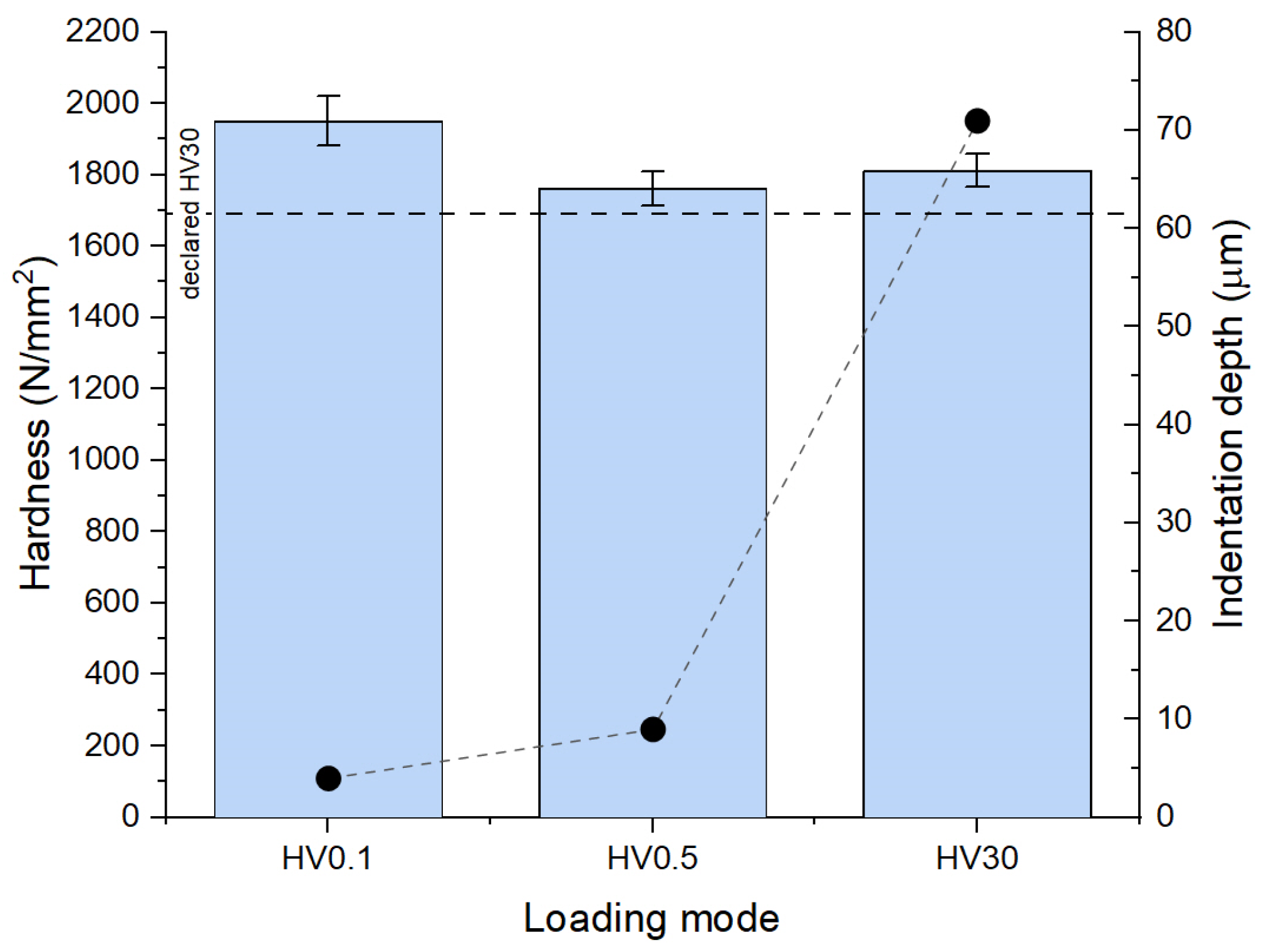
3.2. Vickers Hardness of the Cutting Blade
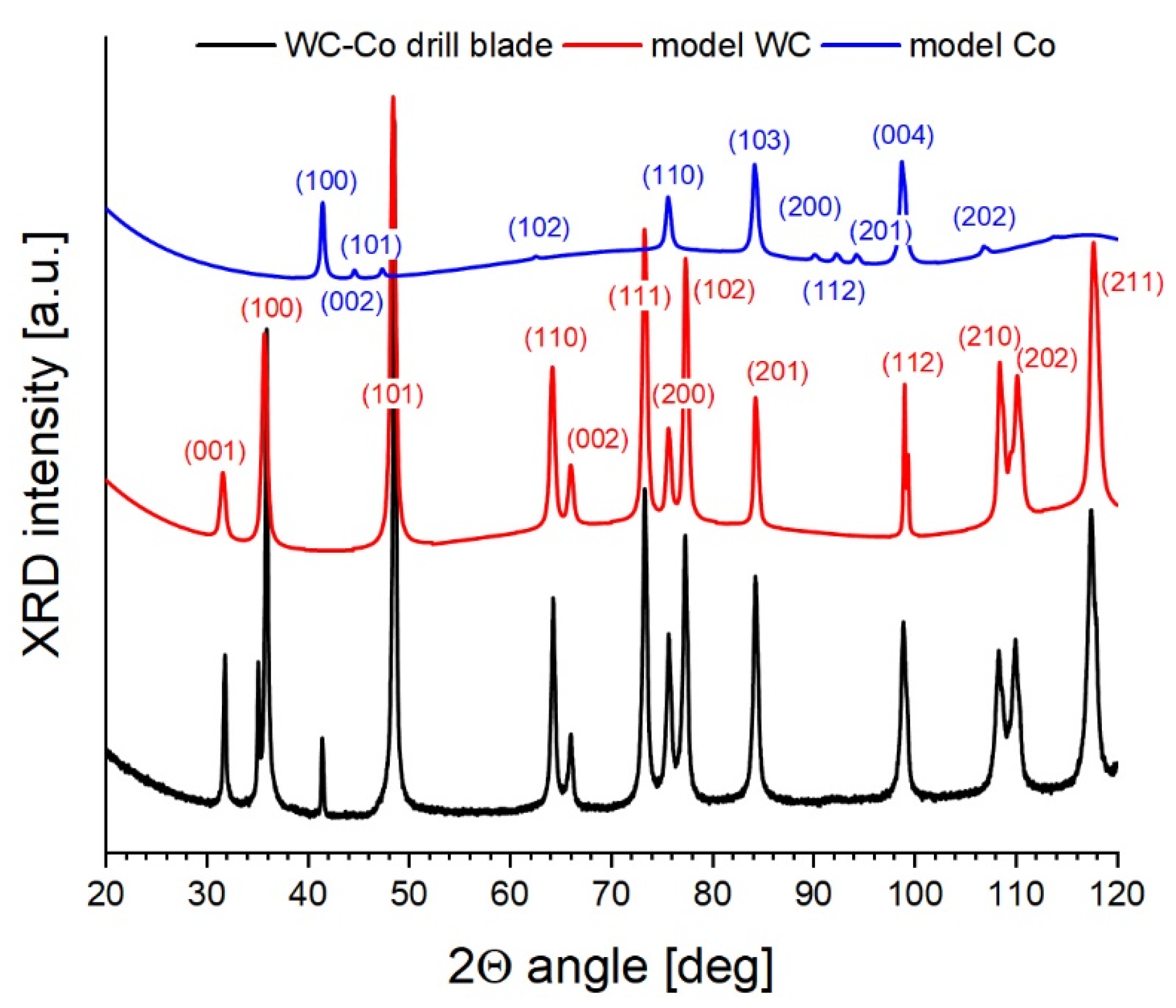
3.3. Structural Analysis by XRD
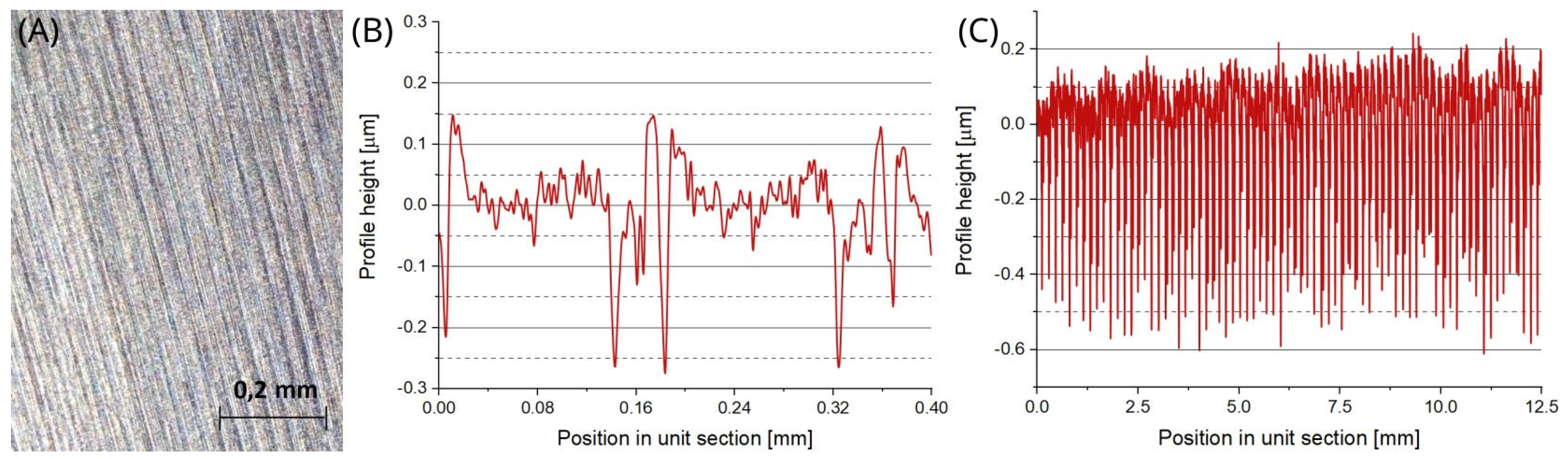
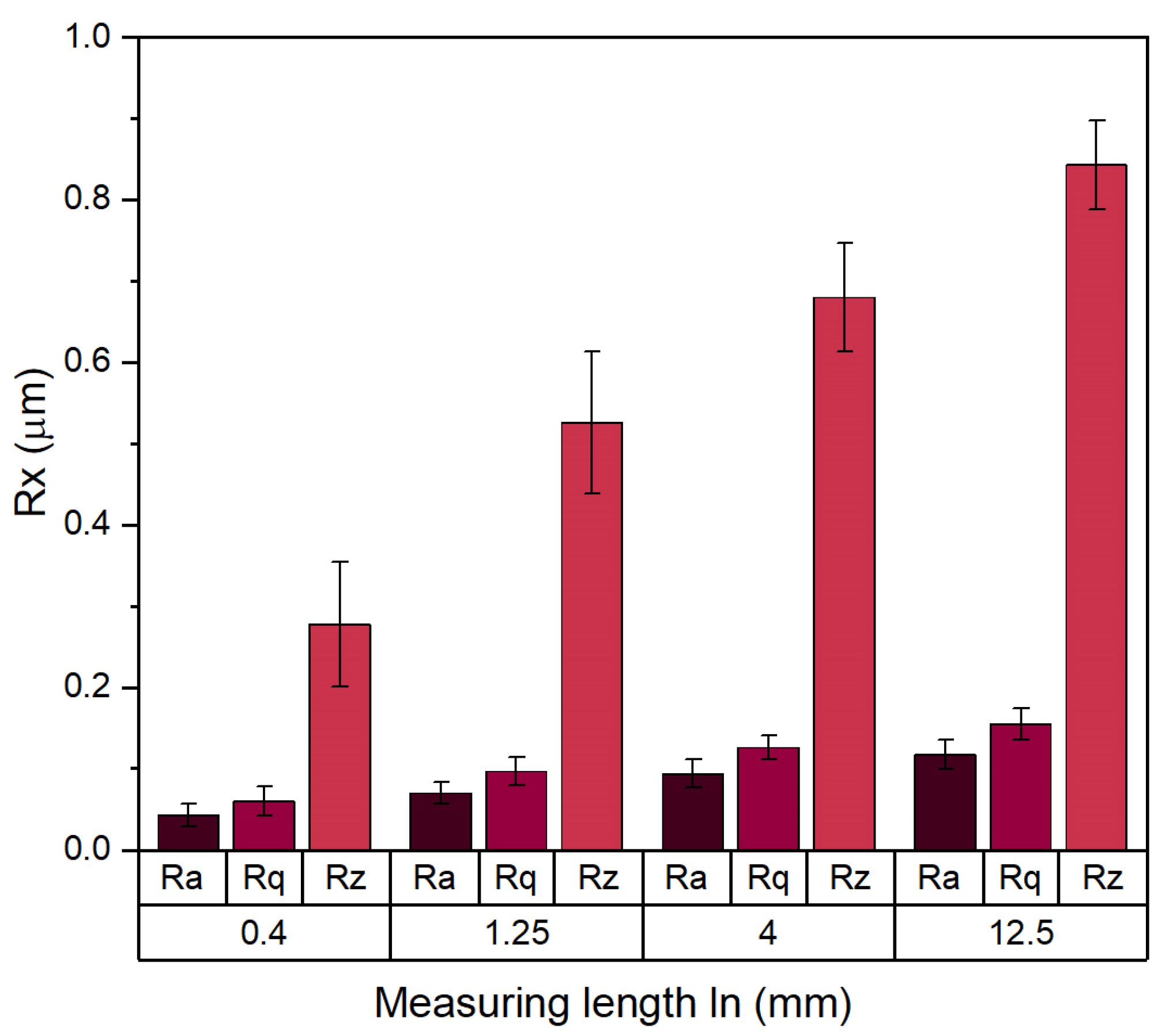
3.4. Geometric and Functional Structure of the Surface
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ortner, H.M.; Ettmayer, P.; Kolaska, H. The history of the technological progress of hardmetals. Int. J. Refract. Met. Hard Mater. 2013, 44, 148–159. [Google Scholar] [CrossRef]
- García, J.; Collado Ciprés, V.; Blomqvist, A.; Kaplan, B. Cemented carbide microstructures: A review. Int. J. Refract. Met. Hard Mater. 2019, 80, 40–68. [Google Scholar] [CrossRef]
- Upadhyaya, G.S. Materials science of cemented carbides—An overview. Mater. Des. 2001, 22, 483–489. [Google Scholar] [CrossRef]
- Straumal, B.B.; Shchur, L.N.; Kagramanyan, D.G.; Konstantinova, E.P.; Druzhinin, A.V.; Nekrasov, A.N. Topology of WC/Co Interfaces in Cemented Carbides. Materials 2023, 16, 5560. [Google Scholar] [CrossRef]
- PN-ISO 513:1999; Zastosowanie twardych materiałów skrawających (Application of Hard Cutting Materials). Polish Committee for Standardization (PKN): Warsaw, Poland, 1999.
- PN-EN 88/H-89500; Sintered Carbides. Polish Committee for Standardization (PKN): Warsaw, Poland, 1988.
- Shilpa, M.K.; Yendapalli, V. Surface roughness estimation techniques for drilled surfaces: A review. Mater. Today Proc. 2022, 52, 1082–1091. [Google Scholar] [CrossRef]
- Amran, M.A.; Salmah, S.; Hussein, N.I.S.; Izamshah, R.; Hadzley, M.; Sivaraos; Kasim, M.S.; Sulaiman, M.A. Effects of machine parameters on surface roughness using response surface method in drilling process. Procedia Eng. 2013, 68, 24–29. [Google Scholar] [CrossRef]
- Kumar, P.K.; Lokeshwar, G.; Reddy, C.U.K.; Jyotis, A.; Shetty, S.; Acharya, S.; Shetty, N. Effect of Drilling Parameters on Surface Roughness and Delamination of Ramie–Bamboo-Reinforced Natural Hybrid Composites. J. Manuf. Mater. Process. 2024, 8, 195. [Google Scholar] [CrossRef]
- Geier, N.; Póka, G.; Jacsó, Á.; Pereszlai, C. A method to predict drilling-induced burr occurrence in chopped carbon fibre reinforced polymer (CFRP) composites based on digital image processing. Compos. B Eng. 2022, 242, 110054. [Google Scholar] [CrossRef]
- Krivokapić, Z.; Spaić, O.; Vučurević, R. Models for prediction of machined surface quality. Qual. Excell. 2015, 1–2, 84–86. (In Serbian) [Google Scholar]
- Nargis, T.; Shahabaz, S.M.; Acharya, S.; Shetty, N.; Malghan, R.L.; Shetty, S.D. A Comprehensive Study on the Optimiza-tion of Drilling Performance in Hybrid Nano-Composites and Neat CFRP Composites Using Statistical and Machine Learning Approaches. J. Manuf. Mater. Process. 2024, 8, 67. [Google Scholar] [CrossRef]
- Wang, L.; Liu, B.; Yang, H.; Guo, Y.; Li, J.; Liu, H. Experimental Study on the Compressive and Shear Mechanical Properties of Cement–Formation Interface Considering Surface Roughness and Drilling Mud Contamination. Energies 2022, 15, 6472. [Google Scholar] [CrossRef]
- Ghazali, M.F.; Abdullah, M.M.A.B.; Abd Rahim, S.Z.; Gondro, J.; Pietrusiewicz, P.; Garus, S.; Stachowiak, T.; Sandu, A.V.; Mohd Tahir, M.F.; Korkmaz, M.E.; et al. Tool Wear and Surface Evaluation in Drilling Fly Ash Geopolymer Using HSS, HSS-Co, and HSS-TiN Cutting Tools. Materials 2021, 14, 1628. [Google Scholar] [CrossRef] [PubMed]
- Nayak, P.R. Some aspects of surface roughness measurement. Wear 1973, 26, 165–174. [Google Scholar] [CrossRef]
- Kurra, S.; Rahman, N.; Regalla, S.; Gupta, A. Modeling and optimization of surface roughness in single point incremental forming process. J. Mater. Res. Technol. 2015, 4, 304–313. [Google Scholar] [CrossRef]
- Echrif, S.B.M.; Hrairi, M. Significant Parameters for the Surface Roughness in Incremental Forming Process. Mater. Manuf. Process. 2014, 29, 697–703. [Google Scholar] [CrossRef]
- Salcedo, M.C.; Coral, I.B.; Ochoa, G.V. Characterization of surface topography with Abbott Firestone curve. Contemp. Eng. Sci. 2018, 11, 3397–3407. [Google Scholar] [CrossRef]
- Solaymani, S.; Ghoranneviss, M.; Elahi, S.M.; Shafiekhani, A.; Kulesza, S.; Ţălu, S.; Bramowicz, M.; Hantehzadeh, M.; Nezafat, N.B. The relation between structural, rugometric and fractal characteristics of hard dental tissues at micro and nano levels. Microsc. Res. Tech. 2019, 82, 421–428. [Google Scholar] [CrossRef]
- Kulesza, S.; Bramowicz, M. A comparative study of correlation methods for determination of fractal parameters in surface characterization. Appl. Surf. Sci. 2014, 293, 196–201. [Google Scholar] [CrossRef]
- Li, C.; Xu, Y.; Jiang, Z.; Yu, B.; Xu, P. Fractal Analysis on the Mapping Relationship of Conductivity Properties in Porous Material. Fractal Fract. 2022, 6, 527. [Google Scholar] [CrossRef]
- Krim, J.; Heyvaert, I.; Van Haesendock, C.; Bruynseraede, Y. Scanning Tuneling Microscopy Observation of Self-Affine Fractal Roughness in Ion-Bombarded Film Surface. Phys. Rev. Lett. 1993, 70, 57–60. [Google Scholar] [CrossRef]
- Bramowicz, M.; Kłysz, S. Application of Atomic Force Microscopy (AFM) in diagnostic of surface layer. Res. Work. AFIT 2007, 22, 167–174. [Google Scholar] [CrossRef]
- Cullity, B.D. Elements of X-Ray Diffraction, 3rd ed.; Pearson Education Limited: London, UK, 2014. [Google Scholar]
- Kraus, W.; Nolze, G. POWDER CELL—A program for the representation and manipulation of crystal structures and calculation of the resulting X-ray powder patterns. J. Appl. Cryst. 1996, 29, 301–303. [Google Scholar] [CrossRef]
- Klysz, S.; Bien, A. Examination of the Structure and Micro-Hardness of a Laser-Constituted Surface Layer Deposited on the Constructional Steel. Res. Work. AFIT 2008, 23, 51–63. [Google Scholar] [CrossRef]
- Scherrer, P. Bestimmung der Grösse und der inneren Struktur von Kolloidteilchenmittels Röntgenstrahlen. Nachr. Ges. Wiss. Göttingen 1918, 26, 98–100. [Google Scholar]
- Stokes, A.R.; Wilson, A.J.C. A method of calculating the integral breadths of Debye-Scherrer lines. Math. Proc. Camb. Philos. Soc. 1942, 38, 313–322. [Google Scholar] [CrossRef]
- Stokes, A.R.; Wilson, A.J.C. The diffraction of X rays by distorted crystal aggregates—I. Proc. Phys. Soc. 1944, 56, 174–181. [Google Scholar] [CrossRef]
- Williamson, G.K.; Hall, W.H. X-ray Line Broadening from Filed Aluminium and Wolfram. Acta Metall. 1953, 1, 22–31. [Google Scholar] [CrossRef]
- Kibasomba, P.M.; Dhlamini, S.; Maaza, M.; Liu, C.-P.; Rashad, M.M.; Rayan, D.A.; Mwakikunga, B.W. Strain and grain size of TiO2 nanoparticles from TEM, Raman spectroscopy and XRD: The revisiting of the Williamson-Hall plot method. Results Phys. 2018, 9, 628–635. [Google Scholar] [CrossRef]
- Dadras, S.; Davoudiniy, M. Analysis of YBCO high temperature superconductor doped with silver nanoparticles and carbon nanotubes using Williamson-Hall and size-strain plot. Phys. C Supercond. Its Appl. 2018, 548, 116–118. [Google Scholar] [CrossRef]
- Shahmoradi, Y.; Souri, D. Growth of silver nanoparticles within the tellurovanadate amorphous matrix: Optical band gap and band tailing properties, beside the Williamson-Hall estimation of crystallite size and lattice strain. Ceram. Int. 2019, 45, 7857–7864. [Google Scholar] [CrossRef]
- Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Available online: https://materialsproject.org (accessed on 10 December 2024).
- PN-ISO 4288:2011; Geometrical Product Specifications (GPS)—Surface Texture: Profile Method—Rules and Procedures for the Assessment of Surface Texture. Polish Committee for Standardization: Warsaw, Poland, 2011.
- Mainsah, E.; Greenwood, J.A.; Chetwynd, D.G. Metrology and Properties of Engineering Surfaces; Kluwer Academic Publishers: Norwell, MA, USA, 2001. [Google Scholar]
- Sayles, R.S.; Thomas, T.R. The spatial representation of surface roughness by means of the structure function: A practical alternative to correlation. Wear 1977, 42, 263–276. [Google Scholar] [CrossRef]
- Available online: http://www.crystallography.net/cod/ (accessed on 9 December 2024).



| Parameter | EB80 GÜHRING |
|---|---|
| Material | Sintered WC |
| Type | K15 |
| Chemical composition (% vol) | WC 94/Co 6 |
| Density | 14,850 kg/m3 |
| Granularity | 1.0 μm |
| Hardness (HV30) | 1690 |
| Lattice Parameters [Å] | Spatial Group No. (Symmetry) | Element | Position of the Atom in the Unit Cell | Unit Cell | ||
|---|---|---|---|---|---|---|
| x | y | z | ||||
| WC | ||||||
| a0 = 2.9065 c0 = 2.8366 γ0 = 120° | 187 (P-6m2) | W | 0 | 0 | 0 | 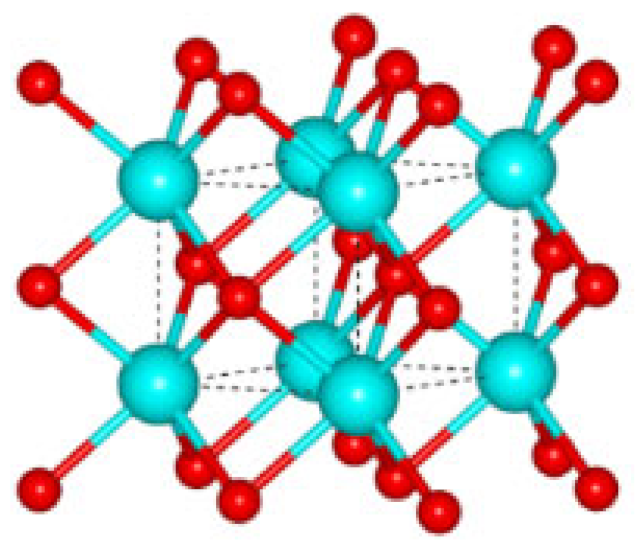 |
| C | 1/3 | 2/3 | 1/2 | |||
| Co | ||||||
| a0 = 2.5071 c0 = 4.0686 γ0 = 120° | 194 (P63/mmc) | Co | 1/3 | 2/3 | 1/4 | 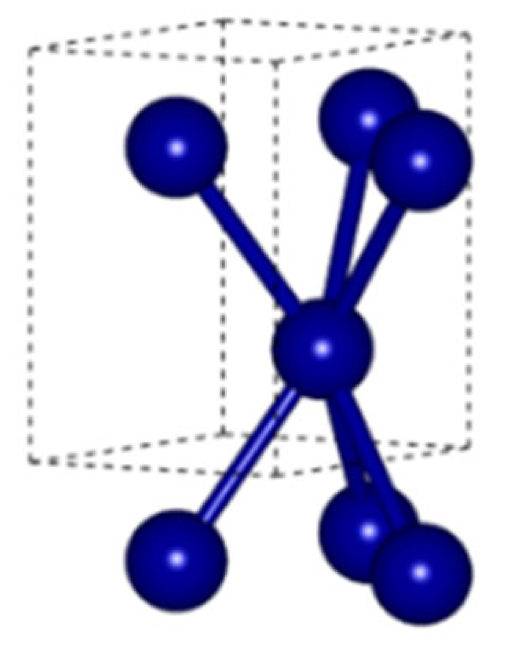 |
| Crystalline Phase | Initial Lattice Parameters [Å] | Final Lattice Parameters [Å] | Volumetric Phase Content [%] | Domain Size [Å] | Lattice Distortion [%] |
|---|---|---|---|---|---|
| WC | a0 = 2.9065 c0 = 2.8366 γ0 = 120° | a0 = 2.9023 c0 = 2.8292 γ0 = 120° | 93.53 | 141.26 | −0.065 |
| Co | a0 = 2.5071 c0 = 4.0686 γ0 = 120° | a0 = 2.5098 c0 = 4.0550 γ0 = 120° | 6.47 | 199.09 | −0.04 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rychlik, K.; Bramowicz, M.; Kulesza, S. Multi-Perspective Characterization of a Performance of a Barrel Drill Made of Tungsten Carbide Composite. Materials 2025, 18, 794. https://doi.org/10.3390/ma18040794
Rychlik K, Bramowicz M, Kulesza S. Multi-Perspective Characterization of a Performance of a Barrel Drill Made of Tungsten Carbide Composite. Materials. 2025; 18(4):794. https://doi.org/10.3390/ma18040794
Chicago/Turabian StyleRychlik, Kazimierz, Mirosław Bramowicz, and Sławomir Kulesza. 2025. "Multi-Perspective Characterization of a Performance of a Barrel Drill Made of Tungsten Carbide Composite" Materials 18, no. 4: 794. https://doi.org/10.3390/ma18040794
APA StyleRychlik, K., Bramowicz, M., & Kulesza, S. (2025). Multi-Perspective Characterization of a Performance of a Barrel Drill Made of Tungsten Carbide Composite. Materials, 18(4), 794. https://doi.org/10.3390/ma18040794






