Large-Scale Metasurface Simulation Using Local-Segmented Approach
Highlights
- We proposed a locally segmented approach for efficient and accurate simulation of large-scale metasurfaces.
- This approach includes the electromagnetic coupling effects between adjacent meta-atoms.
- Fast-responding or more accurate simulations can be conducted by adjusting the simulation parameters.
- Numerical examples of a 2 mm diameter cylindrical metalens with NA = 0.9 and a 1 mm diameter beam splitter are given. Compared with rigorous simulations and local periodic approximation, the precision and effectiveness of our approach are highlighted.
Abstract
1. Introduction
2. Theory of Local-Segmented Approach
2.1. Transverse Localized Electromagnetic Coupling Effects
2.2. Local Segment Approach
2.3. Parameters of Local Segments
- If w and are constant, the deviation tends to convergence as the computing size d increases, which is because more electromagnetic coupling effects are included in the segments for a larger d;
- Comparing Figure 4a with Figure 4b–f, if w and d are constant, the deviation is more likely to tend towards convergence when the edge ratio is a non-zero value. In contrast to other domain decomposition methods to decouple the coupling effects between sub-domains, the coupling effects are included by a decomposed field with the non-zero edge ratio ;
- As for local field width w, a relatively small w () will generate strong transverse effects, which leads to a larger computing size for deviation convergence. Conversely, a larger w takes a longer computing size d to converge. Therefore, a proper w is usually chosen as several times of periods u to the meta-atoms.
3. Numerical Examples
- Global: rigorous methods simulated by FMM of the entire element;
- LPA: fields of an aperiodic element are approximated by individually simulating each meta-atom with periodic boundary conditions as [4]. The amplitude is considered despite the minimal impact.
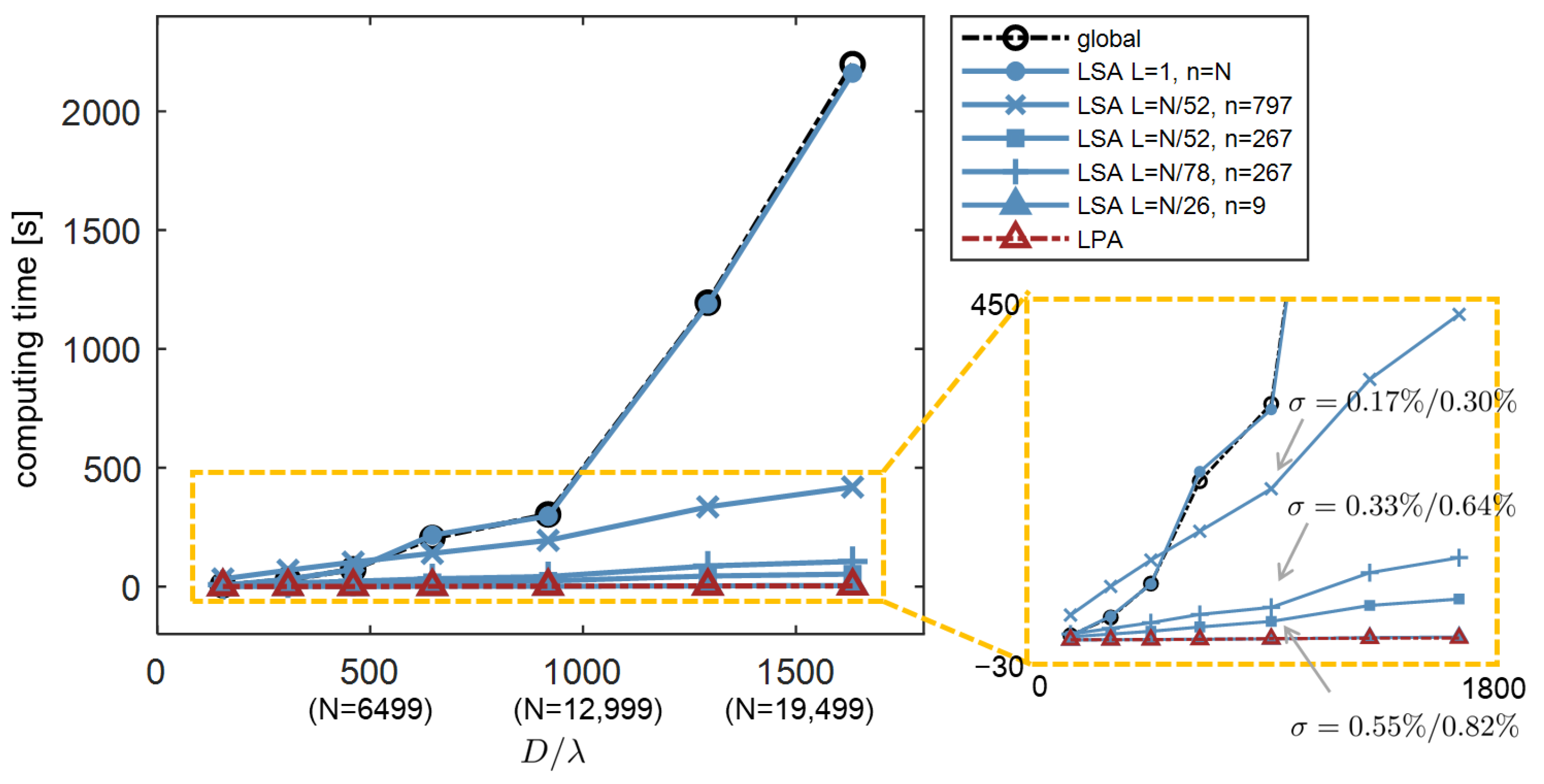
3.1. Numerical Complexity
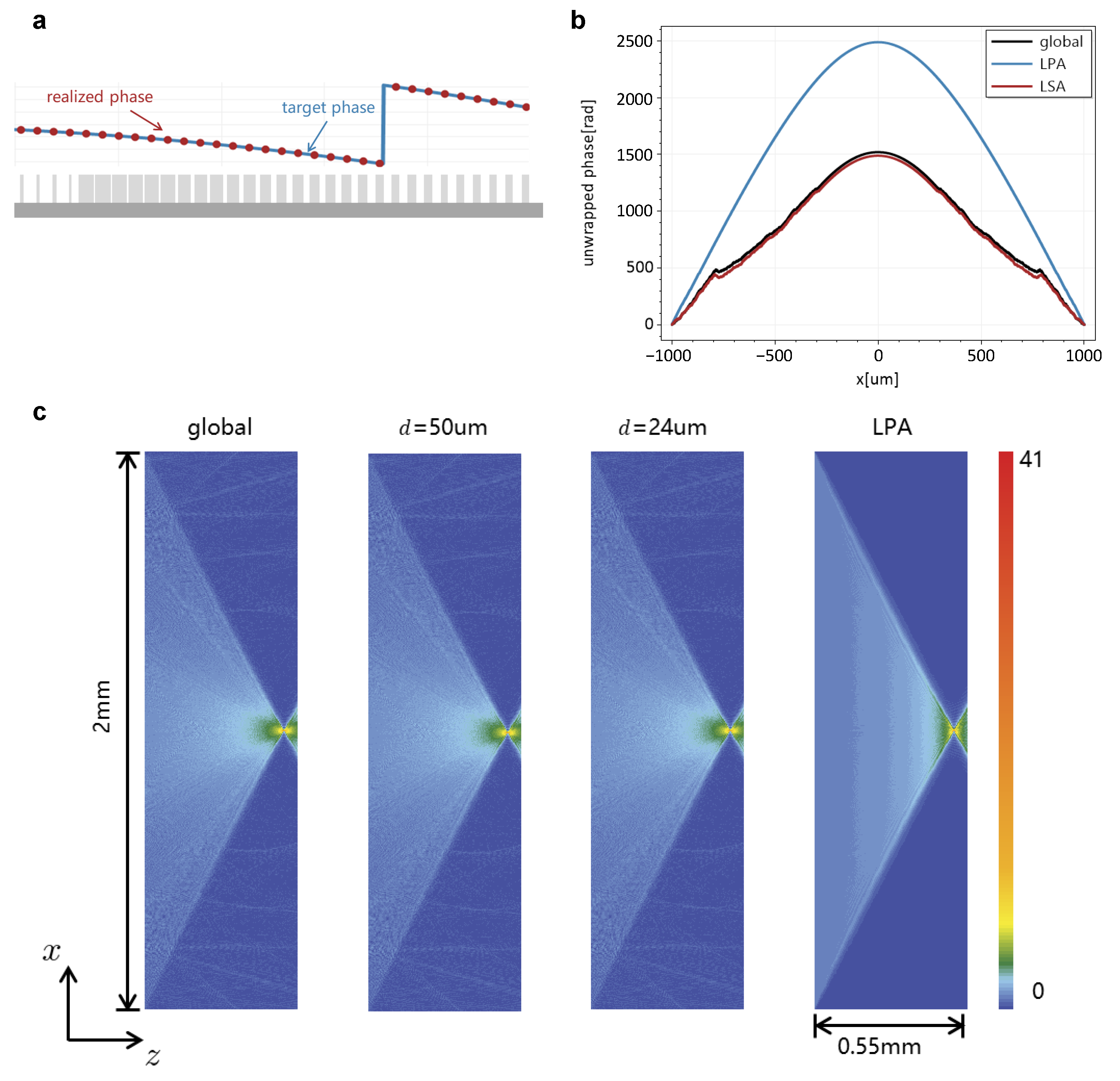
3.2. Simulation of a Metalens
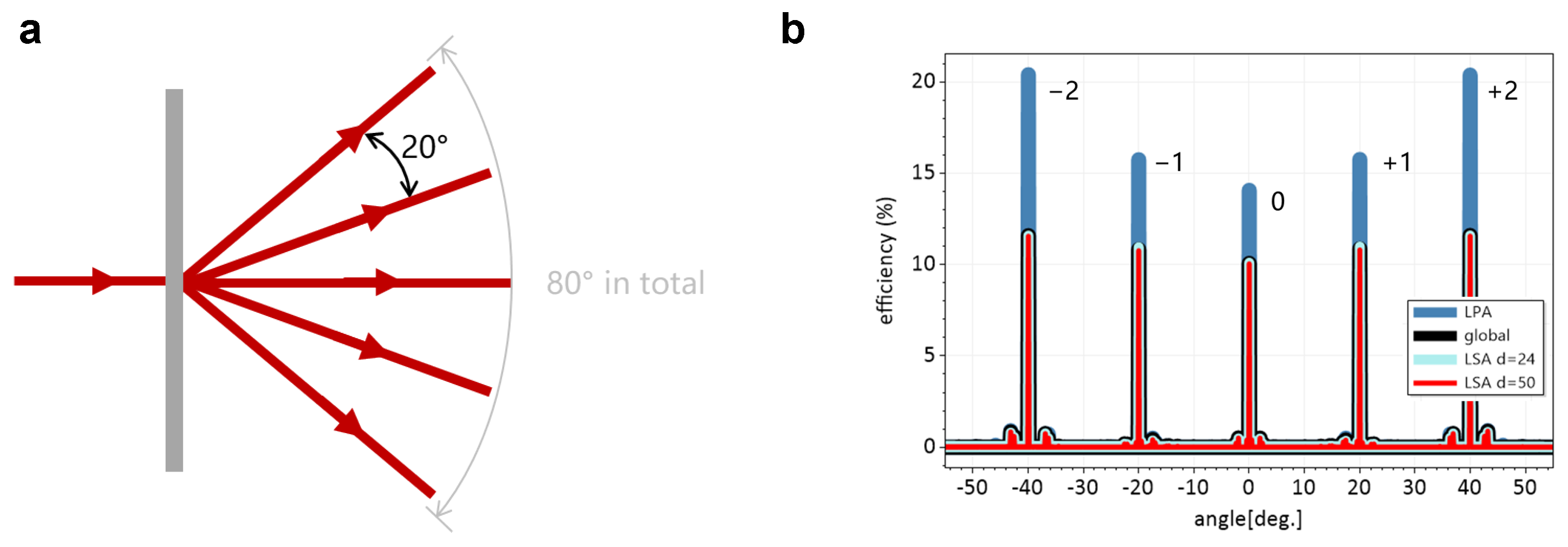
3.3. Simulation of a Beam Splitter
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, W.T.; Zhu, A.Y.; Capasso, F. Flat optics with dispersion-engineered metasurfaces. Nat. Rev. Mater. 2020, 5, 604–620. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Brongersma, M.L.; Yao, J.; Chen, M.K.; Levy, U.; Tsai, D.P.; Zheludev, N.I.; Faraon, A.; Arbabi, A.; Yu, N.; et al. Roadmap for Optical Metasurfaces. ACS Photonics 2024, 11, 816–865. [Google Scholar] [CrossRef] [PubMed]
- Yee, K. Numerical solution of initial boundary value problems involving maxwell’s equations in isotropic media. IEEE Trans. Antennas Propag. 1966, 14, 302–307. [Google Scholar] [CrossRef]
- Robben, B.; Penninck, L. Simulation methods for large-area meta-surfaces: Comparison local periodic, overlapping domains, and full wave calculations. In Proceedings of the High Contrast Metastructures XIII, San Francisco, CA, USA, 29–31 January 2024; SPIE: Bellingham, WA, USA, 2024; Volume 12897, pp. 34–39. [Google Scholar]
- Chen, W.T.; Zhu, A.Y.; Sanjeev, V.; Khorasaninejad, M.; Shi, Z.; Lee, E.; Capasso, F. A broadband achromatic metalens for focusing and imaging in the visible. Nat. Nanotechnol. 2018, 13, 220–226. [Google Scholar] [CrossRef] [PubMed]
- Whiting, E.B.; Campbell, S.D.; Kang, L.; Werner, D.H. Meta-atom library generation via an efficient multi-objective shape optimization method. Opt. Express 2020, 28, 24229–24242. [Google Scholar] [CrossRef]
- Zhang, S.; Khan, K.; Hellmann, C.; Wyrowski, F. Modeling of diffractive-/metasurfaces and their performance evaluations in general optical systems. In Proceedings of the Optical Modeling and Performance Predictions XI, Online, 24 August–4 September 2020. [Google Scholar]
- Zhang, S.; Hellmann, C.; Wyrowski, F. Modeling of high-contrast metasurfaces and their performance in general optical system using fast physical optics (Conference Presentation). In Proceedings of the High Contrast Metastructures IX, San Francisco, CA, USA, 3–6 February 2020; SPIE: Bellingham, WA, USA, 2020; Volume 11290, p. 112900P. [Google Scholar]
- Cai, H.; Srinivasan, S.; Czaplewski, D.A.; Martinson, A.B.F.; Gosztola, D.J.; Stan, L.; Loeffler, T.; Sankaranarayanan, S.K.R.S.; López, D. Inverse design of metasurfaces with non-local interactions. NPJ Comput. Mater. 2020, 6, 116. [Google Scholar] [CrossRef]
- Taflove, A.; Oskooi, A.F.; Johnson, S.G. Advances in FDTD Computational Electrodynamics: Photonics and Nanotechnology; Artech House Publishers: London, UK, 2013. [Google Scholar]
- Lin, Z.; Johnson, S.G. Overlapping domains for topology optimization of large-area metasurfaces. Opt. Express 2019, 27, 32445–32453. [Google Scholar] [CrossRef]
- Fernandez-Mouron, L.-H.; Tremas, l.; Legrand, M.; Urard, P.; Mohamad, H.; Dilhan, L.; Giuseppe Carnemolla, E.; Fissore, M.; Downing, J.; Serradeil, V.; et al. Impact of Numerical Simulation Boundary-Decomposition Errors on Optical Performance of Metadiffusors. In Proceedings of the The 14th International Conference on Metamaterials, Photonic Crystals and Plasmonics, META, Toyama, Japan, 16–19 July 2024. [Google Scholar]
- Edee, K.; Granet, G.; Paladian, F.; Bonnet, P.; Al Achkar, G.; Damaj, L.; Plumey, J.P.; Larciprete, M.C.; Guizal, B. Domain Decomposition Spectral Method Applied to Modal Method: Direct and Inverse Spectral Transforms. Sensors 2022, 22, 8131. [Google Scholar] [CrossRef]
- Gao, H.W.; Xin, X.M.; Lim, Q.J.; Wang, S.; Peng, Z. Efficient Full-Wave Simulation of Large-Scale Metasurfaces and Metamaterials. IEEE Trans. Antennas Propag. 2024, 72, 800–811. [Google Scholar] [CrossRef]
- Phan, T.; Sell, D.; Wang, E.W.; Doshay, S.; Edee, K.; Yang, J.; Fan, J.A. High-efficiency, large-area, topology-optimized metasurfaces. Light Sci. Appl. 2019, 8, 48. [Google Scholar] [CrossRef]
- Linss, S.; Michaelis, D.; Zeitner, U.D. Macroscopic wave-optical simulation of dielectric metasurfaces. Opt. Express 2021, 29, 10879–10892. [Google Scholar] [CrossRef] [PubMed]
- Torfeh, M.; Arbabi, A. Modeling Metasurfaces Using Discrete-Space Impulse Response Technique. ACS Photonics 2020, 7, 941–950. [Google Scholar] [CrossRef]
- Gigli, C.; Li, Q.; Chavel, P.; Leo, G.; Brongersma, M.L.; Lalanne, P. Fundamental Limitations of Huygens’ Metasurfaces for Optical Beam Shaping. Laser Photonics Rev. 2021, 15, 2000448. [Google Scholar] [CrossRef]
- Bayati, E. Design and Characterization of Optical Metasurface Systems. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2022. [Google Scholar]
- Li, L. Multilayer modal method for diffraction gratings of arbitrary profile, depth, and permittivity. J. Opt. Soc. Am. A 1993, 10, 2581–2591. [Google Scholar] [CrossRef]
- Li, L. Formulation and comparison of two recursive matrix algorithms for modeling layered diffraction gratings. J. Opt. Soc. Am. A—Opt. Image Sci. Vis. 1996, 13, 1024–1035. [Google Scholar] [CrossRef]
- Pérez-Arancibia, C.; Pestourie, R.; Johnson, S.G. Sideways adiabaticity: Beyond ray optics for slowly varying metasurfaces. Opt. Express 2018, 26, 30202–30230. [Google Scholar] [CrossRef]
- Asoubar, D.; Zhang, S.; Wyrowski, F.; Kuhn, M. Parabasal field decomposition and its application to non-paraxial propagation. Opt. Express 2012, 20, 23502–23517. [Google Scholar] [CrossRef]
- Li, L. Note on the S-matrix propagation algorithm. J. Opt. Soc. Am. A 2003, 20, 655–660. [Google Scholar] [CrossRef]
- Wyrowski, F.; Kuhn, M. Introduction to field tracing. J. Mod. Opt. 2011, 58, 449–466. [Google Scholar] [CrossRef]
- Wyrowski, F.; Bryngdahl, O. Iterative Fourier-transform algorithm applied to computer holography. J. Opt. Soc. Am. A 1988, 5, 1058–1065. [Google Scholar] [CrossRef]
- Hammond, A.M.; Oskooi, A.; Chen, M.; Lin, Z.; Johnson, S.G.; Ralph, S.E. High-performance hybrid time/frequency-domain topology optimization for large-scale photonics inverse design. Opt. Express 2022, 30, 4467–4491. [Google Scholar] [CrossRef]
- Christiansen, R.E.; Lin, Z.; Roques-Carmes, C.; Salamin, Y.; Kooi, S.E.; Joannopoulos, J.D.; Soljačić, M.; Johnson, S.G. Fullwave Maxwell inverse design of axisymmetric, tunable, and multi-scale multi-wavelength metalenses. Opt. Express 2020, 28, 33854–33868. [Google Scholar] [CrossRef]



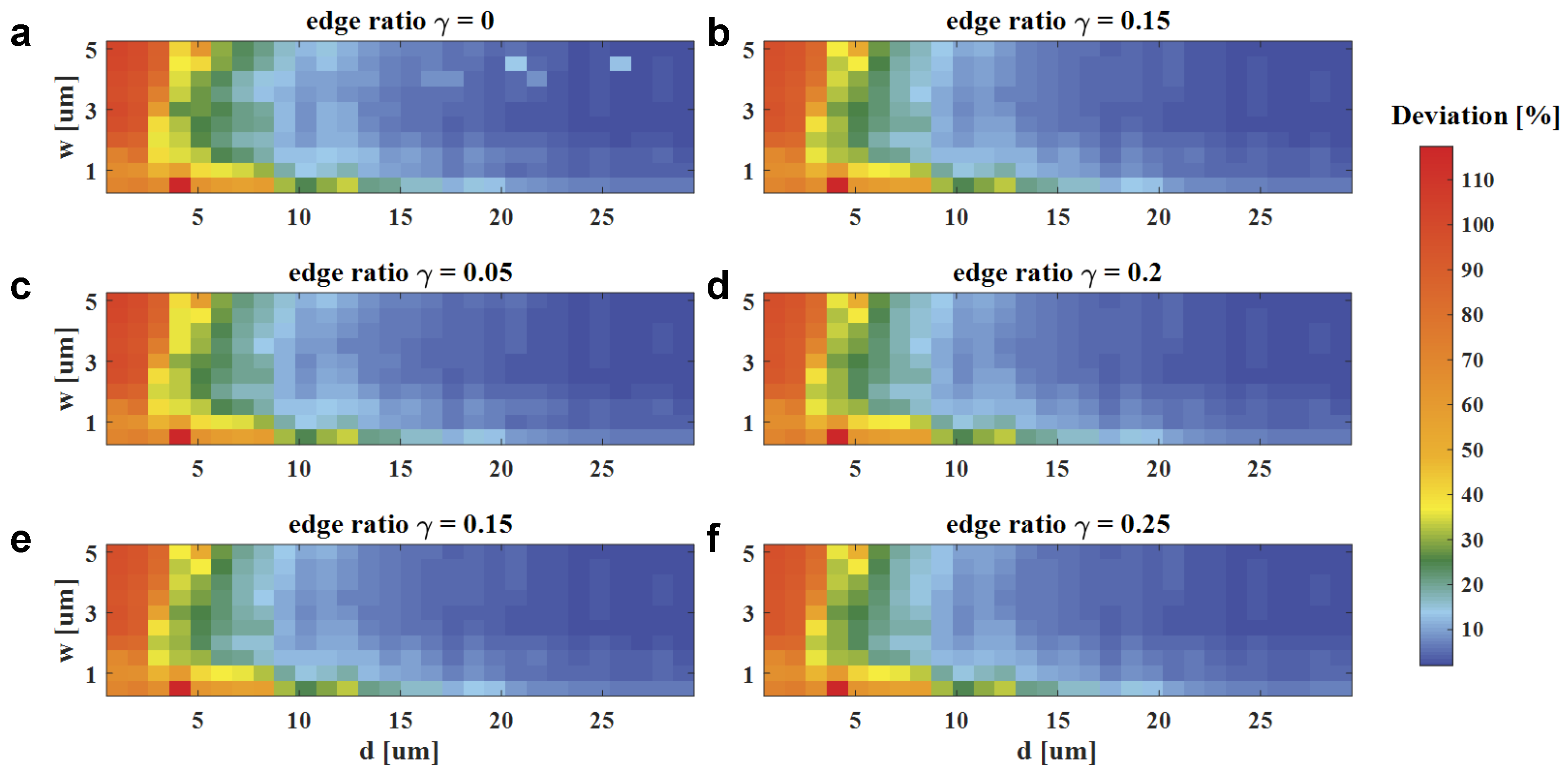
| w** | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d | ||||||||||||
| 0 | N * | N | N | N | 26 | 27 | 27 | N | N | 27 | ||
| 0.05 | N | N | N | N | 26 | 26 | 27 | 27 | 26 | 27 | ||
| 0.1 | N | N | N | N | 25 | 26 | 27 | 26 | 26 | 27 | ||
| 0.15 | N | N | N | N | 25 | 24 | 27 | 26 | 26 | 26 | ||
| 0.2 | N | N | N | N | 25 | 25 | 26 | 26 | 26 | 25 | ||
| 0.25 | N | N | N | N | 24 | 25 | 26 | 26 | 25 | 25 | ||
| Approach | Segments | Number of Harmonics | Complexity |
|---|---|---|---|
| Global | 1 | N | |
| LSA | L | n | |
| LPA | s |
| Approach | Deviation (Without Evan.) | Deviation (With Evan.) | Computing Time | Focusing Efficiency |
|---|---|---|---|---|
| Global | - | - | 1189.89s | 12.52% |
| LSA µm | 1.46% | 2.65% | 124.51s | 12.46% |
| LSA µm | 4.03% | 7.38% | 37.99s | 12.29% |
| LPA | 57.69% | 77.71% | 2.38s | 21.46% |
| Parameters | Global | LSA µm | LSA µm | LPA |
|---|---|---|---|---|
| Deviation (without evan.) | - | 1.33% | 3.56% | 45.09% |
| Deviation (with evan.) | - | 2.09% | 6.65% | 66.15% |
| Computing time | 211.64 s | 57.43 s | 16.65 s | 0.96 s |
| −2 efficiency | 11.59% | 11.55% | 11.59% | 20.41% |
| −1 efficiency | 10.83% | 10.77% | 10.96% | 15.75% |
| 0 efficiency | 10.07% | 10.05% | 10.10% | 14.07% |
| +1 efficiency | 10.87% | 10.81% | 10.99% | 15.76% |
| +2 efficiency | 11.60% | 11.56% | 11.30% | 20.38% |
| Summarized efficiency | 54.96% | 54.73% | 55.25% | 86.37% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Zhang, S.; Song, N.; Xue, D. Large-Scale Metasurface Simulation Using Local-Segmented Approach. Materials 2025, 18, 649. https://doi.org/10.3390/ma18030649
Wang S, Zhang S, Song N, Xue D. Large-Scale Metasurface Simulation Using Local-Segmented Approach. Materials. 2025; 18(3):649. https://doi.org/10.3390/ma18030649
Chicago/Turabian StyleWang, Shiyao, Site Zhang, Naitao Song, and Donglin Xue. 2025. "Large-Scale Metasurface Simulation Using Local-Segmented Approach" Materials 18, no. 3: 649. https://doi.org/10.3390/ma18030649
APA StyleWang, S., Zhang, S., Song, N., & Xue, D. (2025). Large-Scale Metasurface Simulation Using Local-Segmented Approach. Materials, 18(3), 649. https://doi.org/10.3390/ma18030649







