Surface Structure Effects on H and O Adsorption on Gold, Nickel and Platinum Nanoparticles
Abstract
1. Introduction
2. Calculation Details
3. Results
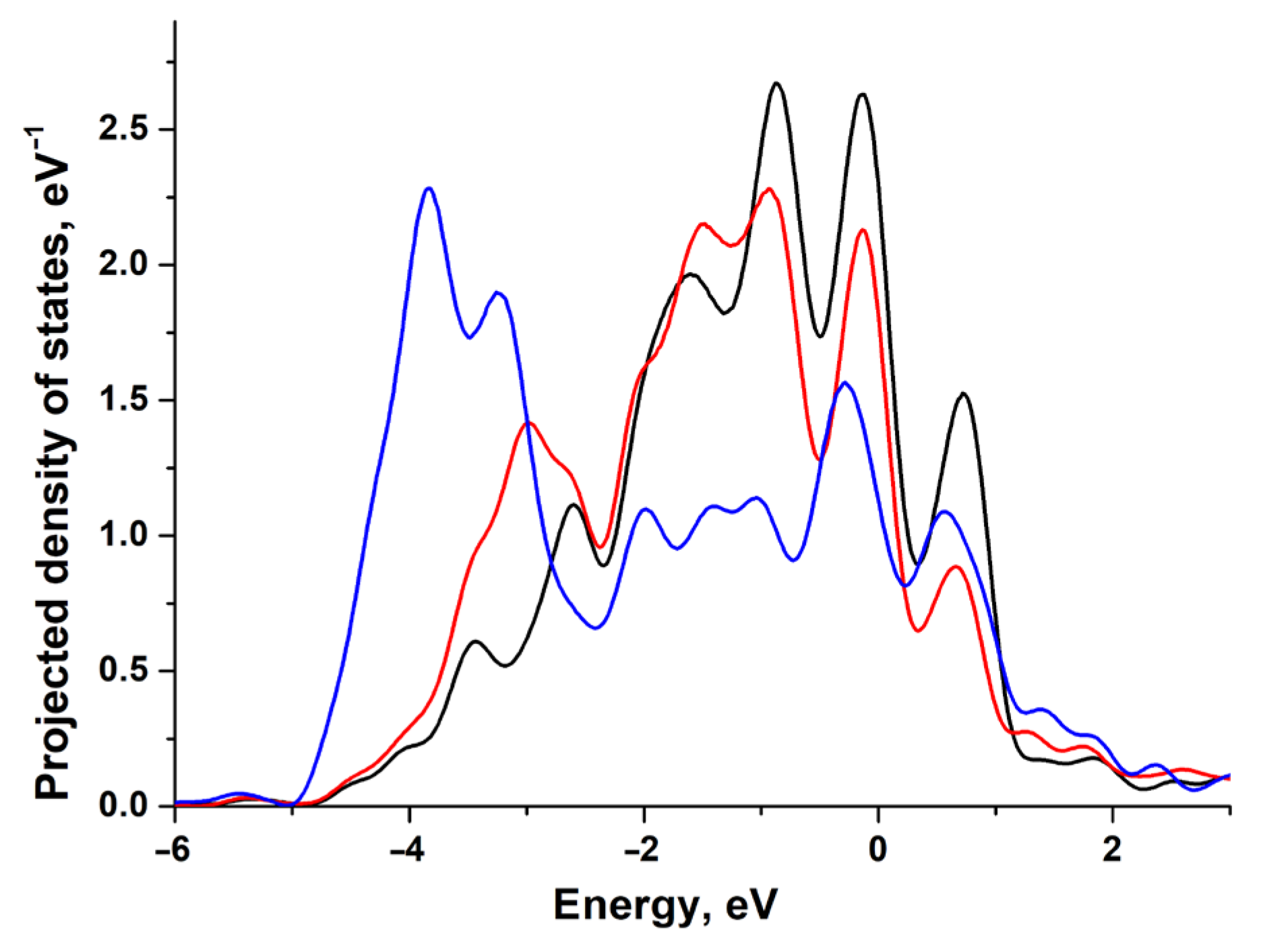
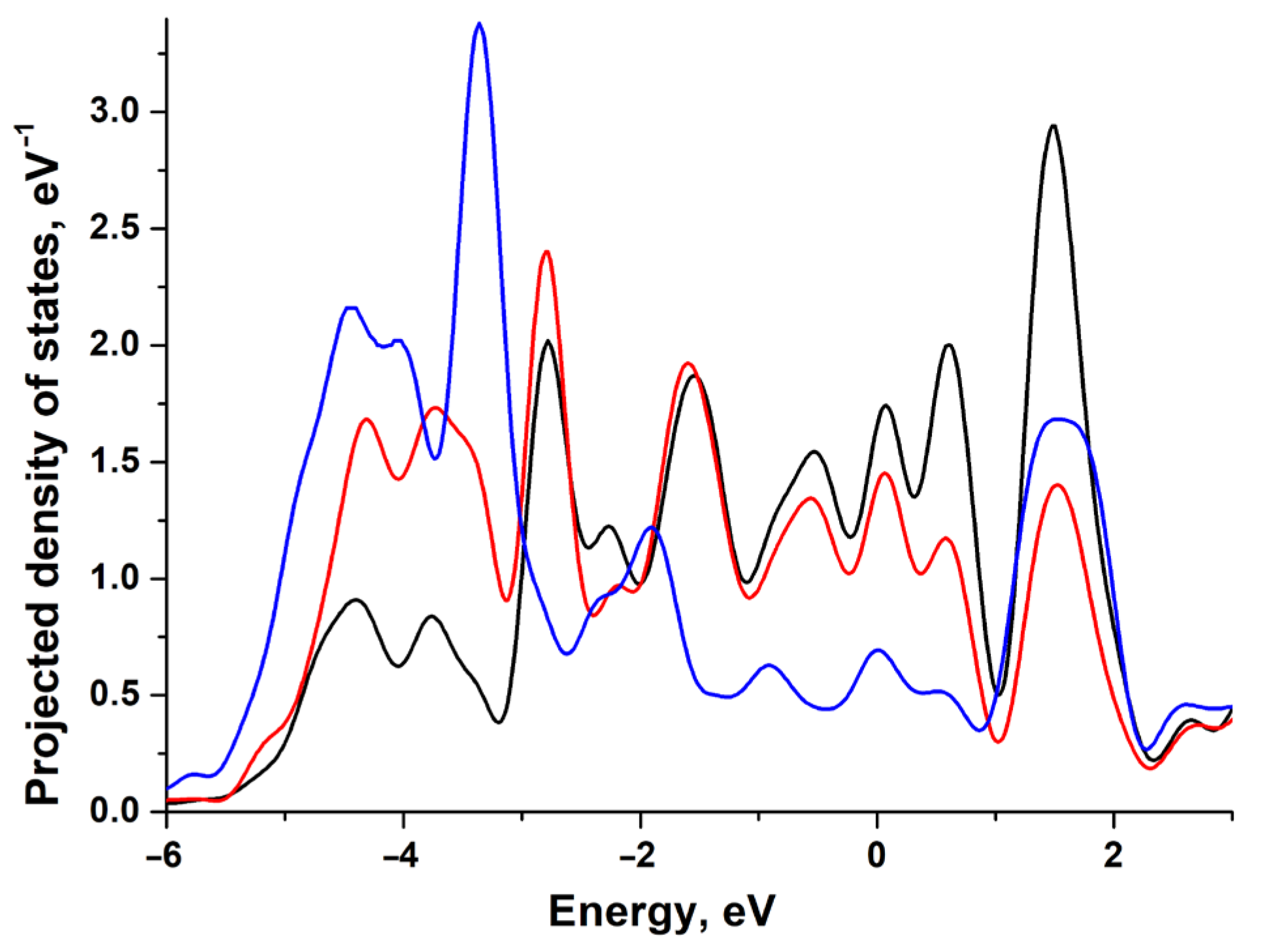
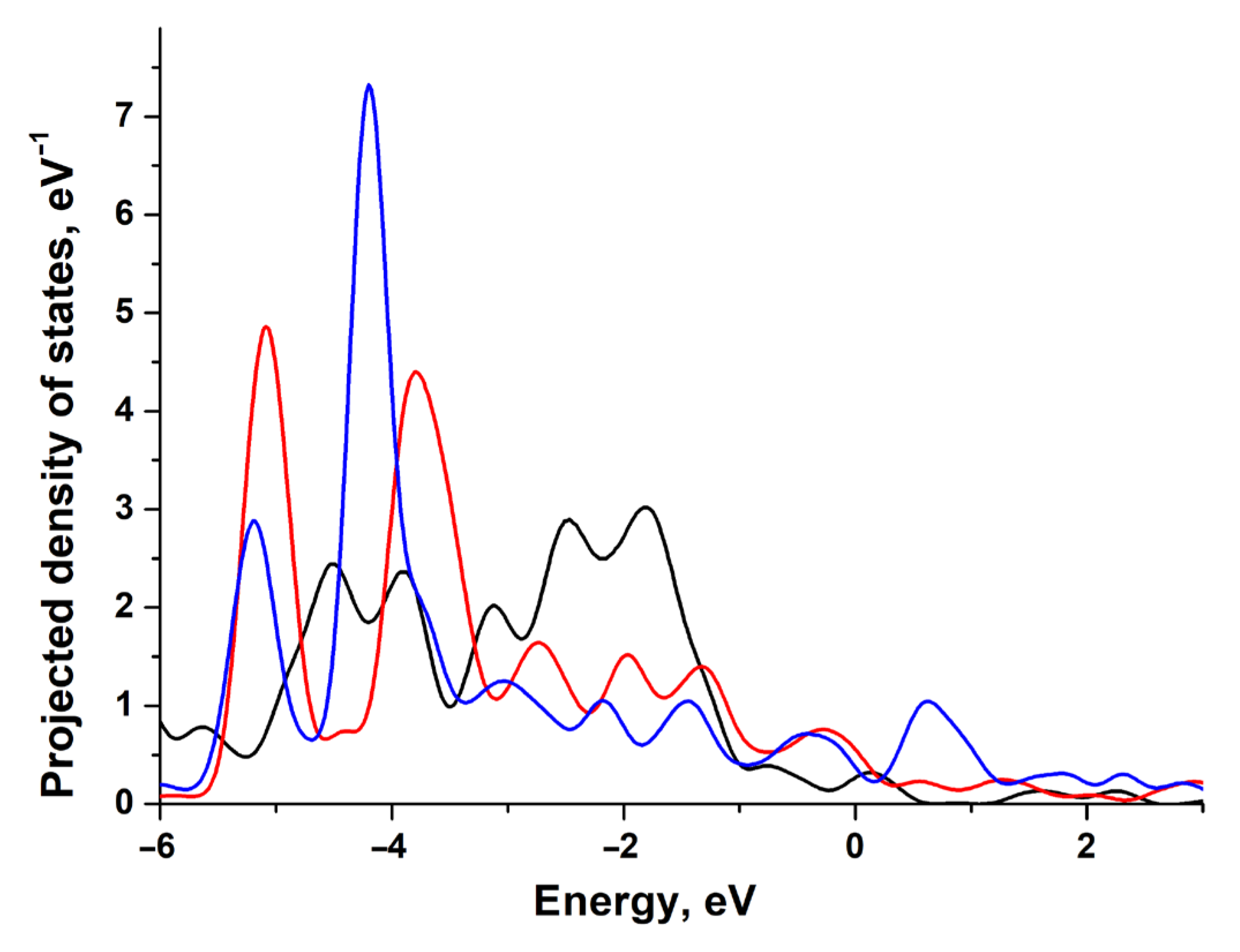
3.1. Electronic and Atomic Structure of the Surface
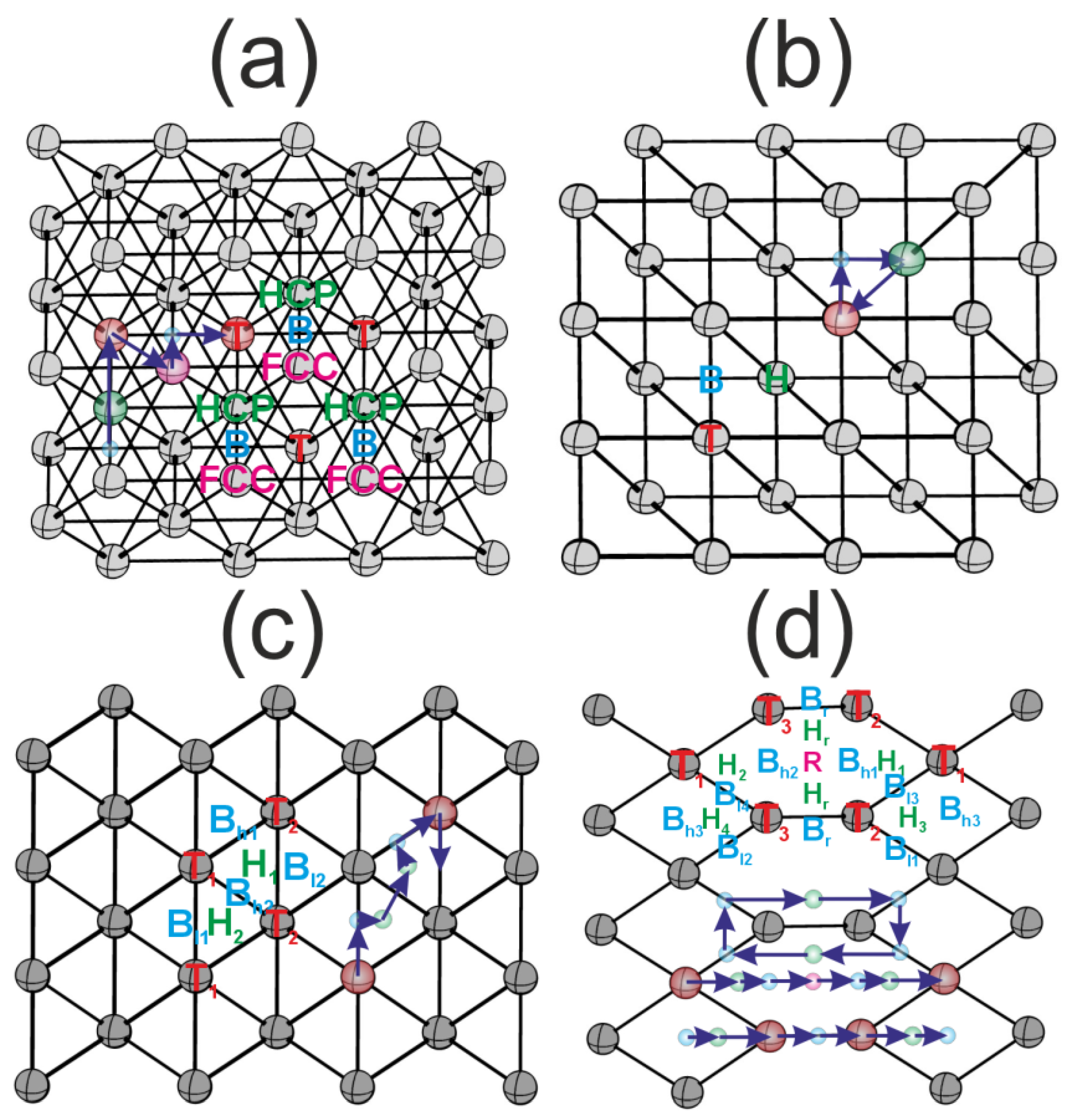
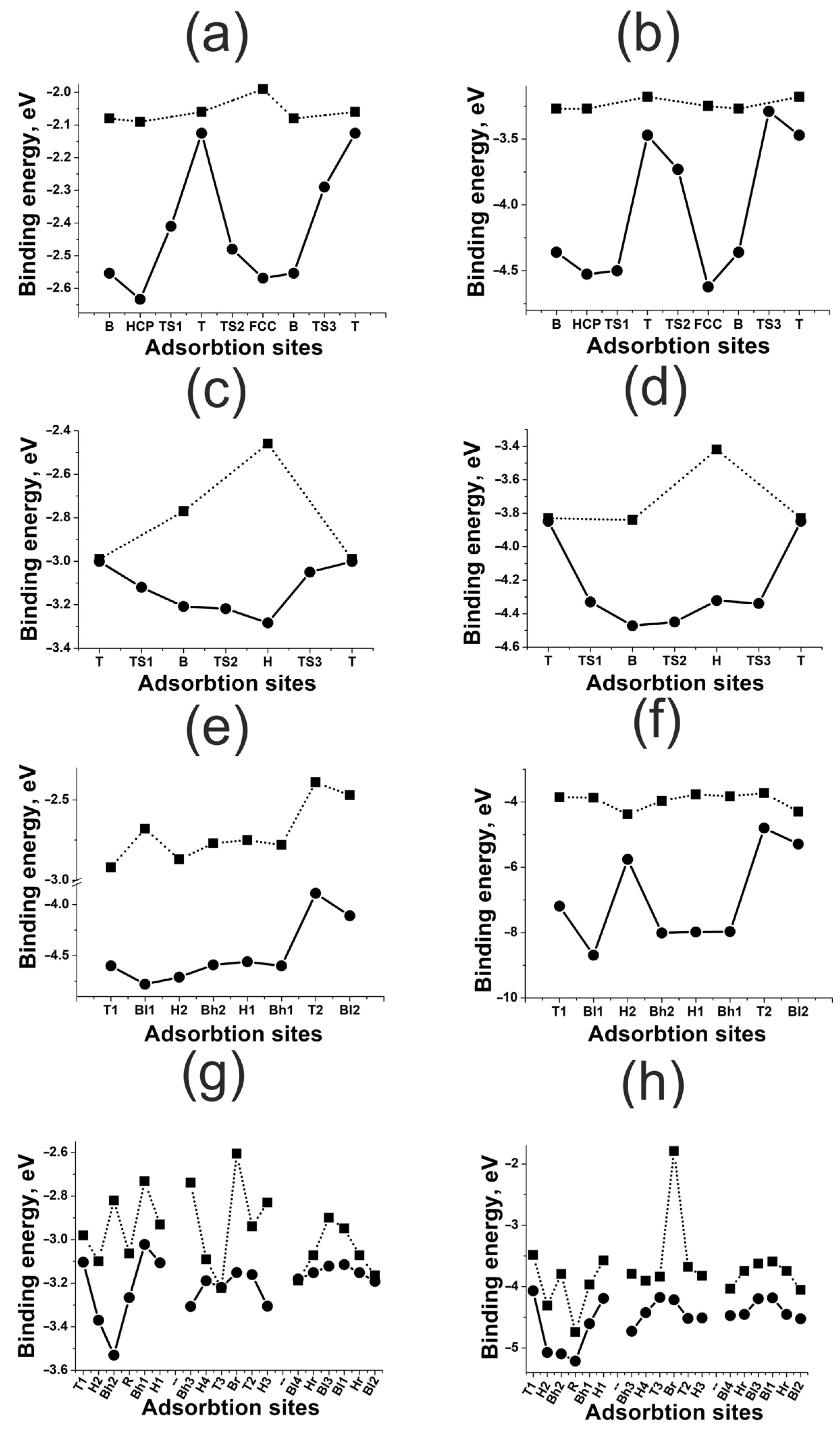
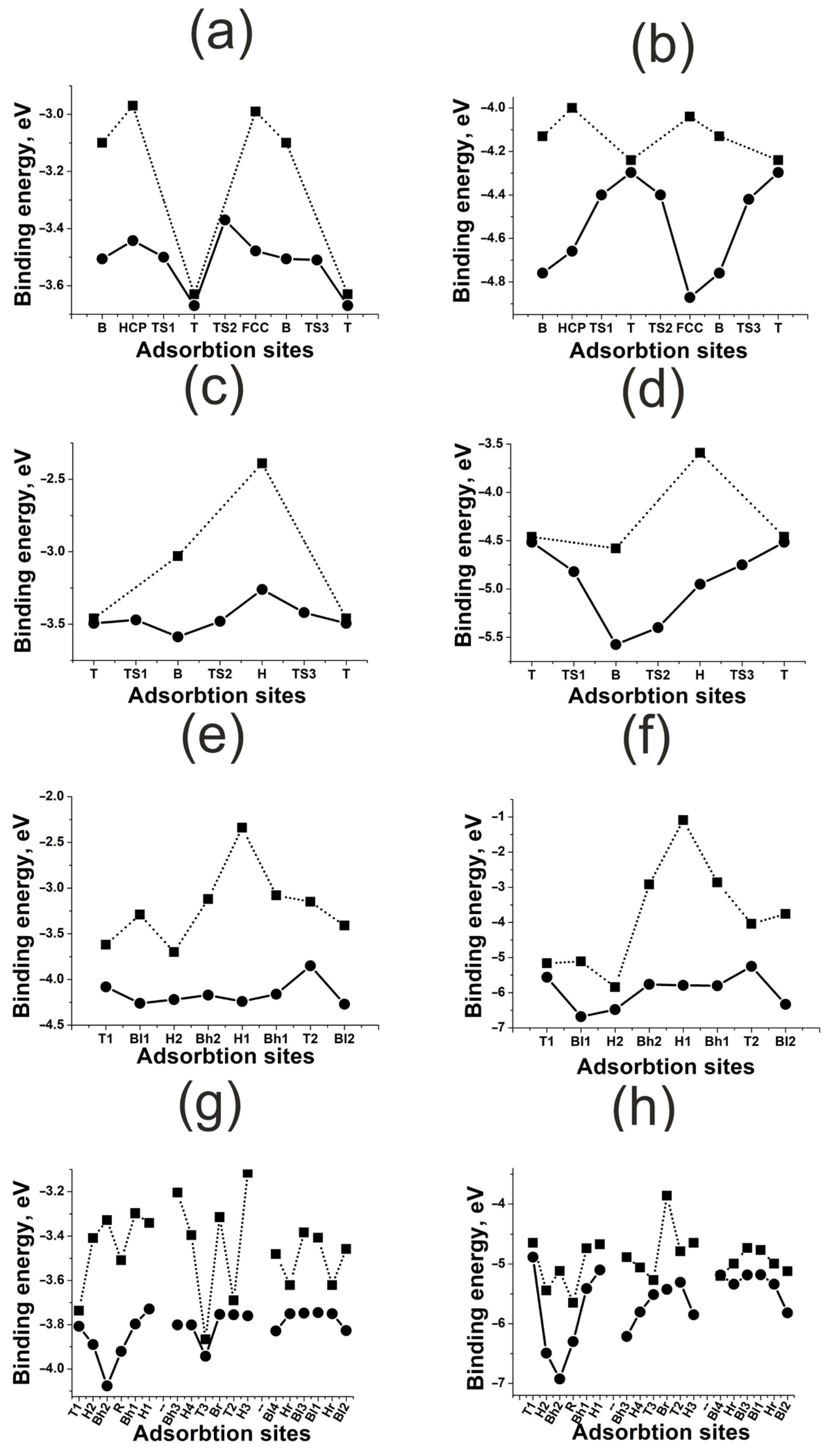
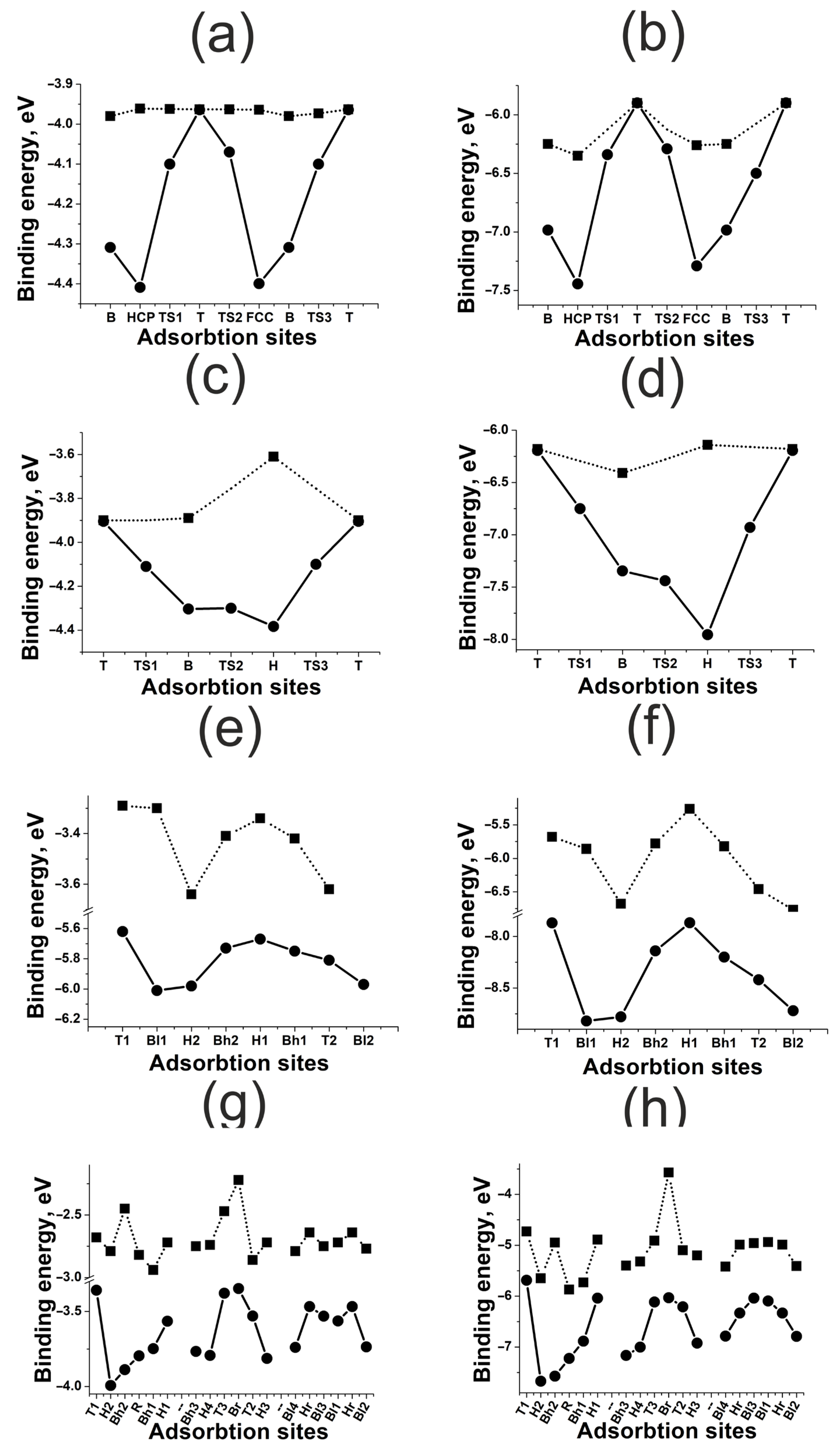
3.2. Highly Symmetric Sites of Nickel Surfaces
3.3. Highly Symmetric Sites of Platinum Surfaces
3.4. Highly Symmetric Sites of Gold Surfaces
4. Conclusions
- For flat (111) and (100) surfaces, only the active sites with a large coordination number are affected significantly by surface deformation. For kinked (110) and (211) surfaces, the surface deformation effect is much stronger than for flat surfaces, though it has no drastic tendency. The surface deformation always results in strong bonding.
- The effect of neighboring atoms depends on the metal type and correlates indirectly with the coupling matrix element. The less the matrix element, the weaker the repulsion in metal–adatom complexes. In the case of weak repulsion, the effect of neighboring atoms increases with the coordination number of the active site. Strong repulsive interaction inverts this tendency.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, F.; Astruc, D. Nanocatalysts and other nanomaterials for water remediation from organic pollutants. Coord. Chem. Rev. 2020, 408, 213180. [Google Scholar] [CrossRef]
- Lee, M.Y.; Ha, H.; Cho, K.H.; Seo, H.; Park, S.; Lee, Y.H.; Kwon, S.J.; Lee, T.W.; Nam, K.T. Importance of interfacial band structure between the substrate and Mn3O4 nanocatalysts during electrochemical water oxidation. ACS Catal. 2020, 10, 1237–1245. [Google Scholar] [CrossRef]
- Choi, H.; Nguyen, P.T.; Tran, C.V.; In, J.B. Micro-patterned metal current collectors for high aspect ratio flexible graphene supercapacitors. Appl. Surf. Sci. 2020, 510, 145432. [Google Scholar] [CrossRef]
- Lambert, R.M.; Pacchioni, G. (Eds.) Chemisorption and Reactivity on Supported Clusters and Thin Films; Springer: Dordrecht, The Netherlands, 1997; 532p. [Google Scholar] [CrossRef]
- Fujitani, T.; Nakamura, I.; Akita, T.; Okumura, M.; Haruta, M. Hydrogen dissociation by gold clusters. Angew. Chem. Int. Ed. 2009, 48, 9515–9518. [Google Scholar] [CrossRef]
- Darling, G.R.; Holloway, S. The dissociation of diatomic molecules at surfaces. Rep. Prog. Phys. 1995, 58, 1595–1672. [Google Scholar] [CrossRef]
- Henry, C.R. Morphology of supported nanoparticles. Prog. Surf. Sci. 2005, 80, 92–116. [Google Scholar] [CrossRef]
- Nørskov, J.K. Chemisorption on metal surfaces. Rep. Prog. Phys. 1993, 53, 1253–1295. [Google Scholar] [CrossRef]
- Hammer, B.; Nørskov, J.K. Theory of adsorption and surface reactions. In Chemisorption and Reactivity on Supported Clusters and Thin Films; Lambert, R.M., Pacchioni, G., Eds.; Springer: Dordrecht, The Netherlands, 1997; 532p. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Bligaard, T.; Rossmeisl, J.; Christensen, C.H. Towards the computational design of solid catalysts. Nat. Chem. 2009, 1, 37–46. [Google Scholar] [CrossRef]
- Hammer, B.; Nørskov, J.K. Electronic factors determining the reactivity of metal surfaces. Surf. Sci. 1995, 343, 211–220. [Google Scholar] [CrossRef]
- Litovchenko, V.G. Models of the adsorbtion-catalytic centers on transition metals. Condens. Matter. Phys. 1998, 1, 383–388. [Google Scholar] [CrossRef]
- Nørskov, J.K.; Abild-Pedersen, F.; Studt, F.; Bligaard, T. Density functional theory in surface chemistry and catalysis. Proc. Natl. Acad. Sci. USA 2011, 108, 937–943. [Google Scholar] [CrossRef] [PubMed]
- Hammer, B.; Nørskov, J.K. Theoretical Surface science and catalysis—Calculations and concepts. Adv. Catal. 2000, 45, 71–129. [Google Scholar] [CrossRef]
- Hammer, B. Special sites at noble and late transition metal catalysts. Top. Catal. 2006, 37, 3–16. [Google Scholar] [CrossRef]
- İnoğlu, N.; Kitchin, J.R. New solid-state table: Estimating d-band characteristics for transition metal atoms. Mol. Simul. 2010, 36, 633–638. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Waghmare, U.V.; Lee, S.C. An improved d-band model of the catalytic activity of magnetic transition metal surfaces. Sci. Rep. 2016, 6, 35916. [Google Scholar] [CrossRef]
- Nilsson, A.; Pettersson, L.G.M.; Hammer, B.; Bligaard, T.; Christensen, C.H.; Nørskov, J.K. The electronic structure effect in heterogeneous catalysis. Catal. Lett. 2005, 100, 111–114. [Google Scholar] [CrossRef]
- Scheffler, M.; Stampfl, C. Theory of Adsorption on Metal Substrates. In Handbook of Surface Science; Horn, K., Scheffler, M., Eds.; Elsevier Science: Amsterdam, The Netherlands, 2000; Volume 2, p. 1058. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Buongiorna Nardelli, M.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter. 2017, 29, 465901. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the density-gradient expansion for exchange in solids and surfaces. Phys. Rev. Lett. 2008, 100, 13640. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B. 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B. 1976, 13, 5188. [Google Scholar] [CrossRef]
- Methfessel, M.; Paxton, A.T. High-precision sampling for Brillouin-zone integration in metals. Phys. Rev. B. 1989, 40, 3616–3621. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H–Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Gatin, A.K.; Sarvadii, S.Y.; Dokhlikova, N.V.; Kharitonov, V.A.; Ozerin, S.A.; Shub, B.R.; Grishin, M.V. Oxidation of supported nickel nanoparticles at low exposure to O2: Charging effects and selective surface activity. Nanomaterials 2022, 12, 1038. [Google Scholar] [CrossRef]
- Dokhlikova, N.V.; Gatin, A.K.; Sarvadii, S.Y.; Rudenko, E.I.; Grishin, M.V.; Shub, B.R. The adsorption of hydrogen on AunNim and AunCum clusters (n + m = 13): Quantum-chemical simulation. Russ. J. Phys. Chem. B. 2020, 14, 733–741. [Google Scholar] [CrossRef]
- Gatin, A.K.; Dokhlikova, N.V.; Mukhutdinova, R.G.; Ozerin, S.A.; Grishin, M.V. Specific features of the interaction of oxidized platinum nanoparticles with molecular hydrogen and carbon monoxide. Colloid J. 2022, 84, 672–680. [Google Scholar] [CrossRef]
- Hammer, B.; Norskov, J.K. Why gold is the noblest of all the metals. Nature 1995, 376, 238–240. [Google Scholar] [CrossRef]
- Gatin, A.K.; Grishin, M.V.; Dokhlikova, N.V.; Kolchenko, N.N.; Shub, B.R. The Effect of hydrogen adsorption on the electronic structure of gold nanoparticles. Dokl. Phys. Chem. 2016, 470, 125–128. [Google Scholar] [CrossRef]

| H | O | |||||
|---|---|---|---|---|---|---|
| Ni(111) | ||||||
| T | –3.96 | 1.47 | 1.47 | –5.90 | 1.67 | 1.67 |
| B | –4.31 | 1.64 | 1.10 | –6.98 | 1.797 | 1.32 |
| FCC | –4.40 | 1.73 | 1.00 | –7.29 | 1.86 | 1.22 |
| HCP | –4.41 | 1.72 | 0.998 | –7.44 | 1.86 | 1.21 |
| Ni(100) | ||||||
| T | –3.90 | 1.46 | 1.46 | –6.19 | 1.65 | 1.65 |
| B | –4.30 | 1.61 | 1.07 | –7.35 | 1.76 | 1.26 |
| H | –4.38 | 1.84 | 0.665 | –7.96 | 1.94 | 0.874 |
| Ni(110) | ||||||
| T1 | –5.62 | 1.48 | 1.48 | –7.89 | 1.64 | 1.64 |
| Bl1 | –6.01 | 1.63 | 1.12 | –8.82 | 1.76 | 1.27 |
| H1 | –5.67 | 1.95 | 1.44 | –7.87 | 2.17 | 1.69 |
| H2 | –5.98 | 1.80 | 1.22 | –8.78 | 1.97 | 1.47 |
| Bh1 | –5.75 | 1.77 | 1.34 | –8.21 | 1.96 | 1.37 |
| Bh2 | –5.73 | 1.77 | 1.38 | –8.14 | 1.95 | 1.44 |
| Bl2 | –5.98 | 1.71 | 1.21 | –8.72 | 1.93 | 1.50 |
| T2 | –5.81 | 1.499 | 1.499 | –8.42 | 1.73 | 1.73 |
| Ni(211) | ||||||
| Bh1 | –3.75 | 1.65 | 1.07 | –6.88 | 1.85 | 1.35 |
| H1 | –3.56 | 1.79 | 1.12 | –6.04 | 1.92 | 1.28 |
| T1 | –3.36 | 1.49 | 1.49 | –5.69 | 1.69 | 1.69 |
| H2 | –3.99 | 1.71 | 1.02 | –7.67 | 1.83 | 1.26 |
| Bh2 | –3.89 | 1.61 | 1.01 | –7.57 | 1.73 | 1.19 |
| R | –3.80 | 2.02 | 1.04 | –7.22 | 2.25 | 1.46 |
| Bl1 | –3.56 | 1.63 | 1.14 | –6.09 | 1.80 | 1.39 |
| Bl2 | –3.74 | 1.68 | 1.195 | –6.79 | 1.798 | 1.39 |
| Hr | –3.47 | 1.98 | 1.48 | –6.33 | 2.19 | 1.71 |
| T2 | –3.53 | 1.53 | 1.53 | –6.21 | 1.77 | 1.77 |
| H3 | –3.81 | 1.68 | 0.93 | –6.92 | 1.84 | 1.26 |
| Bh3 | –3.77 | 1.62 | 1.02 | –7.16 | 1.77 | 1.25 |
| H4 | –3.79 | 1.75 | 1.07 | –7.00 | 1.85 | 1.22 |
| T3 | –3.38 | 1.49 | 1.49 | –6.11 | 1.63 | 1.63 |
| Br | –3.35 | 1.61 | 1.01 | –6.03 | 2.26 | 1.97 |
| Bl3 | –3.53 | 1.65 | 1.16 | –6.04 | 1.82 | 1.34 |
| Bl4 | –3.74 | 1.67 | 1.21 | –6.79 | 1.795 | 1.31 |
| H | O | |||||
|---|---|---|---|---|---|---|
| Pt(111) | ||||||
| T | –3.67 | 1.55 | 1.55 | –4.30 | 1.83 | 1.83 |
| B | –3.51 | 1.77 | 1.18 | –4.76 | 2.00 | 1.515 |
| FCC | –3.48 | 1.88 | 1.08 | –4.87 | 2.09 | 1.40 |
| HCP | –3.44 | 1.88 | 1.07 | –4.66 | 2.11 | 1.46 |
| Pt(100) | ||||||
| T | –3.49 | 1.55 | 1.55 | –4.52 | 1.80 | 1.80 |
| B | –3.59 | 1.74 | 1.13 | –5.57 | 1.94 | 1.405 |
| H | –3.26 | 2.00 | 0.74 | –4.95 | 2.185 | 1.08 |
| Pt(110) | ||||||
| T1 | –4.08 | 1.56 | 1.56 | –5.56 | 1.79 | 1.79 |
| Bl1 | –4.26 | 1.75 | 1.13 | –6.68 | 1.91 | 1.31 |
| H1 | –4.24 | 2.53 | 1.99 | –5.79 | 2.73 | 2.22 |
| H2 | –4.22 | 2.06 | 1.51 | –6.48 | 2.27 | 1.77 |
| Bh1 | –4.16 | 2.19 | 1.84 | –5.80 | 2.40 | 2.07 |
| Bh2 | –4.17 | 2.18 | 1.85 | –5.76 | 2.40 | 2.08 |
| Bl2 | –4.27 | 2.51 | 2.13 | –6.33 | 2.91 | 2.59 |
| T2 | –3.85 | 1.71 | 1.71 | –5.25 | 2.27 | 2.27 |
| Pt(211) | ||||||
| Bh1 | –3.80 | 1.75 | 0.99 | –5.41 | 2.03 | 1.42 |
| H1 | –3.73 | 1.96 | 1.19 | –5.10 | 2.10 | 1.40790 |
| T1 | –3.81 | 1.54 | 1.54 | –4.89 | 1.82 | 1.82029 |
| H2 | –3.89 | 1.84 | 0.998 | –6.49 | 2.02 | 1.32 |
| Bh2 | –4.08 | 1.72 | 0.94 | –6.92 | 1.89 | 1.21 |
| R | –3.92 | 2.205 | 1.03 | –5.18 | 2.47 | 1.58 |
| Bl1 | –3.75 | 1.79 | 1.27 | –5.18 | 1.97 | 1.48 |
| Bl2 | –3.83 | 1.80 | 1.30 | –5.82 | 1.95 | 1.46 |
| Hr | –3.75 | 2.14 | 1.56 | –5.34 | 2.43 | 1.96 |
| T2 | –3.76 | 1.60 | 1.60 | –5.31 | 1.90 | 1.90 |
| H3 | –3.76 | 1.83 | 0.98 | –5.85 | 2.00 | 1.28 |
| Bh3 | –3.80 | 1.74 | 0.98 | –6.21 | 1.96 | 1.34 |
| H4 | –3.80 | 1.96 | 1.26 | –5.80 | 2.10 | 1.37 |
| T3 | –3.94 | 1.56 | 1.56 | –5.51 | 1.77 | 1.77 |
| Br | –3.75 | 2.20 | 1.79 | –5.42 | 2.47 | 2.08 |
| Bl3 | –3.75 | 1.79 | 1.26 | –5.18 | 1.97 | 1.55 |
| Bl4 | –3.83 | 1.77 | 1.29 | –5.18 | 1.95 | 1.45 |
| H | O | |||||
|---|---|---|---|---|---|---|
| Au(111) | ||||||
| T | –2.12 | 1.58 | 1.58 | –3.47 | 1.98 | 1.98 |
| B | –2.55 | 1.78 | 1.28 | –4.36 | 2.00 | 1.28 |
| FCC | –2.57 | 1.88 | 1.12 | –4.62 | 2.10 | 1.15 |
| HCP | –2.63 | 1.89 | 1.01 | –4.53 | 2.11 | 1.19 |
| Au(100) | ||||||
| T | –3.00 | 1.596 | 1.596 | –3.85 | 1.90 | 1.90 |
| B | –3.21 | 1.77 | 1.15 | –4.47 | 2.04 | 1.51 |
| H | –3.28 | 2.01 | 0.65 | –4.32 | 2.29 | 1.24 |
| Au(110) | ||||||
| T1 | –4.6 | 1.60 | 1.60 | –7.19 | 1.88 | 1.88 |
| Bl1 | –4.78 | 1.79 | 1.20 | –8.69 | 1.99 | 1.30 |
| H1 | –4.56 | 2.22 | 1.51 | –7.98 | 2.39 | 1.81 |
| H2 | –4.71 | 2.02 | 1.37 | –5.76 | 2.32 | 1.75 |
| Bh1 | –4.60 | 2.05 | 1.54 | –7.97 | 2.26 | 1.65 |
| Bh2 | –4.59 | 2.00 | 1.57 | –8.01 | 2.21 | 1.67 |
| Bl2 | –4.11 | 1.86 | 1.31 | –5.29 | 2.43 | 2.03 |
| T2 | –3.89 | 1.63 | 1.63 | –4.80 | 2.04 | 2.04 |
| Au(211) | ||||||
| 1Bh1 | –3.02 | 1.81 | 1.11 | –4.61 | 2.33 | 1.84 |
| 2H1 | –3.11 | 2.18 | 1.46 | –4.19 | 2.53 | 1.95 |
| 3T1 | –3.10 | 1.60 | 1.60 | –4.07 | 1.96 | 1.96 |
| 4H2 | –3.37 | 1.90 | 1.04 | –5.07 | 2.197 | 1.54 |
| 5Bh2 | –3.53 | 1.74 | 0.997 | –5.10 | 2.01 | 1.41 |
| 6R | –3.27 | 2.28 | 1.17 | –5.21 | 2.59 | 1.70 |
| 7Bl1 | –3.11 | 1.97 | 1.46 | –4.18 | 2.32 | 1.81 |
| 8Bl2 | –3.19 | 1.88 | 1.298 | –4.53 | 2.16 | 1.65 |
| 9Hr | –3.15 | 2.27 | 1.75 | –4.45 | 2.59 | 2.06 |
| 10T2 | –3.16 | 1.66 | 1.66 | –4.52 | 2.10 | 2.10 |
| 11H3 | –3.31 | 1.936 | 1.07 | –4.51 | 2.31 | 1.66 |
| 12Bh3 | –3.31 | 1.77 | 1.04 | –4.73 | 2.13 | 1.58 |
| 13H4 | –3.19 | 2.06 | 1.27 | –4.42 | 2.34 | 1.66 |
| 14T3 | –3.22 | 1.59 | 1.59 | –4.18 | 1.87 | 1.87 |
| 15Br | –3.15 | 2.30 | 1.95 | –4.22 | 2.63 | 2.34 |
| 16Bl3 | –3.12 | 1.98 | 1.45 | –4.20 | 2.32 | 1.83 |
| 17Bl4 | –3.18 | 1.94 | 1.35 | –4.47 | 2.21 | 1.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dokhlikova, N.V.; Gatin, A.K.; Sarvadii, S.Y.; Tastaibek, D.; Slutskii, V.G.; Grishin, M.V. Surface Structure Effects on H and O Adsorption on Gold, Nickel and Platinum Nanoparticles. Materials 2025, 18, 631. https://doi.org/10.3390/ma18030631
Dokhlikova NV, Gatin AK, Sarvadii SY, Tastaibek D, Slutskii VG, Grishin MV. Surface Structure Effects on H and O Adsorption on Gold, Nickel and Platinum Nanoparticles. Materials. 2025; 18(3):631. https://doi.org/10.3390/ma18030631
Chicago/Turabian StyleDokhlikova, Nadezhda V., Andrey K. Gatin, Sergey Y. Sarvadii, Dinara Tastaibek, Vladislav G. Slutskii, and Maxim V. Grishin. 2025. "Surface Structure Effects on H and O Adsorption on Gold, Nickel and Platinum Nanoparticles" Materials 18, no. 3: 631. https://doi.org/10.3390/ma18030631
APA StyleDokhlikova, N. V., Gatin, A. K., Sarvadii, S. Y., Tastaibek, D., Slutskii, V. G., & Grishin, M. V. (2025). Surface Structure Effects on H and O Adsorption on Gold, Nickel and Platinum Nanoparticles. Materials, 18(3), 631. https://doi.org/10.3390/ma18030631








