Effects of Hypergravity on Phase Evolution, Synthesis, Structures, and Properties of Materials: A Review
Abstract
1. Introduction
2. Principles and Techniques of Hypergravity
2.1. Hypergravity Condition
2.2. Enhanced Interphase Interaction and Mass Transfer Under Hypergravity Conditions
2.3. Hypergravity Techniques
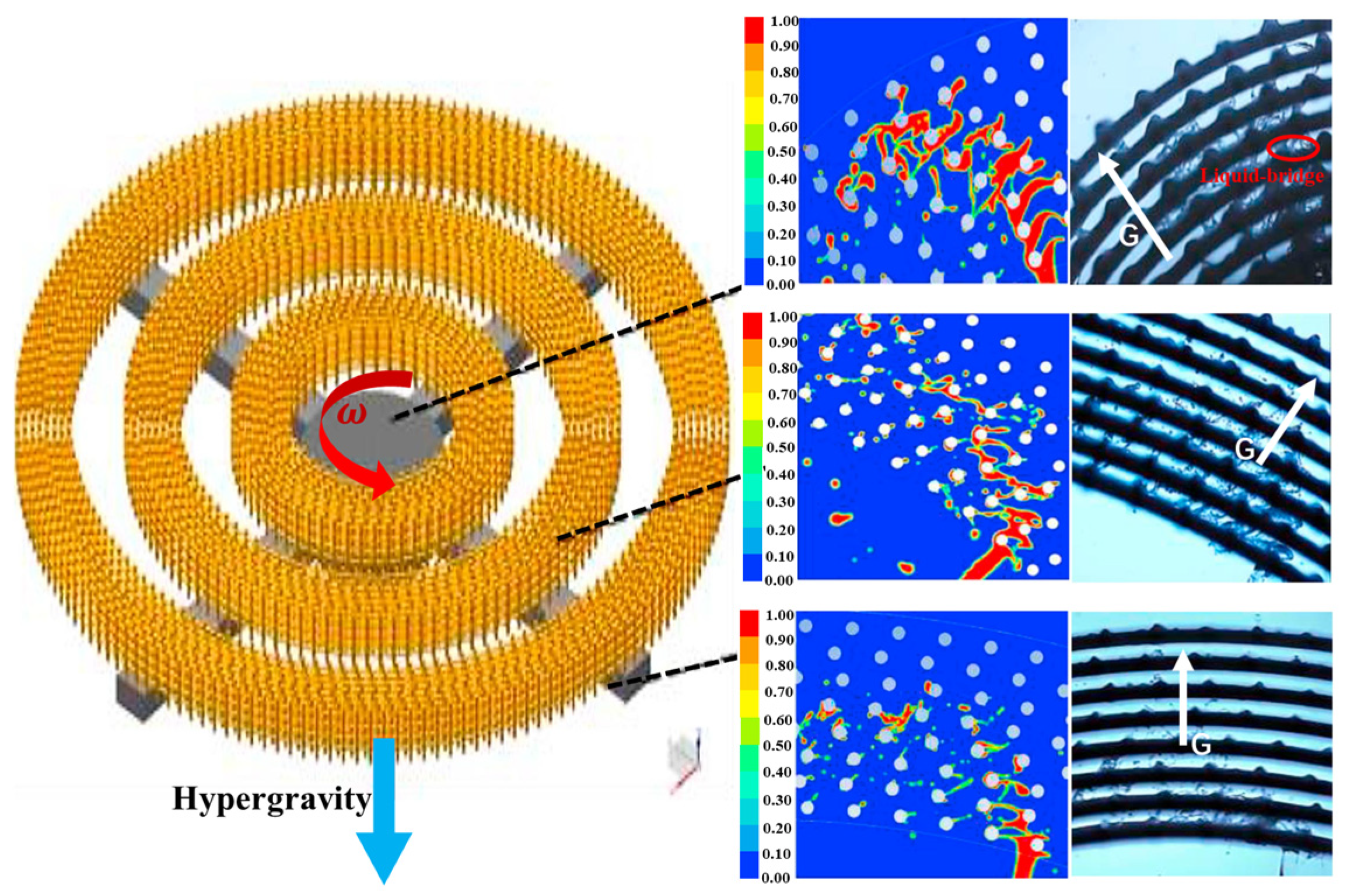
2.3.1. Rotating Packed Bed Techniques
2.3.2. Centrifuge Techniques
3. Liquid-Phase Synthesis and Separation of Materials Under Hypergravity
3.1. The Fluid Dynamics Under Hypergravity
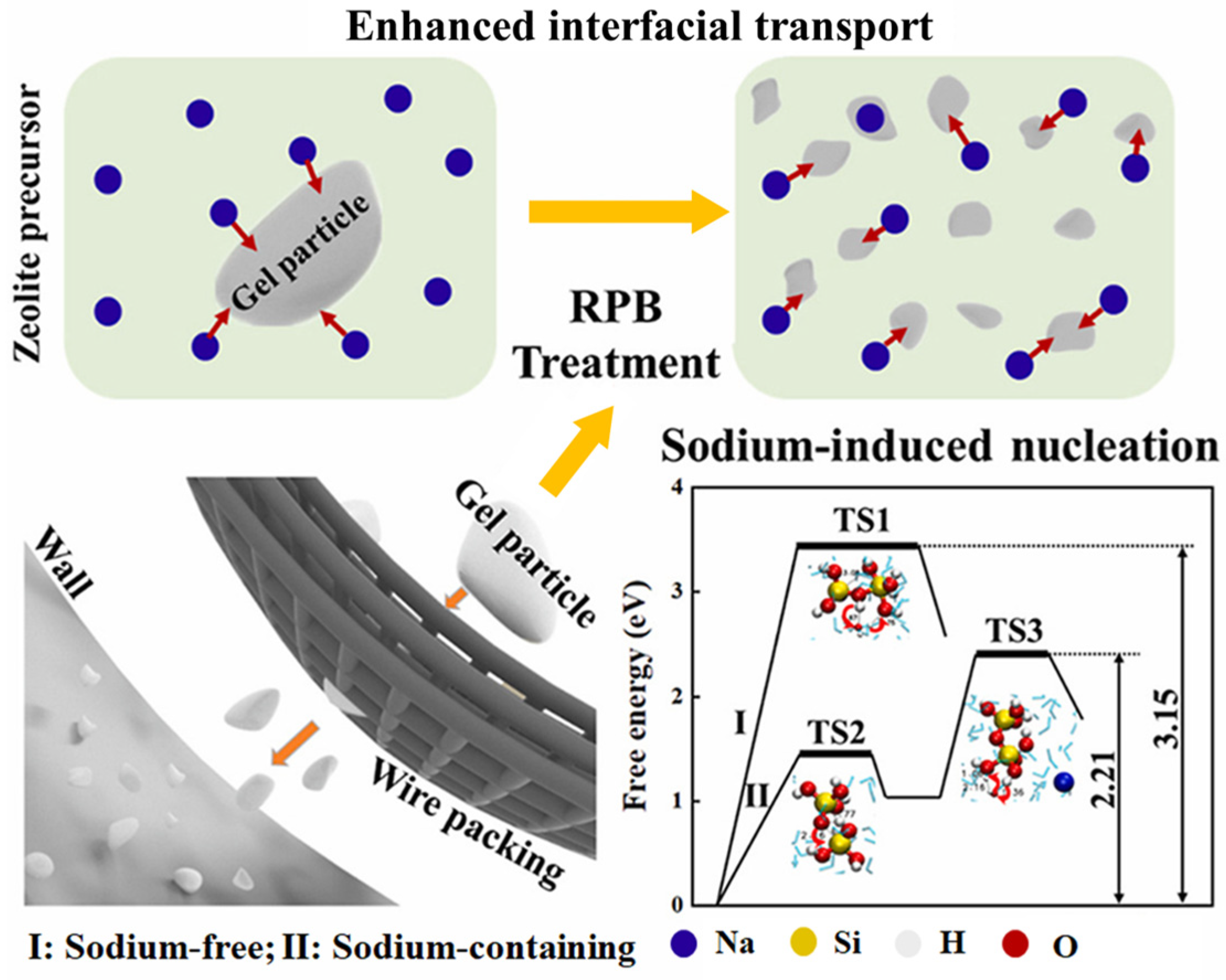
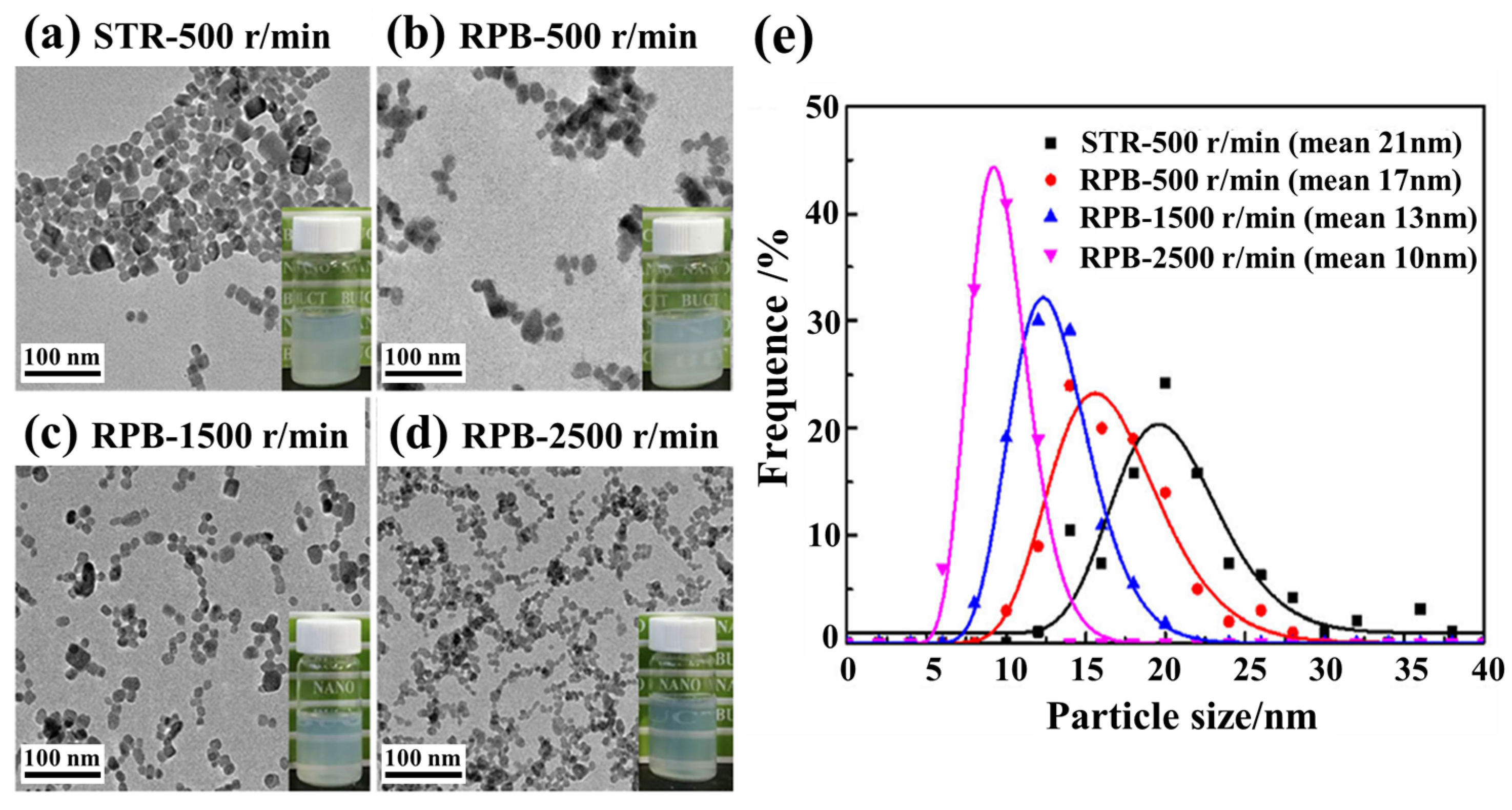
3.2. The Liquid-Phase Synthesis of Materials Under Hypergravity
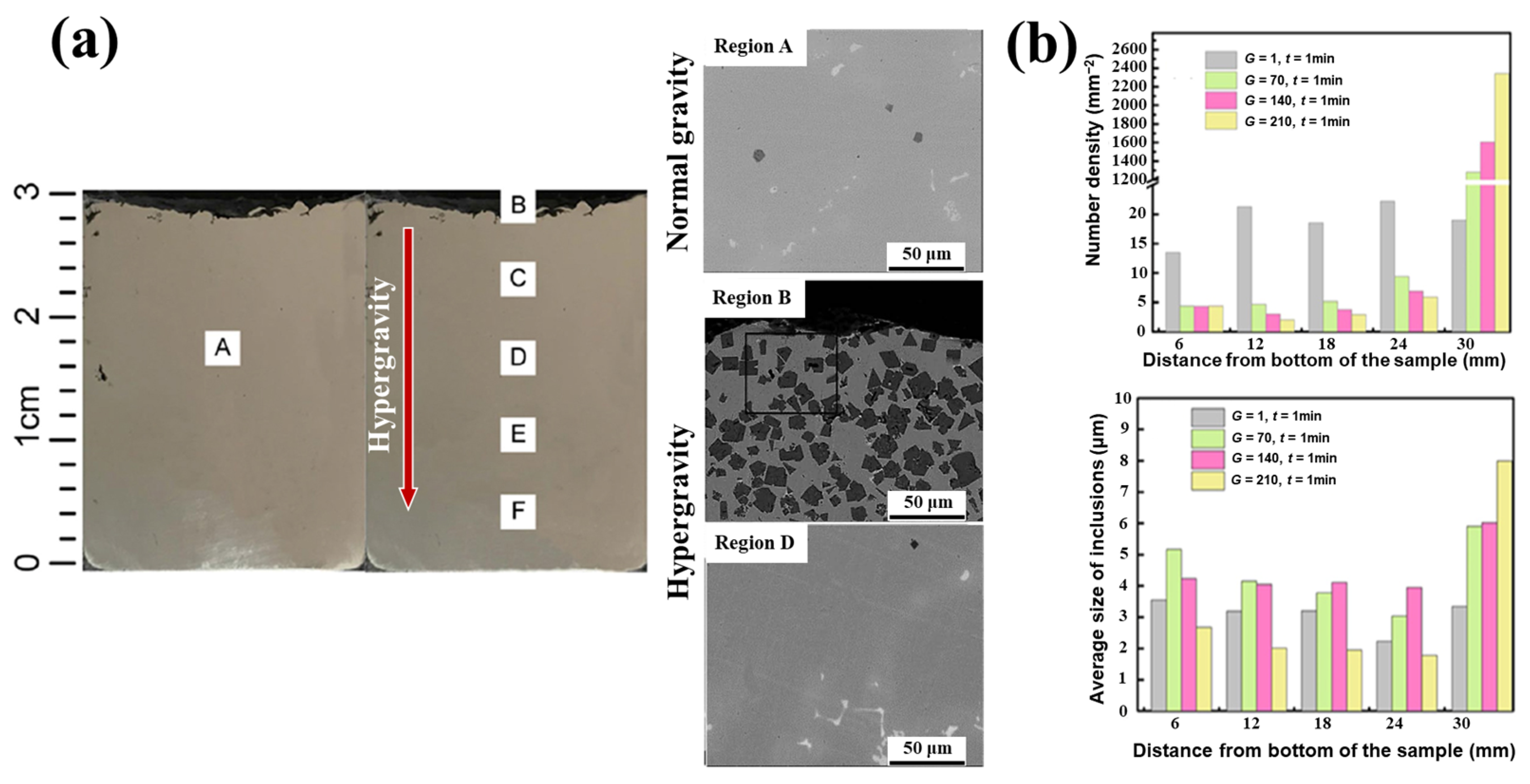
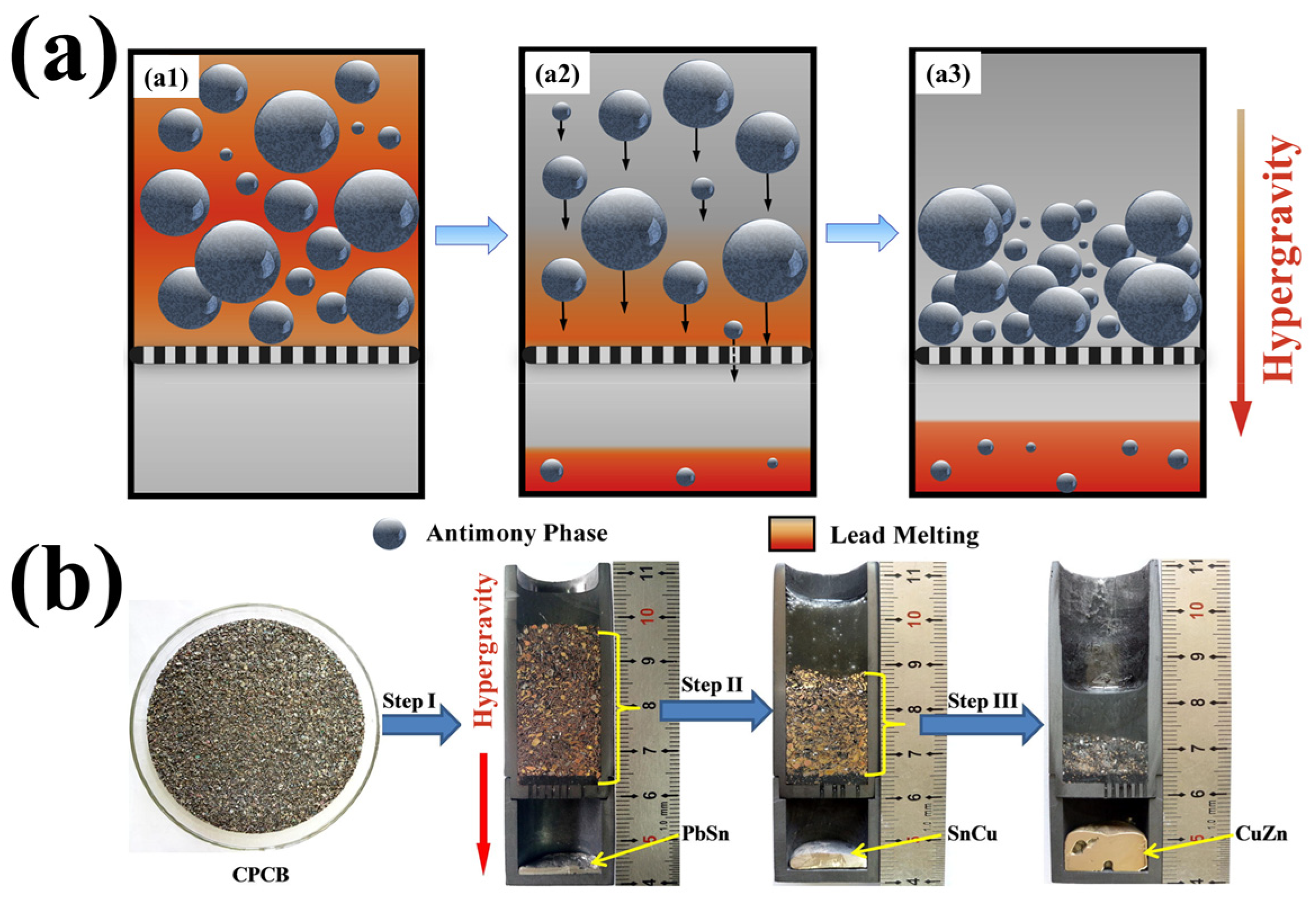
3.3. The Separation of Materials Under Hypergravity
4. Metallurgy of Alloys Under Hypergravity
4.1. Convection and Segregation Under Hypergravity
4.2. Grain Refinement of Solidification
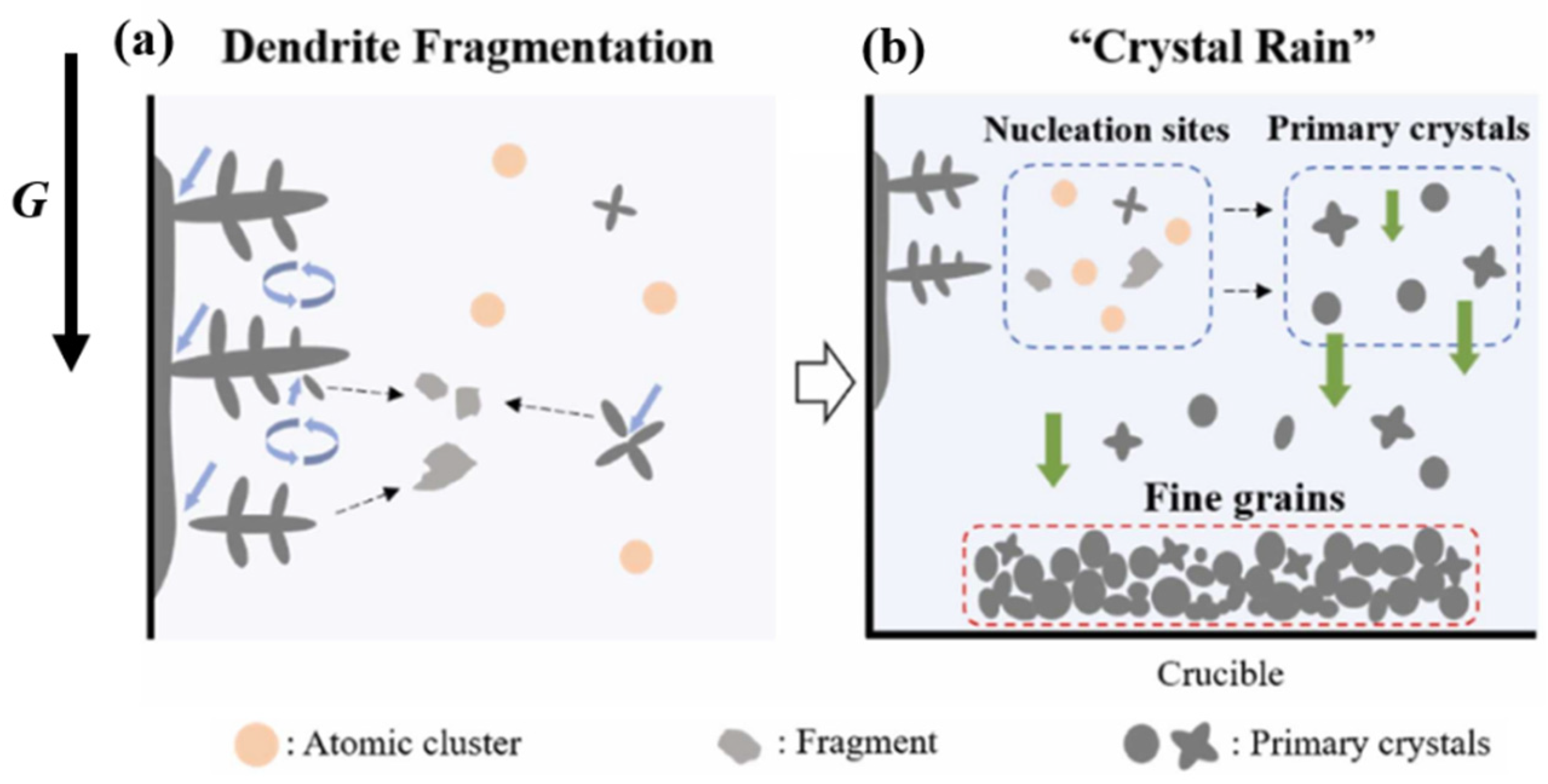
4.3. The Dendrite Structure of Alloy Under Hypergravity Conditions
4.4. The Gradient Structure Under Hypergravity Conditions
5. Structural and Properties of Alloy Materials Under Hypergravity
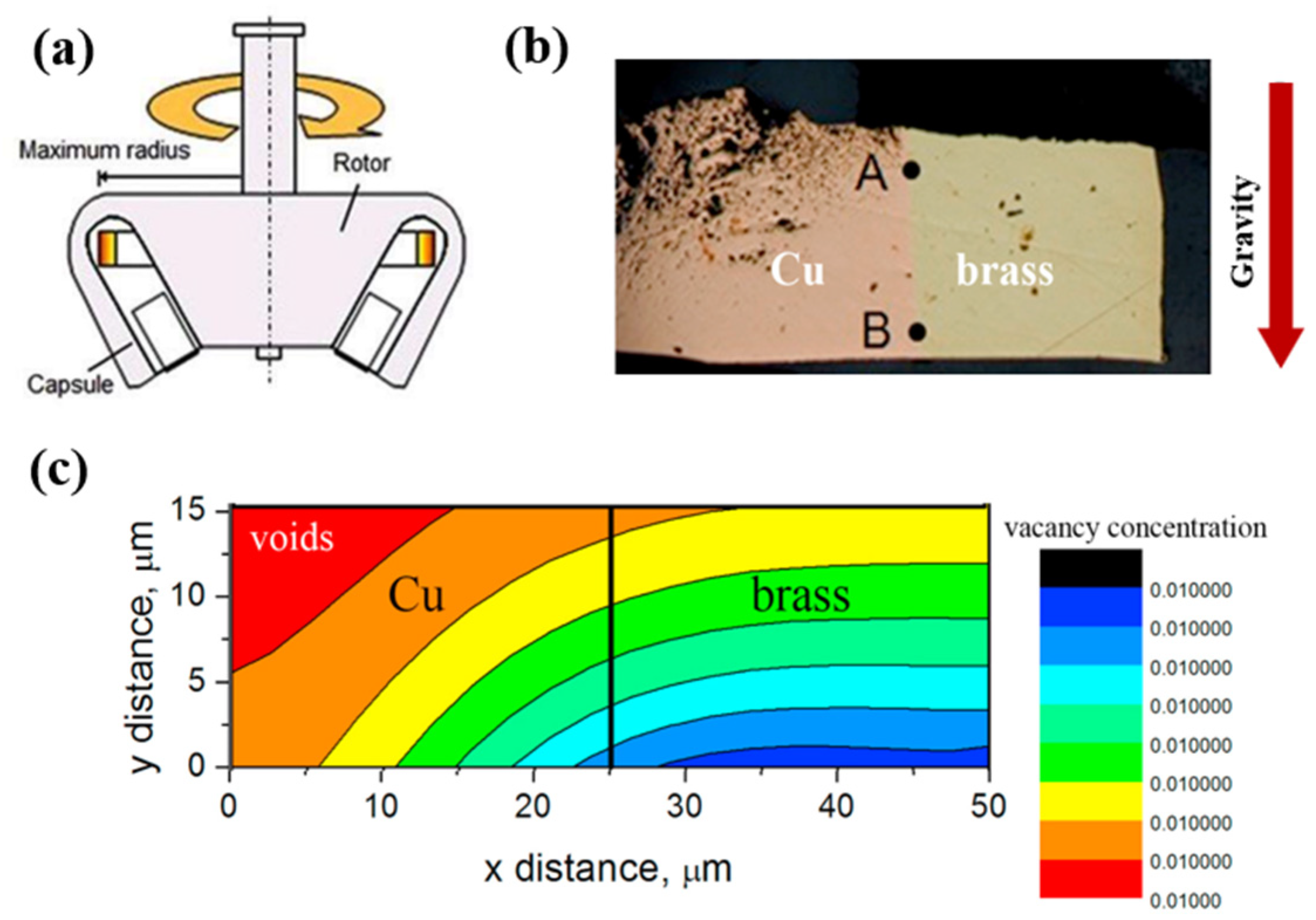
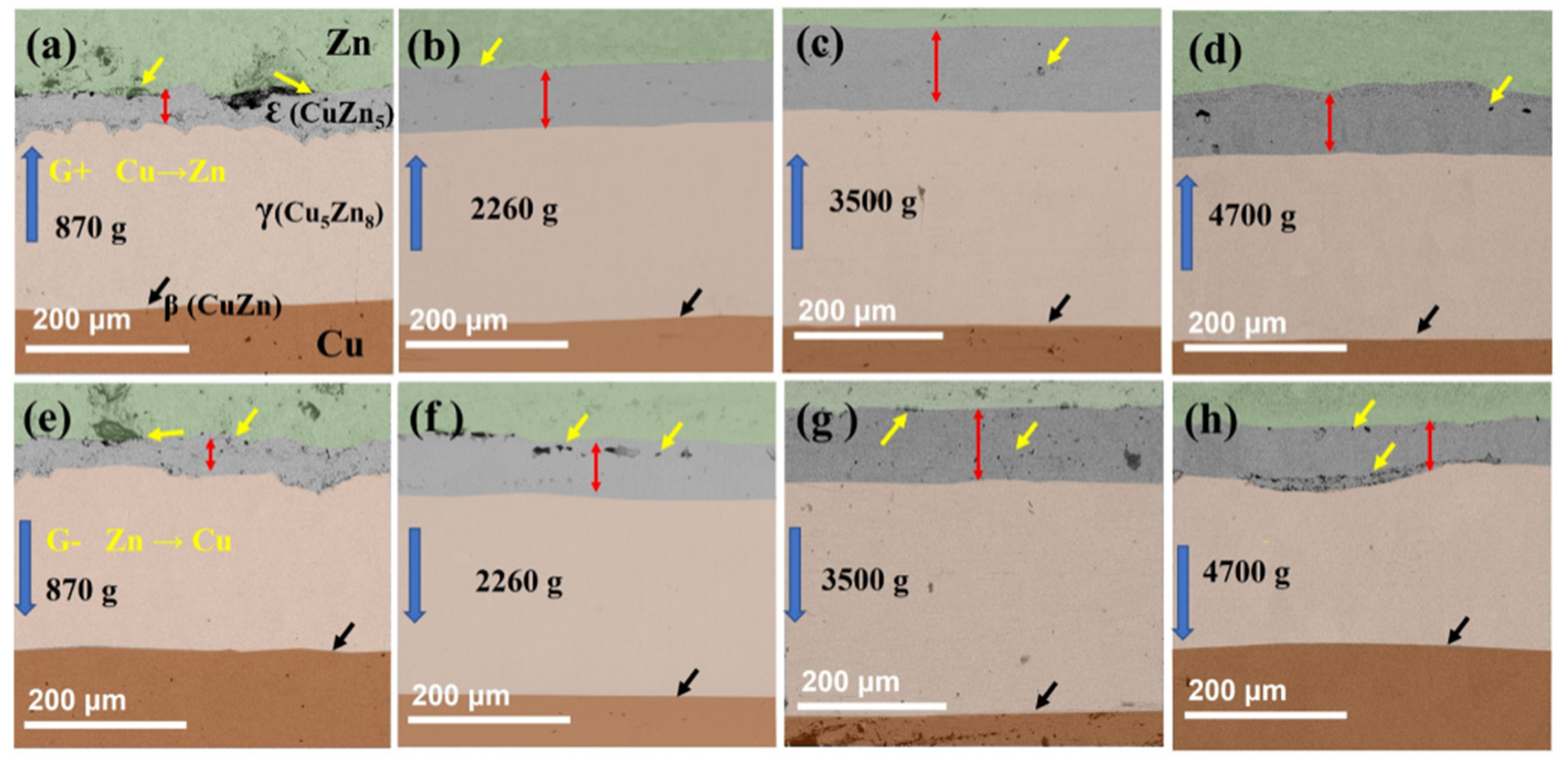
5.1. Solid-State Diffusion Under Hypergravity Conditions
5.2. Structural Evolution of Alloy Materials Under Hypergravity Conditions
5.3. The Properties of Alloy Materials Under Hypergravity Conditions
6. Conclusions and Perspective
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CFD | Computational fluid dynamics |
| DFT | Density functional theory |
| EDS | Energy dispersive spectrometer |
| EBSD | Electron back scatter diffraction |
| GND | Geometrically necessary dislocation |
| HRTEM | High-resolution transmission electron microscope |
| IMC | Intermetallic compound |
| IPF | Inverse pole figure |
| PDAS | Primary dendritic arm spacing |
| RPB | Rotating packed bed |
| SEM | Scanning electron microscope |
| STR | Stirred tank reactor |
| TEM | Transmission electron microscope |
| WPCB | Waste printed circuit boards |
References
- Chen, Y.; Tang, Y.; Ling, D.; Wang, Y. Hypergravity experiments on multiphase media evolution. Sci. China Technol. Sci. 2022, 65, 2791–2808. [Google Scholar] [CrossRef]
- Yang, Y.; Song, B.; Song, G.; Cai, Z. Effect of Super Gravity on the Solidification Structure and C Segregation of High-Carbon Steel. In Proceedings of the 8th International Symposium on High-Temperature; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Takaki, T.; Kashima, H. Numerical investigations of stress in dendrites caused by gravity. J. Cryst.Growth. 2011, 337, 97–101. [Google Scholar] [CrossRef]
- Jiang, H.; Zhu, X.; Mathai, V.; Verzicco, R.; Lohse, D.; Sun, C. Controlling heat transport and flow structures in thermal tur-bulence using ratchet surfaces. Phys. Rev. Lett. 2018, 120, 044501. [Google Scholar] [CrossRef] [PubMed]
- Jiang, H.; Zhu, X.; Wang, D.; Huisman, S.G.; Sun, C. Supergravitational turbulent thermal convection. Sci. Adv. 2020, 6, eabb8676. [Google Scholar] [CrossRef]
- van der Laan, G.P.; Beenackers, A.A.C.M.; Krishna, R. Multicomponent Reaction Engineering Model for Fe-Catalyzed Fischer–Tropsch Synthesis in Commercial Scale Slurry Bubble Column Reactors. Chem. Eng. Sci. 1999, 54, 5013–5019. [Google Scholar] [CrossRef]
- Li, Y.-B.; Wen, Z.-N.; Xu, H.-Z.; Chu, G.-W.; Zhang, L.-L.; Chen, J.-F. Mass transfer modeling for viscous fluids in a disk-distributor rotating packed bed. Chem. Eng. J. 2023, 453, 139604. [Google Scholar] [CrossRef]
- Gao, J.-T.; Guo, L.; Zhong, Y.-W.; Ren, H.-R.; Guo, Z.-C. Removal of phosphorus-rich phase from high-phosphorous iron ore by melt separation at 1573 K in a super-gravity field. Int. J. Miner. Met. Mater. 2016, 23, 743–750. [Google Scholar] [CrossRef]
- Lan, X.; Gao, J.; Li, Y.; Guo, Z. A green method of respectively recovering rare earths (Ce, La, Pr, Nd) from rare-earth tailings under super-gravity. J. Hazard. Mater. 2019, 367, 473–481. [Google Scholar] [CrossRef]
- Aminzadeh, A.; Dimitrova, M.; Meiabadi, M.S.; Karganroudi, S.S.; Taheri, H.; Ibrahim, H.; Wen, Y. Non-Contact Inspection Methods for Wind Turbine Blade Maintenance: Techno–Economic Review of Techniques for Integration with Industry 4.0. J. Nondestruct. Evaluation 2023, 42, 54. [Google Scholar] [CrossRef]
- Xie, Y.; Zhao, J.; Fu, H.; Wei, H. Dependence of microstructural evolution on the geometric structure for serviced DZ125 turbine blades. Front. Mater. 2023, 10, 1165971. [Google Scholar] [CrossRef]
- Ling, D.; Shi, C.; Zheng, J.; Zhao, Y.; Chen, Y. Non-inertial effects on matter motion in centrifugal model tests. Chin. J. Geotech. Eng. 2021, 43, 226. [Google Scholar]
- Patuelli, C.; Tognato, R. Effect of High Gravity on the Solid-Liquid Interfacial Free Energy. In Processing by Centrifugation; Regel, L.L., Wilcox, W.R., Eds.; Springer: Boston, MA, USA, 2001; pp. 361–366. [Google Scholar]
- Wang, M.; Wang, Z.; Gong, X.; Guo, Z. The intensification technologies to water electrolysis for hydrogen production—A review. Renew. Sustain. Energy Rev. 2014, 29, 573–588. [Google Scholar] [CrossRef]
- Liu, T.; Guo, Z.-C.; Wang, Z.; Wang, M.-Y. Effects of gravity on the electrodeposition and characterization of nickel foils. Int. J. Miner. Met. Mater. 2011, 18, 59–65. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Z.; Guo, Z. Deposit structure and kinetic behavior of metal electrodeposition under enhanced gravity-induced convection. J. Electroanal. Chem. 2015, 744, 25. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, T.; Liu, Z.; Wang, S.; Gao, Y.; Wu, M. Mass Transfer in a Rotating Packed Bed: A Critical Review. Chem. Eng. Process. 2019, 139, 78. [Google Scholar] [CrossRef]
- Wenzel, D.; Górak, A. Review and analysis of micromixing in rotating packed beds. Chem. Eng. J. 2018, 345, 492–506. [Google Scholar] [CrossRef]
- Neumann, K.; Gladyszewski, K.; Groß, K.; Qammar, H.; Wenzel, D.; Górak, A.; Skiborowski, M. A guide on the industrial application of rotating packed beds. Chem. Eng. Res. Des. 2018, 134, 443–462. [Google Scholar] [CrossRef]
- Ramshaw, C.; Mallinson, R.H. Mass Transfer Process. U.S. Patent 4283255A, 11 August 1981. [Google Scholar]
- Tung, H.-H.; Mah, R.S. Modeling Liquid Mass Transfer In Higee Separation Process. Chem. Eng. Commun. 1985, 39, 147–153. [Google Scholar] [CrossRef]
- Wang, G.; Xu, Z.; Ji, J. Progress on Higee distillation—Introduction to a new device and its industrial applications. Chem. Eng. Res. Des. 2011, 89, 1434–1442. [Google Scholar] [CrossRef]
- Chen, W.-H.; Syu, Y.-J. Hydrogen production from water gas shift reaction in a high gravity (Higee) environment using a rotating packed bed. Int. J. Hydrogen Energy 2010, 35, 10179–10189. [Google Scholar] [CrossRef]
- Jiang, L.; Chu, G.-W.; Liu, Y.-Z.; Liu, W.; Wen, L.-X.; Luo, Y. Preparation of cordierite monolithic catalyst for α-methylstyrene hydrogenation in a rotating packed bed reactor. Chem. Eng. Process. Process. Intensif. 2020, 150, 107882. [Google Scholar] [CrossRef]
- Jiao, W.; Yang, P.; Qi, G.; Liu, Y. Selective absorption of H2S with High CO2 concentration in mixture in a rotating packed bed. Chem. Eng. Process. Process. Intensif. 2018, 129, 142–147. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, S.; Gao, Y.; Sun, B.; Luo, Y.; Zou, H.; Chu, G.; Chen, J. Absorption of SO2 with calcium-based solution in a rotating packed bed. Sep. Purif. Technol. 2019, 214, 148–155. [Google Scholar] [CrossRef]
- Chu, G.-W.; Fei, J.; Cai, Y.; Liu, Y.-Z.; Gao, Y.; Luo, Y.; Chen, J.-F. Removal of SO2 with Sodium Sulfite Solution in a Rotating Packed Bed. Ind. Eng. Chem. Res. 2018, 57, 2329–2335. [Google Scholar] [CrossRef]
- Freguia, S.; Rochelle, G.T. Modeling of CO2 capture by aqueous monoethanolamine. AIChE J. 2003, 49, 1676–1686. [Google Scholar] [CrossRef]
- Wang, B.-J.; Tang, Z.-Y.; Wang, D.; Luo, Y.; Liu, Z.-H.; Zou, H.-K.; Chu, G.-W. Process intensification of reactive extraction for hydrogen peroxide production in a rotating packed bed reactor. Chem. Eng. J. 2022, 428, 132066. [Google Scholar] [CrossRef]
- Zhan, Y.-Y.; Wan, Y.-F.; Su, M.-J.; Luo, Y.; Chu, G.-W.; Zhang, L.-L.; Chen, J.-F. Spent Caustic Regeneration in a Rotating Packed Bed: Reaction and Separation Process Intensification. Ind. Eng. Chem. Res. 2019, 58, 14588–14594. [Google Scholar] [CrossRef]
- Luo, Y.; Chu, G.-W.; Zou, H.-K.; Xiang, Y.; Shao, L.; Chen, J.-F. Characteristics of a two-stage counter-current rotating packed bed for continuous distillation. Chem. Eng. Process. Process. Intensif. 2012, 52, 55–62. [Google Scholar] [CrossRef]
- Wang, D.; Liu, Y.-Z.; Wang, B.-J.; Chu, G.-W.; Sun, B.-C.; Luo, Y. Process Intensification of Quasi-Homogeneous Catalytic Hydrogenation in a Rotating Packed Bed Reactor. Ind. Eng. Chem. Res. 2020, 59, 1383–1392. [Google Scholar] [CrossRef]
- Wu, K.; Wu, H.; Dai, T.; Liu, X.; Chen, J.-F.; Le, Y. Controlling Nucleation and Fabricating Nanoparticulate Formulation of Sorafenib Using a High-Gravity Rotating Packed Bed. Ind. Eng. Chem. Res. 2018, 57, 1903–1911. [Google Scholar] [CrossRef]
- Tang, Y.-Y.; Su, M.-J.; Chu, G.-W.; Luo, Y.; Wang, Y.-Y.; Zhang, L.-L.; Chen, J.-F. Impact phenomena of liquid droplet passing through stainless steel wire mesh units. Chem. Eng. Sci. 2019, 198, 144–154. [Google Scholar] [CrossRef]
- Wen, Z.-N.; Li, Y.-B.; Liu, W.; Luo, Y.; Zhang, L.-L.; Chu, G.-W. Flow behavior in a rotating packed bed reactor with single-layer mesh: Effect of fiber cross-sectional shape. Chem. Eng. Sci. 2022, 248, 117147. [Google Scholar] [CrossRef]
- Liao, H.-L.; Ouyang, Y.; Zhang, J.-P.; Zou, H.-K.; Chu, G.-W.; Luo, Y. Numerical Studies of a Liquid Droplet Impacting on Single-Layer Hydrophilic and Hydrophobic Wire Meshes. Ind. Eng. Chem. Res. 2022, 61, 7154–7162. [Google Scholar] [CrossRef]
- Wang, Y.; Li, Y.-B.; Su, M.-J.; Chu, G.-W.; Sun, B.-C.; Luo, Y. Liquid droplet dispersion in a rotating packed bed: Experimental and numerical studies. Chem. Eng. Sci. 2021, 240, 116675. [Google Scholar] [CrossRef]
- Chen, Y.-S.; Liu, H.-S. Absorption of VOCs in a Rotating Packed Bed. Ind. Eng. Chem. Res. 2002, 41, 1583–1588. [Google Scholar] [CrossRef]
- Meng, L.; Wang, Z.; Zhong, Y.; Guo, L.; Gao, J.; Chen, K.; Cheng, H.; Guo, Z. Supergravity separation for recovering metals from waste printed circuit boards. Chem. Eng. J. 2017, 326, 540–550. [Google Scholar] [CrossRef]
- Chen, Y.; Han, C.; Ling, D.; Kong, L.; Zhou, Y. Development of geotechnical centrifuge ZJU400 and performance assessment of its shaking table system. Chin. J. Geotech. 2011, 33, 1887–1894. [Google Scholar]
- Ng, C.W.; Li, X.; A Van Laak, P.; Hou, D.Y. Centrifuge modeling of loose fill embankment subjected to uni-axial and bi-axial earthquakes. Soil. Dyn. Earthq. Eng. 2004, 24, 305–318. [Google Scholar] [CrossRef]
- Connolly, J.A.D.; Schmidt, M.W.; Solferino, G.; Bagdassarov, N. Permeability of asthenospheric mantle and melt extraction rates at mid-ocean ridges. Nature 2009, 462, 209–212. [Google Scholar] [CrossRef]
- Van Loon, J.J. Centrifuges for Microgravity Simulation. The Reduced Gravity Paradigm. Front. Astron. Space Sci. 2016, 3, 21. [Google Scholar] [CrossRef]
- Crowley, C.J.; Pughe-Sanford, J.L.; Toler, W.; Krygier, M.C.; Grigoriev, R.O.; Schatz, M.F. Turbulence tracks recurrent solutions. Proc. Natl. Acad. Sci. USA 2022, 119, 2120665119. [Google Scholar] [CrossRef] [PubMed]
- Yeh, H. Geophysical fluid dynamics in the hypergravity field. Acta Mech. Sin. 2024, 40, 723296. [Google Scholar] [CrossRef]
- Nagel, T. Centrifugal hypergravitational scaling experiments of fluid convection with evaluation and correction of Coriolis effect. Phys. Fluids 2023, 35, 0149123. [Google Scholar] [CrossRef]
- Carruthers, J.R.; Nassau, K. Nonmixing Cells due to Crucible Rotation during Czochralski Crystal Growth. J. Appl. Phys. 1968, 39, 5205–5214. [Google Scholar] [CrossRef]
- Müller, G.; Schmidt, E.; Kyr, P. Investigation of convection in melts and crystal growth under large inertial accelerations. J. Cryst. Growth 1980, 49, 387–395. [Google Scholar] [CrossRef]
- Hurle, D. Interface stability during the solidification of a stirred binary-alloy melt. J. Cryst. Growth 1969, 5, 162–166. [Google Scholar] [CrossRef]
- Feigelson, R.S. Crystal growth History: Theory and melt growth processes. J. Cryst. Growth 2022, 594, 126800. [Google Scholar] [CrossRef]
- Zhang, G. Warming-induced contraction of tropical convection delays and reduces tropical cyclone formation. Nat. Commun. 2023, 14, 6274. [Google Scholar] [CrossRef]
- Hartmann, D.L.; Moy, L.A.; Fu, Q. Tropical Convection and the Energy Balance at the Top of the Atmosphere. J. Climate. 2001, 14, 4495. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Z.; Gong, X.; Guo, Z. Progress toward Electrochemistry Intensified by using Supergravity Fields. Chem. Electro. Chem. 2015, 2, 1879–1887. [Google Scholar] [CrossRef]
- Gao, Y.; Qiao, F.; You, J.; Ren, Z.; Li, N.; Zhang, K.; Shen, C.; Jin, T.; Xie, K. Effect of the supergravity on the formation and cycle life of non-aqueous lithium metal batteries. Nat. Commun. 2022, 13, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Burns, J.; Ramshaw, C. Process intensification: Visual study of liquid maldistribution in rotating packed beds. Chem. Eng. Sci. 1996, 51, 1347–1352. [Google Scholar] [CrossRef]
- Wu, W.; Luo, Y.; Chu, G.-W.; Su, M.-J.; Cai, Y.; Zou, H.-K.; Chen, J.-F. Liquid flow behavior in a multiliquid-inlet rotating packed bed reactor with three-dimensional printed packing. Chem. Eng. J. 2020, 386, 121537. [Google Scholar] [CrossRef]
- Sang, L.; Luo, Y.; Chu, G.-W.; Zhang, J.-P.; Xiang, Y.; Chen, J.-F. Liquid flow pattern transition, droplet diameter and size dis-tribution in the cavity zone of a rotating packed bed: A visual study. Chem. Eng. Sci. 2017, 158, 429. [Google Scholar] [CrossRef]
- Anlar, O.; Kisli, M.; Tombul, T.; Ozbek, H. A new impinging stream–rotating packed bed reactor for improvement of mi-cromixing iodide and iodate. J. Neurosci. 2003, 113, 483. [Google Scholar]
- Zhao, H.; Shao, L.; Chen, J.F. High-gravity process intensification technology and application. Chem. Eng. J. 2010, 156, 588–593. [Google Scholar] [CrossRef]
- Chen, J.-F.; Wang, Y.-H.; Guo, F.; Wang, X.-M.; Zheng, C. Synthesis of Nanoparticles with Novel Technology: High-Gravity Reactive Precipitation. Ind. Eng. Chem. Res. 2000, 39, 948–954. [Google Scholar] [CrossRef]
- Sun, Q.; Chen, B.; Wu, X.; Wang, M.; Zhang, C.; Zeng, X.-F.; Wang, J.-X.; Chen, J.-F. Preparation of Transparent Suspension of Lamellar Magnesium Hydroxide Nanocrystals Using a High-Gravity Reactive Precipitation Combined with Surface Modifica-tion. Ind. Eng. Chem. Res. 2015, 54, 666. [Google Scholar] [CrossRef]
- Chen, J.; Li, Y.; Wang, Y.; Yun, J.; Cao, D. Preparation and characterization of zinc sulfide nanoparticles under high-gravity environment. Mater. Res. Bull. 2004, 39, 185–194. [Google Scholar] [CrossRef]
- Qi, T.; Shi, J.; Li, Y.; Chu, G.-W.; Zhang, L.-L.; Sun, B.-C. Interfacial nanoarchitectonics for accelerated growth of zeolite via enlarging gel-liquid interfacial area using rotating packed bed. Microporous Mesoporous Mater. 2022, 342, 112112. [Google Scholar] [CrossRef]
- Fang, L.; Sun, Q.; Duan, Y.-H.; Zhai, J.; Wang, D.; Wang, J.-X. Preparation of transparent BaSO4 nanodispersions by high-gravity reactive precipitation combined with surface modification for transparent X-ray shielding nanocomposite films. Front. Chem. Sci. Eng. 2021, 15, 902–912. [Google Scholar] [CrossRef]
- Song, Z.-M.; Zhang, H. Present Situation of Producing and Quality for Bearing Steel in China. J. Iron Steel Res. 2000, 12, 59–63. [Google Scholar] [CrossRef]
- Reddy, A.; Zitoun, E. Tensile properties and fracture behavior of 6061/Al2O3 metal matrix composites fabricated by low pressure die casting process. J. Mater. Sci. 2011, 6, 147. [Google Scholar]
- Guo, J.; Jiao, W.; Qi, G.; Yuan, Z.; Liu, Y. Applications of high-gravity technologies in gas purifications: A review. Chin. J. Chem. Eng. 2019, 27, 1361–1373. [Google Scholar] [CrossRef]
- Cremer, P.; Driole, J. Effects of the electromagnetic stirring on the removal of inclusions of oxide from liquid steel. Met. Trans. B 1982, 13, 45–52. [Google Scholar] [CrossRef]
- Lou, W.; Zhu, M. Numerical Simulations of Inclusion Behavior in Gas-Stirred Ladles. Met. Mater. Trans. B 2013, 44, 762–782. [Google Scholar] [CrossRef]
- Guo, L.; Gao, J.; Li, C.; Guo, Z. Removal of Fine SiO2 Composite Inclusions from 304 Stainless Steel Using Super-gravity. ISIJ Int. 2020, 60, 238–246. [Google Scholar] [CrossRef]
- Wang, L.; Lan, X.; Wang, Z.; Guo, Z. Removal of Low-Content Impurities from Pure Al by Supergravity Combined with Semi-Solid Method. Metals 2023, 13, 1945. [Google Scholar] [CrossRef]
- Wen, X.-C.; Guo, L.; Bao, Q.-P.; Guo, Z.-C. Rapid removal of copper impurity from bismuth-copper alloy melts via super-gravity separation. Int. J. Miner. Met. Mater. 2021, 28, 1929–1939. [Google Scholar] [CrossRef]
- Shi, A.; Wang, Z.; Shi, C.; Guo, L.; Guo, C.; Guo, Z. Supergravity-Induced Separation of Oxide and Nitride Inclusions from Inconel 718 Superalloy Melt. ISIJ Int. 2020, 60, 205–211. [Google Scholar] [CrossRef]
- Wen, X.; Guo, L.; Bao, Q.; Gao, J.; Guo, Z. Efficient separation of lead and antimony metals from the Pb-Sb alloy by su-per-gravity technology. J. Alloys Compd. 2019, 806, 1012. [Google Scholar] [CrossRef]
- Chen, B.; He, J.; Xi, Y.; Zeng, X.; Kaban, I.; Zhao, J.; Hao, H. Liquid-liquid hierarchical separation and metal recycling of waste printed circuit boards. J. Hazard. Mater. 2019, 364, 388–395. [Google Scholar] [CrossRef] [PubMed]
- Guo, X.-Y.; Liu, J.-X. Optimization of low-temperature alkaline smelting process of crushed metal enrichment originated from waste printed circuit boards. J. Central South. Univ. 2015, 22, 1643–1650. [Google Scholar] [CrossRef]
- Beams, J.W.; Haynes, F.B. The Separation of Isotopes by Centrifuging. Phys. Rev. B 1936, 50, 491–492. [Google Scholar] [CrossRef]
- Cheltsov, A.N.; Sosnin, L.Y.; Khamylov, V.K. Centrifugal enrichment of nickel isotopes and their application to the de-velopment of new technologies. J. Radioanal. Nucl. Chem. 2014, 299, 981. [Google Scholar] [CrossRef]
- Wild, J.F.; Chen, H.; Liang, K.; Liu, J.; Cox, S.E.; Halliday, A.N.; Yang, Y. Liquid solution centrifugation for safe, scalable, and efficient isotope separation. Sci. Adv. 2023, 9, eadg8993. [Google Scholar] [CrossRef]
- Osawa, T.; Ono, M.; Esaka, F.; Okayasu, S.; Iguchi, Y.; Hao, T.; Magara, M.; Mashimo, T. Mass-dependent isotopic fractionation of a solid tin under a strong gravitational field. EPL Europhysics Lett. 2009, 85, 64001. [Google Scholar] [CrossRef]
- Murakami, K.; Fujiyama, T.; Koike, A.; Okamoto, T. Influence of melt flow on the growth directions of columnar grains and columnar dendrites. Acta Metall. 1983, 31, 1425–1432. [Google Scholar] [CrossRef]
- Boden, S.; Eckert, S.; Gerbeth, G. Visualization of freckle formation induced by forced melt convection in solidifying GaIn alloys. Mater. Lett. 2010, 64, 1340–1343. [Google Scholar] [CrossRef]
- Sample, A.K.; Hellawell, A. The mechanisms of formation and prevention of channel segregation during alloy solidification. Met. Trans. A 1984, 15, 2163–2173. [Google Scholar] [CrossRef]
- Yuan, L.; Lee, P.D. A new mechanism for freckle initiation based on microstructural level simulation. Acta Mater. 2012, 60, 4917–4926. [Google Scholar] [CrossRef]
- Mamiya, M.; Nagai, H.; Castillo, M.; Okutani, T. The analysis of CdTe solidification in absence of thermal convection via short-duration microgravity. J. Cryst. Growth 2006, 295, 209–216. [Google Scholar] [CrossRef]
- Polovko, Y.; Sazonov, V.; Yuferev, V. Effect of spacecraft rotation on convection and impurity segregation during the growth of crystals from a melt under microgravity. J. Cryst. Growth 1999, 198–199, 182–187. [Google Scholar] [CrossRef]
- Ananth, R.; Gill, W.N. Dendritic growth in microgravity and forced convection. J. Cryst. Growth 1997, 179, 263–276. [Google Scholar] [CrossRef]
- Li, X.; Fang, X.; Fang, Y.; He, Z.; Shang, H. Experimental study on subcooled pool boiling heat transfer under hypergravity. Int. J. Heat. Mass. Transf. 2023, 217, 124697. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, J.; Yan, Z. Experimental investigation on melting heat transfer characteristics of a phase change material under hypergravity. Int. J. Heat. Mass. Transf. 2021, 181, 122004. [Google Scholar] [CrossRef]
- Weber, W.; Neumann, G.; Müller, G. Stabilizing influence of the coriolis force during melt growth on a centrifuge. J. Cryst. Growth 1990, 100, 145–158. [Google Scholar] [CrossRef]
- Fikri, M.; Labrosse, G.; Betrouni, M. The melt phase hydrodynamics for the “stabilized” Bridgman procedure applied under centrifugation; preliminary analysis and numerical results. J. Cryst. Growth 1992, 119, 41–60. [Google Scholar] [CrossRef]
- Arnold, W.A.; Wilcox, W.R.; Carlson, F.; Chait, A.; Regel, L.L. Transport modes during crystal growth in a centrifuge. J. Cryst. Growth 1992, 119, 24–40. [Google Scholar] [CrossRef]
- Müller, G.; Neumann, G.; Weber, W. Natural convection in vertical Bridgman configurations. J. Cryst. Growth 1984, 70, 78–93. [Google Scholar] [CrossRef]
- Yuferev, V.S. Coriolis Force on Melt Convection During Growth of Crystals. In A Centrifuge and Under Weightlessness, in Growth of Crystals; Givargizov, E.I., Melnikova, A.M., Eds.; Springer: Boston, MA, USA, 1996; pp. 117–127. [Google Scholar]
- Fernández, M.C.; Založnik, M.; Combeau, H.; Hecht, U. Thermosolutal convection and macrosegregation during directional solidification of TiAl alloys in centrifugal casting. Int. J. Heat. Mass. Transf. 2020, 154, 119698. [Google Scholar] [CrossRef]
- Battaglioli, S.; Robinson, A.; McFadden, S. Influence of natural and forced gravity conditions during directional columnar solidification. Int. J. Heat. Mass. Transf. 2018, 126, 66–80. [Google Scholar] [CrossRef]
- Jiang, P.; Gao, S.; Geng, S.; Han, C.; Mi, G. Multi-physics multi-scale simulation of the solidification process in the molten pool during laser welding of aluminum alloys. Int. J. Heat Mass. Transf. 2020, 161, 120316. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, B.; Hou, H.; Chen, W.; Wang, M. Phase-field simulation for the evolution of solid/liquid interface front in directional solidification process. J. Mater. Sci. Technol. 2019, 35, 1044–1052. [Google Scholar] [CrossRef]
- Han, D.; Jiang, W.; Xiao, J.; Li, K.; Lu, Y.; Lou, L. Investigating the evolution of freckles into sliver defects in Ni-based sin-gle-crystal superalloy castings. Mater. Today Commun. 2021, 27, 102350. [Google Scholar] [CrossRef]
- Sun, Q.Y.; Ren, Y.; Liu, D.-R. Numerical investigations of freckles in directionally solidified nickel-based superalloy casting with abrupt contraction in cross section. Results Phys. 2019, 12, 1547–1558. [Google Scholar] [CrossRef]
- Chen, C.; Sun, J.; Diao, A.; Yang, Y.; Li, J.; Zhou, Y. On the dendrite deformation and evolution mechanism of Ni-based sup-eralloy during directional solidification. J. Alloys Compd. 2022, 891, 161949. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, F.; Ma, D.; Yang, Q.; Xu, W.; Zhao, Y.; Dong, H.; Liu, Y.; Li, D. Freckle prediction model incorporating geometrical effects for Ni-based single-crystal superalloy components. Acta Mater. 2024, 266, 119702. [Google Scholar] [CrossRef]
- Nguyen-Thi, H.; Bogno, A.; Reinhart, G.; Billia, B.; Mathiesen, R.H.; Zimmermann, G.; Houltz, Y.; Löth, K.; Voss, D.; Verga, A.; et al. Investigation of gravity effects on solidification of binary alloys with in situ X-ray radiography on earth and in microgravity environment. J. Phys. Conf. Ser. 2011, 327, 012012. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, W.; Xia, Z.; Wei, B. Phase separation and microstructure evolution of ternary Fe–Sn–Ge immiscible alloy under microgravity condition. Comput. Mater. Sci. 2015, 103, 179–188. [Google Scholar] [CrossRef]
- Zhang, Q.; Mo, D.; Moon, S.; Janowitz, J.; Ringle, D.; Mays, D.; Diddle, A.; Rexroat, J.; Lee, E.; Luo, T. Bubble nucleation and growth on microstructured surfaces under microgravity. npj Microgravity 2024, 10, 13. [Google Scholar] [CrossRef]
- Thi, H.N.; Dabo, Y.; Drevet, B.; Dupouy, M.D.; Camel, D.; Billia, B.; Hunt, J.D.; Chilton, A. Directional solidification of Al–1.5 wt% Ni alloys under diffusion transport in space and fluid-flow localisation on earth. J. Cryst. Growth 2005, 281, 654. [Google Scholar]
- Akamatsu, S.; Nguyen-Thi, H. In situ observation of solidification patterns in diffusive conditions. Acta Mater. 2016, 108, 325–346. [Google Scholar] [CrossRef]
- Wen-Jing, Y.; Chun, Y.; Xiu-Jun, H.; Min, C.; Bing-Bo, W.; Zeng-Yuan, G. Rapid dendritic growth in an undercooled Ni-Cu alloy under the microgravity condition. Acta Phys. Sin. 2003, 52, 448–453. [Google Scholar] [CrossRef]
- Kühnen, J.; Scarselli, D.; Schaner, M.; Hof, B. Relaminarization by Steady Modification of the Streamwise Velocity Profile in a Pipe. Flow Turbul. Combust. 2018, 100, 919–943. [Google Scholar] [CrossRef]
- Yang, L.; Chai, L.; Liang, Y.; Zhang, Y.; Bao, C.; Liu, S.; Lin, J. Numerical simulation and experimental verification of gravity and centrifugal investment casting low pressure turbine blades for high Nb–TiAl alloy. Intermetallics 2015, 66, 149–155. [Google Scholar] [CrossRef]
- Kobryn, P.A.; Semiatin, S.L. Determination of interface heat-transfer coefficients for permanent-mold casting of Ti-6Al-4V. Met. Mater. Trans. B 2001, 32, 685–695. [Google Scholar] [CrossRef]
- Wang, J.; Zhao, X.; You, F.; Yue, Q.; Xia, W.; Gu, Y.; Zhang, Z. Effects of high gravity on the nucleation and precipitation of δ phase of GH4169 alloy. Scr. Mater. 2024, 255, 116409. [Google Scholar] [CrossRef]
- Zhao, L.; Guo, Z.; Wang, Z.; Wang, M. Influences of Super-Gravity Field on Aluminum Grain Refining. Met. Mater. Trans. A 2010, 41, 670–675. [Google Scholar] [CrossRef]
- Yang, Y.; Song, B.; Cheng, J.; Song, G.; Yang, Z.; Cai, Z. Effect of Super-gravity Field on Grain Refinement and Tensile Properties of Cu–Sn Alloys. ISIJ Int. 2018, 58, 98–106. [Google Scholar] [CrossRef]
- Zimmermann, G.; Hamacher, M.; Sturz, L. Effect of zero, normal and hyper-gravity on columnar dendritic solidification and the columnar-to-equiaxed transition in Neopentylglycol-(D)Camphor alloy. J. Cryst. Growth 2019, 512, 47–60. [Google Scholar] [CrossRef]
- Yang, Y.; Song, B.; Yang, Z.; Song, G.; Cai, Z.; Guo, Z. The Refining Mechanism of Super Gravity on the Solidification Structure of Al-Cu Alloys. Materials. 2016, 9, 1001. [Google Scholar] [CrossRef] [PubMed]
- Räbiger, D.; Zhang, Y.; Galindo, V.; Franke, S.; Willers, B.; Eckert, S. The relevance of melt convection to grain refinement in Al–Si alloys solidified under the impact of electric currents. Acta Mater. 2014, 79, 327–338. [Google Scholar] [CrossRef]
- Wang, X.; Zhai, W.; Wang, J.; Wei, B. Strength and ductility enhancement of high-entropy FeCoNi2Al0.9 alloy by ultrasonically refining eutectic structures. Scr. Mater. 2023, 225, 115154. [Google Scholar] [CrossRef]
- Huang, C.; Hecht, U.; Bührig-Polaczek, A. Numerical Modeling of Melting and Columnar Solidification with Convection in a Gradient Zone Furnace in a Centrifuge. Met. Mater. Trans. B 2020, 51, 2252–2267. [Google Scholar] [CrossRef]
- Zhang, Z.; Hou, X.; Zhang, Y.; Wei, H.; Wang, J. Phase field simulation of solidification under supergravity. Acta Mech. Sin. 2022, 38, 122031. [Google Scholar] [CrossRef]
- Abou-Khalil, L.; Salloum-Abou-Jaoude, G.; Reinhart, G.; Pickmann, C.; Zimmermann, G.; Nguyen-Thi, H. Influence of gravity level on Columnar-to-Equiaxed Transition during directional solidification of Al-20 wt.% Cu alloys. Acta Mater. 2016, 110, 44–52. [Google Scholar] [CrossRef]
- You, F.; Zhao, X.; Yue, Q.; Wang, J.; Gu, Y.; Zhang, Z. Evolution of solidification structure and mechanical properties of Al7050 alloy under hypergravity. J. Alloy. Compd. 2024, 985, 174014. [Google Scholar] [CrossRef]
- Glicksman, M.E. Fundamentals of Dendritic Growth. In Crystal Growth in Science and Technology; Arend, H., Hulliger, J., Eds.; Springer: Boston, MA, USA, 1989; Volume 210, pp. 167–183. [Google Scholar]
- Cui, C.; Liu, W.; Deng, L.; Wang, Y.; Liu, Y.; Wang, S.; Tian, L.; Su, H. Primary dendrite arm spacing and preferential orientations of the Ni–Si hypereutectic composites at different solidification rates. Appl. Phys. A 2020, 126, 898. [Google Scholar] [CrossRef]
- Grugel, R.N.; Hmelo, A.B.; Battaile, C.C.; Wang, T.G. Microstructural Development in Pb-Sn Alloys Subjected to High-Gravity during Controlled Directional Solidification. In Materials Processing in High Gravity; Regel, L.L., Wilcox, W.R., Eds.; Springer: Boston, MA, USA, 1994; pp. 101–110. [Google Scholar]
- Zhang, Y.; Dou, R.; Wang, J.; Liu, X.; Wen, Z. Numerical simulation of the effect of hypergravity on the dendritic growth characteristics of aluminum alloys. Heliyon 2024, 10, e27008. [Google Scholar] [CrossRef]
- Ren, N.; Panwisawas, C.; Li, J.; Xia, M.; Dong, H.; Li, J. Solute enrichment induced dendritic fragmentation in directional so-lidification of nickel-based superalloys. Acta Mater. 2021, 215, 117043. [Google Scholar] [CrossRef]
- Viardin, A.; Souhar, Y.; Fernández, M.C.; Apel, M.; Založnik, M. Mesoscopic modeling of equiaxed and columnar solidification microstructures under forced flow and buoyancy-driven flow in hypergravity: Envelope versus phase-field model. Acta Mater. 2020, 199, 680–694. [Google Scholar] [CrossRef]
- Naebe, M.; Shirvanimoghaddam, K. Functionally graded materials: A review of fabrication and properties. Appl. Mater. Today 2016, 5, 2352–9407. [Google Scholar] [CrossRef]
- Bui, T.Q.; Do, T.V.; Ton, L.H.T.; Doan, D.H.; Tanaka, S.; Pham, D.T.; Nguyen-Van, T.-A.; Yu, T.; Hirose, S. On the high tem-perature mechanical behaviors analysis of heated functionally graded plates using FEM and a new third-order shear deformation plate theory. Compos. B Eng. 2016, 92, 218. [Google Scholar] [CrossRef]
- Ren, H.; Liu, D.; Tang, H.; Tian, X.; Zhu, Y.; Wang, H. Microstructure and mechanical properties of a graded structural material. Mater. Sci. Eng. A 2014, 611, 362–369. [Google Scholar] [CrossRef]
- Sasaki, M.; Hirai, T. Thermal fatigue resistance of CVD SiC/C functionally gradient material. J. Eur. Ceram. Soc. 1994, 14, 257–260. [Google Scholar] [CrossRef]
- Löffler, J.F.; Johnson, W.L. Crystallization of Mg–Al and Al-Based Metallic Liquids under Ultra-High Gravity. Intermetallics. 2002, 10, 1167–1175. [Google Scholar] [CrossRef]
- Li, R.; Wang, Z.; Guo, Z.; Liaw, P.K.; Zhang, T.; Li, L.; Zhang, Y. Graded microstructures of Al-Li-Mg-Zn-Cu entropic alloys under supergravity. Sci. China Mater. 2019, 62, 736–744. [Google Scholar] [CrossRef]
- Löffler, J.F.; Peker, A.; Bossuyt, S.; Johnson, W.L. Processing of metallic glass-forming liquids under ultra-high gravity. Mater. Sci. Eng. A 2004, 375–377, 341–345. [Google Scholar] [CrossRef]
- Wijmans, J.; Baker, R. The solution-diffusion model: A review. J. Membr. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Sequeira, C.; Amaral, L. Role of Kirkendall effect in diffusion processes in solids. Trans. Nonferrous Met. Soc. China 2014, 24, 1–11. [Google Scholar] [CrossRef]
- Tahir-Kheli, R.A. Correlation factors for atomic diffusion in nondilute multicomponent alloys with arbitrary vacancy concen-tration. Phys. Rev. B 1983, 28, 3049. [Google Scholar] [CrossRef]
- Mundy, J.N. Effect of Pressure on the Isotope Effect in Sodium Self-Diffusion. Phys. Rev. B 1971, 3, 2431–2445. [Google Scholar] [CrossRef]
- Dederichs, P.H.; Schroeder, K. Anisotropic diffusion in stress fields. Phys. Rev. B 1978, 17, 2524–2536. [Google Scholar] [CrossRef]
- Cowern, N.E.B.; Zalm, P.C.; Van Der Sluis, P.; Gravesteijn, D.J.; De Boer, W.B. Diffusion in Strained Si(Ge). Phys. Rev. Lett. 1994, 72, 2585–2588. [Google Scholar] [CrossRef]
- Kringhøj, P.; Larsen, A.N.; Shirayev, S.Y. Diffusion of Sb in Strained and Relaxed Si and SiGe. Phys. Rev. Lett. 1996, 76, 3372–3375. [Google Scholar] [CrossRef]
- Barr, L.W.; Smith, F.A. Observations on the equilibrium distribution of gold diffusing in solid potassium in a centrifugal field. Philos. Mag. 1969, 20, 1293. [Google Scholar] [CrossRef]
- Huang, X.; Ono, M.; Ueno, H.; Iguchi, Y.; Tomita, T.; Okayasu, S.; Mashimo, T. Formation of atomic-scale graded structure in Se-Te semiconductor under strong gravitational field. J. Appl. Phys. 2007, 101, 113502. [Google Scholar] [CrossRef]
- Mashimo, T. Self-consistent approach to the diffusion induced by a centrifugal field in condensed matter: Sedimentation. Phys. Rev. A 1988, 38, 4149–4154. [Google Scholar] [CrossRef]
- Wierzba, B. The vacancies formation and agglomeration under centrifugal force. Phys. A Stat. Mech. Its Appl. 2017, 484, 482–487. [Google Scholar] [CrossRef]
- Xie, L.; Zheng, Y.; Lu, H.; Jiao, Y.; Qu, Y.; Cai, J.; Zhai, Y.; Chen, Y.; Mao, S.; Han, X. Thermal diffusion and microstructural evolution of Cu-Zn binary system under hypergravity. Acta Mater. 2024, 268, 119790. [Google Scholar] [CrossRef]
- Wierzba, B.; Mashimo, T.; Danielewski, M. Competition between Chemical and Gravity Forces in Binary Alloys. High. Temp. Mater. Process. 2017, 37, 285–288. [Google Scholar] [CrossRef]
- Qiao, S.; Chen, Y.; An, Z.; Jiao, Y.; Li, A.; Zhai, Y.; Han, X. Hypergravity suppressed thermal diffusion at the Cu-Sn couple interface. J. Alloy. Compd. 2022, 928, 167231. [Google Scholar] [CrossRef]
- Guo, X.; Zheng, W.; Xiao, C.; Li, L.; Antonov, S.; Zheng, Y.; Feng, Q. Evaluation of microstructural degradation in a failed gas turbine blade due to overheating. Eng. Fail. Anal. 2019, 103, 308–318. [Google Scholar] [CrossRef]
- Alozie, O.; Li, Y.; Diakostefanis, M.; Wu, X.; Shong, X.; Ren, W. Assessment of degradation equivalent operating time for aircraft gas turbine engines. Aeronaut. J. 2020, 124, 549–580. [Google Scholar] [CrossRef]
- Fu, C.; Chen, Y.; Li, L.; Antonov, S.; Feng, Q. Evaluation of service conditions of high pressure turbine blades made of DS Ni-base superalloy by artificial neural networks. Mater. Today Commun. 2020, 22, 100838. [Google Scholar] [CrossRef]
- Lu, H.; Zhang, W.; Chen, Y.; Zhai, Y.; Wang, W.; Long, H.; Li, A.; Han, X. Structural degradation and elemental variations in an ex-service first-stage gas turbine blade. Mater. Charact. 2023, 196, 112596. [Google Scholar] [CrossRef]
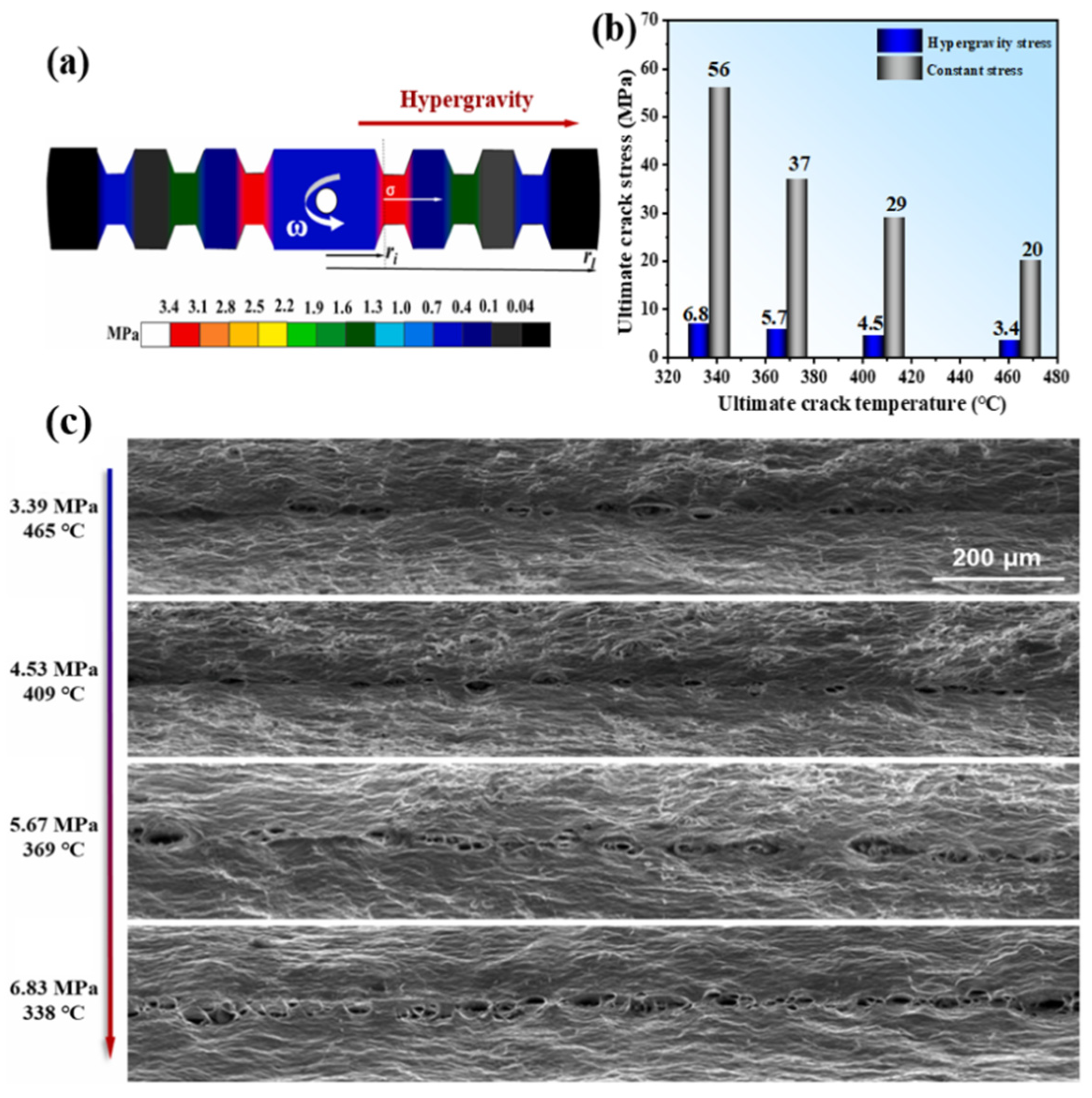
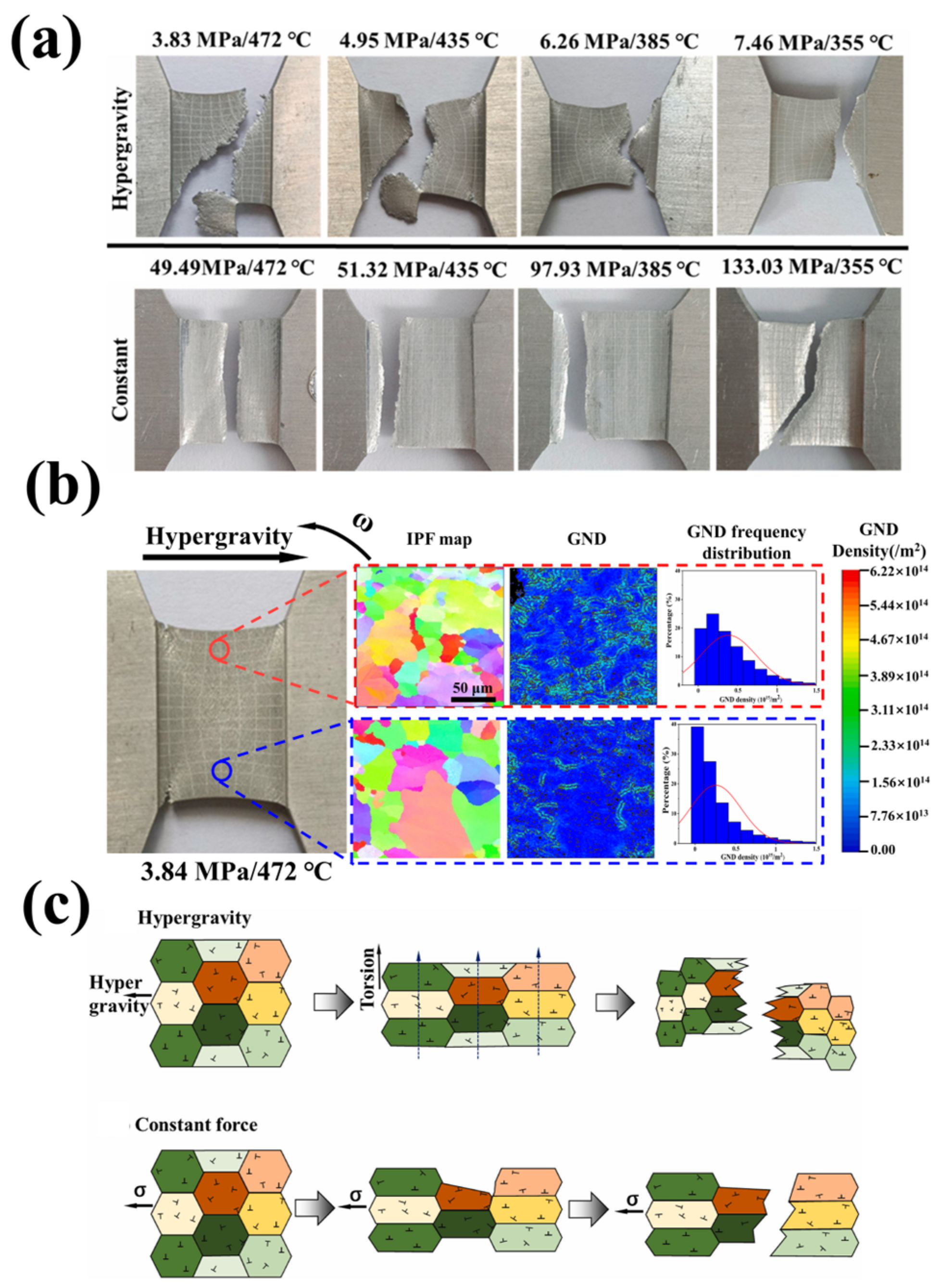
- Yang, F.; Jiao, Y.; Xie, L.; Qiao, S.; Qu, Y.; Zhai, Y.; Li, A.; Chen, Y. Hypergravity prompt thermal crack in 1060 aluminium slat. Mater. Sci. Eng. A 2024, 899, 146437. [Google Scholar] [CrossRef]
- Jiao, Y.; Yang, F.; Niu, H.; Xie, L.; Zhai, Y.; Li, A.; Chen, Y. Hypergravity-exacerbated cracking in high-speed rotating 7075 aluminum blades. J. Mater. Res. Technol. 2024, 30, 542–551. [Google Scholar] [CrossRef]















Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, Y.; Xie, L.; Chen, Y.; Han, X. Effects of Hypergravity on Phase Evolution, Synthesis, Structures, and Properties of Materials: A Review. Materials 2025, 18, 496. https://doi.org/10.3390/ma18030496
Zheng Y, Xie L, Chen Y, Han X. Effects of Hypergravity on Phase Evolution, Synthesis, Structures, and Properties of Materials: A Review. Materials. 2025; 18(3):496. https://doi.org/10.3390/ma18030496
Chicago/Turabian StyleZheng, Yisheng, Lilin Xie, Yanhui Chen, and Xiaodong Han. 2025. "Effects of Hypergravity on Phase Evolution, Synthesis, Structures, and Properties of Materials: A Review" Materials 18, no. 3: 496. https://doi.org/10.3390/ma18030496
APA StyleZheng, Y., Xie, L., Chen, Y., & Han, X. (2025). Effects of Hypergravity on Phase Evolution, Synthesis, Structures, and Properties of Materials: A Review. Materials, 18(3), 496. https://doi.org/10.3390/ma18030496





