Next Article in Journal
Modeling of Heat Treatment Processes in a Vortex Layer of Dispersed Materials
Previous Article in Journal
Structural Effects of Concrete Creep in a Prestressed Balanced Cantilever Bridge Based on Classical and Fractional Rheological Models
Previous Article in Special Issue
Robust Self-Trapped Exciton Emission in Sb3+-Engineered Lead-Free Cs4SnBr6 Zero-Dimensional Perovskites
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 18
Issue 23
10.3390/ma18235458
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Tunable Superconductivity in BSCCO via GaP Quantum Dots

by
Qingyu Hai
,
Duo Chen
,
Ruiyuan Bi
,
Yao Qi
,
Lifeng Xun
,
Xiaoyan Li
and
Xiaopeng Zhao
*
Smart Materials Laboratory, Department of Applied Physics, Northwestern Polytechnical University, Xi’an 710129, China
*
Author to whom correspondence should be addressed.
Materials 2025, 18(23), 5458; https://doi.org/10.3390/ma18235458 (registering DOI)
Submission received: 24 September 2025 / Revised: 28 November 2025 / Accepted: 1 December 2025 / Published: 3 December 2025
(This article belongs to the Special Issue Advances in Luminescent Materials: Fabrication and Technological Applications)
Browse Figures
Versions Notes

Abstract

The enhancement of superconducting properties of high-temperature copper-oxide superconductors like B(P)SCCO remains a hot research topic in the field of superconducting materials. This study introduces GaP quantum dots (QDs) as a heterophase, leveraging their electroluminescent properties to enhance the superconductivity of B(P)SCCO. Experimental results demonstrate that the electroluminescence generated by GaP quantum dots (QDs) under an applied electric field induces tunable superconducting enhancement of B(P)SCCO. A reproducible trend of enhancement in the critical transition temperature (Tc) and depairing current density (Jd) is observed with increasing QD electroluminescent intensity, suggesting a positive correlation. This electroluminescence-induced enhancement dominates over the inherent impurity effects at optimal QD content.

Graphical Abstract

1. Introduction

Bismuth-based superconducting materials (general formula: Bi2Sr2Can−1CunO2n+4+δ) [1,2,3,4,5], as a representative copper-oxide superconductor, exhibit significant application value in power transmission [6], high-field magnets [7], and energy storage due to their high critical temperature (Tc = 110K for Bi-2223 phase [5]), absence of rare-earth elements, and superior processability. However, the intrinsic limitations of BSCCO such as strong anisotropy caused by their layered structure [1,8], weak interlayer coupling, and insufficient intrinsic flux pinning severely constrain performance in high-current and high-field environments [9,10,11]. Traditional elemental doping (e.g., Pb [12,13], Sb [14,15]) can improve phase purity yet offers limited enhancement in critical transition temperature (Tc) and critical current density (Jc). In contrast, the nanocomposite strategy—introducing heterophase nanoparticles as artificial pinning centers (e.g., insulator Al2O3 [16], semiconductor SiC [17], ferromagnet FePb [18])—has emerged as an effective modification approach for (Bi,Pb)-Sr-Ca-Cu-O (B(P)SCCO) superconductors [19,20,21,22,23,24,25,26,27,28]. This strategy leverages interface coupling effects between nanoscale heterophases and the superconducting matrix to create strong pinning sites, significantly enhancing flux pinning force density (Fp) and boosting Jc by 1~2 orders of magnitude [29,30,31,32,33]. However, it typically comes at the cost of a suppressed Tc due to impurity effects and interface scattering. Clearly, although this method has been experimentally confirmed as an effective approach to improve the current carrying capacity of superconductors, it still does not represent the optimal strategy for enhancing the superconductivity of B(P)SCCO materials.
Metamaterials [34,35] are artificially engineered microstructures or composite materials that exhibit extraordinary physical properties unattainable in natural materials, characterized by their structure-determined functionalities. Researchers proposed the concept of metamaterial superconductors [36,37,38], aiming to develop superconducting materials with elevated critical temperatures Tc through precisely engineered superconducting architectures. In recent years, the Max Planck Institute proposed light-induced superconductivity [39,40,41,42,43]. Their research team discovered that under mid-infrared laser irradiation, both YBCO, and K3C60 thin films exhibit transient superconducting behavior. Inspired by the concept of metamaterials, our team proposes a novel modification strategy that incorporates electroluminescent heterophases into superconducting materials. By introducing the electroluminescent heterophase as “meta-atoms” into the superconducting particle “matrix”, we construct a composite structure. The core hypothesis is that photons generated internally via electroluminescence could couple with Cooper pairs, potentially reinforcing the pairing strength and enhancing superconductivity, a system we term a Smart Metamaterial Superconductor (SMSC).
Previous studies demonstrated that although introducing Y2O3:Eu3+/Ag luminescent heterophase enhances superconductivity in MgB2 [44,45,46,47,48,49] (ΔTc = +0.4 K, ΔJc = +20%) and B(P)SCCO [50,51,52] (ΔTc = +1 K, ΔJc = +24%), its performance is severely limited by high electric field dependence, low luminescent intensity, and rapid decay characteristics, compromising the enhancement efficiency of superconductor. In contrast, GaN p-n junction particles exhibit superior advantages including high luminescent quantum efficiency and low turn-on voltage, achieving stronger superconducting enhancement in MgB2 [53,54] (ΔTc = +0.8 K, ΔJc = +35%) and B(P)SCCO [55] (ΔTc = +2 K, ΔJc = +35%). However, their micron-scale dimensions (average ~2 μm) introduce significant impurity effects, which substantially offset the potential superconducting gain from electroluminescence. It is noteworthy that prior research has primarily focused on the influence of heterophase content, leaving the systematic role of the heterophase’s electroluminescence intensity—a key variable in the proposed mechanism—largely unexplored. To address this critical gap and to simultaneously mitigate the limitations of previous electroluminescence phases. we select GaP core–shell quantum dots (QDs) [56] as the electroluminescent heterophase. GaP QDs offer superior stability compared to Y2O3:Eu3+/Ag and a much smaller size (~3.5 nm) than GaN particles. In our preliminary work, incorporating these into MgB2 superconductors [57], we observed an increasing trend in both Tc and Jc with enhanced luminescence intensity, providing the initial validation of light intensity as an independent parameter. Specifically, it was found that both critical temperature Tc and critical current Jc density improved as the luminescence intensity of GaP quantum dots increased.
In this study, we synthesized GaP:Zn2+/GaP–GaInP–GaP:Te2−/GaP core–shell quantum dots [56] with tunable electroluminescent intensities via the thermal injection method. These were incorporated into a B(P)SCCO superconducting matrix to systematically investigate the independent and coupled effects of two variables: the “electroluminescence intensity” and the “addition content” of the luminescent heterophase. This work aims to investigate the potential influence of the heterophase’s electroluminescence intensity on the superconducting properties and to explore a novel modification strategy for B(P)SCCO superconductors.

2. Materials and Methods

2.1. Synthesis of GaP:Zn2+/GaP–GaInP–GaP:Te2−/GaP Core–Shell Quantum Dots

In this study, GaP:Zn2+/GaP–GaInP–GaP:Te2−/GaP core–shell quantum dots (hereinafter referred to as GaP QDs) with tunable electroluminescence intensities were synthesized following the thermal injection strategy reported in Ref. [56]. The synthesis was achieved via a thermal injection approach by modulating the reaction durations of individual layers (GaP:Zn2+/GaP, GaInP, and GaP:Te2−/GaP). GaP:Zn2+ cores were synthesized by rapidly injecting a (TMS)3P–TOP solution into a mixture of Ga(acac)3, Zn(acac)3, oleic acid (OA), and 1-octadecene (ODE) at 300 °C under Ar protection. The GaP active layer was subsequently grown by repeating the hot-injection of (TMS)3P, and a GaInP quantum-well shell was deposited by co-injecting Ga(acac)3 and InCl3 precursors at 300 °C, forming GaP:Zn/GaP/GaInP multilayer QDs. The GaP:Te2−/GaP shell layer was synthesized using an analogous procedure, in which Te powder was used in place of Zn(acac)3. Figure 1b displays the Transmission Electron Microscopy (TEM) image of GaP quantum dots. The inset shows the corresponding size distribution histogram. The nanoparticles demonstrate uniform size distribution, centered at ~3.5 nm (range: 2.5–4.5 nm) and following a normal distribution. The blurring observed in the imaging primarily originates from the oleylamine ligand layer coating the quantum dot surfaces. The samples underwent X-ray diffraction (XRD) characterization, as shown in Figure 1c. The vertical black lines denote the standard XRD pattern of zinc-blende structured bulk GaP. As evidenced in the figure, the diffraction peaks of our samples exhibit precise alignment with the reference pattern, demonstrating three characteristic peaks corresponding to the (111), (220), and (311) crystallographic planes of the zinc-blende GaP structure. Notably, no discernible impurity peaks were observed. This demonstrates that the synthesized samples consist of zinc-blende-structured GaP quantum dots, with Zn2+ and Te2− ions successfully doped into the GaP crystal lattice without detectable elemental segregation or secondary phase formation. Moreover, the absence of XRD peak shifts demonstrates that low-concentration Zn2+/Te2− doping induces no detectable lattice strain. Figure 1a displays the electroluminescence (EL) spectrum of the sample under a 7 V bias voltage. The spectrum reveals red emission centered at ~600 nm with a full width at half maximum (FWHM) of ~200 nm under electric field. The 1:1:1 GaP quantum dots (layer-wise reaction time ratio) exhibit a higher emission intensity of ~2950 a.u., while the 1:1.4:1.4 GaP quantum dots show a reduced intensity of ~2100 a.u. Furthermore, we conducted X-ray photoelectron spectroscopy (XPS) analysis to investigate the elemental composition and valence states of the multilayer core–shell GaP nanoparticles. As shown in Figure 1d–f, distinct emission peaks in the Zn 2p, Te 3d, and In 3d characteristic regions confirm the successful doping of Zn2+, Te2−, and In3+ ions into the GaP lattice via the thermal injection method [56].

2.2. Preparation of B(P)SCCO Superconducting Samples

In this study, B(P)SCCO superconducting samples were synthesized via solid-state sintering. Stoichiometric quantities of high-purity precursors (Bi2O3, PbO, SrCO3, CaCO3, CuO; all Alfa Aesar, 99.99%) were weighed according to the molar ratio of Bi:Pb:Sr:Ca:Cu = 0.9:0.4:2:2:3. To compensate for the potential evaporation of Bi and Pb during the prolonged high-temperature sintering process, a slight excess of these elements was accounted for in the initial weighing. The mixed powder and Φ 5 mm agate balls were loaded into a 50 mL milling jar with anhydrous ethanol as a dispersant. Milling was performed in a planetary ball mill (500 rpm, alternating rotation) for 20 h. The as-milled powder was vacuum-dried at 70 °C for 12 h, then sieved through a 500-mesh sieve to obtain a uniform particle size of 25 ± 3 μm. The raw material powder was calcined in a tubular furnace in air at 840 °C for 50 h (heating rate: 4 °C/min; cooling rate: 2 °C/min, with controlled cooling to 800 °C, followed by furnace cooling). After cooling, the powder was collected and subjected to grinding for one hour using an agate mortar. This thermal-mechanical treatment cycle was repeated twice, ultimately yielding black pre-calcined B(P)SCCO powder.
A measured amount of B(P)SCCO pre-calcined powder was loaded into a mold and compacted under 12 MPa pressure for 10 min to form pellets (Φ 12 × 1 mm). These pellets were then transferred to an alumina boat and sintered in a tubular furnace in air at 840 °C for 30 h (heating rate: 4 °C/min; cooling rate: 2 °C/min with controlled cooling to 800 °C, followed by furnace cooling). After cooling to room temperature, the pellets were removed and ground into B(P)SCCO powder.
To prepare the composite samples, GaP quantum dots with varying electroluminescent intensities were mixed with the B(P)SCCO powder at designated addition ratios (0, 0.15, 0.2 wt.%) by grinding in an agate mortar for 15 min. The mixed powders were then compacted under 12 MPa pressure for 10 min to form pellets (Φ 12 × 1 mm). All composite pellets (S0–S4) were sintered at 840 °C for 120 h in air in a tubular furnace, with the sintering process carefully controlled to ensure uniformity. In this study, the pure B(P)SCCO sample was designated as S0. The sample containing GaP quantum dots without electroluminescence (content: 0.2 wt.%) was designated as S1. The sample with GaP quantum dots added (content: 0.2 wt.%) with an electroluminescence intensity of 2100 a.u. was designated as S2. Samples with GaP quantum dots added (content: 0.15 wt.%, 0.2 wt.%) with an electroluminescence intensity of 2950 a.u. were designated as S3 and S4, respectively, as detailed in Table 1.

2.3. Property Characterization of B(P)SCCO Superconducting Samples

The surface morphology of the samples was examined using an FEI Verios G4 ultra-high-resolution field emission scanning electron microscope (SEM) (Thermo Fisher Scientific, Hillsboro, OR, USA). Energy-dispersive X-ray spectroscopy (EDS) was employed to confirm the elemental composition. To investigate phase formation, X-ray diffraction (XRD) analysis was performed on a Bruker D8 Advance diffractometer (Bruker AXS, Karlsruhe, Germany) with Cu-Kα radiation (λ = 1.5406 Å) over a 2θ range of 10–70°. The electrical transport properties of the samples, including the resistance-temperature (R-T) relationship for determining the critical temperature (Tc) and the current-voltage (I-V) characteristics for determining the depairing current (Id), were measured using the standard four-probe method. First, four indium electrodes, each with dimensions of 1 mm × 1 mm and spaced 1 mm apart, were pressed onto the surface of the sintered samples using the press-contact method. During measurements, the electrodes on the two sides were connected to a Keithley 6221 current source (Keithley Instruments Inc., Cleveland, OH, USA)via enameled copper wires to provide a stable test current, while the two central voltage electrodes were connected to a Keithley 2182A nanovoltmeter (Keithley Instruments Inc., Cleveland, OH, USA) to collect voltage signals. The entire measurement process was conducted in a vacuum low-temperature environment provided by a closed-cycle cryostat manufactured by Advanced Research Systems (Macungie, PA, USA), with a minimum temperature of 10 K. Temperature measurements and control during the experiment were managed by a Lake Shore 335 temperature controller (Lake Shore Cryotronics, Inc., Westerville, OH, USA). The depairing current density (Jd) was determined from current-voltage (I-V) characteristics measured in zero applied magnetic field at various temperatures, using a 1 μV/cm electric field criterion. The DC magnetization of the sample was measured under a magnetic field of 100 Oe in zero-field cooling mode.

3. Results

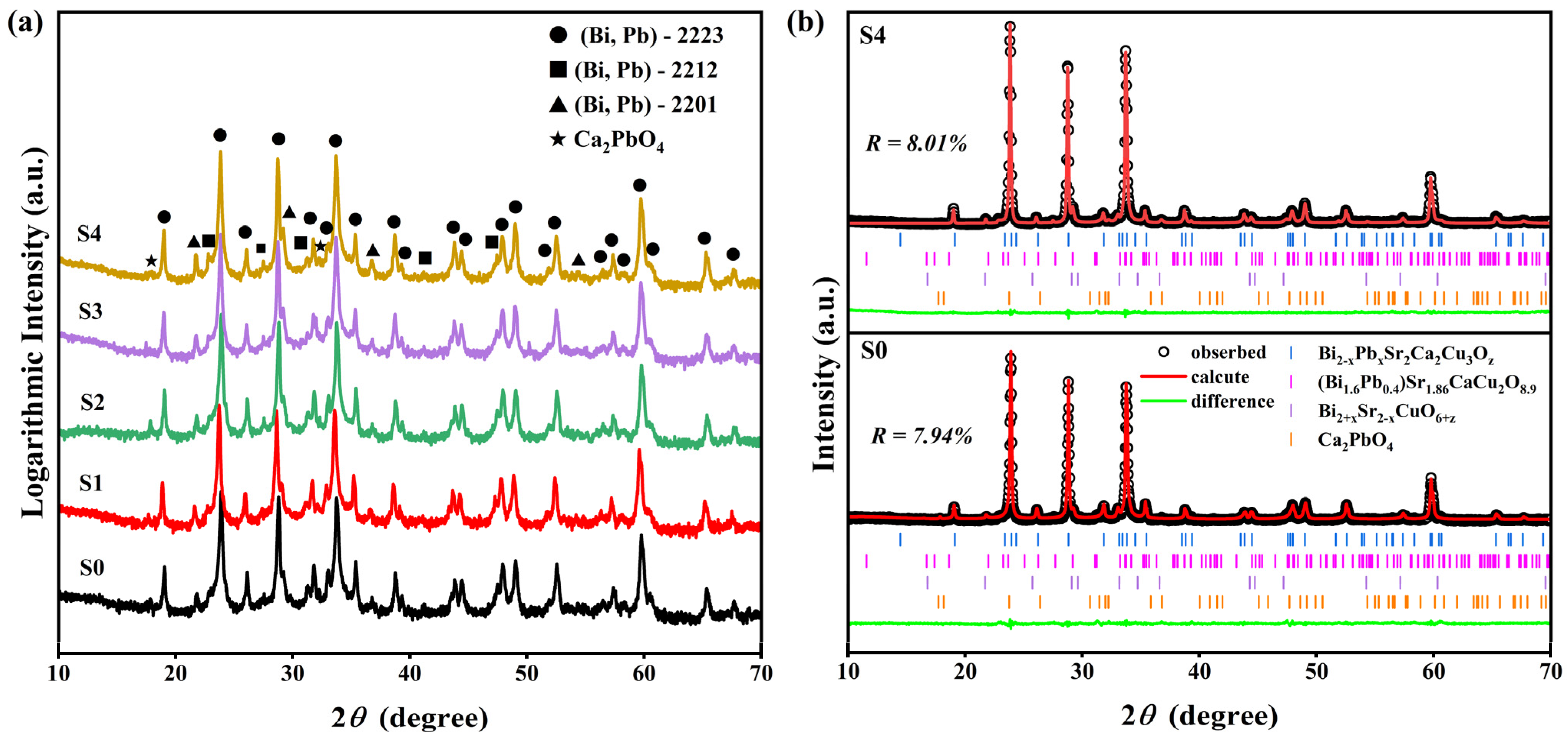
3.1. Phase Analysis

The phase composition of the samples was characterized by X-ray diffraction (XRD). Figure 2a displays the XRD patterns of samples S0 (pure sample) to S4. To enhance the visibility of minor peaks, the diffraction intensity is plotted on a logarithmic scale on the y-axis. It can be observed that all major diffraction peaks correspond to the (Bi,Pb)-2223 high-temperature superconducting phase, while minor peaks originate from the low-temperature phases of (Bi,Pb)-2212 and (Bi,Pb)-2201. In the patterns of samples S1–S4 with added GaP quantum dots, no diffraction peaks corresponding to GaP or its related oxides (such as Ga2O3, P2O5, etc.) were detected, which may be attributed to the low addition content of GaP quantum dots.
Rietveld refinement of the XRD data was performed to analyze the crystallographic parameters of (Bi,Pb)-2223 phase. Figure 2b presents the refinement fitting patterns for the samples S0 and S4. The phase fractions and corresponding lattice parameters, derived from the refinement results, are summarized in Table 2. The data reveal that the content of the dominant (Bi,Pb)-2223 phase remains consistently around 93% across all samples, with no significant variation in lattice parameters. These results indicate that the incorporation of GaP quantum dots does not markedly alter the primary phase composition or crystal structure of the B(P)SCCO matrix.

3.2. Microstructural Analysis

Figure 3 presents representative scanning electron microscopy (SEM) images of the pure B(P)SCCO sample (S0) and the GaP quantum dot-doped samples S1 and S4. All samples exhibit the characteristic defined layered morphology typical of B(P)SCCO superconductors, with a uniform distribution of grain sizes. Comparative analysis demonstrates that the incorporation of GaP quantum dots does not disrupt the intrinsic layered grain structure, nor does it introduce observable microstructural defects or abnormal grain growth. This confirms that the heterophase addition preserves the microstructural integrity of the B(P)SCCO matrix.
To further assess the compositional homogeneity and distribution of constituent elements, backscattered electron (BSE) imaging and energy-dispersive X-ray spectroscopy (EDS) mapping were performed on sample S4. As shown in Figure 4a, the BSE image displays a homogeneous contrast without pronounced brightness variations, suggesting the absence of large-scale elemental segregation or secondary phase agglomeration. The corresponding EDS elemental maps (Figure 4b–f) show continuous and uniform distributions of the principal matrix elements—Bi, Pb, Sr, Ca, and Cu—throughout the scanned region. No localized enrichment or depletion of these elements is detected, confirming the compositional homogeneity of the composite sample at the microscale.
These results collectively confirm that the composite sample maintains compositional homogeneity at the microscale and that the introduced GaP quantum dots do not induce detectable segregation or structural perturbation within the resolution limit of the microscopy techniques employed.

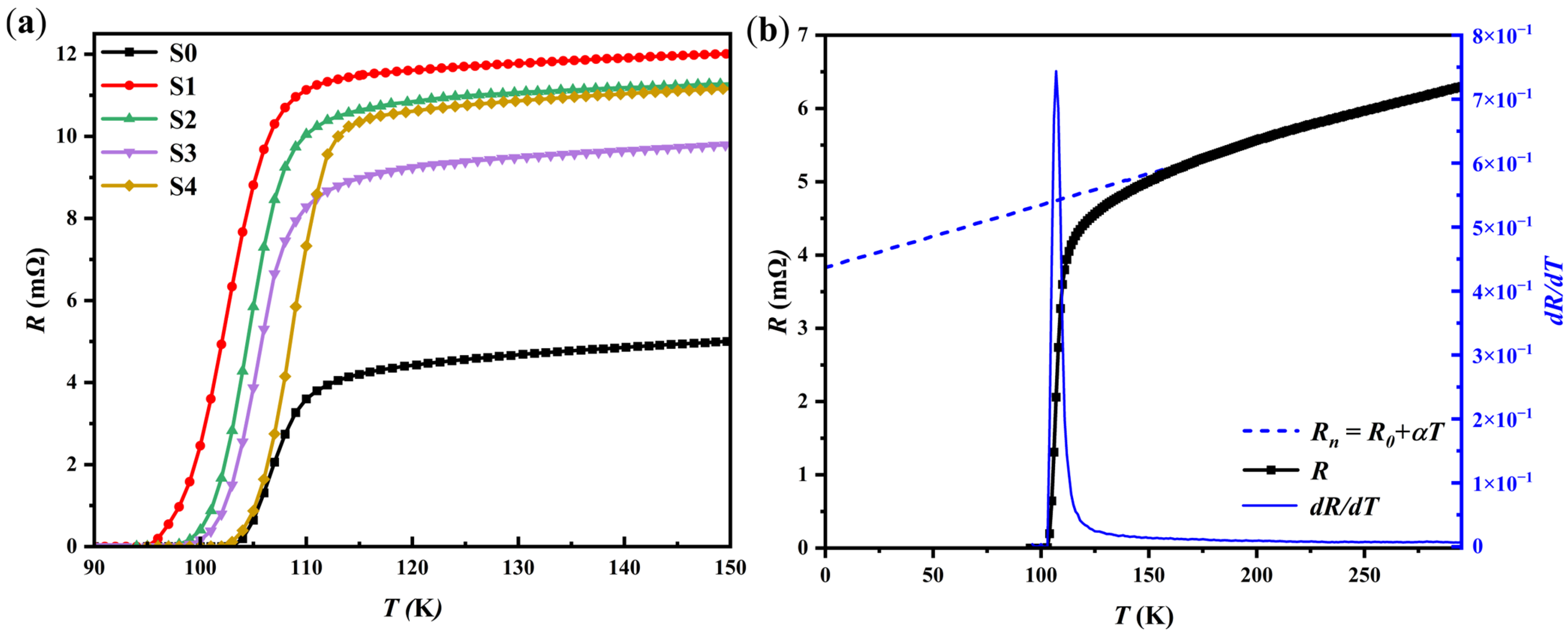
3.3. R–T Curve Measurement

The electrical resistance–temperature relationship of the samples was measured over the temperature range of 90–295 K using the standard four-probe method with a current of 1 mA to prevent Joule heating effects. Figure 5a shows the R–T curves of all the samples within the temperature range of 90–150 K. All samples exhibit characteristic high-temperature superconducting transition behavior of copper oxides. Figure 5b presents the resistance-temperature curve for sample S0 and its derivative, dR/dT. As the temperature decreases, the sample shows strange metal behavior characterized by a linear decrease in resistance, which follows the relation R(T) = αT + R0. Below the characteristic temperature T*—defined as the temperature at which (R(T) − R0)/αT begins to deviate from 1—the resistance gradually departs from the linear temperature dependence, showing an upward curvature, while dR/dT gradually increases. This is generally interpreted as the sample entering the pseudogap state. In this regime, the opening of the pseudogap is accompanied by enhanced electron correlations [58,59], and preformed Cooper pairs begin to emerge, although long-range phase coherence has not yet been established. This phenomenon is commonly observed in underdoped copper-oxide high-temperature superconductors. As the temperature further decreases below the onset transition temperature Tc,on, the resistance drops sharply, accompanied by a steep rise in dR/dT, indicating the establishment of global superconducting coherence. When the temperature falls below the zero-resistance transition temperature Tc,0, the resistance vanishes completely, and the sample enters a fully superconducting state, in which the Cooper pairs achieve long-range phase coherence. It is noteworthy that a two-step transition is universally observed in polycrystalline high-temperature superconductors [60,61,62,63]. This phenomenon, typically characterized by two distinct peaks in dR/dT between the onset transition temperature (Tc,on) and the zero-resistance temperature (Tc,0), is commonly attributed to factors such as weak intergranular links and porosity, the presence of excessive amounts of low-Tc superconducting phases, or Joule heating induced by high excitation currents. In contrast, such a two-step transition is absent in the samples of the present work, where only a single, sharp superconducting transition is observed. Combined with XRD and SEM results, the absence of the two-step transition in our samples can be ascribed to the high phase purity of the (Bi,Pb)-2223 superconductor, excellent intergranular connectivity, and the effective suppression of weak links at grain boundaries. Furthermore, the use of a low measuring current effectively avoided any thermal effects that could arise from current flow.
The superconducting transition intervals for samples S0 to S4 are 103–114, 95–112, 97–113, 98–114, and 102–114, respectively. In this study, the critical transition temperature Tc, is defined as the temperature at which the value of dR/dT reaches its maximum. The parameters extracted from the sample R–T curves, including Tc,0, Tc,on, Tc, and R295K are summarized in Table 3. As shown in Table 3, the introduction of GaP quantum dots (S1–S4) leads to increased room temperature resistance (R295K) and reduced Tc,0 compared with the pure sample S0. This trend reflects the impurity scattering associated with the heterogeneous GaP phases, which affects the normal-state charge transport and weakens superconducting coherence at low temperatures. Overall, the impurity effect induced by the introduction of GaP quantum dots leads to a reduction in the superconducting transition temperature. However, among samples S1, S2, and S4 with the same nominal heterophase addition level (0.2 wt.%), the critical temperature Tc shows a gradual recovery as the electroluminescence intensity of the GaP quantum dots increases. Furthermore, for samples with similar electroluminescence intensity but different addition amounts, S3 (0.15 wt.%) and S4 (0.2 wt.%), the sample with the higher addition content (S4) exhibits a higher Tc. These results collectively demonstrate that the electroluminescence from the GaP quantum dots enhances the superconducting properties of the samples, and this effect exhibits a positive correlation with both the luminescence intensity and the addition content.

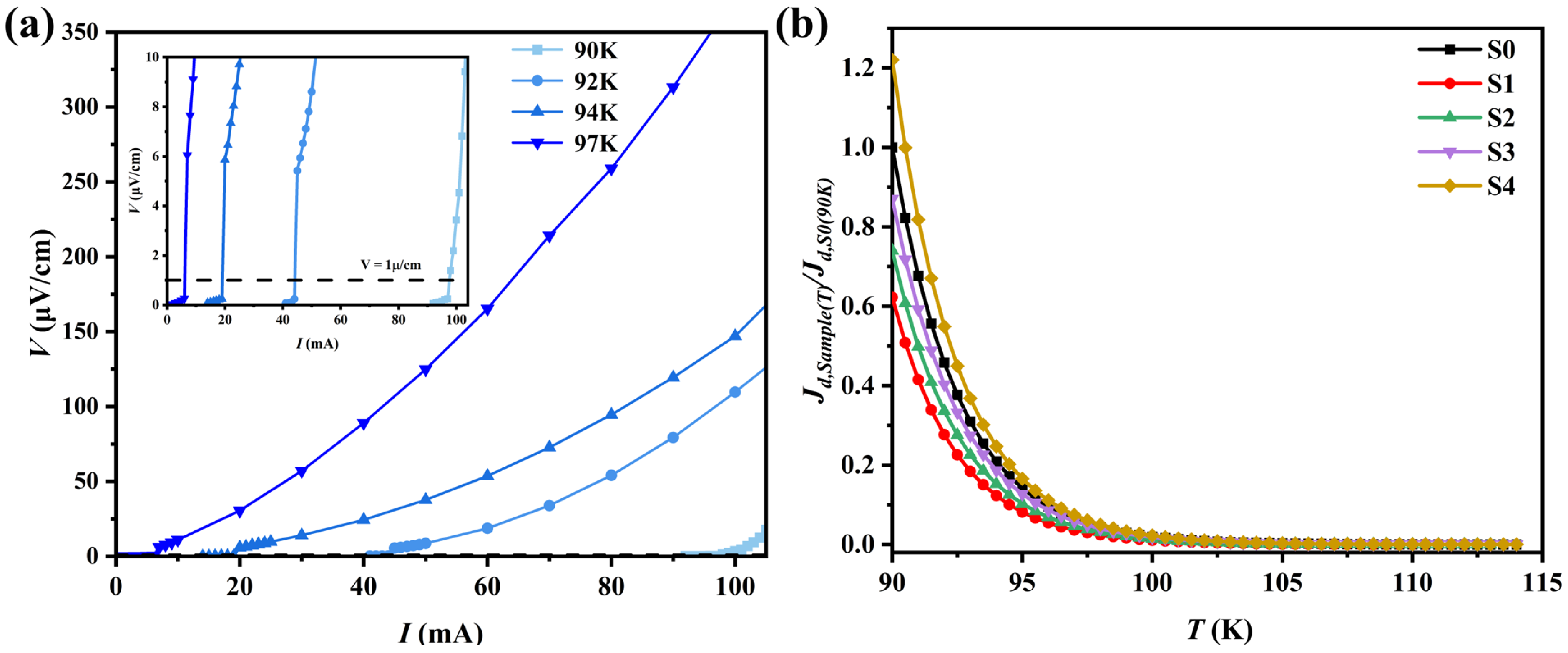
3.4. Jd–T Curve Measurement

The current-voltage (I-V) characteristics of the samples were measured using the standard four-probe method at various temperatures. To eliminate thermal effects and thermoelectric voltages induced by the measuring current, bipolar pulsed currents were employed. Under zero-field conditions, when the current passing through the sample exceeds a certain critical value, the superconducting state is disrupted, and the sample exhibits normal-state behavior; this current is defined as the depairing current Jd [64,65]. The depairing current Id for each sample was determined based on a quench criterion of 1 μV/cm, from which the depairing current density Jd was calculated.
Figure 6a displays the I-V characteristics of sample S4 at different temperatures, As shown in Figure 6b, all samples exhibit typical characteristics of B(P)SCCO superconductors, namely a gradual decrease in Jd with increasing temperature until the superconducting state completely vanishes. Compared to the pristine sample S0, samples S1–S3 with introduced GaP quantum dots show a more pronounced suppression of Jd, which is primarily attributed to the impurity effect resulting from the incorporated heterogeneous phases. This effect reduces the superconducting transition temperature Tc, thereby causing the samples to enter the superconducting-to-normal transition region at an earlier stage.
It can be observed that among samples with the same heterophase addition content (0.2 wt.%), Jd exhibits a systematic increase with enhanced electroluminescence intensity of the GaP quantum dots (from S1, S2 to S4). Furthermore, comparing samples S3 (0.15 wt.%) and S4 (0.2 wt.%) with similar luminescence intensity but different addition amounts reveals that S4, with the higher addition content, demonstrates superior Jd performance, achieving an improvement of approximately 20% compared to S0.
These results indicate that the electroluminescent properties of GaP quantum dots exert an enhancing effect on the current-carrying capacity of B(P)SCCO superconductors. This enhancement not only correlates positively with the electroluminescence intensity but is also influenced by the addition content.

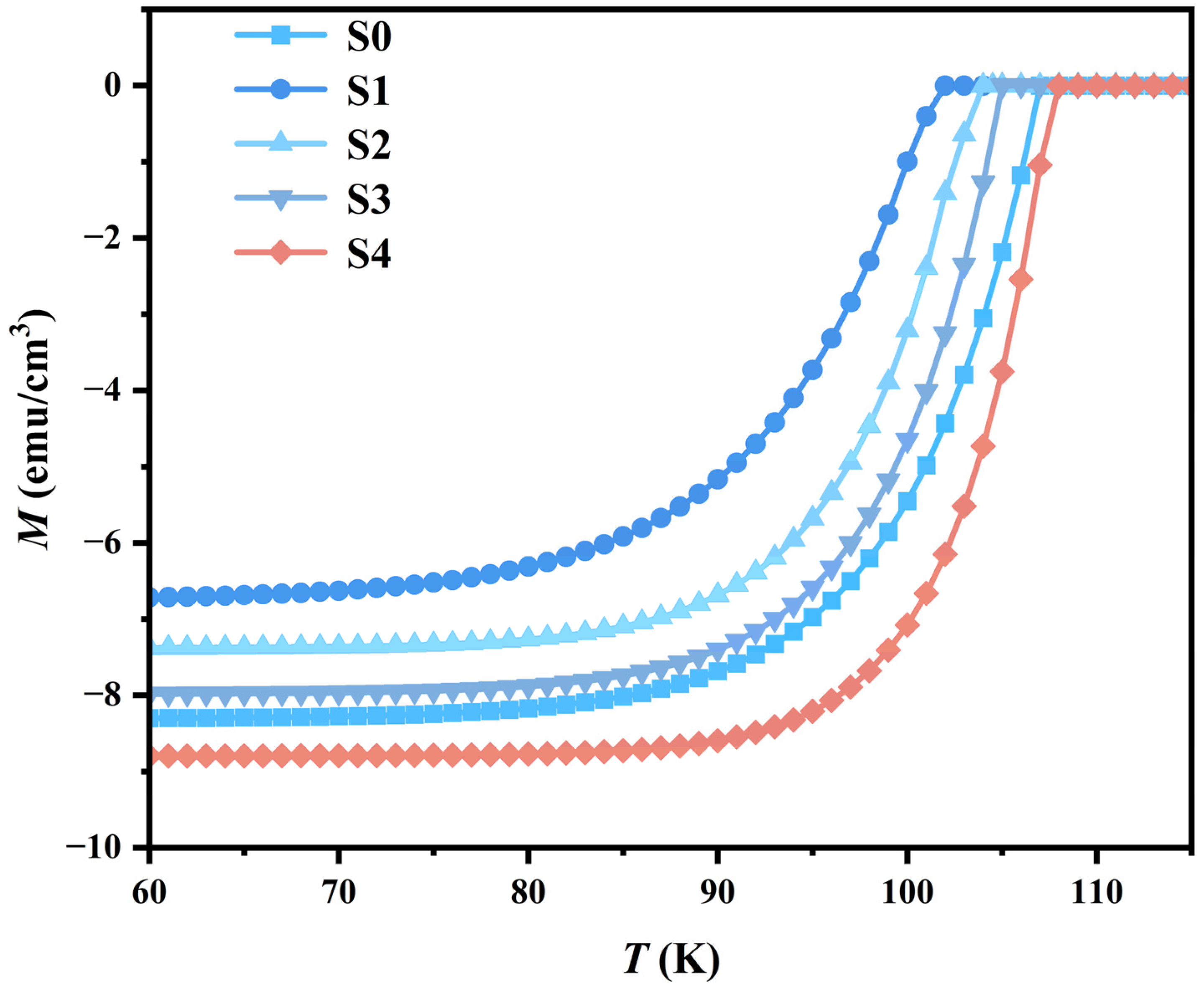
3.5. DC Magnetic Magnetization Measurement

Figure 7 presents the temperature dependence of DC magnetization (M-T) for all samples, measured in zero-field-cooled (ZFC) mode under an applied magnetic field of 100 Oe. The mass magnetization data (in emu/g) were converted to volume magnetization (in emu/cm3) using the geometrically measured density of the pelleted samples. All samples exhibit a clear diamagnetic response upon cooling, signifying the onset of superconductivity. The magnetization gradually weakens with increasing temperature until it approaches the normal-state value, which is consistent with the behavior of B(P)SCCO superconductors. The temperature at which the diamagnetic signal vanishes—defined as the point where the M-T curve merges with the normal-state baseline—is identified as 107 K, 102 K, 104.5 K, 105 K, and 108 K for samples S0, S1, S2, S3, and S4, respectively. Compared to the superconducting transition region revealed by the electrical transport measurements in Figure 5, the transition region displayed in the magnetization measurements is notably broader. This discrepancy is primarily attributed to their distinct underlying physical processes: the resistive transition marks the establishment of a zero-resistance pathway, which emerges as soon as a percolating superconducting network forms. In contrast, the magnetic transition reflects the gradual development of the bulk superconducting state (the Meissner effect), a process that can be hindered by factors such as grain boundaries, weak links, and defects.
Notably, among the samples with an identical heterophase addition content of 0.2 wt.%, the diamagnetic vanishing temperature shows a systematic increase with the enhanced electroluminescence intensity of the GaP quantum dots (progressing from S1 to S2 to S4). Furthermore, a comparison between samples S3 (0.15 wt.%) and S4 (0.2 wt.%), which possess similar luminescence intensity, reveals that S4 with the higher addition content exhibits a superior performance in the characteristic magnetic onset transition temperature (Tm,onset). These magnetic measurements are in good agreement with the electrical transport results. Together, they suggest a systematic tunability of the superconducting properties in B(P)SCCO upon the introduction of GaP quantum dots and indicate a measurable correlation between the electroluminescent characteristics of the dopants and the resultant superconducting parameters.

4. Discussion

This study systematically investigates the influence of incorporating gallium phosphide (GaP) quantum dots with varying electroluminescent characteristics on the superconducting properties of B(P)SCCO. The results indicate that the introduction of GaP quantum dots exerts a dual, competing influence. On one hand, the quantum dots themselves, as a heterogeneous phase, inevitably cause an impurity effect that suppresses superconductivity; on the other hand, their electroluminescence may induce a certain enhancement.
Specifically, sample S1, with the introduction of non-electroluminescent GaP quantum dots, exhibits a reduction in both the critical temperature (Tc) and the depairing current density (Jd) compared to the pure sample S0. This observation directly manifests the impurity effect arising from the incorporated heterogeneous phase. However, as the electroluminescence intensity of the added quantum dots increases (samples S2, S3), a gradual recovery in both Tc and Jd values is observed. Notably, for sample S4, which combines a higher luminescence intensity with a greater addition content, the zero-resistance transition temperature (Tc,0) approaches that of S0, the onset transition temperature (Tc,on) matches that of S0, and both the critical temperature (Tc) and depairing current density (Jd) surpass the values of the pure sample. Although, constrained by the electroluminescence intensity of the GaP quantum dots, the Tc,0 and Tc,on of the samples with added GaP QDs do not exceed those of the pure sample and the enhancement in Jd remains limited, this systematic variation unequivocally demonstrates that the electroluminescent property of the GaP quantum dots exerts a measurable positive influence on the superconducting performance. Furthermore, this positive effect exhibits a clear positive correlation with both the electroluminescence intensity and the addition content.
Integrated characterization results from XRD and SEM confirm that the introduction of GaP quantum dots does not significantly alter the primary phase structure, microstructure, or elemental distribution of the B(P)SCCO matrix. Based on this finding, we compare its effect with that resulting from the addition of conventional non-electroluminescent nanoparticles. The latter typically enhance the depairing current density (Jd) by introducing defects for flux pinning, but often suppress the critical temperature (Tc) due to concomitant impurity scattering, representing a case of “single-effect modulation.” In contrast, the luminescent GaP quantum dots introduced in this work demonstrate the potential for “dual-effect enhancement,” characterized by a concurrent improvement in both Tc and Jd with increasing electroluminescence intensity. This distinction suggests that the electroluminescence property likely governs a physical process distinct from conventional defect-mediated flux pinning.
Building on our previous investigations into light-emitting heterophases as a means to modulate superconducting properties, we further explore the underlying physical mechanisms and propose a preliminary theoretical model. We posit that, under an external electric bias, photons generated by electroluminescence within the heterophase may weakly couple to Cooper pairs in the superconductor. Specifically, such localized optical fields can excite surface plasmons and generate evanescent electromagnetic waves, which in turn modulate the energy matching and transport pathways of carriers at the superconductor’s surface or interface, thereby moderately enhancing the Cooper-pairing interaction [54,66]. This evanescent-field-mediated coupling is expected to exhibit an intensity-dependent resonant enhancement, consistent with our experimental observation that both Tc and Jd increase concurrently with the electroluminescence intensity.
Beyond this “evanescent-field–Cooper-pair coupling” mechanism, numerous studies have shown that optical or high-frequency electromagnetic fields can enhance superconductivity through several distinct pathways. First, non-equilibrium quasiparticle redistribution (Eliashberg mechanism) [67,68], in which an alternating field drives the quasiparticle distribution f(E) away from equilibrium, transiently increasing the superconducting gap Δ and Tc. Second, coherent excitation of the order-parameter amplitude mode (Higgs mode) [69,70], whereby strong THz fields resonantly drive the amplitude mode at ℏω ≈ 2Δ and momentarily reinforce the superconducting order. Third, optically induced nonlinear lattice dynamics and suppression of competing phases. For example, in the stripe-ordered cuprate La1.675Eu0.25Sr0.125CuO4, resonant excitation of the Cu–O stretching mode by the optical field [39] suppresses the stripe phase that competes with superconductivity and restores interlayer Josephson coupling, thereby inducing a transient superconducting state. A similar mechanism has been reported in K3C60, where optical-field-driven excitation of infrared-active phonons triggers nonlinear phonon coupling and consequently enhances the electron–phonon interaction [41]. In addition, interface-related enhancement effects [71,72], widely observed in nanoscale heterostructures, may also contribute in our system: variations in the local dielectric environment, strain state, or interfacial phonon spectrum can subtly modify the pairing interactions and thus elevate the superconducting performance.
Although the local optical fields generated by GaP quantum dots are far weaker than those produced by intense THz or mid-infrared pulses, the associated perturbations—localized electromagnetic fluctuations, slight interfacial charge rearrangements, and modest modifications of the vibrational and phononic environment—may still trigger weak non-equilibrium responses or subtle adjustments to the local pairing landscape. The cooperative action of these microscopic effects may account for the moderate enhancements in Tc and Jd observed in our experiments. The positive correlation between Tc and electroluminescence intensity further supports this integrated theoretical picture. In conclusion, the findings of this study demonstrate that the introduction of electroluminescent GaP quantum dots can induce an enhancement effect in B(P)SCCO superconductors, likely related to photon–Cooper pair coupling. This beneficial effect competes with the inherent impurity effect introduced by the quantum dots, and their interplay collectively governs the final superconducting performance. Although the precise microscopic mechanism requires further elucidation through additional experiments and refined theoretical modeling, the phenomena revealed in this work provide a valuable experimental foundation for exploring novel interactions between photons and the superconducting state.

5. Conclusions

This study investigates the effect of the electroluminescence intensity and addition content of GaP quantum dots on the superconducting properties of B(P)SCCO, including critical temperature (Tc) and depairing current density (Jd). GaP quantum dots with varying luminescence intensities were synthesized via the hot-injection method and subsequently introduced into the B(P)SCCO superconducting matrix. XRD and SEM characterization confirmed that the modified samples maintained high phase purity of the (Bi,Pb)-2223 structure along with a homogeneous microstructure. Electrical transport measurements revealed a dual, competing effect arising from the incorporated quantum dots: acting as a heterogeneous phase, they inherently generate an impurity effect that suppresses superconducting properties, while their electroluminescent characteristics potentially induce an enhancing effect. With the systematic increase in the luminescence intensity of the GaP quantum dots and optimization of their addition content, the superconducting performance of B(P)SCCO exhibited a corresponding upward trend, achieving an enhancement of approximately 1 K in Tc and up to 20% in Jd under optimal conditions. This work demonstrates a positive correlation between electroluminescent properties and superconducting parameters, establishing the potential feasibility of modulating superconducting performance through the controlled introduction of luminescent heterophases and thereby proposing a novel design strategy for the functionalization of superconducting materials.

Author Contributions

Conceptualization, methodology, X.Z.; software, Q.H. and D.C.; validation, Q.H., D.C., and Y.Q.; formal analysis, Q.H., D.C., and R.B.; investigation, Q.H., D.C., Y.Q., L.X., and X.L.; resources, X.Z.; data curation, Q.H., D.C., and Y.Q.; writing—original draft preparation, Q.H.; writing—review and editing, Q.H. and X.Z.; visualization, Q.H., D.C., and R.B.; supervision, X.Z.; project administration, X.Z.; funding acquisition, X.Z. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the National Natural Science Foundation of China for Distinguished Young Scholar under Grant No. 50025207.

Data Availability Statement

The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Maeda, H.; Tanaka, Y.; Fukutomi, M.; Asano, T. A new high-tc oxide superconductor without a rare-earth element. Jpn. J. Appl. Phys. 1988, 27, L209–L210. [Google Scholar] [CrossRef]
  2. Tarascon, J.M.; Lepage, Y.; Greene, L.H.; Bagley, B.G.; Barboux, P.; Hwang, D.M.; Hull, G.W.; McKinnon, W.R.; Giroud, M. Origin of the 110-K superconducting transition in the Bi-Sr-Ca-Cu-O system. Phys. Rev. B 1988, 38, 2504–2508. [Google Scholar] [CrossRef]
  3. Hazen, R.M.; Prewitt, C.T.; Angel, R.J.; Ross, N.L.; Finger, L.W.; Hadidiacos, C.G.; Veblen, D.R.; Heaney, P.J.; Hor, P.H.; Meng, R.L.; et al. Superconductivity in the high-Tc Bi-Ca-Sr-Cu-O system—phase identification. Phys. Rev. Lett. 1988, 60, 1174–1177. [Google Scholar] [CrossRef]
  4. Tallon, J.L.; Buckley, R.G.; Gilberd, P.W.; Presland, M.R.; Brown, I.W.M.; Bowden, M.E.; Christian, L.A.; Goguel, R. High-Tc superconducting phases in the series Bi2.1(Ca, Sr)n+1CunO2n+4+delta. Nature 1988, 333, 153–156. [Google Scholar] [CrossRef]
  5. Ikeda, Y.; Takano, M.; Hiroi, Z.; Oda, K.; Kitaguchi, H.; Takada, J.; Miura, Y.; Takeda, Y.; Yamamoto, O.; Mazaki, H. The High-Tc phase with a new modulation mode in theBi, Pb-Sr-Ca-Cu-O system. Jpn. J. Appl. Phys. 1988, 27, L2067–L2070. [Google Scholar] [CrossRef]
  6. Masuda, T.; Kato, T.; Yumura, H.; Watanabe, M.; Ashibe, Y.; Ohkura, K.; Suzawa, C.; Hirose, M.; Isojima, S.; Matsuo, K.; et al. Verification tests of a 66 kV HTSC cable system for practical use (first cooling tests). Phys. C 2002, 378, 1174–1180. [Google Scholar] [CrossRef]
  7. Kurusu, T.; Ono, M.; Hanai, S.; Kyoto, M.; Takigami, H.; Takano, H.; Watanabe, K.; Awaji, S.; Koyama, K.; Nishijima, G.; et al. A cryocooler-cooled 19 T superconducting magnet with 52 mm room temperature bore. IEEE Trans. Appl. Supercond. 2004, 14, 393–396. [Google Scholar] [CrossRef]
  8. Hao, Z.D.; Clem, J.R. From isotropic to anisotropic superconductors—A scaling approach—Comment. Phys. Rev. Lett. 1993, 71, 301. [Google Scholar] [CrossRef] [PubMed]
  9. Sharma, D.; Kumar, R.; Awana, V.P.S. dc and AC susceptibility study of sol-gel synthesized Bi2Sr2CaCu2O8+δ superconductor. Ceram. Int. 2013, 39, 1143–1152. [Google Scholar] [CrossRef]
  10. Mazwir, M.H.; Balasan, B.A.; Zulkifli, F.H.; Abd-Shukor, R. Effect of Co0.5Ni0.5Fe2O4 Nanoparticles Addition in Ag-Sheathed Bi-2223 Superconductor Tapes Prepared by Co-Precipitation Method. Mater. Sci. Forum 2020, 981, 59–65. [Google Scholar] [CrossRef]
  11. Foltyn, S.R.; Civale, L.; Macmanus-Driscoll, J.L.; Jia, Q.X.; Maiorov, B.; Wang, H.; Maley, M. Materials science challenges for high-temperature superconducting wire. Nat. Mater. 2007, 6, 631–642. [Google Scholar] [CrossRef] [PubMed]
  12. Hudakova, N.; Plechacek, V.; Dordor, P.; Flachbart, K.; Knizek, K.; Kovac, J.; Reiffers, M. Influence of pb concentration on microstructural and superconducting properties of bscco superconductors. Supercond. Sci. Technol. 1995, 8, 324–328. [Google Scholar] [CrossRef]
  13. Asghari, R.; Naghshara, H.; Arsalan, L.; Sedghi, H. Comparing the Effects of Nb, Pb, Y, and La Replacement on the Structural, Electrical, and Magnetic Characteristics of Bi-Based Superconductors. J. Supercond. Nov. Magn. 2018, 31, 3889–3898. [Google Scholar] [CrossRef]
  14. Altin, S.; Aksan, M.A.; Yakinci, M.E. Normal State Electronic Properties of Whiskers Fabricated in Bi-, Ga- and Sb-doped BSCCO System Under Applied Magnetic Fields. J. Supercond. Nov. Magn. 2011, 24, 443–448. [Google Scholar] [CrossRef]
  15. Romero-Sánchez, M.; Sánchez-Mera, T.; Santos-Cruz, J.; Pérez-García, C.E.; Olvera, M.D.; Santillán-Rodríguez, C.R.; Matutes-Aquino, J.; Contreras-Puente, G.; de Moure-Flores, F. Effect of sintering time on structural, morphological and electrical properties of Sb-doped Bi1.6Pb0.4Sr2Ca2Cu3Oy superconductor. Ceram. Int. 2022, 48, 16049–16053. [Google Scholar] [CrossRef]
  16. Annabi, M.; M’Chirgui, A.; Azzouz, F.B.; Zouaoui, M.; Salem, M.B. Effects of nano-Al2O3 particles on the superconductivity of Pb-doped BSCCO. Phys. Stat. Sol. C 2004, 1, 1920–1923. [Google Scholar]
  17. Fallah-Arani, H.; Koohani, H.; Tehrani, F.S.; Noori, N.R.; Nodoushan, N.J. The structural, magnetic, and pinning features of Bi-2223 superconductors: Effects of SiC nanoparticles addition. Ceram. Int. 2022, 48, 31121–31128. [Google Scholar] [CrossRef]
  18. Pham, A.T.; Le, T.; Nguyen, H.L.; Nguyen, H.N.; Nguyen, T.B.; Pham, P.; Nguyen, K.M.; Dang, T.B.H.; Pham, N.T.; Kieu, X.T.; et al. Effect of FePd nanoparticle addition on the superconductivity of Bi1.6Pb0.4Sr2Ca2Cu3O10+δ compounds. Ceram. Int. 2024, 50, 44736–44737. [Google Scholar] [CrossRef]
  19. Dong, Y.; Sun, A.M.; Xu, B.; Zhang, H.T.; Zhang, M. Effect of the BSCCO superconducting properties by tiny Y2O3 addition. Mod. Phys. Lett. B 2016, 30, 1650328. [Google Scholar] [CrossRef]
  20. Qiu, L.P.; Zhang, Y.R.; Gao, S.L.; Zheng, Q.H.; Zhang, T.T.; Cheng, G.T.; Cao, S.Z.; Hang, W.P.; Ramakrishna, S.; Long, Y.Z. Fabrication and magnetic properties of SiO2 nanoparticles-doped BSCCO superconducting nanofibers by solution blow spinning. Phys. C 2023, 608, 1354251. [Google Scholar] [CrossRef]
  21. Zelati, A.; Amirabadizadeh, A.; Kompany, A.; Salamati, H.; Sonier, J. Effect of Eu2O3 Nanoparticles Addition on Structural and Superconducting Properties of BSCCO. J. Supercond. Nov. Magn. 2014, 27, 1369–1379. [Google Scholar] [CrossRef]
  22. Fallah-Arani, H.; Baghshahi, S.; Sedghi, A.; Riahi-Noori, N. Enhancement in the performance of BSCCO (Bi-2223) superconductor with functionalized TiO2 nanorod additive. Ceram. Int. 2019, 45, 21878–21886. [Google Scholar] [CrossRef]
  23. Shalaby, M.S.; Hamed, M.H.; Yousif, N.M.; Hashem, H.M. The impact of the addition of Bi2Te3 nanoparticles on the structural and the magnetic properties of the Bi-2223 high-Tc superconductor. Ceram. Int. 2021, 47, 25236–25248. [Google Scholar] [CrossRef]
  24. Ilhamsyah, A.B.P.; Zabidi, N.A.M.; Hashidi, M.A.H.; Suib, N.R.M.; Mahat, A.M.; Abd-Shukor, R.; Masnita, M.J. Effect of copper (II) sulfide addition on the transport critical current density and AC susceptibility of Bi1.6Pb0.4Sr2Ca2Cu3O10 superconductor. Appl. Phys. A 2024, 130, 590. [Google Scholar] [CrossRef]
  25. Vu, L.H.; Pham, A.T.; Thien, N.D.; Nam, N.H.; Riviere, E.; Pham, Q.N.; Man, N.K.; Binh, N.T.; Hong, N.T.M.; Cuong, L.; et al. Enhancements of critical current density in Bi1.6Pb0.4Sr2Ca2Cu3O10+δ superconductors by additions of SnO2 nanoparticles. Ceram. Int. 2023, 49, 27614–27621. [Google Scholar] [CrossRef]
  26. Suib, N.R.M.; Ilhamsyah, A.B.P.; Mujaini, M.; Mahat, A.M.; Abd-Shukor, R. AC Susceptibility and Electrical Properties of BiFeO3 Nanoparticles Added Bi1.6Pb0.4Sr2Ca2Cu3O10 Superconductor. J. Supercond. Nov. Magn. 2023, 36, 1003–1010. [Google Scholar] [CrossRef]
  27. El Makdah, M.H.; El Ghouch, N.; El-Dakdouki, M.H.; Awad, R.; Matar, M. Synthesis, characterization, and Vickers microhardness for (YIG)x/(Bi, Pb)-2223 superconducting phase. Ceram. Int 2023, 49, 22400–22422. [Google Scholar] [CrossRef]
  28. Karan, S.M.; Chattoraj, T.; Ali, M.A.; Banerjee, S.S. Co2C Nanoparticle-Decorated Grain Boundaries: A Source of Robust, Thermally Stable Vortex Pinning in Bi-2223 High Tc Superconductors. ACS Appl. Electron. Mater. 2024, 7, 202–214. [Google Scholar] [CrossRef]
  29. Llordés, A.; Palau, A.; Gázquez, J.; Coll, M.; Vlad, R.; Pomar, A.; Arbiol, J.; Guzmán, R.; Ye, S.; Rouco, V.; et al. Nanoscale strain-induced pair suppression as a vortex-pinning mechanism in high-temperature superconductors. Nat. Mater. 2012, 11, 329–336. [Google Scholar] [CrossRef]
  30. Scanlan, R.M.; Malozemoff, A.P.; Larbalestier, D.C. Superconducting materials for large scale applications. Proc. IEEE 2004, 92, 1639–1654. [Google Scholar] [CrossRef]
  31. Matsumoto, K.; Horide, T.; Osamura, K.; Mukaida, M.; Yoshida, Y.; Ichinose, A.; Horii, S. Enhancement of critical current density of YBCO films by introduction of artificial pinning centers due to the distributed nano-scaled Y2O3 islands on substrates. Phys. C 2004, 412, 1267–1271. [Google Scholar] [CrossRef]
  32. Feighan, J.P.F.; Kursumovic, A.; MacManus-Driscoll, J.L. Materials design for artificial pinning centres in superconductor PLD coated conductors. Supercond. Sci. Technol. 2017, 30, 123001. [Google Scholar] [CrossRef]
  33. Horide, T.; Kawamura, T.; Matsumoto, K.; Ichinose, A.; Yoshizumi, M.; Izumi, T.; Shiohara, Y. Jc improvement by double artificial pinning centers of BaSnO3 nanorods and Y2O3 nanoparticles in YBa2Cu3O7 coated conductors. Supercond. Sci. 2013, 26, 075019. [Google Scholar] [CrossRef]
  34. Luo, C.R.; Kang, L.; Zhao, Q.; Fu, Q.H.; Song, J.; Zhao, X.P. Effect of nonuniform-defect split ring resonators on the left-handed metamaterials. Acta Phys. Sin. 2005, 54, 1607–1612. [Google Scholar]
  35. Zhang, F.L.; Zhao, Q.; Liu, Y.H.; Luo, C.R.; Zhao, X.P. Behaviour of hexagon split ring resonators and left-handed metamaterials. Chin. Phys. Lett. 2004, 21, 1330–1332. [Google Scholar] [CrossRef]
  36. Smolyaninova, V.N.; Yost, B.; Zander, K.; Osofsky, M.S.; Kim, H.; Saha, S.; Greene, R.L.; Smolyaninov, I.I. Experimental demonstration of superconducting critical temperature increase in electromagnetic metamaterials. Sci. Rep. 2014, 4, 7321. [Google Scholar] [CrossRef]
  37. Smolyaninov, I.I.; Smolyaninova, V.N. Theoretical modeling of critical temperature increase in metamaterial superconductors. Phys. Rev. B 2016, 93, 184510. [Google Scholar] [CrossRef]
  38. Rosen, P.F.; Calvin, J.J.; Woodfield, B.F.; Smolyaninova, V.N.; Prestigiacomo, J.C.; Osofsky, M.S.; Smolyaninov, I.I. Normal state specific heat of a core-shell aluminum-alumina metamaterial composite with enhanced Tc. Phys. Rev. B 2021, 103, 024512. [Google Scholar] [CrossRef]
  39. Fausti, D.; Tobey, R.I.; Dean, N.; Kaiser, S.; Dienst, A.; Hoffmann, M.C.; Pyon, S.; Takayama, T.; Takagi, H.; Cavalleri, A. Light-Induced Superconductivity in a Stripe-Ordered Cuprate. Science 2011, 331, 189–191. [Google Scholar] [CrossRef] [PubMed]
  40. Nicoletti, D.; Casandruc, E.; Laplace, Y.; Khanna, V.; Hunt, C.R.; Kaiser, S.; Dhesi, S.S.; Gu, G.D.; Hill, J.P.; Cavalleri, A. Optically induced superconductivity in striped La2−xBaxCuO4 by polarization-selective excitation in the near infrared. Phys. Rev. B 2014, 90, 100503. [Google Scholar] [CrossRef]
  41. Mitrano, M.; Cantaluppi, A.; Nicoletti, D.; Kaiser, S.; Perucchi, A.; Lupi, S.; Di Pietro, P.; Pontiroli, D.; Riccò, M.; Clark, S.R.; et al. Possible light-induced superconductivity in K3C60 at high temperature. Nature 2016, 530, 461–464. [Google Scholar] [CrossRef]
  42. Cantaluppi, A.; Buzzi, M.; Jotzu, G.; Nicoletti, D.; Mitrano, M.; Pontiroli, D.; Riccò, M.; Perucchi, A.; Di Pietro, P.; Cavalleri, A. Pressure tuning of light-induced superconductivity in K3C60. Nat. Phys. 2018, 14, 837–841. [Google Scholar] [CrossRef]
  43. Fava, S.; De Vecchi, G.; Jotzu, G.; Buzzi, M.; Gebert, T.; Liu, Y.; Keimer, B.; Cavalleri, A. Magnetic field expulsion in optically driven YBa2Cu3O6.48. Nature 2024, 632, 75–80. [Google Scholar] [CrossRef] [PubMed]
  44. Zhang, Z.W.; Tao, S.; Chen, G.W.; Zhao, X.P. Improving the Critical Temperature of MgB2 Superconducting Metamaterials Induced by Electroluminescence. J. Supercond. Nov. Magn. 2016, 29, 1159–1162. [Google Scholar] [CrossRef]
  45. Tao, S.; Li, Y.B.; Chen, G.W.; Zhao, X.P. Critical Temperature of Smart Meta-superconducting MgB2. J. Supercond. Nov. Magn. 2017, 30, 1405–1411. [Google Scholar] [CrossRef]
  46. Chen, H.G.; Li, Y.B.; Chen, G.W.; Xu, L.X.; Zhao, X.P. The Effect of Inhomogeneous Phase on the Critical Temperature of Smart Meta-superconductor MgB2. J. Supercond. Nov. Magn. 2018, 31, 3175–3182. [Google Scholar] [CrossRef]
  47. Li, Y.B.; Chen, H.G.; Qi, W.C.; Chen, G.W.; Zhao, X.P. Inhomogeneous Phase Effect of Smart Meta-Superconducting. J. Low Temp. Phys. 2018, 191, 217–227. [Google Scholar] [CrossRef]
  48. Li, Y.B.; Chen, H.G.; Wang, M.Z.; Xu, L.X.; Zhao, X.P. Smart meta-superconductor MgB2 constructed by the dopant phase of luminescent nanocomposite. Sci. Rep. 2019, 9, 14194. [Google Scholar] [CrossRef]
  49. Li, Y.B.; Han, G.Y.; Zou, H.Y.; Tang, L.; Chen, H.G.; Zhao, X.P. Reinforcing Increase of ΔTc in MgB2 Smart Meta-Superconductors by Adjusting the Concentration of Inhomogeneous Phases. Materials 2021, 14, 3066. [Google Scholar] [CrossRef]
  50. Chen, H.; Li, Y.; Wang, M.; Han, G.; Shi, M.; Zhao, X. Smart Metastructure Method for Increasing Tc of Bi(Pb)SrCaCuO High-Temperature Superconductors. J. Supercond. Nov. Magn. 2020, 33, 3015–3025. [Google Scholar] [CrossRef]
  51. Chen, H.G.; Wang, M.Z.; Qi, Y.; Li, Y.B.; Zhao, X.P. Relationship between the Tc of Smart Meta-Superconductor Bi(Pb)SrCaCuO and Inhomogeneous Phase Content. Nanomaterials 2021, 11, 1061. [Google Scholar] [CrossRef] [PubMed]
  52. Chen, H.G.; Li, Y.B.; Qi, Y.; Wang, M.Z.; Zou, H.Y.; Zhao, X.P. Critical Current Density and Meissner Effect of Smart Meta-Superconductor MgB2 and Bi(Pb)SrCaCuO. Materials 2022, 15, 972. [Google Scholar] [CrossRef] [PubMed]
  53. Qi, Y.; Chen, D.; Li, Y.B.; Sun, C.; Hai, Q.Y.; Shi, M.; Chen, H.G.; Zhao, X.P. Green-light p-n junction particle inhomogeneous phase enhancement of MgB2 smart meta-superconductors. J. Mater. Sci.: Mater. Electron. 2024, 35, 424. [Google Scholar] [CrossRef]
  54. Qi, Y.; Chen, D.; Sun, C.; Hai, Q.Y.; Zhao, X.P. The Influence of Electroluminescent Inhomogeneous Phase Addition on Enhancing MgB2 Superconducting Performance and Magnetic Flux Pinning. Materials 2024, 17, 1903. [Google Scholar] [CrossRef] [PubMed]
  55. Hai, Q.Y.; Chen, H.G.; Sun, C.; Chen, D.; Qi, Y.; Shi, M.; Zhao, X.P. Green-Light GaN p-n Junction Luminescent Particles Enhance the Superconducting Properties of B(P)SCCO Smart Meta-Superconductors (SMSCs). Nanomaterials 2023, 13, 3029. [Google Scholar] [CrossRef]
  56. Chen, D.; Bi, R.Y.; Xun, L.F.; Li, X.Y.; Hai, Q.Y.; Qi, Y.; Zhao, X.P. Core-Shell Composite GaP Nanoparticles with Efficient Electroluminescent Properties. Materials 2025, 18, 487. [Google Scholar] [CrossRef]
  57. Qi, Y.; Chen, D.; Bi, R.Y.; Hai, Q.Y.; Xun, L.F.; Li, X.Y.; Zhao, X.P. The effect of GaP quantum dot luminescent addition on the superconducting properties and electron-phonon coupling in MgB2. Ceram. Int. 2025, 51, 24043–24052. [Google Scholar] [CrossRef]
  58. Timusk, T.; Statt, B. The pseudogap in high-temperature superconductors: An experimental survey. Rep. Prog. Phys. 1999, 62, 61–122. [Google Scholar] [CrossRef]
  59. Bergeal, N.; Lesueur, J.; Aprili, M.; Faini, G.; Contour, J.P.; Leridon, B. Pairing fluctuations in the pseudogap state of copper-oxide superconductors probed by the Josephson effect. Nat. Phys. 2008, 4, 608–611. [Google Scholar] [CrossRef]
  60. Vargas-Pineda, E.M.; Rivera-Contreras, L.J.; Pineda-Peña, G.; Téllez, D.A.L.; Roa-Rojas, J. Observation of the Granular Josephson Mechanism and the Vortex-Glass Transition in the Polycrystalline GdBa2Cu3O7- δ Superconductor. J. Supercond. Novel Magn. 2024, 37, 1957–1963. [Google Scholar] [CrossRef]
  61. Moraitis, P.; Koutsokeras, L.; Stamopoulos, D. AC Magnetic Susceptibility: Mathematical Modeling and Experimental Realization on Poly-Crystalline and Single-Crystalline High-Tc Superconductors YBa2Cu3O7−δ and Bi2−xPbxSr2Ca2Cu3O10+y. Materials 2024, 17, 1744. [Google Scholar] [CrossRef]
  62. Nikolo, M. In Numerical Modeling of Ac Susceptibility and Induced Nonlinear Voltage Waveforms of High-Tc Granular Superconductors. In Proceedings of the 10th International Conference on Application of Mathematics in Technical and Natural Sciences (AMiTaNS), Albena, Bulgaria, 20–25 June 2018. [Google Scholar]
  63. Klamu, P.W. AC Susceptibility and Resistivity of the Granular Nd1.85Ce0.15CuO4.03. Phys. Stat. Sol. (A) 1993, 136, 181–188. [Google Scholar] [CrossRef]
  64. Stamopoulos, D.; Speliotis, A.; Niarchos, D. From the second magnetization peak to peak effect. A study of superconducting properties in Nb films and MgB2 bulk samples. Supercond. Sci. Technol. 2004, 17, 1261–1274. [Google Scholar] [CrossRef]
  65. Ruiz, H.S.; Hänisch, J.; Polichetti, M.; Galluzzi, A.; Gozzelino, L.; Torsello, D.; Milošević-Govedarović, S.; Grbović-Novaković, J.; Dobrovolskiy, O.V.; Lang, W.; et al. Critical current density in advanced superconductors. Prog. Mater. Sci. 2026, 155, 101492. [Google Scholar] [CrossRef]
  66. Zhao, X.P.; Hai, Q.Y.; Shi, M.; Chen, H.G.; Li, Y.B.; Qi, Y. An Improved Smart Meta-Superconductor MgB2. Nanomaterials 2022, 12, 2590. [Google Scholar] [CrossRef]
  67. Ivlev, B.I.; Lisitsyn, S.G.; Eliashberg, G.M. Nonequilibrium Excitations in Superconductors in High-Frequency Fields. J. Low Temp. Phys. 1973, 10, 449–468. [Google Scholar] [CrossRef]
  68. Wyatt, A.F.G.; Dmitriev, V.M.; Moore, W.S.; Sheard, F.W. Microwave-Enhanced Critical Supercurrents in Constricted Tin Films. Phys. Rev. Lett. 1966, 16, 1166–1169. [Google Scholar] [CrossRef]
  69. Zachmann, M.; Croitoru, M.D.; Vagov, A.; Axt, V.M.; Papenkort, T.; Kuhn, T. Ultrafast terahertz-field-induced dynamics of superconducting bulk and quasi-1D samples. New. J. Phys. 2013, 15, 055016. [Google Scholar] [CrossRef]
  70. Matsunaga, R.; Tsuji, N.; Fujita, H.; Sugioka, A.; Makise, K.; Uzawa, Y.; Terai, H.; Wang, Z.; Aoki, H.; Shimano, R. Light-induced collective pseudospin precession resonating with Higgs mode in asuperconductor. Science 2014, 345, 1145–1149. [Google Scholar] [CrossRef] [PubMed]
  71. Yang, B.; Zhao, C.; Xia, B.; Ma, H.; Chen, H.; Cai, J.; Yang, H.; Liu, X.; Liu, L.; Guan, D.; et al. Interface-enhanced superconductivity in monolayer 1T’-MoTe2 on SrTiO3(001). Quantum Front. 2023, 2, 9. [Google Scholar] [CrossRef]
  72. Maggiora, J.; Wang, X.; Zheng, R. Superconductivity and interfaces. Phys. Rep. 2024, 1076, 1–49. [Google Scholar] [CrossRef]
Materials 18 05458 g001
Figure 1. (a) EL spectra of GaP quantum dot electroluminescent particles, (b) TEM images of GaP quantum dot electroluminescent particles, (c) XRD patterns of GaP quantum dot electroluminescent particles, and (d–f) XPS analysis of GaP quantum dot electroluminescent particles.
Figure 1. (a) EL spectra of GaP quantum dot electroluminescent particles, (b) TEM images of GaP quantum dot electroluminescent particles, (c) XRD patterns of GaP quantum dot electroluminescent particles, and (d–f) XPS analysis of GaP quantum dot electroluminescent particles.
Materials 18 05458 g001
Materials 18 05458 g002
Figure 2. (a) XRD patterns of the samples S0 to S4, (b) Refined fitting plots for samples S0 and S4.
Figure 2. (a) XRD patterns of the samples S0 to S4, (b) Refined fitting plots for samples S0 and S4.
Materials 18 05458 g002
Materials 18 05458 g003
Figure 3. SEM images of samples (a) S0, (b) S1, (c) S4.
Figure 3. SEM images of samples (a) S0, (b) S1, (c) S4.
Materials 18 05458 g003
Materials 18 05458 g004
Figure 4. (a) BSE image of sample S4 and the corresponding EDS elemental maps for (b) Bi, (c) Pb, (d) Sr, (e) Ca, and (f) Cu.
Figure 4. (a) BSE image of sample S4 and the corresponding EDS elemental maps for (b) Bi, (c) Pb, (d) Sr, (e) Ca, and (f) Cu.
Materials 18 05458 g004
Materials 18 05458 g005
Figure 5. (a) The curve of samples’ resistance–temperature variation within the temperature range of 90–150 K, (b) the derivatives (dR/dT) of resistance R with respect to temperature T at various temperatures (blue solid line), along with the fitted normal-state resistance Rn (blue dashed line) for the samples S0.
Figure 5. (a) The curve of samples’ resistance–temperature variation within the temperature range of 90–150 K, (b) the derivatives (dR/dT) of resistance R with respect to temperature T at various temperatures (blue solid line), along with the fitted normal-state resistance Rn (blue dashed line) for the samples S0.
Materials 18 05458 g005
Materials 18 05458 g006
Figure 6. (a) I-V curves of sample S4 at different temperatures, (b) depairing current Jd of the samples S0 to S4 within the temperature range of 90–115 K.
Figure 6. (a) I-V curves of sample S4 at different temperatures, (b) depairing current Jd of the samples S0 to S4 within the temperature range of 90–115 K.
Materials 18 05458 g006
Materials 18 05458 g007
Figure 7. The DC magnetic magnetization of the samples S0 to S4.
Figure 7. The DC magnetic magnetization of the samples S0 to S4.
Materials 18 05458 g007
Table 1. Electroluminescence intensity and addition content of the luminescent hetero-phase of the samples S0 to S4.
Table 1. Electroluminescence intensity and addition content of the luminescent hetero-phase of the samples S0 to S4.
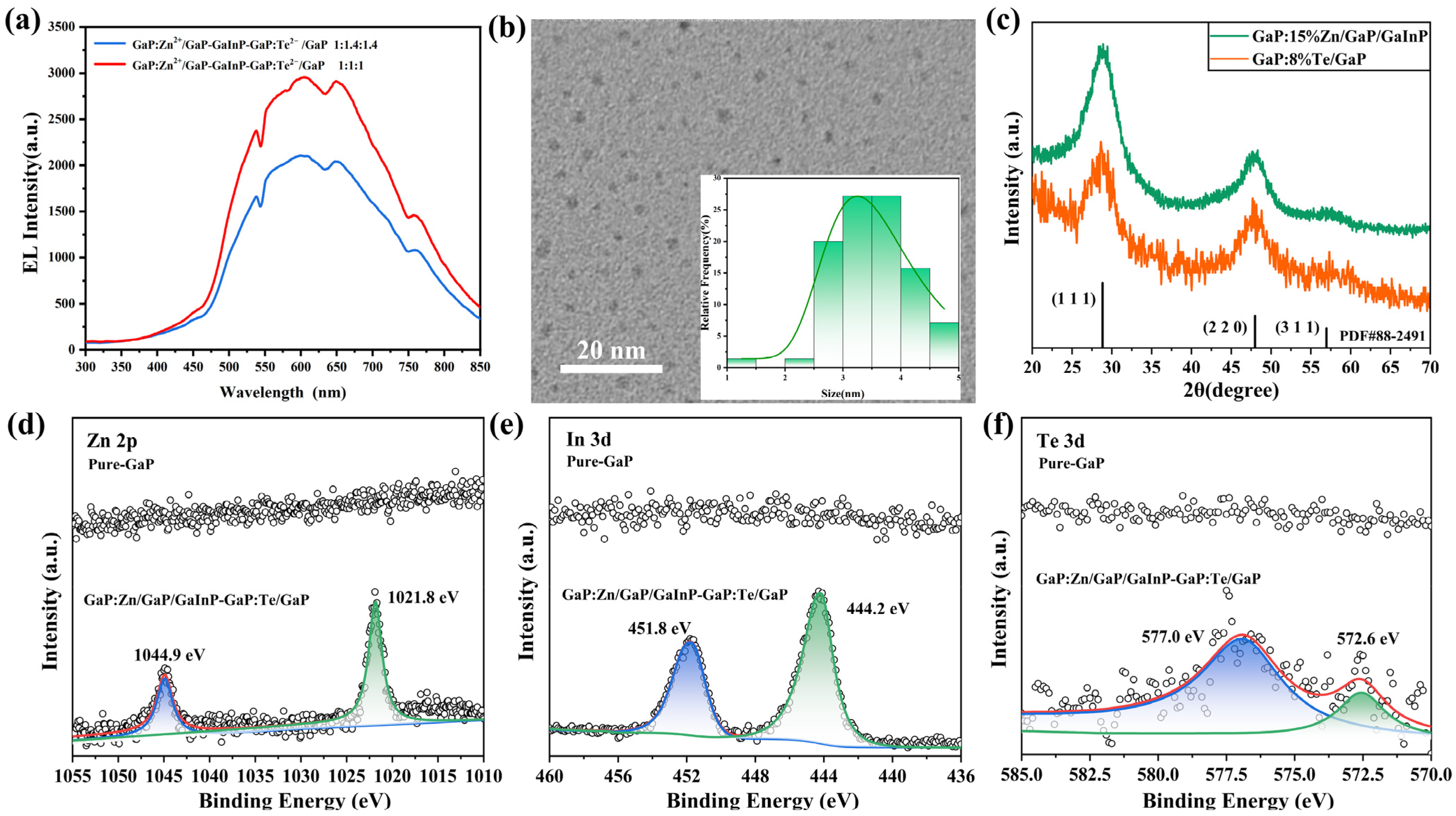
SampleHetero-PhaseEL Intensity a.u.Addition Content wt.%Sintering Process
S0//0840 °C 120 h
S1GaP/0.2840 °C 120 h
S2GaP (1:1.4:1.4)21000.2840 °C 120 h
S3GaP (1:1:1)29500.15840 °C 120 h
S4GaP (1:1:1)29500.2840 °C 120 h
Table 2. Lattice parameters of (Bi,Pb)-2223 and phase volume fractions of the samples S0 to S4.
Table 2. Lattice parameters of (Bi,Pb)-2223 and phase volume fractions of the samples S0 to S4.
SampleLattice Parameters of (Bi,Pb)-2223Phase Volume Fractions
a (Å)b (Å)c (Å)V (Å3)2223%2212%2201%
S05.415.4237.121089.894.492.413.1
S15.415.4137.101086.093.353.453.20
S25.415.4237.121089.192.495.273.24
S35.415.4237.121089.095.392.212.4
S45.415.4237.121080.194.163.642.2
Table 3. Critical transition temperature Tc,0, Tc,on, Tc, and room temperature resistance R295K of the samples S0 to S4.
Table 3. Critical transition temperature Tc,0, Tc,on, Tc, and room temperature resistance R295K of the samples S0 to S4.
SampleTc,0 (K)Tc,on (K)Tc (K)ΔT (K)R295K (mΩ)
S0103 ± 0.14114 ± 0.12107 ± 0.2116.30
S195 ± 0.17112 ± 0.13104 ± 0.181711.90
S297 ± 0.11113 ± 0.16105 ± 0.141610.97
S398 ± 0.15114 ± 0.18106 ± 0.151610.32
S4102 ± 0.19114 ± 0.14109 ± 0.161211.73
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Hai, Q.; Chen, D.; Bi, R.; Qi, Y.; Xun, L.; Li, X.; Zhao, X. Tunable Superconductivity in BSCCO via GaP Quantum Dots. Materials 2025, 18, 5458. https://doi.org/10.3390/ma18235458

AMA Style

Hai Q, Chen D, Bi R, Qi Y, Xun L, Li X, Zhao X. Tunable Superconductivity in BSCCO via GaP Quantum Dots. Materials. 2025; 18(23):5458. https://doi.org/10.3390/ma18235458

Chicago/Turabian Style

Hai, Qingyu, Duo Chen, Ruiyuan Bi, Yao Qi, Lifeng Xun, Xiaoyan Li, and Xiaopeng Zhao. 2025. "Tunable Superconductivity in BSCCO via GaP Quantum Dots" Materials 18, no. 23: 5458. https://doi.org/10.3390/ma18235458

APA Style

Hai, Q., Chen, D., Bi, R., Qi, Y., Xun, L., Li, X., & Zhao, X. (2025). Tunable Superconductivity in BSCCO via GaP Quantum Dots. Materials, 18(23), 5458. https://doi.org/10.3390/ma18235458

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Article metric data becomes available approximately 24 hours after publication online.
Back to TopTop