Analysis of Load-Bearing Capacity and Lateral-Torsional Buckling (LTB) Stability of OSB Laminated and I-Beams Made of Wood and Wood-Based Materials
Abstract
1. Introduction
2. Materials and Methods
- Preparation of OSB laminated beam samples and I-beam samples with identical geometric dimensions,
- Conditioning of samples under constant humidity and temperature conditions (20 ± 2 °C, 55 ± 5% RH),
- Execution of four-point bending tests in accordance with EOTA guidelines,
- Recording of force, displacements, and strains during loading,
- Determination of stiffness, ultimate load-bearing capacity, and failure modes of the tested beams,
- Analysis of the influence of material type (OSB, solid wood) and bonding technology on the repeatability of results,
- Photographic and descriptive documentation of the test process and failure mechanisms.
- Development of 3D spatial models of laminated beams and I-beams in the Abaqus/Standard 2022 environment,
- Assignment of actual material properties for OSB and solid wood,
- Validation of the numerical model in the elastic range based on laboratory test results,
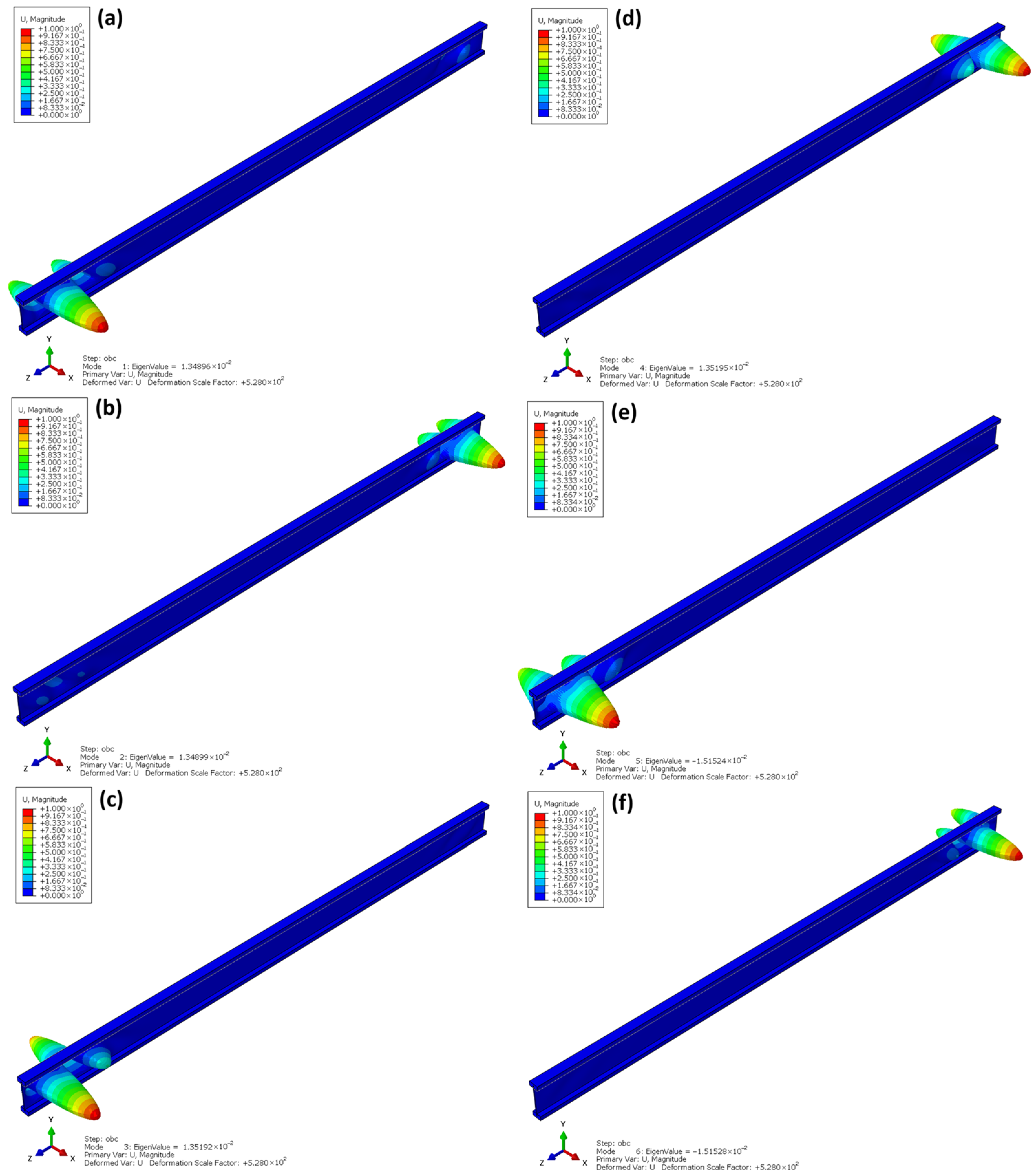
- Execution of linear buckling analysis (Buckle Analysis) to determine buckling modes,
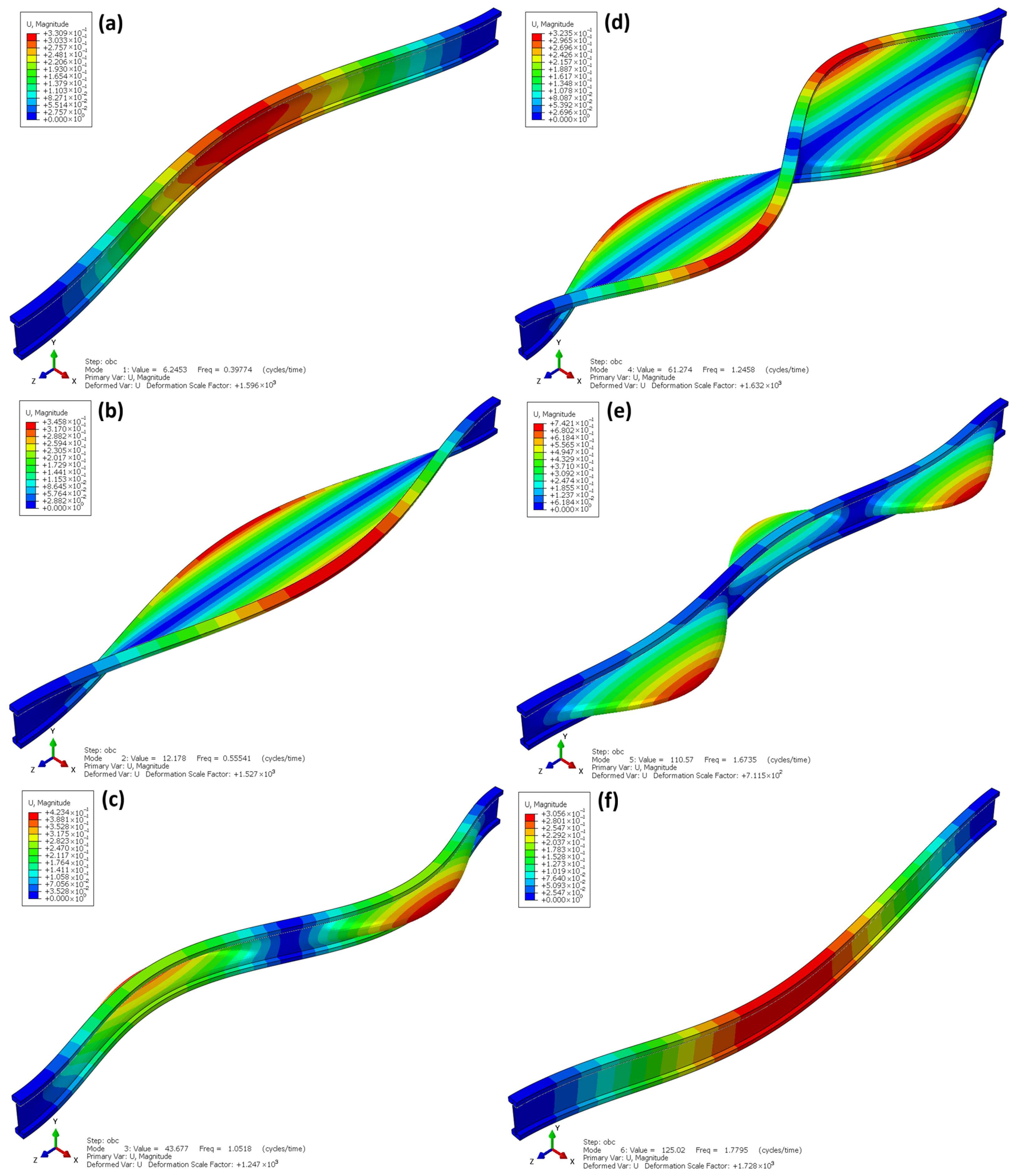
- Performance of modal analysis (Linear Frequency Extraction) to identify natural frequencies and mode shapes,
- Assessment of the influence of geometric and material parameters on the lateral-torsional buckling (LTB) stability of the tested elements.
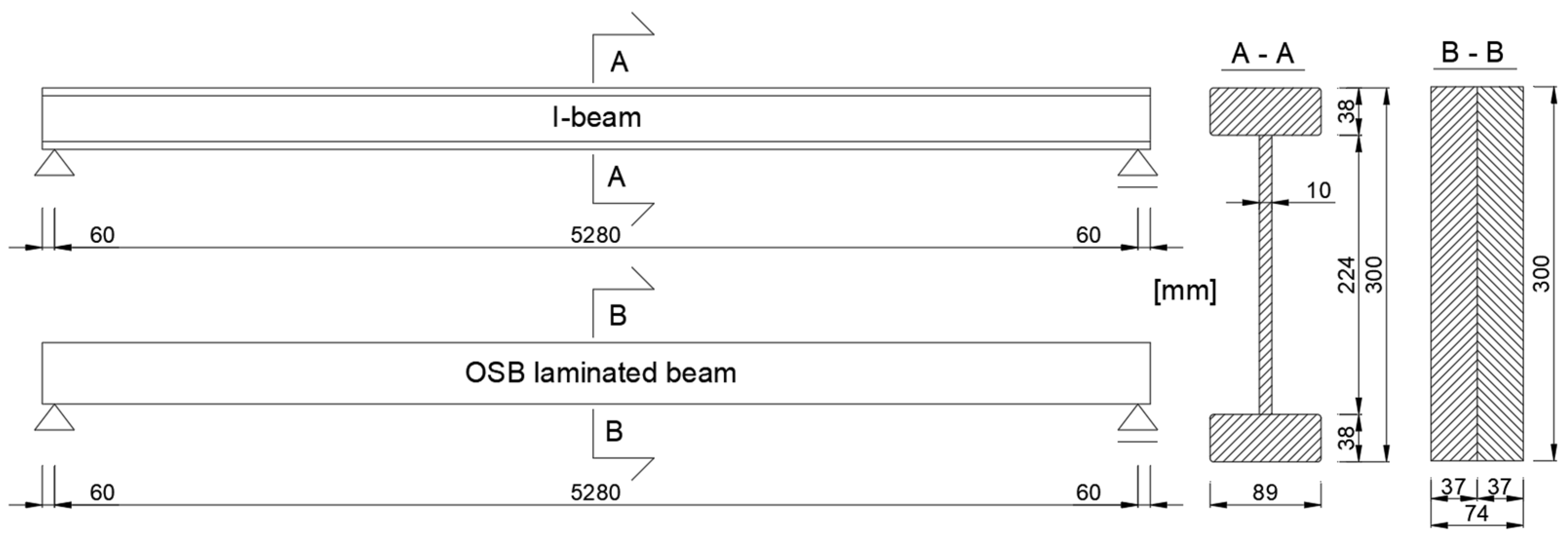
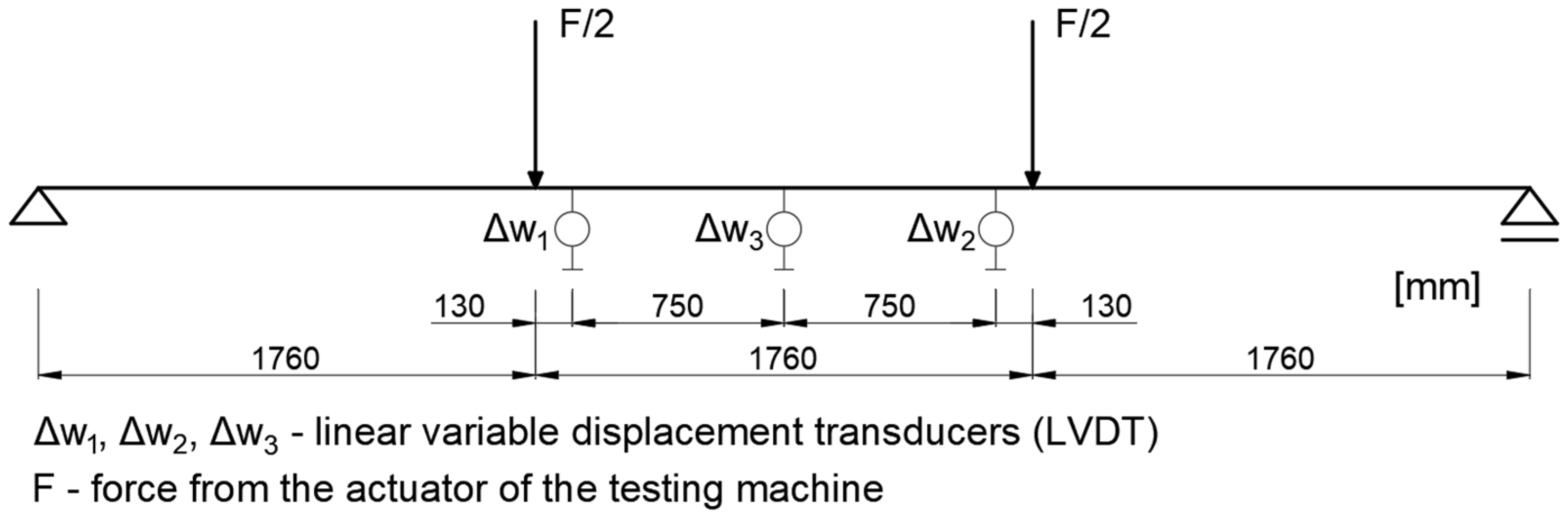
2.1. Laboratory Tests
- —bending stiffness [Nmm2],
- —increase in force during the change in actuator displacement of the testing machine from 2.0 mm to 10.0 mm [N],
- —span of the beam measured between the axes of the supports [mm],
- —span of the deflection measurement system within the pure bending zone [mm],
- —deflection at the midpoint of the deflection measurement system span [mm].
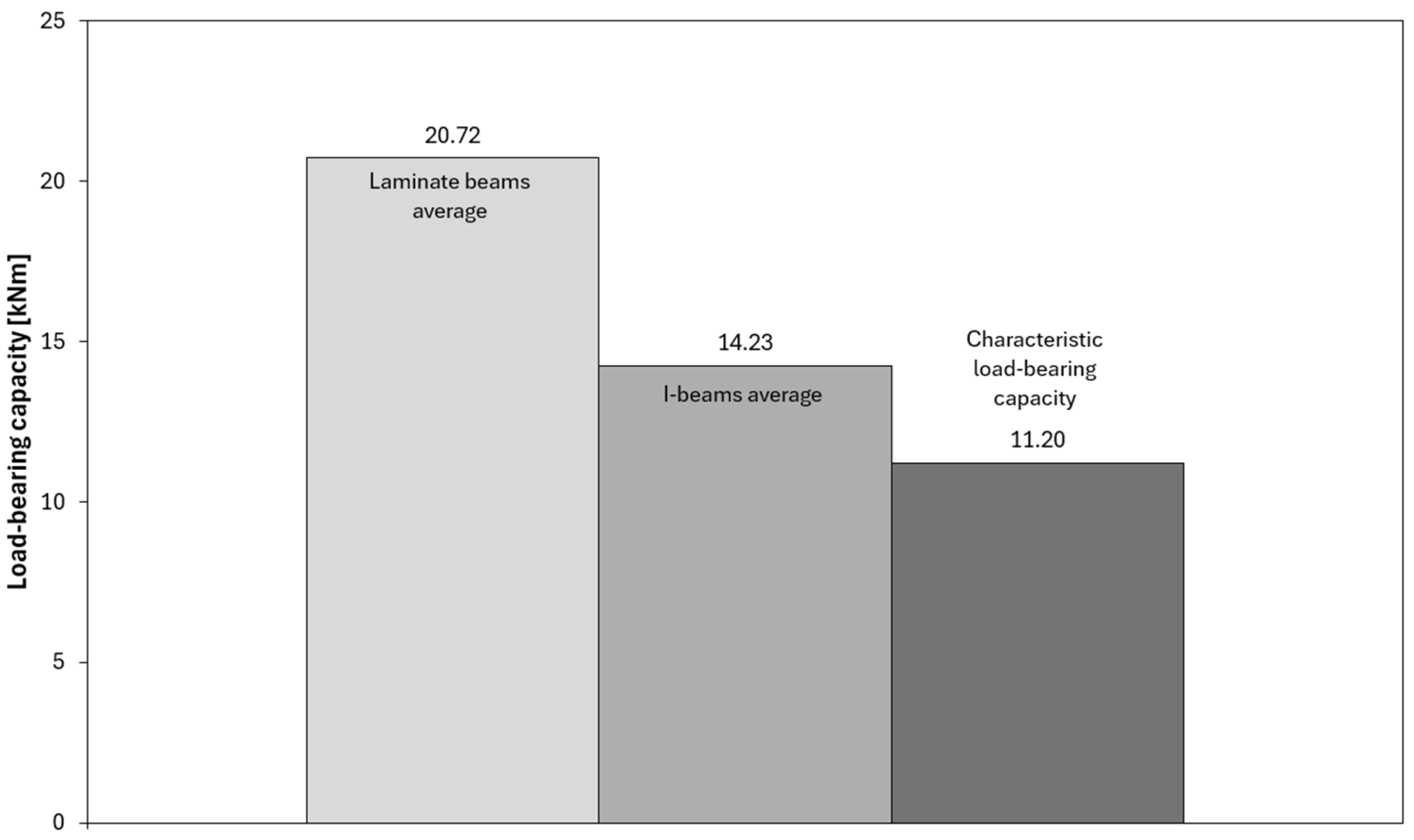
- —bending capacity [kNm]
- —maximum force recorded during the test [kN],
- —span of the beam measured between the axes of the supports [m].
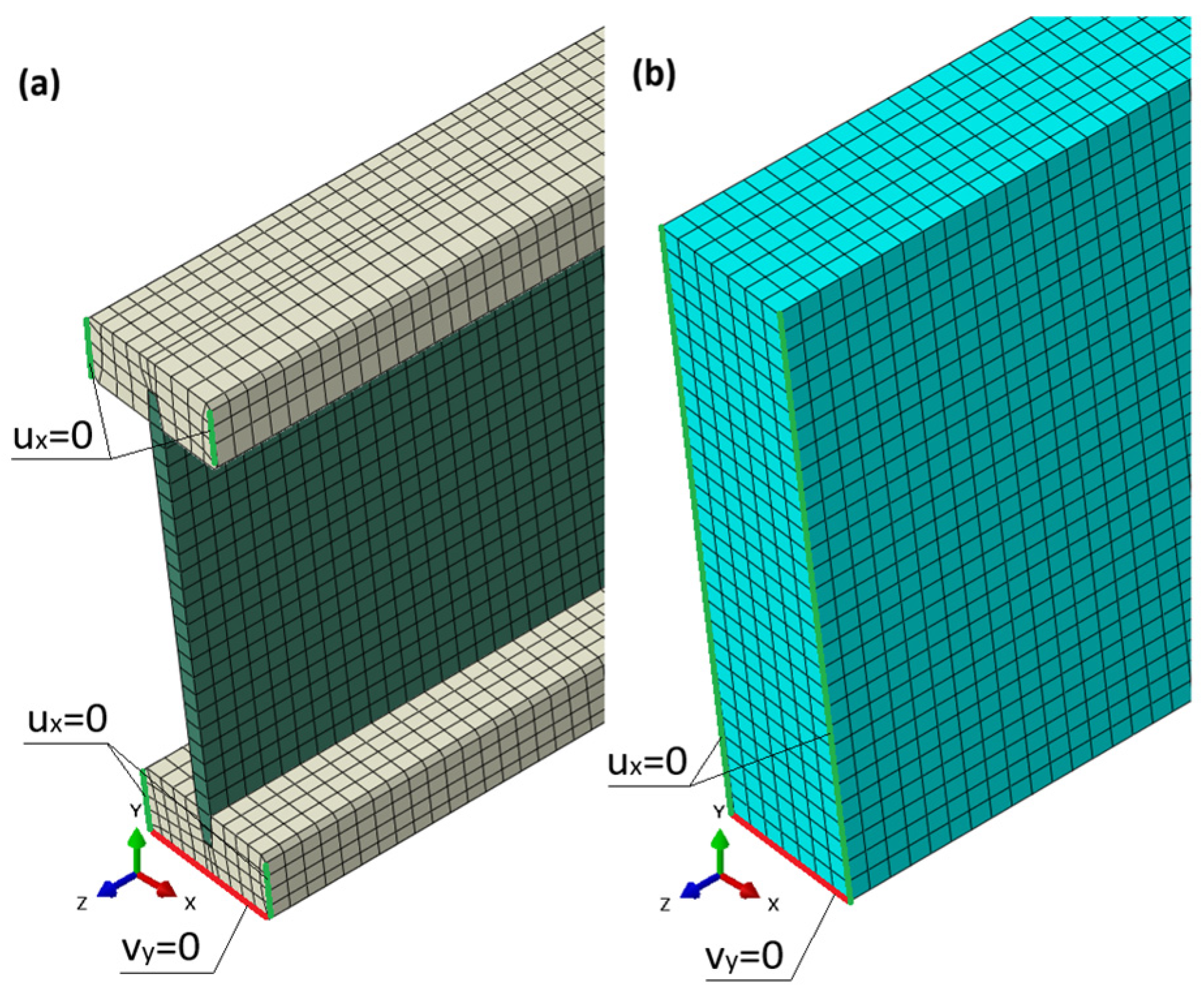
2.2. Numerical Model
- —classical material stiffness matrix,
- —geometric stiffness matrix,
- —eigenvalue (reference load multiplier),
- —eigenvector (buckling mode shape).
- —mass matrix,
- —damping matrix,
- —structural stiffness matrix,
- —displacement vector,
- —external force vector.
- —mode shape vector (eigenmode),
- —angular frequency of natural vibrations [rad/s].
3. Results and Discussion
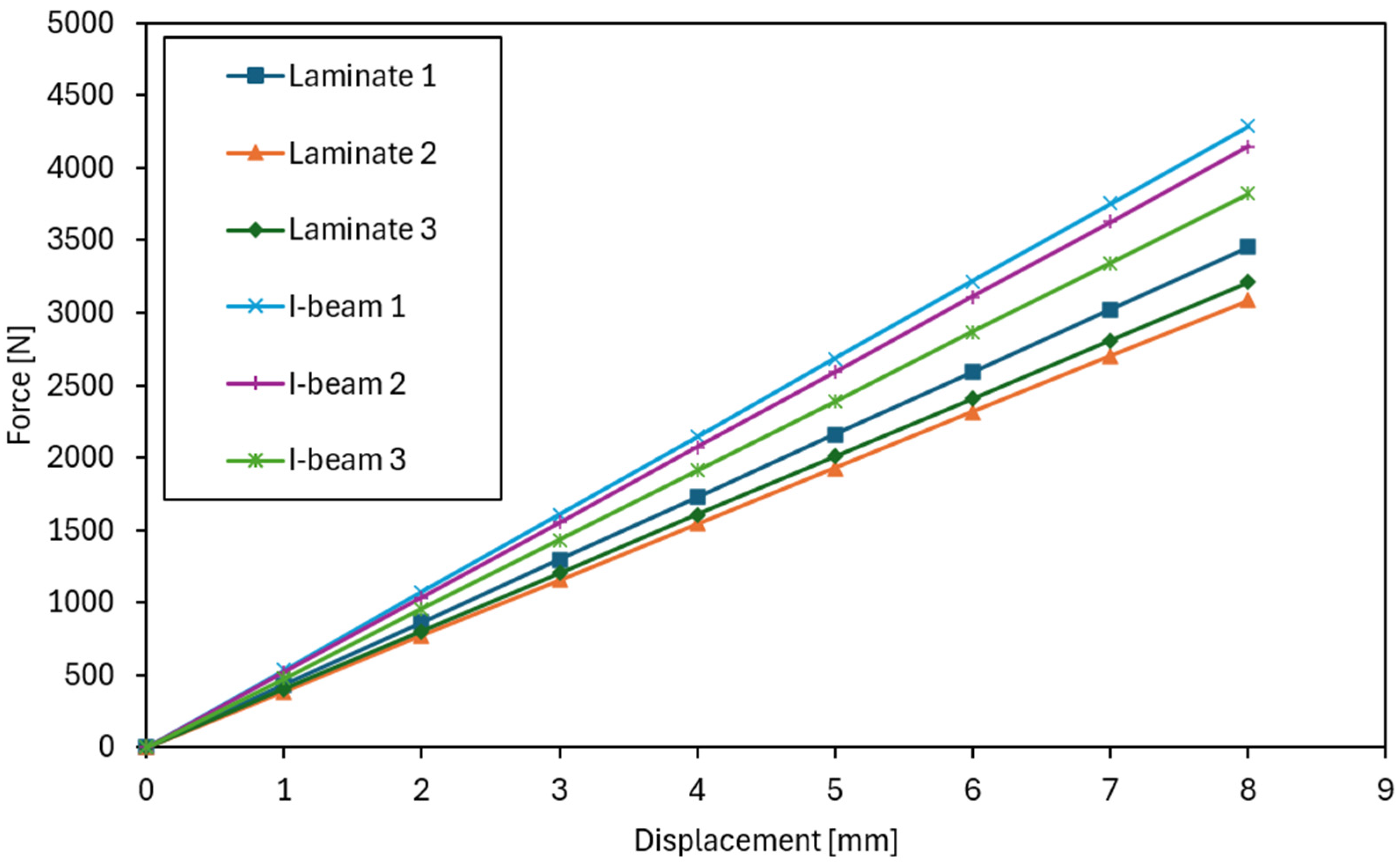
3.1. Results of Laboratory Tests
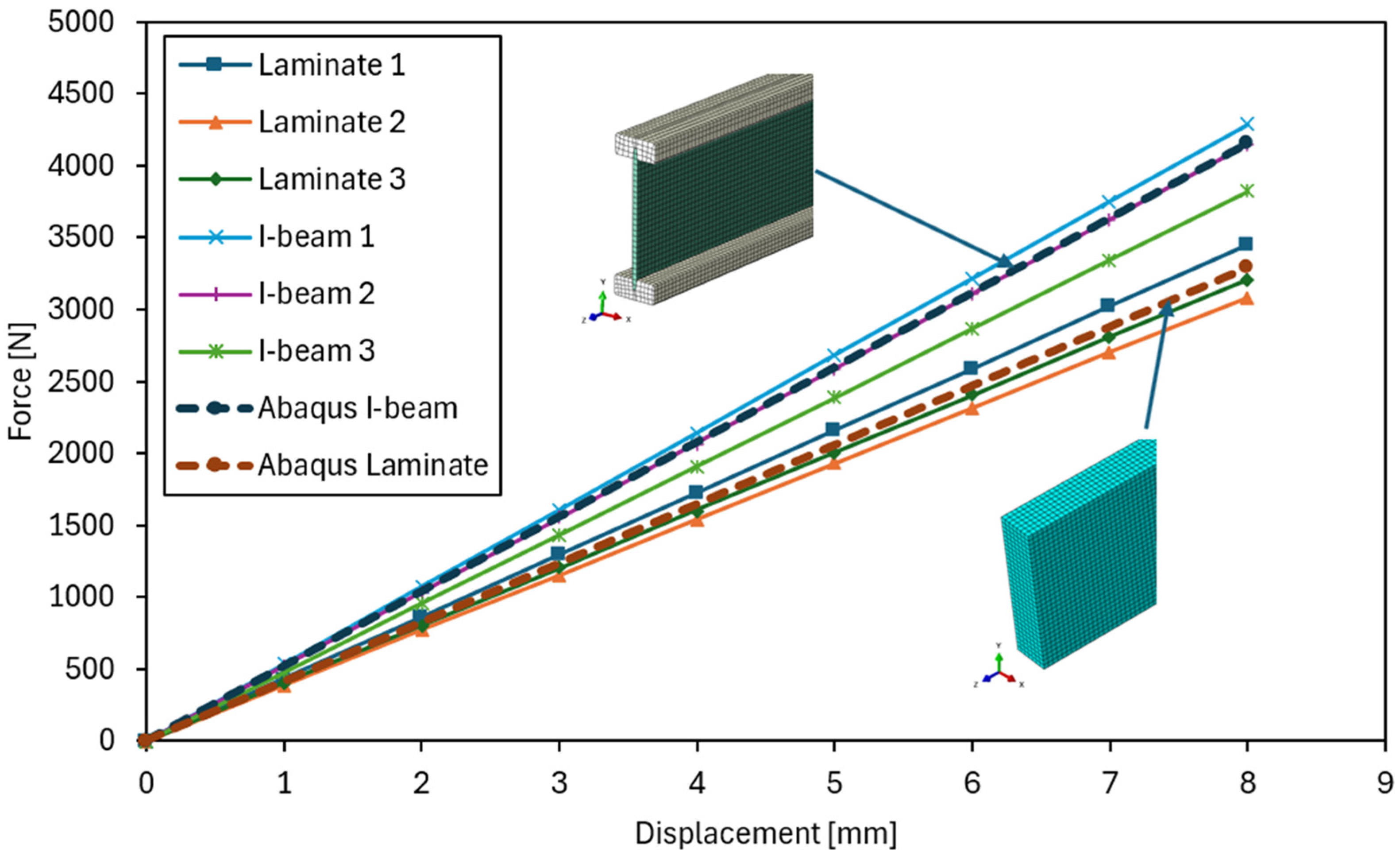
3.2. Results of Numerical Simulations and Model Validation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Maier, D. Wood in Modern Construction: A Scientometric Examination of Sustainable Trends. 2024. Available online: https://www.preprints.org/manuscript/202409.1100 (accessed on 23 November 2025).
- Yang, Y.; Kang, X.; Yang, Y.; Ye, H.; Jiang, J.; Zheng, G.; Wei, K.; Ge, S.; Lam, S.S.; Ouyang, H. Research Progress in Green Preparation of Advanced Wood-Based Composites. Adv. Compos. Hybrid Mater. 2023, 6, 202. [Google Scholar] [CrossRef]
- Ramage, M.H.; Burridge, H.; Busse-Wicher, M.; Fereday, G.; Reynolds, T.; Shah, D.U.; Wu, G.; Yu, L.; Fleming, P.; Densley-Tingley, D.; et al. The Wood from the Trees: The Use of Timber in Construction. Renew. Sustain. Energy Rev. 2017, 68, 333–359. [Google Scholar] [CrossRef]
- Scharai-Rad, M.; Welling, J. Environmental and Energy Balances of Wood Products and Substitutes; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2002. [Google Scholar]
- Masoudnia, R.; Hashemi, A.; Quenneville, P. Predicting the Effective Flange Width of a CLT Slab in Timber Composite Beams. J. Struct. Eng. 2018, 144, 04018084. [Google Scholar] [CrossRef]
- Kodur, V.; Stein, J.; Fike, R.; Tabbador, M. Comparative Fire Performance of Traditional Lumber and Engineered Wood Joists. J. Struct. Fire Eng. 2017, 8, 2–13. [Google Scholar] [CrossRef]
- Pelletier, B.; Doudak, G. Investigation of the Lateral-Torsional Buckling Behaviour of Engineered Wood I-Joists with Varying End Conditions. Eng. Struct. 2019, 187, 329–340. [Google Scholar] [CrossRef]
- Sugahara, E.S.; Arroyo, F.N.; De Campos, C.I.; Botelho, E.C.; Christoforo, A.L.; Costa, M.L.; Lahr, F.A.R. Thermal treatment of OSB panels: A systematic and bibliometric overview. Eur. J. Wood Wood Prod. 2022, 80, 1293–1307. [Google Scholar] [CrossRef]
- Lille, H.; Kiviste, M.; Telling, R.; Leppik, T.; Virro, I.; Kask, R. Evaluation of some mechanical and physical properties of “Oriented Strand Board (OSB/3) following cyclic accelerated aging tests. Eur. J. Wood Wood Prod. 2022, 80, 731–740. [Google Scholar] [CrossRef]
- Jucienė, M.; Dobilaitė, V.; Albrektas, D. An investigation of the impact of water on certain of the mechanical and physical properties of laminated veneer lumber (LVL) as used in construction. Appl. Sci. 2023, 13, 925. [Google Scholar] [CrossRef]
- Romero, A.; Odenbreit, C. Experimental Investigation on Strength and Stiffness Properties of Laminated Veneer Lumber (LVL). Materials 2023, 16, 7194. [Google Scholar] [CrossRef]
- Hasan, K.F.; Bak, M.; Ahmed, A.A.O.; Garab, J.; Horváth, P.G.; Bejó, L.; Alpár, T. Laminated strand lumber (LSL) potential of Hungarian and Central European hardwoods: A review. Eur. J. Wood Wood Prod. 2024, 82, 245–264. [Google Scholar] [CrossRef]
- Moradpour, P.; Pirayesh, H.; Gerami, M.; Jouybari, I.R. Laminated strand lumber (LSL) reinforced by GFRP; mechanical and physical properties. Constr. Build. Mater. 2018, 158, 236–242. [Google Scholar] [CrossRef]
- Oh, S. Experimental study of bending and bearing strength of parallel strand lumber (PSL) from Japanese larch veneer strand. J. Korean Wood Sci. Technol. 2022, 50, 237–245. [Google Scholar] [CrossRef]
- Sukontasukkul, P.; Lam, F.; Mindess, S. Fracture of parallel strand lumber (PSL) under impact loading. Mater. Struct. 2000, 33, 445–449. [Google Scholar] [CrossRef]
- De Araujo, V.; Aguiar, F.; Jardim, P.; Mascarenhas, F.; Marini, L.; Aquino, V.; Santos, H.; Panzera, T.; Lahr, F.; Christoforo, A. Is cross-laminated timber (CLT) a wood panel, a building, or a construction system? A systematic review on its functions, characteristics, performances, and applications. Forests 2023, 14, 264. [Google Scholar] [CrossRef]
- Kang, Y.; Jo, H.H.; Kim, S. Enhancing indoor comfort and building energy efficiency with cross-laminated timber (CLT) in hygrothermal environments. J. Build. Eng. 2024, 84, 108582. [Google Scholar] [CrossRef]
- Fruehwald-Koenig, K.; Heister, L. Compression properties of glued laminated timber and tensile properties of gluelam lamellas from oil palm wood. Wood Mater. Sci. Eng. 2024, 19, 1101–1116. [Google Scholar] [CrossRef]
- Timbolmas, C.; Bravo, R.; Rescalvo, F.J.; Ringhofer, A.; Sieder, R.; Lorenzana, J. Experimental study of hybrid pine–birch glued-laminated timber beams assisted by digital image correlation technique. Eur. J. Wood Wood Prod. 2024, 82, 1187–1199. [Google Scholar] [CrossRef]
- Szeptyński, P.; Jasińska, D.; Mikulski, L. Shape Optimization and Experimental Investigation of Glue-Laminated Timber Beams. Materials 2024, 17, 6263. [Google Scholar] [CrossRef]
- Ghazanfari, A.; Malzl, L.; Pramreiter, M.; Konnerth, J.; Kromoser, B. A Systematic Review of Strand-Based Engineered Wood Products for Construction: Standard Test Methods and Mechanical Properties. Wood Mater. Sci. Eng. 2025. [Google Scholar] [CrossRef]
- Wei, P.X.; Chen, J.X.; Zhang, Y.; Pu, L.J. Wood-based sandwich panels: A review. Wood Res. 2021, 66, 875–890. [Google Scholar] [CrossRef]
- Guo, Z.; Song, Y.; Chen, J.; Xu, Y.; Zhao, C. Relation between the geometric parameters and the composite heat transfer of paper honeycomb plates under cold-above/hot-below conditions and the corresponding influence mechanism. J. Build. Eng. 2021, 43, 102582. [Google Scholar] [CrossRef]
- Leichti, R.J.; Falk, R.H.; Laufenberg, T.L. Prefabricated Wood Composite I-Beams: A Literature Review. Wood Fiber Sci. 1990, 22, 62–79. [Google Scholar]
- Ghanbari-Ghazijahani, T.; Russo, T.; Valipour, H.R. Lightweight Timber I-Beams Reinforced by Composite Materials. Compos. Struct. 2020, 233, 111579. [Google Scholar] [CrossRef]
- Li, J.; Singh, A.; Zhou, Y. Experimental Study on the Flexural Behavior of I-Shaped Laminated Bamboo Composite Beam as Sustainable Structural Element. Buildings 2024, 14, 671. [Google Scholar] [CrossRef]
- Kržan, M.; Pazlar, T.; Ber, B. Composite Beams Made of Waste Wood-Particle Boards, Fastened to Solid Timber Frame by Dowel-Type Fasteners. Materials 2023, 16, 2426. [Google Scholar] [CrossRef] [PubMed]
- Kula, K.; Socha, T.; Denisiewicz, A. Weakened Zones in Wood–Based Composite Beams and Their Strengthening by CFRP: Experimental, Theoretical, and Numerical Analysis. Eng. Trans. 2019, 67, 461–474. [Google Scholar]
- Dassault Systemes. Abaqus Analysis User’s Manual; Dassault Systemes: Johnston, RI, USA, 2022. [Google Scholar]
- EN 300; Oriented Strand Boards (OSB)—Definitions, Classification and Specifications. European Committee for Standardization (CEN): Brussels, Belgium, 2006.
- EN 338; Structural Timber—Strength Classes. European Committee for Standardization (CEN): Brussels, Belgium, 2016.
- Lin, C.P.; Xie, H.; Grimes, R.; Bai, Z. On the Shift-Invert Lanczos Method for the Buckling Eigenvalue Problem. Int. J. Numer. Methods Eng. 2021, 122, 2751–2769. [Google Scholar] [CrossRef]
- Bouckaert, I.; Piedboeuf, A.; Godio, M.; de Almeida, J.P. Modal Analysis and Superposition for Dynamic Response of Structures with Discontinuities Using HybriDFEM. Finite Elem. Anal. Des. 2025, 249, 104360. [Google Scholar]
- EN 408; Timber Structures—Structural Timber and Glued Laminated Timber—Determination of Some Physical and Mechanical Properties. European Committee for Standardization (CEN): Brussels, Belgium, 2012.
- EN 14080; Timber Structures—Glued Laminated Timber and Glued Solid Timber—Requirements. European Committee for Standardization (CEN): Brussels, Belgium, 2013.

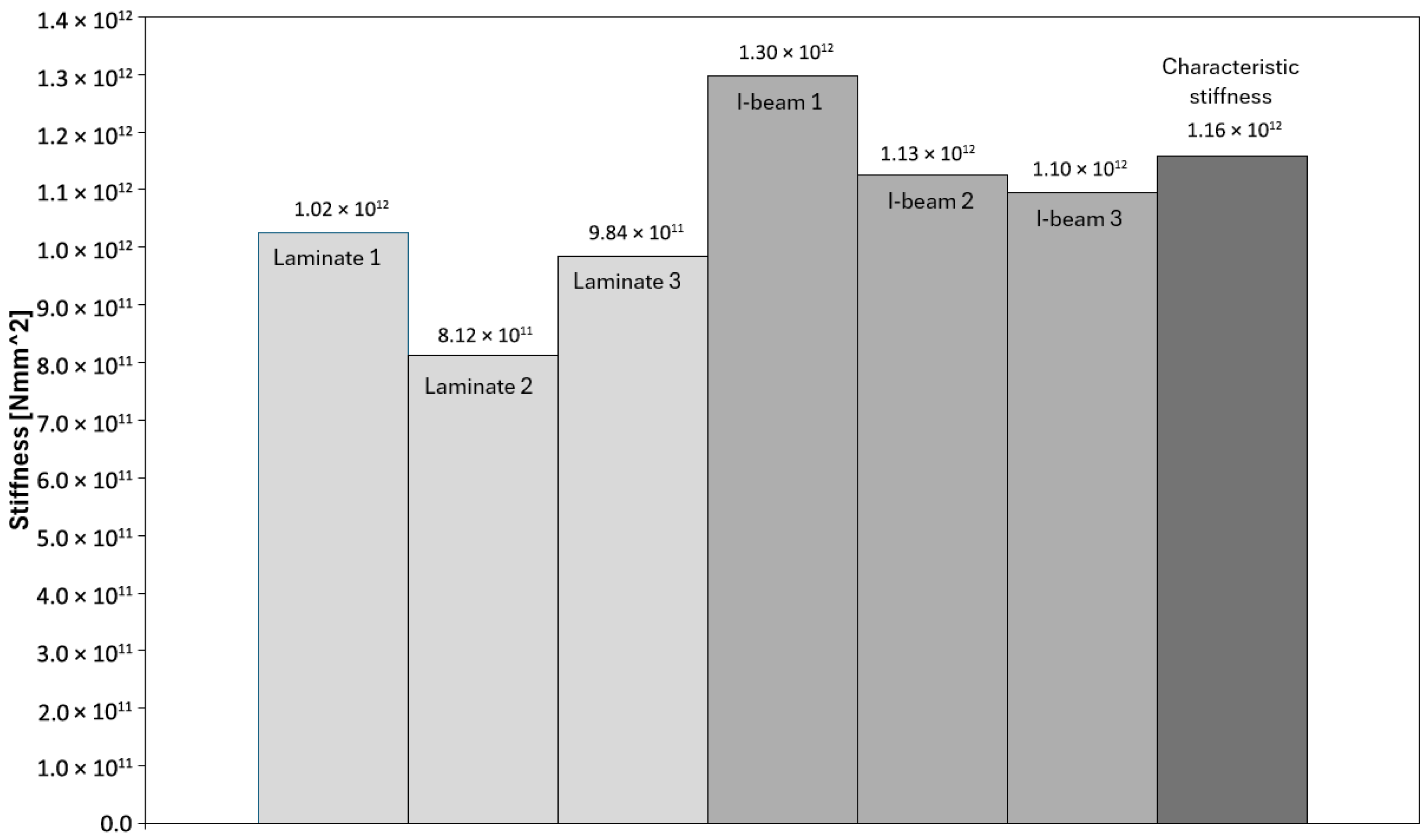
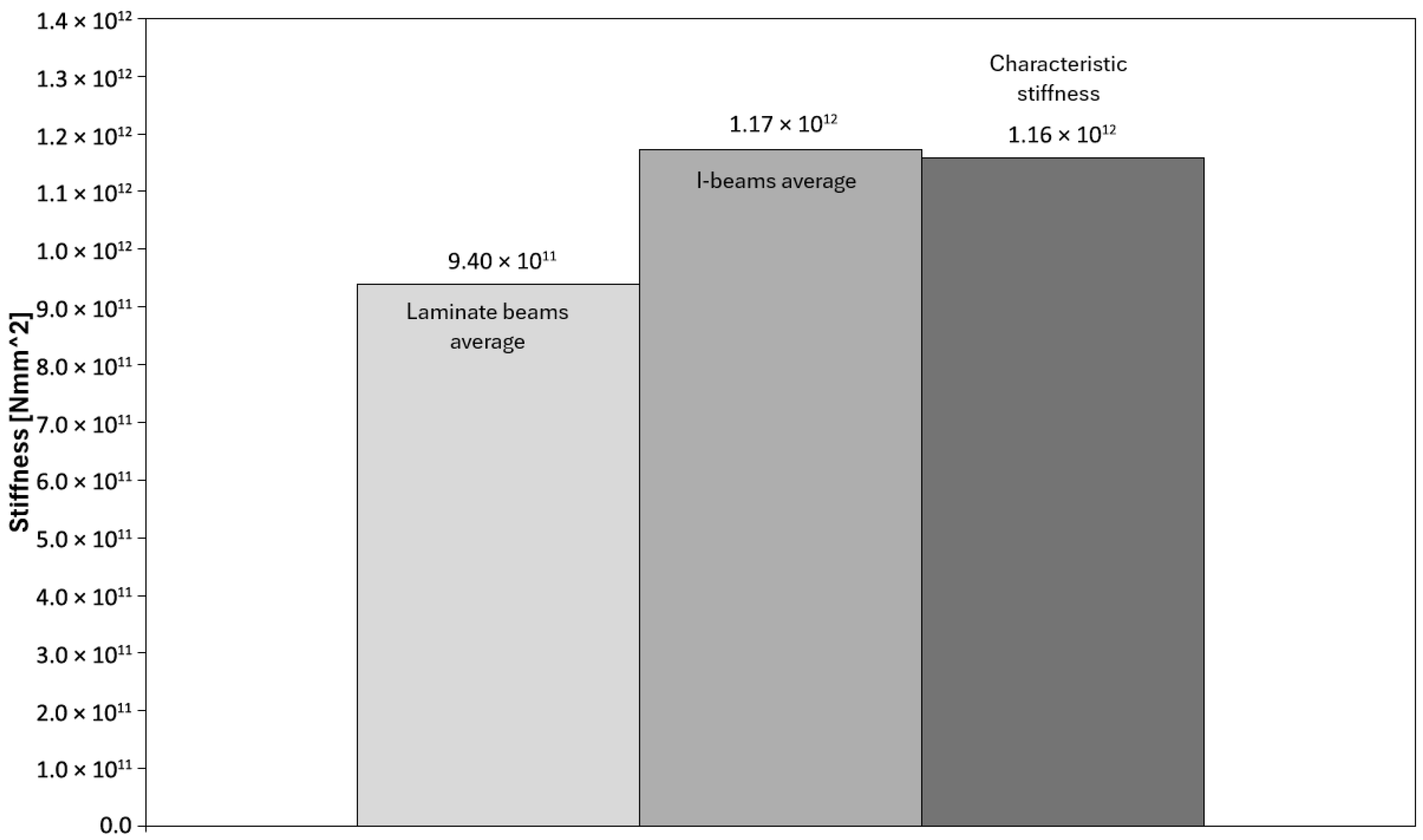
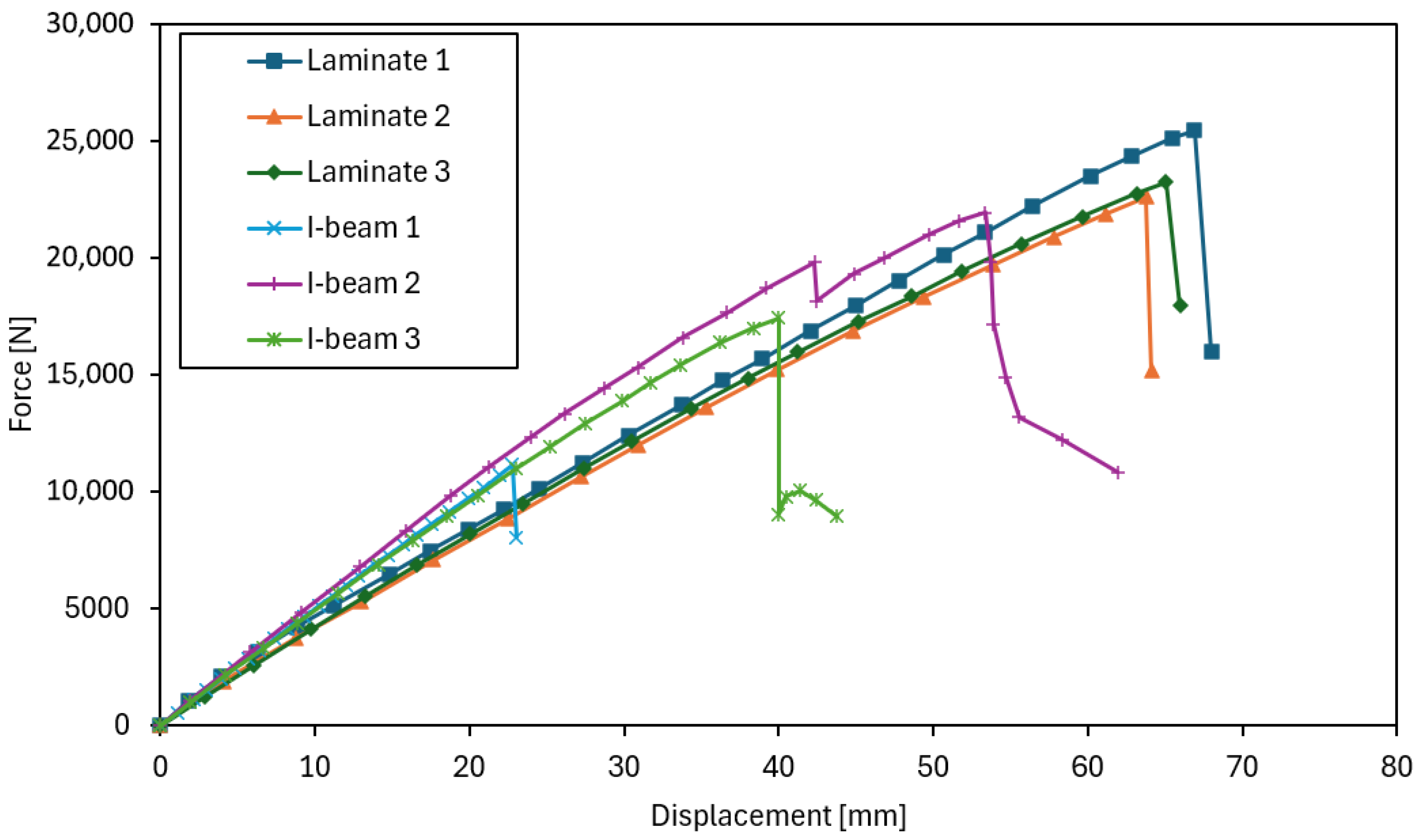
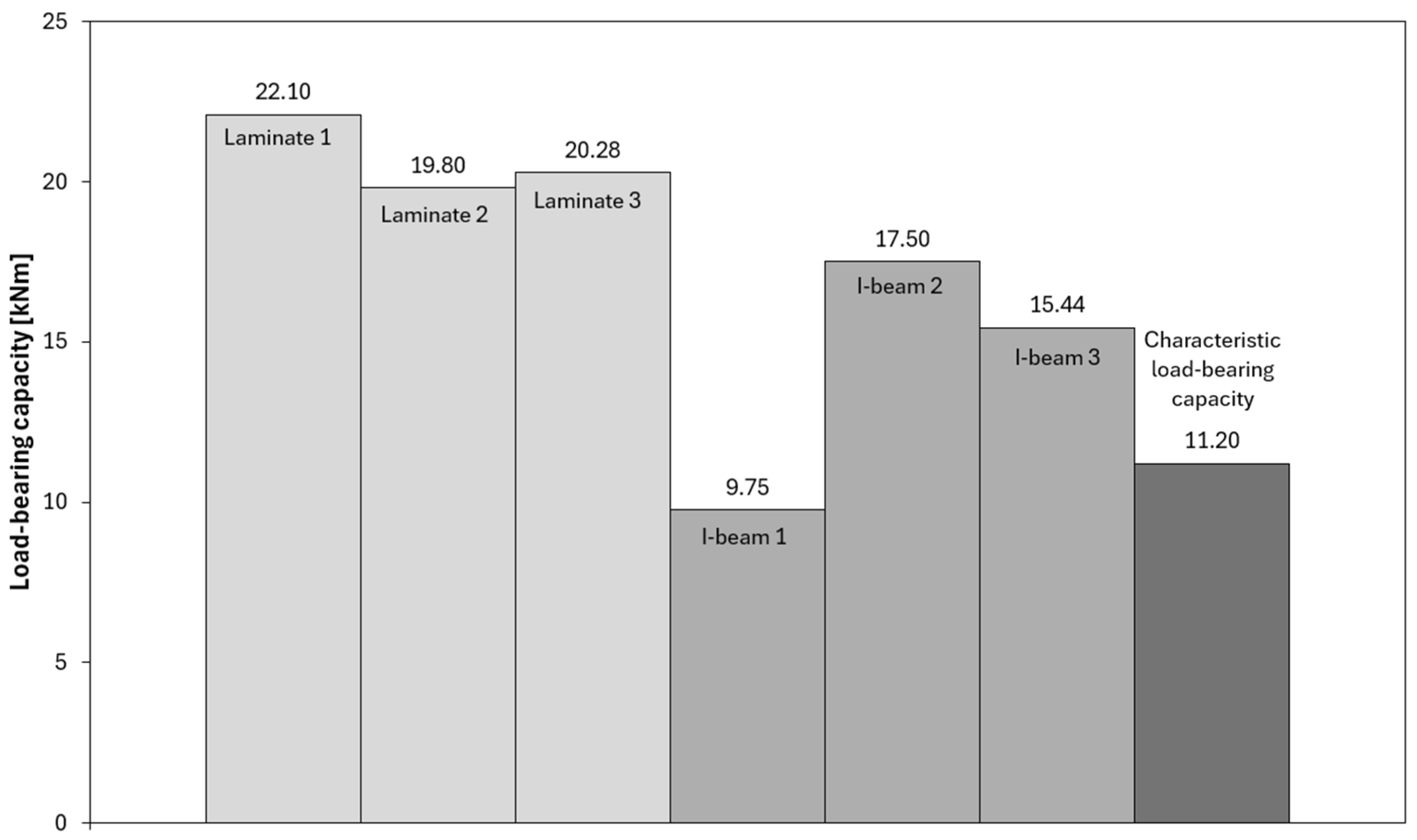





| Material | Density [kg/m3] | E [MPa] | Et [MPa] | G [MPa] | ν [-] | MOR [MPa] |
|---|---|---|---|---|---|---|
| I-beam Pine C24 (flanges) | 470 | 11,000 | 370 | 690 | 0.20 | 24 |
| I-beam OSB (web) | 650 | 4930 | 2100 | 1250 | 0.20 | 18 |
| Laminated beam OSB | 650 | 5430 | 2350 | 1320 | 0.20 | 22 |
| Tested Element/Model | F [N] | Absolute Difference | Relative Error [%] | Mean Relative Error [%] |
|---|---|---|---|---|
| Laminate 1 | 3451 | 159 | 4.60 | 4.63 |
| Laminate 2 | 3085 | 207 | 6.72 | |
| Laminate 3 | 3209 | 83 | 2.58 | |
| I-beam 1 | 4288 | 131 | 3.06 | 3.61 |
| I-beam 2 | 4144 | 13 | 0.32 | |
| I-beam 3 | 3869 | 288 | 7.45 | |
| Abaqus Laminate | 3292 | - | - | - |
| Abaqus I-beam | 4157 | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Denisiewicz, A.; Socha, T.; Kula, K. Analysis of Load-Bearing Capacity and Lateral-Torsional Buckling (LTB) Stability of OSB Laminated and I-Beams Made of Wood and Wood-Based Materials. Materials 2025, 18, 5325. https://doi.org/10.3390/ma18235325
Denisiewicz A, Socha T, Kula K. Analysis of Load-Bearing Capacity and Lateral-Torsional Buckling (LTB) Stability of OSB Laminated and I-Beams Made of Wood and Wood-Based Materials. Materials. 2025; 18(23):5325. https://doi.org/10.3390/ma18235325
Chicago/Turabian StyleDenisiewicz, Arkadiusz, Tomasz Socha, and Krzysztof Kula. 2025. "Analysis of Load-Bearing Capacity and Lateral-Torsional Buckling (LTB) Stability of OSB Laminated and I-Beams Made of Wood and Wood-Based Materials" Materials 18, no. 23: 5325. https://doi.org/10.3390/ma18235325
APA StyleDenisiewicz, A., Socha, T., & Kula, K. (2025). Analysis of Load-Bearing Capacity and Lateral-Torsional Buckling (LTB) Stability of OSB Laminated and I-Beams Made of Wood and Wood-Based Materials. Materials, 18(23), 5325. https://doi.org/10.3390/ma18235325







